Abstract
This paper proposes a new scheme for a brushless wound rotor synchronous machine (WRSM) by generating an additional, two-pole component of magneto-motive force (MMF) with a series-connected additional three-phase winding with the armature three-phase winding. Unlike existing brushless excitation schemes, which use the inverter to inject harmonic currents in the stator windings, the proposed scheme uses series-connected additional winding on the stator with the armature winding in a two-pole configuration. Consequently, as the current flows in the armature winding, it creates a fundamental rotating air gap flux to interact with the field flux. At the same time, additional rotating flux is created from the additional three-phase winding, which cannot synchronize with the field winding. This additional flux can cause the induction of a voltage in a winding with exactly the same number of poles. For this purpose, a harmonic winding is installed in the rotor along with the field winding connected through a diode bridge rectifier, in order to feed the direct current (DC) to the field winding for rotor excitation without an input current from the brush-slip-ring assembly. The 2D finite-element analysis (FEA) was performed to validate the brushless operation of the proposed machine system.
1. Introduction
Research on brushless wound rotor synchronous machines (WRSMs) has gained significant interest in the past decade [1]. Many excitation schemes have been proposed to improve the excitation systems of brushless synchronous machines over the past century, which are briefly summarized here. One of the solutions proposed for brushless excitation is the integration of the exciter into the main machine [2,3,4,5]. This removes the need for the brush-slip-ring assembly required to excite the field winding of a WRSM. In addition, at the same time, it increases the power density of the machine as a solution to the inherent problem of conventional brushless WRSM. In [6,7,8,9,10], more compact machine systems have been investigated by generating and utilizing harmonic flux to induce a voltage in harmonic winding on the rotor with a conventional stator structure. These types of machines are compact in size as they remove the need to install the exciter field winding on the stator. Moreover, recent research has focused on removing the harmonic winding from the rotor and inducing the harmonic alternating current (AC) power in the field winding on the rotor [11,12]. In this type of excitation system, the rotor field winding is connected to a capacitor through a four-switch converter to extract and regulate the required field current for excitation. However, all of the aforementioned machine systems for brushless excitation require more electronic components than the conventional machines, which are expensive and bring new problems [13,14]. In [13], the de-excitation system was investigated for large hydro-generators. In [14], the field current estimation method has been investigated for a brushless wound rotor synchronous starter-generator with asynchronous brushless exciters. However, for small-scale brushless synchronous machines, the cost of the overall system becomes higher compared to the benefits of using a brushless excitation method for WRSM. In this paper, a new cost-effective brushless wound rotor synchronous machine is proposed. The analysis of the machine is conducted using a simple structure in the initial studies. The machine consists of conventional stator and rotor cores; two three-phase series-connected stator windings are supplied current by the same inverter; as well as harmonic and field windings on the rotor connected through a diode bridge rectifier. The two stator windings have a different number of poles, in order for one winding to create a four-pole rotating flux synchronized with the field winding and the second winding to create a rotating two-pole flux intercepted by harmonic winding on the rotor to induce a voltage.
2. Concept of the Proposed Scheme
The proposed brushless scheme is designed to be low-cost for applications where advance control is not needed. In addition, a simplified drive system can achieve the same objective of a redundantly advanced brushless scheme. In the proposed scheme, the stator armature winding is serially connected to an additional three-phase winding on the stator. This additional winding has a two-pole configuration mounted on the stator along with a four-pole armature winding, as shown in Figure 1. The additional winding, namely Wxyz, is inserted in 12 slots by reducing the armature winding (Wacb) conductors in those slots by half.
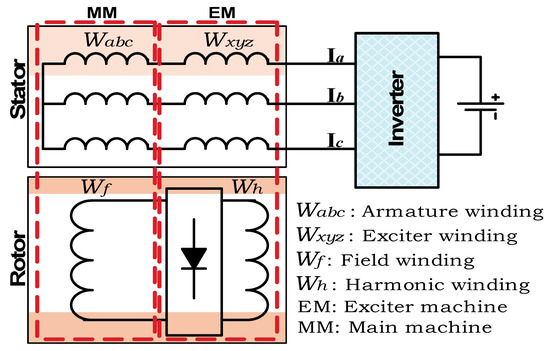
Figure 1.
Schematic diagram of the proposed brushless WRSM.
The three-phase currents flowing through the stator armature winding create a rotating four-pole air gap flux to be synchronized by the four-pole field winding flux of the rotor. Similarly, when these currents flow through the additional two-pole winding (Wxyz), an additional two-pole rotating flux is created in the air gap. This two-pole flux does not synchronize with the four-pole field winding. However, it can be used to induce a voltage in a two-pole harmonic winding mounted on the rotor. The relative speed of the rotor with respect to the rotating two-pole air gap flux component transfers power to the harmonic winding by the induction principle [15].
Therefore, since the voltage is induced in the harmonic winding, it behaves as the excitation source for the field winding. The harmonic winding is connected to the field winding through a diode bridge rectifier to feed the direct current (DC).
For the finite element analysis (FEA), a conventional structure of an 18-slot four-pole machine is selected, as shown in Figure 2, and the parameters are shown in Table 1. The armature winding of the machine has 300 turns, whereas the Wxyz has 150 turns. For the symmetric number of conductors, the turns for Wxyz winding are calculated by keeping the same current density as the armature winding. It turns out that for an 18-slot machine, armature winding can be distributed by considering a room for a 12-slot XYZ winding. It means that the Wxyz can be distributed in only 12 slots with full armature winding turns in the remaining six slots for optimal distribution of both windings. However, the Wxyz can be distributed in four different patterns by a combination of three-phase sequence slot pitch.
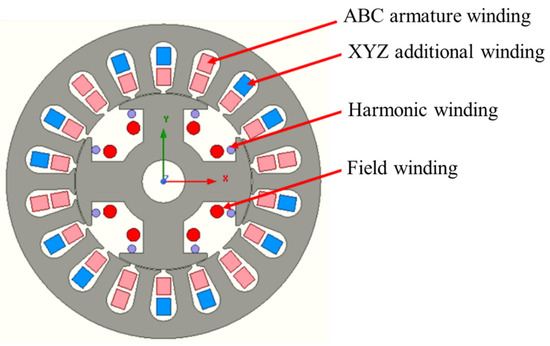
Figure 2.
Machine structure showing the four types of windings.

Table 1.
Machine design parameters.
The winding Wxyz is distributed and arranged in four different patterns for a comparison of the best arrangement for high power transfer possibility. With respect to a phase sequence of ACB for armature winding, the winding Wxyz arrangement patterns are type A with XYZ sequence, type A with XZY sequence, type B with XYZ sequence, and type B with XZY sequence, as shown in Figure 3.
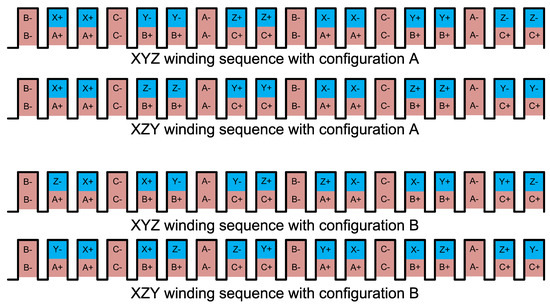
Figure 3.
Winding patterns of Wxyz winding.
Since the stator windings are connected in a series, three-phase currents in both windings and in their respective phases are the same. The instantaneous currents can be given by
where I is the fundamental current maximum amplitude, ω is the electrical angular frequency, and t is time. Considering that the two stator windings are mounted for two-pole and four-pole configurations, the air gap magnetic field must also consist of two-component MMF. Neglecting the effect of harmonics, the MMF equation for the rotating flux is derived by
where Na is the number of Wabc winding turns, Nx is the number of Wxyz winding turns, p is the number of pole pairs, and θ is the spatial angle. Although the additional three-phase winding Wxyz creates a two-pole rotating air gap flux, this flux has a different relative speed of rotation with respect to the rotor. It is illustrated in Figure 4 that the phase sequence changing of Wxyz will induce a six-pole flux linkage with the harmonic winding on the rotor.
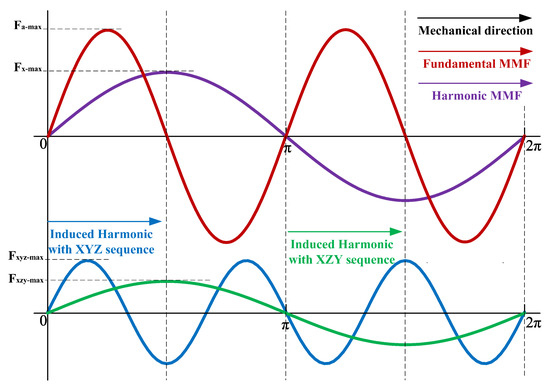
Figure 4.
Illustration of the fundamental MMF, harmonic MMF, and the induced harmonics in the machine.
3. Electromagnetic Performance
The machine structure shown in Figure 2 is used for the simulation of FEA. The simulation was carried out using the JMAG-Designer 19.1 version with a maximum mesh size of 3 mm. The boundary condition for the simulated model is 265.5 mm. The simulation run time was 200 ms with a 0.2 ms time-step for the electromagnetic torque to reach a steady state condition in all of the cases. The 2D simulation showed a good performance of the machine driven with the proposed brushless scheme in terms of harmonic power, field current, and output electromagnetic torque. The results are compared for the four models with winding patterns, as shown in Figure 3. A combination of positive phase sequence with respect to the armature three-phase winding with type A winding XYZ, and type B winding patterns were considered. Similarly, a negative sequence XYZ pattern was used with both type A and type B patterns. Figure 5 shows the harmonic current induced in the harmonic winding of the rotor for all of the four winding patterns. It can be observed that the type-A XYZ pattern has a high magnitude of current compared to all of the other patterns.
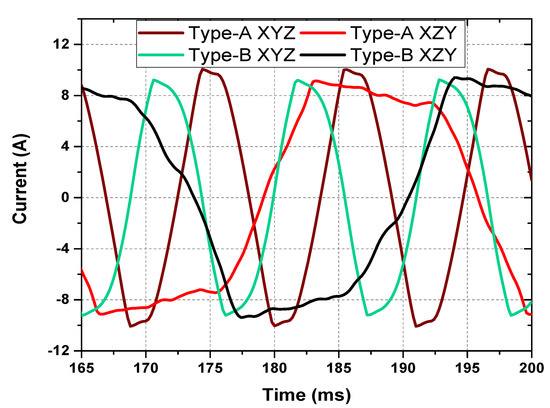
Figure 5.
Harmonic currents comparison.
Similar results of field winding currents are achieved with the type-A XYZ pattern, which has a high field winding current in the stable region, as shown in Figure 6.
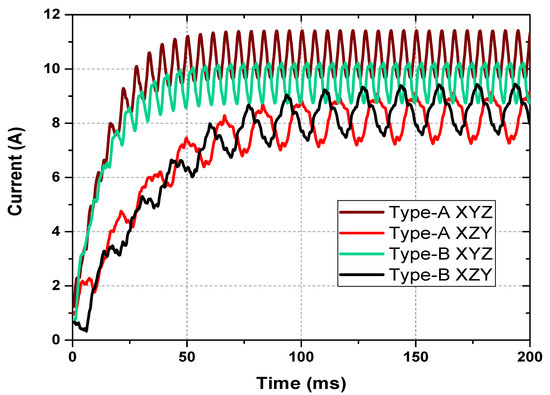
Figure 6.
Field currents comparison.
As the field current in the type-A XYZ pattern is highest compared to all of the other currents, the torque of the machine with this combination must also be highest among all of the patterns. The electromagnetic torque of the machine is compared in Figure 7. The highest torque generated in the type-A XYZ winding sequence is due to the high field current. Since the two-pole MMF component is generated in the air gap with the XZY winding, the interception of rotor harmonic winding induces a harmonic voltage. The frequency of this voltage and thus the current in the harmonic winding matches the two-pole harmonic component in the air gap. However, when the sequence is reversed, i.e., from XZY to XYZ, the relative speed of harmonic winding interception increases to three times. Therefore, the induced voltage and current frequency is three times of the original frequency. Due to the fact that the induced voltage depends on the rotating speed of the flux in the air gap, the voltage generated in the rotor excitation is higher in the XYZ case. Eventually, it will increase the field current and torque of the machine.
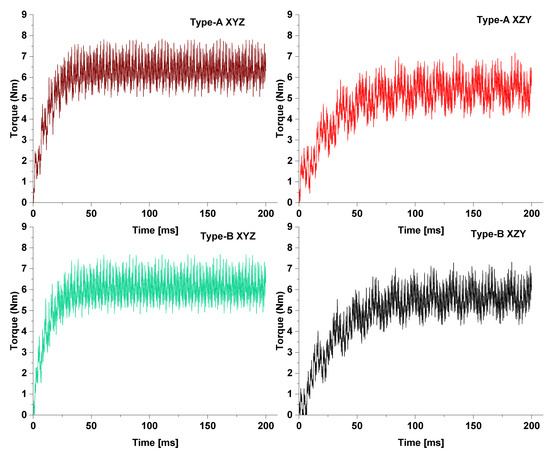
Figure 7.
Torque comparison.
4. Conclusions
This paper proposes a cost-effective brushless three-phase wound rotor synchronous machine. A simplified structure and topology are initially analyzed for the brushless operation of the WRSM. In this topology, two three-phase windings are mounted on the stator namely, an ABC armature winding and XYZ additional three-phase winding for excitation. To create the harmonic air gap component, the XYZ winding is configured for two-poles on a four-pole synchronous machine. The working of the topology was verified by the 2D FEA. Since the machine does not use any additional inverters for harmonic component generation or a specially-built inverter for power supply, it is cost-effective compared to the conventional brushless wound rotor machines.
Author Contributions
Conceptualization, S.S.H.B. and G.J.S.; software, S.S.H.B. and G.J.S.; formal analysis, S.S.H.B. and G.J.S.; writing—original draft preparation, S.S.H.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ayub, M.; Hussain, A.; Jawad, G.; Kwon, B. Brushless Operation of a Wound-Field Synchronous Machine Using a Novel Winding Scheme. IEEE Trans. Magn. 2019, 55, 8201104. [Google Scholar] [CrossRef]
- Chakraborty, C.; Basak, S.; Rao, Y.T. Synchronous Generator with Embedded Brushless Synchronous Exciter. IEEE Trans. Energy Convers. 2019, 34, 1242–1254. [Google Scholar] [CrossRef]
- Bukhari, S.S.H.; Memon, A.A.; Madanzadeh, S.; Sirewal, G.J.; Gandoy, J.D.; Ro, J.-S. Novel Single Inverter-Controlled Brushless Wound Field Synchronous Machine Topology. Mathematics 2021, 9, 1739. [Google Scholar] [CrossRef]
- Bukhari, S.S.H.; Ali, Q.; Gandoy, J.D.; Ro, J.-S. High-Efficient Brushless Wound Rotor Synchronous Machine Topology Based on Sub-Harmonic Field-Excitation Technique. Energies 2021, 14, 4427. [Google Scholar] [CrossRef]
- Ayub, M.; Bukhari, S.S.H.; Sirewal, G.J.; Arif, A.; Kwon, B.-I. Utilization of Reluctance Torque for Improvement of the Starting and Average Torques of a Brushless Wound Field Synchronous Machine. Electr. Eng. 2021, 103, 2327–2333. [Google Scholar] [CrossRef]
- Bukhari, S.S.H.; Ahmad, H.; Chachar, F.A.; Ro, J.-S. Brushless Field-Excitation Method for Wound-Rotor Synchronous Machines. Int. Trans. Electr. Energy Syst. 2021, 31, e12961. [Google Scholar] [CrossRef]
- Yao, F.; Sun, D.; Sun, L.; Lipo, T.A. Dual Third-Harmonic-Current Excitation Principle of a Brushless Synchronous Machine Based on Double Three-Phase Armature Windings. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–4. [Google Scholar]
- Ali, Q.; Lipo, T.A.; Kwon, B.I. Design and analysis of a novel brushless wound rotor synchronous machine. IEEE Trans. Magn. 2015, 51, 8109804. [Google Scholar] [CrossRef]
- Jawad, G.; Ali, Q.; Lipo, T.A.; Kwon, B.I. Novel brushless wound rotor synchronous machine with zero-sequence third-harmonic field excitation. IEEE Trans. Magn. 2016, 52, 8106104. [Google Scholar] [CrossRef]
- Pötter, J.; Pfost, M.; Schullerus, G. A Novel Brushless Excitation System for Synchronous Machines with a Rotating Power Converter. In Proceedings of the 2019 CPE-POWERENG, Sonderborg, Denmark, 23–25 April 2019; pp. 1–6. [Google Scholar]
- Pötter, J.; Pfost, M.; Schullerus, G. Design Aspects of a Novel Brushless Excitation System for Synchronous Machines; IEMDC: San Diego, CA, USA, 2019; pp. 1228–1233. [Google Scholar]
- Rebollo, E.; Blanquez, F.R.; Platero, C.A.; Blazquez, F.; Redondo, M. Improved high-speed de-excitation system for brushless synchronous machines tested on a 20 MVA hydro-generator. IET Electr. Power Appl. 2015, 9, 405–411. [Google Scholar] [CrossRef] [Green Version]
- Bukhari, S.S.H.; Sirewal, G.J.; Ayub, M.; Ro, J.-S. A New Small-Scale Self-Excited Wound Rotor Synchronous Motor Topology. IEEE Trans. Magn. 2021, 57, 8200205. [Google Scholar] [CrossRef]
- Jiao, N.; Liu, W.; Zhang, Z.; Meng, T.; Peng, J.; Jiang, Y. Field Current Estimation for Wound-Rotor Synchronous Starter–Generator with Asynchronous Brushless Exciters. IEEE Trans. Energy Convers. 2017, 32, 1554–1561. [Google Scholar] [CrossRef]
- Lipo, T.A. Magnetic Circuits. In Introduction to AC Machine Design; John Wiley & Sons: New York, NY, USA, 2017; pp. 1–50. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).