Simultaneous Long-Term Planning of Flexible Electric Vehicle Photovoltaic Charging Stations in Terms of Load Response and Technical and Economic Indicators
Abstract
:1. Introduction
2. The General Framework of the Optimization Problem
- (1)
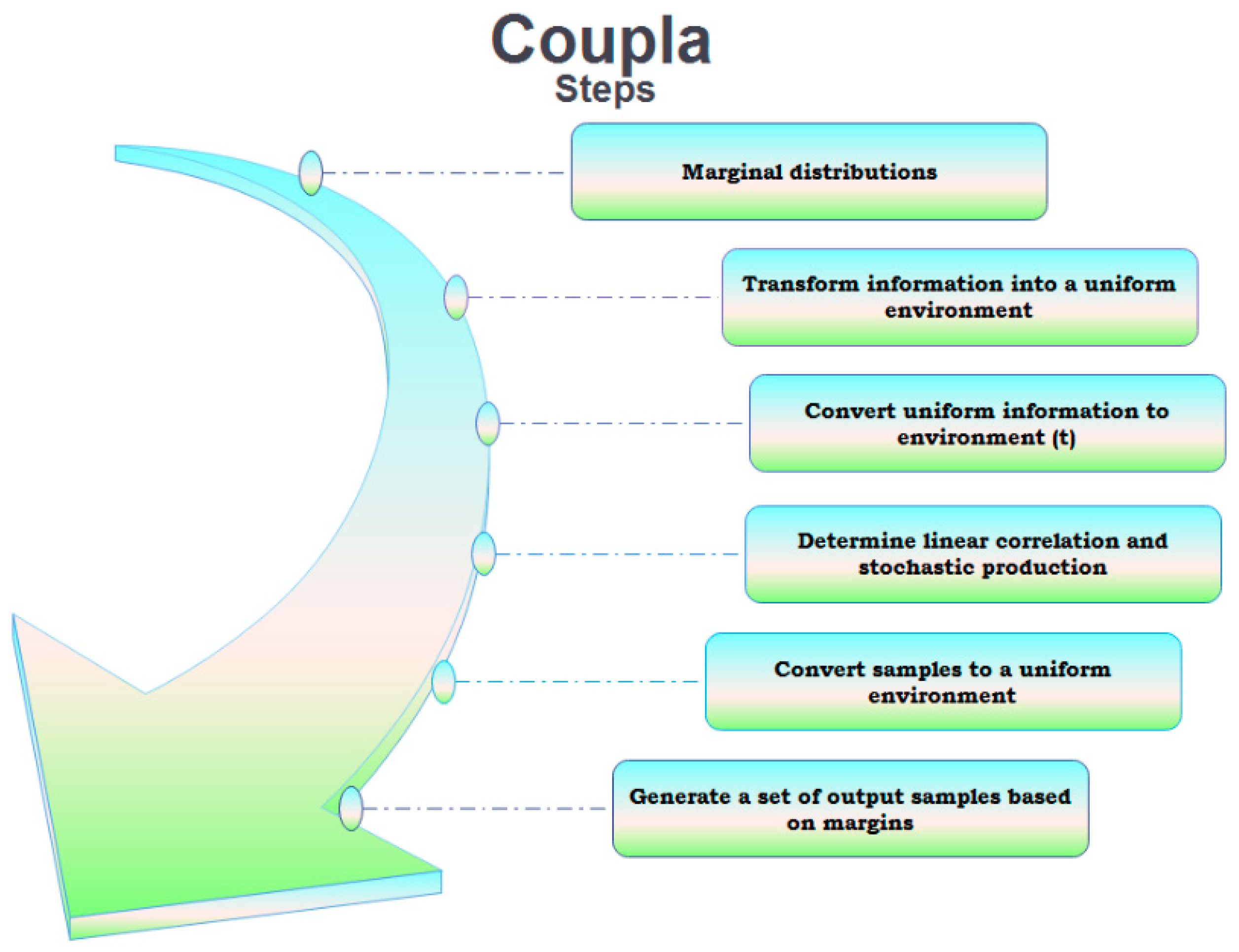
- First, the sample amount of the problem variables that should be examined and analyzed with the information about the problem are determined through the available real statistics.
- (2)
- Then, these amounts are normalized and mapped to zero and one.
- (3)
- The capillary function is then applied to the normalized information, and the correlation coefficients between the variables are obtained.
- (4)
- Then, random samples are produced in large numbers using real normalized information and the obtained correlation coefficients.
- (5)
- Finally, the samples are mapped to their true range from zero to one.
- (1)
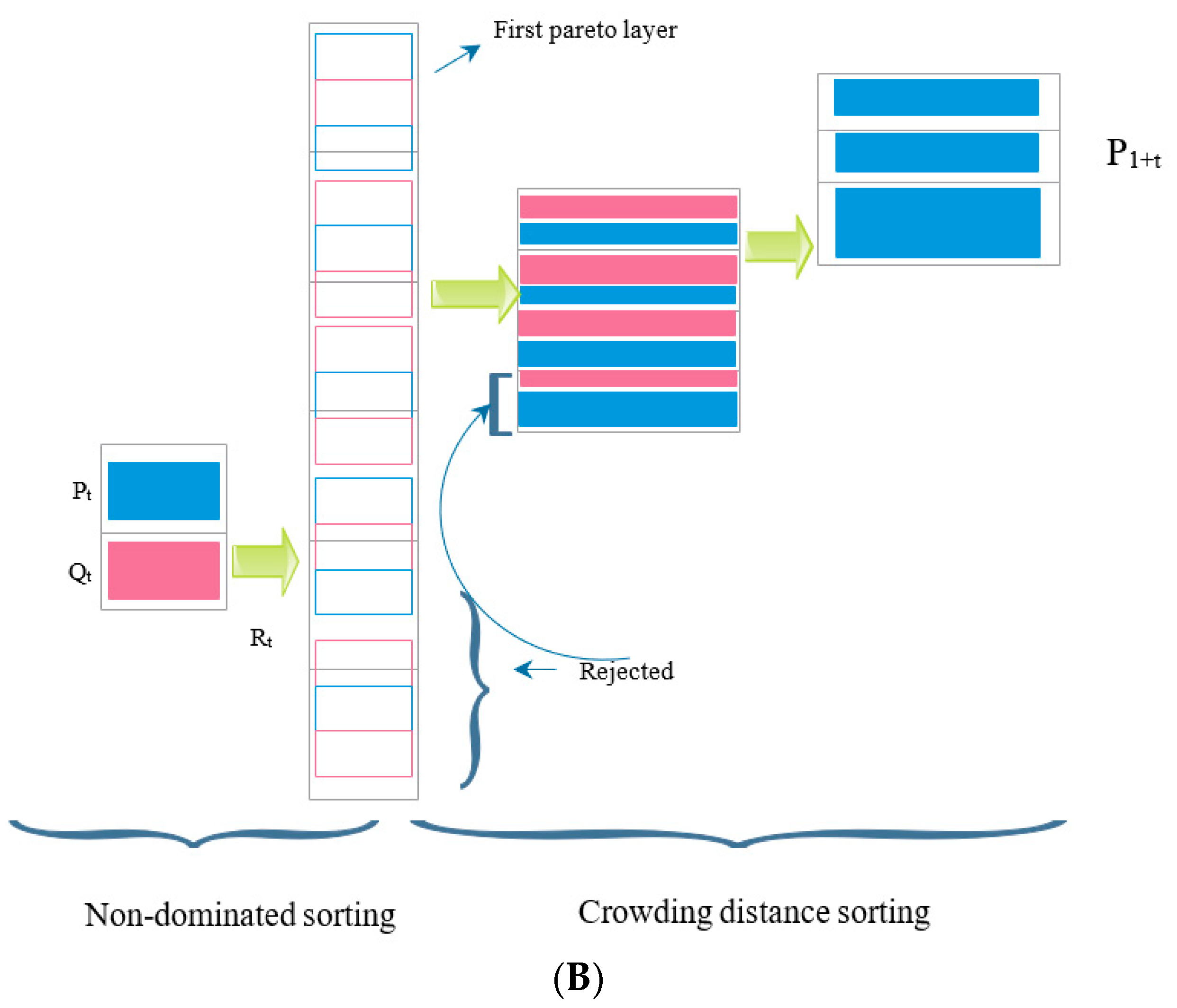
- Combine the population of parents ( =) and children (= ) and form the population () with size 2N.
- (2)
- Run the unsuccessful sort on to specify the different layers . i = 1, 2,…, l.
- (3)
- Create a population of size N by selecting superior solutions from non-dominant layers () in order of priority.
- (4)
- Calculate the population of children of size N using RKGA operators.
- (5)
- Continue steps 1 to 4 until the convergence criteria are reached.
3. Modeling Uncertainties
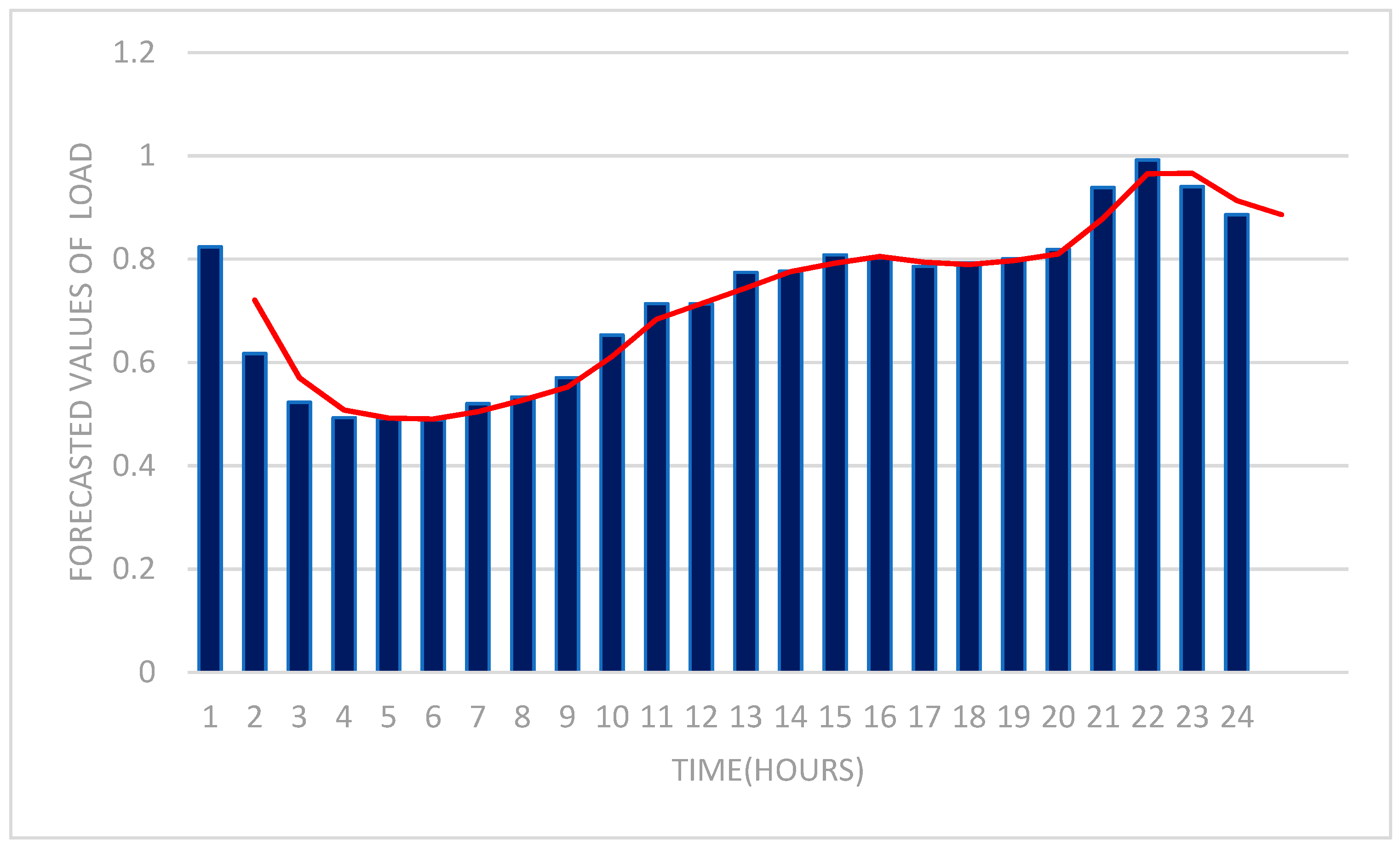
3.1. Load Uncertainty
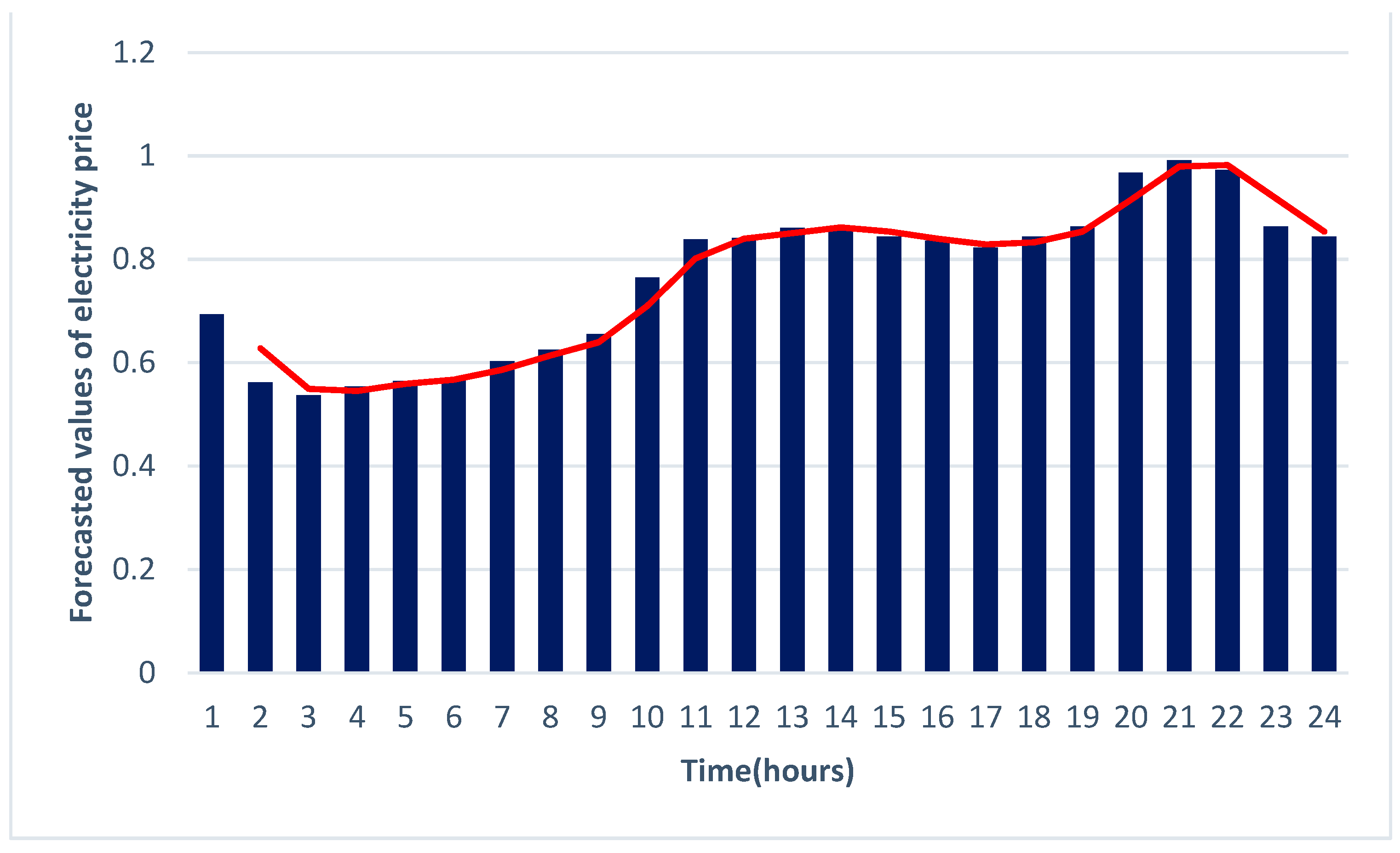
3.2. Electricity Price Uncertainty
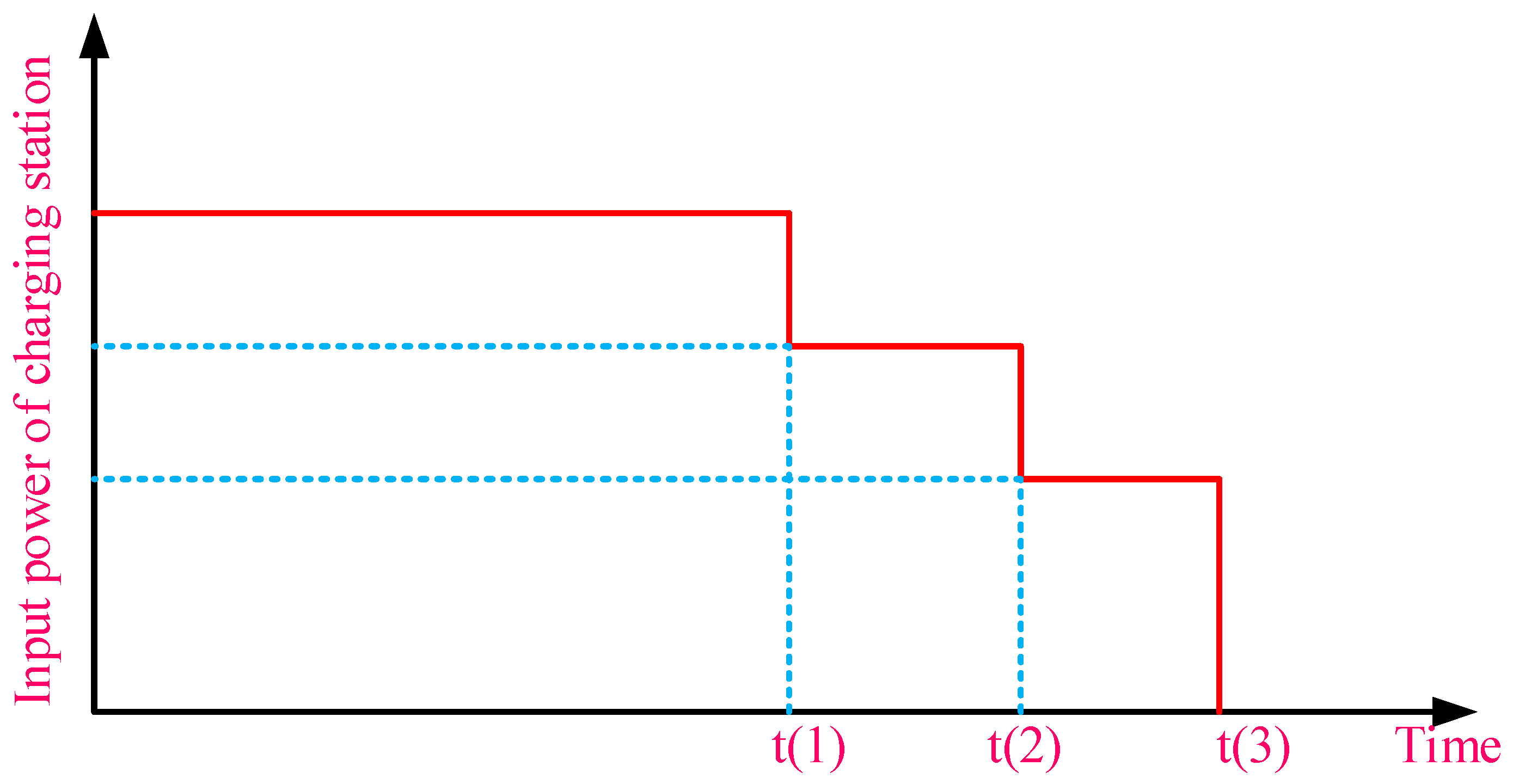
4. Charging Station Modeling
5. Type and Capacity of Vehicle Batteries
5.1. The Initial Charge of Vehicle Batteries
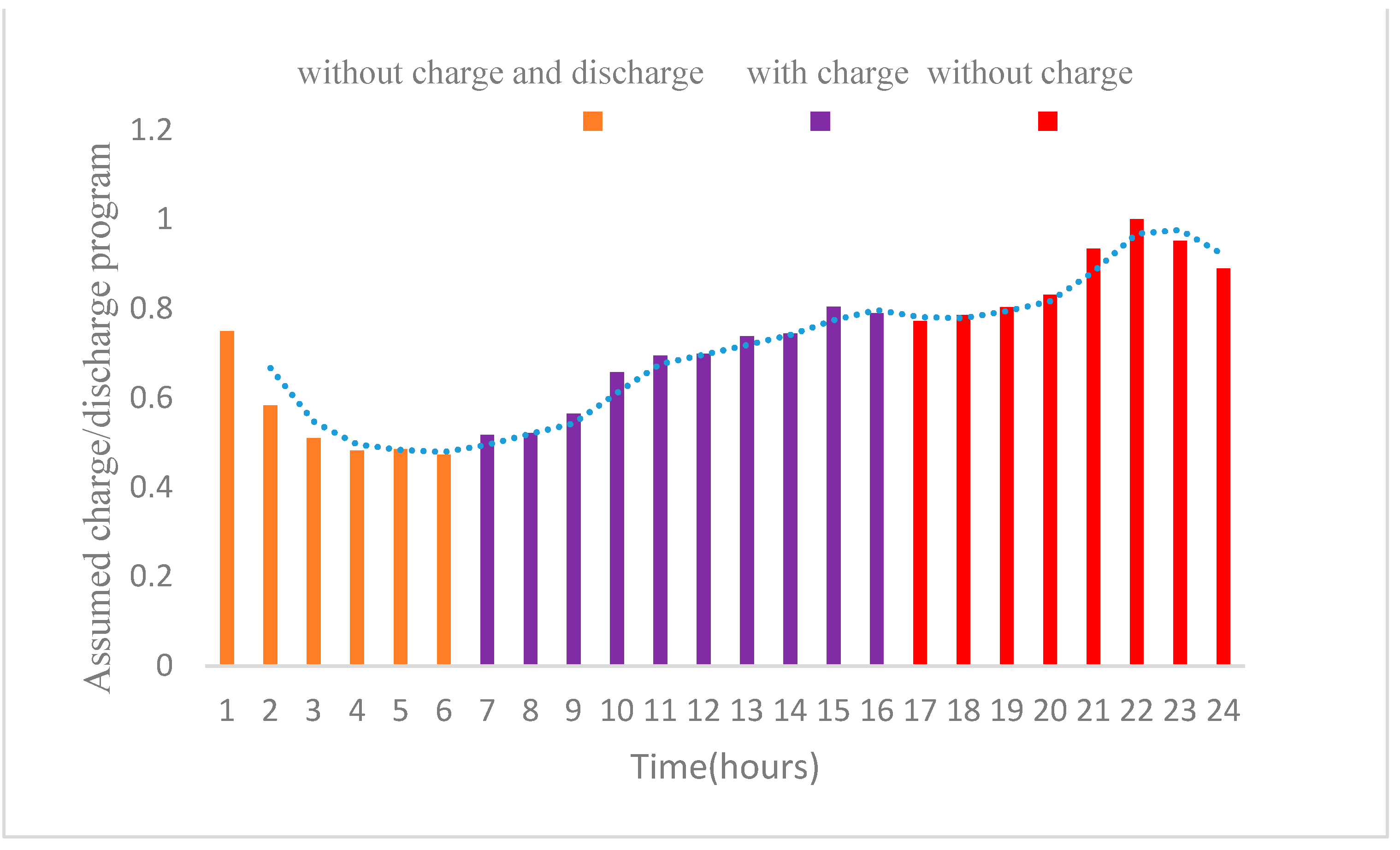
5.2. Vehicle Charging Schedule
6. Modeling the Location Problem
6.1. Profits from Discharge Programs
6.2. Profits from Recharge Programs
6.3. Profits from Reduced Power Purchases from the Upstream Network
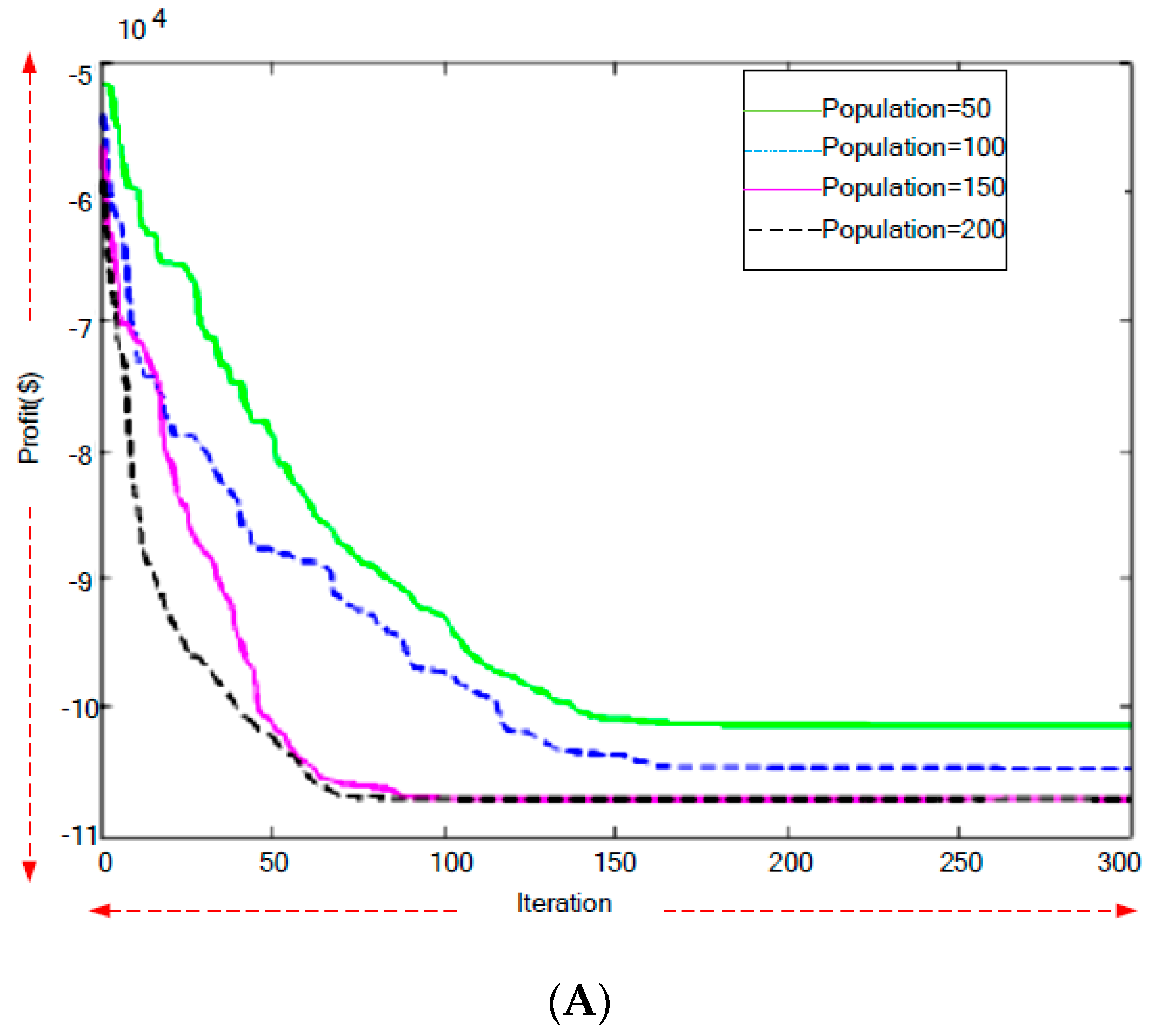
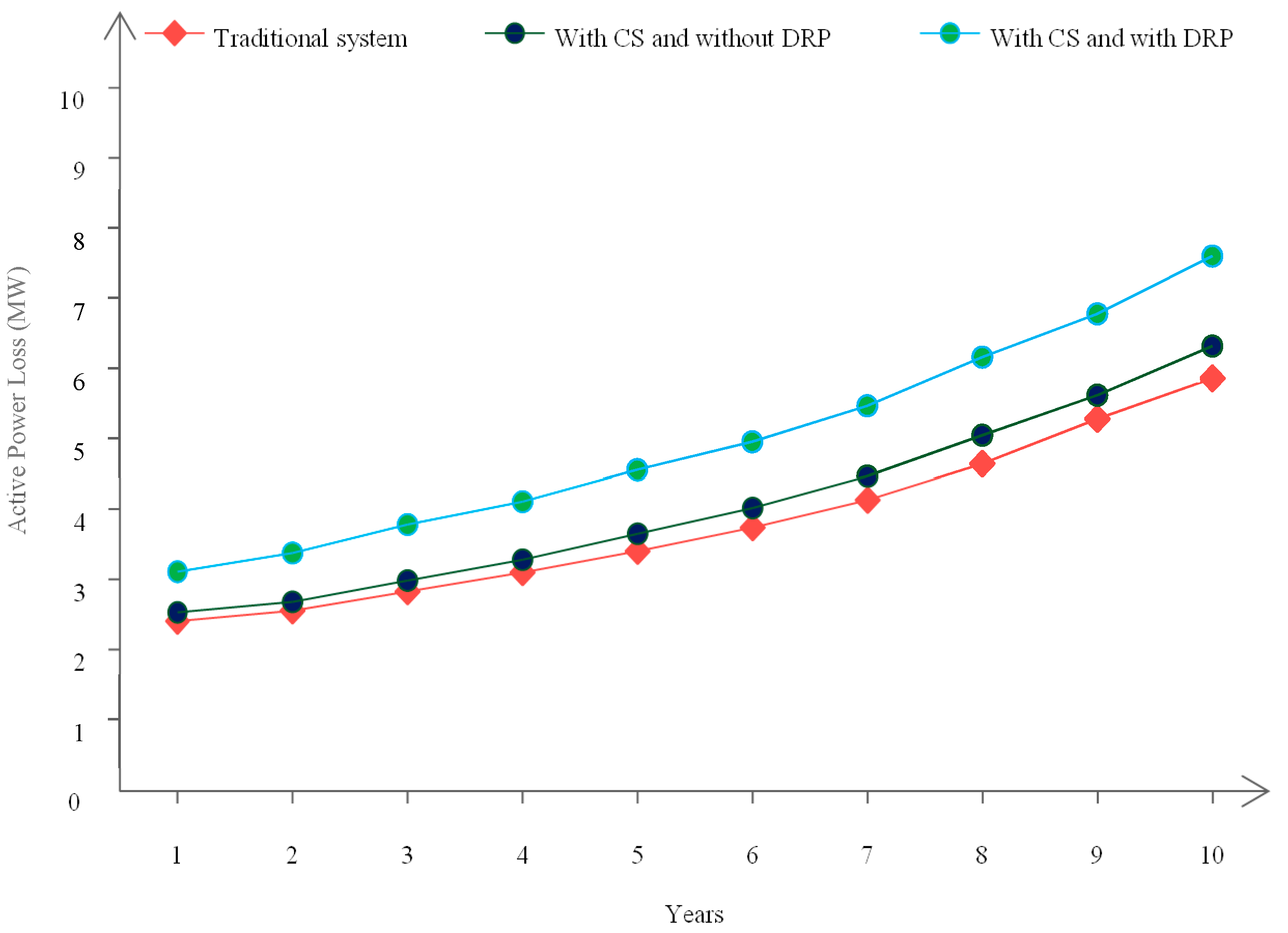
7. Numerical Simulation of the Proposed Method
8. Conclusions
9. Offers
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Parameter | Corresponding Description |
|---|---|
| Demand level factor (in Monte Carlo experiment, in bus i, year t, demand level h) | |
DNO DGOs | Price level factor in year t, demand level h, and Monte Carlo experiment e Distribution network operators Distribution generation owners |
| The forecasted mean value of demand level factor (in bus i, year t, demand level h) | |
| Random demand (in Monte Carlo experiment, in bus i, year t, demand level h) | |
| Standard deviations of demand level factors (in bus i, year t, demand level h) | |
| Base active power demand (in Monte Carlo experiment, in bus i, year t, demand level h) | |
| Base active power (in bus i) | |
| Base reactive power demand (in Monte Carlo experiment, in bus i, first year, demand level h) | |
| Base reactive power (in bus i) | |
| Base apparent power (in Monte Carlo experiment, in bus i, first year, demand level h) | |
| Base apparent power (in bus i) | |
| The base price of power purchased from the grid (year t, demand level h) | |
| The forecasted mean value of price level factor (in bus i, year t, demand level h) | |
| Random demand (in Monte Carlo experiment, in bus i, year t, demand level h) | |
| Standard deviations of demand level factors (in bus i, year t, demand level h) | |
| SOC | Amount of charge of vehicle batteries |
| Power of charging the batteries | |
| Battery capacity | |
| Required time to charging in hours | |
| Required time to discharge in hours | |
| The cost of discharge service | |
| Total gained revenge from discharging vehicle battery | |
| Total profit from discharging vehicle battery | |
| The cost of charge service | |
| Total gained revenge from charging vehicle battery | |
| Total profit from charging vehicle battery | |
| Demand power (year t, demand level h) | |
| Power loss (year t, demand level h) | |
| Transmitted power of charging station (in bus i, year t, demand level h) | |
| Inflation rate (percent) | |
| Interest rate (percent) |
| Indices | Corresponding Description |
|---|---|
| Base i | |
| Year | |
| Demand level | |
| Power price | |
| Demand | |
| Monte Carlo experiment |
References
- Miller, I.; Arbabzadeh, M.; Gençer, E. Hourly Power Grid Variations, Electric Vehicle Charging Patterns, and Operating Emissions. Environ. Sci. Technol. 2020, 54, 16071–16085. [Google Scholar] [CrossRef]
- Wang, B.; Zhao, D.; Dehghanian, P.; Tian, Y.; Hong, T. Aggregated Electric Vehicle Load Modeling in Large-Scale Electric Power Systems. IEEE Trans. Ind. Appl. 2020, 56, 5796–5810. [Google Scholar] [CrossRef]
- Li, M.-W.; Wang, Y.-T.; Geng, J.; Hong, W.-C. Chaos cloud quantum bat hybrid optimization algorithm. Nonlinear Dyn. 2021, 103, 1167–1193. [Google Scholar] [CrossRef]
- Zhang, Z.; Hong, W.-C. Application of variational mode decomposition and chaotic grey wolf optimizer with support vector regression for forecasting electric loads. Knowl. Based Syst. 2021, 228, 107297. [Google Scholar] [CrossRef]
- Sanjeevikumar, P.; Zand, M.; Nasab, M.A.; Hanif, M.A.; Bhaskar, M.S. Using the Social Spider Optimization Algorithm to Determine UPFC Optimal Size and Location for Improve Dynamic Stability. In Proceedings of the ECCE-Asia, Singapore, 24–27 May 2021. [Google Scholar]
- Zand, M.; Nasab, M.A.; Hatami, A.; Kargar, M.; Chamorro, H.R. Using Adaptive Fuzzy Logic for Intelligent Energy Management in Hybrid Vehicles. In Proceedings of the 28th Iranian Conference on Electrical Engineering (ICEE), Tabriz, Iran, 4–6 August 2020; pp. 1–7. [Google Scholar]
- Nasri, S.; Nowdeh, S.A.; Davoudkhani, I.F.; Moghaddam, M.J.H.; Kalam, A.; Shahrokhi, S.; Zand, M. Maximum Power Point Tracking of Photovoltaic Renewable Energy System Using a New Method Based on Turbulent Flow of Water-Based Optimization (TFWO) Under Partial Shading Conditions. In Energy Systems in Electrical Engineering; Springer: Cham, Switzerland, 2021; pp. 285–310. ISBN 9789813364561. [Google Scholar]
- Tightiz, L.; Nasab, M.A.; Yang, H.; Addeh, A. An intelligent system based on optimized ANFIS and association rules for power transformer fault diagnosis. ISA Trans. 2020, 103, 63–74. [Google Scholar] [CrossRef] [PubMed]
- Ghasemi, M.; Akbari, E.; Zand, M.; Hadipour, M.; Ghavidel, S.; Li, L. An Efficient Modified HPSO-TVAC-Based Dynamic Economic Dispatch of Generating Units. Electr. Power Compon. Syst. 2019, 47, 1826–1840. [Google Scholar] [CrossRef]
- Nasab, M.A.; Zand, M.; Eskandari, M.; Sanjeevikumar, P.; Siano, P. Optimal Planning of Electrical Appliance of Residential Units in a Smart Home Network Using Cloud Services. Smart Cities 2021, 4, 1173–1195. [Google Scholar] [CrossRef]
- Zand, M.; Nasab, M.A.; Sanjeevikumar, P.; Maroti, P.K.; Holm-Nielsen, J.B. Energy management strategy for solid-state transformer-based solar charging station for electric vehicles in smart grids. IET Renew. Power Gener. 2020, 14, 3843–3852. [Google Scholar] [CrossRef]
- Ngo, H.; Kumar, A.; Mishra, S. Optimal positioning of dynamic wireless charging infrastructure in a road network for battery electric vehicles. Transp. Res. Part D Transp. Environ. 2020, 85, 102385. [Google Scholar] [CrossRef]
- AlHajri, I.; Ahmadian, A.; Elkamel, A. Stochastic day-ahead unit commitment scheduling of integrated electricity and gas networks with hydrogen energy storage (HES), plug-in electric vehicles (PEVs) and renewable energies. Sustain. Cities Soc. 2021, 67, 102736. [Google Scholar] [CrossRef]
- Zhanhong, W.; Mingbiao, Z.; Zhenheng, L.; Xuejun, C.; Yonghua, H. Improved Genetic Algorithm and XGBoost Classifier for Power Transformer Fault Diagnosis. Front. Energy Res. 2021, 9, 1–10. [Google Scholar] [CrossRef]
- Wang, N.; Tang, L.; Pan, H. A global comparison and assessment of incentive policy on electric vehicle promotion. Sustain. Cities Soc. 2019, 44, 597–603. [Google Scholar] [CrossRef]
- Olatunde, O.; Hassan, M.Y.; Abdullah, P.; Rahman, H.A. Hybrid photovoltaic/small-hydropower microgrid in smart distribution network with grid isolated electric vehicle charging system. J. Energy Storage 2020, 31, 101673. [Google Scholar] [CrossRef]
- Zand, M.; Neghabi, O.; Nasab, M.A.; Eskandari, M.; Abedini, M. A Hybrid Scheme for Fault Locating in Transmission Lines Compensated by the Thyristor-Controlled Series Capacitors. In Proceedings of the 15th International Conference on Protection and Automation of Power Systems (IPAPS), Shiraz, Iran, 30–31 December 2020. [Google Scholar]
- Orsi, F. On the sustainability of electric vehicles: What about their impacts on land use? Sustain. Cities Soc. 2021, 66, 102680. [Google Scholar] [CrossRef]
- Zou, Y.; Zhao, J.; Ding, D.; Miao, F.; Sobhani, B. Solving dynamic economic and emission dispatch in power system integrated electric vehicle and wind turbine using multi-objective virus colony search algorithm. Sustain. Cities Soc. 2021, 67, 102722. [Google Scholar] [CrossRef]
- Li, H.; Rezvani, A.; Hu, J.; Ohshima, K. Optimal day-ahead scheduling of microgrid with hybrid electric vehicles using MSFLA algorithm considering control strategies. Sustain. Cities Soc. 2021, 66, 102681. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Zhang, T.; Gu, Z. Review of the electric vehicle charging station location problem. Commun. Comput. Inf. Sci. 2019, 1123, 435–445. [Google Scholar] [CrossRef]
- Behera, S.; Behera, S.; Barisal, A.K. Dynamic Combined Economic Emission Dispatch integrating Plug-in Electric Vehicles and Renewable Energy Sources. Int. J. Ambient Energy 2021. Accepted for publication. [Google Scholar] [CrossRef]
- Muratori, M.; Elgqvist, E.; Cutler, D.; Eichman, J.; Salisbury, S.; Fuller, Z.; Smart, J. Technology solutions to mitigate electricity cost for electric vehicle DC fast charging. Appl. Energy 2019, 242, 415–423. [Google Scholar] [CrossRef]
- Azimi, Z.; Hooshmand, R.-A.; Soleymani, S. Energy management considering simultaneous presence of demand responses and electric vehicles in smart industrial grids. Sustain. Energy Technol. Assess. 2021, 45, 101127. [Google Scholar] [CrossRef]
- Khan, Z.; Iyer, G.; Patel, P.; Kim, S.; Hejazi, M.; Burleyson, C.; Wise, M. Impacts of long-term temperature change and variability on electricity investments. Nat. Commun. 2021, 12, 1–12. [Google Scholar] [CrossRef]
- Wang, L.; Nian, V.; Li, H.; Yuan, J. Impacts of electric vehicle deployment on the electricity sector in a highly urbanised environment. J. Clean. Prod. 2021, 295, 126386. [Google Scholar] [CrossRef]
- Heinisch, V.; Göransson, L.; Erlandsson, R.; Hodel, H.; Johnsson, F.; Odenberger, M. Smart electric vehicle charging strategies for sectoral coupling in a city energy system. Appl. Energy 2021, 288, 116640. [Google Scholar] [CrossRef]
- Farias, H.O.; Rangel, C.S.; Stringini, L.W.; Canha, L.N.; Bertineti, D.P.; Brignol, W.D.S.; Nadal, Z.I. Combined Framework with Heuristic Programming and Rule-Based Strategies for Scheduling and Real Time Operation in Electric Vehicle Charging Stations. Energies 2021, 14, 1370. [Google Scholar] [CrossRef]
- Mehrjerdi, H. Resilience-robustness improvement by adaptable operating pattern for electric vehicles in complementary solar-vehicle management. J. Energy Storage 2021, 37, 102454. [Google Scholar] [CrossRef]
- Migliavacca, G.; Rossi, M.; Siface, D.; Marzoli, M.; Ergun, H.; Rodríguez-Sánchez, R.; Hanot, M.; Leclerq, G.; Amaro, N.; Egorov, A.; et al. The Innovative FlexPlan Grid-Planning Methodology: How Storage and Flexible Resources Could Help in De-Bottlenecking the European System. Energies 2021, 14, 1194. [Google Scholar] [CrossRef]
- Zeng, B.; Liu, Y.; Xu, F.; Liu, Y.; Sun, X.; Ye, X. Optimal demand response resource exploitation for efficient accommodation of renewable energy sources in multi-energy systems considering correlated uncertainties. J. Clean. Prod. 2021, 288, 125666. [Google Scholar] [CrossRef]
- Nezamabad, H.A.; Zand, M.; Alizadeh, A.; Vosoogh, M.; Nojavan, S. Multi-objective optimization based robust scheduling of electric vehicles aggregator. Sustain. Cities Soc. 2019, 47, 101494. [Google Scholar] [CrossRef]
- Hamwi, M.; Lizarralde, I.; Legardeur, J. Demand response business model canvas: A tool for flexibility creation in the electricity markets. J. Clean. Prod. 2021, 282, 124539. [Google Scholar] [CrossRef]
- Mowry, A.M.; Mallapragada, D.S. Grid impacts of highway electric vehicle charging and role for mitigation via energy storage. Energy Policy 2021, 157, 112508. [Google Scholar] [CrossRef]
- Xiang, Y.; Cai, H.; Liu, J.; Zhang, X. Techno-economic design of energy systems for airport electrification: A hydrogen-solar-storage integrated microgrid solution. Appl. Energy 2021, 283, 116374. [Google Scholar] [CrossRef]
- Zand, M.; Nasab, M.A.; Khoobani, M.; Jahangiri, A.; Hosseinian, S.H.; Kimiai, A.H. Robust Speed Control for Induction Motor Drives Using STSM Control. In Proceedings of the 12th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tabriz, Iran, 2–4 February 2021. [Google Scholar]
- Huang, P.; Sun, Y.; Lovati, M.; Zhang, X. Solar-photovoltaic-power-sharing-based design optimization of distributed energy storage systems for performance improvements. Energy 2021, 222, 119931. [Google Scholar] [CrossRef]
- Kühnbach, M.; Bekk, A.; Weidlich, A. Prepared for regional self-supply? On the regional fit of electricity demand and supply in Germany. Energy Strat. Rev. 2021, 34, 100609. [Google Scholar] [CrossRef]
- Chondrogiannis, S.; Poncela-Blanco, M.; Marinopoulos, A.; Marneris, I.; Ntomaris, A.; Biskas, P.; Bakirtzis, A. Power system flexibility: A methodological analytical framework based on unit commitment and economic dispatch modelling. In Mathematical Modelling of Contemporary Electricity Markets; Academic Press: Cambridge, MA, USA, 2021; pp. 127–156. [Google Scholar]
- Basu, M. Heat and power generation augmentation planning of isolated microgrid. Energy 2021, 223, 120062. [Google Scholar] [CrossRef]
- Alismail, F.; Abdulgalil, M.; Khalid, M. Optimal Coordinated Planning of Energy Storage and Tie-Lines to Boost Flexibility with High Wind Power Integration. Sustainability 2021, 13, 2526. [Google Scholar] [CrossRef]
- Parsa, N.; Bahmani-Firouzi, B.; Niknam, T. A social-economic-technical framework for reinforcing the automated distribution systems considering optimal switching and plug-in hybrid electric vehicles. Energy 2021, 220, 119703. [Google Scholar] [CrossRef]
- Lugovoy, O.; Gao, S.; Gao, J.; Jiang, K. Feasibility study of China’s electric power sector transition to zero emissions by 2050. Energy Econ. 2021, 96, 105176. [Google Scholar] [CrossRef]
- Alshaalan, A. Basic Concepts of Electric Power System Planning. In Advances in Business Information Systems and Analytics; IGI Global: Hershey, PA, USA, 2021; pp. 306–325. [Google Scholar]
- Zand, M.; Nasab, M.A.; Neghabi, O.; Khalili, M.; Goli, A. Fault locating transmission lines with thyristor-controlled series capacitors By fuzzy logic method. In Proceedings of the 14th International Conference on Protection and Automation of Power Systems (IPAPS), Tehran, Iran, 31 December 2019–1 January 2020; pp. 62–70. [Google Scholar] [CrossRef]
- Zand, Z.; Hayati, M.; Karimi, G. Short-Channel Effects Improvement of Carbon Nanotube Field Effect Transistors. In Proceedings of the 28th Iranian Conference on Electrical Engineering (ICEE), Tabriz, Iran, 4–6 August 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Canale, L.; Di Fazio, A.; Russo, M.; Frattolillo, A.; Dell’Isola, M. An Overview on Functional Integration of Hybrid Renewable Energy Systems in Multi-Energy Buildings. Energies 2021, 14, 1078. [Google Scholar] [CrossRef]



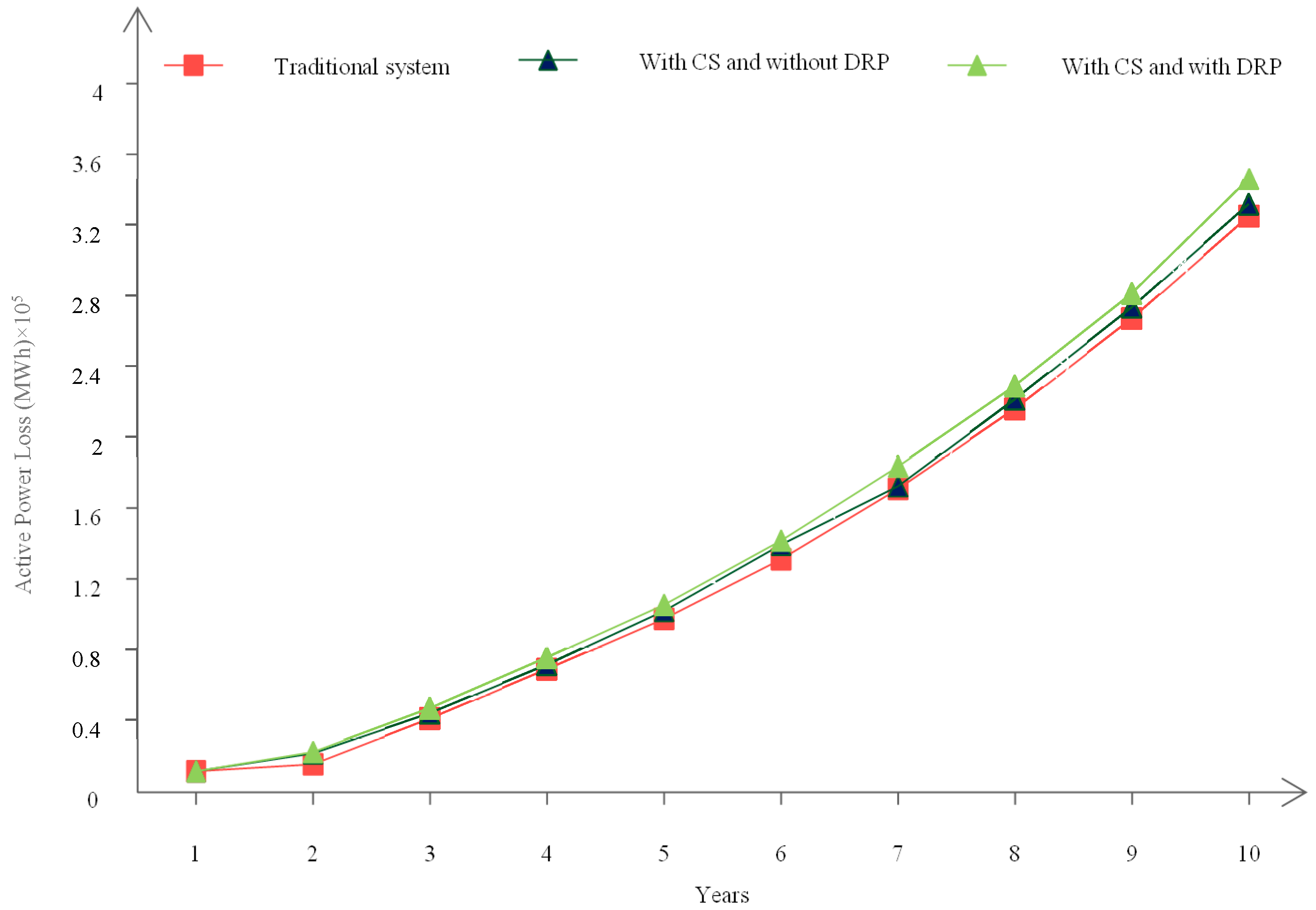

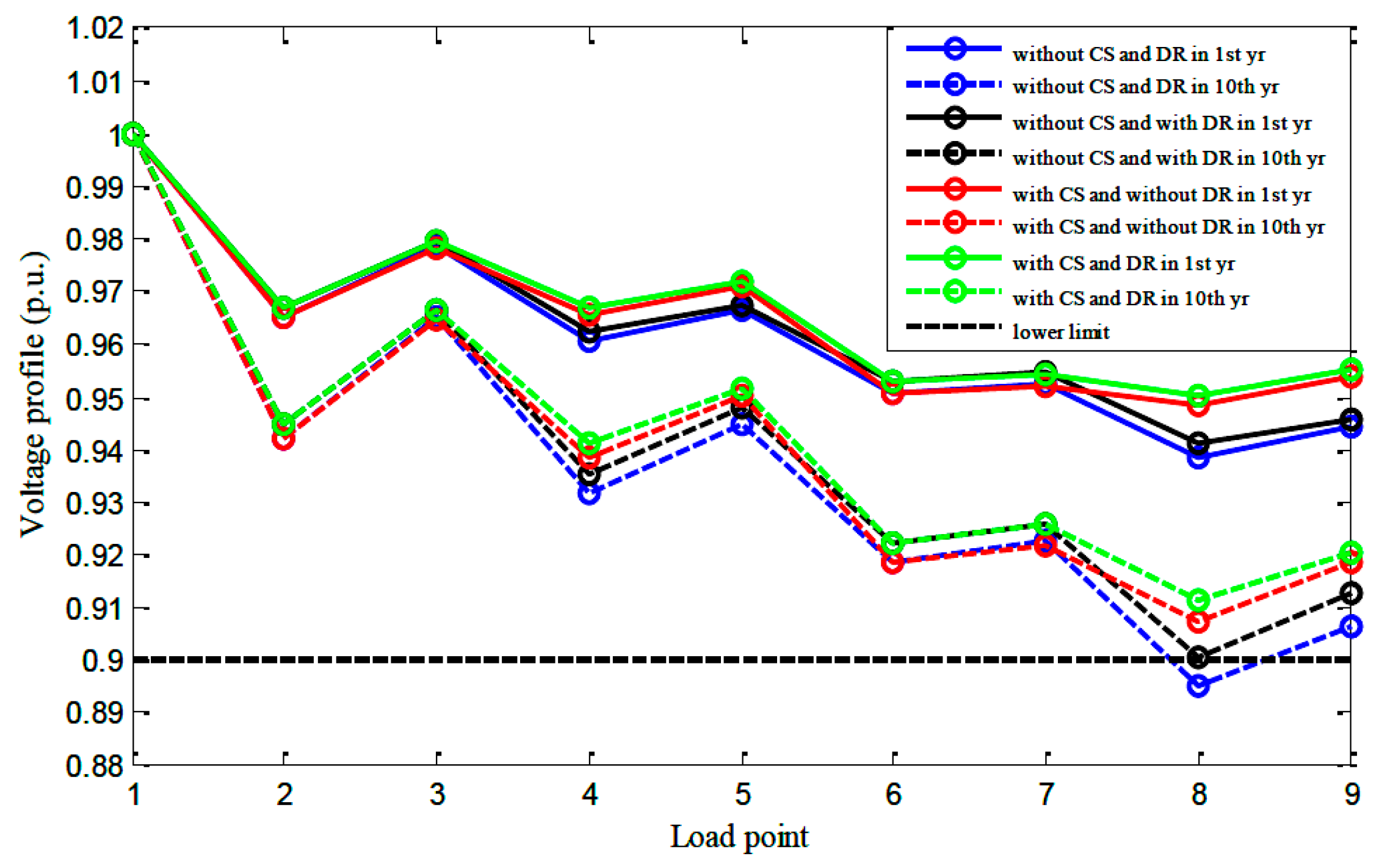
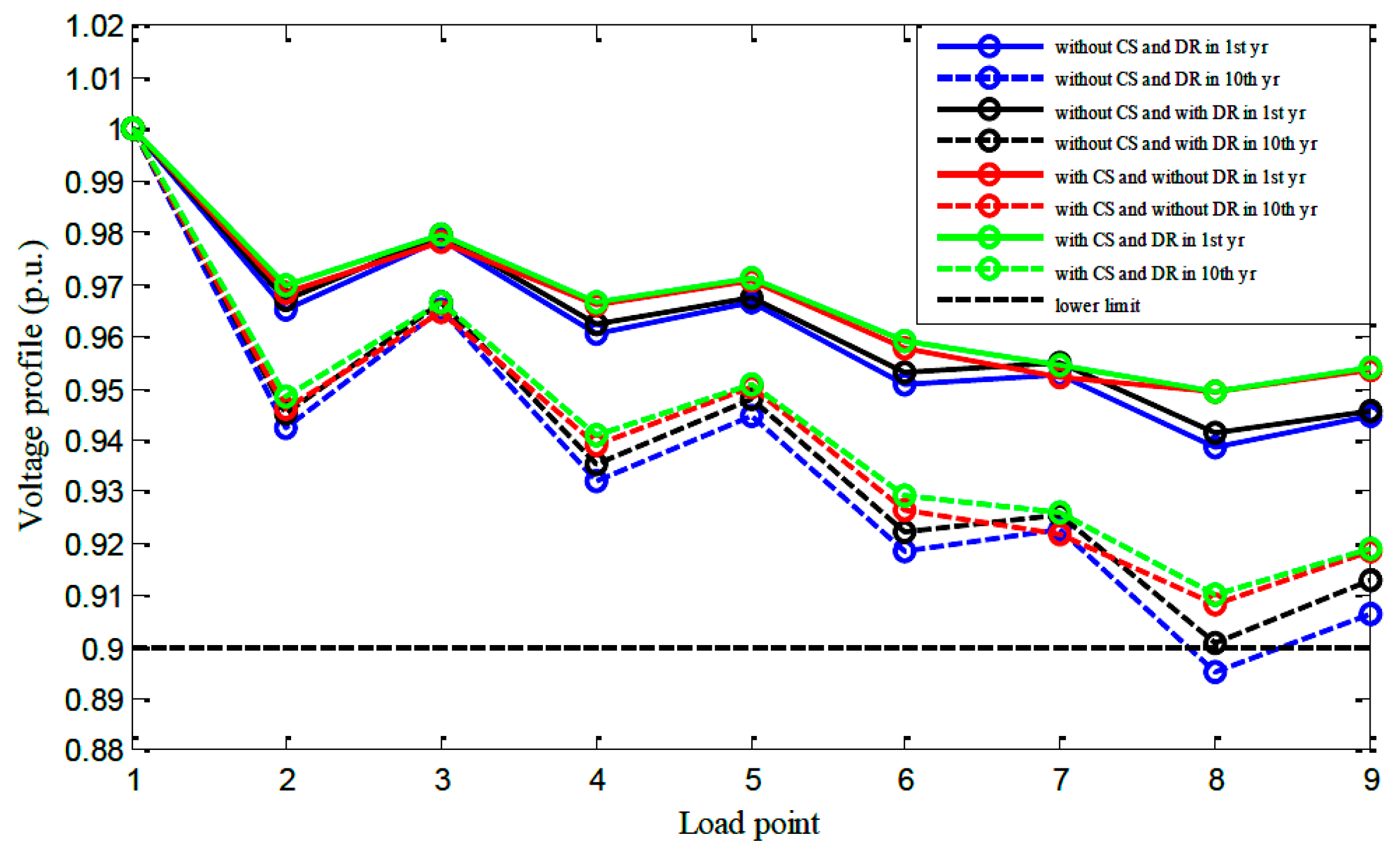
| Parameters | Intended Value |
|---|---|
| Number of population | 150 |
| Maximum repetition | 100 |
| Solving time (seconds) | 159.7 |
| Mutation rates | 0.02 |
| Crossover rate | 0.03 |
| Marriage rate | 0.10 |
| Chromosomes | Representation |
|---|---|
| Chromosome 1 | 11011|00100110110 |
| Chromosome 2 | 11011|11000011110 |
| Offspring 1 | 11011|11000011110 |
| Offspring 2 | 11011|00100110110 |
| The Initial Charge | SOC1 | SOC2 | SOC3 |
|---|---|---|---|
| Number of vehicles | n1 | n2 | n3 |
| Load Information | Without DRP | With DRP |
|---|---|---|
| Maximum load supply profit (USD) | - | - |
| Charge program benefit (USD) | - | - |
| Profit from purchasing energy from the overhead network (USD) | 107 | 107 |
| Profit from loss reduction (USD) | - | 107 |
| Investment cost (USD) | - | - |
| Total profit (USD) | 107 | 107 |
| Load Information | Without DRP | With DRP | ||
|---|---|---|---|---|
| Bass number Optimal capacity of the power plant (kW) | 8 741 | 9 895 | 8 649 | 9 784 |
| Maximum load supply profit (USD) | 106 | 106 | ||
| Charge program benefit (USD) | 105 | 105 | ||
| Profit from purchasing energy from the overhead network (USD) | 107 | 107 | ||
| Profit from loss reduction (USD) | 105 | 106 | ||
| Investment cost (USD) | 107 | 107 | ||
| Total profit (USD) | 107 | 107 | ||
| Load Information | Without DRP | With DRP | ||||
|---|---|---|---|---|---|---|
| Bass number Optimal capacity of the power plant (kW) | 6 547 | 8 791 | 9 895 | 6 463 | 8 580 | 9 654 |
| Maximum load supply profit (USD) | 106 | 106 | ||||
| Charge program benefit (USD) | 105 | 105 | ||||
| Profit from purchasing energy from the overhead network (USD) | 107 | 107 | ||||
| Profit from loss reduction (USD) | 105 | 106 | ||||
| Investment cost (USD) | 107 | 107 | ||||
| Total profit (USD) | 107 | 107 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azimi Nasab, M.; Zand, M.; Padmanaban, S.; Khan, B. Simultaneous Long-Term Planning of Flexible Electric Vehicle Photovoltaic Charging Stations in Terms of Load Response and Technical and Economic Indicators. World Electr. Veh. J. 2021, 12, 190. https://doi.org/10.3390/wevj12040190
Azimi Nasab M, Zand M, Padmanaban S, Khan B. Simultaneous Long-Term Planning of Flexible Electric Vehicle Photovoltaic Charging Stations in Terms of Load Response and Technical and Economic Indicators. World Electric Vehicle Journal. 2021; 12(4):190. https://doi.org/10.3390/wevj12040190
Chicago/Turabian StyleAzimi Nasab, Morteza, Mohammad Zand, Sanjeevikumar Padmanaban, and Baseem Khan. 2021. "Simultaneous Long-Term Planning of Flexible Electric Vehicle Photovoltaic Charging Stations in Terms of Load Response and Technical and Economic Indicators" World Electric Vehicle Journal 12, no. 4: 190. https://doi.org/10.3390/wevj12040190
APA StyleAzimi Nasab, M., Zand, M., Padmanaban, S., & Khan, B. (2021). Simultaneous Long-Term Planning of Flexible Electric Vehicle Photovoltaic Charging Stations in Terms of Load Response and Technical and Economic Indicators. World Electric Vehicle Journal, 12(4), 190. https://doi.org/10.3390/wevj12040190








