State of Health Estimation of Lithium-Ion Batteries Based on Electrochemical Impedance Spectroscopy and Backpropagation Neural Network
Abstract
:1. Introduction
1.1. Experimental Techniques
1.2. Adaptive Models
2. Data Acquisition and Analysis from EIS Measurement
2.1. Battery Degradation
- Internal: Battery Design
- External: Operational Condition
2.1.1. Aging Mechanisms
- Loss of lithium ions: Li-ions that are blocked and unable to be intercalated between electrodes;
- Loss of active material: reduced density of lithium storage sites or reduced electrode area and material;
- Increase of impedance: reduction in cell power and further capacity fade by increased voltage drops due to increased impedance which prevents the battery from being fully discharged.
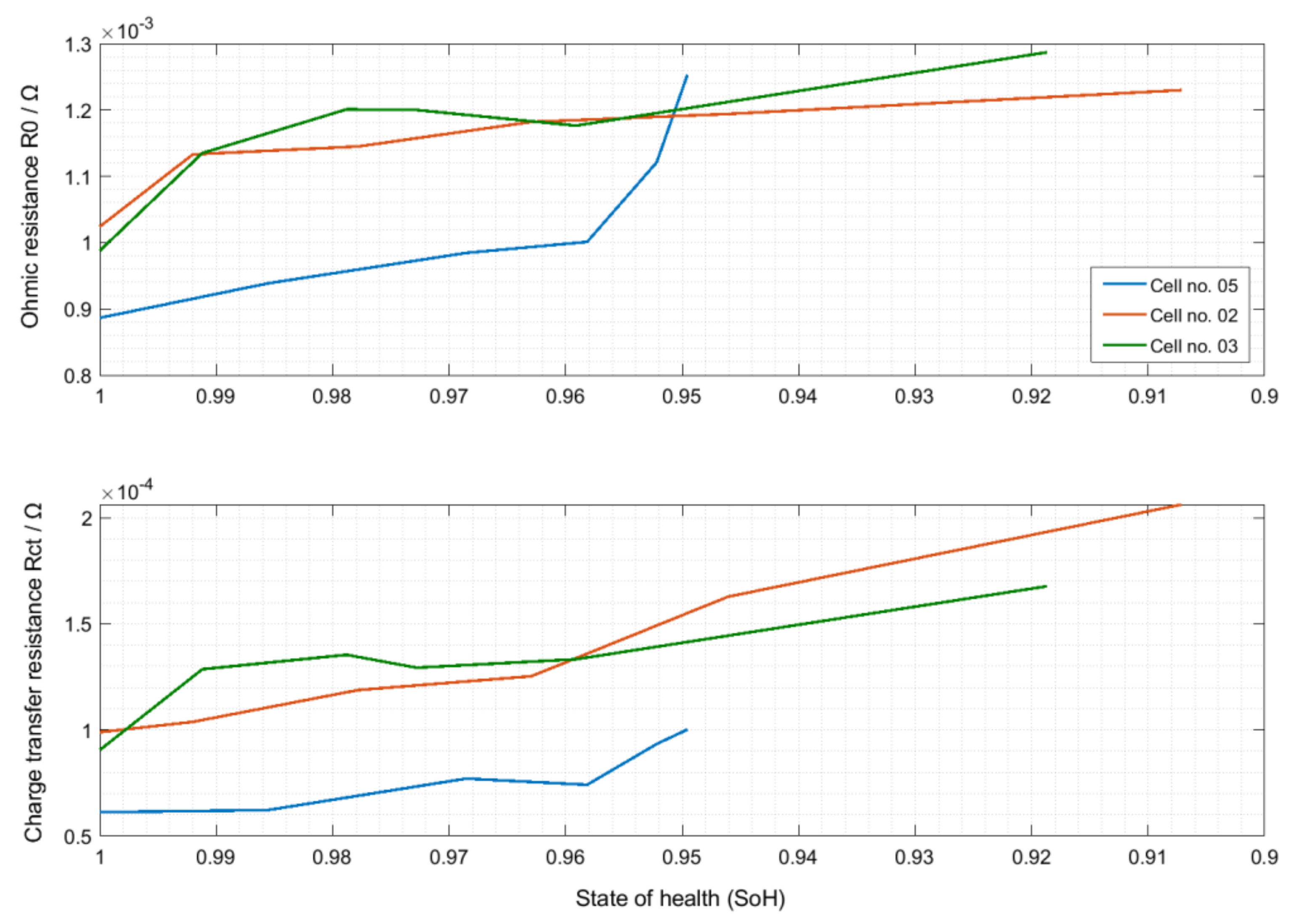
2.1.2. Degradation Indicators
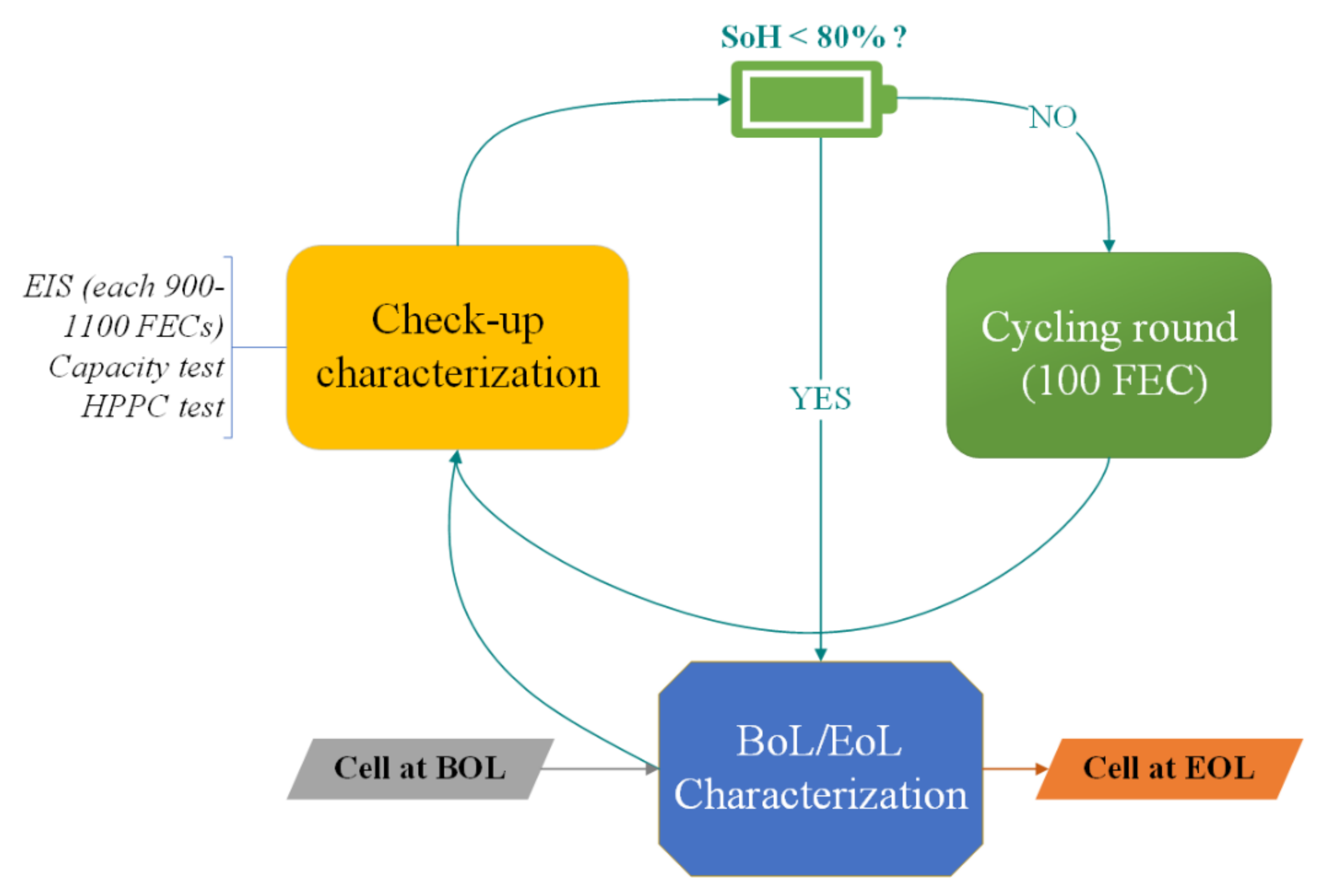
2.2. Data Acquisition
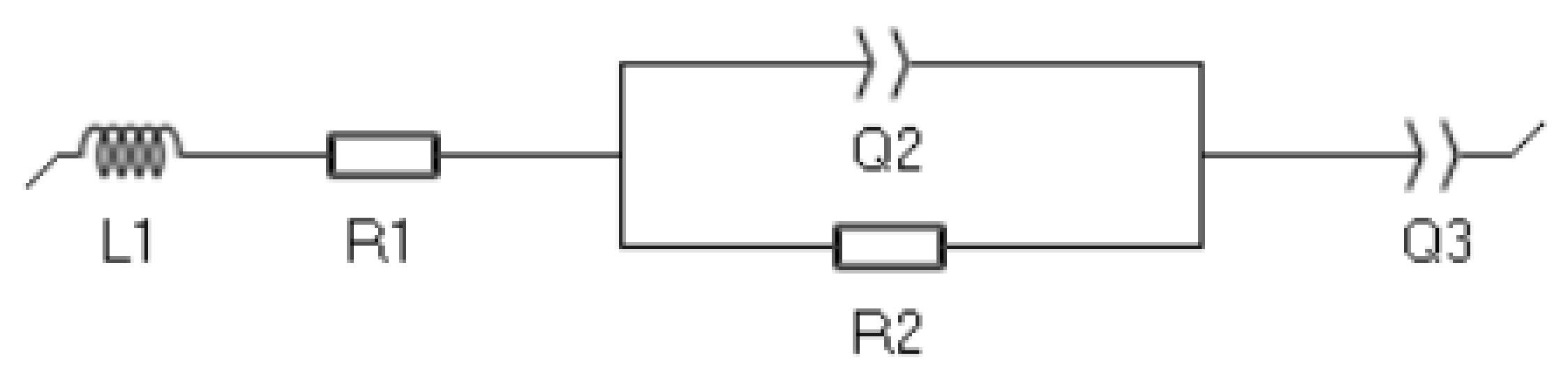
2.3. Impedance Results
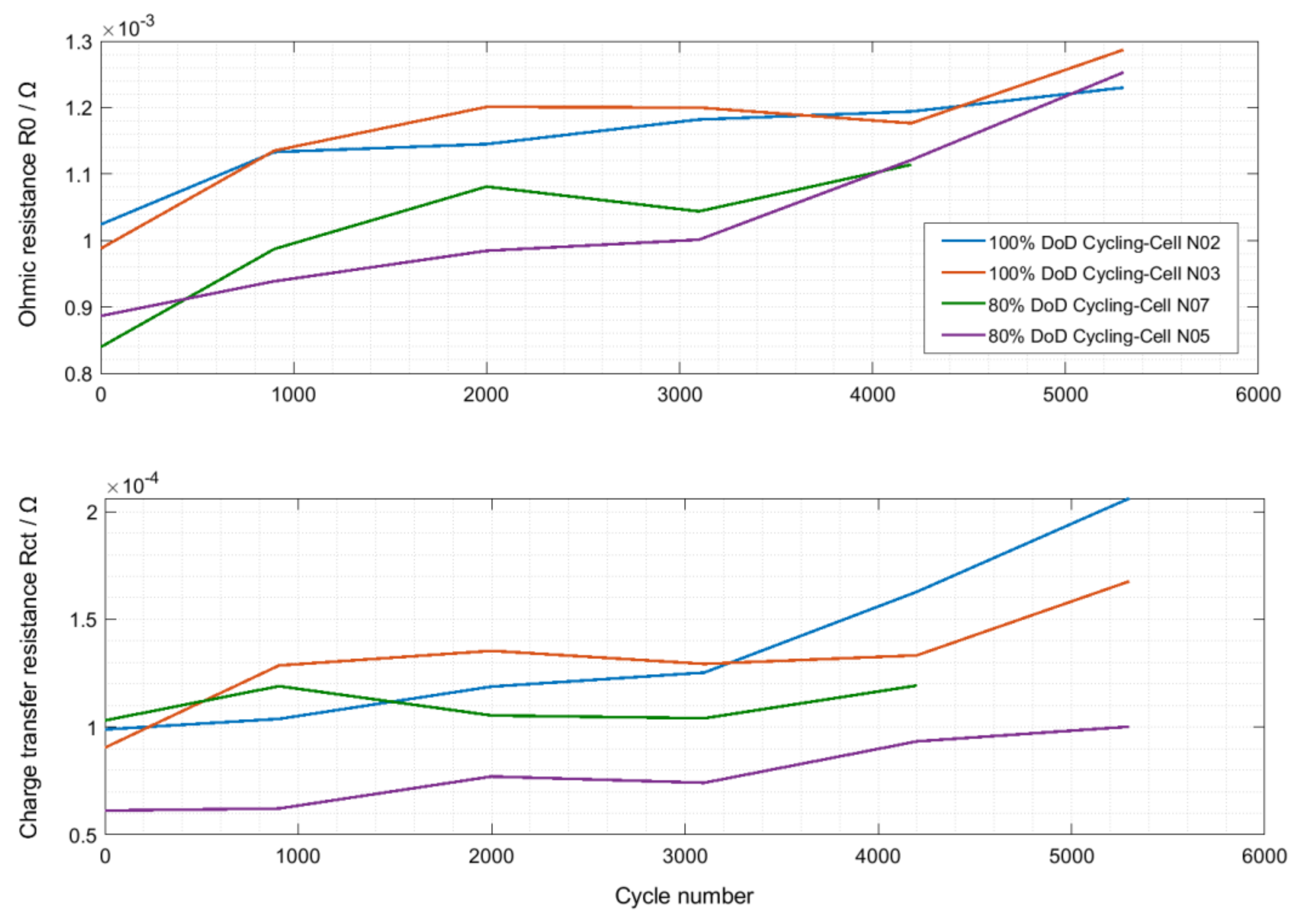
2.3.1. Stress Factor: Depth of Discharge
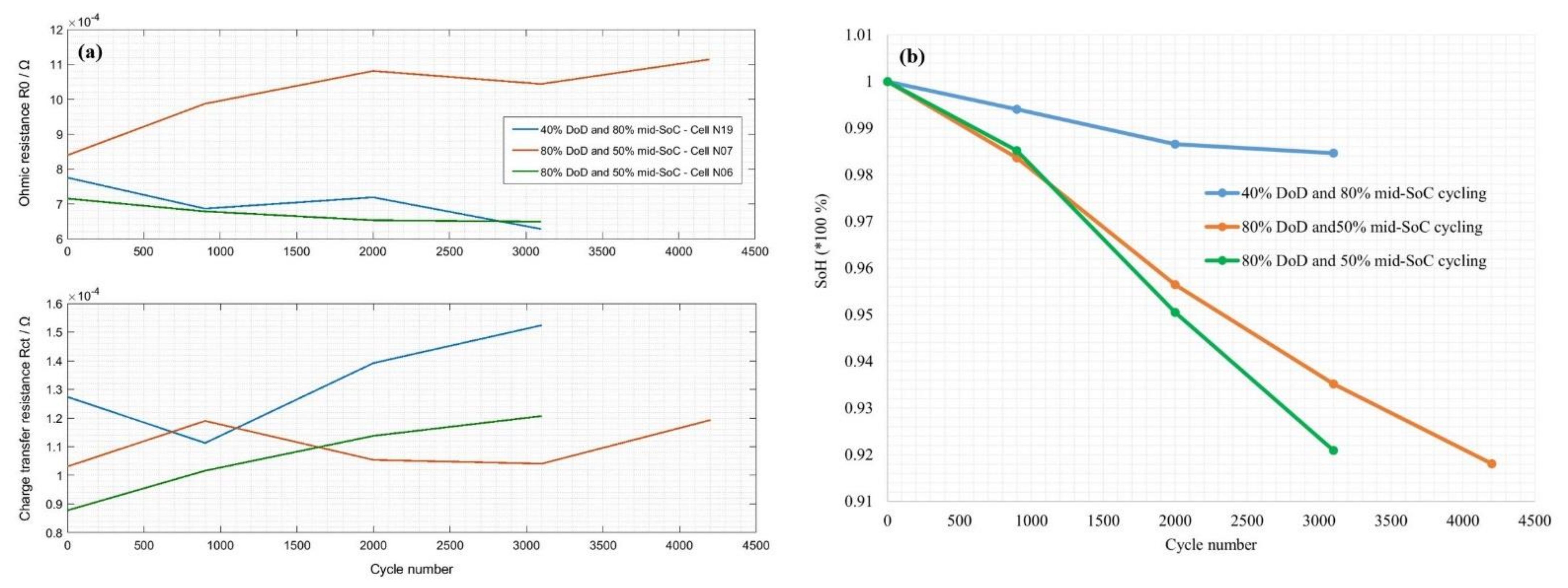
2.3.2. Stress Factor: Middle State of Charge
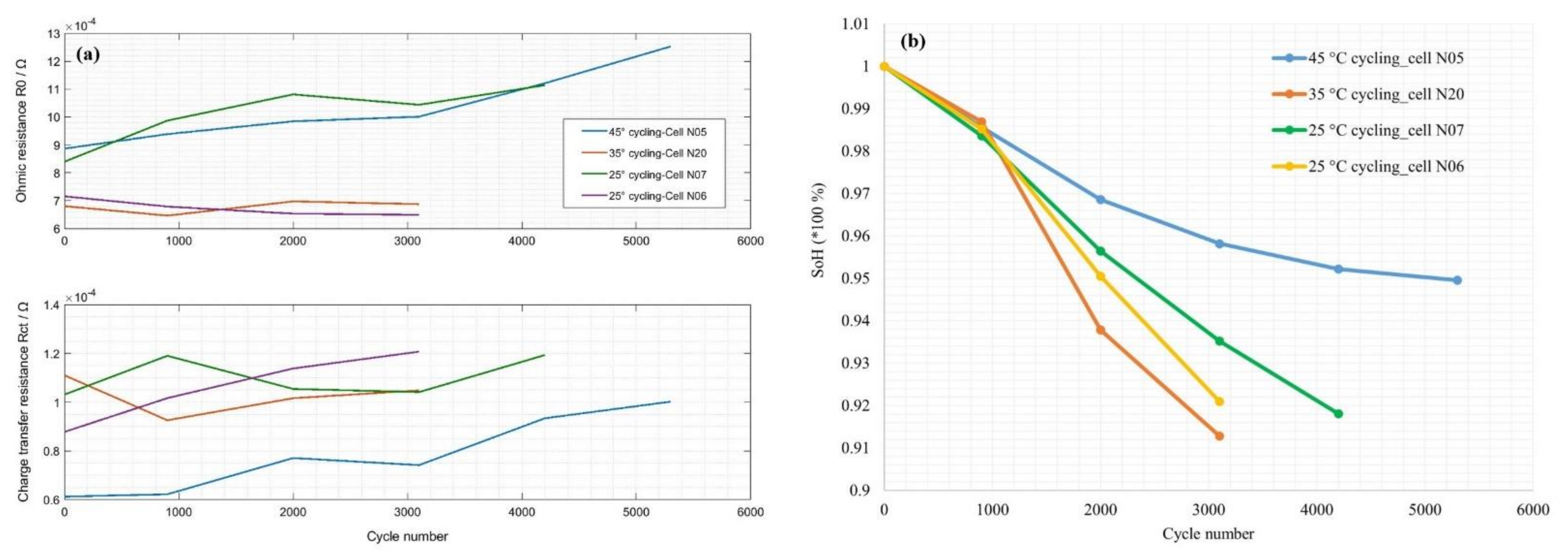
2.3.3. Stress Factor: Temperature
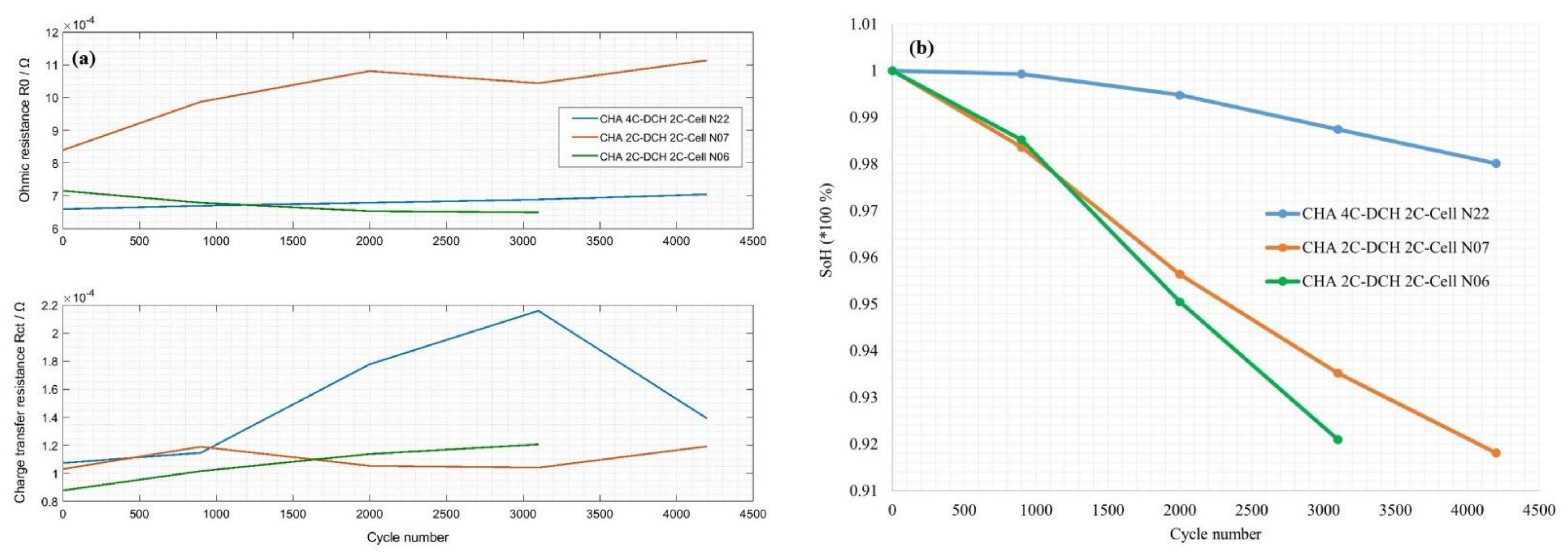
2.3.4. Stress Factor: Charge Rate
3. Model Development
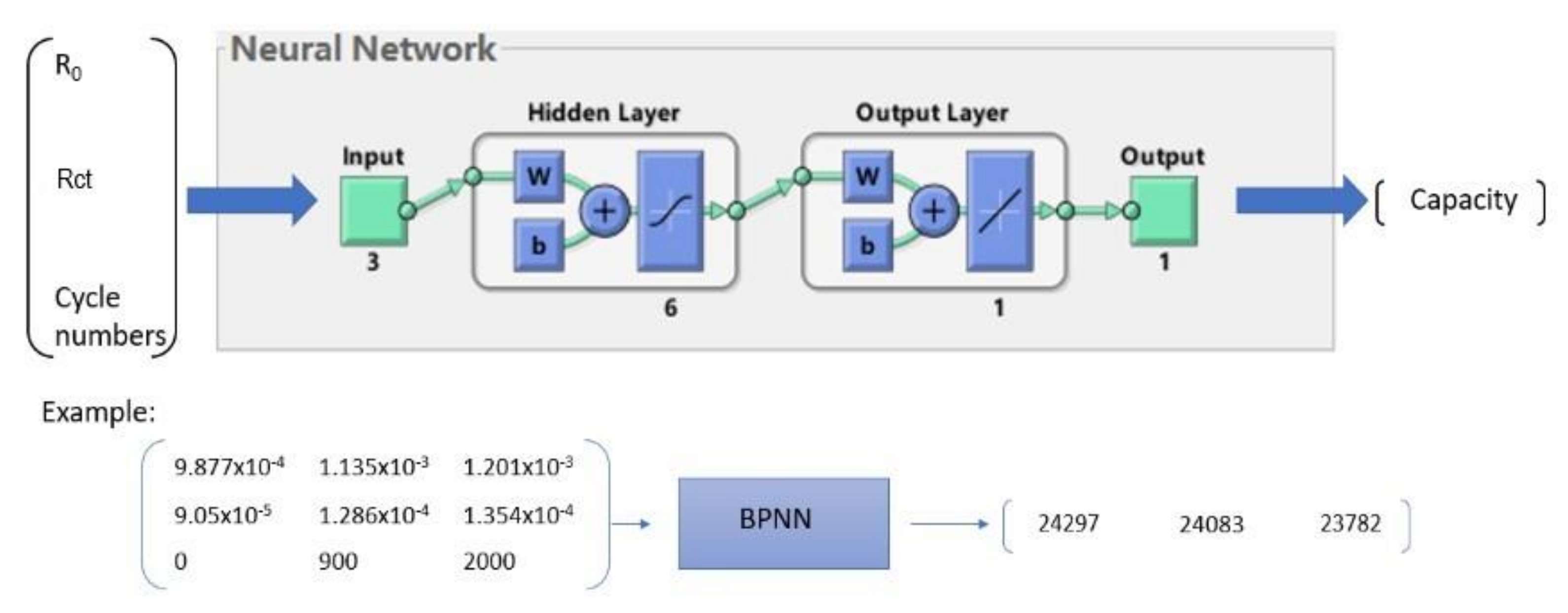
3.1. Back-Propagation Neural Network (BPNN)
- Initialization
- Calculation of output between layers
- Calculation of error and update of weights and threshold
3.2. Training Input
3.2.1. Optimized Model for Cell No. 24 (Cycling Temperature: 25 °C)
- Transfer function: the S-shaped sigmoid function (Equation (6)) where a is set to be 1.
- Training algorithm: Levenberg–Marquardt algorithm.
- Number of hidden layer neurons: 8.
3.2.2. Optimized Model for Cell No. 32 (Cycling Temperature: 35 °C)
- Number of hidden layer neurons: 6
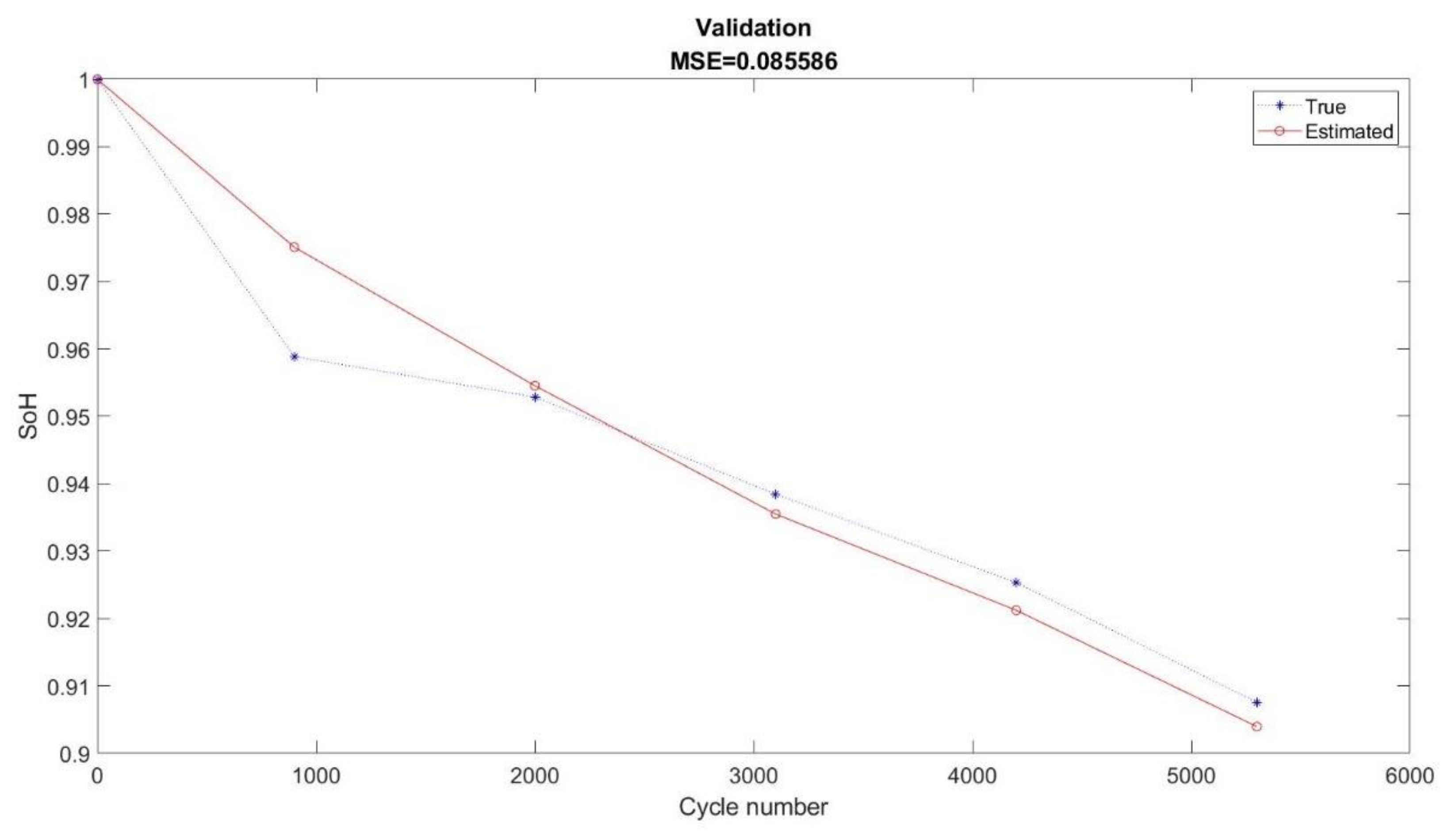
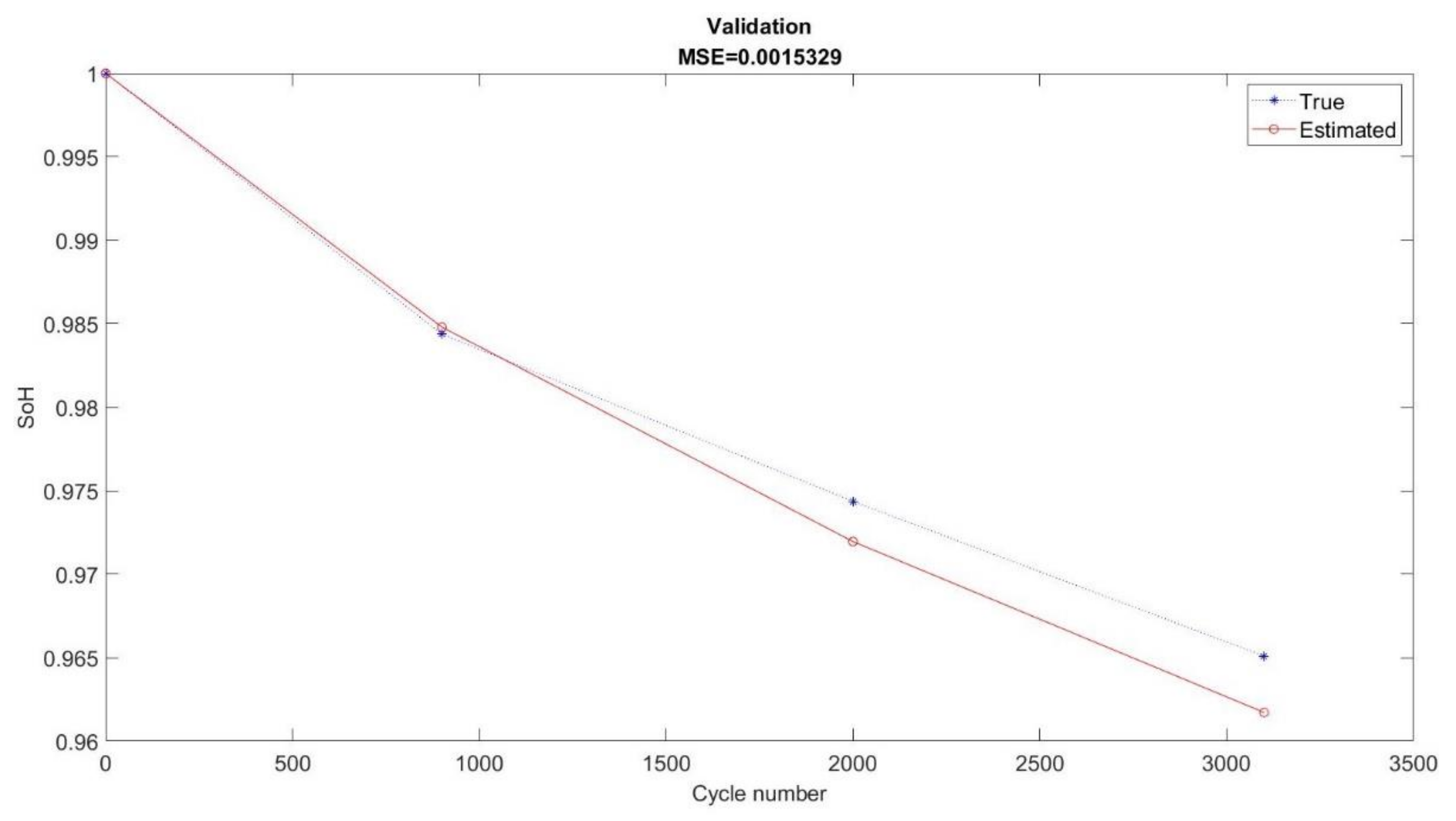
3.3. Validation
3.4. Discussion and Limitation
4. Conclusions
Author Contributions
Funding
Acknowledgments

Conflicts of Interest
References
- Electric Vehicle Market Research Report. Available online: https://www.fortunebusinessinsights.com/industry-reports/electric-vehicle-market-101678 (accessed on 26 March 2021).
- Scrosati, B.; Garche, J. Lithium batteries: Status, prospects and future. J. Power Sources 2010, 195, 2419–2430. [Google Scholar] [CrossRef]
- Cornet d’Elzius, M.; Duerinck, J.; Laes, E.; Lodewijks, P.; Meynaerts, E.; Pestiaux, J.; Renders, N.; Vermeulen, P. Scenarios for a Low-Carbon Belgium by 2050; Climact: Louvain-la-Neuve, Belgium; Vito: Mol, Belgium, 2013. [Google Scholar] [CrossRef]
- Nuhic, A.; Terzimehic, T.; Soczka-Guth, T.; Buchholz, M.; Dietmayer, K. Health diagnosis and remaining useful life prognostics of lithium-ion batteries using data-driven methods. J. Power Sources 2013, 239, 680–688. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Van Mierlo, J.; van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Venugopal, P.T.V. State-of-Health Estimation of Li-ion Batteries in Electric Vehicle Using IndRNN under Variable Load Condition. Energies 2019, 12, 4338. [Google Scholar] [CrossRef] [Green Version]
- Haifeng, D.; Xuezhe, W.; Zechang, S. A new SOH prediction concept for the power lithium-ion battery used on HEVs. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; pp. 1649–1653. [Google Scholar]
- Mingant, R.; Bernard, J.; Moynot, V.S.; Delaille, A.; Mailley, S.; Hognon, J.-L.; Huet, F. EIS Measurements for Determining the SoC and SoH of Li-Ion Batteries. ECS Trans. 2010, 33, 41–53. [Google Scholar] [CrossRef]
- Eddahech, A.; Briat, O.; Bertrand, N.; Delétage, J.-Y.; Vinassa, J.-M. Behavior and state-of-health monitoring of Li-ion batteries using impedance spectroscopy and recurrent neural networks. Int. J. Electr. Power Energy Syst. 2012, 42, 487–494. [Google Scholar] [CrossRef]
- Groot, J. State-of-Health Estimation of Li-Ion Batteries: Cycle Life Test Methods 2012; Chalmers Tekniska Hogskola: Gothenburg, Sweden, 2012. [Google Scholar]
- de Hoog, J.; Timmermans, J.-M.; Ioan-Stroe, D.; Swierczynski, M.; Jaguemont, J.; Goutam, S.; Omar, N.; Van Mierlo, J.; Van Den Bossche, P. Combined cycling and calendar capacity fade modeling of a Nickel-Manganese-Cobalt Oxide Cell with real-life profile validation. Appl. Energy 2017, 200, 47–61. [Google Scholar] [CrossRef]
- Omar, N.; Monem, M.A.; Firouz, Y.; Salminen, J.; Smekens, J.; Hegazy, O.; Gaulous, H.; Mulder, G.; Van Den Bossche, P.; Coosemans, T.; et al. Lithium iron phosphate based battery—Assessment of the aging parameters and development of cycle life model. Appl. Energy 2014, 113, 1575–1585. [Google Scholar] [CrossRef]
- Sarasketa-Zabala, E.; Gandiaga, I.; Laserna, E.M.; Rodriguez-Martinez, L.; Villarreal, I. Cycle ageing analysis of a LiFePO4/graphite cell with dynamic model validations: Towards realistic lifetime predictions. J. Power Sources 2015, 275, 573–587. [Google Scholar] [CrossRef]
- Arora, P.; White, R.E.; Doyle, M. Capacity Fade Mechanisms and Side Reactions in Lithium-Ion Batteries. J. Electrochem. Soc. 1998, 145, 3647–3667. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Liu, K.; Foley, A.; Zülke, A.; Berecibar, M.; Nanini-Maury, E.; Van Mierlo, J.; Hoster, H.E. Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sustain. Energy Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
- Liu, D.; Pang, J.; Zhou, J.; Peng, Y.; Pecht, M. Prognostics for state of health estimation of lithium-ion batteries based on combination Gaussian process functional regression. Microelectron. Reliab. 2013, 53, 832–839. [Google Scholar] [CrossRef]
- Omar, N.; Van Mierlo, J.; Verbrugge, B.; Bossche, P.V.D. Power and life enhancement of battery-electrical double layer capacitor for hybrid electric and charge-depleting plug-in vehicle applications. Electrochim. Acta 2010, 55, 7524–7531. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Dai, H. Estimation of state of health of lithium-ion batteries based on charge transfer resistance considering different temperature and state of charge. J. Energy Storage 2019, 21, 618–631. [Google Scholar] [CrossRef]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
- Liu, H. Research on Estimation of State of Health of Li-Ion Battery Based on Wavelength Spectrum and Time Domain Measurement. Master’s Thesis, Harbin Institute of Technology, Shenzhen, China, 2018. [Google Scholar]
- Ovejas, V.J.; Cuadras, A. Impedance Characterization of an LCO-NMC/Graphite Cell: Ohmic Conduction, SEI Transport and Charge-Transfer Phenomenon. Batteries 2018, 4, 43. [Google Scholar] [CrossRef] [Green Version]
- SPARTACUS Project-Battery 2030. Available online: https://battery2030.eu/research/research-projects/spartacus/ (accessed on 26 March 2021).
- Hosen, S.; Youssef, R.; Kalogiannis, T.; Van Mierlo, J.; Berecibar, M. Battery cycle life study through relaxation and forecasting the lifetime via machine learning. J. Energy Storage 2021, 40, 102726. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Hosen, M.S.; Kalogiannis, T.; Mierlo, J.V.; Berecibar, M. State of Health Estimation of Lithium-Ion Batteries Based on Electrochemical Impedance Spectroscopy and Backpropagation Neural Network. World Electr. Veh. J. 2021, 12, 156. https://doi.org/10.3390/wevj12030156
Zhang S, Hosen MS, Kalogiannis T, Mierlo JV, Berecibar M. State of Health Estimation of Lithium-Ion Batteries Based on Electrochemical Impedance Spectroscopy and Backpropagation Neural Network. World Electric Vehicle Journal. 2021; 12(3):156. https://doi.org/10.3390/wevj12030156
Chicago/Turabian StyleZhang, Sihan, Md Sazzad Hosen, Theodoros Kalogiannis, Joeri Van Mierlo, and Maitane Berecibar. 2021. "State of Health Estimation of Lithium-Ion Batteries Based on Electrochemical Impedance Spectroscopy and Backpropagation Neural Network" World Electric Vehicle Journal 12, no. 3: 156. https://doi.org/10.3390/wevj12030156
APA StyleZhang, S., Hosen, M. S., Kalogiannis, T., Mierlo, J. V., & Berecibar, M. (2021). State of Health Estimation of Lithium-Ion Batteries Based on Electrochemical Impedance Spectroscopy and Backpropagation Neural Network. World Electric Vehicle Journal, 12(3), 156. https://doi.org/10.3390/wevj12030156









