Electronic Differential System Based on Adaptive SMC Combined with QP for 4WID Electric Vehicles
Abstract
:1. Introduction
2. Mathematical Modeling of the Vehicle
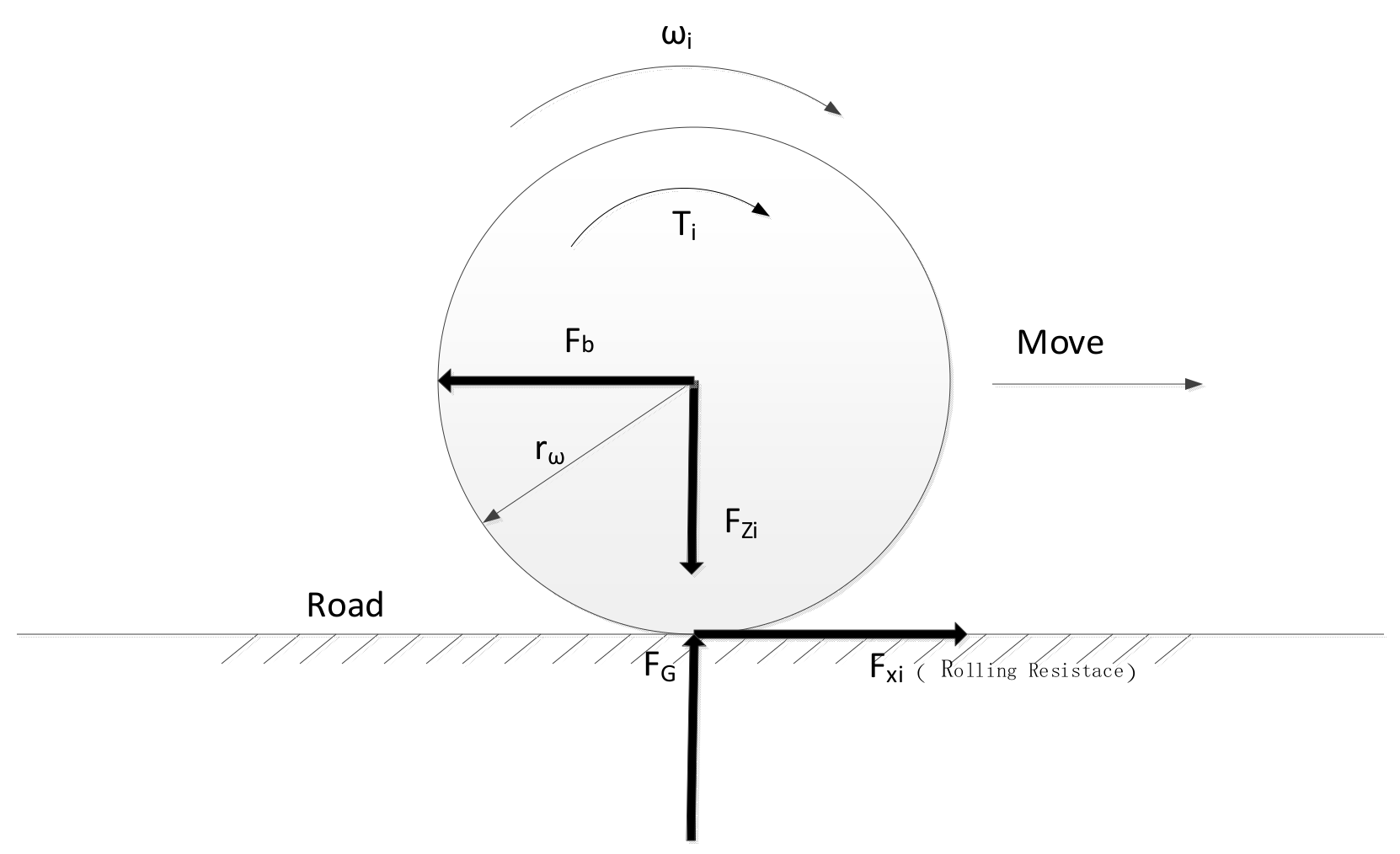
2.1. Vehicle Dynamic Modelling
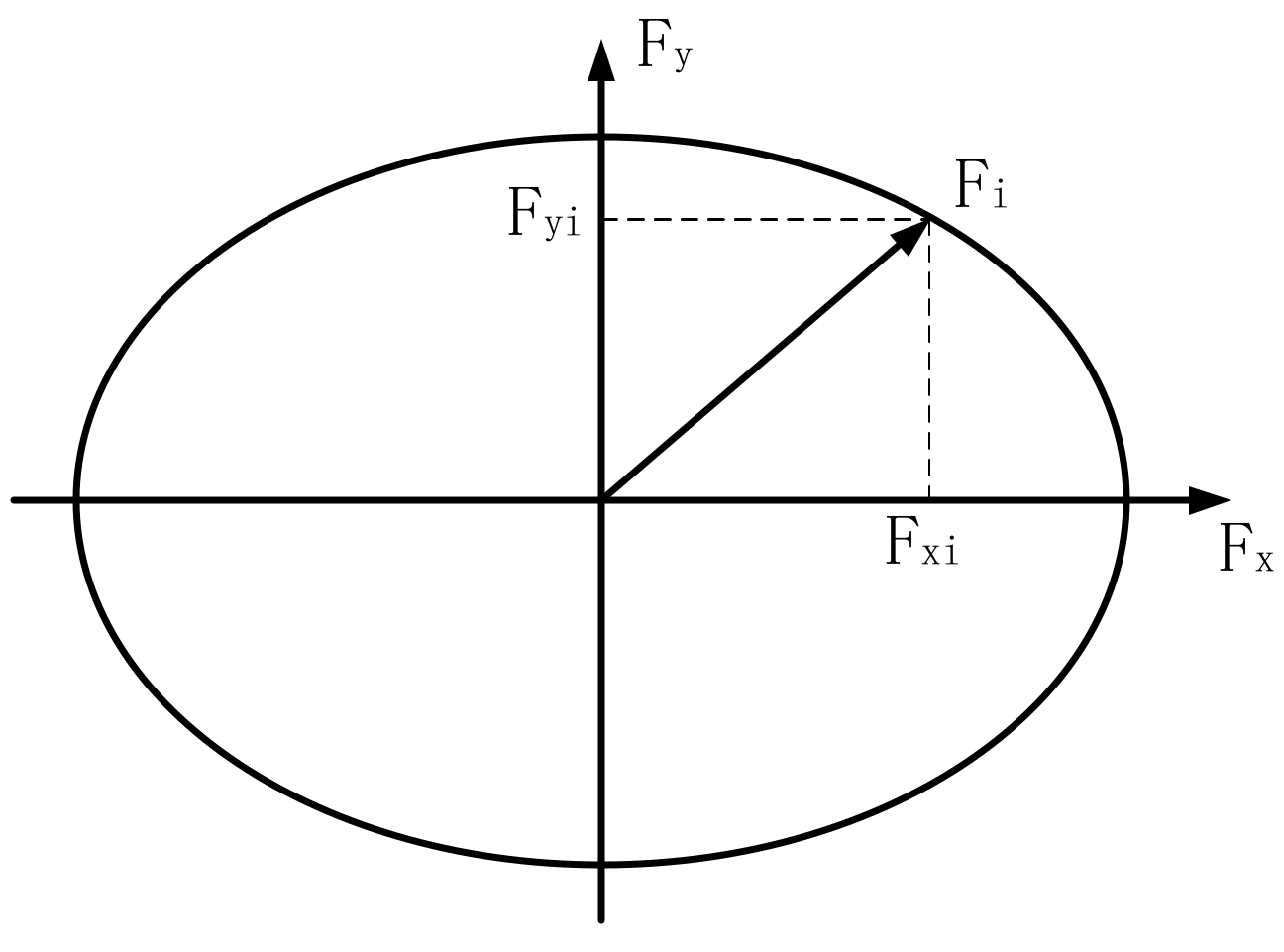
2.2. Tire Model
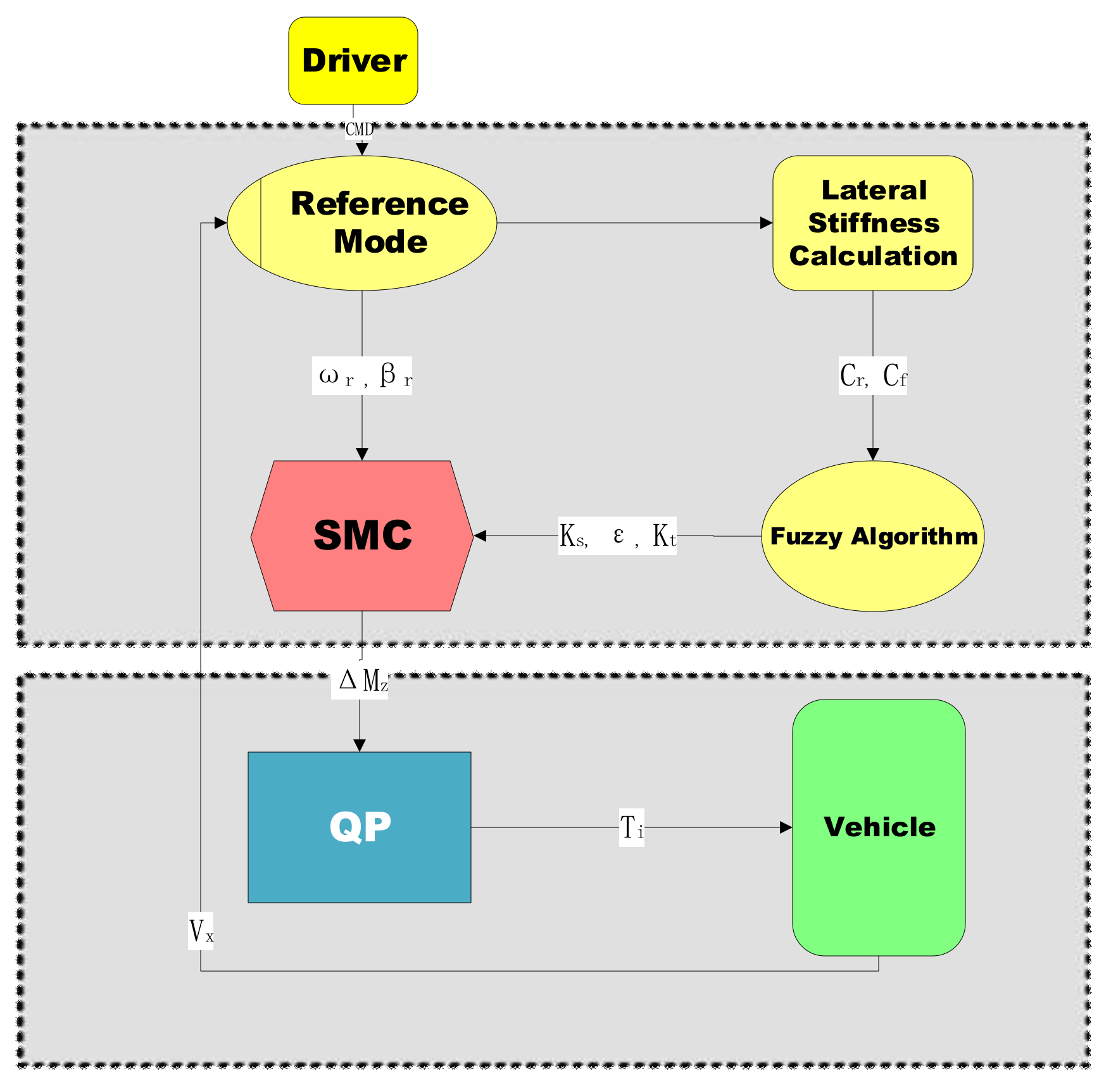
3. Controller Designs
3.1. Reference Model
3.2. Adaptive SMC
3.3. Torque Allocation
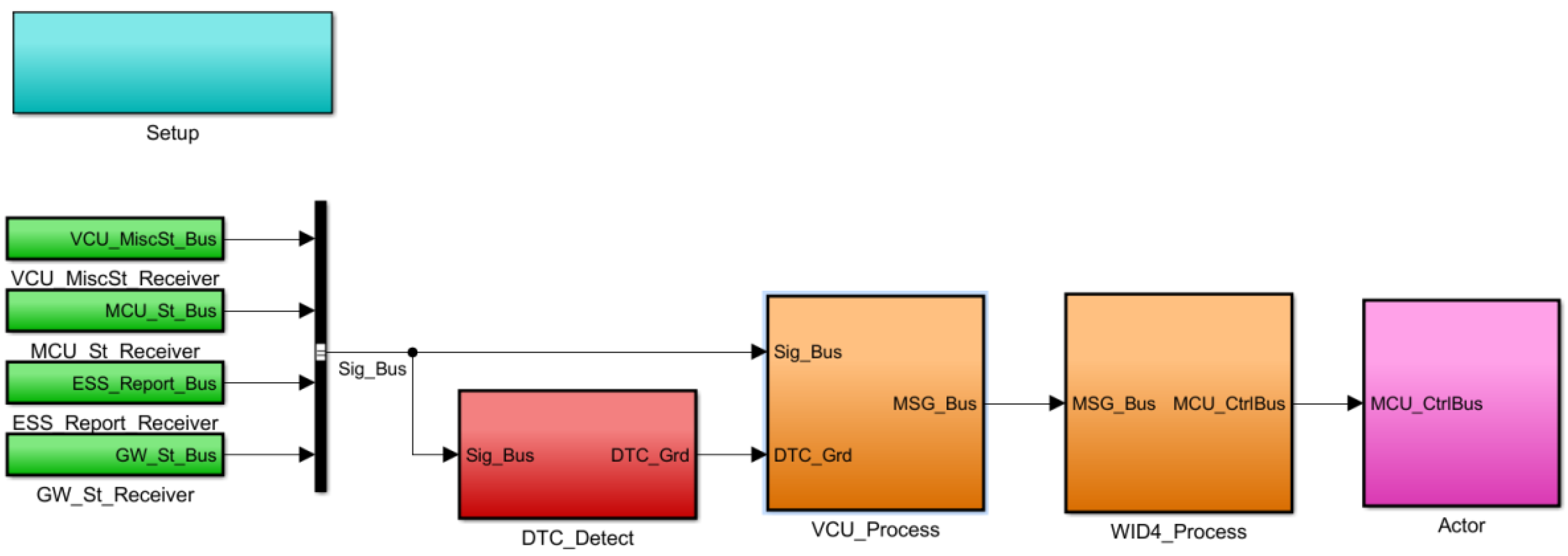
4. Simulation and Experimental Validation
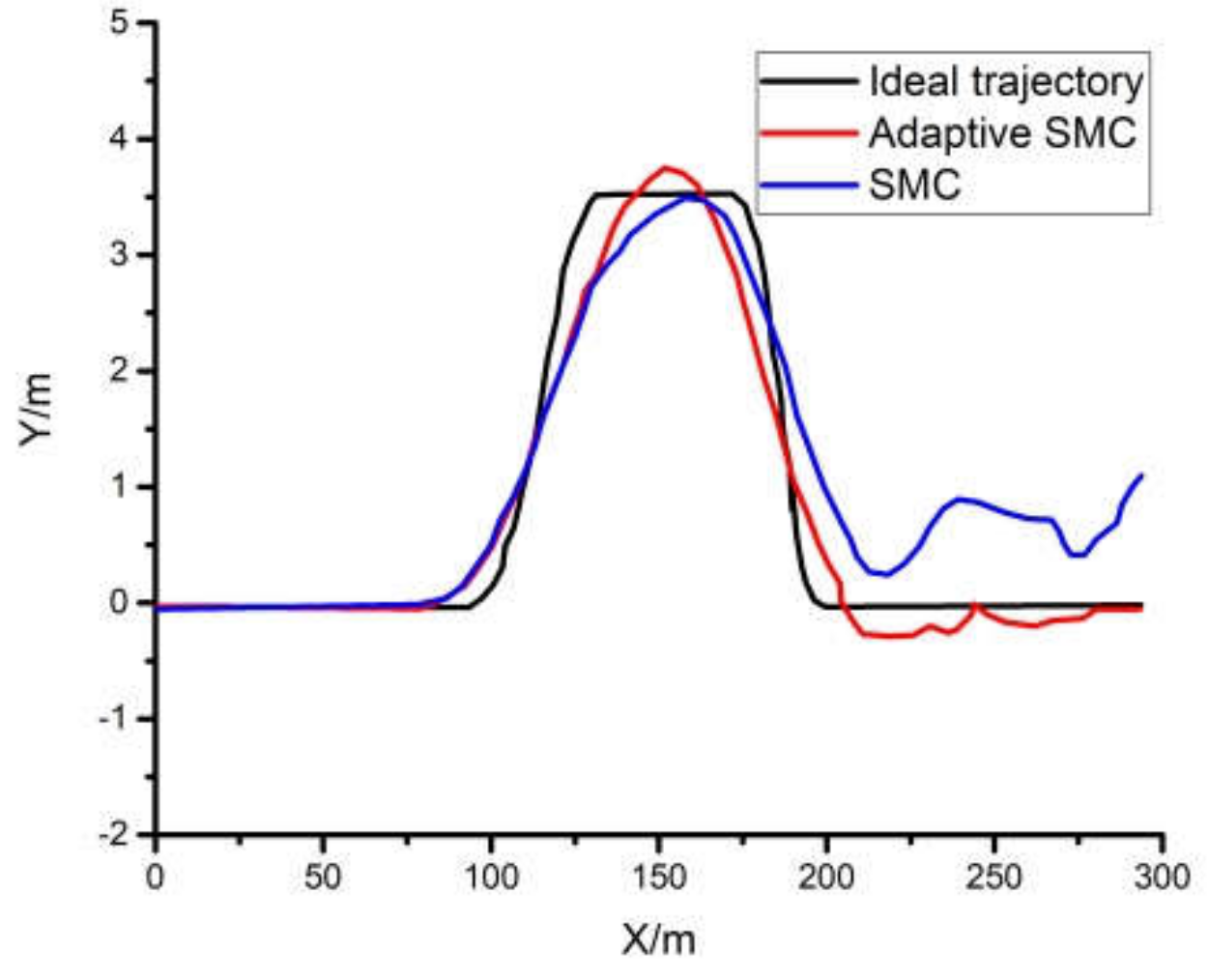
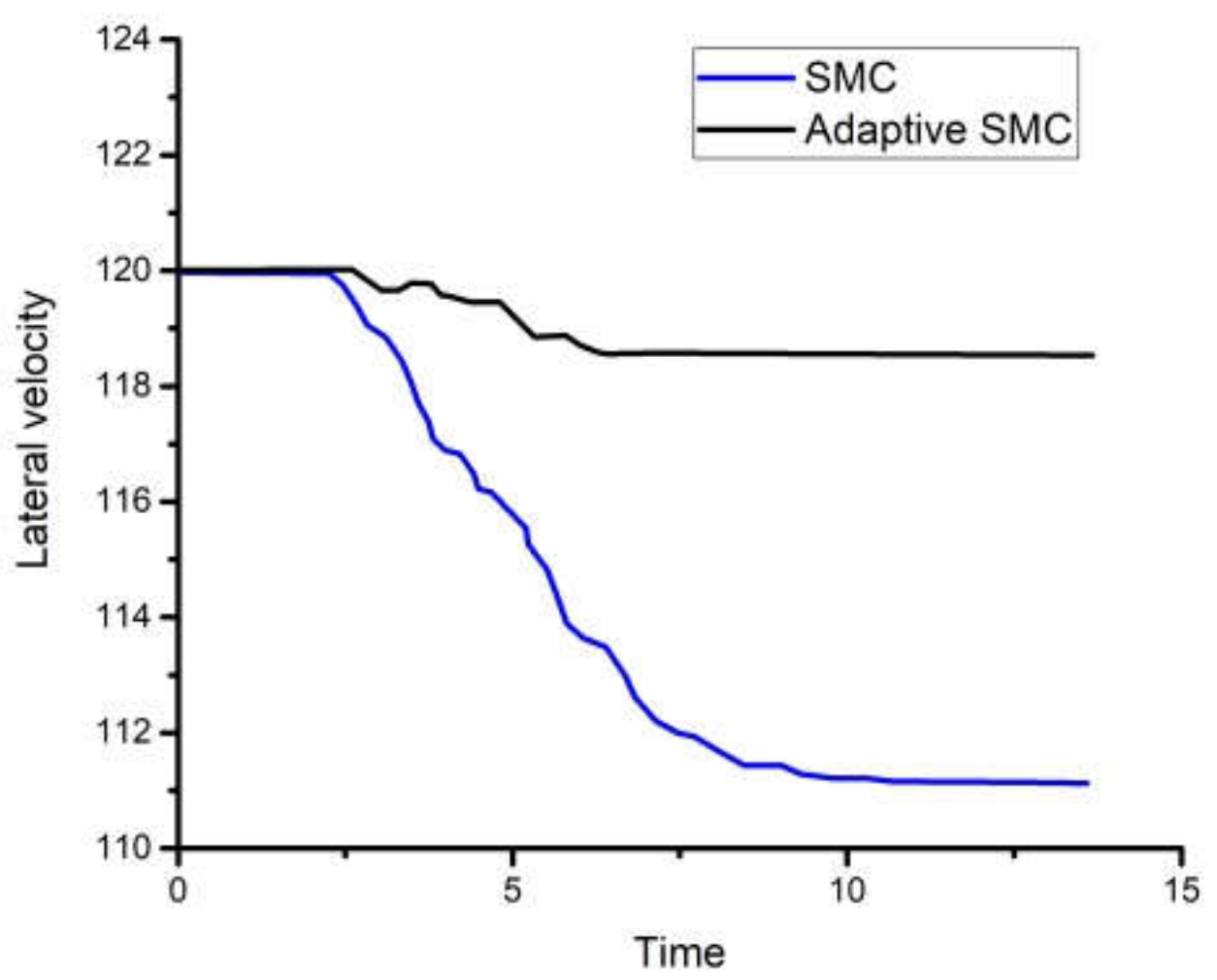
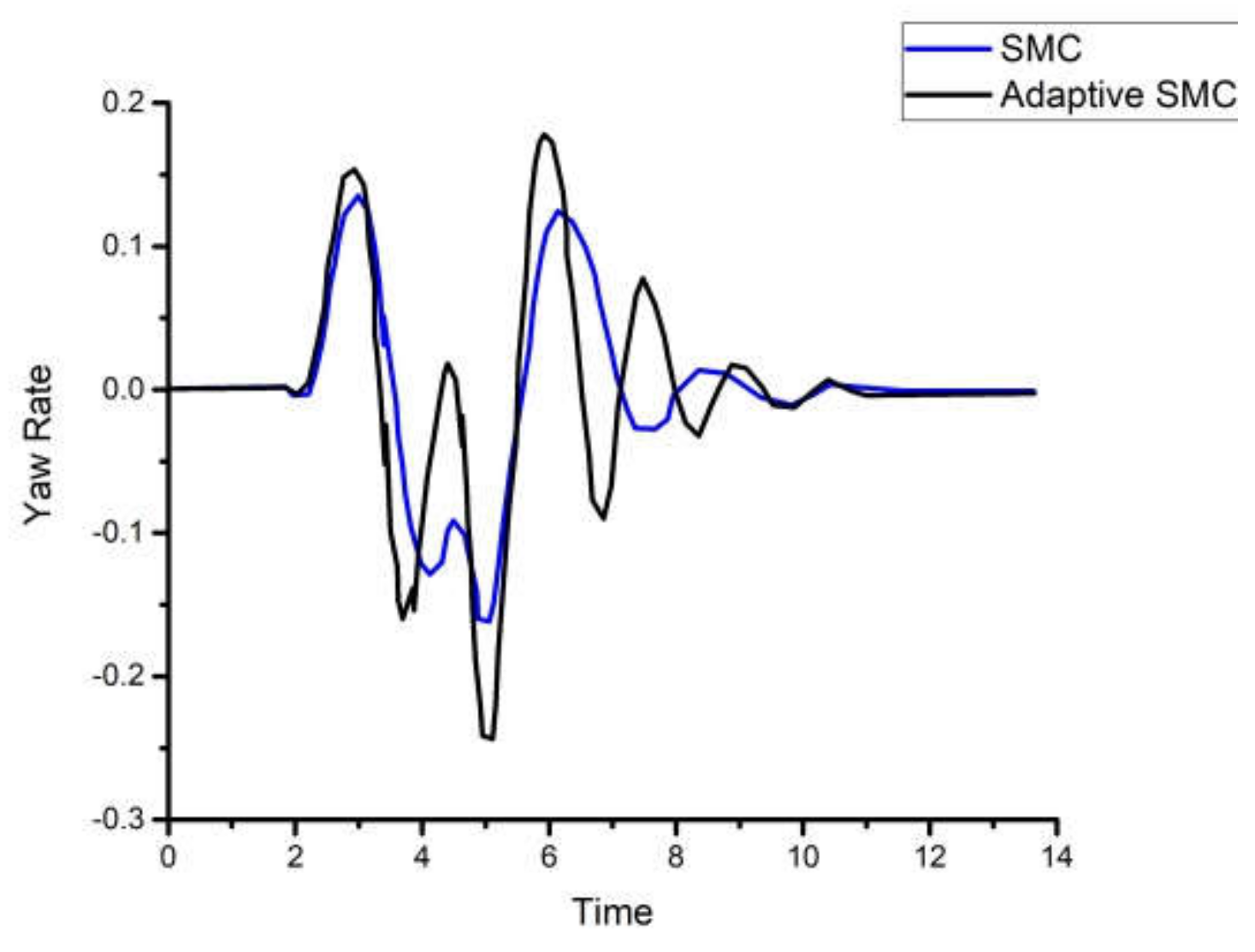
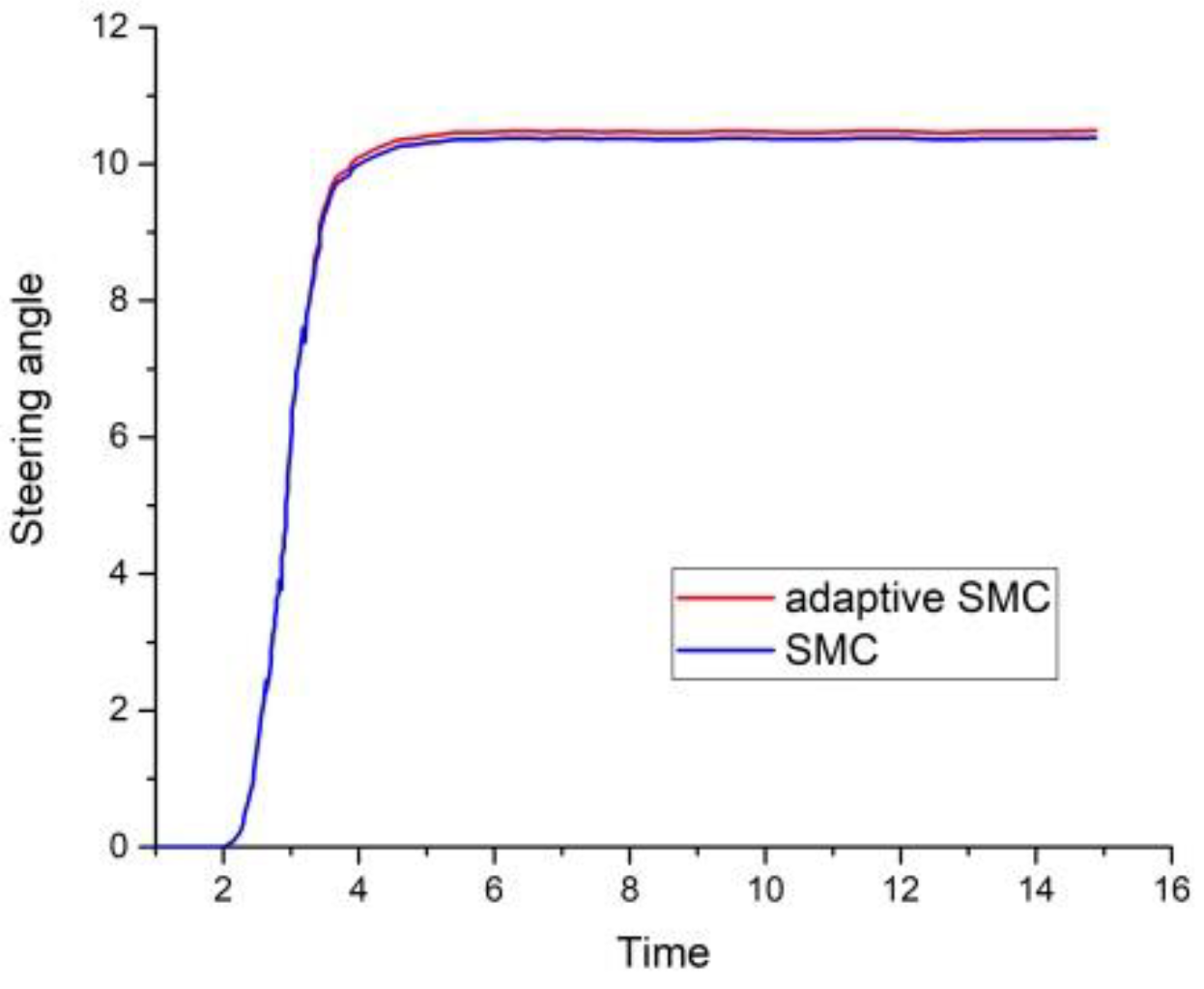
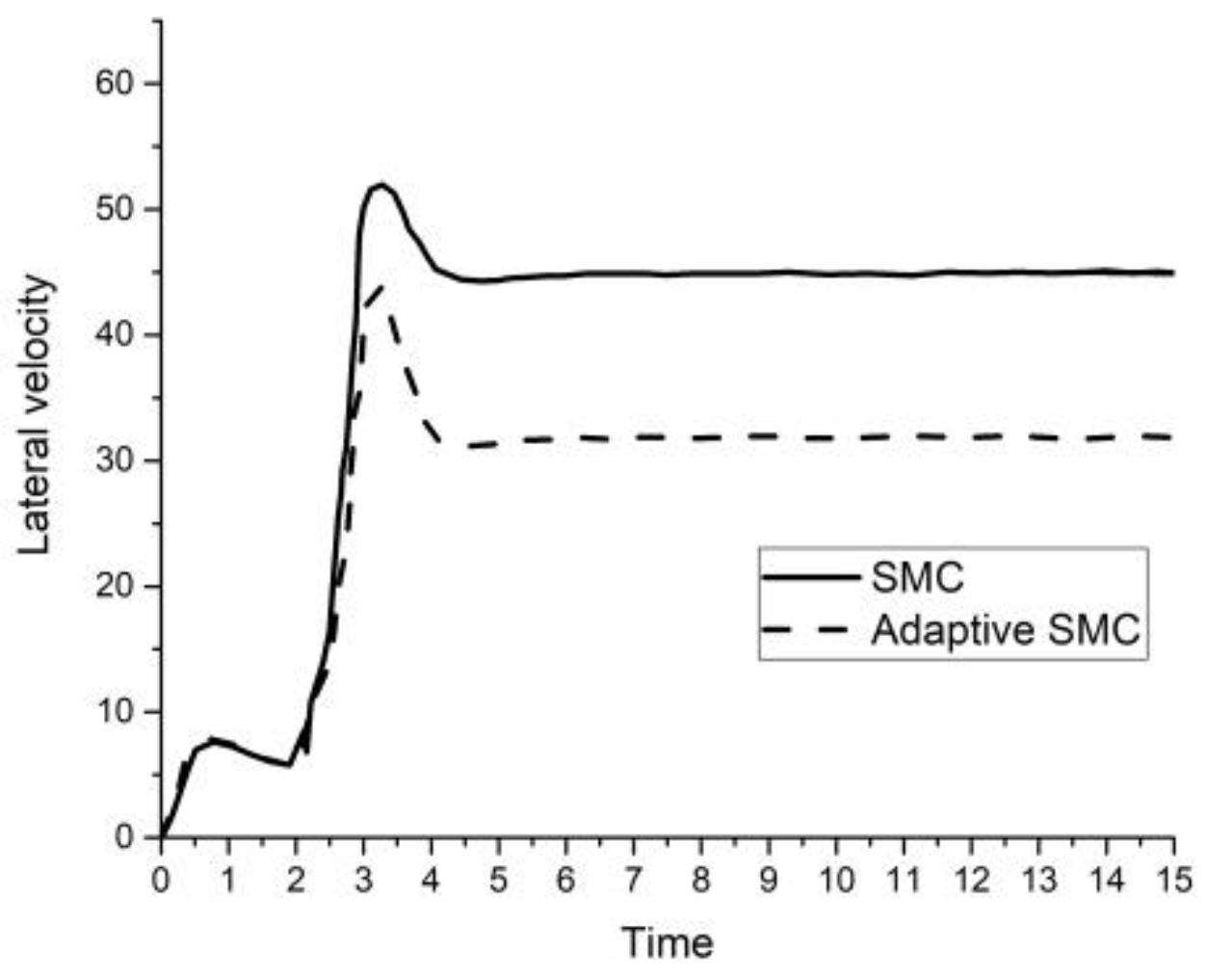
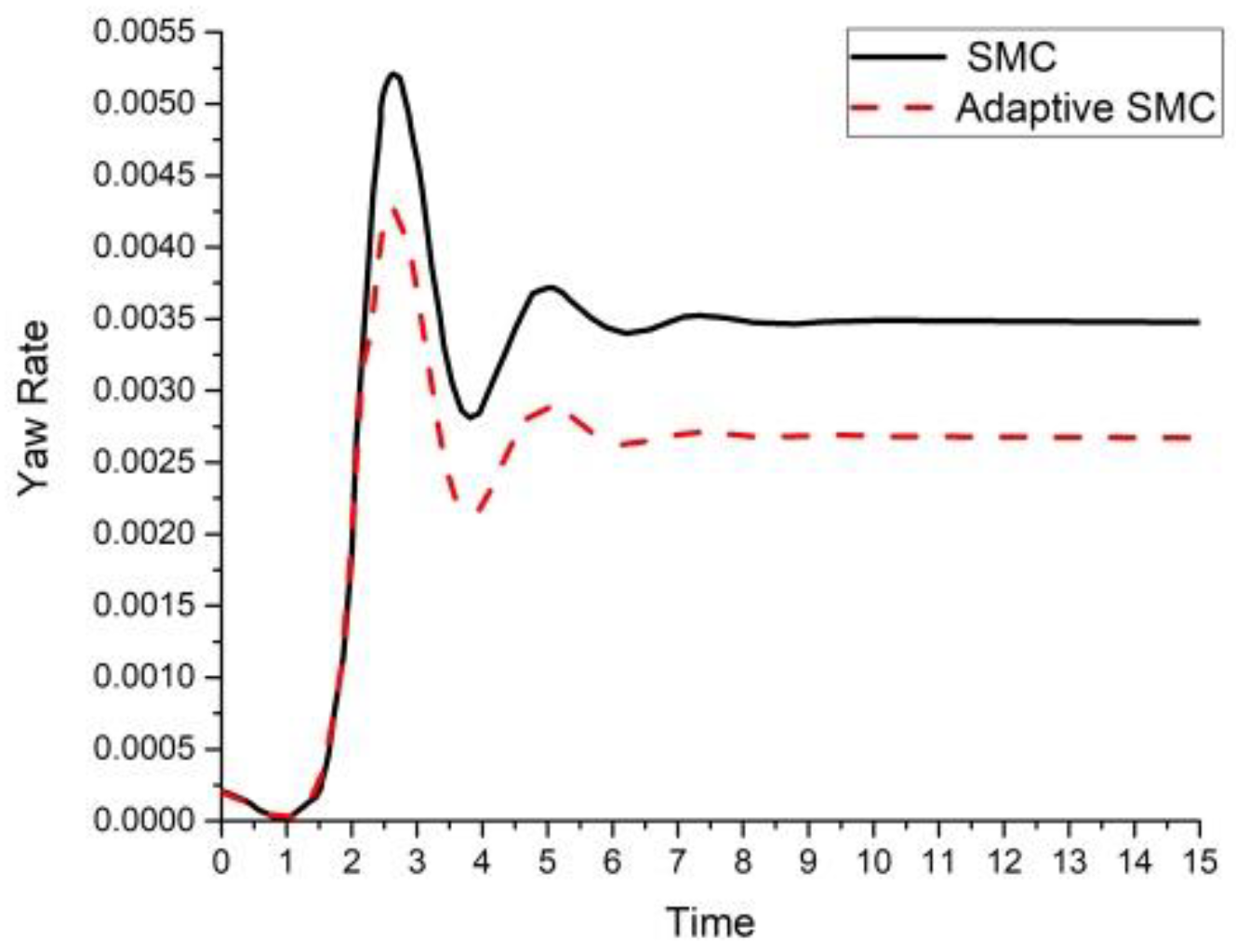
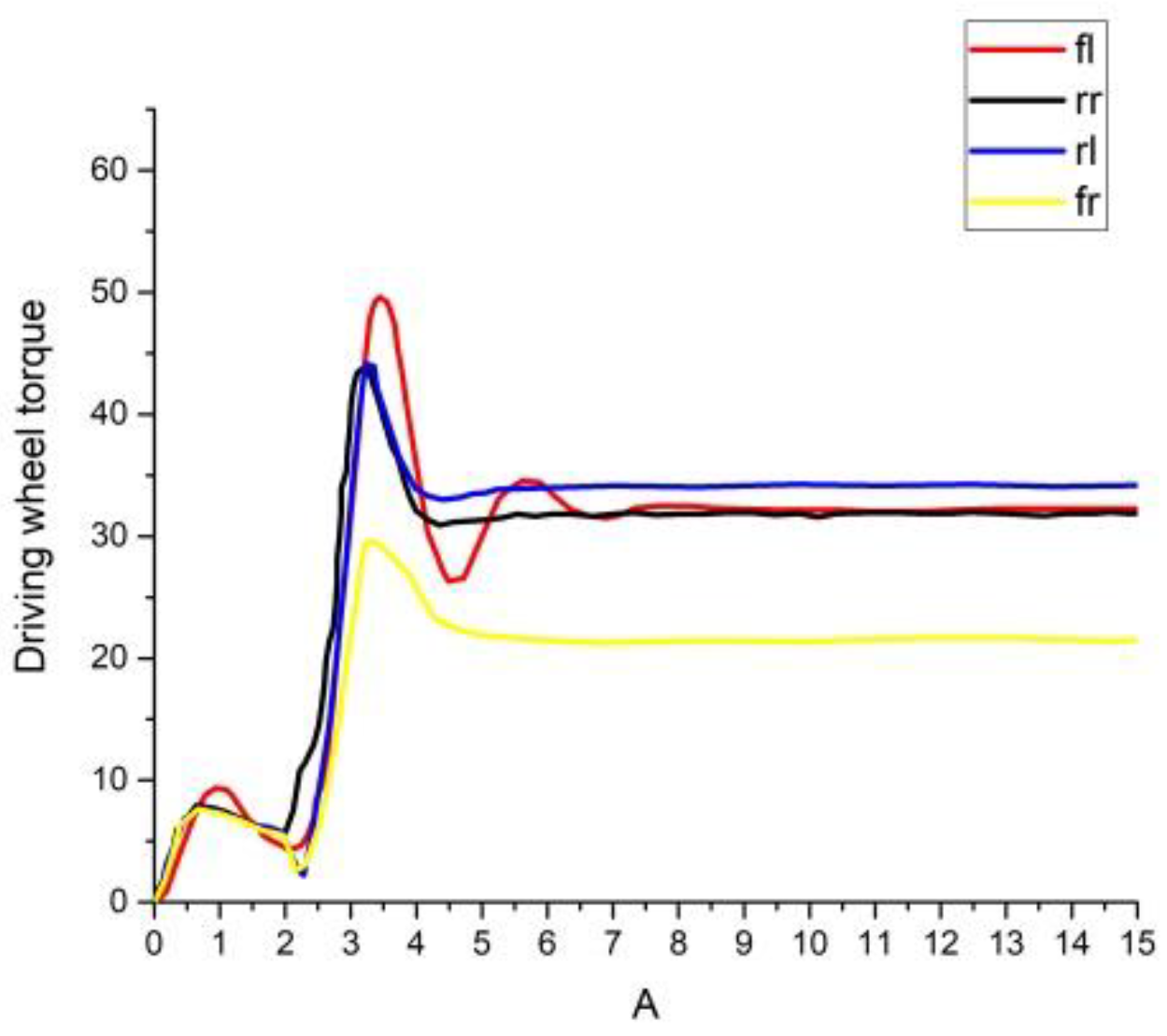
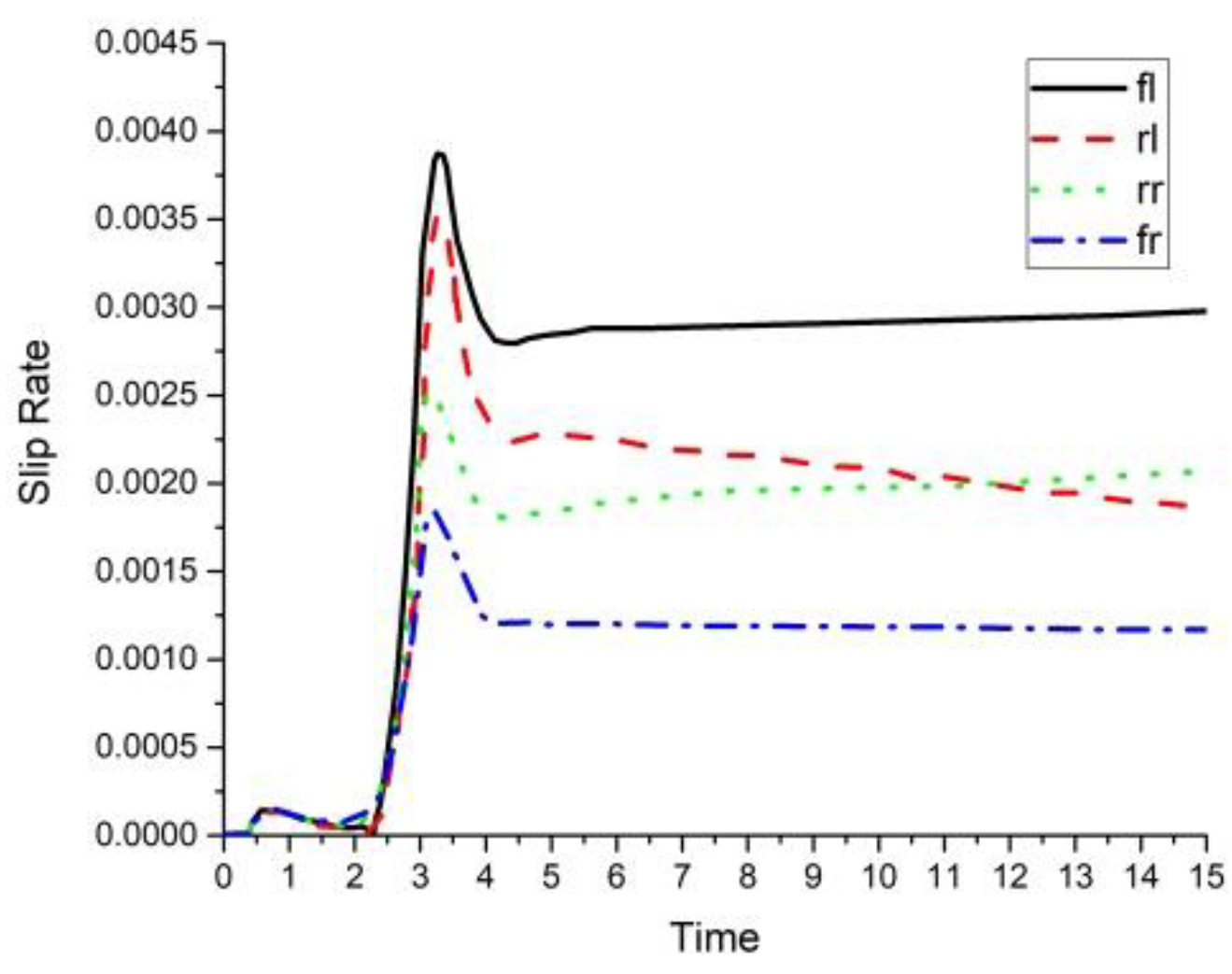
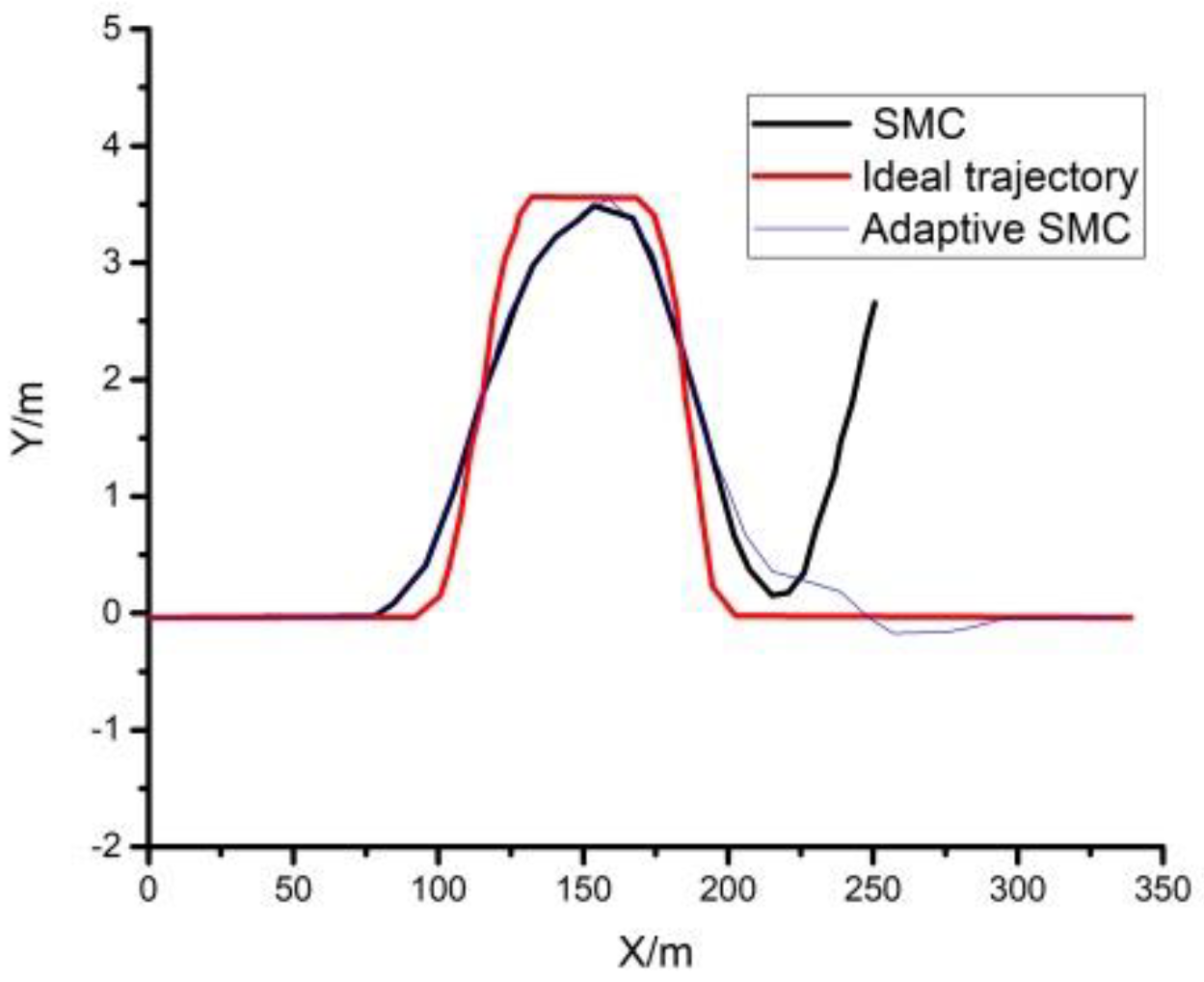
4.1. Numerical Simulations
4.2. Experimental Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Zhao, X.; Yu, Q.; Yu, M.; Tang, Z. Research on an equal power allocation electronic differential system for electric vehicle with dual−wheeled−motor front drive based on a wavelet controller. Adv. Mech. Eng. 2018, 10, 1687814018760039. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Zhang, H. Coupling control strategy of force and displacement for electric differential power steering system of electric vehicle with motorized wheels. IEEE Trans. Veh. Technol. 2018, 67, 8118–8128. [Google Scholar] [CrossRef]
- He, R.; Wang, J.-C. Vertical vibration control of an in-wheel motor-driven electric vehicle using an in-wheel active vibration system. Asian J. Control 2018, 22, 879–896. [Google Scholar] [CrossRef]
- Duan, M.; Sun, M.J.; Gang, L.I. Study on electronic differential control of four wheel drive in−wheel motor electric vehicle. Mach. Tool Hydraul. 2015, 24, 60–66. [Google Scholar]
- Wang, J.-C.; He, R. Varying charge voltage in the steps control method of the coordinated ABS for in-wheel motors driven electric vehicles based on an improved LQG scheme. IEEE Access 2018, 6, 15039–15050. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J. Design and evaluation on electric differentials for over actuated electric ground vehicles with four independent in−wheel motors. IEEE Trans. Veh. Technol. 2012, 61, 1534–1542. [Google Scholar] [CrossRef]
- Hartani, K.; Merah, A.; Draou, A. Stability Enhancement of Four−in−Wheel Motor−Driven Electric Vehicles Using an Electric Differential System. J. Power Electron. 2015, 15, 1244–1255. [Google Scholar] [CrossRef] [Green Version]
- Hua, Y.; Jiang, H.; Geng, G. Electronic differential control of 2WD electric vehicle considering steering stability. In Proceedings of the Advances in Materials, Machinery, Electronics, Tianjin, China, 10–11 June 2017; AIP Conference Proceedings: Beijing, China, March 2017; Volume 1820, pp. 1–8. [Google Scholar]
- Spentzas, K.N.; Alkhazali, I. Generalization of the concept of electronic differential. Forschung im Ingenieurwesen 2001, 66, 273–278. [Google Scholar] [CrossRef]
- Daya, F.J.; Sanjeevikumar, P.; Blaabjerg, F.; Wheeler, P.W.; Olorunfemi Ojo, J.; Ertas, A.H. Analysis of Wavelet Controller for Robustness in Electronic Differential of Electric Vehicles: An Investigation and Numerical Developments. Electr. Mach. Power Syst. 2016, 44, 763–773. [Google Scholar] [CrossRef] [Green Version]
- Perez−Pinal, F.J.; Cervantes, I.; Emadi, A. Stability of an electric differential for traction applications. IEEE Trans. Veh. Technol. 2009, 58, 3224–3233. [Google Scholar] [CrossRef]
- Hartani, K.; Bourahla, M.; Miloud, Y.; Sekour, M. Electronic differential with direct torque fuzzy control for vehicle propulsion system. Turk. J. Electr. Eng. Comput. Sci. 2009, 17, 21–38. [Google Scholar]
- Ozkop, E.; Altas, I.H.; Okumus, H.I.; Sharaf, A.M. A fuzzy logic sliding mode controlled electronic differential for a direct wheel drive EV. Int. J. Electron. 2015, 102, 1919–1942. [Google Scholar] [CrossRef]
- Kim, D.; Hwang, S.; Kim, H. Vehicle Stability Enhancement of Four-Wheel-Drive Hybrid Electric Vehicle Using Rear Motor Control. IEEE Trans. Veh. Technol. 2008, 57, 727–735. [Google Scholar]
- Yildirim, M.; Catalbas, M.C.; Gulten, A.; Kurum, H. Modeling and estimation parameters of electronic differential system for an electric vehicle using radial basis neural network. In Proceedings of the IEEE International Conference on Environment & Electrical Engineering, Florence, Italy, 7–10 June 2016; pp. 1–5. [Google Scholar]
- Yin, D.; Shan, D.; Hu, J.-S. A study on the control performance of electronic differential system for four−wheel drive electric vehicles. Appl. Sci. 2017, 7, 74. [Google Scholar] [CrossRef] [Green Version]
- Jansen, S.T.H.; Oosten, J.J.M.; Pacejka, H.B. Modelling and Simulation of Tyre Behaviour in MADYMO: The Magic Formula Tyre Model; TNO Wegtransportmiddelen; TNO: The Hague, The Netherlands, 1996. [Google Scholar]
- Kozłowski, M.; Choromański, W. Dynamics simulation studies on the electric city car with an electromechanical differential and the rear wheels drive. Bull. Pol. Acad. Sci. Tech. Sci. 2013, 61, 661–673. [Google Scholar] [CrossRef] [Green Version]
- Haddoun, A.; Benbouzid, M.; Diallo, D.; Abdessemed, R.; Ghouili, J.; Srairi, K. Modeling, analysis, and neural network control of an EV electrical differential. IEEE Trans. Ind. Electron. 2008, 55, 2286–2294. [Google Scholar] [CrossRef] [Green Version]
- Zhu, C.Q.; Wu, S.; Yang, Y.Z. Research on Electronic Differential Speed Control for In-wheel Motor Drive Electric Vehicle. Appl. Mech. Mater. 2014, 525, 337–341. [Google Scholar] [CrossRef]









| NB | NS | ZO | PS | PB | ||
|---|---|---|---|---|---|---|
| N | ON | ON | ON | AS | AB | |
| ZO | BS | ON | ON | AB | AB | |
| PS | BS | BS | ON | AS | AB | |
| PM | BB | BS | ON | AS | AS | |
| PB | BB | BS | ON | ON | AS | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Liu, Z.; Chen, Q. Electronic Differential System Based on Adaptive SMC Combined with QP for 4WID Electric Vehicles. World Electr. Veh. J. 2021, 12, 126. https://doi.org/10.3390/wevj12030126
Zhang W, Liu Z, Chen Q. Electronic Differential System Based on Adaptive SMC Combined with QP for 4WID Electric Vehicles. World Electric Vehicle Journal. 2021; 12(3):126. https://doi.org/10.3390/wevj12030126
Chicago/Turabian StyleZhang, Wenjun, Zhuxing Liu, and Qingzhang Chen. 2021. "Electronic Differential System Based on Adaptive SMC Combined with QP for 4WID Electric Vehicles" World Electric Vehicle Journal 12, no. 3: 126. https://doi.org/10.3390/wevj12030126
APA StyleZhang, W., Liu, Z., & Chen, Q. (2021). Electronic Differential System Based on Adaptive SMC Combined with QP for 4WID Electric Vehicles. World Electric Vehicle Journal, 12(3), 126. https://doi.org/10.3390/wevj12030126





