Two-Stage Multi-Period Coordinated Load Restoration Strategy for Distribution Network Based on Intelligent Route Recommendation of Electric Vehicles
Abstract
:1. Introduction
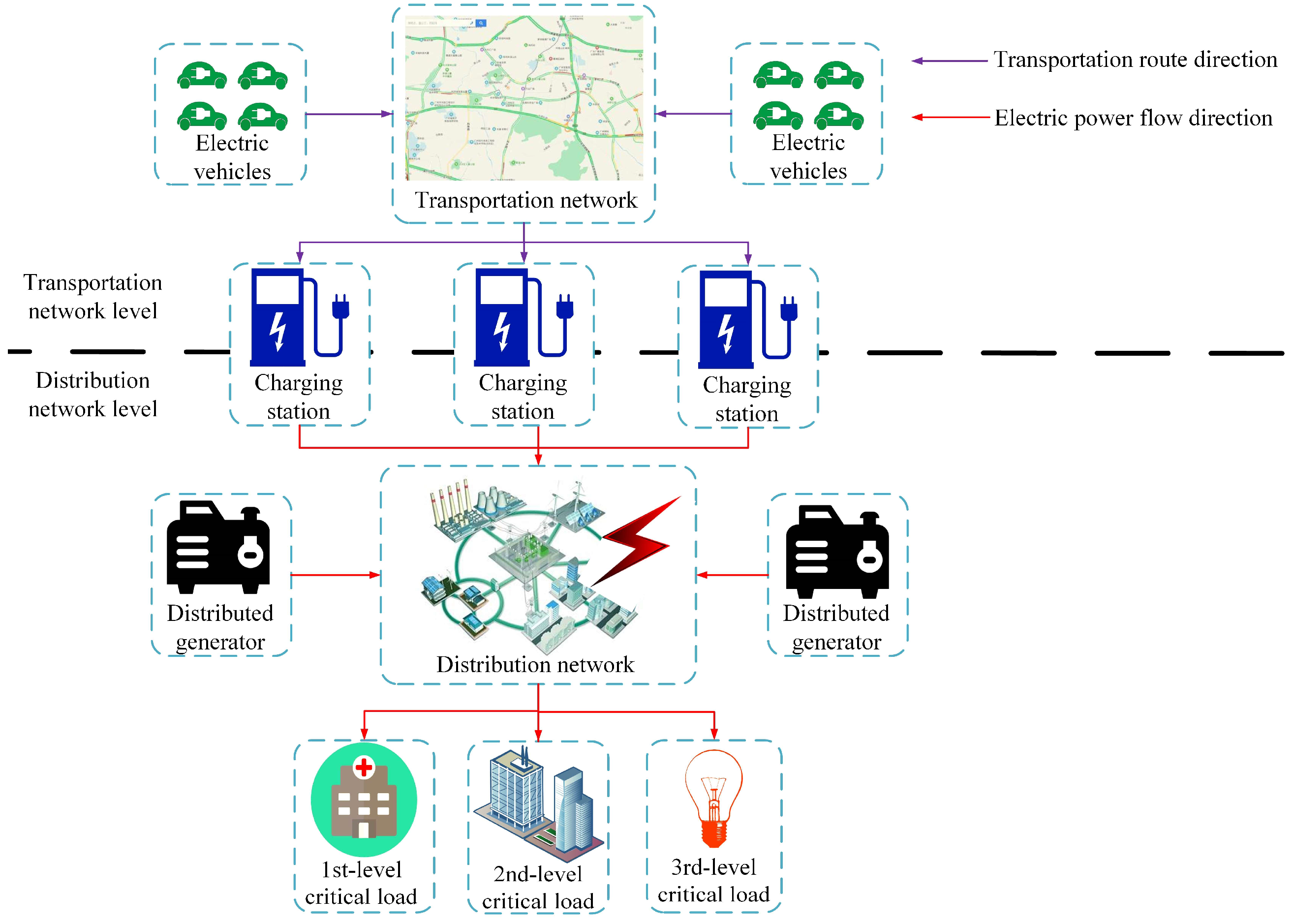
2. The Configuration
3. The Mathematical Modelling
3.1. Multi-Period Coordinated Load Restoration Model
3.1.1. Objective Function
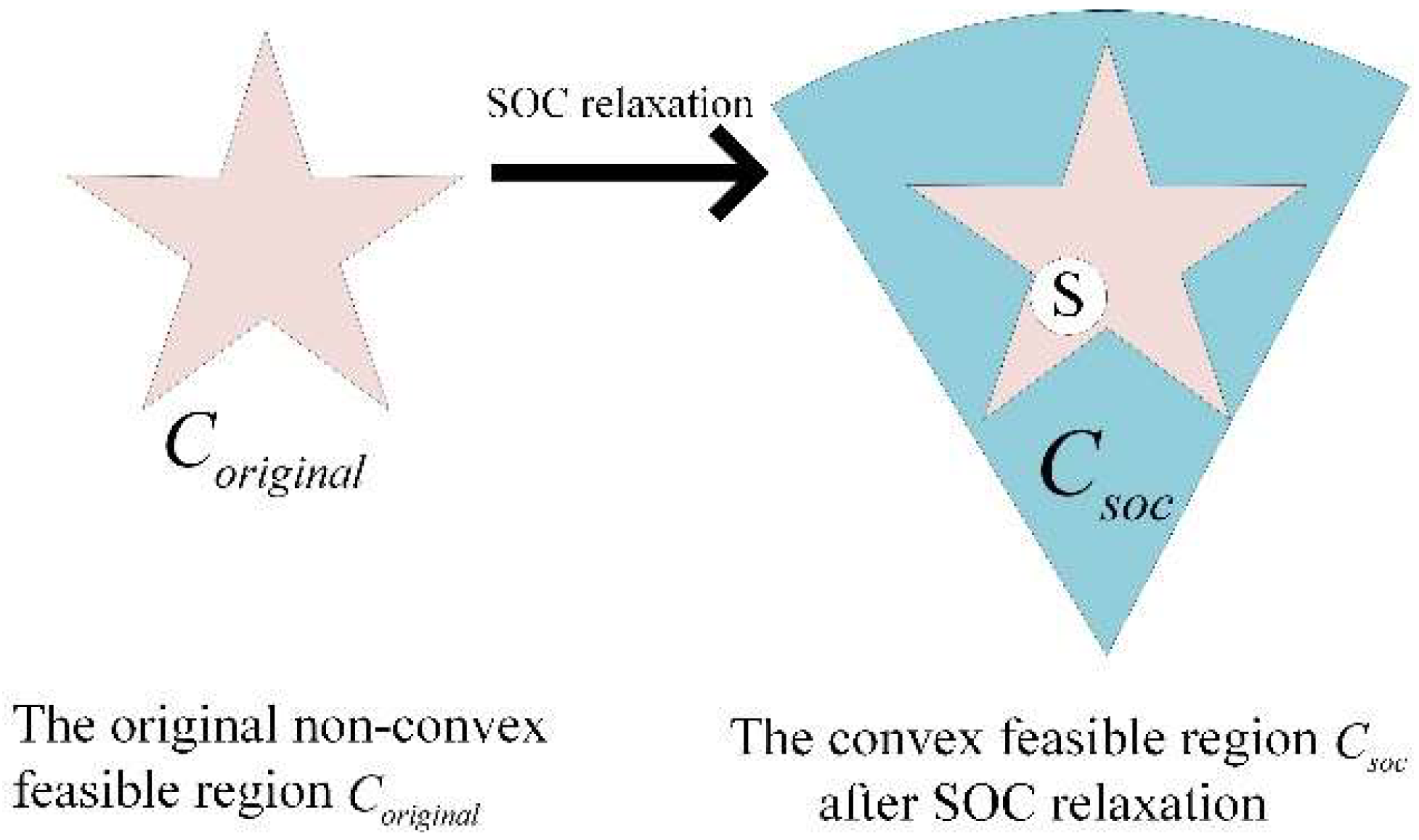
3.1.2. Constraints
- The Radial Topology Constraints of the Distribution Network
- The Operation Constraints of the Distribution Network
- The Energy Limit Constraints of Power Supply Sources
- The Constraints of the Switching Number of Load States
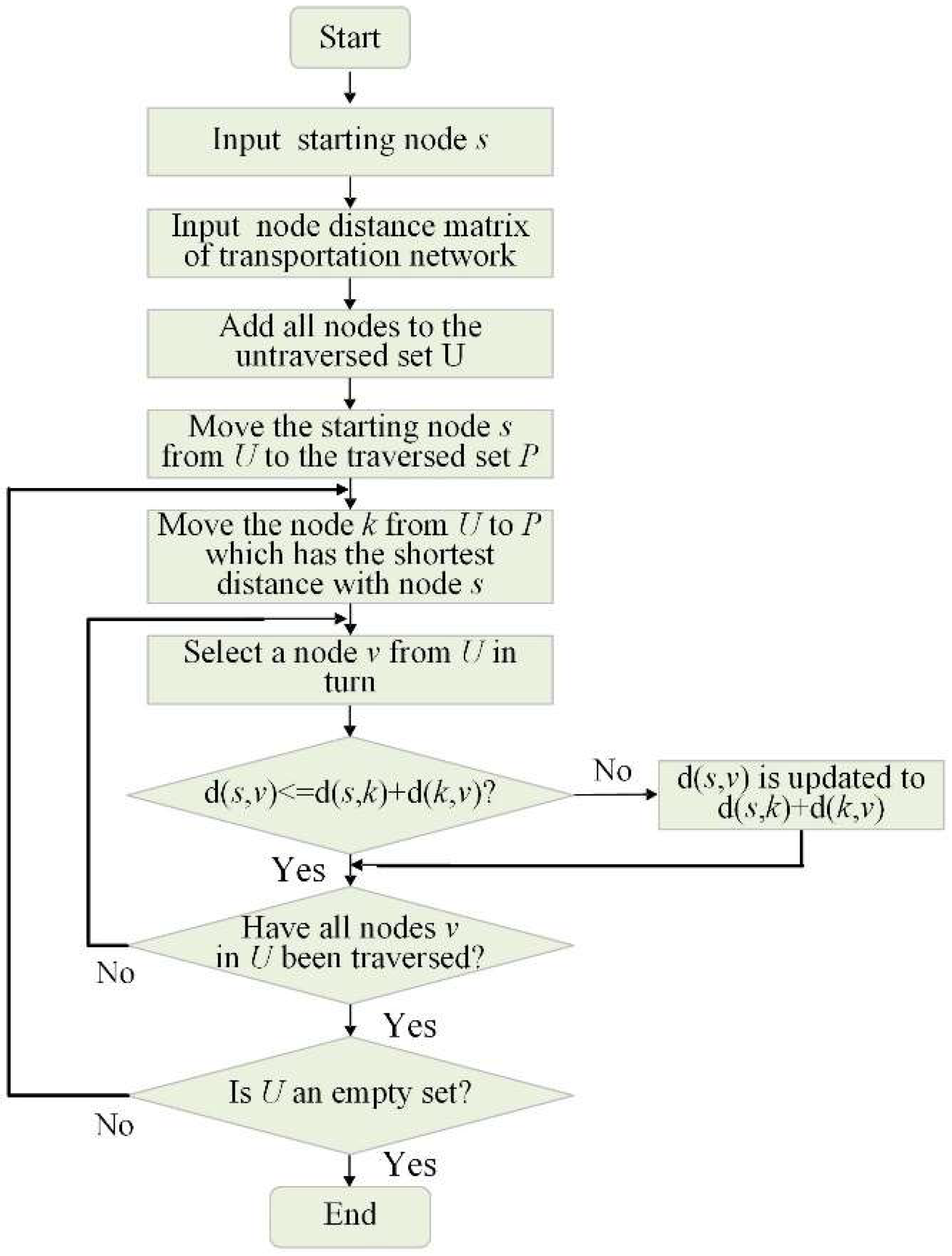
3.2. The Intelligent Recommendation Model of The Shortest Duration Route of EVs
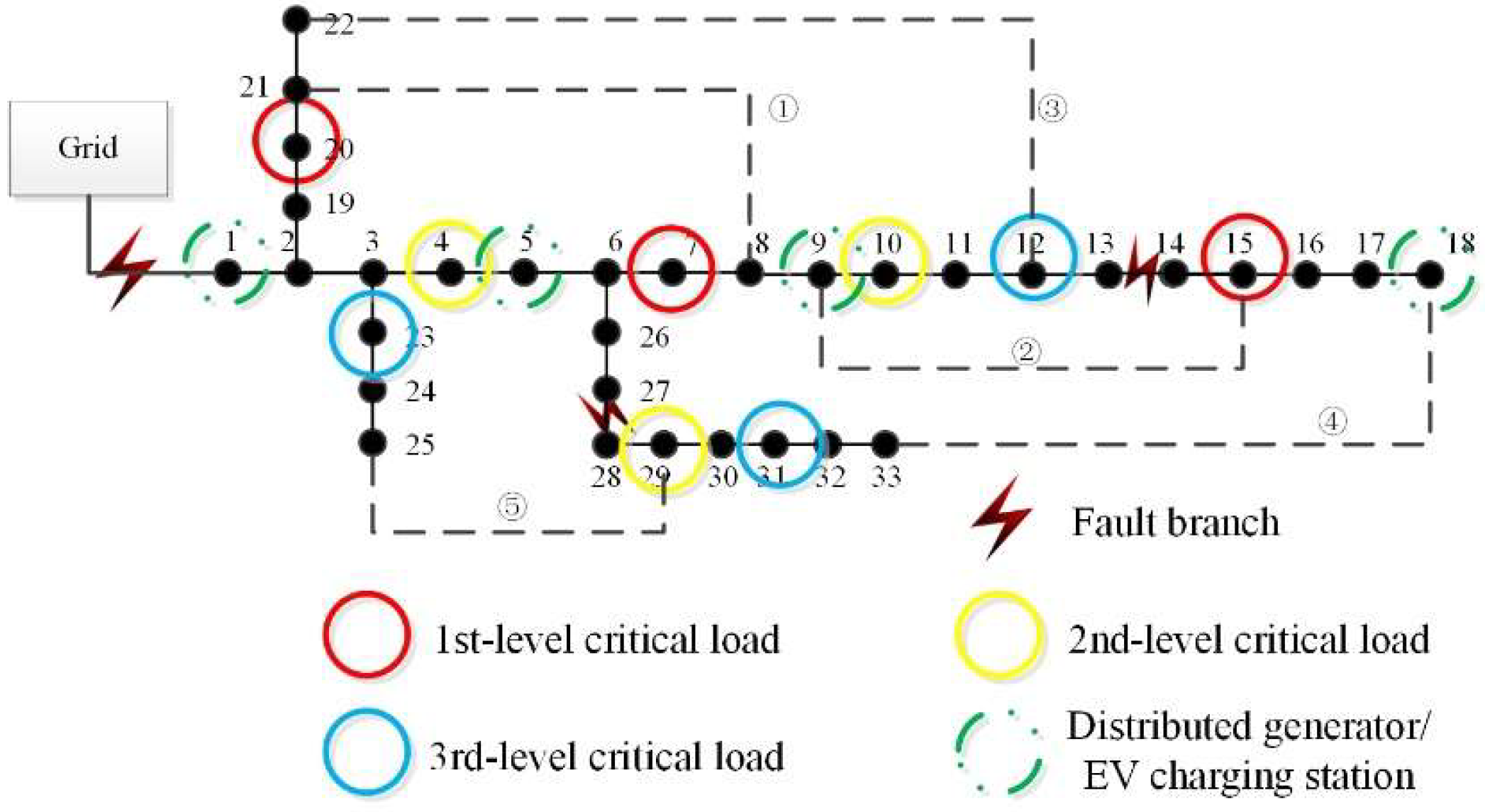
4. Case Study
4.1. Analysis of Critical Load Restoration
4.2. Analysis of Optimal Route Recommendation of EVs
5. Conclusions
- Idle EVs are a large number of usable power generation resources, and reasonable use of these resources during a blackout is very significant. This paper realizes the optimal space assignment of EV power supply resources and verifies that it is helpful to the load restoration of the distribution network.
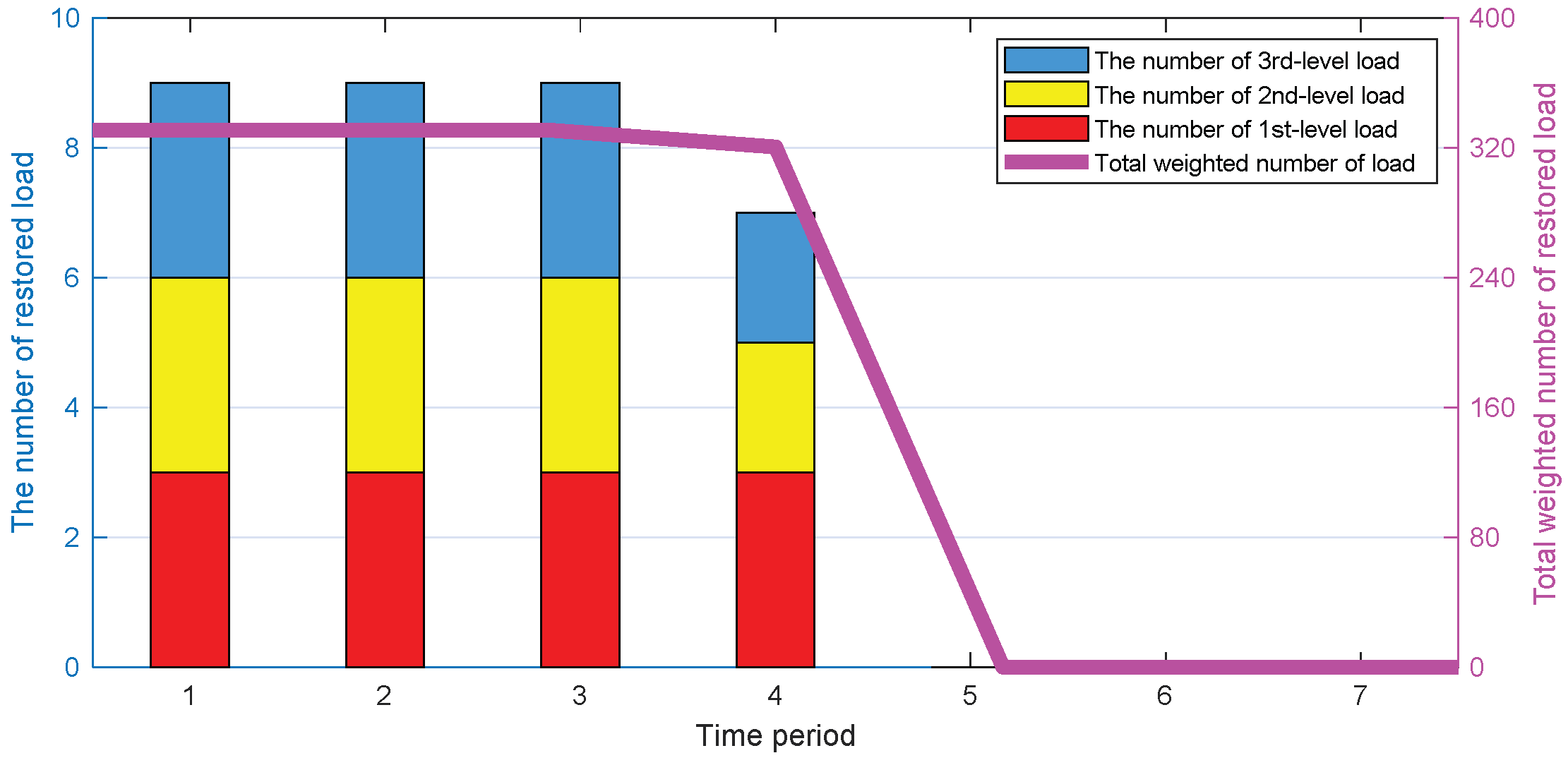
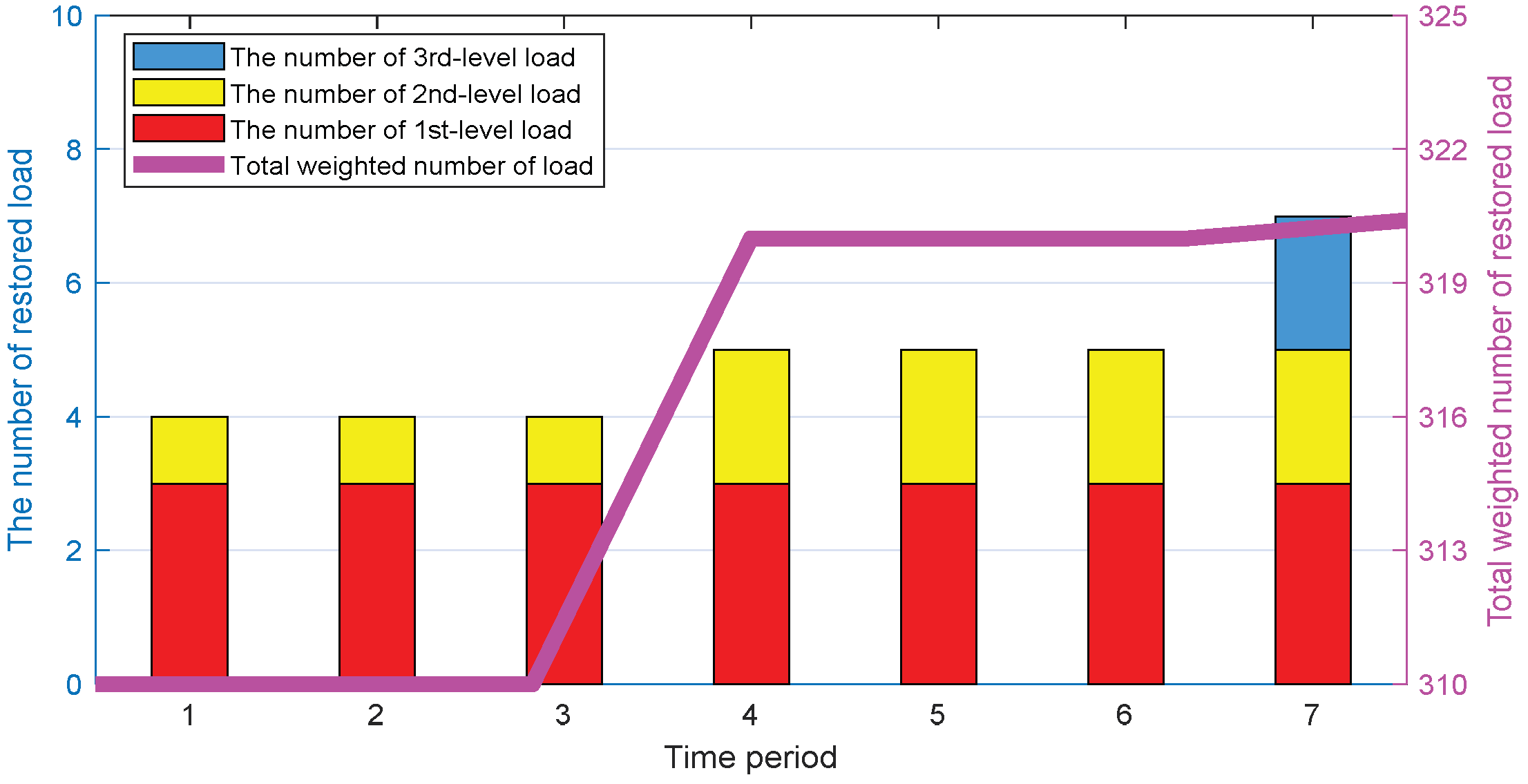
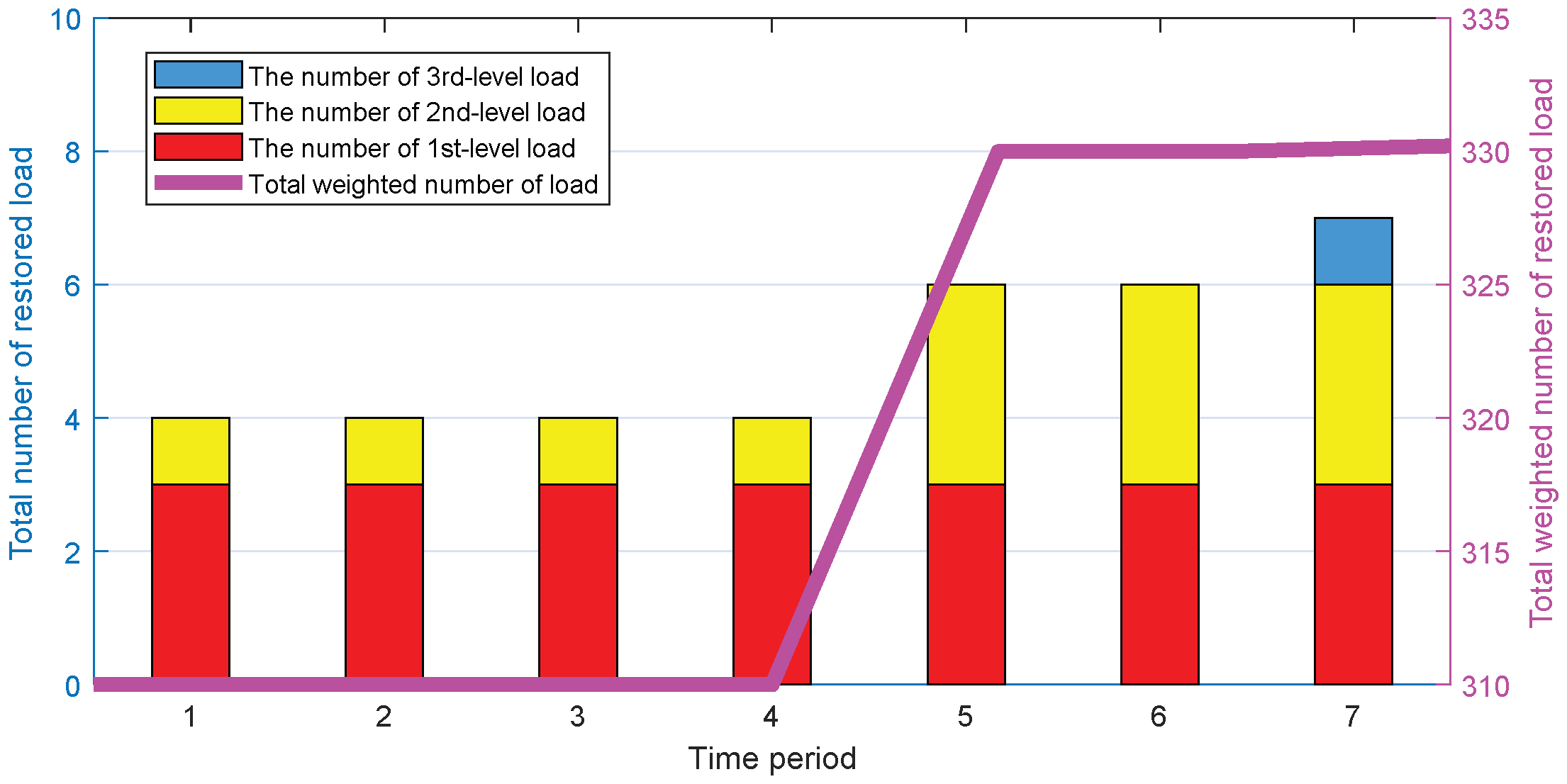
- By comparing the multi-period coordinated load restoration strategy and the single-time section load restoration strategy, this paper verifies that the multi-period coordinated load restoration model used in the proposed strategy can better allocate the limited energy on time scale to extend the weighted power supply time of the critical loads.
- The strategy proposed in this paper is more advantageous than the other two strategies in reducing the total network loss of the system, increasing the minimum voltage magnitude, increasing average voltage, and reducing the standard deviation of voltage, which indicates the proposed strategy also has a good effect in improving the economy and safety of the distribution network during load restoration.
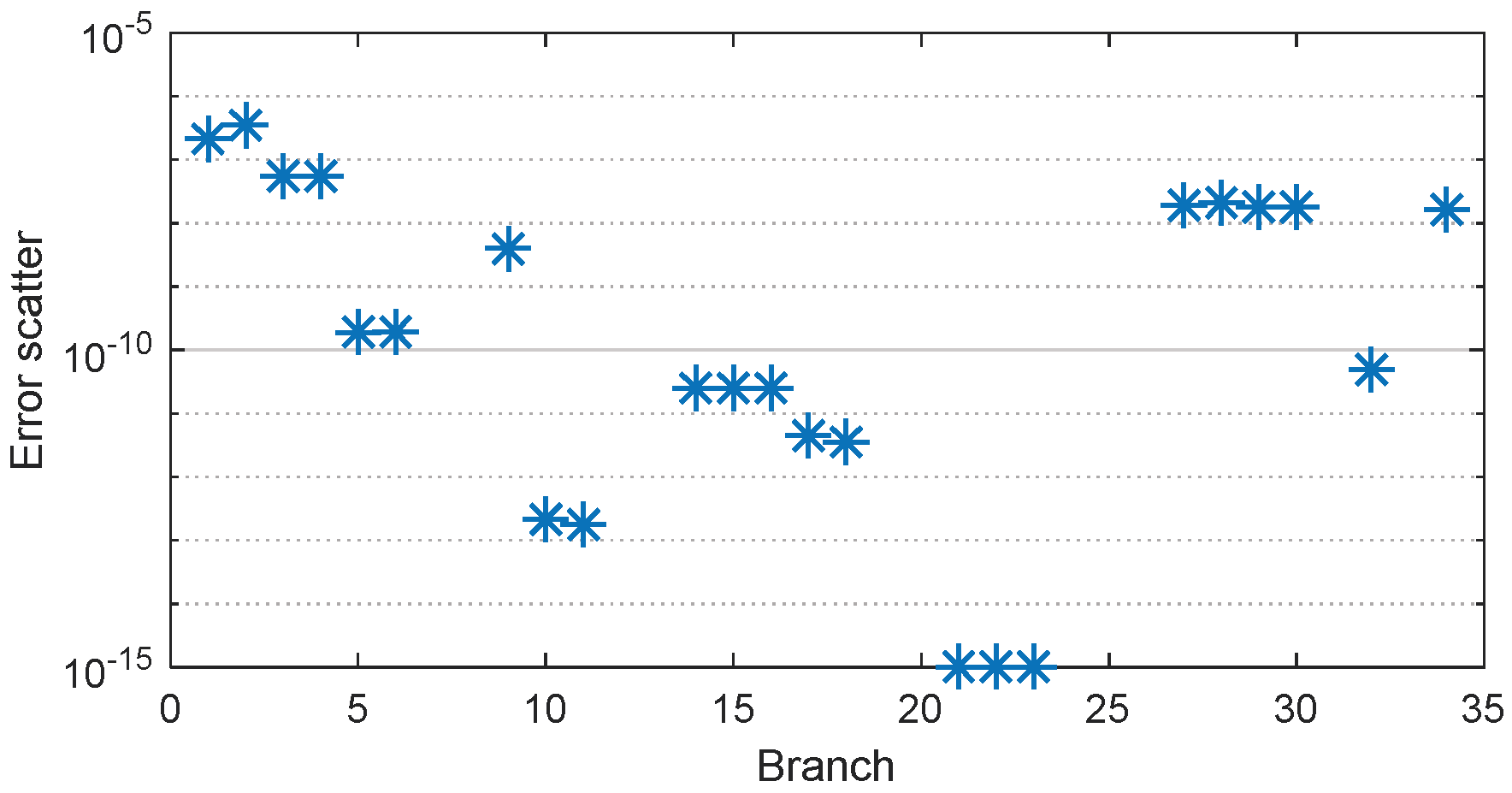
- Based on the error analysis of the model after SOCR, it can be seen that the error index can meet the application requirements of actual engineering, which further verifies the accuracy of the proposed strategy.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kebede, F.S.; Olivier, J.; Bourguet, S.; Machmoum, M. Reliability Evaluation of Renewable Power Systems through Distribution Network Power Outage Modelling. Energies 2021, 14, 3225. [Google Scholar] [CrossRef]
- Gao, H.; Chen, Y.; Huang, S.; Xu, Y. Distribution Systems Resilience: An Overview of Research Progress. Autom. Electr. Power Syst. 2015, 39, 1–8. [Google Scholar]
- Zhang, Z. The Evaluation of Great Blackout Social Integrated Loss of Power Network Planning; North China Electric Power University: Beijing, China, 2017. [Google Scholar]
- Huang, W.; Zhang, X.; Zheng, W. Resilient power network structure for stable operation of energy systems: A transfer learning approach. Appl. Energy 2021, 296, 117065. [Google Scholar] [CrossRef]
- Cieslik, W.; Szwajca, F.; Golimowski, W.; Experimental, A.B. Analysis of Residential Photovoltaic (PV) and Electric Vehicle (EV) Systems in Terms of Annual Energy Utilization. Energies 2021, 14, 1085. [Google Scholar] [CrossRef]
- Irfan, M.M.; Rangarajan, S.S.; Collins, E.R.; Senjyu, T. Enhancing the Power Quality of the Grid Interactive Solar Photovoltaic-Electric Vehicle System. World Electr. Veh. J. 2021, 12, 98. [Google Scholar] [CrossRef]
- Yong, C.; Li, Y.; Zeng, Z.; Zhang, Z.; Zhang, Z.; Liu, Y. Coordinated active and reactive power optimization considering load characteristics for active distribution network. Chin. J. Electr. Eng. 2020, 6, 97–105. [Google Scholar] [CrossRef]
- Chen, H.; Li, Z.; Jin, X.; Jiang, T.; Li, X.; Mu, Y. Modeling and optimization of active distribution network with integrated smart buildings. Proc. CSEE 2018, 38, 6550–6562. [Google Scholar]
- Agrawal, P.; Kanwar, N.; Gupta, N.; Niazi, K.R.; Swarnkar, A. Resiliency in active distribution systems via network reconfiguration. Sustain. Energy Grids Netw. 2021, 26, 100434. [Google Scholar] [CrossRef]
- Li, C.; Miao, S.; Sheng, W. Optimization Operation Strategy of Active Distribution Network Considering Dynamic Network Reconfiguration. Trans. China Electrotech. Soc. 2019, 34, 3909–3919. [Google Scholar]
- Ma, C.; Madaniyazi, L.; Xie, Y. Impact of the Electric Vehicle Policies on Environment and Health in the Beijing-Tianjin-Hebei Region. Int. J. Environ. Res. Public Health 2021, 18, 623. [Google Scholar] [CrossRef]
- Song, Y.; Yang, X.; Lu, Z. Integration of Plug-In Hybrid and Electric Vehicles: Experience from China. In Proceedings of the 2010 IEEE Power Engineering Society General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–5. [Google Scholar]
- Sobol, L.; Dyjakon, A. The influence of Power Sources for Charging the Batteries of Electric Cars on CO2 Emissions during Daily Driving: A Case Study from Poland. Energies 2020, 13, 4267. [Google Scholar] [CrossRef]
- Chen, S. Research on Service Restoration of Active Distribution Network with Microgrids; Shanghai Jiaotong University: Shanghai, China, 2017. [Google Scholar]
- Li, B.; Xiong, Y.; Ren, Z.; Chen, Y.; Zhang, L. Distribution network reconfiguration method considering availability of distribution terminal functions during typhoon disaster. Autom. Electr. Power Syst. 2021, 45, 38–44. [Google Scholar]
- Tang, Y.; Wu, Z.; Gu, W.; Yu, P.; Du, J.; Luo, X. Research on Active Distribution Network Fault Recovery Strategy Based on Unified Model Considering Reconstruction and Island Partition. Power Syst. Technol. 2020, 44, 2731–2737. [Google Scholar]
- Shi, Q.; Li, F.; Olama, M.; Dong, J.; Xue, Y.; Starke, M.; Feng, W.; Winstead, C.; Kuruganti, T. Post-extreme-event restoration using linear topological constraints and DER scheduling to enhance distribution system resilience. Int. J. Electr. Power Energy Syst. 2021, 131, 107029. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, J.; Wang, X.; Xu, Y.; He, J.; Li, J. Critical Load Restoration Method for Distribution Network with Soft Open Point. Autom. Electr. Power Syst. 2021, 45, 104–111. [Google Scholar]
- Gao, T.; Li, J.; Wang, Y.; Xu, Y. Optimization Decision-Making Method for Distribution System Restoration Considering the Interdependency Between Power and Water Distribution Systems. Electr. Power Constr. 2021, 42, 54–60. [Google Scholar]
- Wang, J.; Zheng, X.; Tai, N.; Liu, Y.; Yang, Z.; Wang, J.; Tu, Q. Optimal recovery strategy of DERs integrated distribution network based on scheduling rationality. IET Renew. Power Gener. 2020, 14, 3888–3896. [Google Scholar] [CrossRef]
- Chen, H.; Cong, Q.; Jiang, T.; Zhang, R.; Li, X. Distribution Systems Restoration with Multi-Energy Synergy. Trans. China Electrotech. Soc. 2021, 1–13. [Google Scholar] [CrossRef]
- Ma, T.; Jia, B.; Lu, Z.; Cheng, X.; Wang, D. Multi-energy complement and coordinated post-contingency recovery method of distribution energy networks based on master-slave game theory. Electr. Power Autom. Equip. 2020, 40, 38–46. [Google Scholar]
- Yao, M.; Wang, Y. Restoration Method of Electric Power Supply for Isolated Island with Auxiliary of Electric Vehicles Considering Impact of Cooling Load. Autom. Electr. Power Syst. 2019, 43, 144–150. [Google Scholar]
- Xu, Y.; Wang, Y.; He, J.; Li, C. Optimal Decision-making Method for Multi-period Load Restoration in Distribution Network with Coordination of Multiple Sources. Autom. Electr. Power Syst. 2020, 44, 123–131. [Google Scholar]
- Lv, X.; Yang, L.; An, L.; Lin, Z. Multi-fault repair and recovery strategy for local energy internet integrated with transportation network. Electr. Power Autom. Equip. 2020, 40, 32–38. [Google Scholar]
- Su, M.; Xu, Y.; Wang, Y.; He, J. Placement of Charging Stations for Electric Vehicles Considering Distribution System Resilience and Charging Convenience. J. Glob. Energy Interconnect. 2019, 2, 341–348. [Google Scholar]
- Xu, Y.; Wang, Y.; He, J.; Su, M.; Ni, P. Resilience-Oriented Distribution System Restoration Considering Mobile Emergency Resource Dispatch in Transportation System. IEEE Access 2019, 7, 73899–73912. [Google Scholar] [CrossRef]
- Jiang, T.; Li, Z.; Jin, X.; Chen, H.; Li, X.; Mu, Y. Flexible operation of active distribution network using integrated smart buildings with heating, ventilation and air-conditioning systems. Appl. Energy 2018, 226, 181–196. [Google Scholar] [CrossRef]
- Li, Z. Modeling and Optimization of Active Distribution Network with Integrated Flexible Loads of Smart Buildings; Northeast Electric Power University: Beijing, China, 2019. [Google Scholar]
- Zhang, J.; Nan, Y. Electric car charging path planning under influence of traffic information. J. Comput. Appl. 2016, 36, 282–285. [Google Scholar]
- Zhou, Y.; Yue, Y.; Li, S.; Wei, C.; Li, Z.; Su, S. An Energy Management Method of Active Distribution Network with Integrated Electric Vehicles and Distributed Wind Power. In Proceedings of the 2020 IEEE 3rd Student Conference on Electrical Machines and Systems (SCEMS), Jinan, China, 4–6 December 2020; pp. 847–852. [Google Scholar] [CrossRef]


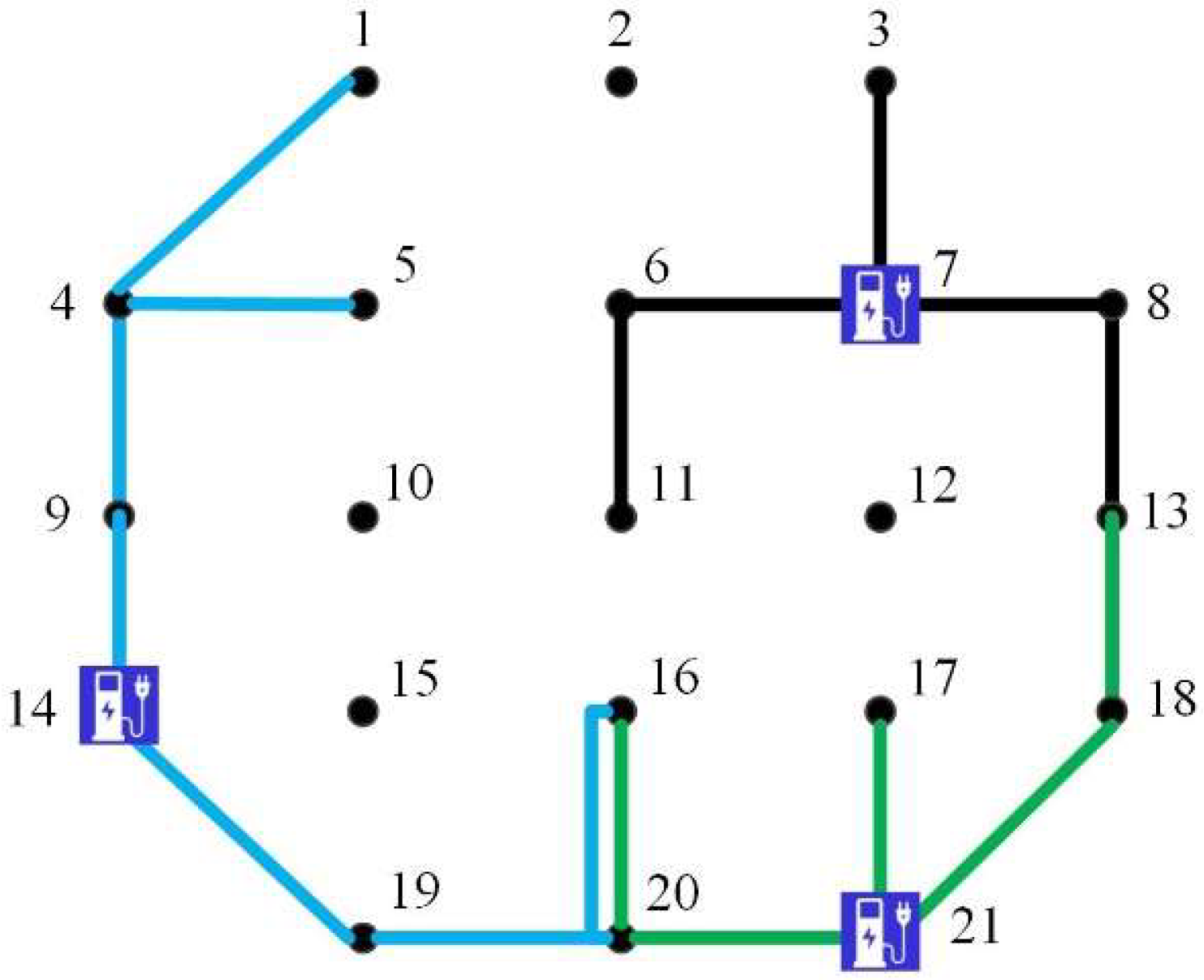
| Transportation Network Node | Distribution Network Bus | Transportation Network Node | Distribution Network Bus | Transportation Network Node | Distribution Network Bus |
|---|---|---|---|---|---|
| 1 | 20 | 8 | 12 | 15 | 7 |
| 2 | 22 | 9 | 3 | 16 | 29 |
| 3 | 10 | 10 | 4 | 17 | 17 |
| 4 | 1 | 11 | 15 | 18 | 33 |
| 5 | 2 | 12 | 16 | 19 | 27 |
| 6 | 23 | 13 | 17 | 20 | 31 |
| 7 | 9 | 14 | 5 | 21 | 18 |
| Strategy | Reasonably Allocate EVs to Charging Stations | Multi-Period Coordinated Load Restoration |
|---|---|---|
| 1 | × | × |
| 2 | × | √ |
| 3 | √ | √ |
| Time Period | DG Output (kW) In Different Strategy | CS1 Output (kW) In Different Strategy | CS2 Output (kW) In Different Strategy | CS3 Output (kW) In Different Strategy | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |
| 1 | 420.8 | 210.8 | 126.2 | 321.1 | 69.9 | 266.4 | 378.9 | 168.5 | 0 | 198.4 | 154.3 | 168.2 |
| 2 | 420.8 | 210.8 | 126.2 | 321.1 | 69.9 | 267.7 | 378.9 | 168.5 | −1.3 | 198.4 | 154.3 | 168.2 |
| 3 | 420.8 | 210.8 | 126.2 | 321.1 | 69.9 | 266.4 | 378.9 | 168.5 | 0 | 198.4 | 154.3 | 168.2 |
| 4 | 128.3 | 210.7 | 187.9 | 320.9 | 196.2 | 266.4 | 378.9 | 168.5 | 0 | 196.6 | 154.2 | 106.6 |
| 5 | 11.7 | 210.7 | 294.4 | −68.1 | 196.2 | 266.4 | −25.5 | 168.5 | 168.4 | 82.1 | 154.2 | 168.2 |
| 6 | 11.7 | 210.7 | 294.4 | −68.1 | 196.2 | 266.4 | −25.5 | 168.5 | 168.4 | 82.1 | 154.2 | 168.2 |
| 7 | 11.7 | 209.5 | 294.4 | −68.1 | 281.5 | 350.6 | −25.5 | 379.5 | 168.4 | 82.1 | 154.3 | 168.2 |
| Remaining Energy(kWh) | Network Loss(kW) | Total Weighted Number of Restored Load | ||||
|---|---|---|---|---|---|---|
| DG | CS1 | CS2 | CS3 | |||
| Strategy 1 | 74.0 | 0.3 | 0.8 | 42.0 | 12.833 | 1312.2 |
| Strategy 2 | 26.1 | 0 | 49.3 | 0 | 12.477 | 2210.4 |
| Strategy 3 | 50.3 | 29.9 | 0 | 0 | 8.041 | 2230.2 |
| (p.u.) | Minimum Voltage Magnitude | Average Voltage | Standard Deviation of Voltage |
|---|---|---|---|
| Strategy 1 | 0.9876 | 0.9969 | 0.0031 |
| Strategy 2 | 0.9881 | 0.9962 | 0.0030 |
| Strategy 3 | 0.9910 | 0.9972 | 0.0021 |
| Transportation Network Node | Strategy 1 | Strategy 2 | Strategy 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 7 | 14 | 21 | 7 | 14 | 21 | 7 | 14 | 21 | |
| 1 | 0 | 10 | 0 | 0 | 10 | 0 | 0 | 10 | 0 |
| 3 | 10 | 0 | 0 | 10 | 0 | 0 | 10 | 0 | 0 |
| 5 | 0 | 10 | 0 | 0 | 10 | 0 | 0 | 10 | 0 |
| 8 | 10 | 0 | 0 | 10 | 0 | 0 | 10 | 0 | 0 |
| 9 | 0 | 10 | 0 | 0 | 10 | 0 | 0 | 10 | 0 |
| 11 | 10 | 0 | 0 | 10 | 0 | 0 | 10 | 0 | 0 |
| 13 | 0 | 0 | 10 | 0 | 0 | 10 | 9 | 0 | 1 |
| 16 | 0 | 0 | 10 | 0 | 0 | 10 | 0 | 8 | 2 |
| 17 | 0 | 0 | 10 | 0 | 0 | 10 | 0 | 0 | 10 |
| 18 | 0 | 0 | 10 | 0 | 0 | 10 | 0 | 0 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, S.; Wei, C.; Li, Z.; Xia, D. Two-Stage Multi-Period Coordinated Load Restoration Strategy for Distribution Network Based on Intelligent Route Recommendation of Electric Vehicles. World Electr. Veh. J. 2021, 12, 121. https://doi.org/10.3390/wevj12030121
Su S, Wei C, Li Z, Xia D. Two-Stage Multi-Period Coordinated Load Restoration Strategy for Distribution Network Based on Intelligent Route Recommendation of Electric Vehicles. World Electric Vehicle Journal. 2021; 12(3):121. https://doi.org/10.3390/wevj12030121
Chicago/Turabian StyleSu, Su, Cunhao Wei, Zening Li, and Dong Xia. 2021. "Two-Stage Multi-Period Coordinated Load Restoration Strategy for Distribution Network Based on Intelligent Route Recommendation of Electric Vehicles" World Electric Vehicle Journal 12, no. 3: 121. https://doi.org/10.3390/wevj12030121
APA StyleSu, S., Wei, C., Li, Z., & Xia, D. (2021). Two-Stage Multi-Period Coordinated Load Restoration Strategy for Distribution Network Based on Intelligent Route Recommendation of Electric Vehicles. World Electric Vehicle Journal, 12(3), 121. https://doi.org/10.3390/wevj12030121






