Abstract
This paper presents a systematic structure and a control strategy for the electric vehicle charging station. The system uses a three-phase three-level neutral point clamped (NPC) rectifier to drive multiple three-phase three-level NPC converters to provide electric energy for electric vehicles. This topology can realize the single-phase AC mode, three-phase AC mode, and DC mode by adding some switches to meet different charging requirements. In the case of multiple electric vehicles charging simultaneously, a system optimization control algorithm is adopted to minimize DC-bus current fluctuation by analyzing and reconstructing the DC-bus current in various charging modes. This algorithm uses the genetic algorithm (ga) as the core of computing and reduces the number of change parameter variables within a limited range. The DC-bus current fluctuation is still minimal. The charging station system structure and the proposed system-level optimization control algorithm can improve the DC-side current stability through model calculation and simulation verification.
1. Introduction
Growing concern about climate change intensifies the trend towards decarbonization and interest in clean technology. As a substitute for internal combustion engine vehicles (ICEVs), electric vehicles (EVs) powered by renewable electricity can reduce petroleum usage and greenhouse emission [1,2]. Furthermore, new technologies on the powertrain of EVs, e.g., a wide-band-gap-component-based motor drive that improves battery-to-wheel efficiency, make EVs more competitive with energy-saving [3]. Besides, the convenience of EV recharging significantly influences EV adoption and utilization. Generally, EVs are powered by charging stations, and the charging power level is generally categorized into two classes-the slow charging (SC) and fast charging (FC) [4,5,6,7]. Typically, the mode of SC is the AC charging mode, including single-phase AC charging and three-phase AC charging; the mode of FC is the DC charging mode.
With the continuous increase in FC power, many researchers are studying the application of FC in EVs [8,9,10,11]. The main research directions of fast charging are efficient power output, reasonable power scheduling, big data analysis of charging stations, and so on [12,13,14,15]. However, fast charging requires high battery performance and battery management systems, while slow charging has lower damage to the battery. Therefore, slow charging has more advantages than fast charging in some cases, such as reducing the load pressure of the charging station. Currently, AC charging connects the car charger directly to the power grid, which will produce a lot of reactive power [16]. Therefore, it is necessary to study the AC charging station for EVs. Moreover, there is no unified standard about EVs’ charging conditions worldwide at present [4,17]. The charging mode, charging interface, and charging voltage of EVs from different manufacturers are different. Some charging stations work at full load in different cities, while others work at no load, which causes a tremendous waste of resources. Therefore, it is necessary to study the charging station with multiple charging modes (MCMs).
In order to meet the multiple charging models (MCMs) of EVs, this paper presents a systematic structure and control strategy to reduce voltage and current ripple for the EVs charging station. The system structure uses the three-phase three-level neutral point clamped (NPC) rectifier to drive multiple three-phase three-level NPC converters, as shown in Figure 1a,b. Additionally, a control switch is added at the front stage of the filter inductance to realize the structural switching between the three-phase converter and the single-phase converter, as shown in Figure 1c. Moreover, multiple EVs can be charged simultaneously by single-phase AC charging mode, three-phase AC charging mode, or DC charging mode.
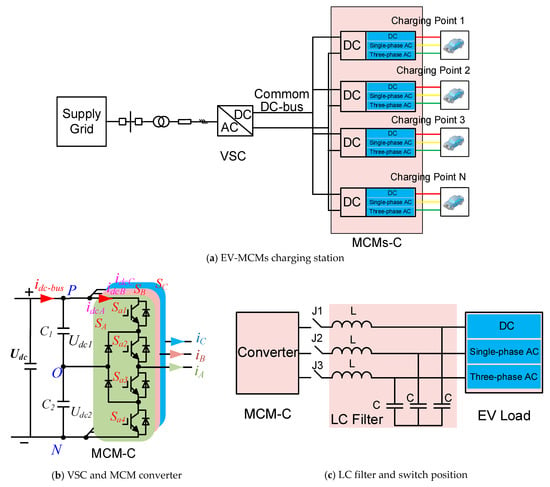
Figure 1.
System Structure of EV-MCMs charging station.
However, different charging modes and power may affect the current fluctuation of the common DC bus and couple to the grid side, impacting the grid. In order to reduce the impact of the charging station system on the power grid, the DC-side current should be linear or constant by reducing the DC bus current fluctuation as much as possible. The work of this paper is as follows:
- The DC-side bus current is expressed and reconstructed in various modes by analyzing the charging power and EVs’ charging mode.
- The current sum of multiple MCMs converters is calculated by current amplitude and current phase offset, and an optimization algorithm is used to control the phase deviation of different EVs charging voltage to reduce the bus current fluctuation.
The rest of this article is organized as follows. The DC-bus Current Analysis of MCMs is introduced in Section 2. An optimal control algorithm is presented in Section 3. In Section 4, simulation results validate the DC-side bus current reconstruction and reduce the bus current fluctuation. The main conclusion is drawn in Section 5.
2. DC-Bus Current Analysis of MCMs
Figure 1b shows the topology of a three-phase three-level NPC converter. UDC, Udc1, and Udc2 represent the DC-link voltages; idcA, idcB, and idcC are the current flowing from the positive bus to the three-phase bridge arm, respectively; IA, IB, and IC are the output current of the three-phase AC side of the inverter, respectively; C1 and C2 are capacitors on DC link. Figure 1c shows the LC filter and switch position between the MCMs converter and EVs. L and C are filters; J1, J2, and J3 are isolating switches.
In the MCMs converter, SK is assumed to be the switching function of the k (k∈{A, B, C}) phase of the three-level inverter and is defined as [18]
If the DC side voltage of MCM is constant and the DC side neutral point potential is balanced, the expression of the voltage uk of the AC side bridge arm neutral point relative to the DC side neutral point O is given
2.1. DC Charging Mode
When S2 is disconnected, the structure of the three-phase converter is changed into a single-phase converter, which can be used as a DC converter or a single-phase AC converter, as shown in Figure 2.
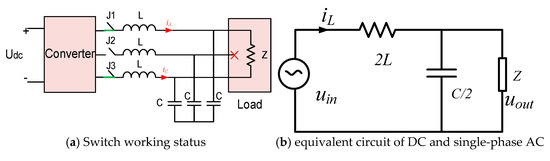
Figure 2.
The structure of DC is charging mode and single-phase AC charging mode.
According to the characteristics of the PWM converter, the mathematical model of the output current in Figure 2b is as follows:
On DC charging mode, the output voltage (out), output current (IL), equivalent impedance of the load (Z), and input voltage (uin) are constant, respectively. The mathematical model of DC bus current Idc-bus is given
Because the converter switching frequency is high, typically up to 5 KHz, the DC side capacitor can filter the high-frequency current ripple. When the output power is constant or linear, there is no need to decrease the ripple of the DC bus current through a system optimization control algorithm in this mode.
2.2. Single-Phase AC Charging Mode
In the single-phase AC charging mode, the topological diagram and equivalent circuit diagram are the same as the DC charging mode, as shown in Figure 2. The amplitude of the output current is defined as Iout; the output voltage amplitudes and the phase are defined as Uout and respectively; the output power factor angle is defined as ;
The output voltage uout and current iL expression are defined as
Through Formulas (1) and (5), the input voltage uin is calculated as follows:
According to the high-frequency mathematical model of NPC three-level PWM converter, assuming that the neutral point potential of DC side is balanced, the mathematical model of DC bus current of the inverter is as follows:
It can be seen that the switching function SK is contained in Equation (7). Obviously, the DC bus current Idc-bus flowing into the converter contains high-frequency components related to the switching frequency. Nevertheless, the bus capacitor can filter out high-frequency components, so it is not considered.
According to input voltage uin in Formula (1), when sinusoidal pulse width modulation (SPWM) strategy is adopted, the average value in switching period of Sk can be approximately expressed as:
Additionally, m is the modulation degree of the fundamental wave.
Through Formulas (6)–(8), the DC-bus current is calculated by
According to the Formula (9) analysis, the DC bus current comprises DC current and second harmonic current. Moreover, the amplitude of the second harmonic current is higher. When multiple EVs use single-phase AC charging mode simultaneously, the harmonic amplitude will be superimposed, which will cause significant fluctuation of DC bus power and lead to grid-side instability. Thus, when the single-phase AC charging mode is used to charge multiple EVs, the second harmonic amplitude can be reduced by changing the initial angle of output voltage.
2.3. Three-Phase AC Charging Mode
When S1, S2, and S3 are connected, the EVs charging system can provide a three-phase charging function, as shown in Figure 3. The output current amplitude is defined as Iout; the output voltage amplitudes and phase are defined as Uout and respectively; the output power factor angle is defined as .
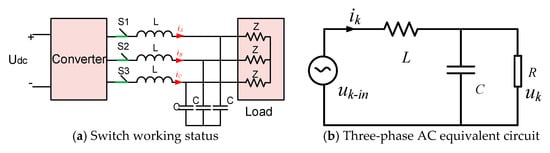
Figure 3.
Structure of three-phase AC charging mode.
According to the characteristics of the PWM converter, the mathematical model of the output current in Figure 3b is as follows:
Due to the symmetry of the three-phase inverter, k is A, B, or C.
The output voltage expression of three-phase AC charging mode is defined as
The output current expression of three-phase AC charging mode is defined as
Through Formulas (10) and (11), the input voltage UA−in is calculated as follows:
Due to the symmetry of the three-phase inverter, the input voltage of phase B and C are calculated
According to the high-frequency mathematical model of NPC three-level PWM converter, assuming that the neutral point potential of DC side is balanced, the mathematical model of DC bus current of the inverter is as follows [6]:
It can be seen that the switching function SK is contained in Equation (15). Obviously, the DC bus current Idc-bus flowing into the converter contains high-frequency components related to the switching frequency. Nevertheless, the high-frequency components can be filtered out by the bus capacitor, so it is not considered.
According to input voltage on-k in Formulas (13) and (14), when sinusoidal pulse width modulation (SPWM) strategy is adopted, the switching function SK can be approximately expressed as [19]:
Additionally, m is the modulation degree of the fundamental wave.
Through Formulas (6)–(8), the DC-bus current is calculated
According to the Formula (17) analysis, the DC bus current comprises DC current and third harmonic current. Moreover, the third harmonic current amplitude is higher. Other modulation strategies can reduce the third harmonic amplitude, such as the zero sequence component compensation method, SVPWM method, etc. [19,20]. However, when multiple EVs use three-phase AC charging mode simultaneously, the harmonic amplitude will be superimposed, which will cause significant fluctuation of DC bus power and lead to grid-side instability. Similarly, when the three-phase AC charging mode is used to charge multiple EVs, the third harmonic amplitude can be reduced by changing the initial angle of output voltage.
3. Optimal Control Algorithm
According to the above analysis, the DC bus current under DC charging mode is the superposition of constant and switching frequency fluctuation, which will not affect the bias current. The low-frequency current component under single-phase AC charging mode and three-phase AC charging mode will significantly influence DC-bus voltage.
The low-frequency current component of DC bus current can be described as follows.
where a is the number of EVs in single-phase charging mode; b is the number of EVs in three-phase charging mode. According to the Formulas (6) and (13), the parameters in the Formula (19) are as follows.
When I = 0, me and Iout-I am also 0. Additionally, when j = 0, mg and Iout-j are also 0.
According to (19), the total fluctuation of bus current can be regarded as the superposition of the third harmonic and the second harmonic. So, the complexity of calculation can be reduced by isolating the three-phase charging mode from the single-phase charging mode. By changing the initial phase angle of different output voltages, the total second or third harmonic amplitude can be reduced. Taking the second harmonic as an example, this paper analyses the second harmonic model of bus current.
When there is a branch by single-phase charging mode, the sum of DC-bus current Idc-sum is calculated as:
Since the charging power or charging current of the same EV is constant, in order to minimize the current fluctuation of the DC-bus, the optimization constraint equation is as follows:
Since the number of charging EVs may increase or decrease one by one in the charging process. This algorithm uses the genetic algorithm (ga) [21,22] as the core of computing and reduces the number of change parameter variables within a limited range. The DC-bus current fluctuation is still minimal. An optimization control algorithm is derived in Algorithm 1.
| Algorithm 1 An Optimization Control Algorithm Implementation |
| /*ga is the Genetic Algorithm that has been Used to Solve Optimization Problems. input:: matrix of n amplitudes; : amplitude of n+1; k: change the number of parameter variables; output: : initial phase matrix of n phases; : phase of n+1; : bus current fluctuation amplitudes; ; /*Sort by initial amplitude; ; /*Calculate the minimum amplitude and the corresponding phase; ; /* Calculate the second harmonic phase of bus current; When is added; /*A new EV with single-phase AC charging mode; for z from 0 to k if then ; k = 1; break; end if then ; k=z; if then break; end end end return matrix , numeric , coefficient k |
According to Formula (20), the initial phase of the output voltage can be calculated by matrix .
4. Simulation and Results
Through literature review, the charging power is generally around 100 KW, the single-phase output voltage is 220 V(RMS), the three-phase output voltage is 380 V(RMS), and the DC charging voltage is generally around 600 V [3]. However, the output voltage of different standards or manufacturers will be different. The simulation circuit parameters can be adjusted according to the actual engineering parameters. Table 1 shows the simulation parameters of the MCMs converter.

Table 1.
Simulation parameters of the MCMs converter.
4.1. DC-Bus Current Error Analysis
In order to analyze the accuracy of DC-bus current reconstruction, the relative error between the DC-bus current reconstruction value and the DC bus current is defined as
where idc-bus-re is the current by the model; idc-bus is the current by simulation
In DC bus current, high-frequency harmonics are generated by the high-frequency action of switching devices, and the high-frequency harmonics can be filtered through the DC side capacitor. According to Figure 4, the DC-bus current is constant in DC charging mode. In single-phase AC charging mode, the DC-bus current has second harmonics. Additionally, in the three-phase AC charging mode, the DC-bus current has third harmonics. By comparing theoretical calculation and simulation, the error of average current is less than 1% in one cycle, which verifies the correctness of DC-bus current Analysis of MCMs.
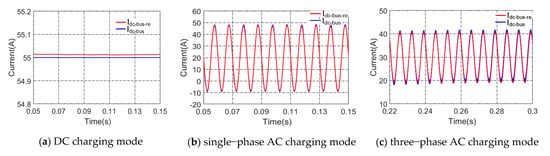
Figure 4.
Comparison of theoretical calculation and simulation.
4.2. Verification of Optimal Control Algorithm
4.2.1. Single-Phase Charging Mode
Since the output power factor of the converter is greater than 95% or higher, this paper takes the unit power factor as an example. It is assumed that there are five sets of converters working in single-phase AC charging mode. Hence, the power factor angle is set to 0; the output voltage amplitudes Uout is 311 V; the output current amplitudes matrix Iout are A.
By calculation, the DC bus current amplitudes matrix Idc-bus are A. The total current amplitude without the algorithm is 163.8 A by theoretical calculation. The total current amplitude is 162 A by simulation. By comparing theoretical calculation and simulation, the error of the average current is less than 2%, as shown in Figure 5a. According to the algorithm’s calculation results, the DC-bus current phase and output voltage phase are calculated as and , respectively. Additionally, DC-bus current fluctuation amplitudes fmin is lower, as shown in region 1 of Figure 5b.
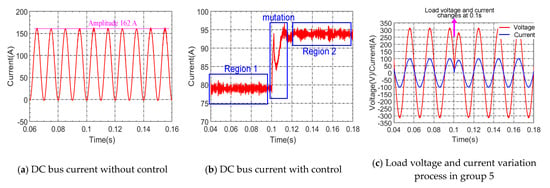
Figure 5.
DC−bus current fluctuation comparison in single-phase charging mode.
At this time, another different group of MCMs is put into operation. When the output current amplitude () is 75 A (random), the DC bus current amplitude is 30.46 A. Only one of the parameters and the phase of group 5 voltage need to be changed through algorithm analysis. The DC-bus current phase and are calculated as and by the algorithm, respectively. Additionally, the output voltage phase and are 0.1083 and 2.3227, respectively. Comparing DC bus current fluctuation is shown in region 2 of Figure 5b, which shows that the proposed algorithm can effectively reduce the bus current fluctuation. The changing process of voltage and current of group 5 is shown in Figure 5c, which shows that the output voltage and current of group 5 are not affected much after group 6 is put into operation.
4.2.2. Three-Phase Charging Mode
Since the output power factor of the converter is greater than 95% or higher, this paper takes the unit power factor as an example. It is assumed that there are five sets of converters working in three-phase AC charging mode. Hence, the power factor angle is set to 0; the output voltage amplitudes UA, UB and UC is 311 V, and the phase difference is in turn; the output current amplitudes matrix Iout are A.
By calculation, the DC bus current amplitudes matrix Idc-bus is A. The total current amplitude without the algorithm is 155.7 A by theoretical calculation. The total current amplitude is 157 A by simulation. The average current error is less than 2% by comparing theoretical calculation and simulation, as shown in Figure 6a. According to the calculation results of the algorithm, DC-bus current phase and output voltage are calculated as and , respectively.
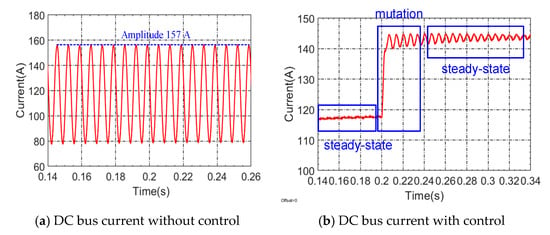
Figure 6.
DC-bus current fluctuation comparison in three-phase charging mode.
At this time, another different group of MCMs is put into operation. When the output current amplitude is 45 A (random), the DC bus current amplitude is 34.81 A. Only one of the parameters and the phase of group 5 voltage need to be changed through algorithm analysis. The DC-bus current phase and are 2.2896 and 0.3343 by the algorithm, respectively. Additionally, the output voltage phase and are 0.7890 and 0.1552, respectively. Comparing DC bus current fluctuation is shown in Figure 6b, which shows that the proposed algorithm can effectively reduce the bus current fluctuation.
5. Conclusions
This paper presents a system architecture and its control structure to achieve three charging modes for the charging station of EVs.
- According to the high-frequency mathematical model of NPC three-level PWM converter, the method of current reconstruction of DC-bus is established in different charging mode. By comparing theoretical calculation and simulation, the average current error is less than 2% in one cycle.
- An optimization algorithm is proposed to reduce the second harmonics current of DC-bus current in single-phase charging mode and reduce the third harmonics current of DC-bus current in three-phase charging mode. When multiple vehicles are charged simultaneously, the harmonic content is reduced by superimposing multiple second and third harmonics so that the bus current is DC by theoretical calculation and simulation.
Because the system is relatively large, many converters are needed, so the experiment is more complicated. We hope that experiments in the future can verify the algorithm.
Author Contributions
Writing—review and editing, T.C.; Conceptualization, S.D.; resources, X.C.; validation, L.H.; investigation, S.H. and Z.W.; Funding acquisition, P.F.; All authors have read and agreed to the published version of the manuscript.
Funding
Plan for Major Provincial Science & Technology Project (202003a05020019).
Acknowledgments
This work was supported in part by Plan for Major Provincial Science & Technology Project (202003a05020019).
Conflicts of Interest
The authors declare no conflict of interests.
References
- Yilmaz, M.; Krein, P.T. Review of Battery Charger Topologies, Charging Power Levels, and Infrastructure for Plug-In Electric and Hybrid Vehicles. IEEE Trans. Power Electron. 2013, 28, 2151–2169. [Google Scholar] [CrossRef]
- Hao, T.; Hao, F.; Srdic, S.; Lukic, S. Extreme Fast Charging of Electric Vehicles: A Technology Overview. IEEE Trans. Transp. Electrif. 2020, 5, 861–878. [Google Scholar]
- Wang, L.; Qin, Z.; Dong, J.; Bauer, P. Design, modelling and evaluation of a GaN based motor drive for a solar car. In Proceedings of the IECON 2019-45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019. [Google Scholar]
- Wang, L.; Qin, Z.; Slangen, T. Grid Impact of Electric Vehicle Fast Charging Stations: Trends, Standards, Issues and Mitigation Measures—An Overview. IEEE Open J. Power Electron. 2021, 2, 56–74. [Google Scholar] [CrossRef]
- Shareef, H.; Islam, M.M.; Mohamed, A. A review of the stage-of-the-art charging technologies, placement methodologies, and impacts of electric vehicles. Renew. Sustain. Energy Rev. 2016, 64, 403–420. [Google Scholar] [CrossRef]
- Pieltain Fernandez, L.; Gomez, S.R.T.; Cossent, R.; Domingo, C.M.; Frias, P. Assessment of the Impact of Plug-in Electric Vehicles on Distribution Networks. IEEE Trans. Power Syst. 2011, 26, 206–213. [Google Scholar] [CrossRef]
- Hilshey, A.D.; Hines, P.D.H.; Rezaei, P.; Dowds, J.R. Estimating the Impact of Electric Vehicle Smart Charging on Distribution Transformer Aging. IEEE Trans. Smart Grid 2013, 4, 905–912. [Google Scholar] [CrossRef]
- Long, T.; Jia, Q.; Wang, G.; Yang, Y. Efficient Real-Time EV Charging Scheduling via Ordinal Optimization. IEEE Trans. Smart Grid 2021. [Google Scholar] [CrossRef]
- Mahfouz, M.; Iravani, R. Autonomous Operation of the DC Fast-Charging Station. IEEE Trans. Ind. Electron. 2021. [Google Scholar] [CrossRef]
- Qin, Z.; Shen, Y.; Loh, P.C.; Wang, H.; Blaabjerg, F. A Dual Active Bridge Converter with an Extended High-Efficiency Range by DC Blocking Capacitor Voltage Control. IEEE Trans. Power Electron. 2017, 33, 5949–5966. [Google Scholar] [CrossRef] [Green Version]
- Mahfouz, M.M.; Iravani, M.R. Grid-Integration of Battery-Enabled DC Fast Charging Station for Electric Vehicles. IEEE Trans. Energy Convers. 2019, 35, 375–385. [Google Scholar] [CrossRef]
- Zahedmanesh, A.; Muttaqi, K.; Sutanto, D. Active and Reactive Power Control of PEV Fast Charging Stations Using a Consecutive Horizon based Energy Management Process. IEEE Trans. Ind. Inform. 2020, 17, 6742–6753. [Google Scholar] [CrossRef]
- Sun, X.; Qiu, J. A Customized Voltage Control Strategy for Electric Vehicles in Distribution Networks with Reinforcement Learning Method. IEEE Trans. Ind. Inform. 2021, 17, 6852–6863. [Google Scholar] [CrossRef]
- Yan, D.; Yin, H.; Li, T.; Ma, C. A Two-Stage Scheme for Both Power Allocation and EV Charging Coordination in A Grid Tied PV-Battery Charging Station. IEEE Trans. Ind. Inform. 2021, 17, 6994–7004. [Google Scholar] [CrossRef]
- Suresh, V.; Bazmohammadi, N.; Janik, P.; Guerrero, J.M.; Kaczorowska, D.; Rezmer, J.; Jasinskia, M.; Leonowicza, Z. Optimal location of an electrical vehicle charging station in a local microgrid using an embedded hybrid optimizer. Int. J. Electr. Power Energy Syst. 2021, 131, 106979. [Google Scholar] [CrossRef]
- Uthra, R.; Suchitra, D. Fault Ride Through in Grid Integrated Hybrid System Using FACTS Device and Electric Vehicle Charging Station. Energies 2021, 14, 3828. [Google Scholar]
- Electric Vehicle Conductive Charging System—Part 1: GeneraL Requirements. IEC Standard 2017, IEC 61851–1. Available online: https://standards.iteh.ai/catalog/standards/iec/c472de67-e272-4734-9103-cf9f4725c597/iec-61851-1-2017 (accessed on 1 March 2021).
- Jung, J.H.; Hwang, S.I.; Kim, J.M. A Common-Mode Voltage Reduction Method Using an Active Power Filter for a Three-Phase Three-Level NPC PWM Converter. IEEE Trans. Ind. Appl. 2021, 57, 3787–3800. [Google Scholar]
- Srivastava, S.; Chaudhari, M.A. Comparison of SVPWM and SPWM Schemes for NPC Multilevel Inverter. In Proceedings of the 2020 IEEE International Students’ Conference on Electrical, Electronics and Computer Science (SCEECS), Bhopal, India, 22–23 February 2020. [Google Scholar]
- Jiang, W.D.; Du, S.W.; Chang, L.C.; Zhang, Y.; Zhao, Q. Hybrid PWM Strategy of SVPWM and VSVPWM for NPC Three-Level Voltage-Source Inverter. IEEE Trans. Power Electron. 2010, 25, 2607–2619. [Google Scholar] [CrossRef]
- Karakati, S. Optimizing nonlinear charging times of electric vehicle routing with genetic algorithm. Expert Syst. Appl. 2020, 164, 114039. [Google Scholar] [CrossRef]
- Jordán, J.; Palanca, J.; del Val, E.; Julian, V.; Botti, V. Localization of charging stations for electric vehicles using genetic algorithms. Neurocomputing 2020, 452, 416–423. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).