Abstract
Permanent magnet traction motor has the advantages of high efficiency, high power density, high torque density and quick dynamic response, which has been widely used in the traction field of electric vehicle. The high-performance control of permanent magnet traction motor depends on accurate rotor position information, which is usually obtained by using mechanical position sensors such as hall sensor, encoder and rotary transformer. However, the traditional mechanical sensor has the disadvantages of high cost, large volume and poor anti-interference ability, which limits the application of permanent magnet motor. The sensorless control technology is an effective way to solve the above-mentioned problem. Firstly, the sensorless control techniques of permanent magnet motor are classified. The sensorless control techniques of permanent magnet motor for rotor initial position, zero-low speed range, medium-high speed range and full speed range are deeply described and compared. Finally, the development trend of sensorless control technology of permanent magnet traction motor is prospected.
1. Introduction
At present, energy and environment are two major themes of social development. A series of social problems such as air pollution, global warming, the shortage of fossil fuel resources and combustion problems related to pollution-free and clean environments have attracted a great of attention for the construction of pollution-free and efficient traction systems in electric vehicles (EV) [1,2,3,4,5,6]. As power electronics technology, automatic control technology and computer technology advance, the performance of AC speed control system has been improved on a continued basis, which challenges the dominant position of DC speed control in the field of high-performance speed regulation [7]. Undoubtedly, the AC speed control system has been increasingly adopted to replace the DC speed control system [8]. The synchronous motor demonstrates advantages such as high-power factor, small inverter capacity and the small moment of inertia over the speed control. In the high-power AC transmission system, the advantages of the synchronous motor speed control system are self-evident. With the development and application of permanent magnet materials, permanent magnet synchronous motor (PMSM) and brushless DC motor (BLDCM) have drawn increasing attention for their high-power density, large torque inertia ratio and fast dynamic response speed, which demonstrates great potential in various areas, especially in the field of advanced manufacturing transmission systems and large ship electric propulsion [9].
When the synchronous motor is in operation, it is necessary for the stator winding current vector to be synchronized with the rotor position, which is used to drive the motor output speed and torque. The motor controller is employed to obtain the information on the rotor position in the motor in real time. When the motor gets started, it is necessary to determine the initial position of the rotor for obtaining the maximum starting torque [10]; otherwise, it may cause motor inversion and reduce motor efficiency [11]. In order to collect information about the rotor position, the commonly used scheme is to install mechanical position sensors, such as photoelectric encoders and rotary transformers. However, the traditional position sensor can not only increase the motor volume and rotation inertia of the shaft, but also reduce the power density of the motor. Nevertheless, the sensor is susceptible to interference caused by temperature and electromagnetic noise, thus reducing the operating reliability of the device. This may lead to problems such as poor sensitivity and temperature drift. Moreover, the installation of the position sensor increases the complexity of motor structure, system cost and maintenance difficulty [12]. Especially for the motors with more poles, the installation accuracy of sensors will have a considerable impact on the performance of motors [13]. The defects caused by mechanical sensors restrict the application of PMSM in some exceptional circumstances. As one of the effective measures to address it, sensorless control technology has been proposed and attracted much attention for the research on motor control technology [14].
Replacing conventional mechanical position sensors with soft sensors provides an effective solution to the aforementioned problems and is conducive to improving the reliability of position detection, extending the service life of motor, simplifying the connection line between inverters and motors, lowering system costs and enhancing the reliability of the system [15]. The sensorless control system is capable of obtaining the information about the rotor position by analyzing the voltage and current of the motor port in real time. As the sensorless control can effectively improve the integration of hub motor drive system, many scholars both at home and abroad have made extensive efforts to come up with practical methods [16]. In [17], the development of a model based on sensorless control is presented, but the compound control and switching methods in full speed range are not introduced. In this paper, the research results obtained in recent years are summarized and presented in Table 1. From Table 1, it can be seen that the rotor position estimation methods presented by many researchers can be divided into initial and low speed, and medium-high speed.

Table 1.
Position detection approaches.
The contribution of this paper is to categorize the state-of-the-art position estimation approaches and advancements in sensorless permanent magnet traction systems of electric vehicles. The paper completely presents the advantages and disadvantages of rotor position estimation techniques, which provide effective guidance for researchers who are working in this field.
2. Sensorless Control Scheme for Rotor Initial and Low Speed Position Detection
As a major difficulty facing the sensorless control technology, the position detection of the motor rotor at zero and low speed is a significant influencing factor in the starting torque and stability of the motor. In sensorless control strategy, the rotor position is determined by using the salient pole characteristic of the motor, saturation characteristic of the magnetic circuit or polarity of the magnetic circuit [18]. These methods are summarized in Figure 1.
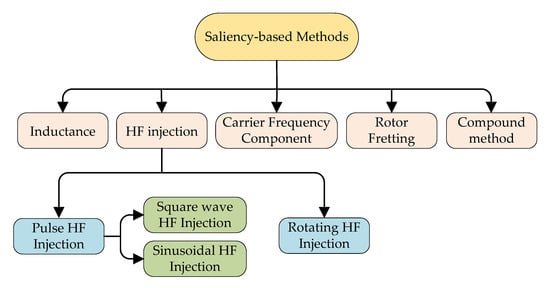
Figure 1.
Sensorless strategies for initial and low speed.
2.1. Inductance Method
Inductance method positioning is premised on the core saturation effect and the magnetization or demagnetization effect produced by the magnetic field of permanent magnet in different directions on the armature. If the change of inductance is detected, the rotor position can be detected as well at zero and low speed [19]. According to the basic theory of motor coordinate transformation, the relationship between the abc of stationary coordinate system and the α-β of a rotating coordinate system can be expressed as:
where, Lo is the constant component of winding self-induction, the Lgm is the m harmonic amplitude of self-inductance, the θe is the rotor electrical angle.
Winding inductance is a function of rotor position and winding current. The rate of current change is subject to a considerable impact from the inverse potential, which renders this method unsuited to the condition of high-speed down-position estimation [20]. In [21], it is indicated that since the method assumes that the motor conforms to the ideal model, the inevitable process problems arising from production will lead to the deviation of the three-phase inductance in the armature winding, and that armature, iron loss, copper loss and demagnetization motor loss will undergo progressive changes as the running time of the motor is extended, thus making detection less consistent. In [19], an analysis was carried out of the im pact caused by saturation on the self-induction and mutual induction of PMSM, based on which it was indicated that the saturation effect was mainly reflected in the first and second harmonic components of these inductors, and that such effect varied with the rotor angle.
According to the operation characteristics of the three-phase six-state brushless DC motor, the three-three conduction method was adopted in [19] to apply the six-channel detection pulse voltage to the motor in order for obtaining the detection pulse voltage in six different states and the rotor position information based on the corresponding current response. The detection of pulse voltage application time is determined by the motor electrical time constant. In [22], an analysis was conducted of the effect caused by voltage vectors at different locations on inductive saturation, as well as the accuracy of rotor position estimation, based on which an improved five-pulse injection method was proposed. In [23], a high level of position detection was achieved by applying a series of voltage pulse vectors with the same magnitude and opposite direction to the stator winding. Nevertheless, this presented even more demanding requirements on the accuracy of the sampling circuit. With the pulse voltage injection method adopted, the inverter may perform multiple switching actions, which is easy to interfere with the sampling circuit and affect the accuracy of sampling. In [24], positioning accuracy was improved by increasing the number of injection pulses. However, the scheme was premised on the motor model as the ideal model, and the excessive pulses required to detect rotor position increased the complexity of algorithm, as a result of which, it was suitable only for the detection of the initial position of the motor rotor.
With regard to non-salient pole brushless DC motor, the inductance ratio of the other two phases was obtained in [25] by detecting the suspension phase voltage, for the rotor position to be determined. In [26], the rotor position was determined by detecting two-phase inductors equal at all times, but inductive deviations had a direct impact on the test results, which led to a compromise on accuracy. An improved high-precision inductive method positioning scheme was proposed in [27,28] to enhance detection accuracy by analyzing the polarity and magnitude of pulse response current simultaneously. In [29], an inductive threshold method based on iron core B-H hysteresis was put forward to detect the rotor position of the PM brushless DC motor at rest and low speeds. According to this method, the detection signal is independent of the motor speed, and it remains capable to obtain a valid position detection signal when the iron center of the motor stator is unsaturated.
2.2. High Frequency (HF) Injection Method
HF injection method is reliant on the salient features of the motor rotor position, rather than the motor model of the counter electromotive force, which makes it the most effective rotor position estimation method for zero-speed and low-speed operation of the PMSM. The HF injection method is adapted to the motor zero speed and low speed control strategy. The injection method of HF pulse signal under the low speed operation is similar to when the rotor is stationary [30]. There are two differences. Firstly, the motor at low speed operation is required to extract the HF response current through the high-pass filter. Secondly, the cross-saturation effect shall be taken into consideration when the motor is running. The comparison of different HF injection methods is shown in voltage pulse vectors with the same magnitude and opposite direction to the stator winding. Nevertheless, this presented even more demanding requirements on the accuracy of the sampling (Table 2).

Table 2.
Comparison of different HF injection methods.
Typically, the injected HF signals include rotating HF voltage signals, rotating HF current signals, and pulse HF voltage signals. Though pulse HF voltage signal injection convex tracking system features a simple structure and the excellent performance in static and dynamic speed regulation, the system with rotating HF voltage signal injection method is more achievable [31]. Depending on the exact type of injection signal, pulse HF voltage is categorized into square-wave and sine-wave signals.
2.2.1. Rotating HF Injection Method
Due to its straightforward working principle, rotating HF carrier signal injection method has now been widely used in the IPMSMS positionless sensor control. The rationale of this method is to inject three-phase symmetrical high frequency sinusoidal voltage signal at the stator end of IPMSM, and then obtain the information on rotor position by detecting and processing the HF response signal in α-β coordinate system; see Equations (6) and (7). The block diagram of this method is presented in Figure 2. The superscript ’*’ in the figures of the paper indicates that the parameter is a reference value.
where, uαi and uβi are the α-β axis components of the HF response voltage, respectively.
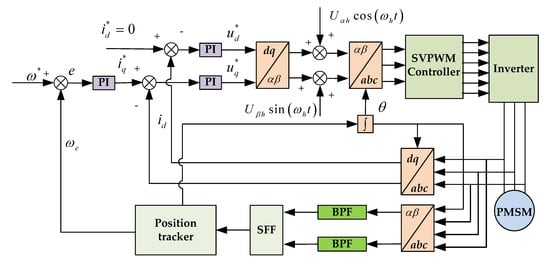
Figure 2.
Block Diagram of rotating HF Voltage injection method.
In [32], low-pass filtering was carried out on the current response of three-phase high-frequency voltage signal, the initial position information of the motor rotor was obtained based on the modulation law of rotor position angle to the amplitude of three-phase HF current response signal, and then the N/S polarity of the motor rotor was distinguished according to the saturation effect of the motor magnetic circuit. In [33], the relationship between the d-axis flux and the stator current of the permanent magnet synchronous motor in the d-q rotating coordinate system was analyzed and a new scheme was proposed to obtain the information on N/S pole polarity according to the nonlinear magnetization characteristics of the stator core. Due to factors such as system hysteresis, stator resistance, cross-coupling effect and inverter nonlinearity, the accuracy of rotor position estimation will decline. In order to solve these problems, a two-way rotating HF carrier signal injection strategy was proposed in [30]. To be specific, two different rotation frequencies and directions of HF carrier voltage were injected, and the complex multi-group filter method was adopted to establish the equation system, as a result of which the rotor position could be directly calculated. However, the method was excessively complex and increased the difficulty of filter design. Besides this, the impact of different frequencies on the system was ignored. In [34,35], the initial IPMSM rotor position estimation method was improved by injecting mixed signal—two short pulse voltage vectors opposite to each other into the stator winding. In this case, the magnetic polarity can be determined in a simple and effective way by comparing the excitation current on the d-axis. Though the robustness of the method is high, it is difficult for the short pulse injection method to determine the pulse width and amplitude. In [36,37], HF rotary voltage signals were injected into the stationary coordinate system, and multiple filters were used to demodulate the inductive current envelope. In doing so, however, the level of complexity could be raised and phase shifts can occur.In [38], the HF rotary carrier signal injection method within 10% of the rated speed of the motor was applied, the sensorless safety operating area (SOA) was introduced, and the quantitative error in the analog digital conversion was taken into account. The estimation error for rotor position in the steady state process was ±5°, while the maximum estimated error in dynamic processes was ±10 degree.
2.2.2. Pulse HF Injection Method
The interior permanent magnet synchronous motor (IPMSM) contains a structural salient pole, while the surface permanent magnet synchronous motor (SPMSM) contains a saturated salient pole. The initial rotor position can be detected by means of HF pulse voltage injection. The stator voltage equation of IPMSM in two-phase rotating coordinate system is:
where, ud and uq are the d-q axis components of the stator voltage, respectively. id and iq are the d-q axis components of the stator current, respectively. p is a differential operator. Rs is the stator armature winding resistance. ωe is the electric angular velocity. ψf is the permanent magnetic flux.
where, Lp = (Ldi + Lqi)/2, Lm = (Ldi − Lqi)/2, Δθ = θe − θe(est). idi and iqi are the d-q axis components of the HF response current, vi is the amplitude of the injected signal, ωi is the frequency of the injected signal, θe is the rotor electrical angle. Injecting a HF pulse voltage signal on the d-axis of the virtual synchronous coordinate system and the stator winding current response carries the information on rotor position, see Equation (4). Since this method is proposed to indicate the spatial convex polarity of the rotor by adding a continuous HF excitation signal, which is irrelevant to the speed, it is possible to make an effective estimate of the speed at low speeds. Besides this, the method is not reliant on the spatial protrusion of the tracking rotor rather than the mathematical equation of the motor, which addresses the sensitivity to the change in motor parameters and leads to a strong robustness.
It is necessary to consider cross saturation effects when pulse voltage is injected into the motor during operation, which is due to its association with the load current of the motor. The negative sequence component of the HF response current in the stator windings contains the information on rotor position, which can be extracted by filtering the fundamental wave component and the positive sequence component of the HF response current [39]. After injecting the HF voltage signal into the synchronous rotating coordinate system, Liu made the initial estimate of the rotor position through closed-loop regulation, and determined the positive direction of the d-axis based on the characteristics that the equivalent circuit time constants vary under different magnetic poles and that the accurate position of rotor can be obtained by combining two points [40]. The basic principle to apply the rotating HF voltage injection method, rotating HF current injection method and pulse vibration HF voltage injection method was analyzed in [41], based on which a position estimation error compensation strategy was proposed. In [42], the d-axis and q-axis carrier currents, not limited to the q-axis carrier current, were combined with the traditional sensorless algorithm based on carrier signal injection, to determine both the initial rotor position of the stationary rotor and the rotor position of the free-running rotor. The position estimation error formula was obtained according to the quadrature axis fundamental wave voltage. In [43], a sensorless control strategy was presented to inject HF pulsating carrier signal into the stationary coordinate system and extract the information on rotor position from the carrier current response of motor convexity modulation. Nevertheless, the control strategy was relatively complicated and reliant on motor parameters in the information extraction process, which affected its robustness.
When the traditional HF injection method was applied (sine voltage injection), low-pass filters (LPFs) are required to capture an error signal. The time delay to the LPF itself reduces the control performance of the positionless sensor. To prevent this effect, square wave voltage injection can be performed instead of sine voltage injection [44]. The block diagram of square wave HF injection method is shown in Figure 3: inject the square wave signal shown in voltage pulse vectors with the same magnitude and opposite direction to the stator winding. Nevertheless, this presented even more demanding requirements on the accuracy of the sampling (Table 2) into the observed d-axis to obtain the envelope of the high frequency response current signal in α-β coordinate system shown in the following formula:
where, iαi and iβi are the α-β axis components of the HF response current, respectively.
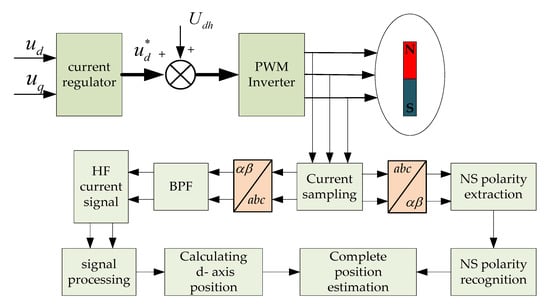
Figure 3.
Block Diagram of the Square Wave HF injection method.
In [45], an IPMSM initial position detection method was proposed on the basis of filterless square wave signal injection, which clearly separated the base frequency from the injection frequency by increasing the square wave frequency of the injection to half the switching frequency. In [46], the HF response current signal was obtained by injecting the pulse square wave voltage signal into the d-axis of the motor, the position deviation signal could be decoupled from the obtained HF signal, and the magnetic pole recognition can be realized by the position tracker. Then, changing the d-axis current bias in a given direction, the filterless carrier signal separation would be realized by simple algebraic operation. This method effectively reduced the consumption, increased the system bandwidth and accelerated the convergence time of position observation strategy. However, this method requires not only the discretization of the HF current response but also high sampling frequency. Though the sampling error was compensated in [47], the outcome remained less than satisfactory due to the high injection frequency and fast current change. In [48], Fourier decomposition was performed to decompose the discrete square wave signal into the sum of sinusoidal signals. In this circumstance, the HF current response is also comprised of sinusoidal basis waves and high-order harmonics, which eliminates the need to calculate the differential current.
In [49], the current was sampled three times during the PWM cycle, the current was compared with two consecutive samples, and then the position error signal was obtained, based on which the correct rotor position was obtained. In the process of extracting the rotor-related information, no filter ingress was required. In [50], an analysis was conducted of the effect caused by the inverter nonlinearity on the injection voltage, the induced current ripple and the position estimation performance, based on which a voltage injection method was developed to adjust the size of the induced current ripple, mitigate the impact of the inverter electromagnetic noise and enhance the position estimation performance.
2.3. Carrier Frequency Component Method
The diagram of carrier frequency component-based logic operation method is shown in Figure 4. To establish the k-l shafting 45 degree in advance of the α-β axis and to conduct the transformation of the mathematical model, the carrier frequency component current was obtained after filtering, whose envelope contained the information on rotor position [51].
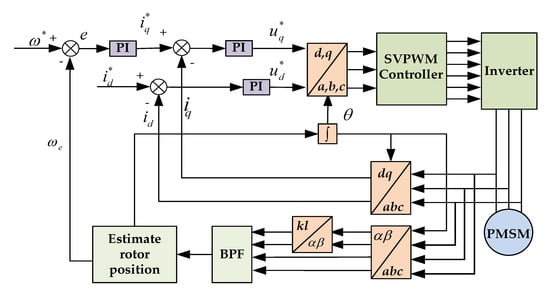
Figure 4.
Block Diagram of the Carrier Frequency Component Method.
Transformation matrix from α-β axis to γ/δ axis:
Put it in Equations (6) and (7):
where, uγi and uδi are the γ/δ axis components of the HF response voltage, respectively. iγi and iδi are the γ/δ axis components of the HF response current.
According to Equations (10) and (11), the rotor position can be calculated as shown in Equation (12):
In [51,52,53], a study was performed on the sensorless control strategy applied in the carrier frequency component method for IPMSM. In this method, a three-phase triangular wave carrier SPWM modulation mode was adopted to provide a continuous carrier frequency component signal, and the rotor position was calculated by analyzing the carrier component in HF current. It took advantage of the structural salient pole effect produced by the motor, which makes it unfit for the SPMSM. In [53], an experiment was conducted on an IPMSM, where a carrier frequency of 20 kHz was adopted. The carrier frequency component of stator current was obtained using an analog bandpass filter. According to the experimental results, the estimated error of the rotor position was ±5 degree, and the estimated error in no-load operation was slightly less significant than in load operation.
2.4. Method Based on Rotor Fretting
In [54], a method based on rotor fretting was proposed to detect the initial position of the rotor. The low frequency rotating voltage vector was applied to the stator winding, which produced the pulsating torque and then made the rotor fretting, thus exerting influence on the current response of the motor. Ultimately, the information on the rotor position was extracted from the current response. With this method applied, however, the detection error remained significant. Moreover, under certain load conditions, the rotor could lose its balance during fretting, which restricts the application of the method in some exceptional circumstances.
2.5. Compound Method
It is possible that a single position detection method is incapable to meet the needs of position detection or the requirement on the accuracy of detection under various working conditions. The combined method of multiple position estimation methods proves effective in improving the accuracy and reliability of detection. In the meantime, however, the complexity of the algorithm could be increased to some extent. Some samples are shown in Table 3.

Table 3.
Hybrid approach sample papers.
The voltage pulse vector method is capable to achieve high accuracy in theory and the software algorithm is simple to apply. Nevertheless, the accuracy of current detection hardware circuit is required to be fairly high. The direction of permanent magnet rotor magnetic pole can be judged accurately and quickly by measuring current change in line with the equal width voltage pulse injection method. In [55], the two methods as mentioned above were combined to determine the initial position by judging the size of equivalent DC current. Despite the ease of implementation, the error of rotor initial position detection is made significant by the small voltage vector applied. On the basis of the conventional pulse vibration HF injection method, the virtual high frequency rotation coordinate was introduced in [56,57,58]. Meanwhile, the carrier frequency component method was brought in as the basis of rotor magnetic pole judgment. The initial rotor position detection involves two steps, which are rotor position initial estimation and magnetic pole judgment as well as pole polarity correction. This method removes the need for PI adjustment and is easy to apply in engineering settings. Moreover, it can help solve the zero-crossing problem encountered when some traditional pulse vibration high frequency injection methods are used.
Figure 5 shows the estimated results obtained by combining pulse HF signal injection method with carrier frequency component method, which is from [58]. (a) and (b) are the sensorless starting waveforms of a given motor starting angle of 1 rad and 4 rad, respectively. The motor is given 60% load torque, and the target speed is 100 rpm. The proposed method can be used to estimate the rotor position of SPMSM in static state. After entering the steady-state operation stage, the estimated speed can still track the actual speed well.
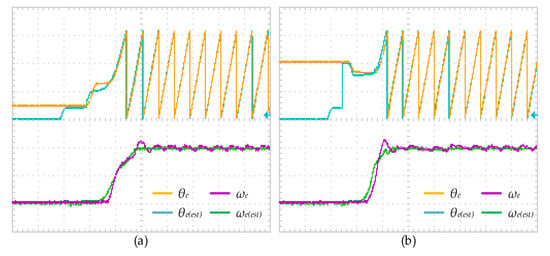
Figure 5.
Waveforms of sensorless estimation at zero-low speed. (Initial rotor angle: (a) 1 rad; (b) 4 rad).
3. Sensorless Control Scheme for Medium-High Speed Operation
In addition to the aforementioned method based on salient pole tracking, the sensorless control technology of PMSM includes the method of fundamental wave model [9], which relies on the back electromotive force related to the rotational speed of the motor in the fundamental wave excitation model for the estimate of rotor position and speed. As the motor runs at zero speed and very low speeds, while the signal-to-noise ratio of useful signals is extremely low, it is usually difficult to conduct extraction.
At present, there are several types of sensorless control technologies applicable for medium-high speed operation, including back EMF method, third harmonic, flux estimation method, model referencing adaptive system (MRAS), state observer method and so on, as shown in Figure 6. A brief introduction of the basic principle that each estimation method follows and an analysis of its advantages and disadvantages are presented as Table 4.
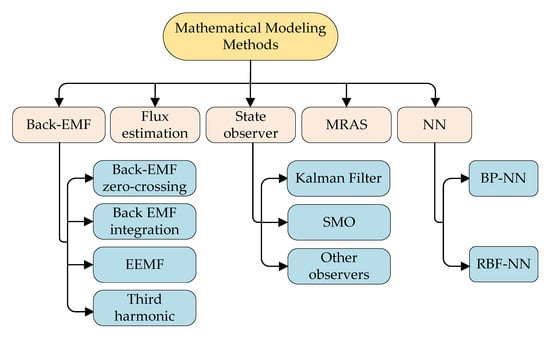
Figure 6.
Sensorless strategies for medium-high speed.

Table 4.
Back EMF methods and analysis.
3.1. Back EMF Methods
3.1.1. Back EMF Zero-Crossing Detection Method
Nowadays, back EMF zero-crossing detection method has been most widely used and represents the relatively most mature position sensorless control method for motors. It is widely used in low-cost equipment, such as pumps, fans and so on. In the operation of BLDC motor, once the zero crossing point of positive and negative alternating potential of back EMF is captured, then the phase 30° is shifted, and the trigger signal of power tube can be obtained according to the phase sequence conduction logic, thus realizing the sensorless control [10].
The three-phase voltage can be obtained by line voltage. The expressions are as follows:
The formula can be transformed and simplified:
In order to resolve the problem that the starting performance of sensorless BLDC motor is easily affected by load, a closed-loop starting method was proposed by Wang [25] on the basis of direct back EMF. In this paper, the principle of commutation was analyzed according to the non-conduction phase terminal voltage in the acceleration process, based on which a method was suggested to determine the voltage threshold at the commutation point. In [59], an anti-potential zero-crossing detection method based on the line-to-line voltage difference was proposed. The three-phase terminal voltage of brushless DC motor stator was subtracted to determine the voltage difference between the lines which contains the information on rotor position. As the armature resistance deviation and the back EMF deviation between different phases are ignored, the reversal error will be amplified significantly when the manufacturing process deviation of the motor is excessively large. In [60], an improved adaptive filter rotor position estimation method based on the effective flux model was proposed. The adaptive notch filter (ANF) was applied to filter the harmonic components of the specified back EMF observations. Based on the harmonic analysis results, the filter parameters were subject to continuous adjustment online by the least mean square (LMS) to ensure the fast convergence of the observer. In Ref. [61], a detection method based on pseudo neutral fundamental voltage was presented. By comparing the relationship between the terminal voltage of the phase winding and the false neutral voltage, the rotor position information was obtained directly. Eliminating the need to change the comparison object, this method has demonstrated its universal applicability. Though the hardware and software implementation of “virtual neutral point method” is simple, the accuracy of neutral point voltage depends on that of the resistance network, and noise interference can result from the process of commutation.
3.1.2. Back EMF Integration Method
There are four methods that can be adopted to realize the back EMF integration method, which are the direct back EMF integration threshold comparison method and the direct back EMF phase-locked loop integral method, third harmonic integral threshold comparison method and third harmonic phase-locked loop integral method [62,63]. The back EMF integration method is reliant on the phase voltage of the non-working phase for the purpose of detection. It is used in places where the load is not fixed such as electric seats.
The motor’s back EMF can be expressed by the following equation:
where, Ke is the back EMF coefficient, B[θ(t)] is the air gap flux density.
When the air gap flux density is standard trapezoid:
When the air-gap flux density is sine wave and the flux density amplitude is constant:
By substituting the commutation time τ = 6 into the above equations, the integral threshold can be obtained. The exact commutation points can be obtained by adjusting the integral threshold.
Distinct from the above-mentioned approach, the former changes the phase through the software delay of 30° electric angle after the zero potential is detected, which makes it possible for commutation error to arise from the motor speed change. The latter starts to integrate the back EMF of the non-conductive phase at zero crossing time, and determines the commutation time by means of voltage comparison. The results are related to the back EMF waveform and independent of the speed of the motor. With adjustment made to the threshold value, the lead or lag commutation can be realized [64]. In this method, it is necessary to introduce an additional integral circuit and increase the complexity of hardware, which may cause additional integral error and reduce the accuracy of commutation. In [65], which aimed at the automobile electric seat, a sensorless DC brushless motor trial starting method based on the back EMF integration method was designed, and an analysis was carried out of the characteristics exhibited by the back EMF integration method and the commutation error caused by the error of zero crossing detection of the back EMF.
3.1.3. Extended EMF (EEMF) Method
The mathematical model of the motor is transformed as follows to obtain the equation [66]:
where, E is the EEMF. Eα and Eβ are the α-β axis components of the EEMF, respectively.
The E term in the equation related to rotor angle and angular velocity. The observer can be established according to the motor model to estimate the E value and obtain the position information.
In [67], the concept of extended reverse EMF was introduced. The DC component and AC component of inductor on axis α and axis β were decoupled, while the AC component was added to the winding back EMF for the formation of EEMF depending on which rotor position is calculated. A disturbance observer was employed to offset the influence of high order harmonics in the EEMF. In [68], an EMF position observer that adopted a second-order generalized integrator (SOGI) was proposed to eliminate harmonic errors. The nonlinearity of the inverter and the harmonic of the magnetic flux space causing the harmonic error of position estimation were analyzed. In multiple selective EMF harmonic cancellation, a harmonic decoupling network comprised of multiple SOGIs-based adaptive filters was used. As an effective extended EEMF-based sensorless strategy for IPMSM, SMO applied the carrier-based synchronous modulation to ensure the symmetry of the output waveform.
3.2. Third Harmonic Method
Due to the magnetic saturation effect produced by the PMSM, or the third harmonic component designed on the PM flux linkage, the stator winding contains the obvious third harmonic back-electromotive force component. In the methods used for the estimate of the rotor position, the third harmonic shows the advantages of simple implementation, which removes the need for depth filtering and the likes. Among these methods of rotor position approaches, not only is the operation range of the motor expanded, the operating characteristic of the motor at low speeds is improved as well. However, the amplitude of the third harmonic is less than that of the anti-potential, which makes it difficult to detect. Besides this, a complex process of Fourier decomposition is required, as a result of which the requirement on the controller is high. The third harmonic back EMF method is unsuitable if the neutral point is incapable to be drawn from the inside of the motor, or the third harmonic component is zero or very small.
The Fourier transform of the motor’s back EMF formula shows that:
where, ki is the Fourier expansion term of i-th power harmonics.
The following formula can be obtained by summing the upper equations:
where, uHF is the Fourier expansion term of higher frequency harmonic components.
In [65], four methods were summarized, including direct back EMF integral threshold comparison method, direct back EMF phase-locked loop integration method, third harmonic integration threshold comparison method and third harmonic phase-locked loop integration method. The third harmonic and phase-locked loop method was proposed to eliminate the effect of the on-off voltage and the noise caused by the PWM switch. In order to address the commutation error of the BLDC motor, a sensorless control and compensation scheme was proposed in [69,70] on the basis of the virtual third-order harmonic back EMF combined with back EMF power factor combining synchronic frequency extractor (BEPF-SFE). By analyzing the zero crossing of the third harmonic back EMF, Liu J M detected the rotor position. The position estimation error was ±9°, while the position estimation error was reduced to ±2° by introducing the continuous signal of PLL analysis. In order to improve the performance of rotor position estimation in sensorless control of flux observer, the three harmonic back EMF was integrated in [71]. Unlike the conventional method, the proposed method takes the continuous signal as a reference, determines the phase difference between the estimated and referenced third harmonic flux and applies it to compensate for the velocity estimation error calculated from the zero-crossing point at each sampling moment. Then, the rotor position can be obtained from the compensated rotor speed. In [72], a rotor position error compensator based on the third harmonic back EMF was presented. The third harmonic flux obtained by the third harmonic back EMF integral shows its superiority to the conventional flux observer in the insensitivity of mechanical parameters.
3.3. Flux Estimation Method
The flux linkage estimation method is applied to estimate the rotor position by detecting the flux linkage information on the rotor. Though it cannot be obtained directly, the first derivative of the rotor flux linkage is calculated to be the Reverse EMF of the motor, which makes the voltage and the current variable value of the motor applicable for integral operation.
The motor flux equation in d-q coordinate system is established as follows:
In [73], a full-order flux observer was suggested to estimate current and flux. The estimated d-q axis currents and fluxes were referenced to predict the rotor position. In [74], a method of PM flux adaptive observer was proposed. With the Popov hyperstability theorem used, a feedback gain design method was proposed on the basis of analyzing the impact of parameters error on the observation results, and the adaptive law PI parameters were optimized. In [75], an implementation method of sensorless control system was proposed on the basis of “active flux” observer in a wide range of rotating speed. A direct torque flux control system with space vector modulation (DTFC-SVM) but without signal injection for IPMSM was put forward.
The flux linkage estimation method is not only simple and feasible, but also suited to SPMSM. However, the algorithm is more sensitive to various motor parameters, especially the stator resistance and inductance. Moreover, the motor parameters tend to vary as the working conditions change.
3.4. State Observer Method
Under this detection strategy, the discrete values of each state variable are obtained by digital filtering, the mathematical model of the system is established, and the rotor position is estimated using the algorithm. The state observer is advantageous in the robustness to interference and the ease of control under high-speed and heavy-load conditions, which requires the system to have high working frequency and excellent digital processing ability.
3.4.1. Extened Kalman Filter (EKF) Method
As an efficient recurrent filter, EKF solves the problem of non-linearity by linearizing the recently estimated state [76]. EKF refers to an optimal estimation algorithm that combines the idea of state space and the theory of optimal filterin [77]. Based on the mathematical model of the motor, the filtering capacity of each state variable is detected within a fixed period, as shown in Table 5. In the meantime, the position signal and speed of the motor rotor are estimated. As for the disadvantage of it, the calculation workload is high and the initial position of the rotor must be known in advance.

Table 5.
EKF algorithm.
In [78], voltage and current were taken as the input and output in the two-phase static coordinate system, respectively, while the stator flux, motor speed and rotor position were treated as state variables. Then, an EKF filter system was constructed to estimate the stator flux, motor speed and rotor position. In [79], the impact of motor parameters on EKF estimation was analyzed. Besides this, the MRAS method was adopted to identify motor parameters and update EKF model for improving the estimation results.
In [80,81], unscented Kalman filter (UKF) was applied to conduct nonlinear state estimation of linear motor sensorless drive system for improving the low-speed performance. In [82], it was proposed to take the modified exponential approach in a sliding mode and EKF to estimate the speed, which improved the performance of low speed. A parallel reduced order EKF algorithm based on field programmable gate array (FPGA) was proposed in [83], where the iterative process was significantly simplified, plenty of resources were saved and the operation accuracy was enhanced at the same time. As revealed by the experimental results on FPGA platform, the position estimation error was approximately 4°.
3.4.2. Sliding Mode Observer (SMO) Method
In essence, the sliding mode control (SMC) is a variable structure-based control observer, which selects an ideal slip face and then drives the state variable rail line along the slip face by making dynamic change to the structure of the system. The SMO method based on anti-electric potential (EMF) or magnetic chain estimation displays advantages such as the insensitivity to system parameters, the insensitivity to disturbance and high robustness, for which it has been widely used in practice [84,85,86]. The block diagram of observers’ method is shown in Figure 7. The traditional sliding mode observation model can be expressed as follows:
where, sign is the switch function; k is the gain coefficient of sliding mode; eα, eβ is the back EMF in α-β coordinate system.
Figure 7.
Block diagram of state observers method.
In [87], a fourth-order hybrid SMO was proposed for SPMSM, as observed with current and magnetic chains. The differences between the actual current and the observation constitute the slide surface, the magnetic chain observation equation is entered after the equivalent signal is multiplied with the feedback matrix, and the magnetic chain observation error gradually converges to zero after the slide mode motion occurs. Then, the position and velocity algorithm were calculated according to the magnetic chain observation results. Zhao adopted MRAS method to independently estimate the rotor speed and decoupled it from position estimation. Combined adaptive line enhancer and SMO are employed to reduce the noise content in the estimated speed, and took the estimated rotor speed as the feedback input signal to reduce the oscillation error in the rotor position estimation.The vector control system was applied for the positionless sensor of the table-mounted permanent magnet synchronous motor in [88]. In [89], a double-surface SMO was proposed based on an IM model in the stationary reference frame. The observer was designed through combining sliding variables produced by combining estimated fluxes of currents error, and the particle swarm optimization method was adopted to optimize these observer parameters and then improve the transient condition by optimally tuning the observer parameters.
In [90], a sensorless control scheme based on a SMO with a fuzzy logic controller (FLC) and a dual second-order generalized integrator-frequency locked loop was proposed. An FLC was designed and integrated into the SMO to adjust the observer gain in a self-adaptive manner and to reduce the chattering. In [91], based on Lyapunov stability theorems, the adaptive fuzzy slide model observer was constructed, the fuzzy control system was designed by analyzing the effect of the slip mode gain on system vibration, and the anti-electric potential observer was established instead of the low-pass filter, which improved the robustness of the system. In [92], EEMF was used for the sensorless control strategy of IPMSM, and the SMO was used to estimate the extended anti-electric potential component in the two-phase stationary coordinate system for detecting the spatial position of the rotor. Based on the Lyapunov function, the convergence of observational parameters was analyzed. In [93,94], an adaptive high-order SMO with super-twisting algorithm was suggested with the motor parameters recognized online. The combination of super-twisting algorithm and SMO achieved the accurate estimate of counter electromotive force.
In response to the vibration problems arising from the conventional slip surface, the Sigmoid function was used in [95,96] instead of the Signum function, which addressed the time delay caused by the LPF while improving the robustness of the entire system. A study was performed on the input switching function selection symbol function, which led to the finding that the estimation error in the high-speed operating area was significant and the precision of position estimation was enhanced significantly after the use of S-type function. In [97], the stator current and the anti-electric potential were taken as the state variables, and a full-order SMO with the variable hyperbolic tangent function of the boundary layer was proposed as the switch function, which can mitigate system vibration. In [98], the feedback of the anti-potential estimation was factored into the stator current observation calculation, and an LPF with rotor speed change was designed, which simplified the hardware structure of the speed control system. Besides, an adaptive algorithm was proposed for the counter-potential feedback gain coefficient.
3.4.3. Other Observers
The state observer method realizes the control of the motor by analyzing state variables such as the speed and current of the motor [99]. In addition to Kalman filter and sliding mode observer, there are also other observers such as Luenberger observer, disturbance observer, D-state-Observer and so on, which can be used for sensorless control of permanent magnet brushless motor.
In [100], a mover flux observer combined a disturbance observer and a feedback controller was proposed. Then, a phase-locked loop was used to detected position information from the mover fluxes. In [101,102], a disturbance observer was employed to observe the motor back EMF. In the current state equation under two-phase stationary coordinates, the back EMF was used as interference quantities to eliminate the differential of state variables and filters, while a rotor position error compensation was added with the change of rotational speed. In [103], a two-dimensional motor mathematical model of PMSM without additional steady-state conditions is established, the D-state-Observer was employed to estimate the rotor flux, which can be used for both SPMSM and IPMSM. In [104], a high-gain nonlinear current-velocity observer was designed on the basis of the reduced order global energy observation subsystem, the observer adaptive gain rate was designed using the observed quadrature -axis current differential, and the rotor position was estimated using the differential difference between the current and the actual measurement as observed by the direct axis. In [105], a support vector machine (SVM) regression observer was proposed using the disturbance observer control method. A reverse electromotive force observer and a torque observer were applied to estimate the rotor position and offset the load torque disturbance, which was simple to implement and required no state vector derivation. In [106], the voltage model method and the current model method were combined, the voltage model method was adopted to estimate the flux, and the current model method was used to estimate the current Iαβ. The error between the measured current and its estimated value was treated as a disturbance, which was fed back to the voltage model method for establishing a disturbance observer based on flux observation. In [107], a complex-vector-based discrete-time synchronous-frame full-order observer with a low-pulse width modulation (PWM) to operating fundamental frequency ratio was proposed, the direct pole assignment in the discrete-time domain was used to ensure the stability and dynamic performance with low-frequency ratios.
3.5. Artificial Neural Network (ANN) Method
ANN technology is the hot spot in artificial intelligence field. A typical NN consists of three layers: input layer, hidden layer and output layer. According to the connection mode there are mainly two kinds: feedforward NN and feedback NN. As shown in Figure 8. The neurons of feedforward NN are arranged in layers, and the neurons in each layer only accept the input from the previous layer, and there is no feedback loop. Feedforward networks can be easily connected in series to build multilayer feedforward networks. This kind of network is suitable for prediction, model recognition and nonlinear function approximation. The feedforward NN include error back propagation (BP-NN), radial basis function (RBF-NN), Support vector machines (SVM) and so on. Some deep learning methods such as deep NN (DNN), deep belief network (DBN) and convolution NN (CNN) are widely used. The input signal of feedback network determines the initial state of feedback system. Stability is one of the most important indexes of feedback network. The common feedback NN includes Hopfield NN, Elman NN, Boltzmann machine, wavelet NN and so on.
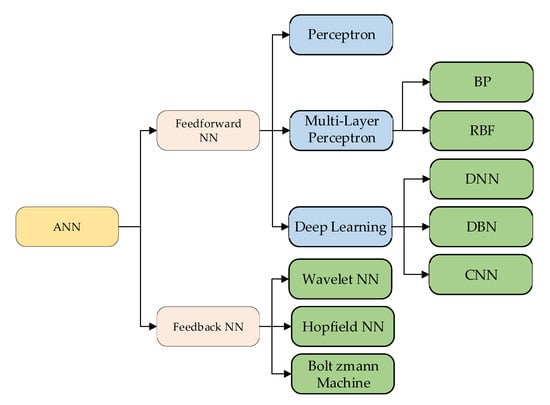
Figure 8.
Artificial neural network (ANN) classification. BP, back propagation; RBF, radial basis function; DNN, deep neural network; DBN, deep belief network; CNN, convolution neural network.
ANN mainly connects the voltage, current and rotor position of the measured phase through adaptive technology and neural network control strategies to capture the rotor position signal [108,109]. There are many kinds of neural networks, and back propagation (BP) network and radial basis function (RBF) network are used more frequently in sensorless estimation.
On the basis of the state equation of the motor in the α-β coordinate system, the NN state space expression is established as follows:
Considering the disadvantages of long training time and slow convergence speed of BP-NN, in [110], an improved method is proposed to transform the fixed weight into a function with adjustable parameters. This method simplifies the complexity of the control system and improves the detection accuracy. The dynamic RBF network model is established [111]. The network gets the initial centers through a k-means algorithm, and gets the weights through recursive least squares (RLS) in off-line training. The network parameters are updated online by gradient descending error algorithm. This method has simpler structure and faster convergence speed. Based on the nonlinear coordinate transformation of the mathematical model under the PMSM α-β coordinate system, the online learning rules of the network right coefficient array were designed by Lyapunov theory in [112], and a nonlinear adaptive observer design method was proposed. In [113], a sensorless control method based on adaptive RBFNN was proposed for SRM. An RBF network with zero initial numbers of hidden layer nodes was constructed. Combining with adaptive algorithm, the number and position of the RBF network hidden layer nodes were determined, while the connection rate between the hidden layer and the output layer was corrected by pushing the least square (LS) online.
3.6. Model Reference Adaptive System (MRAS)
The main idea of model reference adaptive system (MRAS) is as follows. Firstly, the position of the rotor is assumed. Secondly, the voltage and current values of the motor at the hypothetical position are calculated using the motor model. Thirdly, the difference between the two is obtained by comparing it with the measured voltage and current, which is proportional to the angular difference between the hypothetical position and the actual position. When the value decreases to zero, it can be assumed that the hypothetical position is the real location at this time [114]. In this way, the position accuracy is related to the selection of the model. The block diagram of parallel structure MRAS is presented in Figure 9.
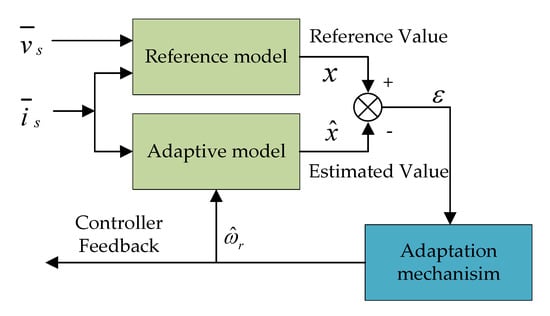
Figure 9.
Block diagram of parallel structure model reference adaptive system (MRAS).
The key point of MRAS lies in the design of adaptive law. A reference model based on motor model is established and the adaptive law is designed by means of Popov hyperstability theory as follows:
In [115], the model reference adaptive observer (MRAO) was applied to estimate the speed and position of the rotor. This method combines the SMC and the MRAS, replaces the PI link in the traditional MRAS algorithm with the SMC algorithm, replaces the traditional current model with the flux model as the adjustable model and simplifies the control algorithm. In [116], an intermediate variable was introduced, and the current equation of the permanent magnetic synchronous motor was transformed into a standard type suitable for the model reference adaptive method. Further with this, the adaptive convergence law of speed was developed. In [117], the current model of the generator was treated as an adjustable model, and the adaptive law was designed to identify the speed and rotor position of PMSM simultaneously. A maximum power point tracking (MPPT) control strategy based on the variable-step climbing method was proposed, which showed advantages such as fast dynamic power tracking and smooth speed when in a steady state. In [118], the SMC was integrated with the MRAS, the current model was taken as the adjustable model, and the slip face was constructed by the error of the two model outputs. In [119], the fuzzy PI regulator was applied to the model reference adaptive observer, based on which a fuzzy PI MRAS observer was proposed.
Figure 10 shows the experimental results in [116]. Figure 10a shows the estimated rotor position and estimation error at different speeds. The MRAS method has a good performance in the extremely low speed region of the motor, and the estimation accuracy of the rotor position is improved with the increase of the speed. The maximum position error of the proposed estimator is 6°. Figure 10b shows the estimated results under variable load. This method is robust to the change of motor parameters and external interference, so it is suitable for situations with variable load and working conditions.
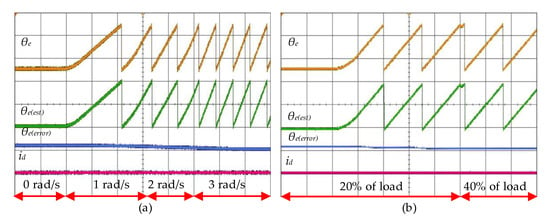
Figure 10.
Experimental results using MRAS. (a) Measured and estimated rotor position and rotor position at 20% of full load. (b) Measured and estimated rotor position and rotor position at 1 rad/s. (Scale: ωe, ωe(est): 3 rad/div; ωe(error): 5 rad/div; iq: 2.5 A/div; θe, θe(est): 150°/div; θe(error): 30°/div; id: 1 A/div).
4. Conclusions
(1) The HF signal injection method is employed for sensorless control of permanent magnet traction motor when it is operating under initial position and low speed. However, this method easily brings additional losses and high digital signal processing capacity. The fundamental wave model of the motor is mainly used to estimate the rotor position by various observers in the medium-high speed range, but attention should be paid to the problems of parameter sensitivity and parameter drift of the motor. The hybrid control algorithm with high reliability and good cohesion should be studied to avoid torque ripple caused by large current during algorithms switching between different speed ranges.
(2) The rotor position can be softly measured through a sensorless technique, which can realize high-performance control of the permanent magnet traction motor. The sensorless control has a broad application prospect in the field of electric vehicle traction systems. At present, the basic principle and control strategy of permanent magnet drive motor without position sensor for electric vehicle have got a certain application. However, in general, the position sensorless control strategy of permanent magnet traction motor and its application are still in the primary stage.
(3) It is a significant research direction to investigate the speed and position estimation approach considering the motor parameters identification techniques, which can realize the stable and reliable operation of the traction motor for EV.
(4) The traction motor for electric vehicle faces complex operation conditions, such as frequent start/stop, rapid acceleration/deceleration, overload and uphill/downhill, which is supposed to operate in a wide speed range. The rotor position estimation methods should be switched frequently, especially while the EV is operating in the urban setting. That means the hybrid rotor position estimation methods for sensorless control should be investigated to improve the reliability and the dynamic performance of the traction motor in the wide speed range.
Author Contributions
Manuscript preparation and writing, H.W.; review and editing, Y.L.; investigation, X.X.; methodology, X.S. and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China, Grant No. 51705213, the Key Laboratory of Automotive Power Train and Electronics (Hubei University of Automotive Technology), Grant No. ZDK1201901, and the China Postdoctoral Science Foundation, Grant No. 2019M660105 and Grant No. 2020T130360.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, Y.; Xu, X.; Sun, X.D.; Jiang, H.B.; Qu, Y.P. Review and Future Development of In-Wheel Motor Drive Technology. Electr. Mach. Control Appl. 2017, 44, 1–7. [Google Scholar]
- Li, Y.; Wu, H.; Zhang, B.H. Frontier techniques and prospect of in-wheel motor for electric vehicle. J. Jiangsu Univ. Nat. Sci. Ed. 2019, 40, 261–268. [Google Scholar]
- Tanwir, N.S.; Hamzah, M.I. Predicting Purchase Intention of Hybrid Electric Vehicles: Evidence from an Emerging Economy. World Electr. Veh. J. 2020, 11, 35. [Google Scholar] [CrossRef]
- Yu, Y.; Jiang, J.; Min, Z.; Wang, P.; Shen, W. Research on Energy Management Strategies of Extended-Range Electric Vehicles Based on Driving Characteristics. World Electr. Veh. J. 2020, 11, 54. [Google Scholar] [CrossRef]
- Sun, X.D.; Hu, C.C.; Lei, G.; Yang, Z.B.; Guo, Y.G.; Zhu, J.G. Speed sensorless control of SPMSM drives for EVs with a binary search algorithm-based phase-locked loop. IEEE Trans. Veh. Technol. 2020, 69, 4968–4978. [Google Scholar] [CrossRef]
- Liu, C.H.; Luo, Y.X. Overview of Advanced Control Strategies for Electric Machines. Chin. J. Electr. Eng. 2017, 3, 53–61. [Google Scholar]
- Sahoo, B.; Routray, S.K.; Rout, P.K. A novel sensorless current shaping control approach for SVPWM inverter with voltage disturbance rejection in a dc grid-based wind power generation system. Wind Energy 2020, 23, 986–1005. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.G.; Chen, Z.; Mao, S.; Meng, T.; Peng, J.C.; Jiao, N.F. A Time-Delay Compensation Method for IPMSM Hybrid Sensorless Drives in Rail Transit Applications. IEEE Trans. Ind. Electron. 2019, 66, 6715–6726. [Google Scholar] [CrossRef]
- Liu, J.L.; Xiao, F.; Shen, Y.; Mai, Z.Q.; Li, C.R. Position-Sensorless Control Technology of Permanent-Magnet Synchronous Motor-a Review. Trans. China Electrotech. Soc. 2017, 32, 76–88. [Google Scholar]
- Chen, S.H.; Liu, G.; Zhu, L.Q. Sensorless Startup Strategy for a 315-kW High-Speed Brushless DC Motor with Small Inductance and Nonideal Back EMF. IEEE Trans. Ind. Electron. 2019, 66, 1703–1714. [Google Scholar] [CrossRef]
- Li, K.; Ling, F.; Sun, X.D.; Cai, Y.F.; Zhao, D.; Yang, Z.B. Displacement sensorless control for bearingless induction motor drives based on the MRAS method. Int. J. Appl. Electromagn. Mech. 2020, 62, 787–805. [Google Scholar] [CrossRef]
- Shinnaka, S.; Takeuchi, S. A New Sensorless Drive Control System for Transmissionless EVs Using a Permanent-Magnet Synchronous Motor. World Electr. Veh. J. 2007, 1, 1–9. [Google Scholar] [CrossRef]
- Lu, Q.; Zhu, X.Y.; Li, Q.; Zuo, Y.F.; Du, S.C. Rotor position estimation scheme with harmonic ripple attenuation for sensorless controlled permanent magnet synchronous motors. IET Electr. Power Appl. 2018, 12, 1200–1206. [Google Scholar] [CrossRef]
- Sun, X.D.; Cao, J.H.; Lei, G.; Guo, Y.G.; Zhu, J.G. Speed Sensorless Control for Permanent Magnet Synchronous Motors Based on Finite Position Set. IEEE Trans. Ind. Electron. 2020, 67, 6089–6100. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, X.Y.; Gao, J.; Mao, Y. Design and Analysis of New Five-Phase Flux-Intensifying Fault-Tolerant Interior-Permanent-Magnet Motor for Sensorless Operation. IEEE Trans. Ind. Electron. 2020, 67, 6055–6065. [Google Scholar] [CrossRef]
- Scicluna, K.; Staines, C.S.; Raute, R. Sensorless Low/Zero Speed Estimation for Permanent Magnet Synchronous Machine Using a Search-Based Real-Time Commissioning Method. IEEE Trans. Ind. Electron. 2020, 67, 6010–6018. [Google Scholar] [CrossRef]
- Wang, G.L.; Valla, M.; Solsona, J. Position Sensorless Permanent Magnet Synchronous Machine Drives—A Review. IEEE Trans. Ind. Electron. 2020, 67, 5830–5842. [Google Scholar] [CrossRef]
- Ren, L.; Cui, R.H.; Wang, Z.P.; Cheng, Z. Saturation Effect of PMSM Windings Inductance. Trans. China Electrotech. Soc. 2000, 15, 21–25. [Google Scholar]
- Wang, C.; Li, Z.; Kang, G.Q.; Zeng, C.Y. BLDC Motor Torque Ripple Control Using Self-Tuning PID Fuzzy Control System. Appl. Mech. Mater. 2016, 851, 459–463. [Google Scholar] [CrossRef]
- Acarnley, P.P.; Watson, J.F. Review of position-sensorless operation of brushless permanent-magnet machines (Review). IEEE Trans. Ind. Electron. 2018, 53, 352–362. [Google Scholar] [CrossRef]
- Shi, T.N.; Li, C.; Jiang, G.K.; Xia, C.L. Model free predictive control method to suppress commutation torqueripple for brushless DC motor. Trans. China Electrotech. Soc. 2016, 31, 54–61. [Google Scholar]
- Wang, Z.H.; Lu, K.Y.; Ye, Y.Y. Initial position estimation method for permanent magnet synchronous motor based on improved pulse voltage injection. Proc. CSEE 2011, 31, 95–101. [Google Scholar]
- Nakashima, S.; Inagaki, Y.Y.; Miki, I. Sensorless initial rotor position estimation of surface permanent-magnet synchronous motor. IEEE Trans. Ind. Appl. 2000, 36, 1598–1603. [Google Scholar]
- Tang, N.P.; Cui, B. A high resolution detectingmethod for rotor zero initial position of sensorlessbrushless DC motor. Trans. China Electrotech. Soc. 2013, 28, 90–96. [Google Scholar]
- Wang, Q.; Wang, Y.R.; Kong, D.M.; Xu, X.M. Initial rotor position estimation for non-salient polebrushless DC Motors. Proc. CSEE 2012, 32, 105–110. [Google Scholar]
- Gambetta, D.; Ahfock, A. New sensorless commutationtechnique for brushless DC motors. IET Electr. Appl. 2009, 3, 40–49. [Google Scholar] [CrossRef]
- Gong, J.; Liao, L.Q.; Ye, B.Q. Brushless DC Motor Starting Based on High Precision Inductance Method and Study on the Stability of BEMF Synchronous Detection. Trans. China Electrotech. Soc. 2017, 32, 105–112. [Google Scholar]
- Meng, G.J.; Yu, H.T.; Huang, L.; Jiu, C.X.; Zhao, D.D. A Novel Initial Rotor Position Estimation Method for PMSM Based on Variation Behavior of Line Inductances. Trans. China Electrotech. Soc. 2015, 30, 1–9. [Google Scholar]
- Sun, W.; Shen, J.X.; Li, P.; Wang, K. Iron Core Hysteresis-Based Position Sensorless Control of PM Brushless DC Motors. Appl. Mech. Mater. 2013, 416, 583–588. [Google Scholar] [CrossRef]
- Tang, Q.P.; Shen, A.W.; Luo, X.; Xu, J.B. IPMSM Sensorless Control by Injecting Bidirectional Rotating HF Carrier Signals. IEEE Trans. Power Electron. 2018, 33, 10698–10707. [Google Scholar] [CrossRef]
- Qin, F.; He, Y.K.; Liu, Y.; Zhang, W. Comparative investigation of sensorless control with two high-frequency signal injection schemes. Proc. CSEE 2005, 25, 118–123. [Google Scholar]
- Lu, J.D.; Liu, J.L.; Wei, L.C. Estimation of the Initial Rotor Position for Permanent Magnet Synchronous Motors. Trans. China Electrotech. Soc. 2015, 30, 105–111. [Google Scholar]
- Zhou, Y.J.; Cai, M.F. Initial rotor position inspection of PMSM based on rotating high frequency voltage signal injection. Electr. Mach. Control 2010, 14, 68–72. [Google Scholar]
- Wang, G.L.; Zhang, G.Q.; Gui, X.G.; Xu, D.G. Hybrid Sensorless Control Strategy for Permanent Magnet Synchronous Motors. Proc. CSEE 2012, 32, 103–109. [Google Scholar]
- Wang, G.L.; Yang, R.F.; Yu, Y.; Xu, D.G. Position Sensorless Control for Interior Permanent Magnet Synchronous Motor. Proc. CSEE 2010, 30, 93–98. [Google Scholar]
- Kim, S.I.; Song, E.Y.; Im, J.H.; Kim, R.Y. A new rotorposition estimation method of IPMSM using all-pass filter on high-frequency rotating voltage signal injection. IEEE Trans. Ind. Electron. 2016, 63, 6499–6509. [Google Scholar] [CrossRef]
- Tian, B.; An, Q.T.; Sun, D.Y.; Sun, L.; Zhao, K. Initial Position Estimation for Surface Permanent Magnet Synchronous Motors Based on Magnetic Saturation Effect. Trans. China Electrotech. Soc. 2016, 31, 155–164. [Google Scholar]
- Zhu, Z.Q.; Gong, L.M. Investigation of effectiveness of sensorless operation in carrier signal injection based sensorless control methods. IEEE Trans. Ind. Electron. 2011, 58, 3431–3439. [Google Scholar] [CrossRef]
- Lin, T.C.; Zhu, Z.Q. Sensorless operation capability of surface-mounted permanent-magnet machine based on high-frequency signal injection methods. IEEE Trans. Ind. Appl. 2015, 51, 2161–2171. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, B.; Li, S.; Feng, Y. Initial Rotor Position Detection of Surface Mounted Permanent Magnet Synchronous Motor. Proc. CSEE 2011, 31, 48–54. [Google Scholar]
- Gong, L.M.; Zhu, Z.Q. Robust initial rotor position estimation of permanent-magnet brushless ac machines with carrier-signal-injection-based sensorless control. IEEE Trans. Ind. Appl. 2013, 49, 2602–2609. [Google Scholar] [CrossRef]
- Liu, H.D.; Zhou, B.; Guo, H.H.; Liu, B.; Li, J.; Xu, X.H.; Shi, R.S. Error Analysis of High Frequency Pulsating Signal Injection Method. Trans. China Electrotech. Soc. 2015, 30, 38–44. [Google Scholar]
- Liu, J.M.; Zhu, Z.Q. Novel sensorless control strategy with injection of high-frequency pulsating carrier signal into stationary reference frame. IEEE Trans. Ind. Appl. 2014, 50, 2574–2583. [Google Scholar] [CrossRef]
- Liu, J.M.; Zhu, Z.Q. Sensorless control strategy by square aveform high-frequency pulsating signal injection into stationary reference frame. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 171–180. [Google Scholar] [CrossRef]
- Yoon, Y.D.; Sul, S.K.; Morimoto, S.; Ide, K. High-Bandwidth Sensorless Algorithm for AC Machines Based on Square-Wave-Type Voltage Injection. IEEE Trans. Ind. Appl. 2011, 47, 1361–1370. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Wang, G.L.; Xu, D.G. Filterless Square-Wave Injection Based Initial Position Detection for Permanent Magnet Synchronous Machines. Trans. China Electrotech. Soc. 2017, 32, 162–168. [Google Scholar]
- Wang, G.L.; Yang, L.; Yuan, B.H. Pseudo-random high frequency square-wave voltage injection basedsensorless control of IPMSM drives for audible noisereduction. IEEE Trans. Ind. Electron. 2016, 63, 7423–7433. [Google Scholar] [CrossRef]
- Li, W.Z.; Liu, J.L.; Chen, S.S. Permanent Magnet Synchronous Motor Rotor Position Detection Method Based on High-Frequency Square-Wave Signal Injection. Trans. China Electrotech. Soc. 2018, 33, 5821–5829. [Google Scholar]
- Wu, T.; Wang, H.; Luo, D.R.; Shao, J.B. A New Initial Position Estimation Method for Interior Permanent Magnet Synchronous Motor. Trans. China Electrotech. Soc. 2018, 33, 3578–3585. [Google Scholar]
- Kim, D.; Kwon, Y.C.; Sul, S.K.; Kim, J.H.; Yu, R.S. Suppression of injection voltage disturbance for High Frequency square-wave injection sensorless drive with regulation of induced High Frequency current ripple. IEEE Trans. Ind. Appl. 2016, 52, 302–312. [Google Scholar] [CrossRef]
- Zhu, J.; Tian, M.; Fu, R.B.; Liu, H.J. Research on rotor position of permanent magnet synchronous motor based on carrier frequency component. Power Syst. Prot. Control 2015, 43, 48–54. [Google Scholar]
- Mamo, M.; Ide, K.; Sawamura, M.; Oyama, J. Novel rotor position extraction based on carrier frequency component method (CFCM) using two reference frames for IPM drives. IEEE Trans. Ind. Electron. 2005, 52, 508–514. [Google Scholar] [CrossRef]
- Gao, H.W.; Yu, Y.J.; Chai, F.; Cheng, S.K. Position sensorless control of interior permanent magnet synchronous motor based on carrier frequency component method. Proc. CSEE 2010, 30, 91–96. [Google Scholar]
- Li, Y.T.; Hu, H.F.; Qu, W.L.; Shuang, S. A novel initial rotor position estimation method for permanent magnet synchronous motors. Proc. CSEE 2013, 33, 75–82. [Google Scholar]
- Wei, K.; Jin, X.H. Initial rotor position estimate technique on surface mounted permanent magnet synchronous motor. Proc. CSEE 2006, 26, 104–109. [Google Scholar]
- Hong, K.; Liu, G.; Mao, K.; Lv, X.Y.; Zhou, X.X. Initial Position Detection of Surface Mounted Permanent Magnet Synchronous Machines Based on Novel High-Frequency Injection Method. Trans. China Electrotech. Soc. 2018, 33, 2914–2922. [Google Scholar]
- Lv, X.Y.; Liu, J.; Mao, K.; Chen, B.D. Initial Position Detection of Permanent Magnet Motor Based on Virtual Pulsating High-Frequency Injection Method. Trans. China Electrotech. Soc. 2017, 32, 34–41. [Google Scholar]
- Li, J.; Zhou, B.; Liu, B.; Wang, L.; Ni, T.H.; Xu, X.H.; Shi, R.S. A Novel Starting Strategy of Sensorless Control for Surface Mounted Permanent Magnet Synchronous Machines. Proc. CSEE 2016, 36, 2513–2520. [Google Scholar]
- Damodharan, P.; Vasudevan, K. Sensorless Brushless DC Motor Drive Based on the Zero-Crossing Detection of Back Electromotive Force (EMF) From the Line Voltage Difference. IEEE Trans. Energy Convers. 2010, 25, 661–668. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Wang, G.L.; Xu, D.G.; Fu, Y.; Ni, R.G. Adaptive Notch Filter Based Rotor Position Estimation for Interior Permanent Magnet. Proc. CSEE 2016, 36, 2521–2527. [Google Scholar]
- Wang, D.F.; Zhu, Y.Q.; Jin, Y.; Liu, Z.Q. A novel research on detecting position of brushless DC motors. Trans. China Electrotech. Soc. 2013, 28, 139–144. [Google Scholar]
- Shen, J.X.; Iwasaki, S. Sensorless control of ultrahigh-speed PM brushless motor using PLL and third-harmonic back EMF. IEEE Trans. Ind. Electron. 2006, 53, 421–428. [Google Scholar] [CrossRef]
- Wang, D.F.; Zhu, Y.Q.; Jin, Y.; Zhao, G.Y. Tentative Strategy of Starting Sensorless BLDCM with the Method of Integrating the Back EMF. Trans. China Electrotech. Soc. 2012, 27, 178–184. [Google Scholar]
- Gupta, N.; Pandey, D.A.K. A Review: Sensorless Control of Brushless DC Motor; Esrsa Publications: Auckland, New Zealand, 2012. [Google Scholar]
- Chen, Z.Q.; Tomita, M.; Doki, S. An extended electromotive force model for sensorless control of interior permanent- magnet synchronous motors. IEEE Trans. Ind. Electron. 2003, 50, 288–295. [Google Scholar] [CrossRef]
- Zhang, B.; Ge, Q.X.; Liu, J.X.; Wang, X.X.; Li, Y.H. Research on Speed Sensorless Control of long Stator Linear Synchronous Motor Based on EEMF. Trans. China Electrotech. Soc. 2017, 32, 91–99. [Google Scholar] [CrossRef]
- Jae, L.Y.; Bak, Y.; LEE, K.B. Restarting Method for EEMF Based Sensorless Permanent Magnet Synchronous Motor Drive Systems. Trans. Korean Inst. Power Electron. 2019, 23, 127–133. [Google Scholar]
- Wang, G.L.; Ding, L.; Li, Z.M.; Xu, J.; Zhang, G.Q.; Zhan, H.L.; Ni, R.G.; Xu, D.G. Enhanced Position Observer Using Second-Order Generalized Integrator for Sensorless Interior Permanent Magnet Synchronous Motor Drives. IEEE Trans. Energy Convers. 2014, 29, 486–495. [Google Scholar]
- Song, X.D.; Han, B.C.; Wang, K. Sensorless Drive of High-Speed BLDC Motors Based on Virtual Third-Harmonic Back EMF and High-Precision Compensation. IEEE Trans. Power Electron. 2018, 34, 8787–8796. [Google Scholar] [CrossRef]
- Song, X.D.; Han, B.C.; Zheng, S.Q.; Chen, S.H. A Novel Sensorless Rotor Position Detection Method for High-Speed Surface PM Motors in a Wide Speed Range. IEEE Trans. Power Electron. 2017, 33, 7083–7093. [Google Scholar] [CrossRef]
- Liu, J.M.; Zhu, Z.Q. Improved sensorless control of permanent-magnet synchronous machine based on third-harmonic back EMF. IEEE Trans. Ind. Appl. 2014, 50, 1861–1870. [Google Scholar] [CrossRef]
- Liu, J.M.; Zhu, Z.Q. Rotor position error compensation based on third harmonic back-EMF in flux observer sensorless control. In Proceedings of the International Conference on Electrical Machine, Berlin, Germany, 2–5 September 2014. [Google Scholar]
- Lee, K.G.; Lee, J.S.; Lee, K.B. Wide-range sensorless control for SPMSM using an improved full-order flux observer. J. Power Electron. 2015, 15, 721–729. [Google Scholar] [CrossRef]
- Qiu, T.F.; Wen, X.H.; Zaho, F.; Wang, Y.X. Design Strategy of Permanent Magnet Flux Linkage Adaptive Observer for Permanent Magnet Synchronous Motor. Proc. CSEE 2015, 35, 2287–2294. [Google Scholar]
- Boldea, I.; Paicu, M.C.; Andreescu, G.D.; Blaabjerg, F. “Active flux” DTFC-SVM sensorless control of IPMSM. IEEE Trans. Energy Convers. 2009, 24, 314–322. [Google Scholar] [CrossRef]
- Abdelmaksoud, H.; Zaky, M. Design of an Adaptive Flux Observer for Sensorless Switched Reluctance Motors Using Lyapunov Theory. Adv. Electr. Comput. Eng. 2020, 20, 123–130. [Google Scholar] [CrossRef]
- Ji, J.H.; Jiang, Y.; Zhao, W.X.; Chen, Q.; Yang, A.C. Sensorless Control of Linear Vernier Permanent-Magnet Motor Based on Improved Mover Flux Observer. IEEE Trans. Power Electron. 2019, 35, 3869–3877. [Google Scholar] [CrossRef]
- Zhao, Q.; Yang, Z.B.; Sun, X.D.; Ding, Q.F. Speed-sensorless control system of a bearingless induction motor based on iterative central difference Kalman filter. Int. J. Electron. 2020, 1524–1542. [Google Scholar] [CrossRef]
- Xiao, X.; Chen, C.M.; Zhang, M. Dynamic permanent magnet flux estimation of permanent magnet synchronous machines. IEEE Trans. Appl. Supercond. 2010, 20, 1085–1088. [Google Scholar] [CrossRef]
- Zhang, M.; Xiao, X. Speed and flux linkage observer for permanent magnet synchronous motor based on EKF. Proc. CSEE 2007, 27, 36–40. [Google Scholar]
- Jiang, B. A Novel Algorithm Based on EKF to Estimate Rotor Position and Speed for Sensorless PMSM Drivers. In Proceedings of the International Conference on Information Engineering and Computer Science, Wuhan, China, 19–20 December 2009. [Google Scholar]
- Yu, P.Q.; Lu, Y.H.; Wang, Y.; Yang, W.M.; Chen, Z.C. Research on Permanent Magnet Linear Synchronous Motor Position Sensorless Control System. Proc. CSEE 2007, 27, 53–57. [Google Scholar]
- Yu, P.Q.; Wang, Y.; Yang, W.M.; Lu, H.C.; Chen, Z.C. Application of UKF in positionless sensor control of permanent magnet linear synchronous motor. J. Mech. Eng. 2007, 11, 149–153. [Google Scholar] [CrossRef]
- Li, J.; Li, J.Z. Speed Sensorless SVM-DTC for Pemanent Magnet Synchronous Motors. Proc. CSEE 2007, 27, 28–34. [Google Scholar]
- Quang, N.K.; Hieu, N.T. FPGA-based sensorless PMSM speed control using reduced-order extended Kalman filters. IEEE Trans. Ind. Electron. 2014, 61, 6574–6582. [Google Scholar] [CrossRef]
- Xu, B.; Shen, X.K.; Ji, W.; Shi, G.D. Adaptive Nonsingular Terminal Sliding Model Control for Permanent Magnet Synchronous Motor Based on Disturbance Observer. IEEE Access 2018, 6, 48913–48920. [Google Scholar] [CrossRef]
- Chen, M.S.; Hwang, Y.R.; Tomizuka, M. A state-dependent boundary layer design for sliding mode control. IEEE Trans. Autom. Control 2010, 47, 1677–1681. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, L.L.; Yang, S.Y.; Cao, R.X. Speed Sensorless Control of Permanent Magnet Synchronous Generators. Proc. CSEE 2014, 34, 3440–3447. [Google Scholar]
- Su, J.Y.; Li, T.C.; Yang, G.J. PMSM sensorless control based on four-order hybrid sliding mode observer. Proc. CSEE 2009, 29, 98–103. [Google Scholar]
- Zhao, Y.; Qiao, W.; Wu, L. Improved Rotor Position and Speed Estimators for Sensorless Control of Interior Permanent-Magnet Synchronous Machines. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 627–639. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Ahmarinejad, A.; Javadi, M.S.; Heidari, R.; Catalao, J.P.S. Improved double-surface sliding mode observer for flux and speed estimation of induction motors. IET Electr. Power Appl. 2020, 14, 1002–1010. [Google Scholar] [CrossRef]
- Ye, S.C. Fuzzy sliding mode observer with dual SOGI-FLL in sensorless control of PMSM drives. ISA Trans. 2019, 85, 161–176. [Google Scholar] [CrossRef]
- Peng, S.Q.; Song, Y.Y. Sensorless vector control of PMSM based on adaptive fuzzy sliding mode observer. Control Des. 2018, 33, 644–648. [Google Scholar]
- Huang, L.; Zhao, G.Z.; Nian, H. Sensorless Control of interior Pemanent Magnet Synchronous Motor by Estimation of an Extended Electromotive Force, motive Force. IET Electr. Power Appl. 2007, 9, 59–63. [Google Scholar]
- Wu, S.F.; Zhang, J.W.; Chai, B.B. Adaptive super-twisting sliding mode observer based robust backstepping sensorless speed control for IPMSM. ISA Trans. 2019, 92, 155–165. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Li, D. Adaptive second-order sliding mode observer with parameter identification for PMSM sensorless vector control. Control Decis. 2019, 34, 1385–1393. [Google Scholar]
- Kim, H.; Son, J. A high-speed sliding-mode observer for the sensorless speed control of a PMSM. IEEE Trans. Ind. Electron. 2011, 58, 4069–4077. [Google Scholar]
- Saadaoui, O.; Khlaief, A.; Abassi, M.; Tlili, I.; Chaari, A.; Boussak, M. A New Full-Order Sliding Mode Observer Based Rotor Speed and Stator Resistance Estimation for Sensorless Vector Controlled Pmsm Drives. Asian J. Control 2019, 21, 1318–1327. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Feng, Y.T.; Qin, M.; Li, M.H. Full-Order Sliding Mode Observation and Control Strategy for Surface Permanent Magnet Synchronous Motor. Trans. China Electrotech. Soc. 2018, 33, 5688–5699. [Google Scholar]
- Lu, W.Q.; Hu, Y.W.; Du, X.Y.; Huang, W.X. Sensorless Vector Control Using a Novel Sliding Mode Observer for PMSM Speed Control System. Proc. CSEE 2010, 30, 78–83. [Google Scholar]
- Lu, X.Q.; Lin, H.Y.; Han, J.L. Position Sensorless Control of Permanent Magnet Synchronous Machine Using a Disturbance Observer. Proc. CSEE 2016, 36, 1387–1394. [Google Scholar]
- Zhao, W.X.; Jiao, S.; Chen, Q.; Xu, D.Z.; Ji, J.H. Sensorless Control of Linear Permanent-Magnet Motor Based on Improved Disturbance Observer. IEEE Trans. Ind. Electron. 2018, 65, 9291–9300. [Google Scholar] [CrossRef]
- Aoshima, I.; Yoshikawa, M.; Ohnuma, N.; Shinnaka, S. Development of Electric Scooter Driven by Sensorless Motor Using D-State-Observer. World Electr. Veh. J. 2009, 3, 48–54. [Google Scholar] [CrossRef]
- Zhu, X.H.; Li, Y.H.; Chen, Y.B. Sensorless Vector Control for PMSM Based on Nonlinear State Observer. Trans. China Electrotech. Soc. 2010, 25, 50–57. [Google Scholar]
- Guven, S.; Usta, M.A.; Okumus, H.I. An improved sensorless DTC-SVM for three-level inverter-fed permanent magnet synchronous motor drive. Electr. Eng. 2018, 100, 2553–2567. [Google Scholar] [CrossRef]
- Zhao, W.X.; Yang, A.C.; Ji, J.H.; Zhu, J.H. Modified Flux Linkage Observer for Sensorless Direct Thrust Force Control of Linear Vernier Permanent Magnet Motor. IEEE Trans. Power Electron. 2018, 99, 7800–7811. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Wang, G.L.; Xu, D.G.; Yu, Y. Discrete-Time Low-Frequency-Ratio Synchronous-Frame Full-Order Observer for Position Sensorless IPMSM Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 870–879. [Google Scholar] [CrossRef]
- Sun, X.D.; Chen, L.; Yang, Z.B.; Zhu, H.Q. Speed-sensorless vector control of a bearingless induction motor with artificial neural network inverse speed observer. IEEE/ASME Trans. Mechatron. 2013, 18, 1357–1366. [Google Scholar] [CrossRef]
- Alsofyani, I.M.; Idris, N.R.N. A review on sensorless techniques for sustainable reliablity and efficient variable frequency drives of induction motors. Renew. Sustain. Energy Rev. 2013, 24, 111–121. [Google Scholar] [CrossRef]
- Xiao, L.; Sun, H.X.; Gao, F. Position Sensorless Control System of SRM Based on Improved BP Neural Network. Adv. Mater. Res. 2012, 1670, 2187–2192. [Google Scholar] [CrossRef]
- Xia, C.L.; Wen, D.; Fan, J.; Yang, X.J. Based on RBF Neural Network Position Sensorless Control for Brushless DC Motors. Trans. China Electrotech. Soc. 2002, 17, 26–29. [Google Scholar]
- Li, H.R.; Gu, S.S. Neural-network-based adaptive observer of position and speed of PMSM. Proc. CSEE 2002, 12, 33–36. [Google Scholar]
- Xia, C.L.; Wang, M.C.; Shi, T.N.; Guo, P.J. Position sensorless control for switched reluctance motors using neural network. Proc. CSEE 2005, 25, 123–128. [Google Scholar]
- Bao, D.Y.; Wang, H.; Wang, X.J.; Zhang, C.R. Sensorless speed control based on the improved Q-MRAS method for induction motor drives. Energies 2018, 11, 235. [Google Scholar]
- Zhu, Y.; Cheng, M.; Hua, W.; Zhang, B.F.; Wang, W. Sensorless control for electrical variable transmission based on sliding mode model reference adaptive system. Trans. China Electrotech. Soc. 2015, 30, 64–72. [Google Scholar]
- Rai, R.; Shukla, S.; Singh, B. Electromagnetic Torque-Based Model Reference Adaptive System Speed Estimator for Sensorless Surface Mount Permanent Magnet Synchronous Motor Drive. IEEE Trans. Ind. Inform. 2020, 16, 4714–4725. [Google Scholar] [CrossRef]
- Hu, W.H.; Wang, Y.; Li, M.X.; Li, M.; Wang, Z.A. Research on sensorless control strategy of direct drive multiphase PMSG wind power generation system based on MRAS. Power Syst. Prot. Control 2014, 42, 118–124. [Google Scholar]
- Wang, Q.L.; Zhang, C.W.; Zhang, X. Variable- structure MRAS speed identification for permanent magnet synchronous motor. Proc. CSEE 2008, 28, 71–75. [Google Scholar]
- Zhang, H.S.; Wang, P.; Han, B.C. Rotor Position Measurement for High-speed Permanent Magnet Synchronous Motors Based on Fuzzy PI MRAS. Proc. CSEE 2014, 34, 1889–1896. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).