Bicycle Speed Modelling Considering Cyclist Characteristics, Vehicle Type and Track Attributes
Abstract
1. Introduction
2. Methodology
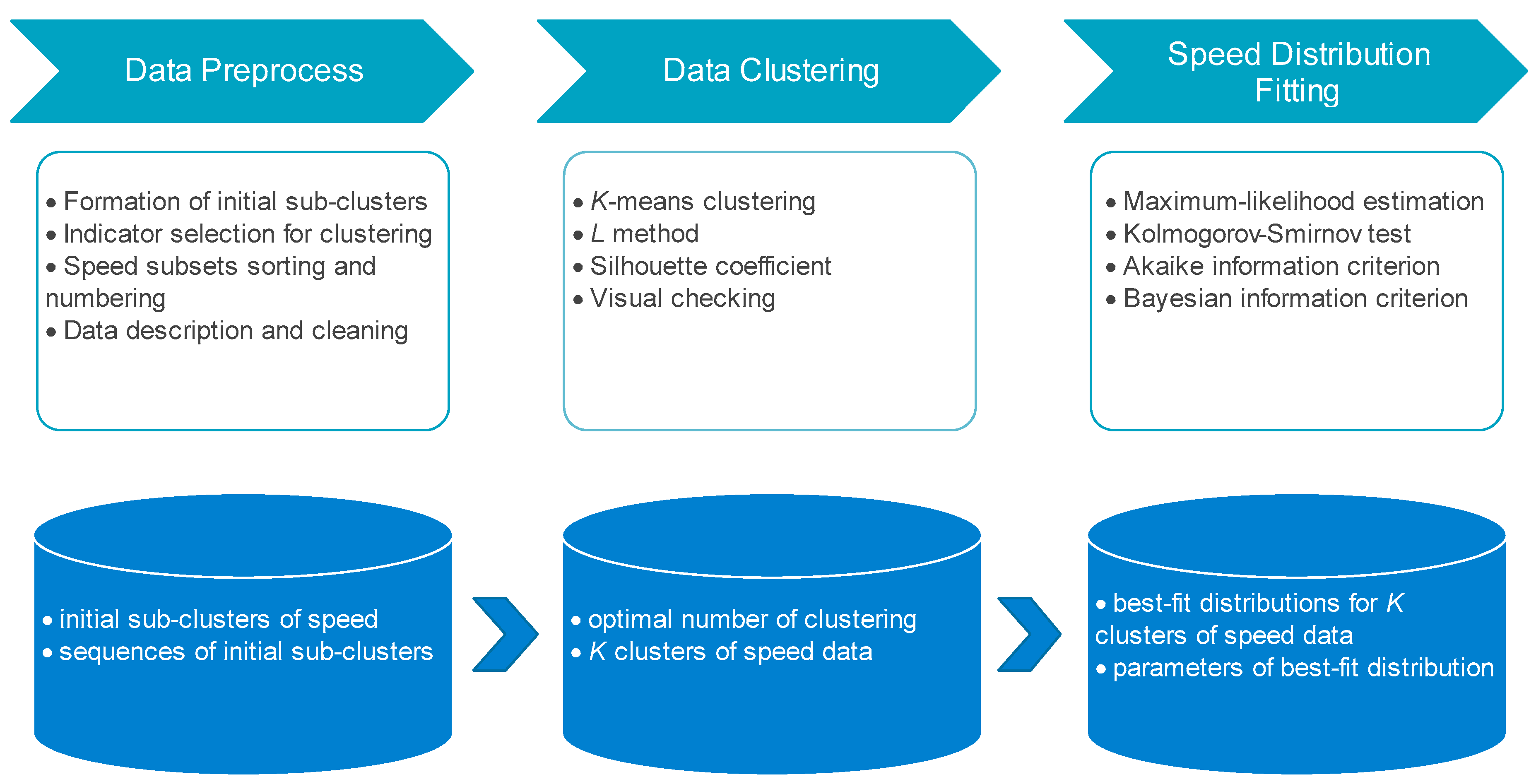
2.1. Study Logic and Technology Pathway
2.1.1. Study Logic
2.1.2. Technology Pathway
2.2. Clustering Algorithm and Validation
2.2.1. K-Means Clustering
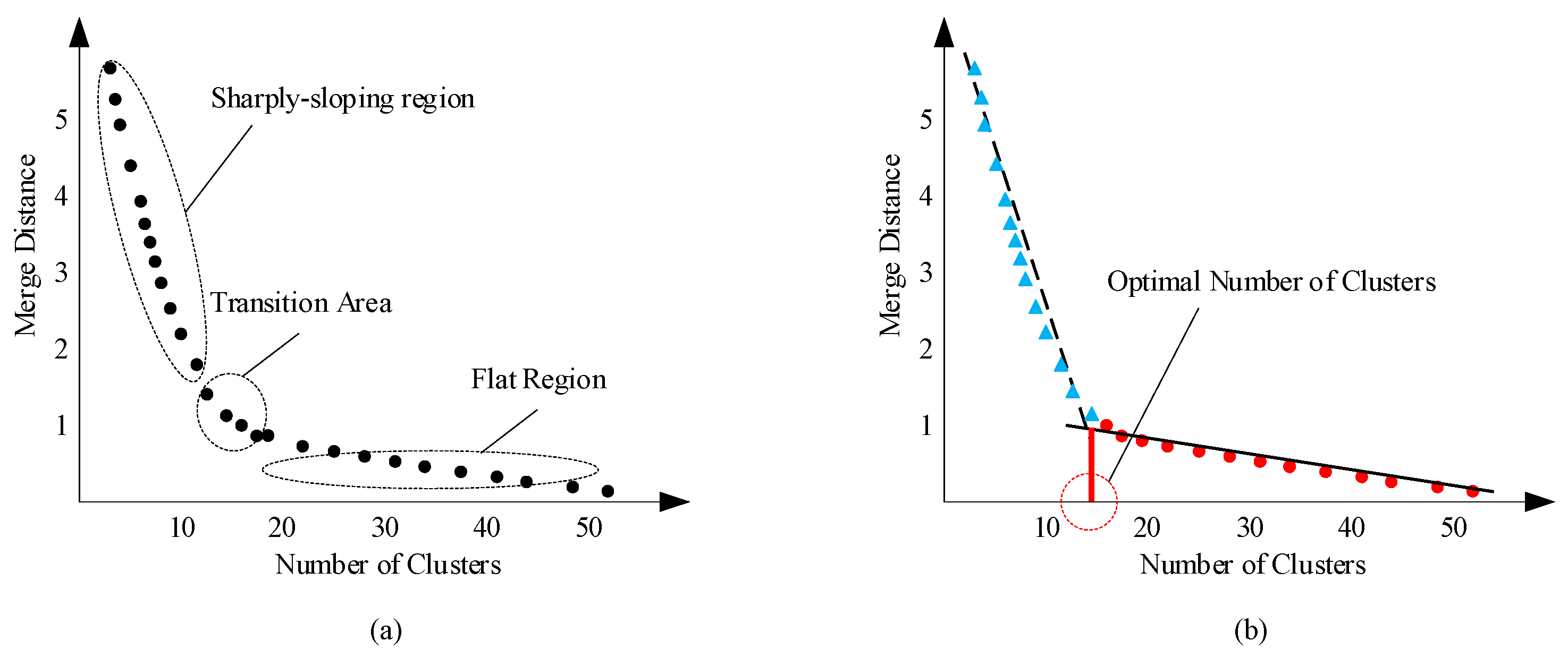
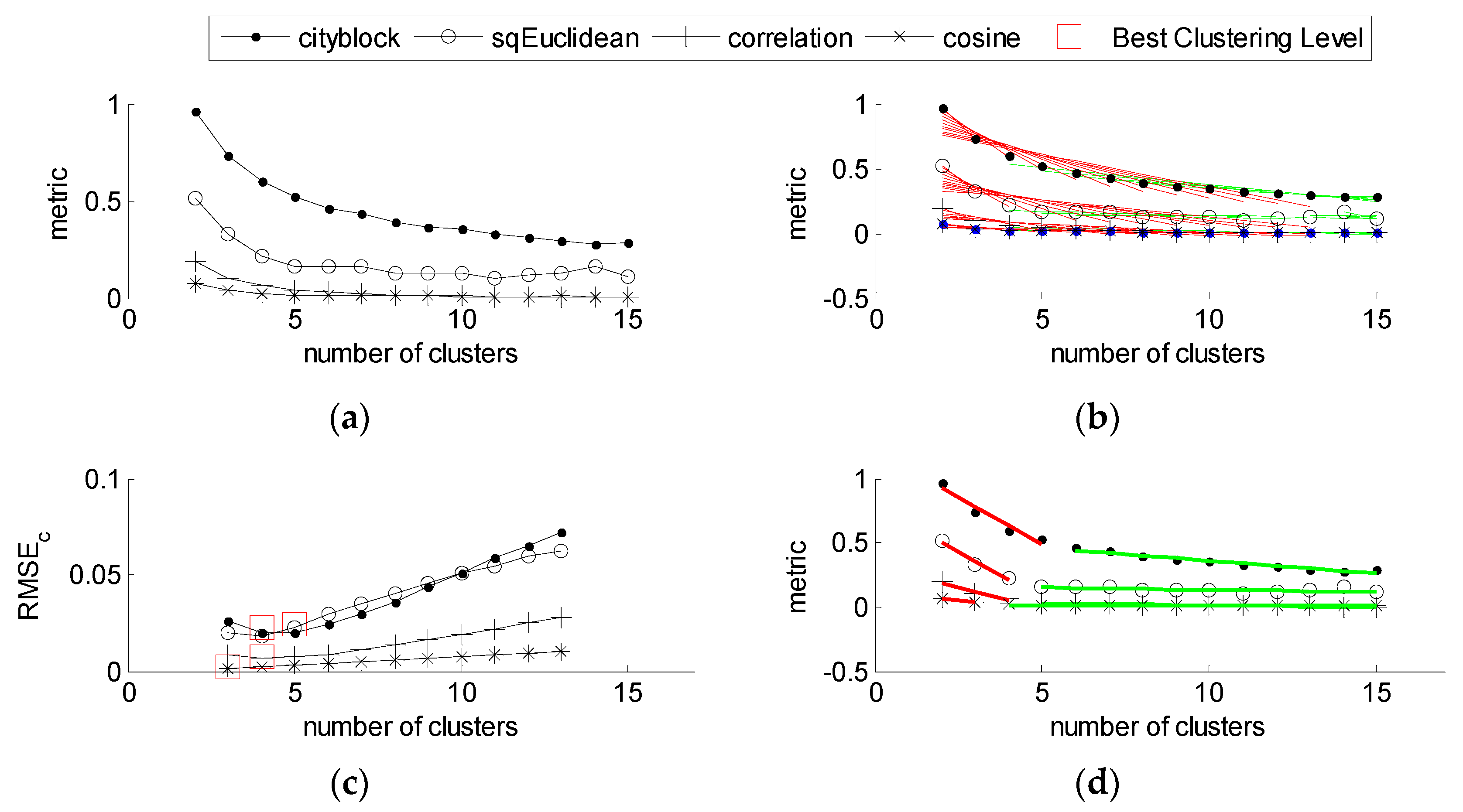
2.2.2. Determining the Optimal Number of Clusters
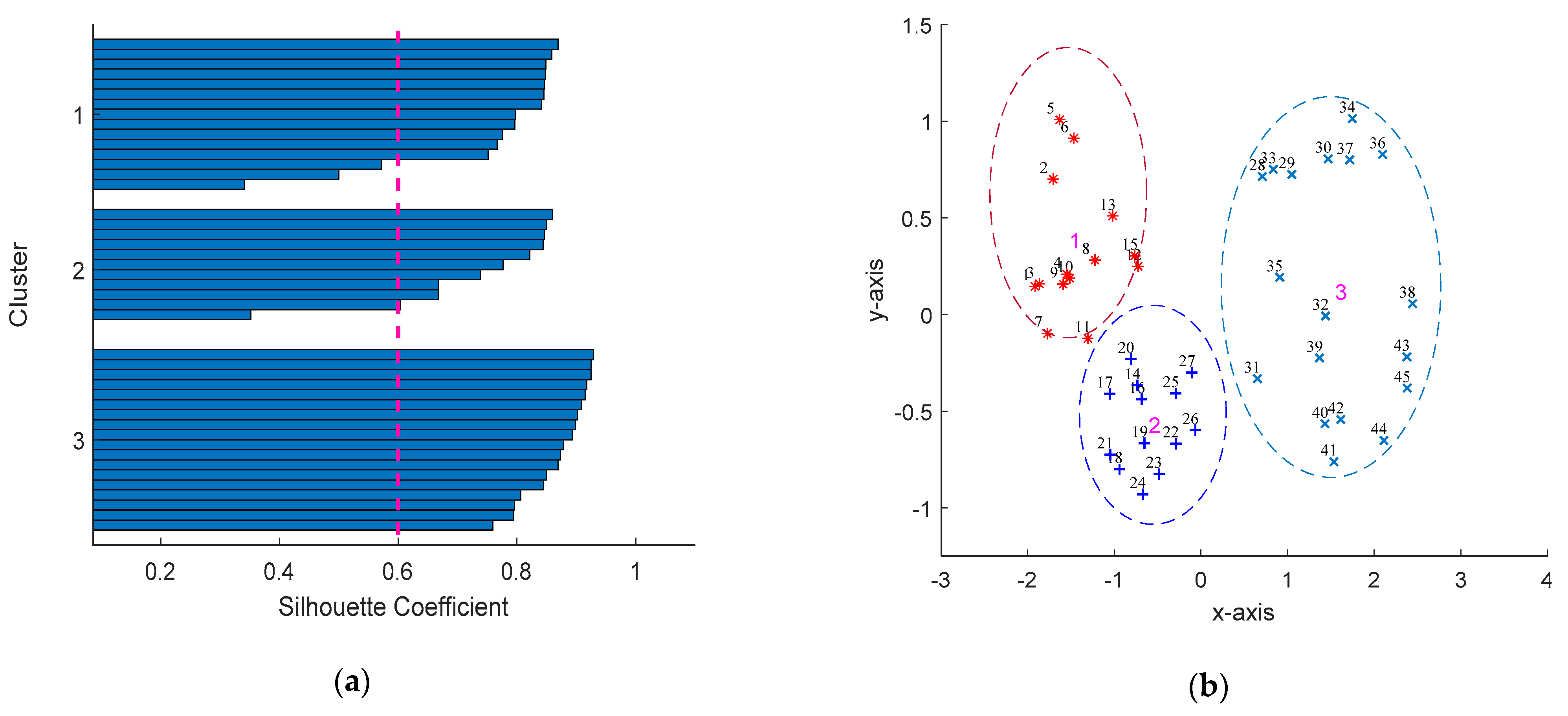
2.2.3. Clustering Validation
2.3. Distribution Fitting
2.3.1. Probability Distribution Models for Fitting
2.3.2. Model Test and Selection
Kolmogorov–Smirnov Test
AIC and BIC
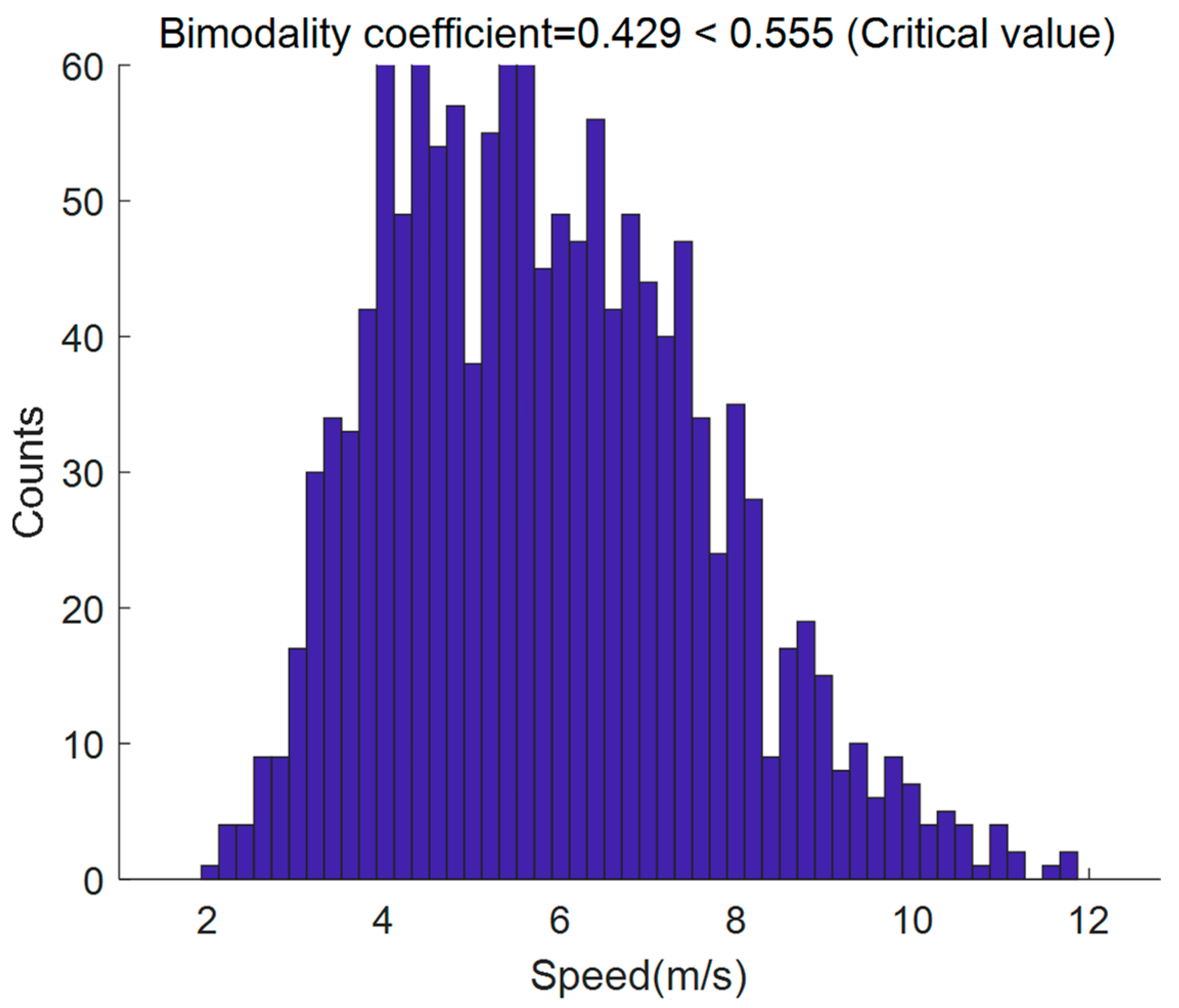
3. Data Preparation and Description
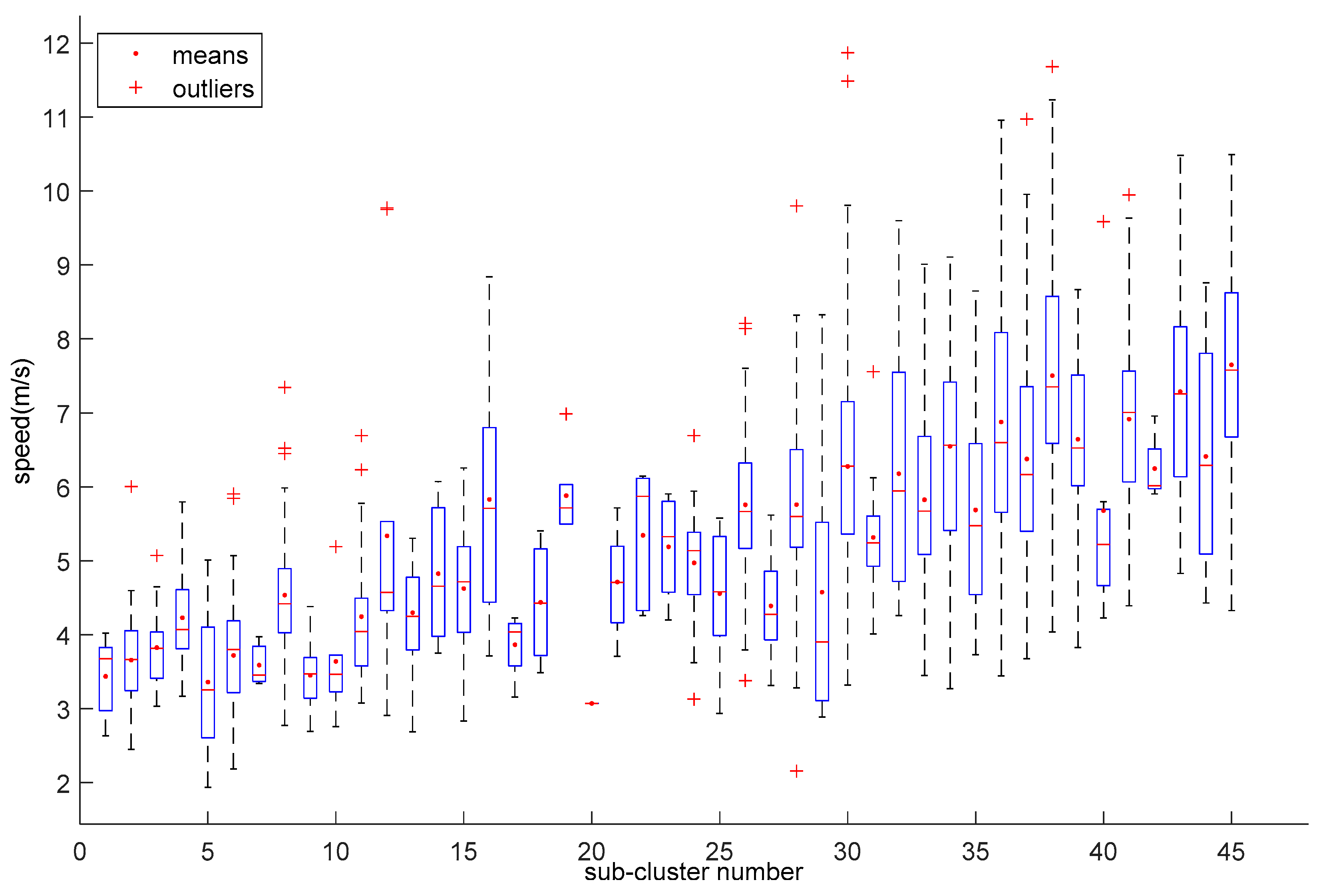
4. Clustering Results
4.1. Optimal Number of Clusters
4.2. Validaty of Clustering
5. Distribution Fitting Results for Speed Clusters
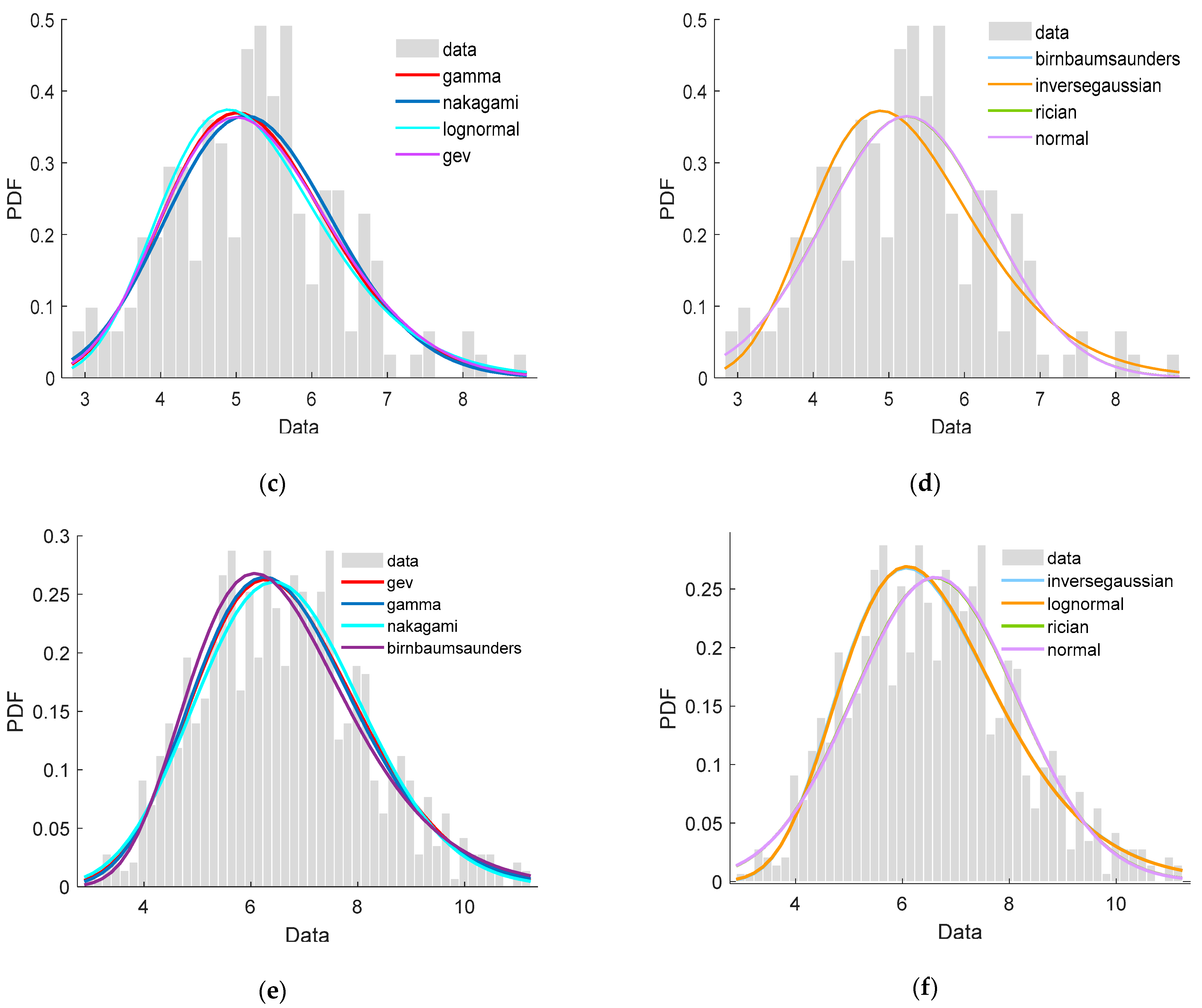
5.1. Speed Distribution of Clusters
- The first 7 distributions were suitable to fit the data of the three clusters according to the K-S test results while Uniform, Rayleigh, Gp, and exponential distribution were not. Nakagami, Rician, normal, logistic remained uncertain due to the failures of passing at least one of K-S tests to the three clusters.
- After considering the sum and variance of the three rankings together, we recommended GEV, Gamma, and Lognormal distributions as the top three tools to fit the three clusters of speed data set.
- Moreover, Tlocationscale, Gamma, and GEV distributions performed best in fitting the data from Clusterss 1, 2, and 3, respectively.
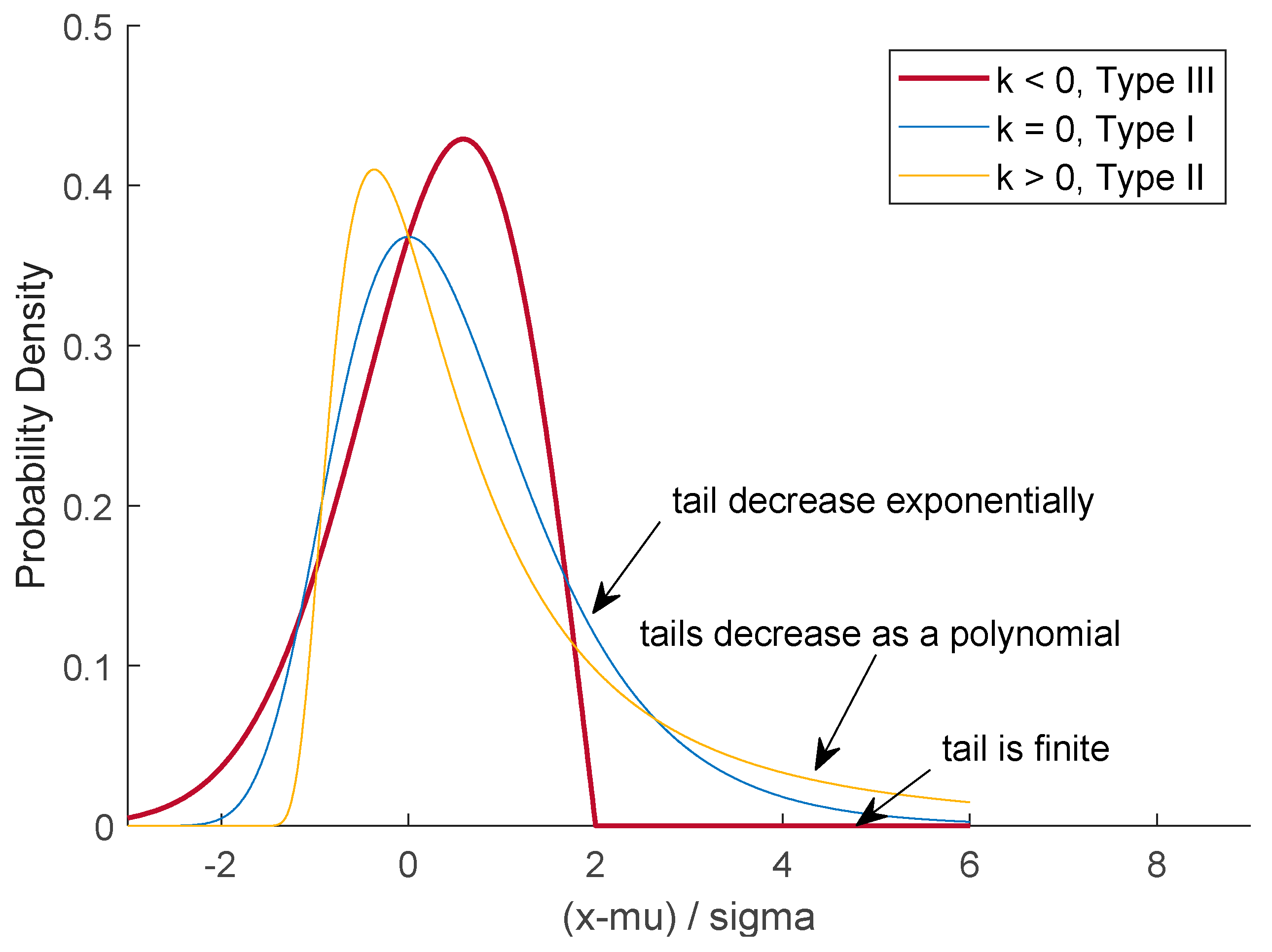
5.2. Discussion on Best-Fit Distribution
- Type Ⅰ—Distributions whose tails decrease exponentially when the shape parameter (k) is equal to zero, see the light blue line.
- Type Ⅱ—Distributions whose tails decrease as a polynomial shown by the yellow line, when k is more than zero.
- Type Ⅲ—Distributions whose tails are finite as illustrated by the red line, when k is less than zero.
6. Conclusions
- 48 initial bicycle speed sub-clusters generated by the combinations of bicycle type, bicycle lateral position, gender, age, and lane width were grouped in three clusters finally.
- Among the common distributions, GEV, Gamma, and lognormal were the top three models to fit the three clusters of speed dataset.
- Integrating stability and overall performance, GEV was the best-fit distribution of bicycle speed. The speeds of the three clusters followed GEV (−0.04, 0.78, 3.66), GEV (−0.17, 1.03, 4.81), and GEV (−0.18, 1.42, 6.00), respectively.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Distribution | Probability Density Function | Parameters |
|---|---|---|
| Birnbaumsaunders | β: scale parameter, β > 0; γ: shape parameter, γ > 0. | |
| Ev | μ: location parameter; σ: scale parameter, σ≥0 | |
| Exponential | θ: inverse scale, θ > 0 | |
| Gamma | α: shape parameter, α: > 0; β: scale paramete, β > 0 | |
| Gev | k: shape parameter σ: scale parameter, σ > 0; θ: location parameter | |
| Gp | k: shape parameter σ: scale parameter, σ≥0; θ: location parameter | |
| Inversegaussian | μ: scale parameter, μ>0; λ: shape parameter, λ>0 | |
| Logistic | μ: mean; β: scale parameter, β > 0 | |
| Loglogistic | μ: mean of logarithmic values, μ>0; σ: scale parameter of logarithmic values, σ > 0; | |
| Lognormal | μ: mean of logarithmic values; σ: standard deviation of logarithmic values, σ > 0; | |
| Nakagami | μ: shape parameter, μ > 0; ω: scale parameter, ω > 0 | |
| Normal | μ: mean; σ: standard deviation, σ ≥ 0; | |
| Rayleigh | b > 0 | |
| Rician | s: noncentrality parameter, s ≥ 0; σ: scale parameter, σ > 0; | |
| Tlocationscale | μ: location parameter; σ: scale parameter, σ > 0; ν: shape parameter, ν > 0. | |
| Uniform | a: lower parameter; b: upper parameter | |
| Weibull | a: scale parameter, a > 0; b scale parameter, b > 0; |
| Number | Gender | Age | Bicycle Type | Lane Width | Lateral Position | Cluster |
|---|---|---|---|---|---|---|
| 1 | Female | >40 years | CB | ≤3.5 m | right | 1 |
| 2 | Female | >40 years | CB | >3.5 m | right | 1 |
| 3 | Female | ≤40 years | CB | ≤3.5 m | right | 1 |
| 4 | Female | ≤40 years | CB | >3.5 m | right | 1 |
| 5 | Male | >40 years | CB | ≤3.5 m | right | 1 |
| 6 | Male | >40 years | CB | >3.5 m | right | 1 |
| 7 | Male | ≤40 years | CB | ≤3.5 m | right | 1 |
| 8 | Male | ≤40 years | CB | >3.5 m | right | 1 |
| 9 | Female | >40 years | CB | ≤3.5 m | center | 1 |
| 10 | Female | >40 years | CB | >3.5 m | center | 1 |
| 11 | Female | ≤40 years | CB | ≤3.5 m | center | 1 |
| 12 | Female | ≤40 years | CB | >3.5 m | center | 1 |
| 13 | Male | >40 years | CB | ≤3.5 m | center | 1 |
| 14 | Male | >40 years | CB | >3.5 m | center | 1 |
| 15 | Male | ≤40 years | CB | ≤3.5 m | center | 1 |
| 16 | Male | ≤40 years | CB | >3.5 m | center | 2 |
| 17 | Female | >40 years | CB | ≤3.5 m | left | 2 |
| 18 | Female | >40 years | CB | >3.5 m | left | 2 |
| 19 | Female | ≤40 years | CB | ≤3.5 m | left | 2 |
| 20 | Female | ≤40 years | CB | >3.5 m | left | 2 |
| 21 | Male | >40 years | CB | ≤3.5 m | left | 2 |
| 22 | Male | >40 years | CB | >3.5 m | left | 2 |
| 23 | Male | ≤40 years | CB | ≤3.5 m | left | 2 |
| 24 | Male | ≤40 years | CB | >3.5 m | left | 2 |
| 25 | Female | >40 years | EB | ≤3.5 m | right | 2 |
| 26 | Female | >40 years | EB | >3.5 m | right | 2 |
| 27 | Female | ≤40 years | EB | ≤3.5 m | right | 2 |
| 28 | Female | ≤40 years | EB | >3.5 m | right | 2 |
| 29 | Male | >40 years | EB | ≤3.5 m | right | 2 |
| 30 | Male | >40 years | EB | >3.5 m | right | 3 |
| 31 | Male | ≤40 years | EB | ≤3.5 m | right | 3 |
| 32 | Male | ≤40 years | EB | >3.5 m | right | 3 |
| 33 | Female | >40 years | EB | ≤3.5 m | center | 3 |
| 34 | Female | >40 years | EB | >3.5 m | center | 3 |
| 35 | Female | ≤40 years | EB | ≤3.5 m | center | 3 |
| 36 | Female | ≤40 years | EB | >3.5 m | center | 3 |
| 37 | Male | >40 years | EB | ≤3.5 m | center | 3 |
| 38 | Male | >40 years | EB | >3.5 m | center | 3 |
| 39 | Male | ≤40 years | EB | ≤3.5 m | center | 3 |
| 40 | Male | ≤40 years | EB | >3.5 m | center | 3 |
| 41 | Female | >40 years | EB | ≤3.5 m | left | 3 |
| 42 | Female | >40 years | EB | >3.5 m | left | 3 |
| 43 | Female | ≤40 years | EB | ≤3.5 m | left | 3 |
| 44 | Female | ≤40 years | EB | >3.5 m | left | 3 |
| 45 | Male | >40 years | EB | ≤3.5 m | left | 3 |
| 46 | Male | >40 years | EB | >3.5 m | left | 3 |
| 47 | Male | ≤40 years | EB | ≤3.5 m | left | 3 |
| 48 | Male | ≤40 years | EB | >3.5 m | left | 3 |
Appendix B
| Order | Name | Parameters | LL | KS | AIC | AICc | BIC |
|---|---|---|---|---|---|---|---|
| 1 | loglogistic | μ: 1.38, σ: 0.12 | −411.6 | Y | 827.3 | 827.3 | 834.9 |
| 2 | tlocationscale | μ: 3.99, σ: 0.67, ν: 4.17 | −416.8 | Y | 839.7 | 839.8 | 851.1 |
| 3 | lognormal | μ: 1.38, σ: 0.22 | −419.2 | Y | 842.5 | 842.5 | 850.0 |
| 4 | inversegaussian | μ: 4.06, λ: 81.49 | −420.2 | Y | 844.4 | 844.5 | 852.0 |
| 5 | birnbaumsaunders | β: 3.97, γ: 0.22 | −420.3 | Y | 844.6 | 844.6 | 852.2 |
| 6 | gev | k: −0.04, σ: 0.78, θ: 3.66 | −420.4 | Y | 846.8 | 846.8 | 858.1 |
| 7 | logistic | μ: 4.00, β: 0.48 | −421.8 | Y | 847.6 | 847.6 | 855.1 |
| 8 | gamma | α: 20.44, β: 0.20 | −423.8 | Y | 851.5 | 851.6 | 859.1 |
| 9 | nakagami | μ: 5.05, ω: 17.42 | −433.7 | N | 871.3 | 871.3 | 878.9 |
| 10 | rician | s: 3.95, σ: 0.96 | −445.3 | N | 894.7 | 894.7 | 902.2 |
| 11 | normal | μ: 4.06, σ: 0.95 | −446.1 | N | 896.3 | 896.3 | 903.9 |
| 12 | rayleigh | b: 2.95 | −584.2 | N | 1170.4 | 1170.5 | 1174.2 |
| 13 | uniform | a: 1.93, b: 9.77 | −673.4 | N | 1350.8 | 1350.8 | 1358.4 |
| 14 | gp | −0.56, θ: 5.53 | −703.1 | N | 1410.1 | 1410.2 | 1417.7 |
| 15 | exponential | θ: 4.06 | −785.5 | N | 1573.1 | 1573.1 | 1576.9 |
| Order | Name | Parameter Values | LL | KS | AIC | AICc | BIC |
|---|---|---|---|---|---|---|---|
| 1 | gamma | α: 22.74, β: 0.23 | −268.2 | Y | 540.5 | 540.6 | 546.9 |
| 2 | nakagami | μ: 5.92, ω: 28.66 | −268.3 | Y | 540.7 | 540.7 | 547.0 |
| 3 | gev | k: -0.17, σ: 1.03, θ: 4.81 | −269.5 | Y | 542.9 | 543.0 | 549.3 |
| 4 | lognormal | μ: 1.63, σ: 0.21 | −268.5 | Y | 542.9 | 543.1 | 552.5 |
| 5 | birnbaumsaunders | β: 5.12, γ: 0.21 | −269.5 | Y | 543.0 | 543.0 | 549.3 |
| 6 | tlocationscale | μ: 5.23, σ: 1.04, ν: 20.78 | −269.5 | Y | 543.1 | 543.1 | 549.4 |
| 7 | inversegaussian | μ: 5.24, λ: 113.26 | −269.7 | Y | 543.4 | 543.5 | 549.8 |
| 8 | rician | s: 5.12, σ: 1.11 | −269.8 | Y | 543.6 | 543.7 | 550.0 |
| 9 | normal | μ: 5.24, σ: 1.09 | −270.2 | Y | 544.4 | 544.4 | 550.7 |
| 10 | logistic | μ: 5.22, β: 0.62 | −270.3 | Y | 544.6 | 544.7 | 551.0 |
| 11 | loglogistic | μ: 1.64, σ: 0.12 | −269.5 | Y | 545.0 | 545.2 | 554.6 |
| 12 | uniform | a: 2.83, b: 8.84 | −321.1 | N | 646.1 | 646.2 | 652.5 |
| 13 | rayleigh | b: 3.79 | −363.0 | N | 728.1 | 728.1 | 731.2 |
| 14 | gp | σ: -1.01, θ: 8.93 | −389.9 | N | 783.7 | 783.8 | 790.1 |
| 15 | exponential | θ: 5.24 | −475.5 | N | 953.0 | 953.1 | 956.2 |
| Order | Name | Parameter Values | LL | KS | AIC | AICc | BIC |
|---|---|---|---|---|---|---|---|
| 1 | gev | k: −0.18, σ:1.42, θ: 6.00 | −1566.6 | Y | 3139.3 | 3139.3 | 3153.5 |
| 2 | gamma | α: 18.40, β: 0.36 | −1567.9 | Y | 3139.8 | 3139.8 | 3149.3 |
| 3 | nakagami | μ: 4.83,46.13 | −1569.2 | Y | 3142.5 | 3142.5 | 3152.0 |
| 4 | birnbaumsaunders | β: 6.43, γ: 0.24 | −1572.8 | Y | 3149.6 | 3149.6 | 3159.1 |
| 5 | inversegaussian | μ: 6.62, λ:114.96 | −1573.0 | Y | 3150.1 | 3150.1 | 3159.6 |
| 6 | lognormal | μ: 1.86, σ: 0.24 | −1573.1 | Y | 3150.1 | 3150.2 | 3159.7 |
| 7 | rician | s: 6.42, σ: 1.56 | −1578.1 | Y | 3160.1 | 3160.2 | 3169.6 |
| 8 | normal | μ: 6.62, σ: 1.53 | −1578.9 | Y | 3161.8 | 3161.9 | 3171.3 |
| 9 | tlocationscale | μ: 6.62, σ: 1.53, ν: 2594780.26 | −1578.9 | Y | 3163.8 | 3163.9 | 3178.1 |
| 10 | loglogistic | μ: 1.87, σ: 0.14 | −1584.9 | Y | 3173.8 | 3173.8 | 3183.3 |
| 11 | logistic | μ: 6.56,β: 0.88 | −1590.1 | Y | 3184.2 | 3184.2 | 3193.7 |
| 12 | uniform | a: 2.89, b: 11.24 | −1814.4 | N | 3632.8 | 3632.8 | 3642.3 |
| 13 | rayleigh | b: 4.8 | −1946.1 | N | 3894.2 | 3894.2 | 3898.9 |
| 14 | gp | −0.98, θ: 11.01 | −2068.1 | N | 4140.2 | 4140.2 | 4149.7 |
| 15 | exponential | θ: 6.62 | −2470.5 | N | 4943.1 | 4943.1 | 4947.8 |
References
- Zhang, H.; Shaheen, S.A.; Chen, X. Bicycle evolution in China: From the 1900s to the present. Int. J. Sustain. Transp. 2014, 8, 317–335. [Google Scholar] [CrossRef]
- Cherry, C.R. Electric Two-Wheelers in China: Analysis of Environmental, Safety, and Mobility Impacts. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2007. [Google Scholar]
- Lin, S.; He, M.; Tan, Y.L.; He, M.W. Comparison study on operating speeds of electric bicycles and bicycles experience from field investigation in Kunming, China. Transp. Res. Rec. 2008, 2048, 52–59. [Google Scholar] [CrossRef]
- Jin, S.; Qu, X.; Zhou, D.; Xu, C.; Ma, D.; Wang, D. Estimating cycleway capacity and bicycle equivalent unit for electric bicycles. Transp. Res. Part A Policy Pract. 2015, 77, 225–248. [Google Scholar] [CrossRef]
- Jin, S.; Shen, L.; Liu, M.; Ma, D. Modelling speed-flow relationships for bicycle traffic flow. Proc. Inst. Civ. Eng. Transp. 2017, 170, 194–204. [Google Scholar] [CrossRef]
- Cheng, X.; Zhao-wei, Q.; Dian-hai, W.; Sheng, J. Speed distribution model for heterogeneous bicycle traffic flow. J. Zhejiang Univ. Eng. Sci. 2017, 51, 1331–1338. [Google Scholar]
- Xu, C.; Guo, H.; Xu, L.; Jin, S. Speeding behavior and speed limits for heterogeneous bicycle flow. Traffic Inj. Prev. 2019, 20, 759–763. [Google Scholar] [CrossRef] [PubMed]
- Parkin, J.; Rotheram, J. Design speeds and acceleration characteristics of bicycle traffic for use in planning, design and appraisal. Transp. Policy 2010, 17, 335–341. [Google Scholar] [CrossRef]
- Buch, G.; Greibe, P. Analysis of bicycle traffic on one-way bicycle tracks of different width. In Proceedings of the European Transport Conference 2015, Association for European Transport (AET), Frankfurt, Germany, 28–30 September 2015. [Google Scholar]
- Fraley, C.; Raftery, A.E. How many clusters? Which clustering method? Answers via model-based cluster analysis. Comput. J. 1998, 41, 578–588. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques, 3rd ed.; Morgan Kaufmann: Burlington, MA, USA, 2011; pp. 83–124. [Google Scholar]
- Estivill-Castro, V.; Yang, J. Fast and robust general purpose clustering algorithms. In Pacific Rim International Conference on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2000; pp. 208–218. [Google Scholar]
- Wu, X.; Kumar, V.; Quinlan, J.R.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Philip, S.Y. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Oakland, CA, USA, 21 June–18 July 1965 and 27 December 1965–7 January 1966; pp. 281–297. [Google Scholar]
- Duda, R.O.; Hart, P.E. Pattern Classification; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Adebisi, A.A.; Olusayo, O.E.; Olatunde, O.S. An exploratory study of k-means and expectation maximization algorithms. J. Adv. Math. Comput. Sci. 2012, 2, 62–71. [Google Scholar] [CrossRef]
- Kearns, M.; Mansour, Y.; Ng, A.Y. An information-theoretic analysis of hard and soft assignment methods for clustering. In Learning in Graphical Models; Springer: Dordrecht, The Netherlands, 1998; pp. 495–520. [Google Scholar]
- Liu, C.; Li, H.C.; Fu, K.; Zhang, F.; Datcu, M.; Emery, W.J. Bayesian estimation of generalized gamma mixture model based on variational EM algorithm. Pattern Recognit. 2019, 87, 269–284. [Google Scholar] [CrossRef]
- Du, Y.; Gui, W. Goodness of fit tests for the log-logistic distribution based on cumulative entropy under progressive type II censoring. Mathematics 2019, 7, 361. [Google Scholar] [CrossRef]
- Yu, L.; Yang, T.; Chan, A.B. Density-preserving hierarchical EM algorithm: Simplifying Gaussian mixture models for approximate inference. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 1323–1337. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, X.; Jiang, J.; Gao, Y. Feature-guided Gaussian mixture model for image matching. Pattern Recognit. 2019, 92, 231–245. [Google Scholar] [CrossRef]
- Gebru, I.D.; Alameda-Pineda, X.; Forbes, F.; Horaud, R. EM algorithms for weighted-data clustering with application to audio-visual scene analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2402–2415. [Google Scholar] [CrossRef] [PubMed]
- McLachlan, G.; Peel, D. Finite Mixture Models, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- McLachlan, G.; Krishnan, T. The EM Algorithm and Extensions, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Bäcklin, C.L.; Andersson, C.; Gustafsson, M.G. Self-tuning density estimation based on Bayesian averaging of adaptive kernel density estimations yields state-of-the-art performance. Pattern Recognit. 2018, 78, 133–143. [Google Scholar] [CrossRef]
- Pagès-Zamora, A.; Cabrera-Bean, M.; Díaz-Vilor, C. Unsupervised online clustering and detection algorithms using crowdsourced data for malaria diagnosis. Pattern Recognit. 2019, 86, 209–223. [Google Scholar] [CrossRef]
- Yang, M.S.; Lai, C.Y.; Lin, C.Y. A robust EM clustering algorithm for Gaussian mixture models. Pattern Recognit. 2012, 45, 3950–3961. [Google Scholar] [CrossRef]
- Celeux, G.; Govaert, G. Gaussian parsimonious clustering models. Pattern Recognit. 1995, 28, 781–793. [Google Scholar] [CrossRef]
- Abbas, O.A. Comparisons between data clustering algorithms. Int. Arab J. Inf. Technol. 2008, 5, 320–325. [Google Scholar]
- Kishor, D.R.; Venkateswarlu, N. Hybridization of expectation-maximization and k-means algorithms for better clustering performance. Cybern. Inf. Technol. 2016, 16, 16–34. [Google Scholar]
- Jung, Y.G.; Kang, M.S.; Heo, J. Clustering performance comparison using K-means and expectation maximization algorithms. Biotechnol. Biotechnol. Equip. 2014, 28, S44–S48. [Google Scholar] [CrossRef]
- Neal, R.M.; Hinton, G.E. A view of the EM algorithm that justifies incremental, sparse, and other variants. In Learning in Graphical Models; Springer: Berlin/Heidelberg, Germany, 1998; pp. 355–368. [Google Scholar]
- Jollois, F.-X.; Nadif, M. Speed-up for the expectation-maximization algorithm for clustering categorical data. J. Glob. Optim. 2007, 37, 513–525. [Google Scholar] [CrossRef]
- Xu, R.; Wunsch, D. Survey of clustering algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef]
- Yan, X.; Chen, J.; Bai, H.; Wang, T.; Yang, Z. Influence factor analysis of bicycle free-flow speed for determining the design speeds of separated bicycle lanes. Information 2020, 11, 459. [Google Scholar] [CrossRef]
- Pfister, R.; Schwarz, K.; Janczyk, M.; Dale, R.; Freeman, J. Good things peak in pairs: A note on the bimodality coefficient. Front. Psychol. 2013, 4. [Google Scholar] [CrossRef]
- Park, B.-J.; Zhang, Y.; Lord, D. Bayesian mixture modeling approach to account for heterogeneity in speed data. Transp. Res. Part B Methodol. 2010, 44, 662–673. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Reddy, C.K. Data Clustering: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Salvador, S.; Chan, P. Learning states and rules for detecting anomalies in time series. Appl. Intell. 2005, 23, 241–255. [Google Scholar] [CrossRef]
- Pham, D.T.; Dimov, S.S.; Nguyen, C.D. Selection of K in K-means clustering. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2005, 219, 103–119. [Google Scholar] [CrossRef]
- Liddle, A.R. How many cosmological parameters. Mon. Not. R. Astron. Soc. 2004, 351, L49–L53. [Google Scholar] [CrossRef]
- Kulkarni, S.; Desai, S. Classification of gamma-ray burst durations using robust model-comparison techniques. Astrophys. Space Sci. 2017, 362, 70. [Google Scholar] [CrossRef]
- Bali, T.G. The generalized extreme value distribution. Econ. Lett. 2003, 79, 423–427. [Google Scholar] [CrossRef]
- EUR-Lex. Available online: https://eur-lex.europa.eu/legal-content/EN/ALL/?uri=CELEX%3A32002L0024 (accessed on 24 January 2021).
- BSI. Available online: https://web.archive.org/web/20110708102035/http://shop.bsigroup.com/en/ProductDetail/?pid=000000000030030402 (accessed on 24 January 2021).
- FINLEX. Available online: https://finlex.fi/fi/laki/ajantasa/2002/20021090 (accessed on 24 January 2021).
- NEWWHEEL.NET. Available online: https://blog.newwheel.net/post/30869093307/eurobike-electric-bike-review-2012 (accessed on 24 January 2021).
- Cycling Resource Centre. Available online: https://www.cyclingresourcecentre.org.au/news/victorians_get_the_power_to_pedal (accessed on 24 January 2021).
- GB17761-2018. Electric Bicycle Safety Technical Specifications; State Market Supervisory Administration; China National Standardization Administration: Beijing, China, 2018; pp. 3–4. [Google Scholar]

| Factor | Original | Merged | ||||
|---|---|---|---|---|---|---|
| Category or Level | Counts | Ratio | Category or Level | Counts | Ratio | |
| gender | Male | 850 | 62.0% | Male | 850 | 62.0% |
| Female | 520 | 38.0% | Female | 520 | 38.0% | |
| age | (~, 20) years | 42 | 3.0% | (~, 40) years | 830 | 67.9% |
| (20, 30) years | 308 | 22.5% | ||||
| (30, 40) years | 580 | 42.4% | ||||
| (40, 50) years | 296 | 21.6% | (40, 60) years | 440 | 32.1% | |
| (50, 60) years | 144 | 10.5% | ||||
| bicycle type | EB | 1028 | 75.1% | EB | 1028 | 75.1% |
| CB | 342 | 24.9% | CB | 342 | 24.9% | |
| lane width | 2 m | 197 | 14.4% | ≤3.5 m | 367 | 26.8% |
| 3.4 m | 170 | 12.4% | ||||
| 3.85 m | 302 | 22.0% | >3.5 m | 1003 | 73.2% | |
| 4 m | 346 | 25.3% | ||||
| 5 m | 355 | 25.9% | ||||
| lateral position | left | 211 | 15.4% | left | 211 | 15.4% |
| center | 745 | 54.4% | center | 745 | 54.4% | |
| right | 421 | 30.8% | right | 421 | 30.8% | |
| Total | ~ | 1370 | ~ | ~ | 1370 | ~ |
| Cluster | Counts | Speed Statistics (m/s) | Distribution Features | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Median | Mean | Std * | 85th Value | Min * | Max * | Kurtosis | Skewness | BC * | ||
| 1 | 327 | 4.00 | 4.06 | 0.95 | 4.81 | 1.93 | 9.77 | 10.37 | 1.63 | 0.35 |
| 2 | 179 | 5.25 | 5.24 | 1.10 | 6.32 | 2.83 | 8.84 | 3.29 | 0.34 | 0.33 |
| 3 | 864 | 6.54 | 6.65 | 1.58 | 8.22 | 2.16 | 11.87 | 3.03 | 0.40 | 0.38 |
| Overall | 1370 | 5.66 | 5.85 | 1.78 | 7.73 | 1.93 | 11.87 | 2.85 | 0.48 | 0.43 |
| Number | Name | Cluster 1 | Cluster 2 | Cluster 3 | Sum | Var. | Suggestions |
|---|---|---|---|---|---|---|---|
| 1 | Gev | 6 | 3 | 1 | 10 | 4.22 | Recommended |
| 2 | Gamma | 8 | 1 | 2 | 11 | 9.56 | Recommended |
| 3 | Lognormal | 3 | 4 | 6 | 13 | 1.56 | Recommended |
| 4 | Birnbaumsaunders | 5 | 5 | 4 | 14 | 0.22 | Suitable |
| 5 | Inversegaussian | 4 | 7 | 5 | 16 | 1.56 | Suitable |
| 6 | Loglogistic | 2 | 6 | 9 | 17 | 8.22 | Suitable |
| 7 | Tlocationscale | 1 | 11 | 10 | 22 | 20.22 | Suitable |
| 8 | Nakagami | 9 | 2 | 3 | 14 | 9.56 | Uncertain |
| 9 | Rician | 10 | 8 | 7 | 25 | 1.56 | Uncertain |
| 10 | Normal | 11 | 9 | 8 | 28 | 1.56 | Uncertain |
| 11 | Logistic | 7 | 10 | 11 | 28 | 2.89 | Uncertain |
| 12 | Uniform | 13 | 12 | 12 | 37 | 0.22 | Unsuitable |
| 13 | Rayleigh | 12 | 13 | 13 | 38 | 0.22 | Unsuitable |
| 14 | GP | 14 | 14 | 14 | 42 | 0.00 | Unsuitable |
| 15 | Exponential | 15 | 15 | 15 | 45 | 0.00 | Unsuitable |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Ye, X.; Chen, J.; Wang, T.; Yang, Z.; Bai, H. Bicycle Speed Modelling Considering Cyclist Characteristics, Vehicle Type and Track Attributes. World Electr. Veh. J. 2021, 12, 43. https://doi.org/10.3390/wevj12010043
Yan X, Ye X, Chen J, Wang T, Yang Z, Bai H. Bicycle Speed Modelling Considering Cyclist Characteristics, Vehicle Type and Track Attributes. World Electric Vehicle Journal. 2021; 12(1):43. https://doi.org/10.3390/wevj12010043
Chicago/Turabian StyleYan, Xingchen, Xiaofei Ye, Jun Chen, Tao Wang, Zhen Yang, and Hua Bai. 2021. "Bicycle Speed Modelling Considering Cyclist Characteristics, Vehicle Type and Track Attributes" World Electric Vehicle Journal 12, no. 1: 43. https://doi.org/10.3390/wevj12010043
APA StyleYan, X., Ye, X., Chen, J., Wang, T., Yang, Z., & Bai, H. (2021). Bicycle Speed Modelling Considering Cyclist Characteristics, Vehicle Type and Track Attributes. World Electric Vehicle Journal, 12(1), 43. https://doi.org/10.3390/wevj12010043






