Analytical Model for the Design of Axial Flux Induction Motors with Maximum Torque Density
Abstract
1. Introduction
2. Materials and Methods
2.1. Thought Experiment
2.2. Model Expression Generation
2.2.1. Stator Resistance
2.2.2. Rotor Cage Resistance
2.2.3. Slot Cross-Sectional Area
2.2.4. General Model Expression
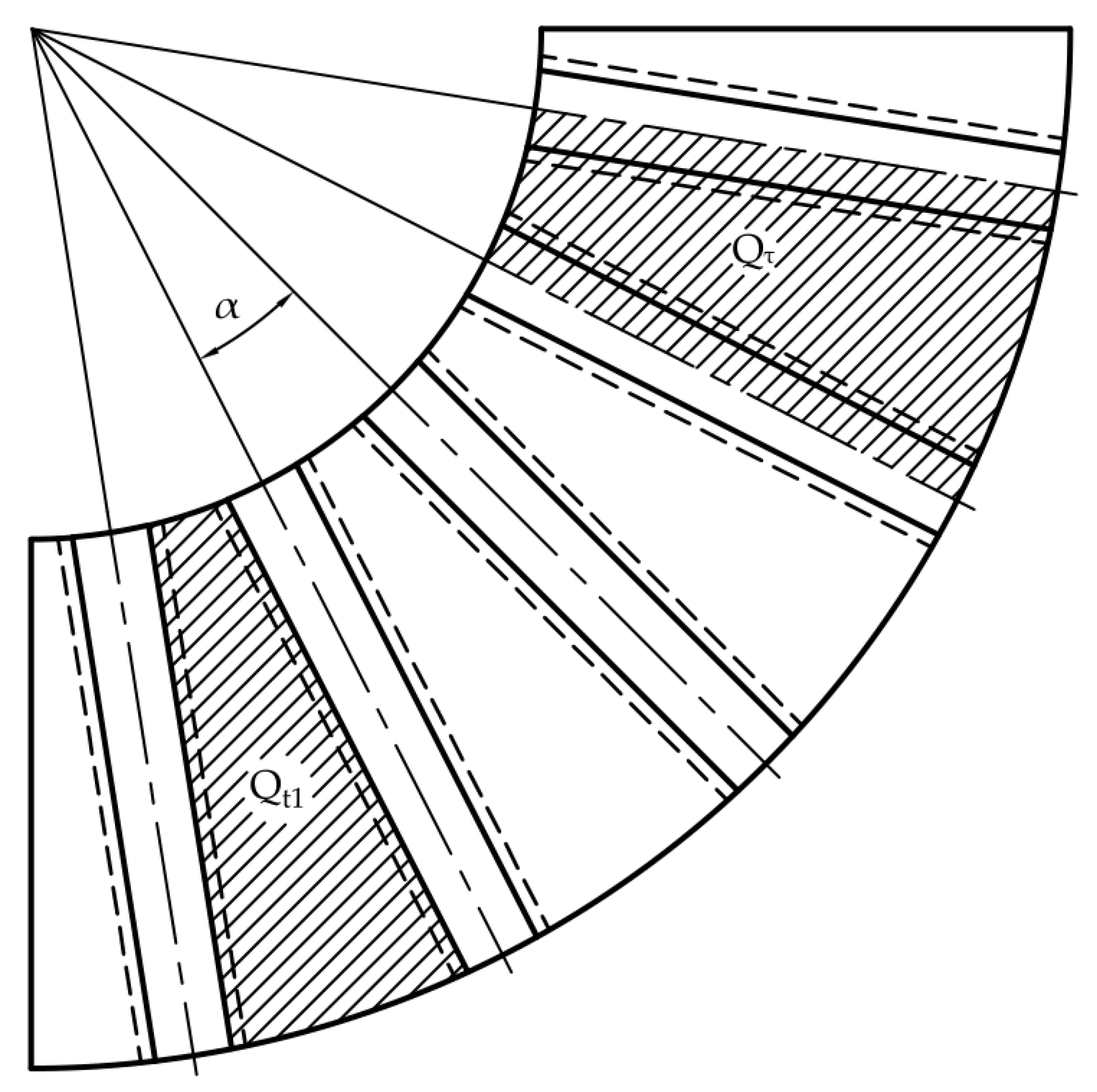
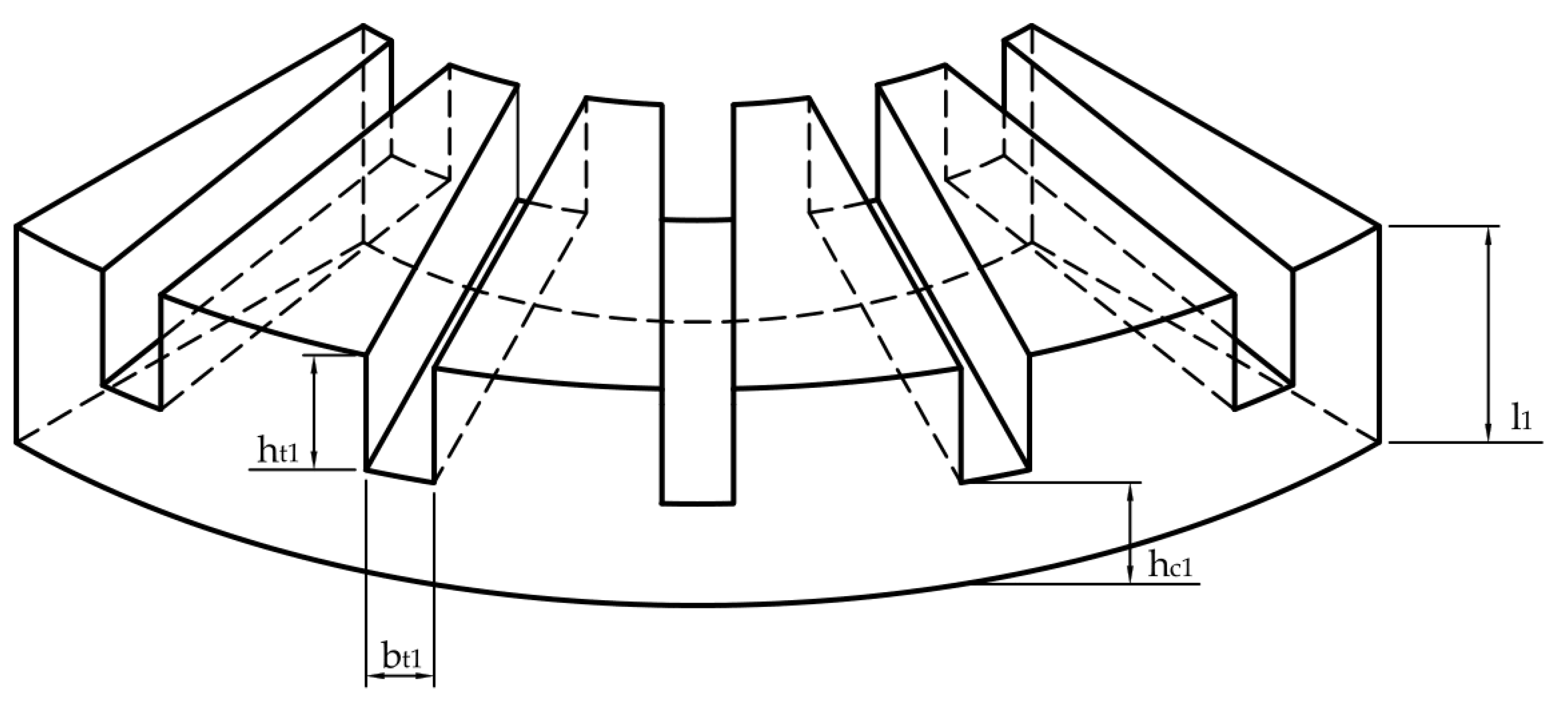
2.2.5. Area of Rectangular Slots
2.2.6. Relative Dimensions
3. Results
3.1. Calculation Example
3.1.1. Design Setup
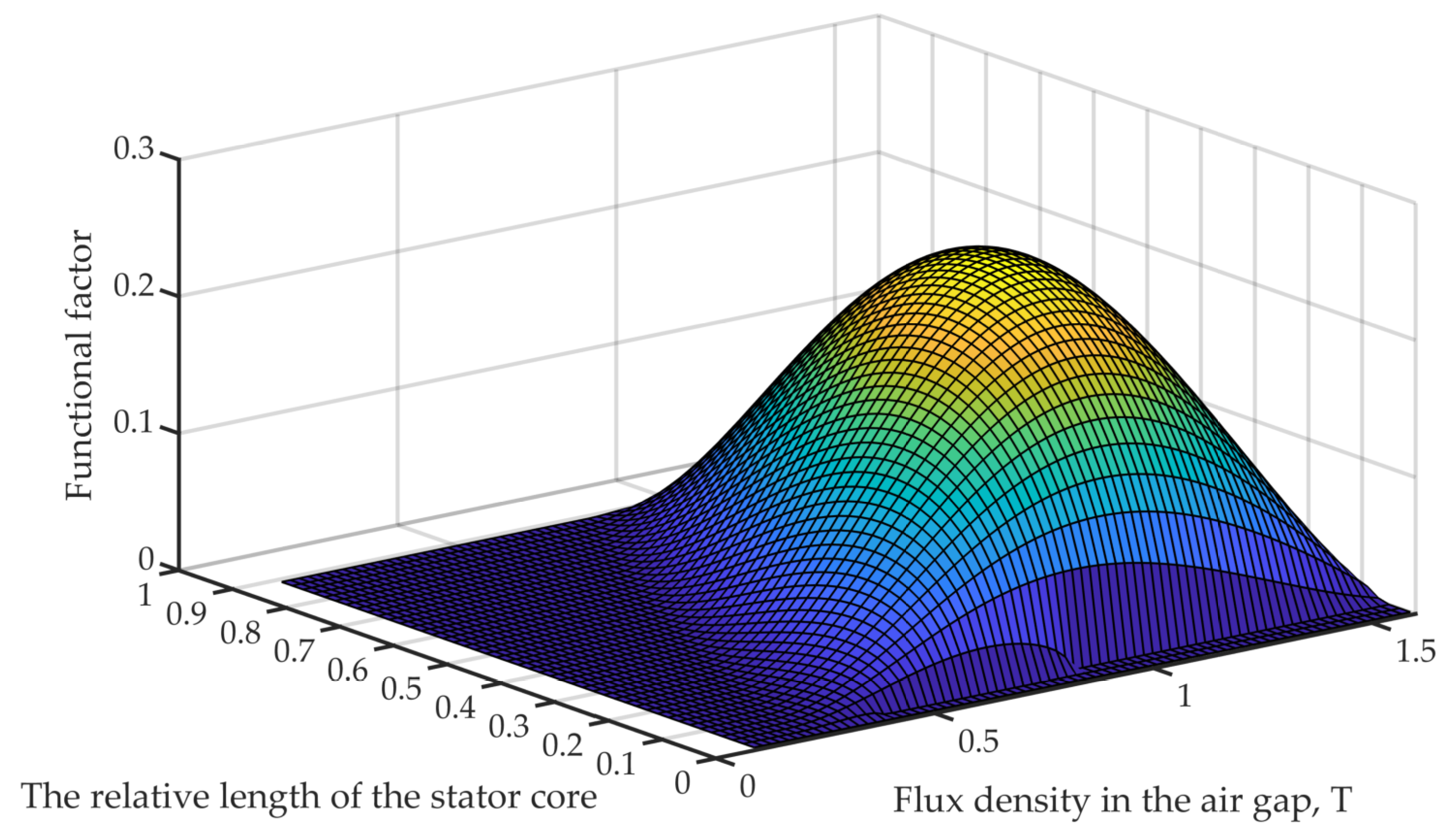
3.1.2. Applications of the Analytical Model
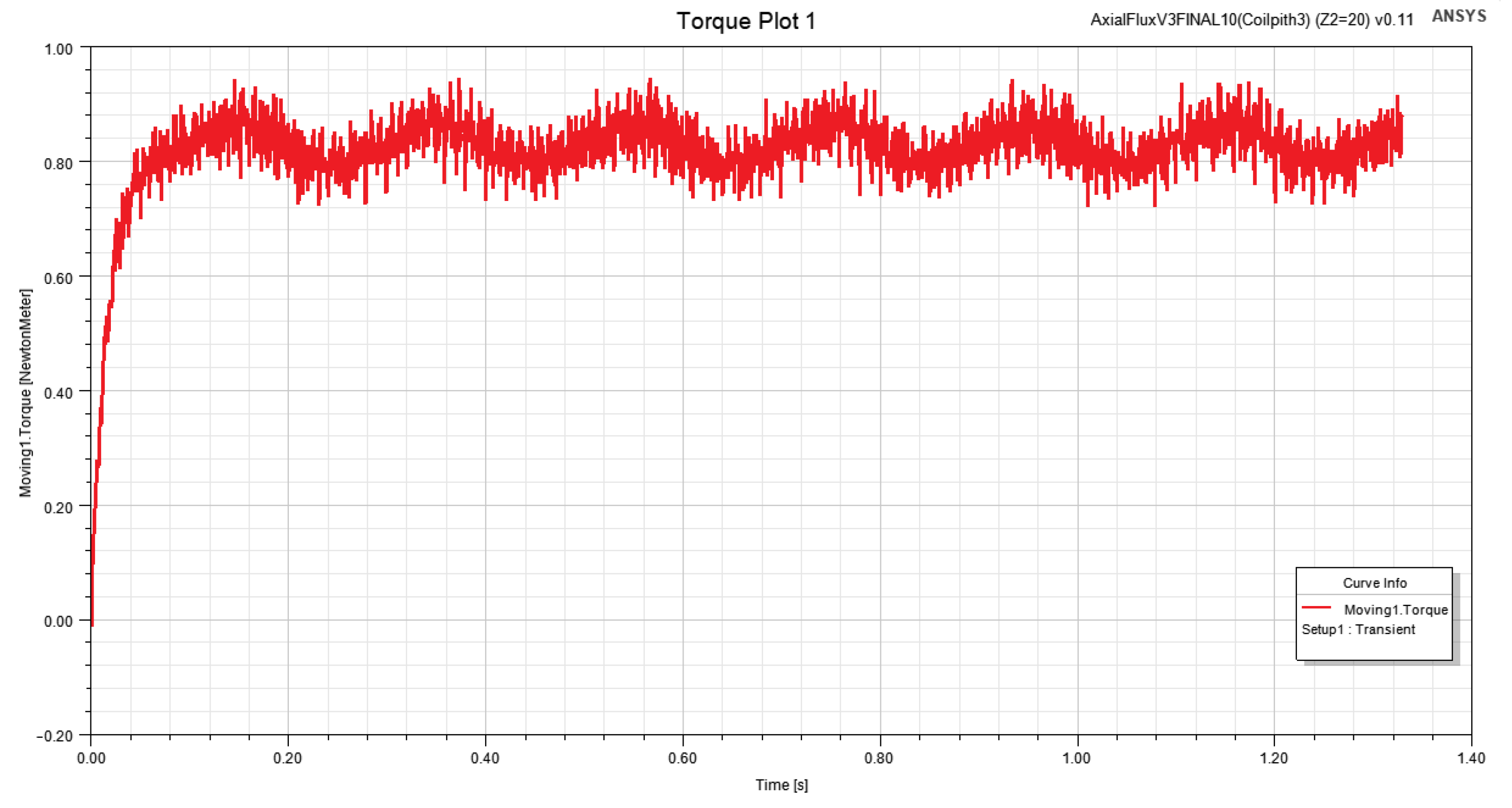
3.2. Validation of Calculated Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AFIM | Axial flux induction motor |
| FEM | Finite element method |
| p | the number of pole pairs |
| electromagnetic toque [] | |
| number of stator phases | |
| the phase voltage of the stator [], RMS | |
| electrical angular velocity | |
| stator resistance [Ohm] | |
| the resistance of the rotor referred to the stator [Ohm] | |
| Coefficient taking into account voltage drop at full resistance of stator winding | |
| stator reactance [Ohm] | |
| the rotor reactance referred to the stator [Ohm] | |
| electromotive force (emf) [], [RMS] | |
| the number of series-connected turns of the stator winding | |
| magnetic flux [] | |
| inner diameter [] | |
| outer diameter [] | |
| pole pitch [] | |
| the stator thickness [] | |
| the rotor thickness [] | |
| thickness of air gap [] | |
| L | the total thickness of the machine [] |
| magnetic flux density in air gap [] | |
| magnetic flux density in stator teeth [] | |
| magnetic flux density in rotor teeth [] | |
| magnetic flux density in stator core [] | |
| magnetic flux density in rotor core [] | |
| the thermal factor of the stator | |
| the thermal factor of the rotor | |
| conductivity of stator conductors [] | |
| conductivity of rotor conductors [] | |
| area of the stator conductor [] | |
| area of the rotor rods [] | |
| area of short-circuited rings [] | |
| current density of rotor rods [] | |
| current density of short-circuited rings [] | |
| the area of the coil pith [] | |
| the area of the stator slot [] | |
| the total area of the all stator slots [] | |
| the area of the stator tooth [] | |
| the area of the rotor slot [] | |
| the total area of the all rotor slots [] | |
| the area of the rotor tooth [] | |
| pitch factor | |
| radial length factor of the end winding | |
| winding factor | |
| space factor for iron | |
| space factor for copper | |
| space factor for aluminum | |
| the number of the stator slots | |
| the number of the rotor slots | |
| the width of the stator slot [] | |
| the width of the rotor slot [] | |
| the height of the stator slot [] | |
| the height of the stator core [] | |
| the height of the rotor slot [] |
References
- Dineva, A.; Mosavi, A.; Faizollahzadeh Ardabili, S.; Vajda, I.; Shamshirband, S.; Rabczuk, T.; Chau, K.W. Review of soft computing models in design and control of rotating electrical machines. Energies 2019, 12, 1049. [Google Scholar] [CrossRef]
- Virtic, P.; Pisek, P.; Marcic, T.; Hadziselimovic, M.; Stumberger, B. Analytical analysis of magnetic field and back electromotive force calculation of an axial-flux permanent magnet synchronous generator with coreless stator. IEEE Trans. Magn. 2008, 44, 4333–4336. [Google Scholar] [CrossRef]
- Krasopoulos, C.T.; Beniakar, M.E.; Kladas, A.G. Multicriteria PM motor design based on ANFIS evaluation of EV driving cycle efficiency. IEEE Trans. Transp. Electrif. 2018, 4, 525–535. [Google Scholar] [CrossRef]
- Virtic, P.; Pisek, P.; Hadziselimovic, M.; Marcic, T.; Stumberger, B. Torque analysis of an axial flux permanent magnet synchronous machine by using analytical magnetic field calculation. IEEE Trans. Magn. 2009, 45, 1036–1039. [Google Scholar] [CrossRef]
- Virtič, P.; Vražić, M.; Papa, G. Design of an axial flux permanent magnet synchronous machine using analytical method and evolutionary optimization. IEEE Trans. Energy Convers. 2015, 31, 150–158. [Google Scholar] [CrossRef]
- Muselli, M.; Notton, G.; Louche, A. Design of hybrid-photovoltaic power generator, with optimization of energy management. Sol. Energy 1999, 65, 143–157. [Google Scholar] [CrossRef]
- Bramerdorfer, G.; Zăvoianu, A.C. Surrogate-based multi-objective optimization of electrical machine designs facilitating tolerance analysis. IEEE Trans. Magn. 2017, 53, 1–11. [Google Scholar] [CrossRef]
- Bramerdorfer, G.; Tapia, J.A.; Pyrhönen, J.J.; Cavagnino, A. Modern electrical machine design optimization: Techniques, trends, and best practices. IEEE Trans. Ind. Electron. 2018, 65, 7672–7684. [Google Scholar] [CrossRef]
- Meo, S.; Zohoori, A.; Vahedi, A. Optimal design of permanent magnet flux switching generator for wind applications via artificial neural network and multi-objective particle swarm optimization hybrid approach. Energy Convers. Manag. 2016, 110, 230–239. [Google Scholar] [CrossRef]
- Hejra, M.; Mansouri, A.; Trabeisi, H. Optimal design of a permanent magnet synchronous motor: Application of in-wheel motor. In Proceedings of the 2014 5th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 25–27 March 2014; pp. 1–5. [Google Scholar]
- Raminosoa, T.; Blunier, B.; Fodorean, D.; Miraoui, A. Design and optimization of a switched reluctance motor driving a compressor for a PEM fuel-cell system for automotive applications. IEEE Trans. Ind. Electron. 2010, 57, 2988–2997. [Google Scholar] [CrossRef]
- Knypiński, Ł.; Pawełoszek, K.; Le Menach, Y. Optimization of Low-Power Line-Start PM Motor Using Gray Wolf Metaheuristic Algorithm. Energies 2020, 13, 1186. [Google Scholar]
- Frederico, L.S.B.F.C.; Min, G.G.J.A.R. Ant colony optimization for the topological design of interior permanent magnet (IPM) machines. Electron. Eng. 2014, 26, 1324–1345. [Google Scholar]
- Mamede, A.C.F.; Camacho, J.R. Evolutionary algorithms for optimization of 4/4 single phase switched reluctance machine. IEEE Lat. Am. Trans. 2018, 16, 1684–1691. [Google Scholar] [CrossRef]
- Benallal, M.; Vaganov, M.; Pantouhov, D.; Ailam, E.; Hamouda, K. Optimal value of air gap induction in an induction motor. In Proceedings of the XIX International Conference on Electrical Machines—ICEM 2010, Rome, Italy, 6–8 September 2010; pp. 1–4. [Google Scholar]
- Pyrhonen, J.; Jokinen, T.; Hrabovcova, V. Design of Rotating Electrical Machines; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Yang, Y.P.; Shih, G.Y. Optimal design of an axial-flux permanent-magnet motor for an electric vehicle based on driving scenarios. Energies 2016, 9, 285. [Google Scholar] [CrossRef]
- Du-Bar, C. Design of an Axial Flux Machine for an In-Wheel Motor Application. Master’s Thesis, Chalmers Reproservice, Göteborg, Sweden, 2011. [Google Scholar]
- Gao, P.; Gu, Y.; Wang, X. The design of a permanent magnet in-wheel motor with dual-stator and dual-field-excitation used in electric vehicles. Energies 2018, 11, 424. [Google Scholar] [CrossRef]
- Kreim, A.; Schäfer, U. An approach to an optimal design of permanent magnet synchronous machines for battery electric vehicles. World Electr. Veh. J. 2013, 6, 673–683. [Google Scholar] [CrossRef]
- Nobahari, A.; Darabi, A.; Hassannia, A. Axial flux induction motor, design and evaluation of steady state modeling using equivalent circuit. In Proceedings of the 2017 8th Power Electronics, Drive Systems & Technologies Conference (PEDSTC), Mashhad, Iran, 14–16 February 2017; pp. 353–358. [Google Scholar]
- Valtonen, M.; Parviainen, A.; Pyrhonen, J. Influence of the air-gap length to the performance of an axial-flux induction motor. In Proceedings of the 2008 18th International Conference on Electrical Machines, Vilamoura, Portugal, 6–9 September 2008; pp. 1–5. [Google Scholar]
- Nasiri-Gheidari, Z.; Lesani, H. Design optimization of a single-phase axial flux induction motor with low torque ripple. Przegląd Elektrotechniczny 2012, 88, 168–172. [Google Scholar]



| Designation | Name | Value | Unit |
|---|---|---|---|
| U | Line voltage, RMS | 7.35 | |
| Maximum line voltage | 36 | ||
| f | Rated frequency | 50 | |
| Maximum frequency | 100 | ||
| Outer diameter | 0.11 | ||
| Inner diameter | 0.05 | ||
| L | Total thickness | 0.03 | |
| The number of phases | 3 | - | |
| p | The number of pole pairs | 4 | - |
| q | The number of slots per pole and phase | 1 | - |
| Step of span in slot pitches | 3 | - | |
| The number of rotor slots | 32 | - | |
| Space factor for copper | 0.5 | - | |
| Space factor for iron | 0.98 | - | |
| Space factor for aluminum | 0.97 | - | |
| Thermal factor | 1.32 | - | |
| Thickness of air gap | 1 | ||
| Overload capability | 2 | - | |
| Inductance of stator core | 1.4 | ||
| Inductance of rotor core | 1.3 | ||
| Inductance in stator teeth | 1.8 | ||
| Cros-section of 1 conductor |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baranov, G.; Zolotarev, A.; Ostrovskii, V.; Karimov, T.; Voznesensky, A. Analytical Model for the Design of Axial Flux Induction Motors with Maximum Torque Density. World Electr. Veh. J. 2021, 12, 24. https://doi.org/10.3390/wevj12010024
Baranov G, Zolotarev A, Ostrovskii V, Karimov T, Voznesensky A. Analytical Model for the Design of Axial Flux Induction Motors with Maximum Torque Density. World Electric Vehicle Journal. 2021; 12(1):24. https://doi.org/10.3390/wevj12010024
Chicago/Turabian StyleBaranov, Georgii, Alexander Zolotarev, Valerii Ostrovskii, Timur Karimov, and Alexander Voznesensky. 2021. "Analytical Model for the Design of Axial Flux Induction Motors with Maximum Torque Density" World Electric Vehicle Journal 12, no. 1: 24. https://doi.org/10.3390/wevj12010024
APA StyleBaranov, G., Zolotarev, A., Ostrovskii, V., Karimov, T., & Voznesensky, A. (2021). Analytical Model for the Design of Axial Flux Induction Motors with Maximum Torque Density. World Electric Vehicle Journal, 12(1), 24. https://doi.org/10.3390/wevj12010024






