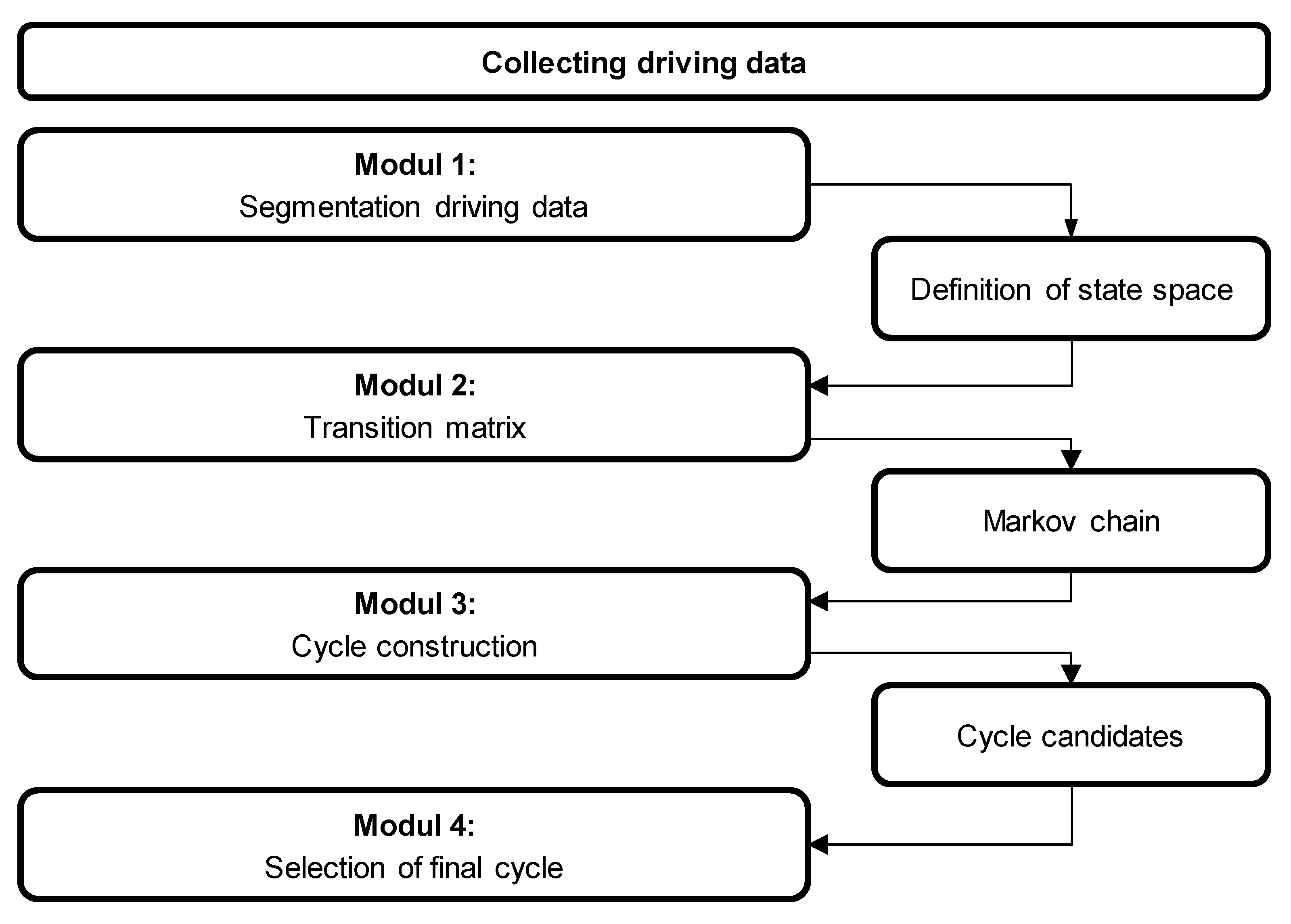
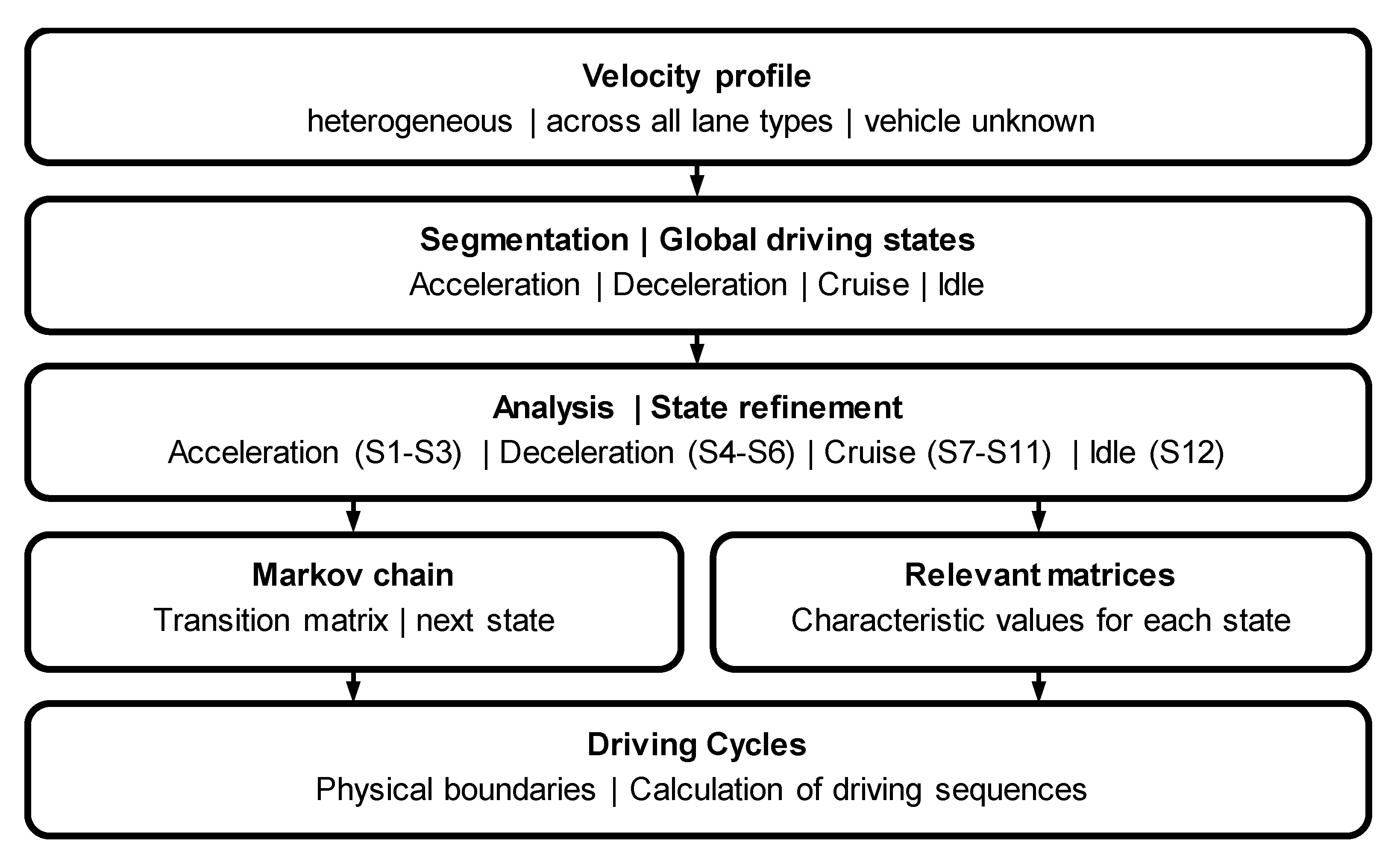
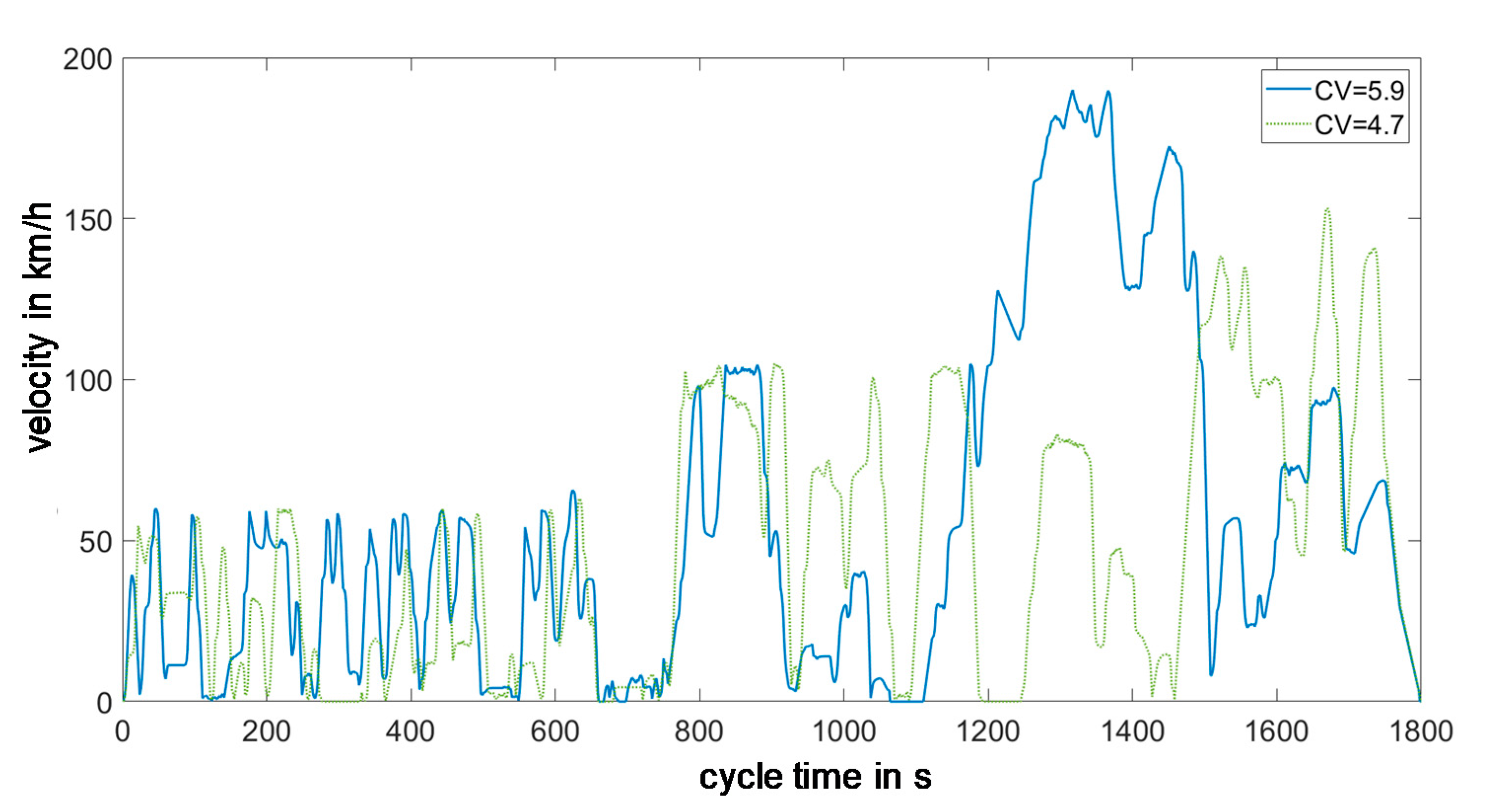
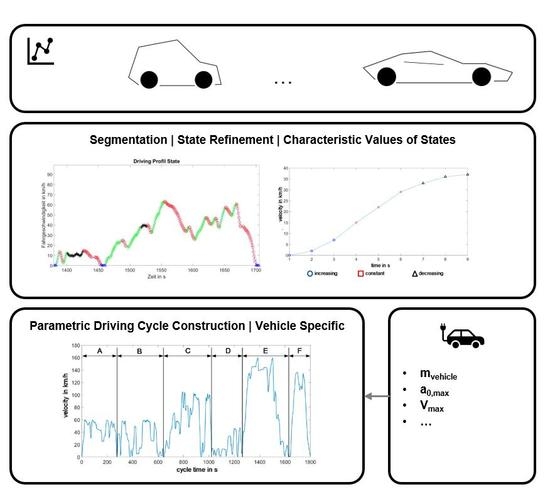
Starting point are the driving profiles of a heterogeneous data set. In the first step, the segmentation into the four global driving states acceleration, deceleration, oscillation and idling takes place. The data analysis in the second step comprises the state refinement and serves to derive characteristic values for each driving state. The results here are, on the one hand, the completely segmented driving profiles, as well as so-called relevant matrices that characterize a driving state. For each driving state S1 to S12, the relevant matrices contain the characteristic values required for the parametric calculation of a driving segment of the corresponding state. More details are shown below. In the third step, the transition matrix can be calculated with this, before a driving cycle is parametrically calculated in the final fourth step.
3.2.2. Data Segmentation
For the EMCC methodology, a new two-stage segmentation approach is shown, which in the first stage prescribes concrete characteristic values for all global driving states. Initially, it is not required that a driving point can only be assigned to exactly one of the four global driving states acceleration, deceleration, oscillation and idling. Note that oscillation in a speed window is composed of acceleration and deceleration. The unambiguousness, which is absolutely necessary to derive the transition matrix, is achieved by the second segmentation stage in a logic.
Step 1: Pre-Segmentation
First, the criteria to be met for each driving condition are set. A driving sequence is identified as an acceleration sequence if for at least 3 s the acceleration in each individual driving point is greater than a
i ≥ 0.01 m/s
2 and the sum of the acceleration values in the driving points is greater than a
sum ≥ 0.1 m/s
2. A deceleration sequence is defined in an analogous manner. A travel sequence is a deceleration sequence if the acceleration is less than a
i ≤ −0.005 m/s
2 for at least 3 s and the sum of the acceleration values in the individual travel points is less than a
sum ≤ −0.1 m/s
2. Previous procedures define all points in a travel profile which have not been identified as acceleration or braking states as oscillating or idling states. Here, however, defined criteria are also to be set for these two driving states. To identify a cruising sequence, a driving sequence with a duration of 10 s is examined. The driving sequence is a cruising sequence if the deviation of the speed in the individual driving points from the average speed of the examined sequence does not exceed a defined tolerance window. This tolerance window is assumed as a function of the average speed of the examined sequence in order to avoid too strong a generalization. The permissible tolerance decreases with increasing speed. The tolerance range is between 25% at very low speeds to 2% at very high speeds. The identification of an idle state is only carried out on the basis of the driving speed. If the driving speed is lower than v
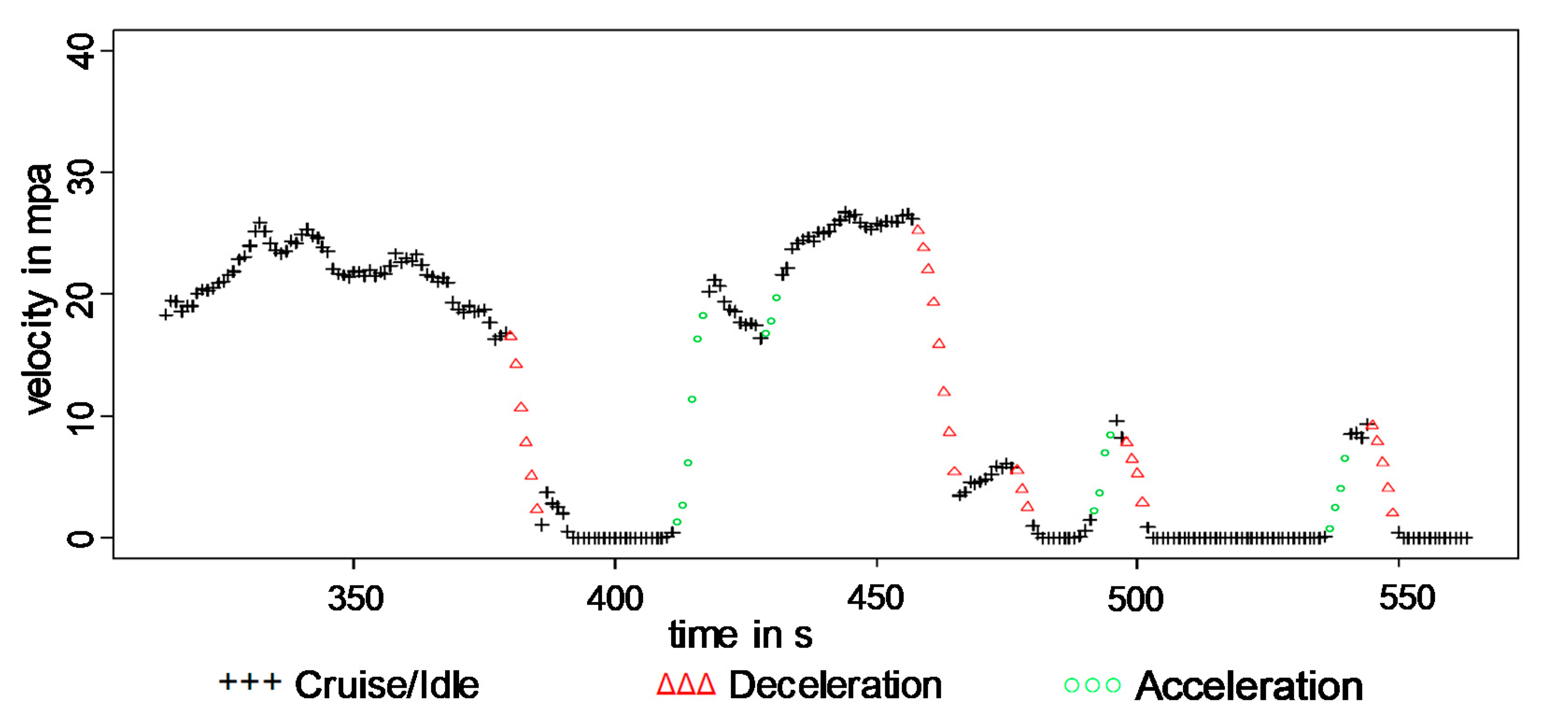
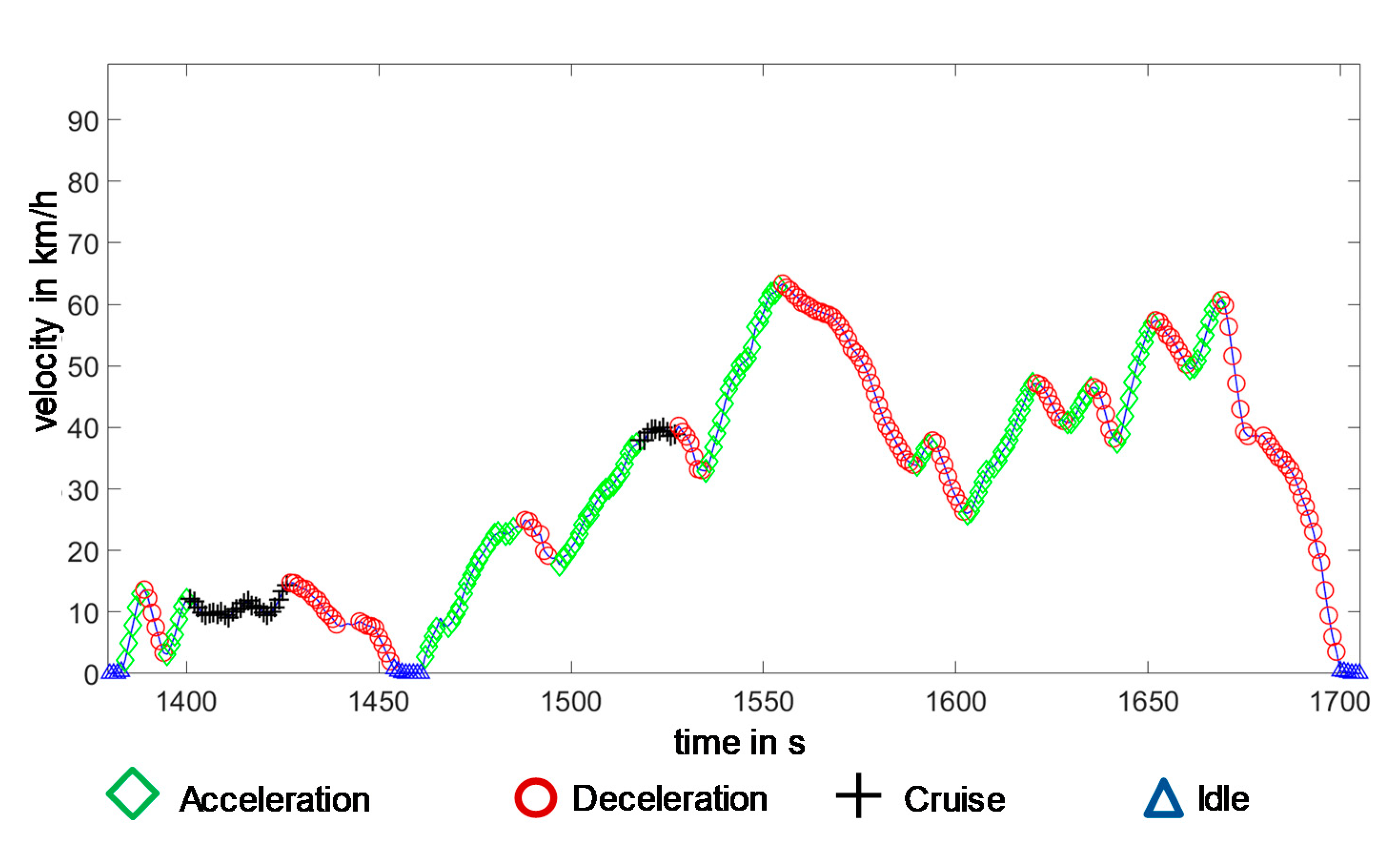
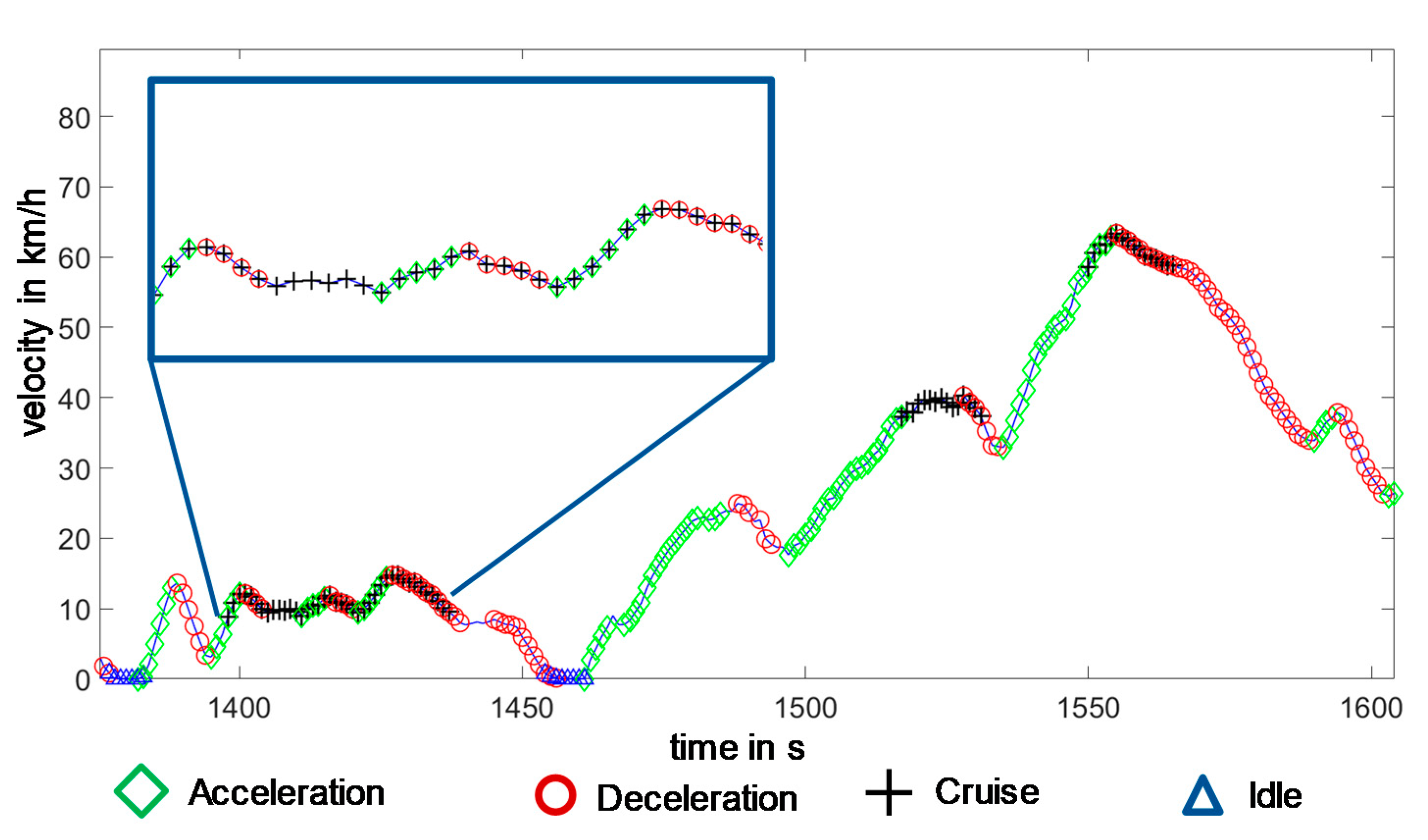
i ≤ 1 km/h for at least 3 s, an idle state is assumed for this sequence. The following figure shows a classified driving sequence according to the criteria mentioned above (
Figure 9).
The figure shows that a cruising sequence is composed of acceleration and deceleration states. Therefore, driving points can be assigned to more than one global driving state.
Step 2: Unambiguousness
To decide whether a driving point belongs to an acceleration, deceleration or cruising sequence, a logic is used which is based on four principles.
A cruising sequence is not interrupted by an acceleration sequence that is shorter than the current cruising sequence, e.g., in
Figure 9. at time 1415 s.
A cruising sequence is not interrupted by a braking sequence that is shorter than the current cruising sequence, e.g., in
Figure 9. at time 1420 s.
An acceleration sequence is not interrupted by a subsequent cruising sequence that is detected, e.g., in
Figure 9. at time 1550 s.
If the deceleration sequence is longer than the cruising sequence which has also been detected, the cruising sequence is interrupted at the starting point of the deceleration sequence. The braking sequence then dominates, e.g., in
Figure 9. at time 1530 s.
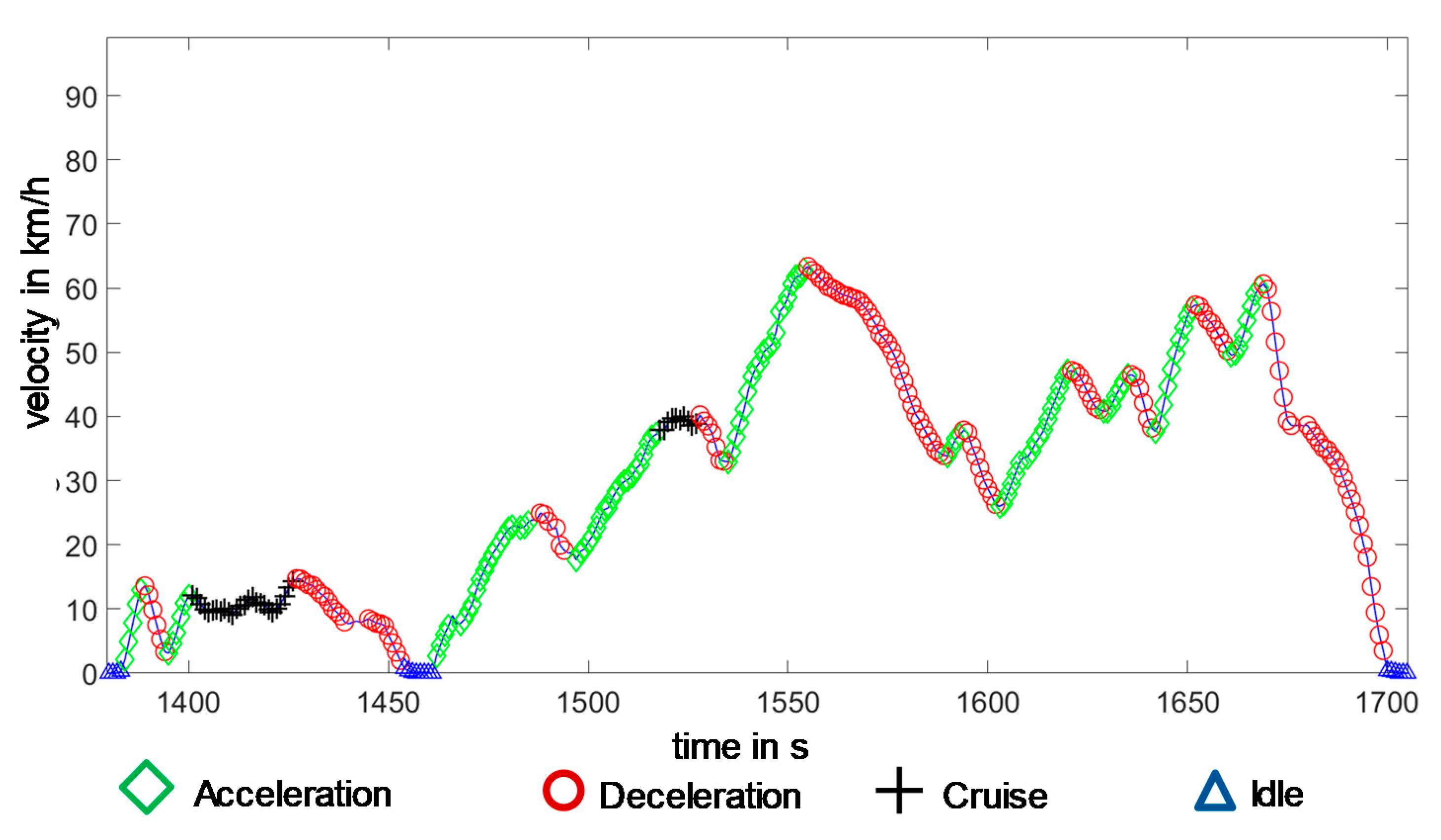
The
Figure 10 below shows the result after applying this logic.
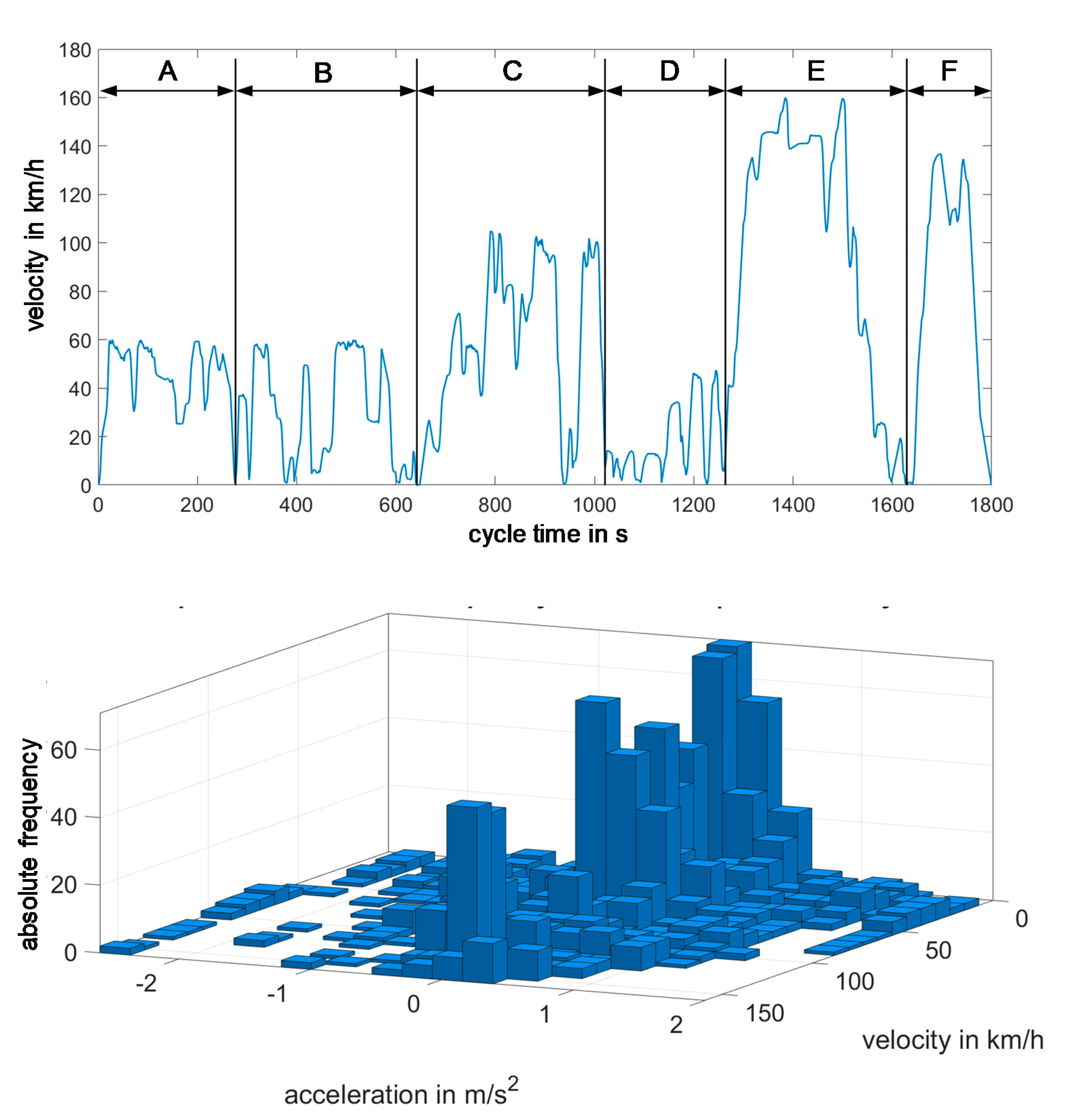
This two-stage classification procedure enables the robust and unambiguous assignment of driving sequences to the four global driving states with fixed criteria. From the nearly 4000 km of driving data, 4410 acceleration, 4204 deceleration, 3368 cruising and 538 idling sequences can be extracted by the two-stage segmentation method. For the data set used, over 95% of all driving points can thus be assigned to one of the four global driving states. Non-assigned points have no influence on the results of cycle construction, as in the approach presented here no real driving segments are linked, but rather these are constructed parametrically.
3.2.3. Data Analysis
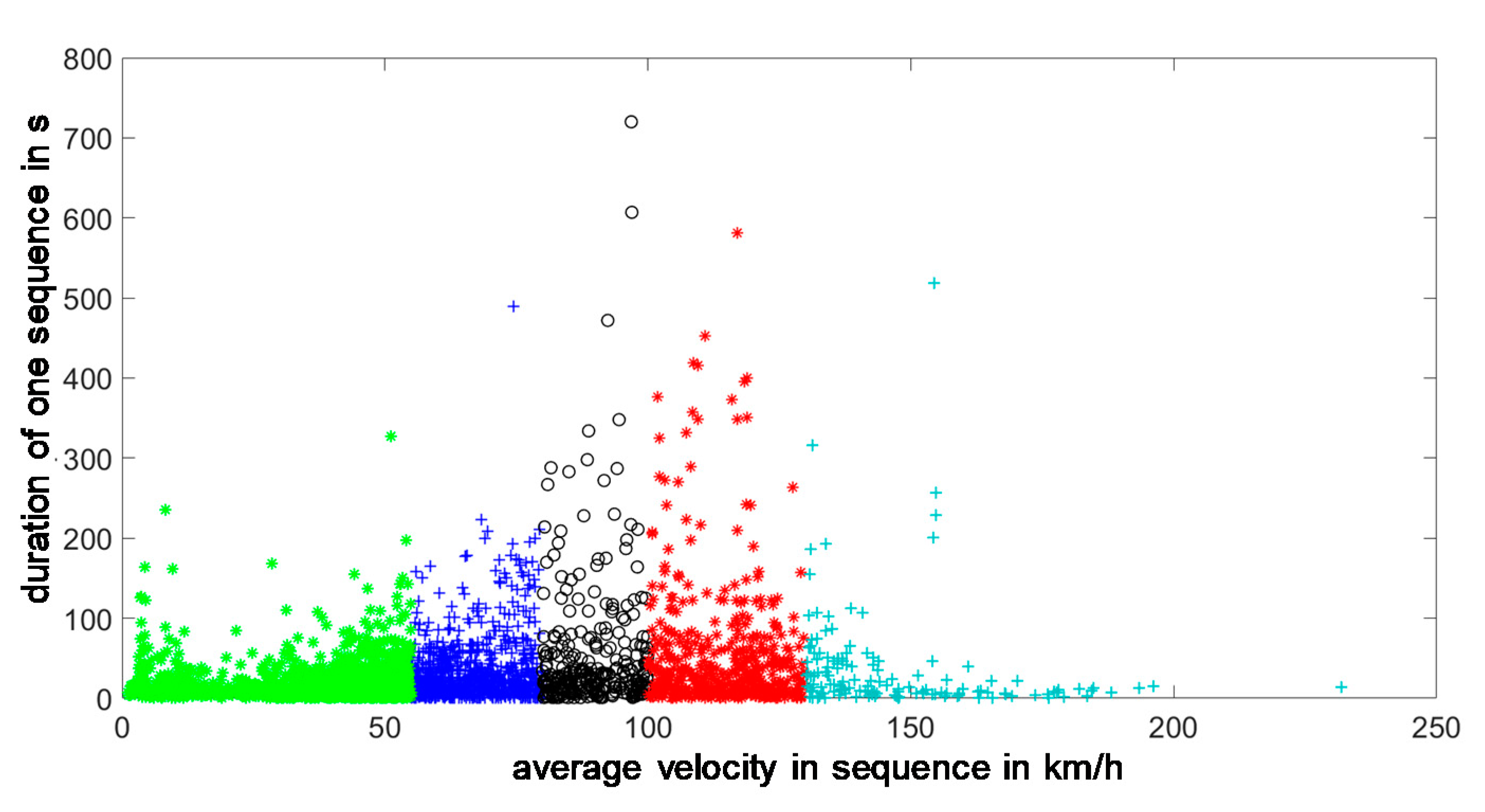
In order to avoid a generalization of the characteristic values of the individual states, the driving sequences are subdivided into different speed ranges analogous to [
10]. For the set of driving sequences of a global driving state and speed range the evaluation and derivation of the characteristic values is done in three steps. In the first step a state refinement is applied to justify the assumption of a 1st order Markov chain. From the four global states, 12 driving states (S
1–S
12) are derived. Accordingly, after this step, a set of driving sequences is available for each driving state S
1–S
12.
For the parametric simulation of a sequence of these driving states, a set of characteristic values is required for each state. These differ from state to state and in general include the duration tseq and initial acceleration astart of the corresponding state. In the second step, therefore, these descriptive characteristic values are identified. Once the variables have been identified for each state, these characteristic values can be assigned in the third step by means of a statistical analysis.
Sequences of acceleration and deceleration:
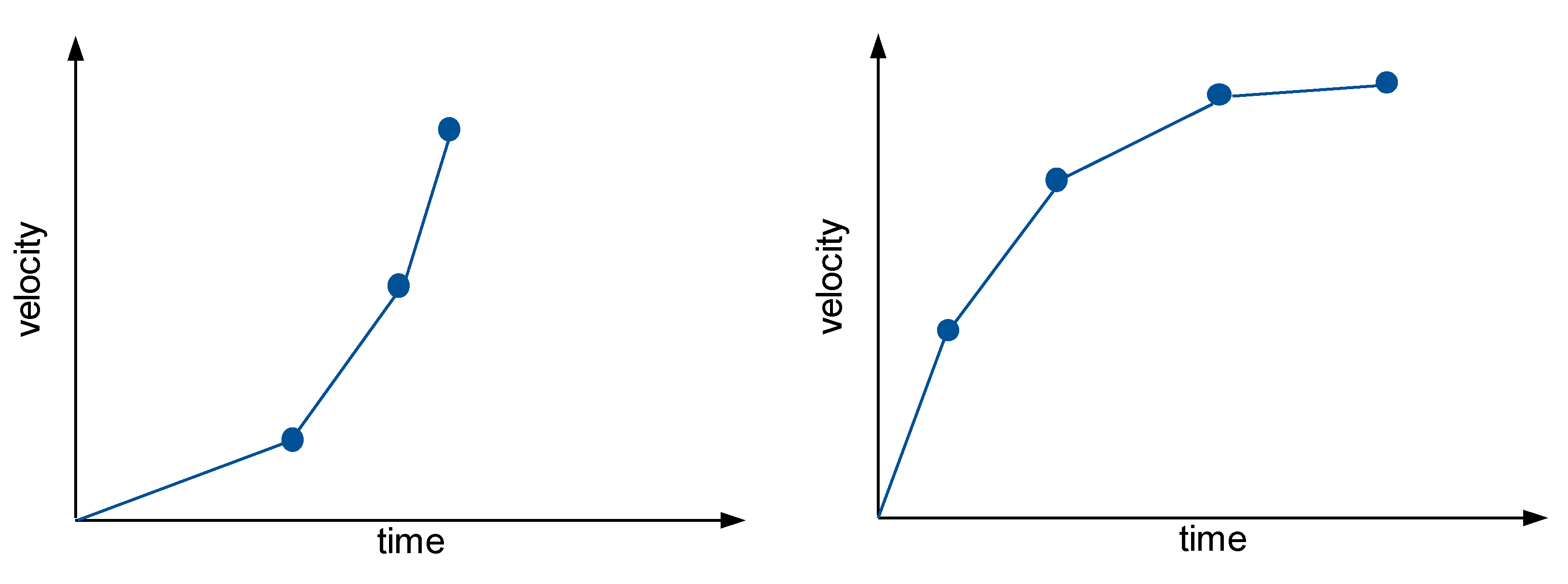
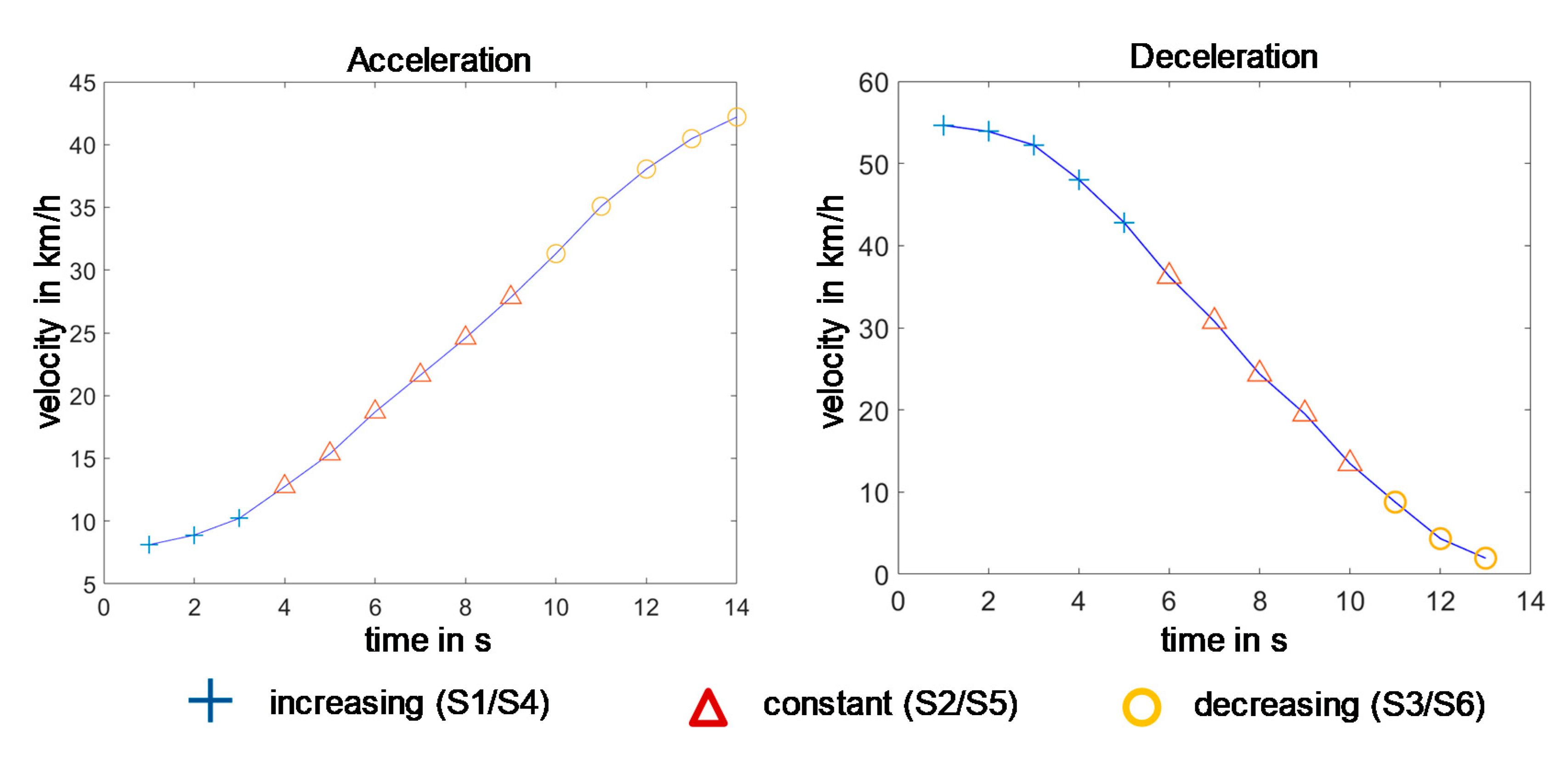
The global acceleration and deceleration sequences are first divided into sub-states (
Figure 8). The following
Figure 11 shows a subdivided global acceleration and deceleration sequence in the corresponding sub-states.
The states of increasing acceleration (S
1) and increasing deceleration (S
4) are defined as follows:
In most cases, one of these states can be detected at the beginning of an acceleration sequence or deceleration sequence. Depending on the total duration of the sequence to be segmented, a state of uniform acceleration usually follows, referred to below as state S
2 or S
5.
This state can last from one to many seconds, depending on the duration of an acceleration or deceleration process. The end of a global acceleration or deceleration sequence is usually characterized by a flattening of the acceleration value. The following applies to states S
3 (acceleration) and S
6 (deceleration):
For the choice of the conditions set in Equations (4) and (6) for state refinement, a compromise between robust state assignment and generalization must be chosen. For each state S1–S6, further characteristic values are derived from the set of corresponding sequences, which allow to construct such sequences parametrically. In the following, the further evaluation for the acceleration states S1–S3 is shown. The evaluation of the deceleration states follows the same procedure and is not shown further here.
The following
Table 1 shows the identified characteristic values which are necessary for the calculation of a driving segment of the corresponding state.
For the driving states S
1 and S
3, the acceleration in the next time step can be calculated using the scaling factor.
For the driving state S1 the acceleration value astart is required for the first time step of this state. Since the state’s steady acceleration (S2) and decreasing acceleration (S3) usually follow on another acceleration state, the initial acceleration value is taken over from the last state in the first time step. After Equation (3) the driving profile can then be calculated for the duration tseq.
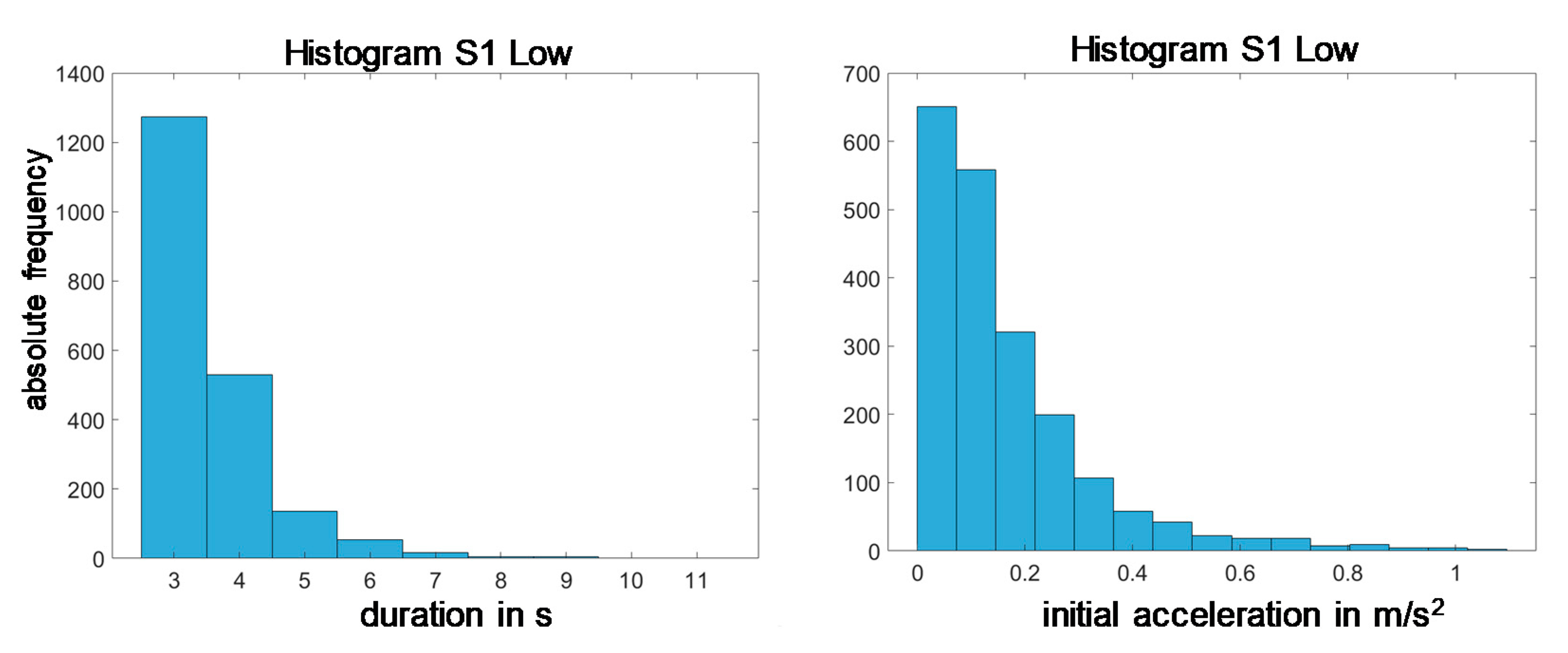
After the state refinement and the identification of the characteristic values that are necessary for the parametric calculation of a driving sequence, the derivation of these values from the extracted real driving sequences is carried out in the third step of the data analysis. The following figure shows an example of the distribution for the sequence duration t
seq and the start acceleration a
start for a speed range of the driving state S
1 (
Figure 12).
For each characteristic value of a driving condition and speed range it must be decided whether a constant value can be assumed or whether a frequency distribution must be taken into account. Furthermore, one of the identified characteristic values can depend on one of the other characteristic values. For the driving state S
1, the statistical evaluation has shown that a constant value can be assumed for the sequence duration t
seq. The start acceleration a
start is selected in accordance with a frequency distribution, for the scaling factor scale
S1 the value is determined as a function of the start acceleration. The characteristic values of a state are summarized in a matrix relevant for this state and velocity range (
Table 2).
If the next state selected by the Markov chain is the driving state S
1 and the current cycle speed is within the range corresponding to this matrix, then the first row of this matrix is selected with a probability of 32.2%. For the further acceleration states S
2 and S
3, as well as the deceleration states S
4–S
6, an analogous data analysis is performed. In the following
Table 3, the identified characteristic values for these states are summarized again.
Sequences of Cruising:
For the acceleration and deceleration sequences, a subdivision into three speed ranges was applied [
10]. For the evaluation of the cruising sequences, the EMCC methodology proposes a finer subdivision into five ranges. The limit values are 55, 80, 100, 130 km/h (
Figure 13).
For each of these speed ranges, an evaluation is carried out according to the procedure described above. In their work,
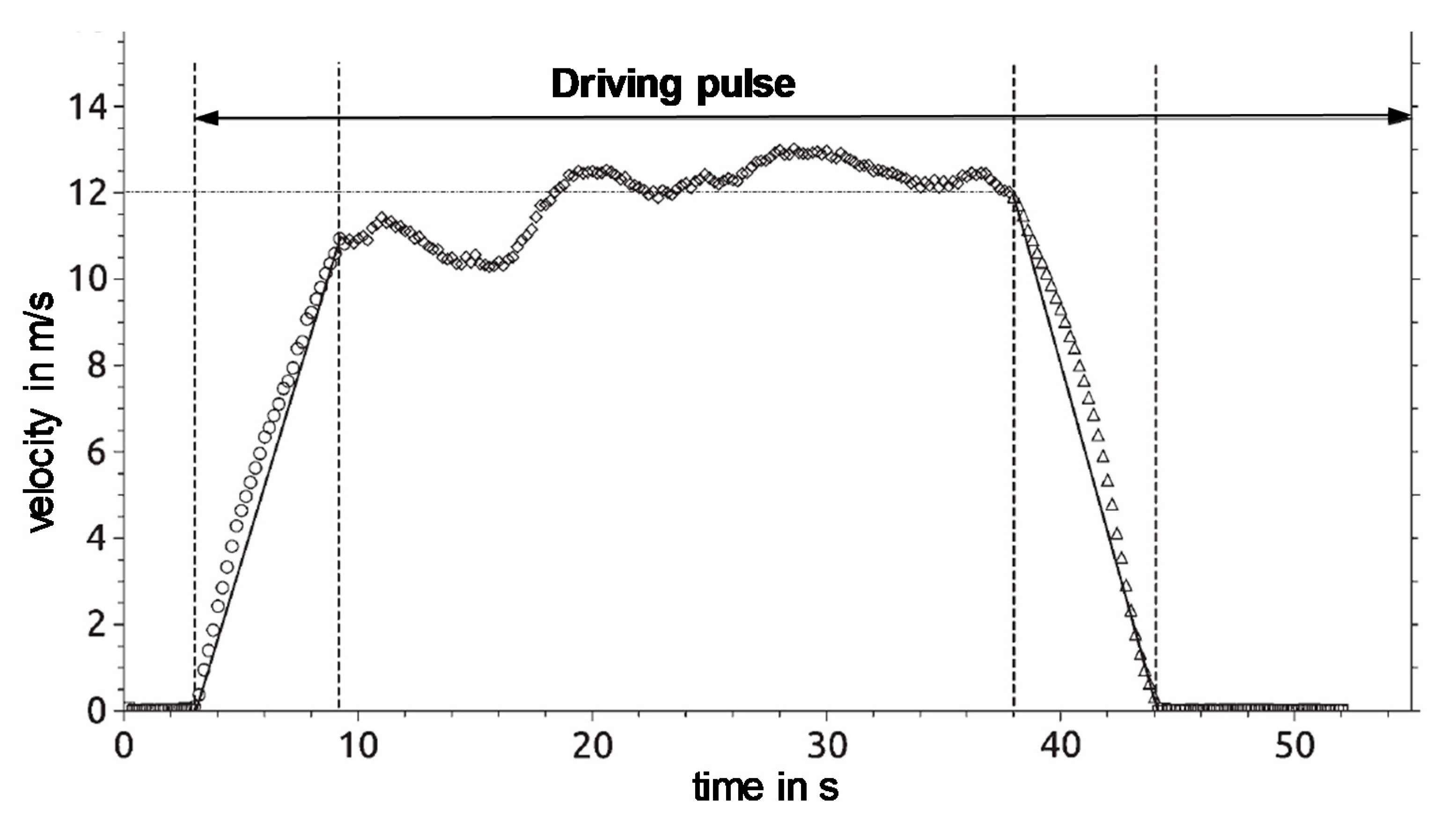
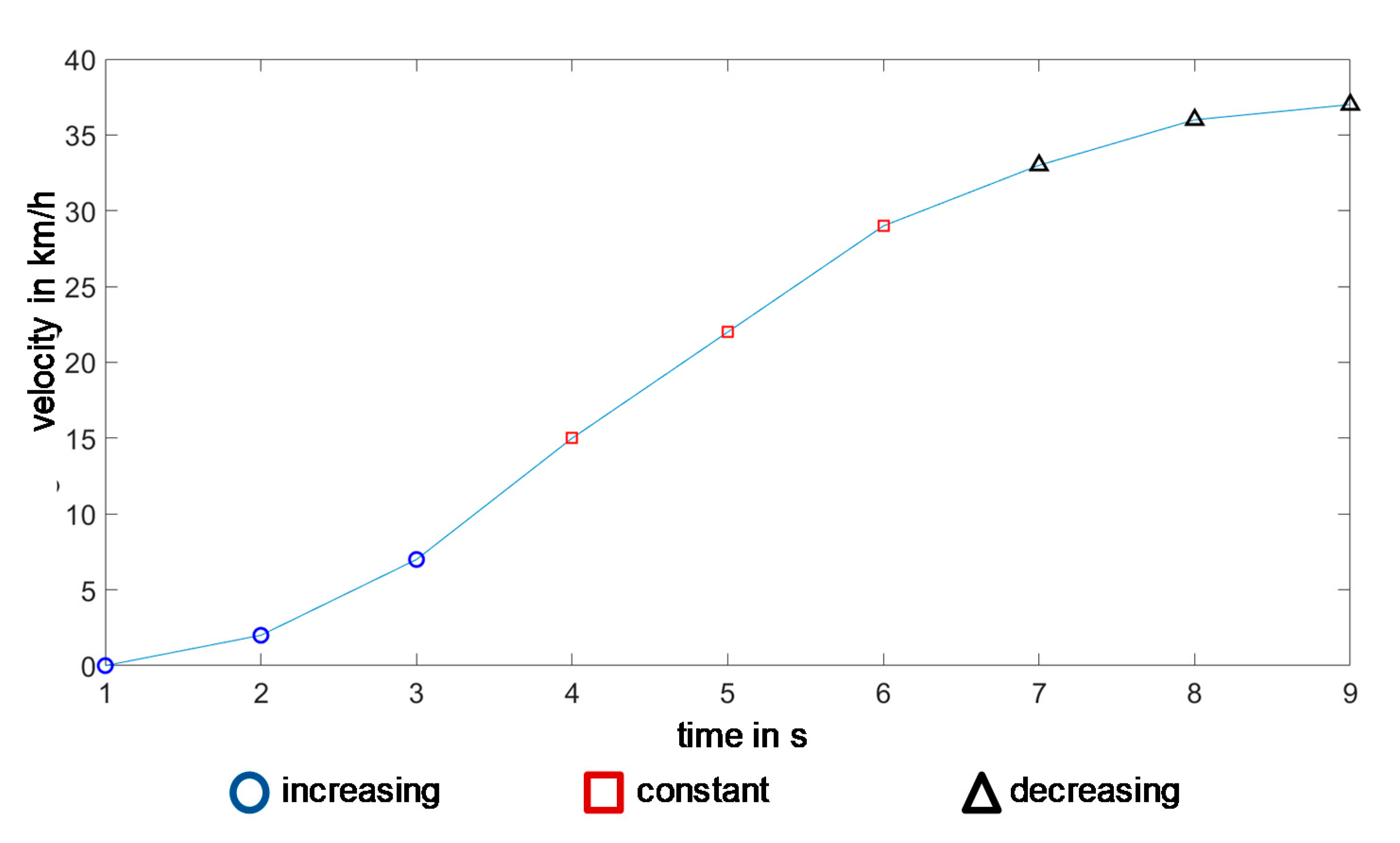
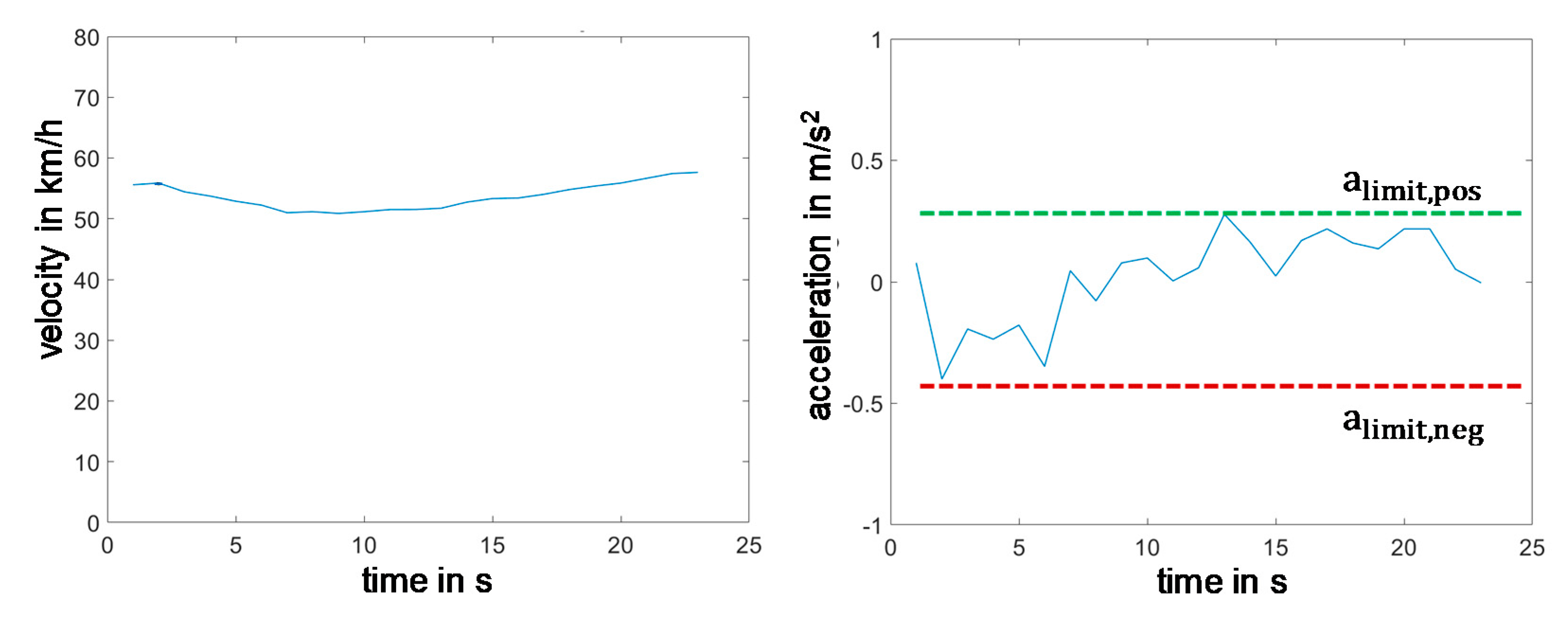
SCHWARZER and GHORBANI show a method that represents cruising sequences as speed noise. For the EMCC method a simplified modelling of a cruising sequence is to be applied. Such a sequence can be described and parametrically modelled by means of three characteristic values (
Figure 14).
Besides the sequence duration tseq the limits of the acceleration value a(limit,pos/neg) are needed. For each point in time of the cruising state, an acceleration value is then randomly selected which lies within these limits. As a result, the driving speed varies in a small window around the initial speed, which corresponds to the definition of a cruising sequence on which this paper is based. This simplified approximation of cruising sequences is considered appropriate for the objective here. However, the method shown by SCHWARZER and GHORBANI certainly offers higher accuracy.
For the consideration of cruising sequences of different lengths, the definition of a global cruising state is not sufficient. Even for speeds up to 55 km/h the duration of the identified cruising sequences in the real data varies from one to more than 100 s. Therefore, a state refinement is also applied here. In each speed range, five cruising states S7–S11 are defined, which are characterized by a different cruising duration. The limit values for the duration of a state vary for each speed range, but are set in such a way that after the cruising sequences have been divided into these driving states S7–S11, a fixed prescribed frequency distribution results. For example, 45% of the extracted cruising sequences of a speed range belong to the driving state S7. As a result of this state refinement, the range of the cruising duration tseq of one state decreases significantly.
For each driving state S
7–S
11 and speed range the statistical evaluation and derivation of the above identified characteristic values t
seq, a
(limit,pos), a
(limit,neg) is carried out according to a uniform procedure. The duration t
seq of a cruising sequence is chosen quasi randomly according to the frequency distribution found in the real data (
Figure 15).
The minimum and maximum acceleration a
(limit,pos/neg) is the average value of a class formed for the duration of a cruising sequence. The following table shows a section of the relevant matrix for the driving state S
7 (<55 km/h) (
Table 4).
If the next state selected by the Markov chain is driving state S7 and the current cycle speed is below 55 km/h, then with a probability of 7% this state will last for 2 s and the acceleration values will be between −0.035 m/s2 and +0.05 m/s2 (class 2). Depending on the speed range and cruising state, these characteristics vary.
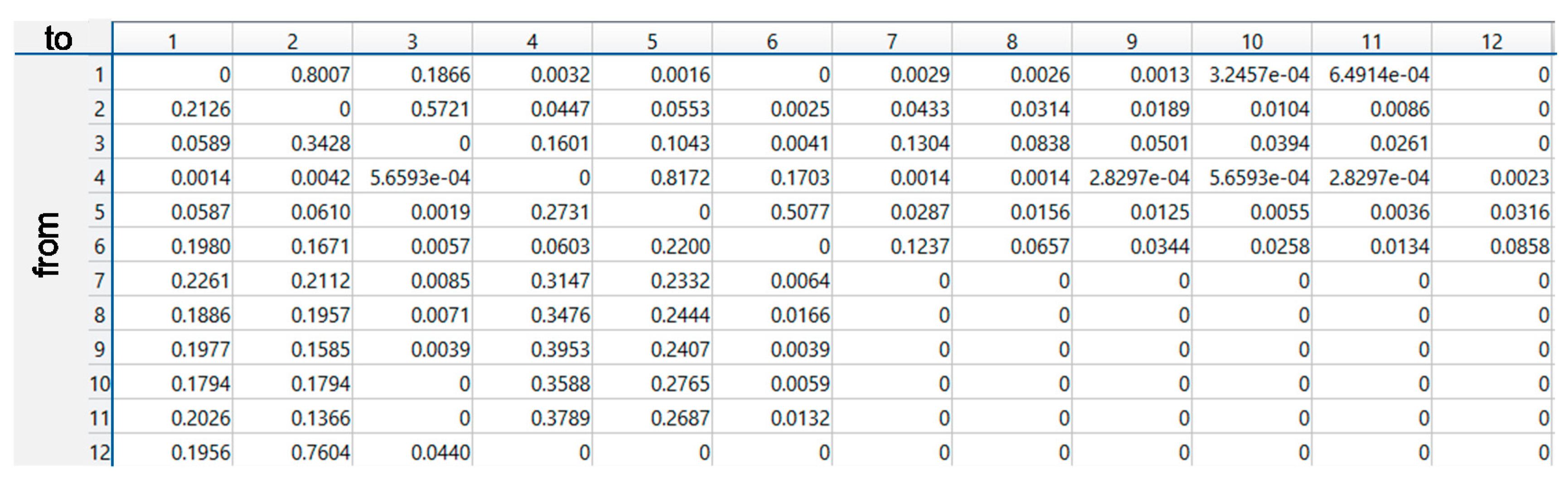
In summary, for each driving state S1–S11 and the different speed ranges such a matrix exists with all relevant characteristic values and the frequency distributions to be taken into account. With the help of this matrix, segments of the driving states can be calculated parametrically.
Sequences of Idle:
For the remaining idle state S
12, the duration of such a state is used as the only characteristic value. The speed and acceleration must be set to zero. In addition to traffic conditions, such as red lights or traffic jams, the duration of an idling sequence is also significantly influenced by the driver and his intentions. The data set used here was recorded with smartphones. Whether the vehicle was actually idling or whether the journey was simply not interrupted manually on the smartphone and the vehicle was already parked cannot be reconstructed from the data set. Therefore, the duration of an idle state will not be derived from the real driving data in this paper. The duration of the driving state S
12 is randomly chosen between one and 90 s. This value corresponds to the maximum circulation time of a traffic light and is considered useful here [
15]. For the results in this paper, an equal distribution for values between 1 to 90 s is used. However, this can be adapted to specific applications, e.g., city cycles.
This means that the characteristic values required for the parametric calculation according to Equation (3) are known for all 12 driving states. The 12 driving states are linked to a driving cycle by a 1st order Markov chain.
3.2.5. Calculation of Driving Cycle
According to Equation (3) the driving cycle can be calculated iteratively. If the state is determined by the Markov chain, the associated travel segment can be calculated using the characteristic values of this state. For this purpose, a state vector is defined which comprises all characteristic values of the selected travel state and the current cycle speed. For the first driving state S
1 of a driving cycle after the initial distribution, the following state vector results as an example.
For this state vector, a driving segment with a duration of 4 s is calculated starting from an initial speed of zero according to the following relationship.
where
t is the current cycle time. In this way, the corresponding travel segment can be calculated for each of the next selected travel states of the Markov chain. This is repeated until the desired cycle length is reached.
The EMCC methodology presented here builds up motion segments for the defined motion states based on the characteristic values. In contrast to the linking of real driving segments in the previous methods according to [
6,
7,
9,
13], the shown EMCC method requires that physically reasonable limit values be observed. The Markov chain has no knowledge that the driving state S
4 (increasing deceleration) cannot be assumed at the current cycle speed close to zero, since otherwise a speed below zero results due to negative acceleration.
The two major interventions to maintain the physical limits are achieved by setting a minimum speed of 0 km/h and a vehicle-specific maximum cycle speed.
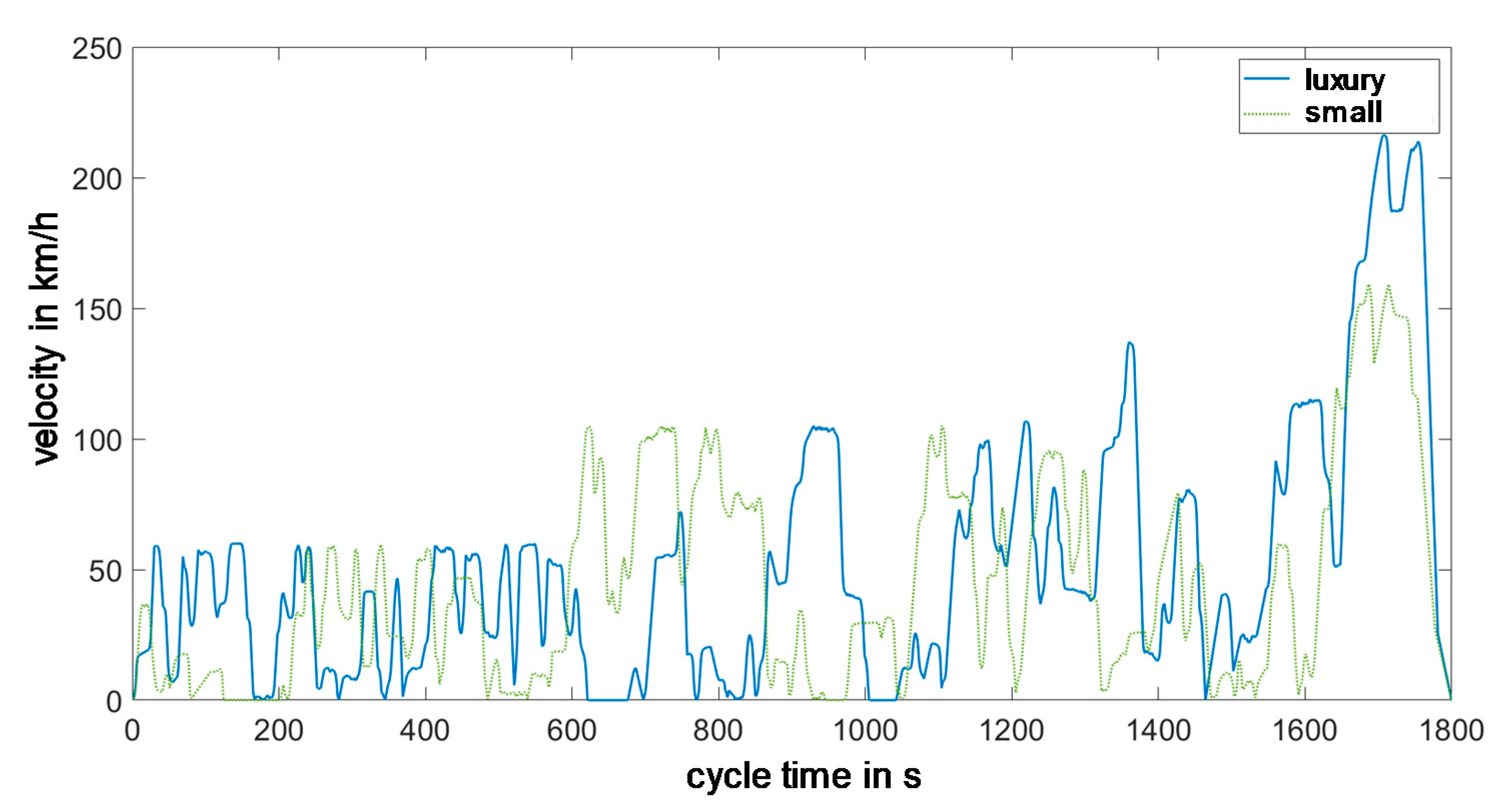
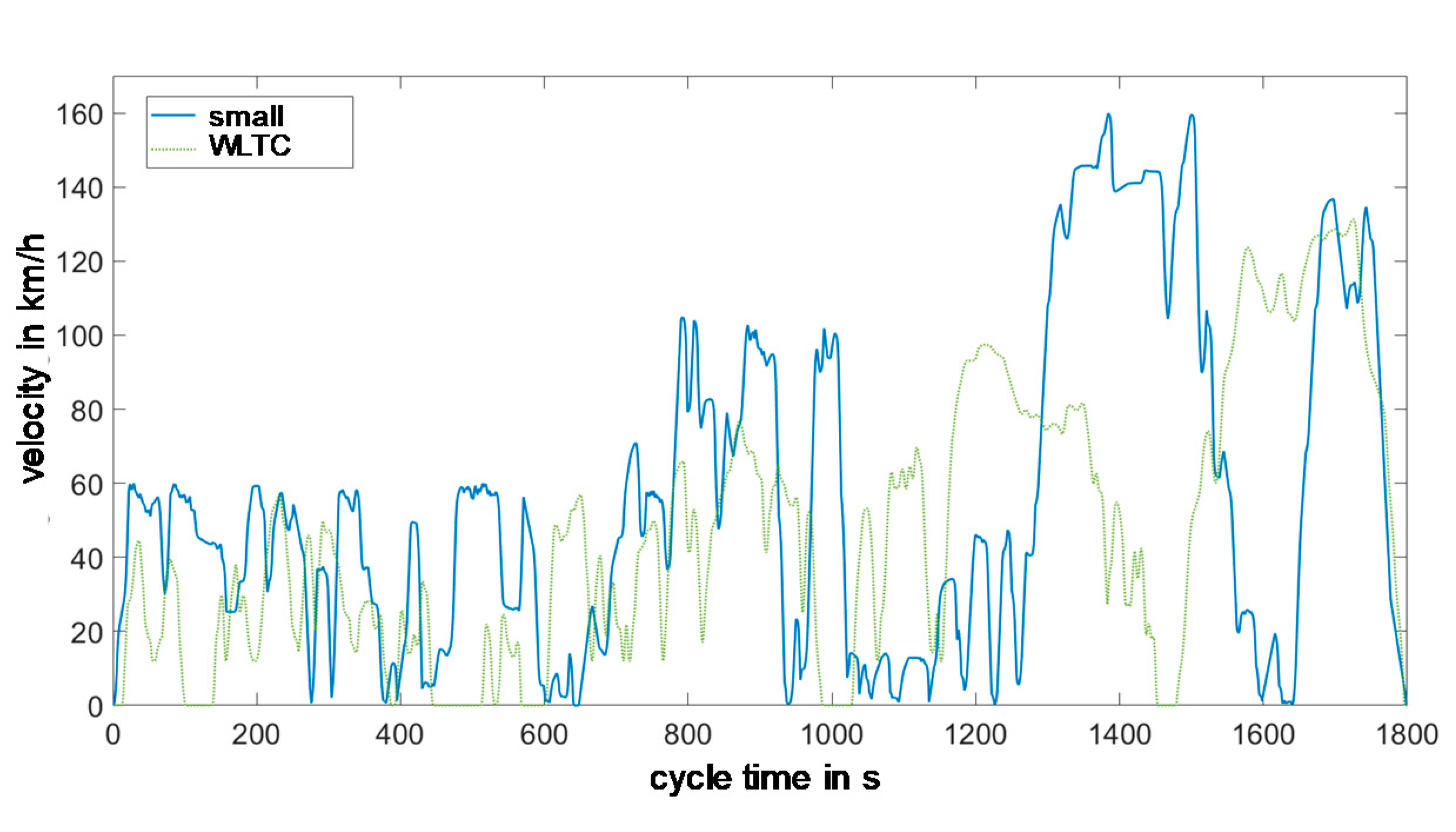
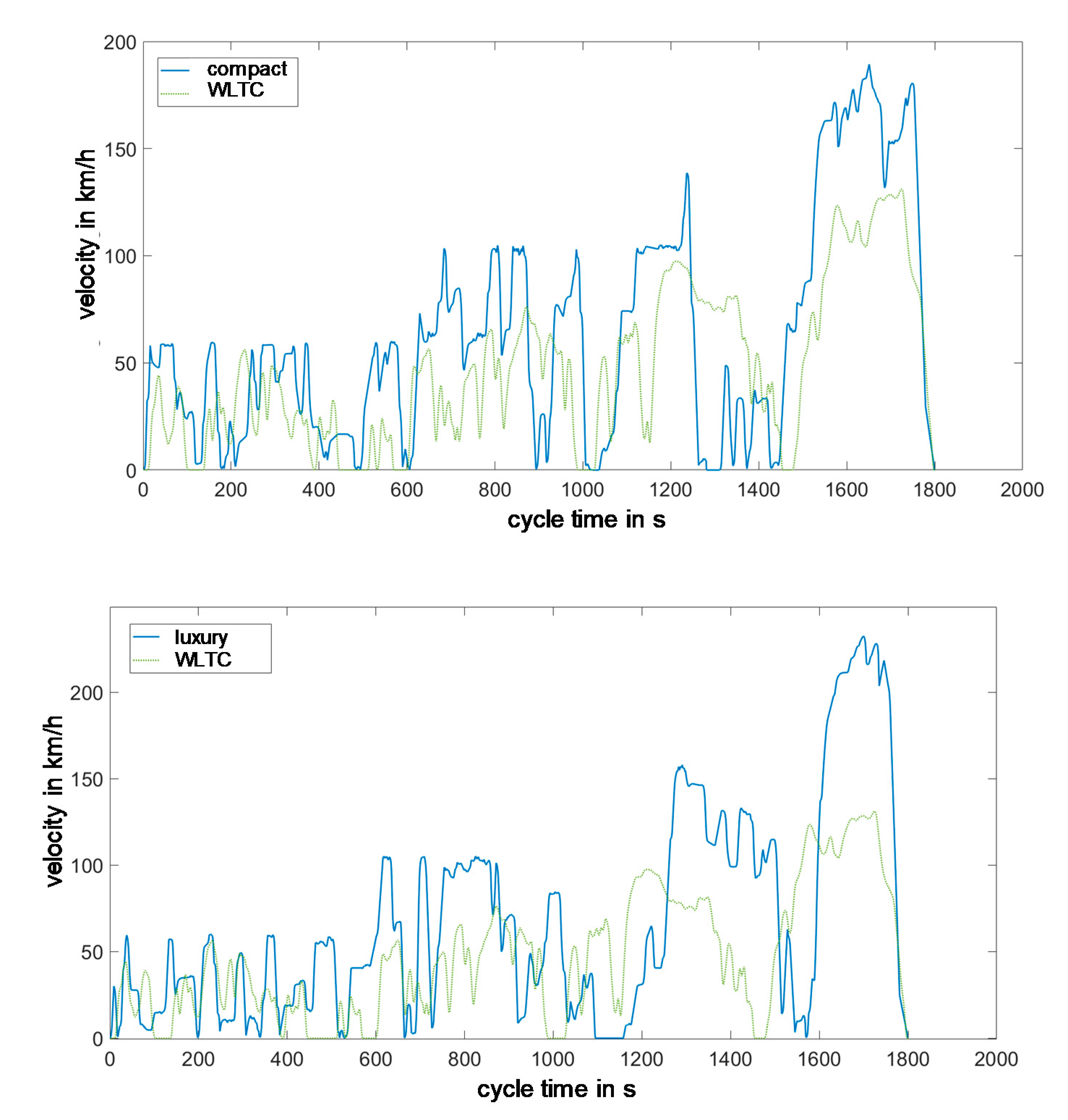
The parametric cycle design presented here allows to generate a driving cycle specifically for one vehicle class based on one global data set. Whether a cycle is drivable for a vehicle depends not only on the already limited maximum speed but also on the acceleration ramps. A sports car will run operating points over its lifetime that a small car cannot reach. By limiting the maximum cycle acceleration, it is possible to react specifically to the vehicle class. Since the acceleration capacity depends on the current vehicle speed, the maximum possible acceleration is not assumed to be constant but is determined by a simplified longitudinal dynamics model based on the current cycle speed.
By means of the parametric cycle calculation shown and the targeted interventions in it, a specific driving cycle can be generated if vehicle-specific characteristic values are known. Exemplary results are presented in the following section.