Measurement-Based Current-Harmonics Modeling of Aggregated Electric-Vehicle Loads Using Power-Exponential Functions
Abstract
1. Introduction
2. Theoretical Background
2.1. Electric Vehicles and Harmonics
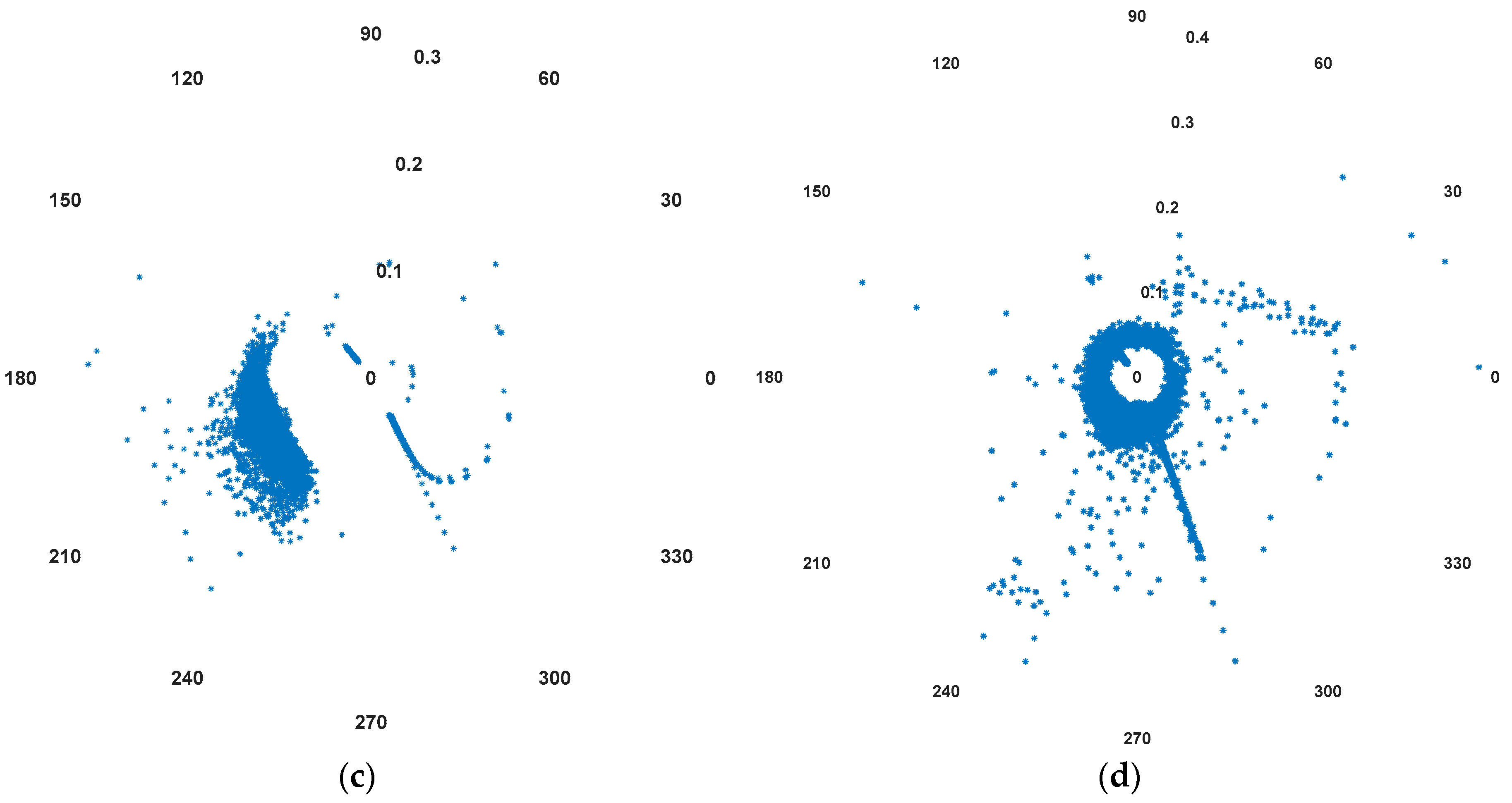
2.2. Harmonic Phasor Aggregation
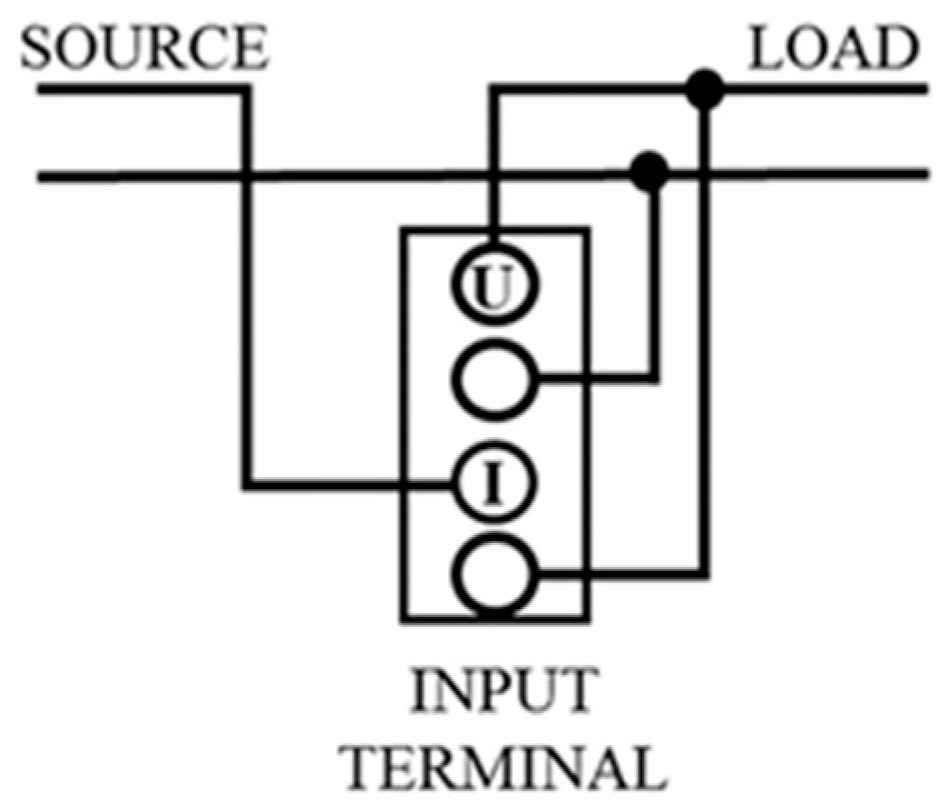
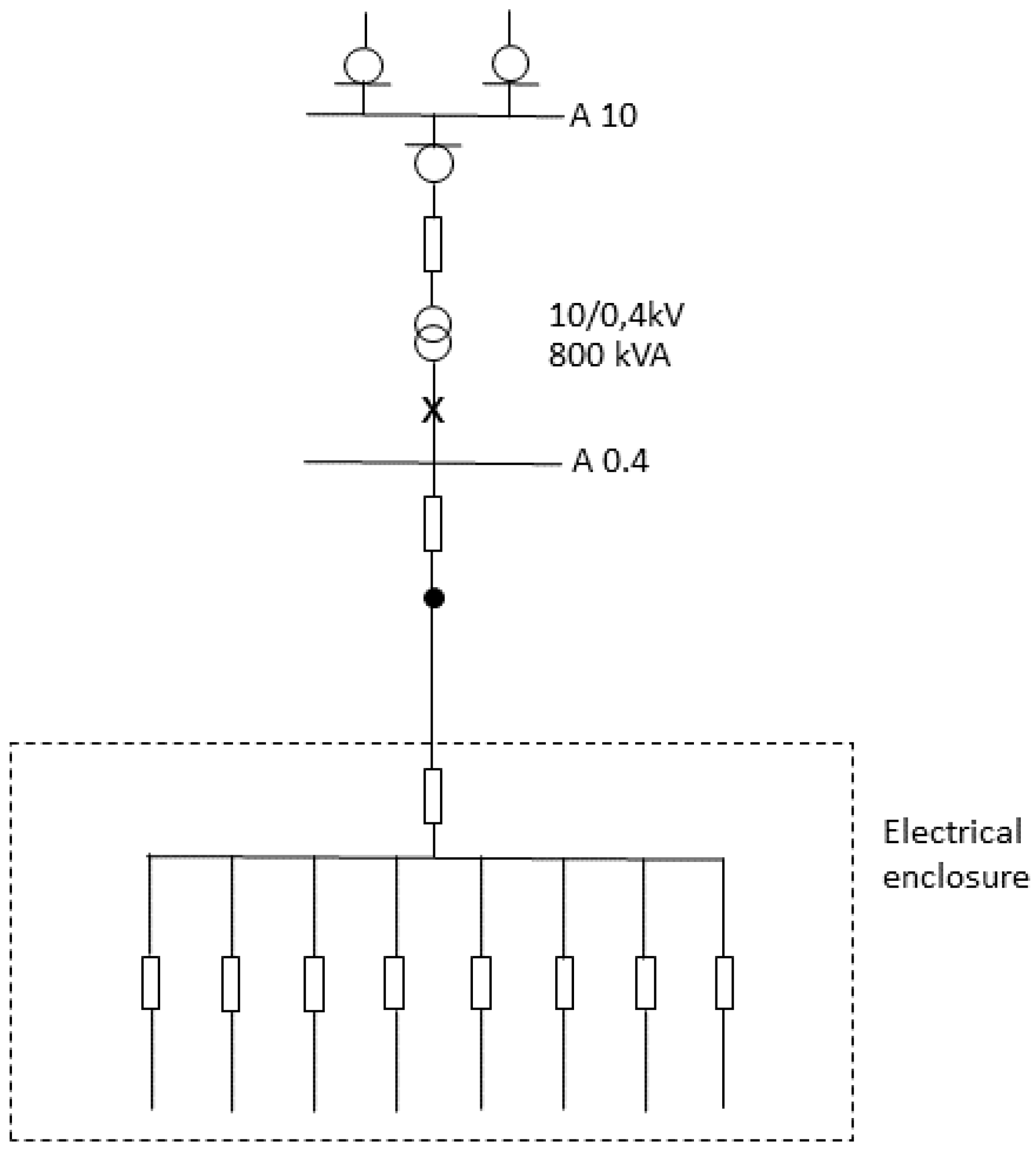
3. Measurement Setup
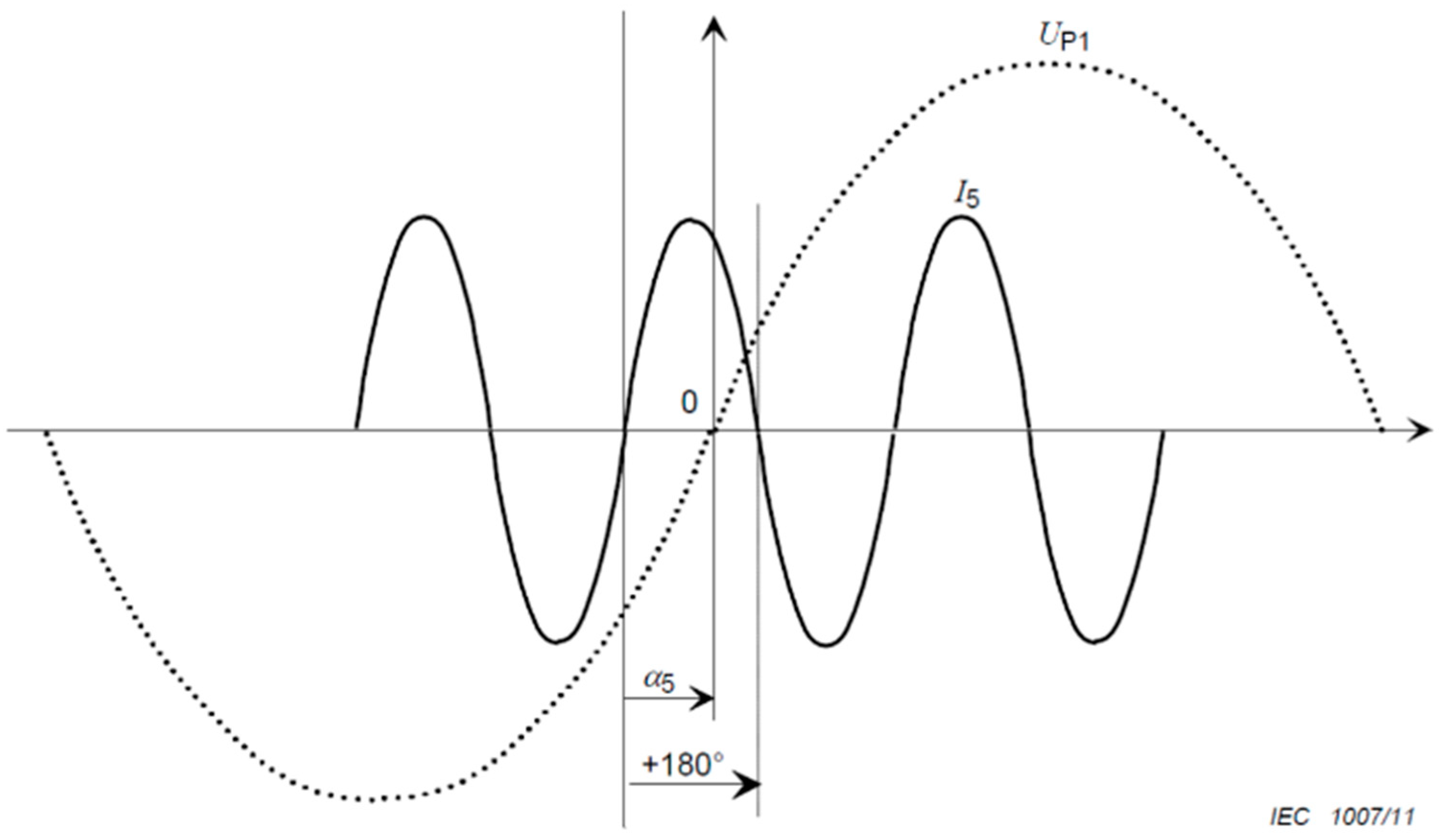
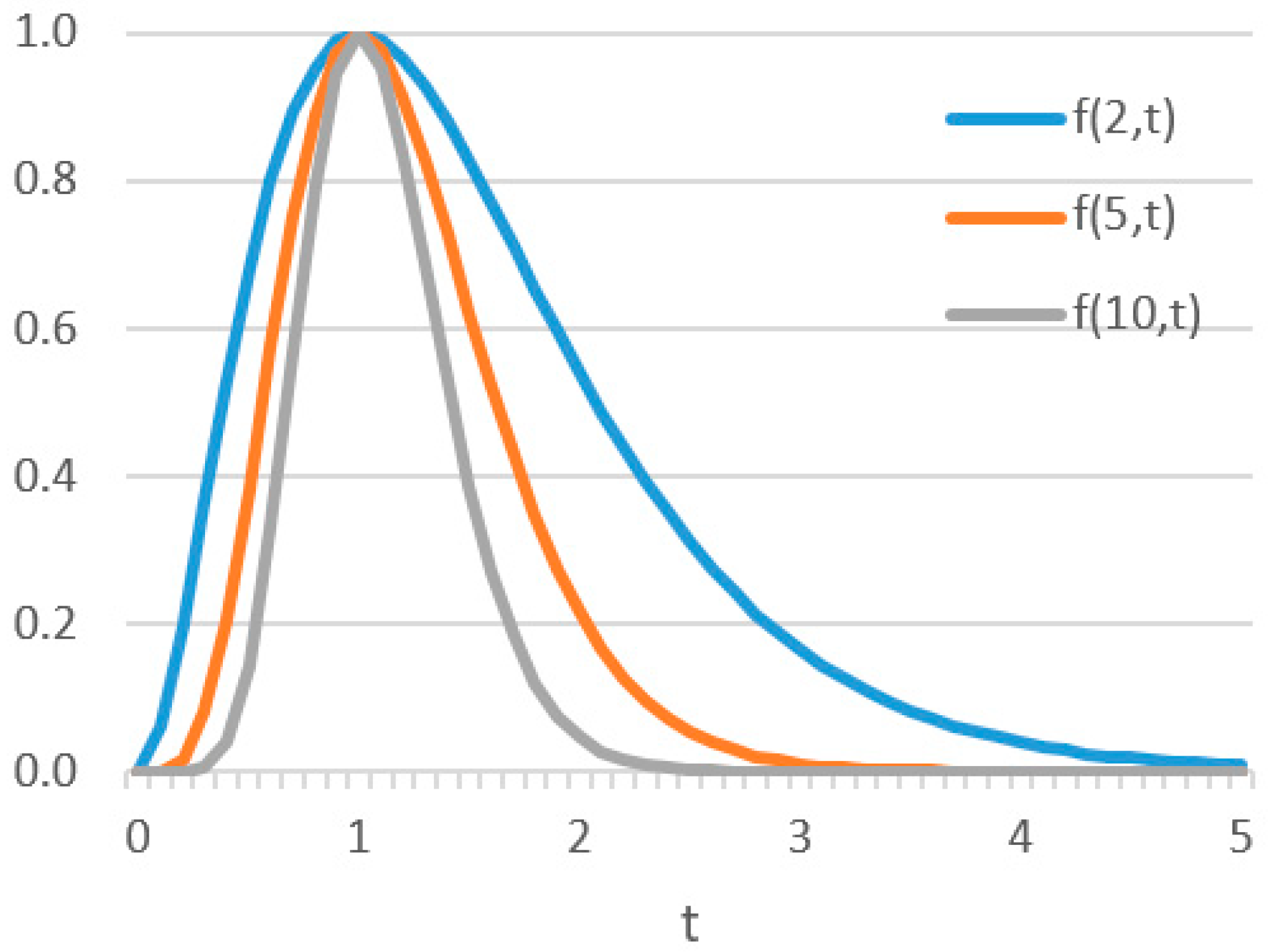
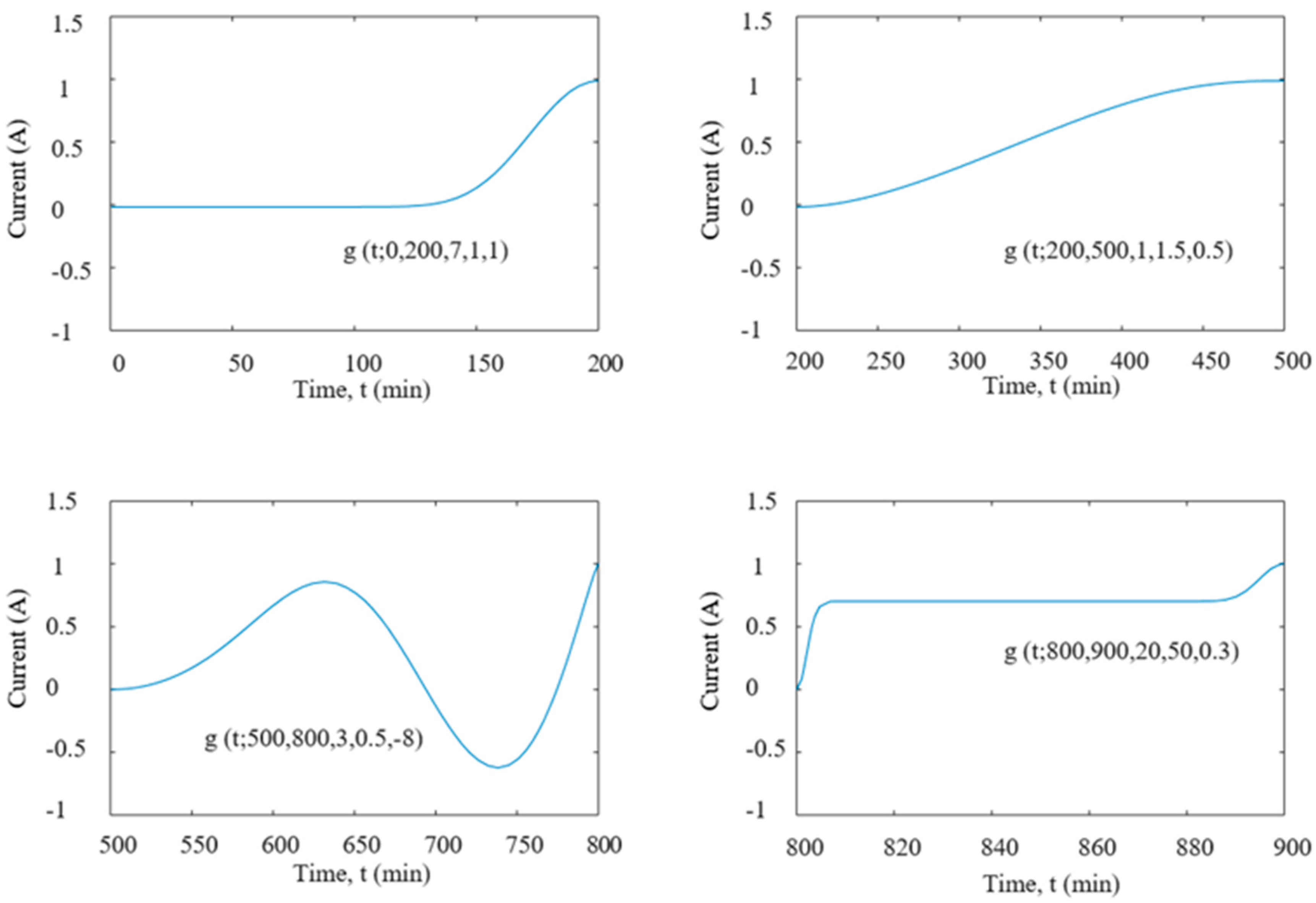
4. Modeling Harmonic Currents Using Power Exponential Functions
- inspection of measured value (imaginary and real part is done separately);
- manually choosing moments in time when peaks occur;
- choosing initial values for p1, p2, and p3 (or q1, q2 and q3);
- applying Function (7) or (8) between peaks;
- least-squares fitting procedure (MATLAB) to find values of p1, p2 and p3 (or q1, q2 and q3) for a function that best fits measured values between peaks;
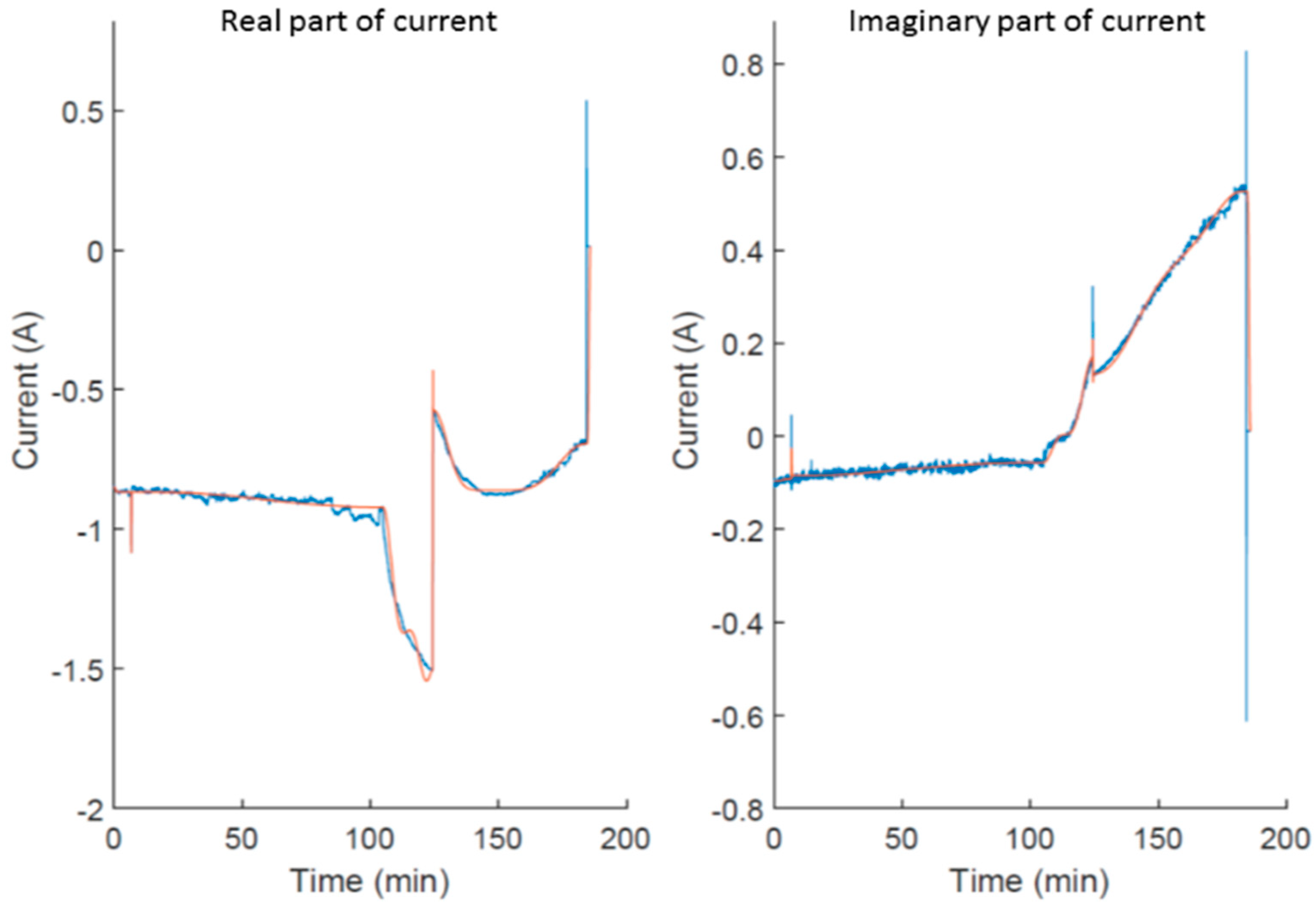
- procedure is repeated until all peaks are handled. Functions between each peak are acquired, and a piecewise combination of the functions is scaled and translated, so that the resulting function is continuous.
Aggregation of Multiple Electric-Vehicle Loads
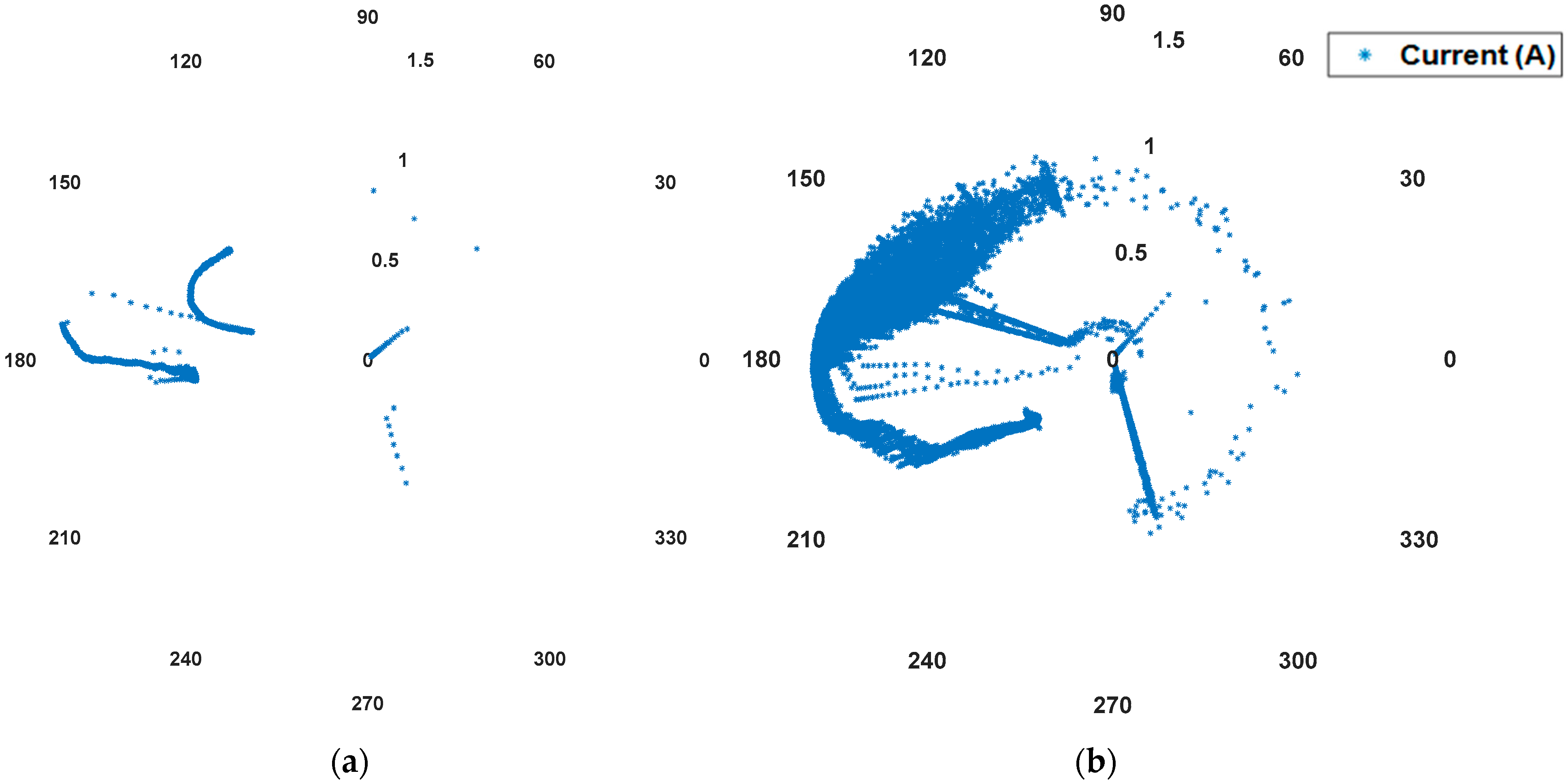
5. Results
6. Discussion and Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- CO2 Emissions from Fuel Combustion Highlights; IEA: Paris, France, 2018. Available online: https://webstore.iea.org/co2-emissions-from-fuel-combustion-2018-highlights (accessed on 11 March 2019).
- UNFCCC. Paris Declaration on Electro-Mobility and Climate Change and Call to Action. In Proceedings of the Paris 2015 UN Climate Change Conference, Paris, France, 30 November–12 December 2015; Available online: https://unfccc.int/gcse?q=the-paris-declaration-on-electro-mobility-and-climate-change-and-call-to-action (accessed on 22 March 2019).
- OECD/IEA. Global EV Outlook 2018: Towards Cross-Modal Electrification. 2018. Available online: https://webstore.iea.org/download/direct/1045?fileName=Global_EV_Outlook_2018.pdf (accessed on 21 March 2019).
- Orr, J.A.; Emanuel, A.E.; Oberg, K.W. Current Harmonics Generated by a Cluster of Electric Vehicle Battery Chargers. IEEE Trans. Power Appar. Syst. 1982, PAS-101, 691–700. [Google Scholar]
- Rahman, S.; Shrestha, G.B. An investigation into the impact of electric vehicle load on the electric utility distribution system. IEEE Trans. Power Deliv. 1993, 8, 591–597. [Google Scholar] [CrossRef]
- Taylor, J.; Maitra, M.; Alexander, M.; Brooks, D.; Duvall, M. Evaluation of the impact of plug-in electric vehicle loading on distribution system operationse. In Proceedings of the IEEE Power Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–6. [Google Scholar]
- Taylor, J.; Maitra, M.; Alexander, M.; Brooks, D.; Duvall, M. Evaluations of plug-in electric vehicle distribution system impacts. In Proceedings of the IEEE Power Energy Society General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–6. [Google Scholar]
- Kutt, L.; Saarijärvi, E.; Lehtonen, M.; Molder, H.; Niitsoo, J. A Review of the Harmonic and Unbalance Effects in Electrical Distribution Networks due to EV Charging. In Proceedings of the 12th International Conference on Environment and Electrical Engineering, Wroclaw, Poland, 5–8 May 2013; pp. 28–33. [Google Scholar]
- Jiang, C.; Torquato, R.; Salles, D.; Xu, W. Method to assess the power quality impact of plug-in electric vehicles. In Proceedings of the 2014 16th International Conference on Harmonics and Quality of Power, Bucharest, Romania, 25–28 May 2014; Volume 29, pp. 177–180. [Google Scholar]
- Wanik, M.Z.C.; Siam, M.F.; Subiyanto, A.A.; Mohamed, A.; HanifahAzit, A.; Sulaiman, S.; Mohamed, A.M.A.; Hussein, Z.F.; MatHussin, A.K. Harmonic Measurement and Analysis during Electric Vehicle Charging. Engineering 2013, 5, 215–220. [Google Scholar] [CrossRef]
- Shareef, H.; Islam, M.M.; Mohamed, A. A review of the stage-of-the-art charging technologies, placement methodologies, and impacts of electric vehicles. Renew. Sustain. Energy Rev. 2016, 64, 403–420. [Google Scholar] [CrossRef]
- Baghzouz, Y.; Burch, R.F.; Capasso, A.; Cavallini, A.; Emanuel, A.E.; Halpin, M.; Langella, R.; Montanari, G.; Olejniczak, K.J.; Ribeiro, P.; et al. Time-varying harmonics. II. Harmonic summation and propagation. IEEE Trans. Power Deliv. 2002, 17, 279–285. [Google Scholar] [CrossRef]
- Kutt, L.; Saarijarvi, E.; Lehtonen, M.; Molder, H.; Niitsoo, J. Estimating the harmonic distortions in a distribution network supplying EV charging load using practical source data—Case example. In Proceedings of the IEEE Power and Energy Society General Meeting, National Harbor, MD, USA, 27–31 July 2014; pp. 4–8. [Google Scholar]
- Meyer, J.; Mueller, S.; Ungethuem, S.; Xiao, X.; Collin, A.; Djokic, S. Harmonic and supraharmonic emission of on-board electric vehicle chargers. In Proceedings of the 2016 IEEE PES Transmission and Distribution Conference and Exposition-Latin America (PES T and D-LA), Morelia, Mexico, 20–24 September 2016. [Google Scholar]
- Hansen, S.; Nielsen, P.; Blaabjerg, F. Harmonic Cancellation by Mixing Nonlinear. IEEE Trans. Ind. Appl. 2000, 36, 152–159. [Google Scholar] [CrossRef]
- Emanuel, A.E.; Orr, J.A.; Pileggi, D.J. Current Harmonics, Voltage Distortion, and Powers Associated with Electric Vehicle Battery Chargers Distributed. IEEE Trans. Ind. Appl. 1984, I, 727–734. [Google Scholar]
- Berisha, S.H.; Karady, G.G.; Ahmad, R.; Hobbs, R.; Karner, D. Current harmonics generated by electric vehicle battery chargers. In Proceedings of the International Conference on Power Electronics, Drives and Energy Systems for Industrial Growth, New Delhi, India, 8–11 January 1996; Volume 1, pp. 584–589. [Google Scholar]
- Bass, R.; Harley, R.; Lambert, F.; Rajasekaran, V.; Pierce, J. Residential harmonic loads and EV charging. In Proceedings of the 2001 IEEE Power Engineering Society Winter Meeting. Conference Proceedings (Cat. No.01CH37194), Columbus, OH, USA, 28 January–1 February 2001; Volume 2, pp. 803–808. [Google Scholar]
- Lu, X.; Jiang, J. Harmonic Study of Electric Vehicle Chargers. In Proceedings of the 2005 International Conference on Electrical Machines and Systems, Nanjing, China, 27–29 September 2005; pp. 2404–2407. [Google Scholar]
- Melo, N.; Mira, F.; De Almeida, A.; Delgado, J. Integration of PEV in Portuguese distribution grid: Analysis of harmonic current emissions in charging points. In Proceedings of the 11th International Conference on Electrical Power Quality and Utilisation, Lisbon, Portugal, 17–19 October 2011; pp. 791–796. [Google Scholar]
- Yang, W.; Wang, J.; Zhang, Z.; Gao, Y. Simulation of electric vehicle charging station and harmonic treatment. In Proceedings of the 2012 International Conference on Systems and Informatics, ICSAI 2012, Yantai, China, 19–20 May 2012; pp. 609–613. [Google Scholar]
- Niitsoo, J.; Kilter, J.; Palu, I.; Taklaja, P.; Kütt, L. Harmonic levels of domestic and electrical vehicle loads in residential distribution networks. In Proceedings of the IEEE AFRICON Conference, Pointe-Aux-Piments, Mauritius, 9–12 September 2013; pp. 1–5. [Google Scholar]
- Nguyen, V.L.; Tran-Quoc, T.; Bacha, S. Harmonic distortion mitigation for electric vehicle fast charging systems. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013. [Google Scholar]
- Kutt, L.; Saarijarvi, E.; Lehtonen, M.; Molder, H.; Niitsoo, J. Current harmonics of EV chargers and effects of diversity to charging load current distortions in distribution networks. In Proceedings of the 2013 International Conference on Connected Vehicles and Expo, Las Vegas, NV, USA, 2–6 December 2013; pp. 726–731. [Google Scholar]
- Kim, K.; Song, C.S.; Byeon, G.; Jung, H.; Kim, H.; Jang, G. Power demand and total harmonic distortion analysis for an EV charging station concept utilizing a battery energy storage system. J. Electr. Eng. Technol. 2013, 8, 1234–1242. [Google Scholar] [CrossRef]
- Lucas, A.; Bonavitacola, F.; Kotsakis, E.; Fulli, G. Grid harmonic impact of multiple electric vehicle fast charging. Electr. Power Syst. Res. 2015, 127, 13–21. [Google Scholar] [CrossRef]
- Deilami, S.; Masoum, A.S.; Moses, P.S.; Masoum, M.A.S. Voltage profile and THD distortion of residential network with high penetration of plug-in electrical vehicles. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Gothenberg, Sweden, 11–13 October 2010; pp. 1–6. [Google Scholar]
- Müller, S.; Möller, F.; Meyer, J.; Collin, A.J.; Djokic, S.Z. Characterisation of harmonic interactions between electric vehicle battery chargers and PV inverters. In Proceedings of the International Conference on Harmonics and Quality of Power (ICHQP), Bucharest, Romania, 25–28 May 2014; pp. 645–649. [Google Scholar]
- Misra, R.; Paudyal, S. Analysis and reduction of total harmonic distortions in distribution system with electric vehicles and wind generators. In Proceedings of the IEEE Power and Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015. [Google Scholar]
- Malano, A.A.; Müller, S.; Meyer, J.; Bachmann, S. Harmonic interaction of electric vehicle chargers in a central charging infrastructure. In Proceedings of the 17th International Conference on Harmonics and Quality of Power (ICHQP), Belo Horizonte, Brazil, 16–19 October 2016; pp. 367–372. [Google Scholar]
- Bollen, M.H.J.; Rönnberg, S.K. Hosting capacity of the power grid for renewable electricity production and new large consumption equipment. Energies 2017, 10, 1325. [Google Scholar] [CrossRef]
- Hu, C.; Song, Y.; Xu, Z.; Luo, Z.; Zhan, K.; Jia, L. Impacts and Utilization of Electric Vehicles Integration Into Power Systems. Proc. Chin. Soc. Electr. Eng. 2012, 32, 1–10. [Google Scholar]
- Sheng, Q.; Chen, M.; Li, Q.; Wang, Y.; Arshad Shehzad Hassan, M. Analysis for the Influence of Electric Vehicle Chargers with Different SOC on Grid Harmonics; Springer: Singapore, 2018; Volume 925, ISBN 978-981-13-2380-5. [Google Scholar]
- Xu, H.; Xia, X.; Liang, W.; Ouyang, F.; Zhu, W.; Li, H. Charging Harmonic Characteristic Analysis of Electric Vehicles Based on Simulation and Analytical Methods. In Proceedings of the 3rd Conference on Energy Internet and Energy System Integration (EI2), Changsha, China, 8–10 November 2019; pp. 1166–1171. [Google Scholar]
- Alame, D.; Azzouz, M.; Kar, N.C. Impact assessment of electric vehicle charging on distribution transformers including state-of-charge. In Proceedings of the 61st International Midwest Symposium on Circuits and Systems (MWSCAS), Windsor, ON, Canada, 5–8 August 2018; pp. 607–610. [Google Scholar]
- Liu, Y.; Li, Y.; Ren, J.; Wang, S.; Li, L. A data-driven harmonic modeling method for electric vehicle charging station. In Proceedings of the 25th International Conference on Electricity Distribution, Madrid, Spain, 3–6 June 2019; pp. 3–6. [Google Scholar]
- Zimmerman, N.; Bass, R. Impacts of Electric Vehicle Charging on Electric Power Distribution Systems; Oregon Transportation Research and Education Consortium: Portland, OR, USA, 2013; Volume OTREC-SS-731. [Google Scholar]
- International Electrotechnical Commission. IEC 61000-3-2 ed. 4 Electromagnetic Compatibility (EMC)—Part 3-2: Limits—Limits for Harmonic Current Emissions (Equipment Input Current ≤16 A per Phase); International Electrotechnical Commission: Geneva, Switzerland, 2014.
- International Electrotechnical Commission. IEC 61000-3-12 ed. 2 Electromagnetic Compatibility (EMC)—Part 3-12: Limits—Limits for Harmonic Currents Produced by Equipment Connected to Public Low-Voltage Systems with Input Current >16 A and ≤75 A per Phase; International Electrotechnical Commission: Geneva, Switzerland, 2011.
- Euopean Standard EN 50160 ed. 3—Voltage Characteristics of Electricity Supplied by Public Distribution Networks; CENELEC: Brussels, Belgium, 2010.
- Vinnal, T.; Kutt, L.; Jarkovoi, M. Harmonic Currents and Voltages in Industrial LV Networks—Case Studies. In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018; pp. 177–182. [Google Scholar]
- Staats, P.T.; Grady, W.M.; Arapostathis, A.; Thallam, R.S. A Statistical Method for Predicting the Net Harmonic Currents Generated by a Concentration of Electric Vehicle Battery Chargers. IEEE Trans. Power Deliv. 1997, 12, 1258–1266. [Google Scholar] [CrossRef]
- Staats, P.T.; Grady, W.M.; Arapostathis, A.; Thallam, R.S. A statistical analysis of the effect of electric vehicle battery charging on distribution system harmonic voltages. IEEE Trans. Power Deliv. 1998, 13, 640–645. [Google Scholar] [CrossRef]
- Au, M.T.; Milanović, J.V. Development of stochastic aggregate harmonic load model based on field measurements. IEEE Trans. Power Deliv. 2007, 22, 323–330. [Google Scholar] [CrossRef]
- Ćuk, V.; Cobben, J.F.G.; Kling, W.L.; Ribeiro, P.F. Analysis of harmonic current summation based on field measurements. IET Gener. Transm. Distrib. 2013, 7, 1391–1400. [Google Scholar] [CrossRef]
- Xiao, Y.; Yang, X. Harmonic summation and assessment based on probability distribution of phase angle. In Proceedings of the 15th International Conference on Harmonics and Quality of Power, Hong Kong, China, 17–20 June 2012; pp. 581–584. [Google Scholar]
- Blanco, A.M.; Meyer, J.; Schegner, P. Calculation of phase angle diversity for time-varying harmonic currents from grid measurement. In Proceedings of the International Conference on Renewable Energies and Power Quality, Cordoba, Spain, 8–10 April 2014; Volume 1, pp. 2–7. [Google Scholar]
- Yokogawa. Wt3001e/wt3002e/wt3003e/wt3004e Precision Power Analyzer—User’s Manual; Yokogawa Meters and Instruments Corporation: Tokyo, Japan, 2015. [Google Scholar]
- International Electrotechnical Commission Electromagnetic Compatibility (EMC) Part 4–7:Testing and Measurement Techniques—General Guide on Harmonics and Interharmonics Measurements and Instrumentation, for Power Supply Systems and Equipment Connected Thereto; International Electrotechnical Commission: Geneva, Switzerland, 2009.
- Lundengård, K. Generalized Vandermonde Matrices and Determinants in Electromagnetic Compatibility. Licentiate Thesis, Mälardalen University, Västerås, Sweden, 2017. [Google Scholar]
- Lundengård, K. Extreme Points of the Vandermonde Determinant and Phenomenological Modelling with Power Exponential Functions. Ph.D. Thesis, Mälardalen University, Västerås, Sweden, 2019. [Google Scholar]
- Lundengård, K.; Rančić, M.; Javor, V.; Silvestrov, S. Application of the multi-peaked analytically extended function to representation of some measured lightning currents. Serb. J. Electr. Eng. 2016, 13, 145–155. [Google Scholar] [CrossRef]
- Javor, V. New function for representing IEC 61000-4-2 standard electrostatic discharge current. Facta Univ. Ser. Electron. Energ. 2014, 27, 509–520. [Google Scholar] [CrossRef]
- MATLAB and Optimization Toolbox Release R2019a; The Math Works, Inc.: Natick, MA, USA, 2019.
- Coleman, T.F.; Li, Y. On the convergence of reflective Newton methods for nonlinear minimization subject to bounds. Math. Progr. 1994, 67, 189–224. [Google Scholar] [CrossRef]
- Coleman, T.F.; Li, Y. An Interior Trust Region Approach for Nonlinear Minimization Subject to Bounds. Siam J. Optim. 1996, 6, 418–445. [Google Scholar] [CrossRef]

| EV 1 | EV 2 | EV 3 | EV 4 | ||
|---|---|---|---|---|---|
| Battery capacity (kWh) | 18.8 | 24 | 24.2 | 18.7 | |
| Motor engine power (kW) | 125 | 80 | 85 | 60 | |
| Maximum charging power (kW) | 7.3 | 6.7 | 3.6 | 3.6 | |
| Charging current (A) | Mean | 20.9 | 16.7 | 13.3 | 14.5 |
| THC (A) | Mean | 1.13 | 0.79 | 0.56 | 0.58 |
| Measurement | Conditions | Maximum Error (±ε) |
|---|---|---|
| Current | Im ≥ 3% of Inom | ±5% of Im |
| Im < 3% of Inom | ±0.15% of Inom |
| Harmonic Order | 3 | 5 | 7 | 9 | 11 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Imax (A) | 6.89 | 2.52 | 1.61 | 1.88 | 1.26 | |||||
| Time (min) at Imax | 400 | 437 | 439 | 598 | 354 | |||||
| Phase-angle location (Quadrant) | Second and third | Second and third | First and second | Third | Second | |||||
| Charging start time (min) | SOC (%) | Charging start time (min) | SOC (%) | Charging start time (min) | SOC (%) | Charging start time (min) | SOC (%) | Charging start time (min) | SOC (%) | |
| EV1 (1) | 229 | 30–40 | 356 | 70–80 | 397 | 70–80 | 508 | 30–40 | 289 | 50–60 |
| EV1 (2) | 281 | 70–80 | 329 | 30–40 | 329 | 70–80 | Not charging | 349 | 50–60 | |
| EV1 (3) | 288 | 50–60 | 280 | 50–60 | 316 | 30–40 | Not charging | 283 | 60–70 | |
| EV1 (4) | 277 | 60–70 | 427 | 60–70 | 395 | 80–90 | 517 | 50–60 | 331 | 80–90 |
| EV2 (1) | Not charging | 309 | 36–40 | Not charging | Not charging | 736 | 60–70 | |||
| EV2 (2) | 357 | 40–50 | 302 | 90–100 | 586 | 90–100 | Not charging | Not charging | ||
| EV2 (3) | 251 | 36–40 | Not charging | 315 | 90–100 | Not charging | 51 | 40–50 | ||
| EV2 (4) | Not charging | Not charging | Not charging | not charging | Not charging | |||||
| EV3 (1) | Not charging | Not charging | Not charging | 373 | 40–50 | Not charging | ||||
| EV3 (2) | Not charging | Not charging | Not charging | 528 | 70–80 | Not charging | ||||
| EV3 (3) | Not charging | Not charging | Not charging | Not charging | Not charging | |||||
| EV3 (4) | Not charging | Not charging | Not charging | Not charging | Not charging | |||||
| EV4 (1) | Not charging | Not charging | Not charging | 472 | 80–90 | Not charging | ||||
| EV4 (2) | Not charging | Not charging | Not charging | 587 | 50–60 | Not charging | ||||
| EV4 (3) | Not charging | Not charging | Not charging | Not charging | Not charging | |||||
| EV4 (4) | Not charging | Not charging | Not charging | Not charging | Not charging | |||||
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Foskolos, G. Measurement-Based Current-Harmonics Modeling of Aggregated Electric-Vehicle Loads Using Power-Exponential Functions. World Electr. Veh. J. 2020, 11, 51. https://doi.org/10.3390/wevj11030051
Foskolos G. Measurement-Based Current-Harmonics Modeling of Aggregated Electric-Vehicle Loads Using Power-Exponential Functions. World Electric Vehicle Journal. 2020; 11(3):51. https://doi.org/10.3390/wevj11030051
Chicago/Turabian StyleFoskolos, Georgios. 2020. "Measurement-Based Current-Harmonics Modeling of Aggregated Electric-Vehicle Loads Using Power-Exponential Functions" World Electric Vehicle Journal 11, no. 3: 51. https://doi.org/10.3390/wevj11030051
APA StyleFoskolos, G. (2020). Measurement-Based Current-Harmonics Modeling of Aggregated Electric-Vehicle Loads Using Power-Exponential Functions. World Electric Vehicle Journal, 11(3), 51. https://doi.org/10.3390/wevj11030051





