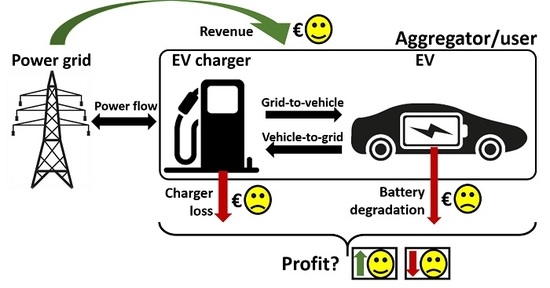
Profitability of Frequency Regulation by Electric Vehicles in Denmark and Japan Considering Battery Degradation Costs

Abstract

This paper determines the profitability of the primary frequency regulation (FR) service considering the wear of the electric vehicle (EV) battery as a cost. To evaluate the profitability of the FR service, the cost of degradation from FR provision is separated from the degradation caused by driving usage. During FR, the power response is proportional to the frequency deviation with full activation power of 9.2 kW, when deviations are larger than 100 mHz. The degradation due to FR is found to be an additional 1–2% to the 7–12% capacity reduction of a 40 kWh Lithium-ion NMC battery pack over 5 years. The overall economic framework is applied in Denmark, both DK1 and DK2, and Japan, by considering historical frequencies. The DK2 FR market framework is taken as reference also for the Japanese and the DK1 cases. Electricity prices and charger efficiency are the two main parameters that affect the profitability of the service. Indeed, with domestic prices there is no profitability, whereas with industrial prices, despite differences between the frequencies, the service is similarly profitable with approx. 3500€ for a five-year period.

1. Introduction

Primary frequency regulation (FR) service has been demonstrated to be technically feasible and economically profitable in different studies worldwide [1,2,3,4,5,6]. In the Nordic grid the bi-directionality of the $\pm 10$ kW DC chargers can give a profit 17 times higher than the unidirectional case [7,8]. The revenue from FR is function of different parameters: electricity, regulation market prices, plugin hours, power capacity of the charger etc. [9]. In the Great Britain depending on the usage FR profit varies between 60 and 400 €/year [10]. In France EVs are found to have a revenue of approximately 100 €/year [11], in Germany the average revenue is 200 €/year [12]. Most of the analyses, particularly in the past, evaluated the profit from FR service as difference between the revenue and the charger losses, without giving the proper attention to the wear the EV battery is exposed to. That is because the battery degradation is a physicochemical process with many uncertainties, non-linearities, and different peculiarities depending on the chemistry considered. Therefore, to account for influence of degradation, different types of models have been derived in a semi-empirical way. Three of the most discussed models in the literature are: NREL model based on NCA and LFP chemistries [13], Wang model based on LMO-NMC chemistry [14] and MOBICUS model based on LMO/NMC chemistry [15]. Therefore, in our battery implementation the Wang model was implemented, as the most complete and appropriate in terms of chemistry. Nevertheless, being the empirical models affected by different limitations due to time resolution, data, cycling definition and chemistry [3], the authors recommend readers to consider also new approaches for future investigations.

In this paper, the authors aim at evaluating the profit of the service including the battery degradation (BD) loss. This loss is technically quantified considering a Simulink model previously developed by the authors [16] to determine the economic loss. The profit from FR service is evaluated as difference between the revenue from FR and the sum of the costs of grid energy exchanged and BD. This paper is organized as follows. Section 2 describes the methodology for the profit evaluation, with details on the revenue, costs of grid energy exchanged and BD loss. Section 3 presents the tested study case, and Section 4 provides the results of the different scenarios analyzed. Section 5 presents a sensitivity analysis and Section 6 concludes the article with the main outcomes. Figure 1 provides the profit evaluation flowchart, from the technical (orange) to the economic (green) characterization which are described in Section 3 and Section 2, respectively. $P_{batt}$ is the battery power output.

2. Profit Evaluation

In this section, the methodology to evaluate the profit of the EV user is described in detailed. By definition, the profit is the difference between the revenue and the costs, therefore the profit from providing FR is determined as in (1):

$$Profi{t}_{FR}=Revenu{e}_{FR}-Cos{t}_{Loss}^{FR}-Cos{t}_{BD}^{FR}$$

(1)

where $Revenu{e}_{FR}$ is the revenue from the FR service, $Cos{t}_{Loss}^{FR}$ is the difference between the cost of the energy sold and the energy purchased with the grid, considering the charger loss, and $Cos{t}_{BD}^{FR}$ is the cost of BD due to the FR service. The next Sections present how revenue and costs are evaluated.

2.1. Revenue Assessment

In Denmark FR is a service which is paid per availability. This means that the price is based on the power capacity that is available for an hour (MW per h) and not on the actual energy that is provided. Thus, when providing FR service, the capacity provided ($P_{cap}$) is known and the revenue is quantified as in (2):

$$Revenu{e}_{FR}=\sum _0^{t_{FR}}{P}_{cap}*CP$$

(2)

where $t_{FR}$ is the number of hours of service availability and $CP$ is the hourly capacity payment.

2.2. Energy Cost Assessment

During FR service, the power provided by the battery is derived from the frequency as follows [17]:

$$P_{batt}=\left\{\begin{array}{ccc}\hfill P_{cap}-c,& \mathrm{if}& f_t<49.9\mathrm{Hz}\hfill \\ \hfill \frac{50-f_t}{0.1}*P_{cap}-c,& \mathrm{if}& 49.9\mathrm{Hz}\le f_t\le 50.1\mathrm{Hz}\hfill \\ \hfill -P_{cap}-c,& \mathrm{if}& f_t>50.1\mathrm{Hz}\hfill \end{array}\right.$$

(3)

where c is the offset, needed to avoid that the vehicle gets too overcharged, $P_{cap}$ is the power capacity of the charger and $f_t$ is the measured frequency at time t. In this analysis $P_{batt}$ is negative when the battery is charging, and positive when it is discharging. From the grid perspective, the power ($P_{grid}$) provided is derived from the battery power and the charger efficiency (4):

$$P_{grid}=\left\{\begin{array}{cc}{P}_{batt}*{\eta }_d\hfill & \mathrm{if}{P}_{batt}\ge 0\hfill \\ {\displaystyle \frac{P_{batt}}{{\eta }_c}}\hfill & \mathrm{if}{P}_{batt}<0\hfill \end{array}\right.$$

(4)

where ${\eta }_d$ and ${\eta }_c$ are the discharging and charging efficiencies, which depend on the different power output, see

Table 1. Bidirectional 10 kW DC charger efficiency [8].

$P_{g_{ch}}$	0	−0.78	−0.91	−1.15	−1.49	−1.99	−2.63	−3.67	−4.68	−5.94	−6.9	−7.97	−9.09	−10
${\eta }_{ch}$	0.01	0.11	0.27	0.42	0.54	0.66	0.73	0.79	0.82	0.85	0.86	0.87	0.87	0.87
$P_{g_{disch}}$	0	0.17	0.33	0.59	0.92	1.29	1.87	2.42	3.27	4.25	5.27	6.08	7.49	8.71
${\eta }_{disch}$	0.01	0.14	0.3	0.45	0.57	0.67	0.74	0.78	0.82	0.84	0.85	0.86	0.86	0.88

. To evaluate the cost due to the energy exchanged with the grid, the energy for driving should be subtracted from the energy consumption as in (5):

$$Cos{t}_{Loss}^{FR}=E_{{disch}_{FR}}*P_{{El}_{sale}}-E_{{ch}_{FR}}*P_{{El}_{purch}}$$

(5)

$E_{{ch}_{FR}}$ is the energy from the grid (charging the EV) and $E_{{disch}_{FR}}$ is the energy to the grid (discharging the EV) during the FR service. $P_{{El}_{purch}}$ is the purchase electricity price and $P_{{El}_{sale}}$ is the sale electricity price.

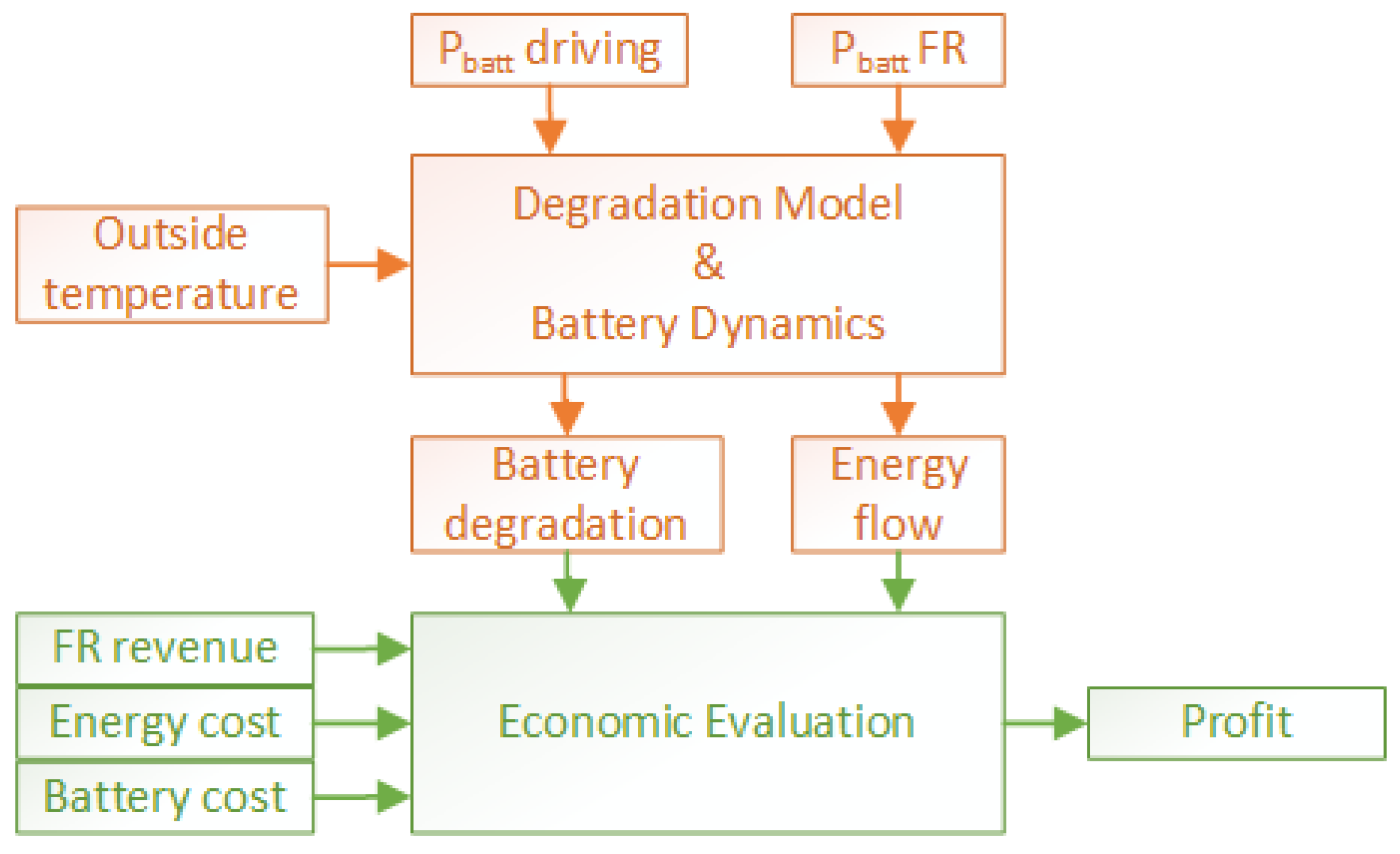
2.3. Degradation Cost Assessment

The battery degradation consists of capacity fade and increase of the internal resistance. For the purpose of this article, only the capacity fade is considered, nevertheless it is in the authors’ interest to include the increase of internal resistance in future investigations [18].

The battery degradation is the sum of two effects: calendar aging and cycle degradation. In this manuscript the authors considered the battery degradation of the Wang model, which is based on a large set of testing data of 1.5 Ah 18650 LMO-NMC Sanyo technology [14]. The formulation was characterized and validated for the considered cells, nevertheless the authors are currently working on the validation of the formulation with the similar cells used in this manuscript [19].

In the Wang model, the calendar loss equation is derived from a combination of the Arrhenius equation and the fit of the model parameters, and then the cycle degradation is calculated as difference between the measurements of the total capacity loss and the calendar ones.

The calendar loss ($Q_{cal}^{*}$), when temperature and SOC are constant, is estimated through the model using the Arrhenius equation in (6) [14,20]:

$$Q_{cal}^{*}=f*e^{-\frac{E_a}{RT}}*t^{0.5}$$

(6)

where $Q_{cal}^{*}$ is the percentage of capacity loss induced by calendar aging, f is the pre-exponential factor, a non-linear function of both SOC and temperature [16], equal to 14,876 day${}^{-1/2}$ for specific SOC and temperature, $E_a$ is the activation energy equal to 24.5 kJ mol${}^{-1}$. R is the gas constant equal to 8.314 J mol${}^{-1}$ K${}^{-1}$. The calendar loss is function of the absolute temperature (T), temperature increases result on larger losses.

The percentage cycle degradation is estimated as in (7) [14,20]:

$$Q_{cycle}^{*}=B_1*e^{B_2*rate}*\mathrm{eqCycles}$$

(7)

$$\begin{array}{cc}\hfill & B_1=a*T^2+b*T+c\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & B_2=d*T+e\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & \mathrm{rate}={\displaystyle \frac{\left|I\right|}{C_{batt}}}\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & \mathrm{eqCycles}={\displaystyle \frac{\mathrm{rate}}{2*3600}}\hfill \end{array}$$

(11)

where a, b, c, d and e are $8.58*{10}^{-6}$ Ah${}^{-1}$ K${}^{-2}$, −0.0051 Ah${}^{-1}$ K${}^{-1}$, 0.759 Ah${}^{-1}$, −0.0067 K${}^{-1}-(C-rate)$ and $2.35{(C-rate)}^{-1}$, respectively. I is the current flowing inside the battery pack and $C_{batt}$ is the initial capacity of the battery, expressed in Ah, considered in the investigation. As for the calendar loss, the cycle degradation is also function of the battery temperature, with the relation provided in Figure 2.

It is relevant to observe that being a semi-empirical model, it does not have absolute validity, as it is limited by time resolution, data limitation, parameters definition and chemistry of the cells. For further information regarding the battery model, please refer to the authors’ works [16,21].

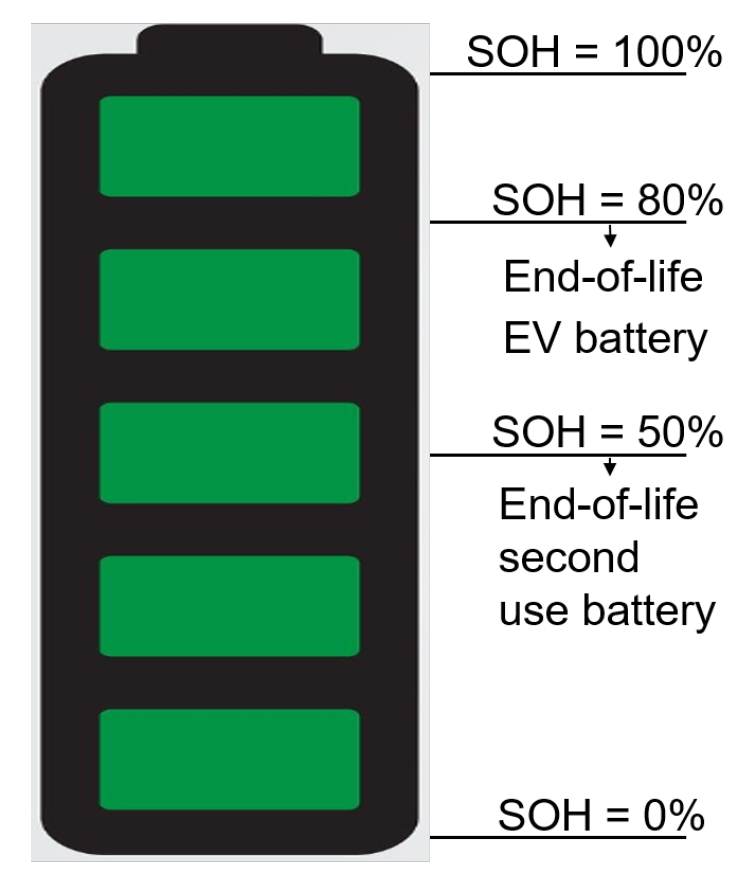
2.3.1. General Assessment

For EV uses the battery end-of-life is usually defined by a 20% reduction of the initial capacity. Nevertheless, a Li-ion battery can still be used when the state-of-health (SOH) is equal to 80% for second-hand uses. The end-of-life of second-hand batteries is set at approx. 50% SOH as shown in Figure 3.

Thus, considering the 50% capacity as usable capacity of the battery, the cost of the BD is evaluated as in (12):

$$Cos{t}_{BD}={\displaystyle \frac{C_{BD}}{50\%}}*Pric{e}_{{batt}_{kWh}}$$

(12)

where $C_{BD}$ is the capacity loss due to degradation and $Pric{e}_{{batt}_{kWh}}$ is the price of the battery per kWh.

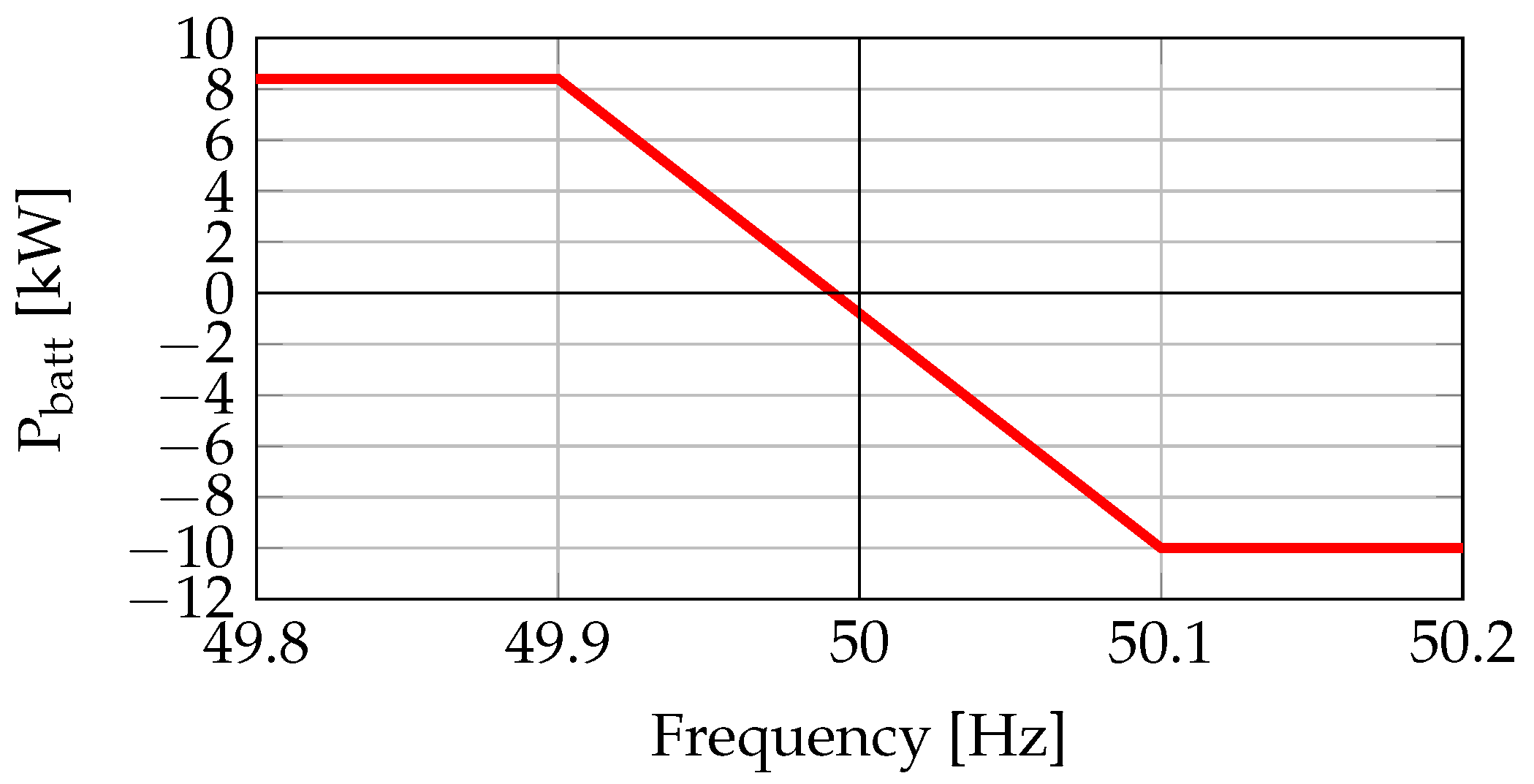
2.3.2. Frequency Regulation Assessment

For the evaluation of the BD costs caused by the FR service provision, two scenarios are defined:

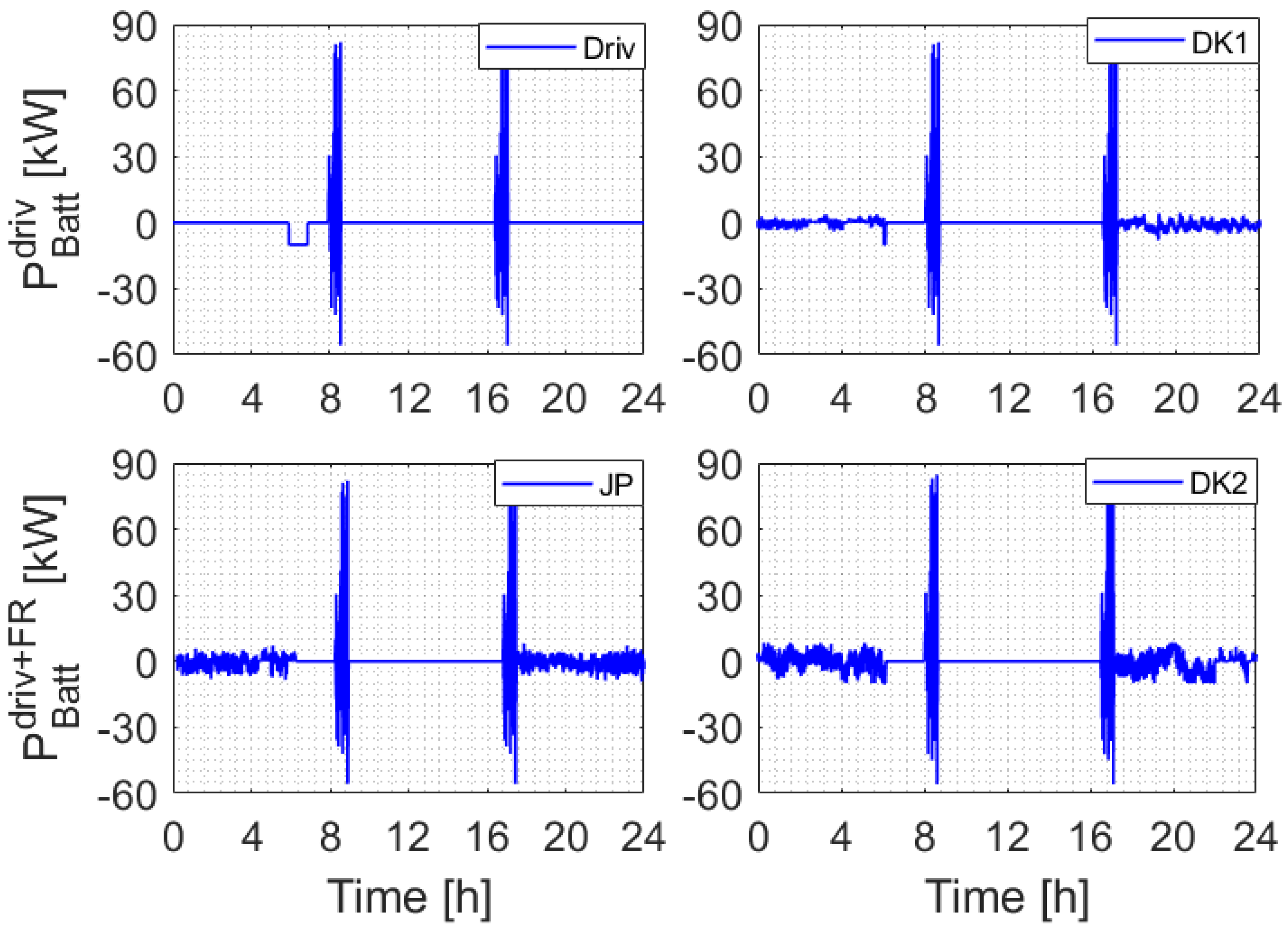
• driving ($driv$): the EV is only driven
• driving plus FR ($driv+FR$): the EV is driven and used for providing FR service.

The lost capacity in the two scenarios is evaluated as in (13):

$$\begin{array}{cc}\hfill C_{BD}^{driv}& =C_{batt}-C_{{batt}_f}^{driv}\hfill \\ \hfill C_{BD}^{driv+FR}& =C_{batt}-C_{{batt}_f}^{driv+FR}\hfill \end{array}$$

(13)

where $C_{batt}$ is the initial battery capacity and $C_{{batt}_f}^{driv}$, $C_{{batt}_f}^{driv+FR}$ are the battery capacities in the two scenarios, at the end of the simulation.

Considering the 50% capacity as the full capacity of the battery, the cost of the BD in the two scenarios is evaluated as in (14):

$$\begin{array}{cc}\hfill Cos{t}_{BD}^{driv}& ={\displaystyle \frac{C_{BD}^{driv}}{50\%}}*Pric{e}_{{batt}_{kWh}}\hfill \\ \hfill Cos{t}_{BD}^{driv+FR}& ={\displaystyle \frac{C_{BD}^{driv+FR}}{50\%}}*Pric{e}_{{batt}_{kWh}}\hfill \end{array}$$

(14)

It is then possible to determine the costs due to FR provision as in (15):

$$Cos{t}_{BD}^{FR}=Cos{t}_{BD}^{driv+FR}-Cos{t}_{BD}^{driv}$$

(15)

3. Test Case

3.1. Technical Characterization Battery

A 40 kWh battery composed of Lithium-ion Nickel Manganese Cobalt pouch cells is taken in consideration in the analysis [16]. The Simulink model simulates the battery EV usage given as input the outside temperature and the battery power profile. The outputs of the model are: current and voltage of the battery, temperature, state-of-charge (SOC) and degradation losses.

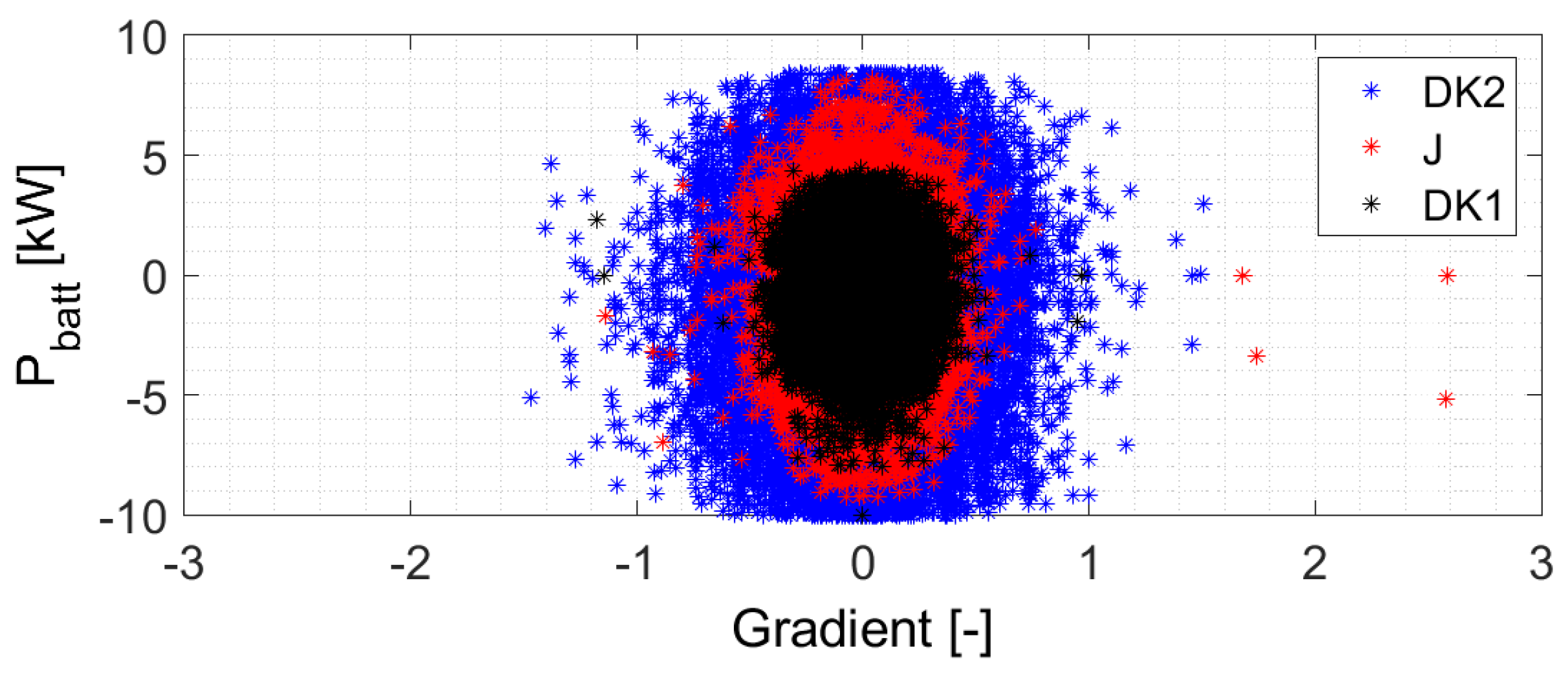
3.1.1. Input: Power

In the $driv$ scenario the EV is considered to be driven 40 km, 20 km in the morning and 20 in the afternoon, and it can charge from 6:00 to 8:00 (for how long, it depends on the driving, approximately 40 min), until when it reaches the requested SOC [22]. In the $driving+FR$ scenario the EV is driving 40 km and performing FR service from 17:15 to 6:00 of the day after (approx. 13 h) and then it can charge from 6:00 to 8:00 to the required SOC. Since the battery degradation is function of the SOC, two simulations are performed: in the first one the average SOC of the simulation is equal to 55% and in the second one it is equal to 75%. To keep the average SOC at these levels, avoiding that the battery gets too charged or discharged, the model is constrained between a maximum and a minimum SOC limits of 20 and 65% in the case with 55% average SOC, and 30 and 85% in the second case.

The battery power during the FR service provision is derived from the frequency values, considering a charger power capacity equal to 9.2 kW and an offset equal to 0.8 kW. From (3) the droop is derived and shown in Figure 4.

In this paper, the Danish frequencies, both DK1 and DK2 [23] (DK1 is the western Denmark part of the European power system, and DK2 is the eastern Denmark part of the Scandinavian countries. The two areas are electrically connected through the DC Great Belt Power Line), and the Japanese (JP) ones are considered. Figure 5 shows the 13 h of frequency both as Gaussian distribution and as frequency versus time.

Given the frequency, the battery and grid powers are derived as in (3) and (4), considering the efficiency of the ±10 kW bidirectional charger as in Table 1. The battery power ($P_{batt}$) for one-day period of the $driv$ scenario and the $driv+FR$ scenario for the three areas DK1, DK2 and JP are provided in Figure 6.

When providing FR, even though the battery could be charged from 6:00 to 8:00, in all three cases the charging time is very short in comparison to the driving scenario. This is due to the fact that the battery is charged more than what it is discharged during the FR hours, thus there is less need for charging to the required SOC level. This is in accordance with the frequency mean values provided in Figure 5, which are slightly higher than 50 Hz in all the three areas.

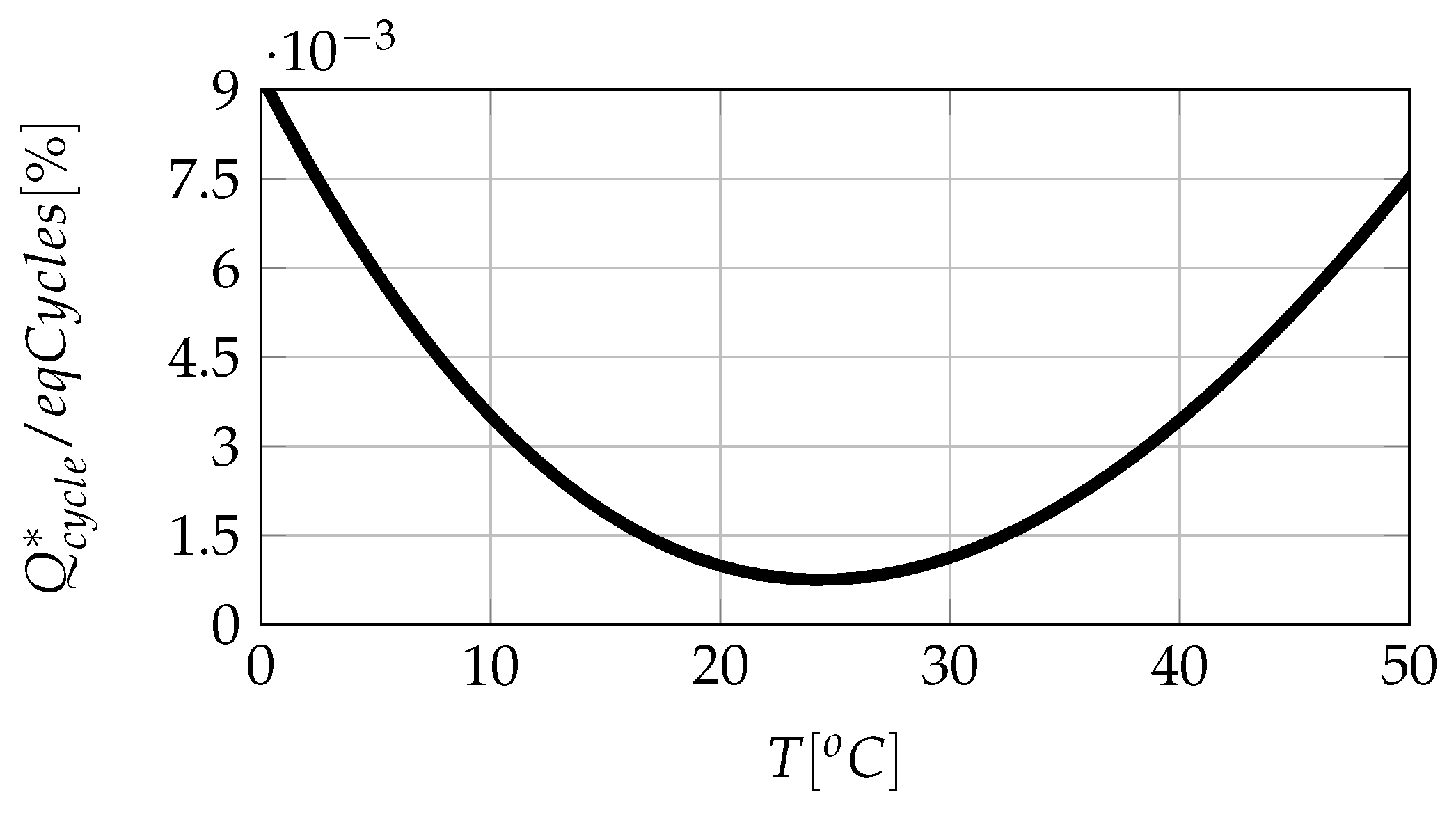
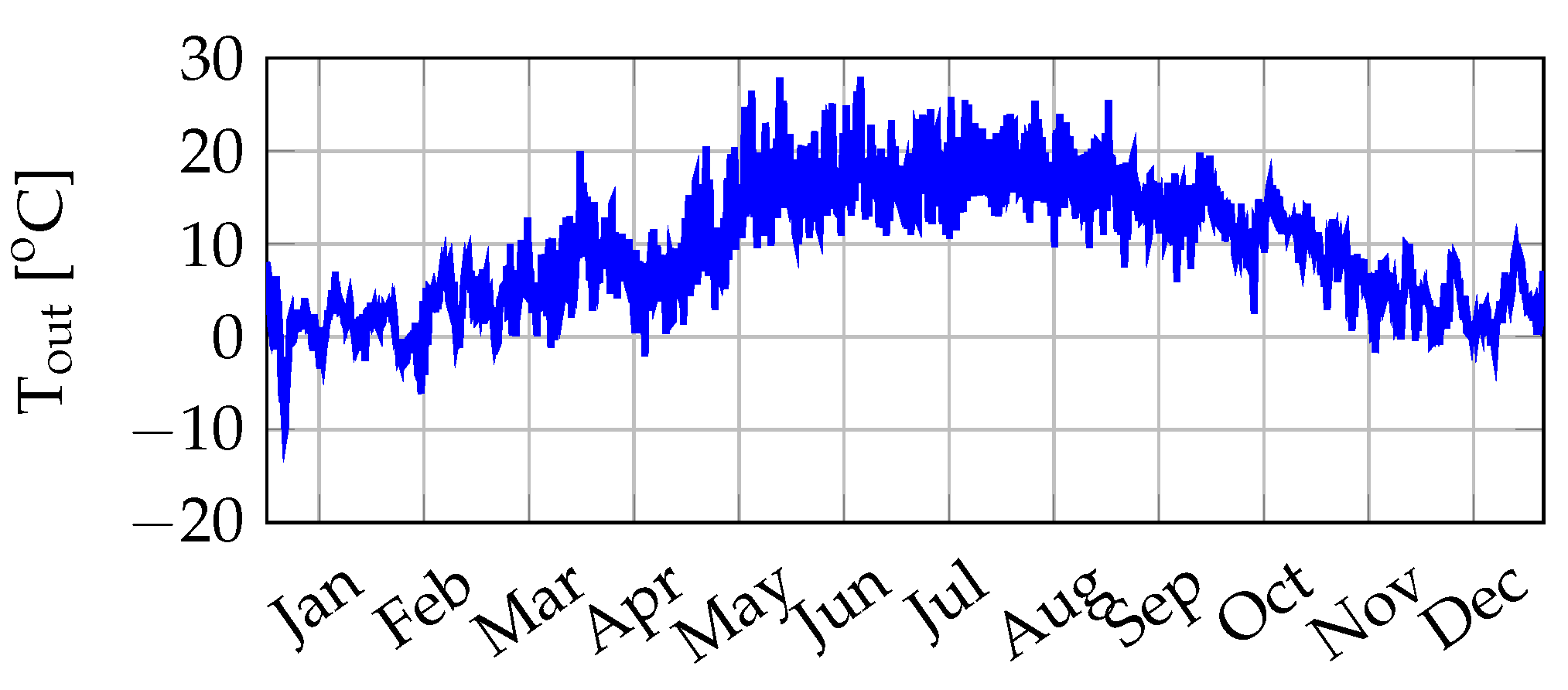
3.1.2. Input: Temperature

Figure 7 shows the outside temperature during year 2017 in Denmark, which is considered during the simulations for DK1, DK2 and JP.

3.2. Economic Characterization

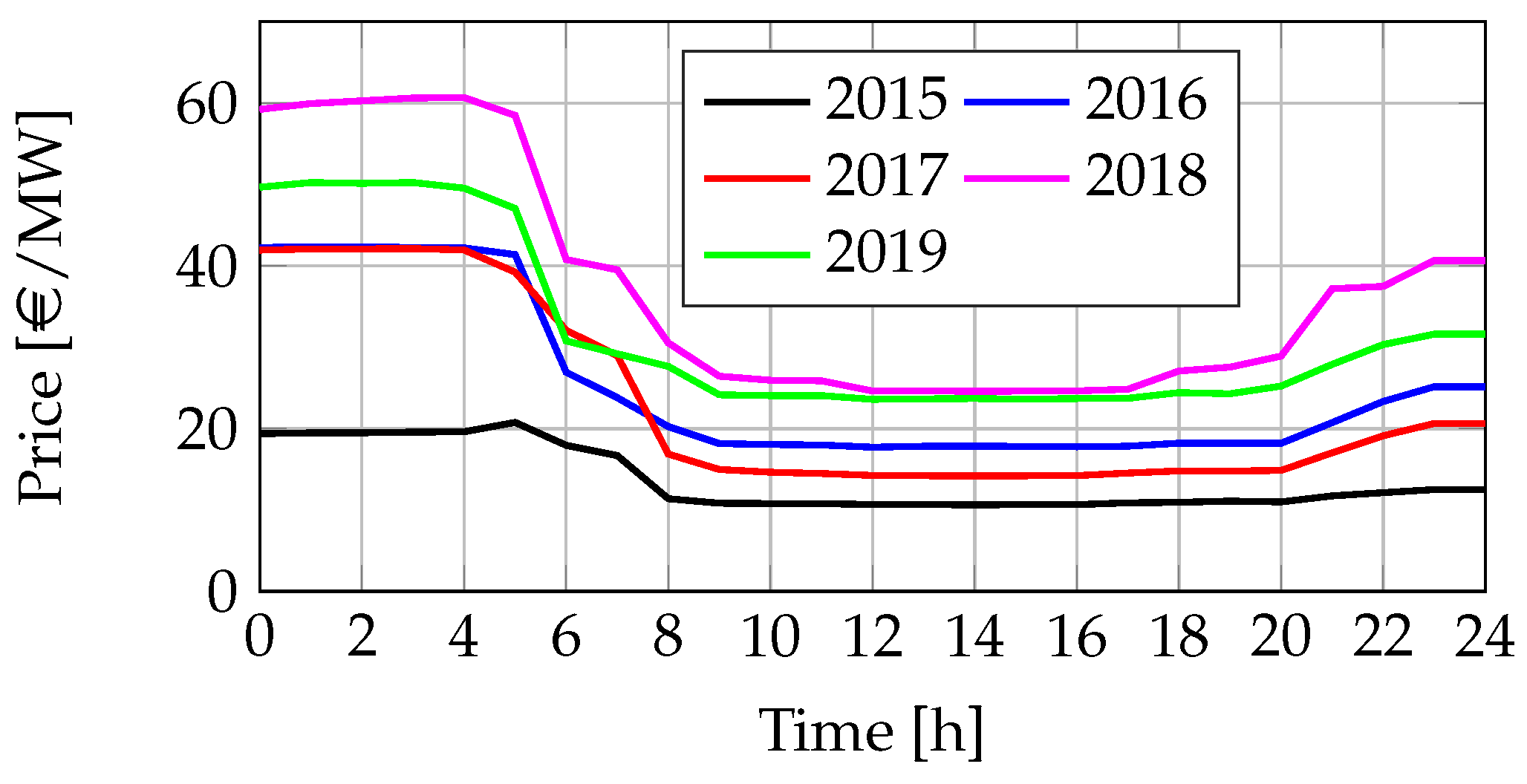
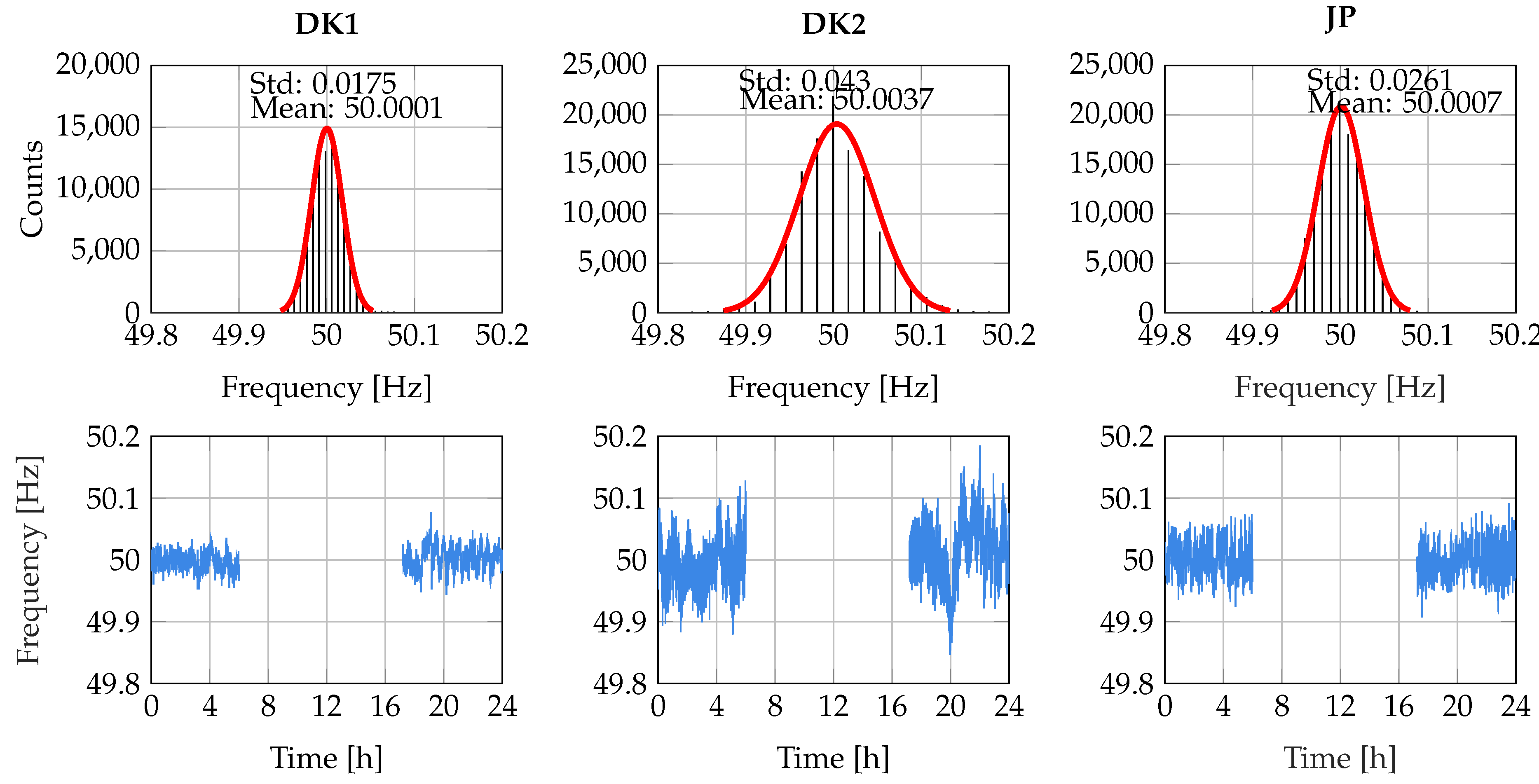
3.2.1. Frequency Regulation Price

The FR market framework in DK2 is taken as reference for all cases, due to the fact that JP does not have a market yet, and in DK1 the prices over the last 10 years are similar to the DK2 ones [24]. The average hourly price of frequency containment reserves in DK1 from 2015 to 2019 is provided in Figure 8. In 2015 the prices were exceptionally low due to high rainfall in the Nordic region, where hydro plants lead the provision of FR decreasing the prices [8,25]. By contrast, 2018 was a “dry” year, where the less FR from hydro plants increased the FR provided by the conventional units, and so did the prices.

3.2.2. Electricity Price

In 2018–2019 the electricity price for the Danish domestic consumers was 0.31 €/kWh, included taxes, whereas the industrial one (mid-size industry) was 0.08 €/kWh, excluded taxes as they are not applied to industrial prices. For what concerns the sale electricity price, over the last 10 years the average price was approx. 0.04 €/kWh.

3.2.3. Battery Price

For the evaluation of the BD costs, the value of 180 €/kWh is considered to be battery pack price per kWh [27]. Nevertheless, this is a conservative assumption since batteries are becoming cheaper and the price is expected to drop to less than 100 €/kWh by 2030 [28,29].

4. Results

During the following analysis, the battery model is considered to receive as input the same outside temperature and battery power for the 5 years of simulation. The scenario $driv$ is run with both SOC equal to 55 and 75%, and it is the same for all the three areas. The scenario $driv+FR$ is run for all the three areas—DK1, DK2 and JP—with both SOC equal to 55 and 75%.

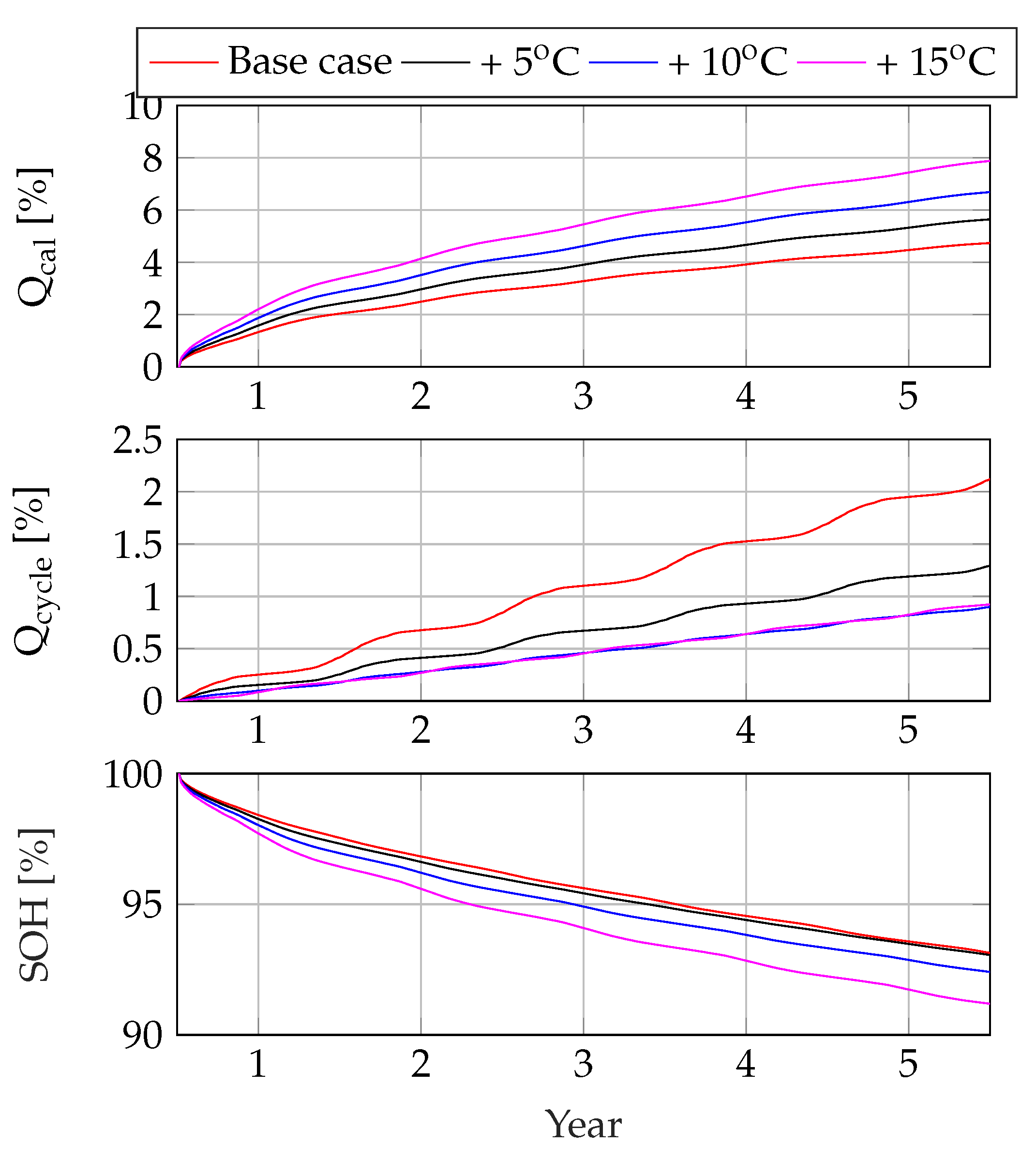
4.1. Technical Results

Figure 9 provides the SOH of the battery over the five years in the different scenarios:

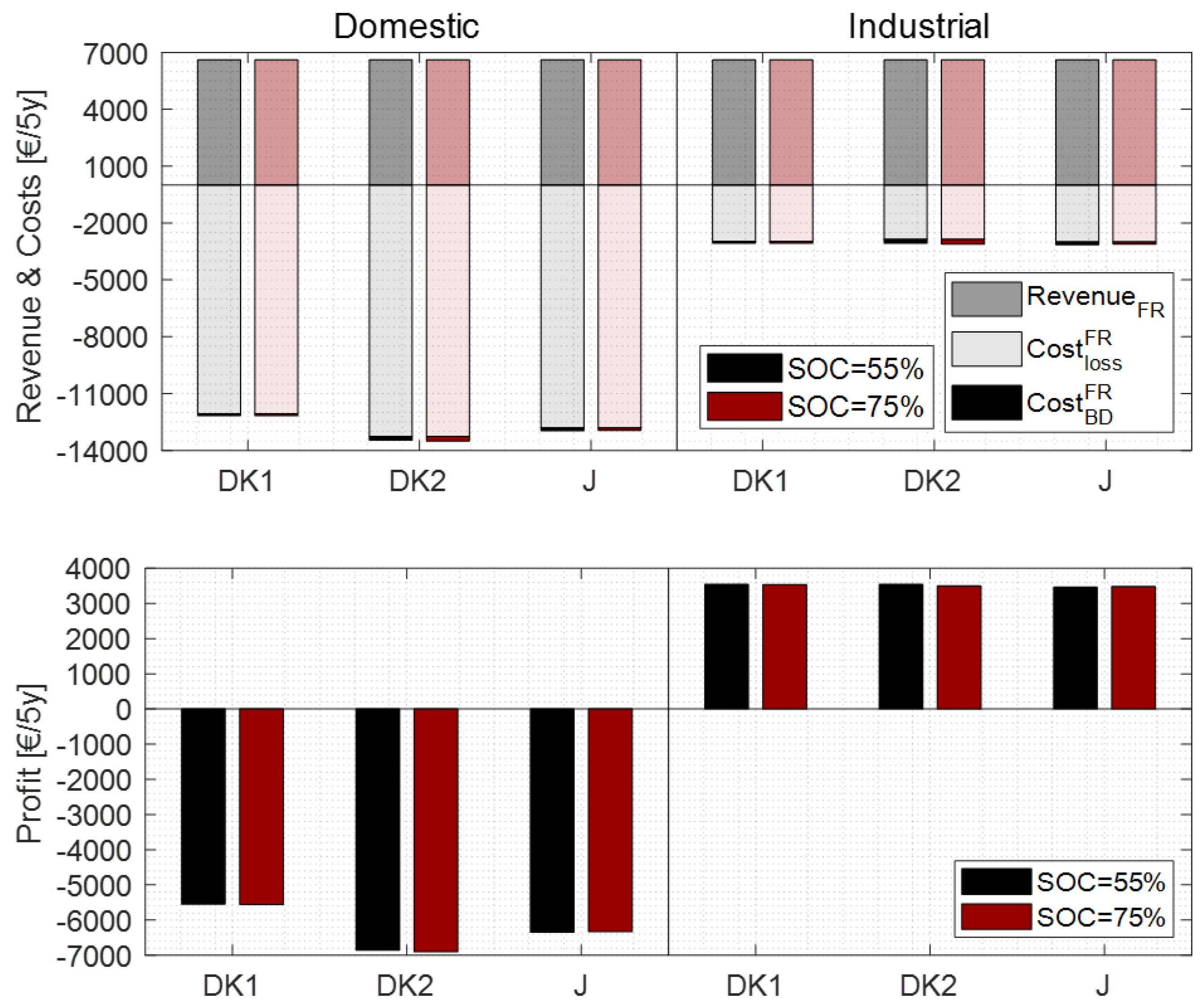
4.2. Economic Results

In this section, the profitability of the FR service is quantified. Revenue, costs and profits are determined as described in Section 2.

Table 2. $Revenu{e}_{FR}$ for the 5 years of frequency regulation and sum of the 5 years.

Year	2015	2016	2017	2018	2019	mean
$Revenu{e}_{FR}$ [€/y]	667	1324	1226	1925	1466	1322
$Revenu{e}_{FR}$ [€/5 y]	6608

provides the $Revenu{e}_{FR}$, which is independent on the SOC, electricity price and area.

Table 3. $Cos{t}_{loss}^{FR}$ for 5-year period of frequency regulation, due to the charging and discharging charger loss.

Electricity Price	Domestic			Industrial
Country	DK1	DK2	JP	DK1	DK2	JP
$Cos{t}_{loss}^{FR}$ [€/5 y]	12,065	13,260	12,815	2970	2860	3000

shows the costs due to energy exchanged with the grid and charger loss, comparing the case with domestic and industrial electricity prices and the three considered areas. The domestic and industrial electricity prices in DK2 are considered for all three areas. Since the power profile of the battery is the same for the 5 years, the cost for 5 years is the $Cos{t}_{loss}^{FR}$ for one year multiplied by 5. It is relevant to observe that with domestic electricity prices the $Cos{t}_{loss}^{FR}$ in DK2 is higher than in DK1 and JP, which is not the case when the industrial electricity prices are considered. This is due to two main reasons: first the frequency in DK2 has a standard deviation of 0.043, larger than in DK1 and JP, meaning that the power request during the regulation is larger. With larger power, both for charging and discharging, losses are lower, because the charger efficiency is closer to the optimal. Second, the domestic electricity price during purchase is higher than the electricity price for sale, making the purchasing component large in comparison to the selling one. The combination of these two shows that during FR the purchase/sale of electricity is causing costs, which are much larger in the domestic case.

The difference between the battery power in the three areas is graphically provided in Figure 10 as battery power in function of the gradient of the battery power.

Table 4. $Cos{t}_{BD}^{driv}$, $Cos{t}_{BD}^{driv+FR}$ and $Cos{t}_{BD}^{FR}$ for 5 years period of battery usage.

Mean SOC	55%			75%
Country	DK1	DK2	JP	DK1	DK2	JP
$Cos{t}_{BD}^{driv}$ [€/5 y]	876			1314
$Cos{t}_{BD}^{driv+FR}$ [€/5 y]	968	1081	1019	1418	1565	1438
$Cos{t}_{BD}^{FR}$ [€/5 y]	92	205	143	104	251	124

provides the costs due to battery degradation when just driving, driving plus FR and just FR. The first two costs are given to underline that the degradation is a relevant cost during the lifetime of the battery, nevertheless the FR provision is not adding a large component to the $driv$ scenario. Furthermore, a difference can be observed between DK2 and the other two areas: in DK2 $Cos{t}_{BD}^{FR}$ represents approximately 16–20% of the total $Cos{t}_{BD}^{driv+FR}$, depending on the SOC level. Differently in DK1 and JP the FR represents approx. the 10% of the total costs. It is important to highlight that, in contrast to the $Cos{t}_{loss}^{FR}$, the costs due to BD are not the same for all the 5 years. This is due to the calendar and cycling degradation, which have an exponential behavior during the first years of the battery lifetime, see Figure 9.

Figure 11 summarizes in the first subplot revenues and costs of the different cases whereas the second subplot compares the profits during the five years period, as calculated with (1). The difference between the SOC, with both domestic and industrial electricity prices, does not have a large impact on the final profitability of the service. By contrast, the energy exchanged with the grid is substantial, causing economic loss when the domestic prices are considered. For what concerns the industrial electricity prices, the cost of the purchase is one fourth of the domestic one and thus the service is profitable with approx. 3500€ for the considered five years and in the different scenarios.

5. Sensitivity Analysis

In this section, three parameters are further investigated, as they provide further highlights for the evaluation of the BD losses and relative costs.

5.1. Outside Temperature

The outside temperature is a relevant parameter during the calculation of the battery degradation, because it influences both the calendar and the cycle processes, as shown in (6) and (7). In this regards, the authors selected the JP case with SOC equal to 55% and investigated the battery degradation when the temperature is increased of 5, 10 and 15 ${}^{°}$C throughout the entire year. Figure 12 compares the results of the different cases, first for the calendar and the cycle degradation and then for the SOH. Results show that despite the temperature increase of 5, 10 and 15 ${}^{°}$C, the maximum SOH difference is 3%, which would result on a contained increase of the BD costs. Furthermore, the calendar losses are observed to be predominant in the total loss and their increase goes with the increase of the temperature. By contrast, the cycle degradation for the 10 and 15 ${}^{°}$C temperature increase is almost the same. This is explained by the relation between the cycle degradation and the temperature provided in Figure 2, which shows that around 25 ${}^{°}$C there is a minimum, and then the degradation starts to increase again.

5.2. Used Capacity

The second parameter is the remaining capacity of the battery. As shown in Figure 3, the battery end-of-life is set to SOH of 50%, after the battery has been used in the vehicle and for a second use. Nevertheless, as presently, not all batteries used in EVs are then used in second life applications. To consider this case the 50% remaining battery capacity in (12) is compared with the 20% used capacity, when the battery end-of-life coincides with the EV end-of-life (final SOH = 80%). The $Cos{t}_{BD}^{FR}$ of the initial case ($Cos{t}_{{BD}_{50\%}}^{FR}$) is compared with the $Cos{t}_{{BD}_{20\%}}^{FR}$ in

Table 5. $Cos{t}_{BD}^{FR}$ for 5 years period of battery usage considering the used capacity equal to 20%, 50%.

Mean SOC	55%			75%
Country	DK1	DK2	JP	DK1	DK2	JP
$Cos{t}_{{BD}_{20\%}}^{FR}$ [€/5 y]	230	513	358	260	628	310
$Cos{t}_{{BD}_{50\%}}^{FR}$ [€/5 y]	92	205	143	104	251	124

:

The results show that the battery degradation is max 5% of the total cost when considering the domestic charger loss present in Table 3. When considering the industrial prices, the battery degradation could represent up to 20% of the cost, resulting on lower profit, but still positive.

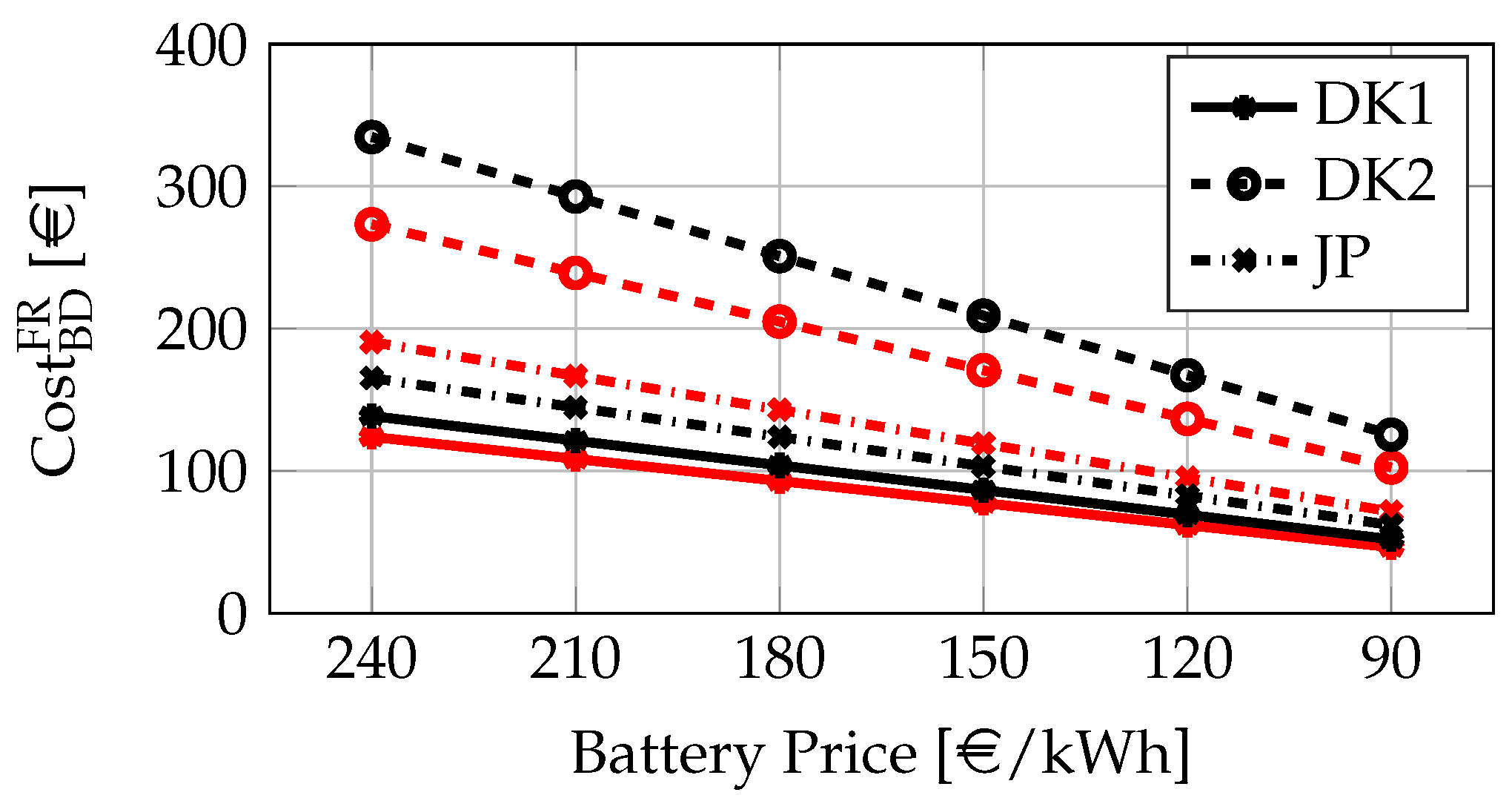
5.3. Battery Price

To evaluate the BD costs, the battery price per kWh has been considered equal to 180€. However, the price of NMC batteries is decreasing year-by-year and forecasts show that the price could become lower than 90 €/kWh by 2030 [29]. Furthermore, to account for price variations among automakers and the price difference between the cost for the automaker and the costumer, prices higher than 180 €/kWh are also considered. In this regard, Figure 13 compares the $Cos{t}_{BD}^{FR}$ evaluated in Table 4, with the BD cost for FR when the battery price per kWh is equal to 240, 210, 180, 150, 120 and 90€. The BD cost due to FR are shown to decrease to less than 100€ for DK1 and JP, meaning that in the future their weight on the final profit can become even lower than what shown in Figure 11.

6. Conclusions

In this manuscript the profitability of primary frequency regulation provided by EVs, taking into account the battery degradation costs has been quantified based on the frequency measured in Denmark, both DK1 and DK2, and Japan. First, the battery power profiles have been derived from the driving pattern and the frequency measurements. Second, the battery model has been simulated to derive the degradation loss and to calculate the related costs the user would encounter while providing frequency regulation. Afterwards the energy exchanged with the grid has been used to determine the economic loss due to the higher purchase electricity price in comparison to the sale one. Finally, revenue and costs were combined to determine the profit. It was noticed that the frequency in DK2 was more spread between the 49.8 and 50.2 Hz causing higher costs due to degradation and energy exchanged with the grid. By contrast, for what concerns the battery degradation, the losses are larger when the frequency is more spread, because the battery is exposed to more cycles during its lifetime. Nevertheless, the battery degradation cost is approx. 1% of the total costs when considering domestic electricity prices, and 3–8% when considering industrial prices, both with 55 and 75% SOC.

Finally, it was observed that the electricity price and the charger efficiency are two main parameters that affect the profitability of the service. Indeed, with domestic prices the charger losses are too large and there are only economic losses in the service provision.

Further considerations and analysis can be done regarding the losses:

• charger efficiency: the charger losses of this analysis are based on the efficiency of a three years old charger. It is interesting to compare the charger efficiency of this charger with new and future chargers, which could have higher efficiency and thus lower costs [30].
• battery capacity: the considered battery has a 40 kWh capacity. Considering the same charging/discharging power profile, larger is the battery, lower is the amount of cycles the battery is exposed to. Thus, for smaller batteries the battery degradation is expected to be a larger component of the total amount of loss. For larger batteries, which are expected in the future, the degradation can be even lower, decreasing further the degradation costs. This would also give more flexibility on the charging power that can be used during the frequency regulation provision.

Even though DK1 (belonging to the continental Europe synchronous areas) has been considered during the analyses, to generalize the results to the all Europe the following aspects should be carefully considered:

• Cost of electricity: in Europe it ranges around 0.21 €/kWh whereas in Denmark it is approx. 0.31 €/kWh, resulting on lower cost of electricity in most European countries.
• Vehicle driving pattern and annual distance: European countries have similar driving patterns, nevertheless distances ranges between 40 and 80 km/day depending on the considered country [31].
• Ambient temperature: European countries are characterized by wide variety of climate zones, meaning that the temperature behavior throughout the year can vary greatly.

Similar aspects must be considered when generalizing the analyses of DK2 to the Scandinavian countries. Further studies of the authors will include the different considerations for the evaluation of the profitability of frequency regulation.