A Novel Algorithm for Controlling Active and Reactive Power Flows of Electric Vehicles in Buildings and Its Impact on the Distribution Network
Abstract
1. Introduction
1.1. Problem Statement
1.2. Literature Review
1.3. Impediments and Barriers of Other Studies
1.4. Contributions
- Main and branch circuit breaker rating into the optimization model,
- Upper and lower limits of both active and reactive power on the distribution transformer,
- real charging and discharging power profiles of the EVs,
- It predicts and calculates the available power to be consumed at each instant and inform the end-user how much energy is left to use every day to charge his EV while respecting the power and energy limits at home,
- It informs the end-user how much energy he should reduce at home in order to attain the desired State of Charge level,
- The discharging mode could be selected according to the EV owner’s desire,
- The algorithm gives the EV owner the choice to participate or not in the ancillary services such as voltage and power flow regulations.
1.5. Paper Organization
2. Problem Formulation
2.1. Objective Function
2.2. Constraints
2.2.1. Mode of Operation
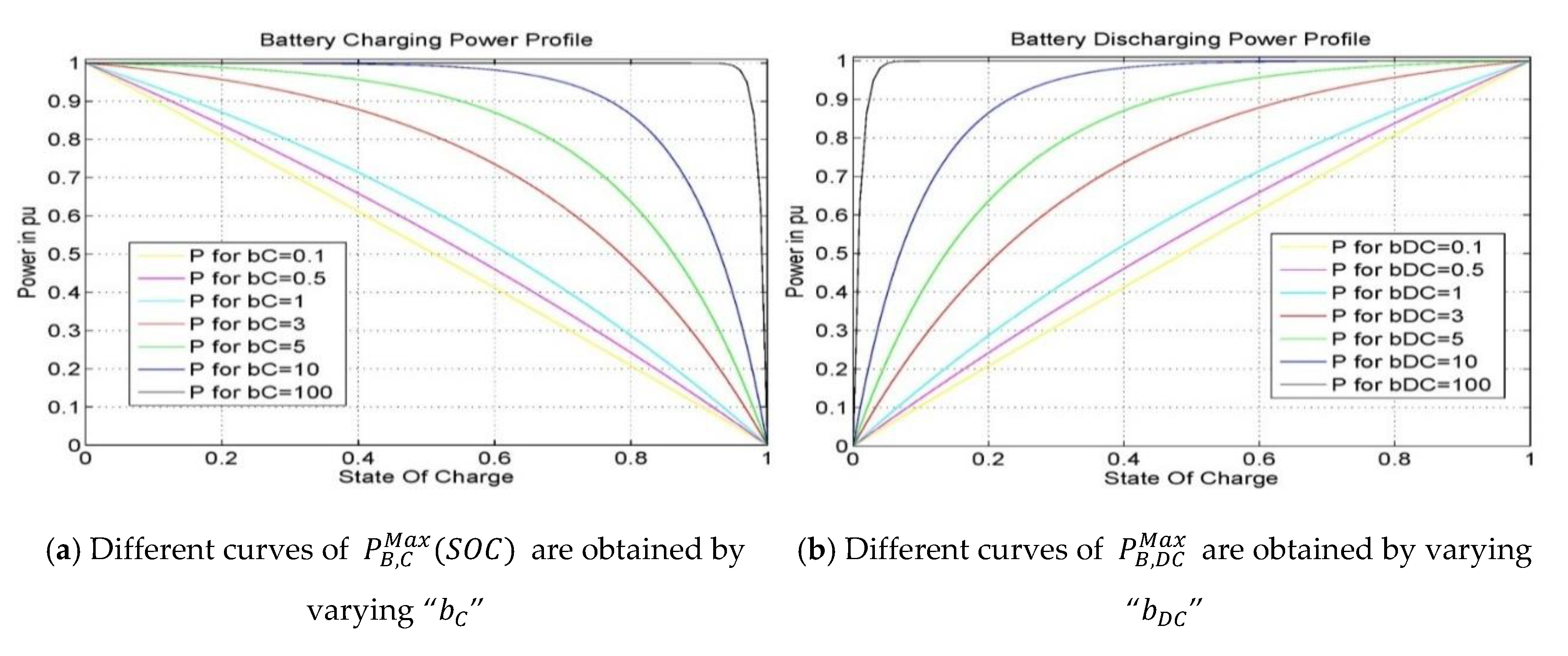
2.2.2. Active Power Constraints
2.2.3. State of Charge (SOC) Constraints
2.2.4. Reactive Power Constraints
2.2.5. Voltage Constraint
2.3. Management of Home Power
2.4. Proposed Algorithm to Solve the Problem
| Proposed Algorithm: |
|
3. Results and Discussions for a Single Home
3.1. Different Scenarios Are Studied at Home
3.2. Considerations for a Single Home
3.3. Results for a Single Home
3.3.1. Power and Charging Rates Profiles
3.3.2. Voltage Profiles
3.3.3. Energy Cost Profiles
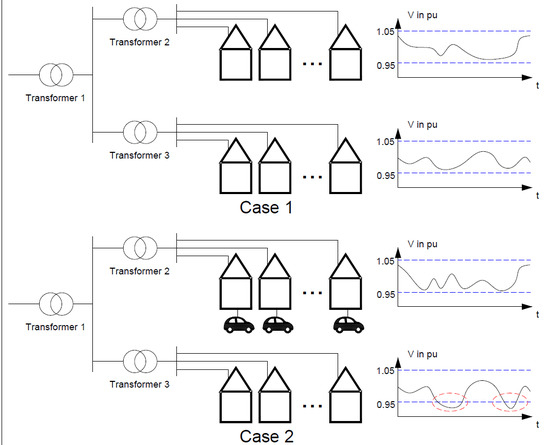
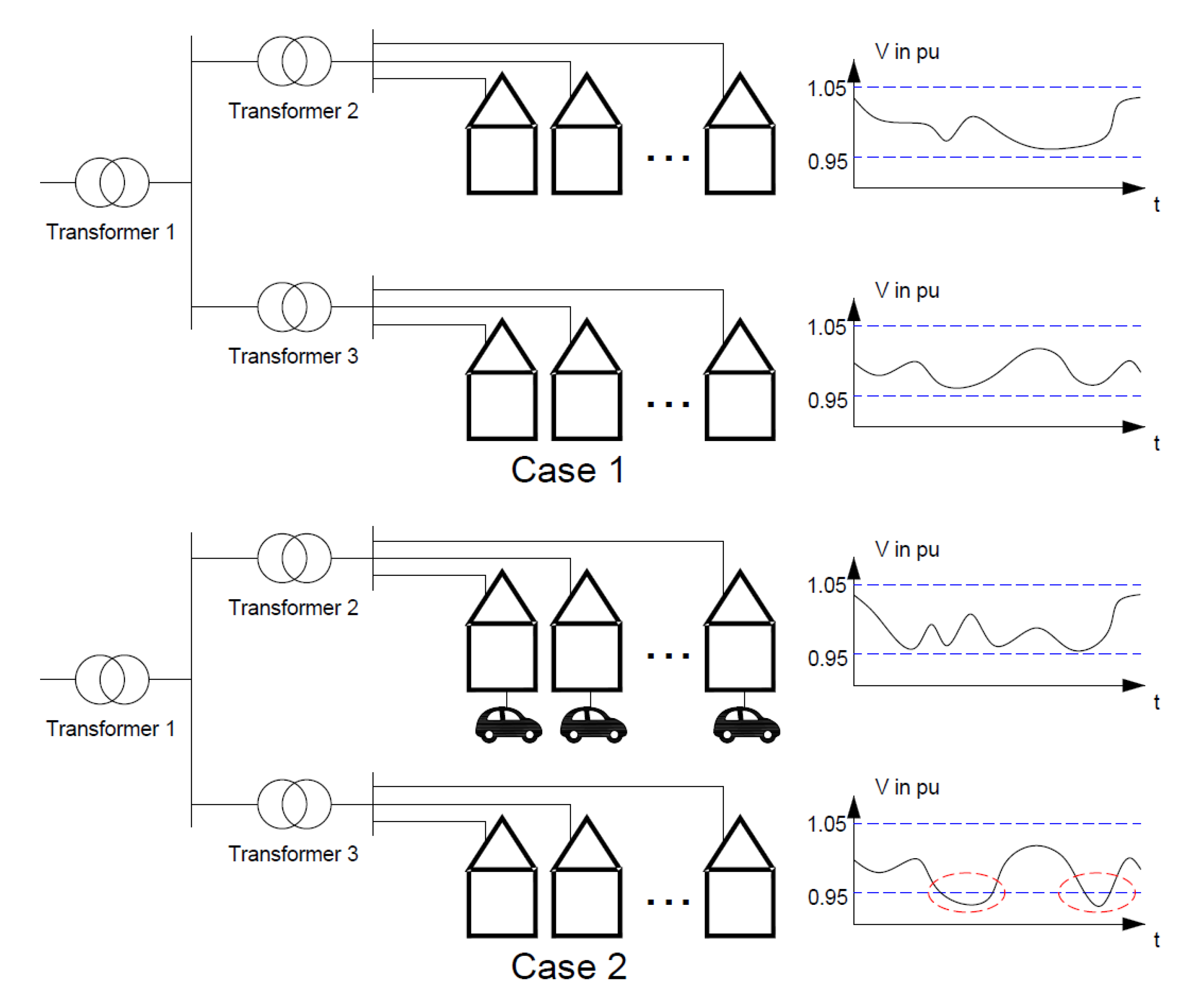
4. Results and Discussions for a Cluster of Homes in the Same Bus
4.1. Considerations for a Cluster of Homes on the Same Bus
4.2. Results for a Cluster of Homes on the Same Bus
5. Summary of the Main Outcomes of the Proposed Algorithm
- The power limit of the transformer is respected,
- The techno-economic losses on the transformer and lines of the network are reduced,
- Voltage limits on the network and transformer are respected,
- The electricity cost at home is minimized.
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Abbreviations | |
| DSO | Distribution system operator |
| DT | Distribution transformer |
| EV | Electric vehicle |
| IEEE | Institute of Electrical and Electronic Engineering |
| RES | Renewable energy sources |
| SOC | State of charge of the battery in the electric vehicle |
| U-EV | Uncoordinated Charging Strategy for Electric Vehicles |
| CC-EV | Coordinated Charging Strategy for Electric Vehicles |
| CCD-EV | Our proposed Coordinated Charging and Discharging Strategy for Electric Vehicles |
| Symbols | |
| , | Avoiding tripping factors of the main and branch circuit breakers [-] |
| Time step interval, e.g., 0.5 h in this study [h] | |
| Phase angle | |
| , | Main and branch circuit breaker nominal rates, respectively [kW] |
| Electricity cost at instant “” [$/kWh] | |
| Maximum available active power at home at instant “” [kW] | |
| Maximum charging power limit for a certain SOC of the battery [kW] | |
| Maximum discharging power limits for a certain SOC of the battery [kW] | |
| Absorbed active power by the EV using charging mode [kW] | |
| Injected active power by the EV using discharging mode [kW] | |
| Baseload power demand of the home without EV [kW] | |
| Power limit not to be overpassed on the EV branch circuit breaker (BCB) [kW] | |
| Active power limit at home [kW] | |
| Active power limit of the main circuit breaker at home [kW] | |
| Active power limit on the distribution transformer [kW] | |
| , | Minimum and maximum power factor limits |
| Absorbed reactive power by the EV [kVAR] | |
| Injective reactive power by the EV [kVAR] | |
| Reactive power demand of the home without EV [kVAR] | |
| Respected Lower Limit of the Active Power for the total load including the EV at instant “” [kW] | |
| Respected Lower Limit of the Reactive Power for the total load including the EV at instant “” [kVAR] | |
| Respected upper limit of active power at instant “” for the total load [kW] | |
| Respected upper limit of reactive power at instant “” for the total load [kVAR] | |
| Algorithm decision result, it is equal to 1 if the decision is about performing charging or discharging, and 0 if no action should be performed [-] | |
| , , | Binary flags of the charging, discharging, and idle modes, respectively. (“1” means the mode is turned on; otherwise, it is “0”, and just one mode at a time could be applied) [-] |
| Status of the load, , and “0” otherwise [-] | |
| Status of the load, if , and “0” otherwise [-] | |
| Plug status of the EV, it is equal to “1” if the vehicle is connected to the grid, and “0” otherwise [-] | |
| Total apparent power at home | |
| Desired final state of charge of the battery in the EV | |
| Period of time for the study [h] | |
| Arrival time of the EV to the home when it is plugged-in [h] | |
| Binary function that is equal to one when , otherwise it is zero [-] | |
| Nominal voltage, (i.e., 220 V) [V] | |
| Voltage measured on the transformer [V] | |
| , | Minimum and maximum voltage limits on the transformer [V] |
References
- Marano, V.; Rizzoni, G. Energy and economic evaluation of PHEVs and their interaction with renewable energy sources and the power grid. In Proceedings of the 2008 IEEE International Conference on Vehicular Electronics and Safety, Columbus, OH, USA, 22–24 September 2008; pp. 84–89. [Google Scholar] [CrossRef]
- Kempton, W.; Tomić, J. Vehicle-to-grid power implementation: From stabilizing the grid to supporting large-scale renewable energy. J. Power Sources 2005, 144, 280–294. [Google Scholar] [CrossRef]
- Tomić, J.; Kempton, W. Using fleets of electric-Drive vehicles for grid support. J. Power Sources 2007, 168, 459–468. [Google Scholar] [CrossRef]
- Al-Awami, A.T.; Sortomme, E. Coordinating Vehicle-to-Grid Services With Energy Trading. IEEE Trans. Smart Grid 2011, 3, 453–462. [Google Scholar] [CrossRef]
- Aravinthan, V.; Jewell, W. Controlled Electric Vehicle Charging for Mitigating Impacts on Distribution Assets. IEEE Trans. Smart Grid 2015, 6, 999–1009. [Google Scholar] [CrossRef]
- Khodayar, M.E.; Wu, L.; Shahidehpour, M. Hourly Coordination of Electric Vehicle Operation and Volatile Wind Power Generation in SCUC. IEEE Trans. Smart Grid 2012, 3, 1271–1279. [Google Scholar] [CrossRef]
- Saber, A.Y.; Venayagamoorthy, G.K. Plug-in Vehicles and Renewable Energy Sources for Cost and Emission Reductions. IEEE Trans. Ind. Electron. 2010, 58, 1229–1238. [Google Scholar] [CrossRef]
- Heydt, G. The Impact of Electric Vehicle Deployment on Load Management Straregies. IEEE Trans. Power Appar. Syst. 1983, 102, 1253–1259. [Google Scholar] [CrossRef]
- Rajakaruna, S.; Shahnia, F.; Ghosh, A. Plug in Electric Vehicles in Smart Grids; Springer: Berlin, Germany, 2016. [Google Scholar]
- Lu, J.; Hossain, J. Vehicle-to-Grid: Linking Electric Vehicles to the Smart Grid; IET: Stevenage, UK, 2015. [Google Scholar]
- Williamson, S.S. Energy Management Strategies for Electric and Plug-in Hybrid Electric Vehicles; Springer Science and Business Media LLC: New York, NY, USA, 2013. [Google Scholar]
- Yao, L.; Lim, W.H.; Tsai, T.S. A Real-Time Charging Scheme for Demand Response in Electric Vehicle Parking Station. IEEE Trans. Smart Grid 2016, 8, 52–62. [Google Scholar] [CrossRef]
- Amjad, M.; Ahmad, A.; Rehmani, M.H.; Umer, T. A review of EVs charging: From the perspective of energy optimization, optimization approaches, and charging techniques. Transp. Res. Part D Transp. Environ. 2018, 62, 386–417. [Google Scholar] [CrossRef]
- Wang, R.; Xiao, G.; Wang, P. Hybrid Centralized-Decentralized (HCD) Charging Control of Electric Vehicles. IEEE Trans. Veh. Technol. 2017, 66, 6728–6741. [Google Scholar] [CrossRef]
- Wang, R.; Wang, P.; Xiao, G. Intelligent Microgrid Management and EV Control under Uncertainties in Smart Grid; Springer Science and Business Media LLC. Springer: Berlin, Germany, 2018. [Google Scholar]
- Verma, A.K.; Singh, B.; Shahani, D. New topology for management of bi-directional power flow between vehicle and grid with reduced ripple current at unity power factor. Int. J. Power Electron. 2013, 5, 216. [Google Scholar] [CrossRef]
- Yilmaz, M.; Krein, P.T. Review of Battery Charger Topologies, Charging Power Levels, and Infrastructure for Plug-In Electric and Hybrid Vehicles. IEEE Trans. Power Electron. 2013, 28, 2151–2169. [Google Scholar] [CrossRef]
- Yilmaz, M.; Krein, P.T. Review of the Impact of Vehicle-to-Grid Technologies on Distribution Systems and Utility Interfaces. IEEE Trans. Power Electron. 2013, 28, 5673–5689. [Google Scholar] [CrossRef]
- Su, W. Smart Grid Operations Integrated with Plug-in Electric Vehicles and Renewable Energy Resources. Ph.D. Thesis, Electrical Engineering, North Carolina State University, Raleigh, NC, USA, 2013. Available online: http://gradworks.umi.com/35/75/3575845.html (accessed on 20 March 2020).
- Su, W.; Eichi, H.; Zeng, W.; Chow, M.-Y. A Survey on the Electrification of Transportation in a Smart Grid Environment. IEEE Trans. Ind. Inform. 2011, 8, 1–10. [Google Scholar] [CrossRef]
- Sortomme, E.; El-Sharkawi, M.A. Optimal Charging Strategies for Unidirectional Vehicle-to-Grid. IEEE Trans. Smart Grid 2010, 2, 131–138. [Google Scholar] [CrossRef]
- Pillai, J.R.; Bak-Jensen, B. Integration of Vehicle-to-Grid in the Western Danish Power System. IEEE Trans. Sustain. Energy 2010, 2, 12–19. [Google Scholar] [CrossRef]
- Masoum, A.S.; Deilami, S.; Abu-Siada, A.; Masoum, M.A.S. Fuzzy Approach for Online Coordination of Plug-In Electric Vehicle Charging in Smart Grid. IEEE Trans. Sustain. Energy 2014, 6, 1–10. [Google Scholar] [CrossRef]
- Deilami, S.; Masoum, A.S.; Moses, P.S.; Masoum, M.A.S. Real-Time Coordination of Plug-In Electric Vehicle Charging in Smart Grids to Minimize Power Losses and Improve Voltage Profile. IEEE Trans. Smart Grid 2011, 2, 456–467. [Google Scholar] [CrossRef]
- Sekyung, H.; Soohee, H.; Sezaki, K. Development of an Optimal Vehicle-to-Grid Aggregator for Frequency Regulation. IEEE Trans. Smart Grid 2010, 1, 65–72. [Google Scholar] [CrossRef]
- Schuller, A.; Ilg, J.; Van Dinther, C. Benchmarking electric vehicle charging control strategies. In Proceedings of the 2012 IEEE PES Innovative Smart Grid Technologies (ISGT), Washington, DC, USA, 16–20 January 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Hua, L.; Wang, J.; Zhou, C. Adaptive Electric Vehicle Charging Coordination on Distribution Network. IEEE Trans. Smart Grid 2014, 5, 2666–2675. [Google Scholar] [CrossRef]
- Clement-Nyns, K.; Haesen, E.; Driesen, J. The Impact of Charging Plug-In Hybrid Electric Vehicles on a Residential Distribution Grid. IEEE Trans. Power Syst. 2009, 25, 371–380. [Google Scholar] [CrossRef]
- El-Bayeh, C.; Mougharbel, I.; Saad, M.; Chandra, A.; Lefebvre, S.; Asber, D. Novel Multilevel Soft Constraints at Homes for Improving the Integration of Plug-in Electric Vehicles. In Proceedings of the 2018 4th International Conference on Renewable Energies for Developing Countries (REDEC), Beirut, Lebanon, 1–2 November 2018; pp. 1–9. [Google Scholar] [CrossRef]
- El-Bayeh, C.; Mougharbel, I.; Saad, M.; Chandra, A.; Asber, D.; Lenoir, L.; Lefebvre, S. Novel Soft-Constrained Distributed Strategy to meet high penetration trend of PEVs at homes. Energy Build. 2018, 178, 331–346. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y.; Zhao, B.; Huang, F.; Chen, Y.; Ren, S. Optimal energy flow control strategy for a residential energy local network combined with demand-side management and real-time pricing. Energy Build. 2017, 150, 177–188. [Google Scholar] [CrossRef]
- Wu, X.; Hu, X.; Teng, Y.; Qian, S.; Cheng, R. Optimal integration of a hybrid solar-battery power source into smart home nanogrid with plug-in electric vehicle. J. Power Sources 2017, 363, 277–283. [Google Scholar] [CrossRef]
- Wu, X.; Hu, X.; Yin, X.; Moura, S.J. Stochastic Optimal Energy Management of Smart Home with PEV Energy Storage. IEEE Trans. Smart Grid 2018, 9, 2065–2075. [Google Scholar] [CrossRef]
- Ghazvini, M.A.F.; Soares, J.; Abrishambaf, O.; Castro, R.; Vale, Z. Demand response implementation in smart households. Energy Build. 2017, 143, 129–148. [Google Scholar] [CrossRef]
- Leou, R.-C.; Su, C.-L.; Lu, C.-N. Stochastic Analyses of Electric Vehicle Charging Impacts on Distribution Network. IEEE Trans. Power Syst. 2014, 29, 1055–1063. [Google Scholar] [CrossRef]
- El-Bayeh, C. Novel Approaches to Optimize and Mitigate the Impact of High Penetration Level of Electric Vehicles on the Distribution Network. Ph.D. Thesis, 2019. Available online: https://espace.etsmtl.ca/id/eprint/2362/1/EL-BAYEH_Claude.pdf (accessed on 29 May 2020).
- El-Bayeh, C.; Mougharbel, I.; Saad, M.; Chandra, A.; Asber, D.; Lefebvre, S. Impact of Considering Variable Battery Power Profile of Electric Vehicles on the Distribution Network. In Proceedings of the 2018 4th International Conference on Renewable Energies for Developing Countries (REDEC), Beirut, Lebanon, 1–2 November 2018; pp. 1–8. [Google Scholar]
- El-Bayeh, C.; Mougharbel, I.; Saad, M.; Chandra, A.; Lefebvre, S.; Asber, D.; Lenoir, L. A novel approach for sizing electric vehicles Parking Lot located at any bus on a network. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar] [CrossRef]
- El-Bayeh, C.; Mougharbel, I.; Saad, M.; Chandra, A.; Lefebvre, S.; Asber, D.; Lenoir, L. A detailed review on the parameters to be considered for an accurate estimation on the Plug-in Electric Vehicle’s final State of Charge. In Proceedings of the 2016 3rd International Conference on Renewable Energies for Developing Countries (REDEC), Boston, MA, USA, 13–15 July 2016; pp. 1–6. [Google Scholar] [CrossRef]
- El-Bayeh, C.; Mougharbel, I.; Asber, D.; Saad, M.; Chandra, A.; Lefebvre, S. Novel Approach for Optimizing the Transformer’s Critical Power Limit. IEEE Access 2018, 6, 55870–55882. [Google Scholar] [CrossRef]
- Qian, K.; Allan, M.; Zhou, C.; Yuan, Y. Modeling of Load Demand Due to EV Battery Charging in Distribution Systems. IEEE Trans. Power Syst. 2010, 26, 802–810. [Google Scholar] [CrossRef]
- Cao, Y.; Tang, S.; Li, C.; Zhang, P.; Tan, Y.; Zhang, Z.; Li, J. An Optimized EV Charging Model Considering TOU Price and SOC Curve. IEEE Trans. Smart Grid 2012, 3, 388–393. [Google Scholar] [CrossRef]
- Bhatia, A. Power factor in electrical energy Management. PDH Online Course E 2012, 144, 1–42. [Google Scholar]
- The Impact of Distributed Generation and Electric Vehicles. In The Future of the Electric Grid; MITei Ed.; MIT Energy Initiative: Cambridge, MA, USA, 2011; Volume 5, pp. 109–126.
- Electric Vehicles Charging Options. PG&E. Available online: http://www.pge.com/en/myhome/saveenergymoney/pev/charging/index.page (accessed on 20 February 2015).
- Hourly Load Profiles Appendix D. Xcel Energy, Report 2012. Available online: http://www.xcelenergy.com/staticfiles/xe/Corporate/Corporate%20PDFs/AppendixD-Hourly_Load_Profiles.pdf (accessed on 20 September 2016).
- OpenDSS EPRI Distribution System Simulator. EPRI. Available online: https://sourceforge.net/projects/electricdss/ (accessed on 20 October 2016).







| Parameters | Without EVs | U-EV | CC-EV | CCD-EV |
|---|---|---|---|---|
| Circuit Breaker (kW) | 7.36 kW | 7.36 kW | 7.36 kW | 7.36 kW |
| Load in (kW) | 4.9282 Min 8.1590 Max | 4.9385 Min 10.079 Max | 4.9385 Min 8.1590 Max | 4.9385 Min 7.3600 Max |
| Circuit Breaker (A) | 40A | 40A | 40A | 40A |
| Line current in (A) | 26.783 Min 44.342 Max | 26.839 Min 54.777 Max | 26.839 Min 44.342 Max | 26.839 Min 40.000 Max |
| Voltage (V) | 225 Min 228.17 Max | 223.12 Min 228.17 Max | 225 Min 228.16 Max | 225.78 Min 228.16 Max |
| Voltage Drop in (%) Advised limit is 2% | 0.797 Min 2.1747 Max | 0.797 Min 2.993 Max | 0.801 Min 2.174 Max | 0.801 Min 1.834 Max |
| Power Losses (kW) | 0.0809 Min 0.2218 Max 6.128 Total 0.0000% | 0.0812 Min 0.3384 Max 7.896 Total +28.8594% | 0.0812 Min 0.2218 Max 7.653 Total +24.8875% | 0.0812 Min 0.1805 Max 7.650 Total +24.8466% |
| Parameters | Without EV | U-EV | CC-EV | CCD-EV |
|---|---|---|---|---|
| Fixed Cost ($) | 0.1692 Min 0.2802 Max 10.023 Total | 0.1692 Min 0.3462 Max 11.264 Total | 0.1692 Min 0.2802 Max 11.264 Total | 0.1692 Min 0.2802 Max 11.264 Total |
| Time-Of-Use ($) | 0.1478 Min 0.4079 Max 10.330 Total | 0.1478 Min 0.5039 Max 11.702 Total | 0.1478 Min 0.4079 Max 11.414 Total | 0.1478 Min 0.4079 Max 11.382 Total |
| Dynamic Price ($) | 0.1467 Min 0.4022 Max 10.960 Total | 0.1467 Min 0.4969 Max 12.356 Total | 0.1467 Min 0.4022 Max 12.151 Total | 0.1467 Min 0.4022 Max 12.135 Total |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Bayeh, C.Z.; Alzaareer, K.; Brahmi, B.; Zellagui, M. A Novel Algorithm for Controlling Active and Reactive Power Flows of Electric Vehicles in Buildings and Its Impact on the Distribution Network. World Electr. Veh. J. 2020, 11, 43. https://doi.org/10.3390/wevj11020043
El-Bayeh CZ, Alzaareer K, Brahmi B, Zellagui M. A Novel Algorithm for Controlling Active and Reactive Power Flows of Electric Vehicles in Buildings and Its Impact on the Distribution Network. World Electric Vehicle Journal. 2020; 11(2):43. https://doi.org/10.3390/wevj11020043
Chicago/Turabian StyleEl-Bayeh, Claude Ziad, Khaled Alzaareer, Brahim Brahmi, and Mohamed Zellagui. 2020. "A Novel Algorithm for Controlling Active and Reactive Power Flows of Electric Vehicles in Buildings and Its Impact on the Distribution Network" World Electric Vehicle Journal 11, no. 2: 43. https://doi.org/10.3390/wevj11020043
APA StyleEl-Bayeh, C. Z., Alzaareer, K., Brahmi, B., & Zellagui, M. (2020). A Novel Algorithm for Controlling Active and Reactive Power Flows of Electric Vehicles in Buildings and Its Impact on the Distribution Network. World Electric Vehicle Journal, 11(2), 43. https://doi.org/10.3390/wevj11020043