Research on the Electromagnetic-Heat-Flow Coupled Modeling and Analysis for In-Wheel Motor
Abstract
1. Introduction
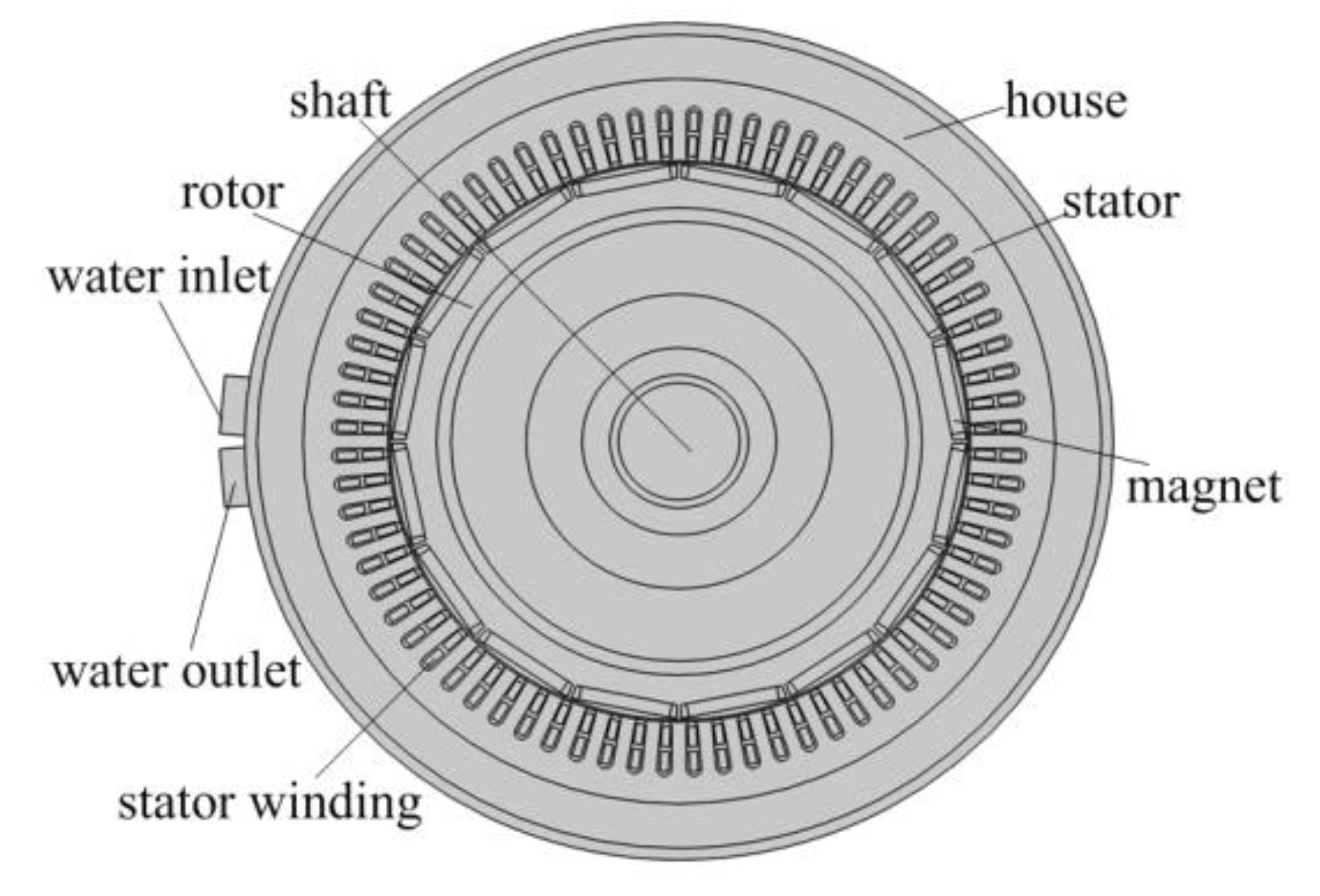
2. Structure of IWM
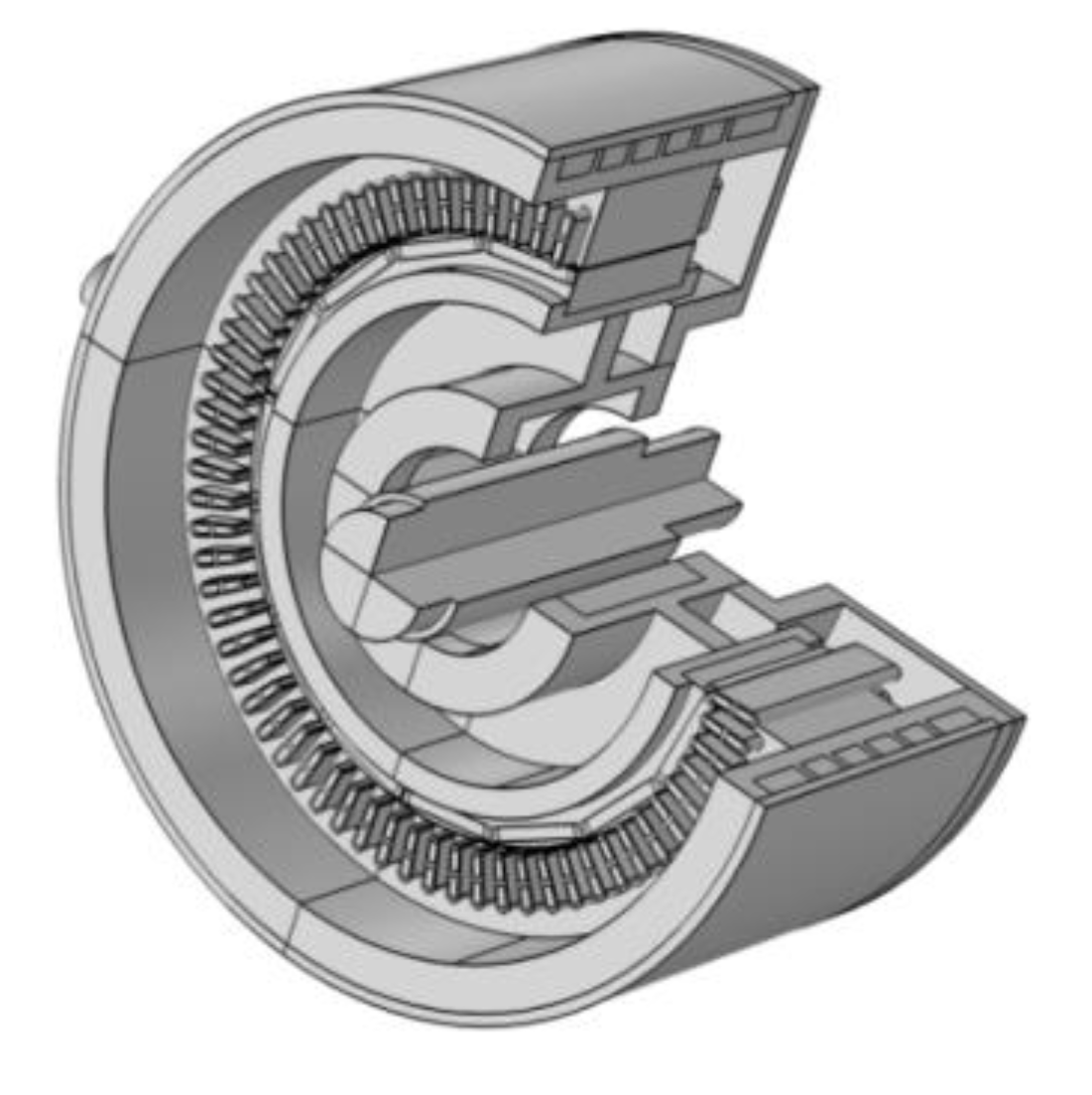
2.1. Basic Structure of IWM
2.2. Basic Parameters of IWM
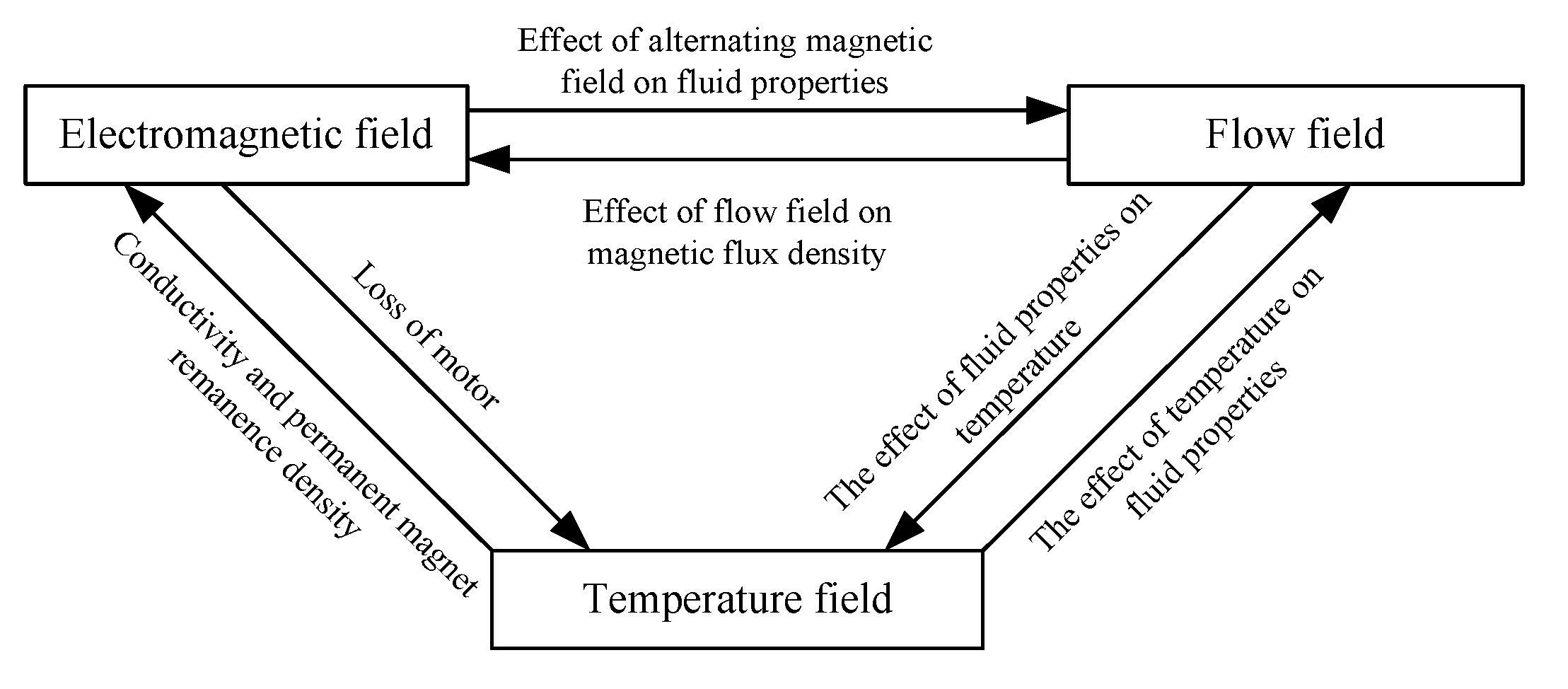
3. Analysis of Electromagnetic-Heat-Flow Coupling Factors
3.1. Analysis of the Coupling Factors of Electromagnetic Field and Temperature Field
3.1.1. Influence Factors of Electromagnetic Field on Temperature Field
(1) Core Loss
(2) Eddy Current Loss of the PM
(3) Copper Loss
3.1.2. Influence of Temperature Field on Electromagnetic Field
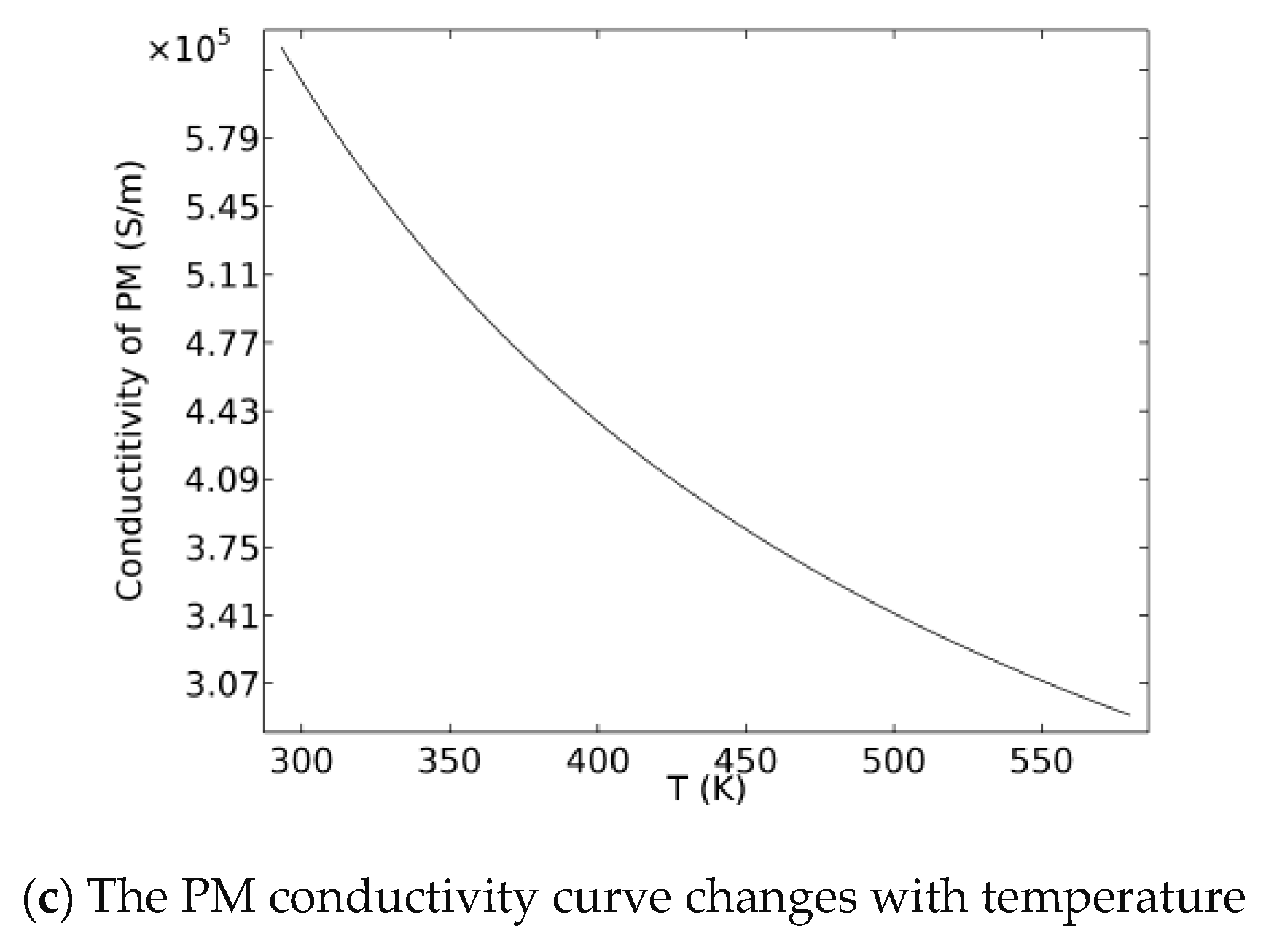
(1) Influence of Temperature on the Conductivity of Materials
(2) Influence of Temperature on Residual Flux Density of PM
3.2. Analysis of the Coupling Factors of Temperature Field and Flow Field
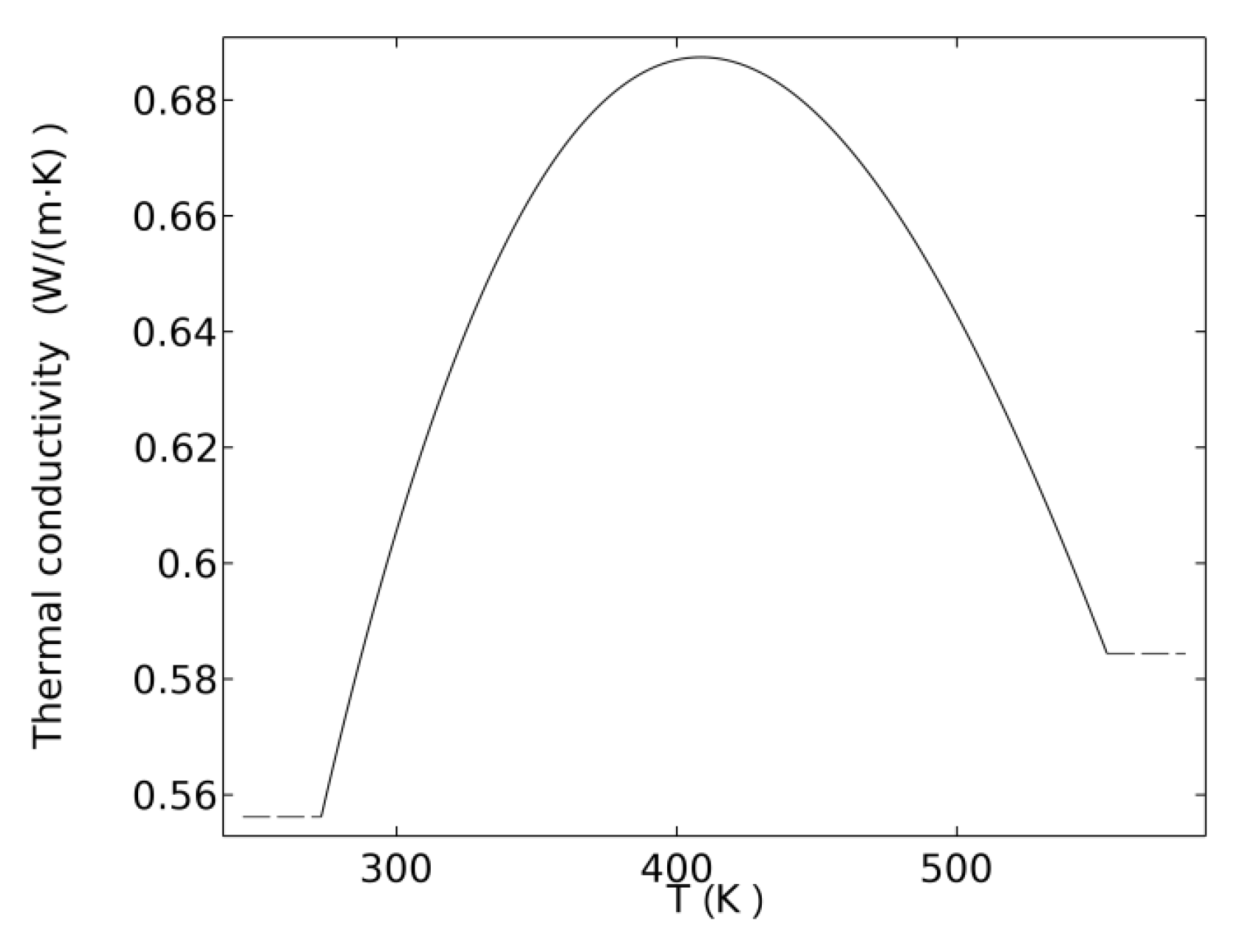
3.2.1. Influence of Temperature on Thermal Conductivity of Fluid
3.2.2. Influence of Temperature on the Specific Heat Capacity of Fluid
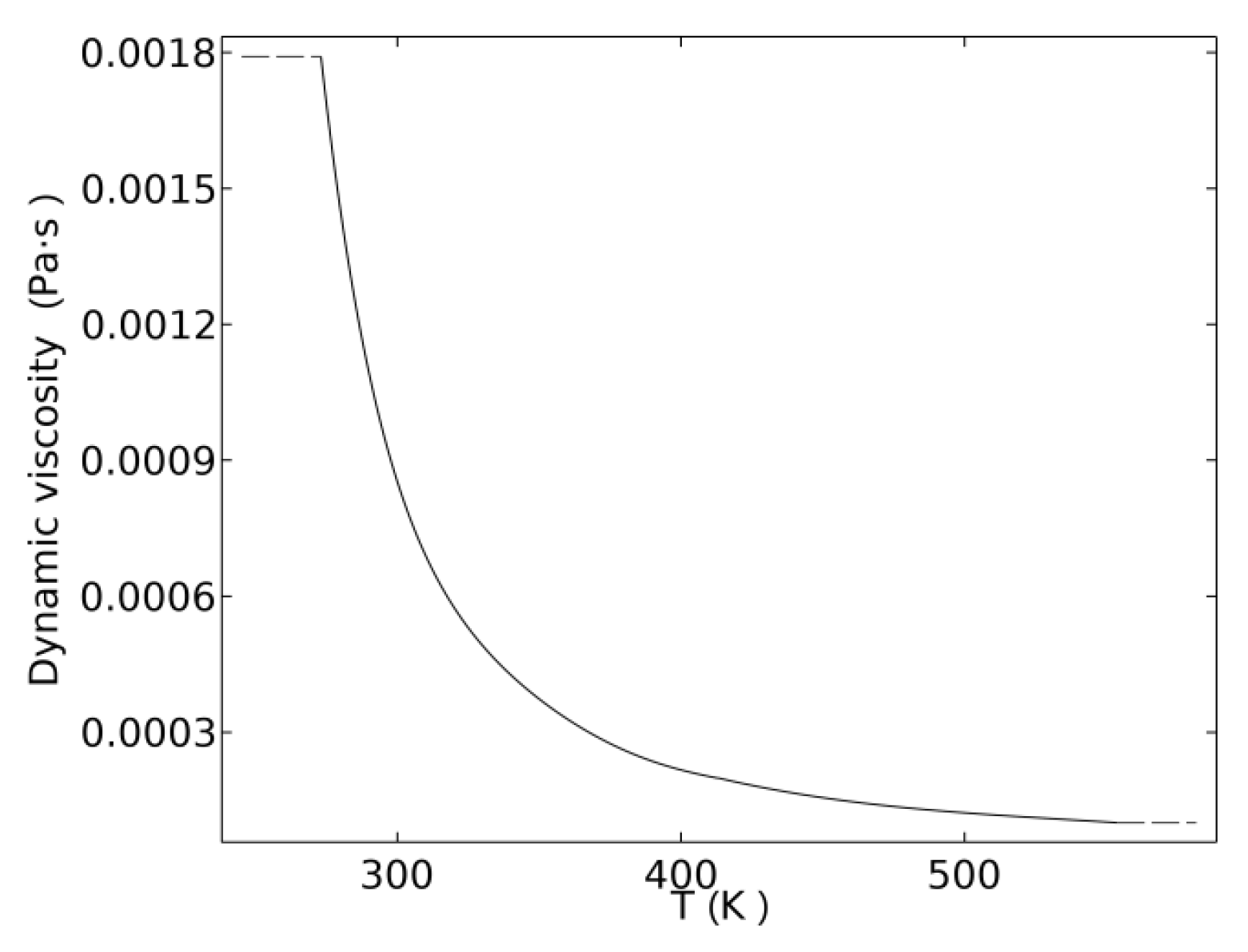
3.2.3. Influence of Temperature on the Dynamic Viscosity of Fluid
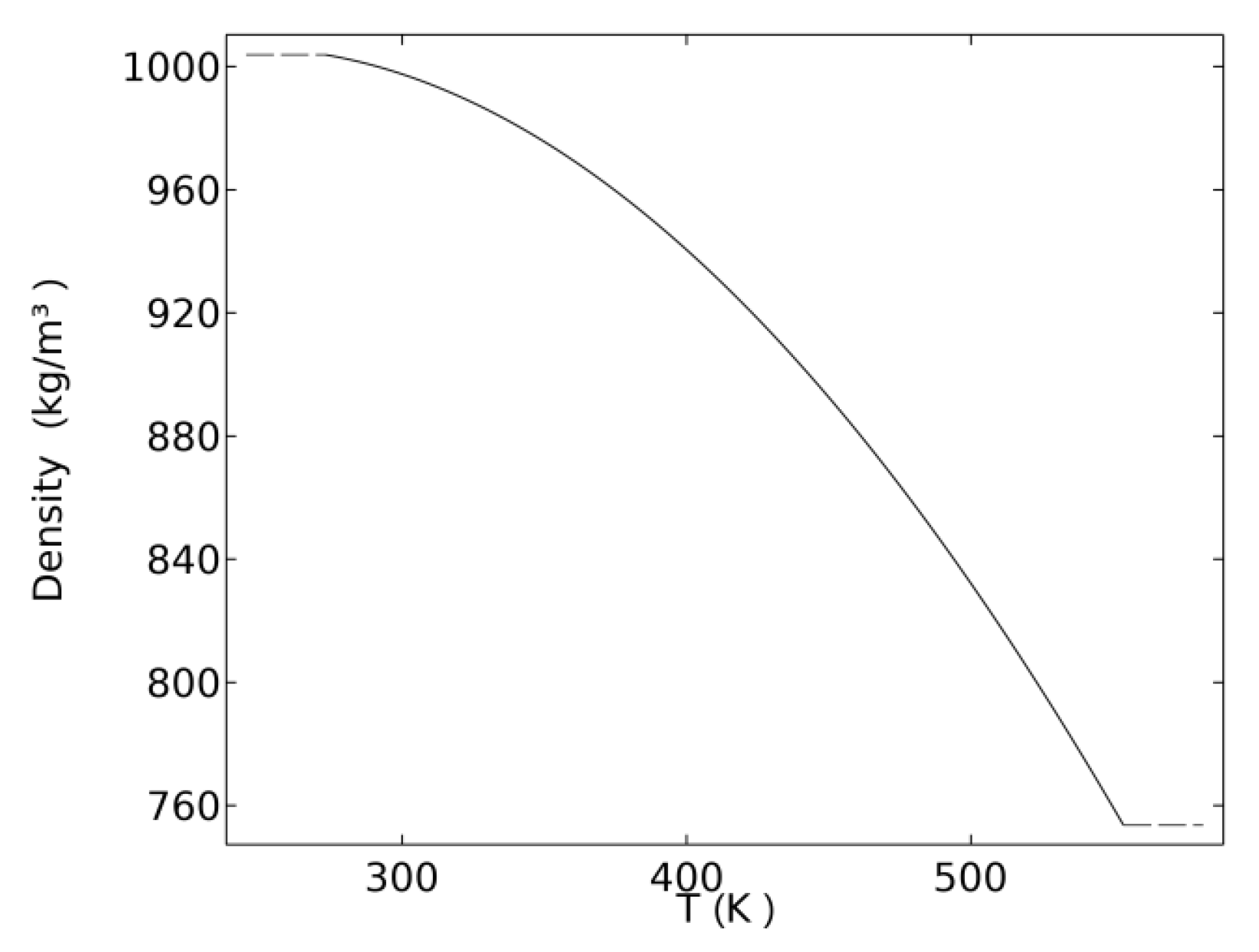
3.2.4. Influence of Temperature on the Density of Fluid
3.3. Analysis of the Coupling Factors of Electromagnetic Field and Flow Field
4. The Establishment of Electromagnetic-Fluid-Thermal Coupling Model for IWM and Model Validity Verification
4.1. The Establishment of the Finite Element Model of IWM
4.2. Determination of Boundary Conditions and Material Properties of IWM
4.2.1. Determination of Material Properties of IWM
4.2.2. Determination of Boundary Conditions of IWM
4.3. Grid Division of IWM
4.4. Model Validity Verification
4.5. Three-Field Coupling Calculation Method
5. Analysis of Electromagnetic-Heat-Flow Coupling, Based on Working Conditions
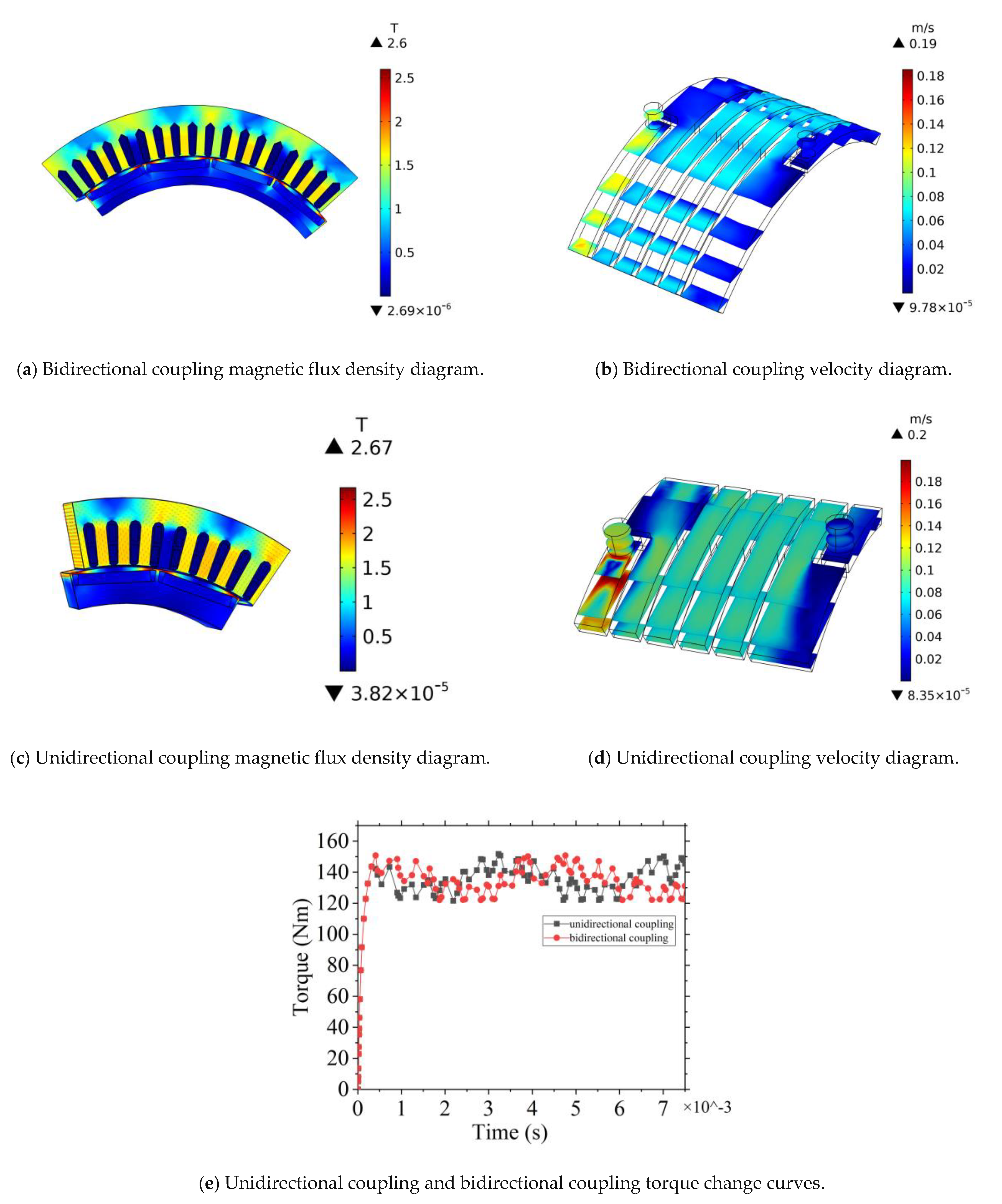
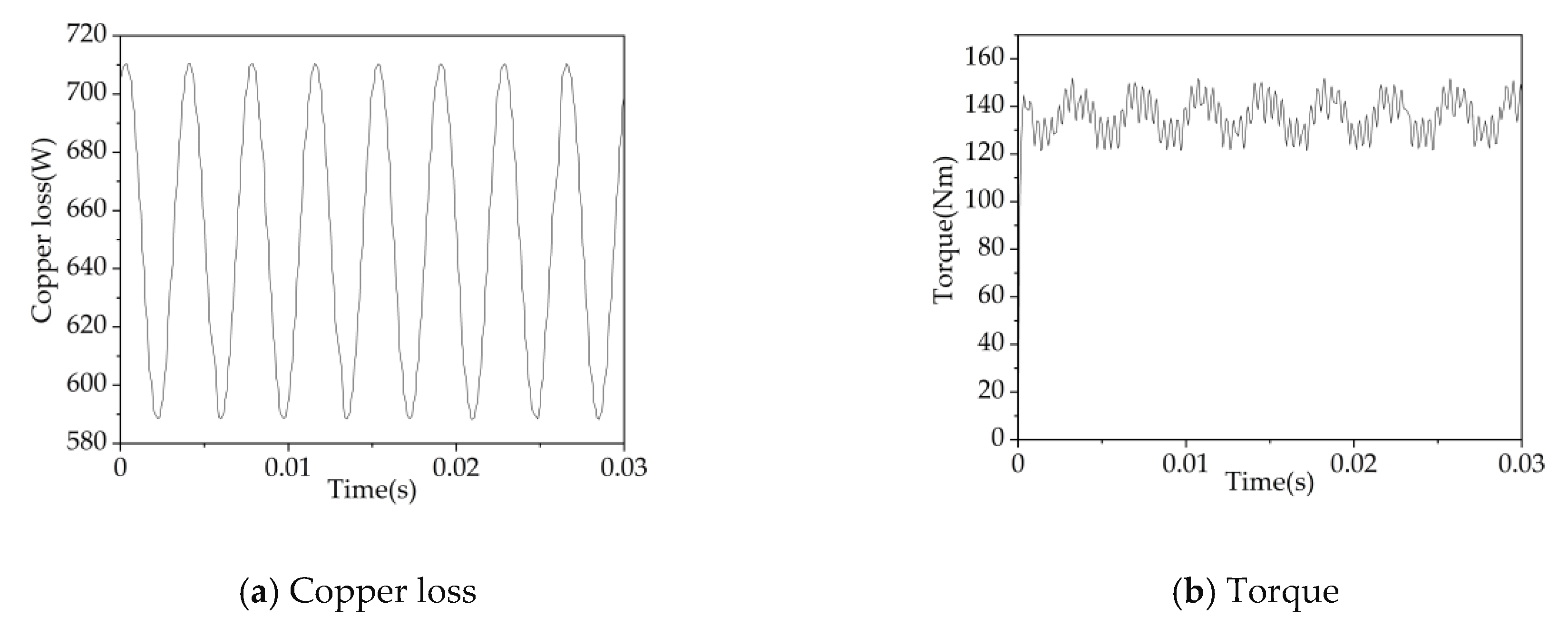
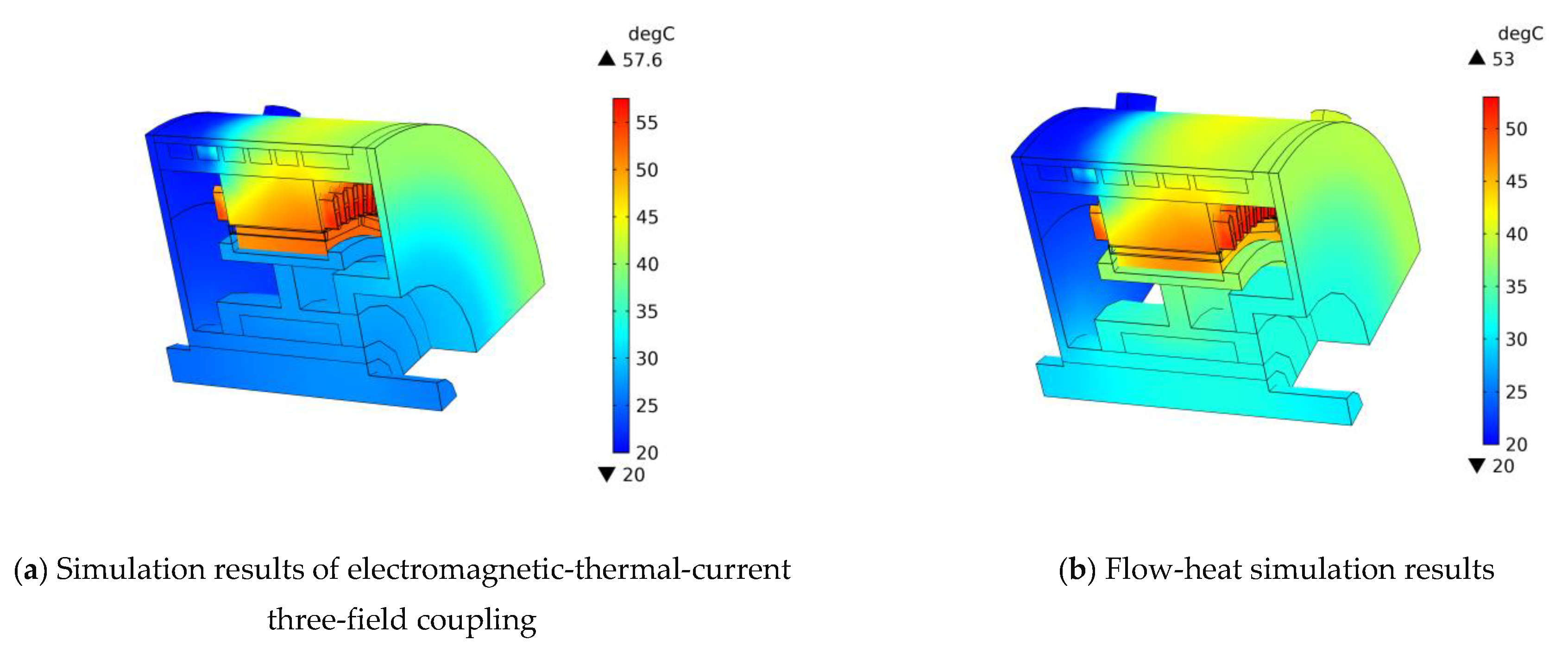
5.1. Comparison and Analysis of the Simulation Results of Unidirectional Coupling and Bidirectional Coupling
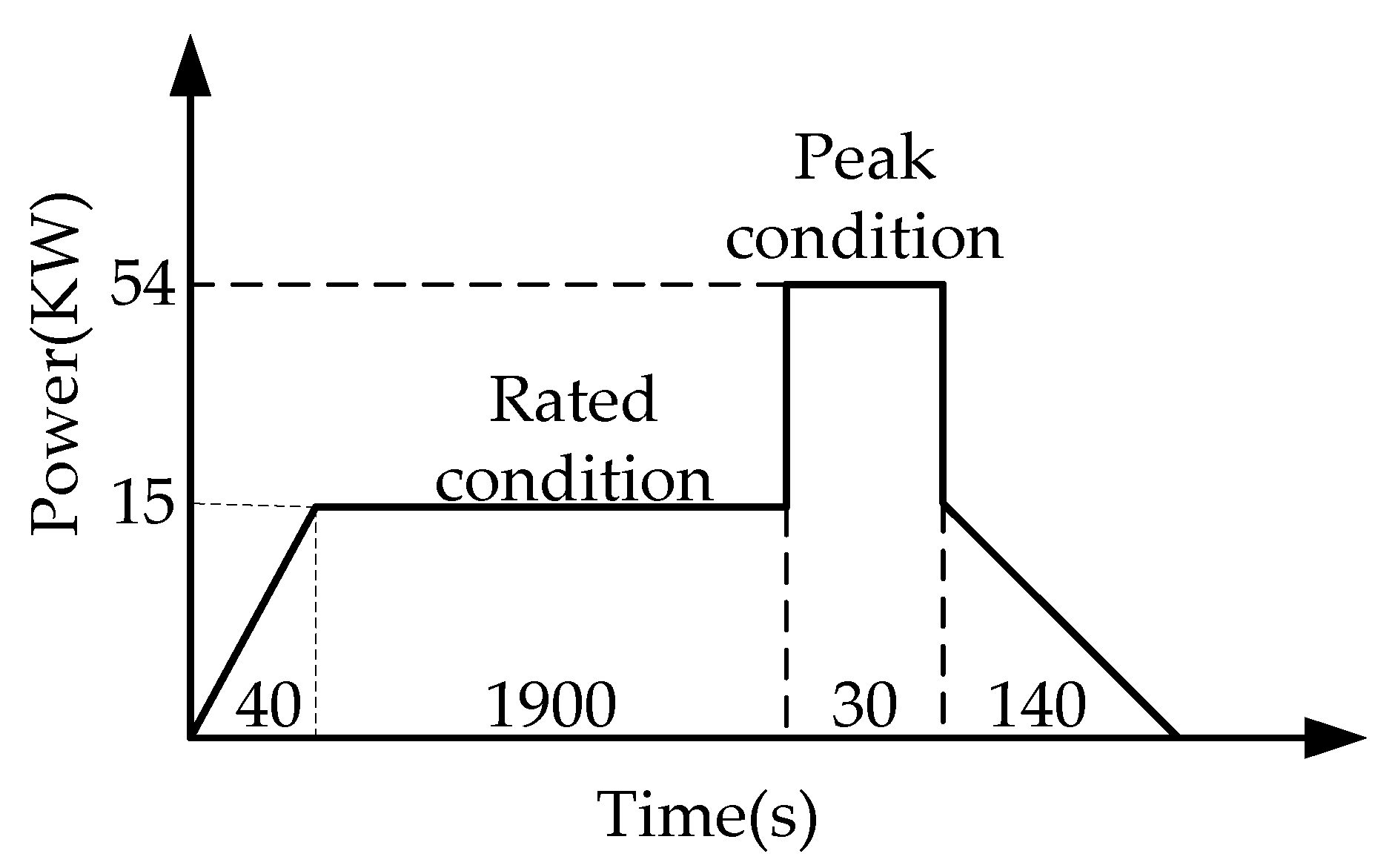
5.2. Vehicle Working Condition Setting
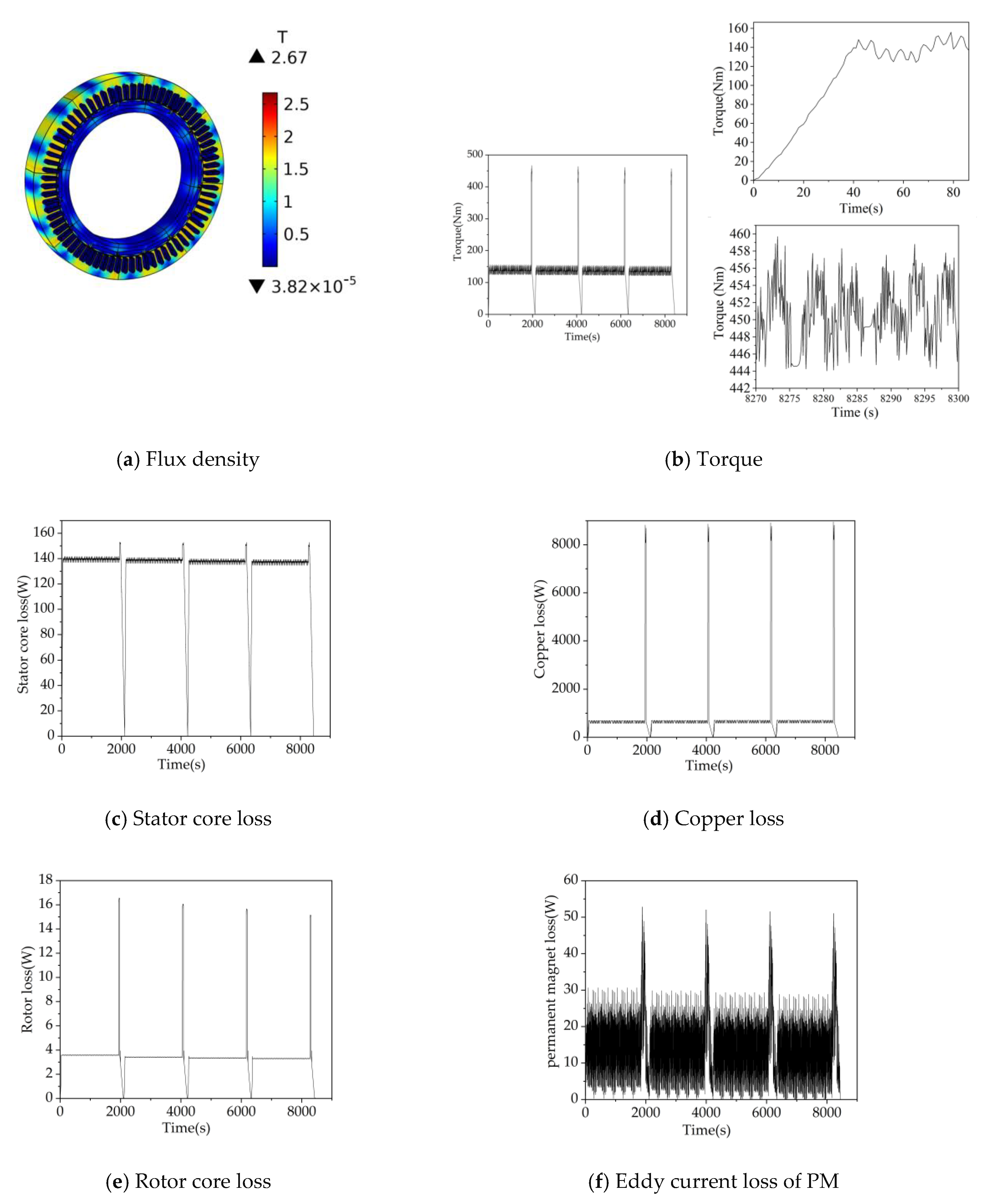
5.3. Analysis of Electromagnetic Field Simulation Results of IWM
5.4. Analysis of Temperature Field Simulation Results of IWM
5.5. Analysis of Flow Field Simulation Results of IWM
5.6. Variation of Maximum Temperature of IWM at Different Flow Rates
6. Results
Author Contributions
Funding
Conflicts of Interest
References
- Shanlin, J. High-Speed Permanent Magnet Synchronous Motor Loss Analysis and Temperature Field Calculation. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2010. [Google Scholar]
- Driesen, J.; Paner, U.; Belmans, R.; Hameyer, K. Transient coupled magnetic thermal analysis of a permanent magnet synchronous electrical vehicle motor. In Proceedings of the International Conference on Electrical Machines (ICEM 2000), Espoo, Finland, 28–30 August 2000; pp. 343–347. [Google Scholar]
- Alberti, L.; Bianchi, N. A Coupled Thermal-Electromagnetic Analysis for a Rapid and Accurate Prediction of IM Performance. IEEE Trans. Ind. Electron. 2008, 55, 3575–3582. [Google Scholar] [CrossRef]
- Mezani, S.; Takorabet, N.; Laporte, B. A Combined Electromagnetic and Thermal Analysis of Induction Motors. IEEE Trans. Magnet. 2005, 41, 1572–1575. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, W.; Huang, S.; Guo, J. Heat transfer simulation of high density permanent magnet motor for vehicles based on fluid-solid coupling method. Electr. Mach. Control Appl. 2012, 8, 1–5. [Google Scholar]
- Wang, X.; Jia, Z.; Gao, P. Coupled electromagnetic-thermal field analysis of out-rotor in-wheel motor. J. Tianjin Univ. Sci. Technol. 2014, 47, 898–902. [Google Scholar]
- Hatziathanassiou, V.; Xypteras, J.; Archontoulakis, G. Electrical-thermal coupled calculation of an asynchronous machine. Archiv ffir Elektrotechnik 1994, 77, 117–122. [Google Scholar] [CrossRef]
- Zhao, N.; Liu, W. Electromagnetic Field and Thermal Field Coupling Analysis of Brushless DC Motor. Small Spec. Electr. Mach. 2009, 3, 9–11. [Google Scholar]
- Gao, N.; Yu, L. Research on loss and electromagnetic heat coupling of high speed permanent magnet synchronous moor. In Proceedings of the 2013 IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 4–7 August 2013. [Google Scholar]
- Zhang, M.; Weiguo, L. Transient Coupled Electro-magnetic Thermal Analysis of a Permanent Magnet Brushless DC Motor. In Proceedings of the 2010 International Conference on Computer, Mechatronics, Control and Electronic Engineering, Changchun, China, 24–26 August 2010. [Google Scholar]
- Xiaowei, W.; Tiecai, L. A 3-D Electromagnetic Thermal Coupled Analysis of Permanent Magnet Brushless. In Proceedings of the 2011 First International Conference on Instrumentation, Measurement, Computer, Communication and Control, Beijing, China, 21–23 October 2012. [Google Scholar]
- Zhang, L.; Li, C.; Wu, Y.; Zhang, K.; Shi, H. Hybrid Prediction Model of the Temperature Field of a Motorized Spindle. Appl. Sci. 2017, 7, 1091. [Google Scholar] [CrossRef]
- Park, J.B.; Moosavi, M.; Toliyat, H.A. Electromagnetic-Thermal Coupled Analysis Method for Interior PMSM. In Proceedings of the 2015 IEEE International Electric Machines & Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 10–13 May 2015; pp. 1209–1214. [Google Scholar]
- Karnavas, Y.L.; Chasiotis, I.D.; Peponakis, E.L. Cooling System Design and Thermal Analysis of an Electric Vehicle’s In-Wheel PMSM. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 1439–1445. [Google Scholar]
- Lamghari-Jamal, M.I.; Fouladgar, J.; Zaim, E.H.; Trichet, D. A Magneto-Thermal Study of a High-Speed Synchronous Reluctance Machine. IEEE Trans. Magn. 2006, 42, 1271–1274. [Google Scholar] [CrossRef]
- Li, J.Q.; Ma, S.L.; Li, H.M. Analysis and calculation on stator temperature field of turbo-generators based on couple physical field. J. North China Electric Power Univ. 2008, 35, 6–10. [Google Scholar]
- Ding, S.Y.; Ge, Y.Z.; Chen, W.J.; Xu, D.G.; Miao, L.J. Coupling calculation and analysis of Three-dimensional temperature field for doubly-fed wind generator. Electric Mach. Control 2012, 16, 83–88. [Google Scholar]
- Song, F. Research on Heating and Cooling System of Hub Motor Drive System. Master’s Thesis, Shandong University of Technology, Harbin, China, 2019. [Google Scholar]
- Yin, H. PMSM Loss Calculation and Temperature Field Analysis. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2015. [Google Scholar]
- Bertotti, G.; Boglietti, A.; Chiampi, M.; Chiarabaglio, D.; Fiorillo, F.; Lazzari, M. An Improved Estimation of Iron Losses in Rotating Electrical Machines. IEEE Trans. Magn. 1991, 27, 5007–5009. [Google Scholar] [CrossRef]
- Ping, C.; Renyuan, T.; Wenming, T.; Jianguo, J.; Qingliang, D. Permanent magnet eddy current loss and its influence of high power density permanent magnet synchronous motor. Trans. China Electrotech. Soc. 2015, 30, 1–9. [Google Scholar]
- Lim, D.H.; Kim, S.C. Thermal performance of oil spray cooling system for in-wheel motor in electric vehicles. Appl. Therm. Eng. 2014, 63, 577–587. [Google Scholar] [CrossRef]
- Chen, W. Desigh and Temperature Analysis of Permanent Magnet Synchronous Motor for Electric Vehicles. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2013. [Google Scholar]
- Tang, R. Modern Permanent Magnet Machines; China Machine Press: Beijing, China, 2015. [Google Scholar]
- Yang, S.; Tao, W. Heat Transfer; Higher Education Press: Beijing, China, 2006.
- Liu, Q.S.; Yan, P.F.; Yang, M.; Tan, Z.C.; Li, C.P.; Welz-Biermann, U. Dynamic viscosity and conductivity of ionic liquids. Acta Phys. Chim. Sin. 2011, 27, 2762–2766. [Google Scholar]
- Sun, J.X.; Sun, Y.X.; Wang, Y.B. Two—Dimensional steady temperature field analysis of interior permanent magnet synchronous motor. Small Special Electr. Mach. 2013, 41, 24–33. [Google Scholar]
- Pechánek, R.; Bouzek, L. Analyzing of Two Types Water Cooling ElectricMotors Using Computational Fluid Dynamics. In Proceedings of the 15th International Power Electronics and Motion Control Conference, Novi Sad, Serbia, 4–6 September 2012; pp. LS2e4-1–LS2e4-5. [Google Scholar]
- Wang, R.-J.; Heyns, G.C. Thermal Analysis of a Water-Cooled Interior Permanent Magnet Traction Machine. In Proceedings of the 2013 IEEE International Conference on Industrial Technology (ICIT), Cape Town, South Africa, 25–28 Febuary 2013; pp. 416–421. [Google Scholar]





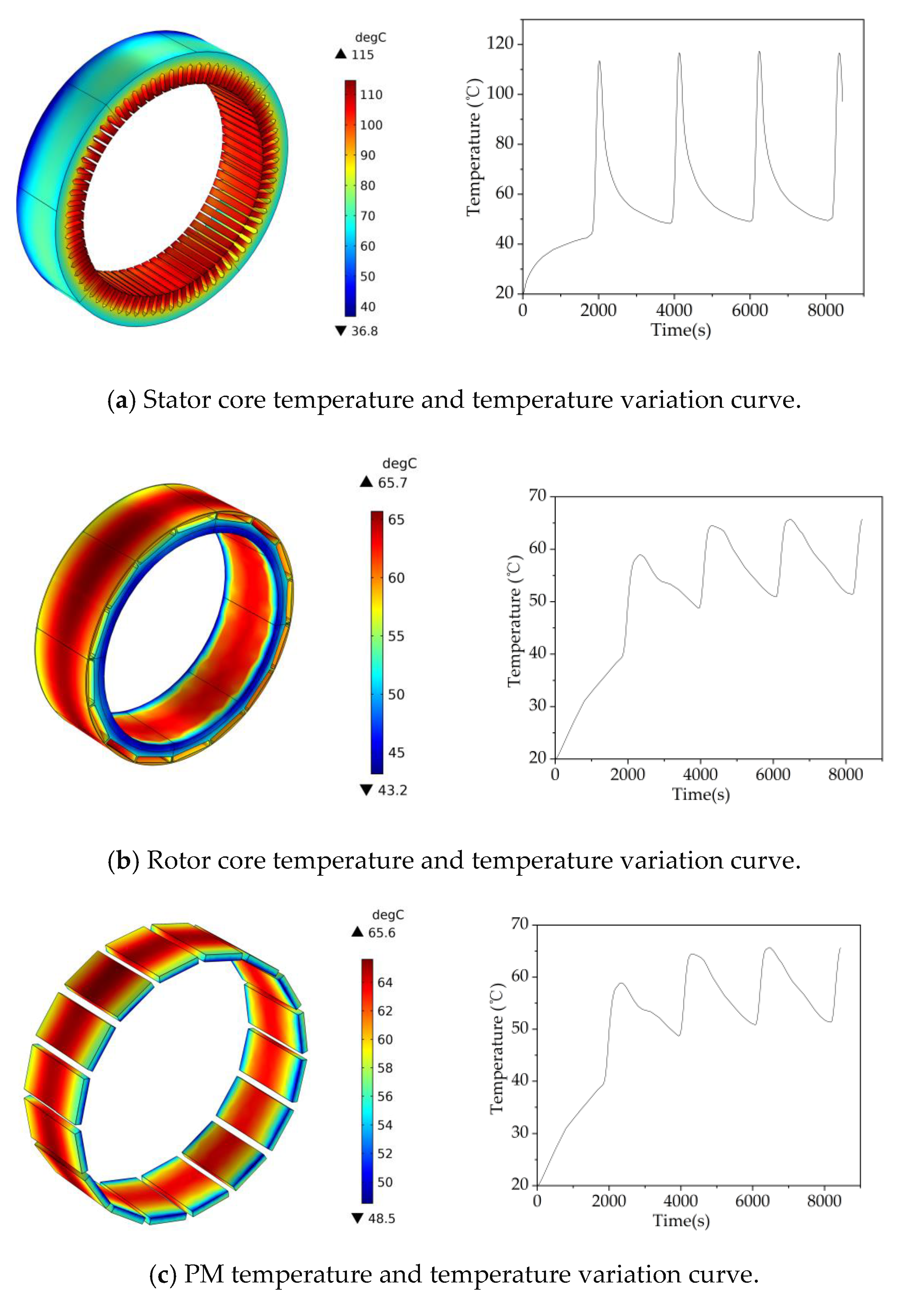
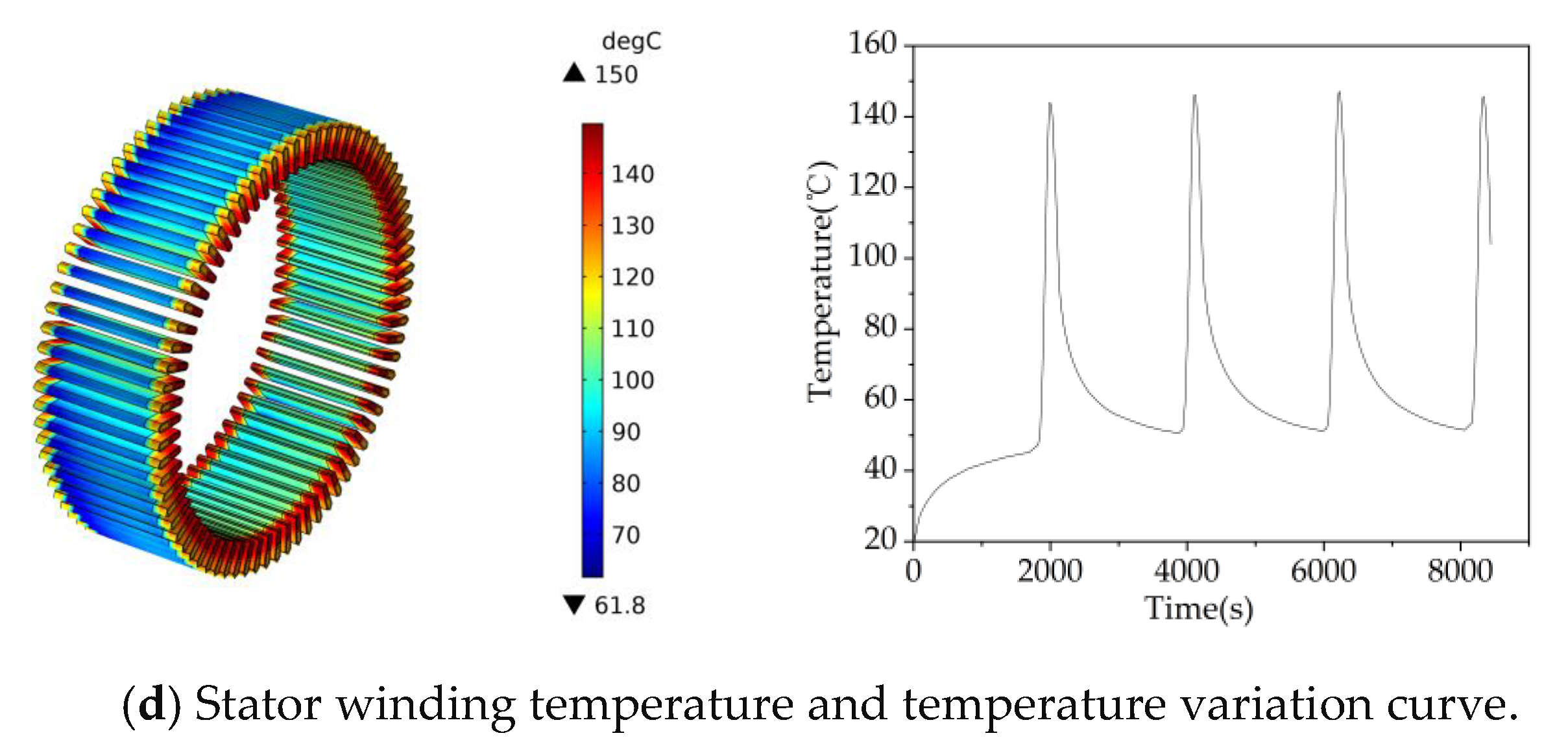
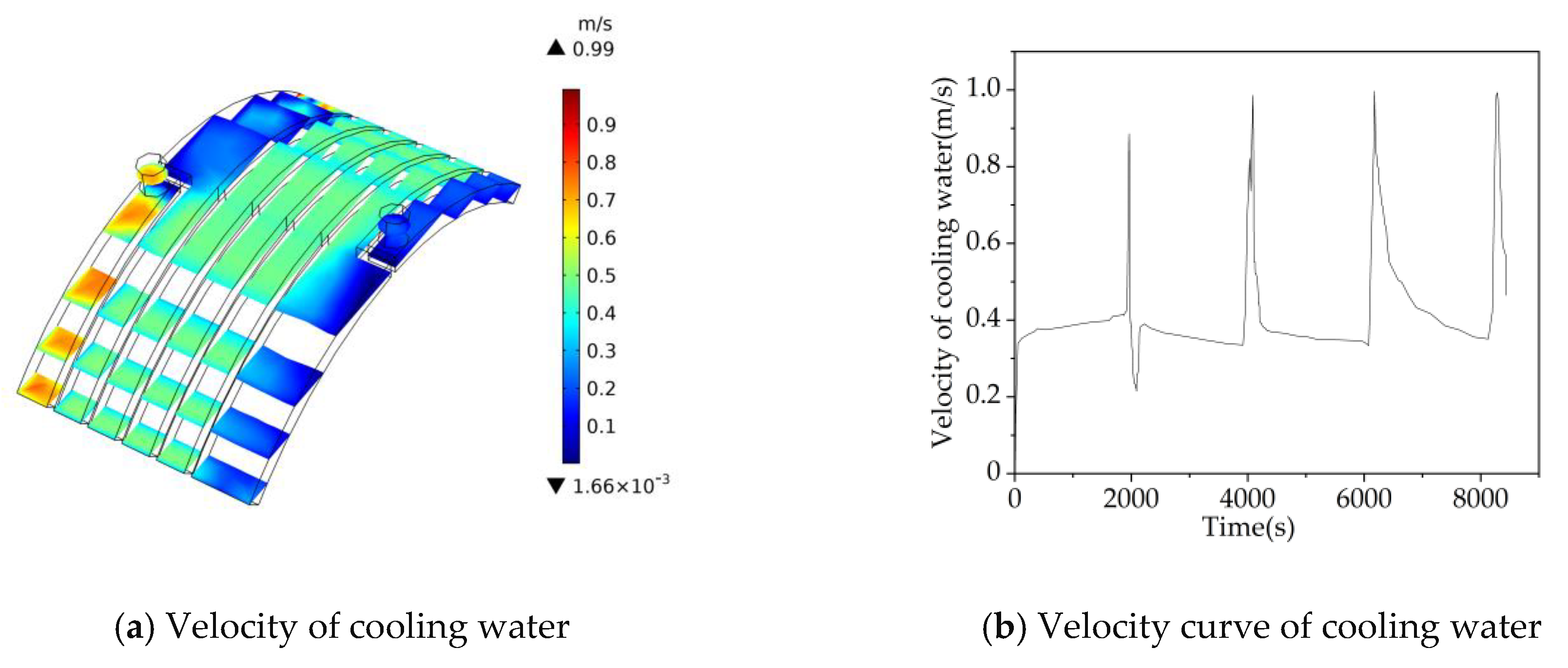
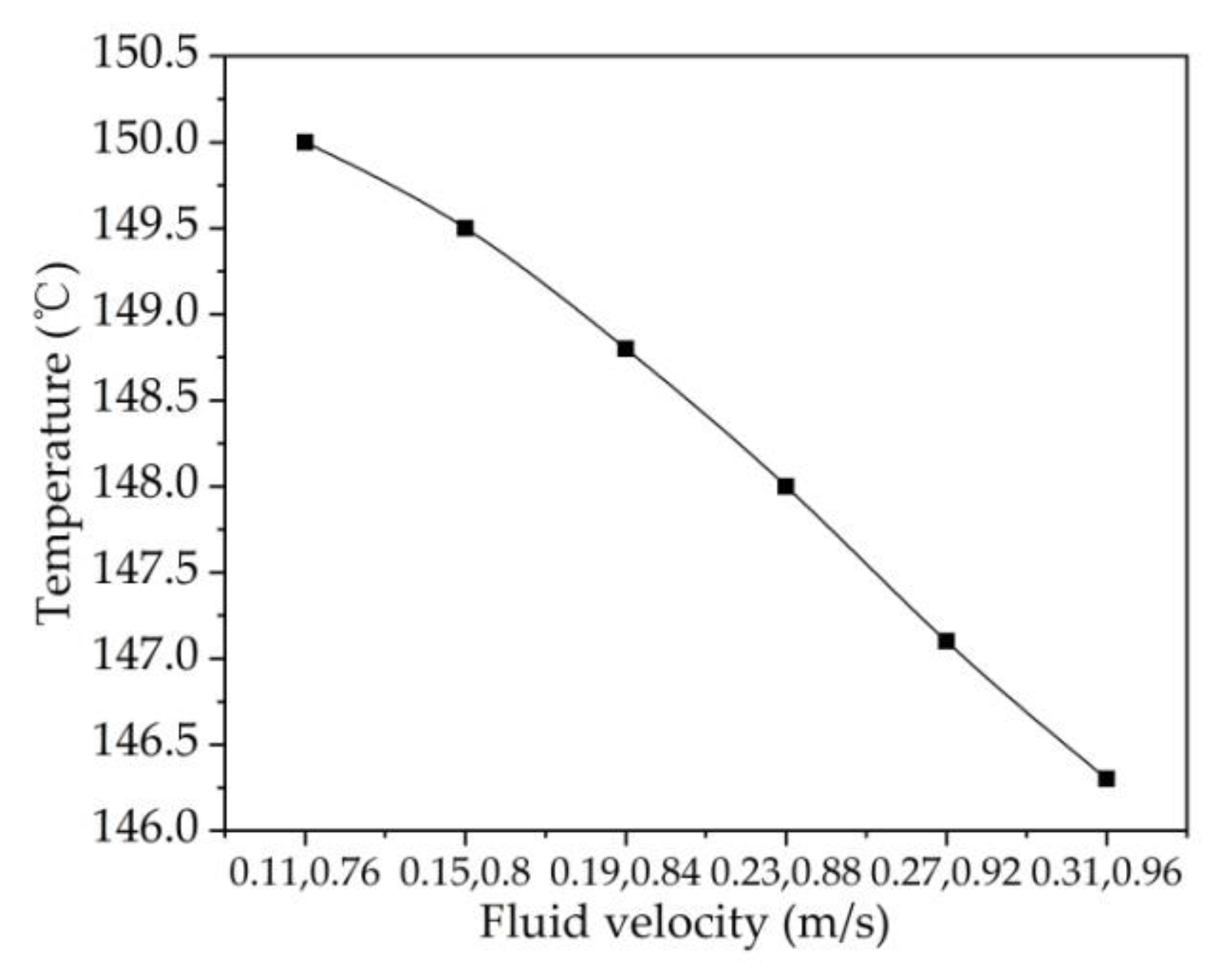
| Name | Numerical Value | Name | Numerical Value |
|---|---|---|---|
| Stator outer diameter | 310 mm | Rotor inner diameter | 200 mm |
| Stator inner diameter | 240 mm | Air gap length | 0.9 mm |
| Stator length | 69 mm | Rotor length | 71 mm |
| Diameter of inlet and outlet | 15 mm | Rib width | 4 mm |
| Channel cross section | 232 mm2 | Channel height | 10 mm |
| Name | Numerical Value | Name | Numerical Value |
|---|---|---|---|
| Rated power | 15 KW | Speak speed | 1100 rpm |
| Peak power | 54 KW | Rated speed | 1000 rpm |
| Component | Material | Thermal Conductivity | Density | Specific Heat Capacity |
|---|---|---|---|---|
| Stator and rotor core | DW465-50 | 40/40/0.95 | 7700 | 426 |
| Winding | copper | 379 | 8900 | 390 |
| PM | NdFeB | 6.16 | 7800 | 460 |
| Insulation layer | Insulation material | 0.3 | 1300 | 1340 |
| Housing | 45 steel | 50.2 | 7850 | 480 |
| Air | Air | 0.0267 | 1.29 | 1000 |
| Maximum Temperature (°C) | ||||
|---|---|---|---|---|
| Stator Core | Rotor Core | Winding | PM | |
| electromagnetic-heat-flow | 54.2 | 52.7 | 57.6 | 51.3 |
| flow-heat | 50.1 | 47.1 | 53 | 46.2 |
| Maximum Temperature (°C) | ||||
|---|---|---|---|---|
| Stator Core | Rotor Core | Winding | PM | |
| flow-heat coupling factors | 54.2 | 52.7 | 57.6 | 51.3 |
| without fluid-heat coupling factors | 52.1 | 50.7 | 55.1 | 50.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, H.; Tan, D.; Liu, S.; Yuan, M.; Zhao, C. Research on the Electromagnetic-Heat-Flow Coupled Modeling and Analysis for In-Wheel Motor. World Electr. Veh. J. 2020, 11, 29. https://doi.org/10.3390/wevj11020029
Xue H, Tan D, Liu S, Yuan M, Zhao C. Research on the Electromagnetic-Heat-Flow Coupled Modeling and Analysis for In-Wheel Motor. World Electric Vehicle Journal. 2020; 11(2):29. https://doi.org/10.3390/wevj11020029
Chicago/Turabian StyleXue, Haojie, Di Tan, Shuaishuai Liu, Meng Yuan, and Chunming Zhao. 2020. "Research on the Electromagnetic-Heat-Flow Coupled Modeling and Analysis for In-Wheel Motor" World Electric Vehicle Journal 11, no. 2: 29. https://doi.org/10.3390/wevj11020029
APA StyleXue, H., Tan, D., Liu, S., Yuan, M., & Zhao, C. (2020). Research on the Electromagnetic-Heat-Flow Coupled Modeling and Analysis for In-Wheel Motor. World Electric Vehicle Journal, 11(2), 29. https://doi.org/10.3390/wevj11020029






