Review on the State of Charge Estimation Methods for Electric Vehicle Battery
Abstract
:1. Introduction
2. The Definition of SOC
3. SOC Estimation Methods
3.1. Traditional Methods Based on Experiments
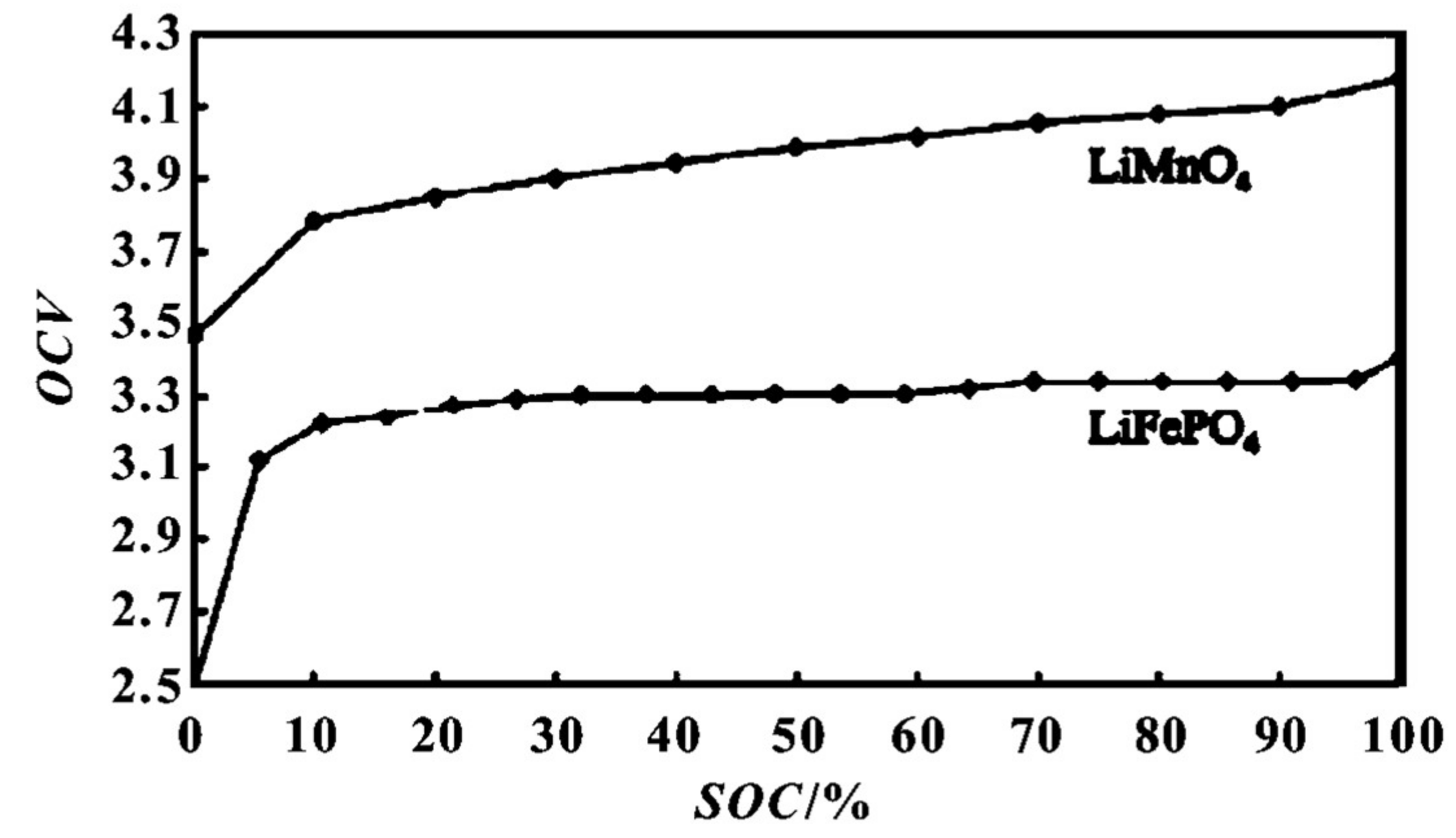
3.1.1. Open Circuit Voltage
3.1.2. Ampere-Hour Integral Method
3.1.3. Internal Resistance Method
3.1.4. Discharge Test Method
3.2. Modern Methods Based on Control Theory
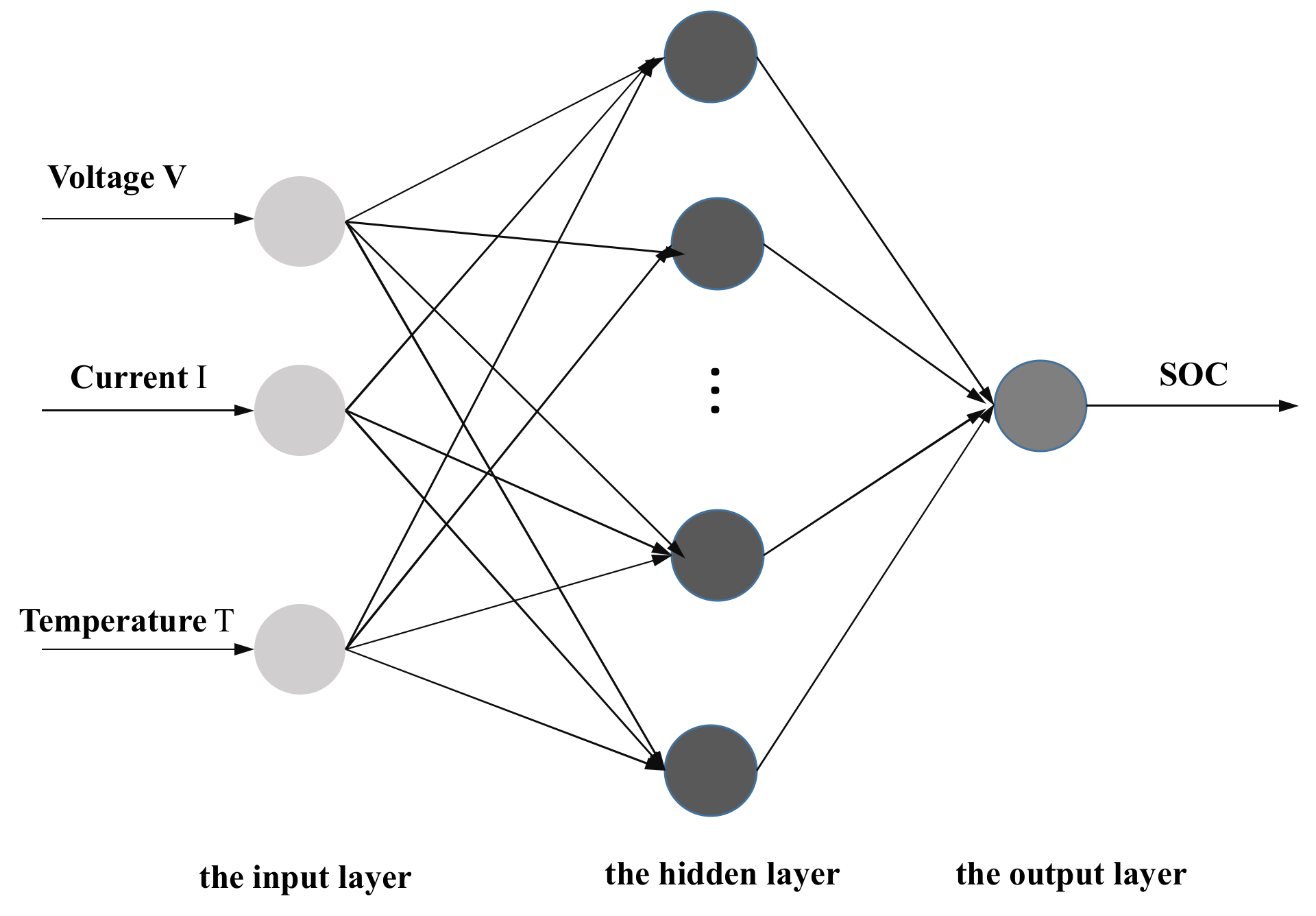
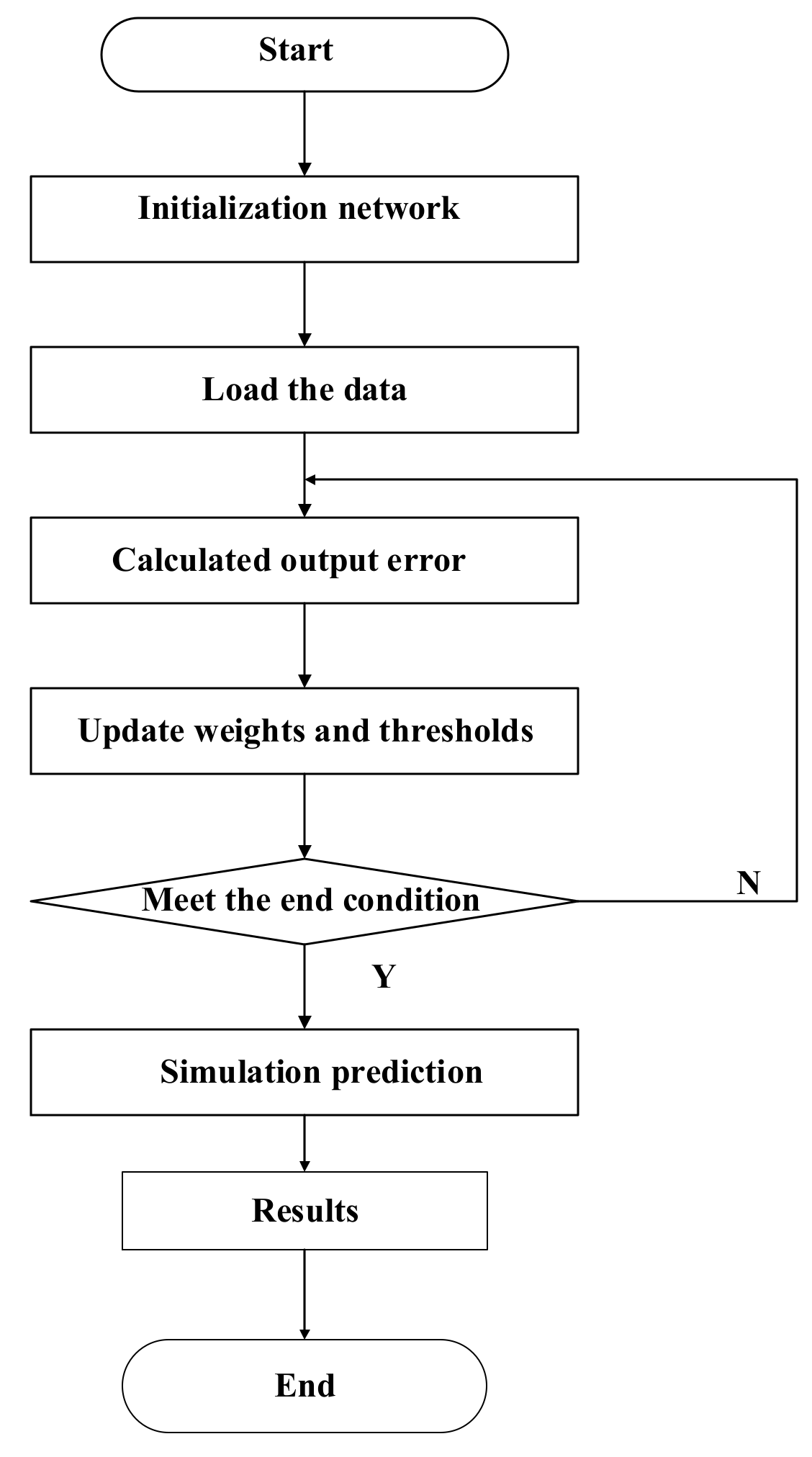
3.2.1. Neural Network Method
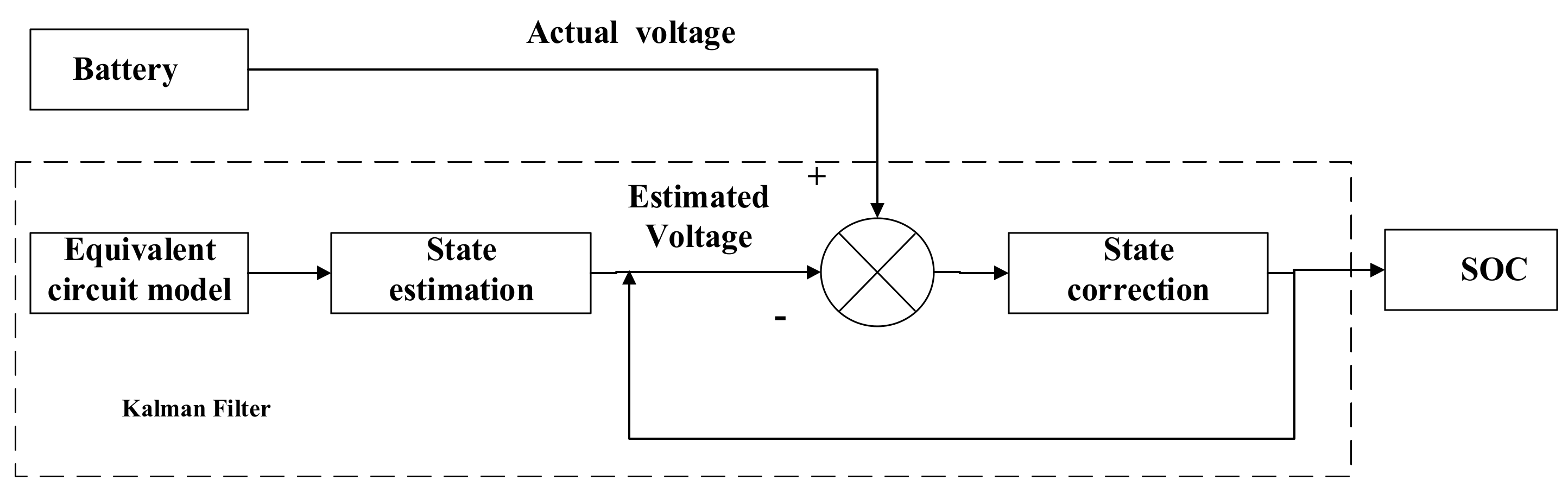
3.2.2. Kalman Filter Method
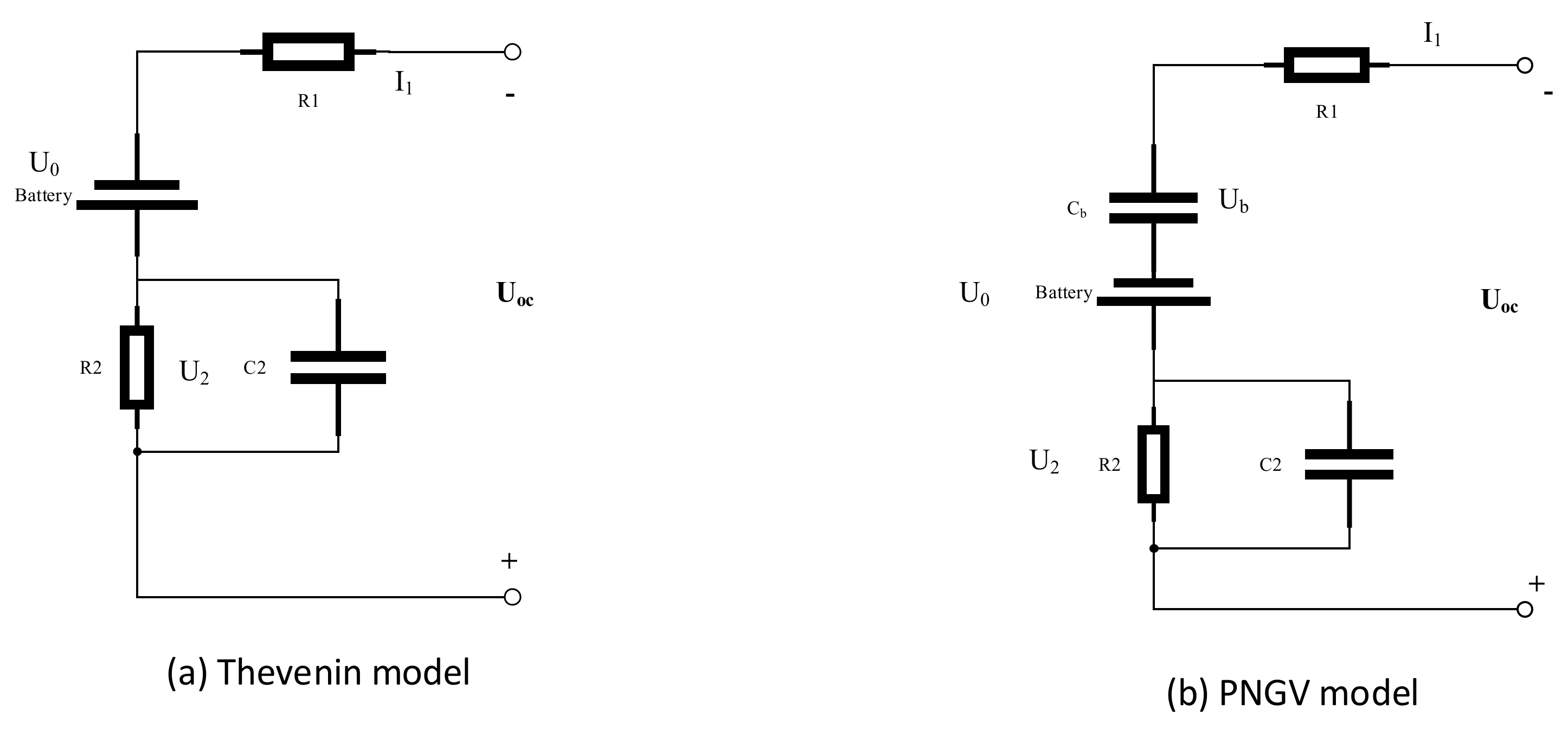
3.2.3. Linear Model Method
3.2.4. Particle Filter Algorithm
3.3. Other Methods Based on the Innovative Ideas
4. Conclusions
5. Current and Future Developments
- A rich database should be established to make the SOC estimation more reliable, which depends on a large number of experiments.
- It is important to improve the hardware technology, improve the accuracy of voltage and current parameters, and strive to ensure the accuracy of SOC.
- A more accurate battery with good dynamic characteristics and versatility model should be built to accurately describe the dynamic characteristics of the battery in use.
- We must carry on the effective synthesis of each kind of method, strives for the biggest degree to display respective superiority, promotes the strong point and avoids the weak point.
- Make full use of interdisciplinary advantages and transfer theoretical knowledge from other disciplines to the remaining electricity estimates.
- Establish theoretical methods with better dynamic adaptability and precision, and improve the processing methods and theoretical basis of nonlinear systems.
- Increase efforts to study more stable batteries, such as battery internal resistance and polarization problems.
Author Contributions
Funding
Conflicts of Interest
References
- Bilgin, B.; Magne, P.; Malysz, P.; Yang, Y.; Pantelic, V.; Preindl, M.; Korobkine, A.; Jiang, W.; Lawford, M.; Emadi, A. Making the case for electrified transportation. IEEE Trans. Transp. Electrif. 2015, 1, 4–17. [Google Scholar] [CrossRef]
- Hu, X.; Zou, C.; Zhang, C.; Li, Y. Technological developments in batteries: A survey of principal roles, types, and management needs. IEEE Power Energy Mag. 2017, 15, 20–31. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, L.Y.; Li, X.; Chen, W.; Yin, G.G.; Jiang, J. Robust and adaptive estimation of state of charge for lithium-ion batteries. IEEE Trans. Ind. Electron. 2015, 62, 4948–4957. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.E.; Yang, Y. Advanced machine learning approach for lithium-ion battery state estimation in electric vehicles. IEEE Trans. Transp. Electrif. 2015, 2, 140–149. [Google Scholar] [CrossRef]
- Xiong, R.; Zhang, Y.; He, H.; Zhou, X.; Pecht, M.G. A double-scale, particle-filtering, energy state prediction algorithm for lithium-ion batteries. IEEE Trans. Ind. Electron. 2017, 65, 1526–1538. [Google Scholar] [CrossRef]
- Yang, R.; Xiong, R.; He, H.; Mu, H.; Wang, C. A novel method on estimating the degradation and state of charge of lithium-ion batteries used for electrical vehicles. Appl. Energy 2017, 207, 336–345. [Google Scholar] [CrossRef]
- Castano, S.; Serrano-Jimenez, D.; Sanz, J. BMS influence on Li-ion packs characterization and modeling. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016. [Google Scholar]
- Hu, X.; Xiong, R.; Egardt, B. Model-based dynamic power assessment of lithium-ion batteries considering different operating conditions. IEEE Trans. Ind. Inform. 2013, 10, 1948–1959. [Google Scholar] [CrossRef]
- Peng, S.; Chen, C.; Shi, H.; Yao, Z. State of charge estimation of battery energy storage systems based on adaptive unscented Kalman filter with a noise statistics estimator. IEEE Access 2017, 5, 13202–13212. [Google Scholar] [CrossRef]
- Chaoui, H.; Golbon, N.; Hmouz, I.; Souissi, R.; Tahar, S. Lyapunov-based adaptive state of charge and state of health estimation for lithium-ion batteries. IEEE Trans. Ind. Electron. 2014, 62, 1610–1618. [Google Scholar] [CrossRef]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Bhatt, D.K.; Darieby, M.E. An Assessment of Batteries form Battery Electric Vehicle Perspectives. In Proceedings of the 2018 IEEE International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 11–13 August 2018. [Google Scholar]
- Sada, T. Battery Diagnosis Method, Battery Diagnosis Program, Battery Management Apparatus, and Power Storage System. U.S. Patent 20190170831A1, 6 June 2019. [Google Scholar]
- Meng, J.; Luo, G.; Breaz, E.; Gao, F. A robust battery state-of-charge estimation method for embedded hybrid energy system. In Proceedings of the IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society, Okohama, Japan, 9–12 November 2015. [Google Scholar]
- Sun, F.; Xiong, R.; He, H. A systematic state-of-charge estimation framework for multi-cell battery pack in electric vehicles using bias correction technique. Appl. Energy 2016, 162, 1399–1409. [Google Scholar] [CrossRef]
- Marcial-Simon, E.; Mehlhorn, R. Method for Controlling Electrical Charging of a Group of Vehicles. U.S. Patent 20190168633A1, 6 June 2019. [Google Scholar]
- VanBlon, R.S.; Peterson, N.J.; Mese, J.C.; Weksler, A.S. Systems and methods to determine time at which battery is to be charged. U.S. Patent 20190148960A1, 16 May 2019. [Google Scholar]
- Cai, C.; Du, D.; Liu, Z.; Ge, J. State-of-charge (SOC) estimation of high power Ni-MH rechargeable battery with artificial neural network. In Proceedings of the 9th International Conference on Neural Information Processing, Singapore, 18–22 November 2002. [Google Scholar]
- Lillehei, C.W.; Cruz, A.B.; Johnsrude, I.; Sellers, R.D. A new method of assessing the state of charge of implanted cardiac pacemaker batteries. Am. J. Cardiol. 1965, 16, 717–721. [Google Scholar] [CrossRef]
- Dincer, I.; Hamut, H.S.; Javani, N. Thermal Management of Electric Vehicle Battery Systems; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Andrea, D.; Li, J. Battery Management Systems for Large Lit-Hium-Lon Battery Packs, 1st ed.; Mechanical Industry Press: Beijing, China, 2016. [Google Scholar]
- Rahn, C.D.; Wang, C.-Y. Battery Systems Engineering; Mechanical Industry Press: Beijing, China, 2018. [Google Scholar]
- Xiaojun, T. Electric vehicle Battery Management System Design; Sun Yat-sen University Press: Guangzhou, China, 2011. [Google Scholar]
- Fang, W.; Jun, X. Design and Manufacture of Battery Management System for Electric Vehicle, 2nd ed.; Science Press: Beijing, China, 2017. [Google Scholar]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Gholizadeh, M.; Salmasi, F.R. Estimation of state of charge, unknown nonlinearities, and state of health of a lithium-ion battery based on a comprehensive unobservable model. IEEE Trans. Ind. Electron. 2013, 61, 1335–1344. [Google Scholar] [CrossRef]
- Weng, C.; Sun, J.; Peng, H. A unified open-circuit-voltage model of lithium-ion batteries for state-of-charge estimation and state-of-health monitoring. J. Power Sources 2014, 258, 228–237. [Google Scholar] [CrossRef]
- Pei, L.; Lu, R.; Zhu, C. Relaxation model of the open-circuit voltage for state-of-charge estimation in lithium-ion batteries. Iet Electr. Syst. Transp. 2013, 3, 112–117. [Google Scholar] [CrossRef]
- Lin, C.; Yu, Q.; Xiong, R.; Wang, L.Y. A study on the impact of open circuit voltage tests on state of charge estimation for lithium-ion batteries. Appl. Energy 2017, 205, 892–902. [Google Scholar] [CrossRef]
- Wentao, W.; Dayang, Z.; Wang, L. Systems and Methods for Battery Management. U.S. Patent 20190148951A1, 16 May 2019. [Google Scholar]
- Tkachenko, O.; Sherstyuk, M. Battery Charging with Charging Parameters Sweep. U.S. Patent 20190081486A1, 14 March 2019. [Google Scholar]
- Farmann, A.; Sauer, D.U. A study on the dependency of the open-circuit voltage on temperature and actual aging state of lithium-ion batteries. J. Power Sources 2017, 347, 1–13. [Google Scholar] [CrossRef]
- Zhang, B.; Lu, C.; Liu, J. Combination Algorithm for State of Charge Estimation. In Proceedings of the 2013 International Conference on Communication Systems and Network Technologies, Gwalior, India, 6–8 April 2013. [Google Scholar]
- Ghantous, D.; Berkowitz, F.; Maluf, N. Method and Circuitry to Calculate the State of Charge of a Battery/Cell. U.S. Patent 8791669B2, 29 July 2014. [Google Scholar]
- Li, X.; Choe, S.-Y. State-of-charge (SOC) estimation based on a reduced order electrochemical thermal model and extended Kalman filter. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013. [Google Scholar]
- Ng, K.S.; Moo, C.-S.; Chen, Y.-P.; Hsieh, Y.-C. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Wenzel, M.J.; Drees, K.H.; Elbsat, M.N. Electrical Energy Storage System with Variable State-of-Charge Frequency Response Optimization. U.S. Patent 10186889B2, 22 January 2019. [Google Scholar]
- Liu, G.; YANG, F.; Zhang, W. Storage battery state of charge (SOC) Estimation Method Based on Extended Kalman Filtering (EKF). CN105093128A, 25 November 2015. [Google Scholar]
- Xu, J.; Ying, Z.; Yu, Z.; Jiuhe, C. Lithium-Ion Battery SOC Estimation Based on Ahh-total Integration Method. Appl. Technol. 2018, 18, 9–11. [Google Scholar]
- Tingting, Y.; Jie, Z.; Linkai, Z.; Yuhua, Z. SOC Estimation and Simulation of Lithium Battery Based on Improved Ampere-hour Integral Method. Energy Sav. New Energy 2018, 6, 58–60. [Google Scholar]
- Kim, J.; Shin, J.; Jeon, C.; Cho, B. High accuracy state-of-charge estimation of Li-Ion battery pack based on screening process. In Proceedings of the 2011 Twenty-Sixth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Fort Worth, TX, USA, 6–11 March 2011. [Google Scholar]
- Windarko, N.A.; Choi, J.; Chung, G.-B. SOC estimation of LiPB batteries using extended Kalman filter based on high accuracy electrical model. In Proceedings of the 8th International Conference on Power Electronics-ECCE Asia, Jeju, Korea, 30 May–3 June 2011. [Google Scholar]
- Yang, W.-R.; Zhu, S.-F.; Chen, Y.; Zhu, J.-B.; Xue, L.-S.; Center, M.R. SOC estimation of lithium-ion battery based on improved ampere-hour integral method. Chin. J. Power Sources 2018, 6, 183–184. [Google Scholar]
- Chen, L.; Lü, Z.; Lin, W.; Li, J.; Pan, H. A new state-of-health estimation method for lithium-ion batteries through the intrinsic relationship between ohmic internal resistance and capacity. Measurement 2018, 116, 586–595. [Google Scholar] [CrossRef]
- Perkins, W.P.; Miller, K.J.; Martin, D.R.; Burke, S.R. Battery State of Charge Target Based on Predicted Regenerative Energy. U.S. Patent 9815373B2, 14 November 2017. [Google Scholar]
- Ping, S.; Lu, L.; Gao, M.; Dong, R.; Xuning, S.F. Combined Estimation Method for Lithium Ion Battery State of Charge, State of Health and State of Function. CN105301509A, 3 February 2016. [Google Scholar]
- Peishan, Y.; Yin, B. Analysis of SOC Estimation Algorithm for Electric Vehicle Power Battery. Automot. Pract. Technol. 2019, 15, 15–17. [Google Scholar]
- Hongwei, L.; Caiying, S. Methods of State of Charge Estimation of Electric Vehicle. Automot. Eng. 2017, 31–33. [Google Scholar]
- Zhou, L. Power Battery SOC Algorithm and Its Information Modeling. Electron. Technol. Softw. Eng. 2018, 88. [Google Scholar]
- Yanhong, Y. Estimation Method and Apparatus for State-of-Charge Value of Battery. WO2017016385A1, 2 February 2017. [Google Scholar]
- Anand, I.; Mathur, B. State of charge estimation of lead acid batteries using neural networks. In Proceedings of the 2013 International Conference on Circuits, Power and Computing Technologies (ICCPCT), Nagercoil, India, 20–21 March 2013. [Google Scholar]
- Chen, J.; Longhui, W.; Wu, C.; Yiheng, Z. Method for Estimating State of Charge of Battery. WO Patent 2019052015A1, 21 March 2019. [Google Scholar]
- Lipu, M.S.H.; Hannan, M.A.; Hussain, A.; Saad, M.H.; Ayob, A.; Blaabjerg, F. State of charge estimation for lithium-ion battery using recurrent NARX neural network model based lighting search algorithm. IEEE Access 2018, 6, 28150–28161. [Google Scholar] [CrossRef]
- Xia, B.; Cui, D.; Sun, Z.; Lao, Z.; Zhang, R.; Wang, W.; Sun, W.; Lai, Y.; Wang, M. State of charge estimation of lithium-ion batteries using optimized Levenberg-Marquardt wavelet neural network. Energy 2018, 153, 694–705. [Google Scholar] [CrossRef]
- Wu, B.-H.; He, J.-M. The trend analysis of China’s stock market based on fractal method and BP neural network model. In Proceedings of the 2014 International Conference on Management Science & Engineering 21th Annual Conference Proceedings, Helsinki, Finland, 17–19 August 2014. [Google Scholar]
- Dong, C.; Wang, G. Estimation of power battery SOC based on improved BP neural network. In Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014. [Google Scholar]
- Sun, B.; Wang, L. The SOC estimation of NIMH battery pack for HEV based on BP neural network. In Proceedings of the 2009 International Workshop on Intelligent Systems and Applications, Wuhan, China, 23–24 May 2009. [Google Scholar]
- Hiwa, S. Secondary Battery state-of-Charge Estimating Device and Secondary Battery State-of-Charge Estimating Method. WO Patent 2016129248A1, 18 August 2016. [Google Scholar]
- Hannan, M.A.; Lipu, M.H.; Hussain, A.; Mohamed, A. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Takechi, H. State-of-Charge Calculation Device, Computer Program, and State-of-Charge Calculation Method. WO Patent 2017183241A1, 26 October 2017. [Google Scholar]
- Zhang, X.; Wang, Y.; Yang, D.; Chen, Z. An on-line estimation of battery pack parameters and state-of-charge using dual filters based on pack model. Energy 2016, 115, 219–229. [Google Scholar] [CrossRef]
- Liu, X.L.; Cheng, Z.M.; Yi, F.Y.; Qiu, T.Y. SOC calculation method based on extended Kalman filter of power battery for electric vehicle. In Proceedings of the 2017 12th International Conference on Intelligent Systems and Knowledge Engineering (ISKE), Nanjing, China, 24–26 November 2017. [Google Scholar]
- Jokić, Ž.Z.; Krstajić, B. State-of-charge estimation of lithium-ion batteries using extended Kalman filter and unscented Kalman filter. In Proceedings of the 2018 23rd International Scientific-Professional Conference on Information Technology (IT), Zabljak, Montenegro, 19–24 February 2018. [Google Scholar]
- Yang, Y.; Cui, N.; Wang, C.; Liu, M.; Gao, R. SOC estimation of lithium-ion battery based on new adaptive fading extended Kalman filter. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017. [Google Scholar]
- Imbomi Device and Method for Estimating State-of-Charge of Battery. WO Patent 2019050330A1, 14 March 2019.
- Cheng, S.; Zhang, Y.; Cheng, X.-F.; Zhang, X. State estimation using physics-based equivalent circuit models of a Li-ion cell and Kalman filter. In Proceedings of the IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017. [Google Scholar]
- Liu, C.; Liu, W.; Wang, L.; Hu, G.; Ma, L.; Ren, B. A new method of modeling and state of charge estimation of the battery. J. Power Sources 2016, 320, 1–12. [Google Scholar] [CrossRef]
- Zou, Y.; Hu, X.; Ma, H.; Li, S.E. Combined state of charge and state of health estimation over lithium-ion battery cell cycle lifespan for electric vehicles. J. Power Sources 2015, 273, 793–803. [Google Scholar] [CrossRef]
- Tang, S.L.I. Method and system for iteratively determining state of charge of a battery cell. EP Patent 3045925A1, 20 July 2016. [Google Scholar]
- Jun, L.; Weiyang, W.; Sihui, G.; Feife, L. Discussion on estimation method of state of charge for power battery on electric vehicle. Automot. Pract. Technol. 2019, 12–16, 21. [Google Scholar]
- Shichang, L.; Jin, Y. Research on SOC Estimation Algorithm of Lithium Battery Based on Iterative Kalman Particle Filter. Ind. Control Comput. 2019, 32, 104–106. [Google Scholar]
- Jianshu, G.; Hao, L.; Mingqiang, W.; Jinglun, S.; Shujian, X. An Improved Particle Filter Algorithm for SOC Estimation of Electric Vehicle Battery. Mech. Sci. Technol. 2017, 36, 1428–1433. [Google Scholar]
- Jun, B.; Dong, Z.; Hai-tao, C.; Sai, S. Estimation for SOC of PEV Battery Based on Artificial Immune Particle Filter. Transp. Syst. Eng. Inf. 2015, 15, 103–108. [Google Scholar]
- Tong, S.; Klein, M.P.; Park, J.W. On-line optimization of battery open circuit voltage for improved state-of-charge and state-of-health estimation. J. Power Sources 2015, 293, 416–428. [Google Scholar] [CrossRef]
- Kim, J.; Song, T.W.; Lim, J.W. Method and Apparatus Estimating State of Battery. EP Patent 3048694A1, 27 July 2016. [Google Scholar]
- Suglia, R.; Pritelli, D.; Aurilio, G. Method for Estimating the Current and the State of Charge of a Battery pack or Cell, Without Direct Detection of Current under Operating Conditions. EP Patent 3410139A1, 11 December 2019. [Google Scholar]
- Haitao, C. Research on Estimation for SOC of PEV Li-ion Battery Based on Artificial Immune Particle Filter. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2013. [Google Scholar]
- Zhang, J.; Pan, G. Comparison and application of multiple regression and BP neural network prediction model. J. Kunming Univ. Sci. Technol. 2013, 38, 61–67. [Google Scholar]
- Zhonghua, H. Estimation Method StudyBased on Principal Component Analysis. Master’s Thesis, Harbin University of Science and Technology, Harbin, China, March 2014. [Google Scholar]
- Wu, H.-D.; Xiao-ming, R.; Wei, N.; Chao, H. Estimating SOC of Li-ion battery by improved AH combined with neural network. Battery Bimon. 2016, 46, 16–19. [Google Scholar]
- Weiqin, L.; Ping, T.; Xu, L.; Dewang, C. Lithium Battery SOC Prediction Based on Multiple Linear Regression Model. Comput. Meas. Control 2018, 26, 145–149. [Google Scholar]
- Qian, Y.Y.; Xiang, Z.; Guanghui, Y.; Kegang, X.; Jiayao, Z. Accurate estimation of charge state of lithium battery base on fuzzy control. Electron. Meas. Technol. 2018, 41, 7–11. [Google Scholar]
- Andersson, H. A System and a Method for Determining State-of-Charge of a Battery. EP Patent 3371613A1, 12 September 2018. [Google Scholar]
- Thomas, M.-P.; Ourabah, A.-D. Method for Managing the Charge State of a Traction Battery of a Hybrid Vehicle. EP Patent 3361601A1, 15 August 2018. [Google Scholar]
- Klass, V.; Behm, M.; Lindbergh, G. Capturing lithium-ion battery dynamics with support vector machine-based battery model. J. Power Sources 2015, 298, 92–101. [Google Scholar] [CrossRef]
- You, K.; Park, S. Method and apparatus for estimating the state of a battery. EP Patent 3048451A1, 27 July 2016. [Google Scholar]
- Wu, Z.; Shang, M.; Shen, D.; Qi, S. SOC estimation for batteries using MS-AUKF and neural network. J. Renew. Sustain. Energy 2019, 11, 1–10. [Google Scholar] [CrossRef]
- XinTian, L.; Hanqi, L.; Zengfu, W.; Yao, H.; Guojian, Z. CKF estimation Li-ion battery SOC based on Drift-Ah integral method. Control Decis. 2019, 34, 535–541. [Google Scholar]



| Estimation | Advantages | Disadvantages |
|---|---|---|
| Traditional methods based on experiments | The simple and stable algorithm is simple and stable Mature technology Easy to implement | High requirements on hardware The effect is usually better in a certain period of battery estimation A large amount of experimental investment is required Obvious cumulative effect of errors |
| Modern methods based on control theory | Better eliminate error accumulation effect Correct the noise well High convergence speed and accuracy | Higher requirements for battery model The algorithm is too complex |
| other methods | Strong pertinence Interdisciplinary and interdisciplinary applications | The practical applicability needs to be further verified Complex algorithm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Fan, X. Review on the State of Charge Estimation Methods for Electric Vehicle Battery. World Electr. Veh. J. 2020, 11, 23. https://doi.org/10.3390/wevj11010023
Zhang M, Fan X. Review on the State of Charge Estimation Methods for Electric Vehicle Battery. World Electric Vehicle Journal. 2020; 11(1):23. https://doi.org/10.3390/wevj11010023
Chicago/Turabian StyleZhang, Mingyue, and Xiaobin Fan. 2020. "Review on the State of Charge Estimation Methods for Electric Vehicle Battery" World Electric Vehicle Journal 11, no. 1: 23. https://doi.org/10.3390/wevj11010023
APA StyleZhang, M., & Fan, X. (2020). Review on the State of Charge Estimation Methods for Electric Vehicle Battery. World Electric Vehicle Journal, 11(1), 23. https://doi.org/10.3390/wevj11010023





