Design Optimization and Analysis of an Outer-Rotor Direct-Drive Permanent-Magnet Motor for Medium-Speed Electric Vehicle
Abstract
:1. Introduction
2. Design of the Outer-Rotor Direct-Drive Brushless DC Motor
2.1. Design Parameters of the Motor
2.1.1. Determination of Motor Power
- Taking the maximum speed as the basis
- Taking the climbing capability as the basis
- Taking the acceleration capability as the basiswhere ua is the acceleration final velocity(km/h), and δ is the mass conversion coefficient whose value is 1.04.
2.1.2. Determination of the Rated Speed and Peak Speed
2.2. Main Dimensions of the Motor and Electromagnetic Load
2.3. Design of the Stator and Rotor of the Motor
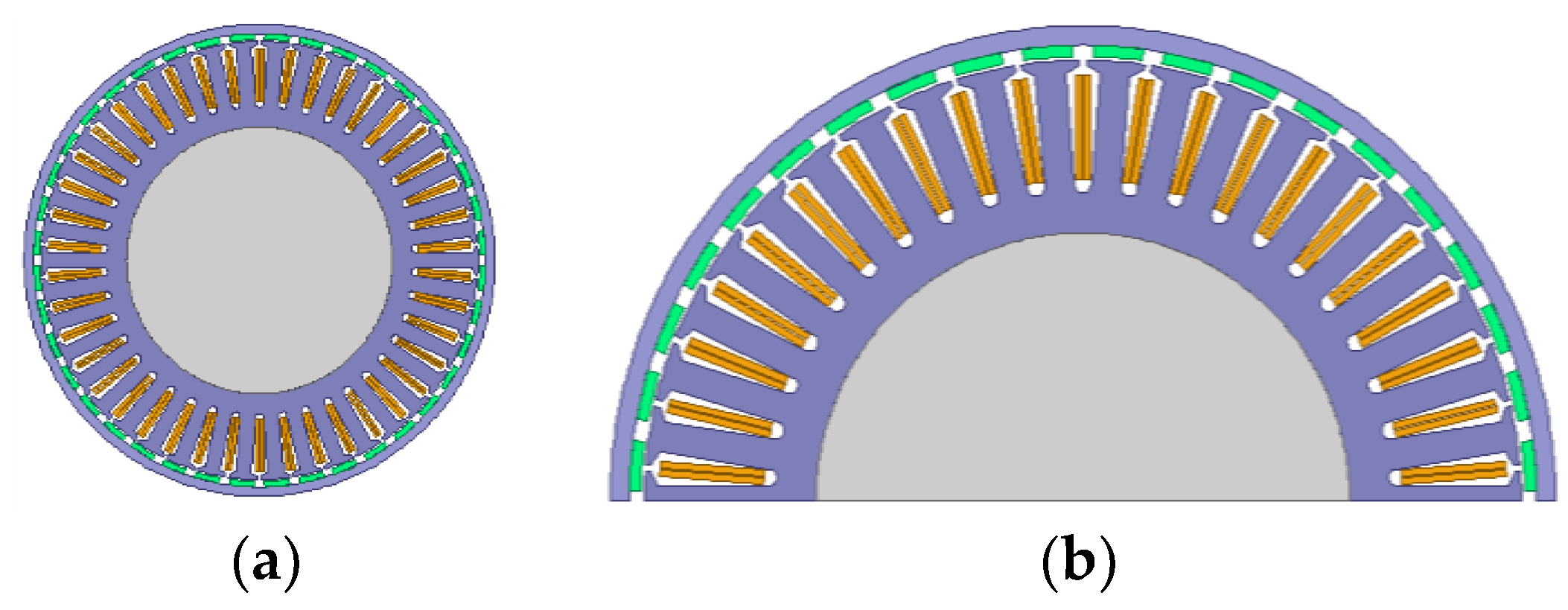
2.3.1. Dimensions of the Stator and Rotor
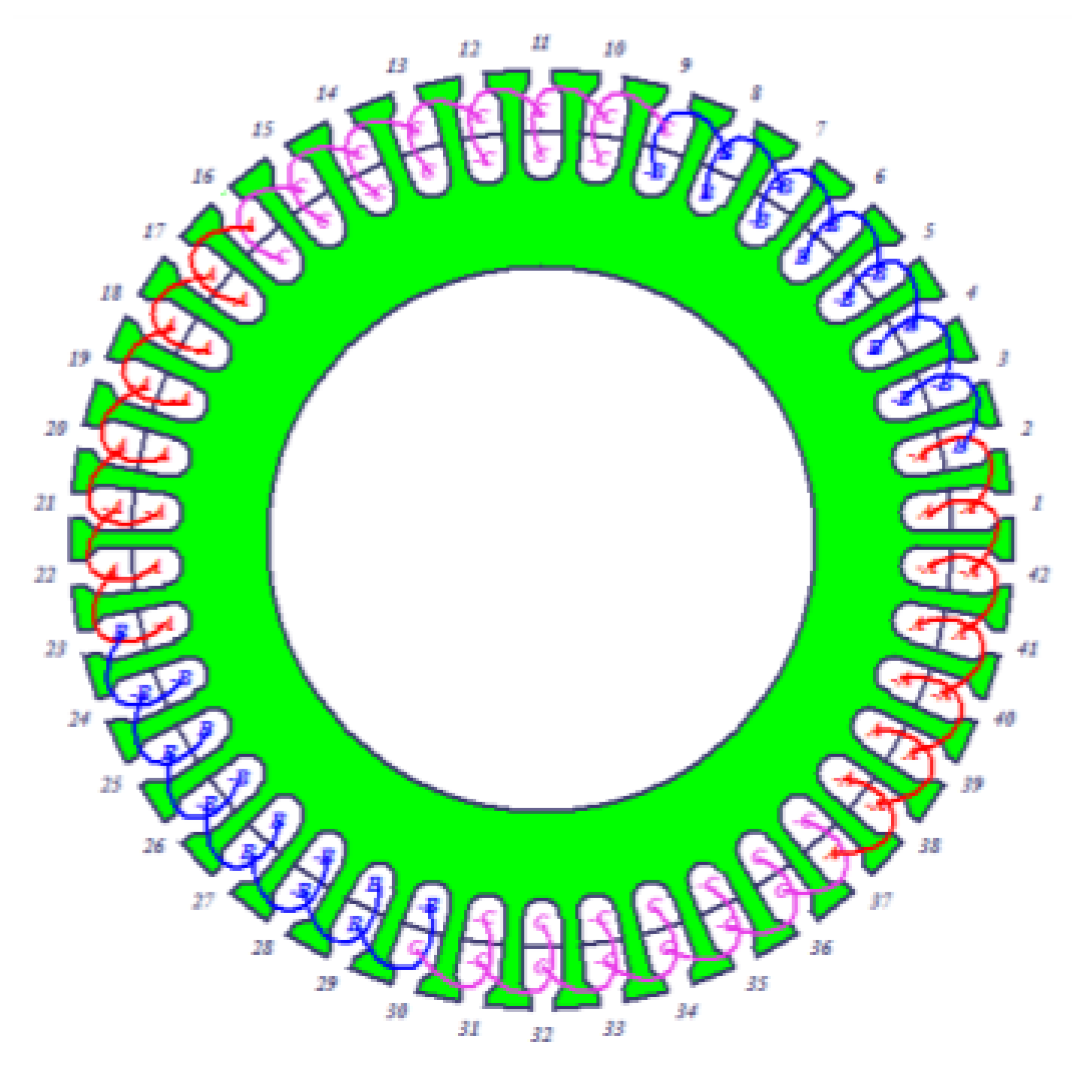
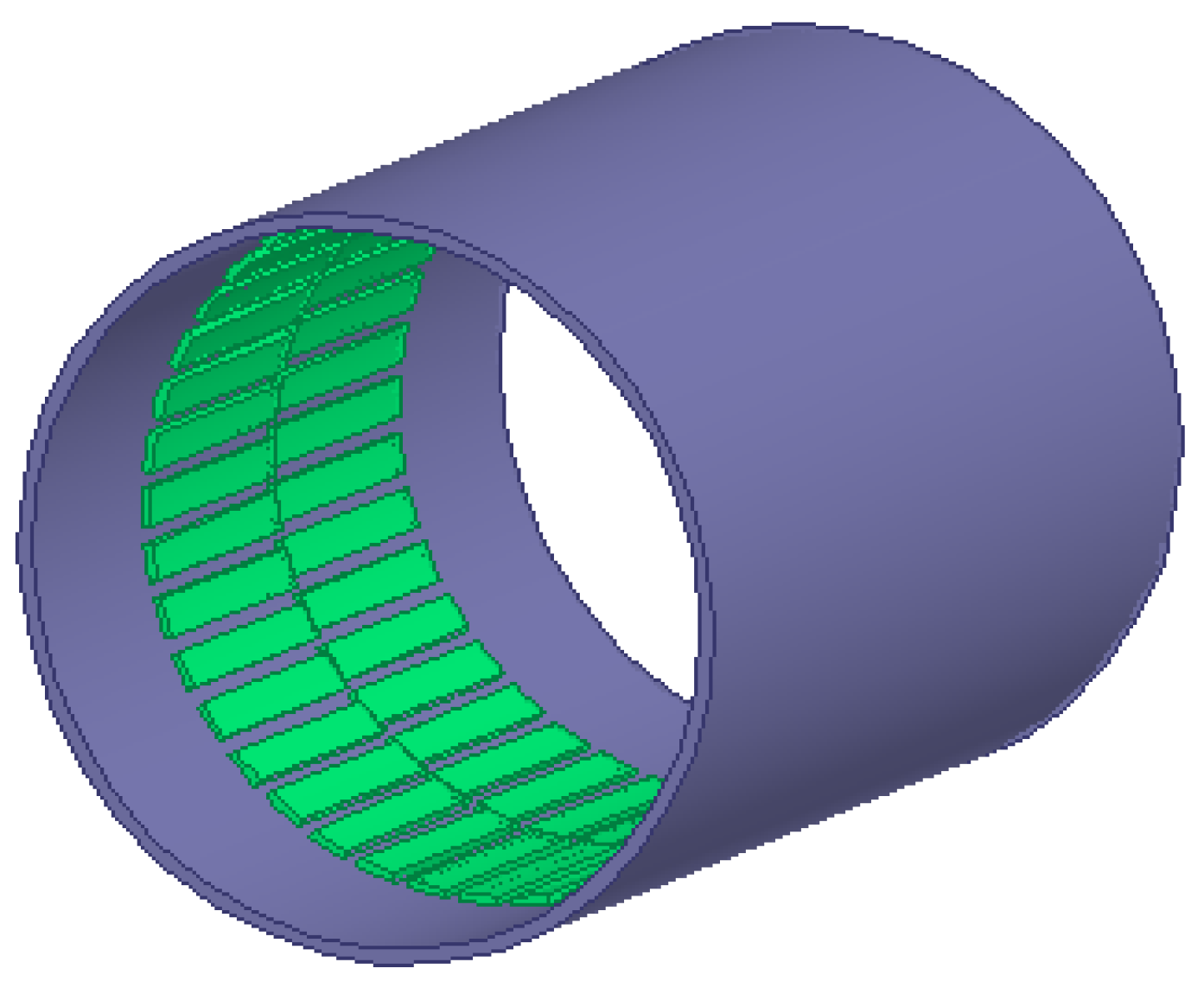
2.3.2. Determination of the Armature Winding
2.3.3. Parameter Optimization Based on the Equivalent Magnetic Circuit Method
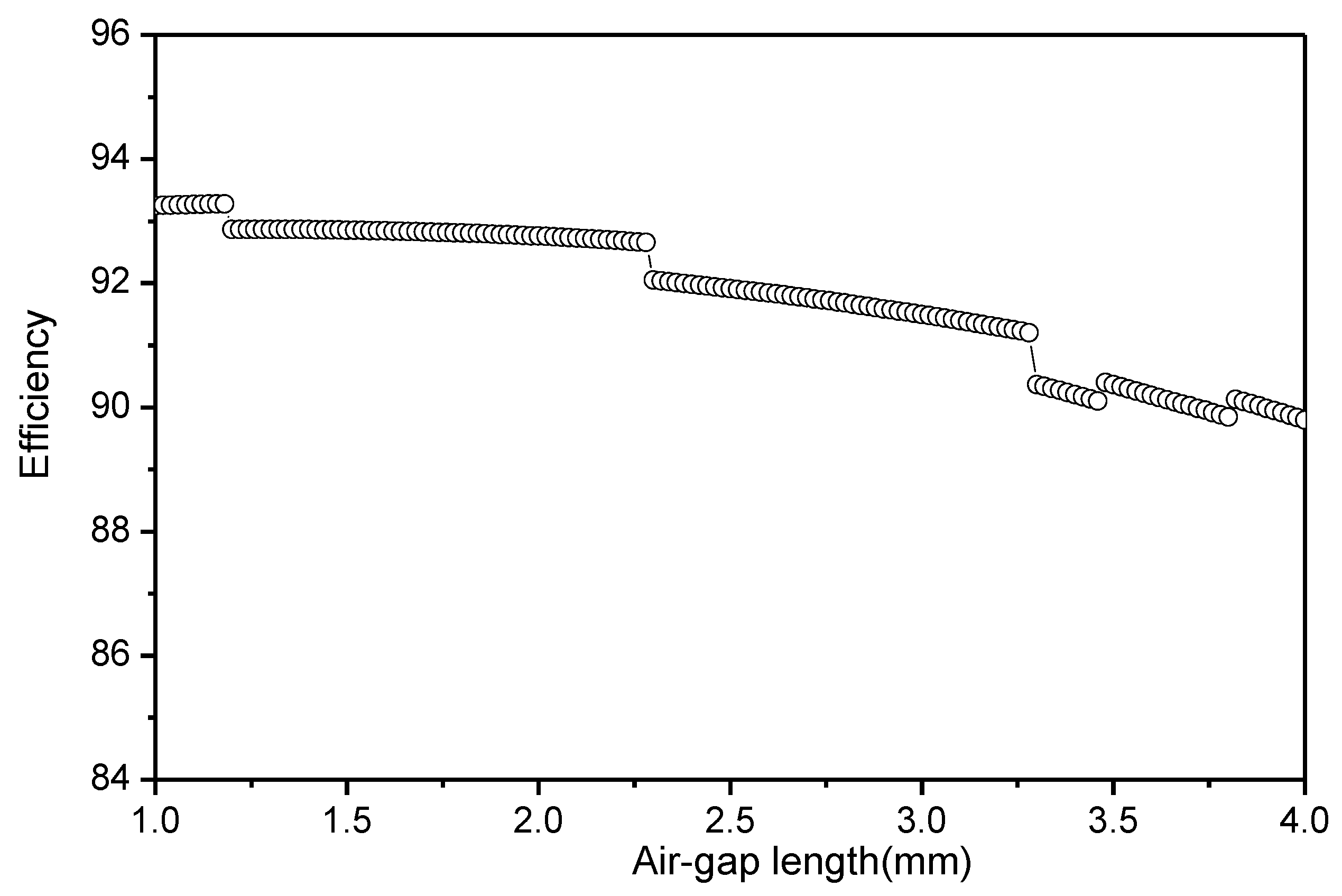
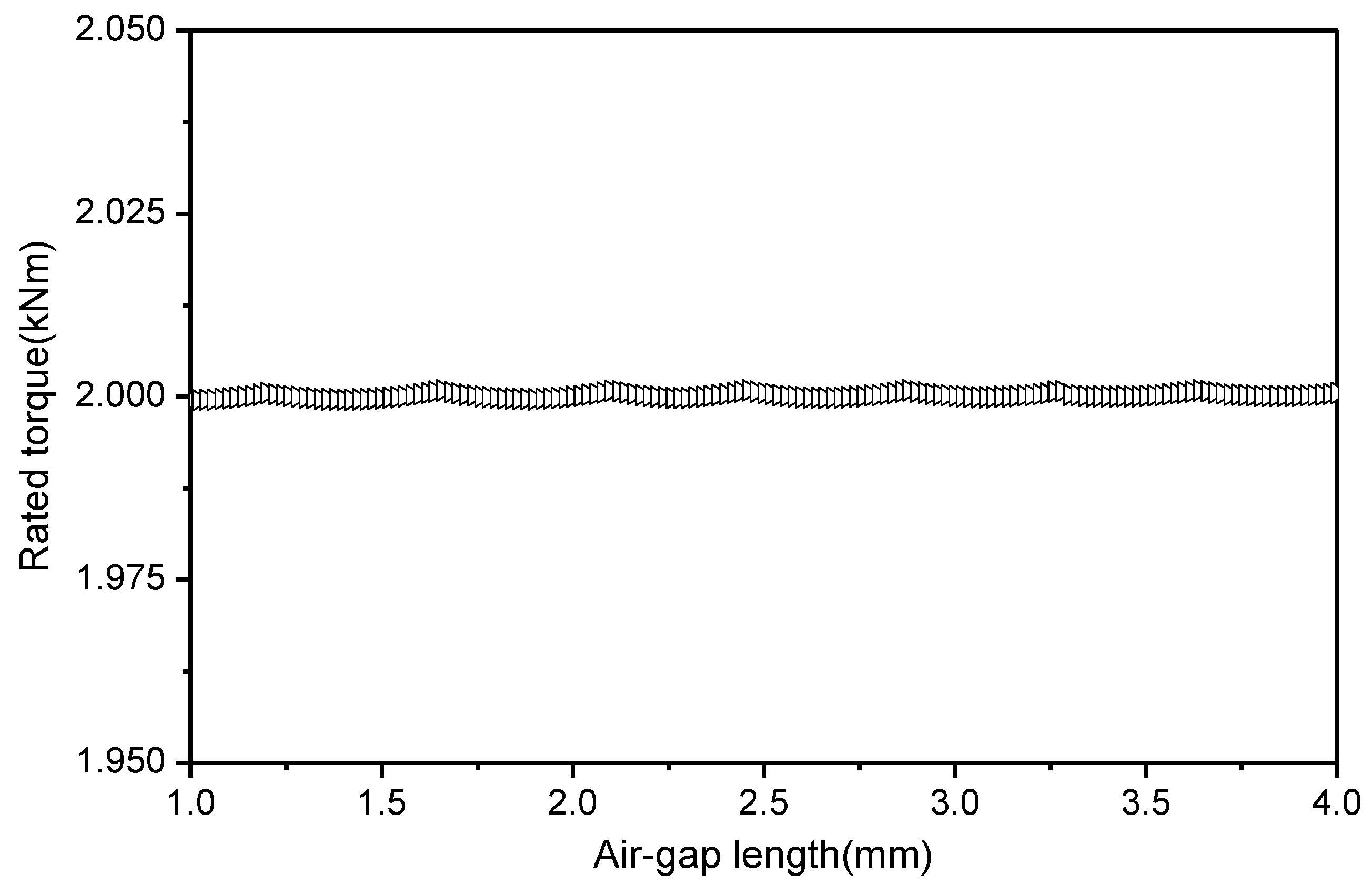
Optimization of the Air-Gap Length
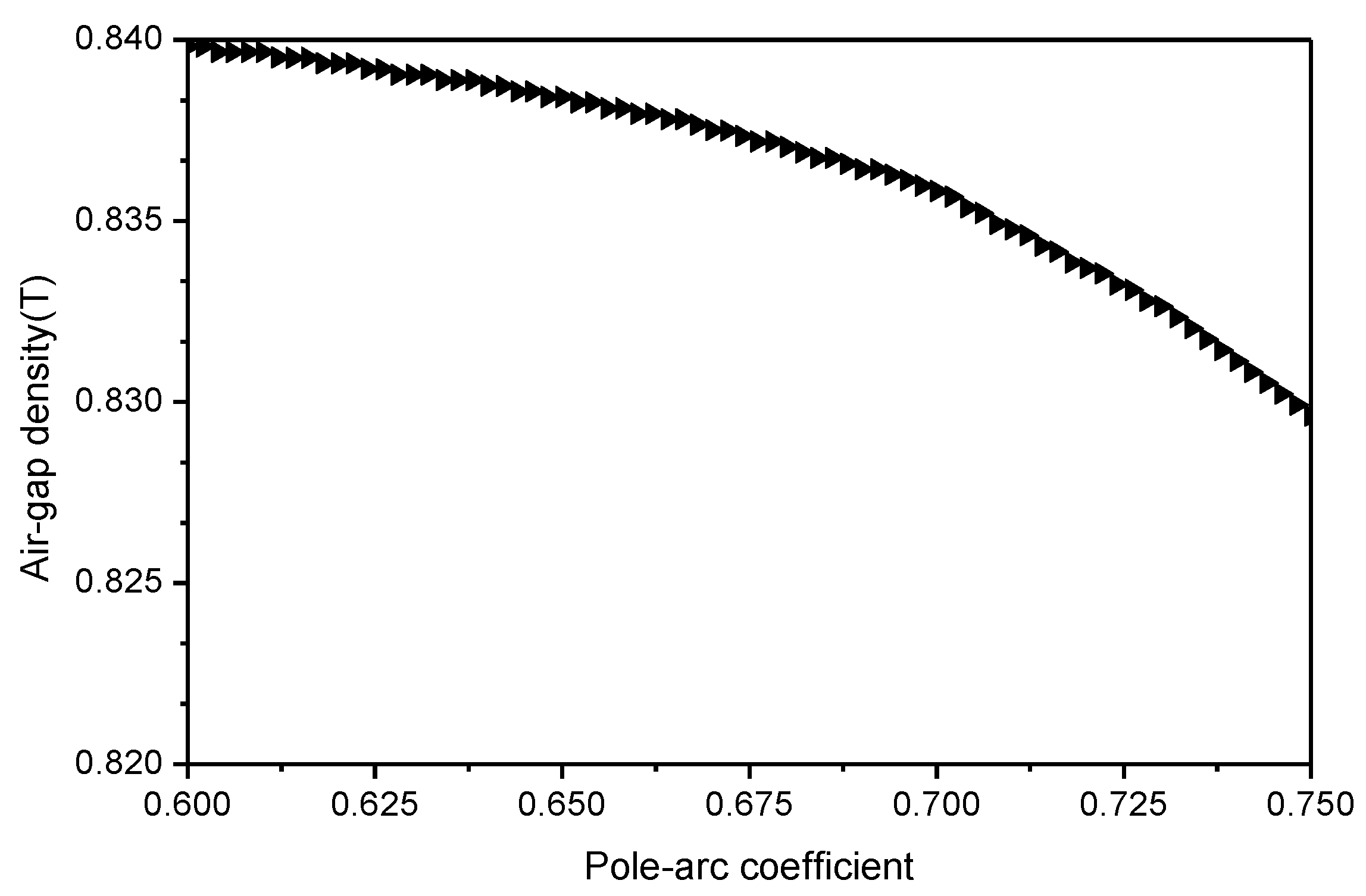
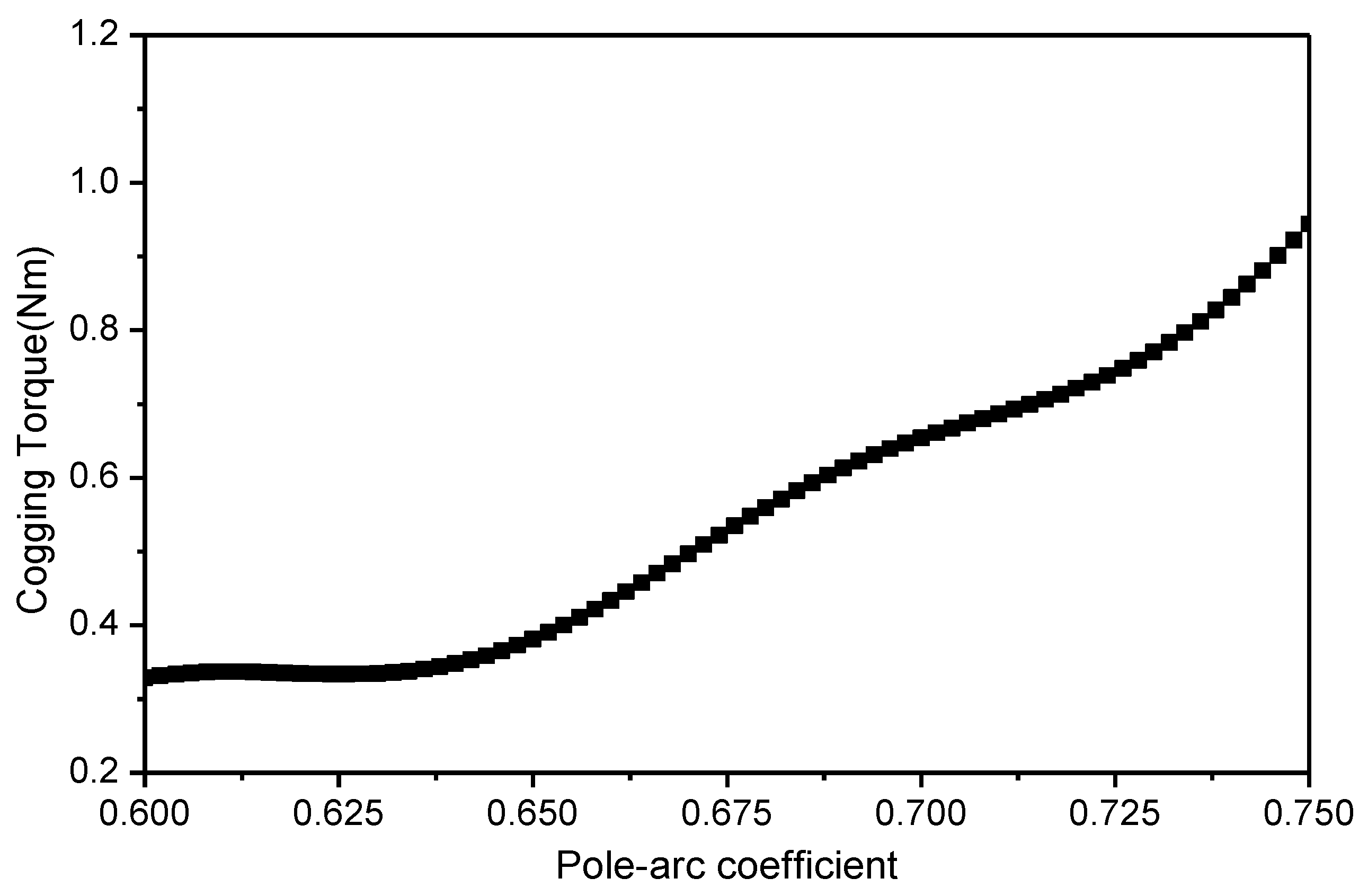
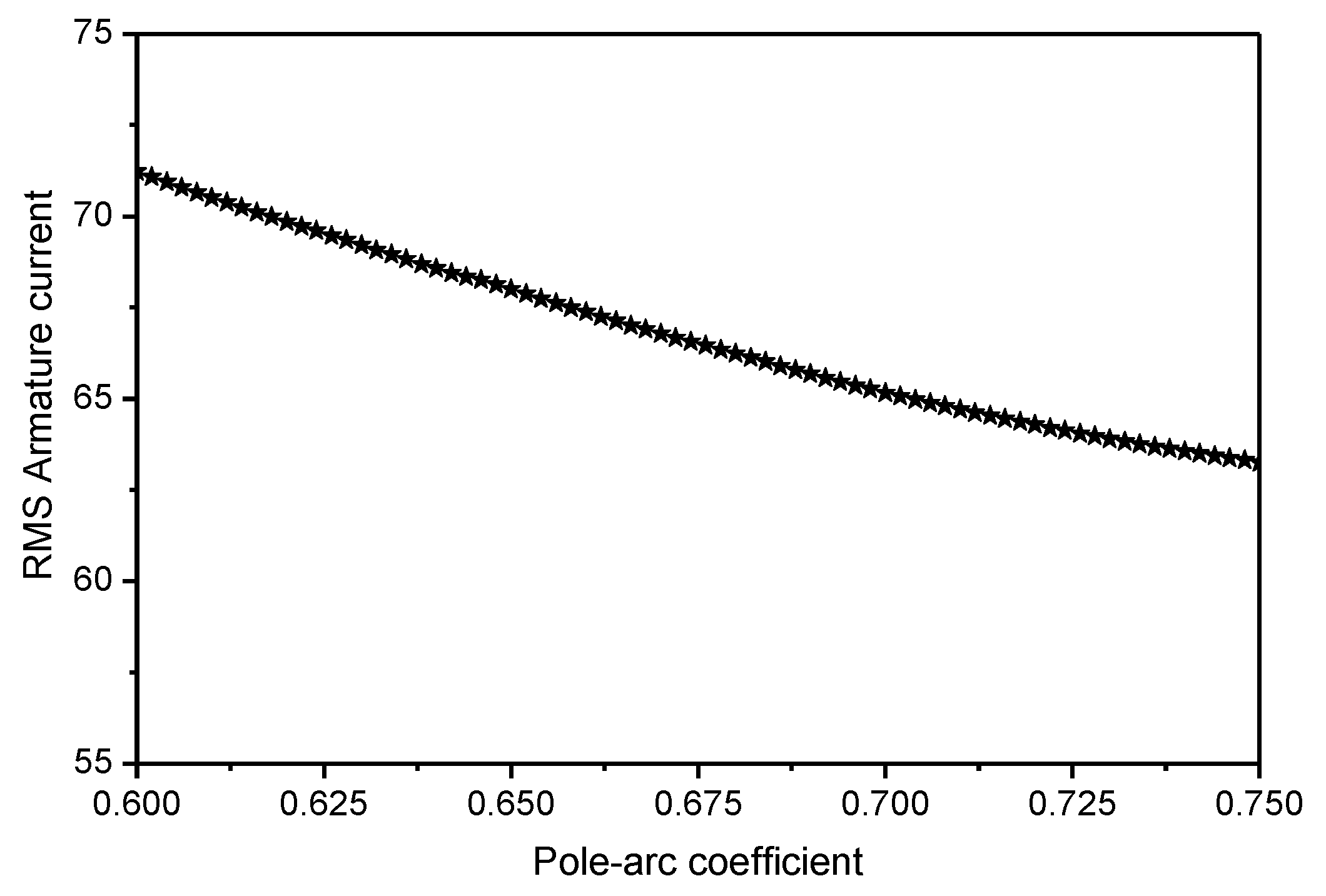
Optimization of the Pole-Arc Coefficient
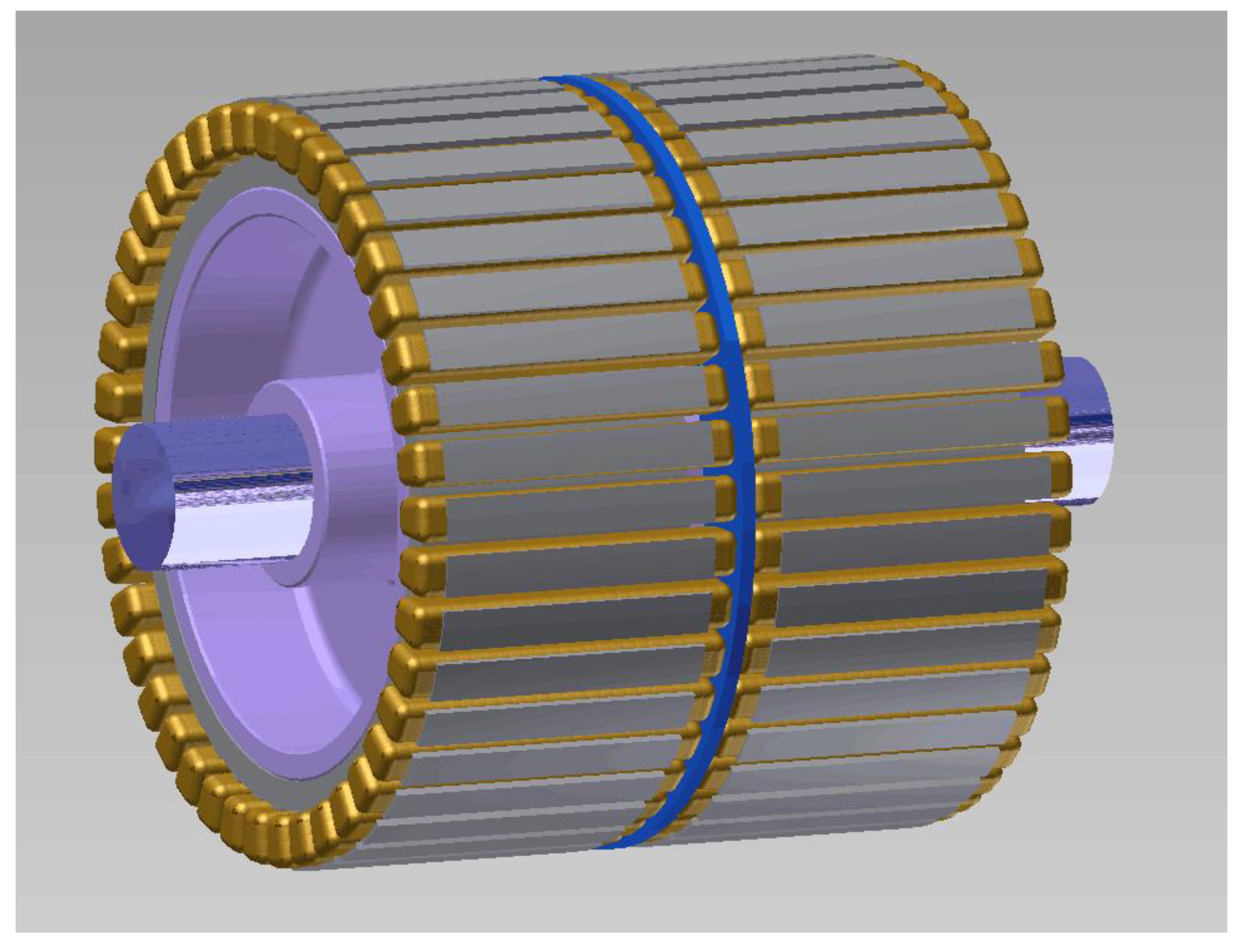
2.3.4. Structural Design of the Motor Stator and Rotor
Mechanical Structure of the Stator
Mechanical Structure of the Rotor
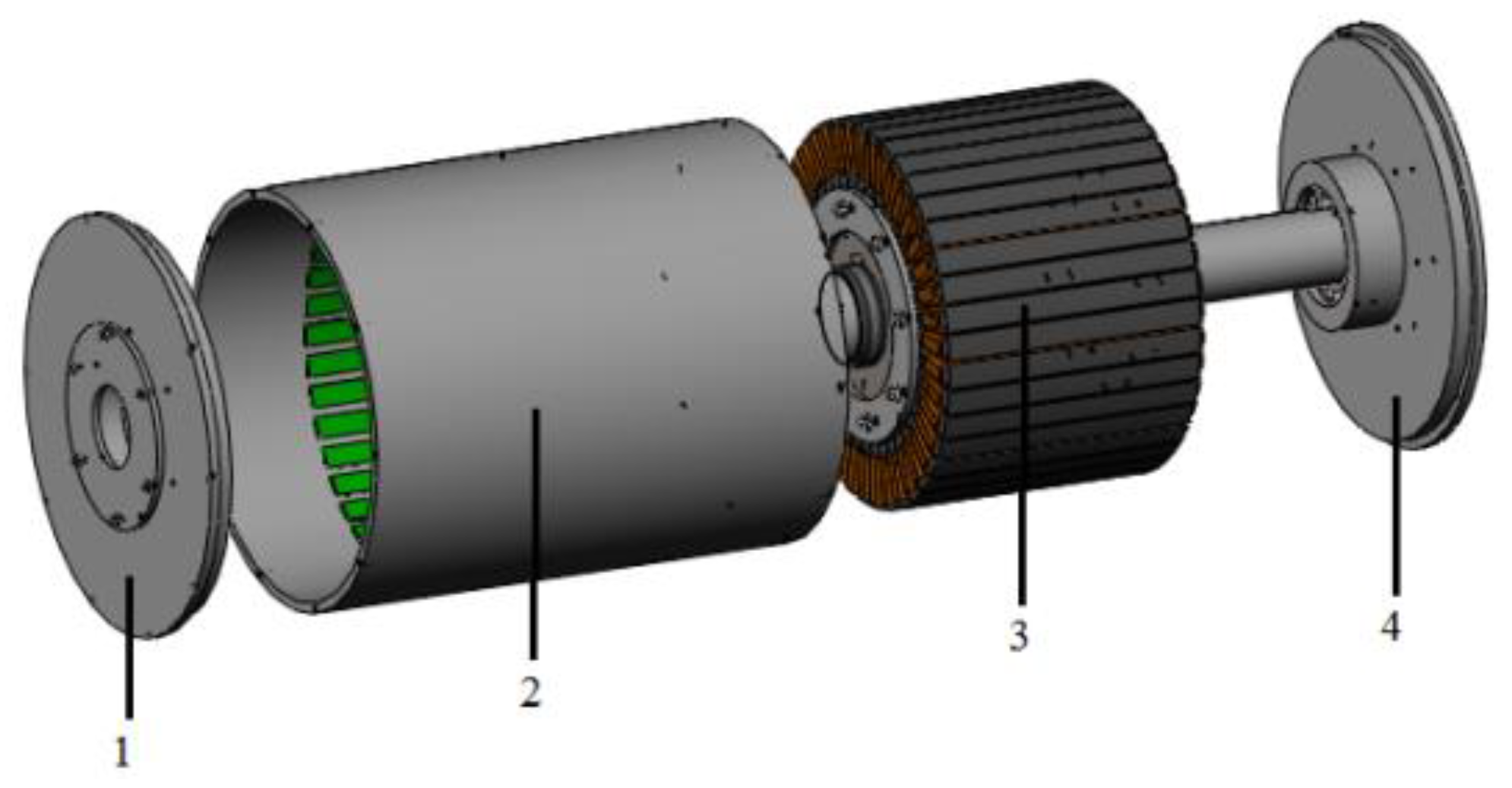
Integral Mechanical Structure of Motor
3. Analysis of the Electromagnetic Field of the Outer-Rotor Direct-Drive Brushless DC Motor
3.1. Establishment of the Motor Model
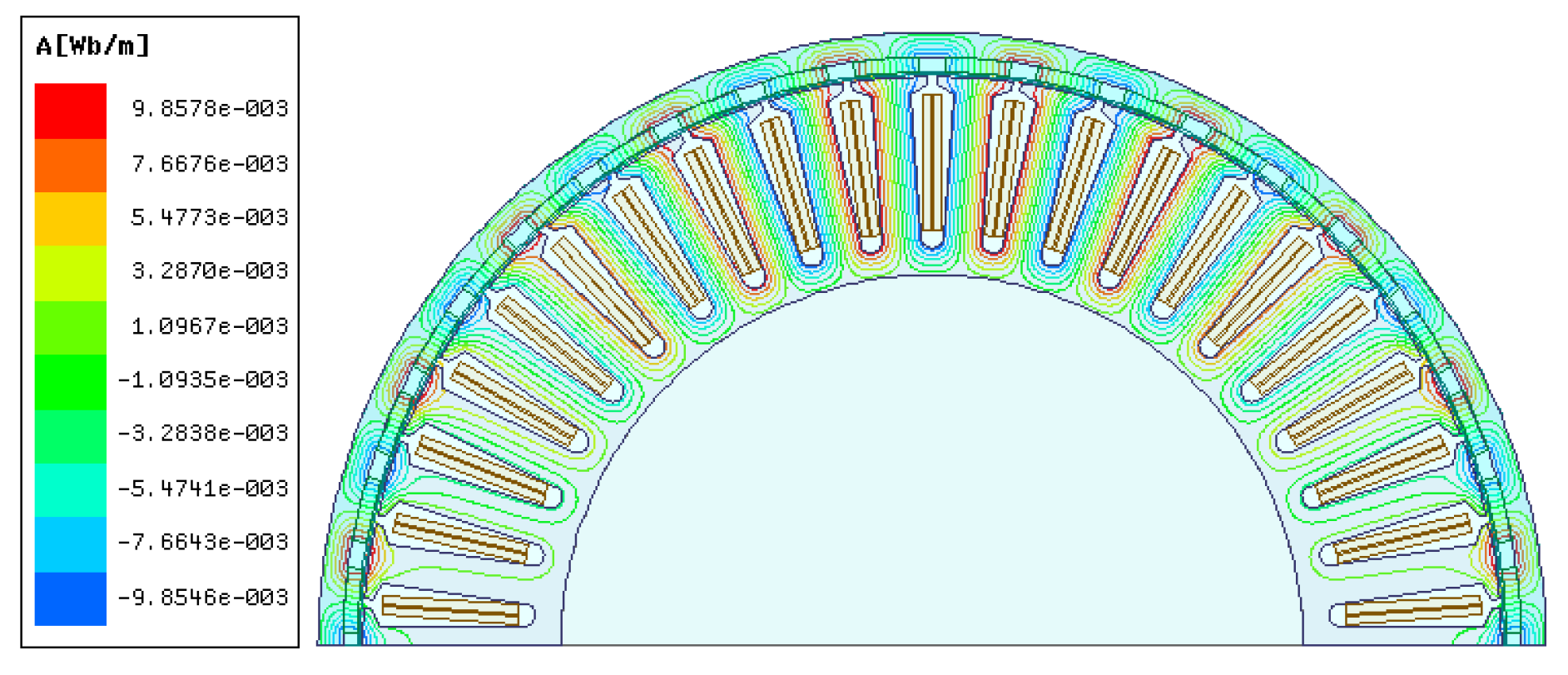
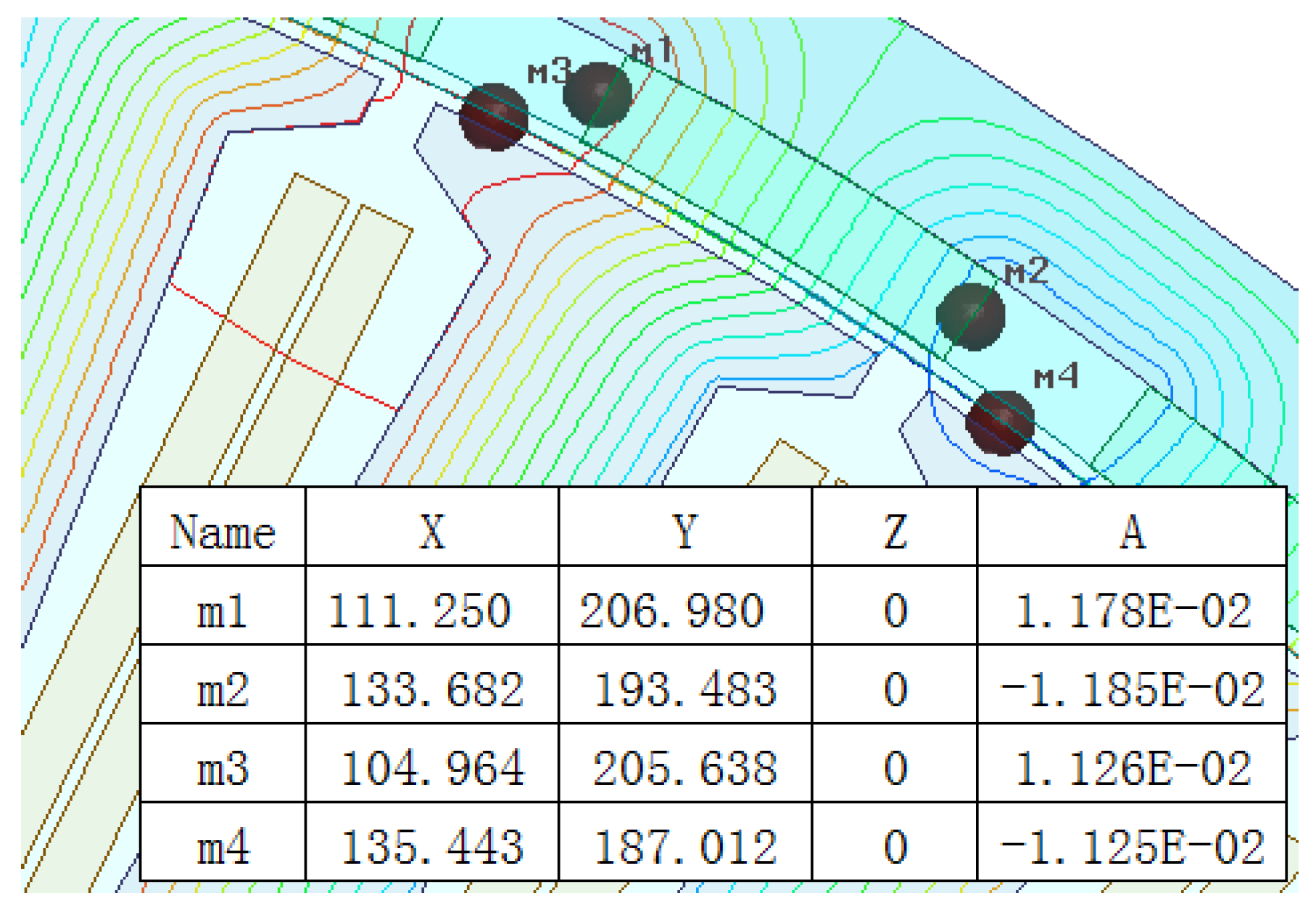
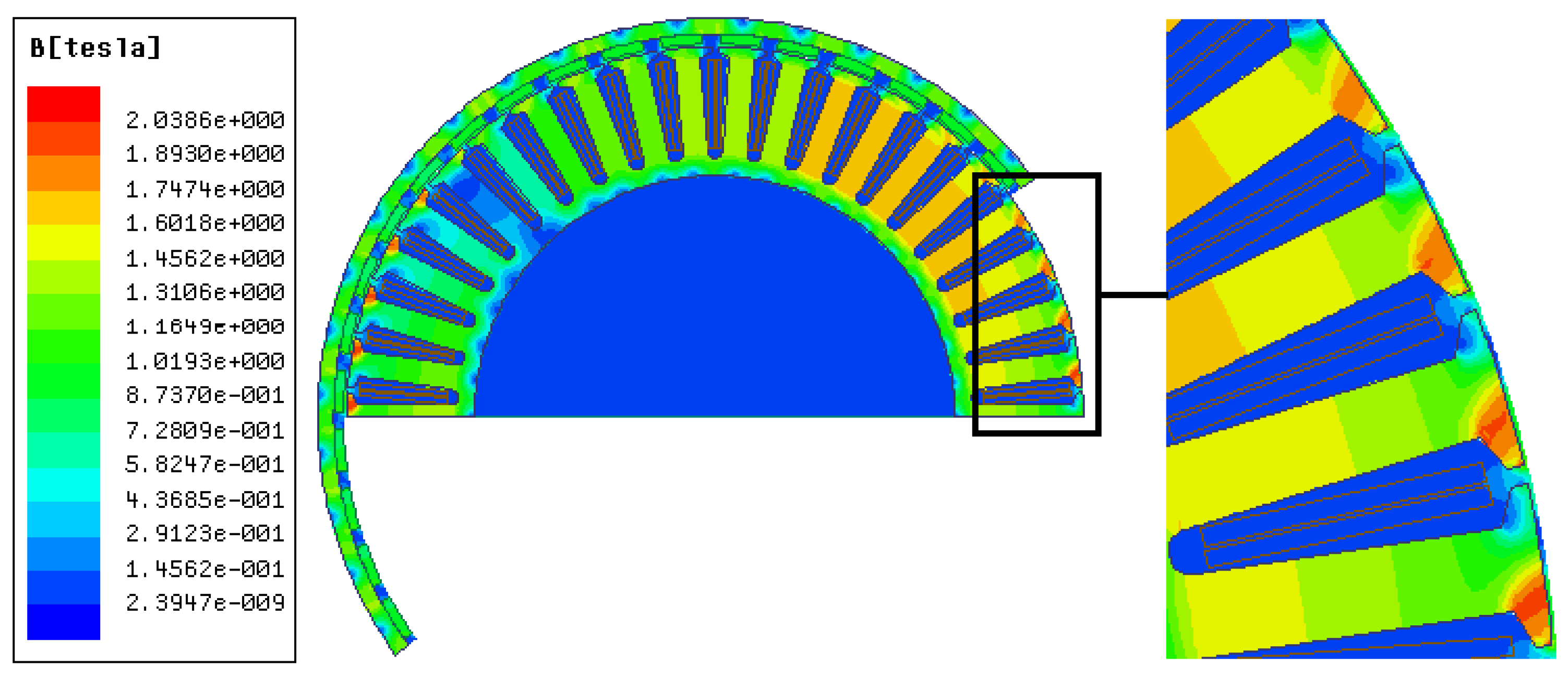
3.2. Analysis of the Static Magnetic Field of the Motor
3.3. Analysis of the Transient Magnetic Field of the Motor
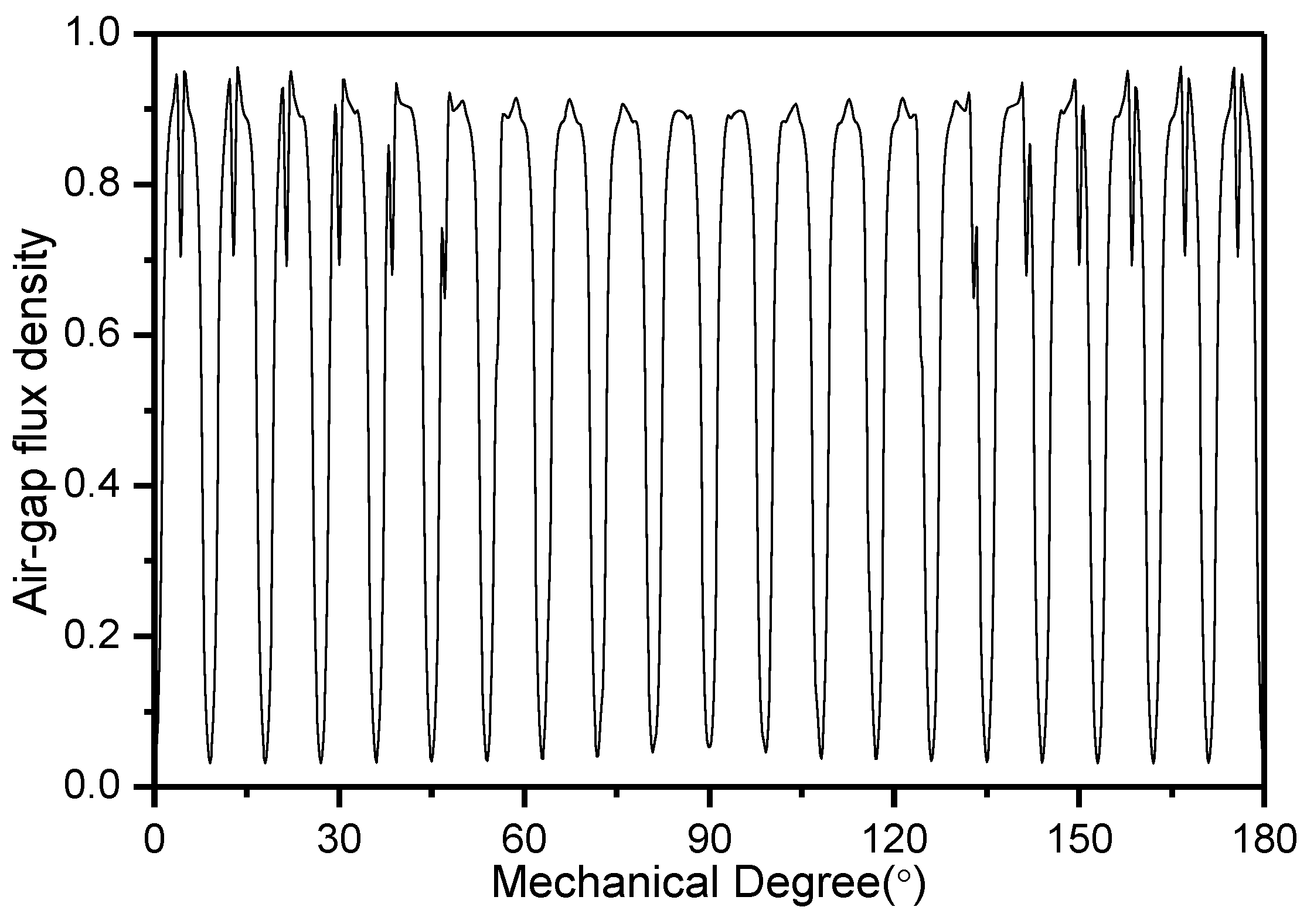
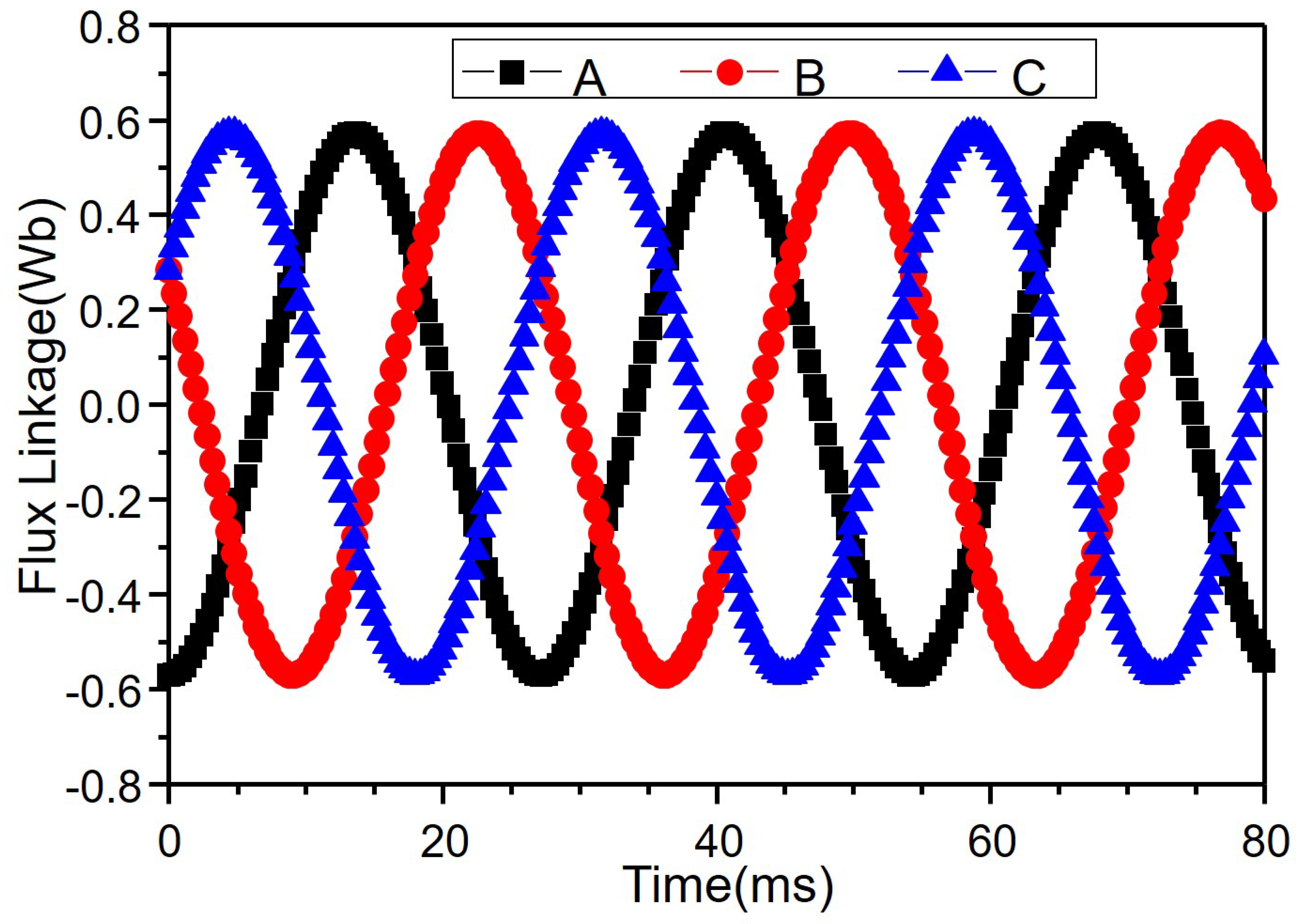
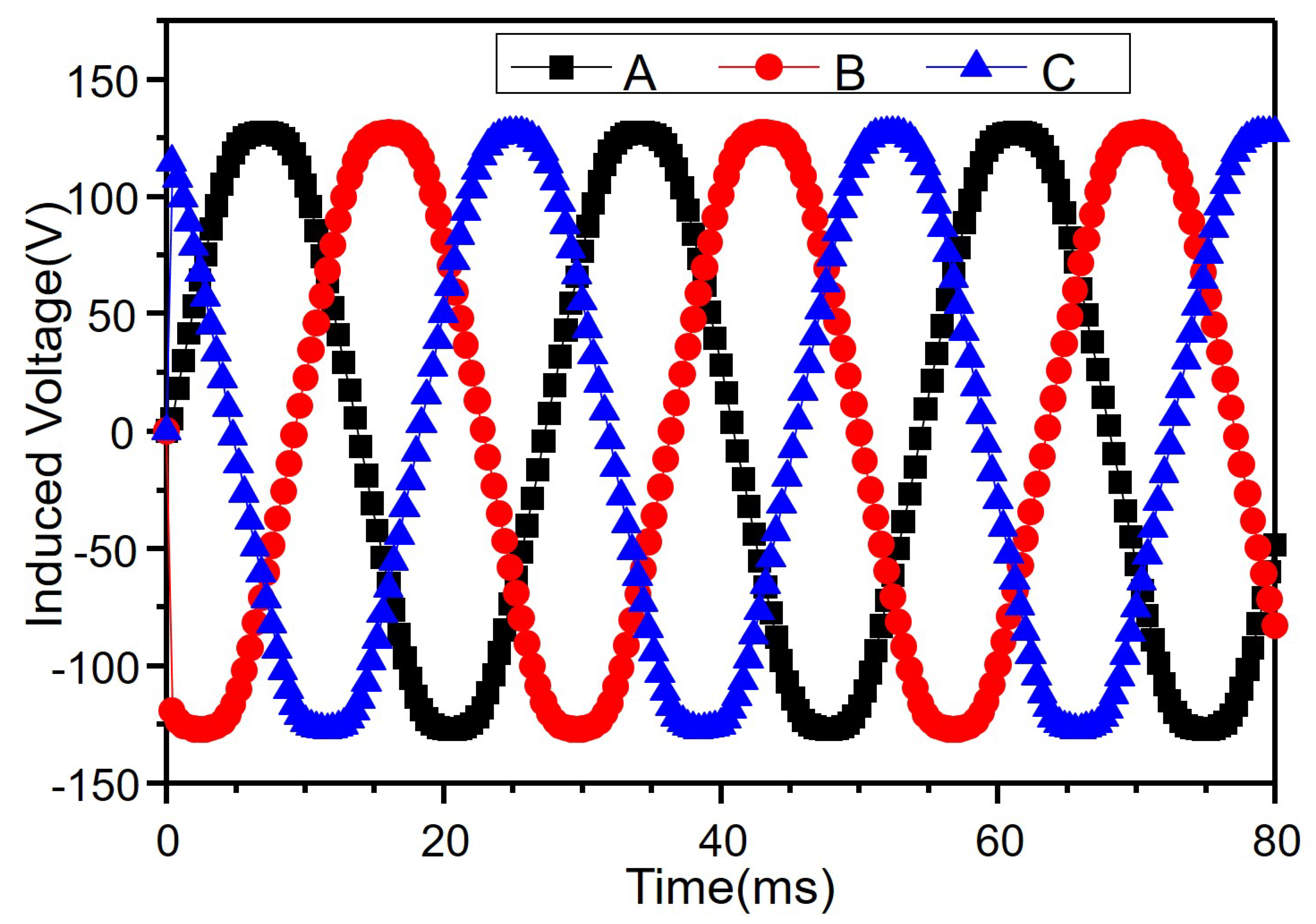
3.3.1. Analysis of the No-Load Transient Magnetic Field
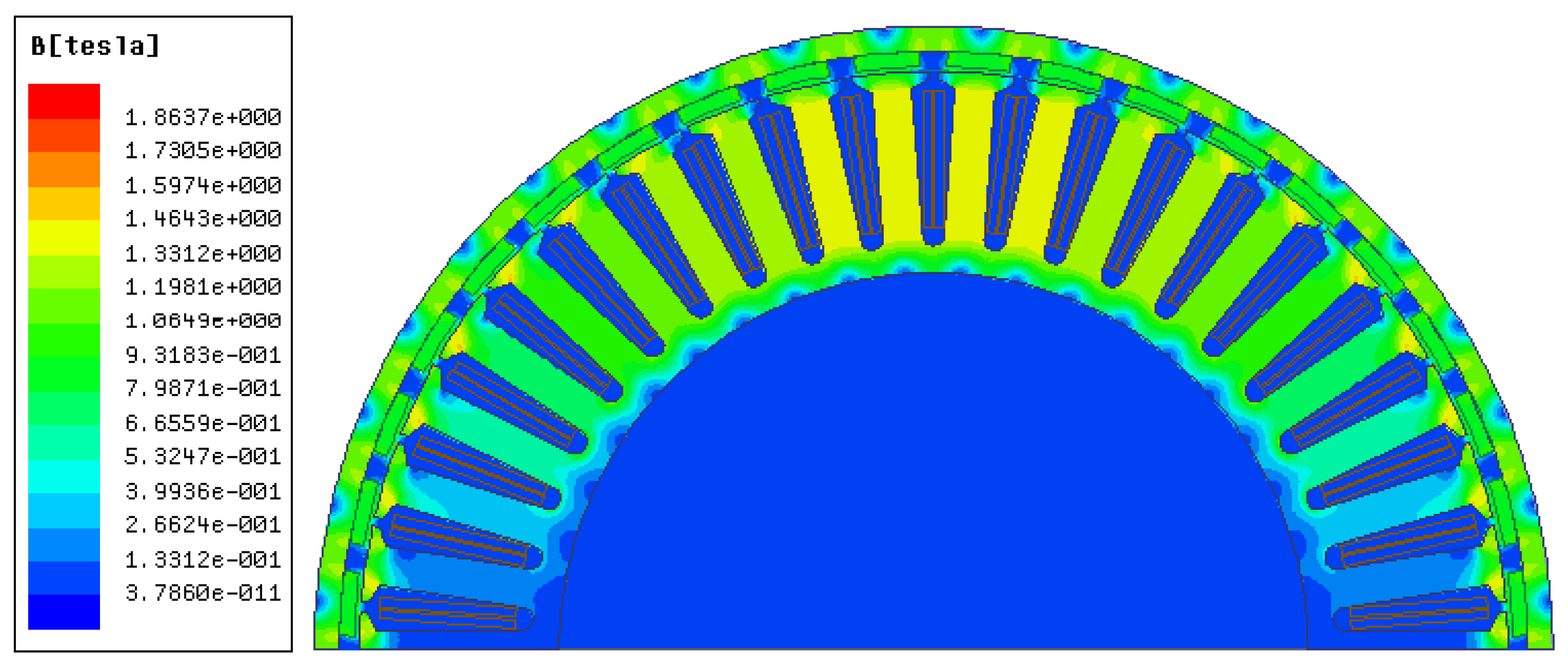
3.3.2. Analysis of the Load Transient Magnetic Field
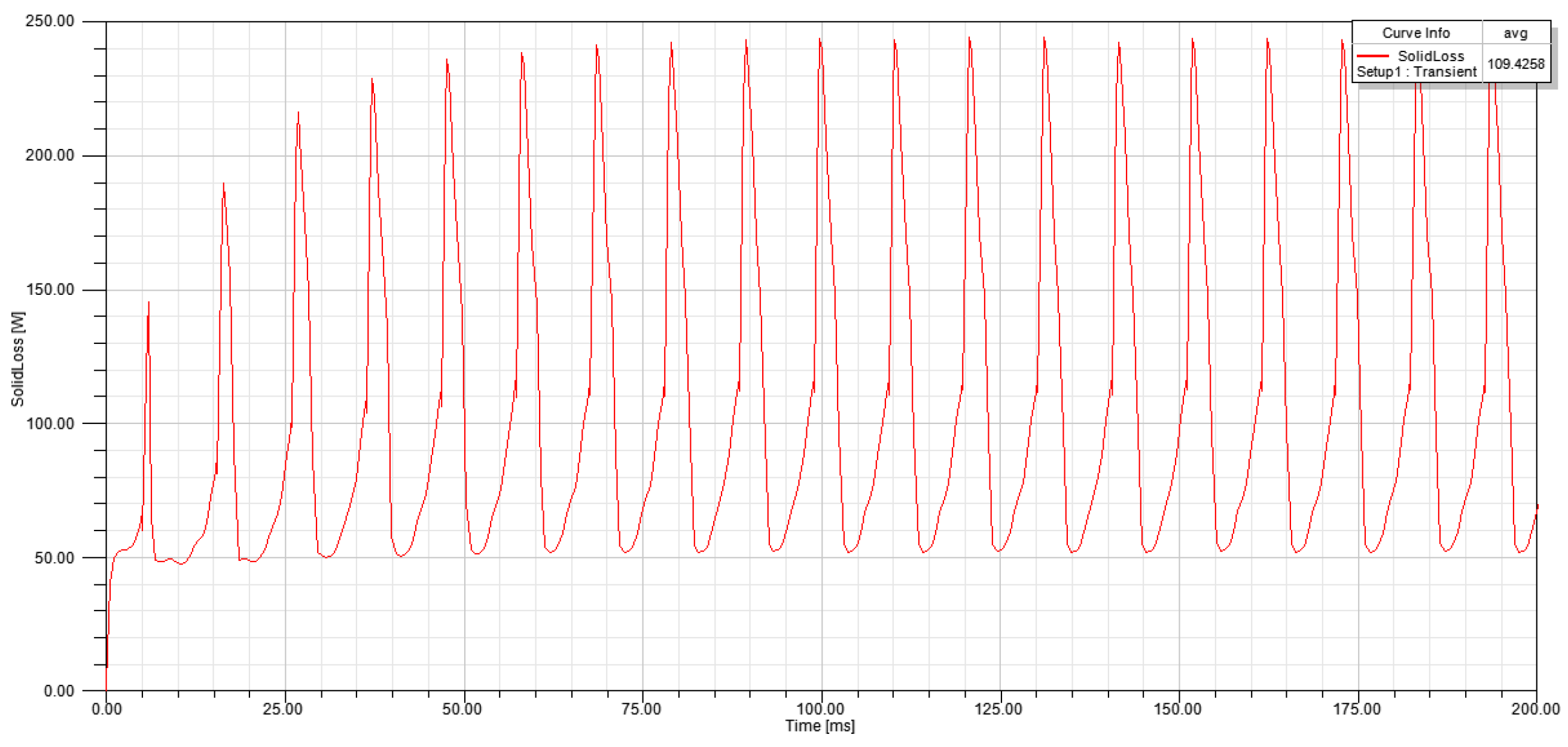
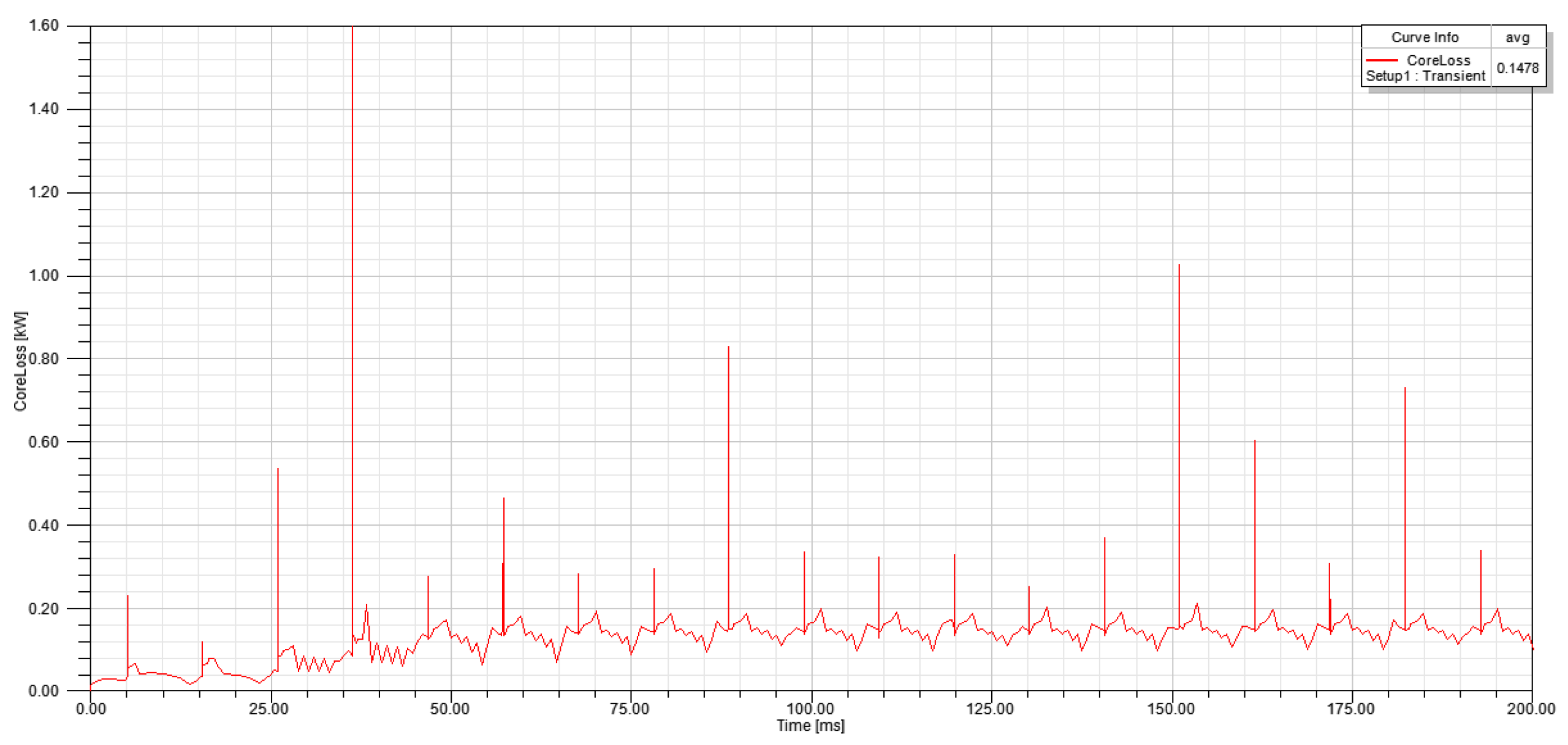
3.4. Loss Analysis of the Motor
4. Analysis of the Torque Ripple Characteristics of the Outer Rotor Direct-Drive Brushless DC Motor
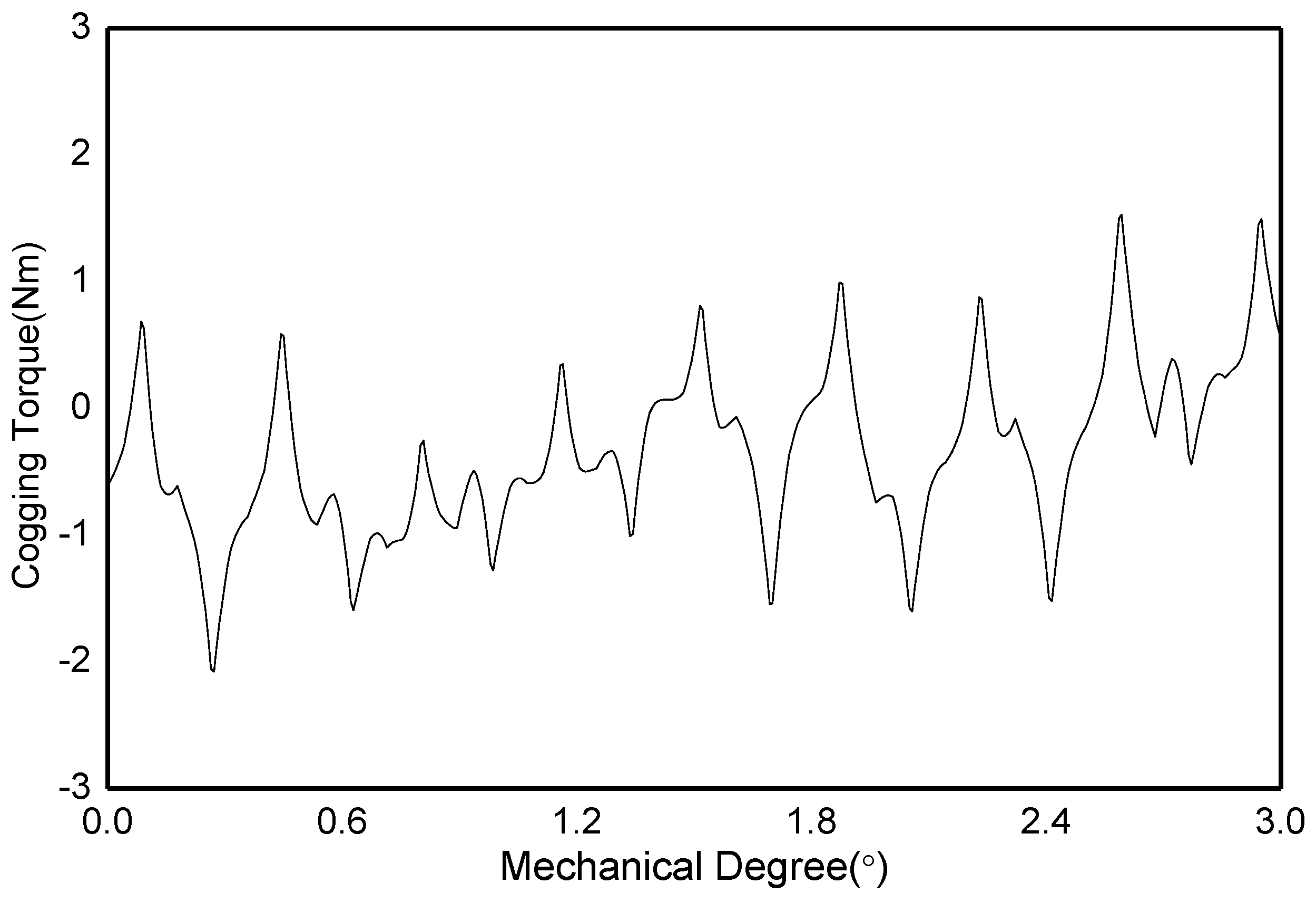
4.1. Analysis of the Cogging Torque
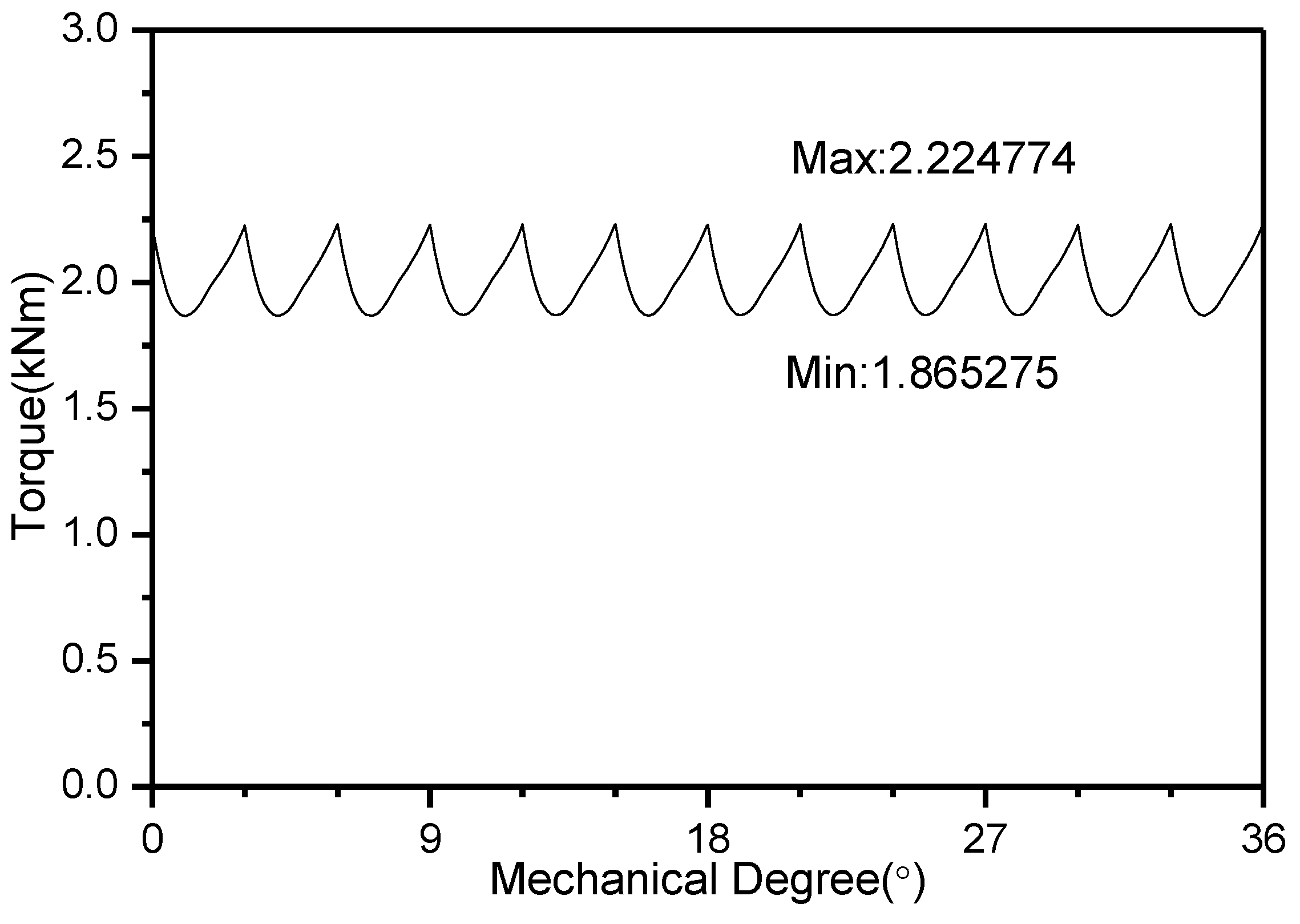
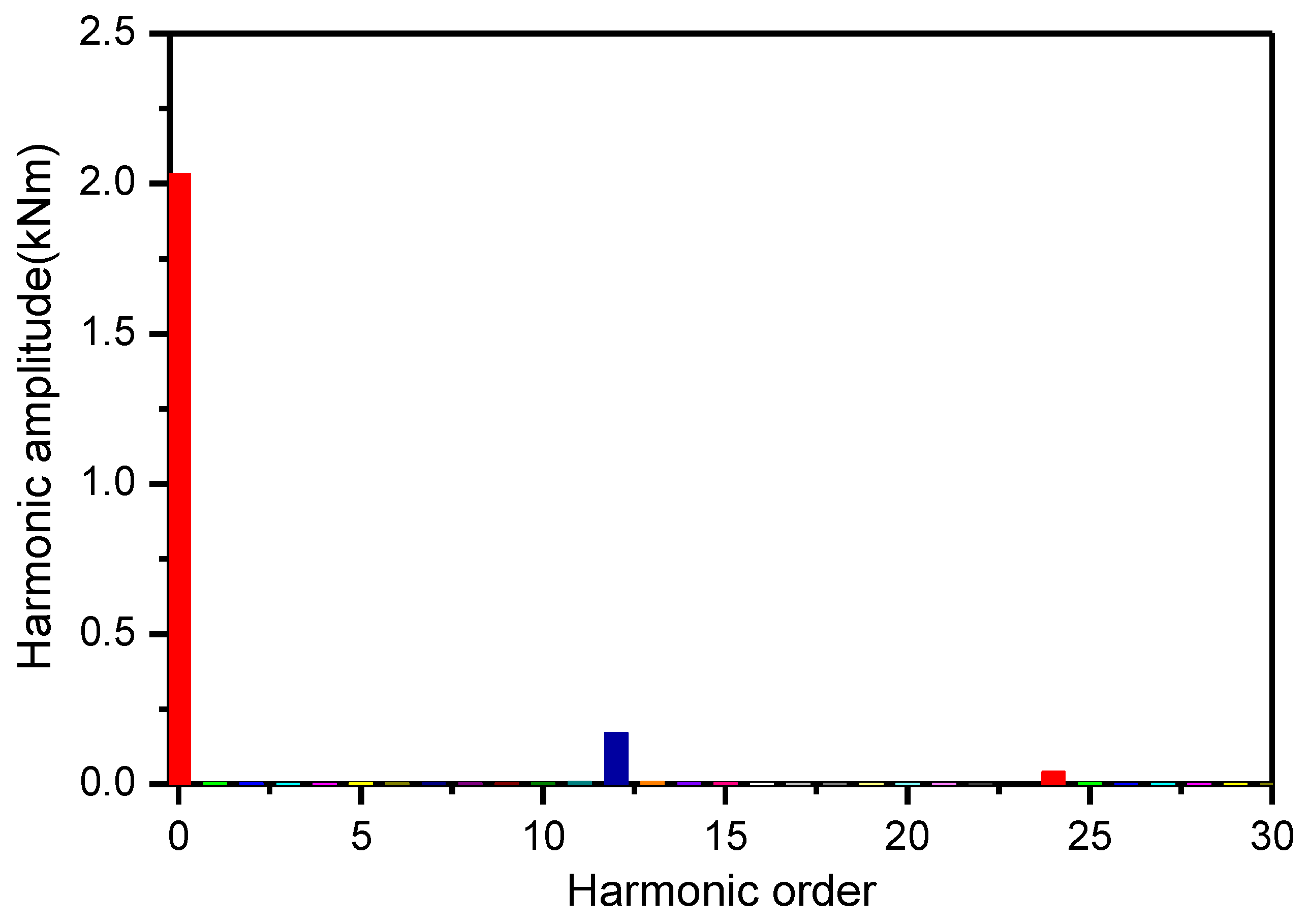
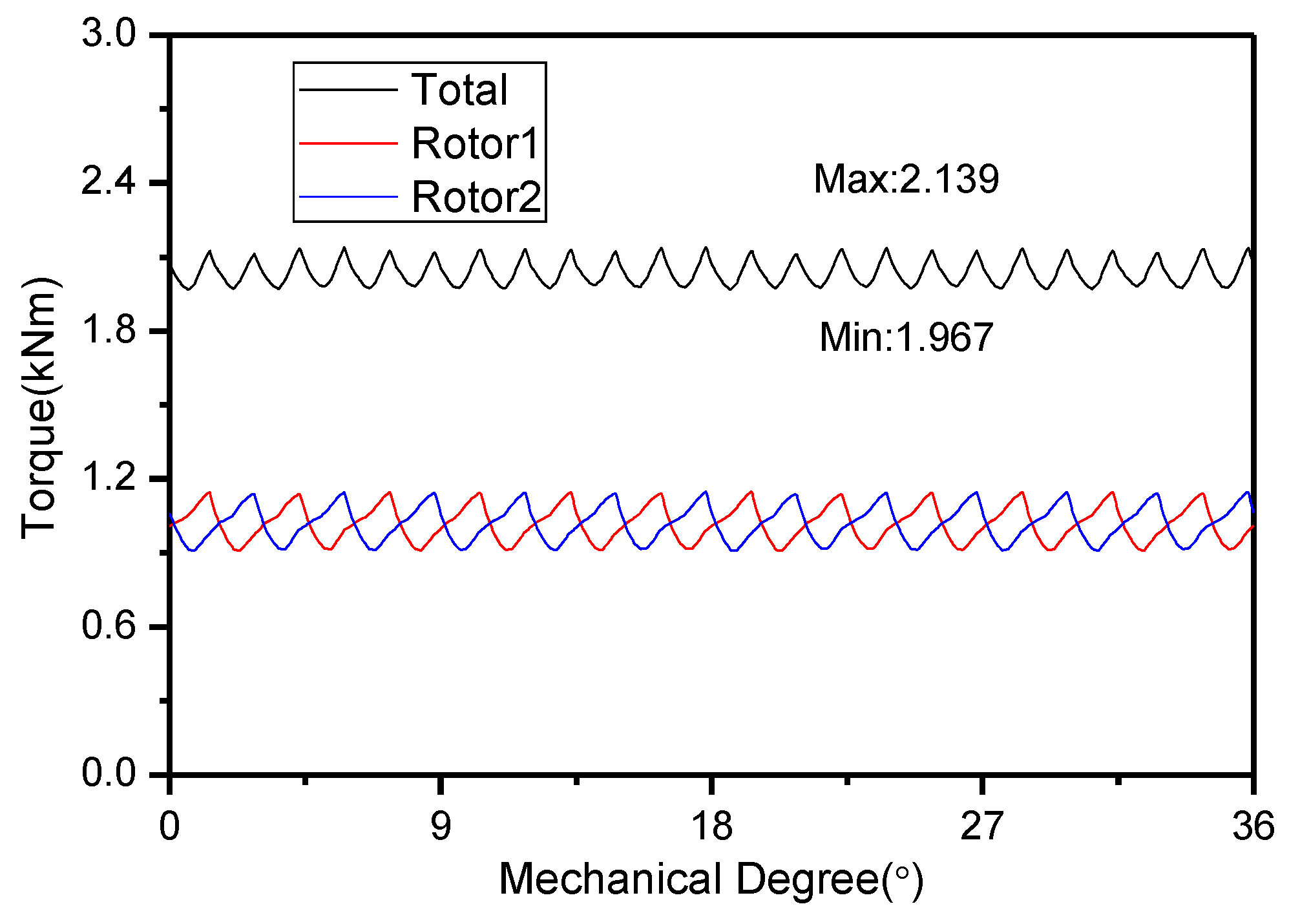
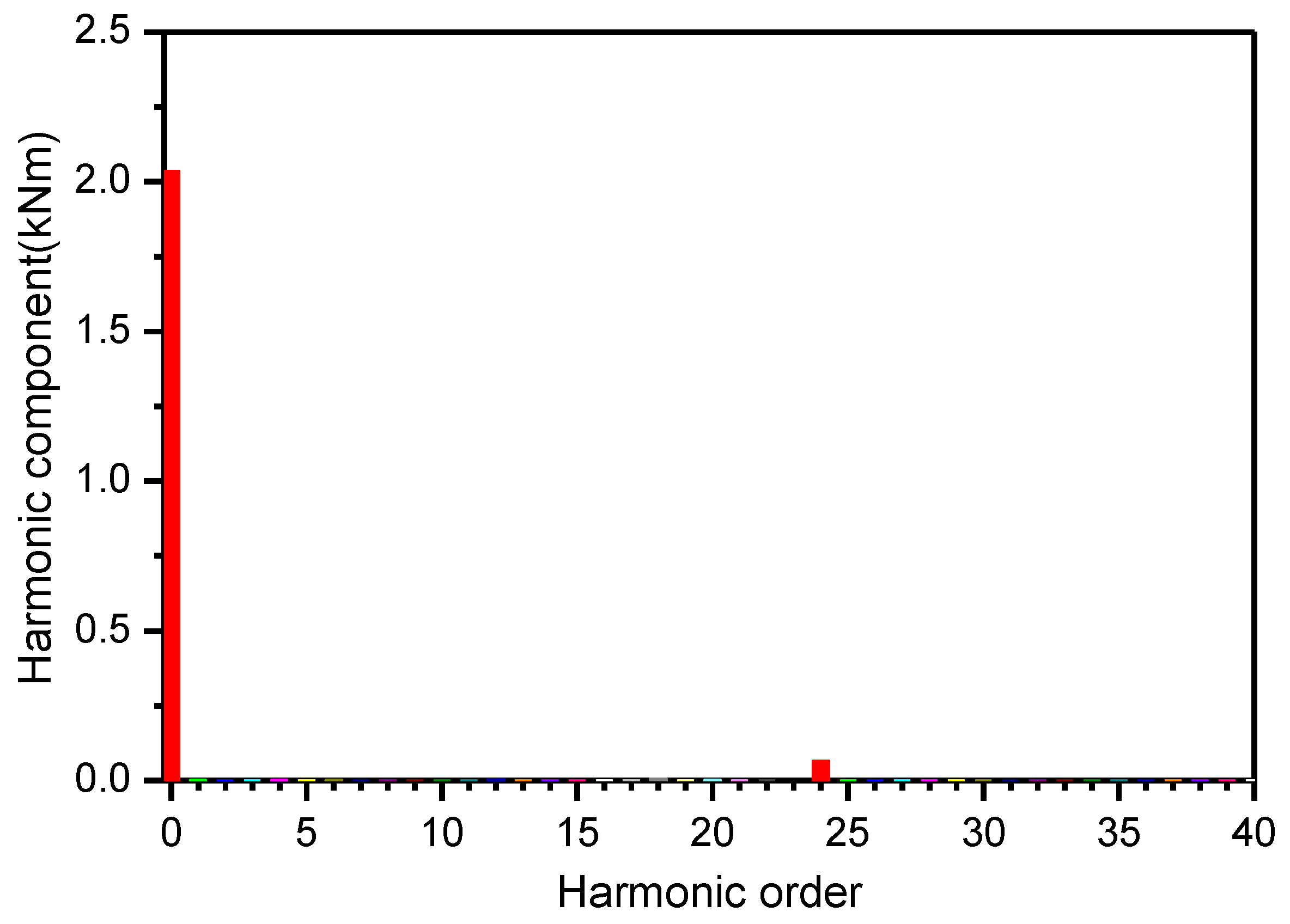
4.2. Analysis of the Electromagnetic Torque
4.3. Reduction of the Torque Ripple of the Motor
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jinghong, L. Drive System Design and Simulation Analysis for Hybrid Electric Vehicles. J. Shanghai Dianji Univ. 2007, 1, 33–35. [Google Scholar]
- Ruiqing, D. New energy vehicles development strategy research. J. New Ind. 2011, 1, 18–24. [Google Scholar]
- Lianqiao, T. The Full Text of China’s 13th Five-Year Plan. Available online: http://www.woc88.com/doc-12659458.html (accessed on 1 March 2018).
- Ningning, T. Finite Element Modeling and Multi-Field Coupling Analysis of BLDC Wheel Motor; Jilin University: Jilin, China, 2014. [Google Scholar]
- Shumei, C.; Junyun, S. The Research of the Direct-driven Wheel Motor Applied in Electric Vehicle. Micromotors Servo Tech. 2006, 39, 68–70. [Google Scholar]
- Xinmei, L. Design and Research of the High-Power Density Permanent Magnet In-Wheel Motor Based on the Reluctance Torque; Harbin Institute of Technology: Harbin, China, 2008. [Google Scholar]
- Tesla Model S. Automotive Observer 2018, 1, 25.
- Zhenpo, W.; Fengchun, S.; Peng, L. The Electric Car Principle and Application Technology; Mechanical Industry Press: Beijing, China, 2015. [Google Scholar]
- Ekram, S.; Mahajan, D.; Fazil, M.; Patwardhan, V.; Ravi, N. Design Optimization of Brushless Permanent Magnet Hub Motor Drive Using FEA. In Proceedings of the International Conference on Electrical Machines and Systems, Seoul, Korea, 8–11 October 2007; Volume 8, pp. 8–11. [Google Scholar]
- Gombert, B.; Fischer, R.; Heinrich, W. Wheel-Hub Motors Criteria of Construction and Vehicle Integrtation. ATZelektronik Worldw. 2010, 5, 4–10. [Google Scholar] [CrossRef]
- Rix, A.J.; Kamper, M.J. Radial-Flux Permanent-Magnet Hub Drives: A Comparison Based on Stator and Rotor Topologies. IEEE Trans. Ind. Electron. 2012, 59, 2475–2483. [Google Scholar] [CrossRef]
- Xiong, S. Motor drive technology research of the electric car. Silicon Val. 2014, 21, 41. [Google Scholar]
- Li, G.; Ojeda, J.; Hoang, E.; Gabsi, M.; Lecrivain, M. Thermal-electromag-netic analysis for driving cycles of embedded flux-switching permanent-magnet motors. IEEE Trans. Veh. Technol. 2012, 61, 140–151. [Google Scholar] [CrossRef]
- Hejra, M.; Mansouri, A. Optimal Design of a Permanent Magnet Synchronous Motor: Application of In-Wheel Motor. In Proceedings of the 15th Intemational Renewable Energy Congress IREC, Hammamet, Tunisia, 25–27 March 2014. [Google Scholar]
- Kock, A.; Groninger, M.; Mertens, A. Fault Tolerant Wheel Hub Drive with Integrated Converter for Electric Vehicle Applications. In Proceedings of the 2012 IEEE Vehicle Power and Propulsion Conference, Seoul, Korea, 9–12 October 2012. [Google Scholar]
- Tashakori, A.; Ektesabi, M. Fault diagnosis of in-wheel BLDC motor drive for electric vehicle application. In Proceedings of the 2013 IEEE Intelligent Vehicles Symposium, Gold Coast, QLD, Australia, 23–26 June 2013. [Google Scholar]
- Li, Y.; Wenjin, D. Theory and Practice of Motor Design; Tsinghua University Press: Beijing, China, 2013. [Google Scholar]
- Sumin, W. The Study on the Optimization for the Structural Parameters of Permanent Magnet Synchronous Motor Based on Ansoft; University of Electronic Science and Technology: Chengdu, China, 2014. [Google Scholar]
- Feng, Y.; Yang, K.; Gu, C. Design and optimization of external-rotor torque motor. In Proceedings of the 12th International Conference on Electrical Machines and Systems, Funabori, Tokyo, 15–18 November 2009; pp. 1–4. [Google Scholar]
- Yuejin, Z.; Chunjiang, L.; Guanzhen, T. Analytical Method for Air-Gap Main Magnetic Field Computation of Surface Mounted Permanent Magnet Torque Motors. Trans. China Electrotech. Soc. 2011, 26, 13–17. [Google Scholar]
- Lei, L. The Study of Thermal Characteristics in Various Conditions and Cooling System of Permanent Magnet Synchronous Motor in Pure Electric Vehicle; Hefei University of Technology: Chengdu, China, 2015. [Google Scholar]
- Zhu, Z.Q. Influence of Design Parameters on Cogging Torque in Permanent Magnet Machines. IEEE Trans. Energy Convers. 2000, 15, 407–412. [Google Scholar] [CrossRef]




| A Geely Automobile | Technical Parameters | Value |
|---|---|---|
| Basic parameters | The entire vehicle mass (kg) | 800 |
| Windward area A () | 2 | |
| Coefficient of air resistance | 0.32 | |
| Rolling resistance coefficient | 0.015 | |
| System transmission efficiency | 0.96 | |
| The wheel radius (m) | 0.27 | |
| Performance index | The maximum speed (km/h) | 80 |
| The maximum gradeability (°) | 11.3 | |
| 0–60 km/h acceleration time () | 9 |
| Parameters | Value |
|---|---|
| Rated power | |
| Peak power | |
| Rated speed | |
| Maximum speed | |
| Rated torque | |
| Phase number | M = 3 |
| Efficiency | |
| Permanent magnet material | N35SH |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Y.; Meng, W.; Sun, X.; Zhang, L. Design Optimization and Analysis of an Outer-Rotor Direct-Drive Permanent-Magnet Motor for Medium-Speed Electric Vehicle. World Electr. Veh. J. 2019, 10, 16. https://doi.org/10.3390/wevj10020016
Yuan Y, Meng W, Sun X, Zhang L. Design Optimization and Analysis of an Outer-Rotor Direct-Drive Permanent-Magnet Motor for Medium-Speed Electric Vehicle. World Electric Vehicle Journal. 2019; 10(2):16. https://doi.org/10.3390/wevj10020016
Chicago/Turabian StyleYuan, Yuan, Wenjun Meng, Xiaoxia Sun, and Liyong Zhang. 2019. "Design Optimization and Analysis of an Outer-Rotor Direct-Drive Permanent-Magnet Motor for Medium-Speed Electric Vehicle" World Electric Vehicle Journal 10, no. 2: 16. https://doi.org/10.3390/wevj10020016
APA StyleYuan, Y., Meng, W., Sun, X., & Zhang, L. (2019). Design Optimization and Analysis of an Outer-Rotor Direct-Drive Permanent-Magnet Motor for Medium-Speed Electric Vehicle. World Electric Vehicle Journal, 10(2), 16. https://doi.org/10.3390/wevj10020016




