Abstract
Device-to-device (D2D) communication is an essential feature for the future cellular networks as it increases spectrum efficiency by reusing resources between cellular and D2D users. However, the performance of the overall system can degrade if there is no proper control over interferences produced by the D2D users. Efficient resource allocation among D2D User equipments (UE) in a cellular network is desirable since it helps to provide a suitable interference management system. In this paper, we propose a cooperative reinforcement learning algorithm for adaptive resource allocation, which contributes to improving system throughput. In order to avoid selfish devices, which try to increase the throughput independently, we consider cooperation between devices as promising approach to significantly improve the overall system throughput. We impose cooperation by sharing the value function/learned policies between devices and incorporating a neighboring factor. We incorporate the set of states with the appropriate number of system-defined variables, which increases the observation space and consequently improves the accuracy of the learning algorithm. Finally, we compare our work with existing distributed reinforcement learning and random allocation of resources. Simulation results show that the proposed resource allocation algorithm outperforms both existing methods while varying the number of D2D users and transmission power in terms of overall system throughput, as well as D2D throughput by proper Resource block (RB)-power level combination with fairness measure and improving the Quality of service (QoS) by efficient controlling of the interference level.
1. Introduction
Device-to-device (D2D) communication is a nascent feature for the Long term evolution advanced (LTE-Advanced) systems. D2D communication can operate in centralized, i.e., Base station (BS) controlled mode, and decentralized mode, i.e., without a BS [1]. Unlike the traditional cellular network where Cellular users (CU) communicate through the base station, D2D allows direct communication between users by reusing the available radio resources. Consequently, D2D communication can provide improved system throughput and reduced traffic load to the BS. However, D2D devices generate interferences while reusing the resources [2,3]. Efficient resource allocation play a vital role in reducing the interference level, which positively impacts the overall system throughput. Fine tuning of power allocation on Resource blocks (RB) has consequences on interference, i.e., a higher transmission power can increase D2D throughput; however, it increases the interference level as well. Therefore, choosing the proper level of transmission power for RBs is a key research issue in D2D communication, which calls for adaptive power allocation methods.
Resource allocators, i.e., D2D transmitters in our system model as described in Section 3 need to perform a particular action at each time step based on the application demand. For example, actions can be selecting power level options for a particular RB [4]. Random power allocation is not suitable in a D2D communication due to its dynamic nature in terms of signal quality, interferences and limited battery capacity [5]. Scheduling of these actions associated with different levels of power helps to allocate the resources in such a way that the overall system throughput is increased and an acceptable level of interference is maintained. However, this is hard to maintain, and therefore, we need an algorithm for learning the scheduling of actions adaptively, which helps to improve the overall system throughput with fairness and the minimum level of interferences.
To illustrate the problem, Figure 1 shows a basic single cell scenario with one Cellular user (CU), two D2D pairs and one base station having two resource blocks operating in an underlay mode. D2D devices contend for resource blocks for reusing. Here, RB1 is allocated to the cellular user. D2D pair Tx and D2D pair Rx are assigned RB2. Now, D2D candidate Tx and D2D candidate Rx will contend for the resources either for RB1 or for RB2 to access. If we allocate RB1 to a D2D pair closer to the BS, there will be high interference between the D2D pair and the cellular user. So, RB1 should be allocated to the D2D candidate Tx which is closer to the cell edge (d2 > d3). For reusing the RB1, there will be interferences. Our goal is to propose an adaptive learning algorithm for selecting the proper level of power for the RB to minimize the level of interferences and maximize the throughput of the system.
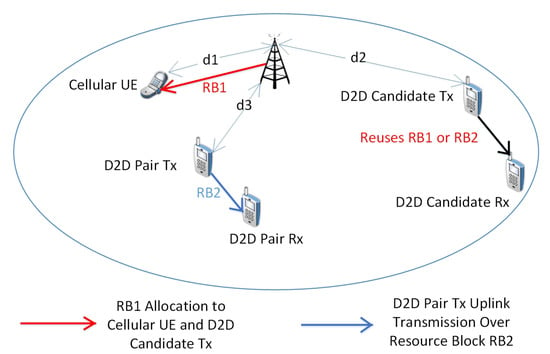
Figure 1.
Device-to-device (D2D) communication in a cellular network. RB1 and RB2 resource allocated to the Cellular User equipments (UE) and the D2D pair TX-D2D pair Rx, respectively. D2D candidate Tx-D2D candidate Rx has joined the network, it will contend for the resources, i.e., either reusing RB1 or RB2.
In contrast with existing works, our proposed algorithm helps to learn the proper action selection for resource allocation. We consider reinforcement learning with the cooperation between users by sharing the value function and incorporating a neighboring factor. In addition, we consider a set of states based on system variables which have an impact on the overall QoS of the system. Moreover, we consider both cross-tier interference (interference that the BS receives from D2D transmitter and that the D2D receivers receive from cellular users) and cotier interference (that the D2D receivers receive from D2D transmitters) [6]. To the best of our knowledge, this is the first work that considers all the above aspects for adaptive resource allocation in D2D communications.
The main contributions of this work can be stated as follows:
- We propose an adaptive and cooperative reinforcement learning algorithm to improve achievable system throughput as well as D2D throughput simultaneously. The cooperation is performed by sharing the value function between devices and imposing the neighboring factor in our learning algorithm. A set of actions is considered based on the level of transmission power for a particular Resource block (RB). Further, a set of states is defined considering the appropriate number of system-defined variables. In addition, the reward function is composed of Signal-to-noise-plus-interference ratio (SINR) and the channel gains (between the base station and user, and also between users). Moreover, our proposed reinforcement learning algorithm is an on-policy learning algorithm which considers both exploitation and exploration. This action selection strategy helps to learn the best action to execute, which has a positive impact on selecting the proper level of power allocation to resource blocks. Consequently, this method shows better performance regarding overall system throughput.
- We perform realistic throughput evaluation of the proposed algorithm while varying the transmission power and the number of D2D users. We compare our method with existing distributed reinforcement learning and random allocation of resources in terms of D2D and system throughput considering the system model where Resource block (RB)-power level combination is used for resource allocation. Moreover, we consider fairness among D2D pairs by computing a fairness index which shows that our proposed algorithm achieves balance among D2D users throughput.
The rest of the paper is organized as follows. Section 2 describes the related works. This is followed by the system model in Section 3. The proposed cooperative reinforcement learning based resource allocation algorithm is described in Section 4. Section 5 presents the simulation results. Section 6 concludes the paper with future works.
2. Related Works
Recent advances in Reinforcement learning (RL) create a broad scope of adaptive applications to apply. Resource allocation in D2D communication is such an application. Here, we describe at first some classical approaches [7,8,9,10,11,12,13,14,15,16] followed by existing RL-based resource allocation algorithms [17,18].
In [7], an efficient resource allocation technique for multiple D2D pairs is proposed considering the maximization of system throughput. By exploring the relationship between the number of Resource blocks (RB) per D2D pair and the maximum power constraint for each D2D pair, a sub-optimal solution is proposed to achieve higher system throughput. However, the interference among D2D pairs is not considered. Local water filling algorithm (LWFA) is used for each D2D pair which is computationally expensive. Feng et al. [8] introduce a resource allocation technique by maintaining the QoS of cellular users and D2D pairs simultaneously to enhance the system performance. A three-step scheme is proposed where the system performs admission control at first and then allocates the power to each D2D pair and its potential Cellular user (CU). A maximum weight bipartite Matching based scheme (MBS) is proposed to select a suitable CU partner for each D2D pair where the system throughput is maximized. However, this work basically focuses on suitable CU selection for the resource sharing where adaptive power allocation is not considered. In [9], a centralized heuristic approach is proposed where the resources of cellular users and D2D pairs are synchronized considering the interference link gain from D2D transmitter to the BS. They formulate the problem of radio resource allocation to the D2D communication as a Mixed integer nonlinear programming (MINLP). However, MINLP is hard to solve and the adaptive power control mechanism is not considered. Zhao et al. [10] propose a joint mode selection and resource allocation method for the D2D links to enhance the system sum-rate. They formulate the problem to maximize the throughput with SINR and power constraints for both D2D links and cellular users. They propose a Coalition formation game (CFG) with transferable utility to solve the problem. However, they do not consider the adaptive power allocation problem. In [11], Min et al. propose a Restricted interference region (RIR) where cellular users and D2D users can not coexist. By adjusting the size of the restricted interference region, they propose the interference control mechanism in a way that the D2D throughput is increased over time. In [12], the authors consider the target rate of cellular users for maximizing the system throughput. Their proposed method shows better results in terms of system interference. However, their work also focuses on the region control for the interference. They do not consider the adaptive resource allocation for maximizing the system throughput. A common limitation to the works as mentioned above is that they are fully centralized, which requires full knowledge of the link state information that produces redundant information over the network.
In addition to above-mentioned works, Hajiaghajani et al. [13] propose a heuristic resource allocation method. They design an adaptive interference restricted region for the multiple D2D pairs. In their proposed region, multiple D2D pairs share the resources where the system throughput is increased. However, their proposed method is not adaptive regarding power allocation to the users. In [14], the authors propose a two-phase optimization algorithm for the adaptive resource allocation which provides better results for system throughput. They propose Lagrangian dual decomposition (LDD) which is computationally complex.
Wang et al. [15] propose a Joint scheduling (JS) and resource allocation for the D2D underlay communication where the average D2D throughput can be improved. Here, the channel assigned to the cellular users is reused by only one D2D pair and the cotier interference is not considered. In [16], Yin et al. propose a distributed resource allocation method where minimum rates of cellular users and D2D pairs are maintained. A Game theoretic algorithm (GTA) is proposed for minimizing the interferences among D2D pairs. However, this approach provides low spectral efficiency.
With regards to machine learning for resource allocation in D2D communication, there are only few works, e.g., [17,18]. Luo et al. [17] and Nie et al. [18] exploit machine learning algorithms for D2D resource allocation. Luo et al. [17] propose Distributed reinforcement learning (DIRL), Q-learning algorithm for resource allocation which improves the overall system performance in comparison to the random allocator. However, the model of Reinforcement learning (RL) is not well structured. For example, the set of states and a set of actions are not adequately designed. Their reward function is composed of only Signal to interference plus noise power ratio (SINR) metric. The channel gain between the base station and the user, and also the channel gain between users are not considered. This is a drawback since channel gains are important to consider as these help the D2D communication with better SINR level and transmission power, which is reflected in increased system throughput [19].
Recently, Nie et al. [18] propose Distributed reinforcement learning (DIRL), Q-learning to solve the power control problem in underlay mode. In addition, they explore the optimal power allocation which helps to maintain the overall system capacity. However, this preliminary study has limitations, for example, in their reward function, the channel gains are not considered. In addition, in their system model only the transmit power level is considered for maximizing the system throughput. To consider RB/subcarrier allocation in the optimization function is a very important issue for mitigating interference [20]. Moreover, the cooperation between devices for resource allocation is not investigated in these existing works. A summary of the features and limitations of classical and RL-based allocation methods is given in Table 1.

Table 1.
Comparison of existing methods with the proposed cooperative reinforcement learning.
We propose adaptive resource allocation using Cooperative reinforcement learning (CRL) considering the neighboring factor, improved state space, and a reward function. Our proposed resource allocation method helps to provide mitigated interference level, D2D throughput and consequently an overall improved system throughput.
Table 1 shows the comparison of all the above mentioned works with our proposed cooperative reinforcement learning. Firstly, we categorize the related methods in two types: classical D2D resource allocation methods and Reinforcement learning (RL) based D2D resource allocation methods. We compare these works based on D2D throughput, system throughput, transmission alignment, online task scheduling for resource allocation, and cooperation. We can observe that almost all the methods consider the D2D and system throughput. None of the existing methods for resource allocation consider the transmission alignment, online action scheduling, and cooperation for the adaptive resource allocation.
3. System Model
We consider a network that consists of one Base station (BS) and a set of Cellular users (CU), i.e., . There are also D2D pairs, coexist with the cellular users within the coverage of BS. In a particular D2D pair, and are the D2D transmitter and D2D receiver respectively. The set of User equipments (UE) in the network is given by UE = . Each D2D transmitter selects an available Resource block (RB) r from the set . In addition, underlay D2D transmitters select the transmit power from a finite set of power levels, i.e., . Each D2D transmitter should select resources, i.e., RB-power level combination refers to transmission alignment [21].
For each RB , there is a predefined threshold for maximum aggregated interference. We consider that the value of is known to the transmitters using the feedback control channels. An underlay transmitter uses a particular transmission alignment in a way that the cross-tier interference should be within the threshold limit. According to our proposed system model, only one CU can be served by one RB where D2D users can reuse the same RB to improve the spectrum efficiency.
For each transmitter , the transmit power over the RBs is determined by the vector where denotes the transmit power level of transmitter over resource block r. If RB is not allocated to the transmitter then the power level . As we assume that each transmitter selects only one RB where only one entity in the power level .
Signal-to-interference-plus-noise-ratio (SINR) can be treated as an important factor to measure the link quality. The received SINR for any D2D receiver over rth RB as follows:
where and denote the uth D2D user and cellular user uplink transmission power on rth RB, respectively. , where is the upper bound of each D2D user’s transmit power. is the noise variance [9].
, and are the channel gains in the uth D2D link, the channel gain from D2D transmitter u to receiver v, and the channel gain from cellular transmitter c to receiver u, respectively. is a D2D pairs set sharing the rth RB.
The SINR of a cellular user on the rth RB is
where and indicate the channel gains on the rth RB from BS to cellular user c and vth D2D transmitter, respectively.
The total path-loss which includes the antenna gain between BS and the user u is:
where is the pathloss between a BS and the user at a distance d meter. is the log-normal shadow path-loss of user u. is the radiation pattern [22].
can be expressed as follows:
where is the carrier frequency in GHz and is the base station antenna height [22].
The linear gain between the BS and a user is .
For D2D communication, the gain between two users u and v is [23]. Here, is the distance between transmitter u and receiver v. is a constant pathloss exponent and is a normalization constant.
The objective of resource allocation problem (i.e., to allocate RB and transmit power) is to assign the resources in a way that maximizes system throughput. System throughput is the sum of D2D users and CU throughput, which is calculated by Equation (6).
The resource allocation can be indicated by a binary decision variable, where
The aggregated interference experienced by RB r can be expressed as follows
Let denote the resource e.g., RB and transmission power allocation. So, the allocation problem can be expressed as follows:
where and is the bandwidth corresponding to a RB. The objective function is to maximize the throughput of the system constrained by that the aggregated interference should be limited by a predefined threshold. The number of RB selected by the transmitter should be one where each can select one power level at each RB. Our goal is to investigate the optimal resource allocation in such a way that the system throughput is maximized by applying cooperative reinforcement learning.
4. Cooperative Reinforcement Learning Algorithm for Resource Allocation
In this section, we describe the basics of Reinforcement learning (RL), followed by our proposed cooperative reinforcement learning algorithm. After that, we describe the set of states, the set of actions and reward function for our proposed algorithm. Finally, Algorithm 1 shows the overall proposed resource allocation method and Algorithm 2 shows the execution steps of our proposed cooperative reinforcement learning.
We apply a Reinforcement learning (RL) algorithm named state action reward state action, SARSA(), for adaptive resource in D2D communication for efficient resource allocation. This variant of standard SARSA() [24] algorithm has some important features like cooperation by using a neighboring factor, a heuristic policy for exploration and exploitation, and a varying learning rate considering the visited state-action pair. Currently, we are applying the learning algorithm for the resource allocation of D2D users considering that the allocation of cellular users is performed prior to the allocation of D2D users. We consider the cooperative fashion of this learning algorithm which helps to improve the throughput as explained in Section 1 by sharing the value function and incorporating weight factors for the neighbors of each agent.
In reinforcement learning, there is no need for prior knowledge about the environment. Agents learn how to behave with the environment based on the previous experience achieved, which is traced by a parameter, i.e., Q-value and controlled by a reward function. There should be some actions/tasks to perform at every time step. After performing every action, the agents shifts from one state to another and it gets a reward that reflects the impact of that action, which helps to decide about the next action to perform. The basic reinforcement learning is a form of Markov decision process (MDP).
Figure 2 depicts the overall model of a reinforcement learning algorithm.
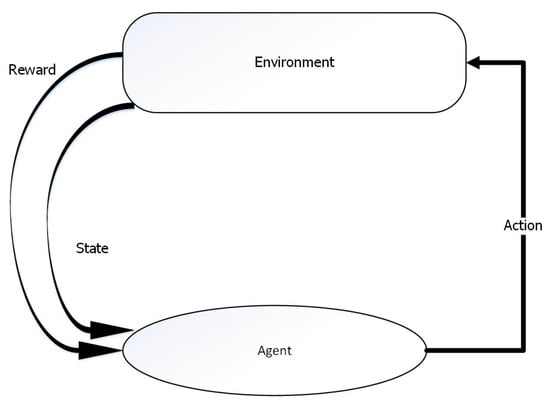
Figure 2.
Basic components of a reinforcement learning. The agent performs an action to the environment which gives a reward and helps to shift from one state to another.
Each agent in RL has the following components [25]:
- Policy: The policy acts as a decision making function for the agents. All other functions/components help to improve the policy for better decision making.
- Reward function: The reward function defines the ultimate goal of an agent. This helps to assign a value/number to the performed action, which indicates the intrinsic desirability of the states. The main objective of the agent is to maximize the reward function in the long run.
- Value function: The value function determines the suitability of action selection in the long run. The value of a state is accumulated reward over long run when starting from the current state.
- Model: The model of the environment mimics the behavior of the environment which consists of a set of states and a set of actions.
In our model of the environment, we consider the components of the reinforcement learning algorithm as follows:
Agent: All the resource allocators: D2D Transmitters.
State: The state of D2D user u on RB r at time t is defined as:
We consider three variables , and for defining the states for maintaining the overall quality of the network. is the SINR of a cellular user on the rth RB. is the channel gain between the BS and an user u. is the channel gain between two users u and v. The variables , and are important to consider for the resource allocation. The SINR is the indicator of the quality of service of the network. In addition, if the channel gains ( and ) quality is good then it is possible to achieve higher throughput without excessively increasing the transmit power, i.e., without causing too much interference to others. On the other hand, if the channel gain is too low, higher transmit power is required, which leads to increased interference.
Now, the state values of these variables can be either 0 or 1 based on following conditions. If the value of the variables are greater than or equal to a threshold value, then this denotes that their state value is ‘0’. On the contrary, if the values are less than the threshold value, then their state value is ‘1’. So, means state value ’1’ and means state value ’0’. Similarly, means state value ‘1’ and means state value ‘0’. Consequently, means state value ‘1’ and means the state value ‘0’. In this way, based on the combination of the value of these variables, the total number of possible states is eight where , and are the minimum SINR and channel gain guaranteeing the QoS performance of the system.
Action/Task: The action of each agent consists of a set of transmitting power levels. It is denoted by
where r represents the rth Resource Block (RB), and means that every agent has power levels. In this work, we consider the power levels to assign within the range of 1 to in the interval of 1 dBm.
Reward Function: The reward function for the reinforcement learning is designed focusing on the throughput of each agent/user which is formulated as follows:
when , and . Otherwise, ℜ = − 1. SINR (u) denotes the signal to interference plus noise power ratio of user u (Step 7–10 in Algorithm 1).
SARSA() is an on-policy reinforcement learning algorithm that estimates the value of the policy being followed where is a parameter such as learning rate [26]. In SARSA learning algorithm, every agent needs to maintain a Q matrix which is initially assigned 0 and the agents may be in any state. Based on performing one particular action, it shifts from one state to another. The basic form of the learning algorithm is , which means that the agent was in state , did action , received reward ℜ, and ended up in state , from which it decided to perform action . This provides a new iteration to update .
SARSA() helps to find out the appropriate sets of actions for some states. The considered state-action pair’s value function as follows:
In Equation (8), is a discount-factor which varies from 0 to 1. The higher the value, the more the agent relies on future rewards than on the immediate reward. The objective of applying reinforcement learning is to find the optimal policy which maximizes the value function . We consider the cooperative fashion of this algorithm where each agent shares the value function with each other.
At each time step, for the iteration , is updated with the temporal difference error and the immediate received reward. The Q value has the following update rules:
for all s, a.
In Equation (9), is the learning rate which decreases with time. is the temporal difference error which is calculated by following rule (Step 7 in Algorithm 2):
In Equation (10), is a discount-factor which varies from 0 to 1. The higher the value, the more the agent relies on future rewards than on the immediate reward. represents the reward received for performing an action. f is the neighboring weight factor of agent i where this factor consists of the effect of neighbor’s Q-value, which helps to update the Q-value of agent i that is calculated as follows [27]:
where is the number of neighbors of agent i within the D2D radius. BS provides the information of number of neighbors for each agent [28].
There is a trade-off between exploration and exploitation in reinforcement learning. Exploration chooses an action randomly in the system to find out the utility of that chosen action. Exploitation deals with the actions which have been chosen based on previously learned utility of the actions.
We use a heuristic for exploration probability at any given time such as:
where and denote upper and lower boundaries for the exploration factor, respectively. represents the maximum number of states which is eight in our work and S represents the current number of states already known [29]. At each time step, the system calculates and generates a random number in the interval . If the selected random number is less than or equal to , the system chooses a uniformly random task (exploration), otherwise it chooses the best task using Q values (exploitation). k is a constant which controls the effect of unexplored states (Step 4 in Algorithm 2).
SARSA() helps to improve the learning technique by eligibility trace. In Equation (9), is the eligibility trace. The eligibility trace is updated by the following rule:
Here, is learning parameter for guaranteed convergence, whereas is the discount factor. In addition, the eligibility trace helps to provide higher impact on revisited states. For example, for a state-action pair , if and , the state-action pair is reinforced. Otherwise, the eligibility trace is removed (Step 8 in Algorithm 2).
The learning rate is decreased in such a way that it reflects the degree to which a state-action pair has been chosen in the recent past. It is calculated as:
where is a positive constant and represents the visited state-action pairs so far [30] (Step 6 in Algorithm 2).
| Algorithm 1: Proposed resource allocation method |
| Input : = 23 dBm, Number of resource blocks = 30, Number of cellular users = 30, Number of D2D user pairs = 12, D2D radius = 20 m, Pathloss parameter = 3.5, Cell radius = 500 m, = 0.004, = 0.2512, = 0.2512 [9] Output: RB-Power level, System Throughput
|
| Algorithm 2: Cooperative SARSA() reinforcement learning algorithm over number of iterations. |
|
Algorithm 1 depicts the overall proposed resource allocation method. After setting the initial input parameters, the system oriented parameters, i.e., pathloss, channel gains, SINR of the D2D users and cellular users on the rth RB are calculated (Step 2–6 in Algorithm 1). Then the reward function is calculated (Step 8) and is assigned when the state values satisfy the constraint in step 7. After that Algorithm 2 is applied for the adaptive resource allocation. Algorithm 2 shows our proposed reinforcement learning algorithm execution steps for resource allocation over number of iterations.
5. Performance Evaluation
We implement our proposed cooperative reinforcement learning algorithm and compare it with the random allocation and existing distributed reinforcement learning algorithm.
The parameters for the simulation are shown in Table 2.

Table 2.
Simulation Parameters.
We consider a single cell with a radius of 500 m where some cellular users and D2D pairs are uniformly distributed within the coverage of the BS. There are 30 cellular users and 12 D2D users. We consider a constraint of resources with only 30 resource blocks.
We consider = 0.004, = 0.2512 and = 0.2512 as constraints to define the states for maintaining the quality of service [9]. In our reinforcement learning algorithm, we consider = 0.3, = 0.1 and k = 0.25 [29]. We set = 1 for learning rate calculation in Equation (14). The discount factor, is considered based on the work [17] for fair comparison with our work.
We compare our method with the distributed reinforcement learning proposed in [17] and a base-line random allocation of resources.
5.1. Throughput Analysis over Number of Iterations
Figure 3a shows that the proposed cooperative reinforcement learning outperforms both the random allocation and the distributed reinforcement learning regarding average system throughput calculated by Equation (6) considering 12 D2D user pairs and other parameter values as in Table 2. We can observe that after the 30th iteration (Figure 3b), our proposed learning algorithm outperforms other methods at almost every iteration when the algorithm reaches the convergence of learning. In addition, there are variations in throughput results for each method and also there are some points where distributed reinforcement learning outperforms proposed cooperative reinforcement learning due to the fact that we consider the heuristic action selection policy based on exploration and exploitation in Equation (13), which avoids to stuck the learning algorithm in a local optimum. Random allocation shows poor results since it does not act appropriately with the changes of the environment. Whereas, distributed reinforcement learning shows moderate results comparing with the both methods. We consider 100 iterations here for the comparison, but the trend of outperformance of our proposed algorithm remains the same with additional iterations.
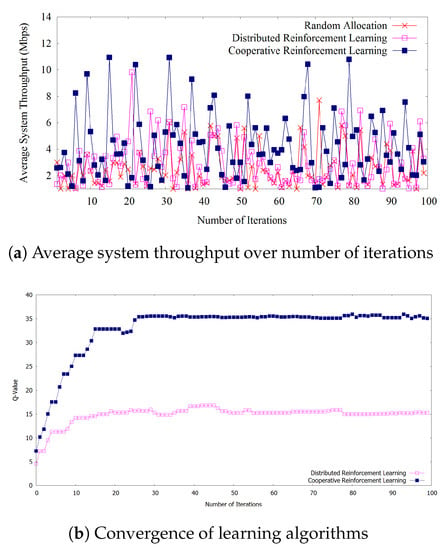
Figure 3.
(a) Average system throughput over number of iterations (b) Convergence of learning algorithms.
Figure 3b shows the Q-values calculated by Equation (9) of distributed reinforcement learning and cooperative reinforcement learning over number of iterations for learning. We can observe that the cooperative reinforcement learning converges faster due to the sharing learned policies between devices. Further, our proposed learning algorithm provides better Q-value at each time step which imposes an impact on the overall improved system throughput. Moreover, higher Q-values denote that action scheduling strategies are performed much better in our proposed algorithm.
5.2. Throughput Analysis by Varying the Transmit Power Level
Figure 4 shows the average D2D throughput over transmit power applying our proposed method, distributed reinforcement learning and random allocation of resources. All the methods follow the same trend that with the increase of transmit power, D2D throughput increases. Our proposed reinforcement learning outperforms others at every level of transmit power due to the appropriate learning of transmission power assignment to the resource blocks. Our proposed method increases D2D throughput by 6.2% as compared with the distributed reinforcement learning. On the other hand, random allocation shows the lowest performance as usual due to the allocation of resources without adaptiveness.
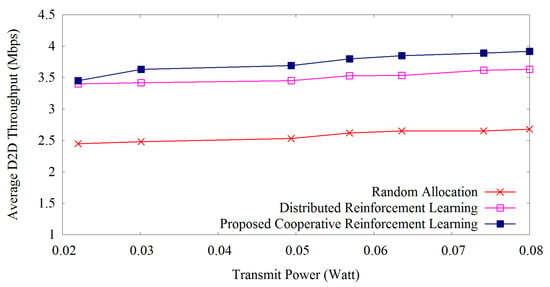
Figure 4.
D2D throughput versus transmit power.
Figure 5 shows the trade-off between D2D throughput and cellular user throughput when varying the transmit power to these values {0.0569, 0.0741, 0.0800} after applying the proposed cooperative reinforcement learning, random allocation, and distributed reinforcement learning where the results are grouped into three sets for each method considering 12 D2D users. For all methods, we can observe the same trends, for example, with the increase of transmit power; D2D throughput increases but cellular user throughput decreases which show the typical phenomena of D2D communication. When the transmit power of the D2D device increases, the D2D throughput also increases. But this provides an impact of interference level to the cellular users which provides lower cellular user throughput. Our proposed method outperforms all methods in terms of D2D and cellular user throughput. For example, when the transmit power is equal to 0.0569, our proposed learning algorithm provides a D2D throughput equal to 3.80, and the cellular user throughput is equal to 2.912. On the other hand, for distributed reinforcement learning, the D2D and the cellular user throughput are 3.53 and 2.734, respectively which is lower than our proposed method. Moreover, random allocation of resources provides the least amount of D2D and cellular user throughput with values equal to 2.62 and 2.27, respectively.
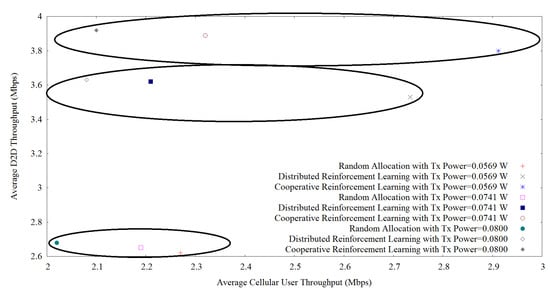
Figure 5.
Joint D2D throughput and cellular user throughput optimization.
5.3. Throughput Analysis over a Number of D2D Users
Figure 6 shows the average D2D throughput, average cellular user throughput and the average system throughput over the number of D2D users. We can observe that D2D throughput increases with the increase of D2D users, but on the other hand, cellular user throughput decreases. System throughput is the summation of D2D and the cellular user throughput, which also increases with the increment of the D2D users. For example, our proposed method provides a cellular user throughput equal to 2.912 for 10 D2D users. The proposed method yields 0.2880 as D2D user throughput, which gives a system throughput equal to 3.2. When we increase the number of D2D users to 20, the figure shows a cellular user throughput, D2D throughput, and overall system throughput of 2.8259, 0.5477 and 3.3736, respectively.
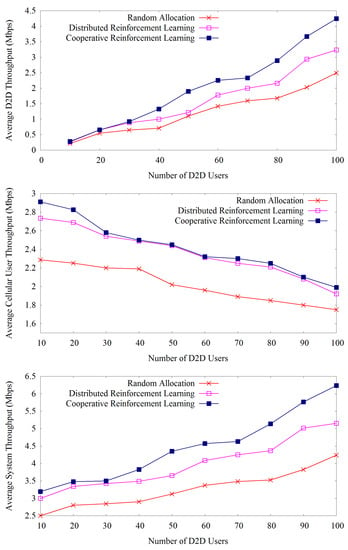
Figure 6.
Throughput analysis over a number of D2D users.
All methods show these same trends over the number of D2D users. From this experiment, we can also investigate the issue about the appropriate number of D2D users which provides the better trade-off between D2D and cellular user throughput in a single cell scenario. Here, we can observe that moderate number of D2D users, for example, 50 D2D users provide suitable amount of D2D and cellular user throughput. Our proposed method outperforms the other methods regarding D2D throughput, cellular user throughput and overall system throughput at every number of D2D users.
5.4. Fairness Analysis
We compute the fairness of our proposed algorithm, the distributed reinforcement learning algorithm, and the random allocation using Jain’s fairness index [31]. Jain’s fairness index can be derived as
where D is the throughput of each device and N is the number of users. Jain’s fairness is used to determine the fairness of the algorithm which helps to make a stable environment of D2D throughput for each D2D pairs.
Figure 7 shows the fairness measure of our proposed learning algorithm, distributed reinforcement learning and random allocation of resources. The higher value of Jain’s index shows a better balance of resources, i.e., fairness. We observe that our proposed algorithm outperforms the two others in terms of fairness. With the increase of D2D pairs, we can see that there is a slight decrease in the fairness level. As our learning algorithm works online based on the proper level of transmit power allocation, we get suitable results in terms of fairness. The distributed reinforcement learning shows comparably less performance with the proposed method. Random allocation of resource provides the worst fairness because it does not use adaptive action scheduling strategy for the resource allocation.
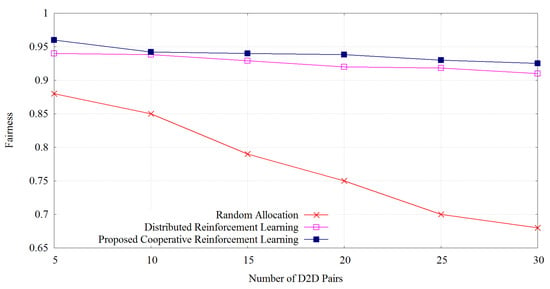
Figure 7.
Fairness index of D2D throughput versus number of D2D pairs.
6. Conclusions
Adaptive resource allocation is a critical issue for the current context in D2D communication. Reinforcement learning can be considered as a suitable method for the adaptive resource allocation by scheduling the actions performed by the resource allocators. In this work, we apply a cooperative reinforcement learning for the resource allocation to improve the system throughput and D2D throughput. A key aspect of our work is that we consider cooperation between agents by sharing the value function and imposing a neighboring factor. In addition, the set of states for our proposed reinforcement learning is composed of important system defined variables which helps to increase the observation space that has to be explored. We measure the fairness of our proposed algorithm considering a fairness index. Our method is compared with the distributed reinforcement learning and random allocation of the resource. The results show better performance regarding system throughput, D2D throughput, and the fairness measure.
All results (showed in Section 5) help us to reach the following decisions:
- Our proposed cooperative reinforcement learning method provides better performance regarding system throughput compared to the distributed reinforcement learning, and random allocation of resources. There are some time steps where distributed reinforcement learning outperforms our proposed method due to our heuristic action selection strategy for exploration and exploitation.
- Our proposed method outperforms the distributed reinforcement learning and random allocation of resources in terms of D2D throughput while varying the transmit power. It is possible to observe that in our proposed method, D2D throughput increases about 6.2% compared to the distributed reinforcement learning.
- The trade-off is observed for D2D and cellular user throughput by varying the transmit power at different values, we can observe that higher transmit power provides higher D2D throughput. Our proposed reinforcement learning provides better results regarding both D2D and cellular user throughput compared to the distributed reinforcement learning and random allocation of resources. By increasing the number of D2D users, we can observe higher D2D and the system throughput.
- Higher index value provides higher fairness measure in Jain’s fairness index. We can observe that our proposed reinforcement learning outperforms the distributed reinforcement learning and random allocation of resources regarding fairness measure.
Currently, we are considering a single cell for our work. As future work, we will consider multiple cells with more dynamics in the environment. Investigating the latency and energy efficiency issues can further be considered. In addition, currently we are not considering the learning algorithms for BS. To include BS as an agent to apply learning algorithm might enhance the QoS for allocating resources to cellular users. Designing the system in a more distributed way considering multiple cells might utilize the full benefits of applying reinforcement learning.
Acknowledgments
This research was supported by the Estonian Research Council through the Institutional Research Project IUT19-11, and by the Horizon 2020 ERA-chair Grant “Cognitive Electronics COEL”-H2020-WIDESPREAD-2014-2 (Agreement number: 668995; project TTU code VFP15051).
Author Contributions
The main concept to solve the problem was conceived by Muhidul Islam Khan. Furthermore, the initial system model was designed and implemented by Muhidul Islam Khan. Muhammad Mahtab Alam worked on to further improve the problem formulation, overall concept of the work and to improve the writing structure of the paper. Elias Yaacoub provided useful suggestions based on to improve the system model and basic components of the method. Yannick Le Moullec helped to enhance the writing style, and review the paper to make it more structured.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Doppler, K.; Rinne, M.; Wijting, C.; Ribeiro, C.B.; Hugl, K. Device-to-device communication as an underlay to LTE-advanced networks. IEEE Commun. Mag. 2009, 47. [Google Scholar] [CrossRef]
- Fodor, G.; Dahlman, E.; Mildh, G.; Parkvall, S.; Reider, N.; Miklós, G.; Turányi, Z. Design aspects of network assisted device-to-device communications. IEEE Commun. Mag. 2012, 50. [Google Scholar] [CrossRef]
- Xiao, X.; Tao, X.; Lu, J. A QoS-aware power optimization scheme in OFDMA systems with integrated device-to-device (D2D) communications. In Proceedings of the 2011 IEEE Vehicular Technology Conference (VTC Fall), San Francisco, CA, USA, 5–8 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–5. [Google Scholar]
- Khan, M.I.; Rinner, B. Resource coordination in wireless sensor networks by cooperative reinforcement learning. In Proceedings of the 2012 IEEE International Conference on Pervasive Computing and Communications Workshops (PERCOM Workshops), Lugano, Switzerland, 19–23 March 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 895–900. [Google Scholar]
- Della Penda, D.; Fu, L.; Johansson, M. Energy efficient D2D communications in dynamic TDD systems. IEEE Trans. Commun. 2017, 65, 1260–1273. [Google Scholar] [CrossRef]
- Boabang, F.; Nguyen, H.H.; Pham, Q.V.; Hwang, W.J. Network-Assisted Distributed Fairness-Aware Interference Coordination for Device-to-Device Communication Underlaid Cellular Networks. Mob. Inf. Syst. 2017, 2017, 1821084. [Google Scholar] [CrossRef]
- Kai, Y.; Zhu, H. In Proceedings of the Resource allocation for multiple-pair D2D communications in cellular networks. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 2955–2960. [Google Scholar]
- Feng, D.; Lu, L.; Yuan-Wu, Y.; Li, G.Y.; Feng, G.; Li, S. Device-to-device communications underlaying cellular networks. IEEE Trans. Commun. 2013, 61, 3541–3551. [Google Scholar] [CrossRef]
- Zulhasnine, M.; Huang, C.; Srinivasan, A. Efficient resource allocation for device-to-device communication underlaying LTE network. In Proceedings of the 2010 IEEE 6th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Niagara Falls, NU, Canada, 11–13 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 368–375. [Google Scholar]
- Zhao, J.; Chai, K.K.; Chen, Y.; Schormans, J.; Alonso-Zarate, J. Joint mode selection and resource allocation for machine-type D2D links. Trans. Emerg. Telecommun. Technol. 2015. [Google Scholar] [CrossRef]
- Min, H.; Lee, J.; Park, S.; Hong, D. Capacity enhancement using an interference limited area for device-to-device uplink underlaying cellular networks. IEEE Trans. Wirel. Commun. 2011, 10, 3995–4000. [Google Scholar] [CrossRef]
- Yu, G.; Xu, L.; Feng, D.; Yin, R.; Li, G.Y.; Jiang, Y. Joint mode selection and resource allocation for device-to-device communications. IEEE Trans. Commun. 2014, 62, 3814–3824. [Google Scholar] [CrossRef]
- An, R.; Sun, J.; Zhao, S.; Shao, S. Resource allocation scheme for device-to-device communication underlying lte downlink network. In Proceedings of the 2012 International Conference on Wireless Communications & Signal Processing (WCSP), Huangshan, China, 25–27 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–5. [Google Scholar]
- Esmat, H.H.; Elmesalawy, M.M.; Ibrahim, I.I. Adaptive Resource Sharing Algorithm for Device-to-Device Communications Underlaying Cellular Networks. IEEE Commun. Lett. 2016, 20, 530–533. [Google Scholar] [CrossRef]
- Wang, F.; Song, L.; Han, Z.; Zhao, Q.; Wang, X. Joint scheduling and resource allocation for device-to-device underlay communication. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 134–139. [Google Scholar]
- Yin, R.; Yu, G.; Zhang, H.; Zhang, Z.; Li, G.Y. Pricing-based interference coordination for D2D communications in cellular networks. IEEE Trans. Wirel. Commun. 2015, 14, 1519–1532. [Google Scholar] [CrossRef]
- Luo, Y.; Shi, Z.; Zhou, X.; Liu, Q.; Yi, Q. Dynamic resource allocations based on Q-learning for D2D communication in cellular networks. In Proceedings of the 2014 11th International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP), Chengdu, China, 19–21 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 385–388. [Google Scholar]
- Nie, S.; Fan, Z.; Zhao, M.; Gu, X.; Zhang, L. Q-learning based power control algorithm for D2D communication. In Proceedings of the 2016 IEEE 27th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Valencia, Spain, 4–8 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Hwang, Y.; Park, J.; Sung, K.W.; Kim, S.L. On the throughput gain of device-to-device communications. ICT Express 2015, 1, 67–70. [Google Scholar] [CrossRef]
- Mehta, M.; Aliu, O.G.; Karandikar, A.; Imran, M.A. A self-organized resource allocation using inter-cell interference coordination (ICIC) in relay-assisted cellular networks. arXiv, 2011; arXiv:1105.1504. [Google Scholar]
- Semasinghe, P.; Hossain, E.; Zhu, K. An evolutionary game for distributed resource allocation in self-organizing small cells. IEEE Trans. Mob. Comput. 2015, 14, 274–287. [Google Scholar] [CrossRef]
- Graziosi, F.; Santucci, F. A general correlation model for shadow fading in mobile radio systems. IEEE Commun. Lett. 2002, 6, 102–104. [Google Scholar] [CrossRef]
- Zulhasnine, M.; Huang, C.; Srinivasan, A. Penalty function method for peer selection over wireless mesh network. In Proceedings of the 2010 IEEE 72nd Vehicular Technology Conference Fall (VTC 2010-Fall), Ottawa, ON, Canada, 6–9 September 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–5. [Google Scholar]
- Khan, M.I. Resource-aware task scheduling by an adversarial bandit solver method in wireless sensor networks. EURASIP J. Wirel. Commun. Netw. 2016, 2016. [Google Scholar] [CrossRef]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998; Volume 1. [Google Scholar]
- Khan, M.I.; Rinner, B. Performance analysis of resource-aware task scheduling methods in Wireless sensor networks. Int. J. Distrib. Sensor Netw. 2014, 10, 765182. [Google Scholar] [CrossRef]
- Chen, M.; Chen, J.; Ma, Y.; Yu, T.; Wu, Z. Base station assisted device-to-device communications for content update network. In Proceedings of the 2015 First International Conference on Computational Intelligence Theory, Systems and Applications (CCITSA), Yilan, Taiwan, 10–12 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 23–28. [Google Scholar]
- Shah, K.; Kumar, M. Distributed independent reinforcement learning (DIRL) approach to resource management in wireless sensor networks. In Proceedings of the 2007 IEEE International Conference on Mobile Adhoc and Sensor Systems (MASS), Pisa, Italy, 8–11 October 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1–9. [Google Scholar]
- Khan, M.I.; Rinner, B. Energy-aware task scheduling in wireless sensor networks based on cooperative reinforcement learning. In Proceedings of the 2014 IEEE International Conference on Communications Workshops (ICC), Sydney, NSW, Australia, 10–14 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 871–877. [Google Scholar]
- Jain, R.; Chiu, D.M.; Hawe, W.R. A Quantitative Measure of Fairness and Discrimination for Resource Allocation in Shared Computer System; Digital Equipment Corporation: Hudson, MA, USA, 1984; Volume 38. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).