Abstract
In this paper, an energy efficient power allocation scheme is proposed for a distributed massive multiple-input multiple-output (MIMO) system with a circular antenna array. Single-antenna users simultaneously transmit signal to the base station (BS) with a large number of distributed antennas. The tight approximation of the energy efficiency (EE) is derived in closed form expressions. Through jointly optimizing the power allocation and the antenna number of BS, an NP-hard problem is formulated to maximize the EE. The equal power allocation is proved to be optimal given the total transmit power and the number of antennas. Finally, the optimal antenna number is determined by one dimension search. It is noteworthy that the NP-hard problem is solved by one dimension search. Simulation results validate the accuracy and the low-complexity of our proposed scheme.
1. Introduction
With the world-wide popularization of fourth-generation networks, mobile data traffic and the number of user equipments (UEs) are increasing exponentially. To satisfy the growing requirement, key technologies have been proposed and studied recently for fifth-generation (5G) networks [1,2].
1.1. Related Work
Massive multiple-input multiple-output (MIMO) with a large antenna array is a promising technology to satisfy the high requirement of 5G. In a massive MIMO system, the base station (BS) equipped with a hundreds of antennas simultaneously provides services for tens of UEs in the same time-frequency resource [3]. Benefiting from the large-scale antenna array, the energy can be concentrated into narrow beams towards receivers. Compared with traditional MIMO systems, massive MIMO systems can achieve higher spectral efficiency (SE) and energy efficiency (EE) [4].
A tight lower bound of achievable rate was derived for the multi-cell multi-user uplink MIMO systems in [5]. Ngo et al. derived exact uplink rate, the symbol error rate (SER), and the outage probability for the uplink of massive single-input multiple-output systems (SIMO) [6]. Zhao et al. derived a tight lower bound of area spectrum efficiency (ASE) for the downlink of a massive MIMO system with zero-forcing (ZF) precoding [7]. Lin et al. derived an approximate expression of the SE for the downlink with maximum-radio transmission (MRT) precoding [8].
To satisfy an achievable rate requirement, Ngo et al. proved that the transmit power of UEs can be made inversely proportional to the number of antennas when the channel state information (CSI) is available at the BS [9]. By contrast, the power consumption of the RF circuits grew linearly with the antenna number. Therefore, the EE is an important metric of 5G networks, since it represents the ratio between the SE and the total power consumption. Ha et al. proved that the EE is quasi-concave with respect to (w.r.t.) the number of antennas [10]. Emil et al. analyze how to maximize the EE by optimizing the transmit power of UEs, active users, and antenna number [11]. A power allocation scheme was proposed to maximize the EE of the downlink massive MIMO system with MRT precoding [12]. Ng et al. investigated power allocation, subcarrier allocation, and antenna allocation policies to improve the EE in orthogonal frequency division multiple access (OFDMA) downlink massive MIMO systems. To solve the NP-hard problem, an efficient iterative algorithm was proposed based on fractional programming [13]. Chunk-based resource allocation was proposed through maximizing the throughput under a total transmit power constraint for OFDMA systems [14,15]. Base on Dinkelbach’s method, an energy-efficient resource allocation algorithm was proposed for multi-cell OFDMA systems with limited backhaul capacity [16]. A low complexity distributed algorithm was proposed to solve the energy efficient user association problem in massive MIMO enabled heterogeneous networks [17]. Emil et al. analyzed and optimized the EE of massive MIMO systems with non-ideal hardware [18].
The achievable rates of cell-boundary users is relatively low due to the path loss. Distributed antenna systems (DAS) can mitigate the near–far problem by using distributed radio remote heads (RRHs) [19]. To reap all the benefits of massive MIMO and DAS, the combination of them has recently been hotly studied. The average SE and the the cell edge SE were compared in downlink multi-cell DAS systems [20]. Senanayake et al. derived closed-form expressions for the signal-to-noise ratio (SNR), the symbol error probability (SEP), and the achievable rate for distributed massive MIMO with zero forcing [21]. The SE of centralized and distributed massive MIMO systems were respectively analyzed and compared [22]. A closed-form optimal precoding scheme was derived to maximize the worst-case SNR for massive distributed MIMO systems [23]. He et al. derived an approximate EE expression for both the idealistic and the realistic power consumption models of distributed massive MIMO systems [24]. Kim et al. jointly optimized time allocation and energy beamforming to maximize the EE of distributed massive MIMO system with energy harvesting [25].
1.2. Motivation and Contribution
For massive MIMO systemS with circularly distributed antennas, higher achievable rates can be achieved with the increase of the transmit power and the number of antennas [26]. Meanwhile, the total power consumption increases as the increasement of power consumption of RF circuits and the transmit power. Inspired by this fact, we jointly optimized the transmit power, the power allocation coefficients, and the number of antennas to maximize the EE. The main contributions of this work are summarized as:
- A tight EE expression is derived in closed-form for the distributed massive MIMO system with circular antenna array.
- To maximize the EE, an optimization problem was formulated to jointly determine the transmit power, power allocation, and the number of antennas. Further, the NP-hard problem is solved by one-dimension search.
- For a given number of antennas and the total transmit power, the optimal power allocation coefficients are derived in closed-form expressions.
- For a given number of antennas, the optimal total transmit power is derived in closed-form.
- To further maximize the EE, the number of transmit antennas are optimized by one-dimension search.
- Simulation results validate the accuracy and the low-complexity of our proposed scheme.
2. System Model
Similarly to [26], we consider the uplink of the single-cell multi-user massive MIMO system as shown in Figure 1, where the BS is equipped with large-scale antennas located on a circle with radius r. The BS equipped with N antennas serves K single-antenna UEs with the same time frequency resource. On one hand, the path-loss fading can be effectively reduced by the distributed antennas. On the other hand, it is more easy to connect the circularly located BS antennas by optical fibres. Similarly to [9], we assume that . All antennas connect with central processing unit through high-speed fiber. The channel fading keeps invariant in one time block, but changes independently from one block to another. We assume that the perfect channel state information is available at the BS by reciprocity in the time division duplex system. Based on the perfect CSI available at the BS, ZF linear technique is used to detect the data from the UEs.
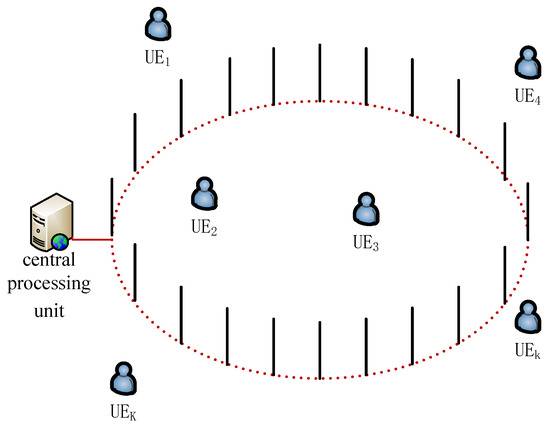
Figure 1.
Massive multiple-input multiple-output (MIMO) system with circularly distributed antennas; K user equipments (UEs) simultaneously transmit signal to the base station (BS) with N antennas located on a circle with radius r.
Assuming that the channel fading between the n-th antenna of BS to the k-th UE is
where represents the fast fading, and represents the path-loss given as
where is the distance between the k-th UE and the n-th antenna of the BS, and v is the path-loss exponent. The channel vector between the BS and the k-th UE is
The channel matrix between the BS and all K UEs is given as
Denote as the normalized data symbol from UE k; i.e., . P is the total transmit power of all the UEs, and is the power allocation vector. That is, the transmit power of the k-th UE is . The vector of the received signal at the BS is
where is the additive white Gaussian noise (AWGN) with variance (i.e., ). The linear detector matrix is given as . After linear processing, the received signal can be given as
The received signal from the k-th UE is given as
where is the k-th column of matrix . Note that the interference terms are eliminated by ZF detector.
3. Energy Efficiency Analysis
The achievable rate of the k-th UE is given as
Then, the sum-rate of the uplink massive MIMO system can be given as
Denoted as , the total power consumption of the system consists of four parts; i.e.,
where denotes the basic power consumption of the system, is the circuit power consumption per the radio frequency (RF) chain, and is the power amplifier efficiency. The EE can be expressed as
Theorem 1.
The EE of the distributed massive MIMO system can be tightly approximated by the following deterministic value
Proof.
Similarly to [26], the achievable rate of the k-th user falls in the interval of [] or [] when N is large, where
and
In addition, we have . Thus, the sum-rate can be tightly approximated by
Combining (10), we can conclude the proof. ☐
4. Energy Efficiency Optimization
4.1. Problem Formulation
It can be seen from (12) that the EE is a function w.r.t. the number of antennas, the total transmit power, and the power allocation coefficients. In this section, we aim to determine the optimal system parameters N, P, and . The optimization problem can be formulated as
where is a predefined threshold of the massive MIMO system. The power allocation vector contains K dependent variables. Thus, the exhaustive search has exponential complexity w.r.t. the number of UEs, which leads to computational infeasibility. In the following subsections, we aim to propose an optimal algorithm with low complexity to solve the NP-hard non-convex problem.
4.2. Optimal Power Allocation for Given P and N
To solve the optimization problem, we first calculated the optimal for given P and N. Given P and N, can be converted to
It is straightforward to prove that achieves the maximal only when . Thus, we can rewrite as
Theorem 2.
Given P and N, the equal power allocation is optimal which can maximize the EE ; i.e.,
Proof.
When N is large enough, the EE can be approximated by
Letting , can be reformulated as
Then, is equivalent to maximizing with the constraint . It is straightforward that . This completes the proof. ☐
Remark 1.
It can be observed from Theorem 2 that the optimal that maximizes the EE for different P and N is the same, so is also the optimal solution of .
4.3. Optimal P for Given N
After obtaining , the optimization problem can be reformulated as for given N.
where .
Theorem 3.
Given N, the optimal transmit power which maximizes the EE is given as
where , and the corresponding EE is
Proof.
Since EE is a quasiconcave function w.r.t. P, the first-order derivative shall be zero to maximize EE. Thus, the optimal transmit power should satisfy the following equation:
which can be reformulated as
Then, we can conclude that
Substituting , we have
Thus, t can be expressed as
where W is the lambert W function defined as . Thus, the optimal transmit power can be given as
Substituting (30) into the objective function of , we have
This completes the proof. ☐
4.4. Optimal N
After obtaining the optimal power allocation and the total transmit power for the given number of antennas. It can be seen from (31) that the maximized EE is a function w.r.t. N. Thus, we can obtain the optimal number of antennas by one-dimension exhaustive search. It is noteworthy that the NP-hard problem is solved by simple one-dimension exhaustive search w.r.t. N.
5. Numerical and Simulation Results
In this section, we will verify the tightness of our closed-form expressions. The path-loss exponent is set as . Unless stated otherwise, we set , m, , mW, dBm, and dBm. Since the EE depends on the path-loss, we only adopt one realization of the spatial distribution of UEs to evaluate our performance. The distances from UEs to the the centre of the distributed circle are set as m.
Figure 2 shows the EE versus the number of antennas. The graph indicates that EE is concave with the number of antennas. In addition, the derived closed-form expressions are in agreement with the simulation results.
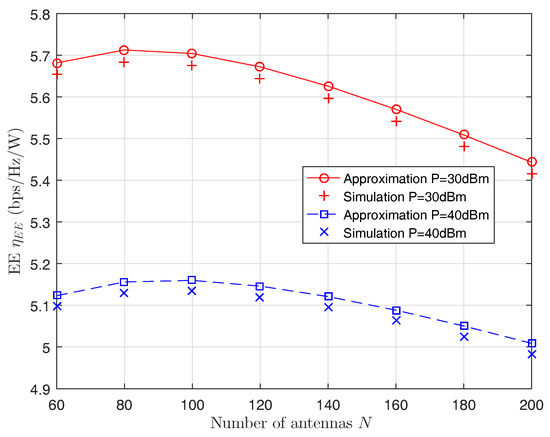
Figure 2.
The energy efficiency (EE) versus the number of antennas.
Figure 3 compares our closed-form power allocation and the optimal power allocation using exhaustive search in terms of the EE. It shows that our closed-form power allocation agrees reasonably well with the optimal power allocation when the number of antennas is large enough.
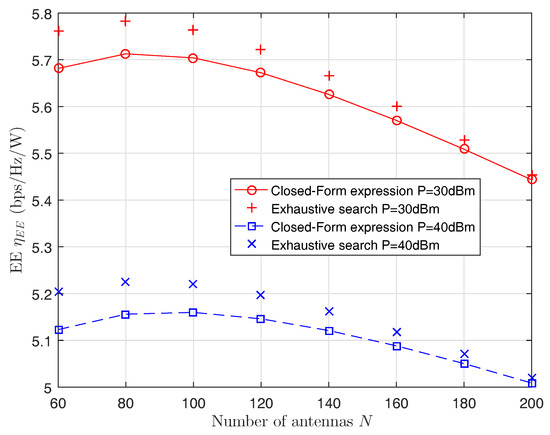
Figure 3.
Comparison of power allocation schemes between closed-form expressions and the exhaustive search.
Figure 4 illustrates the EE versus the total transmit power. It indicates that EE is concave with the total transmit power. Figure 5 plots the optimal total transmit power versus the number of antennas. Figure 6 shows the maximized EE versus the number of antennas. As expected, the maximized EE becomes larger when the circuit power per RF chain decreases.
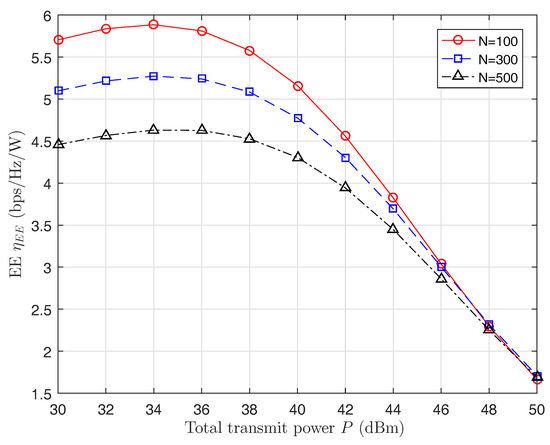
Figure 4.
The energy efficiency versus the total transmit power.
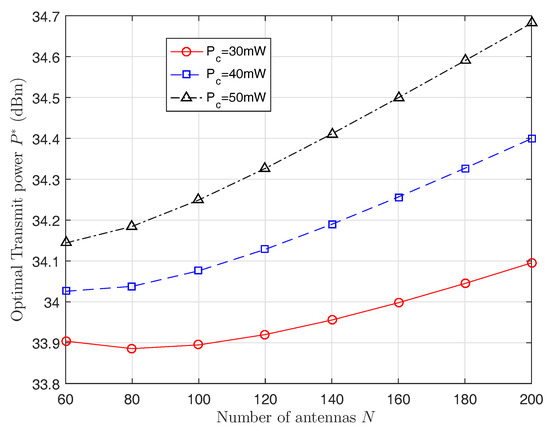
Figure 5.
The optimal total transmit power versus the number of antennas.
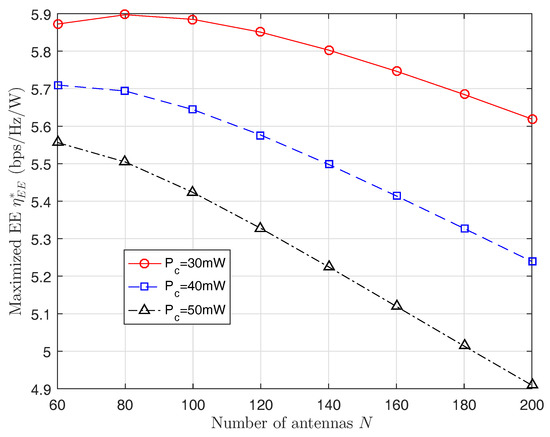
Figure 6.
The maximized energy efficieny versus the number of antennas.
6. Conclusions
We investigate and optimize the energy efficiency of the uplink of a massive MIMO system with circularly distributed antennas. The energy efficiency is tightly approximated by a closed-form expression. To maximize the energy efficiency, the power allocation, the total transmit power, and the number of antennas are jointly optimized and determined. Given the number of antennas and the total transmit power, the optimal power allocation coefficients are derived in closed-form. Given the number of antennas, the total transmit power and the maximized EE are verified functions w.r.t. the number of antennas. Then, the NP-hard problem can be solved by one-dimension search.
Acknowledgments
This work was supported by the Chongqing Science and Technology Plan Project (cstc2016jcyjA0516).
Author Contributions
Xinhua Wang created the main ideas and wrote the paper; Yan Yang and Jinlu Sheng critically reviewed and revised the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gupta, A.; Jha, R.K. A survey of 5G network: Architecture and emerging technologies. IEEE Access 2015, 3, 1206–1232. [Google Scholar] [CrossRef]
- Wong, V.; Schober, R.; Ng, D.W.K.; Wang, L. Key Technologies for 5G Wireless Systems; Cambridge University Press: Oxford, UK, 2017. [Google Scholar]
- Larsson, E.G.; Edfors, O.; Tufvesson, F.; Marzetta, T.L. Massive MIMO for next generation wireless systems. IEEE Commun. Mag. 2006, 52, 186–195. [Google Scholar] [CrossRef]
- Zheng, K.; Zhao, L.; Mei, J.; Shao, B.; Xiang, W.; Hanzo, L. Survey of large-scale MIMO systems. IEEE Commun. Surv. Tutor. 2015, 17, 1738–1760. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Larsson, E.G.; Marzetta, T.L. The multicell multiuser MIMO uplink with very large antenna arrays and a finite-dimensional channel. IEEE Trans. Commun. 2013, 61, 2350–2361. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Matthaiou, M.; Duong, T.Q.; Marzetta, T.L. Uplink performance analysis of multicell MU-SIMO systems with ZF receivers. IEEE Trans. Veh. Technol. 2012, 62, 4471–4483. [Google Scholar]
- Zhao, L.; Zheng, K.; Long, H.; Zhao, H. Performance analysis for downlink massive MIMO system with ZF precoding. Trans. Emerg. Telecommun. Technol. 2014, 25, 1219–1230. [Google Scholar] [CrossRef]
- Lin, Y.; Li, X.; Fu, W.; Hei, Y. Spectral efficiency analysis for downlink massive MIMO systems with MRT precoding. China Commun. 2015, 12, 67–73. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Larsson, E.G.; Marzetta, T.L. Energy and spectral efficiency of very large multiuser MIMO systems. IEEE Trans. Commun. 2013, 61, 1436–1449. [Google Scholar]
- Ha, D.; Lee, K.; Kang, J. Energy efficiency analysis with circuit power consumption in massive MIMO systems. In Proceedings of the 2013 IEEE 24th International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC Workshops), London, UK, 8–9 September 2013; pp. 938–942. [Google Scholar]
- Bjornson, E.; Sanguinetti, L.; Hoydis, J.; Debbah, M. Optimal design of energy-efficient multi-user MIMO systems: Is massive MIMO the answer? IEEE Trans. Wirel. Commun. 2015, 14, 3059–3075. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, H.; Zheng, K.; Zhang, J. Energy efficient power allocation algorithm for downlink massive MIMO with MRT precoding. In Proceedings of the 2013 IEEE 78th Vehicular Technology Conference (VTC2013-Fall), Las Vegas, NV, USA, 2–5 September 2013; pp. 1–5. [Google Scholar]
- Ng, D.W.K.; Lo, E.S.; Schober, R. Energy-efficient resource allocation in OFDMA systems with large numbers of base station antennas. IEEE Trans. Veh. Technol. 2012, 11, 3292–3304. [Google Scholar]
- Zhu, H.; Wang, J. Chunk-based resource allocation in OFDMA systems—Part I: Chunk allocation. IEEE Trans. Commun. 2009, 57, 2734–2744. [Google Scholar]
- Zhu, H.; Wang, J. Chunk-based resource allocation in OFDMA systems—Part II: Joint chunk, power and bit allocation. IEEE Trans. Commun. 2012, 60, 499–509. [Google Scholar] [CrossRef]
- Ng, D.W.K.; Lo, E.S.; Schober, R. Energy-efficient resource allocation in multi-cell OFDMA systems with limited backhaul capacity. IEEE Trans. Wirel. Commun. 2012, 11, 3618–3631. [Google Scholar] [CrossRef]
- Liu, D.; Wang, L.; Chen, Y.; Zhang, T. Distributed energy efficient fair user association in massive MIMO enabled HetNets. IEEE Commun. Lett. 2015, 19, 1770–1773. [Google Scholar] [CrossRef]
- Bjornson, E.; Hoydis, J.; Kountouris, M.; Debbah, M. Massive MIMO systems with non-ideal hardware: Energy efficiency, estimation, and capacity limits. IEEE Trans. Inf. Theory 2014, 60, 7112–7139. [Google Scholar] [CrossRef]
- Guo, K.; Guo, Y.; Ascheid, G. Security-Constrained power allocation in MU-Massive-MIMO with distributed antennas. IEEE Trans. Wirel. Commun. 2016, 15, 8139–8153. [Google Scholar] [CrossRef]
- Zhu, H. Performance comparison between distributed antenna and microcellular systems. IEEE J. Sel. Areas Commun. 2011, 29, 1151–1163. [Google Scholar] [CrossRef]
- Senanayake, R.; Smith, P.; Yeoh, P.L.; Evans, J. An SNR approximation for distributed massive MIMO with zero forcing. IEEE Commun. Lett. 2016, 19, 1885–1888. [Google Scholar] [CrossRef]
- Kamga, G.N.; Xia, M.; Aissa, S. Spectral-Efficiency analysis of massive MIMO systems in centralized and distributed schemes. IEEE Trans. Commun. 2016, 64, 1930–1941. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, J.; Wang, Z.; Jin, J. Optimal precoder design maximizing the worst-case average received SNR for massive distributed MIMO systems. IEEE Commun. Lett. 2015, 19, 589–592. [Google Scholar] [CrossRef]
- He, C.; Yin, J.; He, Y.; Huang, M.; Zhao, B. Energy efficiency of distributed massive MIMO systems. J. Commun. Netw. 2016, 18, 649–657. [Google Scholar]
- Kim, W.; Yoon, W. Energy efficiency maximisation for WPCN with distributed massive MIMO system. Electron. Lett. 2016, 19, 1642–1644. [Google Scholar] [CrossRef]
- Yang, A.; Jing, Y.; Xing, C.; Fei, Z. Performance analysis and location optimization for massive MIMO systems with circularly distributed antennas. IEEE Trans. Wirel. Commun. 2015, 14, 5659–5671. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).