A Novel DOA Estimation Algorithm Using Array Rotation Technique
Abstract
:1. Introduction
2. The MUSIC Algorithm of 2-D UCA
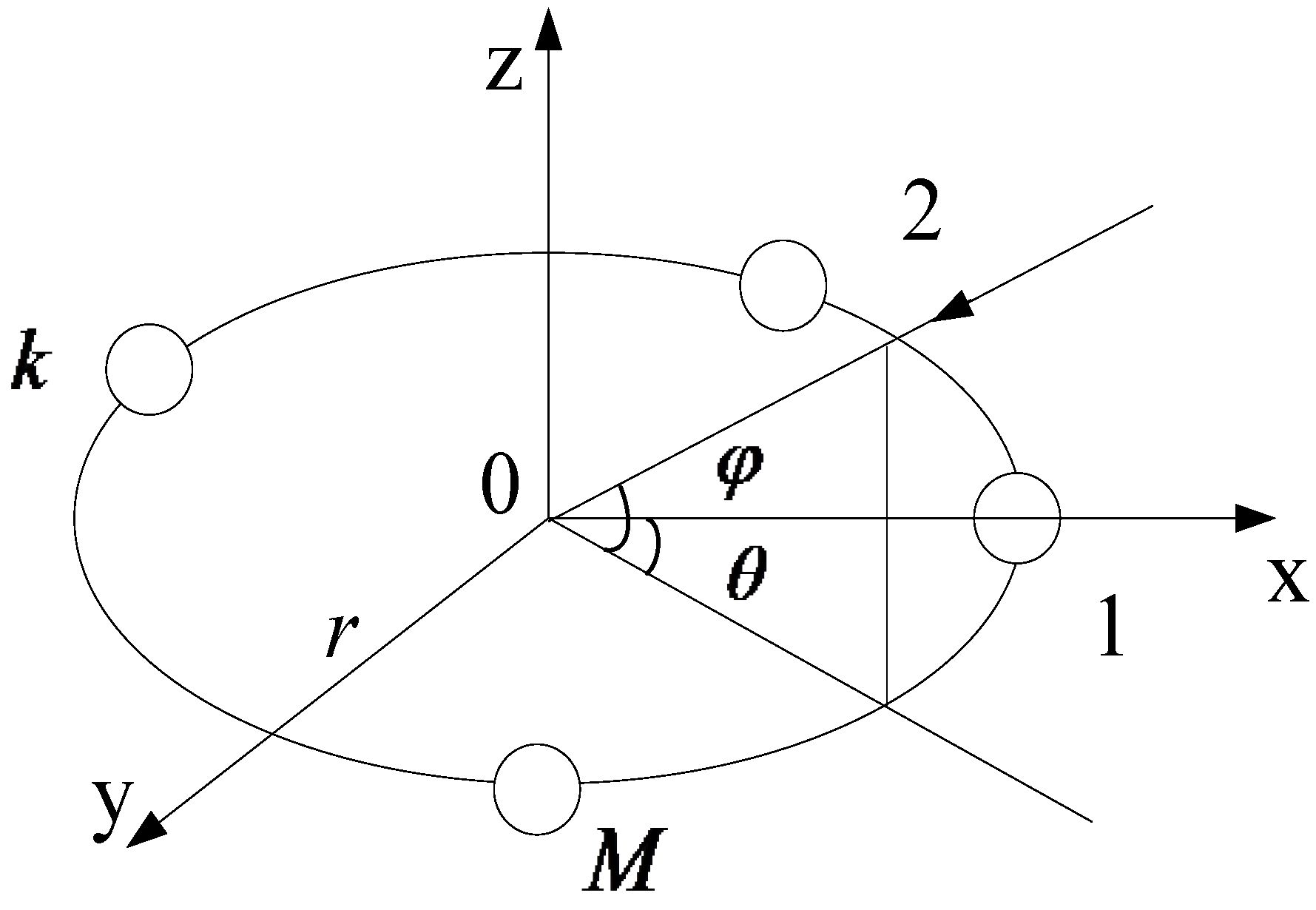


 can be written as
can be written as

 , respectively. In ideal conditions, λ1 ≥ λ2 ⋯ ≥ λD ≥ λD +1 = ⋯ = λM = σ2. Assume that the number of incident signals D is known,
, respectively. In ideal conditions, λ1 ≥ λ2 ⋯ ≥ λD ≥ λD +1 = ⋯ = λM = σ2. Assume that the number of incident signals D is known,  can be described as
can be described as


3. The Proposed Algorithm
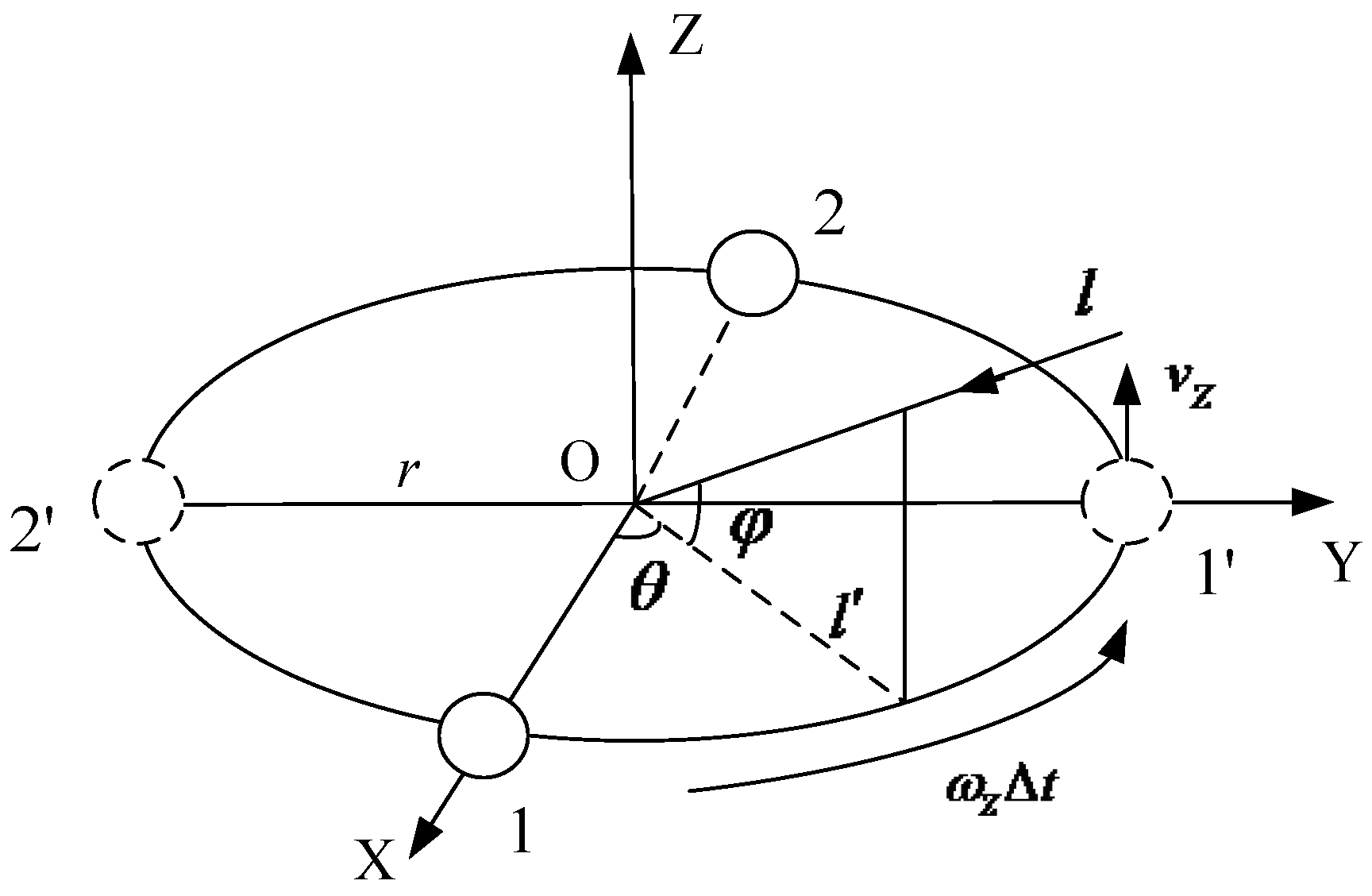
3.1. The Rotation Array Structure of Proposed Algorithm
- (1)
- While the baseline 1–2 is rotating, the baseline is certainly vertical to Z-axis with absolute uniform velocity;
- (2)
- Select 2M elements at uniformly-time interval to make them form the virtual UCA within T/2 period;
- (3)
- The signals remain static during the measurement time.

= 2πƒzr sin(θ − ωzt) cos φ •ƒ / c


 ; m = 1,2⋯, M; i = 1,2, ⋯, D.
; m = 1,2⋯, M; i = 1,2, ⋯, D.

 .
.3.2. How to Choose Array Rotation Velocity




4. The Cramer-Rao Bound








5. Simulation Examples
5.1. Resolution Performance Simulation

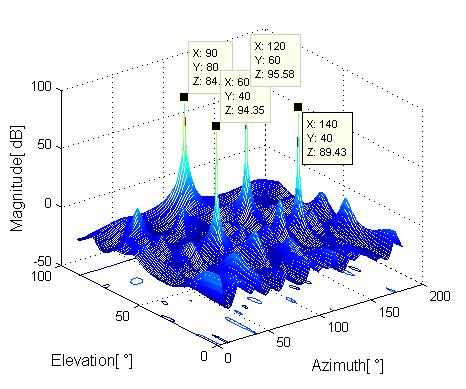
5.1.1. The Spatial Spectrum of the R-MUSIC Algorithm
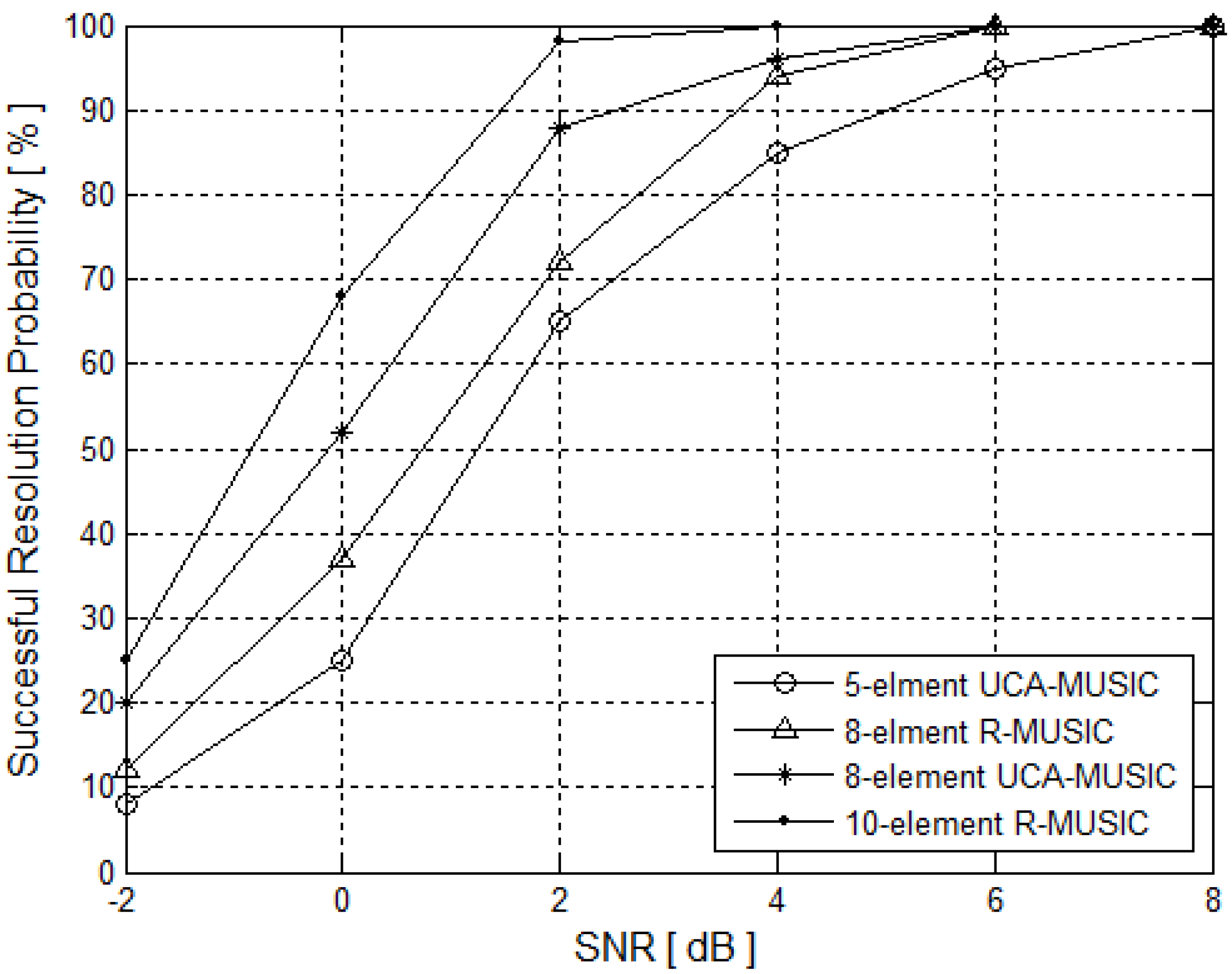
5.1.2. The Resolution Probability versus SNR

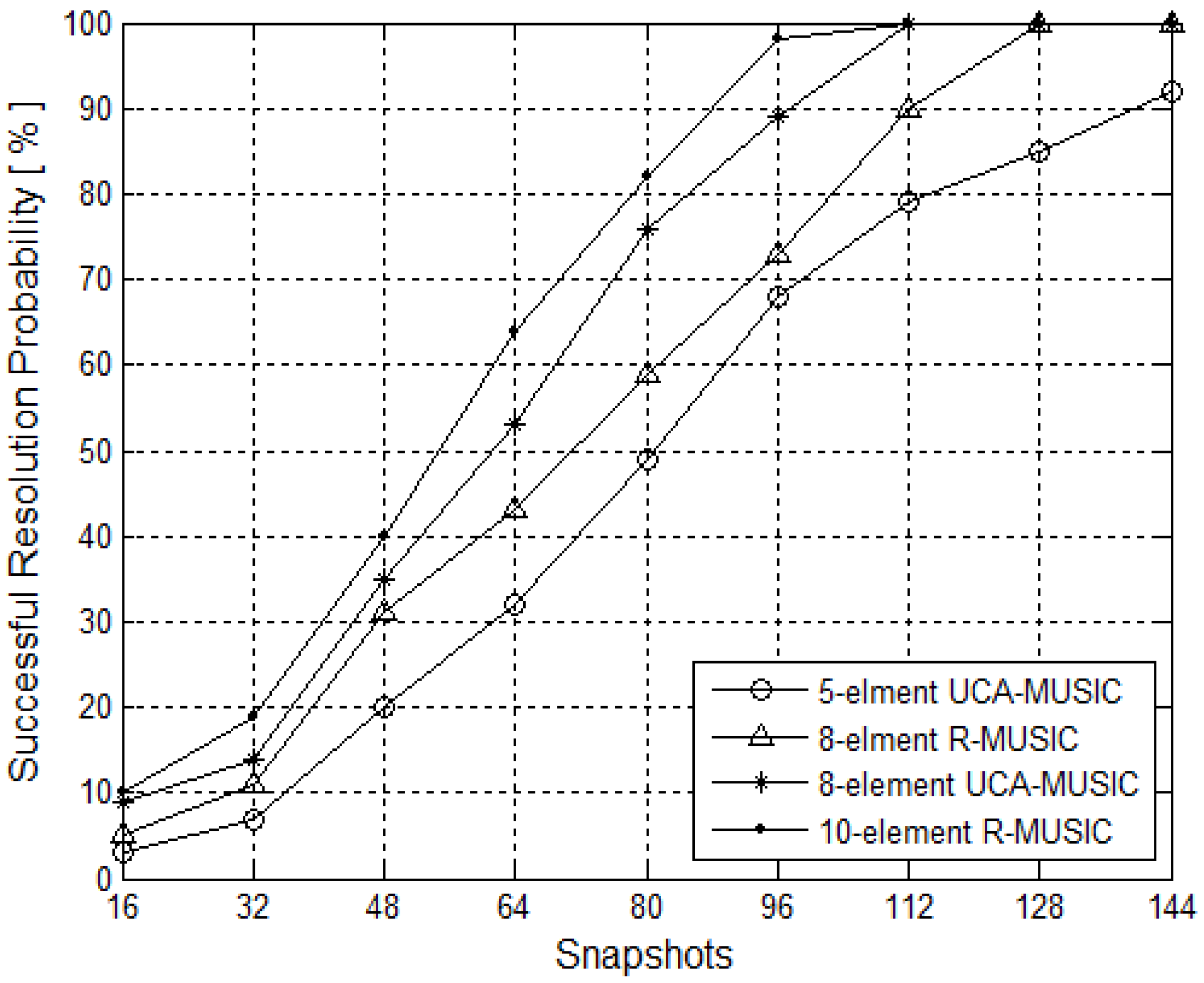
5.2. Estimation Accuracy Performance Simulation
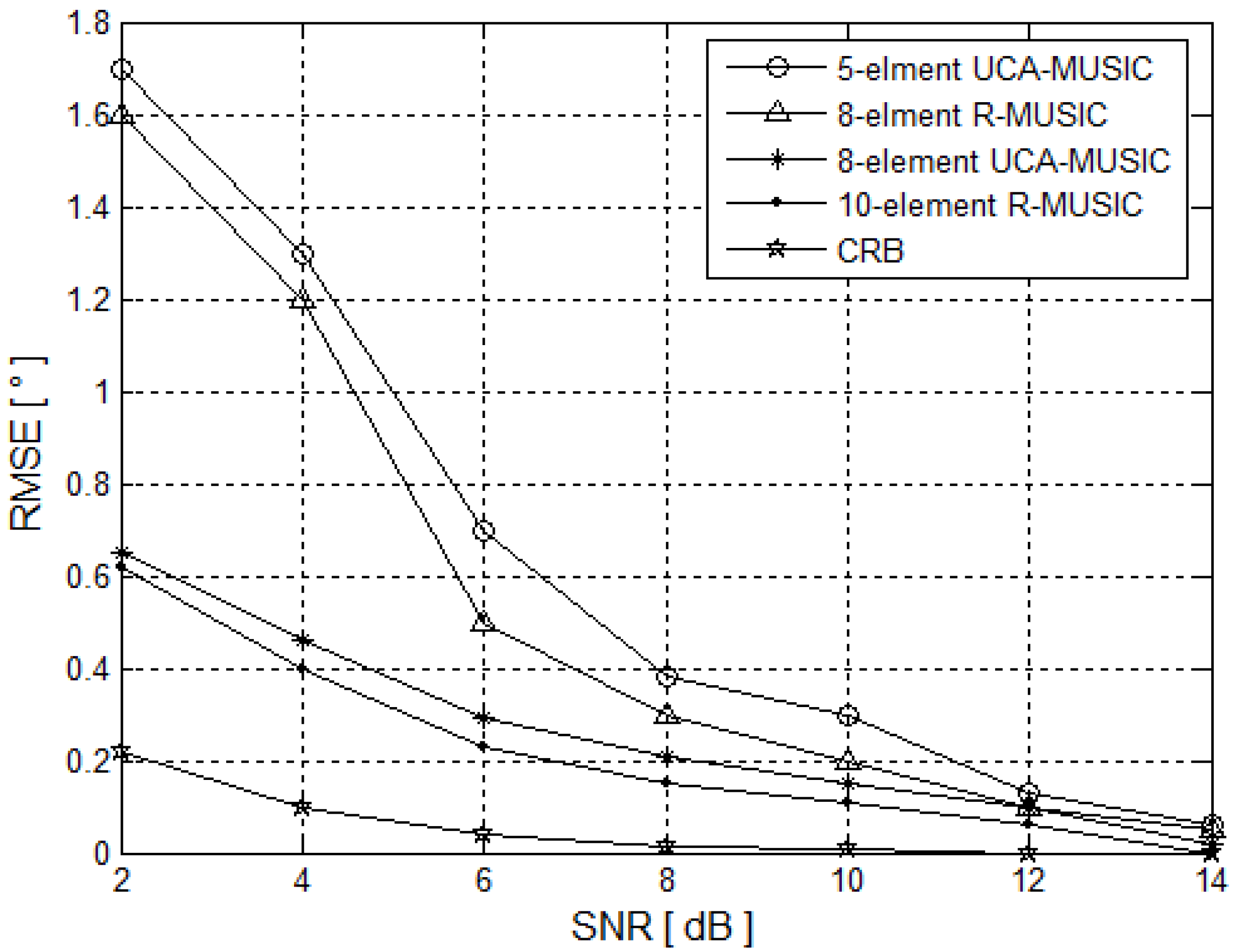
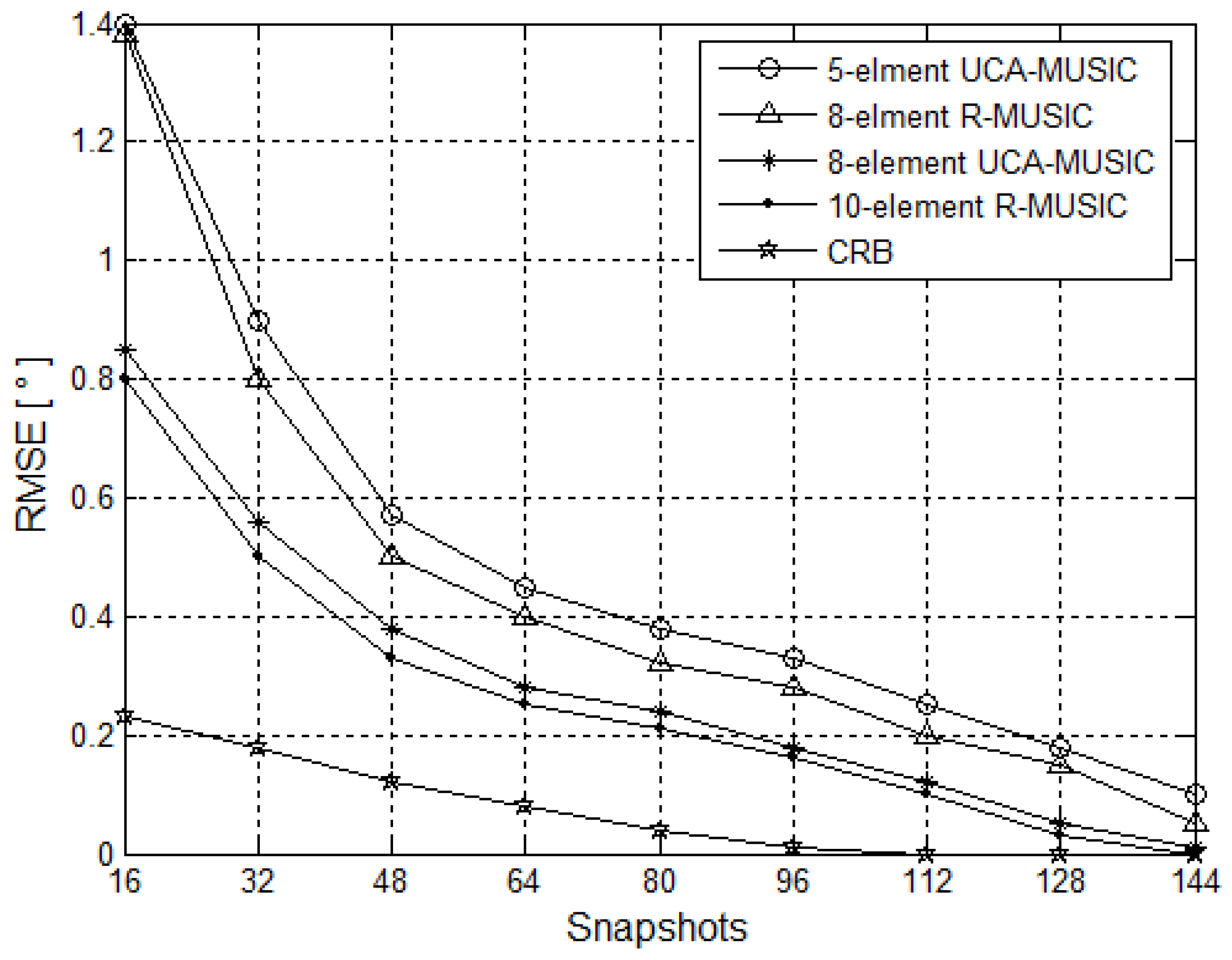
5.3. Channel Mismatch Errors Simulation
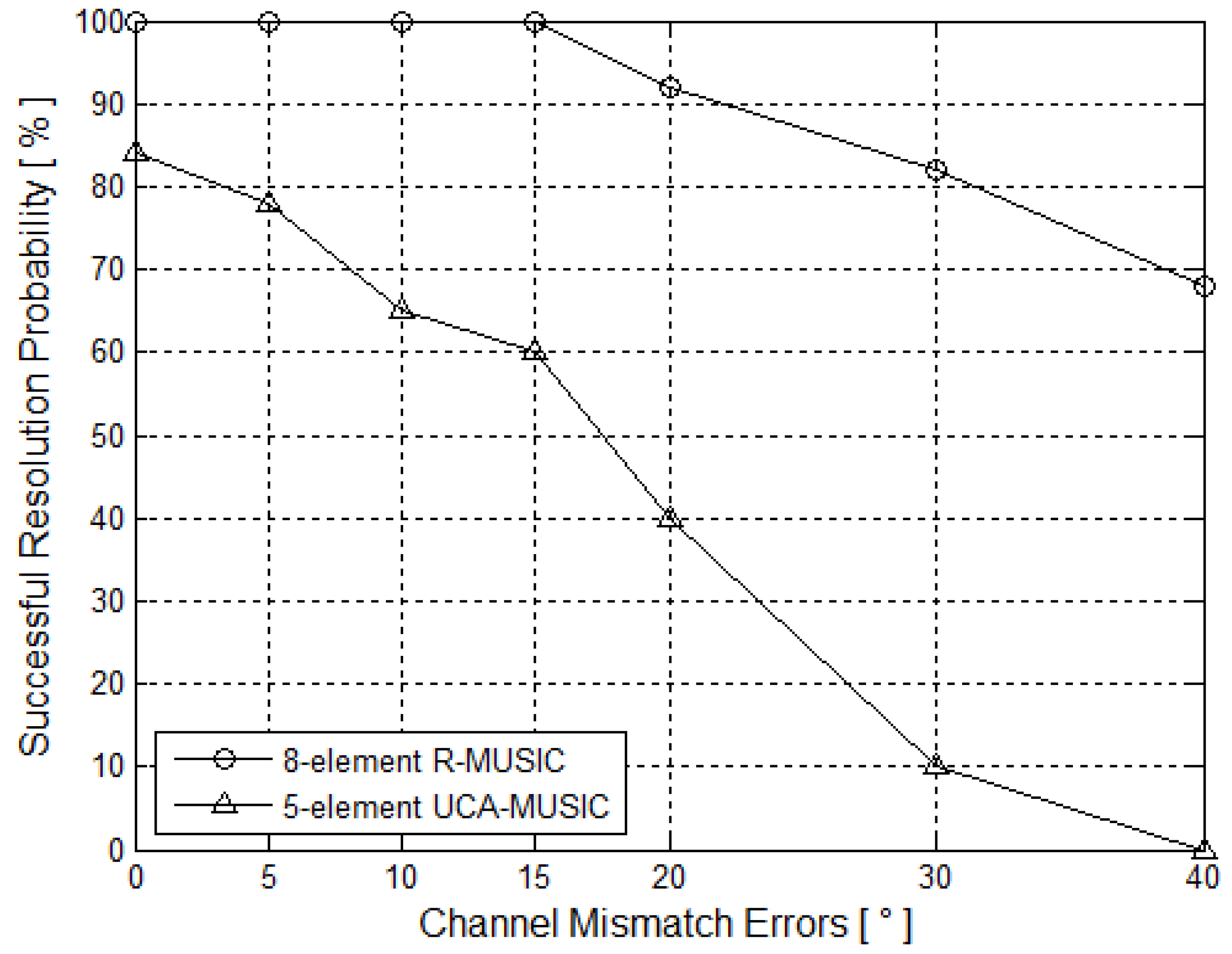
| Channel mismatch errors [degree] | 5-elment UCA-MUSIC | 8-element R-MUSIC |
|---|---|---|
| 0 | 0.1414 | 0.2739 |
| 5 | 0.2191 | 0.2162 |
| 10 | 0.4817 | 0.4000 |
| 15 | 0.5441 | 0.4427 |
| 20 | 0.6132 | 0.4336 |
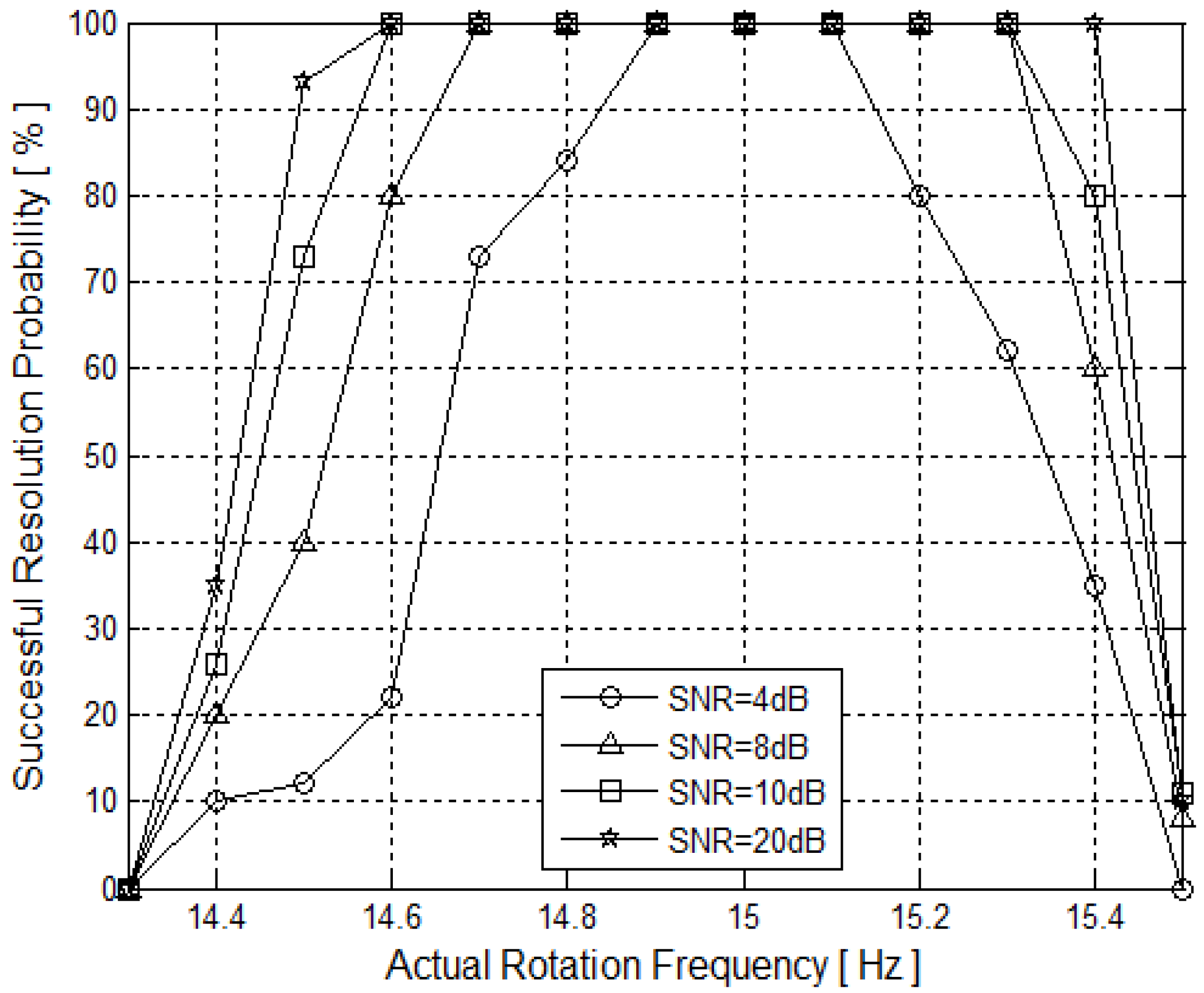
5.4. Resolution Performance versus Rotation Frequency Errors
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Schmidt, R.O. Multiple Emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Rubsamen, M.; Gershman, A.B. Direction of arrival estimation for nonuniform sensor arrays: From manifold separation to Fourier domain MUSIC methods. IEEE Trans. Signal Process. 2009, 57, 588–599. [Google Scholar] [CrossRef]
- Gao, F.F.; Nallanathan, A.; Wang, Y.D. Improvd MUSIC under the coexistence of both circular and noncircular sources. IEEE Trans. Signal Process. 2008, 56, 3033–3038. [Google Scholar] [CrossRef]
- You, H.; Huang, J.G.; Jin, Y. Improving MUSIC performance in snapshot deficient scenario via weighted signal-subspace projection. Syst. Eng. Electron. 2008, 30, 792–794. [Google Scholar]
- Mestre, X.; Lagunas, M. Modified subspace algorithms for DOA estimation with large arrays. IEEE Trans. Signal Process. 2008, 56, 598–614. [Google Scholar] [CrossRef]
- Mccloud, M.L.; Scharf, L.L. A new subspace identification algorithm for high-resolution DOA estimation. IEEE Trans. Antennas Propag. 2002, 50, 1382–1390. [Google Scholar] [CrossRef]
- Liu, J.; Yu, H.Q.; Huang, Z.T. Conjugate extended MUSIC algorithm based on second-order preprocessing. Syst. Eng. Electron. 2008, 30, 57–60. [Google Scholar]
- Liu, H.S.; Xiao, X.C. An approach to designing linear array with high accuracy doa estimate based on minimal manifold length. Acta Aeronaut. Etastronautica Sin. 2008, 29, 462–466. [Google Scholar]
- He, M.H.; Yin, Y.X.; Zhang, X.D. UCA-ESPRIT algorithm for 2-D angle estimation. IEEE Trans. Signal Process. 2000, 1, 437–440. [Google Scholar]
- Goosens, R.; Rogier, H.; Werbrouck, S. UCA Root-MUSIC with sparse uniform circular arrays. IEEE Trans. Signal Process. 2008, 56, 4095–4099. [Google Scholar] [CrossRef]
- Wu, Y.T.; So, H.C. Simple and accurate two-dimensional angle estimation for a single source with uniform circular array. IEEE Antennas Wirel. Propag. Lett. 2008, 7, 78–80. [Google Scholar] [CrossRef]
- Pajsusco, P.; Pagani, P. On the use of uniform circular array for characterizing UWB time reversal. IEEE Trans. Antennas Propag. 2009, 57, 102–109. [Google Scholar] [CrossRef]
- Huang, L.; Wu, S.; Feng, D. Low complexity method for signal subspace filtering. IEEE Electron. Lett. 2004, 40, 34–38. [Google Scholar] [CrossRef]
- Goosens, R.; Rogier, H. A hybrid UCA RARE or root MUSIC approach of 2D direction of arrival estimation in uniform circular arrays in the presence of mutual coupling. IEEE Trans. Antennas Propag. 2007, 55, 841–849. [Google Scholar] [CrossRef]
- Tao, J.W.; Shi, Y.W.; Chang, W.X. The estimation of 2-D DOA of scattered sources with UCAs. J. China Inst. Commun. 2003, 24, 10–17. [Google Scholar]
- Tao, J.W.; Shi, Y.W.; Chang, W.X. Cross correlation estimator of azimuth-elevation with UCAs. Acta Electron. Sin. 2003, 31, 575–575. [Google Scholar]
- Tang, Z.L.; Wu, S.J.; Zhang, S. Estimation of 2-D DOA based on uniform circle array. J. Harbin Eng. Univ. 2005, 26, 247–252. [Google Scholar]
- Xu, D.C.; Liu, Z.W.; Qi, X.D. A unitary transformation method for DOA estimation with uniform circular array. Radio Eng. 2010, 40, 13–16. [Google Scholar]
- Lu, L.Q.; Hu, X.P.; Wu, M.P. Fast orientation determination by Twin-Star system through method of rotating baseline. J. Astronaut. 2004, 25, 158–162. [Google Scholar]
- Si, W.J.; Cheng, W. Study on solving ambiguity Method of rolling interferometer and implemention. J. Proj. Rocket. Missiles Guid. 2010, 30, 199–202. [Google Scholar]
- Yaqoob, M.A.; Tufvesson, F.; Mannesson, A.; Bernhardsson, B. Direction of arrival estimation with arbitrary virtual antenna arrays using low cost inertial measurement units. In Proceedings of the IEEE ICC 2013 Workshop on Advances in Network Localization and Navigation, Budapest, Hungary, 9–13 June 2013.
- de Jong, Y.L.C.; Herben, M.H.A.J. High-resolution angle-of arrival measurement of the mobile radio channel. IEEE Trans. Antennas Propag. 1999, 47, 1677–1687. [Google Scholar] [CrossRef]
- Broumandan, A.; Lin, T.; Moghaddam, A. Direction of Arrival Estimation of GNSS Signals Based on Synthetic Antenna Array. In Proceedings of the International Technical Meeting (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007.
- Yuan, X.H.; Zhen, H.; Yu, F.Q. Cramer-Rao bound for 2-D angle estimation with uniform circular array. J. Telecommun. Eng. 2013, 53, 44–51. [Google Scholar]
- Han, G.J.; Xu, H.; Duong, T.Q.; Jiang, J.; Takahiro, H. Localization algorithms of wireless sensor networks: A survey. Telecommun. Syst. 2013, 52, 2419–2436. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lan, X.; Wan, L.; Han, G.; Rodrigues, J.J.P.C. A Novel DOA Estimation Algorithm Using Array Rotation Technique. Future Internet 2014, 6, 155-170. https://doi.org/10.3390/fi6010155
Lan X, Wan L, Han G, Rodrigues JJPC. A Novel DOA Estimation Algorithm Using Array Rotation Technique. Future Internet. 2014; 6(1):155-170. https://doi.org/10.3390/fi6010155
Chicago/Turabian StyleLan, Xiaoyu, Liangtian Wan, Guangjie Han, and Joel J. P. C. Rodrigues. 2014. "A Novel DOA Estimation Algorithm Using Array Rotation Technique" Future Internet 6, no. 1: 155-170. https://doi.org/10.3390/fi6010155
APA StyleLan, X., Wan, L., Han, G., & Rodrigues, J. J. P. C. (2014). A Novel DOA Estimation Algorithm Using Array Rotation Technique. Future Internet, 6(1), 155-170. https://doi.org/10.3390/fi6010155