Abstract
The performance of traditional direction of arrival (DOA) estimation algorithm based on uniform circular array (UCA) is constrained by the array aperture. Furthermore, the array requires more antenna elements than targets, which will increase the size and weight of the device and cause higher energy loss. In order to solve these issues, a novel low energy algorithm utilizing array base-line rotation for multiple targets estimation is proposed. By rotating two elements and setting a fixed time delay, even the number of elements is selected to form a virtual UCA. Then, the received data of signals will be sampled at multiple positions, which improves the array elements utilization greatly. 2D-DOA estimation of the rotation array is accomplished via multiple signal classification (MUSIC) algorithms. Finally, the Cramer-Rao bound (CRB) is derived and simulation results verified the effectiveness of the proposed algorithm with high resolution and estimation accuracy performance. Besides, because of the significant reduction of array elements number, the array antennas system is much simpler and less complex than traditional array.
1. Introduction
With the development of array signal processing, the direction of arrival (DOA) estimation algorithms are used widely in radar, sonar, atmosphere, communication and so on. Since the 1980s, many high resolution 2-dim (2-D) DOA algorithms were proposed in succession. Among them, the multiple signal classification (MUSIC) algorithm [1,2] marks a symbolic method of the spatial spectrum estimation algorithm. In ideal conditions, MUSIC algorithm has better estimation accuracy and resolution performance and nowadays there are still a lot of scholars devoting themselves to MUSIC algorithm [3,4,5,6,7]. However, in practice, MUSIC algorithm has strict requirements with the placement of array elements, which has a great influence on DOA estimation accuracy, resolution and stability [8]. As a symbolic plane array, the uniform circular array (UCA) can provide both azimuth and elevation information ranging from 0° to 360° and also has other excellent performance such as circular symmetry properties [9,10,11,12,13,14]. Utilizing array manifold directly, the algorithm proposed in [15] could estimate the 2-D DOAs of a single extended signal combining least-squares (LS) method with weighted total LS (WTLS), which leads to a better performance. A much amplifier algorithm proposed in [16,17] can achieve a better stability, but only apply to one single source. A unitary transformation method was proposed in [18] based on array space; this method can reduce the computational complexity and improve the practicability of the MUSIC algorithm. By base-line rotation and phase integration, the algorithm proposed in [19,20] utilized rotating interferometer to solve the ambiguity problem. However, the algorithms mentioned above have not solved the problem as below: (1) DOA estimation performance has strict restrictions with the radius r of antenna dish in UCA; the larger the radius is, the better the resolution is; (2) More antenna elements can provide better resolution and estimation accuracy, but too many elements will cause high energy loss and that will make it difficult to calibrate channel mismatches. On the other hand, the number of elements cannot be too high because of the space restrictions of the antenna dish. To solve these issues, a virtual antenna array technique can be used by moving the receiver antenna to various locations and then measuring the static signal at those locations. In addition, another method for DOA estimation using single antenna devices was presented in [21,22,23].
In this paper, a novel rotation MUSIC (R-MUSIC) algorithm for static targets based on the array rotating technique is proposed. This algorithm can obtain any even number of elements by rotating only two elements, so that it can receive the signal data at multiple positions. Besides, the R-MUSIC algorithm can break the constraints that the number of antenna elements must be more than the number of incident signals. Most importantly, the array system will be much simpler than the traditional array. Computer simulations verified the effectiveness and superior performance of the proposed method.
The remainder of this paper is organized as follows. Section 2 introduces the MUSIC algorithm based on 2-D UCA. Section 3 elaborates the structure model of the rotation array and contains the core work of this paper, in which the R-MUSIC method is proposed for 2D-DOA estimation. Section 4 derives the Cramer-Rao bound (CRB). Section 5 presents the computer simulation result. Section 6 gives the final conclusions.
2. The MUSIC Algorithm of 2-D UCA
Consider a UCA with M elements impinged by D narrowband signals si(t), i = 1, 2, …, D (D < M), where t is the time variable, as shown in Figure 1. The D sources are assumed to be from far-field with azimuth θi and elevation φi, i = 1, 2, …, D. Assume the radius of UCA is r and the noise is additive white Gaussian noise (AWGN).
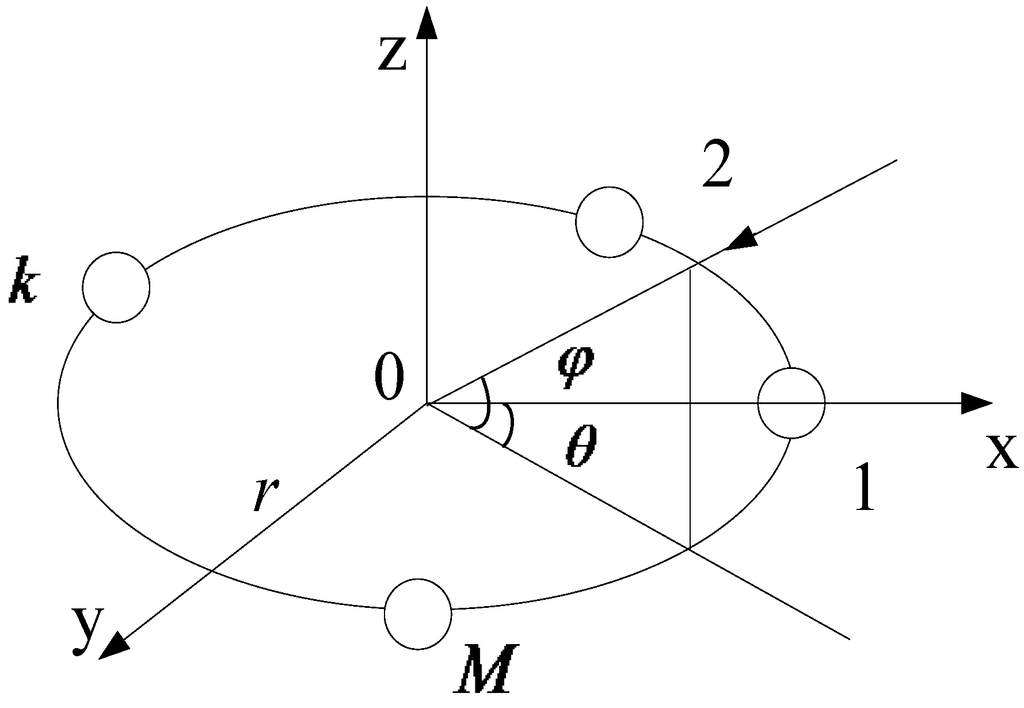
Figure 1.
Uniform circular array diagram.
Consider the reference point is 0, the ideal steering matrix can be obtained from the array geometry as
where k = 1, 2, …, M; i = 1, 2, …, D; λ is wavelength; d = 2π/λ. The array output of the kth element at time t can be written as
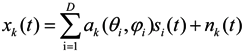
A(θ,φ) = [a(θ1,φ1), a(θ2,φ2), ⋯, a(θD,φD)]
a(θi,φi) = [a1(θi,φi),a2(θi,φi), ⋯, aM (θi,φi)]T
ak (θi,φki) = exp(− jωτi) = exp(− j dr cos (2π(k − 1)/ M − θi) cos φi)
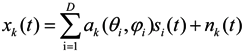
Equation (4) can be written in matrix form as
where X(t) is M × 1 array output vector; A is M × D array steering matrix; S(t) is D × 1 signal vector; N(t) is M × 1 noise vector. X(t), S(t) and N(t) are abbreviated as X, S and N, respectively, and the array covariance matrix of X can be written as
where P = E[SSH] = diag[P1, P2, …, Pi, …, PD]; Pi is the power of the ith signal; σ2 is noise power; I is M × 1 identity matrix. E[•] and [•]H denote the statistical expectation and the Hermitian transpose, respectively. In real systems, the covariance matrix R can be estimated from a finite set of sample snapshots as
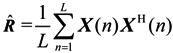 where L is the total number of snapshots. Then the eigendecomposition of
where L is the total number of snapshots. Then the eigendecomposition of 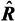 can be written as
can be written as
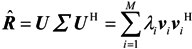 where ∑ = diag{λ1 ≥ λ2, ⋯, λM}; λi and vi are the eigenvalue and corresponding eigenvector of
where ∑ = diag{λ1 ≥ λ2, ⋯, λM}; λi and vi are the eigenvalue and corresponding eigenvector of 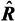 , respectively. In ideal conditions, λ1 ≥ λ2 ⋯ ≥ λD ≥ λD +1 = ⋯ = λM = σ2. Assume that the number of incident signals D is known,
, respectively. In ideal conditions, λ1 ≥ λ2 ⋯ ≥ λD ≥ λD +1 = ⋯ = λM = σ2. Assume that the number of incident signals D is known, 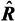 can be described as
can be described as
 where US = [v1, v2, ⋯, vD] and UN = [vD+1, vD+2, ⋯, vM] are the signal subspace and noise subspace, respectively; ∑S = diag{λ1, ⋯, λD} and ∑N = diag{λD+1, ⋯, λM} are diagonal matrices related to the signal and noise power, respectively. Because the D-incident sources spanning the signal space are orthogonal to the noise space, so the MUSIC algorithm can estimate the DOA as
where US = [v1, v2, ⋯, vD] and UN = [vD+1, vD+2, ⋯, vM] are the signal subspace and noise subspace, respectively; ∑S = diag{λ1, ⋯, λD} and ∑N = diag{λD+1, ⋯, λM} are diagonal matrices related to the signal and noise power, respectively. Because the D-incident sources spanning the signal space are orthogonal to the noise space, so the MUSIC algorithm can estimate the DOA as
 where PMUSIC (θ,φ) is expected to show a large positive value if (θ,φ) is a true DOA, because aH (θ,φ) vi = 0, i = D +1, ⋯, M. Here, the signal is processed before the data is demodulated, where the carrier phase information is maintained through the sampling.
where PMUSIC (θ,φ) is expected to show a large positive value if (θ,φ) is a true DOA, because aH (θ,φ) vi = 0, i = D +1, ⋯, M. Here, the signal is processed before the data is demodulated, where the carrier phase information is maintained through the sampling.
X(t)=AS(t)+N(t)
R = E[XXH]=APAH+σ2I
 can be written as
can be written as
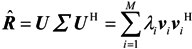
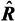 , respectively. In ideal conditions, λ1 ≥ λ2 ⋯ ≥ λD ≥ λD +1 = ⋯ = λM = σ2. Assume that the number of incident signals D is known,
, respectively. In ideal conditions, λ1 ≥ λ2 ⋯ ≥ λD ≥ λD +1 = ⋯ = λM = σ2. Assume that the number of incident signals D is known, 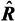 can be described as
can be described as
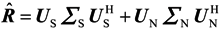
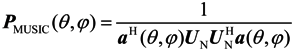
3. The Proposed Algorithm
3.1. The Rotation Array Structure of Proposed Algorithm
As shown in Figure 2, D narrowband far-field sources are observed by a rotation array with two antenna elements, “1” and “2”. Assume the baseline 1–2 is rotating around Z-axis in XOY plane at a constant velocity by anticlockwise direction. The rotate velocity is vZ, vZ = ωZr = 2πƒzr, where ωZ is rotational angular frequency; ƒz is rotation frequency. The rotation period is T. After time Δt (Δt < T), the elements 1 and 2 are rotating to the position 1ʹ and 2ʹ, respectively. Assume the array radius is r; l is the incident signal direction; lʹ is the projection of l onto the XOY plane; θ and φ are azimuth and elevation, respectively.
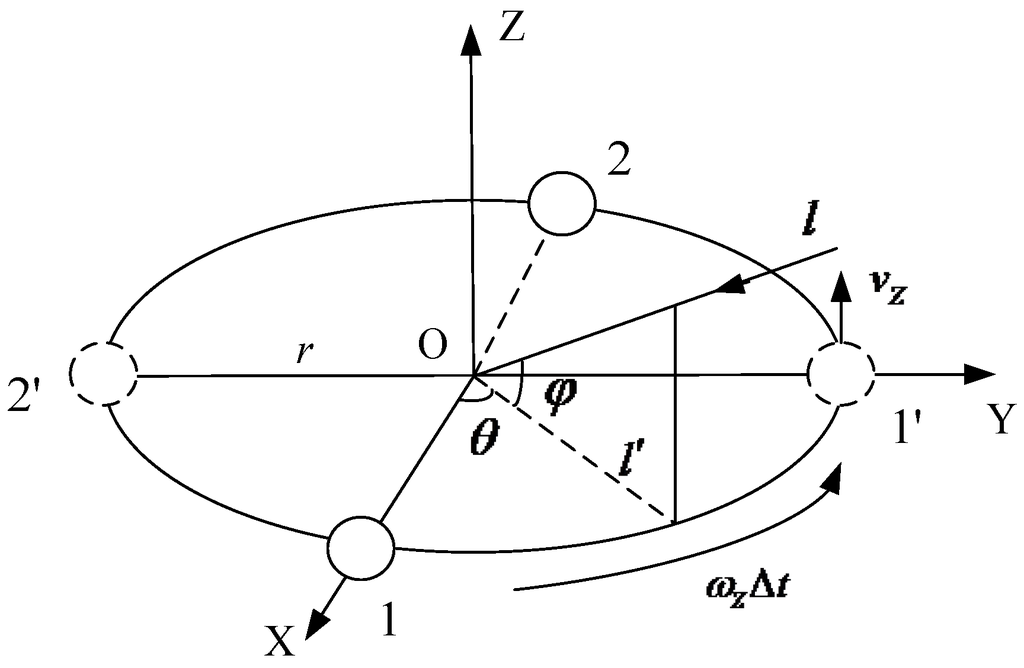
Figure 2.
Rotation array structure diagram.
In order to derive the proposed algorithm, some assumptions are clarified at first,
- (1)
- While the baseline 1–2 is rotating, the baseline is certainly vertical to Z-axis with absolute uniform velocity;
- (2)
- Select 2M elements at uniformly-time interval to make them form the virtual UCA within T/2 period;
- (3)
- The signals remain static during the measurement time.
At time tm, the elements 1 and 2 start to sample the received signal data, so tm can be expressed as
where t1 = 0, m = 1,2, ⋯,M ; ∆τ is the time delay which is needed for selecting two neighboring elements, 0 < ∆τ < T / 2. As we know, the wave path difference between the reference point O and the mth element for the ith signal is τmi. In the rotation array model, the element m is obtained by rotating element 1 through time (m − 1)∆τ, so the total wave path difference τ1m is
(12)
tm = t1 + (m − 1)∆τ
τ1m = τmi + (m−1) ∆τ
Then Equation (4) is modified as
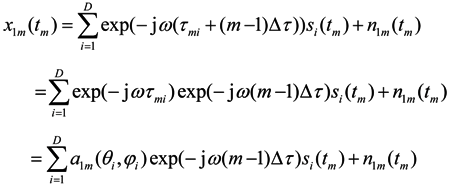
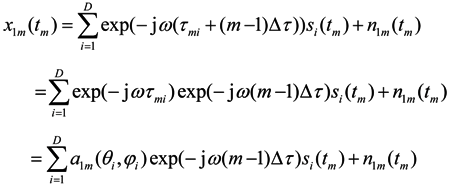
Assuming the signal sources remain static, the element rotation will cause the Doppler frequency shift. As shown in Figure 2, v is denoted as the velocity component of vz in the source incident direction Ɩʹ, we obtain
v = vz sin(θ − ωzt) cos φ
According to the Doppler frequency formula ƒd = v•ƒ /c, ƒd can be written as
where ƒ is signal frequency. Therefore, in (13), ω should be modified as
ƒd = vz sin(θ − ωzt) cos φ •ƒ /c
= 2πƒzr sin(θ − ωzt) cos φ •ƒ / c
= 2πƒzr sin(θ − ωzt) cos φ •ƒ / c
ω = 2π(ƒ + ƒd)
Let ϕtm = exp(− j ω(m − 1)∆τ), the vector received by element 1 within T/2 period can be expressed by
 where ϕtm is the phase difference of element 1 at time tm relative to the initial position. Equation (17) can be further simplified as
where ϕtm is the phase difference of element 1 at time tm relative to the initial position. Equation (17) can be further simplified as
 where X1 = [x11, x12, ⋯, x1M]T is M × 1 array output matrix; N1 = [n1(t1), n1(t2), ⋯, n1(tM)]T is M × 1 noise matrix. The steering matrix A1 can be written as
where a1m(θi,φi) = exp(− j ωτmi);
where X1 = [x11, x12, ⋯, x1M]T is M × 1 array output matrix; N1 = [n1(t1), n1(t2), ⋯, n1(tM)]T is M × 1 noise matrix. The steering matrix A1 can be written as
where a1m(θi,φi) = exp(− j ωτmi);  ; m = 1,2⋯, M; i = 1,2, ⋯, D.
; m = 1,2⋯, M; i = 1,2, ⋯, D.

A1 = [a1(θ1, φ1), a1(θ2, φ2), ⋯, a1(θD, φD)]
a1(θj, φj) = [a11(θ1, φ1), a12(θ2, φ2), ⋯, a1M (θD, φD)]T
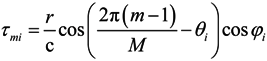 ; m = 1,2⋯, M; i = 1,2, ⋯, D.
; m = 1,2⋯, M; i = 1,2, ⋯, D.Denote Φ1 = diag[ϕt1,ϕt2, ⋯, ϕtM], (17) can be expressed by
X1 = Φ1A1S + N1
In the same way, the vector received by element 2 within T/2 period is
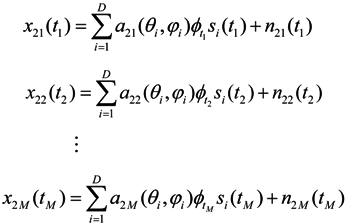
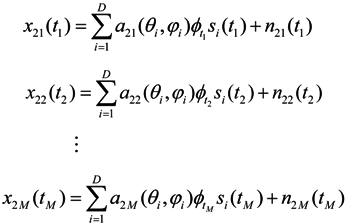
Similarly, denoting Φ2 = diag[ϕt1, ϕt2, ⋯, ϕtM]; ϕtm is the phase difference of element 2 at time tm relative to the initial position; therefore, the array output matrix of element 2 within T/2 is modeled as
X2 = Φ2A2S + N2
When the array elements are rotating more than T/2 period, we can select 2M elements to construct a virtual UCA. Then, integrate X1 with X2, X can be represented by X1 and X2
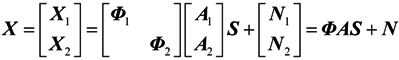 where
where 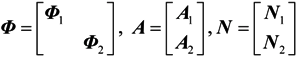 .
.
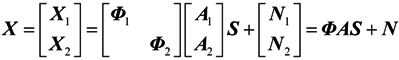
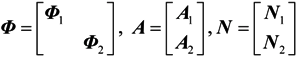 .
.Using Equations (7), (9) and (10), MUSIC spectrum function will be obtained.
Seen from the analysis above, the key advantages of the proposed method is, by sampling the received signal date at a uniform time interval while the array antennas are rotating, more than two antenna elements can be obtained and it can estimate more than two DOAs. Besides, because the number of antennas is much smaller, the array system is greatly simplified than the traditional array and it will become much easier to calibrate with channel phase errors in practice.
3.2. How to Choose Array Rotation Velocity
Consider the rotation frequency is ƒz, and ƒz = 1/T, ƒs is the sampling frequency of the receiver. Select 2M antenna elements within T/2 period while array rotating. Because the characteristics of element 1 are the same as element 2, we only need to analyze element 1 in this subsection. As we know, the received signal data is sampled while the array is rotating, which will cause a tiny phase difference between every two sampled data. In order to ensure the stability of sampled data, ∆τ should satisfy the following equation
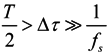 where ∆τ is much greater than the sampling time interval. We have
where ∆τ is much greater than the sampling time interval. We have
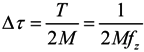
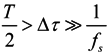
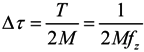
Assume the snapshots is L, then
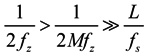
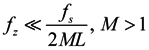
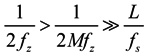
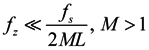
As a result, if (28) is satisfied, the stability of the algorithm could be ensured. Consider the sampling frequency of a receiver is 50 MHz, the elements number is 8, the snapshots number L is 100, according to (28), we can get ƒz ≪ 31 250 Hz. If the antenna rotation frequency is much smaller than 31,250 Hz, the stability of the sampled data will be guaranteed.
4. The Cramer-Rao Bound
Cramer-Rao bound (CRB) gives a lower bound of unbiased parameter estimation. In this section, some assumptions are considered to hold throughout this section first: (1) The number of selected array elements should be greater than that of signals (M > D); (2) The noise {n(t)} is Gaussian distributed and E{n(t)nH(t)} = σ2I, E{n(t)nT(t)} = 0; (3) The signal covariance matrix RS = E{SSH} is positive definite. Furthermore, the signals and noise are uncorrelated for all time. Under these conditions, we derive the Cramer-Rao bound (CRB) formula for the algorithm proposed in this paper. The derivation process approximates the method proposed in [24].
Define u is the angle parameters vector contained in the signal covariance matrix RS,
where θ = [θ1, ⋯, θD]T, φ = [φ1, ⋯, φD]T. The CRB of the angle parameters is defined as
u = [θT,φT]T
var(u) ≥ CRB
var(u) = E[(û - u)(û - u)T]
CRB = F-1
The 2D × 2D Fisher information matrix (FIM) for the parameter u is given by
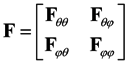 where Fθθ is the block matrix of azimuth estimator and Fφφ is the block matrix of elevation estimator. The m, n elements of F is represented as
where Fθθ is the block matrix of azimuth estimator and Fφφ is the block matrix of elevation estimator. The m, n elements of F is represented as
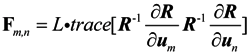 where trace[●] is the trace of matrix[●]. L is the snapshot. Define
where trace[●] is the trace of matrix[●]. L is the snapshot. Define
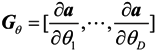
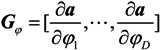
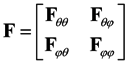
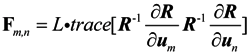
G = [Gθ,Gφ]
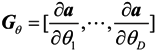
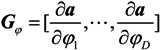
Then the matrix Fθθ, Fφφ, Fφθ, Fθφ, is represented as
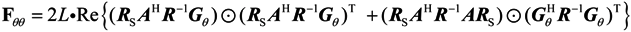
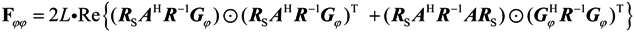
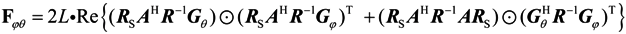
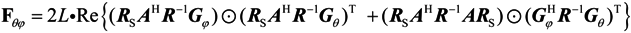 where ʘ denotes the Hadamard product.
where ʘ denotes the Hadamard product.
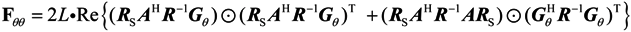
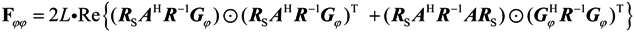
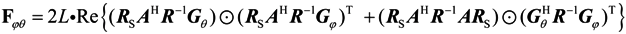
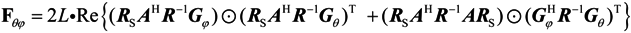
5. Simulation Examples
This section demonstrates the performance of the proposed method via numerical simulation. In all simulation examples, we use the rotation array structure shown in Figure 2. The radius r is 0.124 m, the rotation frequency ƒz is 15 Hz, and the noise background is AWGN. Select M = 8 and M = 10 elements for forming the UCA to estimate DOAs. To verify the performance of the R-MUSIC algorithm, some comparison simulations of MUSIC algorithm with five elements UCA and eight elements UCA are carried as well.
5.1. Resolution Performance Simulation
In this part, the resolution is defined as
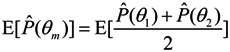 where θm = (θ1 + θ2)/ 2. When the right-hand side of (30) is smaller than the left-hand side, the two angles can be distinguished; while the right-hand sides of (30) is great than the left-hand sides, then the two angles cannot be distinguished. Furthermore, the successful resolution probability is defined as the ratio of successful test numbers to the total test numbers.
where θm = (θ1 + θ2)/ 2. When the right-hand side of (30) is smaller than the left-hand side, the two angles can be distinguished; while the right-hand sides of (30) is great than the left-hand sides, then the two angles cannot be distinguished. Furthermore, the successful resolution probability is defined as the ratio of successful test numbers to the total test numbers.
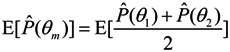
5.1.1. The Spatial Spectrum of the R-MUSIC Algorithm
In order to verify the effectiveness of the proposed method, some spatial spectrum figures are shown in this section. Assume there are several incoherent signals impinging on the array, the signal frequencies are 6 GHz, SNR (signal to noise ratio) is 20 dB and the snapshots are 100. Figure 3 shows the spatial spectrum of two, three, and four incident signals, respectively. It can be seen that the proposed method has better resolution and estimation accuracy performance. In addition, it can estimate more than two sources successfully.
5.1.2. The Resolution Probability versus SNR
Two signal DOAs are (90°, 81°) and (90°, 85°), respectively, and both the signal frequencies are 6 GHz. Figure 4 displays the resolution probability of the eight-element R-MUSIC, 10-element R-MUSIC, five-element UCA MUSIC, and eight-element UCA MUSIC versus the SNR from −2 to 8 dB with snapshots number L = 100. While Figure 5 displays the resolution probability of the four methods versus the snapshots number from 16 to 144 with SNR = 20 dB. Every data is averaged over 200 Monte Carlo simulations. It can be seen from Figure 4 and Figure 5 that the resolution performance of the proposed eight-element R-MUSIC is close to that of the five-element UCA-MUSIC, but the successful probability is lower than that of the eight-element UCA-MUSIC. However, if we select 10 elements to form a UCA, then the resolution performance will be better than that of the eight-element UCA-MUSIC.
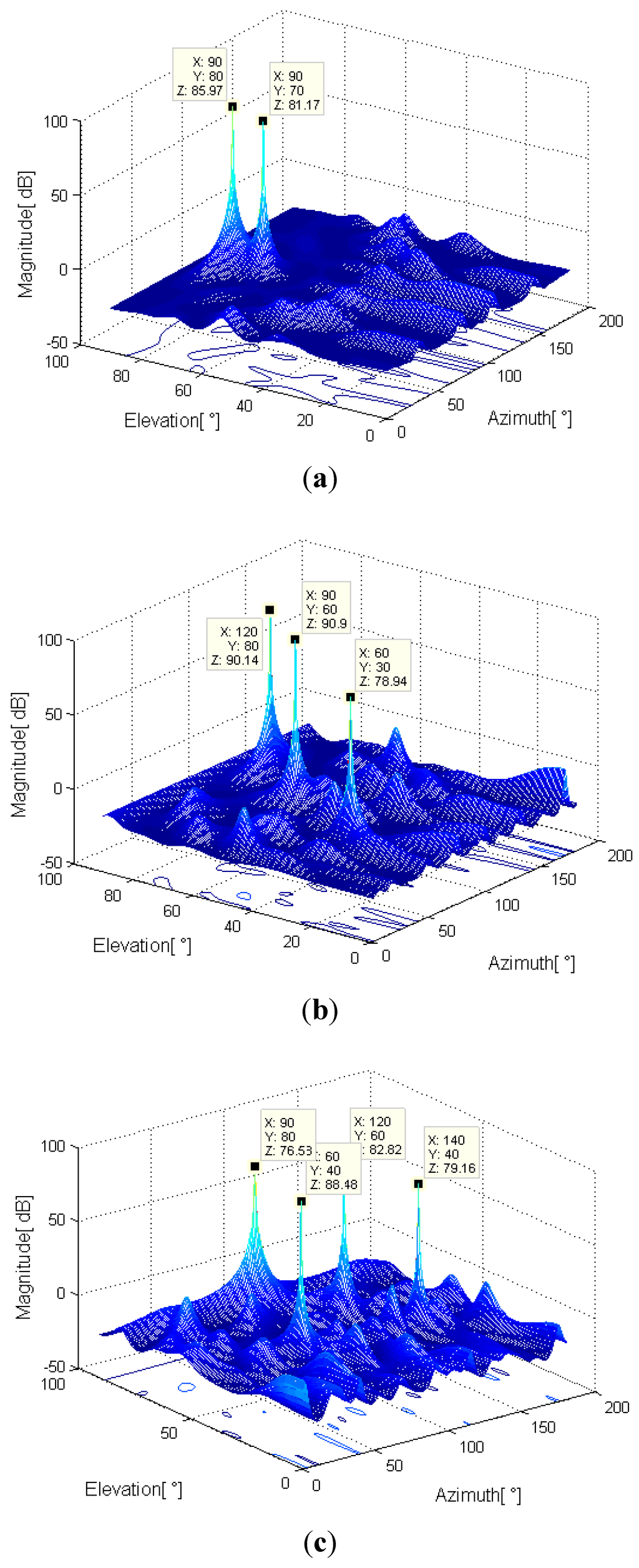
Figure 3.
Spatial spectrum with multiple signals. (a) Two signal DOAs are (90°, 70°) and (90°, 80°); (b) Three DOAs are (60°, 30°), ( 90°, 60°) and ( 120°, 80°); (c) Four DOAs are (60°, 40°), (90°, 80°), (120°, 60°) and (140°, 40°).
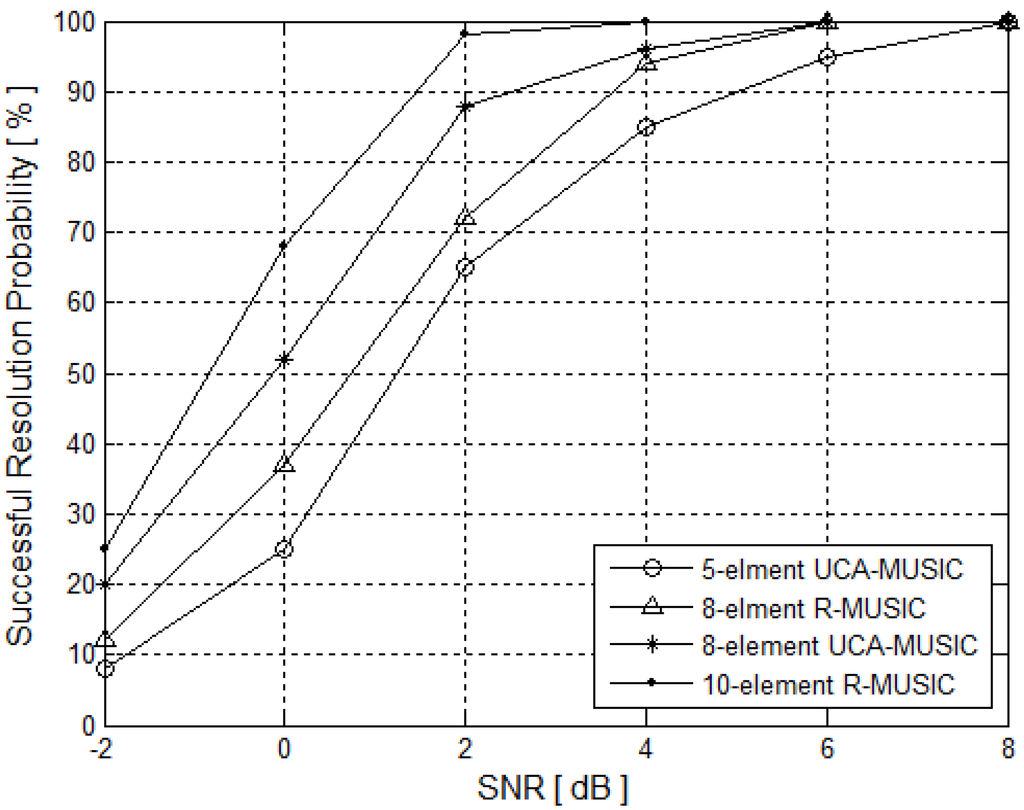
Figure 4.
Successful resolution probability versus SNR.
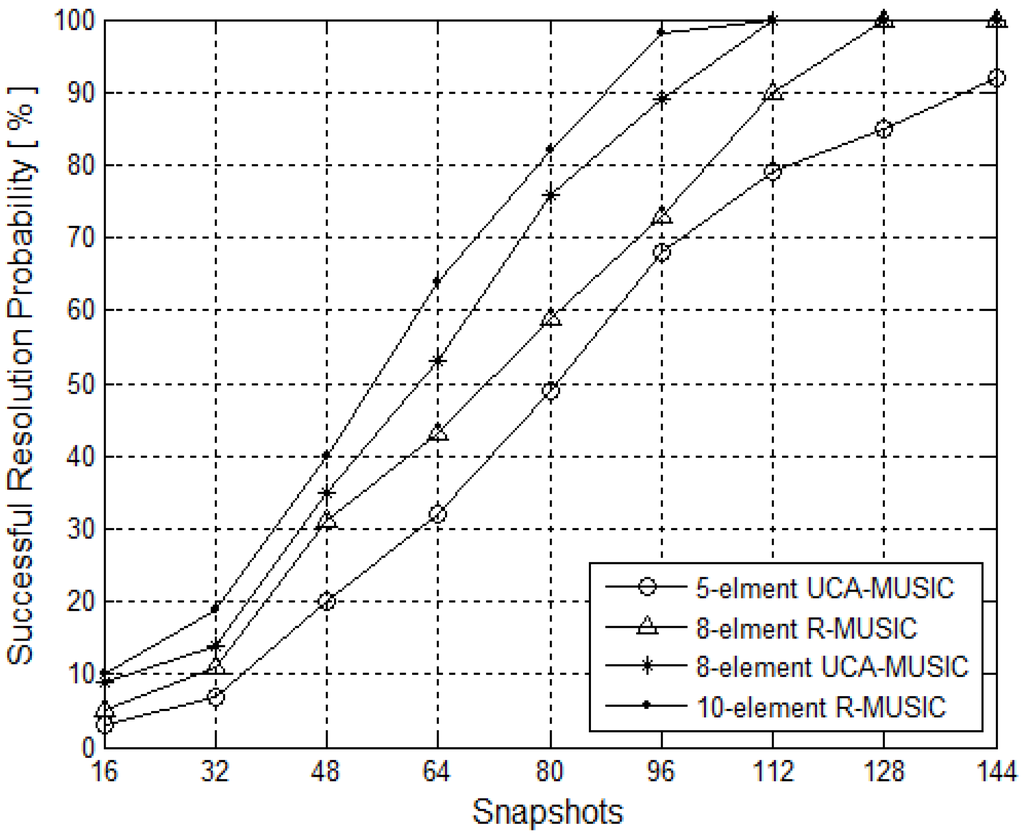
Figure 5.
Successful resolution probability versus snapshots number.
5.2. Estimation Accuracy Performance Simulation
Two signal DOAs are (90°, 81°) and (90°, 85°), respectively, both the signal frequencies are 6 GHz. Figure 6 displays the root mean square error (RMSE) of the eight-element R-MUSIC, 10-element R-MUSIC, five-element UCA MUSIC, and eight-element UCA MUSIC versus the SNR from 2 to 14 dB with snapshots L = 100. While Figure 7 displays the resolution probability of the four methods versus the snapshots from 16 to 144 with SNR = 10 dB. Every data is averaged over 200 Monte Carlo simulations. It can be seen from Figure 6 and Figure 7 that the RMSE of the proposed algorithm approximates to the CRB and the RMSE of the four methods is decreasing with increasing snapshots. Besides, the estimation accuracy performance of the proposed eight-element R-MUSIC is better than that of the five-element UCA-MUSIC, but which is lower than that of the eight-element UCA-MUSIC. However, the estimation accuracy of the 10-element R-MUSIC is better than that of the eight-element UCA-MUSIC.
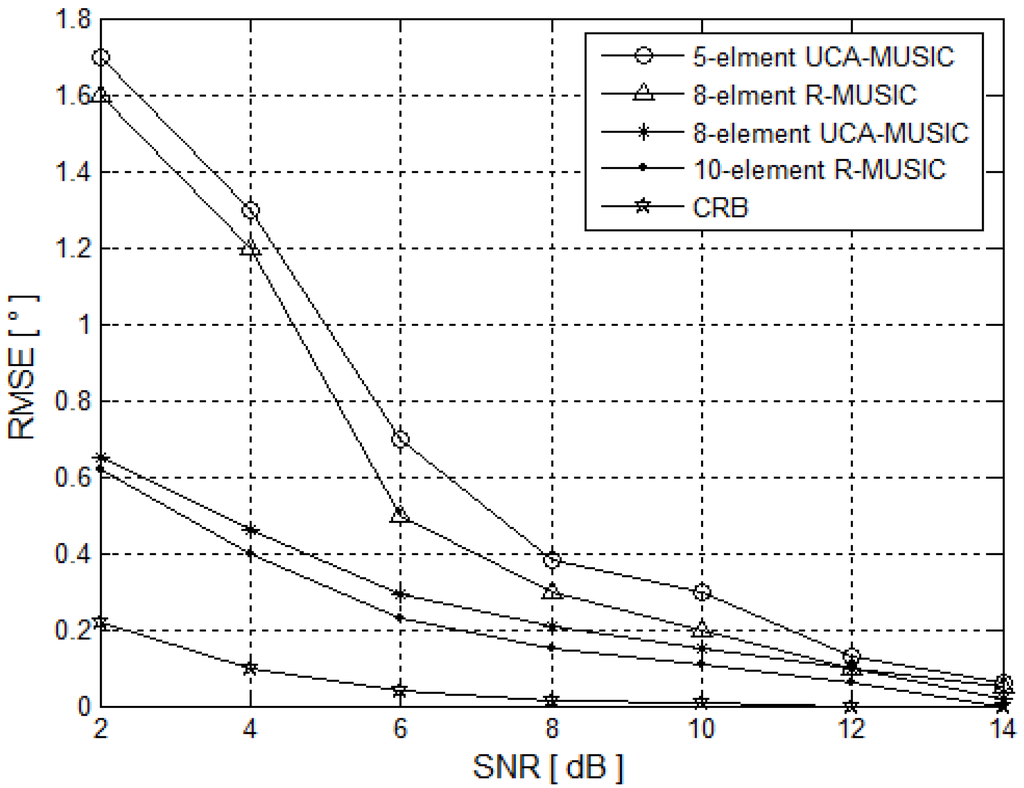
Figure 6.
RMSE versus SNR.
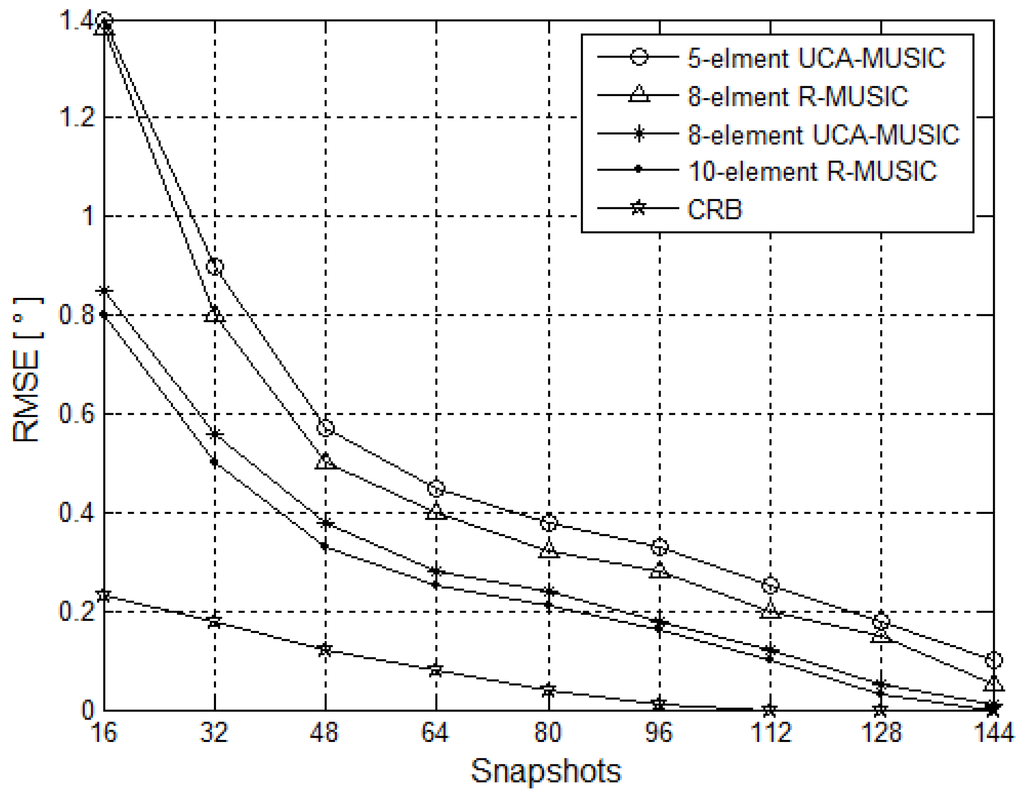
Figure 7.
RMSE versus snapshots.
5.3. Channel Mismatch Errors Simulation
The influence of channel mismatch errors on the resolution probability of the eight-element R-MUSIC and five-element MUSIC is shown in Figure 8. The channel mismatch errors range from 0 to 40°, SNR is 6 dB and the snapshots number is 100. The two DOAs are the same as the simulation in Subsection 5.2. Every data is averaged over 200 Monte Carlo simulations. Table 1 shows the RMSE versus the channel mismatch errors. Because the statistical characteristics of the two DOAs are the same, both Figure 8 and Table 1 shows the estimation results of DOA = (90°, 85°).
It can be seen from the Figure 8 that the proposed R-MUSIC algorithm can provide better robustness than that of the classical MUSIC in large channel mismatch errors. Table 1 shows the estimation accuracy performance of R-MUSIC is much better than that of the classical MUSIC, when the channel mismatch errors exist. This is because the R-MUSIC algorithm only needs two elements; the number of elements of R-MUSIC is much less than that of the classical MUSIC. Furthermore, the problem of element channel calibration is easier to solve too.
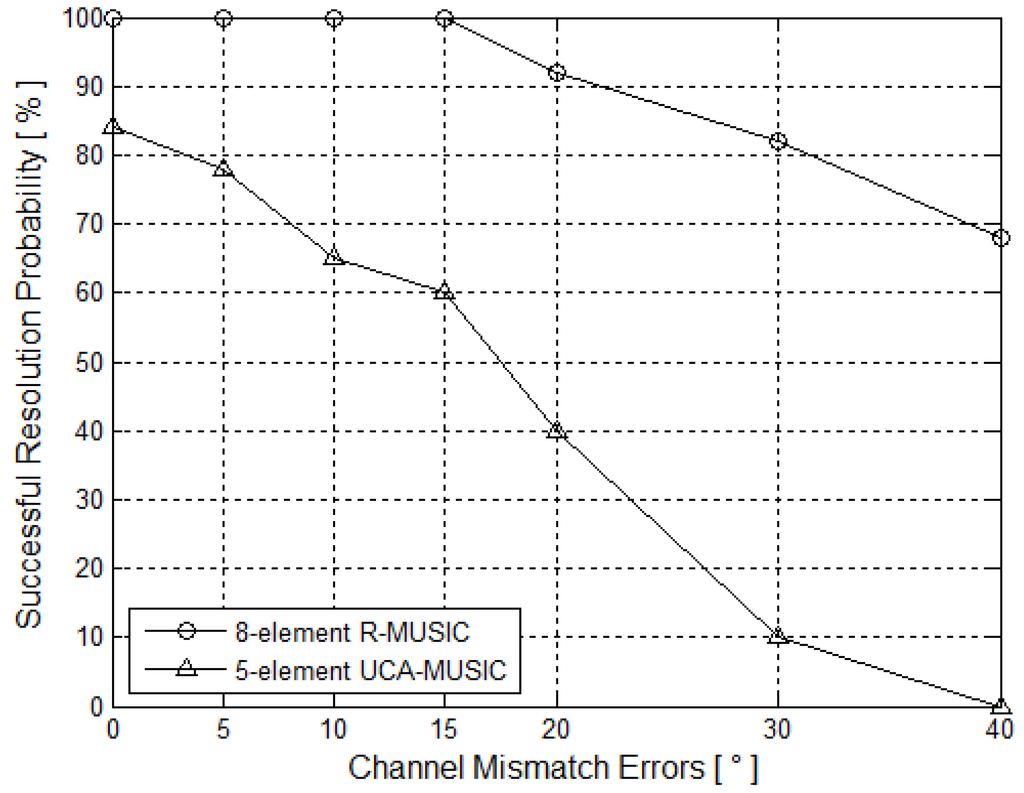
Figure 8.
Successful resolution probability versus different channel mismatch errors.

Table 1.
The RMSE versus different channel mismatch errors [degree]
| Channel mismatch errors [degree] | 5-elment UCA-MUSIC | 8-element R-MUSIC |
|---|---|---|
| 0 | 0.1414 | 0.2739 |
| 5 | 0.2191 | 0.2162 |
| 10 | 0.4817 | 0.4000 |
| 15 | 0.5441 | 0.4427 |
| 20 | 0.6132 | 0.4336 |
5.4. Resolution Performance versus Rotation Frequency Errors
There are two inherent incident signals with DOAs are (90°, 81°) and (90°, 85°) respectively, both the signal frequencies are 6 GHz. The snapshots number is L = 100, and in theory, the rotation frequency is ƒz = 15HZ. However, in fact, the rotation velocity will be greater or smaller than the theory rotation frequency ƒz. Now, assume the actual rotation frequency is ƒʹ, and let ƒʹ range from 14.3 to 15.5 Hz by the step 0.1 Hz in this simulation. So, the rotation frequency error is ∆ƒ = ƒʹ − ƒz. shows the successful resolution probability versus rotation frequency error when SNR = 4 dB, 8dB, 10 dB and 20 dB, successively.
As shown in Figure 9, when ƒʹ = ƒz and the SNR>8 dB, the successful resolution probability of the R-MUSIC is 100%; However, when the actual rotation frequency ƒʹ is larger or smaller than ƒz, the successful resolution probability will decrease. The larger the |∆ƒ| is, the lower the successful resolution probability is. On the other hand, when SNR = 4 dB, the successful rotation frequency (>60%) ranges from 15 − 0.3 ~ 15 + 0.3 Hz; When SNR = 10 dB, the successful rotation frequency ranges from 15−0.4 ~ 15 + 0.4 Hz; When SNR = 20 dB, the successful rotation frequency ranges from 15 − 0.5 ~ 15 + 0.4 Hz; that is to say, with increases in SNR, the rotation array system can tolerate wider rotation frequency error range. However, when ∆ƒ is larger than a certain value, even increasing SNR would not improve resolution. That is because according to Equation (15), a larger rotation frequency error will cause a Doppler frequency shift, which has a great influence on the estimation and resolution performance of the proposed algorithm.
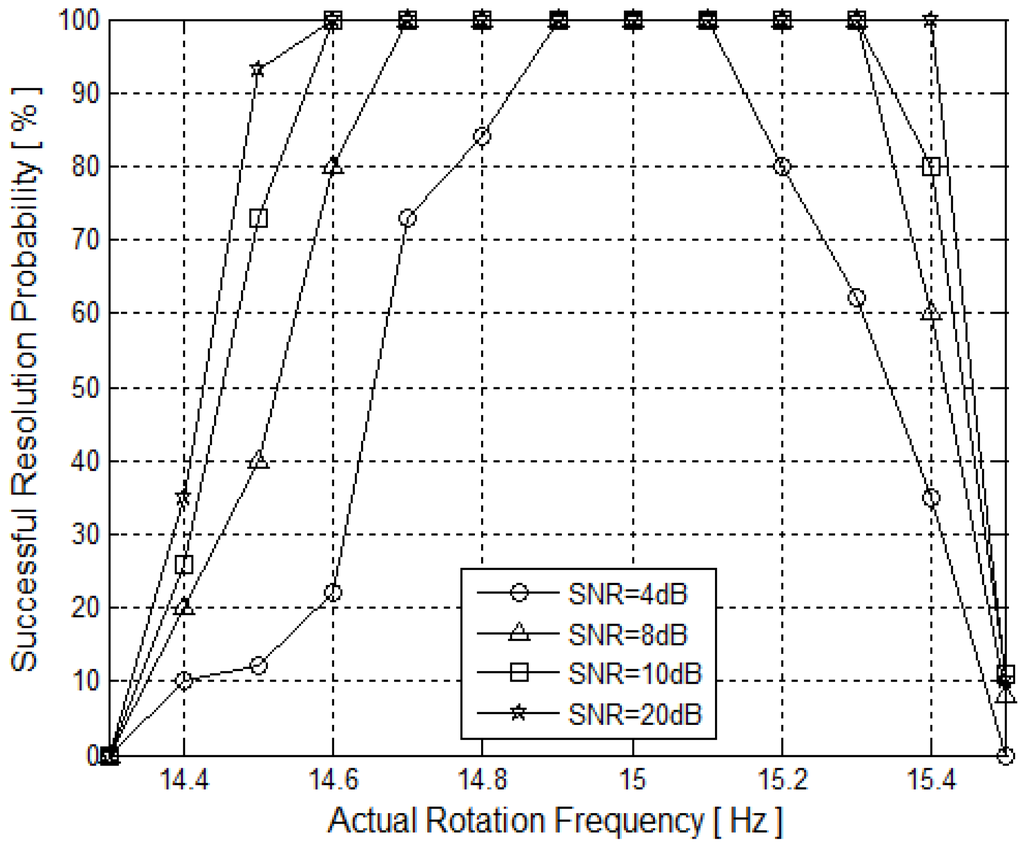
Figure 9.
Successful resolution probability versus rotation frequency errors.
6. Conclusions
The performance of classical MUSIC algorithm based on UCA is constrained by array aperture greatly, and most DOA estimation algorithms demand that the number of elements be larger than that of incident signals. Focusing on this problem, a novel multiple DOAs estimation algorithm based on rotation array is proposed in this paper, which has lower energy loss and complexity. Computer simulations verify the effectiveness of the proposed method, and the number of incident signals that the algorithm could estimate is more than that of the elements. Besides, the proposed array model could be used for any algorithm based on UCA. In the future work, we will focus on the application of the proposed algorithm [25].
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No 61101161). Guangjie Han’s work is supported by “Natural Science Foundation of Jiangsu Province of China, No.BK20131137”. This work has been partially supported by Instituto de Telecomunicações, Next Generation Networks and Applications Group (NetGNA), Covilhã Delegation, by National Funding from the FCT—Fundação para a Ciência e a Tecnologia through the Pest-OE/EEI/LA0008/2013 Project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schmidt, R.O. Multiple Emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Rubsamen, M.; Gershman, A.B. Direction of arrival estimation for nonuniform sensor arrays: From manifold separation to Fourier domain MUSIC methods. IEEE Trans. Signal Process. 2009, 57, 588–599. [Google Scholar] [CrossRef]
- Gao, F.F.; Nallanathan, A.; Wang, Y.D. Improvd MUSIC under the coexistence of both circular and noncircular sources. IEEE Trans. Signal Process. 2008, 56, 3033–3038. [Google Scholar] [CrossRef]
- You, H.; Huang, J.G.; Jin, Y. Improving MUSIC performance in snapshot deficient scenario via weighted signal-subspace projection. Syst. Eng. Electron. 2008, 30, 792–794. [Google Scholar]
- Mestre, X.; Lagunas, M. Modified subspace algorithms for DOA estimation with large arrays. IEEE Trans. Signal Process. 2008, 56, 598–614. [Google Scholar] [CrossRef]
- Mccloud, M.L.; Scharf, L.L. A new subspace identification algorithm for high-resolution DOA estimation. IEEE Trans. Antennas Propag. 2002, 50, 1382–1390. [Google Scholar] [CrossRef]
- Liu, J.; Yu, H.Q.; Huang, Z.T. Conjugate extended MUSIC algorithm based on second-order preprocessing. Syst. Eng. Electron. 2008, 30, 57–60. [Google Scholar]
- Liu, H.S.; Xiao, X.C. An approach to designing linear array with high accuracy doa estimate based on minimal manifold length. Acta Aeronaut. Etastronautica Sin. 2008, 29, 462–466. [Google Scholar]
- He, M.H.; Yin, Y.X.; Zhang, X.D. UCA-ESPRIT algorithm for 2-D angle estimation. IEEE Trans. Signal Process. 2000, 1, 437–440. [Google Scholar]
- Goosens, R.; Rogier, H.; Werbrouck, S. UCA Root-MUSIC with sparse uniform circular arrays. IEEE Trans. Signal Process. 2008, 56, 4095–4099. [Google Scholar] [CrossRef]
- Wu, Y.T.; So, H.C. Simple and accurate two-dimensional angle estimation for a single source with uniform circular array. IEEE Antennas Wirel. Propag. Lett. 2008, 7, 78–80. [Google Scholar] [CrossRef]
- Pajsusco, P.; Pagani, P. On the use of uniform circular array for characterizing UWB time reversal. IEEE Trans. Antennas Propag. 2009, 57, 102–109. [Google Scholar] [CrossRef]
- Huang, L.; Wu, S.; Feng, D. Low complexity method for signal subspace filtering. IEEE Electron. Lett. 2004, 40, 34–38. [Google Scholar] [CrossRef]
- Goosens, R.; Rogier, H. A hybrid UCA RARE or root MUSIC approach of 2D direction of arrival estimation in uniform circular arrays in the presence of mutual coupling. IEEE Trans. Antennas Propag. 2007, 55, 841–849. [Google Scholar] [CrossRef]
- Tao, J.W.; Shi, Y.W.; Chang, W.X. The estimation of 2-D DOA of scattered sources with UCAs. J. China Inst. Commun. 2003, 24, 10–17. [Google Scholar]
- Tao, J.W.; Shi, Y.W.; Chang, W.X. Cross correlation estimator of azimuth-elevation with UCAs. Acta Electron. Sin. 2003, 31, 575–575. [Google Scholar]
- Tang, Z.L.; Wu, S.J.; Zhang, S. Estimation of 2-D DOA based on uniform circle array. J. Harbin Eng. Univ. 2005, 26, 247–252. [Google Scholar]
- Xu, D.C.; Liu, Z.W.; Qi, X.D. A unitary transformation method for DOA estimation with uniform circular array. Radio Eng. 2010, 40, 13–16. [Google Scholar]
- Lu, L.Q.; Hu, X.P.; Wu, M.P. Fast orientation determination by Twin-Star system through method of rotating baseline. J. Astronaut. 2004, 25, 158–162. [Google Scholar]
- Si, W.J.; Cheng, W. Study on solving ambiguity Method of rolling interferometer and implemention. J. Proj. Rocket. Missiles Guid. 2010, 30, 199–202. [Google Scholar]
- Yaqoob, M.A.; Tufvesson, F.; Mannesson, A.; Bernhardsson, B. Direction of arrival estimation with arbitrary virtual antenna arrays using low cost inertial measurement units. In Proceedings of the IEEE ICC 2013 Workshop on Advances in Network Localization and Navigation, Budapest, Hungary, 9–13 June 2013.
- de Jong, Y.L.C.; Herben, M.H.A.J. High-resolution angle-of arrival measurement of the mobile radio channel. IEEE Trans. Antennas Propag. 1999, 47, 1677–1687. [Google Scholar] [CrossRef]
- Broumandan, A.; Lin, T.; Moghaddam, A. Direction of Arrival Estimation of GNSS Signals Based on Synthetic Antenna Array. In Proceedings of the International Technical Meeting (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007.
- Yuan, X.H.; Zhen, H.; Yu, F.Q. Cramer-Rao bound for 2-D angle estimation with uniform circular array. J. Telecommun. Eng. 2013, 53, 44–51. [Google Scholar]
- Han, G.J.; Xu, H.; Duong, T.Q.; Jiang, J.; Takahiro, H. Localization algorithms of wireless sensor networks: A survey. Telecommun. Syst. 2013, 52, 2419–2436. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).