Ensemble Learning for Software Requirement-Risk Assessment: A Comparative Study of Bagging and Boosting Approaches

Abstract

In software development, software requirement engineering (SRE) is an essential stage that guarantees requirements are clear and unambiguous. However, incomplete inconsistency, and ambiguity in requirement documents often occur, which can cause project delay, cost escalation, or total failure. In response to these challenges, this paper introduces a machine learning method to automatically identify the risk levels of software requirements according to ensemble classification methods. The labeled textual requirement dataset was preprocessed utilizing conventional preprocessing techniques, label encoding, and oversampling with the synthetic minority oversampling technique (SMOTE) to handle class imbalance. Various ensemble and baseline models such as extra trees, random forest, bagging with decision trees, XGBoost, LightGBM, gradient boosting, decision trees, support vector machine, and multi-layer perceptron were trained and compared. Five-fold cross-validation was used to provide stable performance evaluation on accuracy, area under the ROC curve (AUC), F1-score, precision, recall, root mean square error (RMSE), and error rate. The bagging (DT) classifier achieved the best overall performance, with an accuracy of 99.55%, AUC of 0.9971 and an F1-score of 97.23%, while maintaining a low RMSE of 0.03 and error rate of 0.45%. These results demonstrate the effectiveness of ensemble-based classifiers, especially bagging (DT) classifiers, in accurately predicting high-risk software requirements. The proposed method enables early detection and mitigation of requirement risks, aiding project managers and software engineers in improving resource planning, reducing rework, and enhancing overall software quality.

1. Introduction

Software development is a highly complex and dynamic process requiring a high level of focus on quality right from its initial stages, especially in the requirements engineering phase [1]. Of all the phases of the software development life cycle (SDLC), the requirements phase is the most vital, since vagaries, inconsistencies, or gaps at this phase have the potential to cascade down to the succeeding development phases with typically catastrophic effects in the form of delays in the project, increased costs, or even outright failures. The increasing use of waterfall and iterative development paradigms has further raised the volatility of requirement specifications, where regular changes due to changing stakeholder demands and market requirements are the norm [2]. In such environments, manual tracking of risks becomes less reliable, time-consuming, and susceptible to human error.

Consequently, requirement-risk analysis has become a vital activity for early defect detection, enabling well-informed design decisions and ensuring that the resulting software aligns with business objectives and stakeholder expectations [3]. Research has further demonstrated the viability of using test cases in agile development processes as substitutes for formal requirement specifications. This practice helps reduce ambiguity and improves the effectiveness of risk mitigation [4]. With the advancement of artificial intelligence, particularly in ML [5] and NLP, automated approaches to requirement-risk analysis have gained significant attention. These techniques aim to eliminate manual intervention and improve the objectivity and accuracy of identifying faulty or high-risk requirement statements [6,7].

Manual checks, checklists, and expert opinion were conventionally used for risk detection in requirement specifications. These are normally non-reproducible, biased, and non-scalable in large, dynamic projects. In reaction, recent research has shifted towards ML and NLP techniques for the automation of risk detection and enhancing objectivity and consistency in predictions. ML classifiers can be learned from past requirement datasets, while NLP techniques can learn semantic and syntactic features from text data for identifying imprecise, conflicting, or incomplete requirement statements. While past models like naïve Bayes and Support Vector Machines have proved promising, their dependency on manual feature engineering restricts their applicability across different domains [8].

Ensuring guaranteeing software reliability and quality has long been a problem area in software engineering, with predictive modeling taking the central position of detecting emerging risks at initial development phases. Previous work has investigated different statistical and machine learning approaches for that aim. For instance, Kumar et al. [9] used Bayesian belief networks to forecast fault-prone software modules, confirming the feasibility of probabilistic models for early defect identification. On a larger scale, Kumar et al. [10] carried out an extensive scientometric study of quality and reliability engineering research with an emphasis on the rising use of computational intelligence techniques in software dependability advancements.

With the advent of deep learning, more specifically transformer-based models such as BERT, RoBERTa, and DistilBERT, the landscape of requirement-risk analysis has also seen a dramatic shift. These models leverage contextual embeddings to more effectively capture the rich nuances of language, enhancing the accuracy of classifying difficult or ambiguous requirement text [11,12]. Although having better performance, these models are susceptible to requiring a massive number of computational resources, large numbers of labeled data, and familiarity with fine-tuning, thus being less feasible on large scales within industrial environments, more so where labeled requirement-risk data are limited. Additionally, their black-box nature will be likely to restrict interpretability as a critical aspect in software engineering where transparency and justification of decisions are paramount.

To solve these challenges, this paper suggests an efficient yet effective ensemble learning-based approach towards automated risk-prone software requirement statement classification. In particular, we investigate employing bagging algorithms such as decision tree bagging, random forest, and extra trees, and boosting algorithms such as LightGBM, Gradient Boosting, and XGBoost. Ensemble algorithms leverage the collective power of many base learners—bagging reduces variance by parallel training, and boosting minimizes bias and improves generalization by sequential optimization. These models find the optimal trade-off among accuracy, interpretability, and computational overhead and are therefore inherently well-suited for structured, medium-sized requirement sets. The suggested framework uses these ensemble classifiers to classify a preprocessed set of requirement statements into risk-prone and non-risk-prone sets, providing an efficient, cost-effective, and explainable solution for requirement-level risk analysis.

The rest of this paper is organized as follows: Section 2 overviews the related literature on requirement-risk analysis. Section 3 describes the proposed methodology, dataset description, and evaluation setup. Section 4 presents the experimental results and main findings. Section 5 concludes the research and outlines future work directions.

2. Related Work

Predicting software risk has become an important research area with the goal of enhancing software quality and reducing costs associated with project failure and defect remediation particularly in the early phases of the SDLC. Several recent studies have advanced the field by applying ML techniques and intelligent systems to accurately forecast and manage software-related risks.

Gupta et al. [13] executed a systematic mapping study of requirements engineering in software startups. Out of 461 initial papers, they selected 20 primary studies, revealing that startups focus heavily on achieving product/market fit through iterative RE activities (e.g., elicitation, prioritization, validation) in uncertain environments. The review also noted a lack of adaptation of traditional RE practices to startup contexts.

Jimoh et al. [14] applied neuro-fuzzy inference system (ANFIS) for selection of appropriate risk factors in each stage of software development process. They examined how each risk factor influences security risk at different phases of the SDLC and used this analysis to design a weighting method that contributes to building an effective scoring system for security risk assessment. Alharbi et al. [15] proposed an analytical risk-assessment model for concurrent multi-project environments using classification techniques. By evaluating classifiers like simple logistic and REP Tree on a dataset of multiple projects, they achieved 93–98% accuracy in risk-level prediction, validating the use of supervised learning in this domain.

Naseem et al. [16] empirically evaluated ten ML classifiers on a published software requirements-risk dataset. Their study included KNN, naïve Bayes, decision tree variants (e.g., J48, RF, Credal DT), and hybrid models. Credal decision trees (CDT) showed the best performance, with a minimal mean absolute error (MAE 0.013) and high predictive accuracy. Naumcheva [17] explored deep learning for automated requirement generation using a vanilla sentence autoencoder. The generated sentences were mostly incoherent, suggesting that larger datasets or more advanced architectures are necessary for producing syntactically valid requirement statements.

Mahmud et al. [18] performed a systematic review of ML-based software risk prediction methods between 2007 and 2022, where 16 studies were found relevant. While ML models showed promising performance, only a few satisfied stringent quality criteria. Khan et al. [19] proposed a novel “Tree-Family” ML model for software requirement-risk prediction using a public dataset. Their experiments with various ensemble techniques (e.g., Credal DT, GB, RF) concluded that CDT consistently outperformed other models in both accuracy and error rate.

Mamman et al. [20] introduced fuzzy-rule learning for requirements-risk prediction. They enhanced the FURIA fuzzy induction algorithm by adding nested dichotomy-based splitting and rule-stretching methods. These models were evaluated on a benchmark requirements-risk dataset against conventional ML and rule-based baselines. The enhanced FURIA variants achieved superior results roughly 98% in accuracy, AUC, and MCC outperforming the standard FURIA and other comparison models. Xu et al. [21] presented a hybrid ML and fuzzy logic framework using ANFIS, tuned with an Enhanced Crow Search Algorithm (ECSA). Applied to the NASA-93 dataset, this model offered better interpretability and accuracy compared to existing risk-assessment methods.

Pemmada et al. [22] proposed a deep learning-based memetic firefly algorithm-optimized risk prediction model. A deep neural network (DNN) whose hyperparameters were optimized with a novel “memetic” firefly optimizer with a perturbation operator to avoid local optima was proposed. The DNN-MFF model was compared against other hybrid optimizers (DNN with standard firefly, DNN with PSO, etc.) on requirement-risk data. The memetic firefly-tuned DNN achieved the highest classification accuracy (98.8%), outperforming all alternatives, making it a strong candidate for precise early software requirement-risk prediction.

From the above literature, it is evident that ML techniques are essential for the accurate prediction of software requirement risks. While traditional tree-based and rule-based models remain strong, newer approaches such as deep learning and hybrid neuro-fuzzy models offer superior precision and adaptability. Furthermore, incorporating optimization algorithms like the memetic firefly enhances predictive performance. This justifies the adoption of ensemble learning and deep optimization strategies to build robust and scalable risk-assessment frameworks.

3. Methodology

The workflow of this work offers a formal pipeline for building an AI-based software risk classification system through ensemble learning methods, as shown in Figure 1. The methodology focuses on enhancing the prediction accuracy and reliability by employing sophisticated preprocessing and heterogeneous ML models [23]. The dataset is initially preprocessed by converting categorical features into numerical features and deleting missing values to maintain the quality of the data. For handling the imbalance of classes in the target variable (risk levels), SMOTE generates minority class synthetic samples, therefore making a balanced dataset. Models that bag, such as RF and ET, are utilized in order to reduce variance and enhance stability, while models that boost, such as GB, XGB, and LGBM, reduce errors iteratively in an attempt to maximize accuracy. Five-fold cross-validation ensures the unbiased measurement of performance across a range of metrics including accuracy, AUC, RMSE, precision, error rate, F1-score, and recall with scoring metrics of interest being user-customizable for further insight. Results are mechanistically collated and compared fold-wise, emphasizing the power of ensemble models for risk classification. The method produces a strong, interpretable, and data-driven solution, using cutting-edge techniques to facilitate accurate and trustworthy software risk predictions. The step-by-step process is presented in Algorithm 1.

Algorithm 1 Proposed Ensemble Learning Method for Software Risk Classification

1: Input: Dataset D with software requirements and risk levels. 2: Output: Trained ensemble models with performance metrics. 3: Step 1: Data Preprocessing 4:     Load the dataset. 5:     Drop the ‘Requirements’ column to focus on measurable attributes. 6:     Encode categorical features numerically using LabelEncoder. 7:     Remove rows containing missing values to ensure data quality. 8: Step 2: Feature and Target Separation 9:     Let X be the feature matrix (all columns except ‘Risk Level’). 10:   Define y as the target variable, scaling ‘Risk-Level’ values to zero-based indexing. 11: Step 3: Class Balancing with SMOTE 12:    Apply SMOTE with random state = 42 to generate synthetic samples. 13:    Obtain balanced feature matrix X_resampled and target vector y_resampled. 14: Step 4: Model Initialization 15:    Define bagging models: Mbag = {Random Forest, Extra Trees, Bagging Classifier} 16:    Define boosting models: Mboost = {Gradient Boosting, XGBoost, LightGBM} 17:    Define Baseline models: M_base = {Decision Tree, SVM, MLP} 18: Step 5: Model Training and Cross-Validation 19:    for each model M ∈ Mbag ∪ Mboost do 20:        Perform 5-fold cross-validation on X_resampled and y_resampled 21:        for each fold f = 1 to 5 do 22:             Train model M on training subset. 23:             Validate model on validation subset. 24:             Record metrics: Accuracy, F1-Score, AUC, Precision, Recall, RMSE, and Error Rate. 25:        end for 26:    end for 27:  Step 6: Performance Analysis 28:    Aggregate fold-wise metrics for each model. 29:    Compare bagging, boosting, and baseline models. 30:    Identify best-performing model(s) based on evaluation metrics then perform statistical tests. 31: Step 7: Result Interpretation 32:    Compute feature importance and visualize grouped impacts (Bagging, Boosting, Baseline) 33:   Summarize findings with performance tables and interpretability insights 34:   Highlight models most effective for software risk classification

3.1. Dataset

The dataset used in this research includes 299 labeled software requirement records that are all enriched with several risk-related attributes [24]. It contains 13 fields encompassing both textual and numerical/categorical features. The requirements field includes natural language statements, with 292 unique entries. Each requirement is linked to a project category (e.g., transaction processing system), a requirement category (e.g., functional, non-functional), and a risk target category (e.g., quality, budget, schedule), providing essential contextual metadata relevant to software engineering. Additionally, the dataset includes several quantitative attributes include probability (likelihood of risk occurrence, ranging from 1% to 100%), fixing duration (in days), fix cost (as a percentage of the total project), and priority. Additionally, categorical descriptors such as magnitude of risk, dimension of risk, and impact offer further granularity regarding the nature and scope of the associated risks.

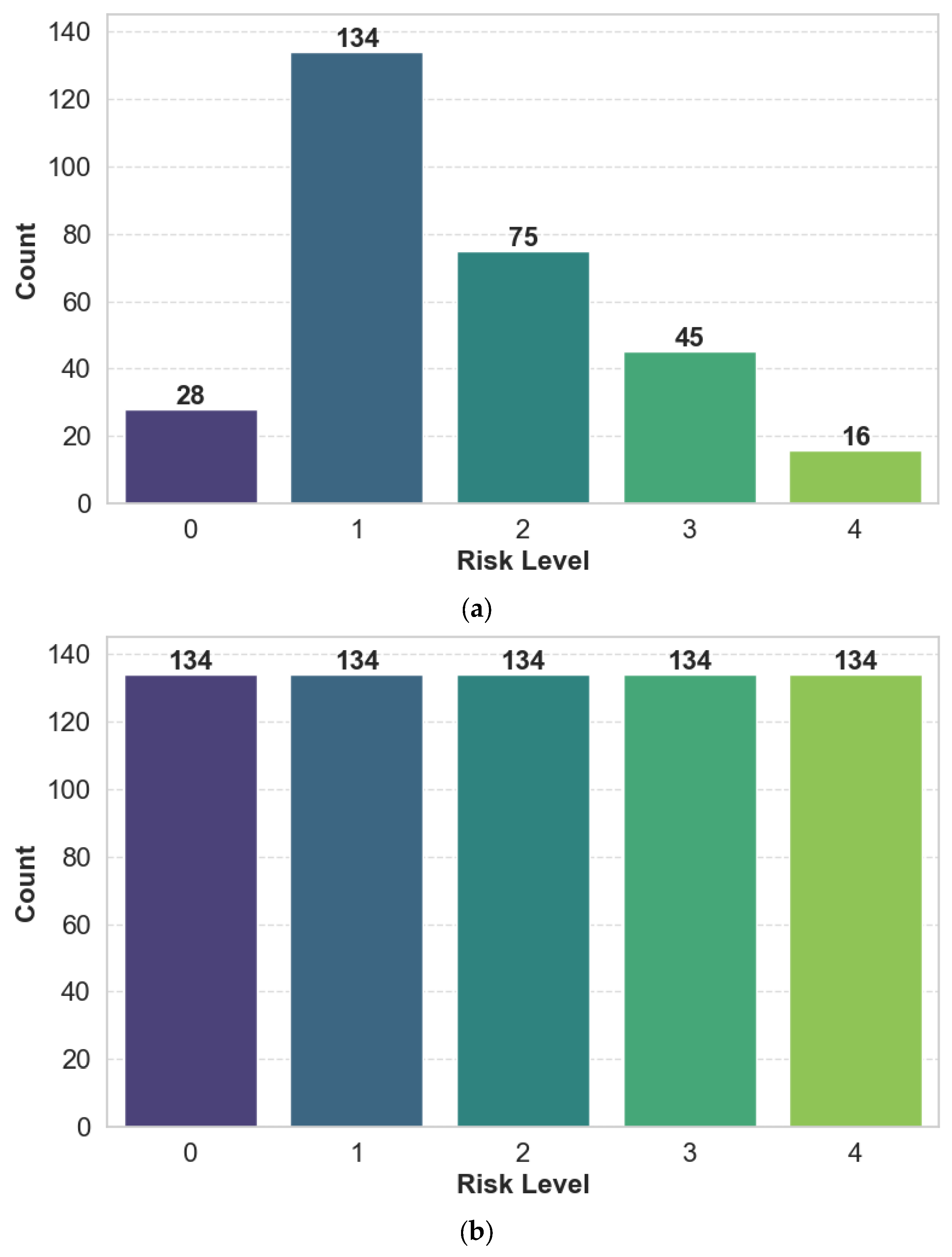
The target variable, risk level, is an integer-labeled value between 1 and 5, with 1 being the least risky and 5 being the most risky. Figure 2a illustrates the distribution of risk levels in the dataset. The distribution is moderately imbalanced, with a higher concentration of instances in the mid-range categories (levels 2 and 3), while the extreme classes (levels 1 and 5) contain fewer samples. This suggests that most requirements are associated with moderate levels of risk, with only a minority falling into the very low or very high-risk categories. Given this imbalance, special attention must be paid during model training to mitigate potential bias toward the majority classes. Overall, the dataset’s rich feature composition and labeled risk levels make it well-suited for supervised ML approaches [25] aimed at automated software requirement-risk classification and prioritization.

3.2. Data Preprocessing

Prior to exposing the raw dataset to ML algorithms, a systematic pipeline of preprocessing was adopted. Initially, the unstructured requirements column was removed to retain only measurable and structured risk-related attributes. Categorical variables such as project category and risk target category were transformed into numerical representations using Scikit-learn’s LabelEncoder (scikit-learn v1.2.2, Python v3.10), preserving ordinal semantics where applicable. To ensure data integrity and eliminate inconsistencies, rows containing missing values were discarded, resulting in a final dataset of 298 samples from the original 299 (99.7% retention). This conservative filtering approach ensures a complete-case analysis while minimizing the introduction of preprocessing artifacts.

3.3. Feature-Label Segmentation

After preprocessing, the dataset was split into a feature matrix X and a target vector y. The feature matrix comprises all columns except the target variable, while the label vector consists of risk-level values, re-indexed to a zero-based scale (i.e., 0–4) to conform with Scikit-learn’s classification conventions. This segmentation facilitates proper alignment of feature dimensions and ensures compatibility with standard supervised learning pipelines. Moreover, maintaining the ordinal nature of the risk levels preserves the semantic ordering required for meaningful classification outcomes.

3.4. Class Balancing with SMOTE

To deal with the problem of class imbalance among the risk-level distribution Figure 2a, we used SMOTE [26]. SMOTE generates new samples of the minority classes by interpolating between the original samples in the feature space, via a k-nearest neighbors algorithm (with default k = 5). Using SMOTE created a better balanced class distribution, as depicted in Figure 2b.

Importantly, SMOTE was applied only after feature-label segmentation to prevent target leakage, and synthetic samples were generated exclusively from training folds within the cross-validation procedure. This ensures that the test data remain untouched by synthetic augmentation, preserving their role as an unbiased estimator of generalization performance. The balanced dataset enhances model sensitivity to underrepresented risk levels and enables fairer evaluation across all risk categories.

3.5. Model Selection

Our research adopts a comparative evaluation of state-of-the-art ensemble learning techniques for software risk prediction. We categorize these models into three major paradigms bagging, boosting, and baseline models, each offering unique strengths for imbalanced, high-dimensional datasets.

3.5.1. Bagging Models

Bagging models are ensemble methods that train multiple base learners in parallel on random subsets of the data, reducing variance and improving stability. Popular algorithms include RF, which also randomizes feature selection, enhancing model robustness. Bagging works well with high variance models and helps prevent overfitting by averaging predictions or voting. Unlike boosting, bagging does not focus on correcting errors but rather on creating diverse, independent models.

Random Forest

Random forest (RF) constructs a forest of decision trees, with each tree trained on a bootstrapped sample of data and a random sample of features (with max_features set to ‘sqrt’) [27]. Each tree is expanded fully without pruning and uses Gini impurity for split selection [28]. The ensemble of 100 trees (n_estimators = 100) effectively reduces variance and captures ambiguous patterns in software requirement attributes. RF’s built-in feature importance mechanism enhances interpretability, highlighting influential predictors such as “Probability” and “Fixing Cost”. Its parallel architecture supports efficient training, even on smaller datasets.

Extra Trees

Extra trees (ET) also known as extremely randomized trees differ from RF by selecting split thresholds randomly, increasing variance among the 100 base estimators and reducing training time by approximately 25% [29,30]. ET’s stochastic nature is advantageous when handling redundant or correlated attributes like “Impact” and “Magnitude”. While inheriting RF’s robustness and interpretability, ET’s added randomness further decorrelates trees, improving generalization on small datasets.

Bagging Classifier with Decision Trees

The bagging meta-estimator aggregates 50 unregularized decision tree predictions (n_estimators = 50) trained on bootstrap samples [31]. Contrary to RF, it uses all the features at each node (max_features = 1.0) and is a baseline to check the effect of feature randomization. Decision trees are grown to pure leaves (min_impurity_decrease = 0) so that complex risk interactions are captured but there could be overfitting. This one showcase bagging’s primary advantage variance reduction via majority vote without RF/ET’s optimizations [32]. For software risk data, the simplicity of the model allows it to identify whether feature randomization (in RF/ET) or boosting methods provide better performance with the moderate sample size available.

3.5.2. Boosting Models

Boosting models are ensemble learning techniques that combine multiple weak learners sequentially, correcting errors from previous models. Popular algorithms include GB, XGB, and LGBM, which improve prediction accuracy by focusing on misclassified data. They reduce bias and variance, often outperforming single models in tasks like classification and regression. Boosting requires careful tuning to avoid overfitting but is powerful for complex datasets.

Gradient Boosting

Gradient boosting (GB) constructs 100 weak learners sequentially (n_estimators = 100) with regression trees of max depth 3, optimizing exponential loss by gradient descent [33]. New trees update residuals from past predictions, which makes GB very well-suited for ordinal risk ranges (0–4). The learning rate (η = 0.1) is how contribution per tree is controlled, and overfitting is avoided with L2 regularization (λ = 1). GB’s stage-wise strategy is good at picking up on weak patterns of risk (e.g., non-linear interaction between “Priority” and “Fixing Duration”) but needs precise tuning [34]. The computational cost of GB constrains scalability compared to bagging procedures, as boosting builds trees sequentially rather than in parallel.

XGBoost

XGBoost (XGB) enhances GB by incorporating second-order derivatives and regularization techniques [35]. We use 100 estimators (n_estimators = 100), histogram-based splitting (max_bin = 256), and default regularization parameters (lambda = 1, gamma = 0). This design accelerates training and enhances robustness to missing values. XGB’s gain-based feature importance frequently prioritizes “Probability” and “Dimension of Risk” [36]. It also offers internal pruning mechanisms (min_split_loss = 0) and automatic validation to mitigate overfitting.

LightGBM

LightGBM (LGBM) utilizes leaf-wise growth of trees with depth limitations (max_depth = 31) and integrates GOSS (Gradient-based one-side sampling) and EFB (exclusive feature bundling) to speed up learning [37]. With 100 estimators (n_estimators = 100) and early stopping (n_iter_no_change = 10), LGBM achieves high performance with reduced memory usage. Although prone to overfitting on small datasets, its categorical handling (e.g., “Project Category”) and O(n) complexity make it an efficient choice for real-world software risk datasets [38].

3.5.3. Baseline Models

Baseline models such as DT, SVM, and MLP are basic machine learning methods for classification and regression. SVMs determine optimal hyperplanes to discriminate data, performing well in high-dimensional spaces, whereas DTs divide data hierarchically along features, providing understandability but with potential overfitting. MLPs, which are neural networks, learn complicated patterns via layers of neurons but need architecture and hyperparameter tuning. They yield good baselines but are frequently surpassed by ensemble algorithms such as boosting or bagging on more difficult tasks.

Decision Tree

Decision tree (DT) classifier recursively splits the feature space along axis-aligned directions [39]. We utilize Gini impurity as the split criterion with default depth, enabling the model to learn hierarchical patterns among requirement attributes like “Priority” and “Complexity.” Though DT is intuitive, easy to interpret and computationally minimal (O(n log n)), it suffers from overfitting issues, especially for small datasets like PROMISE. Feature importance scores often highlight “Probability” and “Project Category,” aligning with domain-specific risk drivers.

Support Vector Machine

Support vector machine (SVM) baseline implements an RBF kernel to transform features into a higher dimensional space, allowing the classifier to distinguish non-linear boundaries in risk classification [40]. We standardize features to provide stability during margin maximization. SVM optimizes a hinge loss function with regularization (C) to regulate margin width and Platt scaling offers probabilistic outputs. This structure enables SVM to pick up on fine-grained non-linearities in requirement risks.

Multi-Layer Perceptron

Multi-layer perceptron (MLP) is a two-hidden-layer feed-forward neural network with 128 and 64 neurons, employing ReLU activation and Adam optimization [41]. The model is optimized using cross-entropy loss with L2 regularization (α = 1 × 10⁻⁴) and learning rate η = 1 × 10⁻³. Early stopping is employed to avoid overfitting. MLP can capture intricate non-linear relationships between requirement attributes and has high predictive stability across folds. Nonetheless, its “black-box” form diminishes interpretability relative to tree models, making it harder to attribute features.

3.6. Cross-Validation

To provide robust and unbiased estimation, we utilized stratified five-fold cross-validation, which maintains proportional risk-level representation in all folds. This is especially relevant to class imbalance in software risk data where some risk categories are rare. By maintaining class ratios, stratification compensates for sampling bias and guarantees each fold to be representative of the entire dataset. We did this with Scikit-learn’s cross_validate function, which defaults to StratifiedKFold for classification problems [42]. This ensured consistent and equitable evaluations of generalization performance of each model. It also helped to eliminate variability in performance between folds, giving stable and trustworthy metric estimates. Utilizing stratified cross-validation greatly facilitated the reliability of model comparison and enabled more confident selection of good predictors. Average performance between folds gave an equal measure of performance that accounted for the difficulties of imbalanced classification.

3.7. Evaluation Metrics

In order to provide a solid and well-rounded assessment of model performance, we utilized seven highly regarded measures. These measures encapsulate the various facets of effectiveness, specifically with regard to imbalanced, multi-class software requirement-risk prediction. In order to calculate assessment criteria like accuracy, precision, recall, and F1-score, knowledge of the terms true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN) is critical. TP is defined as the number of positive instances predicted correctly, while TN is correctly predicted negative instances. FP is negative samples wrongly predicted positive, and FN are positive samples wrongly predicted negative. These are the values on which all significant classification metrics are based. The total number of predictions is the sum of all four components and is expressed as follows:

Total Predictions = TP + TN + FP + FN

(1)

To further validate the reliability of the reported results, we complemented these metrics with statistical significance testing. Specifically, we applied paired t-tests and the Wilcoxon signed-rank test on the cross-validation fold results. These tests assess whether the performance differences between models are statistically meaningful or merely due to random variation. The paired t-test assumes normally distributed differences across folds, while the Wilcoxon signed-rank test provides a non-parametric alternative, making it robust to non-normal distributions. By incorporating these tests alongside traditional performance metrics, we ensured that the comparative analysis of models reflects not only raw performance values but also their statistical credibility.

3.7.1. Accuracy

Accuracy measures the ratio of correct predictions to total predictions. Although it is a good baseline, it can be too optimistic in unbalanced datasets, where the majority class tends to dominate.

$$\mathrm{Accuracy}={\displaystyle \frac{\mathrm{T}\mathrm{P}+\mathrm{T}\mathrm{N}}{\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s}}}$$

(2)

3.7.2. Area Under the Curve (AUC)

AUC calculates the area under the receiver operating characteristic (ROC) curve, assessing the power of the model to separate classes for all classification thresholds. For multi-class problems, macro-averaged AUC with a one-vs-rest strategy provides equitable assessment of all classes.

3.7.3. Precision

Precision measures the ratio of true positives to all predicted positives. In risk prediction, high precision guarantees that the high-risk requirements that have been identified are actually risky.

$$\mathrm{Precision}(\mathrm{P})={\displaystyle \frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}}}$$

(3)

3.7.4. Recall

Alternatively, recall quantifies the percentage of actual positives correctly predicted. In risk assessment, high recall reduces the likelihood of underestimating high-risk demands.

$$\mathrm{Recall}(\mathrm{R})={\displaystyle \frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}}$$

(4)

3.7.5. Error Rate

Error rate is the complement of accuracy and reflects the proportion of incorrect predictions. It highlights misclassifications, making it valuable for performance analysis in imbalanced settings.

Error Rate = 1 − Accuracy

(5)

3.7.6. Root Mean Squared Error

RMSE, while generally employed in regression tasks, is employed here because of the ordinal nature of the risk labels. It estimates the average size of prediction error and penalizes larger errors more severely.

$$\mathrm{RMSE}=\sqrt{({\displaystyle \frac{1}{\mathrm{n}}}{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{(\mathrm{y}\mathrm{i}-\widehat{\mathrm{y}\mathrm{i}})}^2)}$$

(6)

3.7.7. F1-Score

The F1-score is the harmonic mean of precision and recall. Macro-averaged F1-score is what we report to give equal weights to all classes. The measure is particularly valuable in ordinal and imbalanced classification tasks.

$$\mathrm{F}1-\mathrm{Score}={\displaystyle \frac{2\mathrm{\ast }\mathrm{R}\mathrm{\ast }\mathrm{P}}{\mathrm{R}+\mathrm{P}}}$$

(7)

3.7.8. Paired t-Test

Paired t-test is a statistical technique employed to ascertain if a difference in the mean difference in the performance between two models over the same cross-validation folds is significant statistically. Using the paired t-test in risk prediction assists in providing assurance that improvements observed are not random but instead represent significant differences in model performance. The test presupposes differences to be normally distributed.

$$\mathrm{Paired}t-\mathrm{test}\mathrm{statistic}(\mathrm{t}){\displaystyle \frac{\mathrm{d}}{{\mathrm{s}}_{\mathrm{d}}/\surd \mathrm{n}}}$$

(8)

where d is the mean of differences between paired results, ${\mathrm{s}}_{\mathrm{d}}$ is the standard deviation of differences, and n is the number of folds.

3.7.9. Wilcoxon Signed-Rank Test

Wilcoxon signed-rank test is a non-parametric version of the paired t-test. It tests whether two related samples have significantly different median ranks without normality assumptions about the differences. In software requirement-risk estimation, Wilcoxon test checks robustness by establishing if the estimated performance improvements are valid under fewer distributional assumptions.

The procedure involves ranking the absolute differences between paired results, assigning signs based on direction, and computing the test statistic W, which is the smaller of the sums of positive and negative ranks.

W = min(∑ R⁺, ∑ R⁻)

(9)

where R⁺, R⁻ denote the ranks of positive and negative differences.

4. Results and Discussion

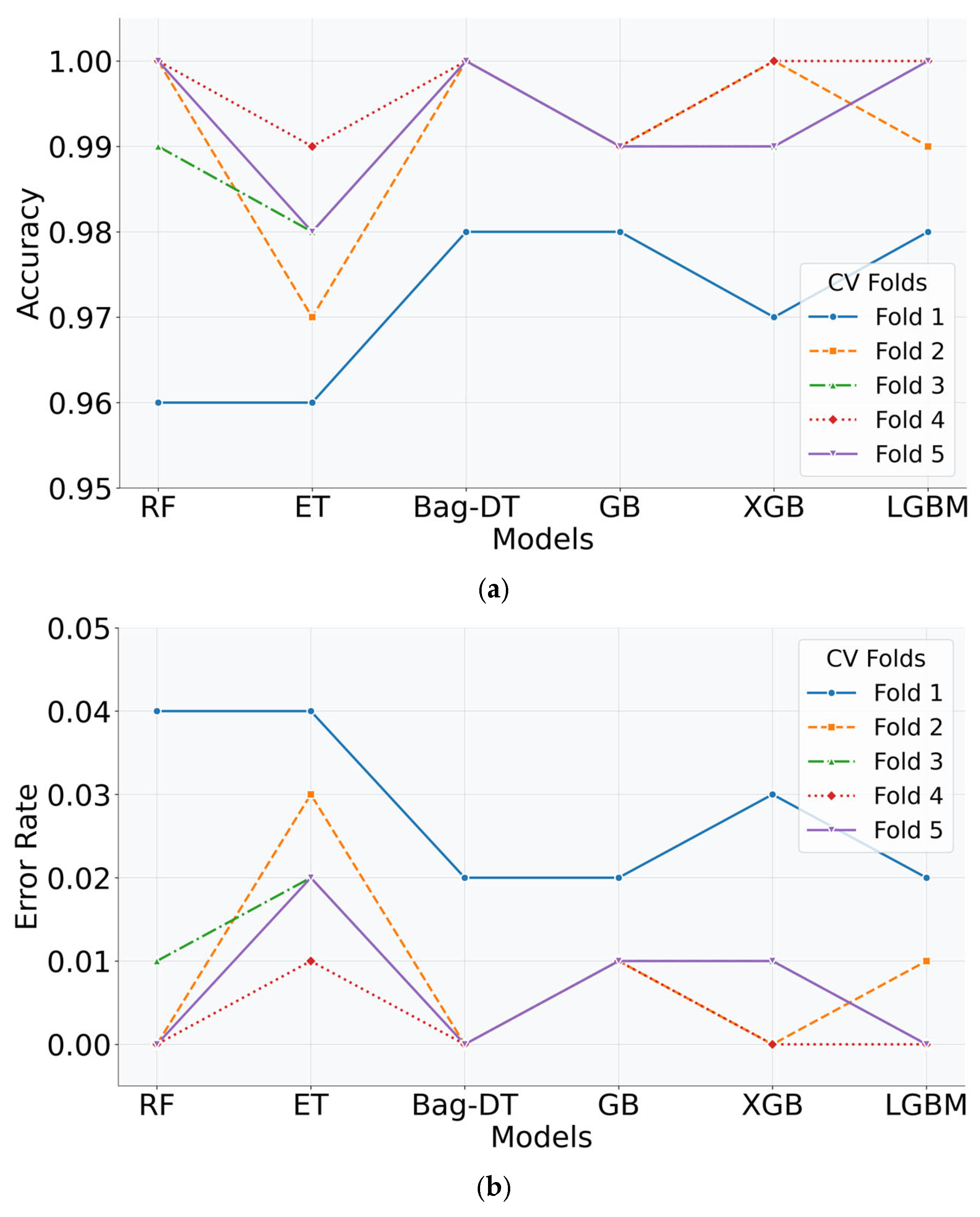
Comparative evaluation of ensemble ML models and baseline ML/DL models such as RF, ET, Bag-DT, LGBM, XGB, GB, DT, SVM, and MLP using stratified five-fold cross-validation provided substantial insights into their classification performance in software requirement-risk prediction. Important evaluation measures such as accuracy, AUC, error rate, F1-score, recall, precision, and RMSE were calculated to examine the predictive accuracy and robustness of the models. The models all had high AUC values, reflecting strong class-separation strength, with low error rates and repeatable results for small folds. Bag-DT and LGBM were the best performing classifiers in both near-perfect accuracy and lowest RMSE. RF and XGB also performed highly competitively, confirming the strength of ensemble-based and boosting models. The marginal difference between the metrics like RMSE and Error Rate also testifies to the stability and reliability of such models.

4.1. Performance Comparison

In order to compare the performance of the suggested ensemble and baseline models, we performed a stratified five-fold cross-validation on the preprocessed and balanced dataset. Every model was assessed against seven performance metrics: AUC, error rate, accuracy, F1-score, precision, RMSE, and recall. The results are shown in

Table 1. Performance measures of RF.

Fold	RMSE	Recall	AUC	F1-Score	Precision	Error Rate	Accuracy
1	0.19	0.96	1.00	0.96	0.96	0.04	0.96
2	0.00	1.00	1.00	1.00	1.00	0.00	1.00
3	0.09	0.99	1.00	0.99	0.99	0.01	0.99
4	0.00	1.00	1.00	1.00	1.00	0.00	1.00
5	0.00	1.00	1.00	1.00	1.00	0.00	1.00

,

Table 2. Performance measures of ET.

Fold	RMSE	Recall	AUC	F1-Score	Precision	Error Rate	Accuracy
1	0.19	0.96	1.00	0.96	0.96	0.04	0.96
2	0.17	0.97	1.00	0.97	0.97	0.03	0.97
3	0.15	0.98	1.00	0.98	0.98	0.02	0.98
4	0.12	0.98	1.00	0.98	0.99	0.01	0.99
5	0.15	0.98	1.00	0.98	0.98	0.02	0.98

,

Table 3. Performance measures of Bag-DT.

Fold	RMSE	Recall	AUC	F1-Score	Precision	Error Rate	Accuracy
1	0.15	0.98	0.99	0.98	0.98	0.02	0.98
2	0.00	1.00	1.00	1.00	1.00	0.00	1.00
3	0.00	1.00	1.00	1.00	1.00	0.00	1.00
4	0.00	1.00	1.00	1.00	1.00	0.00	1.00
5	0.00	1.00	1.00	1.00	1.00	0.00	1.00

,

Table 4. Performance measures of GB.

Fold	RMSE	Recall	AUC	F1-Score	Precision	Error Rate	Accuracy
1	0.15	0.98	0.99	0.98	0.98	0.02	0.98
2	0.09	0.99	1.00	0.99	0.99	0.01	0.99
3	0.09	0.99	1.00	0.99	0.99	0.01	0.99
4	0.09	0.99	1.00	0.99	0.99	0.01	0.99
5	0.09	0.99	1.00	0.99	0.99	0.01	0.99

,

Table 5. Performance measures of XGB.

Fold	RMSE	Recall	AUC	F1-Score	Precision	Error Rate	Accuracy
1	0.17	0.97	1.00	0.97	0.97	0.03	0.97
2	0.00	1.00	1.00	1.00	1.00	0.00	1.00
3	0.09	0.99	1.00	0.99	0.99	0.01	0.99
4	0.00	1.00	1.00	1.00	1.00	0.00	1.00
5	0.12	0.99	0.99	0.99	0.99	0.01	0.99

,

Table 6. Performance measures of LGBM.

Fold	RMSE	Recall	AUC	F1-Score	Precision	Error Rate	Accuracy
1	0.15	0.98	1.00	0.98	0.98	0.02	0.98
2	0.09	0.99	1.00	0.99	0.99	0.01	0.99
3	0.00	1.00	1.00	1.00	1.00	0.00	1.00
4	0.00	1.00	1.00	1.00	1.00	0.00	1.00
5	0.00	1.00	1.00	1.00	1.00	0.00	1.00

,

Table 7. Performance measures of DT.

Fold	RMSE	Recall	AUC	F1-Score	Precision	Error Rate	Accuracy
1	0.15	0.98	0.99	0.98	0.98	0.02	0.98
2	0.15	0.98	0.99	0.98	0.98	0.02	0.98
3	0.15	0.98	0.99	0.98	0.98	0.02	0.98
4	0.00	1.00	1.00	1.00	1.00	0.00	1.00
5	0.09	0.99	1.00	0.99	0.99	0.01	0.99

,

Table 8. Performance measures of SVM.

Fold	RMSE	Recall	AUC	F1-Score	Precision	Error Rate	Accuracy
1	0.38	0.88	0.98	0.88	0.90	0.12	0.88
2	0.31	0.90	0.99	0.90	0.91	0.10	0.90
3	0.19	0.96	1.00	0.96	0.96	0.04	0.96
4	0.30	0.91	1.00	0.91	0.93	0.09	0.91
5	0.32	0.90	1.00	0.89	0.92	0.10	0.90

and

Table 9. Performance measures of MLP.

Fold	RMSE	Recall	AUC	F1-Score	Precision	Error Rate	Accuracy
1	0.35	0.88	0.99	0.88	0.89	0.12	0.88
2	0.24	0.94	0.99	0.94	0.94	0.06	0.94
3	0.23	0.95	1.00	0.95	0.95	0.05	0.95
4	0.21	0.95	1.00	0.95	0.96	0.04	0.96
5	0.29	0.92	1.00	0.92	0.94	0.08	0.92

.

4.1.1. Bagging-Based Models

Table 1, Table 2 and Table 3 provide fold-wise results for the RF, ET, and Bag-DT classifiers, respectively. Among these, Bag-DT achieved near-perfect performance, with F1-score, precision, accuracy, and recall reaching 1.00 in folds 2 through 5. It also reported the lowest RMSE values, demonstrating strong generalization and robustness.

RF also maintained an excellent AUC (1.00 in all folds) and high accuracy (0.96–1.00), with low error rates and RMSE, confirming its effectiveness in handling multi-class classification tasks. ET performed consistently with an AUC of 1.00 and an accuracy between 0.96–0.99, slightly trailing Bag-DT and RF.

4.1.2. Booting-Based Models

Table 4, Table 5 and Table 6 provide fold-wise results for the GB, XGB, and LGBM classifiers, respectively. LGBM outperformed other models with perfect accuracy in the last three folds, lowest RMSE values, and consistently high scores across all metrics.

XGB achieved high accuracy and AUC, maintaining a strong balance between precision and recall. GB performed steadily with F1 and Recall values consistently near 0.99.

4.1.3. Baseline-Based Models

Table 7, Table 8 and Table 9 give fold-wise results for decision tree, SVM, and MLP classifiers, respectively. Decision tree performed almost perfectly with accuracy, precision, recall, and F1-scores ranging uniformly between 0.98 and 1.00, complemented by highly minimal RMSE. SVM yielded competitive results with AUC trending around 1.00 but slightly inferior accuracy and greater RMSE across folds.

The MLP performed better than SVM, delivering greater accuracy and balanced precision–recall with smaller RMSE values, indicating better predictive stability.

4.1.4. Model Summary and Comparative Analysis

To summarize the comparative performance, average metric values (with standard deviations) across folds are shown in

Table 10. Performance evaluation of bagging models.

Metric	RF	ET	Bag-DT
AUC	0.9992 (±0.0017)	0.9989 (±0.0014)	0.9971 (±0.0058)
F1-Score	0.9910 (±0.0145)	0.9746 (±0.0075)	0.9955 (±0.0090)
Error Rate	0.0090 (±0.0145)	0.0254 (±0.0076)	0.0045 (±0.0090)
Precision	0.9912 (±0.0143)	0.9760 (±0.0074)	0.9956 (±0.0089)
Recall	0.9910 (±0.0146)	0.9745 (±0.0074)	0.9955 (±0.0090)

and

Table 11. Performance evaluation of boosting models.

Metric	GB	XGB	LGBM
AUC	0.9973(±0.0054)	0.9979 (±0.0022)	0.9996 (±0.0008)
F1-Score	0.9895 (±0.0060)	0.9895 (±0.0112)	0.9940 (±0.0087)
Error Rate	0.0104 (±0.0060)	0.0104 (±0.0112)	0.0060 (±0.0087)
Precision	0.9898 (±0.0060)	0.9900 (±0.0108)	0.9941 (±0.0086)
Recall	0.9895 (±0.0060)	0.9895 (±0.0112)	0.9940 (±0.0087)

. Bag-DT achieved the best overall results among bagging models, while LGBM slightly outperformed XGB and GB in the boosting category.

Figure 3a–g provide a visual comparison of the performance of the seven ensemble models for all five cross-validation folds. Each subplot depicts a different evaluation metric accuracy, AUC, error rate, F1-score, recall, precision, and RMSE. Most models performed uniformly well with near-perfect values in important metrics like accuracy, AUC, and F1-score, indicating their good generalization and robustness in software requirement-risk classification.

4.2. Statistical Significance Analysis

The statistical tests compare all model performances against the bagging decision tree (DT) baseline to identify significant improvements. This analysis employs both parametric (paired t-test) and non-parametric (Wilcoxon) approaches to validate results across different distributional assumptions. The reference model was selected for its balanced performance and interpretability in ensemble methods.

4.2.1. Parametric Test (Paired t-Test)

Paired t-test analysis compared mean performance differences between models on the assumption of normally distributed metric scores.

Table 12. Paired t-test values of all models.

Metric	RF	ET	GB	XGB	LGBM	DT	SVM	MLP
Accuracy	0.2080	0.0017	0.0161	0.0993	0.3739	0.1079	0.0022	0.0023
AUC	0.3739	0.4599	0.4615	0.7722	0.3739	0.1122	0.0039	0.2080
F1-Score	0.2088	0.0016	0.0161	0.0985	0.3739	0.1075	0.0023	0.0021
Recall	0.2095	0.0015	0.0162	0.0977	0.3739	0.1065	0.0021	0.0021
Precision	0.2096	0.0026	0.0161	0.0980	0.3739	0.1086	0.0015	0.0020
RMSE	0.2074	0.0048	0.0161	0.1337	0.3739	0.0830	0.0005	0.0001
Error Rate	0.2080	0.0017	0.0161	0.0993	0.3739	0.1079	0.0022	0.0023

shows that SVM and MLP exhibited strongest significance (p < 0.01) on all classification metrics like A=accuracy, F1-score, and precision, indicating their better discriminative power. The tests also revealed gradient boosting’s moderate but consistent significance (p < 0.05) in classification and regression tasks, while tree-based models such as random forest and XGBoost were less statistically different from baseline performance. Interestingly, for RMSE—the only regression measure—SVM and MLP had outstanding significance (p < 0.001), which reflects their strong performance on continuous prediction tasks. The parametric tests were highly sensitive in picking up performance disparities in models that had normally distributed errors.

4.2.2. Non-Parametric Test (Wilcoxon Signed-Rank)

The Wilcoxon signed-rank tests offered distribution-free median performance difference assessment as a strong t-test alternative.

Table 13. Wilcoxon signed-rank values of all models.

Metric	RF	ET	GB	XGB	LGBM	DT	SVM	MLP
Accuracy	0.1797	0.0625	0.0455	0.1025	0.3173	0.1025	0.0625	0.0625
AUC	0.3173	0.7150	0.6547	1.0000	0.3173	0.1441	0.0625	0.3125
F1-Score	0.1797	0.0625	0.0656	0.1088	0.3173	0.1088	0.0625	0.0625
Recall	0.1797	0.0625	0.0588	0.1088	0.3173	0.1088	0.0625	0.0625
Precision	0.1797	0.0625	0.0455	0.1088	0.3173	0.1088	0.0625	0.0625
RMSE	0.1797	0.0625	0.0455	0.1088	0.3173	0.1025	0.0625	0.0625
Error Rate	0.1797	0.0625	0.0455	0.1025	0.3173	0.1025	0.0625	0.0625

shows more conservative results, where gradient boosting was the most consistently significant model (p < 0.05 accuracy, precision and RMSE). While SVM and MLP had borderline significance (p ≈ 0.06) by several metrics, their effects were weaker than in parametric tests, because of the reduced sensitivity of the Wilcoxon test to outlier values. The tests were most interesting for extra trees, which was highly significant in t-tests but only at the edge of significance (p = 0.0625) in Wilcoxon tests. This difference may indicate some normality deviations in some metric distributions that are worthy of further study. Non-parametric method was useful in verifying the stability of gradient boosting performance under varying evaluation settings.

4.3. Interpretability Analysis

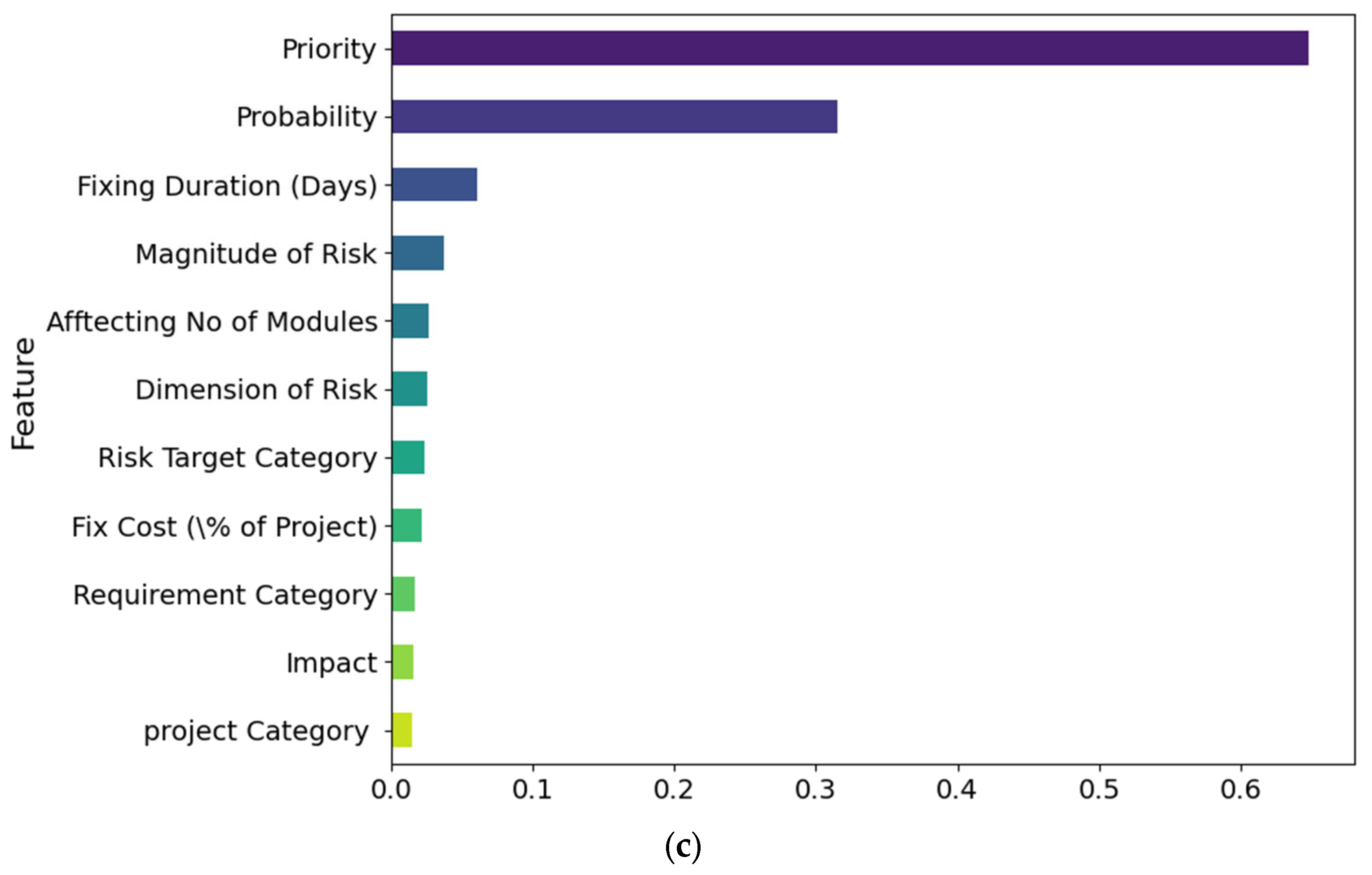
As a supplement to the performance assessment, we conducted an interpretability analysis to see the impact of individual features on the classification of software requirement risks. Feature importance scores were calculated for every model, and grouped visualizations for the bagging, boosting, and baseline groups were generated. For each group, the average importance across its models was computed, and the top 15 most influential features were identified. Figure 4a–c illustrates the interpretability analysis of every model group type (bagging, boosting, and baselines).

The findings consistently demonstrated that features like probability, dimension of risk, and priority were the most crucial predictors of requirement-risk levels for both ensemble and baseline classifiers. Bagging-based models (RF, ET, and Bag-DT) were significantly dependent on categorical features such as project category, whereas boosting models (GB, XGB, LGBM) focused more on finer-grained numerical attributes such as fixing duration. Baseline models such as DT, SVM, and MLP also highlighted similar characteristics, but with greater consistency in feature ranking.

This interpretability analysis strengthens the pragmatic significance of the suggested approach. By breaking down the important drivers of risk classification, it offers project managers and software engineers usable knowledge about which requirement attributes most significantly affect risk. So, in addition to predictive performance, the models provide explainability and transparency, which are crucial for real-world utilization in software engineering projects.

4.4. Comparison Analysis

This part provides an extensive comparison of ensemble learning models to software requirement-risk classification. As indicated in

Table 14. Performance comparison against existing approaches.

Method	Accuracy
Mamman et al., (2024) [20]	97.99%
Naseem et al., (2021) [16]	97.99%
Pemmada et al., (2023) [22]	98.80%
Proposed Methodology	99.55%

, the suggested ensemble-based models have superior performance compared to a number of state-of-the-art methods documented in the literature. Among the tested models, Bag-DT registered a maximum average accuracy of 99.55%, followed by LGBM (99.40%) and RF (99.10%). These are a remarkable improvement on earlier techniques, including Mamman et al. [20] (97.99%), Naseem et al. [16] (97.993%), and Pemmada et al. [22] (98.80%).

The enhanced performance of our ensemble models can be attributed to their ability to capture complex feature interactions and reduce overfitting through collective decision-making. In particular, the Bag-DT model demonstrated remarkable consistency, achieving perfect classification in multiple folds and an exceptionally low error rate of 0.45%. Boosting-based models, namely LGBM, XGB, and GB, also performed exceptionally well, reaffirming the efficacy of sequential error correction mechanisms in software risk prediction.

The results clearly demonstrate that ensemble learning techniques set a new benchmark in software requirement-risk prediction. Even marginal improvements in predictive accuracy have a substantial impact on reducing project delays, cost overruns, and system failures. The significantly high-performance values in all the metrics such as AUC, F1-score, precision, and recall further establish the reliability and strength of the presented ensemble models for real-world, safety-critical software engineering scenarios.

5. Conclusions

This study gives a comprehensive evaluation of ensemble learning techniques to software requirement-risk classification using the PROMISE_exp dataset. The results of the experiment show that ensemble-based techniques perform significantly better than previous techniques in terms of classification accuracy, stability, and generalizability. Of the models utilized, the bagging with decision trees (Bag-DT) classifier performed best with an accuracy and F1-score of 99.55% and an error rate of 0.45%. LGBM and RF classifiers were also highly competitive, with accuracy percentages of 99.40% and 99.10%, respectively. The models also had area under the curve (AUC) values close to 1.00, showing high discriminant power for all the risk classes.

All ensemble models demonstrated excellent capacity to identify complex patterns of data hidden within the requirement statements. The ensemble techniques, more specifically, brought some significant advantages:

i.

improved class imbalance management through techniques such as bootstrapped sampling and weighted learning.

ii.

integrated feature selection procedures that cut down on the level of manual feature engineering.

iii.

improved robustness to noise and vagueness inherent in textual requirement specifications.

Moreover, the models consistently recorded very high precision scores well above 99% and RMSE ranging from 0.00 to 0.19 for all cross-validation folds. The results point to the real-world applicability and reliability of ensemble learning methods to mission-critical software requirement-risk prediction tasks, particularly where high classification precision and data inconsistency insensitivity are most essential.

Apart from performing better than native single learners, the ensemble models also displayed better consistency between folds, validating their generalization capacity over imbalanced and domain-specific text datasets. The interpretability and simplicity of tree-based models such as RF and Bag-DT also qualify them for real-world deployment in software engineering pipelines. These results indicate the promise of ensemble learning not just as a research capability but also as an implementation tool for automated decision-making in requirement engineering. The success shown with structured risk datasets provides new avenues for scaling such models over diverse SDLC documentation in future research.

Future research will target improving the real-world deployment of the suggested framework into software development pipelines. Intended extensions are:

• Domain-specific adaptations tailored to verticals like finance, healthcare, and embedded systems.
• Integration with development platforms such as Jira (v9.4), GitHub (August 2025 release), and Azure DevOps (2023 update) for real-time risk alerts.
• Model interpretability enhancements using SHAP and LIME to explain prediction outcomes.
• Expanded risk taxonomy, incorporating hierarchical risk categories (e.g., security, usability, compliance) and severity scores.
• Lightweight deployment strategies using model distillation and quantization for edge or resource-constrained environments.
• Hybrid ensemble-transformer architectures to leverage contextual embeddings for deeper semantic understanding.
• Continuous learning pipelines for periodic model retraining and real-time validation in dynamic environments.

Special emphasis will be placed on reducing false positives and enhancing robustness under uncertainty, ensuring that the proposed models remain reliable across diverse operational scenarios. These enhancements aim to support scalable, interpretable, and actionable risk assessment across the software development lifecycle.