AUV Trajectory Planning for Optimized Sensor Data Collection in Internet of Underwater Things
Abstract
1. Introduction
1.1. Contribution
- A trajectory planning method is proposed for a single AUV operating in collaboration with a USV to support data collection in UASNs and enable IoUT. The method ensures that essential data with important information from all sensor nodes is delivered to the surface before it loses its value to enable timely intervention.
- This paper utilizes the VoI concept to quantify the time-sensitive importance of data based on its abnormality and urgency. Important data experiences rapid value decay, whereas normal data diminishes more slowly [1]. A realistic VoI formulation, as proposed in [1], is adopted to accurately capture this behaviour.
- An optimization problem is formulated to maximize the total residual VoI collected from sensor nodes by the time it is delivered to the USV. A forward DP algorithm is used to solve this problem, providing the AUV’s optimal waypoints and their best visiting order and the USV’s starting and ending positions. This collectively maximizes the total residual VoI at mission completion.
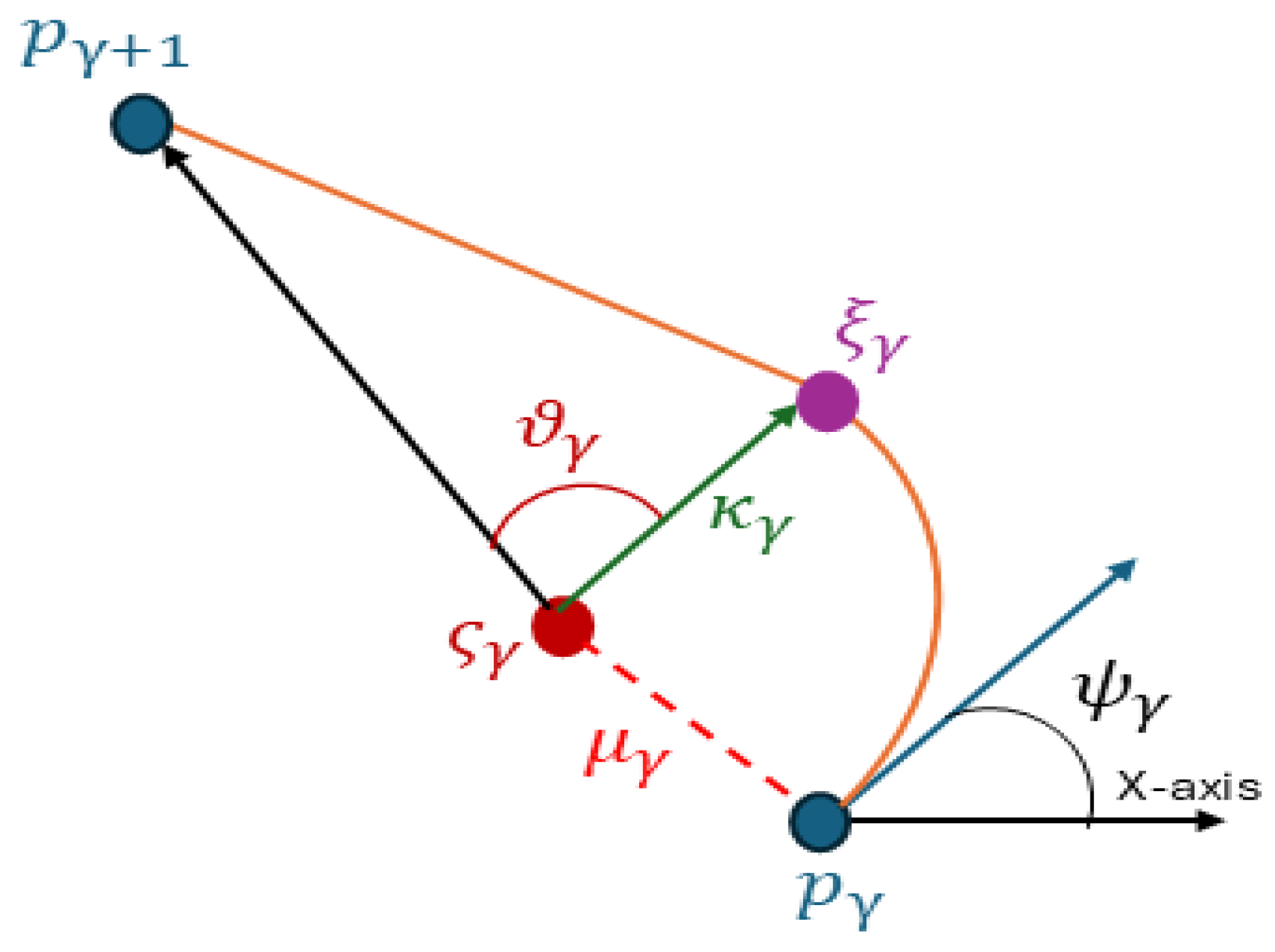
- To minimize the AUV’s energy consumption and avoid long travel distances, a path design, as in [24], is proposed to reduce unnecessary movement. The AUV first determines the optimal turning angle to align with the next waypoint. If alignment is achieved, it proceeds directly to the next position, following the shortest feasible trajectory.
- The communication range of sensor nodes is adjusted to facilitate data transmission without requiring the AUV to reach the exact node location or hover for extended periods. The AUV only needs to navigate within the communication region and remain there just long enough to complete the transmission. This ensures successful data delivery while minimizing travel time, hence maintaining residual VoI.
- The proposed method is assessed using MATLAB R2022b simulations and benchmarked against alternative approaches to validate its performance.
1.2. Related Work
1.3. Article Organization
2. Materials and Methods
2.1. System Model
2.1.1. Network Architecture
2.1.2. AUV Kinematic Model
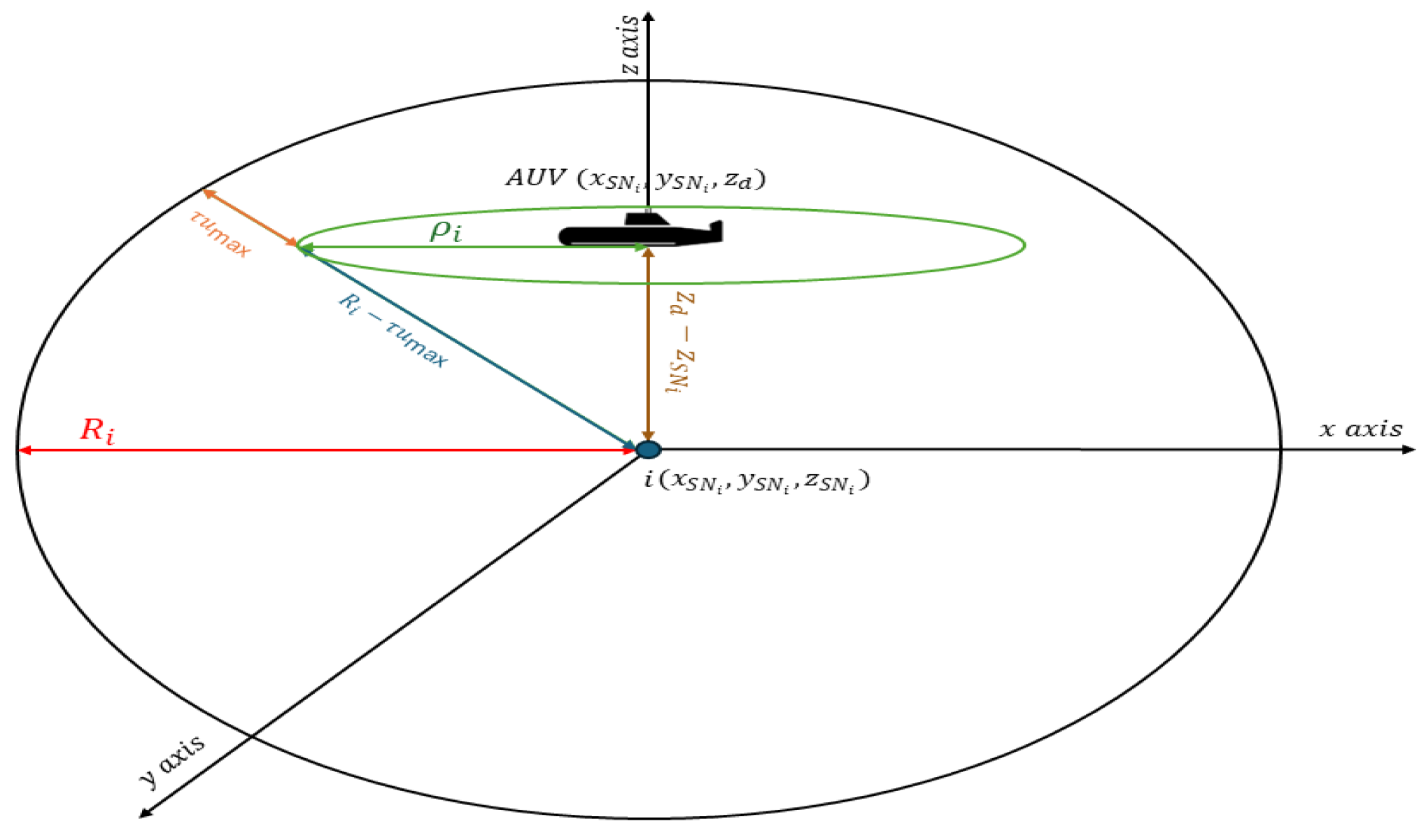
2.1.3. Communication Region Model
2.2. Problem Formulation
2.2.1. Objective Function
2.2.2. Problem Statement
2.3. Proposed Solution
2.3.1. AUV Trajectory Optimization Algorithm
| Algorithm 1. Forward DP-based Algorithm for AUV Trajectory Optimization | |
| Input: Candidate waypoint sets {}, all permutations , VoI parameters: and for each CH i, decay factor β. | |
| Output: Optimal CH visit sequence , optimal waypoint path , and maximum total residual VoI . | |
| 1 | Initialize |
| 2 | for each permutation : |
| 3 | for stage i = 1 |
| 4 | for each : |
| 5 | Compute |
| 6 | Compute residual VoI: |
| 7 | Set |
| 8 | for i = 2 to M: |
| 9 | for each : |
| 10 | for each : |
| 11 | Compute travel time: |
| 12 | Compute arrival time: |
| 13 | Compute new VoI: |
| 14 | Update |
| 15 | Store |
| 16 | Compute upper bound |
| 17 | If : prune path |
| 18 | After stage M, find |
| 19 | If a new maximum is found, update and record |
| 20 | Backtrack from final q using to build |
| 21 | Return and |
2.3.2. Path Design
3. Results and Discussion
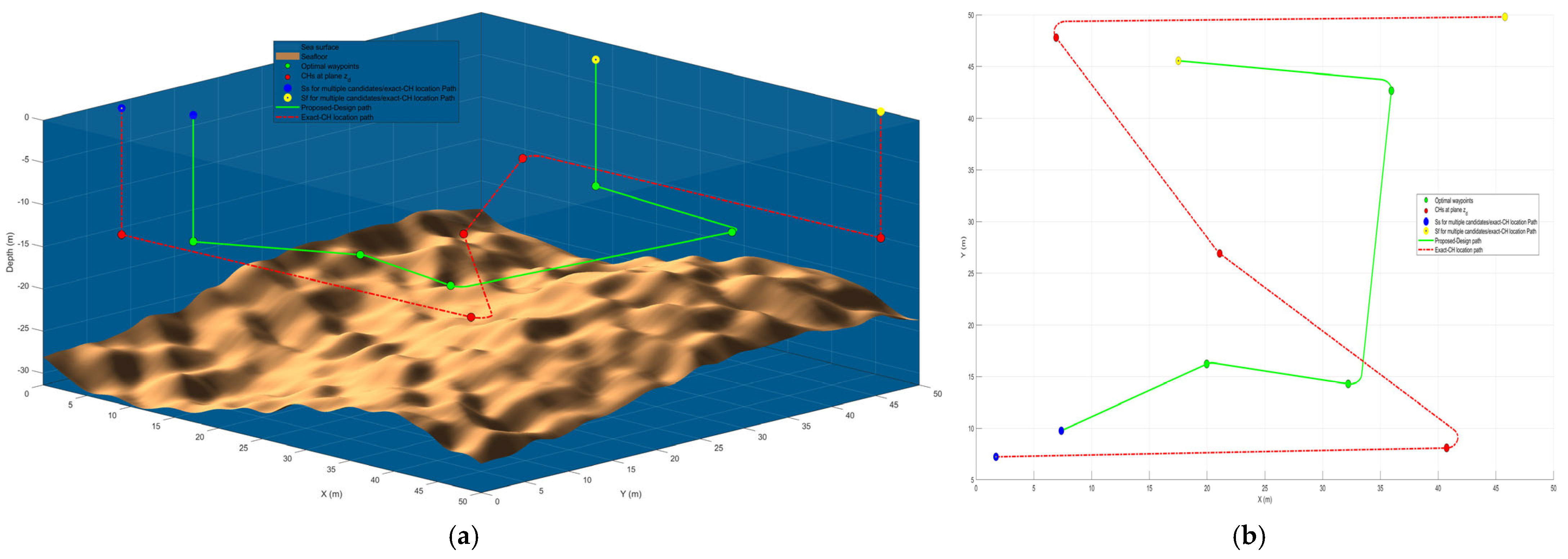
3.1. Straight-Line Trajectory Design Comparison
3.2. Single-Point Design Comparison
3.3. TSP-Based Method Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| IoUT | Internet of Underwater Things |
| UASN | The Underwater Acoustic Sensor Network |
| AUV | Autonomous Underwater Vehicle |
| USV | Unmanned Surface Vehicle |
| VoI | Value of Information |
| DP | Dynamic Programming |
| CH | Cluster Head CH |
| TSP | Traveling Salesman Problem |
References
- Liu, Z.; Meng, X.; Liu, Y.; Yang, Y.; Wang, Y. AUV-Aided Hybrid Data Collection Scheme Based on Value of Information for Internet of Underwater Things. IEEE Internet Things J. 2022, 9, 6944–6955. [Google Scholar] [CrossRef]
- Jahanbakht, M.; Xiang, W.; Hanzo, L.; Azghadi, M.R. Internet of Underwater Things and Big Marine Data Analytics—A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2021, 23, 904–956. [Google Scholar] [CrossRef]
- Petritoli, E.; Leccese, F. Autonomous Underwater Glider: A Comprehensive Review. Drones 2025, 9, 21. [Google Scholar] [CrossRef]
- Greco, M.; Leccese, F.; Giarnetti, S.; De Francesco, E. A Multiporpouse Amphibious Rover (MAR) as Platform in Archaeological Field. In Proceedings of the 2022 IMEKO TC-4 International Conference on Metrology for Archaeology and Cultural Heritage, University of Calabria, Arcavacata, Italy, 19–21 October 2022; pp. 19–21. [Google Scholar]
- Tang, Y.; Jing, L.; Shi, W.; He, C. Dynamic Data Collection of AUV Based on Deep Reinforcement Learning. In Proceedings of the 2023 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Zhengzhou, China, 14–17 November 2023. [Google Scholar]
- Duan, R.; Du, J.; Jiang, C.; Ren, Y. Value-Based Hierarchical Information Collection for AUV-Enabled Internet of Underwater Things. IEEE Internet Things J. 2020, 7, 9870–9883. [Google Scholar] [CrossRef]
- Liu, Z.; Liang, Z.; Yuan, Y.; Chan, K.Y.; Guan, X. Energy-Efficient Data Collection Scheme Based on Value of Information in Underwater Acoustic Sensor Networks. IEEE Internet Things J. 2024, 11, 18255–18265. [Google Scholar] [CrossRef]
- Yan, J.; Yang, X.; Luo, X.; Chen, C. Energy-Efficient Data Collection over AUV-Assisted Underwater Acoustic Sensor Network. IEEE Syst. J. 2018, 12, 3519–3530. [Google Scholar] [CrossRef]
- Gjanci, P.; Petrioli, C.; Basagni, S.; Phillips, C.A.; Boloni, L.; Turgut, D. Path Finding for Maximum Value of Information in Multi-Modal Underwater Wireless Sensor Networks. IEEE Trans. Mob. Comput. 2018, 17, 404–418. [Google Scholar] [CrossRef]
- Li, Y.; Bai, J.; Chen, Y.; Lu, X.; Jing, P. High Value of Information Guided Data Enhancement for Heterogeneous Underwater Wireless Sensor Networks. J. Mar. Sci. Eng. 2023, 11, 1654. [Google Scholar] [CrossRef]
- Wang, C.; Shen, X.; Wang, H.; Xie, W.; Zhang, H.; Mei, H. Multi-Agent Reinforcement Learning-Based Routing Protocol for Underwater Wireless Sensor Networks With Value of Information. IEEE Sens. J. 2024, 24, 7042–7054. [Google Scholar] [CrossRef]
- Felemban, E.; Shaikh, F.K.; Qureshi, U.M.; Sheikh, A.A.; Qaisar, S.B. Underwater Sensor Network Applications: A Comprehensive Survey. Int. J. Distrib. Sens. Netw. 2015, 11, 896832. [Google Scholar] [CrossRef]
- Khan, M.T.R.; Ahmed, S.H.; Jembre, Y.Z.; Kim, D. An Energy-Efficient Data Collection Protocol with AUV Path Planning in the Internet of Underwater Things. J. Netw. Comput. Appl. 2019, 135, 20–31. [Google Scholar] [CrossRef]
- López-Barajas, S.; Sanz, P.J.; Marín-Prades, R.; Echagüe, J.; Realpe, S. Network Congestion Control Algorithm for Image Transmission—HRI and Visual Light Communications of an Autonomous Underwater Vehicle for Intervention. Future Internet 2025, 17, 10. [Google Scholar] [CrossRef]
- Hu, T.; Zhuo, X.; Tang, L.; Li, Z.; Lu, W.; Qu, F. Multi-AUV Collaborative Data Collection and Trajectory Planning in Integrated Sensing and Communication for Underwater Acoustic Networks. In Proceedings of the IEEE Vehicular Technology Conference, Singapore, 24–27 June 2024. [Google Scholar]
- Wang, J.; Liu, S.; Shi, W.; Han, G.; Yan, S. A Multi-AUV Collaborative Ocean Data Collection Method Based on LG-DQN and Data Value. IEEE Internet Things J. 2024, 11, 9086–9106. [Google Scholar] [CrossRef]
- Savkin, A.V.; Verma, S.C.; Anstee, S. Optimal Navigation of an Unmanned Surface Vehicle and an Autonomous Underwater Vehicle Collaborating for Reliable Acoustic Communication with Collision Avoidance. Drones 2022, 6, 27. [Google Scholar] [CrossRef]
- Françolin, C.C.; Rao, A.V.; Duarte, C.; Martel, G. Optimal Control of a Surface Vehicle to Improve Underwater Vehicle Network Connectivity. J. Aerosp. Comput. Inf. Commun. 2012, 9, 1–13. [Google Scholar] [CrossRef]
- Lv, Z.; Zhang, J.; Jin, J.; Liu, L. Link Strength for Unmanned Surface Vehicle’s Underwater Acoustic Communication. In Proceedings of the 2016 IEEE/OES China Ocean Acoustics (COA), Harbin, China, 9–11 January 2016; pp. 1–4. [Google Scholar]
- Eskandari, M.; Savkin, A.V. Kinodynamic Motion Model-Based MPC Path Planning and Localization for Autonomous AUV Teams in Deep Ocean Exploration. In Proceedings of the 33rd Mediterranean Conference on Control and Automation (MED’ 2025), Tangier, Morocco, 10–13 June 2025. [Google Scholar]
- Bertsekas, D. Dynamic Programming and Optimal Control: Volume I; Athena Scientific: Nashua, NH, USA, 2012; Volume 4, ISBN 1886529434. [Google Scholar]
- Zhao, L.; Bai, Y. Data Harvesting in Uncharted Waters: Interactive Learning Empowered Path Planning for USV-Assisted Maritime Data Collection under Fully Unknown Environments. Ocean Eng. 2023, 287, 115781. [Google Scholar] [CrossRef]
- Huang, M.; Zhang, K.; Zeng, Z.; Wang, T.; Liu, Y. An AUV-Assisted Data Gathering Scheme Based on Clustering and Matrix Completion for Smart Ocean. IEEE Internet Things J. 2020, 7, 9904–9918. [Google Scholar] [CrossRef]
- Huang, H.; Savkin, A.V.; Ni, W. Online UAV Trajectory Planning for Covert Video Surveillance of Mobile Targets. IEEE Trans. Autom. Sci. Eng. 2022, 19, 735–746. [Google Scholar] [CrossRef]
- Almutairi, A.; Carpent, X.; Furnell, S. Recommendation-Based Trust Evaluation Model for the Internet of Underwater Things. Future Internet 2024, 16, 346. [Google Scholar] [CrossRef]
- Kotis, K.; Stavrinos, S.; Kalloniatis, C. Review on Semantic Modeling and Simulation of Cybersecurity and Interoperability on the Internet of Underwater Things. Future Internet 2023, 15, 11. [Google Scholar] [CrossRef]
- Fu, X.; Kang, S. Deep Reinforcement Learning-Based Collaborative Data Collection in UAV-Assisted Underwater IoT. IEEE Sens. J. 2025, 25, 1611–1626. [Google Scholar] [CrossRef]
- Lai, R.; Zhang, B.; Gong, G.; Yuan, H.; Yang, J.; Zhang, J.; Zhou, M. Energy-Efficient Scheduling in UAV-Assisted Hierarchical Wireless Sensor Networks. IEEE Internet Things J. 2024, 11, 20194–20206. [Google Scholar] [CrossRef]
- Han, S.; Zhu, K.; Zhou, M.; Liu, X. Joint Deployment Optimization and Flight Trajectory Planning for UAV Assisted IoT Data Collection: A Bilevel Optimization Approach. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21492–21504. [Google Scholar] [CrossRef]
- Cheng, M.; Guan, Q.; Ji, F.; Cheng, J.; Chen, W. Mobile Relaying-Based Reliable Data Collection in Underwater Acoustic Sensor Networks. IEEE Wirel. Commun. Lett. 2022, 11, 1795–1799. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, J.; Xie, G.; Wang, J.; Han, Z.; Ren, Y. Environment- and Energy-Aware AUV-Assisted Data Collection for the Internet of Underwater Things. IEEE Internet Things J. 2024, 11, 26406–26418. [Google Scholar] [CrossRef]
- Al-Bzoor, M.; Al-assem, E.; Alawneh, L.; Jararweh, Y. Autonomous Underwater Vehicles Support for Enhanced Performance in the Internet of Underwater Things. Trans. Emerg. Telecommun. Technol. 2021, 32, e4225. [Google Scholar] [CrossRef]
- Nandyala, C.S.; Cho, H.-S. AUV-Aided Isolated Sub-Network Prevention for Reliable Data Collection by Underwater Wireless Sensor Networks. Comput. Netw. 2025, 262, 111154. [Google Scholar] [CrossRef]
- Shi, W.; Tang, Y.; Jin, M.; Jing, L. An AUV-Assisted Data Gathering Scheme Based on Deep Reinforcement Learning for IoUT. J. Mar. Sci. Eng. 2023, 11, 2279. [Google Scholar] [CrossRef]
- Zhuo, X.; Wu, W.; Tang, L.; Qu, F.; Shen, X. Value of Information-Based Packet Scheduling Scheme for AUV-Assisted UASNs. IEEE Trans. Wirel. Commun. 2024, 23, 7172–7185. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Y.; Ren, Q.; Li, S. AUV-Aided Data Collection Considering Adaptive Ocean Currents for Underwater Wireless Sensor Networks. China Commun. 2023, 20, 356–367. [Google Scholar] [CrossRef]
- Cheng, W.; Teymorian, A.Y.; Ma, L.; Cheng, X.; Lu, X.; Lu, Z. Underwater Localization in Sparse 3D Acoustic Sensor Networks. In Proceedings of the IEEE INFOCOM 2008—The 27th Conference on Computer Communications, Phoenix, AZ, USA, 13–18 April 2008; pp. 236–240. [Google Scholar]
- Santhiya, V.; Siron, N.; Simon, J. An Energy Efficient Multi-Level Clustering and Optimized Path Planning with Data Fusion (EEMLC-OPPDF) for Autonomous Underwater Vehicles (AUVs) in Underwater Wireless Sensor Networks. Int. J. Commun. Syst. 2025, 38, e6130. [Google Scholar] [CrossRef]
- Xia, N.; Luo, L.; Wang, Y.; Zhang, K.; Yang, J.; Wu, Q.; Yuan, C. Improved AP-Clustering-Based AUV-Aided Data Collection Method for UWSNs. Electronics 2023, 12, 3116. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Lawler, E.L.; Wood, D.E. Branch-and-Bound Methods: A Survey. Oper. Res. 1966, 14, 699–719. [Google Scholar] [CrossRef]
- Guang, X.; Liu, C.; Qu, W.; Qiu, T. A Joint Optimized Data Collection Algorithm Based on Dynamic Cluster-Head Selection and Value of Information in UWSNs. Veh. Commun. 2022, 38, 100530. [Google Scholar] [CrossRef]
- Khan, W.; Hua, W.; Anwar, M.S.; Alharbi, A.; Imran, M.; Khan, J.A. An Effective Data-Collection Scheme with AUV Path Planning in Underwater Wireless Sensor Networks. Wirel. Commun. Mob. Comput. 2022, 2022, 8154573. [Google Scholar] [CrossRef]
- Zhuo, X.; Liu, M.; Wei, Y.; Yu, G.; Qu, F.; Sun, R. AUV-Aided Energy-Efficient Data Collection in Underwater Acoustic Sensor Networks. IEEE Internet Things J. 2020, 7, 10010–10022. [Google Scholar] [CrossRef]





| 1 | 0.8336 | 0.5507 | 66.1% |
| 2 | 0.9626 | 0.6175 | 64.1% |
| 3 | 0.7272 | 0.4921 | 67.7% |
| 4 | 0.6432 | 0.4437 | 69% |
| 5 | 0.9518 | 0.6121 | 64.3% |
| Total | 4.1184 | 2.7161 | 65.9% |
| Proposed Method | Straight-Line Trajectory | Single-Point Design | TSP-Based Method | |
|---|---|---|---|---|
| Total Residual VoI | 2.7161 | 2.7080 | 2.0749 | 2.4568 |
| Total time (s) | 45.0167 | 45.3374 | 74.1794 | 55.8793 |
| Preserved VoI Ratio | 65.95% | 65.75% | 50.38% | 59.65% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almuzaini, T.S.; Savkin, A.V. AUV Trajectory Planning for Optimized Sensor Data Collection in Internet of Underwater Things. Future Internet 2025, 17, 293. https://doi.org/10.3390/fi17070293
Almuzaini TS, Savkin AV. AUV Trajectory Planning for Optimized Sensor Data Collection in Internet of Underwater Things. Future Internet. 2025; 17(7):293. https://doi.org/10.3390/fi17070293
Chicago/Turabian StyleAlmuzaini, Talal S., and Andrey V. Savkin. 2025. "AUV Trajectory Planning for Optimized Sensor Data Collection in Internet of Underwater Things" Future Internet 17, no. 7: 293. https://doi.org/10.3390/fi17070293
APA StyleAlmuzaini, T. S., & Savkin, A. V. (2025). AUV Trajectory Planning for Optimized Sensor Data Collection in Internet of Underwater Things. Future Internet, 17(7), 293. https://doi.org/10.3390/fi17070293







