Topology-Aware Anchor Node Selection Optimization for Enhanced DV-Hop Localization in IoT
Abstract
1. Introduction
- (1)
- The impact of non-uniform node distribution on hop count and average hop distance was analyzed. A binary Grey Wolf Optimization (BGWO) algorithm was employed to encode anchor nodes and establish an optimal anchor node selection mechanism.
- (2)
- During the multilateration stage, a continuous GWO algorithm was applied to replace the least squares method for position optimization, enhancing the accuracy of solving the distance equations.
- (3)
- The overall performance of the proposed algorithm was thoroughly evaluated through simulation experiments.
2. Related Works
3. Theoretical Backgrounds
3.1. Original DV-Hop Algorithm
3.2. Effects of Non-Uniform Node Topology on the Localization Accuracy of the DV-Hop Algorithm
4. Grey Wolf Optimization Algorithm and Its Binary Variant
4.1. Continuous Version of the Grey Wolf Optimization Algorithm
4.2. Binary Grey Wolf Optimization Algorithm
5. Proposed Algorithm
5.1. Anchor Node Selection Mechanism Using BGWO
5.2. Localization Optimization Using GWO
5.3. The Complete Procedure of the Improved Localization Algorithm Is Outlined as Follows
6. Simulation and Results Analysis
6.1. Network Simulation Model
6.2. Performance Evaluation Criteria
- (1)
- The normalized localization error for a single unknown node
- (2)
- Computation of the network-wide normalized average localization error
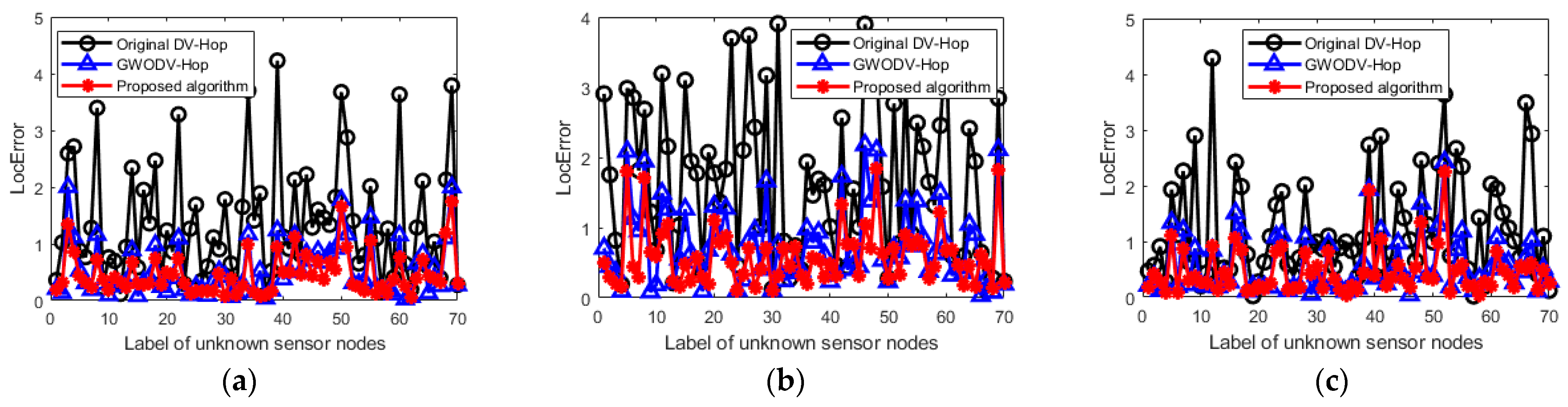
6.3. Comparison of Localization Errors in Non-Uniform Network Topologies
- (1)
- Normalized localization error of unknown nodes
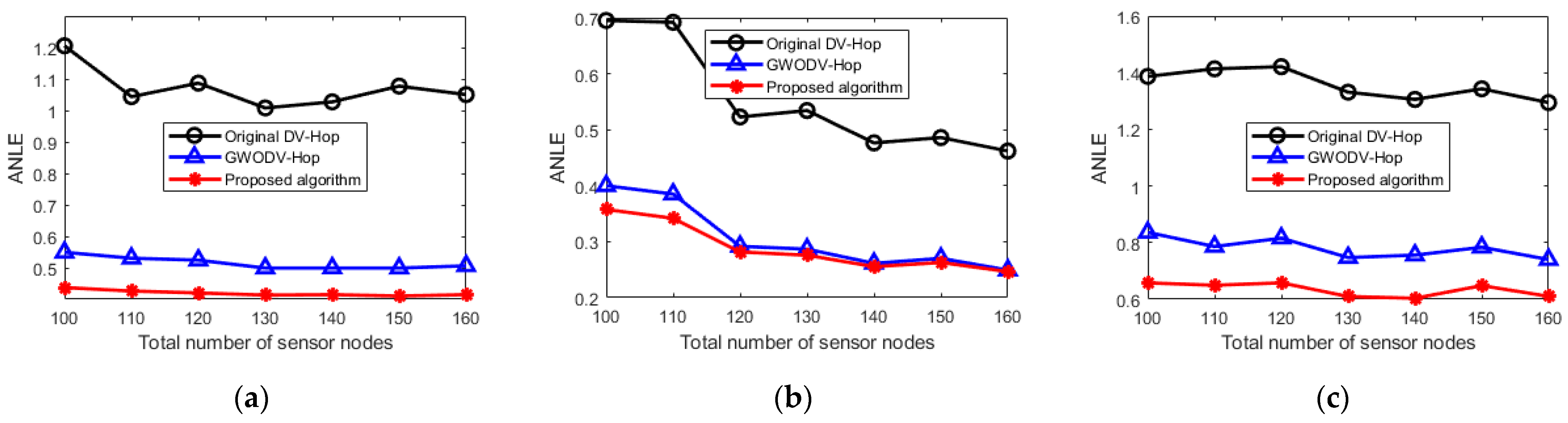
- (2)
- Impact of total number of nodes on localization performance
- (3)
- Impact of different number of anchor nodes on localization performance
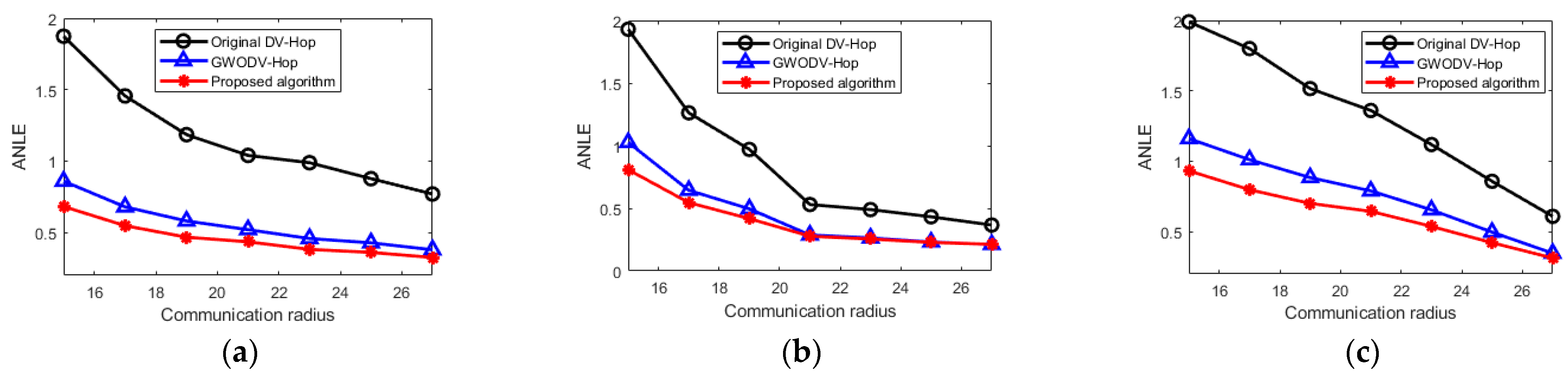
- (4)
- The impact of different communication radius on localization performance
6.4. Comparison of Localization Stability Under Non-Uniform Network Topology
6.5. Node Localization Time Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Čolaković, A.; Hadžialić, M. Internet of Things (IoT): A review of enabling technologies, challenges, and open research issues. Comput. Netw. 2018, 144, 17–39. [Google Scholar] [CrossRef]
- Perwej, Y.; Haq, K.; Parwej, F.; Mohamed Hassan, M.M. The internet of things (IoT) and its application domains. Int. J. Comput. Appl. 2019, 182, 36–49. [Google Scholar] [CrossRef]
- Ghorpade, S.; Zennaro, M.; Chaudhari, B. Survey of localization for internet of things nodes: Approaches, challenges and open issues. Future Internet 2021, 13, 210. [Google Scholar] [CrossRef]
- Singh, P.; Mittal, N.; Salgotra, R. Comparison of range-based versus range-free WSNs localization using adaptive SSA algorithm. Wirel. Netw. 2022, 28, 1625–1647. [Google Scholar] [CrossRef]
- Chen, H.; Liu, B.; Huang, P.; Liang, J.; Gu, Y. Mobility-assisted node localization based on TOA measurements without time synchronization in wireless sensor networks. Mob. Netw. Appl. 2012, 17, 90–99. [Google Scholar] [CrossRef]
- Ennasr, O.; Tan, X. Time-difference-of-arrival (TDOA)-based distributed target localization by a robotic network. IEEE Trans. Control Netw. Syst. 2020, 7, 1416–1427. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X.; Li, M.; Wang, Z.H.; Wang, C. Optimizing node localization in wireless sensor networks based on received signal strength indicator. IEEE Access 2019, 7, 73880–73889. [Google Scholar] [CrossRef]
- Xu, J.; Ma, M.; Law, C.L. Cooperative angle-of-arrival position localization. Measurement 2015, 59, 302–313. [Google Scholar] [CrossRef]
- Chen, T.; Hou, S.; Sun, L. An enhanced DV-Hop positioning scheme based on spring model and reliable beacon node set. Comput. Netw. 2022, 209, 108926. [Google Scholar] [CrossRef]
- Wang, J.; Urriza, P.; Han, Y.; Cabric, D. Weighted centroid localization algorithm: Theoretical analysis and distributed implementation. IEEE Trans. Wirel. Commun. 2011, 10, 3403–3413. [Google Scholar] [CrossRef]
- Sun, K.; Sun, L.; Chen, T. Indoor Positioning Model Based on Principal Component Extraction of Support Vector Regression. In Proceedings of the 2024 36th Chinese Control and Decision Conference (CCDC), Xi’an, China, 25–27 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 2667–2672. [Google Scholar]
- Liu, J.; Wang, Z.; Yao, M.; Qiu, Z.H. VN-APIT: Virtual nodes-based range-free APIT localization scheme for WSN. Wirel. Netw. 2016, 22, 867–878. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Cheng, L.; Wu, C.; Zhang, Y.; Wu, H.; Li, M.; Maple, C. A survey of localization in wireless sensor network. Int. J. Distrib. Sens. Netw. 2012, 8, 962523. [Google Scholar] [CrossRef]
- Kuriakose, J.; Joshi, S.; Vikram Raju, R.; Aravind, K. A review on localization in wireless sensor networks. In Advances in Signal Processing and Intelligent Recognition Systems, Proceedings of the first International Symposium on Signal Processing and Intelligent Recognition Systems (SIRS-2014), Trivandrum, India, 13–15 March 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 599–610. [Google Scholar]
- Shen, S.; Yang, K.; Qian, K.; She, Y.; Wang, W. On Improved DV-Hop Localization Algorithm for Accurate Node Localization in Wireless Sensor Networks. Chin. J. Electron. 2019, 28, 658–666. [Google Scholar] [CrossRef]
- Liu, C.H.; Zhang, L. Optimization of Localization Accuracy of Wireless Sensor Network Based on DV-Hop Algorithm. Laser Optoelectron. Prog. 2021, 58, 2228007. [Google Scholar]
- Chen, T.; Sun, L.; Wang, Z.; Wang, Y.; Zhao, Z.; Zhao, P. An enhanced nonlinear iterative localization algorithm for DV_Hop with uniform calculation criterion. Ad Hoc Netw. 2021, 111, 102327. [Google Scholar] [CrossRef]
- Song, G.; Tam, D. Two Novel DV-Hop Localization Algorithms for Randomly Deployed Wireless Sensor Networks. Int. J. Distrib. Sens. Netw. 2015, 11, 187670. [Google Scholar] [CrossRef]
- Abd EIGhafour, M.G.; Kamel, S.H.; Abouelseoud, Y. Improved DV-Hop based on Squirrel search algorithm for localization in wireless sensor networks. Wirel. Netw. 2021, 27, 2743–2759. [Google Scholar] [CrossRef]
- Chen, T.; Sun, L. A Connectivity Weighting DV_Hop Localization Algorithm Using Modified Artificial Bee Colony Optimization. J. Sens. 2019, 2019, 1464513. [Google Scholar] [CrossRef]
- Shi, Q.; Xu, Q.; Zhang, J. Improvement for DV-Hop Based on Distance Correcting and Grey Wolf Optimization Algorithm. Chin. J. Sens. Actuators 2019, 32, 1549–1555. [Google Scholar]
- Sun, B.; Wei, S.; Li, D. Localization Algorithm for Wireless Sensor Network Based on Accumulated Hop Distance and Calibration Factor. Instrum. Tech. Sens. 2019, 2, 109–113. [Google Scholar]
- Lv, J.; Long, M.; Yin, K. DV-Hop Location Algorithm Based on Weighted Least Squares Optimization. Chin. J. Sens. Actuators 2020, 33, 450–455. [Google Scholar]
- Kumar, S.; Lobiyal, D.K. Power efficient range-free localization algorithm for wireless sensor networks. Wirel. Netw. 2014, 20, 681–694. [Google Scholar] [CrossRef]
- Tang, D.; Wang, Y.; Ma, X. Sensor node localization mechanism based on improved DV-Hop algorithm. J. Jilin Univ. (Eng. Technol. Ed.) 2022, 52, 3015–3021. [Google Scholar]
- Gui, L.; Val, T.; Wei, A.; Dalce, R. Improvement of range-free localization technology by a novel DV-hop protocol in wireless sensor networks. Ad Hoc Netw. 2015, 24, 55–73. [Google Scholar] [CrossRef]
- Kaur, A.; Kumar, P.; Gupta, G.P. Improving DV-Hop-Based Localization Algorithms in Wireless Sensor Networks by Considering Only Closest Anchors. Int. J. Inf. Secur. Priv. 2020, 14, 1–15. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, B. 3D DV–hop localisation scheme based on particle swarm optimisation in wireless sensor networks. Int. J. Sens. Netw. 2014, 16, 100–105. [Google Scholar] [CrossRef]
- Xu, Z. Wireless Sensor Network Localization Incorporating Gray Wolf Optimization and DVHop Algorithm. IEEE Access 2024, 12, 168594–168606. [Google Scholar] [CrossRef]
- Sun, H.; Li, H.; Meng, Z.; Dong, W. An improvement of dv-hop localization algorithm based on improved adaptive genetic algorithm for wireless sensor networks. Wirel. Pers. Commun. 2023, 130, 2149–2173. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, X.; Song, Q. Improved DV-Hop algorithm based on artificial bee colony. Int. J. Control Autom. 2015, 8, 135–144. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X. Comprehensive review of grey wolf optimization algorithm. Comput. Sci. 2019, 46, 30–38. [Google Scholar]
- Zhang, M.; Long, D.; Wang, X.; Yang, J. Research on convergence of grey wolf optimization algorithm based on Markov chain. Acta Anat. Sin. 2020, 48, 1587–1595. [Google Scholar]
- Sun, L.; Feng, B.; Chen, T. Global convergence analysis of grey wolf optimization algorithm based on martingale theory. Control Decis. 2022, 37, 2839–2848. [Google Scholar]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing 2016, 172, 371–381. [Google Scholar] [CrossRef]
- Liu, X.; Han, F.; Ji, W.; Liu, Y.; Xie, Y. A Novel Range-Free Localization Scheme Based on Anchor Pairs Condition Decision in Wireless Sensor Networks. IEEE Trans. Commun. 2020, 68, 7882–7895. [Google Scholar] [CrossRef]
- Niculescu, D.; Nath, B. DV Based Positioning in Ad Hoc Networks. Telecommun. Syst. 2003, 22, 267–280. [Google Scholar] [CrossRef]
- Sun, B.; Wei, S. DV-Hop Localization Algorithm Based on Grey Wolf Optimization Algorithm with Adaptive Adjutment Strategy. Comput. Sci. 2019, 46, 77–82. [Google Scholar]





| Parameter | Value |
|---|---|
| Node deployment | random |
| Monitoring region | 100 m × 100 m |
| Sensor nodes | 100 |
| Anchor nodes | 30 |
| Communication range | 20 m |
| Channel Irregularity Degree (DOI) | 0.05 |
| Number of iterations in the GWO | 50 |
| Population size of the GWO | 30 |
| Algorithm | Original DV-Hop | GWODV-Hop | Proposed Scheme | ||||||
|---|---|---|---|---|---|---|---|---|---|
| C-Type | O-Type | W-type | C-Type | O-Type | W-Type | C-Type | O-Type | W-Type | |
| Average value | 1.0712 | 0.5526 | 1.3565 | 0.5154 | 0.3063 | 0.7808 | 0.4195 | 0.2888 | 0.6339 |
| Algorithm | Original DV-Hop | GWODV-Hop | Proposed Scheme | ||||||
|---|---|---|---|---|---|---|---|---|---|
| C-Type | O-Type | W-Type | C-Type | O-Type | W-Type | C-Type | O-Type | W-Type | |
| Average value | 1.1665 | 0.7373 | 1.4176 | 0.5561 | 0.3950 | 0.8214 | 0.4554 | 0.3603 | 0.6742 |
| Algorithm | Original DV-Hop | GWODV-Hop | Proposed Algorithm | ||||||
|---|---|---|---|---|---|---|---|---|---|
| C-Type | O-Type | W-Type | C-Type | O-Type | W-Type | C-Type | O-Type | W-Type | |
| Average value | 1.1699 | 0.8545 | 1.3217 | 0.5577 | 0.4512 | 0.7635 | 0.4571 | 0.3920 | 0.6210 |
| Algorithm | Running Times (s) |
|---|---|
| Original DV-Hop | 8.46 |
| GWODV-Hop | 27.38 |
| Proposed algorithm | 40.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, H.; Li, Y.; Hou, S.; Chen, T.; Sun, L.; Gu, M.; Abdullah, M.I. Topology-Aware Anchor Node Selection Optimization for Enhanced DV-Hop Localization in IoT. Future Internet 2025, 17, 253. https://doi.org/10.3390/fi17060253
Niu H, Li Y, Hou S, Chen T, Sun L, Gu M, Abdullah MI. Topology-Aware Anchor Node Selection Optimization for Enhanced DV-Hop Localization in IoT. Future Internet. 2025; 17(6):253. https://doi.org/10.3390/fi17060253
Chicago/Turabian StyleNiu, Haixu, Yonghai Li, Shuaixin Hou, Tianfei Chen, Lijun Sun, Mingyang Gu, and Muhammad Irsyad Abdullah. 2025. "Topology-Aware Anchor Node Selection Optimization for Enhanced DV-Hop Localization in IoT" Future Internet 17, no. 6: 253. https://doi.org/10.3390/fi17060253
APA StyleNiu, H., Li, Y., Hou, S., Chen, T., Sun, L., Gu, M., & Abdullah, M. I. (2025). Topology-Aware Anchor Node Selection Optimization for Enhanced DV-Hop Localization in IoT. Future Internet, 17(6), 253. https://doi.org/10.3390/fi17060253






