Abstract
Distributed inference in resource-constrained heterogeneous edge clusters is fundamentally limited by disparities in device capabilities and load imbalance issues. Existing methods predominantly focus on optimizing single-pipeline allocation schemes for partitioned sub-models. However, such approaches often lead to load imbalance and suboptimal resource utilization under concurrent batch processing scenarios. To address these challenges, we propose a non-uniform deployment inference framework (NUDIF), which achieves high-throughput distributed inference service by adapting to heterogeneous resources and balancing inter-stage processing capabilities. Formulated as a mixed-integer nonlinear programming (MINLP) problem, NUDIF is responsible for planning the number of instances for each sub-model and determining the specific devices for deploying these instances, while considering computational capacity, memory constraints, and communication latency. This optimization minimizes inter-stage processing discrepancies and maximizes resource utilization. Experimental evaluations demonstrate that NUDIF enhances system throughput by an average of 9.95% compared to traditional single-pipeline optimization methods under various scales of cluster device configurations.
1. Introduction
With the development of edge computing, the demand for deploying deep neural networks (DNNs) and large language models (LLMs) for inference at the network edge is becoming increasingly strong [1]. By directly executing machine learning models such as DNNs at the edge, edge inference can support relatively high-reliability and low-latency AI services by reducing the requirements for communication, computation, and storage resources. However, running large-scale DNN models on a single resource-constrained device poses significant challenges [2]. To address this challenge, distributed inference is one of the viable solutions. It involves partitioning a complete model into multiple sub-models, which are then deployed across several computing nodes that collaborate to complete the inference process [3].
In edge or open shared environments, the computational capabilities of heterogeneous devices vary significantly, and at the same time, the resource requirements of the partitioned sub-models differ as well [4]. Additionally, the prompt calculation and token generation stages of LLM inference exhibit even more diverse resource demands [5,6]. Current distributed inference methods primarily focus on how to partition the model and adapt it to appropriate nodes, employing methods such as dynamic programming [3,6], linear programming [2,5], and heuristic algorithms to solve the problem, with the core objective of minimizing single-inference latency. However, these methods typically employ a single-instance deployment approach, which has the following two limitations: (1) The parallel computing potential of heterogeneous devices is not fully utilized, resulting in some low-load devices being underutilized for extended periods; (2) A “weak link effect” arises due to differences in the running speeds of device-sub-model combinations at each stage, which severely restricts overall system throughput.
To address these issues, this paper proposes a non-uniform deployment method for heterogeneous clusters focused on throughput optimization. Unlike existing approaches that concentrate on single-instance deployment, this methodology adopts a system-level resource collaboration perspective, allowing multiple instances of each sub-model to be configured and appropriately distributed based on the heterogeneous characteristics of devices. Specifically, the framework establishes a mechanism to balance the processing speeds across stages by quantifying the total processing capabilities of the instance clusters for each sub-model. This mechanism converts originally idle device resources into parallel computing units, thereby enhancing overall throughput. The design enables the system to flexibly scale the number of sub-model instances in response to load changes, maximizing the global utilization rate of cluster resources.
Our framework simultaneously optimizes instance allocation and resource distribution among devices, enabling system throughput to dynamically adapt to varying scenarios while maintaining load balancing. Consequently, effectively addressing the complex constraints and multifaceted objectives inherent in non-uniform deployment strategies becomes imperative. In edge computing, these optimization problems are often NP-hard [7], presenting significant challenges. Existing methods such as dynamic programming struggle with scalability in large-scale scenarios, while linear programming cannot effectively address complex nonlinear constraints. While heuristic methods may provide feasible solutions, they often fall short of ensuring global optimality and risk becoming trapped in local optima. To tackle these challenges, this study adopts mixed-integer nonlinear programming (MINLP). MINLP allows for the simultaneous handling of discrete and continuous variables, facilitating precise modeling of complex nonlinear constraints [8], including throughput, communication latency, and task dependencies. This approach enables the construction of the optimization problem with an objective function centered on system throughput. Moreover, our model’s constraints comprehensively encompass hardware limitations, such as device computational power, memory capacity, and communication latency, while ensuring balanced processing speeds across stages to avoid pipeline bottlenecks.
In summary, the overall contributions of this paper are as follows:
- Non-Uniform Deployment Framework: We propose a non-uniform deployment-based inference framework (NUDIF) that allocates sub-model instances across heterogeneous devices to optimize inter-stage processing speed alignment. This framework enhances overall resource utilization through non-uniform deployment.
- Optimization Modeling and Solving: A mixed-integer nonlinear programming (MINLP) model is formulated to maximize system throughput through the joint optimization of sub-model deployment, load balancing, and communication efficiency, providing theoretical guidance for heterogeneous resource adaptation.
- Experimental Validation: Evaluations on real-world edge device clusters demonstrate an average throughput improvement of 9.95% compared to traditional single-pipeline optimization methods, validating the effectiveness of non-uniform deployment strategies in batch inference scenarios.
2. Related Work
In the context of distributed inference deployment, optimization methods have become a core component in enhancing performance and resource utilization. These methods can be categorized into two primary categories: joint optimization of model partitioning and deployment, and staged deployment optimization methods.
The first category emphasizes the joint optimization of model partitioning and resource allocation to enhance overall system performance. For example, CoopAI [9] uses dynamic programming to refine model partitioning while dynamically adjusting the computation–communication balance. SCADS [10] applies piecewise convex optimization for task scheduling, aiming to minimize system latency. EosDNN [11] employs intelligent algorithms to optimize cross-platform migration strategies for deep neural networks. JointDNN [2] optimizes distributed computing in mobile cloud environments using integer linear programming, focusing on minimizing energy consumption and maximizing computational efficiency.
Conversely, the second category targets deployment optimization following model partitioning to improve system adaptability. DINA [12] facilitates adaptive task offloading within multi-layer fog computing architectures using matching theory, aiming to balance load and reduce latency in heterogeneous environments. TREND-WANT [13] optimizes hierarchical deployment in 5G networks using dynamic programming techniques to balance the trade-off between computation and communication. DistInference [14] and OULD [15] focus on optimizing CNN layer allocation for unmanned aerial vehicle (UAV) clusters, minimizing end-to-end latency while considering mobility and communication constraints. In the domain of model compression, EdgenAI [16] achieves distributed parallel inference through class-aware pruning, while DeepThings [17] enhances throughput using block fusion and dynamic load balancing. EdgeShard [6] employs dynamic programming to optimize task allocation for large language model (LLM) inference, focusing on reducing inference time and enhancing scalability in edge environments.
The existing methods primarily exhibit a limitation in optimizing deployment for single-instance models, which fails to fully utilize resources and often leads to bottlenecks due to imbalances between processing stages during batch processing. In contrast, our NUDIF framework leverages non-uniform deployment and optimized constraints to achieve enhanced resource utilization and balanced capabilities across stages. By modeling the deployment strategy as a mixed-integer nonlinear programming (MINLP) problem, we are able to optimize both resource allocation and throughput, overcoming the limitations of traditional approaches and enabling scalable, flexible deployment strategies.
3. Non-Uniform Deployment Framework
This chapter presents the non-uniform deployment inference framework (NUDIF). Its three-phase workflow (profiling–optimization–execution) addresses device heterogeneity, while a mixed-integer nonlinear programming (MINLP) model optimizes instance distribution for maximal throughput.
3.1. Framework Overview
Aiming at the issues of resource idleness and speed imbalance between stages caused by single-instance deployment in heterogeneous edge clusters, particularly in the context of batch processing, this paper proposes a non-uniform deployment distributed inference framework (NUDIF). As shown in Figure 1, through a multi-instance deployment strategy and an optimization mechanism for processing rates between stages, NUDIF divides the deep neural network (DNN) or large language model (LLM) into multiple sub-models. It differentiates the configuration of the number of instances of each sub-model within the heterogeneous device cluster, forming a throughput-adaptive distributed inference pipeline. The core process of the framework is divided into three stages:
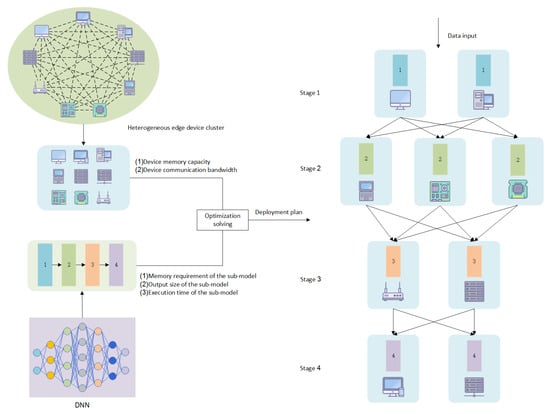
Figure 1.
Framework of NUDIF.
In the first stage, heterogeneous resource profiling is conducted to quantify the hardware characteristics of the cluster and the execution features of sub-models, thereby constructing the dataset required for optimization decisions. This involves collecting device attributes, such as memory capacity, peak computing power, and communication bandwidth. Additionally, sub-model requirements, including memory footprint, output data volume, and single-computation latency on different devices, are measured. The transmission latency across stages is estimated based on device bandwidth and output data of sub-models, allowing for the calculation of communication costs.
In the second stage, the non-uniform deployment is modeled as a mixed-integer nonlinear programming problem, with core design principles including resource adaptation, rate balance, and elastic expansion. Resource adaptation ensures that the total memory requirement of sub-model instances on each device does not exceed its capacity. Rate balance adjusts the number of instances for each sub-model to align the processing capabilities of adjacent stages. Elastic expansion allows multiple instances of the same sub-model to be deployed across various devices, enabling low-performance devices to participate in lightweight sub-tasks by stacking instances. The optimization solver outputs the optimal deployment configuration for each sub-model instance. Communication delays between devices are considered a cost factor to prevent potential bottlenecks in cross-stage transmission.
Finally, in the inference execution stage, the system executes tasks in a pipeline mode. Input data are split into batches and allocated to idle instances of the first stage. Once the instance cluster of each stage completes processing, intermediate results select the optimal transmission path based on the real-time load status of downstream instances, balancing computational and communication overheads through a batch processing mechanism.
3.2. MINLP-Based Deployment Optimization Modeling
The modeling of the optimization problem in the deployment planning stage is the core step of the entire system, which we detail as follows. Consider a heterogeneous edge cluster with N devices, each exhibiting distinct computational power, memory capacity, and communication bandwidth. A complete model is partitioned into M sub-models. Our objective is to allocate one or multiple devices to each sub-model, forming M instance clusters that sequentially execute the inference pipeline to maximize system throughput.
For the convenience of description, the main symbols used are shown in Table 1.

Table 1.
Notations and their explanations.
We use a binary variable to represent whether the sub-model i is executed on device j. It is 1 if so, and 0 otherwise. We use a binary variable to represent whether device j belongs to stage s. It is 1 if so, and 0 otherwise. We use to represent the computation time of the i-th sub-model on device j. Assume that the -th sub-model is executed on device j and the i-th sub-model is executed on device . We use to represent the communication time for transmitting the output of the -th sub-model from device j to device . The data transmission time is determined by the output size of the sub-task and the bandwidth between the two devices. Since the constraint requires that only one sub-model can be deployed on a device, the -th sub-model and the i-th sub-model are not on the same device. Then the communication time for transmitting the output of the -th sub-model from device j to device is:
We use to represent the total time for device j to perform the inference of sub-model s, which includes the computation time and the communication time, and it can be expressed by the formula as:
The throughput of each device is the reciprocal of its execution time. For each stage, the throughput of that stage is the sum of the throughputs of all the devices in that stage. The throughput of stage s can be expressed by the formula as:
Our optimization objective is to make full use of the device resources in the cluster, enabling the devices in each stage to execute collaboratively, complete the inference of the entire model, and maximize the throughput of the entire system. Since the throughput of the entire system is determined by the stage with the minimum throughput among all stages, the objective function is to maximize the throughput of the stage with the minimum throughput, that is:
The constraint conditions for the optimization objective are as follows:
- (1)
- The sub-model i can only be assigned to the devices of stage i:
- (2)
- The total memory requirement of all sub-models on device j cannot exceed its memory capacity:
- (3)
- A device can have at most one model:
- (4)
- Regarding whether there is a sub-model on a device, if there is, a device can be in at most one stage. A binary auxiliary variable is introduced to represent whether device j is assigned a sub-model:If device j is assigned a sub-model; then , otherwise, :
- (5)
- For each stage, the number of devices in that stage is greater than or equal to 1:
- (6)
- In each stage s there is at least one device processing sub-model s:
- (7)
- For each stage s, sub-models from other stages cannot be executed in the current stage s:
- (8)
- is not greater than the throughput of any stage:
3.3. Optimization Problem Solving
In this section, we present a detailed description of the optimization problem solving process using mixed-integer nonlinear programming (MINLP). We use Gurobi [18] as the solver to maximize the system’s minimum throughput while satisfying the computational and communication constraints of the devices.
First, we define the system parameters, including: M, N, , , , , and . Next, we establish the optimization model and define the decision variables. These variables include binary variables , , and . In addition, we define execution time and communication time variables, including and . Here, represents the execution time of stage s. Furthermore, we introduce throughput-related variables, such as , , and . represents the throughput of device j in stage s. Subsequently, we define the constraints consistent with the mathematical modeling.
Before solving the optimization problem, we calculate the execution time and throughput for each device in each stage and compute the throughput for each stage. The execution time of a device in a stage includes computation time and communication time. The computation time is determined by the time required for the device to process its assigned sub-model, while the communication time is the time for transmitting the output of the sub-model from the device to the device in the next stage that will process the next sub-model. The communication time is calculated as the output size of the sub-model on the device divided by the communication bandwidth between the two devices. The total execution time is the sum of the computation time and the communication time. The throughput of a device in a stage is defined as the inverse of the execution time of the device in that stage, and the throughput of each stage is the sum of the throughputs of all devices in that stage. Subsequently, we set the optimization objective to maximize the minimum throughput across all stages to ensure that the system achieves the highest possible throughput even at the slowest stage. Once the optimization problem is formulated, we solve it using the solver.
4. Experimental Results
This section aims to verify the effectiveness of the proposed non-uniform deployment framework (NUDIF) in heterogeneous edge clusters through systematic experiments. The experiment focuses on evaluating the throughput performance of NUDIF under different device scales and conducts a comparative analysis with traditional single-pipeline optimization methods.
4.1. Experimental Setting
To comprehensively evaluate the effectiveness of the proposed non-uniform deployment inference framework (NUDIF) in heterogeneous edge clusters, we designed a series of experiments focusing on throughput performance under different device scales. The experimental environment simulates a heterogeneous edge computing environment, where the devices used have varying performance capabilities. For edge devices, smartphones typically have 6 to 12 GB of memory, while Jetson Orin NX devices have 8 to 16 GB of memory. Therefore, in our experiments, we set the device memory capacity range between 8 GB and 10 GB to reflect the typical memory constraints in edge environments. The bandwidth between edge devices typically ranges from tens of Kbps to 1000 Mbps. In our experiments, we set the bandwidth range between 100 Mbps and 1000 Mbps. The selection of these simulated devices is representative and can reflect the heterogeneity, resource constraints, and scalability of real-world edge computing scenarios. To study the performance of NUDIF in clusters of different scales, we varied the number of devices from 4 to 24, covering both small-scale edge deployments and large-scale industrial edge environments. We consider the scenario where there are a large number of devices in the cluster, the device resources are limited, and each device can deploy only one sub-model at most. In our experiments, we assume that a complete model is divided into four sub-models, each with different output sizes and memory requirements. Specifically, Sub-model 0 has an output size of 8 MB and a memory requirement of 5 GB; Sub-model 1 has an output size of 6 MB and a memory requirement of 6 GB; Sub-model 2 has an output size of 9 MB and a memory requirement of 7 GB; and Sub-model 3 has an output size of 7 MB and a memory requirement of 6 GB. The execution time for each sub-model on different devices is set between 1 and 3 s, reflecting differences in computational complexity and device capabilities. The communication delay between devices is calculated based on the output size of the sub-model and the bandwidth of the communication link between devices. When the number of devices is 8, the data used is shown in Table 2.

Table 2.
Data used in the experiments when the number of devices is eight.
We compare our method with the one in EdgeShard [6]. The method in EdgeShard partitions a complete model into multiple sub-models, which are then deployed onto devices. During deployment, dynamic programming is utilized to select the optimal combination of devices to minimize overall processing latency. These devices collaborate to complete the inference of a set of complete models. To fully demonstrate the effectiveness of the method proposed in this paper, we also repeatedly apply the EdgeShard method to deploy multiple sets of instances. The specific approach is as follows: after selecting a set of devices from the cluster to complete the inference instance of a complete model, we continue to select another set of devices from the remaining edge devices to form another inference instance, until the remaining devices can no longer constitute a complete inference instance. For clarity, we refer to the original EdgeShard as EdgeShard-single, while the method that repeatedly applies EdgeShard to deploy multiple sets of instances is called EdgeShard-multi. This variation significantly improves the utilization of devices and increases the throughput of the system.
4.2. Experimental Results Analysis
Our evaluation metric is the system throughput. Since this paper considers a batch execution scenario, the system throughput in our method is determined by the throughput of the sub-model instance cluster with the longest execution time. For the EdgeShard-single method, the throughput is dictated by the device exhibiting the longest execution time. In contrast, the throughput of the EdgeShard-multi method is the sum of the throughputs of multiple inference instance clusters.
In Figure 2, we illustrate the throughput of our non-uniform deployment framework (NUDIF), as well as EdgeShard-single and EdgeShard-multi, with the number of sub-models fixed at 4 while the number of devices increases from 4 to 24. It can be observed that with the increase in the number of available devices, both NUDIF and EdgeShard-multi consistently exhibit growth, whereas EdgeShard-single shows a slower increase.
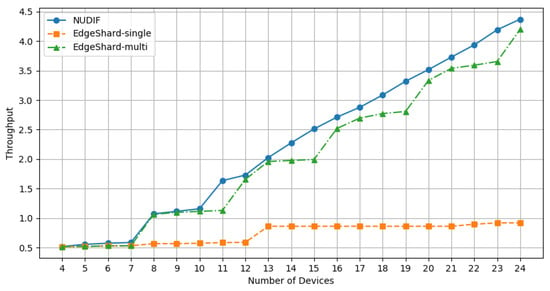
Figure 2.
Throughput comparison among three methods.
As illustrated in Figure 2, when the number of sub-models equals the number of devices, the throughputs of all three methods are identical, at 0.5192. This occurs because the number of devices matches the number of sub-models, resulting in the same sub-model deployment result for all three methods, as detailed in Table 3.

Table 3.
Deployment plan and throughput of EdgeShard-single, EdgeShard-multi, and NUDIF under N = 4.
For the EdgeShard-single method, the introduction of new devices prompts a change in the optimal deployment plan. The new plan selects devices with superior capabilities, thereby reducing the execution time of the device with the longest execution time compared to the original plan, which ultimately increases throughput. Conversely, if the newly introduced devices do not possess greater capabilities than the existing ones, they will not lead to a change in the deployment plan, resulting in unchanged throughput. For example, during the aforementioned experimental process, the addition of the 9th device, as well as devices 13 through 21 and the 24th device, did not improve the throughput of the original system.
In the case of the EdgeShard-multi method, when the number of devices is five, six, or seven, only one instance cluster can be formed, and since the new devices do not offer better resources than the original ones, its throughput matches that of EdgeShard-single. However, when the number of devices reaches eight, two complete models can be executed, leading to a throughput that equals the sum of the throughputs of the two cluster instances, totaling 1.0643. Even as the number of devices increases further, the total number of instance clusters remains two. However, with the addition of more powerful devices, the allocation scheme for each group adjusts, resulting in an increase in throughput. The continuing trend aligns with previous observations.
In Table 4, we present the deployment plan for each sub-model along with the corresponding throughput during the experiment when N = 12, 13, and 14. It is evident that whether the introduction of new devices leads to an increase in the number of instance clusters or modifies the existing deployment plan, overall throughput is increased.

Table 4.
Deployment plan and throughput of EdgeShard-multi under N = 12, 13, 14.
In our NUDIF method, as the number of devices increases, throughput consistently rises. Table 5 displays the deployment plan for each sub-model along with the corresponding throughput of our method when N = 12, 13, and 14. It is apparent that non-uniform deployment offers distinct advantages over the deployment of multiple sets of instances. This arises because our non-uniform deployment strategy allows for optimal utilization of each newly added device, resulting in a superior deployment plan of sub-models, which in turn continuously elevates the throughput of the stage with the longest execution time.

Table 5.
Deployment plan and throughput of NUDIF under N = 12, 13, 14.
To quantify the throughput improvement of NUDIF, we present its performance gains over EdgeShard-multi across all tested device counts, as illustrated in Figure 3. In all experiments, NUDIF consistently outperforms EdgeShard-multi, with throughput improvements ranging from 0.91% to 44.67%, averaging 9.95% with a standard deviation of 10.11%. Although the magnitude of improvement fluctuates with the number of devices, all experimental results indicate that NUDIF’s throughput remains consistently higher than that of EdgeShard-multi. The 95% confidence interval is [5.34%, 14.55%], and the p-value is 0.00021, indicating that this improvement is statistically significant.
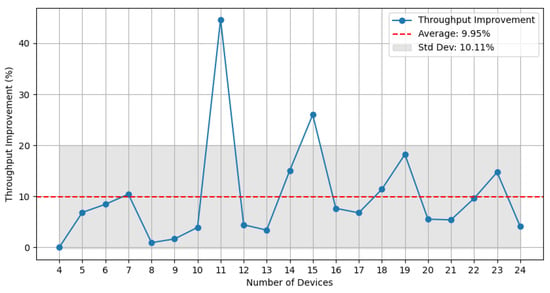
Figure 3.
Throughput improvement of NUDIF over EdgeShard-multi for each device count.
NUDIF’s higher throughput compared to EdgeShard-multi can be attributed to its superior resource utilization. To better explain the throughput improvement, we further analyzed the average resource utilization of devices in clusters with varying numbers of devices. The resource utilization of a device is defined as the ratio of the memory required by the deployed sub-model to the device’s total memory capacity. If no sub-model is deployed, the resource utilization is zero. The average resource utilization of the cluster is given by:
where N is the total number of devices, is the memory required by the sub-model deployed on device i, and is the total memory capacity of device i.
The results depicted in Figure 4 indicate that as the number of devices increases, the average resource utilization of the EdgeShard-single cluster gradually decreases. This is because EdgeShard-single can only form one set of inference instances. As the number of devices increases, the number of idle devices correspondingly increases, leading to a decrease in the average resource utilization of the cluster.
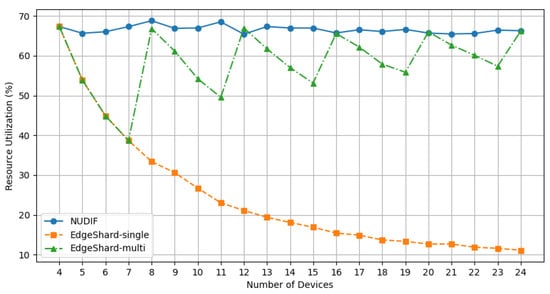
Figure 4.
Resource utilization comparison among three methods.
For EdgeShard-multi, when the number of devices is 8, 12, 16, 20, and 24, the average resource utilization of the cluster is enhanced. This is due to EdgeShard-multi’s ability to utilize all devices in the cluster to form multiple sets of inference instances, thereby making full use of the cluster resources. However, when the number of devices falls within ranges such as 4–7, 8–11, 12–15, 16–19, and 20–23, the increase in the number of devices does not result in the formation of new inference instance sets, leading to an increase in the number of idle devices and consequently causing a decline in the average resource utilization of the cluster.
In contrast, as the number of devices in the cluster increases, NUDIF maintains a high average resource utilization rate without significant fluctuations. This is attributed to its non-uniform deployment strategy, which allows multiple instances of each sub-model to be deployed across multiple devices. By dynamically allocating sub-model instances based on the computational power and memory capacity of each device, NUDIF ensures efficient operation within device capabilities and avoids idleness. Consequently, compared to EdgeShard-single, NUDIF’s average resource utilization rate is 42.27% higher, and compared to EdgeShard-multi, it is 8.07% higher.
Additionally, we performed a comparative analysis of inference latency, as shown in Figure 5. EdgeShard-single exhibits shorter inference latency, as it only needs to complete a single set of inference instances. The inference latencies of EdgeShard-multi and NUDIF are nearly identical. Calculations show that NUDIF increases the average inference latency by 2.03 s compared to EdgeShard-single, and by 0.086 s compared to EdgeShard-multi, with both differences falling within an acceptable range. Although NUDIF introduces a slight increase in inference latency, it significantly enhances throughput and device resource utilization, making it a more advantageous choice.
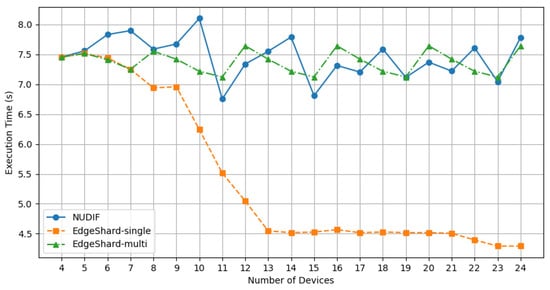
Figure 5.
Inference latency comparison among three methods.
4.3. Discussion
This study illustrates the throughput improvements achieved by the NUDIF framework across clusters of varying sizes. However, it is important to note that the NUDIF framework is specifically designed for batch inference optimization, focusing on balancing the processing time at each stage while maximizing the throughput for each phase. While this approach enhances overall throughput, it does not achieve optimal latency for individual inference tasks. Additionally, the mixed-integer nonlinear programming (MINLP) problem, by its nature, is NP-hard, and the solving time increases exponentially with the scale of the problem. Therefore, in large-scale clusters with a significant number of devices, it is essential to adopt multi-level optimization strategies, such as decomposition methods (including Benders decomposition and Lagrangian relaxation), heuristic and metaheuristic algorithms (such as genetic algorithms and simulated annealing), and machine-learning-based techniques. These approaches can effectively reduce computational complexity and enhance efficiency while minimizing the loss of optimality, thereby providing more viable solutions for optimizing distributed inference tasks in expansive edge computing environments.
5. Conclusions
This paper addresses the deployment optimization of distributed inference in heterogeneous edge clusters by proposing a non-uniform deployment framework (NUDIF). This framework treats differences in device capabilities as core constraints, ensuring a balanced processing speed across various sub-models while maximizing overall throughput through modeling and constraint conditions. Experiments demonstrate that NUDIF effectively alleviates throughput bottlenecks caused by speed mismatches, maintaining optimal throughput across different scales of device deployment. Its primary advantage lies in employing a nonlinear programming model to align resources and loads, with the objective of optimizing for minimal stage throughput to ensure balanced processing capabilities. Furthermore, by leveraging redundant device resources, the framework enhances cluster utilization and addresses the issue of resource idleness. This study provides an efficient solution for optimizing the deployment of distributed inference in edge environments, with significant implications for improving inference efficiency and supporting real-time AI services in resource-constrained scenarios.
Author Contributions
Conceptualization, P.L. and C.Q.; methodology, P.L. and C.Q.; software, P.L. and H.L.; validation, P.L., C.Q. and H.L.; formal analysis, P.L.; investigation, P.L.; resources, P.L.; data curation, P.L. and H.L.; writing—original draft preparation, P.L.; writing—review and editing, C.Q.; visualization, P.L.; supervision, P.L.; project administration, P.L.; funding acquisition, P.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhou, Z.; Chen, X.; Li, E.; Zeng, L.; Luo, K.; Zhang, J. Edge intelligence: Paving the last mile of artificial intelligence with edge computing. Proc. IEEE 2019, 107, 1738–1762. [Google Scholar] [CrossRef]
- Eshratifar, A.E.; Abrishami, M.S.; Pedram, M. JointDNN: An efficient training and inference engine for intelligent mobile cloud computing services. IEEE Trans. Mob. Comput. 2019, 20, 565–576. [Google Scholar] [CrossRef]
- Hu, Y.; Imes, C.; Zhao, X.; Kundu, S.; Beerel, P.A.; Crago, S.P.; Walters, J.P. Pipeedge: Pipeline parallelism for large-scale model inference on heterogeneous edge devices. In Proceedings of the 2022 25th IEEE Euromicro Conference on Digital System Design (DSD), Maspalomas, Spain, 31 August–2 September 2022; pp. 298–307. [Google Scholar]
- Duan, S.; Wang, D.; Ren, J.; Lyu, F.; Zhang, Y.; Wu, H.; Shen, X. Distributed artificial intelligence empowered by end-edge-cloud computing: A survey. IEEE Commun. Surv. Tutor. 2022, 25, 591–624. [Google Scholar] [CrossRef]
- Zhao, J.; Wan, B.; Peng, Y.; Lin, H.; Wu, C. Llm-pq: Serving llm on heterogeneous clusters with phase-aware partition and adaptive quantization. arXiv 2024, arXiv:2403.01136. [Google Scholar]
- Zhang, M.; Shen, X.; Cao, J.; Cui, Z.; Jiang, S. Edgeshard: Efficient llm inference via collaborative edge computing. IEEE Internet Things J. 2024. [Google Scholar] [CrossRef]
- Feng, C.; Han, P.; Zhang, X.; Yang, B.; Liu, Y.; Guo, L. Computation offloading in mobile edge computing networks: A survey. J. Netw. Comput. Appl. 2022, 202, 103366. [Google Scholar] [CrossRef]
- Boukouvala, F.; Misener, R.; Floudas, C.A. Global optimization advances in mixed-integer nonlinear programming, MINLP, and constrained derivative-free optimization, CDFO. Eur. J. Oper. Res. 2016, 252, 701–727. [Google Scholar]
- Yang, C.Y.; Kuo, J.J.; Sheu, J.P.; Zheng, K.J. Cooperative distributed deep neural network deployment with edge computing. In Proceedings of the ICC 2021-IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Liu, H.; Zheng, H.; Jiao, M.; Chi, G. SCADS: Simultaneous computing and distribution strategy for task offloading in mobile-edge computing system. In Proceedings of the 2018 IEEE 18th International Conference on Communication Technology (ICCT), Chongqing, China, 8–11 October 2018; pp. 1286–1290. [Google Scholar]
- Xue, M.; Wu, H.; Li, R.; Xu, M.; Jiao, P. EosDNN: An efficient offloading scheme for DNN inference acceleration in local-edge-cloud collaborative environments. IEEE Trans. Green Commun. Netw. 2021, 6, 248–264. [Google Scholar] [CrossRef]
- Mohammed, T.; Joe-Wong, C.; Babbar, R.; Di Francesco, M. Distributed inference acceleration with adaptive DNN partitioning and offloading. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications, Toronto, ON, Canada, 6–9 July 2020; pp. 854–863. [Google Scholar]
- Lin, C.Y.; Wang, T.C.; Chen, K.C.; Lee, B.Y.; Kuo, J.J. Distributed deep neural network deployment for smart devices from the edge to the cloud. In Proceedings of the ACM MobiHoc Workshop on Pervasive Systems in the IoT Era, Catania, Italy, 2 July 2019; pp. 43–48. [Google Scholar]
- Dhuheir, M.; Baccour, E.; Erbad, A.; Sabeeh, S.; Hamdi, M. Efficient real-time image recognition using collaborative swarm of uavs and convolutional networks. In Proceedings of the 2021 IEEE International Wireless Communications and Mobile Computing (IWCMC), Harbin, China, 28 June– 2 July 2021; pp. 1954–1959. [Google Scholar]
- Jouhari, M.; Al-Ali, A.K.; Baccour, E.; Mohamed, A.; Erbad, A.; Guizani, M.; Hamdi, M. Distributed CNN inference on resource-constrained UAVs for surveillance systems: Design and optimization. IEEE Internet Things J. 2021, 9, 1227–1242. [Google Scholar] [CrossRef]
- Hemmat, M.; Davoodi, A.; Hu, Y.H. EdgenAI: Distributed Inference with Local Edge Devices and Minimal Latency. In Proceedings of the 2022 27th IEEE Asia and South Pacific Design Automation Conference (ASP-DAC), Taipei, Taiwan, 17–20 January 2022; pp. 544–549. [Google Scholar]
- Zhao, Z.; Barijough, K.M.; Gerstlauer, A. Deepthings: Distributed adaptive deep learning inference on resource-constrained iot edge clusters. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2018, 37, 2348–2359. [Google Scholar] [CrossRef]
- Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual. 2024. Available online: https://www.gurobi.com (accessed on 6 April 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).