Eavesdropper Detection in Six-State Protocol Against Partial Intercept–Resend Attack

Abstract

This work presents and evaluates two threshold-based detection methods for the Six-State quantum key distribution protocol, considering a realistic scenario involving partial intercept–resend attack and channel noise. The statistical properties of the shared quantum bit error rate (QBER) are analyzed and used to estimate the attacker interception density from observed data. Building on this foundation, the work derives two optimal QBER detection thresholds designed to minimize both false positive and false negative rates, following, respectively, upper theoretical bounds and limit probability density function approach. A developed Qiskit simulation environment enables the evaluation and comparison of the two detection methods on simulated and real-inspired quantum systems with differing noise characteristics. This framework moves beyond theoretical analysis, allowing practical investigation of system noise effects on detection accuracy. Simulation results confirm that both methods are robust and effective, achieving high detection accuracy across all the tested configurations, thereby validating their applicability to real-world quantum communication systems.

1. Introduction

Quantum key distribution (QKD) has emerged as the only proven method to achieve information-theoretically secure key exchange between two legitimate parties, conventionally referred to as Alice and Bob [1,2]. Unlike classical cryptographic schemes, whose security relies on computational assumptions such as the hardness of integer factorization or discrete logarithms [3,4], QKD derives its security directly from the fundamental principles of quantum mechanics. The impossibility of perfectly cloning an unknown quantum state, guaranteed by the no-cloning theorem [5], together with the Heisenberg uncertainty principle [6], ensures that any attempt by an eavesdropper (Eve) to intercept the quantum channel inevitably introduces detectable disturbances. In principle, this enables QKD to provide unconditional security for key exchange, provided the system is implemented without imperfections [7].

In this context, an alternative promising paradigm is quantum secure direct communication (QSDC) [8,9,10], which enables the direct transmission of secret messages with information-theoretic security, thereby eliminating the need for prior key establishment and potentially enhancing efficiency in scenarios that require immediate secure data exchange. However, many practical QSDC implementations demand substantially different physical resources or operational models—such as hyperentangled states with complete Bell-state discrimination, two-way quantum operations, or variants employing forward error correction—and they exhibit distinct error and loss characteristics that complicate direct comparison with prepare-and-measure QKD schemes [10]. Moreover, QKD protocols currently benefit from greater experimental maturity, scalability, and integration with existing communication infrastructures, thereby motivating our focus on improving the practical security of QKD through realistic eavesdropper detection methods.

The strategic relevance of QKD extends well beyond academic interest. Its potential applications in the military and defense domains are particularly critical, as it promises to secure tactical and strategic communications, protect diplomatic and intelligence channels, and enable resilient satellite-based secure networks [11,12]. Beyond defense, QKD has potential applications in protecting critical infrastructure such as energy grids, transportation systems, and global financial networks [13,14,15]. This is of growing importance as advances in quantum computing threaten the long-term security of classical cryptographic systems. For military and governmental use, it is, therefore, imperative to develop quantum-resistant solutions that can ensure the confidentiality of classified information over extended time horizons. Nevertheless, despite rapid progress in recent years, significant obstacles remain to the widespread deployment of QKD, including hardware limitations, channel imperfections, and the need for scalable and cost-effective implementations [16].

Among the many QKD protocols, the Six-State protocol [17,18] represents a natural extension of the well-known BB84 scheme, offering increased robustness against noise by employing three mutually unbiased bases. Its design allows for enhanced detection of eavesdropping attempts, particularly in channels affected by collective-rotation noise [19]. This makes the Six-State protocol an attractive candidate for environments where transmission imperfections are unavoidable, though the presence of realistic noise sources and imperfections still poses challenges to its implementation.

In this work, we address one of the key challenges in deploying QKD: the reliable detection of an eavesdropper under realistic attack models [20]. Specifically, we investigate the Six-State protocol under a partial intercept-and-resend attack, in which Eve targets only a fraction of the transmitted qubits in order to reduce her chances of detection. Additionally, we incorporate system noise into our network model, as it can further complicate the assessment of both the protocol security and the overall system performance [21]. In practice, distinguishing with absolute certainty between quantum errors induced by an eavesdropping attack and those resulting from imperfections in the quantum channel remains a significant challenge. Consequently, as emphasized in [22], most studies on QKD protocols have concentrated on evaluating performance in terms of the achievable secret key rate rather than on detecting the presence of an eavesdropper. This work addresses this fundamental issue by explicitly proposing and evaluating two threshold-based detection methods specifically designed to identify eavesdropping attempts while accounting for both channel noise and the statistical properties of the quantum bit error rate (QBER). Through extensive simulation on backends inspired by real IBM quantum devices, we demonstrate the effectiveness and accuracy of the proposed methods, thereby contributing to the advancement in practical, secure implementations of Six-State QKD.

Paper Contribution

The primary contributions are as follows:

• The paper proposes a generalization to the Six-State protocol of threshold-based eavesdropper detection techniques proposed for the BB84 scheme in [23,24]. We explicitly derive two optimal QBER detection thresholds designed to minimize both the false positive rate (FPR) and false negative rate (FNR), following, respectively, upper Hoeffding’s theoretical bounds [25] and limit probability density function approach, thereby broadening the applicability of threshold-based detection strategies.
• The analysis explicitly incorporates the scenario of partial intercept–resend attack (characterized by a constant interception density), also accounting for channel noise. This scenario enables a nuanced evaluation of detection performance under variable attack intensities.
• A comprehensive simulation model, developed on the Quantum Solver framework and implemented using the Qiskit library, is presented. This model facilitates both the testing of detection methods on real quantum systems and the isolation of different noise sources through controlled simulations. The simulation framework is used to systematically compare both methods in terms of detection accuracy and robustness. By doing so, we move beyond purely theoretical analysis and this allows the investigation of practical system noise effects on detection performance.

2. Related Work

The standard security proof for Six-State QKD has been available since 2005 [26], and more recently a simpler proof has been proposed in [27]. The latter work entirely avoids the use of Rényi entropies, applying state smoothing directly in the Bell basis. Another class of studies investigates eavesdropping in the Six-State protocol when signal states are mixed with white noise [28,29]. In these works, the white noise is assumed to originate either from deliberate addition by Alice before the states leave her laboratory or from a realistic scenario in which Eve cannot replace the noisy quantum channel with a noiseless one. The authors analyze Eve’s optimal mutual information with Alice, for individual attacks, as a function of the qubit error rate. Their main finding is that added quantum noise reduces Eve’s mutual information more significantly than Bob’s. In contrast, our work focuses on the definition of a detection method for identifying Eve’s presence in intercept–resend attacks.

Garapo et al. [19] study the effect of collective-rotation noise on the security of the Six-State protocol under intercept–resend attacks. They first introduce a collective-rotation noise model for the Six-State protocol and provide a parametrization of the mutual information between Alice and Eve. The authors also derive the QBER for three intercept–resend scenarios, concluding that the Six-State protocol is robust against such attacks when the rotation angle remains within certain bounds. However, their work does not investigate detection methods for Eve’s presence.

Other studies have explored eavesdropping in combination with depolarizing errors in quantum channels [30]. In particular, the authors propose the use of a k-means clustering algorithm to analyze potential attacks in the BB84 protocol under depolarizing noise. Their results show that the shared keys remain secure even in the presence of both noise and eavesdropping, and they demonstrate that clustering is an efficient approach for detecting eavesdroppers, particularly when channel noise is relatively high. Different from this approach, our work extends the detection techniques presented in [23,24] and develops a theoretical framework based on statistical analysis to define threshold-based detection methods for the Six-State protocol. These methods optimize FNR and FPR, while also allowing the user to adjust the balance between them depending on the application scenario.

Ding et al. [31] propose a machine-learning-based attack detection scheme (MADS) for continuous-variable QKD (CVQKD). Their method combines density-based spatial clustering of applications with noise (DBSCAN [32]) and multiclass support vector machines (MCSVMs [33]). MADS demonstrates high effectiveness in detecting quantum hacking attacks. However, it is specifically designed for CVQKD and requires the prior definition of attack-related features, which are used to construct feature vectors. These vectors serve as inputs for DBSCAN to identify and filter noise or outliers, after which trained MCSVMs are employed for classification and prediction. The output immediately determines whether a final secret key can be generated. Beyond its application to discrete-variable QKD, our approach distinguishes itself from these works by eliminating the need for a model training phase, relying instead on statistical analysis.

3. Background on Six-State Protocol

The Bechmann-Pasquinucci and Gisin protocol extends the BB84 scheme by using three mutually unbiased bases (MUBs) in a d-dimensional Hilbert space [17]. For the special case where $d=2$ (qubit), these three bases correspond to the eigenbases of the Pauli X, Y, and Z operators. Explicitly, the three MUBs are defined as follows:

• The Computational basis (Z basis): $|0\rangle ,|1\rangle$.
• The Hadamard basis (X basis): $|+\rangle ,|-\rangle$.
• The Circular basis (Y basis): $|+i\rangle ,|-i\rangle$.

By introducing a third MUB, the protocol increases the uncertainty for an eavesdropper (Eve), thereby enhancing the security margin. In particular, having three MUDs implies six possible states, shown in

Table 1. Six-State protocol states.

State	Z Basis	X Basis	Y Basis
$|0\rangle$	$|0\rangle$	${\displaystyle \frac{\left(\right|+\rangle +|-\rangle )}{\sqrt{2}}}$	${\displaystyle \frac{\left(\right|+i\rangle +|-i\rangle )}{\sqrt{2}}}$
$|1\rangle$	$|1\rangle$	${\displaystyle \frac{\left(\right|+\rangle -|-\rangle )}{\sqrt{2}}}$	${\displaystyle \frac{\left(\right|+i\rangle -|-i\rangle )}{\sqrt{2}}}$
$|+\rangle$	${\displaystyle \frac{\left(\right|0\rangle +|1\rangle )}{\sqrt{2}}}$	$|+\rangle$	${\displaystyle \frac{e^{(-i\pi /4)}\left(\right|+i\rangle +i|-i\rangle )}{\sqrt{2}}}$
$|-\rangle$	${\displaystyle \frac{\left(\right|0\rangle -|1\rangle )}{\sqrt{2}}}$	$|-\rangle$	${\displaystyle \frac{e^{(i\pi /4)}\left(\right|+i\rangle -i|-i\rangle )}{\sqrt{2}}}$
$|+i\rangle$	${\displaystyle \frac{\left(\right|0\rangle +i|1\rangle )}{\sqrt{2}}}$	${\displaystyle \frac{e^{(i\pi /4)}\left(\right|+\rangle -i|-\rangle )}{\sqrt{2}}}$	$|+i\rangle$
$|-i\rangle$	${\displaystyle \frac{\left(\right|0\rangle -i|1\rangle )}{\sqrt{2}}}$	${\displaystyle \frac{e^{(-i\pi /4)}\left(\right|+\rangle +i|-\rangle )}{\sqrt{2}}}$	$|-i\rangle$

. Having two more states than BB84 reduces the effectiveness of certain eavesdropping strategies, as Eve’s probability of correctly guessing the basis decreases.

The objective of the protocol is to enable Alice and Bob to establish a secure shared key. If an eavesdropper is detected during execution, the protocol must abort immediately. In its standard configuration, Alice utilizes a quantum source capable of generating states that encode randomly produced key bits. These qubits are subsequently transmitted to Bob via an insecure quantum channel. During transmission, an adversary (Eve) may interact with the system in an attempt to extract maximal information. Additionally, the protocol requires an authenticated classical channel through which Eve can observe all the exchanged messages but cannot alter them.

The protocol begins with the state preparation. Alice randomly selects one of the three MUBs and then randomly chooses one of the basis states within that basis to encode a key symbol. Each basis has a probability of being chosen equal to $1/3$. After that, Alice generates the corresponding quantum state using, for example, the quantum coding scheme shown in

Table 2. Qubit coding scheme.

Classical Bit	Z Basis	X Basis	Y Basis
0	$|0\rangle$	$|+\rangle$	$|+i\rangle$
1	$|1\rangle$	$|-\rangle$	$|-i\rangle$

, and sends it over the insecure quantum channel. During the quantum state transmission, Eve can execute an intercept–resend attack.

Upon receipt, Bob independently and randomly selects one of the three bases to measure the received state. The randomness in the choice of the measurement basis is fundamental. Eve should not be able to predict the chosen basis for the protocol to work correctly. These two steps are repeated K times so that at the end, both Alice and Bob have a list of K pairs (bit, basis). The bit transmitted by Alice is denoted as b, while the received bit of Bob is ${\widehat{b}}_B$.

After transmission, Alice and Bob, via a public channel, publicly announce the basis used for each state (but not the actual state). Only those states obtained when their choices of basis coincide are retained for key generation. The others are discarded. This procedure is denoted as key sifting. The a priori probability for Alice and Bob to choose the same basis is $1/3$. Hence, after the key sifting $2/3$ of the exchanged bits are removed on average.

Alice and Bob publicly and randomly disclose a subset of their remaining bits, denoted as shared key length, $n\subset K$. The comparison of the shared bits is used to estimate the QBER, which is a critical metric for evaluating communication security and detecting potential eavesdropping. In an ideal noiseless scenario, the disclosed bits should exhibit perfect correlation. However, in practice, discrepancies may arise due to channel noise, measurement imperfections, or adversarial interference (e.g., by Eve). By analyzing a sufficiently large sample of shared bits, Alice and Bob can accurately estimate the QBER, which serves two key purposes: (1) to detect an eavesdropping analysing if the QBER is higher than expected, (2) to quantify information leakage, given that the magnitude of the QBER provides an upper bound on the information Eve may have obtained. If the computed QBER exceeds a predefined security threshold, the protocol must be aborted, as the key exchange is no longer deemed secure. This threshold ensures that any excessive information leakage to an adversary results in immediate termination, preserving the system integrity. This step is essential in QKD, as it allows Alice and Bob to dynamically assess whether the key establishment process can proceed securely or must be halted.

Alice and Bob execute a classical error correction protocol to reconcile discrepancies between their respective keys. Subsequently, they verify key equality by computing the bitwise XOR of their corrected keys and comparing the result. A successful verification (i.e., a null result) confirms key agreement, while any mismatch indicates residual errors requiring further correction or protocol abortion.

The protocol concludes with privacy amplification, a critical post-processing step designed to exponentially reduce any partial information that Eve may have obtained about the key [22]. In essence, this step compresses the reconciled key into a shorter, highly secure version that is statistically uncorrelated with Eve’s data. It is implemented through the application of a universal hash function—a class of mathematical functions ensuring that even minimal differences in input produce statistically independent outputs. Although this operation inevitably reduces the final key length, it provides an information-theoretic guarantee that Eve’s mutual information with the key becomes negligible. The compression ratio, which quantifies the degree of shortening during the hashing process, is carefully chosen by the legitimate parties based on the estimated QBER to ensure the required level of security while maximizing the usable key rate. It is important to note that the final two stages of the process—error correction and privacy amplification—are considered classical post-processing procedures rather than intrinsic components of the QKD protocol itself and are, therefore, not further analyzed in this work.

Upon completion of all the protocol steps, two mutually exclusive outcomes emerge. If the presence of Eve is detected by excessive QBER or verification failures, Alice and Bob immediately abort the protocol. In this case, all the exchanged information is securely discarded, and the key establishment process restarts from the initial phase. This action ensures no potentially compromised key material is retained or utilized. On the contrary, if all the security checks are passed, Alice and Bob obtain a shared secret key that is both identical and information-theoretically secure. The key is guaranteed to be free from eavesdropper interference, as any attempted interception would have been detected during earlier verification stages.

The protocol is designed such that it never produces a compromised key; either a secure key is successfully established, or the protocol terminates without generating any key material. This fail-safe property is fundamental to the protocol security guarantees, and ensures that Alice and Bob only proceed with communication when unconditional security can be assured.

4. Model with System Noise

In practical QKD applications, the accurate measurement of qubits is affected by various imperfections in the components of the system and by Eve interference. These imperfections introduce errors that can impact the final key generation and overall security of the QKD protocol [34]. The main sources of errors can be categorized into transmitter imperfections, receiver imperfections, and channel imperfections. Transmitter imperfections could include, for example, misalignment of optical components or imperfect coupling between the transmitter and the quantum channel (optical fiber). Moreover, there could also be some flaws in the generation of the quantum states. All these imperfections could result in some signal loss and distortions. Receiver imperfections also negatively affect the measurements. Dark counts in detectors can introduce false positive detections even when there are no incoming photons [35,36]. Finally, the transmitting medium can introduce errors by itself. Path loss can reduce the number of photons reaching the detectors [37]. All these imperfections contribute to increasing the QBER of the system. Since the QBER is a crucial parameter in QKD systems, it is fundamental to carefully characterize these imperfections to achieve secure key distribution.

In this work, we make several fundamental assumptions regarding both the quantum channel noise and the potential Eve actions.

System Noise Model Assumption. We assume that bit-flip events induced by ”system noise” can be accurately modeled as Bernoulli random variables. Specifically, for each qubit transmitted between Alice and Bob, the occurrence of a bit-flip due to noise is treated as an independent and identically distributed (i.i.d.) Bernoulli process. Let $e_{ch}$ denote the probability of a bit-flip event for a single qubit. This assumption implies that, for l qubits transmitted, the number of bit-flip events follows a binomial distribution with parameters l and $e_{ch}$ [38]. In this context, an additional assumption adopted throughout the remainder of this work is that the channel and device conditions are stationary with respect to noise; that is, $e_{ch}$ remains constant over the duration of the QKD protocol execution. The validity of this assumption has been substantiated in practical implementations by [39], who reported that fluctuations in the error rate did not exceed 0.16% during a 70 h monitoring period. Furthermore, we assume that Alice and Bob can estimate $e_{ch}$ from a preliminary measurement of quantum interference visibility prior to the actual QKD transmission. As demonstrated by [40], the discrepancy between the estimated and experimentally measured QBER values remains within 1% for QKD transmission over 122 km of standard telecommunication fiber.

Eavesdropping Model Assumption. A second key assumption concerns the capabilities of a potential eavesdropper. In this study, we consider the partial intercept–resend attack, a variant of the standard intercept–resend attack. In this scenario, Eve intercepts only a fraction of the qubits transmitted from Alice to Bob, rather than all of them.

Let p denote the interception density, defined as the probability that Eve intercepts a given qubit during its transmission. By adjusting p, Eve balances the trade-off between information gain and risk of detection: a lower p reduces her detection probability but limits the information she acquires, while a higher p increases both the detection probability and her information gain. For the purposes of this analysis, p is assumed to be constant during the entire protocol execution.

The main notations are summarized in

Table 3. Notations.

Symbol	Meaning
p	Interception Density
$\widehat{p}$	Sample interception density
$e_{ch}$	“System noise” error probability
b	Alice’s Bit
$\widehat{b_B}$	Bob’s bit
$\widehat{b_E}$	Eve’s bit
$SB$	Event: Alice’s and Bob’s bases are the same
K	Key length
n	Shared key length
$QBE{R}_{AB}$	Theoretical QBER
$\widehat{QBE{R}_{AB}}$	Sample QBER

.

4.1. Logical Model

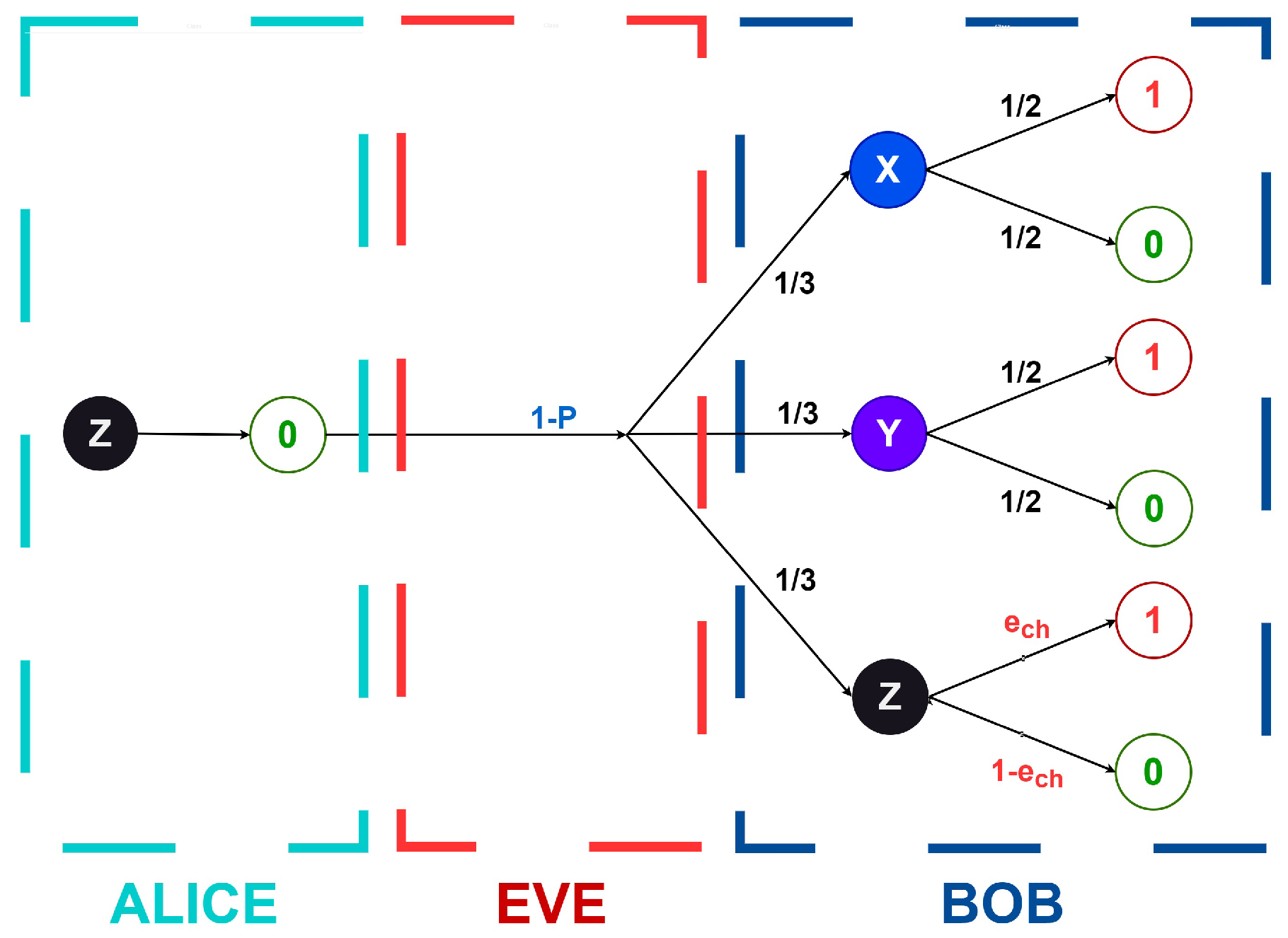
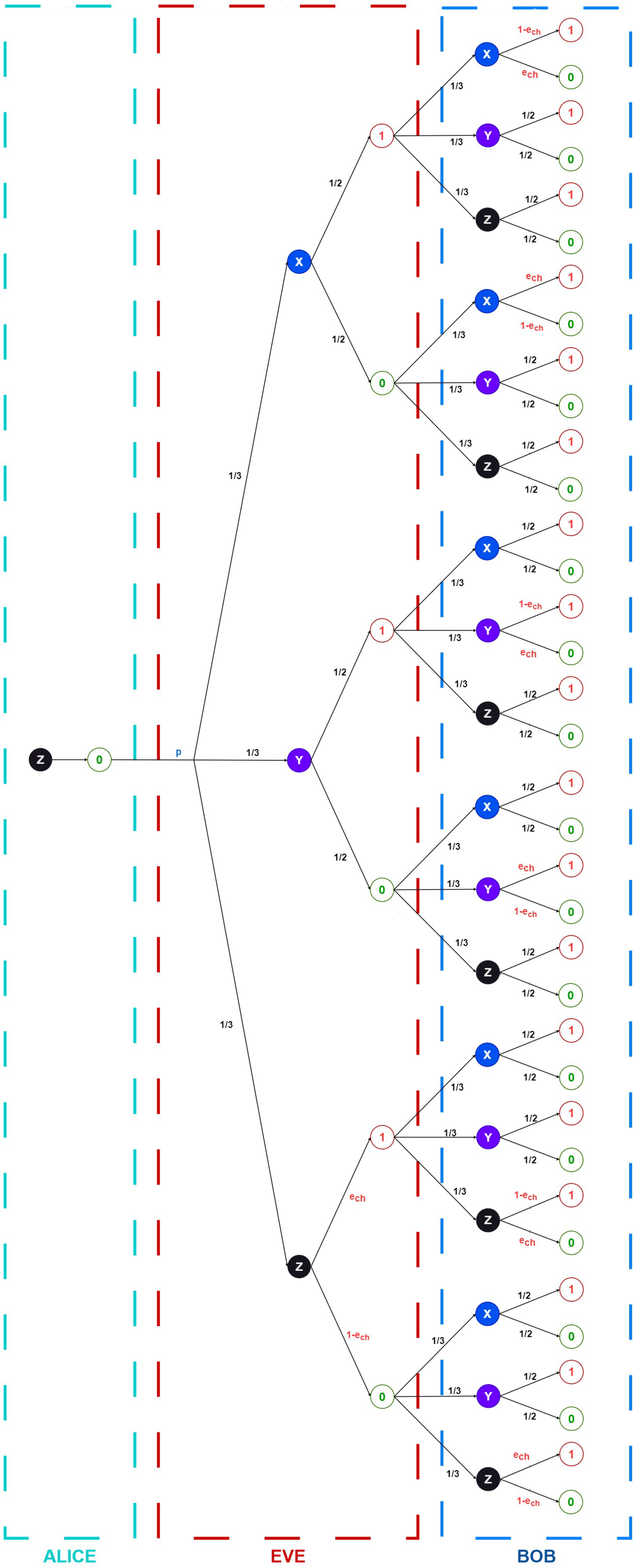
For systematic analysis, we constructed logical diagrams (Figure 1 and Figure 2) enumerating all the possible protocol outcomes in both non-eavesdropped and eavesdropped scenarios. These diagrams explicitly represent bit values rather than qubit states, though the underlying quantum phenomena are implicitly accounted for in determining these values.

These figures illustrate the impact of system noise on qubit transmission. In particular, the presented analysis focuses on Alice transmitting a 0 encoded in the Z basis; however, due to the inherent symmetry of the protocol, these results generalize straightforwardly to other cases. Each transition path in the diagrams is annotated with the corresponding probability of occurrence, including basis selection probabilities and measurement outcomes.

Notably, when all the possible outcomes occur with equal probability, the noise becomes statistically indistinguishable from the inherent randomness of the quantum system, effectively rendering it benign. This equiprobable case represents an important boundary condition where the noise contribution vanishes from an information-theoretic perspective.

The $QBE{R}_{AB}$ is defined as follows:

$$\begin{array}{c}\hfill QBE{R}_{AB}={\displaystyle \frac{\mathrm{Number}\mathrm{of}\mathrm{mismatched}\mathrm{bits}}{\mathrm{Total}\mathrm{number}\mathrm{of}\mathrm{compared}\mathrm{bits}}}.\end{array}$$

(1)

The numerator represents the number of instances where a bit sent by Alice differs from the bit measured by Bob, considering only the cases in which the same basis is used. The denominator, on the other hand, is the total number of bits in the sifted key that are compared. From this definition, it is possible to derive a $QBE{R}_{AB}$ theoretical expression as follows:

$$\begin{array}{cc}\hfill P\left\{\widehat{b_B}\ne b|SB\right\}& ={\displaystyle \frac{\left\{\widehat{b_B}\ne b\cap SB\right\}}{P\left\{SB\right\}}}=3P\left\{\widehat{b_B}\ne b\cap SB\right\}.\hfill \end{array}$$

(2)

Indeed, the probability for Alice and Bob to choose the same basis in this protocol is $1/3$. By applying the total probability law, we get the following:

$$\begin{array}{cc}\hfill P\left\{\widehat{b_B}\ne b\cap SB\right\}& =P\left\{\widehat{b_B}\ne b\cap SB|0\right\}P\left\{0\right\}\hfill \\ & +P\left\{\widehat{b_B}\ne b\cap SB|1\right\}P\left\{1\right\}=\hfill \\ & =2{\displaystyle \frac{1}{2}}P\left\{\widehat{b_B}\ne b\cap SB|0\right\}=\hfill \\ & =P\left\{\widehat{b_B}\ne b\cap SB|0\right\}.\hfill \end{array}$$

(3)

As per the protocol definition, it is known that $P\left\{0\right\}=P\left\{1\right\}=0.5$ and $P\{\widehat{b_B}\ne b\cap SB|0\}=P\{\widehat{b_B}\ne b\cap SB|1\}$. Leveraging this symmetry, $P\{\widehat{b_B}\ne b\cap SB|0\}$ can be computed as follows:

$$\begin{array}{cc}\hfill P\left\{\widehat{b_B}\ne b\cap SB|0\right\}=& P\left\{\widehat{b_B}\ne b\cap SB|0\cap Z\right\}P\left\{Z\right\}+\hfill \\ & P\left\{\widehat{b_B}\ne b\cap SB|0\cap X\right\}P\left\{X\right\}+\hfill \\ & P\left\{\widehat{b_B}\ne b\cap SB|0\cap Y\right\}P\left\{Y\right\}.\hfill \end{array}$$

(4)

Referring to Figure 1 and Figure 2, $P\{\widehat{b_B}\ne b\cap SB|0\cap Z\}$ can be graphically obtained as follows:

$$\begin{array}{cc}\hfill P\left\{\widehat{b_B}\ne b\cap SB|0\cap Z\right\}& =p\left({\displaystyle \frac{1}{36}}+{\displaystyle \frac{1}{36}}+{\displaystyle \frac{1}{36}}+{\displaystyle \frac{1}{36}}\right)\hfill \\ & +{\displaystyle \frac{2}{9}}p{e}_{ch}\left(1-e_{ch}\right)+{\displaystyle \frac{1}{3}}\left(1-p\right)e_{ch}=\hfill \\ & ={\displaystyle \frac{1}{9}}p+{\displaystyle \frac{2}{9}}p{e}_{ch}\left(1-e_{ch}\right)+{\displaystyle \frac{1}{3}}\left(1-p\right)e_{ch}.\hfill \end{array}$$

(5)

Using Equation (5) and combining it with Equations (2) and (4), we obtain the following:

$$\begin{array}{cc}\hfill QBE{R}_{AB}& =P\left\{\widehat{b_B}\ne b|SB\right\}=\hfill \\ & =3P\left\{\widehat{b_B}\ne b\cap SB|0\cap Z\right\}=\hfill \\ & =-{\displaystyle \frac{2}{3}}p{e}_{ch}^2+e_{ch}\left(1-{\displaystyle \frac{1}{3}}p\right)+{\displaystyle \frac{1}{3}}p.\hfill \end{array}$$

(6)

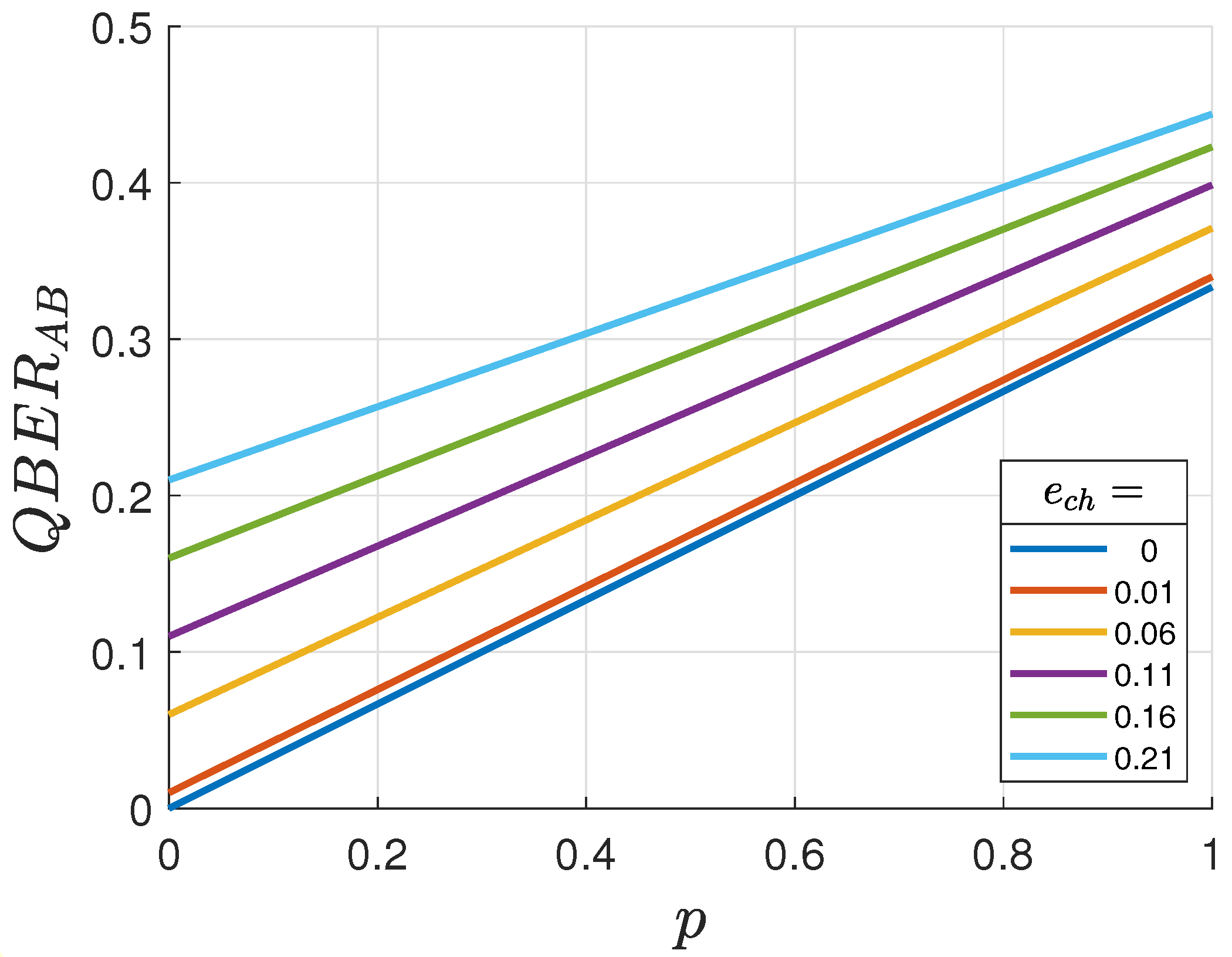
The theoretical $QBE{R}_{AB}$ versus p is shown in Figure 3. Its analysis reveals several key insights. First, the relationship between $QBE{R}_{AB}$ and p exhibits a linear dependence. Second, $e_{ch}$ introduces a vertical offset in the QBER curve, displacing it from the origin. Furthermore, the slope of the QBER curve becomes slightly less steep when accounting for both noise and Eve presence compared to the scenario involving only Eve intervention. Notably, the combined effects of noise and eavesdropping can produce a cancellation phenomenon, where a qubit undergoes two consecutive bit flips—one induced by noise and another by Eve—resulting in no net observable change to the transmitted state.

4.2. Interception Density Estimation

The sharing of parts of their keys after the sifting allows Alice and Bob to estimate $\widehat{QBE{R}_{AB}}$. As a result, it is possible for them to obtain an estimation of the interception density p by inverting the theoretical expression of $QBE{R}_{AB}$ when $\widehat{QBE{R}_{AB}}$ is available:

$$\begin{array}{c}\hfill \widehat{p}={\displaystyle \frac{3\left(\widehat{QBE{R}_{AB}}-e_{ch}\right)}{1-e_{ch}-2e_{ch}^2}}.\end{array}$$

(7)

In a practical implementation, Alice and Bob are expected to determine the value of $e_{ch}$ either through precise calibration measurements during the system installation or from technical specifications provided by the installer. Numerous studies have demonstrated that $e_{ch}$ can be estimated with high precision, with errors below $1\%$ reported over fiber lengths up to $122\mathrm{km}$ [39]. To assess the accuracy in estimating the interception density p, it is useful to analyze the statistical properties of $\widehat{QBE{R}_{AB}}$. Alice and Bob use n bits for the estimation of $\widehat{QBE{R}_{AB}}$. As a result, since the events are assumed to be i.i.d., it follows that the mean of $\widehat{QBE{R}_{AB}}$ should be $QBE{R}_{AB}$ and its variance can be expressed as $QBE{R}_{AB}(1-QBE{R}_{AB})/n$. These results are derived from the assumption that $\widehat{QBE{R}_{AB}}$ is obtained as the ratio of the number of errors in the shared key to its total length, assuming each bit is an independent Bernoulli random variable. By calculating the expected value from Equation (7) the following is obtained:

$$\begin{array}{cc}\hfill E\left\{\widehat{p}\right\}& ={\displaystyle \frac{3(\widehat{QBE{R}_{AB}}-e_{ch})}{1-e_{ch}-2e_{ch}^2}}={\displaystyle \frac{3\left(-\frac{2}{3}p{e}_{ch}^2+e_{ch}\left(1-\frac{1}{3}p\right)+\frac{1}{3}p-e_{ch}\right)}{1-e_{ch}-2e_{ch}^2}}=p.\hfill \end{array}$$

(8)

This result demonstrates that the proposed estimator for p is unbiased.

The variance in $\widehat{p}$ is

$$\begin{array}{cc}\hfill Var\left\{\widehat{p}\right\}& ={\displaystyle \frac{QBE{R}_{AB}(1-QBE{R}_{AB})}{n{\left(\frac{1}{3}-\frac{1}{3}{e}_{ch}-\frac{2}{3}{e}_{ch}^2\right)}^2}}.\hfill \end{array}$$

(9)

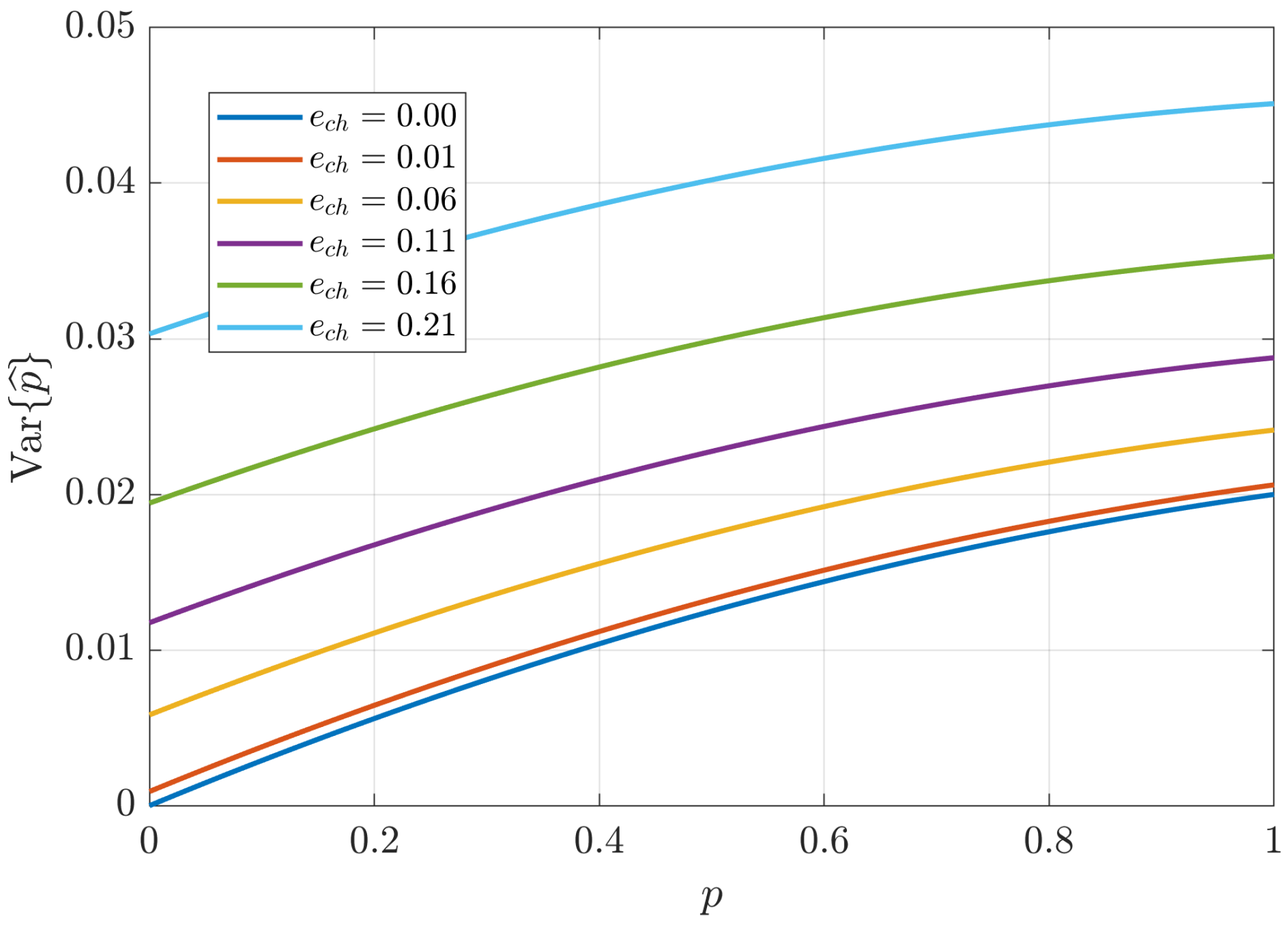
Equation (9) shows that the sample size n directly affects the accuracy of the estimate: as the length of the shared key between Alice and Bob increases, the variance in the estimator decreases, resulting in a more accurate determination of p. This observation aligns with the well-established statistical principle that larger sample sizes yield more precise estimates. Figure 4 illustrates the dependence of the variance in $\widehat{p}$ on the true values of p and $e_{ch}$. Higher values of p correspond to increased variance in $\widehat{p}$, indicating that as the extent of eavesdropping rises, the difficulty of accurately estimating the interception density also increases. This effect may be attributed to the additional uncertainty introduced by more frequent eavesdropping interventions. Additionally, higher system noise levels ($e_{ch}$) lead to further degradation in the accuracy of the estimation. This outcome is intuitive, as elevated noise makes it increasingly challenging to distinguish between errors arising from eavesdropping and those inherent to the quantum channel.

5. Detection Methods

To detect Eve’s presence, two threshold-based methods are proposed, both designed to minimize FPR and FNR. To evaluate the performance of the proposed detection methods, the Accuracy, FNR, and FPR are defined as follows:

$$\begin{array}{c}\hfill \mathit{Accuracy}={\displaystyle \frac{\mathit{TP}+\mathit{TN}}{\mathit{TP}+\mathit{TN}+\mathit{FP}+\mathit{FN}}},\end{array}$$

(10)

$$\begin{array}{c}\hfill \mathit{FNR}={\displaystyle \frac{\mathit{FN}}{\mathit{FN}+\mathit{TP}}},\end{array}$$

(11)

$$\begin{array}{c}\hfill \mathit{FPR}={\displaystyle \frac{\mathit{FP}}{\mathit{FP}+\mathit{TN}}},\end{array}$$

(12)

where $TP$ denotes true positives, $TN$ true negatives, $FP$ false positives, and $FN$ false negatives.

5.1. Method “A”

Given the assumption of i.i.d. channel error events and the possibility of a partial intercept–resend attack by Eve with interception density p, the central limit theorem allows us to approximate $\widehat{QBE{R}_{AB}}$ by a normal distribution when n is sufficiently large. Accordingly, the probability density function of $\widehat{QBE{R}_{AB}}$ can be approximated as $\mathcal{N}({\mu }_{ch},{\sigma }_{ch}^2)$ in the absence of Eve, and as $\mathcal{N}({\mu }_{eve},{\sigma }_{eve}^2)$ when Eve is present. Here, ${\mu }_{ch}$ and ${\mu }_{eve}$ denote the theoretical values of $QBE{R}_{AB}$ for the respective scenarios, while ${\sigma }_{ch}^2$ and ${\sigma }_{eve}^2$ are the corresponding binomial variances. Specifically, ${\mu }_{ch}=e_{ch}$. The detection algorithm decides the presence of eavesdropping by comparing the measured $\widehat{QBE{R}_{AB}}$ to a threshold ${\theta }_{QBER}$, which is assumed to lie within the interval $({\mu }_{ch},{\mu }_{eve})$.

By applying Hoeffding’s inequality [25], it is possible to derive an upper bound for both FNR and FPR. Both bounds exhibit exponential dependence on the threshold, the mean of $\widehat{QBE{R}_{AB}}$, and the number of shared bits n. Let $QBE{R}_{ch,n}$ denote the value of ${\widehat{QBER}}_{AB}$ computed over n bits when Eve is absent. The upper bound for the FPR is then given by the following:

$$\begin{array}{cc}\hfill \mathrm{FPR}& =Pr\left[QBE{R}_{\mathrm{ch},n}\ge {\theta }_{\mathrm{QBER}}\right]\hfill \\ \hfill & =Pr\left[QBE{R}_{\mathrm{ch},n}-{\mu }_{\mathrm{ch}}\ge {\theta }_{\mathrm{QBER}}-{\mu }_{\mathrm{ch}}\right]\hfill \\ \hfill & =Pr\left[QBE{R}_{\mathrm{ch},n}-{\mu }_{\mathrm{ch}}\ge {\epsilon }_{\mathrm{FP}}\right]\le e^{-2{\epsilon }_{\mathrm{FP}}^{2}n}.\hfill \end{array}$$

(13)

Similarly, defining $QBE{R}_{eve,n}$ as the value of ${\widehat{QBER}}_{AB}$ over n bits when Eve is present, the upper bound for the FNR is given by the following:

$$\begin{array}{cc}\hfill \mathrm{FNR}& =Pr\left[QBE{R}_{\mathrm{eve},n}\le {\theta }_{\mathrm{QBER}}\right]\hfill \\ \hfill & =Pr\left[{\mu }_{eve}-QBE{R}_{\mathrm{eve},\mathrm{n}}\ge {\mu }_{\mathrm{eve}}-{\theta }_{\mathrm{QBER}}\right]\hfill \\ \hfill & =Pr\left[{\mu }_{eve}-QBE{R}_{\mathrm{eve},\mathrm{n}}\ge {\epsilon }_{\mathrm{FN}}\right]\le e^{-2{\epsilon }_{\mathrm{FN}}^{2}n},\hfill \end{array}$$

(14)

where ${\epsilon }_{FN}={\mu }_{eve}-{\theta }_{QBER}$ and ${\epsilon }_{FP}={\theta }_{QBER}-{\mu }_{ch}$.

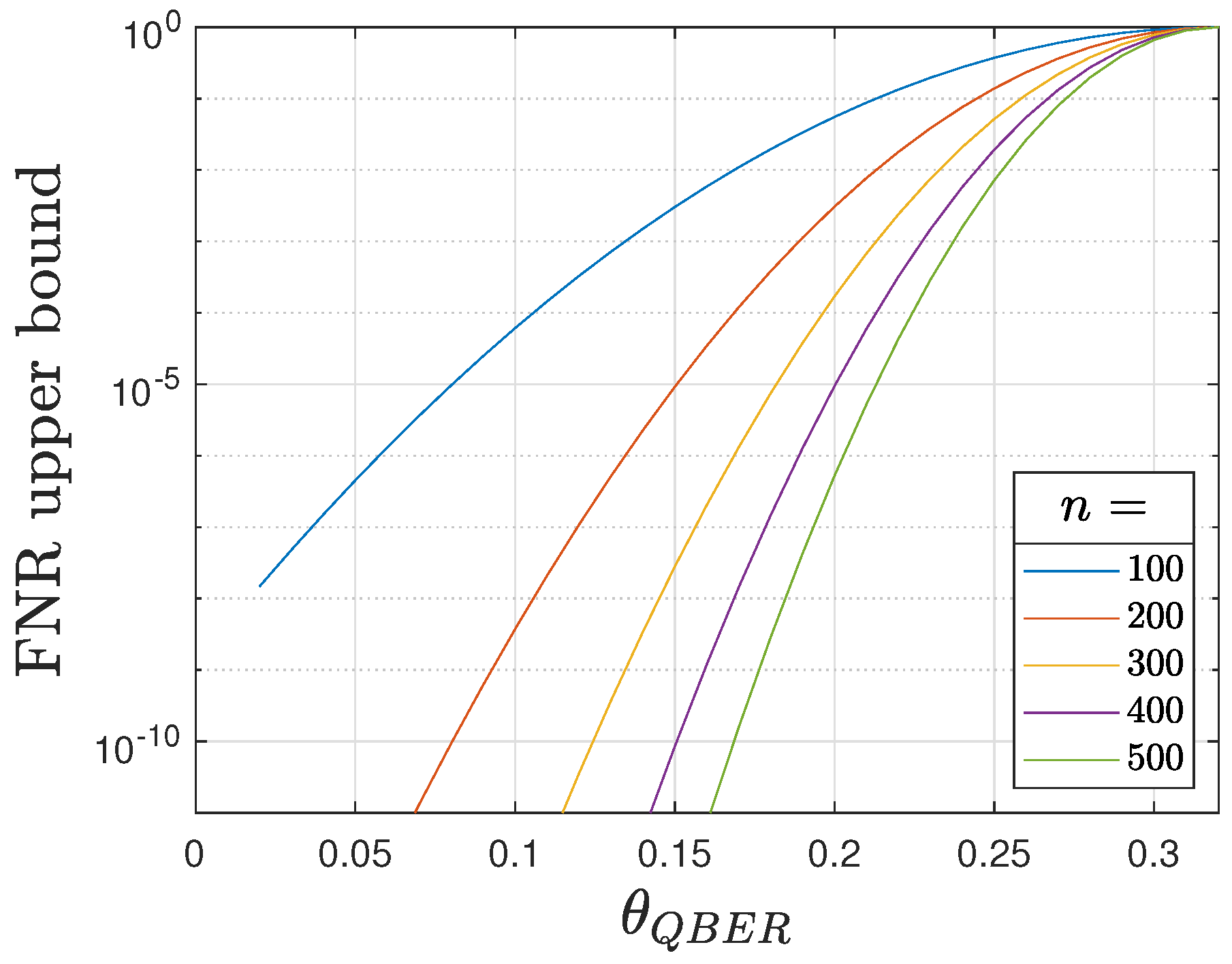
Figure 5 and Figure 6 illustrate the upper bounds for the FNR and FPR, respectively. Assuming ${\mu }_{ch}=2\%$, various values of n are considered. The curves confirm that the upper bounds decrease exponentially as n increases. Furthermore, decreasing ${\theta }_{QBER}$ lowers the upper bound for the FNR but raises the one for the FPR; conversely, increasing ${\theta }_{QBER}$ has the opposite effect. Therefore, the selection of ${\theta }_{QBER}$ is critical for balancing detection performance. The optimal value of ${\theta }_{QBER}$ can be found by solving

$${\theta }_{\mathrm{QBER}}^{\ast }=arg\underset{{\theta }_{\mathrm{QBER}}}{min}\left(e^{-2{\epsilon }_{\mathrm{FN}}^{2}n}+\alpha e^{-2{\epsilon }_{\mathrm{FP}}^{2}n}\right),$$

(15)

where the optimal threshold minimizes the weighted sum of the upper bounds of FNR and FPR. The parameter $\alpha \in (0,1)$ weights the importance of the FPR relative to the FNR. Both terms in Equation (15) are differentiable with respect to ${\theta }_{QBER}$. Therefore, by differentiating with respect to ${\theta }_{QBER}$ and solving, we obtain the following:

$$\begin{array}{c}\hfill \alpha {\displaystyle \frac{e^{-2n{({\theta }_{QBER}-{\mu }_{ch})}^2}}{e^{-2n{({\theta }_{QBER}-1/3p+2/3p{\mu }_{ch}^2-{\mu }_{ch}(1-1/3p))}^2}}}={\displaystyle \frac{(1/3p-2/3p{\mu }_{ch}^2+{\mu }_{ch}-1/3{\mu }_{ch})-{\theta }_{QBER}}{{\theta }_{QBER}-{\mu }_{ch}}},\end{array}$$

(16)

which can be rearranged as follows:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\alpha }{e^{\frac{2n}{9}\left[p^2+(6p-2p^2){\mu }_{ch}-(3p^2+6p){\mu }_{ch}^2+(4p^2-12p){\mu }_{ch}^3+4p^2{\mu }_{ch}^4\right]}}}=\hfill \\ \\ & =e^{4/3n{\theta }_{QBER}(-2p{\mu }_{ch}^2-p{\mu }_{ch}+p)}{\displaystyle \frac{(1/3p-2/3p{\mu }_{ch}^2+{\mu }_{ch}-1/3{\mu }_{ch})-{\theta }_{QBER}}{{\theta }_{QBER}-{\mu }_{ch}}}.\hfill \end{array}$$

(17)

It follows:

$$\begin{array}{cc}\hfill & {\left({\displaystyle \frac{\alpha }{e^{\frac{2n}{9}\left[p^2+(6p-2p^2){\mu }_{ch}-(3p^2+6p){\mu }_{ch}^2+(4p^2-12p){\mu }_{ch}^3+4p^2{\mu }_{ch}^4\right]}}}\right)}^{{\displaystyle \frac{1}{4/3n(-2p{\mu }_{ch}^2-p{\mu }_{ch}+p)}}}=\hfill \\ \\ \hfill & =e^{4/3n{\theta }_{QBER}}\underset{\approx 1}{\underbrace{{\underset{>0}{\underbrace{\left({\displaystyle \frac{(1/3p-2/3p{\mu }_{ch}^2+{\mu }_{ch}-1/3{\mu }_{ch})-{\theta }_{QBER}}{{\theta }_{QBER}-{\mu }_{ch}}}\right)}}}^{{\displaystyle \frac{1}{4/3n(-2p{\mu }_{ch}^2-p{\mu }_{ch}+p)}}}}}.\hfill \end{array}$$

(18)

By restricting ${\theta }_{QBER}$ to the interval $({\mu }_{ch},{\mu }_{eve})$, the expression within the brackets remains strictly positive. Given that ${\mu }_{ch}\ll 1$, the corresponding exponent approaches zero, allowing the last term to be approximated as unity. Under this approximation, the optimal threshold ${\theta }_{QBER}^{\ast }$ can be readily computed:

$$\begin{array}{c}\hfill {\theta }_{\mathrm{QBER}}^{\ast }={\displaystyle \frac{ln\left(\alpha \right)-\frac{2n}{9}\left[p^2+(6p-2p^2){\mu }_{ch}-(3p^2+6p){\mu }_{ch}^2+(4p^2-12p){\mu }_{ch}^3+4p^2{\mu }_{ch}^4\right]}{\frac{16}{9}{n}^2\left(-2p{\mu }_{ch}^2-p{\mu }_{ch}+p\right)}}.\end{array}$$

(19)

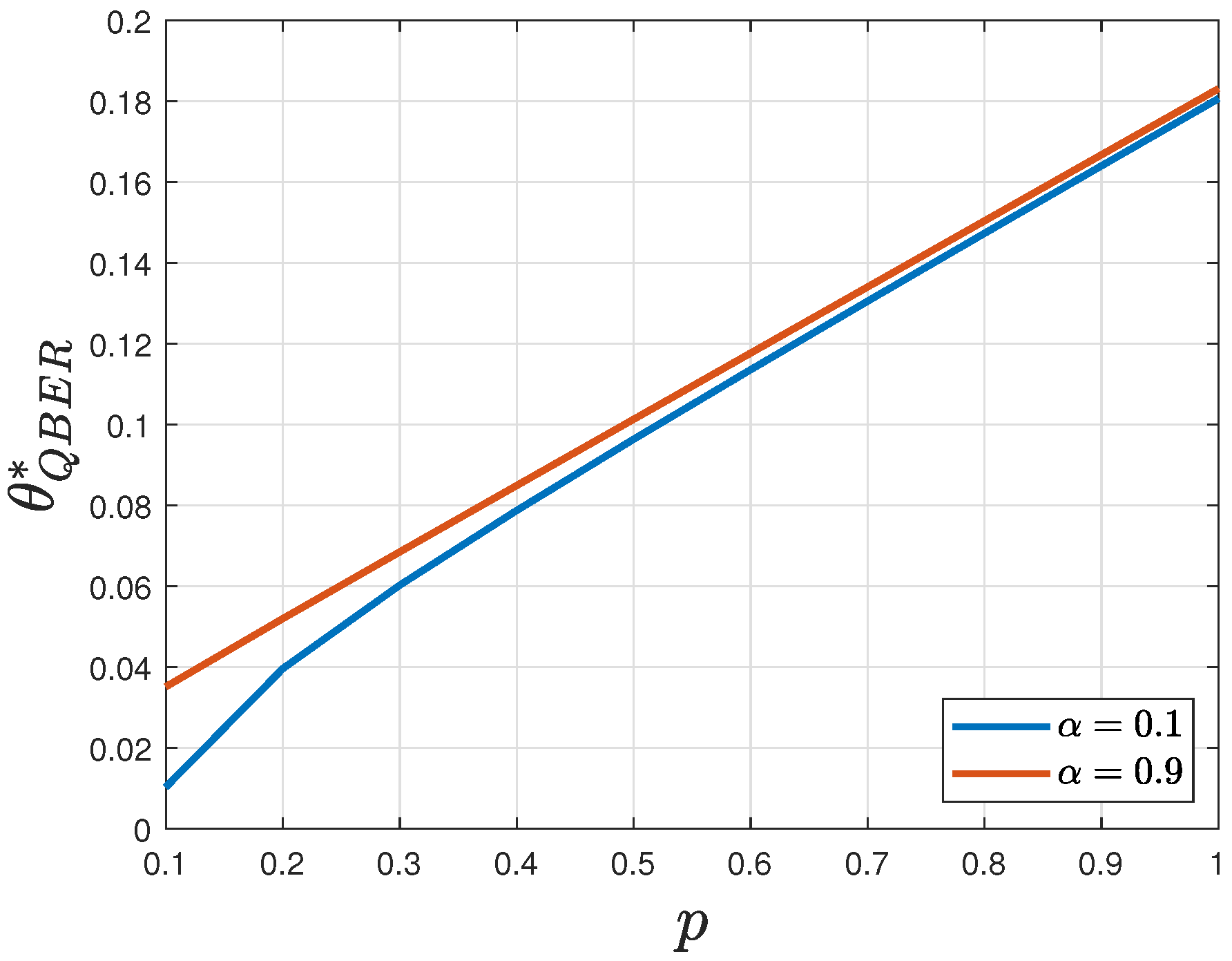
Figure 7 illustrates the optimal threshold as a function of $\alpha$. As $\alpha$ increases, the threshold also increases, leading to a reduction in the FNR but at the expense of a higher FPR. This effect is particularly pronounced at lower values of p. Thus, by selecting an appropriate $\alpha$, it is possible to assign greater weight to either the FPR or the FNR. For the purpose of a fair comparison between Method A and Method B, we set $\alpha =1$ in this work.

5.2. Method “B”

Recalling that $QBE{R}_{AB}\sim \mathcal{N}({\mu }_{ch},{\sigma }_{ch}^2)$ when Eve is absent and $QBE{R}_{AB}\sim \mathcal{N}({\mu }_{eve},{\sigma }_{eve}^2)$ when she is present, an alternative approach to determining the optimal threshold can be considered. In this context, the variances of each distribution are given by:

$$\begin{array}{c}\hfill {\sigma }_{ch}=\sqrt{{\displaystyle \frac{{\mu }_{ch}(1-{\mu }_{ch})}{n}}},\end{array}$$

(20)

$$\begin{array}{c}\hfill {\sigma }_{eve}=\sqrt{{\displaystyle \frac{{\mu }_{eve}(1-{\mu }_{eve})}{n}}}.\end{array}$$

(21)

Moreover, assuming n sufficiently large, FPR and FNR can be expressed as:

$$\begin{array}{c}\hfill \mathrm{FPR}={\int }_{{\theta }_{\mathrm{QBER}}}^{\infty }{\displaystyle \frac{1}{{\sigma }_{ch}\sqrt{2\pi }}}{e}^{-{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{x-{\mu }_{ch}}{{\sigma }_{ch}}}\right)}^2}dx=1-\mathrm{\Phi }\left({\displaystyle \frac{{\theta }_{\mathrm{QBER}}-{\mu }_{ch}}{{\sigma }_{ch}}}\right),\end{array}$$

(22)

$$\begin{array}{c}\hfill \mathrm{FNR}={\int }_0^{{\theta }_{\mathrm{QBER}}}{\displaystyle \frac{1}{{\sigma }_{\mathrm{eve}}\sqrt{2\pi }}}{e}^{-{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{y-{\mu }_{\mathrm{eve}}}{{\sigma }_{\mathrm{eve}}}}\right)}^2}dy=\mathrm{\Phi }\left({\displaystyle \frac{{\theta }_{\mathrm{QBER}}-{\mu }_{\mathrm{eve}}}{{\sigma }_{\mathrm{eve}}}}\right),\end{array}$$

(23)

where $\mathrm{\Phi }(·)$ denotes the cumulative distribution function of the standard normal distribution.

By adopting the same criterion for the optimal threshold as in the previous method, and noting that both FPR and FNR are differentiable functions of ${\theta }_{QBER}$, the following relation holds:

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{{\sigma }_{\mathrm{eve}}\sqrt{2\pi }}}{e}^{-{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{{\theta }_{QBER}^{\ast }-{\mu }_{eve}}{{\sigma }_{eve}}}\right)}^2}={\displaystyle \frac{1}{{\sigma }_{ch}\sqrt{2\pi }}}{e}^{-{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{{\theta }_{QBER}^{\ast }-{\mu }_{ch}}{{\sigma }_{ch}}}\right)}^2}.\end{array}$$

(24)

Hence:

$$\begin{array}{c}\hfill 2ln{\displaystyle \frac{{\sigma }_{ch}}{{\sigma }_{\mathrm{eve}}}}={\left({\displaystyle \frac{{\theta }_{QBER}^{\ast }-{\mu }_{eve}}{{\sigma }_{\mathrm{eve}}}}\right)}^2-{\left({\displaystyle \frac{{\theta }_{QBER}^{\ast }-{\mu }_{ch}}{{\sigma }_{ch}}}\right)}^2.\end{array}$$

(25)

Finally, the optimal threshold can be written as follows:

$$\begin{array}{cc}\hfill {\theta }_{QBER}^{\ast }& ={\displaystyle \frac{1}{{\sigma }_{ch}^2-{\sigma }_{eve}^2}}\left\{\left({\sigma }_{ch}^2{\mu }_{eve}-{\sigma }_{eve}^2{\mu }_{ch}\right)-{\sigma }_{ch}{\sigma }_{eve}\mathrm{\Gamma }\right\},\hfill \end{array}$$

(26)

where:

$$\begin{array}{cc}\hfill \mathrm{\Gamma }& =\sqrt{{\left({\mu }_{eve}-{\mu }_{ch}\right)}^2+2\left({\sigma }_{ch}^2-{\sigma }_{eve}^2\right)ln{\displaystyle \frac{{\sigma }_{ch}}{{\sigma }_{eve}}}}.\hfill \end{array}$$

(27)

Considerations on the Optimal Threshold. Several considerations arise in the determination of the optimal threshold. Both approaches require knowledge of ${\mu }_{ch}$, n, and p. The value of n is directly available, as it is set during protocol execution. In contrast, accurately measuring ${\mu }_{ch}$ during the protocol is challenging; consequently, this parameter must be provided by the installer or measured prior to protocol initiation. The interception density p, on the other hand, cannot be known a priori by Alice and Bob. In this work, it is assumed that Eve maintains a constant interception density, compatible with a passive attack strategy, allowing Alice and Bob to accurately estimate p as described in Section 4.2.

6. Experimental Setup

To verify the effectiveness of the proposed algorithms, we employed a simulator based on the QuantumSolver (QS) library [41]. To allow the replication of the results, the developed code is publicly available on GitHub [42]. Leveraging the open-source Qiskit framework, we can simulate quantum circuits and their associated operations. Qiskit also provides the capability to execute programs locally using a backend that incorporates a realistic noise model, closely reflecting the performance of contemporary quantum hardware. Although execution on an actual IBM quantum device was technically feasible, it was rendered impractical due to excessive queue times.

The simulator initiates with the Key Generation step. During this operation, the following parameters must be specified as inputs:

• Key length (K): The number of qubits exchanged during the transmission process.
• Shared key length (n): The number of qubits used for the estimation of QBER.
• Interception density (p).
• Number of iterations: The number of repetitions of the proposed algorithm.
• System noise error probability ($e_{ch})$: The expected error rate associated with the quantum channel.

The simulation procedure begins with Alice generating two random binary arrays of length K, corresponding to the key bits and the bases used for encoding, respectively. Bob and Eve each independently generate one random array of the same length to determine their measurement bases. In the encoding phase, three MUBs are available: Z, X, and Y. All the qubits are initialized in the $|0\rangle$ state.

The encoding of each bit proceeds as follows: If the bit value to be transmitted is “1”, an X gate (logical NOT) is first applied. Subsequently, depending on the selected encoding basis, further operations are performed depending on the selected basis. In particular, no additional gate is applied when the Z-basis is selected, while an H gate is applied in the case of X-basis. To generate the quantum information when the Y-basis is selected, an H gate followed by an S gate is applied in sequence.

The H gate is defined as follows:

$$H={\displaystyle \frac{1}{\sqrt{2}}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right],$$

(28)

while the S gate is defined as follows:

$$S=\left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right].$$

(29)

During this process, an alphanumeric message of length K is generated. Following the encoding phase, Eve intervenes by choosing to intercept each qubit with probability p. For intercepted qubits, Eve performs a measurement in her randomly chosen basis by applying the appropriate gates (either H or $HS$) prior to the resend phase. In contrast, Bob receives all the transmitted qubits (i.e., $p=1$) and measures each according to his randomly assigned basis.

Following the measurement, Alice and Bob publicly share their chosen bases over an authenticated classical channel. The sifting phase is then executed, wherein only the bits corresponding to matching bases are retained; typically, m bits survive this phase. Subsequently, $\widehat{QBE{R}_{AB}}$ and $\widehat{p}$ are computed.

7. Simulation Results

The simulation analysis is designed to evaluate the estimation procedures for both QBER and p, which are essential for the proposed eavesdropping detection methods. Subsequently, the performance and effectiveness of these detection methods are discussed.

7.1. QBER Estimation

For this study, multiple IBM backend simulators were employed to model realistic quantum noise environments. The characteristics of the selected backends are summarized in

Table 4. Considered backend.

Backend	Number of Qubits	Noise Error Rate
$fake\text{\_}armonk$	1	$2.36\%$
$fake\text{\_}casablanca$	7	$2.04\%$
$fake\text{\_}quito$	5	$4.72\%$
$fake\text{\_}rome$	5	$3.11\%$
$fake\text{\_}tenerife$	5	$8.27\%$

. These simulators were chosen specifically for their different $e_{ch}$ values, which allow for a comprehensive assessment of the proposed methods under diverse channel conditions.

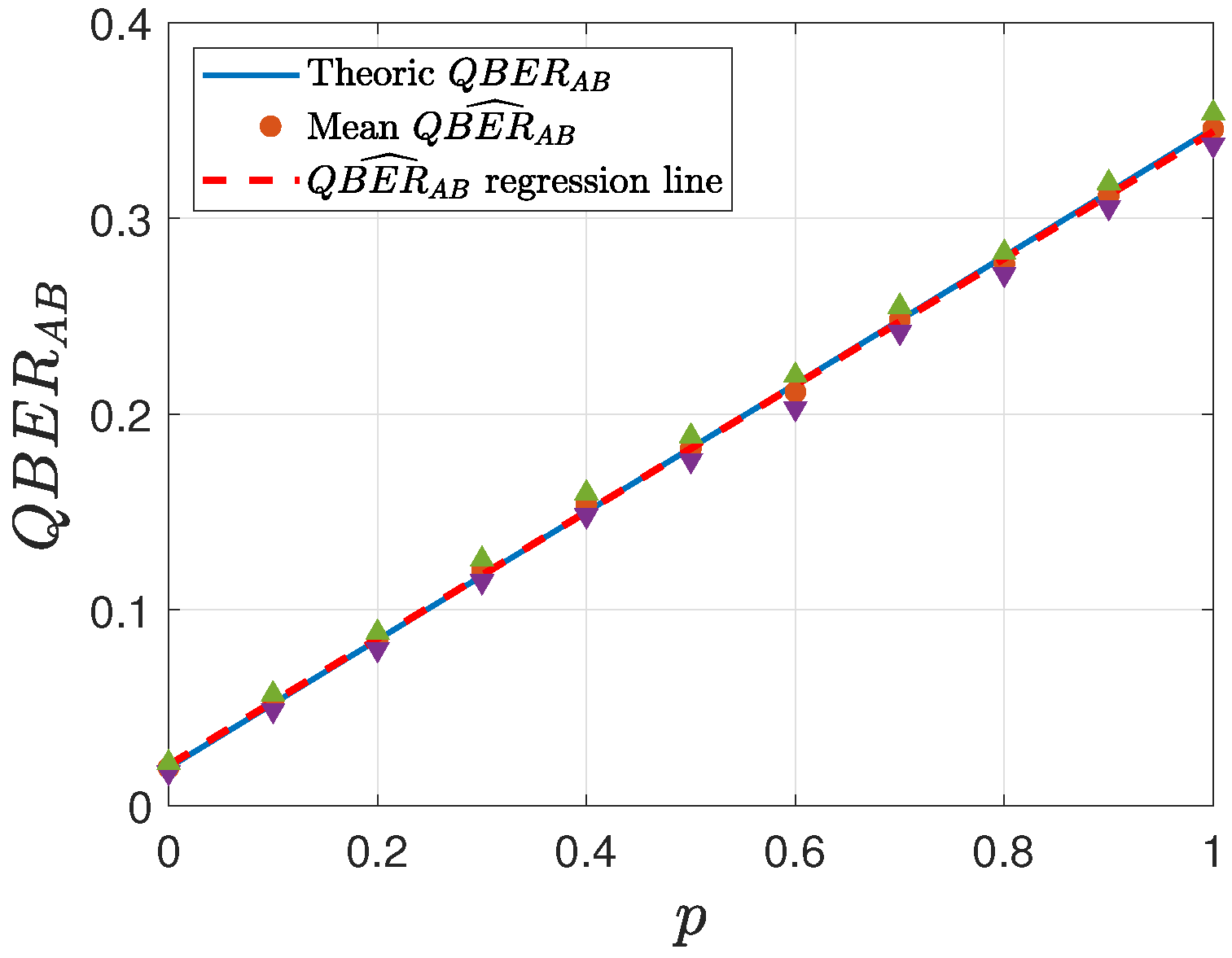
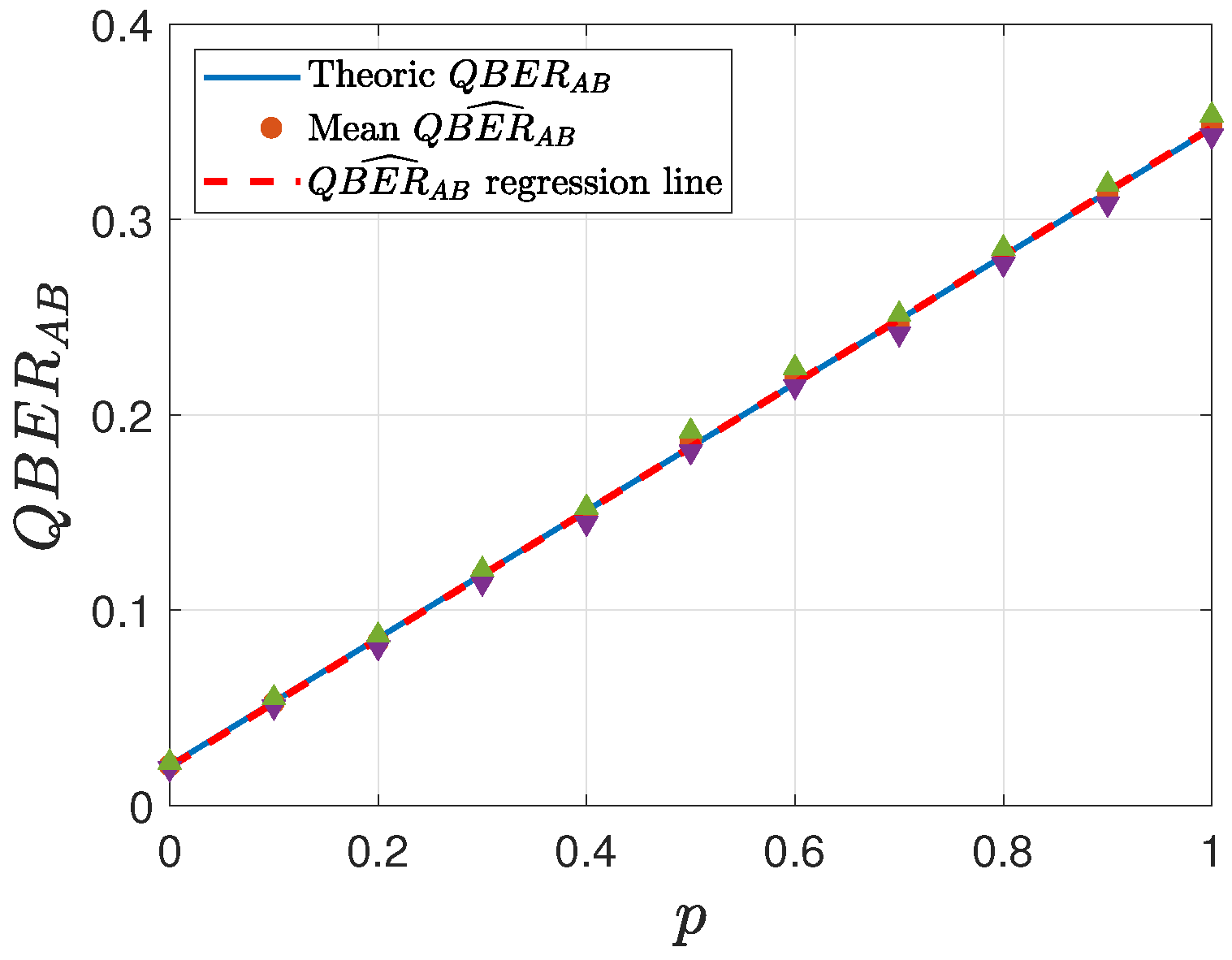
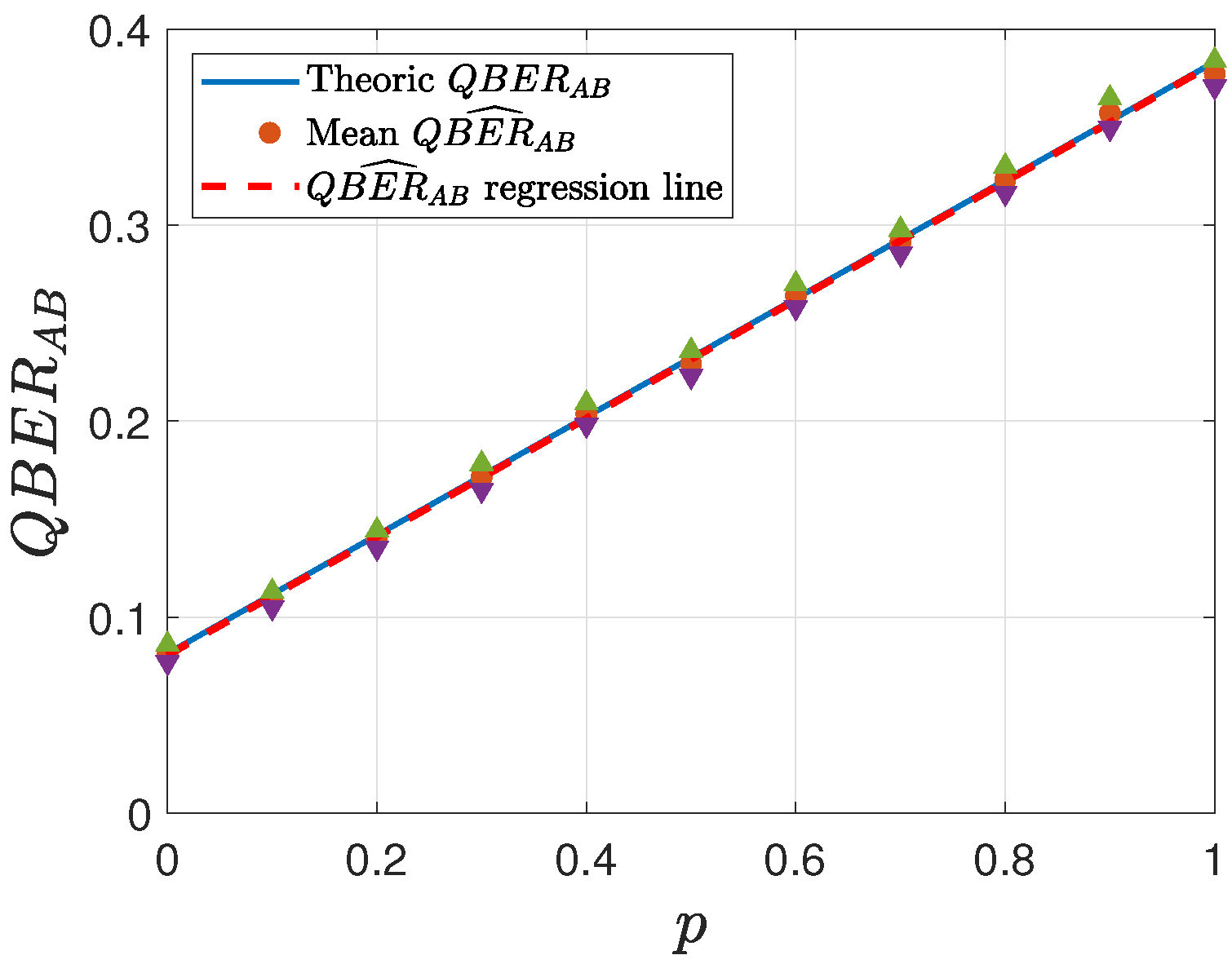
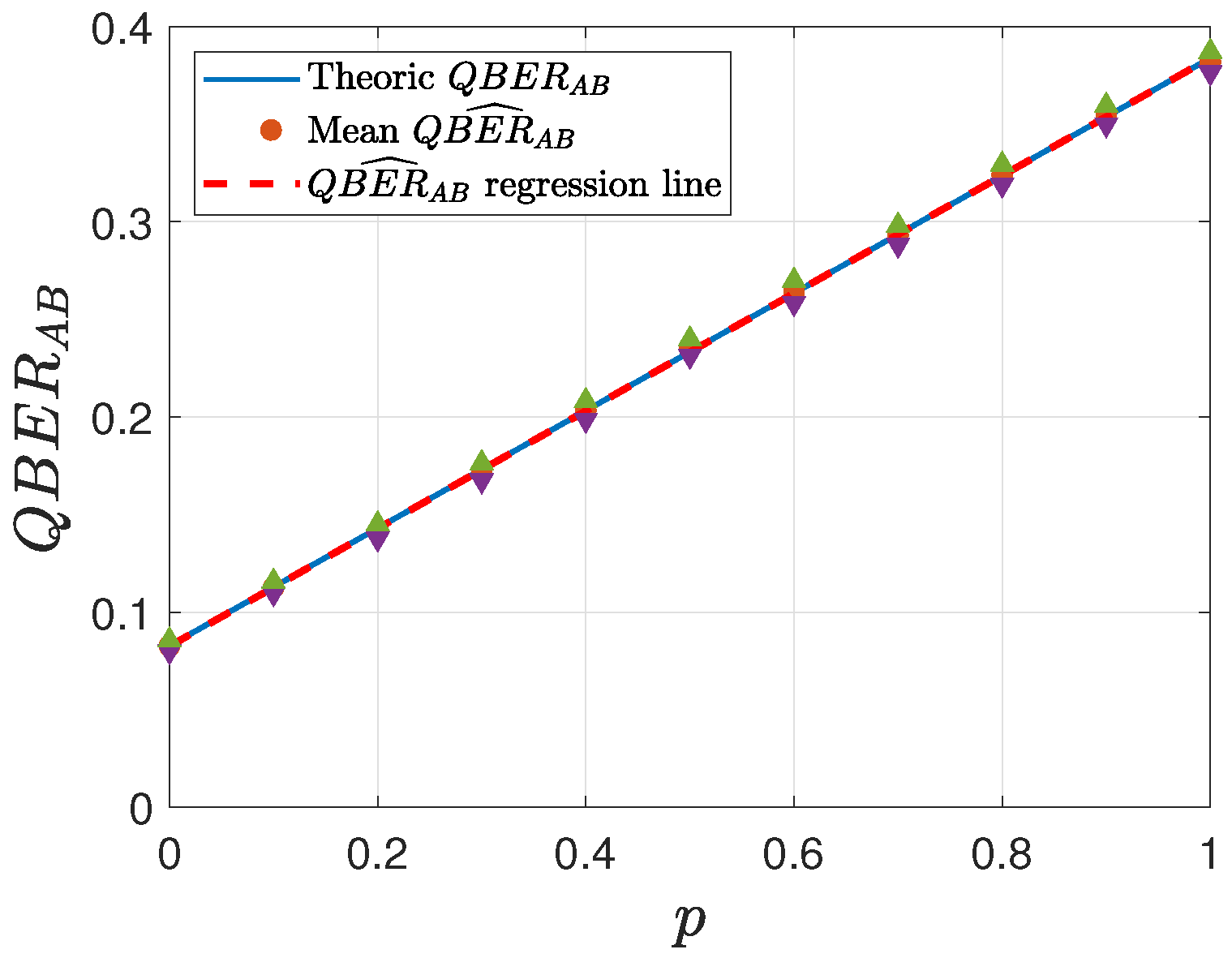
For clarity, we present the results corresponding to the backends with the lowest and highest $e_{ch}$, namely fake_casablanca ($e_{ch}=2.04\%$) and fake_tenerife ($e_{ch}=8.27\%$). The results obtained with the remaining backends are consistent with the conclusions drawn from these two representative cases. Figure 8, Figure 9, Figure 10 and Figure 11 report the corresponding estimated values of ${\widehat{QBER}}_{AB}$, with the regression line and the $95\%$ confidence intervals (indicated by triangle symbols). For each value of p, every simulation was repeated 50 times, and the mean value was subsequently computed. This study considers two different settings for K, i.e., $K=2048,4096$. Considering a sifting factor of $1/3$ arising from the basis reconciliation phase, and assuming that n corresponds to half of the sifted key length, these choices ensure, in a conservative manner, at least a twofold security margin with respect to the standard key sizes employed in AES-128 and AES-256. Consequently, they satisfy the post-quantum security requirement against Grover’s algorithm [43]. This selection, thus, provides a reasonable trade-off between computational robustness and protocol feasibility.

In all the analyzed cases, the regression line consistently lies within the confidence intervals, indicating the robustness of the estimation procedure. Furthermore, as the key length K increases, the accuracy of the ${\widehat{QBER}}_{AB}$ estimation improves, following statistical theory. Additionally, it is evident that lower values of $e_{ch}$ yield greater precision in the estimation, as expected.

7.2. Interception Density Estimation

Building upon the $\widehat{QBE{R}_{AB}}$ estimation, we also obtained estimates for the interception density p. The corresponding results are reported in

Table 5. p estimation results (fake_casablanca).

	K = 2048		K = 4096
$\mathit{p}$	$\widehat{\mathit{p}}$	$\widehat{\mathit{\sigma }}\{\widehat{\mathit{p}}$}	$\widehat{\mathit{p}}$	$\widehat{\mathit{\sigma }}\{\widehat{\mathit{p}}$}
0	0	0.0237	0	0.0170
0.1	0.1025	0.0385	0.0989	0.0273
0.2	0.1982	0.0477	0.1948	0.0339
0.3	0.3084	0.0559	0.2970	0.0393
0.4	0.4119	0.0621	0.3929	0.0435
0.5	0.4995	0.0664	0.5088	0.0476
0.6	0.5877	0.0701	0.6099	0.0506
0.7	0.7012	0.0743	0.6931	0.0527
0.8	0.7887	0.0770	0.7997	0.0550
0.9	0.8956	0.0797	0.8968	0.0567
1	0.9990	0.0818	1.0047	0.0582

and

Table 6. p estimation results (fake_tenerife).

	K = 2048		K = 4096
$\mathit{p}$	$\widehat{\mathit{p}}$	$\widehat{\mathit{\sigma }}\left\{\widehat{\mathit{p}}\right\}$	$\widehat{\mathit{p}}$	$\widehat{\mathit{\sigma }}\left\{\widehat{\mathit{p}}\right\}$
0	0	0.0586	0	0.0420
0.1	0.0909	0.0668	0.0992	0.0482
0.2	0.1933	0.0744	0.1946	0.0532
0.3	0.2984	0.0808	0.2961	0.0576
0.4	0.4045	0.0863	0.4005	0.0614
0.5	0.4901	0.0901	0.5073	0.0647
0.6	0.6045	0.0945	0.6021	0.0672
0.7	0.6959	0.0974	0.6986	0.0695
0.8	0.8007	0.1003	0.8016	0.0714
0.9	0.9132	0.1027	0.9031	0.0730
1	0.9801	0.1039	0.9931	0.0741

. For both the considered values of K, the estimation of p demonstrates good precision. Specifically, the sample standard deviation $\widehat{\sigma }$ decreases as K increases, confirming that longer key lengths yield more accurate estimates. Conversely, $\widehat{\sigma }$ increases with larger values of p, indicating that higher interception densities are more challenging to estimate precisely. Additionally, an increase in the system error rate $e_{ch}$ leads to a degradation in estimation accuracy.

7.3. Detection

The performance of the proposed thresholding methods is quantitatively assessed through numerical evaluation of FPR and FNR, as defined in Equations (22) and (23). To formalize the accuracy metric, recall Equation (10):

$$1-\mathit{Accuracy}={\displaystyle \frac{\mathit{FP}+\mathit{FN}}{\mathit{TP}+\mathit{TN}+\mathit{FP}+\mathit{FN}}}.$$

(30)

Rewriting the definitions of FPR and FNR, we have the following:

$$FP=FPR·(FP+TN),FN=FNR·(FN+TP).$$

(31)

Noting that $FP+TN$ accounts for all the trials where Eve is not present (with probability $1-p$), and $FN+TP$ accounts for all the trials where Eve is present (with probability p), we have:

$${\displaystyle \frac{FP+TN}{TP+TN+FP+FN}}=1-p,{\displaystyle \frac{FN+TP}{TP+TN+FP+FN}}=p.$$

(32)

Thus, $1-\mathit{Accuracy}$ can be rewritten as:

$$1-\mathit{Accuracy}=(1-p)·FPR+p·FNR.$$

(33)

This result highlights how the overall detection error is a weighted combination of the two principal error types, modulated by the true prevalence of eavesdropping events in the communication. The practical implications are twofold:

• Sensitivity to Interception Density (p): As p increases, the contribution of $FNR$ to the total error becomes more significant, emphasizing the importance of minimizing false negatives in high-threat environments.
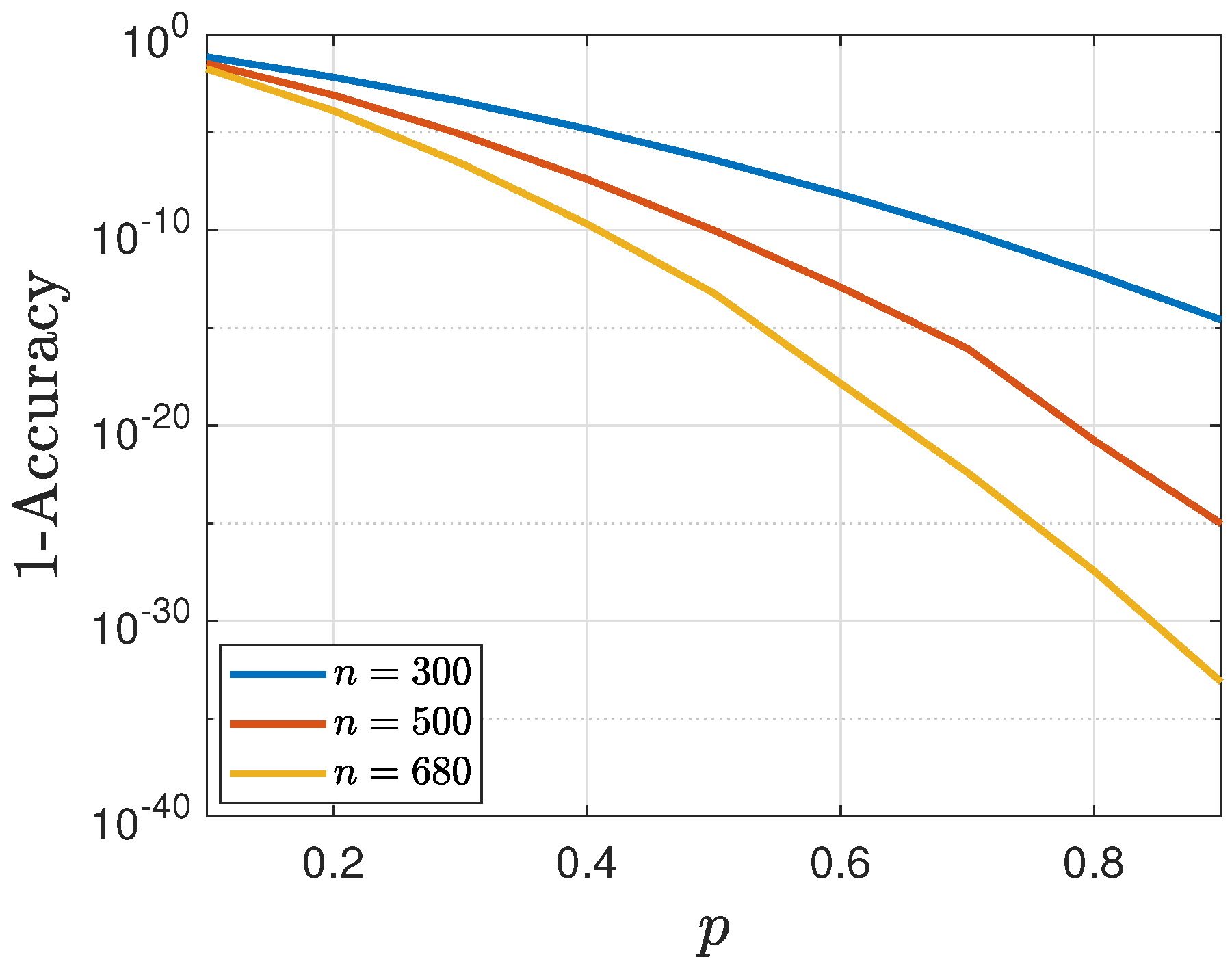
• Role of Shared Key Length (n): The accuracy of both methods is found to improve with increasing key length, as shown in Figure 12. This is a direct consequence of the reduction in statistical uncertainty with larger samples, which enhances the reliability of threshold-based detection.

Figure 12 further demonstrates that the optimal thresholding method (method “B”) maintains high accuracy across the range of p values tested. Notably, for longer keys, the accuracy asymptotically approaches the theoretical maximum, thereby supporting the adoption of larger key sizes in practical implementations.

It is noteworthy that higher values of p are associated with improved detectability of eavesdropping. At first glance, this observation may appear counterintuitive, as previous analysis established that increasing p also increases the variance in $\widehat{QBE{R}_{AB}}$, potentially degrading the accuracy of the optimal threshold calculation. However, this apparent contradiction can be resolved by examining the relationship between the sample QBER and the detection threshold.

Specifically, although a larger p induces greater variance in $\widehat{QBE{R}_{AB}}$, it also leads to a greater separation between the expected system noise mean (${\mu }_{ch}$) and the mean QBER in the presence of eavesdropping (${\mu }_{eve}$). Consequently, the average distance between the sample QBER and the detection threshold increases with p, which compensates for the increased variance and enhances the overall probability of correctly identifying an eavesdropper.

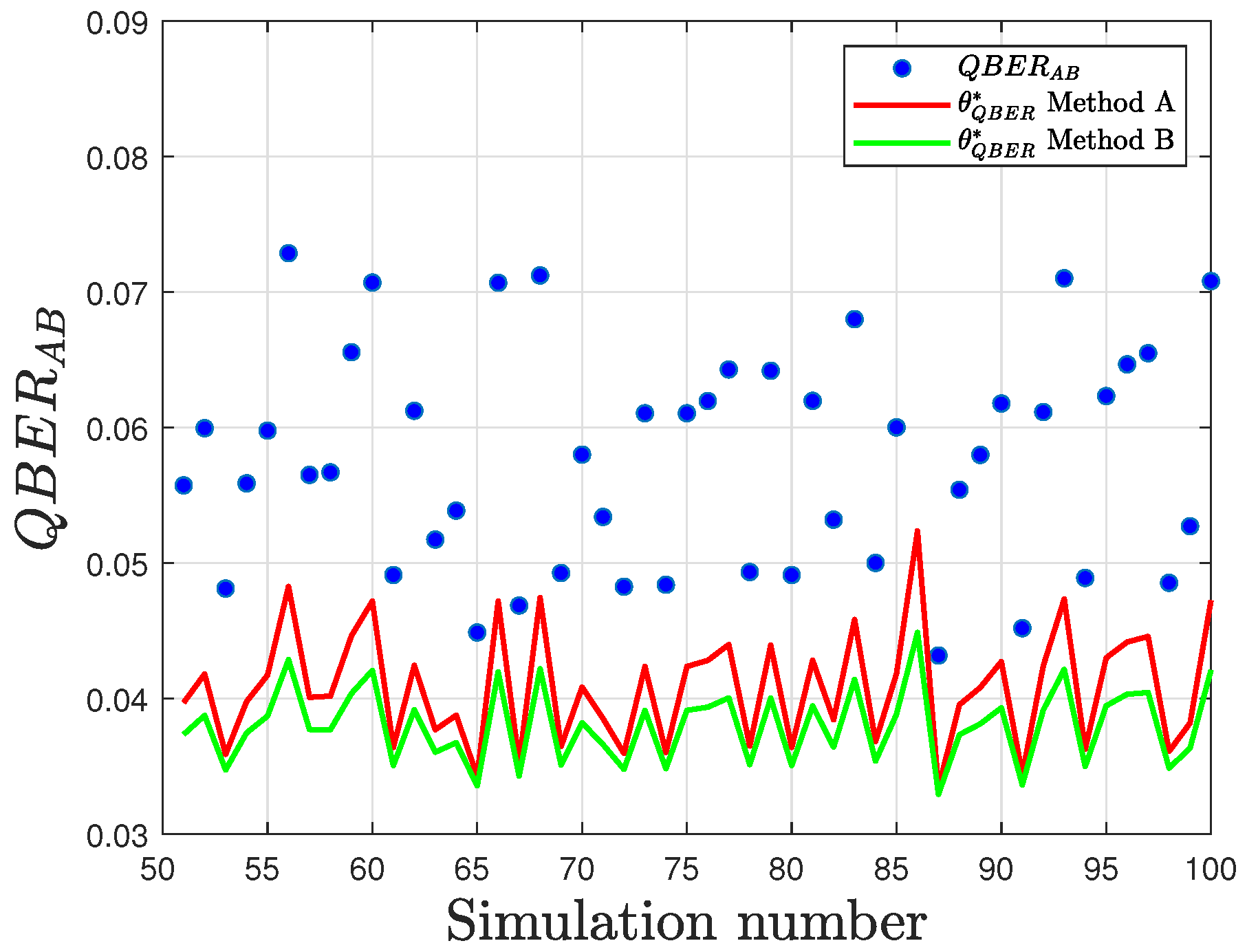
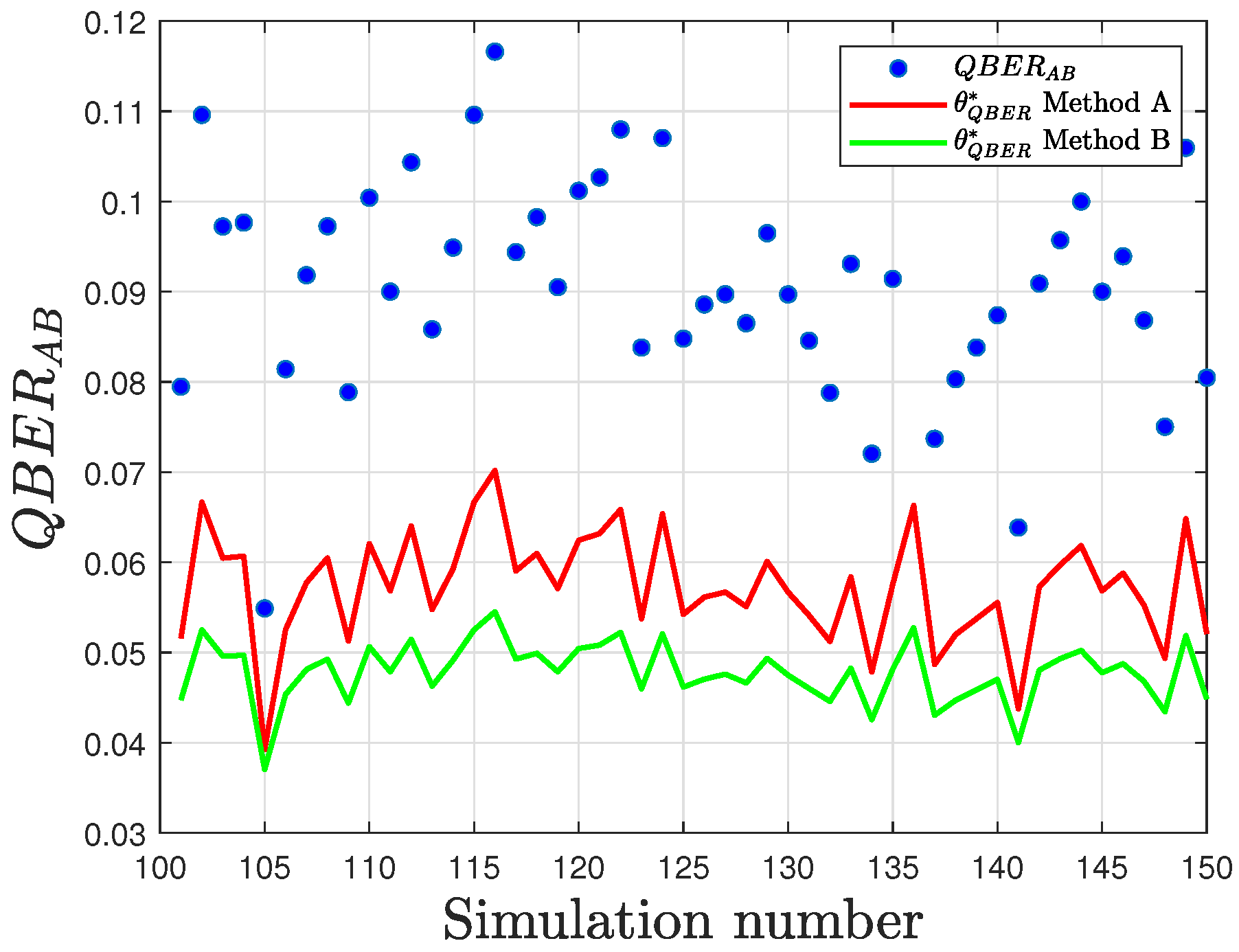
This phenomenon is evident in both the proposed detection methods, as demonstrated by the results in Figure 13 and Figure 14. For this analysis, the experimental results obtained using the fake_armonk backend simulator with a key length of $K=4096$ was considered. For each value of p (ranging from 0 to 1 in increments of $0.1$), the simulation was repeated 50 times. Thus, simulation runs 1–50 correspond to $p=0$, 51–100 to $p=0.1$, and so forth.

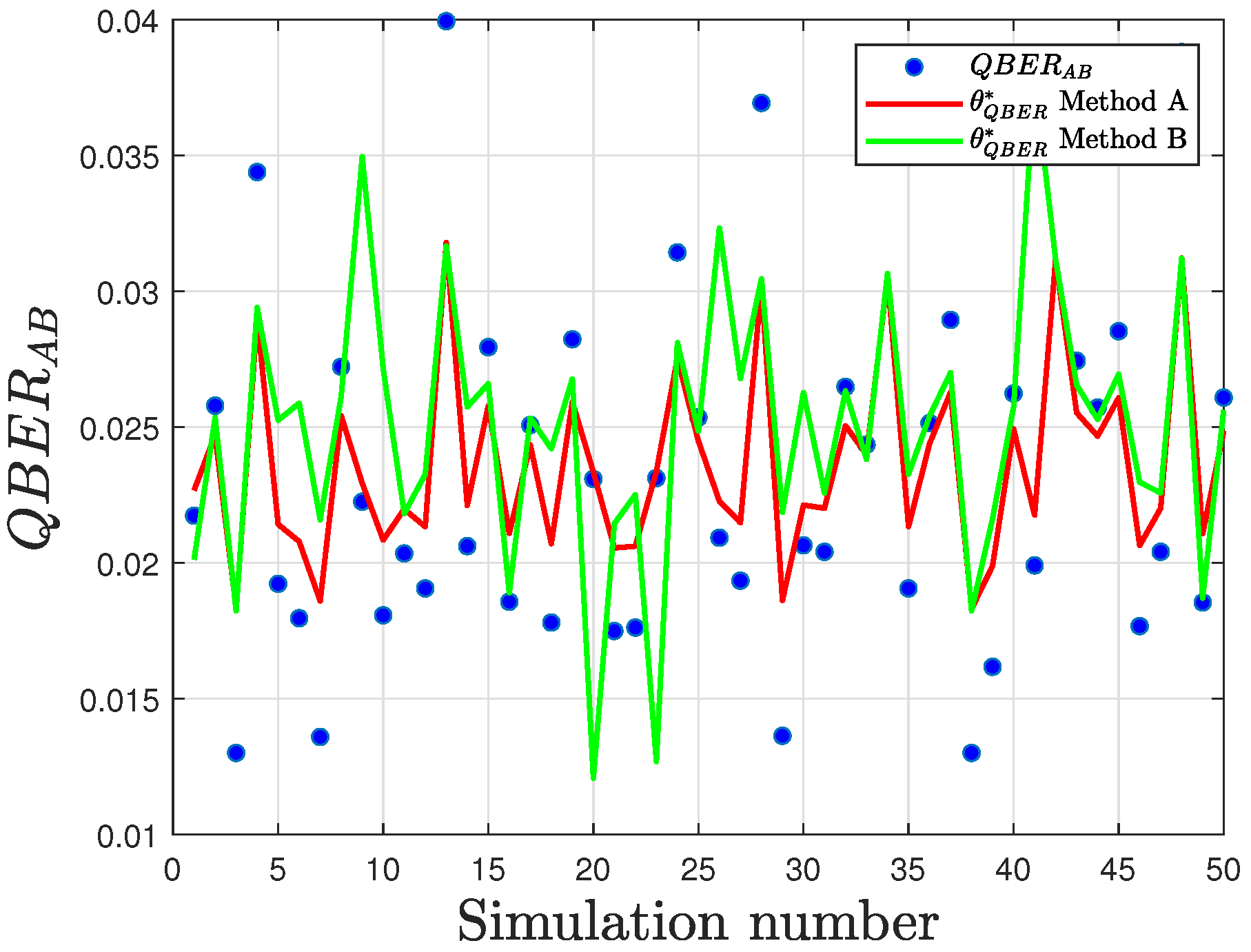
The quantitative analysis presented in

Table 7. Distance between $\widehat{QBE{R}_{AB}}$ and ${\theta }_{QBER}^{\ast }$.

p	Method A	Method B
0.1	0.0172	0.02
0.2	0.0336	0.0432
0.3	0.0488	0.0657
0.4	0.0671	0.0940
0.5	0.0814	0.1164
0.6	0.0980	0.1424
0.7	0.1137	0.1676
0.8	0.1317	0.1965
0.9	0.1456	0.2187
1	0.1628	0.2461

reports the measured distances between the sample QBER and the optimal threshold for both methods. Notably, method “B” consistently exhibits a larger separation, resulting in higher detection accuracy, particularly at greater values of interception density.

Table 8. Accuracy obtained from experimental results.

Backend	Accuracy Method A	Accuracy Method B
fake_amronk (K = 2048)	$95.64\%$	$96.00\%$
fake_amronk (K = 4096)	$96.00\%$	$95.82\%$
fake_casablanca (K = 2048)	$95.45\%$	$95.82\%$
fake_casablanca (K = 4096)	$94.55\%$	$96.00\%$
fake_quito (K = 2048)	$94.91\%$	$94.73\%$
fake_quito (K = 4096)	$95.09\%$	$94.75\%$
fake_rome (K = 2048)	$94.73\%$	$94.73\%$
fake_rome (K = 4096)	$95.27\%$	$95.45\%$
fake_tenerife (K = 2048)	$94.18\%$	$94.73\%$
fake_tenerife (K = 4096)	$94.00\%$	$94.91\%$

summarizes the results obtained obtained by the two considered methods for all the considered backends.

Across all the simulations, both the detection methods consistently achieve accuracies exceeding $90\%$. As anticipated, lower levels of system noise (${\mu }_{ch}$) correspond to higher detection accuracy. This trend underscores the importance of minimizing channel noise in practical QKD systems to maximize the reliability of eavesdropping detection.

A more detailed examination of the error distribution can be obtained by closely analyzing Figure 13 and Figure 14. By further inspecting Figure 15, Figure 16 and Figure 17, it becomes evident that as p increases, the separation between the sample quantum bit error rate ($QBE{R}_{AB}$) and the detection threshold also increases. This observation directly confirms the previously discussed relationship between p and detection performance.

Moreover, these figures validate the consistency between the theoretical analysis (as shown in Figure 12) and the experimental outcomes: the vast majority of detection errors are concentrated at low values of p, where the distinction between normal channel noise and eavesdropping-induced errors is less pronounced.

An additional noteworthy result is that for higher values of p, the difference between the thresholds determined by Method B increases. This divergence arises from Method A employs a static threshold, which does not adjust to sample variance and is thus less robust in scenarios with higher p or increased channel noise.

7.4. Final Remarks

The detailed comparative analysis of the two threshold-based detection methods highlights both their operational differences and the practical implications for QKD security.

Method B incorporates not only the expected value but also the variance in $\widehat{QBE{R}_{AB}}$ in the threshold calculation. The resulting threshold, ${\theta }_B^{\ast }$, thus adapts to the uncertainty inherent in the estimation process and can be expressed as:

$${\theta }_B^{\ast }={\mu }_{ch}+\alpha ·{\sigma }_{\widehat{QBE{R}_{AB}}},$$

(34)

where ${\sigma }_{\widehat{QBE{R}_{AB}}}$ is the standard deviation of the sample QBER and $\alpha$ is the design parameter determined by the desired balance between the FPR and FNR.

As shown in Table 7, the mean distance between the sample QBER and the threshold is consistently greater for Method B compared to Method A across all the tested values of p. This increased separation is particularly pronounced at higher values of p, where the presence of an eavesdropper introduces a significant shift in the mean QBER. By incorporating variance, Method B dynamically adjusts the threshold to maintain robust discrimination even as sample variability increases.

The experimental results across all the simulated scenarios confirm that Method B yields higher detection accuracy, especially for moderate to high interception densities. Method A, while simple and less computationally demanding, is more susceptible to errors when sample variability is high, as it lacks the ability to adapt to statistical fluctuations in the QBER. Conversely, Method B use of variance enables it to more effectively distinguish between normal channel noise and genuine eavesdropping events.

Both methods benefit from larger key lengths K, which reduce statistical uncertainty and thus improve estimation precision. However, the performance gap between the two methods widens at higher values of $e_{ch}$ (system noise) and p. In particular, Method B adaptive threshold offers superior performance under challenging conditions, as it is less prone to both false positives and false negatives.

In summary, the comparative analysis demonstrates that Method B consistently outperforms Method A in terms of both accuracy and robustness, especially in scenarios with high variability or elevated interception density. The findings support the adoption of variance-aware adaptive thresholds for secure and reliable eavesdropping detection in practical QKD systems.

8. Conclusions

This work has advanced the state of the art in eavesdropper detection for the Six-State QKD protocol by proposing, optimizing, and evaluating two threshold-based detection methods in the context of partial intercept–resend attacks with constant interception density. A rigorous system model was adopted, including an explicit and realistic characterization of system noise as independent Bernoulli bit-flip events, and the consequent impact on transmission fidelity was thoroughly analyzed.

The first part of this study focused on the statistical properties of the quantum bit error rate ($QBE{R}_{AB}$) and the estimation of the eavesdropper’s interception density p. By employing statistical estimators and variance analysis, we highlighted the critical dependence of estimation accuracy on key system parameters, notably key length and noise rate.

We then presented two detection strategies tailored to the Six-State protocol: a Hoeffding-based thresholding method and an analytically extended probabilistic approach. Both methods aim to minimize the sum of FPR and FNR, but differ fundamentally in their construction. Method B exploits the full probabilistic structure of the QBER estimator. Notably, this study represents the first extension and practical evaluation of these detection schemes in the Six-State context, encompassing realistic partial interception scenarios.

A key strength of this work lies in its comprehensive simulation campaign, implemented in Python using the Qiskit library and the Quantum Solver framework. This approach enabled testing on simulated backends modeled after real IBM quantum hardware, thereby capturing a range of practical noise conditions. The simulation results demonstrate that both detection methods are highly accurate across all the tested scenarios, with performance consistently exceeding $90\%$, and Method B exhibiting clear superiority in more challenging noise and attack regimes due to its variance-aware thresholding.

In summary, this research confirms the practical feasibility and robustness of advanced eavesdropper detection in Six-State QKD systems, bridging the gap between theoretical security analysis and real-world implementation. The paper also provides actionable guidance for selecting appropriate thresholding methods based on specific channel conditions. Future research may extend this framework to account for time-varying noise conditions and dynamic eavesdropping strategies through the development of adaptive threshold optimization techniques. Additionally, future work could involve collaborations with experimental groups and industry partners to facilitate real-world validation and practical deployment of the proposed methods.