A Three-Party Evolutionary Game Model and Stability Analysis for Network Defense Strategy Selection

Abstract

Traditional cyber attack-defense strategies have traditionally focused solely on the attacker and defender, while neglecting the role of government-led system administrators. To address strategic selection challenges in cyber warfare, this study employs an evolutionary game theory framework to construct a tripartite game model involving cyber attackers, defenders, and system administrators. The replicator dynamic equation is utilized for stability analysis of behavioral strategies across stakeholders, with Lyapunov theory applied to evaluate the equilibrium points of pure strategies within the system. MATLAB (2021a) simulations were conducted to validate theoretical findings. Experimental results demonstrate that the model achieves evolutionary stability under various scenarios, yielding optimal defense strategies that provide theoretical support for addressing cybersecurity challenges.

1. Introduction

As cyberspace continues to expand, information technology has been widely adopted across industries, effectively driving societal development in the information age. However, this advancement also brings severe security threats and challenges. The primary form of confrontation among cyberspace entities is cyber warfare. To minimize damage or further reduce losses, it is essential to implement scientifically sound and feasible defense strategies to enhance cybersecurity capabilities [1]. Therefore, applying game theory-based approaches to analyze cybersecurity and strengthening the construction of defensive technology systems hold significant practical importance. Traditional decision-making approaches typically assume a static decision environment where decision-makers independently make choices with minimal consideration for other participants’ reactions. This makes them ill-suited to dynamic environments and struggle to analyze information asymmetry in detail. Decision-makers often focus on optimizing single objectives without mechanisms to predict adversaries’ actions or assess the system’s equilibrium state. Game theory, however, can quantify the impact of strategies between attackers and defenders, enabling analysis and optimization of decision-making processes in uncertain, complex, and interdependent network environments. It helps predict attack behaviors, formulate corresponding defense strategies, and innovatively propose incentive mechanisms to guide specific participant behaviors. These contributions have significantly advanced cybersecurity fields such as network security situation assessment, cyber warfare confrontation, and information warfare.

However, existing studies focus primarily on the attacker–defender dyad, overlooking the critical influence of a third participant: the government-led system administrator. This omission constitutes a significant limitation, as it fails to capture the regulatory dimension that fundamentally shapes real-world cybersecurity ecosystems. The administrator, through mechanisms such as audits, penalties, and rewards, alters the cost–benefit structure for both attackers and defenders, thereby critically changing the game dynamics and resulting equilibria. This intervention breaks the self-reinforcing dynamics of the bilateral game and introduces a feedback and control loop, steering the system towards more desirable equilibria that are unattainable without regulatory oversight. A typical scenario is the protection of Critical Information Infrastructure (e.g., the power grid), where a national regulatory body mandates security standards, penalizes non-compliance, and incentivizes robust defense, thereby fundamentally reshaping the strategic landscape for both utility companies and potential attackers. Therefore, incorporating the regulator as a strategic player is essential for a more accurate and realistic representation of cybersecurity governance.

To bridge this gap, this study constructs a tripartite evolutionary game model incorporating attackers, defenders, and a system administrator. The main contributions of this work are threefold:

• We propose a novel theoretical framework that endogenizes the system administrator as a core decision-maker, moving beyond traditional bilateral models.
• We derive the replicator dynamics and employ Lyapunov stability theory to identify and analyze the Evolutionary Stable Strategies (ESSs) under various realistic conditions.
• We validate our theoretical findings through numerical simulations and translate the equilibrium results into actionable insights for cybersecurity policy and defense strategy selection.

The remainder of this paper is structured as follows: Section 2 reviews related work. Section 3 details the model formulation. Section 4 presents the stability analysis of equilibrium points. Section 5 discusses the simulation results. Finally, Section 6 concludes the study and suggests future research directions.

2. Related Work

Significant progress has been made in cybersecurity through game-theoretic modeling approaches. Specifically, ref. [2] developed a game-theoretic matching optimization model and proposed a distributed algorithm to find Nash equilibria in strategic interactions. The work in [3] proposes a Bayesian-game-driven, charging-guided co-defense framework to enhance the resilience of the coupled transportation–cyber–physical power system against attacks. The study also improved existing strategy evaluation methods by incorporating defender countermeasures and attack success rates. The work in [4] introduced an Adversarial Game Theory (ADGM) model that defines network security status through node density distribution across various security states. This approach analyzes transition paths of cybersecurity conditions, effectively mapping macro-level network dynamics from micro-level adversarial behaviors. The work in [5] developed a signal game model integrating active defense technology, solving and analyzing pure-strategy complete Bayesian Nash equilibrium. Ref. [6] combined qualitative differential analysis with evolutionary game theory to construct a cybersecurity threat dynamic game model featuring continuous attack–defense interactions and bounded rational decision-makers. The study derived the evolution trajectory of cybersecurity states and validated the feasibility of the dynamic threat assessment algorithm. Ref. [7] designs a Bayesian Stackelberg game to optimally allocate IoV security resources against advanced persistent threats. Ref [8] presents a complex-probability attack graph framework to quantify concurrent exploits and backtracking cycles for large-scale IoT risk assessment.

Traditional game theory (such as Nash equilibrium analysis) typically focuses on static equilibrium states, assuming that participants select optimal strategies once and for all within a given strategy space and remain unchanged in equilibrium. It fails to account for dynamic adjustments and adaptive changes in participants’ strategies, often assumes complete rationality, neglects learning processes and bounded rationality, emphasizes individual-level equilibrium while ignoring collective behavioral patterns and evolutionary trends, lacks stability and sustainability, and features singular, inflexible strategies. Evolutionary game theory, however, is premised on bounded rationality [9], allowing participants to dynamically evolve based on their specific capabilities and gains from offensive–defensive interactions to select optimal solutions. In the context of cyber warfare, ref. [10] designs an evolutionary-game-based proactive defense to predict and mitigate DoS attacks in islanded microgrid secondary control. Subsequently, ref. [11] builds a three-player evolutionary game to evolve stable strategies for dynamic array–honeypot defense beyond static traps. Ref. [12] proposes a global learning particle swarm optimization algorithm for calculating Nash equilibria and quantifying evolutionary game parameters. Ref. [13] establishes an evolutionary game decision model for cyber attack–defense based on RM algorithms, deriving optimal defense strategies through solving stable equilibrium points and describing evolutionary trajectories of two-sided optimal strategies. Ref. [14] develops an attack–defense evolutionary game model based on network topology learning mechanisms and designs defense strategy selection algorithms. Through research on wireless sensor networks, ref. [15] systematically reviews multiple game-theoretic defense studies, classifying by warfare type, game class, and player structure, and identifies gaps.

To provide a clearer delineation between existing studies and the proposed work, a systematic comparison of related game-theoretic cybersecurity models is presented in

Table 1. Comparison of related work on game-theoretic cybersecurity models.

Reference	Players	Game Theory Type	Dyn/ Evol	Regulator	Key Findings/ Focus
Yang et al. [3]	Attacker, Defender	Static Bayesian Game	No	No	Security defense of coupled transportation and cyber–physical power system.
Halabi et al. [7]	Attacker, Defender	Bayesian Stackelberg Game	No	No	Optimal resource allocation against advanced persistent threats in IoV.
Zhang et al. [10]	Attacker, Defender	Evolutionary Game Theory	Yes	No	Evolutionary strategy for DoS attack in islanded microgrid.
Shi et al. [11]	Attacker, Defender	Evolutionary Game Theory	Yes	No	Optimization of array honeypot defense strategies.
Jin et al. [13]	Attacker, Defender	Evolutionary Game Theory (Regret Minimization)	Yes	No	Network attack–defense decision-making based on regret minimization.
Tosh et al. [9]	Attacker, Defender, Info Exchange Center	Evolutionary Game Theory	Yes	Yes (diff. role)	Establishing evolutionary game models for cybersecurity information exchange.
Our Work	Attacker, Defender, System Admin	Evolutionary Game Theory	Yes	Yes (Core)	Analyzes tripartite stable strategies under regulation, providing quantitative basis for cybersecurity policy.

. The table compares key aspects, including the players involved, the game theory type, dynamic nature, and consideration of a regulator. It clearly shows that most existing research is confined to an attacker–defender dyad and generally overlooks the role of an active regulatory third party. Even when a third party is considered, its role typically differs from the system administrator with enforcement power investigated in this study. This comparison highlights a gap in the literature and provides a clear justification for the necessity of our work.

3. Methodology

3.1. Basic Concepts

Evolutionary game theory originated from biological evolution theory [16], among which the learning mechanism with replication dynamics as the core is most widely used. Under the condition of bounded rationality, this paper constructs an evolutionary game model of attack, defense, and user in network attack and defense based on evolutionary game theory.

Definition 1.

The three-way evolutionary game model of network attack and defense can be expressed as a four-tuple $(N,S,\theta ,U)$.

(1) $N=(N_A,N_D,N_M)$ represents the set of three participants in network attack and defense. Here, $N_A$ represents the network attacker, $N_D$ represents the network defender, and $N_M$ represents the system manager.

(2) $S=(S_A,S_D,S_M)$ represents the set of strategy spaces for the evolution game of three-party attack and defense, where $S_A=\{S_{A1},S_{A2},\dots ,S_{Am}\}$ is the strategy set of network attacker; $S_D=\{S_{D1},S_{D2},\dots ,S_{Dn}\}$ is the strategy set of network defender; $S_M=\{S_1,S_2,\dots ,S_h\}$ is the strategy set of system manager. $m,n,h$ respectively represent the number of strategies of attacker, defender, and system manager; $m,n,h\le 2$ and are all positive integers.

(3) The $\theta =(P_A,P_D,P_M)$ belief set for the evolution game of attack, defense, and tripartite $S_{Ai}$$S_A$$x_i$. Here, $P_A=(x_1,x_2,\dots ,x_m)$ represents the probability distribution of the attacker’s strategy $S_A$ set; $\forall x_i\in P_A$ represents the probability $x_i$ that the attacker chooses to adopt an attack strategy $S_{Ai}$; $P_D=\left(y_1,y_2,\dots ,y_n\right)$ represents the probability distribution of the defender’s strategy $S_D$ set; and $P_M=\left(z_1,z_2,\dots ,z_h\right)$ represents the probability distribution of the system manager’s strategy $S_M$ set. ${\displaystyle \sum _{i=1}^m}{x}_i=1,{\displaystyle \sum _{j=1}^n}{y}_j=1,{\displaystyle \sum _{k=1}^h}{z}_k=1(i\in \left[1,m\right],j\in \left[1,n\right],k\in \left[1,h\right])$

(4) $U=(U_A,U_D,U_M)$ is the set of payoff functions of the three-party evolutionary game model, which represents the game payoff of each participant. $U_A,U_D,U_M$ respectively represent the payoff function obtained by network attackers, network defenders, and system managers when choosing strategy $(S_{Ai},S_{Dj},S_{Mk})$ sets.

Definition 2.

The payoff matrix of the three-party evolution game of network attack and defense consists of the benefits obtained by the three parties under the three-party strategy , and there are $\left(m\times n\times h\right)$ elements in the matrix.

(1) Use $R_A$,$R_D$,$R_M$ respectively represent the total revenue of the implementation actions of network attackers, network defenders, and system managers, and use $C_A$,$C_D$,$C_M$ respectively represent the costs of network attackers, network defenders, and system managers.

(2) Use $a_{ijk}$,$b_{ijk}$, $c_{ijk}$ respectively represent the net benefits of network attackers, network defenders, and system managers, which are shown as follows:

 $a_{ijk}=U_A(S_{Ai},S_{Dj},S_{Mk})=R_A-C_A$    $b_{ijk}=U_D(S_{Ai},S_{Dj},S_{Mk})=R_D-C_D$    $c_{ijk}=U_M(S_{Ai},S_{Dj},S_{Mk})=R_M-C_M$

(3) $M=(M_A,M_D,M_M)$ represents a set of three-party benefit matrices for network attack and defense, where $M_A$ represents the benefit matrix of network attackers, $M_D$ represents the benefit matrix of network defenders, and $M_M$ represents the benefit matrix of system managers. Based on the above theory, the benefit matrices of the three parties are shown as follows:

$$M_A=\left(\begin{array}{ccc}{a}_{111}& \cdots & a_{1n1}\\ ⋮& \ddots & ⋮\\ a_{m11}& \cdots & a_{mn1}\end{array}\right)\left(\begin{array}{ccc}{a}_{112}& \cdots & a_{1n2}\\ ⋮& \ddots & ⋮\\ a_{m12}& \cdots & a_{mn2}\end{array}\right)\cdots \left(\begin{array}{ccc}{a}_{11h}& \cdots & a_{1nh}\\ ⋮& \ddots & ⋮\\ a_{m1h}& \cdots & a_{mnh}\end{array}\right)$$

$$M_D=\left(\begin{array}{ccc}{b}_{111}& \cdots & b_{1n1}\\ ⋮& \ddots & ⋮\\ b_{m11}& \cdots & b_{mn1}\end{array}\right)\left(\begin{array}{ccc}{b}_{112}& \cdots & b_{1n2}\\ ⋮& \ddots & ⋮\\ b_{m12}& \cdots & b_{mn2}\end{array}\right)\cdots \left(\begin{array}{ccc}{b}_{11h}& \cdots & b_{1nh}\\ ⋮& \ddots & ⋮\\ b_{m1h}& \cdots & b_{mnh}\end{array}\right)$$

$$M_M=\left(\begin{array}{ccc}{c}_{111}& \cdots & c_{1n1}\\ ⋮& \ddots & ⋮\\ c_{m11}& \cdots & c_{mn1}\end{array}\right)\left(\begin{array}{ccc}{c}_{112}& \cdots & c_{1n2}\\ ⋮& \ddots & ⋮\\ c_{m12}& \cdots & c_{mn2}\end{array}\right)\cdots \left(\begin{array}{ccc}{c}_{11h}& \cdots & c_{1nh}\\ ⋮& \ddots & ⋮\\ c_{m1h}& \cdots & c_{mnh}\end{array}\right)$$

In cyber warfare scenarios, attackers, defenders, and system administrators employ distinct strategies. Through strategic imitation of competitive tactics and adaptive adjustments driven by mutual interests, the confrontation evolves into a dynamic process. To clarify the quantified benefits of each stakeholder in this tripartite framework, we integrate and visualize the attack payoff matrix, defense payoff matrix, and management payoff matrix using game theory diagrams, as illustrated in Figure 1. Each terminal node of the game tree is associated with a payoff vector $(a_{ijk},b_{ijk},c_{ijk})$, where $a_{ijk},b_{ijk}$, and $c_{ijk}$ represent the payoffs for the attacker, defender, and administrator, respectively, under the corresponding strategy combination $(S_{Ai},S_{Dj},S_{Mk})$. For instance, the vector $(a_{111},b_{111},c_{111})$ denotes the payoffs for all parties when the attacker chooses strategy 1, the defender chooses strategy 1, and the administrator chooses strategy 1.

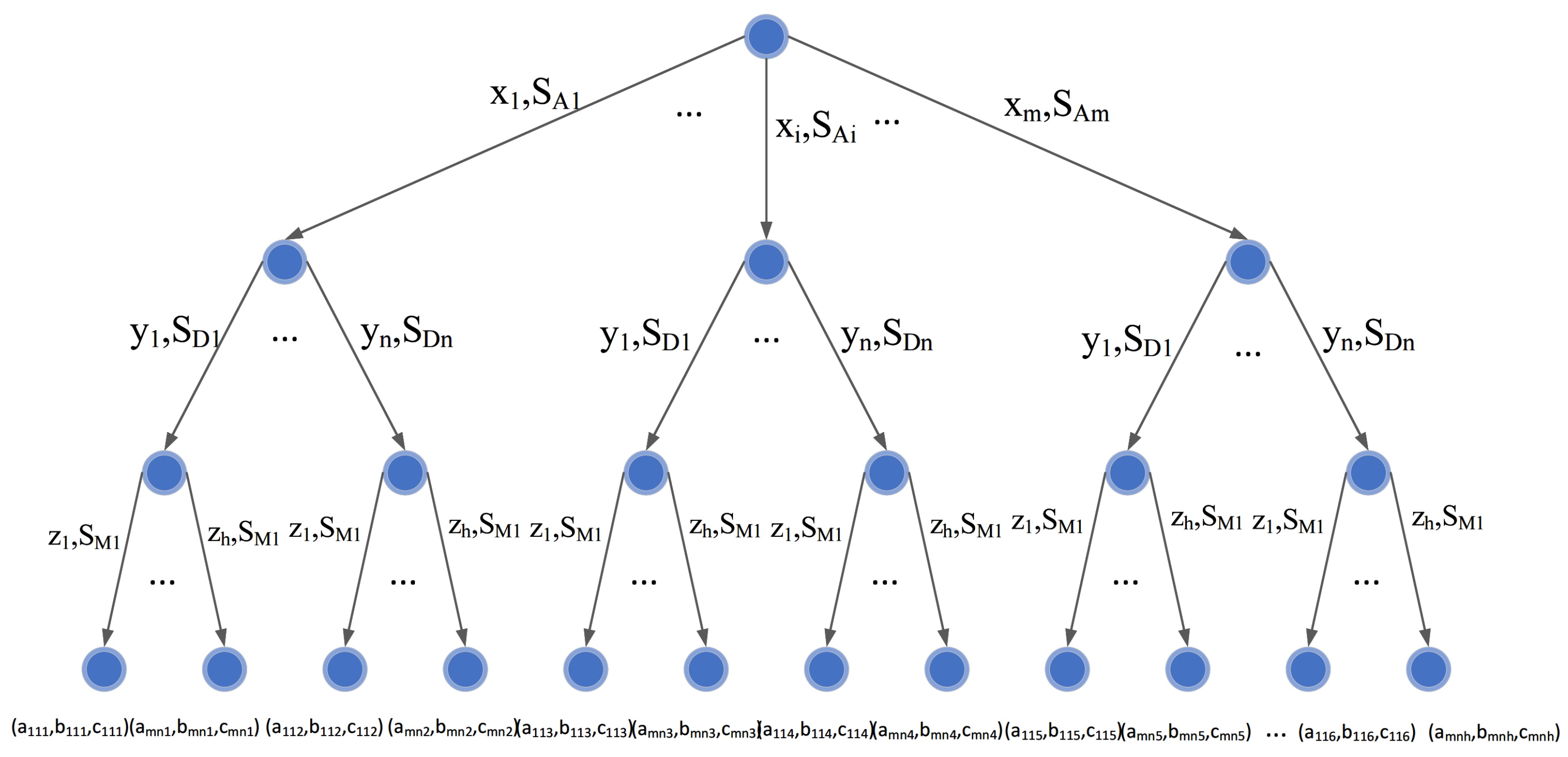
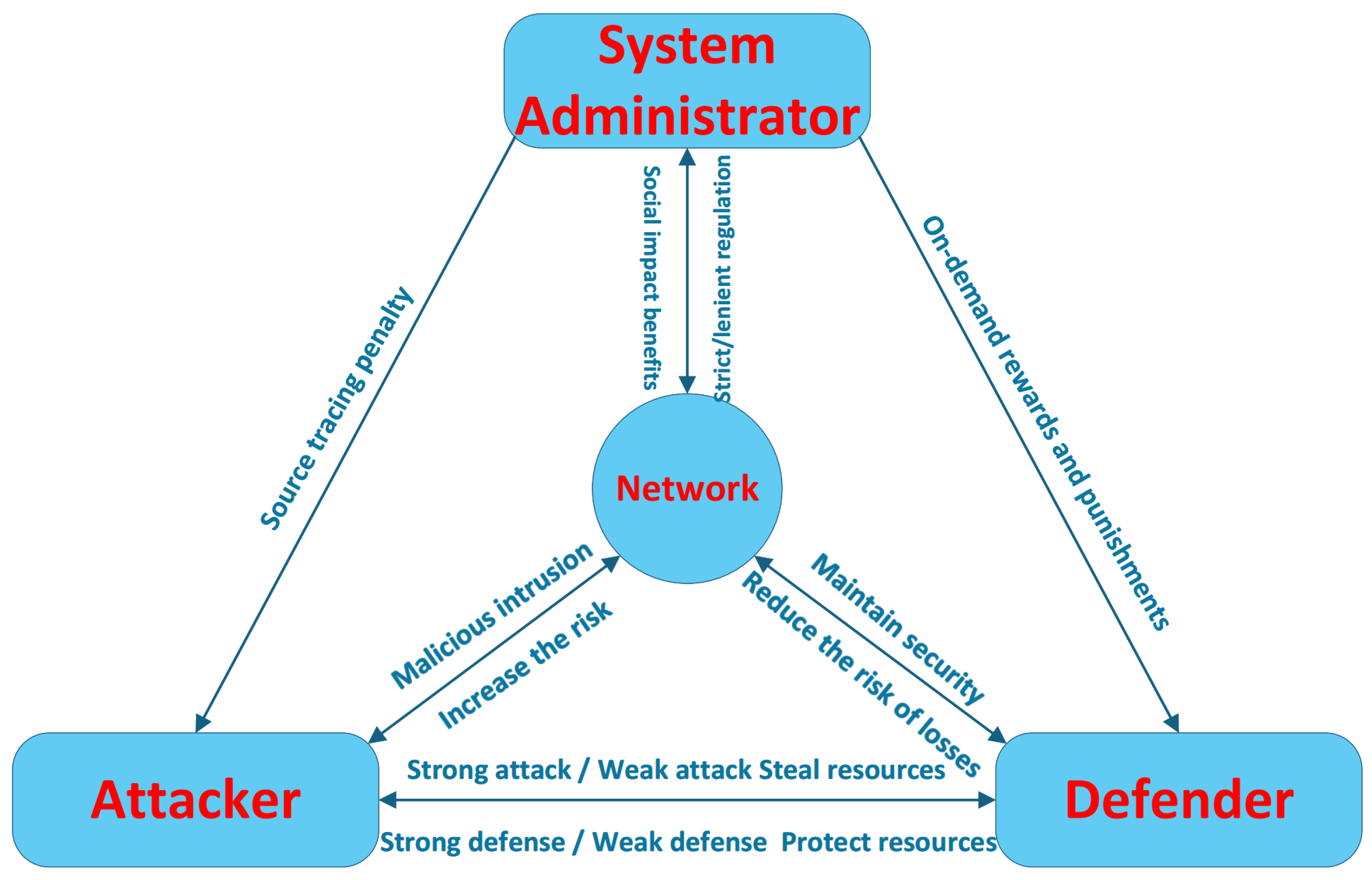
3.2. Tripartite Evolution Game Model

The network defense strategy constructed in this paper selects the logical relationship between the three parties of evolutionary game subjects as shown in Figure 2:

Assuming the three parties have distinct strategy sets: (1) $S_A=\{S_{A1},S_{A2}\}$ Strong Attack $S_{A1}$ vs. Weak Attack $S_{A2}$, (2) $S_D=\{S_{D1},S_{D2}\}$ Strong Defense $S_{D1}$ vs. Weak Defense $S_{D2}$, (3) $S_{\mathrm{M}}=\{S_{M1},S_{M2}\}$ Strict $S_{M1}$ vs. Lenient Regulation $S_{M2}$. Strong Attack denotes sophisticated, resource-intensive offensive actions (e.g., Advanced Persistent Threats), modeled by a substantial cost $C_1$. Weak Attack refers to simple, low-effort opportunistic attacks, whose cost is assumed to be negligible. Strong Defense represents the deployment of proactive and advanced security measures (e.g., threat intelligence platforms and automated incident response systems), incurring a cost $C_2$. Weak Defense implies relying only on basic, foundational security controls (e.g., conventional firewalls, basic patch management), with assumed negligible cost but resulting in reduced defense effectiveness. Strict supervision means the administrator enforces high-intensity oversight, including mandatory audits, forensic investigation, and the imposition of rewards/penalties, at a cost $C_3$. Loose Regulation describes a basic, reactive supervisory approach, with assumed negligible cost. V represents the value of defensive resources, E $(E>V)$ represents the fixed returns generated by these defenses. When attackers employ strong strategies, defenders adopt weak defenses and administrators implement lenient regulation, resulting in continuous ransomware intrusions causing losses L (L increasing with V). During network attacks, strict regulation administrators conduct traceability investigations and impose penalties $P_1$ on attackers. If defenders adopt strong defense strategies, they receive administrative rewards $R_D$; otherwise, penalties $P_2$ apply. Implementing strong defense strategies yields positive benefits $R_S$ for system administrators, whereas adopting weak defenses under lenient regulation leads to negative outcomes $P_3$ $(P_3>C_3)$.

When attackers employ strong attacks with defenders implementing robust defenses, or when attackers use weak attacks with defenders adopting inadequate defenses, the probability of successful cyberattacks remains constant ∂. Specifically, (1) when attackers launch strong attacks against defenders using weak defenses, the success rate of cyberattacks equals $\beta$ $(\beta >2\alpha )$. (2) When attackers employ weak attacks against defenders with strong defenses, the probability of successful cyberattacks becomes negligible.

Based on the above assumptions, the payoff matrix of a mixed strategy game between network attackers, network defenders, and system managers is shown in

Table 2. Setting of relevant parameters of the three parties in the game model.

Main Body	Parameter	Meaning
Cyber attackers	x	The probability of choosing a strong attack strategy
	$C_1$	The cost of choosing a strong attack strategy
Cyber defenders	y	The probability of choosing a strong defense strategy
	$C_2$	The cost of choosing a strong defense strategy
	V	Value of owned data assets
	E	Resources provide a fixed benefit to the defensive side
	L	The loss incurred when a resource attack is successful
System Administrator	z	Choose the probability of strict supervision
	$C_3$	Choose the cost of strict regulation
	$P_1$	Strictly regulate the punishment of cyber attackers
	$R_D$	Strict regulation and strong defense strategies reward the defender
	$P_2$	Strict regulation and lax regulation are the punishment for defenders
	$R_S$	The positive benefits of strong defense for system managers
	$P_3$	Weak defense brings negative benefits to system managers
	$\alpha$	The probability of success of a network attacker when the network defender takes strong defense measures, and the network attacker carries out weak attack while the network defender takes weak defense
	$\beta$	The probability of success of a network attacker when the network attacker adopts a strong attack and the network defender adopts a weak defense

.

Based on the above benefit matrix, we can obtain the expected benefit matrix and average benefit matrix under different strategy combinations of the three parties. Among them, the benefit of strong attack strategy of network attackers is $E_{A1}$, the benefit of weak attack is $E_{A2}$, and the average benefit of selected strategies is $\overline{E_A}$:

$$\left\{\begin{array}{c}{E}_{A1}=yz\left(\alpha V-C_1-P_1\right)+y\left(1-z\right)\left(\alpha V-C_1\right)+\hfill \\ \left(1-y\right)z\left(\beta V-C_1-P_1\right)+\left(1-y\right)\left(1-z\right)\left(\beta V-C_1\right)\hfill \\ =L-C_1+Vb-Ly-Lz-p_{1}z+V\alpha y-V\beta y+Ly\hfill \\ E_{A2}=yz(-P_1)+y(1-z)\times 0+(1-y)z(\alpha V-P_1)+\hfill \\ (1-y)(1-z)\left(\alpha V\right)\hfill \\ =V\alpha -P_{1}z-V\alpha y\hfill \\ \overline{E_A}=x{E}_{A1}+(1+x)E_{A2}\hfill \end{array}\right.$$

(1)

The benefits of the strong defense strategy for network defenders are $E_{D1}$, and the benefits of the weak defense strategy are $E_{D2}$. The average benefits of the selected strategies are $\overline{E_D}$:

$$\left\{\begin{array}{c}{E}_{D1}=xz(E-\alpha V-C_2+R_D)+x(1-z)(E-\alpha V-C_2)+\hfill \\ (1+x)z(E-C_2+R_D)+(1-x)(1-z)(E-C_2)\hfill \\ =E-C_2+R_{D}z-V\alpha x\hfill \\ E_{D2}=xz(E-\beta V-P_2)+x(1-z)(E-\beta V-L)+\hfill \\ (1-x)z(E-\alpha V-P_2)+x(1-z)(E-C_2)\hfill \\ =E-V\alpha -Lx-P_{2}z+V\alpha x-V\beta x+Lxz\hfill \\ \overline{E_D}=y{E}_{D1}+(1-y)E_{D2}\hfill \end{array}\right.$$

(2)

The returns of the system regulator’s strict supervision strategy are $E_{S1}$, the returns of the loose supervision strategy are $E_{S2}$, and the average returns of the selected strategies are $\overline{E_S}$:

$$\left\{\begin{array}{c}{E}_{S1}=xy(P_1-R_D-C_3+R_S)+x(1-y)(P_1+P_2-C_3)+\hfill \\ (1-x)y(P_1-R_D-C_3)+(1-x)(1-y)(P_1+P_2-C_3)\hfill \\ =P_1-C_3+P_2-P_{2}y-R_{D}y+R_{S}xy\hfill \\ E_{S2}=-P_{3}xy-P_{3}x(1-y)-P_3(1-x)y-P_3(1-x)(1-y)\hfill \\ =-P_3\hfill \\ \overline{E_S}=z{E}_{S1}+(1-z)E_{S2}\hfill \end{array}\right.$$

(3)

3.3. Analysis of Three-Way Evolution Path

3.3.1. Analysis of Network Attacker Strategy Evolution Path

According to Equation (1), the dynamic equation of attack replication and its first partial derivative can be obtained as follows:

$$\left\{\begin{array}{c}F\left(x\right)={\displaystyle \frac{dx}{dt}}=x(E_{A1}-\overline{E_A})\hfill \\ =x(x-1)(C_1-L+V\alpha -V\beta +Ly+Lz-2V\alpha y+V\beta y-Lyz)\hfill \\ {\displaystyle \frac{\mathrm{d}\left(\mathrm{F}\left(\mathrm{x}\right)\right)}{\mathrm{dx}}}=(2x-1)(C_1-L+V\alpha -V\beta +Ly+Lz-2V\alpha y+V\beta y-Lyz)\hfill \end{array}\right.$$

If $G\left(y\right)=C_1-L+V\alpha -V\beta +Ly+Lz-2V\alpha y+V\beta y-Lyz$. According to the stability theorem of differential equations, if a cyber attacker chooses to launch a strong attack, they must satisfy the following conditions to maintain stability: $F\left(x\right)=0$ and $d\left(F\right(x\left)\right)/dx<0$. Since $\partial G\left(y\right)/\partial y>0$ is an increasing function of y, we have that when $y=-(C_1-L+V\alpha -V\beta +Lz)/(L-2V\alpha +V\beta -Lz)=y^{*}$, $G\left(y\right)=0$, $d\left(F\right(x\left)\right)/dx\equiv 0$ and thus the attacker cannot determine a stable strategy; when $y<y^{*}$, $G\left(y\right)>0$, $d\left(F\left(x\right)\right)/dx{|}_{x=0}>0$ and $x=1$ becomes the attacker’s evolutionary stable strategy; conversely, when $x=0$, it represents the Evolutionarily Stable State (ESS). The phase diagram of the attacker’s strategy evolution is shown in Figure 3.

The volume in the figure $A_1$ is $V_{A1}$, where is the probability that the attacker chooses a strong attack, and the $A_2$ volume is $V_{A2}$, where is the probability that the attacker chooses a weak attack. Calculations can be obtained as follows:

$$\left\{\begin{array}{c}{V}_{A1}=\int {\int }_0^1(-{\displaystyle \frac{C_1-L+V\alpha -V\beta +Lz}{L-2V\alpha +V\beta -Lz}}dzdx)\hfill \\ ={\displaystyle \frac{L}{2}}-C_1-3L{\alpha }^2+2V{\beta }^2-{\displaystyle \frac{1}{2}}\hfill \\ V_{A2}=1-V_{A1}\hfill \end{array}\right.$$

According to the $V_{A1}$ expression of the probability that network attackers adopt strong attack strategy, the first-order partial derivatives of each element are obtained: $\partial V_{A1}/\partial L>0$, $\partial V_{A1}/\partial \beta >0$, $\partial V_{A1}/\partial V>0$, $\partial V_{A1}/\partial C_1<0$, $\partial V_{A1}/\partial \alpha <0$. It is also found that the probability of adopting strong attack is positively correlated with $L,\beta ,V$ and negatively correlated with $C_1,\alpha$.

When the attacker is analyzed for strategic stability, $x=1$ is an evolutionally stable strategy when $z<-(C_1-L+V\alpha -V\beta +Ly-2V\alpha y+V\beta y)/(L-Ly),y<y^{*}$. As $y,z$ gradually increased, the attacker’s stable strategy gradually changed from $x=1$ (taking a strong attack strategy) to $x=0$ (taking a weak attack strategy).

3.3.2. Analysis of Evolution Path of Network Defender Strategy

According to Equation (2), the dynamic equation of attack replication and its first partial derivative are obtained as follows:

$$\left\{\begin{array}{c}F\left(y\right)={\displaystyle \frac{dy}{dt}}=y(E_{D1}-\overline{E_D})\hfill \\ =y(y-1)(-V\alpha +C_2-Lx-P_{2}z-R_{D}z+2V\alpha x-V\beta x+Lxz)\hfill \\ {\displaystyle \frac{d\left(F\right(y\left)\right)}{dy}}=2(2y-1)(-V\alpha +C_2-Lx-P_{2}z-R_{D}z+2V\alpha x-V\beta x+Lxz)\hfill \end{array}\right.$$

If $J\left(z\right)=-V\alpha +C_2-Lx-P_{2}z-R_{D}z+2V\alpha x-V\beta x+Lxz$. According to the stability theorem of differential equations, if a network defender chooses to implement $F\left(y\right)=0$ strong $y=0$ defense, $y=1$ they must satisfy the following conditions to maintain stability: $F\left(y\right)=0$ and $d\left(F\right(y\left)\right)/dy<0$. Since $\partial J\left(z\right)/\partial z<0$ is a decreasing function of z, we have that when $z=-(V\alpha -C_2+(L-2V\alpha +V\beta )x)/(P_2+R_D-Lx)=z^{*}$, $J\left(z\right)=0$, $d\left(F\right(y\left)\right)/dy\equiv 0$, indicating the defender cannot determine a stable strategy; when $z<z^{*}$, $J\left(z\right)>0,d\left(F\left(y\right)\right)/dy{|}_{y=0}<0$, in which $y=0$ becomes the defender’s final stable strategy; conversely, when $y=1$, it represents an Equilibrium Stable State (ESS). The phase diagram of the defender’s strategy evolution is shown in Figure 4.

In the figure, the volume is $V_{B1}$, the probability of the defender choosing strong defense is $B_1$, and the volume is $V_{B2}$, the probability of the defender choosing weak defense is $B_2$. Calculations can be obtained as follows:

$$\left\{\begin{array}{c}{V}_{B2}=\int {\int }_0^1({\displaystyle \frac{V(\alpha -2\alpha x+Lx)+V\beta x-C_2}{(-P_2-R_D+Lx)dxdy}})\hfill \\ ={\displaystyle \frac{L}{2^2}}-2R_D+{\displaystyle \frac{2LV}{2^2}}+{\displaystyle \frac{2V\beta }{2^2}}+{\displaystyle \frac{C_2}{P_2}}\hfill \\ V_{B1}=1-V_{B2}=1-{\displaystyle \frac{L}{2}}+R_D-{\displaystyle \frac{LV}{2}}-{\displaystyle \frac{V\beta }{2}}-{\displaystyle \frac{C_2}{P_2}}\hfill \end{array}\right.$$

According to the $V_{B1}$ expression of the probability $V_{B1}$ of network defenders adopting strong defense strategy, the first-order partial derivatives of each element are obtained as $\partial V_{B1}/\partial R_D>0$, $\partial V_{B1}/\partial P_2>0$, $\partial V_{B1}/\partial C_2<0$, $\partial V_{B1}/\partial \beta <0$, $\partial V_{B1}/\partial L<0$, and $\partial V_{B1}/\partial V<0$. Therefore, the probability of adopting strong defense is positively correlated with $R_D,P_2$ and negatively correlated with $C_2,\beta ,L,V$.

When the defender is analyzed for strategic stability, $y=0$ is an evolutionally stable strategy when $x<(V\alpha -C_2+P_{2}z+R_{D}z)/(2V\alpha -V\beta -L+Lz)$, $z<z^{*}$. As $x,z$ gradually increases, the defender’s stable strategy changes from $y=0$ (taking a weak defense strategy) to $y=1$ (taking a strong defense strategy).

3.3.3. Analysis of Evolution Path of System Manager Strategy

According to Equation (2), the dynamic equation of attack replication and its first partial derivative are obtained as follows:

$$\left\{\begin{array}{c}F\left(z\right)={\displaystyle \frac{dz}{dt}}=z(E_{S1}-\overline{E_S})\hfill \\ =z(z-1)(-P_1+C_3-P_2-P_3+P_{2}y+R_{D}y-R_{S}xy)\hfill \\ {\displaystyle \frac{d\left(F\right(z\left)\right)}{dz}}=(2z-1)(-P_1+C_3-P_2-P_3+P_{2}y+R_{D}y-R_{S}xy)\hfill \end{array}\right.$$

if $H\left(x\right)=-P_1+C_3-P_2-P_3+P_{2}y+R_{D}y-R_{S}xy$. According to the stability theorem of differential equations, if a system manager adopts a strict supervision strategy x, the system must satisfy the following conditions to maintain stability: $H\left(x\right)=0$ and

$$d\left(F\right(z\left)\right)/dz<0.$$

Since $\partial H\left(x\right)/\partial x<0$ is a decreasing function of x, we have that when

$$x=(-P_1+C_3-P_2-P_3+P_{2}y+R_{D}y)/\left(R_{S}y\right)=x^{*},$$

 $H\left(x\right)=0$, $d\left(F\right(z\left)\right)/dz\equiv 0$ and the system manager cannot determine a stable strategy; when $x<x^{*}$, $H\left(x\right)>0,d\left(F\left(z\right)\right)/dz{|}_{z=0}<0$, $z=0$ becomes the final stable strategy for the system manager; conversely, when $z=1$, it reaches ESS. The phase diagram of the system manager’s strategy evolution is shown in Figure 5:

The volume $V_{S1}$ in the $S_1$ figure is, where is the probability that the system administrator chooses strong defense, and the volume $V_{S2}$ of is $S_2$, where is the probability that the system administrator chooses weak defense. Calculations can be obtained as follows:

$$\left\{\begin{array}{c}{V}_{S2}=\int {\int }_0^1{\displaystyle \frac{-P_1+C_3-P_2-P_3+P_{2}y+R_{D}y}{R_{S}y}}dydz\hfill \\ =C_3-P_1-{\displaystyle \frac{P_2}{2}}-P_3+{\displaystyle \frac{R_D}{3R_S}}\hfill \\ V_{S1}=1-V_{S2}=1-C_3+P_1+{\displaystyle \frac{P_2}{2}}+P_3-{\displaystyle \frac{R_D}{3R_S}}\hfill \end{array}\right.$$

According to the $V_{S1}$ expression of the probability of system managers adopting strict supervision strategies, the first-order partial derivatives of each element are obtained as $\partial V_{S1}/\partial P_1>0$, $\partial V_{S1}/\partial P_2>0$, $\partial V_{S1}/\partial P_3>0$, $\partial V_{S1}/\partial R_S>0$, $\partial V_{S1}/\partial C_3<0$, $\partial V_{S1}/\partial R_D<0$. The probability of adopting strict supervision is positively correlated with $P_1,P_2,P_3,R_S$ and negatively correlated with $C_3,R_D$. When the system manager conducts a stability analysis of strategies, when

$$y=(P_1-C_3+P_2+P_3)/(P_2+R_D-R_{S}x)=y^{*}$$

and $x>x^{*}$, $H\left(x\right)<0,d\left(F\left(z\right)\right)/dz{|}_{z=0}<0$ , $z=1$ is considered an evolutionary stable strategy; when $y>y^{*}$ and $x<x^{*}$,$H\left(x\right)>0,d\left(F\left(z\right)\right)/dz{|}_{z=0}<0$, $z=0$ becomes a final stable strategy. Therefore, as x increases and y decreases, the system manager’s strategy gradually shifts from $z=0$ (loose regulation) to $z=1$ (strict regulation).

4. Model Solution and Analysis

4.1. Solving the Three-Party Evolutionary Game Model

According to Lyapunov stability theory, the equilibrium point of the system $K_1=(0,0,0)$, $K_2=(1,0,0),K_3=(0,1,0),K_4=(0,0,1)$, $K_5=(1,1,0),K_6=(1,0,1)$, $K_7=(0,1,1),K_8=(1,1,1)$ can be calculated with $F\left(x\right)=0, F\left(y\right)=0, F\left(z\right)=0$. The Jacobian matrix of the three-party evolutionary game is as follows:

$$\begin{array}{l}\mathrm{E}=\left[\begin{array}{ccc}{E}_1& E_2& E_3\\ E_4& E_5& E_6\\ E_7& E_8& E_9\end{array}\right]=\left[\begin{array}{ccc}{\displaystyle \frac{\partial F\left(x\right)}{\partial x}}& {\displaystyle \frac{\partial F\left(x\right)}{\partial y}}& {\displaystyle \frac{\partial F\left(x\right)}{\partial z}}\\ {\displaystyle \frac{\partial F\left(y\right)}{\partial x}}& {\displaystyle \frac{\partial F\left(y\right)}{\partial y}}& {\displaystyle \frac{\partial F\left(y\right)}{\partial z}}\\ {\displaystyle \frac{\partial F\left(z\right)}{\partial x}}& {\displaystyle \frac{\partial F\left(z\right)}{\partial y}}& {\displaystyle \frac{\partial F\left(z\right)}{\partial z}}\end{array}\right]=\\ \left[\begin{array}{cc}(2x-1)(C_1-L+V\alpha -V\beta +Ly& \\ +Lz-2V\alpha y+V\beta y-Lyz)& x(x-1)(L-2V\alpha +V\beta -Lz)& x(1-x)(y-1)L\\ y(1-y)(L-2V{\alpha }^2+V{\beta }^2-Lz)& (1-2y)\left(V\alpha -C_2+Lx+P_2{z}^2+R_D{z}^2-2V\alpha x^2+2V\beta x^2-Lxz\right)& y(1-y)(P_2+R_D-Lx)\\ z(1-z)R_{S}y& z(1-z)(P_2+R_D-R_{S}x)& (1-2z)\left(P_1-C_3+P_2+P_3-P_{2}y-R_{D}y+R_{S}xy\right)\end{array}\right]\end{array}$$

The eigenvalues at each equilibrium point are solved, as shown in

Table 3. Payoff matrix of the three-party mixed-strategy game.

Cyber Attackers	Defender	System Administrator	Payoff Vector (Attacker, Defender, SysAdmin)
x	y	Strict supervision (z)	$\begin{array}{c}\alpha V-C_1-P_1\hfill \\ E-\alpha V-C_2+R_D\hfill \\ P_1-R_D-C_3+R_S\hfill \end{array}$
		Loose regulation ($1-z$)	$\begin{array}{c}\alpha V-C_1\hfill \\ E-\alpha V-C_2\hfill \\ -P_3\hfill \end{array}$
	$1-y$	Strict supervision (z)	$\begin{array}{c}\beta V-C_1-P_1\hfill \\ E-\beta V-P_2\hfill \\ P_1+P_2-C_3\hfill \end{array}$
		Loose regulation ($1-z$)	$\begin{array}{c}\beta V-C_1+L\hfill \\ E-\beta V-L\hfill \\ -P_3\hfill \end{array}$
$1-x$	y	Strict supervision (z)	$\begin{array}{c}-P_1\hfill \\ E-C_2+R_D\hfill \\ P_1-R_D-C_3\hfill \end{array}$
		Loose regulation ($1-z$)	$\begin{array}{c}0\hfill \\ E-C_2\hfill \\ -P_3\hfill \end{array}$
	$1-y$	Strict supervision (z)	$\begin{array}{c}\alpha V-P_1\hfill \\ E-\alpha V-P_2\hfill \\ P_1+P_2-C_3\hfill \end{array}$
		Loose regulation ($1-z$)	$\begin{array}{c}\alpha V\hfill \\ E-\alpha V\hfill \\ -P_3\hfill \end{array}$

:

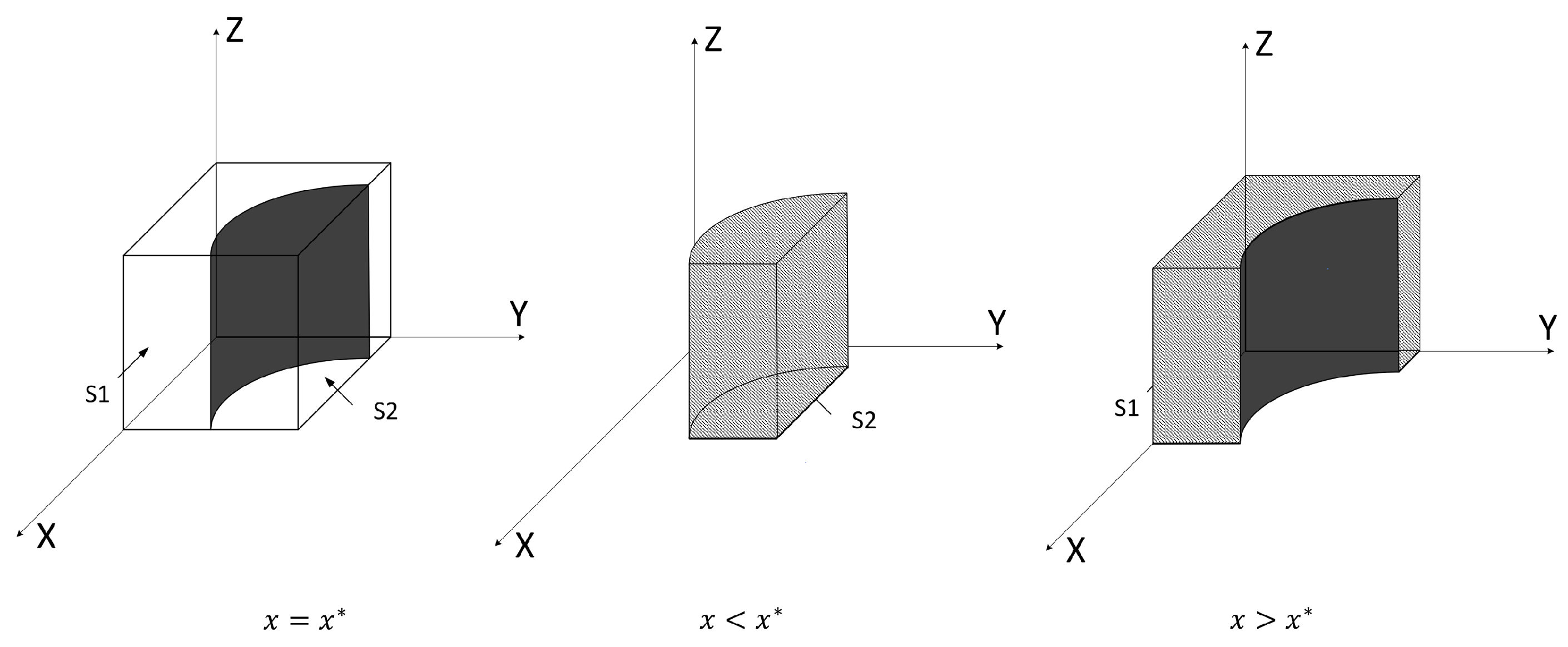
4.2. Stability Analysis of Balance Point

According to the first law of Lyapunov, when the corresponding eigenvalues of each equilibrium point are negative, the equilibrium point is stable; when there is at least one positive eigenvalue, the equilibrium point is unstable. The corresponding eigenvalues of each equilibrium point are analyzed under different circumstances, according to

Table 4. Payoff matrix of three-party mixed-strategy game (order as original).

Equilibrium	${\mathit{N}}_{\mathit{A}}$	${\mathit{N}}_{\mathit{D}}$	${\mathit{N}}_{\mathit{M}}$
$(0,0,0)$	$V\alpha -C_2$	$L-C_1-V\alpha +V\beta$	$P_1-C_3+P_2+P_3$
$(1,0,0)$	$C_1-L+V\alpha -V\beta$	$L-C_2-V\alpha +V\beta$	$P_1-C_3+P_2+P_3$
$(0,1,0)$	$V\alpha -C_1$	$C_3-P_1-P_2-P_3$	$P_1-C_3+P_3-R_D$
$(0,0,1)$	$V\beta -V\alpha -C_1$	$C_3-P_1-P_2-P_3$	$P_2-C_2+R_D+V\alpha$
$(1,1,0)$	$C_1-V\alpha$	$C_2-L+V\alpha -V\beta$	$P_1-C_3+P_3-R_D+R_S$
$(1,0,1)$	$C_1+V\alpha -V\beta$	$C_3-P_1-P_2-P_3$	$P_2-C_2+R_D-V\alpha +V\beta$
$(0,1,1)$	$V\alpha -C_1$	$C_2-P_2-R_D-V\alpha$	$C_3-P_1-P_3+R_D$
$(1,1,1)$	$C_1-V\alpha$	$C_3-P_1-P_3+R_D-R_S$	$C_2-P_2-R_D+V\alpha -V\beta$

.

Scenario 1. When the conditions are met , the stable strategies of the three parties are strong attack, strong defense, and loose supervision, and the stability determination is shown in

Table 5. Stability analysis of $K_5=(1,1,0)$.

Equilibrium	${\mathit{\lambda }}_1$	${\mathit{\lambda }}_2$	${\mathit{\lambda }}_3$	ESS
$(0,0,0)$	+	+	$-,+$	Instability point
$(1,0,0)$	−	+	$-,+$	Instability point
$(0,1,0)$	+	−	−	Instability point
$(0,0,1)$	+	$+,-$	+	Instability point
$(1,1,0)$	−	−	−	ESS
$(1,0,1)$	−	$+,-$	+	Instability point
$(0,1,1)$	+	−	+	Instability point
$(1,1,1)$	−	+	−	Instability point

.

In Scenario 1, cyber attackers derive far greater benefits from launching aggressive attacks than the costs incurred in implementing strong countermeasures. When an attack occurs, system administrators fail to impose retrospective penalties, leading attackers to adopt aggressive strategies. For network defenders facing frequent and highly sophisticated cyberattacks, the perceived risk of losses far outweighs the costs of proactive defense measures, making aggressive defense strategies nearly inevitable. When all defenders implement rigorous protective measures during cyberattacks, the overall network environment remains largely intact. System administrators not only avoid negative consequences but also gain positive returns, resulting in a near-zero probability of adopting strict supervision. When all three parties reach equilibrium, the optimal defensive strategy becomes aggressive defense.

Scenario 2. When the conditions are met $V\alpha <C_1,C_2<V\alpha +P_2+R_D,C_3<P_1+P_3-R_D$, the three-party evolutionary stable strategy is $K_7=(0,1,1)$ (weak attack, strong defense, strict supervision), and the stability determination situation is shown in

Table 6. Stability analysis of $K_7=(0,1,1)$.

Equilibrium	${\mathit{\lambda }}_1$	${\mathit{\lambda }}_2$	${\mathit{\lambda }}_3$	ESS
$(0,0,0)$	+	+	$-,+$	Instability point
$(1,0,0)$	−	+	$-,+$	Instability point
$(0,1,0)$	+	−	−	Instability point
$(0,0,1)$	+	$+,-$	+	Instability point
$(1,1,0)$	−	−	−	ESS
$(1,0,1)$	−	$+,-$	+	Instability point
$(0,1,1)$	+	−	+	Instability point
$(1,1,1)$	−	+	−	Instability point

.

In Scenario 2, cyber attackers face significantly higher costs than potential gains from adopting aggressive attack strategies, coupled with traceability penalties imposed by system administrators. This incentivizes attackers to adopt passive defense tactics. Conversely, when system administrators implement strict oversight and provide corresponding rewards for defenders adopting robust defenses, it substantially reduces defensive losses, thereby encouraging stronger protective measures. The dynamic between defenders’ aggressive strategies and attackers’ passive approaches generates substantial positive social benefits for system administrators, driving them to enforce stricter regulations. When all three stakeholders reach equilibrium, the optimal defense strategy becomes aggressive defense.

Scenario 3. When the conditions are met $C_1<V\alpha , C_3+R_D<P_1+P_3+R_S,C_2-P_2-R_D<V\beta -V\alpha$, the stable strategies of the three parties are $K_8=(1,1,1)$ (strong attack, strong defense, strict supervision), and the stability determination is shown in

Table 7. Stability analysis of $K_8=(1,1,1)$.

Equilibrium	${\mathit{\lambda }}_1$	${\mathit{\lambda }}_2$	${\mathit{\lambda }}_3$	ESS
$(0,0,0)$	+	+	+	Instability point
$(1,0,0)$	−	+	+	Instability point
$(0,1,0)$	+	−	+	Instability point
$(0,0,1)$	+	−	+	Instability point
$(1,1,0)$	−	−	+	Instability point
$(1,0,1)$	−	−	+	Instability point
$(0,1,1)$	+	−	−	Instability point
$(1,1,1)$	−	−	−	ESS

.

In Scenario 3, when the network defender possesses sufficiently high resource value, attackers may still opt for aggressive attack strategies to maximize gains despite facing traceability penalties from system regulators. When both resource value and regulatory incentives are sufficient, defenders tend to adopt strong defense strategies over time to minimize losses. Meanwhile, system regulators implement strict oversight policies that increase rewards for defenders while intensifying penalties against attackers. Given that the costs of rigorous supervision and reward expenditures are lower than fines and positive benefits from penalties, the probability of adopting strict supervision approaches tends toward 1. When all three parties reach equilibrium, the optimal defense strategy becomes aggressive defense.

4.3. Optimal Strategy Selection Algorithm

In the process of a three-party game of network attack and defense, each subject can maximize its expected benefit by constantly learning, adjusting, and improving its strategy selection, and gradually tend to a certain equilibrium state. At this time, the strategy selected by each subject is the optimal strategy.

In the initial phase of a three-party evolutionary game, participants fully utilize available information resources to assess expected economic returns from their strategies. Subsequently, they employ evolutionary dynamic equations to precisely calculate optimal defensive strategies that maximize benefits, continuously refining and optimizing their choices to achieve better outcomes. This ongoing process of information gathering and strategy adjustment forms the cornerstone enabling the three-party evolutionary game model to operate effectively and sustainably. See Algorithm 1.

Algorithm 1. Algorithm for deriving the optimal network defense strategy
1	Input the initial three-party evolutionary game model $(N,S,\theta ,U)$.
	Construct the attacker’s strategy set $S_A=\{S_{A1},S_{A2},\dots ,S_{Am}\}$ and belief set
2	$P_A=(x_1,x_2,\dots ,x_m)$, where $x_i\in P_A$ is the probability that the attacker adopts attack strategy $S_{Ai}$.
	Construct the defender policy set $S_D=\{S_{D1},S_{D2},\dots ,S_{Dn}\}$ and belief set
3	$P_D=(y_1,y_2,\dots ,y_n)$, where $y_j\in P_D$ is the probability that the defender adopts defense strategy $S_{Dj}$.
	Construct the system manager’s strategy set $S_M=\{S_1,S_2,\dots ,S_h\}$ and belief set
4	$P_M=(z_1,z_2,\dots ,z_h)$, where $z_k\in P_M$ is the probability that the system manager adopts supervision strategy $S{M}_k$.
5	/* Calculate the attack and defense benefit matrices $M_A,M_D,M_M$ for each strategy combination $(S_{Ai},S_{Dj},S_{Mk})$ */
6	for i←1 to m do
7	for j←1 to n do
8	for k←1 to h do
9	$a_{ijk}=U_A(S_{Ai},S_{Dj},S_{Mk})=R_A-C_A$
10	$b_{ijk}=U_D(S_{Ai},S_{Dj},S_{Mk})=R_D-C_D$
11	$c_{ijk}=U_M(S_{Ai},S_{Dj},S_{Mk})=R_M-C_M$
12	end for
13	end for
14	end for
15	/* Complex dynamic equations are constructed*/
16	for i←1 to m do
17	${\displaystyle \frac{d{x}_i}{dt}}=x_i[U_{SAi}-\overline{U_{SAi}}]$
18	end for
19	for j←1 to n do
20	${\displaystyle \frac{d{y}_j}{dt}}=y_j[U_{SDj}-\overline{U_{SDj}}]$
21	end for
22	for k←1 to h do
23	${\displaystyle \frac{d{z}_k}{dt}}=z_k[U_{SMk}-\overline{U_{SMk}}]$
24	Solve ${\displaystyle \frac{d{x}_i}{dt}}=0,{\displaystyle \frac{d{y}_j}{dt}}=0,{\displaystyle \frac{d{z}_k}{dt}}=0$
25	Output the optimal network defense strategy
26	end

5. Results and Discussion

To validate the aforementioned analysis, we conducted simulation experiments using a tripartite cyber attack–defense model based on evolutionary game theory proposed in this paper. Through deploying network information systems, we used Matlab R2020b to analyze the evolutionary patterns and behavioral tendencies of three stakeholders in cyber warfare scenarios, while exploring how critical influencing parameters affect the strategic models.

This study analyzes the evolution process of key influencing parameters for three strategic equilibrium points, with all initial $x,y,z$ values set to 0.2. The ode 45 function was employed to solve differential equations over a time range from 0 to 50, where different parameter values were assigned to each dataset and plotted using distinct colors and line types. Subsequent analyses examined evolutionary processes under varying initial probabilities while keeping other parameters constant. A three-layer nested loop was implemented to modify initial strategy combinations of $x,y,z$, with variables within each iteration ranging from 0.1 to 1 at 0.2-step intervals. This resulted in 125 datasets, which were analyzed through ode45 to determine system state evolution over time. The plot3 function transformed these results into visual 3D graphics, enabling observation of evolutionary trajectories under different initial strategies and facilitating deeper understanding of system behavior patterns.

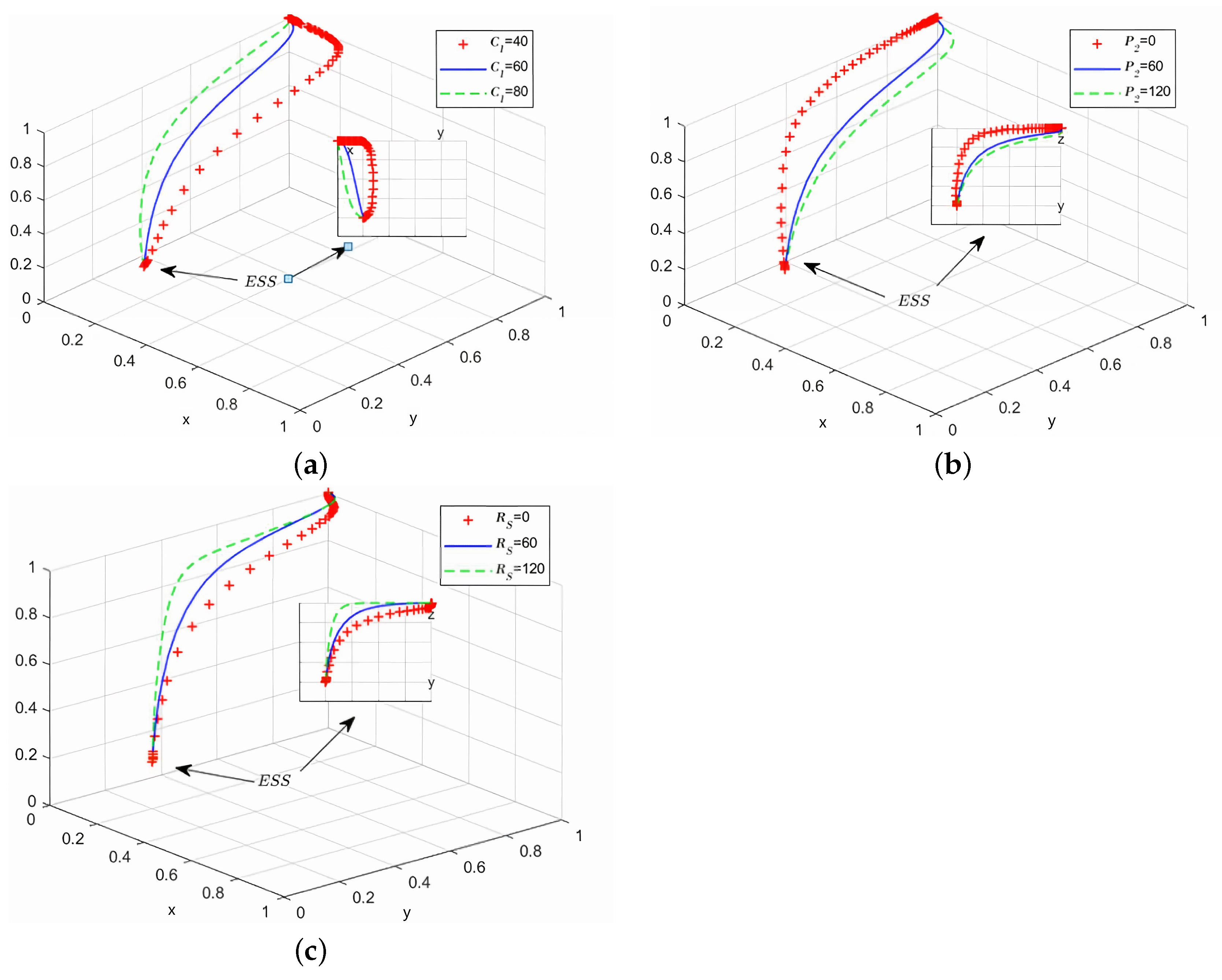
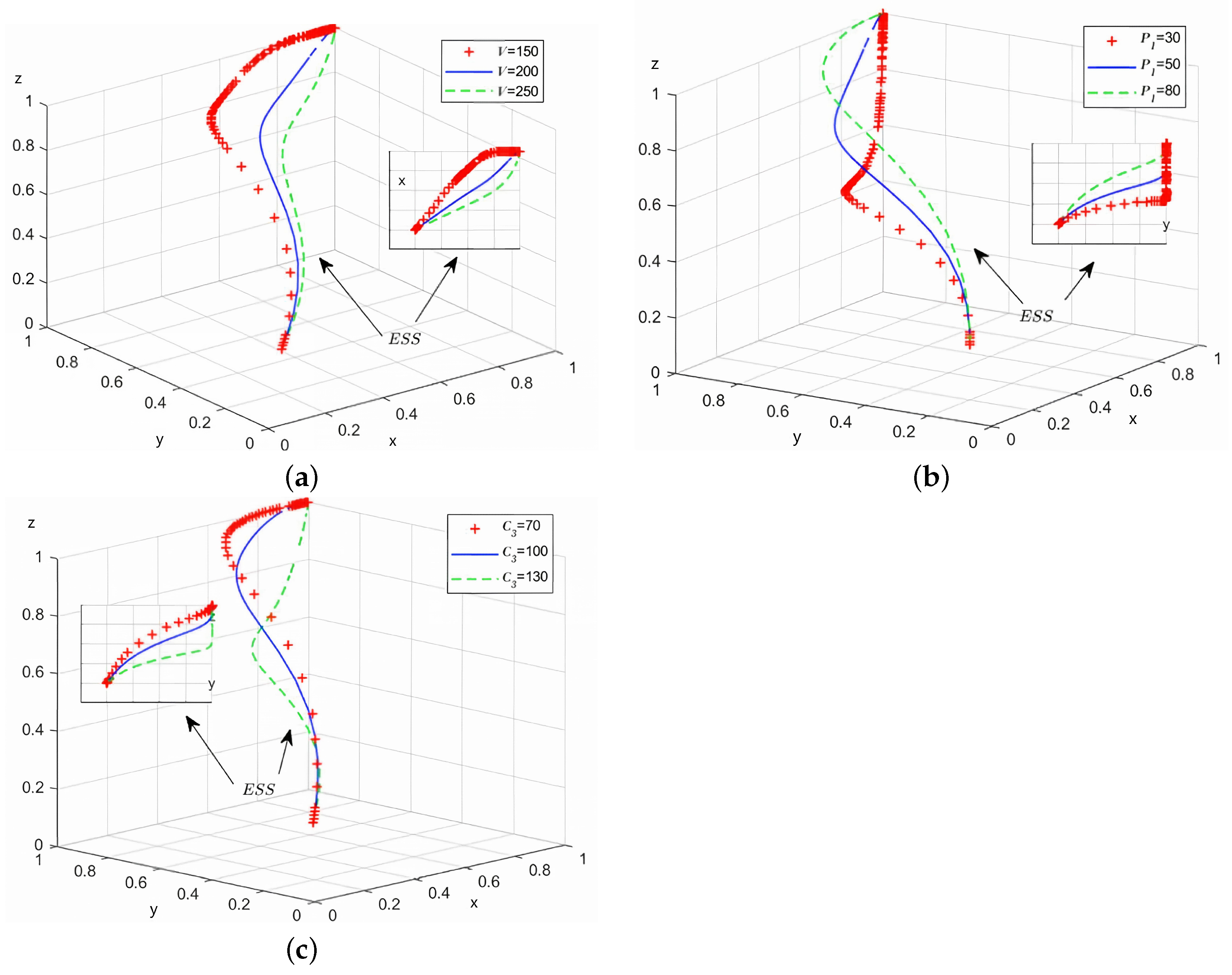
5.1. Simulation Result Analysis of the Evolution Process of Key Influence Parameters

5.1.1. Simulation Analysis of Strategy Point (1,1,0)

Select the data that meet the conditions to form array 1, and analyze the influence of the process and results of the three-party evolutionary game under this situation, and analyze the influence brought by the change of the core influence parameter value $V,C_1,P_1$.

Analyze the correlation between $V,C_1,P_1$ variable changes and evolutionary game process and results, assign parameters $V=200,240,280$, $C_1=30,50,70$, $P_1=55,65,75$, respectively, while keeping other parameters unchanged. During the simulation evolution process, 50 iterative operations are carried out to obtain the simulation results of the replication dynamic equation, as shown in Figure 6a–c:

As shown in Figure 6a, the enhancement of network users’ resource value accelerates attackers’ evolution toward sustained use of aggressive strategies. With increasing risks V, both attackers’ probability of adopting aggressive tactics and defenders’ probability of implementing robust defenses rise simultaneously, while system administrators’ adoption of strict monitoring decreases. In this scenario, defenders invest more resources to protect their assets, aiming to minimize losses during large-scale aggressive attacks. Figure 6b reveals that as risks $C_1$ escalate, attackers’ probability of choosing aggressive strategies declines while defenders’ probability of adopting strong defense measures increases. By continuously upgrading cybersecurity technologies, updating security protocols, and implementing robust defense strategies, defenders significantly increase the difficulty of attacks and raise the costs of aggressive tactics, ultimately reducing attackers’ propensity to use aggressive approaches. Figure 6c indicates that as risks $P_1$ grow, attackers’ probability of using aggressive strategies decreases while system administrators’ preference for strict monitoring intensifies. Therefore, to curb cyberattacks, system administrators should enhance cybersecurity frameworks by increasing penalties, establishing comprehensive governance regulations, developing efficient incident response mechanisms, and improving regulatory oversight capabilities. These measures combined with stricter enforcement can effectively reduce attackers’ reliance on aggressive tactics.

5.1.2. Simulation Analysis of Strategy Point (0,1,1)

Select the data that meet the conditions to form array 2, analyze the process and results of the three-party evolutionary game under this situation, and analyze the influence brought by the change of the core influencing parameter value $C_1,P_2,R_S$.

Analyze the correlation between $C_1,P_2,R_S$ variable changes and evolutionary game process and results, assign parameters $C_1=40,60,80$, $P_2=0,60,120$, $R_S=0,60,120$, respectively, while keeping other parameters unchanged. During the simulation evolution process, 50 iterative operations are carried out to obtain the simulation results of the replication dynamic equation, as shown in Figure 7a–c:

As shown in Figure 7a, as the value of $C_1$ increases, both the probability of cyber attackers adopting aggressive attack strategies and the probability of defenders implementing robust defense measures decrease. In such scenarios, attackers may opt for more cost-effective, covert, and harder-to-detect tactics to reduce operational costs and enhance attack success rates. This necessitates system administrators to adopt stricter regulatory policies. Consequently, defenders must intensify research and monitoring of emerging attack patterns while promptly adjusting their defense strategies. Continuous enhancement of cybersecurity expertise and vigilance is essential to maintain sensitivity to evolving threats and respond effectively to dynamic security environments. Figure 7b reveals that as the value of $P_2$ rises, the probability of attackers choosing aggressive strategies and defenders implementing strong defenses increases simultaneously, while the probability of administrators adopting strict oversight decreases. The graph indicates that to strengthen overall network security, administrators should focus on technical enhancements that increase attackers’ intrusion difficulty rather than merely raising penalties for non-compliant defenders. Figure 7c demonstrates that as the value of $R_S$ grows, administrators’ adoption of strict supervision intensifies. Strengthening public recognition and awareness of administrators’ roles through transparent regulatory frameworks and accountability mechanisms will ensure fair enforcement practices, thereby collectively advancing cybersecurity development and maximizing regulatory effectiveness and social benefits.

5.1.3. Strategy Point (1,1,1) Simulation Analysis

Select the data that meet the conditions to form array 3, and analyze the process and results of the three-party evolutionary $V,P_1,C_3$$V,P_1,C_3$ game under this situation, and analyze the influence brought by the change of the core influencing parameter value.

Analyze the correlation between $V,P_1,C_3$ variable changes and evolutionary game process and results, assign parameters

$$V=150,200,250,$$

$P_1=30,50,80$ and $C_3=70,100,130$, respectively, while keeping other parameters unchanged. During the simulated evolution process, 50 iterative operations are carried out to obtain simulation results of the replication dynamic equation, as shown in Figure 8a–c.

As shown in Figure 8a, as the value of V increases, cyber attackers’ probability of adopting aggressive attack strategies rises, while both defenders’ adoption of robust defense measures and system administrators’ implementation of strict supervision decrease. To curb attacks and enhance cybersecurity, system administrators should proactively fulfill their supervisory responsibilities by providing technical support subsidies to defenders. This reduces the resource costs for defenders, elevates overall network security, and consequently decreases attackers’ propensity to employ aggressive tactics. Figure 8b demonstrates that increased penalties incentivize administrators to maintain rigorous oversight. As the value of $P_1$ rises, the probability of strict supervision intensifies, making attacks more costly and reducing aggressive strategy adoption, thereby strengthening network security. Figure 8c reveals that higher $C_3$ increases attackers’ probability of using aggressive strategies while decreasing administrators’ adoption of strict supervision. By establishing innovative regulatory frameworks and implementing cutting-edge cybersecurity technologies, we can reduce administrative and human resource costs associated with strict supervision, effectively lowering attackers’ probability of choosing aggressive tactics.

5.2. Analysis of Simulation Results of Evolution Process Under Different Initial Probabilities

Figure 9a–c respectively illustrate the results after 125 iterations of Array 1, Array 2, and Array 3. As shown in Figure 9a, when the conditions $C_1<V\alpha ,C_2<L-V\alpha +V\beta ,P_1-C_3+P_3-R_S+R_D<0$ are met, the system exhibits a uniquely stable strategy combination (strong attack, strong defense, lenient supervision). Network defenders should strengthen cybersecurity measures by conducting regular vulnerability scans and repairs, establishing backup systems and emergency response mechanisms. Simultaneously, they should actively foster public awareness to encourage system administrators to fulfill their duties diligently, thereby enhancing overall network security.

As shown in Figure 9b, when the conditions $V\alpha <C_1,C_2<V\alpha +P_2+R_D,C_3<P_1+P_3-R_D$ are met, the system exhibits a unique evolutionary stable strategy combination (weak attack, strong defense, strict supervision). System administrators must establish comprehensive legal frameworks, enhance reward and penalty mechanisms for both attackers and defenders, and spearhead the development of network defense systems. Through systematic defensive measures, this approach not only reduces the operational costs for defenders implementing robust defenses but also boosts their motivation to strengthen cybersecurity, thereby effectively curbing cyber intrusions to the greatest extent possible.

As shown in Figure 9c, when the conditions $C_1<V\alpha ,C_3+R_D<P_1+P_3+R_S,C_2-P_2-R_D<V\beta -V\alpha$ are met, the system exhibits a unique evolutionary stable strategy combination (strong attack, strong defense, strict supervision). Under this configuration, defenders hold higher resource value while system administrators impose relatively low penalties on attackers. Given that attackers perceive higher returns than risks, they tend to adopt aggressive offensive measures. Frequent cyberattacks drive defenders and administrators to actively implement defensive and regulatory measures. This can enhance traceability capabilities for cyberattacks and increase penalty, while boosting rewards for defenders. Consequently, more resources will be allocated to accelerate technological research in areas like intrusion detection systems and information security defenses. These efforts aim to maintain network environment security through more efficient and rapid methods.

In conclusion, the results obtained through numerical simulation analysis align with theoretical analyses of strategy stability, thereby validating the effectiveness of the analysis. This discovery holds significant practical implications and guiding value for cybersecurity regulation, helping us better understand and address challenges posed by cyber attacks.

5.3. Discussion and Implications

To fully demonstrate the practical value of our model, we take Scenario 2 (Weak Attack, Strong Defense, Strict Supervision) as an example and delve into a concrete case study of Critical Information Infrastructure protection (e.g., a smart grid). In this case, the defender is a grid operator protecting high-value assets V; the attacker is a hostile entity aiming to disrupt the infrastructure; and the administrator is a national cybersecurity regulatory agency.

Our model analysis reveals that to achieve and maintain this ideal state, the regulator must implement a precise combination of policies: First, it must ensure, through robust threat attribution and law enforcement capabilities, that the penalty $P_1$ is high enough to make the cost of a strong attack $C_1$ significantly exceed its expected gain $V\alpha$. Second, it needs to provide adequate rewards $R_D$ or subsidies for the operator to deploy strong defense measures (e.g., advanced threat detection systems), while simultaneously imposing clear fines $P_2$ for security negligence, thereby making “strong defense” the only rational choice for the operator both economically and compliantly.

The unique value of our model lies in its transformation of qualitative goals, such as “effective deterrence,” into quantitative relationships among key parameters like $P_1$, $R_D$, and $C_1$. Policymakers can use our stability conditions (e.g., $V\alpha <C_1$) to calculate the minimum threshold for required regulatory intensity (e.g., $P_1$), thereby advancing cybersecurity governance from experience-based to scientifically quantitative.

6. Conclusions

Cyber warfare constitutes a dynamic and complex process. This study employs bounded rationality theory to construct a tripartite evolutionary game model for attackers, defenders, and system administrators, grounded in practical cyber defense scenarios. Through replicating dynamic equations, we comprehensively analyze the strategic evolution of all parties’ behaviors and their ultimate stable states under different conditions, thereby identifying optimal defensive strategies for each scenario. By simulating key variable control at three strategic equilibrium points, the analysis reveals critical factors influencing behavioral patterns across stakeholders. These findings provide actionable insights for evolving cyber defense strategies, ultimately contributing to the development of more secure cyberspace environments.

This study establishes a foundational tripartite evolutionary game model, providing a theoretical cornerstone for understanding the regulator’s role in cybersecurity. Future research can be pursued in the following directions to extend this work:

• Incorporating Complex Attack Models: Future work will align attack strategies with frameworks like MITRE ATT&CK to model multi-stage and adaptive attack behaviors, alongside investigating the dynamic, stage-dependent responses of defenders and administrators.
• Exploring Advanced Learning Mechanisms: Going beyond replicator dynamics, investigating learning rules based on historical actions or belief updates (e.g., reinforcement learning) would capture more sophisticated strategic adaptation.
• Extending Model Assumptions: Incorporating continuous strategy spaces and scenarios with incomplete information would enhance the model’s realism and generalizability.