Hybrid GOMP–ROMP Algorithm for Sparse Channel Estimation in mmWave MIMO: Enhancing Convergence and Reducing Computational Complexity

Abstract

This paper proposes an efficient sparse channel estimation method for millimeter wave (mmWave) hybrid multiple-input multiple-output (MIMO) systems. The performance of orthogonal matching pursuit (OMP) and its advanced variants—generalized OMP (GOMP), simultaneous OMP (SOMP), and regularized OMP (ROMP)—is evaluated based on normalized mean square error (NMSE) and computational complexity. A new hybrid GOMP–ROMP algorithm is proposed to achieve faster convergence and lower computational costs while maintaining the desired estimation accuracy. Simulation results reveal that the proposed algorithm reduces NMSE by 0.040823 compared to OMP and attains ROMP’s accuracy with significantly less complexity. For a MIMO system with 32 ×32 configuration, the method offers up to a fourfold reduction in computational complexity compared to OMP, ROMP, and SOMP. These findings highlight the potential of the hybrid algorithm for real-time mmWave massive MIMO applications in fifth-generation (5G) and sixth-generation (6G) systems, where high bandwidth and low latency are essential.

1. Introduction

Next-generation wireless communication systems often strive for data transfer speeds of gigabits per second. Around 2029, there will be over 5.6 billion fifth-generation (5G) subscribers worldwide, and mobile data traffic is anticipated to increase by 20% yearly until the end of 2029 [1]. Millimeter wave (mmWave)-based communication can handle such large data rates because of their wide bandwidth [2]. Microwaves (1 GHz to 30 GHz) and infrared (IR) portions of the electromagnetic (EM) spectrum are separated by mmWave frequencies, which range from 30 GHz to 300 GHz. The potential bandwidth in 5G frequency range 2 (FR2) bands is ten times more than that of sub-6 GHz 5G frequency range 1 (FR1) bands. Consequently, mmWave networks are able to support more connections with higher peak individual data rates [3,4]. Furthermore, the atmosphere’s gas absorption creates considerable attenuation, and mmWave systems face significant challenges such as atmospheric absorption, severe pathloss, penetration loss, and limited scattering. In densely populated metropolitan places, including stadiums, airports, and sports arenas, mobile providers are implementing mmWave 5G networks. These work best in situations where incredibly fast wireless communication is needed in crowded spaces with minimal obstacles [5,6].

Analog beamforming is a cost-effective solution for mmWave multiple-input multiple-output (MIMO) systems, but it has limitations due to its reliance on a single radio-frequency (RF) chain, limited spatial multiplexing, phase-only control, and it support of single-user, single-symbol transmission. Digital beamforming offers flexibility and spectral efficiency but also has high power consumption, complicated hardware, and higher expenses. Real-time beamforming becomes more complex due to computational complexity and thermal noise problems. Hybrid beamforming is a promising technique that efficiently combines analog and digital techniques, requiring fewer RF chains and reducing hardware complexity. It supports multi-stream transmission and spatial multiplexing, improving spectral efficiency without the high costs associated with digital systems [7,8].

Accurate channel estimation is crucial for mmWave systems. Conventional channel estimation methods designed for sub-6 GHz frequencies are not directly applicable to mmWave systems, as they assume a rich scattering environment. In contrast, mmWave channels typically have only a few dominant paths due to limited scattering, making them sparse in nature. This sparsity significantly reduces the complexity of channel estimation for mmWave systems. A simple and powerful paradigm for recovering sparse signals from a limited number of linear measurements is provided by compressed sensing (CS) techniques. It is feasible to correctly estimate the channel using a substantially smaller number of pilot symbols by addressing mmWave channel estimation as a sparse signal recovery problem. Orthogonal matching pursuit (OMP) is a prominent CS method because of its resistance to noise, low computational complexity, and most importantly, its simple and straightforward structure, making it easy to implement. OMP builds a sparse representation of the channel by iteratively determining which dictionary elements have the highest correlation with the current residual [9]. To reduce the computational complexity of traditional OMP, a number of variants are being developed.

This paper is structured as follows: related works are covered in Section 2, and the system model, which includes mmWave channel modeling and a hybrid architecture, is presented in Section 3. In Section 4, the channel estimation problem is formulated, and various OMP variants related to channel estimation are explored. The simulation results are analyzed in Section 5, and the paper is concluded in Section 6.

2. Related Works

This section discuss the works related to traditional channel estimation methods in mmWave communication systems, including OMP-based channel estimation and its variants.

2.1. Traditional Channel Estimation Schemes

The channel estimation problem for mmWave MIMO orthogonal frequency division multiplexing (OFDM) systems with hybrid architectures was examined in [10]. The angle of departure (AoD), angle of arrival (AoA), and transmission delays were estimated using a beam space multiple signal classification (MUSIC) algorithm. Systems with uniform planar arrays were included in the focus of the suggested channel estimator. High channel estimate accuracy was achieved using the suggested method. In [11], the authors used spatial sparsity and correlation for MIMO mmWave channel estimation in a hybrid analog–digital architecture through compressive covariance estimation. A novel Gaussian-prior model was suggested, which takes inspiration from sparse Bayesian learning (SBL), used an expectation-maximization procedure to update posterior channel values. The algorithm’s online version minimized latency and performance loss and was created for real-world use. The normalized mean squared error (NMSE) of the channel estimation was also examined in the study.

A new method for acquiring precise channel state information (CSI) in mmWave communication systems was presented in [12]. Two sub-problems had been derived from the non-convex mmWave channel estimation problem using the alternative direction method of multipliers (ADMM) technique. The first sub-problem had been resolved using a fast gradient descent matrix completion algorithm, and the precise CSI estimate matrix was obtained by CS. The suggested method was important for MIMO channel estimation, as it reduced training overhead and improved channel estimate accuracy.

2.2. Deep Learning-Based Channel Estimation

In [13], the authors introduced a model-driven approach to estimate the channel for mmWave massive MIMO broadband systems. The low estimation accuracy in low signal-to-noise ratios (SNRs) was addressed by considering the beam squint effect and applying the iterative shrinkage threshold technique to the deep iterative network. This method accelerated convergence and optimized the contraction threshold network, ensuring an efficient and reliable solution. In [14], a deep learning (DL) method for hybrid beamforming and channel estimation in frequency-selective, wideband mm-wave systems was presented. It suggested three distinct DL frameworks while considering the massive MIMO-OFDM system. This technique provided more tolerance against defects in received pilot data and the propagation environment, as well as improved spectrum efficiency (SE), reduced processing costs, and fewer pilot signals than current optimization and DL techniques.

The authors of [15] presented a DL-based channel estimation technique by constructing a deep neural network (DNN) using SBL. The DNN efficiently captured intricate channel sparsity structures by updating the Gaussian variance parameters in each SBL layer. The method also improved the performance by optimizing the measurement matrix. Compared to SBL, which took 28 s, the suggested DL-based method took less than 1 s. In [16], a DL-based CS (DLCS) channel estimation system was suggested to predict beamspace channel amplitude using simulated environments. After that, dominating beamspace channel entries were used to rebuild the channel. The suggested DL-quantized phase (DLQP) hybrid precoder design technique achieved better SE and NMSE than existing systems.

2.3. OMP-Based Channel Estimation

In [17], the authors suggested an open-loop channel estimator for hybrid MIMO systems in mmWave communications using a CS problem. The channel estimation process employed a redundant dictionary of array response vectors with highly quantized angle grids using the OMP technique. Analytical derivations of the lower and upper bounds of the sum of squared errors were provided, taking into account the performance of the oracle estimator and OMP. Simulation results demonstrated that the suggested OMP method with a redundant dictionary outperforms least square (LS) techniques. The authors of [18] presented an OMP-based sparse channel estimation technique for mmWave massive MIMO systems with a mixed analog-to-digital converter (ADC) architecture. Within a specific SNR range, the numerical results clearly indicated that the OMP algorithm outperformed the LS method. Near-optimal performance may be obtained using a range of ADC combinations with varying resolutions.

In [19], the authors discussed an iterative channel estimation approach based on OMP for orthogonal chirp division multiplexing (OCDM) systems. The suggested system’s SE was better than that of current techniques. In the frequency domain, a pilot pattern was created to guarantee precision and to lower pilot power. The method also minimized the impact of data symbols on channel estimation. In high-speed communication environments, simulation findings demonstrated not only improved bit error rate (BER) performance but also faster convergence, highlighting the efficiency of the system.

Low-complexity and low pilot-overhead channel estimation for reconfigurable intelligent surface (RIS)-aided single-input multiple-output (SIMO) OFDM systems was investigated in [20]. The authors presented two low-complexity SBL channel estimators and a low-complexity OMP estimator. These techniques effectively addressed the challenges of phase shifter design and pilot overhead reduction in RIS-assisted SIMO-OFDM systems, achieving a favorable balance between CSI estimation performance and complexity. In [21], the authors suggested methods for enhancing channel estimation in mmWave networks based on CS. The approach was evaluated against OMP and an oracle estimator in various mmWave MIMO configurations using a hybrid MIMO architecture. According to simulation results, the suggested approach significantly reduced NMSE and took 16.9 times less computation time. The hybrid MIMO approach provided nearly ideal performance when compared to a fully digital precoder, making it a feasible substitute for practical applications.

2.4. OMP Variant-Based Channel Estimation

A novel iterative technique based on alternating minimization was introduced for creating the ideal sensing matrix in [22]. This method enhanced the performance of multi-stage CS-based mmWave channel estimation and recovery. The optimization problem was formulated as the nearest Kronecker product (NKP) problem, which aimed to jointly identify the best hybrid precoders and combiners derived from the optimally developed sensing matrix. Compared to existing codebook-based systems, the generalized orthogonal matching pursuit (GOMP) algorithm, along with the suggested joint hybrid design, offered superior channel prediction accuracy and spectral efficiency.

In [23], the authors used the spatially joint sparsity structure of channels to analyze sparse channel estimation through weighted distributed simultaneous OMP (WDiSOMP), which was the outcome of combining the suggested distributed method with the traditional simultaneous orthogonal matching pursuit (SOMP) algorithm. Performance was evaluated using the NMSE. The study contrasted WDiSOMP with other techniques, such as local SOMP, distributed SOMP (DiSOMP), and a centralized strategy built on structured SOMP. Also, in [24], the authors suggested an improved SOMP for channel estimation and a sensing algorithm for mmWave MIMO-OFDM systems. The algorithm also developed a reliable sensing scheme for user localization and mapping of scattering environments. Simulation results showed that the suggested algorithm had better channel estimation and sensing performance than existing algorithms. To enhance channel estimation in massive MIMO systems, in [25], the authors suggested a hybrid-field channel estimation approach in conjunction with the simultaneous weighted OMP (SWOMP) algorithm. The suggested method eliminated the difference between far-field and near-field estimation techniques by using the SWOMP algorithm for unknown channel sparsity. The suggested strategy convincingly outperformed conventional techniques in terms of channel estimation performance. In [26], the performance of OMP and regularized OMP (ROMP) is compared with that of subspace pursuit (SP), a high-speed, accurate greedy method. Simulation findings indicated that SP outperforms OMP and ROMP in terms of runtime and SE.

Table 1. Comparison of proposed work with existing papers.

Ref.	mmWave	Hybrid MIMO	OMP Based	OMP Variant	Sensing Matrix Design	Channel Sparsity	Performance Metric	Computa-tional Complexity Analysis	Massive MIMO Configuration
[10]	✓	✓	×	×	×	×	NMSE	×	8 × 16
[11]	✓	✓	×	×	×	✓	NMSE	✓	128 × 16
[12]	✓	✓	×	×	×	✓	NMSE	✓	64 × 64
[13]	✓	×	×	×	×	✓	NMSE	✓	32 × 32
[14]	✓	✓	×	×	×	✓	NMSE,SE	✓	16 × 128
[15]	✓	✓	×	×	×	×	NMSE	✓	32 × 32
[16]	✓	✓	✓	×	×	✓	NMSE,SE	×	1 × 64
[17]	✓	✓	✓	×	✓	✓	NMSE,SE	✓	16 × 16, 32 × 32
[18]	✓	✓	✓	×	×	✓	NMSE	×	16 × 32
[19]	✓	✓	✓	×	×	✓	BER	×	×
[20]	✓	×	✓	×	×	✓	NMSE	✓	×
[21]	✓	✓	✓	×	×	✓	NMSE	✓	32 × 32
[22]	✓	✓	✓	✓ (GOMP)	✓	✓	NMSE,SE	✓	32 × 32
[23]	✓	×	×	✓ (SOMP)	×	✓	NMSE	✓	×
[24]	×	✓	×	✓ (SOMP)	×	✓	RMSE	✓	9 × 64
[25]	✓	✓	×	✓ (SWOMP)	×	✓	NMSE	✓	1 × 512
[26]	✓	✓	✓	✓ (ROMP)	×	✓	NMSE	×	16 × 32
This Work	✓	✓	✓	✓ (GOMP, ROMP, SOMP, Hybrid GOMP–ROMP)	✓	✓	NMSE	✓	16 × 16, 32 × 32

compares the proposed work with existing works, highlighting performance metrics, computational complexity, massive MIMO configurations, and other aspects.

2.5. Contributions

The main contributions of this paper are summarized as follows:

• Hybrid algorithm innovation: A new hybrid GOMP–ROMP algorithm is introduced that combines the group selection efficiency of GOMP and the stability and regularization of ROMP. The hybridization facilitates faster convergence with much less computational complexity and preserves NMSE performance equivalent to ROMP.
• Comprehensive performance benchmarking: A thorough quantitative comparison between OMP, GOMP, SOMP, ROMP, and the new hybrid approach with regards to NMSE and computational complexity is performed. Genie-aided and SBL estimators are also added to establish upper-bound performance references.
• Trade-off between complexity and accuracy: This research examines computational complexity scaling behavior with rising antenna dimensions and assesses normalized performance efficiency measures that balance both NMSE and computational cost.
• Practical relevance: The suggested algorithm shows four times reduced computational complexity and  0.04 NMSE gain over OMP for 32 × 32 MIMO configurations, making it appropriate for real-time mmWave massive MIMO deployments in 5G/6G systems.

3. System Model

The mmWave channel model and hybrid architecture for mmWave massive MIMO systems are discussed in this section. The variables and notations are listed in

Table 2. Variables and notations.

Notation	Description
H	mmWave channel
$\widehat{\mathbf{H}}$	Estimated channel
L	Total number of multipath components
d	Distance between antennas
${\alpha }_l$	Complex gain of lth multipath component
$\lambda$	Wavelength
${\mathit{a}}_{\mathit{T}}$	Array response vector at transmitter
${\mathit{a}}_{\mathit{R}}$	Array response vector at receiver
$N_t$	Number of transmitting antennas
$N_r$	Number of receiving antennas
${\theta }_l^t$	AoD of lth multipath component
${\theta }_l^r$	AoA of lth multipath component
${\mathit{A}}_{\mathit{T}}$	Dictionary of array response vectors at transmitter
${\mathit{A}}_{\mathit{R}}$	Dictionary of array response vectors at receiver
${\mathbf{H}}_{\mathit{m}}$	mmWave beam space channel matrix
${\mathbf{F}}_{\mathit{BB}}$	Baseband precoding matrix
${\mathbf{F}}_{\mathit{RF}}$	RF precoding matrix
${\mathit{W}}_{\mathit{RF}}$	RF combining matrix
${\mathit{W}}_{\mathit{BB}}$	Baseband combining matrix
${\mathit{I}}_{{\mathit{N}}_{\mathit{T}}^{\mathit{Beam}}}$	Pilot matrix
$\tilde{\mathit{N}}$	Noise matrix
$\mathbf{Y}$	Received signal matrix
${\mathit{N}}_{\mathit{t}}^{\mathit{Beam}}$	Number of pilot symbols at transmitter side
${\mathit{N}}_{\mathit{r}}^{\mathit{Beam}}$	Number of pilot symbols at receiver side
P	Power of pilot signal
$\mathit{Q}$	Sensing matrix for OMP
$\mathit{D}$	Sensing matrix for genie-aided estimation
${\mathit{h}}_{\mathit{m}}$	Vectorization of ${\mathbf{H}}_{\mathit{m}}$
$\mathbf{y}$	Vectorization of $\mathbf{Y}$
$\mathbf{h}$	Vectorization of $\mathbf{H}$
$\epsilon$	Threshold
$\mathit{c}$	Correlation vector
$\mathit{r}$	Residue vector
n	Iteration counter
$\mathit{S}$	Support set
j	Index of the maximum value of correlation vector in OMP
k	Index of the maximum value of correlation vector in GOMP
$J_1, J_2$ …	Candidate groups in ROMP
${(.)}^H$	Hermitian operator
${(.)}^T$	Transpose operator
⊗	Kronecker product
${\parallel ·\parallel }_F$	Frobenius norm
$\mathbb{E}[·]$	Expectation operator
vec(.)	Vectorization operator

.

3.1. mmWave Channel Model

The mmWave channel can be modelled as follows [19]:

$$\mathbf{H}=\sqrt{{\displaystyle \frac{N_t{N}_r}{L}}}{\displaystyle \sum _{l=1}^L}{\alpha }_l{\mathit{a}}_R\left({\theta }_l^r\right){\mathit{a}}_T\left({\theta }_l^t\right)$$

(1)

where L is the total number of multipath components. A few multipaths are significant in mmWave communication because the signals are greatly attenuated by the strong atmospheric absorption and low scattering at mmWave frequencies [27]. There are $N_t$ and $N_r$ antennas at the transmitter and receiver, respectively. Therefore, the channel becomes sparse in nature. Here, ${\alpha }_l$ is the complex gain, and ${\theta }_l^r$ and ${\theta }_l^t$ are the AoA and AoD of the lth multipath component, respectively. A uniform linear array (ULA) is considered, where each antenna is separated by a distance $d={\displaystyle \frac{\lambda }{2}}$. To efficiently receive or transmit signals along with the dominant paths in mmWave systems, beamforming and channel modeling depend on the array response vectors with AoD and AoA; this describes the phase shifts across antenna elements for a signal arriving or departing from a certain direction. The array response vectors at the transmitter side and receiver side are specified as ${\mathit{a}}_Tϵ{\mathbb{C}}^{N_t\times 1}$ and ${\mathit{a}}_Rϵ{\mathbb{C}}^{N_r\times 1}$, respectively. For the lth multipath component, they are given as follows:

$${\mathit{a}}_T\left({\theta }_l^t\right)={\displaystyle \frac{1}{\sqrt{N_t}}}\left[1,e^{-j{\displaystyle \frac{2\pi }{\lambda }}dcos{\theta }_l^t},\dots ,e^{-j{\displaystyle \frac{2\pi }{\lambda }}\left(N_t-1\right)dcos{\theta }_l^t}\right]$$

(2)

$${\mathit{a}}_R\left({\theta }_l^r\right)={\displaystyle \frac{1}{\sqrt{N_r}}}\left[1,e^{-j{\displaystyle \frac{2\pi }{\lambda }}d\cos {\theta }_l^r},\dots ,e^{-j{\displaystyle \frac{2\pi }{\lambda }}\left(N_r-1\right)d\cos {\theta }_l^r}\right]$$

(3)

From Equation (1), the mmWave channel model can be written in matrix form as

$$\mathbf{H}={\mathbf{A}}_R{\mathbf{H}}_m{\mathit{A}}_T^H$$

(4)

where ${\mathit{A}}_R=\left[{\mathit{a}}_R\left({\theta }_1^r\right),{\mathit{a}}_R\left({\theta }_2^r\right),\dots {\mathit{a}}_R\left({\theta }_L^r\right)\right]$ and ${\mathit{A}}_T=\left[{\mathit{a}}_T\left({\theta }_1^t\right),{\mathit{a}}_T\left({\theta }_2^t\right),\dots {\mathit{a}}_T\left({\theta }_L^t\right)\right]$ are the dictionary of array response vectors at the receiver and transmitter side, respectively. ${\mathbf{H}}_m=\sqrt{{\displaystyle \frac{N_t{N}_r}{L}}}diag({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_L)$ is the mmWave beam space channel matrix.

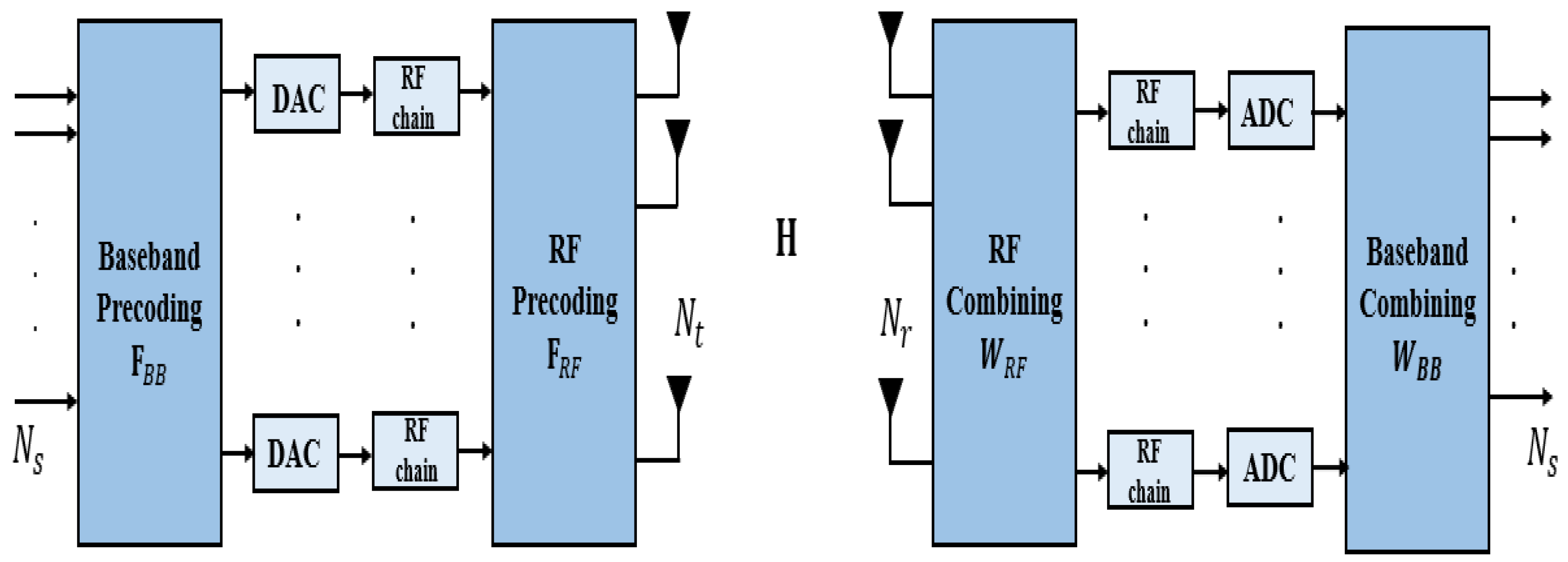
3.2. Hybrid Architecture

In mmWave MIMO systems, analog beamforming is a cost-effective solution that consumes less power. However, it has notable limitations. It relies on a single RF chain, which restricts its ability to support multi-user MIMO and reduces spectral efficiency due to limited spatial multiplexing. Furthermore, the use of phase-only control limits flexibility and advanced beam shaping. Other challenges include strong multi-path effects and inter-cell interference, which complicate the effectiveness of analog beamforming [9]. On the other hand, digital beamforming in mmWave MIMO communication systems provides flexibility and spectral efficiency, but it also has its limitations. High power consumption, complicated hardware, and higher expenses are significant factors to consider in system design. Real-time beamforming becomes increasingly complicated due to the computational complexity imposed by several RF chains. Significant signal conversion is necessary at high data rates, which raises energy consumption and causes thermal noise problems. Massive MIMO systems have extra difficulties because there are so many RF chains [8].

Hybrid beamforming is a promising technique for mmWave systems, as it efficiently combines analog and digital techniques. This approach requires fewer RF chains than fully digital beamforming, resulting in lower power consumption and reduced hardware complexity. Hybrid beamforming also supports multi-stream transmission and spatial multiplexing, which improves spectral efficiency without the high costs typically associated with digital systems. Because of its efficiency with large antenna arrays, it is a viable option for massive MIMO applications [28]. There are two types of hybrid architectures based on the connection between RF chains and antennas. The first is a fully connected architecture, in which every antenna is controlled by each RF chain. The second is a partially connected architecture, in which each RF chain controls a sub-array of the antennas.

The hybrid architecture of the massive MIMO system is illustrated in Figure 1. Hybrid precoding combines baseband precoding ${\mathbf{F}}_{BB}$ $ϵ{\mathbb{C}}^{N_t\times N_t^{Beam}}$ and RF precoding

${\mathbf{F}}_{RF}ϵ{\mathbb{C}}^{N_t\times N_t}$. $\mathbf{H}ϵ{\mathbb{C}}^{N_r\times N_t}$ is the mmWave channel matrix. On the receiver side, RF combining ${\mathbf{W}}_{RF}ϵ{\mathbb{C}}^{N_r\times N_r}$ is followed by baseband combining ${\mathbf{W}}_{BB}ϵ{\mathbb{C}}^{N_r\times N_r^{Beam}}$. It is always assumed that $N_r$, $N_t$ are multiples of ${\mathrm{N}}_{RF}$ [5]. The number of pilot symbols transmitted is $N_t^{Beam}\le N_t$, and the receiver uses $N_r^{Beam}\le N_r$ pilot symbols.

Pilot signals are known signals sent by the transmitter to help the receiver characterize the channel. For a pilot matrix $\sqrt{\mathit{P}{\mathit{I}}_{N_T^{Beam}}}$, the received signal matrix $\mathbf{Y}$ is given as

$$\mathbf{Y}=\sqrt{P}{\mathit{W}}_{BB}^H{\mathit{W}}_{RF}^H\mathbf{H}{\mathbf{F}}_{RF}{\mathbf{F}}_{BB}{\mathit{I}}_{N_T^{Beam}}+\tilde{\mathit{N}}$$

(5)

where $\tilde{\mathit{N}}ϵ{\mathbb{C}}^{N_r^{Beam}\times N_t^{Beam}}$ is the noise matrix, and P the transmitted power of the pilot signal.

4. mmWave Channel Estimation

In this section, various methods for channel estimation are discussed. These include genie-aided channel estimation, OMP, and its variants such as GOMP, ROMP, and SOMP.

Applying the vector operator for (1) yields the following:

$$\mathbf{y}=\mathrm{vec}(\mathbf{Y})=\sqrt{P}({\mathbf{F}}_{BB}^T{\mathbf{F}}_{RF}^T\otimes {\mathit{W}}_{RF}^H{\mathit{W}}_{BB}^H)\mathrm{vec}(\mathbf{H})+\tilde{\mathit{n}}$$

(6)

where $\tilde{\mathit{n}}ϵ{\mathbb{C}}^{N_r^{Beam}{N}_t^{Beam}\times 1}$ is the vectorization of $\tilde{\mathit{N}}$. Here, vec(·) denotes the vectorization operator that converts a matrix into a column vector by stacking its columns sequentially. Substituting (4) in (6) gives

$$\mathbf{y}=\underset{\mathbf{Q}}{\underbrace{\sqrt{P}{\mathbf{F}}_{BB}^T{\mathbf{F}}_{RF}^T{\mathit{A}}_T^H\otimes {\mathit{W}}_{RB}^H{\mathit{W}}_{BB}^H{\mathbf{A}}_R}}{\mathit{h}}_{\mathit{m}}+\tilde{\mathit{n}}$$

(7)

where ${\mathit{h}}_{\mathit{m}}$ = $\mathrm{vec}({\mathbf{H}}_m)$ and $\mathbf{Q}ϵ{\mathbb{C}}^{N_r^{Beam}{N}_t^{Beam}\times N_r{N}_t},$ is the sensing matrix. The model for mmWave MIMO channel estimation can be simplified as follows:

$$\mathbf{y}=\mathrm{vec}(\mathbf{Y})=\mathbf{Q}{\mathit{h}}_{\mathit{m}}+\tilde{\mathit{n}}$$

(8)

4.1. Genie-Aided Channel Estimation

Genie-aided channel estimation assumes that the receiver has the AoA and AoD dictionary matrices, which helps establish the best-case performance [29]. Applying the vector operator for the mmWave channel model in (1) gives the following:

$$\mathbf{h}=\mathrm{vec}\left(\mathbf{H}\right)={\displaystyle \sum _{l=1}^L}{\mathit{a}}_T^H\left({\theta }_l^t\right)\otimes {\mathit{a}}_R\left({\theta }_l^r\right){\alpha }_l=\mathbf{\Phi }{\mathit{h}}_{\mathit{m}}$$

(9)

where $\mathbf{\Phi }=[{\mathit{a}}_T^H({\theta }_1^t)\otimes {\mathit{a}}_R({\theta }_1^r),{\mathit{a}}_T^H({\theta }_2^t)\otimes {\mathit{a}}_R({\theta }_2^r),\dots ,{\mathit{a}}_T^H({\theta }_L^t)$ $\otimes {\mathit{a}}_R({\theta }_L^r)]$ and ${\mathit{h}}_m={[{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_L]}^T$.

For a pilot matrix $\sqrt{P{\mathit{I}}_{N_t^{Beam}}}$, the output matrix $\mathit{Y}$ is given as follows:

$$\mathit{Y}=\sqrt{P}{\mathit{W}}_{BB}^H{\mathit{W}}_{RF}^H\mathit{H}{\mathit{F}}_{RF}{\mathit{F}}_{BB}{\mathit{I}}_{N_t^{Beam}}+\tilde{\mathit{N}}$$

(10)

Substituting Equation (9) into (10) and applying the vector operator, the genie-aided channel model can be given as follows:

$$\mathit{y}=\mathit{D}{\mathit{h}}_{\mathit{m}}+\tilde{\mathit{n}}$$

(11)

where $\mathit{D}=\sqrt{P}\left({\mathit{F}}_{BB}^T{\mathit{F}}_{RF}^T\otimes {\mathit{W}}_{RF}^H{\mathit{W}}_{BB}^H\right)\mathbf{\Phi }$ The genie-aided LS estimate is given as follows:

$${\widehat{\mathit{h}}}_{\mathit{m}}={\left({\mathit{D}}^H\mathit{D}\right)}^{-1}{\mathit{D}}^H\mathit{y}$$

(12)

4.2. OMP

OMP uses inherent sparsity in channels to lower computation needs and pilot overhead. OMP provides a high-resolution estimate even at low SNR by iteratively choosing significant multipath components. In hybrid beamforming arrangements, it improves beam tracking and alignment by collecting AoA and AoD. OMP’s low complexity and scalability make it perfect for real-time utilization in next-generation networks and massive MIMO applications [8]. The OMP algorithm can be used to estimate ${\mathit{h}}_{\mathit{m}}$ from (9). The OMP algorithm for mmWave channel estimation is given in Algorithm 1.

In step 1, the algorithm will initialize the required variables. In step 2, the algorithm computes the correlation of the sensing matrix, $\mathit{Q}$ and residue, $\mathit{r}\left(n-1\right)$. Then, it will select the index that has maximum correlation and support set, and $\mathit{S}$ is also updated. The corresponding column of $\mathit{Q}$, i.e., ${\mathit{Q}}_S$ is selected, and least square analysis is performed based on the chosen column. Then, the residue is updated by removing the approximation, and n is incremented. These steps will continue until the thresholding criterion is not satisfied, i.e., $∥\mathit{r}\left(n-1\right)-\mathit{r}\left(n-2\right)∥>\epsilon$, where $\epsilon$ is the predefined threshold. Finally, ${\widehat{\mathbf{h}}}_{\mathit{m}}$ is constructed by substituting ${\mathbf{h}}_m^n$ in the corresponding places, and all other entries of ${\widehat{\mathbf{h}}}_{\mathit{m}}$ are set as zeros.

Algorithm 1 mmWave channel estimation based on OMP

Input: $\mathit{Q}$, $\mathit{y}$, $\epsilon$ Output: ${\mathbf{h}}_{\mathit{m}}$

Step 1. Initialize the variables $\mathit{r}\left(0\right)=\mathit{y}$, $\mathit{r}\left(-1\right)=\mathbf{0}$, $n=1$, $\mathit{S}$ = { }

Step 2. While $∥\mathit{r}\left(n-1\right)-\mathit{r}\left(n-2\right)∥>\epsilon$ 2.1 Compute correlations: $\mathit{c}={\mathit{Q}}^H$$\mathit{r}\left(n-1\right)$ 2.2 Select index of the largest correlation: $j\left(n\right)$ = arg max (|$\mathit{c}$|) 2.3 Update support set: $\mathit{S}$ =$\mathit{S}$ ∪{ $j\left(n\right)\}$ 2.4 Solve LS ${\mathbf{h}}_m^n$ = ${\left({\left({\mathit{Q}}_S\right)}^H{\mathit{Q}}_S\right)}^{-1}{\left({\mathit{Q}}_S\right)}^H$ y 2.5 Update residual:   $\mathit{r}\left(n\right)=\mathit{y}-{\mathit{Q}}_s{\mathbf{h}}_m^n$ 2.6 $n=n+1$

Step 3. Construct sparse solution: $${\widehat{\mathbf{h}}}_{\mathit{m}}\left[n\right]=\left\{\begin{array}{c}{\mathbf{h}}_m^n,n\in \mathit{S}\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.$$

4.3. GOMP

GOMP is a variant of the OMP algorithm that reduces the complexity and execution time compared to conventional OMP [30]. Although OMP chooses one column per iteration based on the maximum correlation with the current residual, GOMP chooses K multiple columns, which has higher correlations. The GOMP becomes OMP if $K=1$. The GOMP algorithm converges faster, requiring fewer iterations to reach the desired sparsity level. When K increases, the probability of choosing the wrong indices also increases. The GOMP algorithm is described in Algorithm 2.

Algorithm 2 mmWave channel estimation based on GOMP

Input: $\mathit{Q}$, $\mathit{y}$, $\epsilon$ Output: ${\mathbf{h}}_{\mathit{m}}$

Step 1. Initialize the variables $\mathit{r}\left(0\right)=\mathit{y}$, $\mathit{r}\left(-1\right)=0$, $n=1$, $\mathit{S}$ = { }

Step 2. While $∥\mathit{r}\left(n-1\right)-\mathit{r}\left(n-2\right)∥>\epsilon$ 2.1 Compute correlations: $\mathit{c}={\mathit{Q}}^H$$\mathit{r}\left(n-1\right)$ 2.2 Find the top K indices of | $\mathit{c}$ |: $k\left(n\right)$ 2.3 Update support set: $\mathit{S}$ = $\mathit{S}$ ∪ { $k\left(n\right)\}$ 2.4 Solve LS: ${\mathbf{h}}_m^n$ = ${\left({\left({\mathit{Q}}_S\right)}^H{\mathit{Q}}_S\right)}^{-1}{\left({\mathit{Q}}_S\right)}^H$ y 2.5 Update residual:   $\mathit{r}\left(n\right)=\mathit{y}-{\mathit{Q}}_s{\mathbf{h}}_m^n$ 2.6 $n=n+1$

Step 3. Construct sparse solution: $${\widehat{\mathbf{h}}}_{\mathit{m}}\left[n\right]=\left\{\begin{array}{c}{\mathbf{h}}_m^n,n\in \mathbf{S}\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.$$

LS is performed based on the chosen columns. Then, the residue is updated by subtracting the estimate from the original signal, and n is incremented. These steps will continue until the thresholding criterion is not satisfied. Finally, ${\widehat{\mathbf{h}}}_{\mathit{m}}$ is constructed by substituting ${\mathbf{h}}_m^n$ in the corresponding places, and all other entries of ${\widehat{\mathbf{h}}}_{\mathit{m}}$ are set as zeros.

4.4. ROMP

The ROMP algorithm is an effective method for recovering sparse signals [31].  It chooses components with high correlations of comparable magnitude to prevent unstable selection. By recognizing stable groups, resolving a LS problem, and updating the residual, ROMP iteratively finds the best possible solution. ROMP is more reliable and accurate because of the balance between structured regularization and selection. The ROMP algorithm is described in Algorithm 3.

In step 1, the variables are initialized. In step 2, the algorithm computes the correlation between $\mathit{Q}$ and $\mathit{r}\left(n-1\right)$. Then, the algorithm starts grouping indices with similar magnitudes, and it creates several candidate groups $J_1,J_2,\dots$. It selects the group with the highest sum of squared correlations, J and updates the support set, S = $\mathit{S}$ ∪ {$\mathit{Q}(J)\}$, based on the selected group. Then, LS analysis is performed based on the chosen columns, the residue is updated by subtracting the estimate from the original signal, and n is incremented. These steps will continue until the thresholding criterion is not satisfied. Finally, ${\widehat{\mathbf{h}}}_{\mathit{m}}$ is constructed by substituting ${\mathbf{h}}_m^n$ in the corresponding places, and all other entries of ${\widehat{\mathbf{h}}}_{\mathit{m}}$ are set as zeros.

Algorithm 3 mmWave channel estimation based on ROMP

Input: $\mathit{Q}$, $\mathit{y}$, $\epsilon$ Output: ${\mathbf{h}}_{\mathit{m}}$

Step 1. Initialize the variables $\mathit{r}\left(0\right)=\mathit{y}$, $\mathit{r}\left(-1\right)=0$, $n=1$, $\mathit{S}$ = { }

Step 2. While $∥\mathit{r}\left(n-1\right)-\mathit{r}\left(n-2\right)∥>\epsilon$ 2.1 Compute correlations: $\mathit{c}={\mathit{Q}}^H$$\mathit{r}\left(n-1\right)$ 2.2 Sort | $\mathit{c}$ | in descending order 2.3 Form groups: - Group columns with similar magnitudes - Create several candidate groups $J_1,J_2,\dots$ 2.4 Select the group with the highest sum of squared correlations, J. 2.5 Update support set: $\mathit{S}$ = $\mathit{S}$ ∪ { $\left(J\right)\}$ 2.6 Solve LS: ${\mathbf{h}}_m^n$ = ${\left({\left({\mathit{Q}}_S\right)}^H{\mathit{Q}}_S\right)}^{-1}{\left({\mathit{Q}}_S\right)}^H$ y 2.7 Update residual:   $\mathit{r}\left(n\right)=\mathit{y}-{\mathit{Q}}_s{\mathbf{h}}_m^n$ 2.8 $n=n+1$

Step 3. Construct sparse solution: $${\widehat{\mathbf{h}}}_{\mathit{m}}\left[n\right]=\left\{\begin{array}{c}{\mathbf{h}}_m^n,n\in \mathbf{S}\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.$$

4.5. SOMP

A variant of OMP, known as SOMP, is employed to recover multiple sparse signals that share the same sensing matrix [32]. By utilizing a common sparse representation, this approach enhances the basic OMP method to address multiple measurement vector (MMV) scenarios. The objective is to reconstruct several signals from their linear measurements. The SOMP algorithm for mmWave channel estimation is shown in Algorithm 4.

Algorithm 4 mmWave channel estimation based on SOMP

Input: $\mathit{Q}$, $\mathbf{Y}$, $\epsilon$ Output: ${\mathbf{h}}_{\mathit{m}}$

Step 1. Initialize the variables $\mathit{R}\left(0\right)=\mathit{Y}$, $n=0$, $\mathit{S}$ = { }

Step 2. While $∥\mathit{R}\left(n\right)∥>\epsilon$ 2.1 Compute correlations: $\mathit{c}={\mathit{Q}}^H$$\mathit{R}\left(n\right)$ 2.2 Select index of the largest correlation: $j\left(n\right)$ = $\arg {\max }_i{\sum }_{m=1}^T|{\mathit{c}}_{i,m}|$ 2.3 Update support set: $\mathit{S}$ = $\mathit{S}$ ∪ $\left\{i\right(n\left)\right\}$ 2.4 Solve LS: ${\mathbf{H}}_{\mathit{m}}^n$ = ${\left({\left({\mathit{Q}}_S\right)}^H{\mathit{Q}}_S\right)}^{-1}{\left({\mathit{Q}}_S\right)}^H$ $\mathbf{Y}$ 2.5 Update residual:   $\mathbf{R}\left(n\right)=\mathbf{Y}-{\mathit{Q}}_s{\mathbf{H}}_{\mathit{m}}^n$ 2.6 $n=n+1$

Step 3. Construct sparse solution: $${\widehat{\mathbf{h}}}_{\mathit{m}}\left[n\right]=\left\{\begin{array}{c}{\mathbf{h}}_m^n,n\in \mathit{S},\mathrm{where}{\mathbf{h}}_m^n=\mathrm{vec}\left({\mathbf{H}}_{\mathit{m}}^n\right)\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.$$

The residue matrix is initialized as $\mathit{R}\left(0\right)$ as $\mathit{Y}$, the iteration counter as $n=0$, and the support set as a null set. In step 2, the algorithm computes the correlation between $\mathit{Q}$ and $\mathit{R}\left(n\right)$. Then, the index of the largest correlation is selected, and S is updated. Based on the chosen columns, the least square is calculated, and the residue is updated. Then, n is incremented. These steps will continue until the thresholding criterion, $∥\mathit{R}\left(n\right)∥>\epsilon$, is not satisfied. Finally, in step 3, ${\mathbf{h}}_m^n$ is constructed by applying the vector operator to ${\mathbf{H}}_{\mathit{m}}^n$, and ${\widehat{\mathbf{h}}}_{\mathit{m}}$ is constructed by substituting ${\mathbf{h}}_m^n$ into the corresponding places.

4.6. Hybrid GOMP–ROMP

The regularized GOMP combines the multiple group selection property of GOMP with the regularization of ROMP. It enhances the faster convergence of the algorithm by preserving the stability mechanism of ROMP. The proposed hybrid GOMP–ROMP algorithm is described in Algorithm 5.

In step 1, the variables are initialized. In step 2, the algorithm computes the correlation between $\mathit{Q}$ and $\mathit{r}\left(n-1\right)$. Then, it chooses K multiple columns with higher correlations based on GOMP. The regularization of ROMP is applied within the selected group. The algorithm then groups the indices corresponding to elements with similar magnitudes and creates several candidate groups $J_1,J_2,\dots$. The group with the highest sum of squared correlations, J, is selected, and the support set is updated. Then, LS analysis is performed based on the chosen columns, the residue is updated, and n is incremented. These steps will continue until the thresholding criterion is not satisfied. Finally, ${\widehat{\mathbf{h}}}_{\mathit{m}}$ is constructed by substituting ${\mathbf{h}}_m^n$ into the corresponding places, and all other entries of ${\widehat{\mathbf{h}}}_{\mathit{m}}$ are set as zeros.

Algorithm 5 mmWave channel estimation based on hybrid GOMP–ROMP

Input: $\mathit{Q}$, $\mathit{y}$, $\epsilon$ Output:${\mathbf{h}}_{\mathit{m}}$

Step 1. Initialize the variables $\mathit{r}\left(0\right)=\mathit{y}$, $\mathit{r}\left(-1\right)=0$, $n=1$, $\mathit{S}$ = { }

Step 2. While $∥\mathit{r}\left(n-1\right)-\mathit{r}\left(n-2\right)∥>\epsilon$ 2.1 Compute correlations: $\mathit{c}={\mathit{Q}}^H$ $\mathit{r}\left(n-1\right)$ 2.2 Find the top K indices of | $\mathit{c}$ |: $k\left(n\right)$ (GOMP selection) 2.3 Apply ROMP regularization within the selected group - Extract the correlation magnitude - Sort | $\mathit{c}$ | in descending order - Group columns with similar magnitudes - Create several candidate groups $J_1,J_2,\dots$ - Select the group with the highest sum of squared correlations, J. 2.4 Update support set: $\mathit{S}$ = $\mathit{S}$ ∪ { $\left(J\right)\}$ 2.5 Solve LS: ${\mathbf{h}}_m^n$ = ${\left({\left({\mathit{Q}}_S\right)}^H{\mathit{Q}}_S\right)}^{-1}{\left({\mathit{Q}}_S\right)}^H$ y 2.6 Update residual:   $\mathit{r}\left(n\right)=\mathit{y}-{\mathit{Q}}_s{\mathbf{h}}_m^n$ 2.7 $n=n+1$

Step 3. Construct sparse solution: $${\widehat{\mathbf{h}}}_{\mathit{m}}\left[n\right]=\left\{\begin{array}{c}{\mathbf{h}}_m^n,n\in \mathbf{S}\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.$$

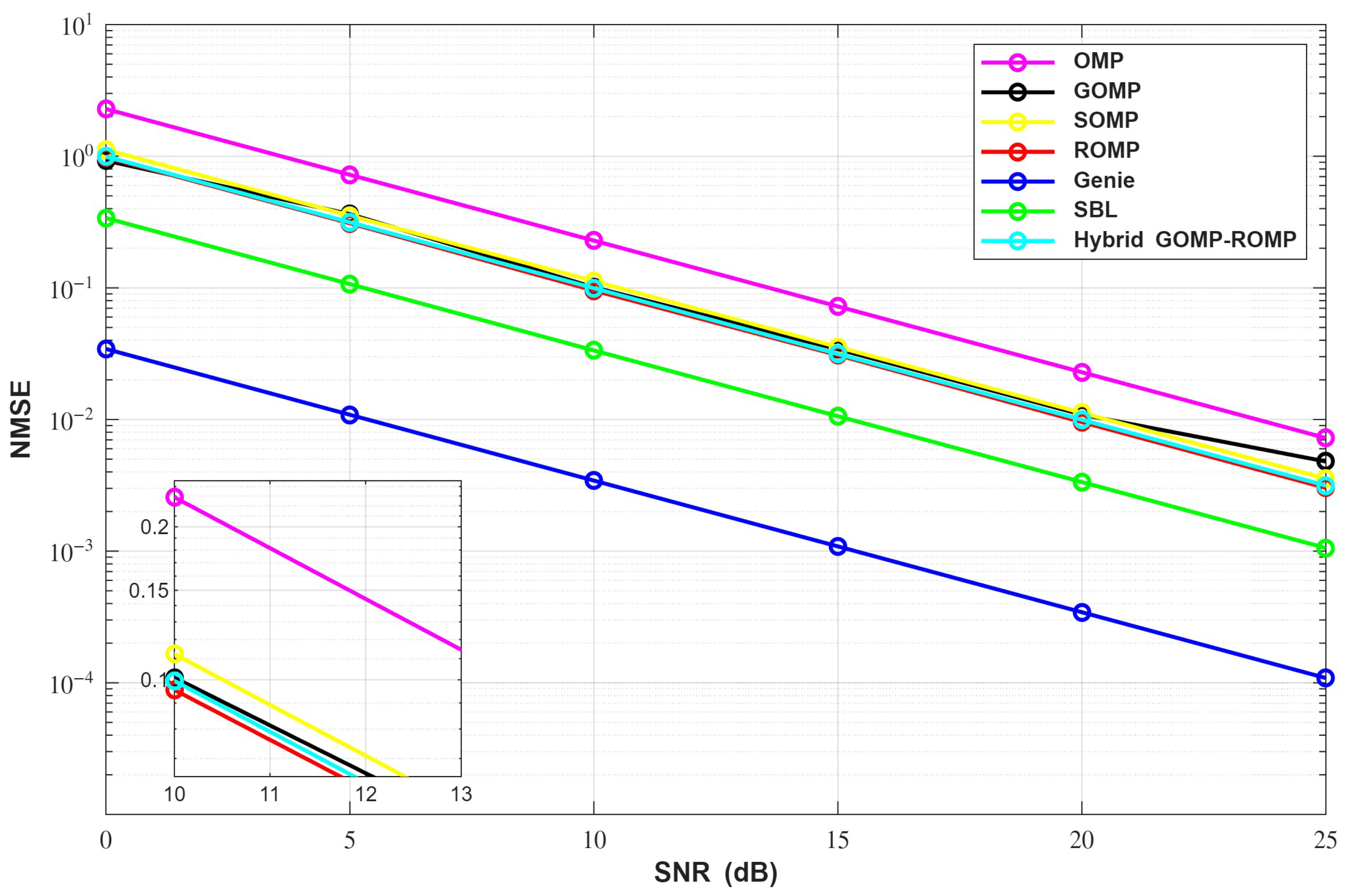
5. Results and Discussion

This section validates the simulation of the NMSE performance of various channel estimation techniques, including genie-aided, standard SBL [11], and OMP and its variants such as GOMP, SOMP, and ROMP, as well as the proposed hybrid approach, GOMP–ROMP. The simulation is carried out in MATLAB R2023b in a workstation model of a Dell PowerEdge R740 server with dual Intel Xeon Silver 4208 CPUs (16 cores/32 threads total), 128 GB DDR4 RAM, and Windows 10. The simulation parameters are listed in

Table 3. Simulation parameters.

Simulation Parameters	Values
Number of transmit antennas $(N_t)$	16, 32
Number of receive antennas $(N_r)$	16, 32
Number of RF chains	4, 8
Sparsity level $(L)$	5
Number of pilot beams $(N_r^{Beam},N_t^{Beam})$	12, 24
Threshold $(ϵ)$	1
Number of columns selected in GOMP $(K)$	4

.

The NMSE is widely used for evaluating the accuracy of channel estimation algorithms. This quantifies how close the estimated channel matrix ($\widehat{\mathbf{H}}$) is to the true channel matrix ($\mathbf{H}$) while normalizing the error relative to the actual channel power. The NMSE is computed as follows:

$$\mathrm{NMSE}=\mathbb{E}\left[{\displaystyle \frac{{∥\mathbf{H}-\widehat{\mathbf{H}}∥}_F^2}{{∥\mathbf{H}∥}_F^2}}\right]$$

(13)

Figure 2 shows the NMSE performance of conventional OMP, variants such as GOMP, ROMP, SOMP, and genie-aided channel estimation with 16 transmitting and receiving antennas. In contrast, Figure 3 illustrates the NMSE performance for 32 transmitting and receiving antennas. Genie-aided estimation shows the best performance compared to OMP and its variants. The genie-aided estimation eliminates the need for a complex sparse recovery problem, using LS estimation with the support of known AoA and AoD dictionary matrices to compute the channel coefficients with the least error. This results in lower NMSE and higher reliability. Even though prior information of complete AoA and AoD dictionary matrices are not practically possible, making genie-aided estimation as an ideal condition. In contrast to OMP algorithms, SBL improves estimation accuracy by iteratively updating channel coefficients to find significant paths. Therefore, the NMSE performance of SBL is better than all other OMP variants.

Table 4. NMSE comparison of OMP and its variants at an SNR of 15 dB for 16 × 16 and 32 × 32 MIMO configurations.

Algorithms	NMSE of 16 × 16 MIMO	NMSE of 32 × 32 MIMO
OMP	0.072291	0.077927
GOMP	0.034216	0.035162
ROMP	0.03083	0.032603
SOMP	0.035533	0.036967
Hybrid GOMP–ROMP	0.031468	0.034540

presents a comprehensive NMSE comparison of OMP and its variants at an SNR of 15 dB for 16 × 16 and 32 × 32 MIMO configurations. Variants of OMP have almost similar performance. However, ROMP has less NMSE than other variants. For a MIMO configuration of 16 × 16, at 15 dB SNR, the NMSE of ROMP is 0.03083, whereas the NMSE of OMP, GOMP, SOMP, and the proposed hybrid GOMP–ROMP are 0.072291, 0.034216, 0.035533, and 0.031468, respectively. Compared to traditional OMP, the NMSE of ROMP and the proposed algorithm is reduced by 0.041461 and 0.040823, respectively. ROMP is the most stable variant of OMP, which selects a group of columns with similar correlations, applying a regularization step to choose a more significant column. This method reduces the possibility of selecting the wrong column in each iteration, making the system more stable. Therefore, ROMP achieves lower NMSE values than other variants, and it is a more robust choice for mmWave sparse channel estimation compared to the other OMP and its variants.The hybrid GOMP–ROMP algorithm performs nearly as well as ROMP and surpasses GOMP because it combines the advantages of both: ROMP’s regularization and GOMP’s best correlation selection in each iteration. However, the hybrid GOMP–ROMP is slightly inferior to ROMP in terms of accuracy. Since it balances GOMP’s speed with ROMP’s accuracy, it is faster but slightly less accurate than ROMP due to its multiple initial choices.

GOMP outperforms OMP because instead of selecting single column in each iteration, GOMP selects multiple columns. Selecting multiple columns increases the convergence of the algorithm, reducing the number of iterations. Still, choosing many atoms raises the possibility of incorporating the wrong selection of columns in a sparse environment like mmWave, particularly when dictionary matrix columns are correlated. GOMP typically performs better than simple OMP in terms of NMSE, providing a trade-off between speed and accuracy in sparse mmWave channel estimation. When employing GOMP and SOMP instead of conventional OMP, the NMSE is decreased by 0.03875 and 0.036758, respectively, at 15 dB SNR for the 16 × 16 MIMO configuration. Both SOMP and GOMP exhibit comparable NMSE performance, and because SOMP employs joint sparsity across several measurement vectors, it performs better than traditional OMP and can accurately estimate the sparse channel. When compared to OMP, this leads to a much reduced NMSE, enhanced resistance to noise, and significantly greater channel estimation accuracy.

The conventional OMP performs the worst, and it has a higher NMSE than its variants. The OMP is the basic greedy algorithm that selects only one column in each iteration based on the maximum correlation. Therefore, it increases the computational time. An incorrect selection in the early iteration of OMP can seriously affect the final estimate, and the performance of OMP degrades if the columns of the sensing matrix are highly correlated. Even though OMP is computationally efficient among other sparse recovery algorithms, it has higher NMSE and worse support recovery than more sophisticated variants like SOMP, ROMP, and GOMP.

When the number of antennas at the transmitter and receiver increases to 32, there is a slight increase in the NMSE for OMP and its variants. As $N_t$ and $N_r$ increase, the channel matrix also expands, resulting in a larger dictionary matrix and more values to estimate. OMP and its variants work by finding the most significant path from a large set of dictionary matrices. But, as number of antennas increases, the size dictionary matrix will also increase, which makes it harder for OMP to correctly identify the correct support set. As the number of antennas increases, the complexity of the sparse recovery rises, resulting in higher NMSE values. It is observed that the proposed hybrid GOMP–ROMP algorithm maintains robust NMSE performance even for larger MIMO configurations, demonstrating improved scalability and stability.

Computational Complexity

The computational complexity of genie-aided estimation, OMP, and its variants is discussed in this section. From Equation (12), the computational complexity of genie-aided estimation can be calculated as $\mathcal{O}({(N_r{N}_t)}^3)$. The complexity of the OMP algorithm is explained as follows. From step 2.1 in Algorithm 1, the complexity required is $\mathcal{O}(N_r^{Beam}{N}_t^{Beam}{N}_r{N}_t)$. Then, in step 2.2, for the index selection, it is $\mathcal{O}(N_r{N}_t)$. The complexity of the LS solution for n iterations in step 2.4 is $\mathcal{O}(N_r^{Beam}{N}_t^{Beam}+n^3)$. For the residual update in step 2.5, the complexity will be $\mathcal{O}(N_r^{Beam}{N}_t^{Beam}n)$. The number of multipath components, L, also depends on the iteration. Therefore, the total complexity of OMP can be approximated as $\mathcal{O}(L{N}_r^{Beam}{N}_t^{Beam}{N}_r{N}_t+L^3)$.

The complexity analyses of OMP and GOMP are similar. The GOMP selects the top K columns in each iteration. Therefore, for LS estimation—step 2.4 in Algorithm 2—the matrix size will be $(N_r^{Beam}{N}_t^{Beam}\times nK)$. The overall complexity of GOMP will be $\mathcal{O}(L/K\times N_r^{Beam}{N}_t^{Beam}{N}_r{N}_t+{(LK)}^3)$. Compared to OMP or GOMP, ROMP adds a more difficult selection criterion that includes magnitude comparisons and candidate groups; however, the fundamental operations such as correlation calculations, LS estimation, and residue update are the same as OMP only. Therefore, the complexity of ROMP can be approximated as $\mathcal{O}(L{N}_r^{Beam}{N}_t^{Beam}{N}_r{N}_t+L^3)$. When recovering multiple sparse signals at once, SOMP’s complexity increases linearly with the number of channels, but recovering a single channel maintains the same complexity as OMP, i.e., $(L{N}_r^{Beam}{N}_t^{Beam}{N}_r{N}_t+L^3)$. The complexity of the hybrid GOMP–ROMP algorithm is comparable to GOMP and ROMP and can be readily inferred from their respective complexity derivations. From step 2.1 in Algorithm 5, the complexity required is $\mathcal{O}(N_r^{Beam}{N}_t^{Beam}n)$. Then, after selecting the top K indices based on GOMP, complexity will reduce to $\mathcal{O}(L/K\times (N_r^{Beam}{N}_t^{Beam}{N}_r{N}_t))$. This is followed by regularization, LS estimation, and residue update, and finally, the computational complexity of the hybrid GOMP–ROMP can be approximated as $\mathcal{O}(L/K\times (N_r^{Beam}{N}_t^{Beam}{N}_r{N}_t+L^3))$. The primary factors affecting the complexity of SBL are covariance updates and repetitive matrix inversions. Therefore, the computational complexity of standard SBL [11] is roughly described as $\mathcal{O}({(N_r{N}_t)}^3)$. Detailed analyses of computational complexity for genie-aided estimation and OMP and its variants are shown in

Table 5. Computational complexity analysis.

Algorithm	Computational Complexity	${\mathit{N}}_{\mathit{r}}={\mathit{N}}_{\mathit{t}}=16,$${\mathit{N}}_{\mathit{t}}^{\mathit{Beam}}={\mathit{N}}_{\mathit{r}}^{\mathit{Beam}}=12$	${\mathit{N}}_{\mathit{r}}={\mathit{N}}_{\mathit{t}}=32,$${\mathit{N}}_{\mathit{t}}^{\mathit{Beam}}={\mathit{N}}_{\mathit{r}}^{\mathit{Beam}}=24$
Genie	$\mathcal{O}({(N_r{N}_t)}^3)$	16,777,216	1,073,741,824
SBL	$\mathcal{O}({(N_r{N}_t)}^3)$	16,777,216	1,073,741,824
OMP	$\mathcal{O}(L{N}_r^{Beam}{N}_t^{Beam}{N}_r{N}_t+L^3)$	184,445	2,949,120
GOMP	$\mathcal{O}(L/K\times (N_r^{Beam}{N}_t^{Beam}{N}_r{N}_t+{(LK)}^3))$	52,489	745,280
ROMP	$\mathcal{O}(L{N}_r^{Beam}{N}_t^{Beam}{N}_r{N}_t+L^3)$	184,445	2,949,120
SOMP	$\mathcal{O}(L{N}_r^{Beam}{N}_t^{Beam}{N}_r{N}_t+L^3)$	184,445	2,949,120
Hybrid GOMP–ROMP	$\mathcal{O}(L/K\times (N_r^{Beam}{N}_t^{Beam}{N}_r{N}_t+L^3))$	46,205	737,405

. For the complexity analysis, $L=5$ and $K=4$ are considered.

The computational complexity of various algorithms for 16 and 32 antennas at the transmitter and receiver are analyzed. The computational complexity of genie and SBL are very high, and by increasing antennas from 16 to 32, the computational complexity increases by 64 times. Conventional OMP, ROMP, and SOMP have approximately similar complexity—much less than genie-aided estimation. For these algorithms, when the antennas are increased from 16 to 32, complexity is increased by 16 times. For the 16 × 16 MIMO configuration, the computational complexity of the proposed hybrid GOMP–ROMP algorithm is almost similar to GOMP, and it is 4 times less than conventional OMP, ROMP, and SOMP and 363 times less than genie and standard SBL. The proposed hybrid algorithm has less computational complexity among all of the other algorithms because it utilizes the advantages of both GOMP and ROMP, such as selecting the top correlations in each iteration in GOMP and regularization in ROMP, so this method significantly reduces the computational complexity. Therefore, it is concluded that the suggested hybrid algorithm is computationally more efficient than all other algorithms. The hybrid GOMP–ROMP can achieve similar NMSE performance to ROMP with reduced complexity. Even though SBL and genie have the lowest NMSE values, practically, they are not possible to implement because of their higher complexity.

Figure 4 presents a comparative analysis of the proposed hybrid GOMP–ROMP algorithm and OMP variants with 16 × 16 and 32 × 32 MIMO configurations. The bar plots show the computational complexity of each algorithm, while the line plot shows NMSE, reflecting channel estimation accuracy. The combined illustration of both NMSE and computational complexity allows a clear trade-off comparison of these algorithms. From this plot, it is clear that increasing the order of the MIMO configuration results in a drastic increase in computational complexity and a reduction in NMSE across all algorithms. The proposed algorithm maintains a better balance with accuracy and complexity, as it achieves the NMSE value nearest to ROMP with reduced complexity.

The normalized efficiency index (EI) is a performance metric used to evaluate and compare the estimation algorithm in terms of accuracy and computational complexity. In general, for a channel estimation algorithm to achieve better accuracy (low NMSE), it requires a higher computational cost. The normalized EI offers a single normalized metric that quantifies performance per computing unit so that methods may be fairly compared. Higher EI can be achieved by lower denominator values, which indicates better algorithm efficiency. It is defined and normalized within the range [0, 1] as follows:

$$\mathrm{Normalized}\mathrm{EI}={\displaystyle \frac{\frac{1}{\mathrm{NMSE} \times \mathrm{Computational}\mathrm{Complexity}}}{\max \left(\frac{1}{\mathrm{NMSE} \times \mathrm{Computational}\mathrm{Complexity}}\right)}}$$

(14)

The normalized EI comparison of the proposed hybrid algorithm and the OMP variants for 16 × 16 and 32 × 32 MIMO configurations at an SNR of 15 dB is summarized in

Table 6. Normalized EI comparison of various algorithms for SNR of 15 dB.

Algorithm	$\mathit{Nt}=\mathit{Nr}=16$			$\mathit{Nt}=\mathit{Nr}=32$
	NMSE	Complexity	Normalized EI	NMSE	Complexity	Normalized EI
OMP	0.072291	184,445	0.1090	0.077927	2,949,120	0.1090
GOMP	0.034216	52,489	0.8095	0.035162	745,280	0.8096
ROMP	0.030834	184,445	0.2556	0.032603	2,949,120	0.2557
SOMP	0.035533	184,445	0.2218	0.036967	2,949,120	0.2218
Hybrid GOMP–ROMP	0.031468	46,205	1.0000	0.034539	737,405	1.0000

, with the corresponding bar plot shown in Figure 5.

For the 16 × 16 MIMO configuration, the normalized EI values of OMP, GOMP, ROMP, SOMP, and the proposed hybrid GOMP–ROMP algorithms are 0.1090, 0.8096, 0.2557, 0.2218, and 1.0000, respectively, at an SNR of 15 dB. The conventional OMP has the lowest EI due to its higher computational complexity and NMSE. Across all OMP variants, ROMP achieved a lower NMSE; however, it could not achieve a better EI due to its higher computational complexity. The proposed hybrid GOMP–ROMP achieves the highest EI with a good NMSE at lower computational complexity for both MIMO configurations. This indicates that the proposed algorithm maintains a balance between computational complexity and accuracy.

6. Conclusions

This paper examines the effectiveness of OMP in sparse channel estimation and discusses improvements using its advanced variants— GOMP, ROMP, SOMP. A new hybrid GOMP–ROMP algorithm is introduced to reduce computational costs and enable faster convergence, all while meeting the desired performance requirements. This paper also analyzes the NMSE performance and computational complexity of genie-aided estimation, OMP, and its variants, focusing on practical implications for system design and implementation. Genie-aided estimation shows the best NMSE performance compared to OMP and its variants, but it is practically difficult to implement. ROMP is the most stable variant of OMP, which selects a group of columns with similar correlations, applying a regularization step to choose a more significant column. The conventional OMP has a higher NMSE than its variants. Simulation results show that the proposed algorithm reduces the NMSE by 0.040823 compared to OMP and achieves ROMP’s accuracy with lower complexity. As the number of antennas increases, computational complexity increases drastically. Channel estimation using the hybrid GOMP–ROMP presents a promising method for achieving accurate and efficient results in mmWave massive MIMO systems. Future research could consider integrating DL techniques to decrease computational complexity while preserving, or possibly enhancing, estimation accuracy, particularly in dynamic or large-scale deployment environments.