SFC-GS: A Multi-Objective Optimization Service Function Chain Scheduling Algorithm Based on Matching Game

Abstract

Service Function Chain (SFC) is a framework that dynamically orchestrates Virtual Network Functions (VNFs) and is essential to enhancing resource scheduling efficiency. However, traditional scheduling methods face several limitations, such as low matching efficiency, suboptimal resource utilization, and limited global coordination capabilities. To this end, we propose a multi-objective scheduling algorithm for SFCs based on matching games (SFC-GS). First, a multi-objective cooperative optimization model is established that aims to reduce scheduling time, increase request acceptance rate, lower latency, and minimize resource consumption. Second, a matching model is developed through the construction of preference lists for service nodes and VNFs, followed by multi-round iterative matching. In each round, only the resource status of the current and neighboring nodes is evaluated, thereby reducing computational complexity and improving response speed. Finally, a hierarchical batch processing strategy is introduced, in which service requests are scheduled in priority-based batches, and subsequent allocations are dynamically adjusted based on feedback from previous batches. This establishes a low-overhead iterative optimization mechanism to achieve global resource optimization. Experimental results demonstrate that, compared to baseline methods, SFC-GS improves request acceptance rate and resource utilization by approximately 8%, reduces latency and resource consumption by around 10%, and offers clear advantages in scheduling time.

1. Introduction

5G, representing the latest generation of mobile communication networks, delivers substantial enhancements in device connectivity, data transmission rates, and latency management, thereby establishing the foundation for the Internet of Everything. However, the proliferation of users and the diversification of service demands result in increased network traffic and greater complexity in service processing. Inefficient virtual network function mapping can result in excessive resource consumption, reduced request acceptance rates, increased end-to-end delays, and other performance issues, thereby directly affecting network service quality and resource utilization efficiency. To address this challenge, Service Function Chain (SFC), a pivotal technology arising from the integration of Network Function Virtualization (NFV) and Software-Defined Networking (SDN), not only improves resource utilization and service quality but also enables end-to-end service processing by sequentially orchestrating multiple Virtualized Network Functions (VNFs) according to a defined network service orchestration strategy. It thus provides a flexible and efficient solution to accommodate differentiated and dynamic service demands in the 5G environment [1].

Based on the virtualization capabilities of NFV, Service Function Chains (SFCs) abstract the underlying computing, communication, storage, and other resources, enabling network function instances—such as firewalls and deep packet inspection—to be flexibly deployed on general-purpose hardware [2]. Efficiently orchestrating and scheduling VNF instances in SFCs to handle dynamic fluctuations in resource supply and demand, while simultaneously optimizing end-to-end Quality of Service (QoS), has become a critical challenge. Although the introduction of SFCs enhances the flexibility of network services, it also brings more complex scheduling problems. Traditional scheduling approaches struggle to meet the high concurrency and low-latency requirements of 5G networks, creating an urgent need for intelligent scheduling mechanisms that optimize resource utilization and service performance. As SFCs assume an increasingly central role in network services, their scheduling faces key challenges, including competition for computing, network, and storage resources, strict temporal constraints, and significant operational overhead. Moreover, resource preemption among VNF instances and nonlinear fluctuations in service demand result in imbalanced resource utilization [3]. The strict ordering constraints of SFC topologies further conflict with the scheduling complexity of parallel service chains, exacerbating the mismatch between scheduling behavior and actual demand, and ultimately degrading scheduling efficiency while increasing computational overhead.

Existing SFC scheduling methods (reinforcement learning, mathematical programming, generative/matching theory) have critical limitations: reinforcement learning faces data dependency and slow convergence in large scales, mathematical programming lacks stability and has high complexity, and generative/matching theory struggles with multi-objective balance, which creating an urgent need for an efficient, low-overhead approach to achieve stable multi-objective optimization and global resource coordination.

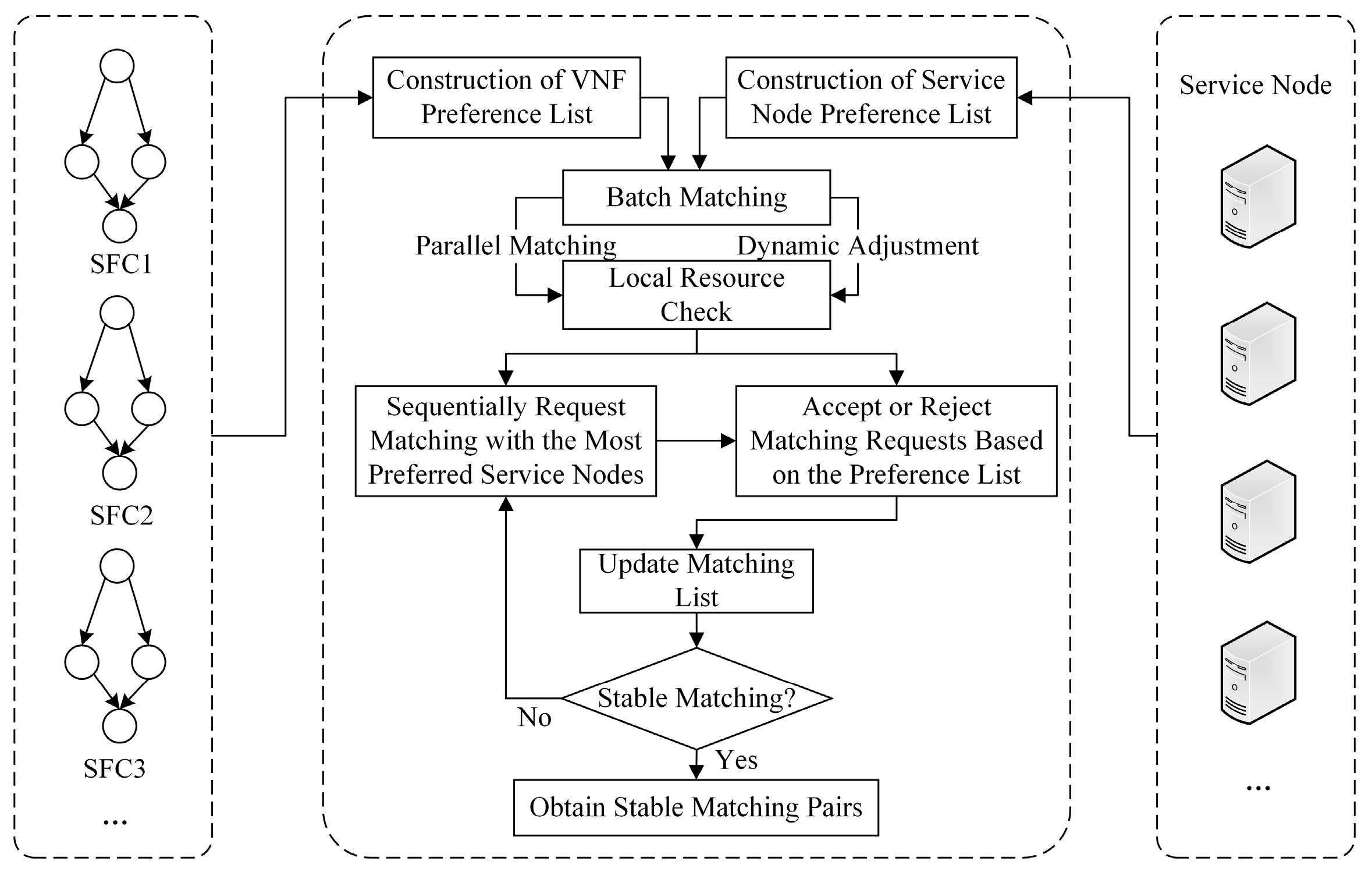
To address the above challenges, this paper proposes a service function chain scheduling algorithm based on matching game (SFC-GS). By leveraging bidirectional preference matching and a hierarchical batch-processing mechanism, the proposed approach achieves global resource optimization with low overhead, effectively tackling the core challenges in SFC scheduling. The main contributions of this paper are as follows:

• We develop a multi-objective SFC scheduling model that considers four objectives: maximizing request acceptance rate, minimizing end-to-end delay, minimizing resource consumption, and minimizing scheduling execution time. This model improves SFC orchestration efficiency and 5G network resource utilization, thereby enhancing the network’s overall service-carrying capacity.
• We further propose a two-way preference matching mechanism based on a matching game. The mechanism accounts for VNF resource demands—including computation, storage, and bandwidth—along with physical service node availability and local topology. Multiple rounds of iterative games enable rapid local matching, improving scheduling responsiveness, refining fitness evaluation, and strengthening dynamic adaptability.
• We introduce a hierarchical batch scheduling strategy based on resource demand. Service requests are processed in priority-based batches, with resource allocation for subsequent batches dynamically adjusted according to feedback from previous results, enabling iterative optimization. This mechanism ensures timely response to high-priority requests, maintains fairness for low-priority requests, and balances overall resource utilization, thereby enhancing scheduling flexibility and allocation efficiency.
• The remainder of this paper is organized as follows: Section 2 summarizes previous related work conducted by other researchers; Section 3 describes the system model and problem description; Section 4 describes in detail the matching model setting and matching preference list construction, and presents the algorithmic steps of multi-objective optimal service function chain scheduling based on matching game; Section 5 describes the simulation experiment environment construction and design and systematically analyzes the experimental results; Section 6 summarizes the work of this paper and discusses directions for future work.

2. Related Work

In recent years, research on SFC scheduling has focused on reducing end-to-end latency, improving load balancing, and enhancing system reliability [4]. This paper reviews existing approaches from three perspectives: reinforcement learning-based methods, mathematical programming-based methods, and methods based on generative models and matching theory. Their respective strengths and limitations are analyzed, and the potential of matching game-based methods for SFC scheduling is further explored. The details are as follows:

(1) Reinforcement Learning-Based Methods

Jia et al. [5] proposed a reconfigurable time-expanded graph and further developed a dynamic SFC scheduling model. The algorithm, combined with deep reinforcement learning, is proposed to solve the SFC scheduling problem formulated as integer linear programming under limited resources and time constraints. Zhang et al. [6] formulated the SFC scheduling problem as a multi-Markov decision process and employed a multi-state action deep reinforcement learning algorithm to learn the optimal scheduling policy, aiming to minimize the weighted total delay. Song et al. [7] proposed a deep reinforcement learning-based approach for virtual network function deployment, which reduced transmission delay by identifying the shortest matching paths. Additionally, they introduced a service function chain rescheduling mechanism based on network calculus theory to minimize queuing delay and enhance the flexibility of the scheduling algorithm. Cao et al. [8] proposed a task-oriented service provisioning and scheduling model for networks’ dynamic complexity. Building on this model, they formulated the SFC scheduling problem as maximizing the number of task completions under limited resource and time constraints and proposed a deep reinforcement learning algorithm to solve it as an integer linear programming problem. Baharvand et al. [9] proposed a deep Q-learning-based service function chain scheduling method that used a scheduling mechanism to reorder the functions in the chain. The method explored the simultaneous scheduling of multiple SFCs, aiming to reduce the total completion time of the scheduling, and improved the resource utilization and request acceptance rate.

However, there are problems with training data dependency, slow convergence, and lagging policy updates in the mega-scale scenarios. Most of the existing research focuses on unidirectional resource allocation, ignoring the service function chain and resource nodes, such as the bidirectional preference of performance demand and load balancing, which is prone to trigger local optimum, resource conflict and high computational overhead. Notably, in VPN (Virtual Private Network)-secured scenarios, these methods’ high computational overhead from training makes it hard to accommodate additional encryption/decryption resource demands, a gap SFC-GS’s lightweight local resource check can address.

(2) Mathematical Programming-Based Methods

Jia et al. [10] represented the SFC scheduling problem for NFV-enabled 5G networks as a mixed-integer nonlinear programming problem and proposed an efficient algorithm to identify redundant virtual neural networks, aiming to maximize the number of requests that satisfy both latency and reliability constraints. E. Nagireddy et al. [11] conducted a rigorous evaluation of different action spaces within the model to optimize the action space across various paths. The results demonstrated that the proposed algorithm served as a feasible and effective optimization solution to the problem of SFC request scheduling within the given scope. Wang et al. [12] formulated the service function chain scheduling problem as a 0–1 nonlinear integer programming problem and proposed a two-stage heuristic algorithm to solve this problem. In the first phase, if resources were sufficient, the service function chains were deployed in parallel to the UAV edge servers based on the proposed pairing principle between the service function chains and the UAVs in order to minimize the sum of task completion times. Instead, when resources were insufficient, a revenue maximization heuristic was used to deploy arriving SFCs in a serial service mode.

Despite their theoretical optimality, mathematical programming methods share key drawbacks: they lack stability guarantees (often forming “blocking pairs” that reduce resource utilization and waste network resources) and incur extremely high solution costs in large-scale complex network environments. Adding VPN-specific resource constraints (e.g., secure tunnel bandwidth) would further increase their solving complexity, conflicting with VPN services’ low-latency needs—an issue SFC-GS’s batch matching avoids via simplified local computation.

(3) Generative Model and Matching Theory-Based Methods

Liao et al. [13] addressed SFC scheduling as an integer linear programming problem by dynamically sensing resource availability under different time slots. They proposed a resource-aware SFC scheduling algorithm that combined VNFs and time slots. The algorithm efficiently coordinates computing and network resources in the spatiotemporal domain, optimized resource utilization while strictly adhering to application latency requirements. Zhang et al. [14] proposed a novel network diffuser based on a conditional generative model. This model formulated the SFC optimization problem as a state sequence generation task for planning purposes and performed graph diffusion over state trajectories, conditioning the extraction of SFC decisions on the optimization constraints and objectives. Pham et al. [15] proposed a matching-based algorithm to solve the NP-hard VNF scheduling problem, aiming to address the challenges of high computational cost and the inability to perform online scheduling while ensuring scheduling stability and satisfying the allocation requirements of all network services.

However, these methods face a shared challenge: when simultaneously optimizing multi-objectives, they struggle with resource trade-offs and coordination difficulties. How to achieve efficient and fair resource scheduling under the constraints of uncertainty in resource requirements and request priorities such as computing, communication, and storage is still a key challenge in current SFC scheduling. Notably, existing matching theory methods here rarely consider VPN security, whereas SFC-GS’s bilateral preference list can explicitly weight VPN resource fitness, thereby filling this practical gap.

In summary, current SFC scheduling methods have distinct but overlapping limitations. Additionally, few methods address bidirectional preferences between VNFs and resource nodes or adapt to the uncertainty in computing/communication/storage demands. This highlights an urgent need for a VNF scheduling method that synergizes resource states, enables efficient decisions, and scales well-while simultaneously optimizing scheduling efficiency, resource cost, and QoS to enhance overall 5G network service performance. In the SFC scheduling problem, how to determine the execution order of VNF instances at each node based on satisfying the location constraints and priority constraints to achieve the optimal solution is an urgent problem. Matching game is a game-theoretic approach applicable to the resource allocation problem, which can make two-way preference choices among multiple subjects to achieve efficient and fair resource scheduling. The complex supply and demand relationship between VNF instances and server resources and the dynamic nature of service requests require scheduling algorithms with fast adaptation capabilities. Compared to the traditional integer planning or heuristic search-based methods, the matching game has higher scalability and real-time performance, which enables SFC scheduling to be more efficient and flexible to adapt to the dynamic demands of 5G networks. Therefore, the SFC scheduling method based on matching game has an important research value in improving resource utilization and optimizing resources.

3. System Model and Problem Formulation

3.1. System Model

In order to construct a reasonable VNF mapping model, a formal description of the topology of the physical network is required, and the mapping model is shown in Figure 1. In this paper, the underlying physical network is defined as an undirected graph $G\left(N,L\right)$, $N=\left\{n_1,n_2,\cdots ,n_{\max }\right\}$ denotes the set of physical nodes in NFV, and max represents the maximum number of service nodes. These nodes are composed of generalized high-performance server clusters $Server$, which serve as the fundamental hardware infrastructure for hosting VNFs. They possess capabilities in computation, storage, and network communication. Each physical service node is equipped with a certain number of CPU cores, memory modules, and network interface cards, which collectively determine the node’s resource capacity and processing capability. For each physical node $n_i\in N$, there are computational resources $C_{ni}$ such as the number of CPU cores, storage resources $S_{ni}$ such as memory capacity, and network bandwidth resources $B_{ni}$. The set $L=\{l_1,l_2,l_3,\cdots ,l_n\}$ denotes the physical links between NFV nodes, which serve as communication channels connecting the physical nodes. These links determine the maximum amount of data that can be transmitted between nodes per unit of time, thereby ensuring the smooth transmission of data within the service function chain. For a physical link $l_{i,j}\in L$ connecting a physical node $n_i$ and a physical node $n_j$ has a link capacity $C{l}_{i,j}$ denotes the upper limit of the amount of data that can be transmitted over the link, where $n_i,n_j\in N$, and $n_i\ne n_j$. Let $V=\{v_1,v_2,\dots ,v_n\}$ denote the set of all VNFS. The set of service function chains is defined as $S=\{s_1,s_2,\cdots ,s_k\}$, where each service function chain $s_k=\{VN{F}_{k1},VN{F}_{k2},\cdots ,VN{F}_{kq}\}$ consists of a set of sequence of VNFs arranged in a specific order. For example, to run a web application, a firewall function must first inspect incoming data packets before forwarding them to the web service function.

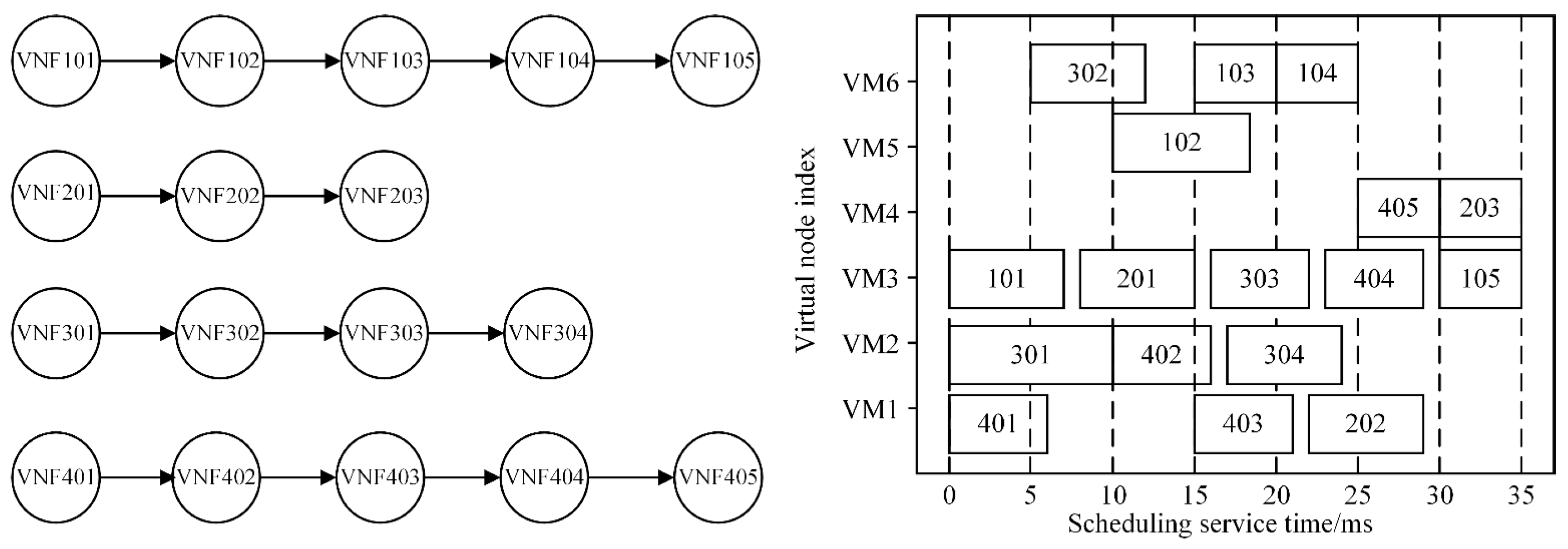
SFC instances have differentiated service requirements and need to be reasonably scheduled based on resource constraints, efficient utilization, and quality of service requirements. This paper investigates how to optimize scheduling algorithms in resource-constrained computing environments to achieve efficient VNF placement on heterogeneous virtual machines, thereby meeting the diverse requirements of different SFC instances. Assuming that there are four SFC instances with differentiated service demands for scheduling, namely, SFC1: VNF101–105, SFC2: VNF201–203, SFC3: VNF301–304, and SFC4: VNF401–405. The scheduling algorithm is required to perform dynamic mapping within a resource pool composed of six heterogeneous virtual machines (VM1–VM6), aiming to allocate VNFs in a demand-driven manner based on the predefined VNF–VM mapping relationships, under the constraint of limited computing resources. The VNF scheduling example is shown in Figure 2.

3.2. Display Style

In this paper, we divide the processing of a service request into multiple time intervals, denote these time slots by the set $T=\{1,2,\cdots ,t\}$, and set each time slot $t\in T$ as a processing period for a link mapping. Define a binary Boolean variable $x_{ij}^n$ that indicates whether the VNF $i$ requested by the SFC is scheduled on physical node $n_j$, if yes then $x_{ij}^n=1$, otherwise $x_{ij}^n=0$. Define a binary Boolean variable $y_{ab}^l$, which indicates whether the virtual link $(a,b)$ connecting nodes $a$ and $b$ in the service function chain is mapped to the physical link $l_{a,b}$, if yes then $y_{ab}^l=1$, otherwise $y_{ab}^l=0$. In this paper, the end-to-end delay mainly consists of the processing delay ${\delta }_{proc}^v$ of the VNF at the physical node and the propagation delay ${\delta }_{trans}^l$ of the data traffic on the physical link, defining the maximum tolerable delay $D_{\max }^{s_k}$. The total end-to-end delay $D_{total}^{s_k}$ is shown in Equation (1).

$$D_{total}^{s_k}={\displaystyle \sum _{n_i,n_j\in N}{\displaystyle \sum _{v\in V}{x}_{ij}^n}}\times {\delta }_{proc}^v+{\displaystyle \sum _{l\in L}{\displaystyle \sum _{a,b\in (a,b)}{y}_{ab}^l}{\delta }_{trans}^l\le D_{\max }^{s_k}}$$

(1)

In VNF architecture design, physical node selection, along with strategies for VNF mapping and sequencing, are key factors influencing both link transmission delay and processing delay. As critical components of overall network service latency, these factors are directly related to network performance and user experience. In order to optimize network operations and reduce resource consumption and service delay, systematic optimization of key indicators such as end-to-end delay, average request acceptance rate, and resource consumption is required based on actual scenarios to improve VNF performance and network service quality.

In NFV scenarios, the Average Acceptance Rate (AAR) is a key metric for evaluating the system’s service capability. It represents the proportion of SFC requests that are successfully accepted out of the total incoming requests. At any time between 1 and $T$, when request $s$ is successfully accepted, the binary Boolean variable $X_s$ takes the value of 1; when request $s$ is rejected due to insufficient resources or constraint conflicts, the binary Boolean variable $X_s$ takes the value of 0. The Average Acceptance Rate is expressed as shown in Equation (2).

$$R_{AAR}={\displaystyle \frac{1}{T}}{\displaystyle \sum _{t=1}^T(\frac{{\displaystyle \sum s_k\in S\times X_s}}{\left|S\right|}} \times 100\%)$$

(2)

The resource consumption $R_{total}$ of the SFC request scheduling represents the normalized sum of the CPU resource consumption $R_{\mathrm{CPU}}$, storage resource consumption $R_{\mathrm{Storage}}$, and bandwidth resource consumption $R_{\mathrm{BW}}$ of each virtual network node in the SFC, where ${\omega }_{\mathrm{CPU}}+{\omega }_{\mathrm{Storage}}+{\omega }_{\mathrm{BW}}=1$, as shown in Equation (3).

$$\begin{array}{l}{R}_{total}={\omega }_{\mathrm{CPU}}\cdot {\displaystyle \sum _{s_k\in \mathcal{S}}}{\displaystyle \sum _{v\in V}}{\displaystyle \sum _{n\in N}}{C}_{ni}\cdot x_{ij}^n+{\omega }_{\mathrm{Storage}}\cdot {\displaystyle \sum _{s\in \mathcal{S}}}{\displaystyle \sum _{v\in V}}{\displaystyle \sum _{n\in N}}{S}_{ni}\cdot x_{ij}^n\\ +{\omega }_{\mathrm{BW}}\cdot {\displaystyle \sum _{s\in \mathcal{S}}}{\displaystyle \sum _{l\in L}}{\displaystyle \sum _{a,b\in l_{a,b}}}{B}_{ni}\cdot y_{ab}^l\end{array}$$

(3)

Given that the actual network environment and service requirements are extremely complex, the following constraints need to be introduced in the SFC orchestration process in order to ensure service quality.

(1) Resource constraints aspects

Computational resource constraints: For each physical node $n_j$, there is ${\displaystyle \sum _{k=1}^p{\displaystyle \sum _{i=1}^q{x}_{ki}^n}}\times C_{ki}\le C_{n_j}$, $C_{ki}$ denotes the amount of computational resources required by the $VN{F}_{ki}$, which limits the computational resource occupancy of the VNF on a physical node so that it always remains within the available computational capacity of that node to prevent resource overload.

Storage resource constraints: ${\displaystyle \sum _{k=1}^p{\displaystyle \sum _{i=1}^q{x}_{ki}^n}}\times S_{ki}\le S_{n_j}$, $S_{ki}$ where denotes the number of storage resources required by the $VN{F}_{ki}$ to ensure that the storage resources of the node meet the demand.

Network bandwidth constraint: For each physical link $l_{a,b}$, ${\displaystyle \sum _{k=1}^p{\displaystyle \sum _{i=1}^{q-1}{x}_{ki}^l}}\times r_{ki,k(i+1)}\le C_{l_{ij}}$, where $r_{ki},k(i+1)$ denotes the traffic demand in the service function chain $s_k$ from $VN{F}_{ki}$ to $VN{F}_{k(i+1)}$ in the service function chain, ensuring that the link is not congested due to traffic overload.

(2) Sequential constraint aspects

Define the variable $t_{ki}$ to denote the start execution time of $VN{F}_{ki}$ and $p_{ki}$ to denote the execution time of $VN{F}_{ki}$, with the formula $p_{ki}={\displaystyle \frac{w_{ki}}{C_{node}}}$, $w_{ki}$ where is the amount of task computation and $C_{node}$ is the computation speed. For the order of VNFs in each service function chain $s_k$, there is $t_{ki}+p_{ki}\le t_{k(i+1)}$, which ensures that the VNFs are executed sequentially in the specified order.

4. Service Function Chain Scheduling Algorithm Based on Matching Game

4.1. Matching Model and Preference List Construction

4.1.1. Matching Model Settings

Based on the constraints of the matching game framework, both participants in the model design must establish a two-way preference ranking for all potential objects of the other group. In this paper, let ${\succ }_{k1}$ denote the preference ranking of $VN{F}_{k1}$ over the service nodes, and let ${\succ }_n$ represent the preference ranking of service node $n$ over the VNF instances. For $\forall s\in S$, $n_1{\succ }_s{n}_2$ indicates that service function chain $s$ prefers service node $n_1$ over $n_2$, while $\varnothing {\succ }_{s}n$ denotes that $s$ does not accept service node $n$; $VN{F}_{k1}{\succ }_{n}VN{F}_{k2}$ indicates that service node $n$ prefers VNF instance $k_1$ over $k_2$, while $\varnothing {\succ }_{n}VN{F}_k$ denotes that service node $n$ does not accept VNF instance $k$. Meanwhile, the scheduling of VNF instances onto the selected service nodes yields a many-to-one matching sequence, defined by the matching function $\mu :s_k\cup N\to 2^{s_k\cup N}$, which represents the set of matching pairs formed between the set of VNF instances constituting the service function chain $s_k$ and the set of service nodes $N$ after the matching process. When there exists a service node $n_x\in N$ such that $VN{F}_{k1}$ prefers $n_x$ over the currently matched service node and the preference order received by the service node $n_x$ is lower than the preference ordering of $VN{F}_{k1}$ in the service node $n_x$, then both the service node $n_x$ and $VN{F}_{k1}$ will reject the current match and form a new match queue. If the service node $n_m$ has no match with the VNF instance $VN{F}_{km}$, but both are mutually better matching choices than the current match, i.e., $(n_m,VN{F}_{km})\notin \mu$, $n_m{\succ }_s{n}_i$, and $VN{F}_{km}{\succ }_{ni}VN{F}_{kn}$, then the $\mu :(n_m,VN{F}_{km})$ is said to be a blocking pair.

The establishment of a stable matching must satisfy dual constraints. Firstly, within the bounds of resource availability, service nodes, and VNF instances establish mutually non-rejective relationships through bilateral selection—where service nodes preferentially accept VNFs that meet their resource constraints, and VNFs, in turn, prioritize matching with available nodes. Secondly, no inactive server–VNF pair exists that can mutually improve their utility through rematching. This absence of blocking pairs ensures that the current matching not only guarantees all established connections meet the minimum quality of service (QoS) thresholds but also adheres to the Pareto optimality principle—namely, no reallocation of resources can improve any participant’s utility without degrading that of others—thus leading to an equilibrium-optimal resource allocation scheme.

4.1.2. Preference List Construction

In each time slot $t$, VNF scheduling requires separate preference lists of VNFs to physical nodes and physical nodes to VNF instances in order to establish the preference lists of the two parties of the game, and then the matching game performs game selection to find a stable solution based on the preference lists of the two parties.

Define the preference utility function of the VNF as shown in Equation (4). The preference of the VNF over the physical nodes combines the communication latency and resource fitness to calculate the preference value, where $\alpha +\beta =1$, $\alpha$ and $\beta$ are the weighting coefficients belonging to the range between 0 and 1, reflecting the relative importance of the latency and resource fitness in the preference.

$$Preference(v_j,n_i)=-\alpha \cdot {\displaystyle \frac{1}{1+L(v_j,n_i)}}+\beta \cdot R_{fit}(v_j,n_i)$$

(4)

$L(v_j,n_i)$ denotes the communication delay as shown in Equation (5). $p_{ji}$ denotes the set of physical paths from the virtual location where $v_j$ is located to $n_i$. $F_{l_{pq}},B_{l_{pq}},d_{l_{pq}}$ denote the data traffic, bandwidth, and base delay on link $l_{pq}$, respectively. $R_{fit}(v_j,n_i)$ denotes the resource fitness as shown in Equation (6).

$$L(v_j,n_i)={\displaystyle \sum _{l_{pq}\in p_{ji}}(\frac{F_{l_{pq}}}{B_{l_{pq}}}+d_{l_{pq}})}$$

(5)

$$R_{fit}(v_j,n_i)=1-{\displaystyle \frac{R(n_i)-D{(v_j)}_2}{R{(n_i)}_2}}$$

(6)

The algorithmic process for constructing the VNF preference list for matching is presented in Algorithm 1.

Algorithm 1: Algorithm for construction of VNF matching preference list

Input: VNF instance set $V$, service node set $N$, physical infrastructure graph $G$ Output: Matching preference list for VNFs $T_v$ (1) for each $n\in N$ do (2)   Initialize the empty match preference list $T_v$ (3)   for each $v\in V$ do (4)     Calculation of resource preference values according to Equation (4) (5)     Select the service node with the smallest value $n_i$ (6)     Put $n_i$ into the matching preference list $T_v$ (7)     Update the position of the untraversed service node $P_{center}$ (8)   end for (9)   While There are untraversed nodes in N do (10)   Find the nearest service node to $P_{center}$ that satisfies the resource (11) end for (12) return $T_v$

This algorithm is used to construct the VNF matching preference list, with the input being the set of VNF instances $V$, the set of service nodes $N$, and the physical infrastructure graph $G$, and the output being the VNF matching preference list $T_v$. In Lines (1)–(8), an empty list $T_v$ is initialized for each service node $n\in N$. Then, each $v\in V$ is traversed, the resource preference value is calculated according to the formula, the service node with the smallest value is selected and added to the list, and the position is updated. In Lines (9)–(11), when there are untraversed nodes in $N$, the service node that meets the conditions is searched for. Finally, in Line (12), $T_v$ is returned.

To construct the service node matching preference list, set the physical node’s preference for the VNF. Ranked according to the fitness of the resource requirements to the remaining resources, as shown in Equation (7).

$$Preference(n_i,v_j)=R_{fit}(v_j,n_i)$$

(7)

For VNFs in the service function chain, the execution order is adjusted to ensure sequential execution as shown in Equation (8).

$$T_{start}(v_k)\ge T_{end}(v_k-1)=T_{start}(v_j)+t(v_j)$$

(8)

The implementation flow of the service node matching preference list generation algorithm is shown in Algorithm 2.

Algorithm 2: Algorithm for constructing the service node matching preference list.

Input: VNF instance set $V$, service node set $N$ Output: Matching preference list for VNFs $T_f$ (1) for each $v\in V$ do (2)   Initialize the empty match preference list $T_f$ (3)   for each $n\in N$ do (4)   Calculation of resource preference values according to Equation (7) (5)   According to the priority order of $C_{ni}>S_{ni}>B_{ni}$ (6)   Put $v_j$ into the matching preference list $T_f$ (7)   end for (8)   Perform an ascending ordering of $v\in V$ and update $T_f$ (9) end for (10) return $T_v$

The algorithm takes the VNF instance set $V$ and service node set $N$ as input and outputs the matching preference list for VNFs $T_f$. Lines (1)–(7) involve, for each $v\in V$, initializing an empty match preference list $T_f$, then for each $n\in N$, calculating resource preference values as per Equation (7), and putting $v_j$ into $T_f$ following the priority order $C_{in}>S_{in}>B_{in}$. Line (8) performs ascending ordering on $v\in V$ and updates $T_f$. Finally, Line (10) returns $T_f$.

4.2. Description of the Matching Game Algorithm

The Gale–Shapley (GS) algorithm [16] is a classical stable matching algorithm, widely applied in solving problems such as communication resource allocation, organ transplantation matching, and the stable marriage problem. It requires that, within the two groups involved in the matching process, each individual from one group can potentially be matched with any individual from the other group. In addition, each individual is required to rank the preferences of the individuals in the other group, and this is used as the basis for the matching decision. During the matching process, a series of “propose” and “accept/reject” operations are performed iteratively to progressively achieve a stable matching. One party sequentially sends match requests to individuals in its preference list, while the other party selects the currently optimal match based on its preference order and rejects other requests. This process is iterated until all individuals have been successfully matched or no superior matches can be found. The final matches are stable and there are no unmatched individuals who have a preference for each other over their current matches. The core of the GS algorithm lies in achieving a globally stable matching solution through an individual preference ranking and a progressive optimization matching process.

In this paper, each VNF instance is assigned to a single server for deployment, while ensuring that the server has sufficient computing power to support the parallel operation of VNFs from multiple SFC tasks. Additionally, the server can host multiple VNFs from the same SFC, ensuring the independence of VNFs while fully utilizing the server’s resources, thus enhancing the system’s flexibility and efficiency.

4.2.1. Batch Matching

The traditional matching game algorithm handles the matching requests of each VNF one by one. The VNFs make matching requests to the physical nodes in turn according to their own preference lists, and the physical nodes accept or reject the VNFs according to their remaining resources. However, in the SFC scheduling scenario, a large number of VNFs and servers may participate in matching at the same time. The pre-requested VNFs may occupy a large number of resources, leading to a decrease in the overall matching quality. In addition, the matching requests of each VNF increase the number of matching rounds, leading to higher computational complexity of the GS algorithm.

To solve the above problems, this paper introduces the Batch Matching strategy, which divides each round of the matching process into multiple batches based on the resource demands strategy and matches in parallel within each batch. Within each batch, all VNFs submit matching requests to the physical node simultaneously, while the physical node makes a unified decision to accept the optimal match according to the preference list after receiving all the requests to ensure the overall allocation efficiency. At the same time, the matching strategy of subsequent batches is optimized based on the matching results of the previous batch to reduce the probability of resource conflicts and to cope with complex scheduling scenarios such as dynamic and parallel computing environments more efficiently to enhance the global scheduling effect.

(1) Batch-wise Strategy

All VNFs are divided into batches $B_1,B_2,\dots ,B_k$. The VNFs within each batch are matched simultaneously and are classified according to the total amount of resource demand $D(v_j)=D^c(v_j)+D^s(v_j)$. The batching strategy is shown in Equation (9).

$$B_k=\{v_j\mid {\displaystyle \frac{k-1}{K}}\cdot D_{\max }\le D(v_j)<{\displaystyle \frac{k}{K}}\cdot D_{\max }\}$$

(9)

To clarify the resource composition and calculation logic of the demand vector $D_v$: $D_v$ is a normalized multi-dimensional vector integrating three core resources of VNFs, specifically $D_v={\omega }_1\times r_{v,CPU}+{\omega }_2\times r_{v,RAM}+{\omega }_3\times r_{v,BW}$. Among them, CPU demand $r_{v,CPU}$ ranges from 5 to 20, memory demand $r_{v,RAM}$ ranges from 5 to 15, bandwidth demand $r_{v,BW}$ ranges from 5 to 10 Mbps; ${\omega }_1=0.4$, ${\omega }_2=0.3$, ${\omega }_3=0.3$ are weight coefficients to balance dimension differences, and all resource demands are normalized to the [0, 1] interval (e.g., normalized CPU demand = $r_{v,CPU}$/$\max (r_{v,CPU})$, where $\max (r_{v,CPU})=20$) before weighting. Notably, $D_v$ is determined by VNF’s inherent resource requirements, not by deep learning (deep learning is only used in DQN/DDPG baselines).

$K$ is the number of batches, and $D_{\max }$ is the maximum resource requirement in all VNFs. Setting low latency priority batches by latency sensitivity $L(v_j,n_i)$ grouping is shown in Equation (10).

$$B_k=\{v_j\mid {\displaystyle \frac{k-1}{K}}\cdot L_{\max }\le L(v_j,n_i)<{\displaystyle \frac{k}{K}}\cdot L_{\max }\}$$

(10)

(2) Intra-Batch Parallel Matching and Dynamic Adjustment

Within batch $B_k$, find the optimal physical node $n_i$ for all VNF $V_j\in B_k$ simultaneously. For the matched batch $B_k$, update the remaining resources of the physical nodes $R(n_i)$. The dynamic adjustment is shown in Equation (11).

$$R(n_i)\leftarrow R(n_i)-{\displaystyle \sum _{v_j\in B_k}D(v_j)\cdot x_{ij}}$$

(11)

When there is a $\mu (v_j,n_i)$ match, $x_{ij} = 1$, the unmatched VNFs will go to the next batch for matching until all batches are processed or resources are exhausted.

4.2.2. Local Resource Check

During the execution of the matching game algorithm, VNFs may submit matching requests to physical nodes with insufficient resources, leading to many matching failures and wasting computation time. The local resource check verifies whether the target physical node has enough resources to satisfy the demand before sending the match request. If the resources are insufficient, the node is skipped and a request is sent directly to the next preference node to quickly screen out the options that do not satisfy the resource constraints to reduce invalid matching attempts and improve the matching efficiency. Meanwhile, when adding new VNF requests, the entire matching game algorithm is not re-run and only incremental adjustments are made based on the existing matching results. Local resource checking reduces the invalid attempts of matching, reduces the computational cost, improves the matching efficiency, and makes the algorithm lighter by introducing resource constraints.

(1) Resource Constraint Conditions

For each physical node $n_i$, define its residual resource vector as $R(n_i)=R^c(n_i)+R^s(n_i)$. If the node fails to satisfy the demand $D(v_j)=D^c(v_j)+D^s(v_j)$ for any VNF $v_j$, then it directly proceeds to the next bit of filtering as shown in Equation. (12).

$$R(n_i)<D(v_j)\Rightarrow x_{ij}=0,\forall v_j\in V$$

(12)

The computational resource constraints and storage resource constraints are $D^c(v_j)\le R^c(n_i)$ and $D^s(v_j)\le R^s(n_i)$, respectively.

(2) Post-Check Matching

For a set of nodes: $N(v_j)$, $N(v_j)=\{n_i\mid R(n_i)\ge D(v_j)\}$, preferences are computed only for nodes in $N(v_j)$, $Preference(v_j,n_i)={\displaystyle \frac{1}{1+L(v_j,n_i)}},n_i\in N(v_j)$, physical node $n_i$ also handles only the requested VNFs in $N(v_j)$, $M(n_i)=\{v_j\mid n_i\in N(v_j)\}$.

(3) Dynamic Resource Updating

For a successfully matched VNF $v_j$: $if x_{ij}=1$, $R(n_i)\leftarrow R(n_i)-D(v_j)$, recheck that the unmatched VNFs still have available nodes after the update $N(v_j)\leftarrow \{n_i\mid R(n_i)\ge D(v_j)\}$.

4.2.3. Matching Game Scheduling Algorithm

Service function chain scheduling can be achieved through the matching game between service functions and service nodes, with the process modeled as a bilateral matching optimization problem. Through the establishment of a multi-dimensional evaluation index system to construct the service node matching resource fitness priority sequence and service function matching sorting set. Through multiple rounds of matching game requests, the optimized service function chain scheduling strategy of stable matching is finally achieved. The flow of the matching game scheduling algorithm is shown in Figure 3.

In each matching cycle, VNFs actively send matching requests to physical nodes strictly following their preference lists. If a network node receives deployment requests from multiple VNFs, it accepts the most preferred request and rejects the rest based on its preferences. The rejected VNFs will initiate sub-sequent matching proposals to the next preferred physical nodes in their preference lists during the following rounds until a stable matching state is achieved. Stable matching implies that no VNF is motivated to change its current placement due to increased network traffic costs, and no physical node is inclined to alter its allocation as it would result in greater computational resource waste. In other words, all VNFs and physical nodes lack the incentive to disrupt the existing matching configuration. The flow of VNF scheduling algorithm based on matching game is shown in Algorithm 3.

Algorithm 3: VNF scheduling algorithm based on matching game.

Input: VNF instance set $V$, service node set $N$, matching preference list for VNFs $T_v$, matching preference list of service nodes $T_f$ Output: Stable matching sequence $\mu$, scheduling strategy ${\pi }^{\mu }$ (1) Initialize all nodes to unmatched state and create an empty result list $\mu =\varnothing$ (2) for each $v\in V$ do (3)   Match the VNF’s matching preference list $T_v$ with its most preferred service node $n_i$ (4)   if $n_i{\succ }_{vi}{n}_1$ and $n_1$ $in$ $T_f$ (5)     then establish the matching for the pair (6)     Update the node information based on the matching results. If VNF $v_j$ is accepted by node $n_i$, then update the remaining resources $R(n_i)\leftarrow R(n_i)-D(v_j)$ of node $n_i$ accordingly (7)   else traverse $n_x{\succ }_{vi}{n}_i$ (8)   Node $n_i$ accepts the highest-priority request $v_j$ according to its matching preference list and rejects all other requests (9)   Remove node $n_i$ from the VNF’s matching preference list $T_v$ (10)   Remove VNF $v_j$ from the service node’s matching preference list $T_f$ (11)   Submit a request to the next node (12)   end (13) end for (14) return $\mu$

This algorithm is for VNF scheduling based on matching game, taking VNF instance set $V$, service node set $N$, VNF matching preference list $T_v$, and service node matching preference list $T_f$ as input, and outputting stable matching sequence $\mu$ and scheduling strategy $\pi$. Line (1) initializes all nodes to an unmatched state and creates an empty result list $\mu =\varnothing$. Lines (2)–(12) involve, for each $\mathrm{v}\in V$, matching the VNF’s matching preference list $T_v$ with its most preferred service node $n_i$; if $n_i\succ v_j{n}_i^{\prime }$ and $n_i$ is in $T_f$, a matching for the pair is established, node information is updated based on matching results (if VNF $v_j$ is accepted by node $n_i$, the remaining resources $R(n_{\mathrm{i}})$ of node $n_i$ are updated as $R(n_{\mathrm{i}})\leftarrow R(n_{\mathrm{i}})-D({\mathrm{v}}_{\mathrm{j}})$; otherwise, $n_i\succ v_j{n}_j^{\prime }$ is traversed, node $n_i$ accepts the highest-priority request $v_j$ according to its matching preference list and rejects other requests, node $n_i$ is removed from the VNF’s matching preference list $T_v$, VNF $v_j$ is removed from the service node’s matching preference list $T_f$, and a request is submitted to the next node. Finally, Line (14) returns $\mu$.

4.3. Algorithm Complexity Analysis

4.3.1. Complexity Analysis of Traditional Algorithm

In the original Gale-Shapley stable matching algorithm, each VNF can initiate a matching request to each physical node, and each physical node sorts and selects all the received requests. In the worst-case scenario, when there are $n$ service nodes initiating $n$ matching requests, the time complexity is $O(n^2)$. The decision-making process of each service function to accept or reject the matching request from a service node has a time complexity of $O(1)$. Therefore, the overall time complexity is $O(n^2)$. During the construction of preference lists, each VNF includes $m$ physical nodes in its preference list, and each physical node includes $n$ VNFs in its list. In the matching process, influenced by the preference order, each VNF can submit requests to up to $m$ nodes. The processing complexity of each request is $O(logn)$, resulting in a total matching iteration complexity of $O(n\cdot m\cdot logn)$.

4.3.2. Complexity Analysis of the Optimized Algorithm

Suppose $n$ VNFs are divided into $b$ batches, each of size ${\displaystyle \frac{n}{b}}$, with intra-batch matching complexity: $O({\displaystyle \frac{n}{b}}\cdot m\cdot log{\displaystyle \frac{n}{b}}\cdot )$, and there are $b$ batches in total, so the batch matching complexity of all batches is: $O(b\cdot {\displaystyle \frac{n}{b}}\cdot m\cdot log{\displaystyle \frac{n}{b}}\cdot )=O(n\cdot m\cdot log{\displaystyle \frac{n}{b}}\cdot )$. Local resource checking performs a resource verification before each request to avoid invalid attempts. The complexity of each resource check is $O(1)$, and the total number of requests is limited by the number of successful matches. Therefore, the overall complexity of resource checking for all VNFs is $O(n\cdot m\prime )$, where $m\prime \le m$ denotes the average number of nodes satisfying the resource constraints. The local resource check filters out the nodes that do not satisfy the resource constraints and reduces the number of candidate nodes that need to be processed in the matching, which reduces the node size from $m$ to $m\prime$, and significantly reduces the computational effort in matching. The combined complexity is $O(n\cdot m^{\prime }\cdot log{\displaystyle \frac{n}{b}}\cdot )$.

Compared to the standard algorithm, the optimized matching game scheduling algorithm demonstrates significant advantages. Its computational complexity is substantially reduced—from a relatively high level to a much lower one—while the integration of local resource checking effectively minimizes invalid matching attempts, thereby greatly enhancing resource utilization efficiency. Moreover, the optimized algorithm exhibits superior scalability, making it particularly well-suited for large-scale scheduling scenarios, and remains highly efficient even under resource-constrained environments. In summary, the optimized algorithm comprehensively outperforms the traditional Gale-Shapley (GS) algorithm in terms of computational complexity, matching efficiency, and adaptability. As a result, it enables more efficient execution of SFC scheduling tasks and significantly enhances the overall performance of the system.

5. Experimental Design and Results Analysis

5.1. Experimental Setup

To comprehensively evaluate the performance of the SFC-GS algorithm, this paper constructs a dynamic service function chain scheduling scenario based on a simulation platform. The algorithm simulation is implemented in an environment with the Windows 11 operating system, an Intel(R) Core (TM) i5-12490F CPU @3.00 GHz, 16 GB DDR4 RAM, and an NVIDIA GTX 3070 GPU, using tools such as Python 3.6.12 and TensorFlow 2.4.1.

This paper employs the Monte Carlo method [17], with the physical node topology randomly generated. To mitigate the impact of randomness, the average value of 100 simulation tests is taken as the result. The setup of this experimental scenario refers to the commonly used load testing scenarios and resource demand distribution methods in existing research. It is important to clarify two points here: First, the Monte Carlo method is only used to generate random physical node topologies and reduce randomness in simulation results, not to model real data center environments—for real-world applications, SFC-GS can directly adopt actual data center resource parameters to construct the demand vector ($D$), eliminating reliance on random generation. Second, the proposed SFC-GS algorithm does not use deep learning to generate the demand vector ($D$) or scheduling decisions; deep learning is only applied in the DQN and DDPG baseline algorithms for performance comparison. SFC-GS’s core logic relies on matching game and batch scheduling, which avoids the additional system load caused by deep learning and aligns with the resource efficiency goal emphasized in the paper.

The experimental parameters are set as follows: set the maximum number of service function chains to 100–500 SFC requests, covering light to overloaded scenarios, with an increase of 100 requests per phase to simulate load increment. The total input/output bandwidth range for each node is from 5 to 10 Mbps. It is assumed that SFC requests arrive dynamically and follow a Poisson distribution. Each SFC request consists of one or more VNFs, with the number of VNFs uniformly distributed between 2 and 5. The CPU required for each VNF to operate normally is randomly distributed between 5 and 20, and the memory resource consumption follows a uniform distribution between 5 and 15. The neural network employs the Adam optimizer and the ReLU activation function, with a four-layer fully connected architecture comprising 256, 128, 64, and 32 neurons, respectively. The learning rate is set to 0.0005, the batch size is 128, and the discount factor is set to 0.7. The simulation parameters are detailed in

Table 1. Simulation Parameter Settings.

Simulation Parameters	Numerical Value
VNF	[2, 5]
CPU	[5, 20]
RAM	[5, 15]
Fully Connected Layer	256- 128- 64- 32
Bandwidth	[5, 10]
Learning Rate	0.0005
Batch Size	128
Discount Factor	0.7

. The experimental design covers a comprehensive load spectrum ranging from 100 to 500 requests and incorporates multi-dimensional performance metrics for comparison, thereby providing a thorough validation of the superiority of the SFC-GS algorithm across varying scale scenarios.

5.2. Baselines

Three benchmark algorithms are selected for performance comparison with SFC-GS, with brief descriptions as follows:

(1) Deep Q-Network [18]

A deep reinforcement learning algorithm that approximates the Q-value function via a neural network, learning optimal scheduling policies by interacting with the environment; it is widely used in dynamic resource allocation tasks but faces challenges of slow convergence in large-scale scenarios.

(2) Deep Deterministic Policy Gradient [19]

DDPG is a reinforcement learning algorithm suitable for continuous action spaces, widely applied in resource allocation, such as bandwidth allocation in communication networks and computing resource scheduling in data centers. It outputs specific resource allocation amounts via the actor network, evaluates the allocation scheme with the critic network, and achieves stable learning by combining experience replay and target networks, thereby dynamically optimizing resource allocation strategies to improve core objectives like resource utilization.

(3) Random [20]

A naive scheduling algorithm that randomly allocates VNFs to physical nodes without optimization strategies; it serves as a baseline to verify the effectiveness of optimized algorithms.

5.3. Performance Metrics

Five core metrics are used to evaluate the scheduling performance of all algorithms:

(1) Average Request Acceptance Rate

The proportion of successfully accepted SFC requests to total incoming requests, reflecting the algorithm’s ability to handle service demands.

(2) End-to-End Delay

The total latency of data transmission in SFCs, including VNF processing delay and physical link propagation delay, a key indicator of service quality.

(3) Resource Utilization

The ratio of used resources (CPU, memory, bandwidth) to total available resources in physical nodes, measuring resource allocation efficiency.

(4) Runtime

The total computation time of the scheduling algorithm, reflecting its real-time performance and scalability for large-scale tasks.

(5) Resource Consumption

The normalized sum of CPU, memory, and bandwidth resources consumed by SFC scheduling, evaluating the algorithm’s resource-saving ability.

5.4. Results and Discussion

(1) Comparison of average request acceptance rate

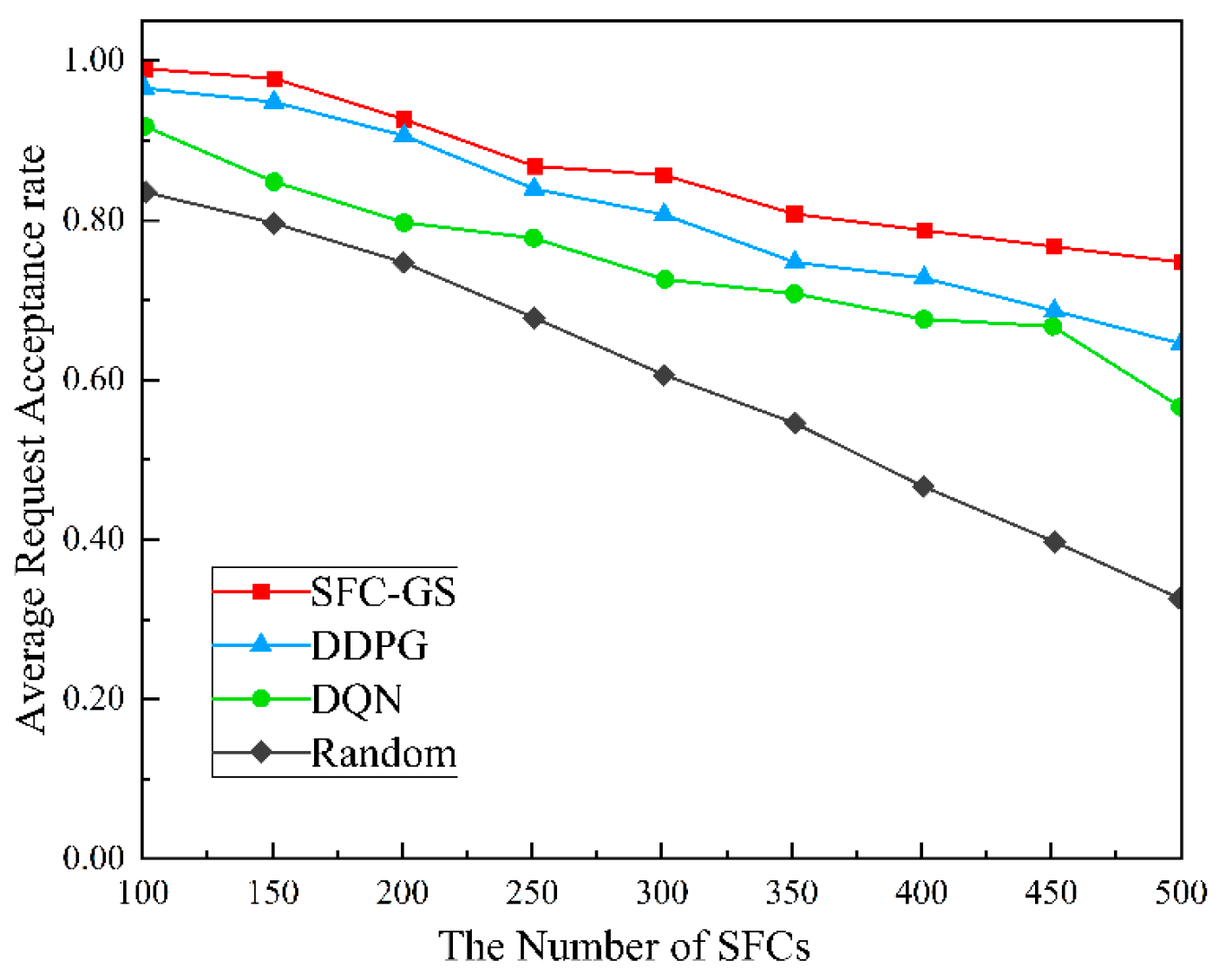
Figure 4 illustrates the trend of the average request acceptance rate with respect to the number of SFCs for different algorithms dealing with SFC scheduling. As the number of SFCs increases, the acceptance rate of all algorithms declines due to higher resource demands and increased scheduling complexity. However, the SFC-GS algorithm consistently outperforms the other three algorithms, achieving an average request acceptance rate that is more than 8.108% higher, thereby demonstrating a significant advantage. Batch-based matching enables SFC-GS to handle a large volume of requests more efficiently, while local resource checking helps prevent conflicts and resource waste during allocation. This mechanism ensures that data packets traverse multiple network service nodes as required by users, maintaining stable and reliable service delivery even under highly complex network conditions. So, the algorithm sustains a high acceptance rate under substantial request loads. In comparison, DDPG and DQN, as deep reinforcement learning algorithms, demonstrate superior performance in certain scenarios. However, in large-scale SFC scheduling, their learning complexity leads to less stable performance compared to SFC-GS. The Random algorithm allocates resources in a completely arbitrary manner without any optimization strategy, leading to the most rapid decline in the average request acceptance rate under intense resource competition.

(2) Delay comparison

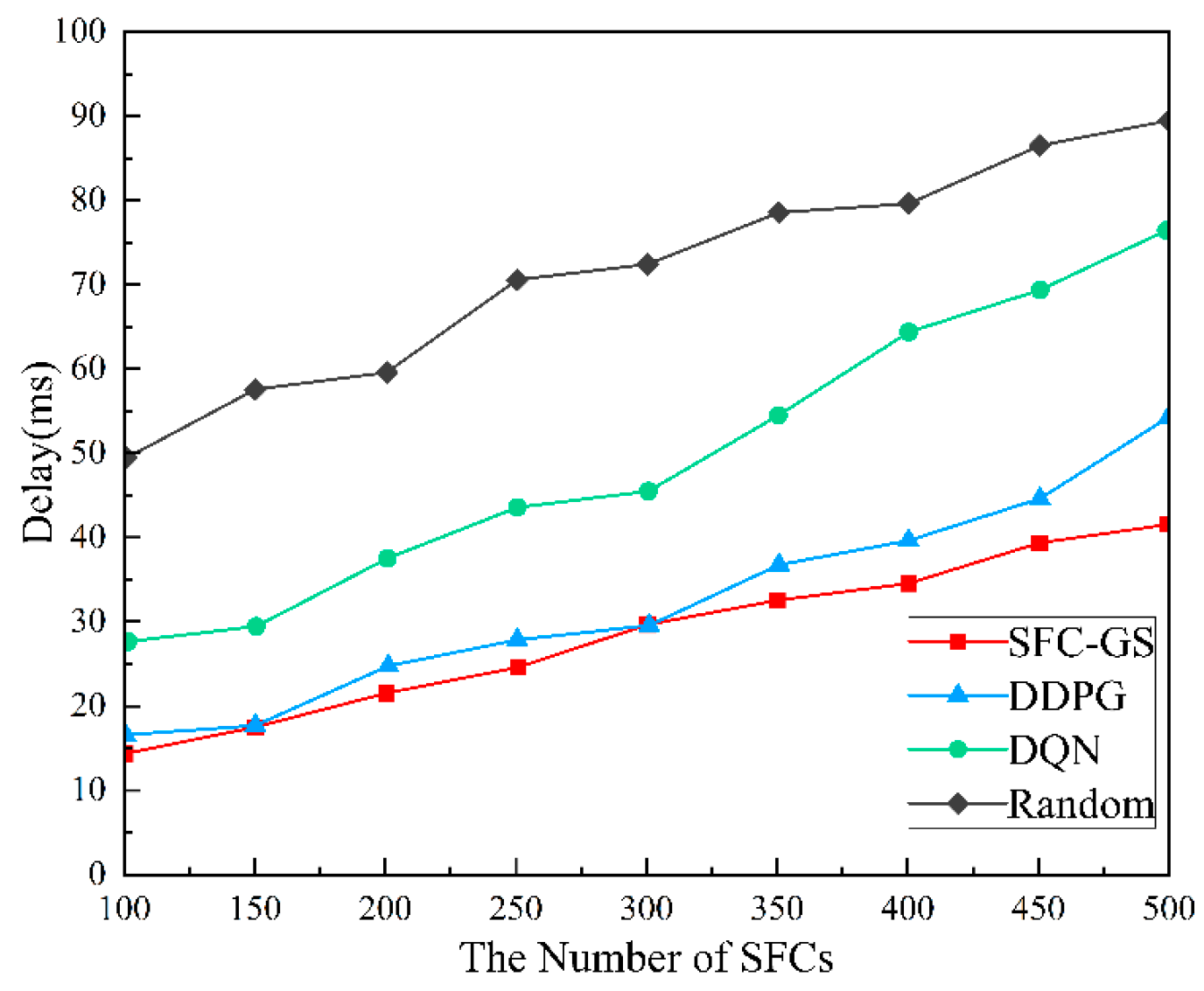
Figure 5 illustrates the delay performance of different algorithms in handling SFC requests. As the number of SFC requests increases, the end-to-end delay for all algorithms shows an upward trend. However, the SFC-GS algorithm exhibits a delay growth rate that is reduced by more than 10.2% compared to the baseline algorithms, indicating that SFC-GS effectively mitigates the delay increase when handling large-scale SFCs. The SFC-GS algorithm combines the batch matching approach of the Gale-Shapley stable matching algorithm with an improved local resource check method, resulting in more efficient resource allocation. This avoids resource waste and conflicts, thereby reducing delays. The SFC-GS curve remains relatively smooth across the entire range, without the drastic fluctuations observed in the Random algorithm, indicating that it can maintain stable performance under varying loads.

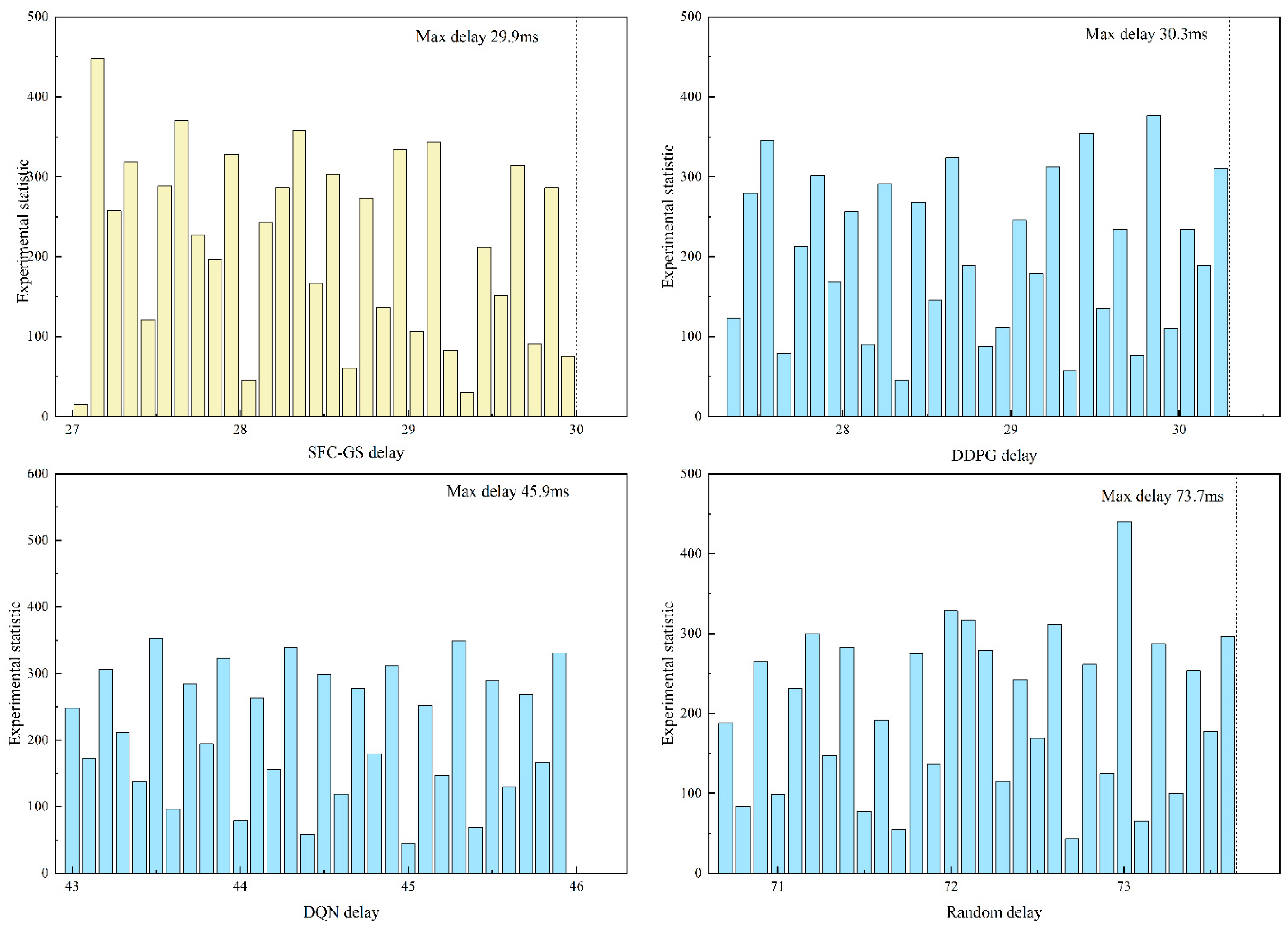
In the training process of this paper, to better simulate real-world network environments and conduct effective research under limited resources, the scenario with 300 SFCs was selected to evaluate the distribution of end-to-end delay. The distribution of training episode counts corresponding to specific latency levels is illustrated in Figure 6. The SFC-GS algorithm exhibits a higher frequency of lower latency occurrences and achieves the lowest maximum latency among all compared algorithms, indicating its clear advantage in mitigating latency escalation trends. The analysis of the experimental data distribution, shows that SFC-GS has a large statistic of small end-to-end delay bias and the lowest end-to-end delay compared to other algorithms. These results demonstrate that SFC-GS exhibits significant stability in latency control for SFC scheduling. Meanwhile, SFC-GS reduces computational redundancy through local resource checking, iteratively refines the matching process over multiple rounds to approximate the global optimum, and enhances allocation efficiency via batched parallel processing. This approach effectively avoids premature acceptance of locally optimal requests that may lead to global resource imbalance, thereby significantly improving the overall network latency performance.

(3) Comparison of resource utilization rate

Figure 7 illustrates the resource utilization performance of different scheduling algorithms under varying numbers of service function chains. As the number of SFCs increases, the resource utilization of all algorithms improves, indicating that the degree of optimization in resource scheduling enhances with the growth of task load. The SFC-GS algorithm performs best in all SFC number intervals and outperforms the comparison algorithm by more than 8.57%. It indicates that its collaborative matching game strategy that takes into account the bilateral states can effectively improve the resource utilization rate. Reinforcement learning is affected by the exploration efficiency and training effect in resource allocation in a short period. In contrast, SFC-GS improves matching efficiency and reduces computational resource consumption by employing batch matching to minimize the waiting time of individual matches, and by incorporating local resource checking to avoid invalid matching attempts.

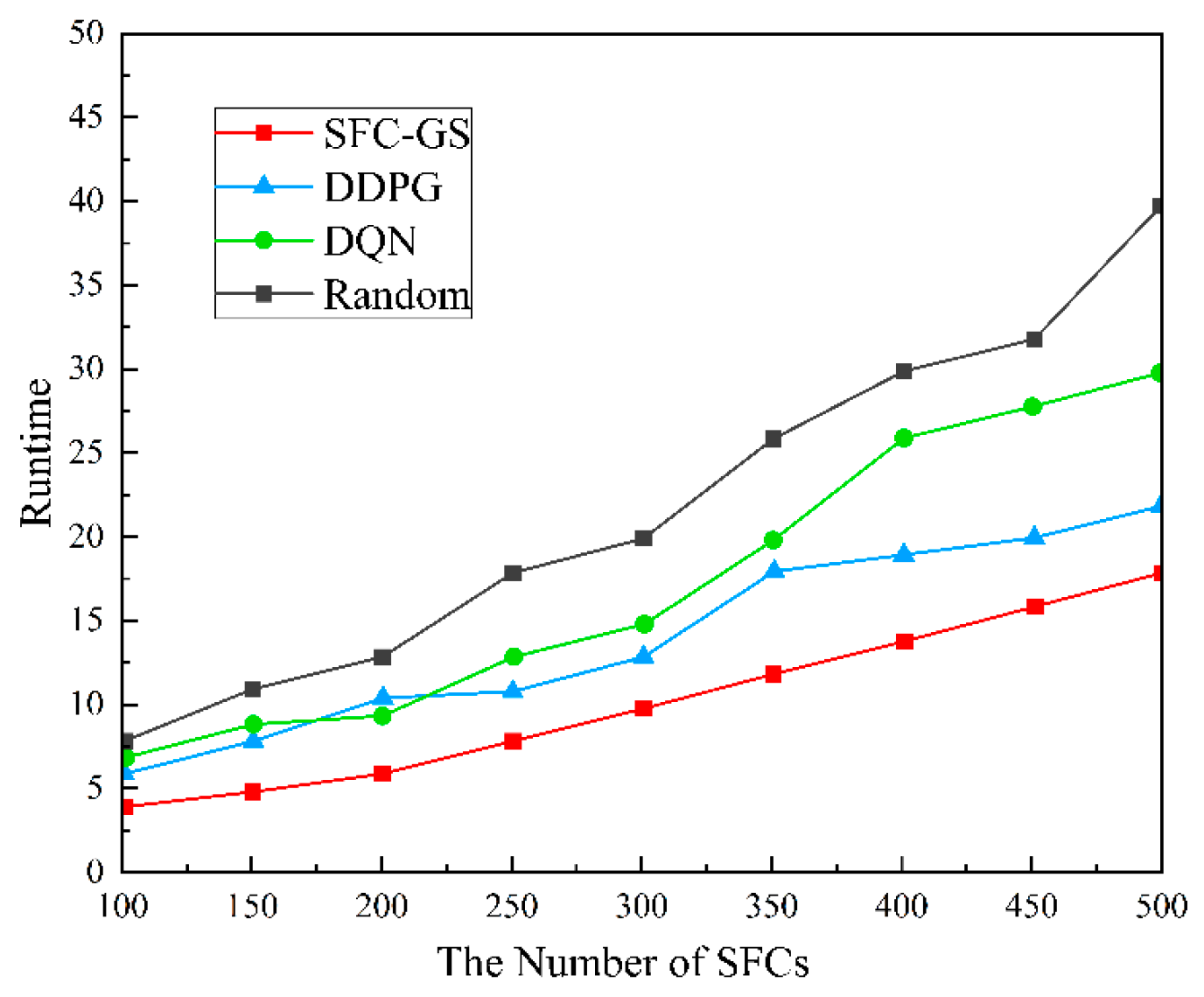
(4) Comparison of Runtime

Figure 8 illustrates the differences in runtime performance of various scheduling algorithms under different numbers of service function chains. The runtime increases with the number of SFCs, indicating that the scheduling computation complexity is positively correlated with the number of SFCs. When the number of SFCs is 500, SFC-GS reduces the computation time by about 25% and 40% compared to DDPG and DQN, respectively. It indicates that reinforcement learning methods still have high computational resource overheads, while SFC-GS reduces unnecessary computations and improves execution efficiency using batch matching and local resource checking. As the number of SFCs increases, the runtime of the Random algorithm rises sharply. When SFC = 500, the runtime of SFC-GS is only 1/3 of that of Random, indicating that unoptimized scheduling incurs extremely high computational overhead and is incapable of effectively adapting to large-scale SFC scheduling scenarios. SFC-GS consistently maintains the lowest runtime throughout the entire process, indicating that its optimized matching game strategy is highly effective in controlling computational complexity. This advantage becomes even more pronounced as the number of SFCs increases, demonstrating its superior scalability and efficiency in large-scale scenarios.

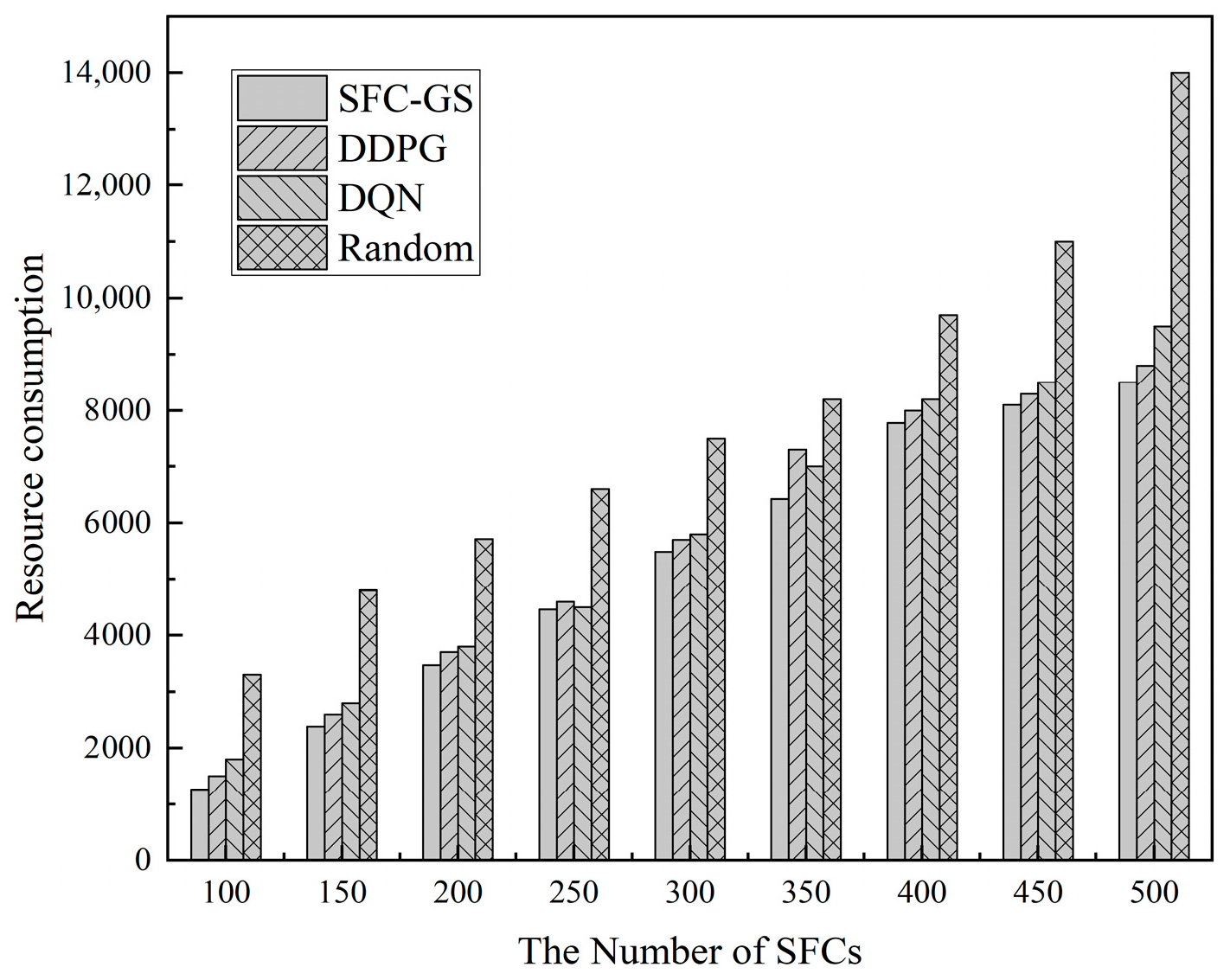
(5) Comparison of Resource Consumption

The resource consumption under varying service request arrival intensities is illustrated in Figure 9. As the number of SFCs increases, the overall resource consumption also rises, which aligns with the principle that resource demand is positively correlated with the scale of SFC deployments. The highest resource consumption observed in the Random algorithm indicates that scheduling without an optimization strategy results in significant resource waste. In this paper’s algorithm, the matching strategy of each batch optimizes the subsequent batch matching process, thereby enhancing the overall resource utilization efficiency. The reinforcement learning algorithm optimizes resource scheduling, but the resource consumption is still higher than that of SFC-GS due to the fact that there are still redundant computations during training and inference. Through the optimization of batch matching and local resource inspection, SFC-GS achieves lower resource consumption compared to DQN, DDPG, and Random algorithms. In large-scale SFC scheduling scenarios, SFC-GS reduces resource consumption by approximately 10.5–15%, demonstrating higher resource utilization and scheduling efficiency, making it a superior choice for scheduling algorithms.

In summary, the SFC-GS algorithm demonstrates significant comprehensive advantages in large-scale SFC scheduling scenarios. When the number of SFCs increases, SFC-GS exhibits the smallest decline in acceptance rate, the slowest growth in delay, with steady fluctuations, and consistently maintains the highest level of resource utilization. At the same time, its running time is reduced by 25–40%, and resource consumption is reduced by 10.5–15% compared with the comparison algorithm. Especially when the number of SFCs reaches 500, the running time is only 1/3 of the Random algorithm. The algorithm in this paper outperforms DQN, DDPG, and Random algorithms in five core metrics: average request acceptance rate, delay control, resource utilization, running time, and resource consumption through the co-optimization of batch matching and local resource checking. The algorithm effectively balances the resource allocation efficiency and computational complexity through the matching game strategy, providing an efficient and stable scheduling solution for NFV environments under high load.

6. Conclusions

This paper proposes SFC-GS, a multi-objective SFC scheduling algorithm based on matching games, which innovatively integrates three core designs: a bilateral preference matching model for VNFs and service nodes, a local resource check mechanism to reduce invalid attempts, and a hierarchical batch scheduling strategy for iterative optimization. Experimental results show that the proposed method improves request acceptance rate and resource utilization by approximately 8% and reduces latency and resource consumption by approximately 10% compared with DQN, DDPG, and Random algorithms.

Existing SFC scheduling methods still exhibit certain limitations, particularly in multi-objective collaborative optimization and algorithm efficiency. Future research will focus on designing multi-dimensional optimization frameworks for scheduling strategies, aiming to maximize system resource utilization, minimize task response latency, and achieve load-balancing metrics superior to current benchmark algorithms, while exploring novel scheduling paradigms with significantly reduced computational complexity.