Bi-Scale Mahalanobis Detection for Reactive Jamming in UAV OFDM Links

Abstract

Reactive jamming remains a critical threat to low-latency telemetry of Unmanned Aerial Vehicles (UAVs) using Orthogonal Frequency Division Multiplexing (OFDM). In this paper, a Bi-scale Mahalanobis approach is proposed to detect and classify reactive jamming attacks on UAVs; it jointly exploits window-level energy and the Sevcik fractal dimension and employs self-adapting thresholds to detect any drift in additive white Gaussian noise (AWGN), fading effects, or Radio Frequency (RF) gain. The simulations were conducted on 5000 frames of OFDM signals, which were distorted by Rayleigh fading, a ±10 kHz frequency drift, and log-normal power shadowing. The simulation results achieved a precision of 99.4%, a recall of 100%, an F1 score of 99.7%, an area under the receiver operating characteristic curve (AUC) of 0.9997, and a mean alarm latency of 80 μs. The method used reinforces jam resilience in low-power commercial UAVs, yet it needs no extra RF hardware and avoids heavy deep learning computation.

1. Introduction

Nowadays, electronic warfare (EW) is an emerging field that is growing at a rapid pace. In this context, securing communication between various embedded systems such as UAVs and base stations can easily fall victim to various types of advanced enemy jamming. To protect and immunize these communication links, various techniques can be used, ranging from statistical methods to machine learning. The paper published in [1] shows that UAVs generally use wireless networks such as Wi-Fi, Long-Term Evolution (LTE) and fifth-generation (5G) technology. Among these, 5G systems predominantly use OFDM modulation techniques for their immunity to jamming interference. However, this modulation technique is still limited against selective interference of the transmission signal, as in the case of reactive jamming, which only works when there is active transmission between the drone and the base station receiver, making it very difficult to intercept this type of jamming.

Currently, machine learning (ML) techniques are widely used to detect various types of jamming in OFDM UAVs. The authors proposed in [2] six conventional ML algorithms—decision tree (DT), k-nearest neighbors (KNN), logistic regression (LR), multilayer perceptron (MLP), naïve Bayes (NB), and random forest (RF)—to detect four basic proactive jamming signals, namely, Barrage, Tone, Success pulse, and P-aware. All algorithms were quantitatively validated with measurements, including detection and false-alarm rates, and the results revealed that interference was detected and classified with 92.2% confidence and a false-alarm rate of 1.35%.

Exploring further into the embedded ML, we find that Viana in [3] offers a principal component analysis (PCA)-featured transformer for 5G-UAV networks. The PCA compresses the RSSI/SINR time series, and the transformer captures the long dependencies. This approach is characterized by detecting complex scenarios (multiple jammers, variable channels), but it requires memory and computational power, which poses the problem of embedding it in a microcontroller. The authors in [4] applied several ML algorithms, including AlexNet, VGG16, ResNet-50, and EfficientNet-B0, based on spectrogram signal images in their training and testing phases to detect the same types of jamming attacks treated in [2]. The detection rate of all ML algorithms was around 99%. In the paper proposed in [4], a 3.20 GHz central processing unit (CPU) with 128 GB RAM and a Tesla P100 graphics processing unit (GPU) with 16 GB RAM were used to train and test the ML models. In reality, most commercial drones do not have microprocessors suitable for techniques such as deep learning and machine learning. This raises questions about the actual implementation in commercial drones, which generally use limited and restricted hardware.

In [5], the authors simulated three types of interference, including constant, reactive, and random, using the Network Simulator-3 (ns-3) environment and trained five ML algorithms. The gradient boosting model showed 93–95% detection accuracy, and random forest showed 91% accuracy. The approach uses a synthetic dataset that does not take into consideration environmental noise and fading effects.

The state of the art shows that ML methods used for reactive jamming detection are computationally intensive and less effective when the environment changes abruptly or contains significant AWGN. Therefore, an area for improvement compared to the literature is the lack of simple methods that can manage multiple features simultaneously and efficiently, such as signal energy and variation in signal complexity over multiple samples.

From another angle, some recent studies of reactive jamming detection use probabilistic methods that better account for the uncertainty associated with the radio channel by avoiding dependence on data and its environment.

In his study [6], Altun employed a statistical test dedicated to OFDM-IM by utilizing the energy distribution between active and inactive subcarriers to detect the intrusion of a reactive jammer. This method proved to be simple and interpretable but was sensitive to additive noise and required accurate calibration of thresholds.

The authors in [7] implemented a Hidden Markov Model (HMM) that uses the received signal strength as a binary clean/jammed string and estimates the parameters using Expectation and Maximization (EM). This method achieved detection probabilities greater than 95% for average SNR values ranging from −10 dB to −4 dB. However, the performance of this probabilistic model decreased when the fraction of victim frames was very short and when the noise distribution deviated from the Gaussian shape.

The authors in [8] used the Sequential Probability Ratio Test (SPRT), which is fed with bit errors associated with radio frequency interference received signal strength (RSS) to distinguish between ambient and real noise. This method can detect jamming in near real time, but it requires an accurate measurement of the RSS per bit and is sensitive to sudden fluctuations in data traffic.

Spühler in [9] proposed a statistical method based on the difference between the predicted packet delivery ratio (PDR) and the actually observed PDR. They used preamble symbols and were able to keep the total detection error (FP + FN) below 8% even when the jammer attacked all of the transmitted packets. The method is very simple, but it does not work if the preamble is also corrupted, and even more so if the received signals are fluctuating too much to estimate the expected PDR.

From a more theoretical point of view, Thai in his study [10] created a Trigger Identification Service, which is a non-adaptive fault-tolerant group testing scheme that uses specific transmission patterns to identify a subset of nodes that will trigger a reactive jammer. This solution has been demonstrated analytically, but it seems to be difficult to implement once the network grows.

Based on a 2 × 2 free-space-optical multiple-input multiple-output (MIMO) link, Sliti et al. in [11] monitored the multichannel ratio (MCR) between two receiver apertures. Any significant deviation above the threshold indicates an interference attempt, and the same ratio is used to subtract the interference from the desired signal. Simulations in log-normal free-space-optical (FSO) channels showed that recalculating the MCR removed approximately 90% of the interference power every five samples, but this efficiency decreased as the interference-to-signal ratio increased. Although the method is lightweight, its assumption of quasi-static channels and a single-antenna attacker could weaken robustness in swarms of fast-moving UAVs facing smarter jammers.

Additionally, within UAV swarms using Impulse Radio Ultra-Wide-band (IR-UWB) links, Gupta et al. [12] applied thresholding on Channel State Information (CSI) together with lightweight machine learning models to detect jamming attacks in real time while preserving range accuracy. However, the inherent specificity of IR-UWB limits the direct transfer of this approach to OFDM systems.

Zeng, in his tutorial [13], showed that UAV platforms operate under severe size, weight, and power (SWaP) constraints that directly cap on-board computing power and energy. In contrast, Li [4], Ray [14], and Immonen [15] described deep learning-based jamming or modulation classifiers that achieve high accuracies from spectrogram inputs and large datasets, but their methods require GPU-accelerated training and memory footprints that are incompatible with microcontroller-class hardware. In addition, the study of Perenda [16] highlights the vulnerability of these models to channel/material domain shifts and proposes dedicated augmentation schemes, while Deng [17] confirms the need for transfer and adaptation pipelines to restore robustness. In this context, Ray [14] and Immonen [15] emphasize that a detector based on low-order statistics and closed-form decision rules guarantees deterministic time/space complexity and interpretable decisions, making it suitable for real-time embedded systems under SWaP constraints. These elements justify, in line with Zeng’s analysis [13], the option of a lightweight statistical approach for reactive jamming detection on resource-constrained UAVs.

Beyond detection, resilience to jamming requires intelligent allocation of resources in a contested environment. Recent deep reinforcement learning studies jointly optimize transmit power, channel/carrier selection, beamforming and IRS phases to maintain Quality of Service (QoS) while maximizing energy efficiency. For example, Ma et al. [18] modeled energy efficiency maximization in an RSMA-IRS system for ISAC and learned a proximal control policy that simultaneously adjusts transmitter-side beamforming and Intelligent Reflecting Surface (IRS) phases under service constraints.

Building on previous work in the literature, this study proposes a method that combines two key parameters: the local root-mean-square (RMS) energy, used to flag sudden changes in the received signal, and the Sevcik fractal dimension (SFD), which serves as a complexity detector for that signal. The final decision is made by computing the Mahalanobis distance between the current feature vector and a baseline distribution, enabling robust outlier-based discrimination of jamming events. The simulation results show that the proposed approach achieved a detection accuracy above 99%, with minimal false negative and false positive rates.

As a second key contribution, we replaced the conventional single fixed threshold with a self-adjusting threshold, enabling the proposed algorithm to automatically track variations in the jamming landscape and remain effective across a broad spectrum of real-world conditions. We show that the method couples high detection accuracy with very modest computational demands, making it deployable on unmanned aircraft with limited onboard resources.

The approach blends the Sevcik fractal dimension with local effective energy, equips them with an adaptive threshold for added flexibility, and proves its value under realistic stressors such as a Rayleigh channel with reactive jamming through targeted simulation campaigns.

The rest of the article is organized as follows. Section 2 presents the reactive interference models commonly used to defeat UAV missions. Section 3 presents the methods and models used to simulate OFDM signals and reactive jamming and the detection model used. Finally, Section 4 shows an analysis of the evaluation results.

2. Reactive Jamming

2.1. Reactive DATA/ACK Jammer

A reactive DATA/ACK jammer is explained by Grover in [19] as a special type of reactive jammers designed to interfere with the two-way acknowledgement process in networks with short data to ACK cycles (e.g., IEEE 802.11, IEEE 802.15.4, or Bluetooth Low Energy (BLE)). Unlike active jammers, which transmit interference continuously, this jammer listens passively to the channel and activates only when it detects the start of a legitimate transmission. Upon detecting the data frame’s wiring and header sequence, the jammer calculates the ACK frame’s acknowledgment time and sends a short alarm pulse at the correct time in a response time that does not exceed the Short Inter-Frame Space (SIFS) interval or return time. The purpose is either to interfere with the decoding of the received data at the receiving end so that no ACK is generated or to interfere with the ACK itself so that the transmitting end does not receive an acknowledgment, and the transmission has to be retransmitted with an exponential delay.

Technically, pulses can be broadband noise, narrow-band “tones”, or signals that mimic sacrificial modulation. Since the ACK frame duration in a typical WLAN network is less than 30 µs, the cumulative effect of such interference can be less than 1%, which significantly limits detection with average RSS monitoring methods or PDR statistics. Moreover, the selectivity of the attack allows attackers to save energy and bypass simple signature detectors, as it takes only a few microseconds to capture the maximum resource value.

2.2. Reactive RTS/CTS Jammer

The RTS/CTS jammer as mentioned in [19] is a highly sophisticated UAV jammer. Rather than blocking the entire band, it attacks only the request-to-send (RTS) or clear-to-send (CTS) control messages, which are transmitted before data are transmitted according to the IEEE 802.11 protocol. Attacking this negotiation phase breaks the connection, but not the user’s data.

The first strategy is to block the connection as soon as an RTS is detected. The eavesdropper listens to the channel and sends a short radio pulse as soon as it detects an RTS packet, preventing the receiver from reading the RTS. The receiver cannot understand the request and sends no CTS acknowledgment. The sending node determines that the receiver is busy or out of range and drops the transmission. This method is very cost-effective because a microburst during RTS is sufficient, but it can be compensated by a retransmission mechanism or an adaptive timer.

The second strategy is for CTS. The jammer first allows the RTS packet to reach the receiver undamaged and then monitors the channel until the CTS response begins. It then only jams this confirmation message. Thus, the transmitter does not hear the expected CTS response. It assumes that there is noise on the channel or that the receiver is overloaded and cancels the data transfer. This solution is more discreet because the interference occurs later, but it requires a longer listening time and therefore slightly higher power consumption.

3. Methodology

Wilhelm in [20] showed that reactive jamming is among the most insidious threats to OFDM communication, as it is extremely difficult to detect due to its minimal activation time and maximal energy efficiency. The method presented in this article is based on a mathematical model of this instantaneous interference. We model (i) the activation process based on excess received energy, (ii) a response delay $\Delta N$ that mimics the hardware latency observed in software-defined radios (SDRs), and (iii) additive white Gaussian noise (AWGN) with power $P_J$ determined by the jammer-to-signal ratio (JSR). This model is then used to derive the detection features (RMS energy and Sevcik fractal dimension, FD) and to calibrate the adaptive thresholds.

3.1. Signal Model

Consider a complex OFDM signal $s\left[n\right]$ passing through a time-selective channel $h\left[n\right]$ and disturbed by additive Gaussian noise AWGN $w\left[n\right]$∼$\mathcal{CN}(0,{\sigma }^2)$.

$\mathcal{CN}(0,{\sigma }^2)$ denotes a circularly symmetric complex Gaussian with mean zero and variance ${\sigma }^2$.

The receiver observes

$$r\left[n\right]=\left(h\right[n]\ast s[n\left]\right)+w\left[n\right],n\in \mathbb{Z},$$

(1)

where $r\left[n\right]$ is the received signal before any jamming activity;

• $s\left[n\right]$ is the transmitted OFDM symbol;
• $h\left[n\right]$ is the Rayleigh channel impulse response;
• $w\left[n\right]$∼$\mathcal{CN}(0,{\sigma }^2)$ is the AWGN, or additive white Gaussian noise;
• “∗” is the discrete convolution.

An OFDM signal with 64 carriers and a cyclic prefix corresponding to 16 is sampled at

$$f_s=20\mathrm{MS}/\mathrm{s}$$

At this sampling frequency, and the subcarrier spacing is 312.5 kHz (fs/64), which is a value often chosen for OFDM UAVs links with low data rates. This choice reproduces a compact OFDM scheme, which is commonly used in low-speed UAV systems, where the useful width (5 MHz) can be achieved by sub-carrier in-band filtering while maintaining the standard SDR sampling rate. Recent work on UAV links such as [21] confirms the use of a comparable bandwidth for the OFDM/SC-FDM physical layer. In addition, several technical studies, such as [22], confirm that a sampling rate of 20 mega-samples per second (MS/s) is an important parameter when modeling or mapping an OFDM link in UAVs.

Each frame ($T_{\mathrm{active}}$) is followed by a silence of equal duration. Then, the reactive jammer is launched with variable parameters as follows:

$$P_k\in [-40,40]\mathrm{dB},\Delta f_k\in [0,500]\mathrm{kHz},{\varphi }_k\in [0,2\pi ].$$

The interval $P_{\mathrm{k}}$ covers the full spectrum of hazards, from stealth interference (−40  dB below the signal) to near handheld 10 W interference (+40 dB) at the receiver). The ranges suggested are of the same order of magnitude as those found by reactive LoraWan jamming tests used in [23].

The frequency offset also ranges from 0 (full channel) to 500 kHz (≈13 subcarriers), allowing testing of both full channel jamming and off-tone attacks with no observations or partial offset. In [24], the authors showed that such a spacing is sufficient to seriously degrade OFDM synchronization.

The initial phase of the jammer, noted ${\varphi }_k\in [0,2\pi ]$, is modeled as a uniform random variable to represent the lack of synchronization, both at the carrier and symbol clock, between the jammer and the OFDM target link. A reactive jammer starts operation without prior locking of the Phase-Locked Loop (PLL). By scanning the entire domain $[0,2\pi ]$, the simulation covers all phase-shift configurations (constructive, destructive, or intermediate), which avoids distortions caused by arbitrary phase alignment and faithfully reproduces real operating conditions in which neither the UAV receiver’s PLL nor the attacker’s PLL can converge within the duration of a single OFDM symbol. This assumption is corroborated by Rahbari in [25], who demonstrated that a swift reactive jammer can inject interference in less than one OFDM symbol (≈4 μs) after frame detection, leaving no time for a carrier-phase lock.

3.2. The Activation Process Based on the Excess Received Energy

The reactive jammer remains silent as long as no significant radio activity is detected. Its activation is triggered as soon as the RMS energy observed in the current window exceeds the adaptive threshold. ε_k. The hypothesis test is written as follows:

$$\sqrt{{\displaystyle \frac{1}{B-A+1}}\sum _{n=A}^B{\left|r\left[n\right]\right|}^2}>{\epsilon }_k,0<{\epsilon }_k<1,$$

(2)

For frame k, we use

$$W_k\triangleq \{n\mid A_k\le n\le B_k\},S_k\triangleq \{m\mid A_k-L\le m\le A_k-1\},$$

where $W_k$ is the current analysis window, and $S_k$ is the preceding silence segment. $r\left[n\right]$ is the sample; A and B delimit the current window. Therein, we also define the following:

• L: Integer length (in samples) of the silence segment $S_k$ used to estimate the noise variance.
• m: Sample index that ranges over the silence segment $S_k$, i.e., $m\in \{A_k-L,\dots ,A_k-1\}$.
• n: Sample index that ranges over the analysis window $W_k$, i.e., $n\in \{A_k,\dots ,B_k\}$.

We determine the maximum probability of a false alarm $P_{\mathrm{FA}}$, and the noise variance is estimated in situ ${\sigma }_k^2$ on the silence section in front of the useful frame as follows:

$${\sigma }_k^2={\displaystyle \frac{1}{L}}\sum _{m=1}^L{\left|r_{\mathrm{sil}}\left[m\right]\right|}^2,r_{\mathrm{sil}}\left[m\right]=r\left[A-L+m-1\right].$$

(3)

The resulting threshold, calculated according to the Neyman–Pearson criterion, is

$${\epsilon }_k={\sigma }_k\sqrt{-2ln{P}_{\mathrm{FA}}}.$$

(4)

The $P_{\mathrm{FA}}$ settles the ratio sensibility/false positives. With $N_{\mathrm{FFT}}+N_{\mathrm{CP}}=80$ samples, the duration of an OFDM frame is $T_{\mathrm{frm}}\simeq 40$ μs. $P_{\mathrm{FA}}$ of ${10}^{-3}$ ensures that, on average, less than one parasitic activation occurs every $T_{\mathrm{avg}}=T_{\mathrm{frm}}/P_{\mathrm{FA}}\approx 40$ ms, which is a false-alarm frequency well below RF reconfiguration times. The $P_{\mathrm{FA}}={10}^{-3}$, derived from the Neyman–Pearson criterion, ensures an optimal compromise between sensitivity and false alarms. It limits spurious activations to a frequency well below RF reconfiguration delays, guaranteeing practical robustness.

Then, the reactive jammer switches to the ON state during the current sub-frame. A fixed delay is injected to reproduce hardware response latency (RF detection, as well as decision and switching times).

$$\Delta N=4\left(N_{\mathrm{FFT}}+N_{\mathrm{CP}}\right)$$

(5)

where

• $N_{\mathrm{FFT}}=64$ is the FFT size;
• $N_{\mathrm{CP}}=16$ is the cyclic prefix;
• $\Delta N$ is the delay (in samples) before jammer transmission.
• Experiments with SDR devices show that there is often a material delay of 12–16 μs between the detection of radioactivity by the receiver and the first noise emission by the transmitter. Shin, in his study [26], reported a typical response time of 15 μs to Universal Software Radio Peripheral (USRP)-B210/N210 for an 802.11 n Wi-Fi jammer, while Wilhelm in [20] measured an initialization time of about 15 μs on the field-programmable gate array (FPGA) and the USRP-N210 after the decision.

Using 20 MS/s, an OFDM symbol ($N_{\mathrm{FFT}}=64$, and $N_{\mathrm{CP}}=16$) lasted 4 µs. Therefore, $\Delta N$ = 320 samples corresponds to 16 µs at 20 MS/s, which reflects the latencies measured on SDR platforms (12–16 µs on USRP-B210/N210). This choice is theoretically based on the OFDM symbol duration (4 µs) and corresponds to four symbols. With this configuration, the simulation becomes more destructive, as it avoids preambles and targets the payload directly.

From a functional point of view, several studies recommend a deliberate offset of three to four symbols to avoid jamming the preamble. This leaves the victim station to complete its synchronization, after which it destroys only the payload, which is a scenario considered by authors in [19] to be the most difficult to detect.

Then, the jamming is effectively injected into the sampling window, whose limits are noted (js, je) as follows:

$${\mathcal{W}}_J=\{n\in \mathbb{Z}\left|n=A+\Delta N,\dots ,B\right\}.$$

(6)

where

• ${\mathcal{W}}_J$ denotes all indices affected by jamming.

3.3. Analytical Form of the Jamming Signal

During activation, the reactive jammer emits a complex white noise defined as follows:

$$j\left[n\right]=\sqrt{P_J}(u_I\left[n\right]+\mathrm{j}{u}_Q\left[n\right]),u_I,u_Q\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }\mathcal{N}(0,1),P_J={10}^{\mathrm{JSR}/10}.$$

(7)

3.4. Signal Received with Jamming

The merged signal at the detector input is

$$r_J\left[n\right]=r\left[n\right]+j\left[n\right],\forall n,$$

(8)

Explicitly, it is defined as

$$r_J\left[n\right]=\left\{\begin{array}{c}\left(h\right[n]\ast s[n\left]\right)+w\left[n\right]\hfill \\ +\sqrt{P_J}\left(u_I\left[n\right]+\mathrm{j}{u}_Q\left[n\right]\right),\hfill & n\in {\mathcal{W}}_J,\hfill \\ \left(h\right[n]\ast s[n\left]\right)+w\left[n\right],\hfill & \mathrm{else}.\hfill \end{array}\right.$$

(9)

3.5. Feature Extraction

The method adopted for reactive jamming detection is based firstly on splitting the received signal into small sample windows. Then, for each window, two parameters are calculated: the energy and fractal dimension. These two features are estimated directly in the time domain on sliding windows. This method avoids any recourse to FFT, which reduces complexity to $\mathcal{O}\left(N\right)$ and guarantees real-time implementation on a digital signal processor (DSP) or low-power microcontroller, such as the case in [27], where twelve features have been extracted from the time domain of the received signal in order to reduce processing and calculation complexity.

Detecting reactive jamming in UAVs RF links requires descriptors capable of capturing both energy bursts and structural irregularity in the interfered signal, which are two dynamics already exploited in frequency hopping systems for interference recognition, as reported by the authors of the published study [28]. According to a contribution done by Zeng in [29], RMS energy is the basic non-coherent indicator for detecting the presence of a signal, since it only requires knowledge or estimation of the noise power. Furthermore, published work [30] by Cortés-Leal points out that, in practice, energy-related metrics such as RSSI and node energy consumption vary in characteristic ways under attack and serve as reliable symptoms for operational detectors. Concerning complexity measurement, Sevcik proposed the fractal dimension (SFD) which, as recalled in [31], normalizes the signal into the unit square and estimates its curve length, making it a fast and inexpensive estimator. More broadly, the authors in [32] show that the fractal dimension applied to waveforms is a powerful tool for the detection of transients, with an accuracy/robustness trade-off depending on the algorithm chosen, which motivates its use as a feature sensitive to fast interference-induced disturbances. Finally, comparative studies published by authors in [33] demonstrate that SFD efficiently discriminates modulated signals while displaying the shortest execution time among several fractal dimension variants, thus reinforcing its relevance for embedded implementations. In sum, RMS energy ensures sensitivity to the power increases expected during reactive jamming, SFD captures the increase in pattern irregularity, and their combination, validated by the literature, remains an ambitious choice for reactive jamming detection in UAVs.

3.5.1. Sliding Windowing

The signal received $x\left[n\right]=r_J\left[n\right]$ is segmented using a rectangular window $N_{\mathrm{win}}=1024$ samples, which is shifted by $N_{\mathrm{hop}}=512$ samples. This length corresponds to 51.2 µs at 20 MS/s, which is a compromise that is long enough to reduce the variance of the estimators but short enough to detect brief bursts, giving the following:

$$x_w\left[n\right]=x[n+(w-1)N_{\mathrm{hop}}],w=1,2,\dots ,W,$$

where

• $W=⌊\frac{N-N_{\mathrm{win}}}{N_{\mathrm{hop}}}⌋+1$ is the total number of windows. Each segment $x_w\left[n\right]$ is then analyzed independently.

3.5.2. Local Energy

For each window, signal intensity is quantified using the root mean square (RMS) and then converted into decibels as follows:

$$E_w=20{log}_{10}\left(\mathrm{RMS}\left\{x_w\left[n\right]\right\}+\epsilon \right),$$

(10)

with $\mathrm{RMS}\left\{x_w\left[n\right]\right\}=\sqrt{\frac{1}{N_{\mathrm{win}}}{\sum }_{n=0}^{N_{\mathrm{win}}-1}{\left|x_w\left[n\right]\right|}^2}$ and $\epsilon =2.2\times {10}^{-16}$ being regularization terms to avoid $log\left(0\right)$, which corresponds to the IEEE-754 double-precision floor scale. This metric captures the power surges introduced by the reactive jammer, even for moderate signal-to-jammer ratios (SJRs).

3.5.3. Fractal Dimension

Sevcik’s fractal dimension is used to estimate the geometric complexity of the signal. $D_w$ is calculated from standardized envelopes.

• ${\tilde{x}}_w\left[n\right]=\frac{|x_w\left[n\right]|-min|x_w|}{max|x_w|-min|x_w|+\epsilon }$.

$$D_w=1+{\displaystyle \frac{log{L}_w}{log\left(2(N_{\mathrm{win}}-1)\right)}},$$

(11)

where the cumulative length $L_w$ of the normalized curve is

$$L_w=\sum _{n=1}^{N_{\mathrm{win}}-1}\sqrt{1+{\left({\tilde{x}}_w\left[n\right]-{\tilde{x}}_w[n-1]\right)}^2}$$

(12)

The temporal roughness is strongly affected and increased by the injection of high-power additive Gaussian noise. $D_w$ rises above the median computed over the quiet intervals, highlighting a second discrimination criterion orthogonal to the energy.

3.6. Decision Making Using Mahalanobis Distance

Detecting reactive jamming introduced into traffic requires adaptive thresholds that can cope with rapid channel fluctuations and changes in background noise depending on environmental conditions. In [34], they demonstrated that thresholds based on fixed limits quickly become obsolete as SNR or AWGN changes. This part proposes adaptive thresholds based on local OFDM frame statistics, which are complemented by multiscale analysis to reduce the detection delay.

After extraction, each window is represented b the vector ${\mathbf{f}}_w={[E_w,D_w]}^{\top },$ where $E_w$ is the local energy defined in Equation (10), and $D_w$ is the fractal dimension defined in Equation (11). The objective of this part is that the algorithm should be able to differentiate between jammed windows and normal windows.

For each frame t, the reference set ${\mathcal{R}}_t$ is computed from the windows belonging to the silence interval post-OFDM. The mean and covariance are then predicted as follows:

$$\begin{array}{cc}\hfill {\mathit{\mu }}_t& ={\displaystyle \frac{1}{|{\mathcal{R}}_t|}}\sum _{\mathbf{z}\in {\mathcal{R}}_t}\mathbf{z},\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\mathbf{\Sigma }}_t& =cov\left({\mathcal{R}}_t\right)+{10}^{-6}{\mathbf{I}}_2,\hfill \end{array}$$

(14)

where

$$\mathbf{z}={[E_w,D_w]}^{\top }$$

The addition of the term ${10}^{-6}{\mathbf{I}}_2$ corresponds to a Tikhonov-type regularization, commonly used to stabilize the inversion of covariance matrices estimated from a limited number of samples. This patch prevents numerical degeneration when $|{\mathcal{R}}_t|$ is small, guaranteeing the definite positivity of ${\mathbf{\Sigma }}_t$. This is standard practice in statistical signal processing and machine learning, where it ensures the robustness of Mahalanobis distance estimators in the face of singularity.

For each window in the frame, the Mahalanobis distance is calculated, as shown in [35], as follows:

$$d_w^2={({\mathbf{z}}_w-{\mathit{\mu }}_t)}^{\top }{\mathbf{\Sigma }}_t^{-1}({\mathbf{z}}_w-{\mathit{\mu }}_t).$$

(15)

Under the null hypothesis $H_0$ (no jamming), the test statistic $d_w^2$ still follows a ${\chi }^2\left(2\right)$ law when the background noise is strictly Gaussian. Rather than relying on a fixed theoretical quantile, we re-estimate the decision threshold frame-by-frame from the most recent silent windows ${\mathcal{S}}_t$ as follows:

$${\tau }_{\mathrm{eff},t}=Q_{1-P_{\mathrm{FA}}}\{d_{\ell }^2\left|\ell \in {\mathcal{S}}_t\right\},$$

(16)

where $Q_{1-P_{\mathrm{FA}}}\{·\}$ denotes the empirical $(1-P_{\mathrm{FA}})$ quantile of the set of silent-window distances within frame t. This adaptive rule guarantees a constant false-alarm probability, even under slow noise or channel drifts.

We keep

$$P_{\mathrm{FA},\mathrm{long}}=0.02,P_{\mathrm{FA},\mathrm{short}}=0.01,$$

for long windows ($N_1=512$, $H_1=256$) and short windows ($N_2=20$, $H_2=10$), respectively. The choice of $P_{\mathrm{FA},\mathrm{long}}=0.02$ and $P_{\mathrm{FA},\mathrm{short}}=0.01$ is the result of a compromise between the speed of detection and the control of the false-alarm rate. On the long scale, a more permissive value ($0.02$) preserves the sensitivity in the presence of slow noise and channel drifts, while on the short scale, a stricter threshold ($0.01$) limits the inflation of false positives induced by the higher variance of estimators over reduced windows. This differentiation of $P_{FA}$ levels is in line with the principles of multi-scale CFAR described in the literature on adaptive detection by the authors in [36]. Then, the binary decision becomes the following:

$$d_w^2>{\tau }_{\mathrm{eff},t}⟹\mathrm{Reactive}\mathrm{Jamming}\mathrm{detected}$$

(17)

3.7. Multi-Scale Fusion

Two independent Mahalanobis detectors operate in parallel:

$${\mathcal{D}}_1=\left\{d_{\ell ,1}^2>{\tau }_{\mathrm{eff},\mathrm{long},t}\right\},{\mathcal{D}}_2=\left\{d_{\ell ,2}^2>{\tau }_{\mathrm{eff},\mathrm{short},t}\right\},$$

(18)

where the adaptive thresholds ${\tau }_{\mathrm{eff},\mathrm{long},t}$ and ${\tau }_{\mathrm{eff},\mathrm{short},t}$ are the $(1-P_{FA})$ quantiles of the silent-window distances at the long and short scales (see Equation (16)).

The short-scale decisions ${\mathcal{D}}_2$ are re-sampled onto the long window grid and then combined by logical disjunction as follows:

$$D={\mathcal{D}}_1\vee {\mathcal{D}}_2.$$

This logical OR fusion preserves the target false-alarm probabilities for both time scales while capturing jamming events ranging from very brief spikes to bursts lasting several $N_2/f_s$ seconds.

Because ${\mathit{\mu }}_t$ and ${\mathbf{\Sigma }}_t$ are updated only once per frame (Equations (13) and (14)), each window requires just two scalar multiplications and one comparison. The resulting workload is compatible with real-time execution on low-power DSPs or microcontrollers.

The authors in [37] demonstrated that updating key metrics in a single frame has been shown to keep CPU, memory, and power budgets very low, making it compatible with real-time execution on modest onboard systems.

A fixed threshold, even if theoretically matched to the ${\chi }^2\left(2\right)$ law, presumes that the background noise, the receiver-front gain and the propagation channel remain stationary. In practice, every RF chain exhibits gain drift (temperature, aging), every channel undergoes quasi-lognormal slow fading, and the additive noise floor varies with adjacent-band interference. A fixed $\tau$ therefore slides, in real units, away from the optimal decision surface: too low of a value inflates the false-alarm rate, whereas too high of a value blinds the detector to weak or short jamming attempts. By contrast, the adaptive thresholds ${\tau }_{\mathrm{eff},\mathrm{long},t}$ and ${\tau }_{\mathrm{eff},\mathrm{short},t}$ are re-anchored at every frame on the empirical distribution of genuinely silent windows. This re-centering guarantees that the test statistic always lies on the same probabilistic scale, whatever the instantaneous SNR.

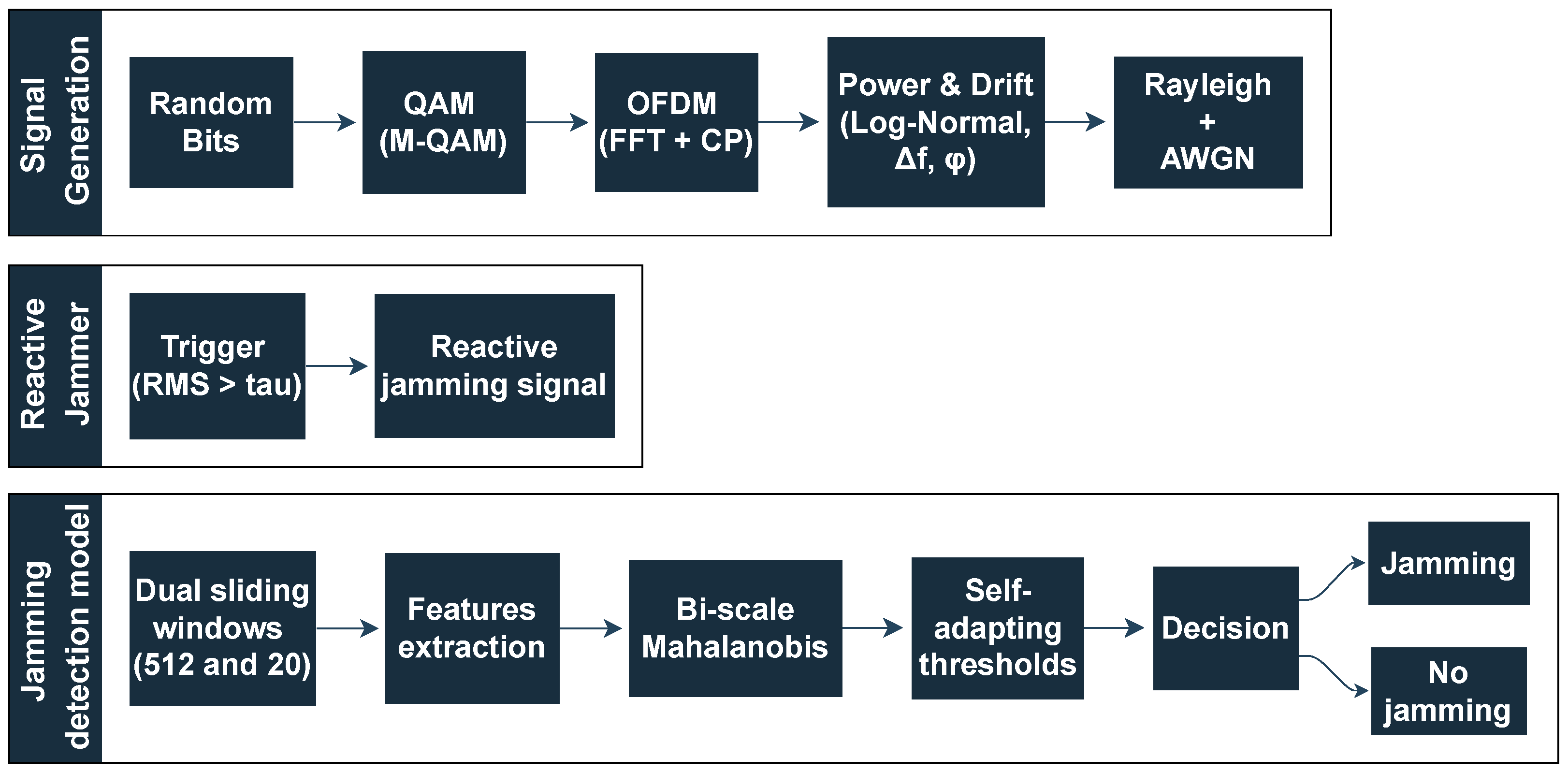
The pipeline in Figure 1 summarizes the end-to-end reactive jamming detection from the OFDM transmission signal modeling, going through the reactive interference triggering and ending with the implemented detection process.

3.8. Simulation Framework and TX/RX/Jammer Setup

The simulation setup shown below is described in detail in order to ensure clarity and reproducibility.

• Transmitter

Consider a transmission frame indexed by k. The emitted power is modeled with its logarithmic expression $P_{\mathrm{dB}}\left(k\right)$ used for generation. The useful signal is carried by a set of orthogonal subcarriers, and then symbols are mapped and assembled into an OFDM frame. Two multiplicative impairments are applied per frame—a carrier-frequency offset $\Delta f_k$ and a phase rotation ${\varphi }_k$—which are both drawn from bounded ranges. The useful frame is followed by a deterministic silent interval so that a repeating useful + silence structure spans the entire sequence.

• Receiver

The received signal results from propagation over a time-selective channel modeled as a two-path Rayleigh channel [0, 1, 2 μs] with average earnings [0, −6] dB and maximum Doppler of 10 Hz, followed by AWGN noise at 10 dB measured SNR.

• Reactive Jammer

The reactive scrambler makes a frame-by-frame decision via a CFAR energy test applied to the received signal before injection, local noise variance ${\sigma }_k$ is estimated on the segment of silence immediately preceding the frame, and then a Neyman–Pearson threshold is determined as ${\epsilon }_k={\sigma }_k\sqrt{-2ln{P}_{\mathrm{FA}}}$.

Afterwards, the reactive jammer is triggered if $\mathrm{RMS}>{\epsilon }_k$. To model realistic hardware latency (detection $to$ decision $to$ RF switching chain), injection starts after a fixed delay $\mathtt{delay}=4(\mathtt{FFT}+\mathtt{CP})=320$ samples, i.e., 16 μs, and continues until the end of the frame, producing a jamming burst of 144 μs.

The jamming amplitude is drawn frame by frame according to the law ${\mathrm{JNR}}_{\mathrm{dB}}$∼$\mathcal{N}(12,3^2)$, while the useful signal undergoes independent frequency and phase shifts per frame ($\Delta f$∼$\mathcal{U}[-10\mathrm{kHz},+10\mathrm{kHz}]$, $\varphi$∼$\mathcal{U}[0,2\pi )$).

• Feature Windowing

Two analysis scales are used: a long scale with parameters $(wi{n}_{\ell },ho{p}_{\ell })$ and a short scale with parameters $(wi{n}_s,ho{p}_s)$. For each temporal window w, a two-dimensional feature vector is extracted, consisting of the logarithmic energy

$$E\left(w\right)=20{log}_{10}\left(\mathrm{rms}\left(w\right)+ϵ\right)$$

where $ϵ$ is a small regularization constant, and the Sevcik fractal dimension is computed on the signal magnitude $\left|w\right|$. Window-level labels are obtained by aggregating the ground truth at the window scale (for example, any jamming present within the window implies label 1), thus providing inputs for subsequent two-scale detection stages.

3.9. Channel Model Configuration

The channel introduces small-scale fading, noise, and carrier impairments.

• Fading Channel

The propagation environment is modeled as a multipath Rayleigh block-fading channel. It consists of a finite set of propagation paths, with each characterized by a specific delay and average gain. The channel is assumed to remain constant during the duration of a frame and to vary independently between frames. A maximum Doppler shift parameter controls the temporal correlation of the fading process, capturing the effect of mobility or oscillator instabilities.

• Additive Noise

The received signal is further corrupted by additive white Gaussian noise (AWGN). The noise is characterized by a measured signal-to-noise ratio, which determines the variance of the Gaussian distribution added to the received samples. This noise component models thermal and electronic disturbances in the receiver chain.

• Carrier Impairments

In addition to fading and noise, carrier impairments are applied at the transmitter side. These include a frequency offset, denoted $\Delta f$, and a phase offset, denoted as $\varphi$. Both quantities are modeled as random variables drawn from bounded ranges, to emulate practical imperfections such as oscillator mismatch or residual synchronization errors.

3.10. Adaptive Mahalanobis Detector

The detection algorithm exploits features extracted at two time scales (long and short windows). For each scale, the features are arranged into vectors containing the logarithmic energy and the fractal dimension. Detection is based on the squared Mahalanobis distance, which compares each feature vector x against a statistical model estimated from silent windows as follows:

$$d^2={(x-\mu )}^T{C}^{-1}(x-\mu ),$$

where $\mu$ is the mean vector, and C is the covariance matrix of features computed over silence-only windows. A constant false-alarm rate (CFAR) is achieved by adapting thresholds per frame.

Additional constraints are imposed for robustness:

• A minimum number of silence windows must be available to compute $\mu$ and C.
• Guard windows adjacent to potential transitions are excluded.
• If silence statistics are insufficient, the test falls back to a fixed ${\chi }^2$ threshold.

If these conditions are not satisfied, the threshold falls back to the quantile of a ${\chi }^2$ distribution with two degrees of freedom. The final frame-level decision results from the logical fusion of long- and short-window detectors.

The following Algorithm 1 summarizes the complete functioning of the two-scale Mahalanobis detector.

Algorithm 1 Two-scale detection

1: Initialize: $x={\sum }_{k=1}^{N_{\mathrm{frm}}}{x}_k$ (frame+silence), $r\leftarrow \mathcal{H}\left(x\right)+n$; $g\left[n\right]=0$, $j\left[n\right]=0$   2: Global noise.  ${\sigma }_g=\mathrm{rms}\left(r|\mathrm{global}\mathrm{silence}\right)$   3: Per-frame noise & CFAR: for k: ${\sigma }_k=\mathrm{rms}\left(r|{\mathrm{silence}}_k\right)$; if $k=1$ then ${\sigma }_k\leftarrow {\sigma }_g$; ${\epsilon }_k={\sigma }_k\sqrt{-2ln{P}_{\mathrm{FA},\mathrm{jam}}}$   4: Reactive jamming: if $\mathrm{rms}\left(r|{\mathrm{frame}}_k\right)>{\epsilon }_k$ then inject j on last $L_{\mathrm{delay}}$; set $g\left[n\right]=1$ there   5: Compose:   $r_J=r+j$   6: Windows & features: build $W{L}_{\ell },W{L}_s$; $z_{\alpha }\left(w\right)={\left[20{log}_{10}(\mathrm{rms}\left(r_J{|}_{[i_w,j_w]}\right)+\epsilon ),FD\left(\right|r_J{|}_{[i_w,j_w]})\right]}^{\top }$; $G\left(w\right)=maxg$   7: Select per frame/scale: ${\mathcal{W}}_f=\{w\in W{L}_{\alpha }:[i_w,j_w]\subseteq {\mathrm{frame}}_f\cup {\mathrm{silence}}_f\}$; ${\mathcal{S}}_f=\{w\in {\mathcal{W}}_f:G\left(w\right)=0\}$; if $|{\mathcal{S}}_f| < m^{★}$ then ${\mathcal{S}}_f\leftarrow {\mathcal{W}}_f$; trim $g^{★}$   8: Silence stats: ${\mu }_{\alpha ,f}=\mathrm{mean}{z}_{\alpha }\left({\mathcal{S}}_f\right)$; $C_{\alpha ,f}=\mathrm{cov}{z}_{\alpha }\left({\mathcal{S}}_f\right)+\lambda I_2$   9: Mahalanobis Distance: for $w\in {\mathcal{W}}_f$: $d_{\alpha }^2\left(w\right)={(z_{\alpha }\left(w\right)-{\mu }_{\alpha ,f})}^{\top }{C}_{\alpha ,f}^{-1}(z_{\alpha }\left(w\right)-{\mu }_{\alpha ,f})$ 10: Threshold & decision: ${\tau }_{\alpha ,f}=Q_{1-P_{\mathrm{FA},\alpha }}\{d_{\alpha }^2\left(w\right):w\in {\mathcal{S}}_f\}$; if undefined then ${\tau }_{\alpha ,f}={\chi }_2^{2-1}(1-P_{\mathrm{FA},\alpha })$; ${\delta }^{\left(\alpha \right)}\left(w\right)=[d_{\alpha }^2\left(w\right)>{\tau }_{\alpha ,f}]$ 11: Fuse: ${\delta }^{(s\uparrow )}=\mathrm{NN}\text{-}\mathrm{up}({\delta }^{\left(s\right)}\to W{L}_{\ell })$; ${\delta }^{\left(\mathrm{fuse}\right)}={\delta }^{(\ell )}\vee {\delta }^{(s\uparrow )}$

3.11. Simulation Setup

The simulations were executed on a workstation equipped with an Intel Core i9-9880H processor (Intel Corporation, Santa Clara, CA, USA; 8 cores, 16 threads, 2.30 GHz) and 32 GB RAM. The entire framework, including signal generation, feature extraction, and Mahalanobis detection, was implemented in MATLAB R2024a with the Communications Toolbox (The MathWorks, Inc., Natick, MA, USA).

4. Simulations and Results

4.1. Overview of the Evaluation Protocol

To assess the proposed bi-scale Mahalanobis detector, we simulated $N_{\mathrm{frm}}=5000$ OFDM frames corrupted by a reactive jammer over a Rayleigh channel (

Table 1. Main simulation parameters.

Parameter (Symbol)	Value/Setting
OFDM configuration
Sampling frequency $f_s$	20 MS/s
FFT size $N_{\mathrm{FFT}}$	64
Cyclic prefix $N_{\mathrm{CP}}$	16 samples (25 %)
Quadrature amplitude modulation (QAM) of order M	4, i.e., quadrature phase-shift keying (QPSK)
Symbols per frame $N_{\mathrm{sym}}$	40
Frames simulated $N_{\mathrm{frm}}$	5000
Windowing
Long window/hop $(w_1,h_1)$	512/256 samples
Short window/hop $(w_2,h_2)$	20/10 samples
Detector settings
Min. silence windows $N_{\mathrm{sil},\min }$	5
False-alarm target $P_{\mathrm{FA}}$	$2\%$ (long), $1\%$ (short)
Channel & jammer
Fading model	2-tap Rayleigh (0 and 1.2 μs; 0/−6 dB)
Jammer trigger	reactive (power-driven)
Jammer JSR	∼$\mathcal{N}\left(12\mathrm{dB},3^2{\mathrm{dB}}^2\right)$
Jammer power range $P_{\mathrm{jam}}$	$[-40,40]\mathrm{dB}$
Carrier-frequency offset (CFO) range range $\Delta f$	−10–+10 kHz; phase $\varphi \in [0,2\pi ]$

). Two window lengths were adopted (512 samples and 20 samples) to capture both macro- and micro-temporal statistics of the received signals. The energy (E) and Sevcik’s fractal dimension ($\mathrm{FD}$) were extracted from every window and fed to the detector under $P_{\mathrm{FA}}=2\%$ (long) and $P_{\mathrm{FA}}=1\%$ (short). A decision was finally taken by the logical OR between the two scales.

4.2. Confusion Matrix and Core Metrics

The detection model creates for each window a confusion matrix, shown in Figure 2, which summarizes the detection results for the long and short windows. The detector correctly marked each jamming window with a of recall = 100%. On the other hand, 370 quiet windows were misclassified as jammed (FP/TN = 0.5%), resulting in an accuracy of 99.4% and an F1 score of 99.7%. All results are summarized in

Table 2. Detection metrics.

Metric	Value
Precision	$99.4\%$
Recall	$100.0\%$
Accuracy	$99.7\%$
F1 score	$99.7\%$
AUC (receiver operating characteristic (ROC) curve)	$0.9997$
Average detection time	$80\mu \mathrm{s}$

.

The detection model produces, for each analysis window (long and short), a confusion matrix, as shown in Figure 2, summarizing the classification of jamming versus quiet intervals. Each window is labeled as either Jam (positive class) or Quiet (negative class). Let $TP$ denote true positives (jammed windows correctly detected), $FN$ denote false negatives (jammed windows missed), $FP$ denote false positives (quiet windows spuriously flagged), and $TN$ denote true negatives (quiet windows correctly rejected). In this simulation, all jammed windows were correctly detected so that $FN=0$, and thus, the window-level recall attained $\mathrm{Recall}=TP/(TP+FN)=1.000(100\%)$. Conversely, $FP=370$ quiet windows were misclassified as jammed.

Given the reported internal ratio $FP/TN=0.005(0.5\%)$, we infer $TN=FP/0.005=\mathrm{74,000}$. This yields an overall accuracy of 99.7% and a harmonic mean $F1=2·(\mathrm{Precision}·\mathrm{Recall})/(\mathrm{Precision}+\mathrm{Recall})=0.997(99.7\%)$ under the stated performance summary. All aggregated results are listed in Table 2.

The four cells $(TP,FN,FP,TN)$ furnish the sufficient statistics for all standard classification metrics.

Precision quantifies the reliability of positive detections:

$$\mathrm{Precision}={\displaystyle \frac{TP}{TP+FP}}$$

A high precision indicates a low false-alarm burden on mitigation resources.

Recall captures completeness of detection:

$$\mathrm{Recall}={\displaystyle \frac{TP}{TP+FN}}$$

With $FN=0$, the detector achieves perfect sensitivity, ensuring no jamming window escapes detection.

The overall correctness is measured by

$$\mathrm{Accuracy}={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

blending performance on both positive and negative classes. When the accuracy is high, it can mask class imbalance; hence, complementary metrics remain essential.

The $F1$ score is the harmonic mean balancing precision and recall:

$$F1=2·{\displaystyle \frac{\mathrm{Precision}·\mathrm{Recall}}{\mathrm{Precision}+\mathrm{Recall}}}$$

Because the recall is perfect, $F1$ is chiefly governed by precision.

The false positive rate (FPR) is

$$\mathrm{FPR}={\displaystyle \frac{FP}{FP+TN}}={\displaystyle \frac{FP/TN}{1+FP/TN}}$$

which with $FP/TN=0.005$ gives $\mathrm{FPR}\approx 0.005$ (0.5%). The specificity (true negative rate) is

$$\mathrm{TNR}={\displaystyle \frac{TN}{TN+FP}}=1-\mathrm{FPR}$$

The absence of false negatives prioritizes operational safety (no missed jamming events). Any remaining improvement leverage lies mainly in reducing $FP$ to minimize unnecessary countermeasure activations and downstream processing load. Once definitive $TP$ values and total window counts are finalized, a consistency check should be performed to verify that the triplet $(\mathrm{Precision}, \mathrm{Recall}, F1)$ numerically aligns with the raw confusion counts.

For every jam onset, the first positive decision occurred, on average, $80\mu \mathrm{s}$ after the actual jamming start, with only four OFDM symbols at the current sampling frequency. This microsecond responsiveness plainly outperformed the millisecond-level latency reported in recent works that rely on machine learning models [28], yet it remains to be verified on hardware simulation; convenience must not be mistaken for real-time guarantee.

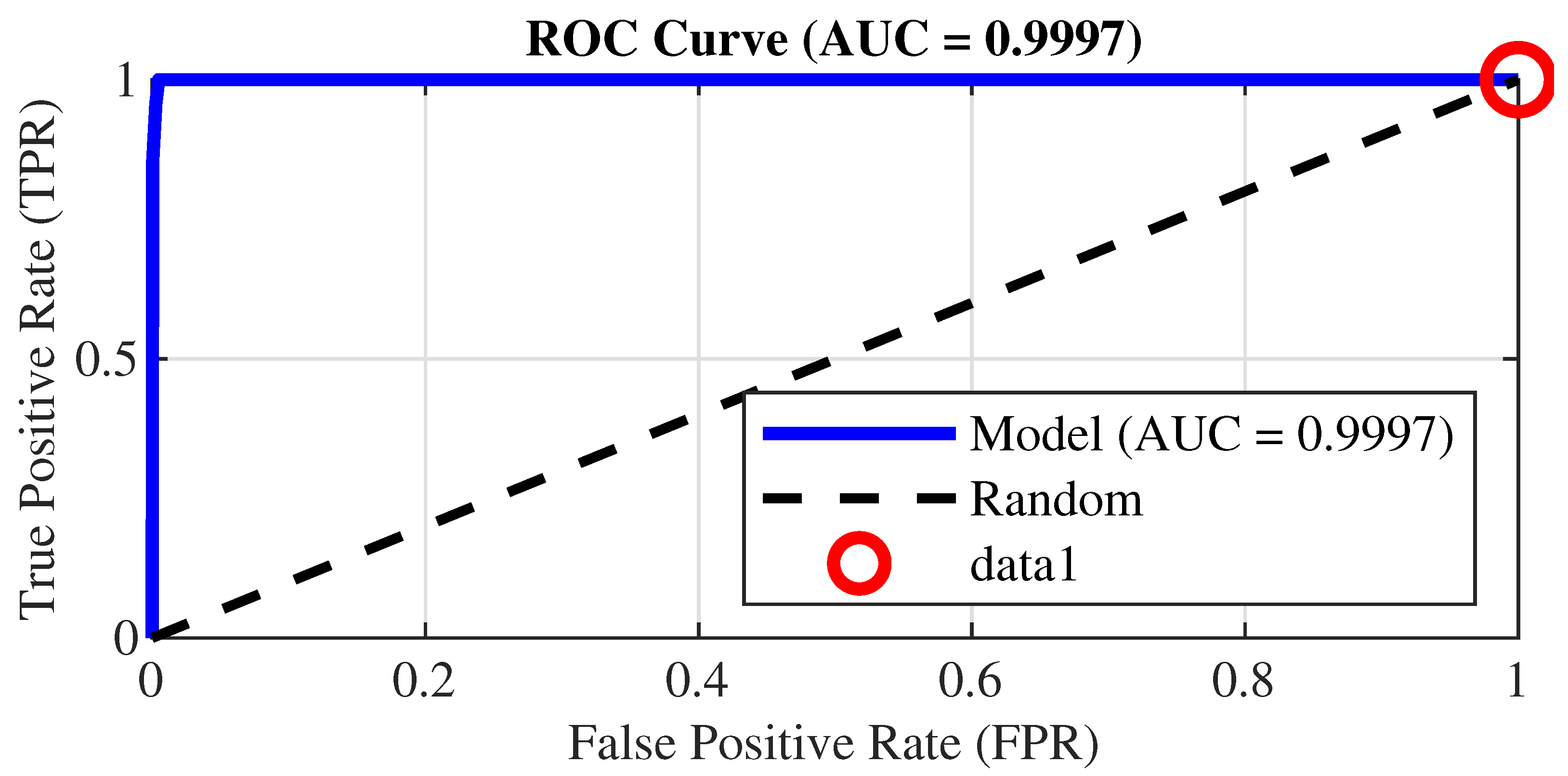
4.3. ROC Curve

Figure 3 shows the detector’s ROC curve rising almost vertically from $(0,0)$ to the upper left-hand corner, where it then remained on the ceiling with a rate of true positives $\mathrm{TPR}\approx 1$ across the entire width. This pattern reveals a near-perfect discrimination capability, which is corroborated by the area under the curve $\mathrm{AUC}=0.9997$. In concrete terms, if we select at random one jamming window and one silence window, the detector ranks them correctly (${\mathrm{score}}_{\mathrm{jamming}}>{\mathrm{score}}_{\mathrm{silence}}$) in 99.97% of cases. Accordingly, the area under the ROC curve is $\mathrm{AUC}=0.9997=1-3\times {10}^{-4}$, which is well above the chance level ($\mathrm{AUC}=0.5$).

Given the total number of windows tested ($N\simeq 1.27\times {10}^5$), the standard error associated with AUC estimate is

$${\sigma }_{\mathrm{AUC}}=\sqrt{{\displaystyle \frac{\mathrm{AUC}(1-\mathrm{AUC})}{N}}}\approx 4\times {10}^{-4}$$

which places the confidence interval at $95\%$ in $[0.9990,1]$. The probability of the model’s AUC falling below 0.99 is therefore statistically negligible.

4.4. Robustness to Jammer Power

The scatter plot in Figure 4 shows, for all 5000 frames simulated, the instantaneous power of the jammer $P_{\mathrm{jam}}$ (x axis, dB scale) and the average Mahalanobis distance ${\overline{d}}^2$ calculated over the long and short windows of the bi-scale detector (ordinate axis, linear scale). The almost exponential growth of ${\overline{d}}^2$ between $-20$ dB and $-5$ dB confirms the sensitivity of the model as soon as jamming exceeds the background noise by approximately 10 dB. The peak observed around $P_{\mathrm{jam}}\simeq -7$ dB corresponds exactly to the time when SJR ratio remains sufficiently balanced to maximize the statistical divergence without inducing clipping on the communication channel. When $P_{\mathrm{jam}}$ is above 0 dB, the slight decrease in ${\overline{d}}^2$ reflects intra-frame normalization, which means the situation when the jammer becomes dominant, but the overall variance remains controlled, avoiding detector saturation. This non-monotonic response also validates bi-scale dimensioning; it guarantees recall rate of 100% and a precision of 99.4% while preserving a margin against false positives when jamming reaches extreme powers.

4.5. Adaptive Thresholds Dynamics

Figure 5 plots only the first 500 frames so that the frame-to-frame fluctuations can be seen clearly on a single axis. The long-window threshold, ${\tau }_{\mathrm{eff},\mathrm{long}}$ (red), remains in the range between 2 and 6 because it was computed from windows of 512 samples, whose statistics evolve slowly. The short-window threshold, ${\tau }_{\mathrm{eff},\mathrm{short}}$ (orange), spans roughly 10 to 30 with only 20 samples per window; it responded much more sharply to any rapid shift in SNR or noise floor. In both traces, rises correspond to fading or interference peaks, whereas drops mark calmer channel conditions—demonstrating that the quantile update accurately tracks the real-time spread of Mahalanobis distances.

These visible swings underline the weakness of a single, fixed decision level. A constant threshold low enough to capture weak bursts during quiet periods would overshoot the target false-alarm rate whenever the noise increases. Conversely, a level high enough to withstand noisy episodes would miss low-power jamming once the channel quiets down. By recalibrating $\tau$ from silent windows at every frame, the adaptive method keeps the false-alarm probability $P_{FA}$ under control and retains sensitivity across the full spectrum of real-world channel and noise variations without manual re-tuning.

4.6. CPU Time Consumption

To substantiate the claim of low CPU intensity, instrumentation of the CPU time per frame was added to the simulation loop. Figure 6 plots, for 500 consecutive frames, the processing time per frame of the proposed detector, with a horizontal line serving as an average CPU time budget.

The curve shows minimal CPU consumption for the most part; the time per frame is closely clustered around the global mean 6.875 ms, with a low, steady trend. This plan reflects the low intrinsic cost of the proposed pipeline and constant complexity per window, without trained models. As it stands, the average value and the cloud density around this average indicate a load compatible with real-time execution on embedded targets.

Visible point elevations were rare among the 500 frames and did not alter the nominal regime, with most frames remaining in the immediate vicinity of the mean. The distribution appears asymmetrically right-tailed, which is typical of a light algorithmic core occasionally disturbed by non-recurrent operations. In practice, the cloud’s median and concentration support the idea that the sustained cost is low, with the rare peaks having a negligible cyclical duty.

Deep learning approaches (e.g., convolutional neural networks) have achieved high jamming detection accuracy, especially using spectrogram or IQ-sample representations, but often at the expense of higher computational burden. Li et al., in [4], developed a spectrogram-based CNN classifier to detect jamming against OFDM receivers on UAVs. The study reported an outstanding accuracy 99.8% detection and 0.03% false alarm with deep CNNs, but a trade-off in processing cost was noted. The training and testing times for the CNN models were significantly higher than those obtained by the conventional ML algorithms, which is attributed to the CNNs’ deep and complex architectures.

In other words, the CNN-based approach required far more computation to achieve its accuracy. For instance, their best CNN (EfficientNet-B0) took on average 0.005 s per frame with a GPU and 0.066 s per frame on a CPU (i.e., 66 ms per OFDM frame) for inference, which is more than 9.6 times higher than the average CPU time observed for the bi-scale Mahalanobis detector. This implies that without GPU acceleration, a deep model might only process 15 frames per second on a CPU, indicating a substantial computational load. Such heavy models involve millions of parameters and numerous matrix operations per evaluation, contributing to high CPU usage.

In positioning the propsed method against the literature, it aligns with the push for “lightweight yet efficient” reactive jamming detection in IoT/UAV networks explained by Alia in [38]. Unlike deep learning solutions that demand substantial computational resources and hindering scalability in distributed networks, a lightweight statistical detector imposes minimal CPU and energy burden. Thus, the proposed approach can be presented as a lower-cost alternative that sacrifices some complexity in exchange for speed, accuracy, simplicity, and ease of deployment on resource-limited platforms. This is supported by evidence from prior work [39], such as simple metric-based detectors that have been successfully used to catch jamming with negligible overhead. By operating in the time domain and using an adaptive threshold, the method is also well suited to reactive jamming, which often manifests as subtle changes in the timing or variance of signals. Time-domain anomaly detection can catch the transient interference bursts of reactive jammers quickly, without needing intensive spectral analysis.

4.7. Complexity Analysis

Per-window operation counts are reported for feature extraction (local energy $E_w$ and Sevcik fractal dimension $D_w$) and for the frame-level adaptive Mahalanobis decision. Additive operations include both additions and subtractions; divisions, square roots, and logarithms are itemized separately.

4.7.1. Energy on a Window of Length w

Using $E_w=20{log}_{10}(\mathrm{rms}(·)+\epsilon )$ with $\mathrm{rms}=\sqrt{{\displaystyle \frac{1}{w}}\sum {\left|r\left[n\right]\right|}^2}$ gives

$$\underset{\mathrm{mult}({\mathrm{Re}}^2+{\mathrm{Im}}^2)}{\underbrace{2w}}+\underset{\mathrm{adds}(\mathrm{sum}\mathrm{of}\mathrm{squares})}{\underbrace{2w}}+\underset{\mathrm{division}}{\underbrace{1}}+\underset{\mathrm{sqrt}}{\underbrace{1}}+\underset{{log}_{10}}{\underbrace{1}}+\underset{\mathrm{constant}\mathrm{mult}(\times 20)}{\underbrace{1}}.$$

4.7.2. Sevcik $D_w$ on a Window of Length w

With normalization $x^{\prime }=(x-min)/(max-min+\epsilon )$ and $L={\sum }_{i=2}^w\sqrt{1+{(x_i^{\prime }-x_{i-1}^{\prime })}^2}$, then $D_w=1+{\displaystyle \frac{logL}{log\left(2\right(w-1\left)\right)}}$, and we have

$$\underset{\mathrm{comparisons}}{\underbrace{2w}}+\underset{\mathrm{adds}(\mathrm{norm}+\mathrm{diff}+\mathrm{accum})}{\underbrace{(3w-2)}}+\underset{\mathrm{mult}\left(\mathrm{squares}\right)}{\underbrace{(w-1)}}+\underset{\mathrm{divisions}(\mathrm{norm}+\mathrm{final})}{\underbrace{w+1}}+\underset{\mathrm{sqrt}}{\underbrace{(w-1)}}+\underset{log}{\underbrace{1}}.$$

4.7.3. Mahalanobis Distance per Window (Given $\mu$ and $C^{-1}$)

For feature vector $x\in {\mathbb{R}}^2$, $d=x-\mu$, and $d^2=d^{\top }{C}^{-1}d$,

$$\underset{\mathrm{mult}}{\underbrace{6}}+\underset{\mathrm{adds}}{\underbrace{5}}+\underset{\mathrm{comparison}\mathrm{vs}.\mathrm{threshold}}{\underbrace{1}}.$$

The per-frame overhead to estimate $\mu$ and C on s silence windows is linear in s:

$$\mathrm{mean}:2s\mathrm{adds}+2\mathrm{divs};\mathrm{covariance}:(3s\mathrm{mult}+5s\mathrm{adds})+3\mathrm{divs},$$

plus a constant-cost $2\times 2$ matrix inversion. The adaptive threshold is computed by a quantile of the silent $d^2$ values (sorting $O(slogs)$), with fixed windowing s bounded per frame; hence, the amortized cost is constant. If desired, the ${\chi }_p^2$ fallback (df = 2) yields $O\left(1\right)$ per frame.

Let N be the number of samples. The number of windows at hop h is $N_w\approx N/h$. Since each window incurs a constant number of primitive operations (independent of N), the total cost scales linearly as

$$\mathrm{Cost}\left(N\right)=\Theta \left({\displaystyle \frac{N}{h_{\mathrm{long}}}}{c}_{\mathrm{feat},\mathrm{long}}+{\displaystyle \frac{N}{h_{\mathrm{short}}}}{c}_{\mathrm{feat},\mathrm{short}}+{\displaystyle \frac{N}{h_{\mathrm{long}}}}{c}_{d^2}\right)=O\left(N\right).$$

4.7.4. Numerical Counts with Simulation Parameters

For the long windows $(w_1=512,h_1=256)$ and short windows $(w_2=20,h_2=10)$, we find the following:

Per Window	Mult	Adds	Divs	Sqrt	Log	Comps
Energy ($w=512$)	$1024+1$	1024	1	1	1	0
Sevcik FD ($w=512$)	511	1534	513	511	1	1024
Mahalanobis $d^2$	6	5	0	0	0	1
Energy ($w=20$)	$40+1$	40	1	1	1	0
Sevcik FD ($w=20$)	19	58	21	19	1	40

With hops $(h_1=256,h_2=10)$, the window counts scale as $N/h_1$ and $N/h_2$, so the aggregate complexity remains linear in N and avoids any $O(NlogN)$ term inherent to FFT-based features. This supports real-time feasibility on lightweight embedded UAVs hardware.

5. Quantitative Comparison with State-of-the-Art Methods

In order to reinforce the validity of the proposed contribution, a quantitative comparison with representative reactive jamming detection algorithms from the last decade was conducted. The objective of this section is to position the bi-scale Mahalanobis detector with respect to existing state-of-the-art methods by considering the most relevant performance indicators, namely, the precision, recall, detection latency, and computational requirements.

Several recent proposals illustrate the diversity of approaches in this domain. The “JamShield system” developed by the authors in [40] exemplifies a dynamic machine-learning based approach capable of online adaptation. When evaluated with real 802.11 traffic, it reported a 88.5% precision and 90.3% recall, with a detection rate of 97.9% and a false-alarm rate of approximately 3.9%. Although robust in realistic conditions, its precision values remain below those of the bi-scale Mahalanobis detector, which consistently exceeds 99%. Nevertheless, JamShield demonstrates the importance of online adaptability and minimal misdetection rates.

Another recent study introduced a lightweight XGBoost-based detector implemented on an STM32H7 microcontroller used by the authors in [41]. This model employed a reduced set of time-frequency features and achieved 96% precision and 93% recall, with an overall accuracy of 98%. A notable strength of this method was its ultra-low decision latency of 20 μs, which is faster than the 80 μs latency measured for the proposed detector. However, the slight reduction in precision highlights a trade-off between speed and accuracy. The hardware requirements of the XGBoost approach were minimal, making it suitable for embedded deployment.

Deep learning solutions have also been introduced, such as the dual-threshold DNN with wavelet preprocessing designed for 5G New Radio signals. This approach shown by the authors in [42] achieved 94% precision and 97% recall, corresponding to an AUC greater than 0.95. Despite the strong classification performance, this method required substantial training effort, initially more than 40 h—later reduced to 144 min—and powerful computational platforms. Such requirements significantly limit deployment on lightweight or embedded hardware, whereas the bi-scale Mahalanobis detector executes distance calculations in microseconds without any training overhead.

Complementary efforts can be found in cluster-based detection schemes for wireless sensor networks (WSNs). Ganeshkumar et al. [43] reported a detection rate of 99.88% in simulation, indicating near-perfect recall. However, no details on latency or hardware feasibility were provided, which limits the relevance of this approach for real-world deployments.

More recently, collaborative detection algorithms (CDRA) for IoT networks have been proposed by Ashraf and Sagheer [38]. Their method emphasized efficiency rather than raw accuracy, reporting a 17% reduction in energy consumption and a 10% reduction in detection delay compared to prior models. While promising for resource-constrained environments, precision and recall metrics were not explicitly reported, leaving uncertainty regarding detection reliability. In contrast, the bi-scale Mahalanobis detector achieves both high accuracy and computational efficiency.

Overall, the comparative analysis highlights that the bi-scale Mahalanobis detector achieves performance that is at least competitive with, and often superior to, state-of-the-art alternatives. With a precision of approximately 99.4%, recall at similarly high levels, and latency in the order of tens of microseconds, the proposed method demonstrates a favorable balance between accuracy, speed, and simplicity. Unlike deep learning models, it does not incur significant training or hardware costs, and unlike cooperative schemes, it does not require inter-node coordination. These characteristics make the bi-scale Mahalanobis detector highly suitable for real-time applications in resource-constrained platforms such as IoT nodes or embedded devices. A side-by-side tabular comparison of the most representative approaches and their reported metrics is shown below in

Table 3. Quantitative comparison with state-of-the-art reactive jamming detectors.

Method/Reference	Precision	Recall	Latency	AUC	Hardware and Computational Cost
Bi-scale Mahalanobis (Proposed)	99.4%	100%	80 μs	0.9997	No extra RF hardware, average CPU time per frame under 5.07 ms
JamShield (Panitsas et al. [40])	88.5%	90.3%	Not reported	0.95	PC-class device or embedded board
Real-Time XGBoost (Zafari et al. [41])	96%	93%	20 μs	0.98	STM32H7 microcontroller, memory footprint ≤3.5%
Deep DNN (Sadeghi et al. [42])	94%	97%	Platform-dependent	0.95	Requires GPU/PC or high-power board, computational cost very high (144 min of training)
WSN Cluster-based (Ganeshkumar et al. [43])	N/A	99.88%	Not reported	N/A	Not reported
IoT Collaborative CDRA (Ashraf & Sagheer [38])	Not reported	Not reported	Improved (≥10% faster)	N/A	Low-power IoT nodes with 17% energy savings

.

5.1. Analytical Baseline: Energy-Only CFAR

To provide a comparator evaluated under identical conditions without relying on external implementations, an analytical baseline was included: a constant false-alarm-rate (EO–CFAR) energy detector applied to the same analysis windows, dataset, and MATLAB configuration as the proposed detector. For each frame, silent windows were used to estimate the reference distribution of the short-window energy $E_w$. The ON/OFF thresholds $({\tau }_{\mathrm{on}},{\tau }_{\mathrm{off}})$ were derived from the empirical $(1-\mathrm{PFA})$ quantile of the silent-window distribution, and decisions were produced as $D_{\mathrm{EO}}\left(w\right)=\mathbf{1}\{E_w>{\tau }_{\mathrm{on}}\}$.

EO–CFAR and the proposed bi-scale Mahalanobis (BM) detector were executed on the same set of 5000 OFDM frames and jamming scenarios. Operating points were aligned by matching the global false-positive rate (FPR) across methods. The following metrics were reported: precision, recall, F₁ score, area under the ROC curve (AUC), and mean decision latency per frame. Receiver operating characteristic (ROC) and precision–recall (PR) curves were generated. Uncertainty was quantified using 95% confidence intervals estimated via bootstrap over frames (1000 resamples).

• Findings

Under the evaluation protocol of Section 5.1, the EO–CFAR baseline achieved as shown in

Table 4. Head-to-head comparison under identical simulation setup.

Method	Precision	Recall	F1	AUC	Latency
EO–CFAR	78.4%	98.6%	87.1%	0.774	68 μs
Bi-scale Mahalanobis (proposed)	99.4%	100%	99.7%	0.9997	80 μs

: 78.4% precision, 98.6% recall, 87.1% F₁, and an AUC of 0.774, with a mean decision latency of 68 μs. By contrast, the proposed bi-scale Mahalanobis (BM) detector reached 99.4% precision, 100% recall, 99.7% F₁, and a 0.9997 AUC at 80 μs. Relative to EO–CFAR, BM improved the precision by +21.0 percentage points and F₁ by +12.6 points, while increasing the recall by +1.4 points and incurring only a 12 μs latency overhead. The low AUC of EO–CFAR indicates limited score separability between jammed and clean windows when using energy alone, which is consistent with susceptibility to transient energy micro-peaks, fading fluctuations, and baseline drift. The BM formulation, combining bi-scale features with adaptive hysteresis, short-term persistence, and drift veto, suppresses isolated positives and yields near-perfect separability without a material latency penalty.

6. Conclusions

This paper presented a bi-scale Mahalanobis detector with adaptive thresholds that combines short- and long-window energy with the Sevcik fractal dimension to detect reactive jamming in an unmanned aircraft telemetry OFDM link. Across 5000 jammed frames, the detection model achieved 99.4% precision, 100% recall, 99.7% F₁ score, an AUC of 0.9997, and an 80 μs mean alarm latency, meeting the sub-millisecond intervals of lightweight autopilots. Because the decision process is recalculated per frame, AWGN drift, fading, or RF-gain shifts require no manual retuning, making the approach attractive and suitable for radios that lack spare DSP cycles or additional RF hardware.

Several gaps remain before field deployment:

• The 80 μs latency is analytical; therefore, micro-benchmarks on an microcontroller unit (MCU) or FPGA must confirm deterministic timing and power draw.

7. Future Work

Future work will therefore (i) port the algorithm to a 168 MHz Cortex-M4 autopilot and a low-cost FPGA to obtain measured latency–throughput–power trade-offs; (ii) extend Monte Carlo trials to negative JSR scenarios and real over-the-air captures; and (iii) integrate the detector with evasive counter-measures such as adaptive waveform hopping to quantify end-to-end link survival probability.

To further increase accuracy beyond 99.4%, it is proposed to add a light decision layer above the Mahalanobis bi-scale detector. This layer is designed to suppress isolated false alarms due to energy micro-peaks to transient shifts in background noise, all while retaining microsecond latency and ease of implementation on embedded hardware. The whole system will remain analytical, with no learning curve and a constant cost per window.

The principle is based on four complementary mechanisms. Firstly, scale-adaptive hysteresis, based on local quantiles, avoids “floating” decisions. Secondly, a coherence gate requires that the local energy and the fractal dimension rise together, thus eliminating energetic bursts. A short time persistence will only validate an alarm if several recent windows converge, filtering out orphaned positives. Finally, a CFAR drift veto will momentarily suspend the decision when the baseline changes abruptly, while silent statistics are re-estimated.

Integration will take place in the post-processing of long- and short-range decisions by replacing the raw OR with an OR conditioned by these tests. The evaluation will report the gain in precision, the impact on recall and latency stability, as well as an ablation isolating the contribution of each mechanism.

The pseudo code that follows Algorithm 2 summarizes the precision-boosting post-processor described above and will be the subject of future work. It builds the design by establishing a frame-adaptive reference for constant false-alarm control, gating detections on the joint rise of energy and fractal complexity, enforcing adaptive hysteresis at both time scales to prevent chatter, applying a short temporal-persistence rule to suppress isolated positives, and introducing a drift veto that withholds decisions during rapid baseline shifts. The final decision arises from a gated fusion of the long and short scales.

Algorithm 2 Precision-boosted

bi-scale Mahalanobis (PB-BM) Require: Windowed signal, per-window features $E_w$ (local energy) and $D_w$ (local Sevcik   fractal dimension, FD), per-scale Mahalanobis distances $d_{w,\mathrm{long}}^2$ and $d_{w,\mathrm{short}}^2$ computed   from the feature vector ${[E_w,D_w]}^{\top }$ against the frame-level reference distribution esti-   mated from silent windows. Ensure: Final binary decision $D\left(w\right)\in \{\mathrm{False},\mathrm{True}\}$ for each analysis window w   1: Frame-level CFAR setup (constant false-alarm rate): using silent windows (segments without useful signal) in the current frame, estimate the reference mean and covariance of the feature vectors. Then, for each time scale, compute adaptive quantiles of the silent-window distance distribution and define an ON threshold ${\tau }_{\mathrm{on}}$ and an OFF threshold ${\tau }_{\mathrm{off}}$ with ${\tau }_{\mathrm{off}}<{\tau }_{\mathrm{on}}$.   2: for each window w do   3:   Feature-coherence gate: standardize $E_w$ and $D_w$ using frame-local means and standard deviations. Set $\mathrm{Gate}\left(w\right)\leftarrow \mathrm{True}$ if both standardized scores are simultaneously elevated relative to their baselines, otherwise $\mathrm{Gate}\left(w\right)\leftarrow \mathrm{False}$.   4:   for each scale $s\in \{\mathrm{long},\mathrm{short}\}$ do   5:           Adaptive hysteresis state $S_s\left(w\right)\in \{\mathrm{False},\mathrm{True}\}$:   6:           if $S_s(w-1)=\mathrm{False}$ and $d_{w,s}^2>{\tau }_{\mathrm{on}}$ and $\mathrm{Gate}\left(w\right)=\mathrm{True}$ then   7:     $S_s\left(w\right)\leftarrow \mathrm{True}$           ▹ activation when distance exceeds ON threshold and features are coherent   8:           else if $S_s(w-1)=\mathrm{True}$ and $d_{w,s}^2<{\tau }_{\mathrm{off}}$ then   9:     $S_s\left(w\right)\leftarrow \mathrm{False}$       ▹ deactivation when distance falls below OFF threshold 10:          else 11:     $S_s\left(w\right)\leftarrow S_s(w-1)$ 12:          end if 13:          Short temporal persistence: define the persistent decision ${\widehat{D}}_s\left(w\right)\in \{\mathrm{False},\mathrm{True}\}$ to be True only if at least K states $S_s(·)$ are True within the most recent M windows (the K-of-M rule), otherwise set ${\widehat{D}}_s\left(w\right)\leftarrow \mathrm{False}$. K is the required count and M is the persistence window length. 14:   end for 15:   CFAR drift veto: if the median energy of silent windows has shifted by more than a drift threshold $\kappa$ over a recent horizon of S frames, refresh the frame-level reference (mean, covariance and quantiles) and set $\mathrm{DriftOK}\left(w\right)\leftarrow \mathrm{False}$ for the current window, otherwise set $\mathrm{DriftOK}\left(w\right)\leftarrow \mathrm{True}$. $\kappa$ controls the sensitivity to baseline changes and S is the drift-checking horizon. 16:   Fusion: produce the gated OR of the two scales, $$D\left(w\right)\leftarrow \left({\widehat{D}}_{\mathrm{long}}\left(w\right)\mathbf{OR}{\widehat{D}}_{\mathrm{short}}\left(w\right)\right)\mathbf{AND}\mathrm{DriftOK}\left(w\right).$$ 17: end for