1. Introduction
In the current age of digital advancement, the internet depends heavily on the utilization of content delivery networks (CDNs) to ensure efficient access to the enormous amount of content available to users across the globe. The increasing popularity of streaming services like Amazon Prime and Netflix, along with the widespread cloud and web services, has highlighted the importance of secure and efficient content delivery. CDNs are strategically deployed with an extensive network of servers, spanning various locations worldwide. The surge in massive content traffic and the high-quality service expectations of users have placed considerable strain on backbone networks. To meet these demands, edge caching servers are implemented to optimize the positions of CDN infrastructure, ensuring that these servers are in close proximity to users’ networks. This approach aims to reduce the burden on the source CDN servers and enable efficient content delivery to users that improves scalability, enhances reliability, and reduces bandwidth usage, all of which contribute to a better user experience [
1,
2,
3].
CDNs are essential for enhancing the performance, reliability, and security of websites by caching content at various locations globally. This helps reduce latency and improve load times for users regardless of their geographic location. Cache replacement algorithms play a vital role in CDNs by deciding which content stays in the cache memory and which is replaced, which significantly affects the cache hit ratio and the overall performance of CDNs. The primary goal of CDNs is to maximize the server’s hit rate, which represents the proportion of requests served directly from the cache. The dynamic nature of caching environments makes cache replacement challenging, as these algorithms must effectively identify popular content and determine which content to replace. Effective cache replacement algorithms help optimize the performance of a CDN by ensuring that the most relevant and frequently accessed content remains readily available.
The choice of algorithm can significantly impact the overall performance and cost-effectiveness of a CDN. Conventional approaches like least recently used (LRU), least frequently used (LFU), First-In-First-Out (FIFO), and Random Replacement (RR), along with their variations, offer scalability and ease of implementation. However, they often rely on heuristics and lack adaptability to diverse network configurations. Additionally, these strategies do not provide the flexibility to incorporate custom costs or utility functions. Furthermore, existing conventional algorithm models are designed for single-cache systems and do not account for cooperative caching scenarios [
4,
5].
In recent years, many research fields have utilized machine learning-based approaches to solve the cache replacement problem. Researchers have investigated the use of different reinforcement learning methods to address cache replacement in networks [
6,
7]. ML-based cache replacement solutions for CDNs face several challenges, including high computational overhead, significant data requirements, and the need for constant adaptation to dynamic content and user behavior. Additionally, single-agent approaches make decisions based on their own local data and experiences, which limits their effectiveness in the highly distributed and collaborative environment of CDNs. Multiple cache nodes should work together to optimize the overall performance of CDNs, and a single-agent system might not efficiently coordinate these nodes, potentially leading to suboptimal caching decisions and reduced hit rates.
In the context of CDNs, the state space can become exceedingly large due to the vast amount of content, varied user behaviors, and dynamic network conditions. Managing this immense state space can be computationally intensive and memory-heavy, leading to scalability issues. As the number of states grows, the model becomes more complex and harder to manage, often resulting in slower learning rates and less effective performance. Deep-Q networks (DQNs) have been instrumental in addressing the challenge of large state spaces in reinforcement learning, particularly through their ability to approximate complex state–action value functions using deep neural networks [
8,
9]. Traditional Q-learning methods struggle with scalability due to their reliance on tabular representations of state–action pairs, which become infeasible as the state space grows. In contrast, DQNs leverage deep neural networks to approximate the Q-values, allowing them to generalize across similar states and actions, thus effectively managing large and continuous state spaces. Key techniques employed in DQNs to handle this complexity include experience replay and target networks. Experience replay involves storing past experiences in a replay buffer and randomly sampling mini-batches for training, which breaks the correlation between consecutive samples and stabilizes learning. This technique helps improve data efficiency and convergence by smoothing out updates over time. Target networks, on the other hand, are used to stabilize Q-value updates by decoupling the action-value targets from the main network being updated. By periodically updating the target network with the weights of the primary Q-network, DQNs reduce the oscillations and divergence issues common in traditional Q-learning [
8,
9]. Together, these techniques enable DQNs to scale effectively to problems with large state spaces, making them particularly suitable for applications such as content delivery networks, where the environment is highly dynamic and complex. Hence, our motivation lies in investigating the performance of a cooperative DQN algorithm in a CDN cache replacement scenario.
To this end, this study proposes a cache replacement policy for CDNs, focusing on a multi-agent deep-Q network (MADQN)-based reinforcement learning approach that is scalable for larger environments. We consider a caching environment with the edge servers acting as agents, where they share information and cooperatively learn through the deep-Q network with the objective of maximizing the cache hit ratio of CDNs. Initially, we model our problem as a Markov decision process (MDP) and extend it to a multi-agent reinforcement learning problem. We consider each edge caching server as an agent equipped with a deep-Q network, working cooperatively to maximize the cache hit ratio on each edge server. The proposed cooperative cache replacement algorithm is capable of surpassing traditional cache replacement policies in terms of the cache hit ratio and the average delay in catering to content requests during the considered time interval. A set of experimental results are presented to validate our claims.
The rest of this paper is structured as follows.
Section 2 provides the background and related works. The network model is outlined in
Section 3.
Section 4 presents the formulation of the MDP problem. Our proposed MADQN cache replacement policy is detailed in
Section 5. The experimental results are discussed in
Section 6, and
Section 7 concludes this paper and includes suggestions for future work.
2. Background and Related Works
Compared to traditional centralized server architectures, CDNs utilize distributed servers in multiple geographic locations, referred to as Points of Presence (PoPs), to cache content closer to end users, which increases content availability, decreases latency, and enhances delivery speeds. The distributed servers within CDNs work together to offload traffic from the source servers, enabling more efficient content delivery. CDNs direct user requests to nearby edge servers through intelligent routing, which allows users to access content from a server physically closer to them, thus optimizing resource usage and minimizing latency.
Content caching systems typically employ both admission and eviction algorithms to efficiently manage the contents of the cache. When a user requests a specific object, such as an image or a file, the request is directed to a nearby edge server in close proximity to the user. If the requested object is already stored in the cache of the edge server, resulting in a “hit”, the user promptly obtains the desired object from the cache. Otherwise, if it results in a “miss” and the edge server does not have a local cached copy, it retrieves the object from the content provider’s source server and subsequently delivers it to the user [
10]. The object can then be saved as a local cache copy for future use. The admission algorithm is responsible for deciding whether to cache a requested object by evaluating multiple factors such as the popularity of the object, the predicted likelihood of future requests for the object, and the available space in the cache.[
11]. Meanwhile, the eviction algorithm comes into play when the cache reaches its capacity and needs to make room for the newly retrieved object. Various strategies can be employed to determine which object(s) to remove from the cache to accommodate new entries. Content caching systems can optimize resource utilization and improve overall performance by ensuring that frequently accessed content is readily available while efficiently managing the limited space in the cache.
Efficient content caching algorithms have been the subject of extensive research. Over time, numerous solutions have been proposed to address this problem. Traditional algorithms for content replacement, such as LRU, LFU, and FIFO, as well as their hybrid methodologies, have some limitations. The LFU and LRU techniques suffer from static decision making, as they cannot adapt to changes in content popularity and lack contextual comprehension. Although hybrid strategies combine elements of both LFU and LRU, they might still encounter challenges in dynamic scenarios and may not fully leverage contextual information for efficient content caching [
12,
13,
14]. In [
15], the authors presented “Octopus”, a cooperative hierarchical caching strategy for cloud-based radio access networks (C-RANs) to minimize the network costs of content delivery and improve users’ quality of experience. A delay-cost model was introduced to characterize and formulate the cache placement optimization problem. The authors proposed two heuristic algorithms: the proactive cache distribution (PCD) algorithm and the reactive cache replacement (RCR) algorithm. However, due to their dependence on pre-established heuristics, these algorithms are not as capable as machine learning algorithms in recognizing complicated patterns and learning from data, as the latter are able to extract non-obvious caching techniques from data. Moreover, it has been shown in the literature that simple cooperative heuristic algorithms are suitable for environments with many nodes available in the network [
7]. C-RANs are networks based on base stations. However, for content delivery networks where the server count is lower than the base station count, it is more suitable to explore reinforcement learning-based machine learning techniques for implementing efficient cache replacement algorithms [
7].
In recent years, machine learning, particularly deep learning, has revolutionized CDN web caching by predicting user behavior from web data, thus enhancing content delivery and web adaptability. However, traditional approaches to cache replacement often overlook factors such as cost and size learning [
16]. Reinforcement learning effectively addresses these challenges by considering various cache-related factors through dynamic optimization and agent-based trial-and-feedback learning. Machine learning- and reinforcement learning-based policies offer adaptability, contextual understanding, and the ability to learn from experience, leading to more efficient content caching in modern environments.
The paper authored by Kirilin et al. [
11] introduced RL-Cache, an algorithm employing model-free reinforcement learning to determine the admission of a requested object into the cache of a CDN. Zhong et al. [
17] presented an actor-critic-based reinforcement learning framework for content caching at base stations in wireless networks, which enhances the cache hit rates over the long term without relying on prior knowledge of content popularity distribution. The paper authored by Sung et al. [
18] addressed the content replacement problem in a wireless content delivery network with cooperative caching, using reinforcement learning (Q-learning) to maximize the hit ratio and alleviate network congestion caused by growing mobile content demands. Jiang et al. proposed a content caching algorithm based on deep Q-learning networks (DQNs) to achieve an optimal content caching strategy and introduced a content update policy that incorporates user preferences and predictions of content popularity [
19].
Nevertheless, a notable challenge encountered in the application of Q-learning is the management of a substantial increase in the number of states within larger dynamic environments. This surge in complexity can pose difficulties for the system in effectively updating Q-values and achieving stability [
20,
21,
22]. In [
7], Wang et al. introduced MacoCache, an intelligent edge caching framework that leverages a policy-based actor-critic reinforcement learning approach to enhance content access latency and minimize traffic costs at the network edge. The authors of [
23] demonstrated that combining deep learning with Q-learning enhances the Q-value update process and addresses the problem of increasing state variables in larger environments.
In our work, we primarily focus on the development and evaluation of the MADQN algorithm itself and emphasize the impact of using it specifically for CDN cache replacement. The comparison of our work with existing reinforcement-learning algorithms is limited, mainly due to the unavailability of open-source code. Moreover, the scarcity of suitable benchmarks in the field also leads most works to use private datasets or simulation data. We noticed that most existing works [
17,
18,
24,
25] only compare the performance of their models with that of non-learning-based (heuristic) cache algorithms. Thus, we compare our algorithm’s performance with that of traditional cache replacement policies.
3. Network Model
We examine a CDN with edge servers interconnected as a mesh, where each edge server handles some load of end-user requests, as shown in
Figure 1. We designate the set of edge servers as
. The links connecting these edge servers are represented as
, where
x and
y denote the IDs of the respective edge servers forming the connection. For example,
is the link between edge servers 1 and 2. Each edge server is connected to a CDN source server via a backbone link
, where
z denotes the corresponding edge server that forms the link to the source server. Moreover, the traffic costs of links
and
are denoted as
and
, respectively. We assume that the source server has
M number of slots to store all the contents distributed and populated in the network. We assign an ID to each content in the source server, ranging from 1 to
M. A uniform content volume is assumed for simplicity. The capacity of each edge server is limited to a size of
C (
), and the cache of each edge server is initially filled with some content. We model the request pattern as an independent reference model with a Zipf probability distribution, which reflects the common pattern of content popularity observed in traffic measurements [
26]. Hence, the content popularity is modeled by a Zipf distribution [
27,
28]. For simplicity, the analysis does not explicitly account for individual user devices or the connections between these devices and their respective edge servers.
The requests from users to the ith edge server can be represented as a temporal sequence of content IDs , where is the content request at time t for the ith edge server. Similarly, the cached content of the ith edge server at time t can be written as a sequence of content IDs such that , where . It can be seen that varies with content requests at each time instance t. A cache miss occurs when and after the replacement occurs.
We use the temporal sequence of content IDs to represent the requests to the ith edge server, where denotes the content request received at time t for the corresponding ith edge server. Similarly, the cache content of the ith edge server at time t can be written as a sequence of content IDs such that , where . The composition of can be updated in response to the content requests received at each time step t. If the requested content is not found in , a cache miss occurs, and will differ from after the replacement process has taken place.
In a network architecture, intercommunication among edge servers is crucial for optimizing content retrieval. When a user requests specific content from their designated edge server, the request is processed through the following steps: First, if the content is available in the local cache of the edge server, it is retrieved immediately. If the local cache does not contain the requested content, the edge server searches its neighboring peer edge servers. If a neighboring server has the content, it is retrieved and sent to the user. If neither the local cache nor the neighboring servers have the content, the edge server fetches it directly from the source server and stores it in the local cache. This final scenario, known as a cache miss, indicates that all local and adjacent caches were exhausted before retrieving the content from the source server.
4. Formulation of Markov Decision Process Problem
The content replacement problem can initially be defined as a Markov decision process (MDP) and then decomposed into sub-problems. These sub-problems can be implemented individually on edge servers and solved as single-agent reinforcement learning problems [
18]. In traditional single-agent deep reinforcement learning, an agent aims to make effective decisions by considering its past experiences and the rewards it receives. The MDP consists of a finite state space
, an action space
, a reward function
, and a transition probability
. The problem starts with an initial state
. At every
tth decision epoch, the agent takes action
and transitions its state
to
. For each action taken by the agent, the agent receives a reward
r. Hence, the transition probability
and the reward
are functions of the current state, next state, and the taken action. In our model, the decision epoch is defined when a cache miss occurs. Every cache miss is handled on the decision epoch, and action is taken only on a cache miss.
4.1. State Space
In the multi-agent scenario, we consider each edge server as an agent. These agents collaborate to explore the optimal edge caching strategy. For a given edge server
i, we consider both the currently requested content and the currently cached content for the state space. Furthermore, we consider that each agent
i communicates with its neighboring agents
. Hence, in the state space
, it is important to include the cache states of the neighboring servers as well. Thus, every state
at the
tth decision epoch can be represented by
, where
. However, in this case, the state space would be significantly large, which would make the learning model difficult to converge. Hence, we resort to an alternative way of representing the state vector by employing numerical feature vectors to encode each state at time
t by concatenating the feature vectors of the current request and the cached contents of the considered agent and neighboring servers. Then,
can be written as
where
,
, and
are the feature vectors of the current request, the feature vector of the
kth cached content (
) of the considered edge server
i, and the feature vector of the
jth neighboring server, respectively. In (
1),
,
, and
can be defined as
where
. Moreover, the elements in (
2),
,
, and
, represent the short-term, middle-term, and long-term recent access times, respectively. The use of access time frequencies also serves the purpose of implementing the LFU policy. Maintaining perpetual access records necessitates a memory cost of O(N), which is notably prohibitive. Consequently, to circumvent this high memory expenditure, a strategic approach involves retaining only a limited subset of historical data. This subset is then subjected to regression and exploration through the utilization of a neural network, facilitating the extraction of latent information. By implementing this methodology, a commendable level of efficacy is achieved while concurrently mitigating the burdensome memory costs. In our empirical investigations, we consider varying historical windows, namely the past 10, 100, and 1000 accesses, to assess the performance and effectiveness of this approach.
4.2. Action Space
Next, we define the action space for the
ith edge server at the
tth decision epoch. In order to restrict the action space
, we assume that at most one cached content is replaced in each decision epoch. This reduces the computational complexity in each decision epoch [
17]. Let
be the action selected at decision epoch
t, transitioning states from
to
. If the current content in the cache is replaced with the requested content, then
; otherwise,
.
4.3. Reward Function
To maximize the cache hit ratio of an edge server, a reward function is designed to encourage the server to cache content efficiently. The agent is given the reward immediately after taking an action. Hence, our reward function is designed based on short-term feedback. We define the reward for transitioning from state
to
by taking action
a as
where
is the reward term and
is the penalty term.
is a weight parameter that balances the reward and penalty terms. Moreover,
if
causes a cache miss; otherwise,
. The reward term
is defined as the weighted sum of hit counts in each cache slot of the
ith edge server and is written as
where
is the cumulative hit count of the
kth cached slot at the
tth decision epoch. We employ a weight parameter
to highlight the differences among cache slots. For instance, we can increase the weight for newly cached content to emphasize the latest selected actions. The penalty term is implemented to impose a reduction on the total reward when the action taken causes a cache miss, thereby signifying that it was not an optimal action. Furthermore, it is defined such that the penalty decreases as the cumulative hit count increases between two decision epochs. Then, the term
in (
3) can be written as
where
,
, and
are hyperparameters of the penalty terms satisfying
,
, and
.
5. Multi-Agent Deep-Q Network Learning Model
For the formulated MDP, a reinforcement learning approach is necessary to acquire knowledge of the rewards and the probabilistic distribution of transitions. We adopt a model-free reinforcement learning approach that does not require specifically learning the dynamics of the environment. Traditional Q-learning, a value-based model-free technique, involves agent
i observing state
and selecting the best possible action
a at time
t to transition to state
. Subsequently, the agent receives an immediate reward
at time
, and updates the Q-value that represents this scenario as
where
denotes the learning rate,
is a discount factor in reinforcement learning, and
represents the discounted reward. For agent
i, a two-dimensional look-up table with the dimensions
is used to store the Q-values for each possible state and action. Thus, in a complex environment, the size of the Q-table increases exponentially with the number of states and actions. This introduces the curse of dimensionality, leading to longer convergence times to obtain the optimal action [
29].
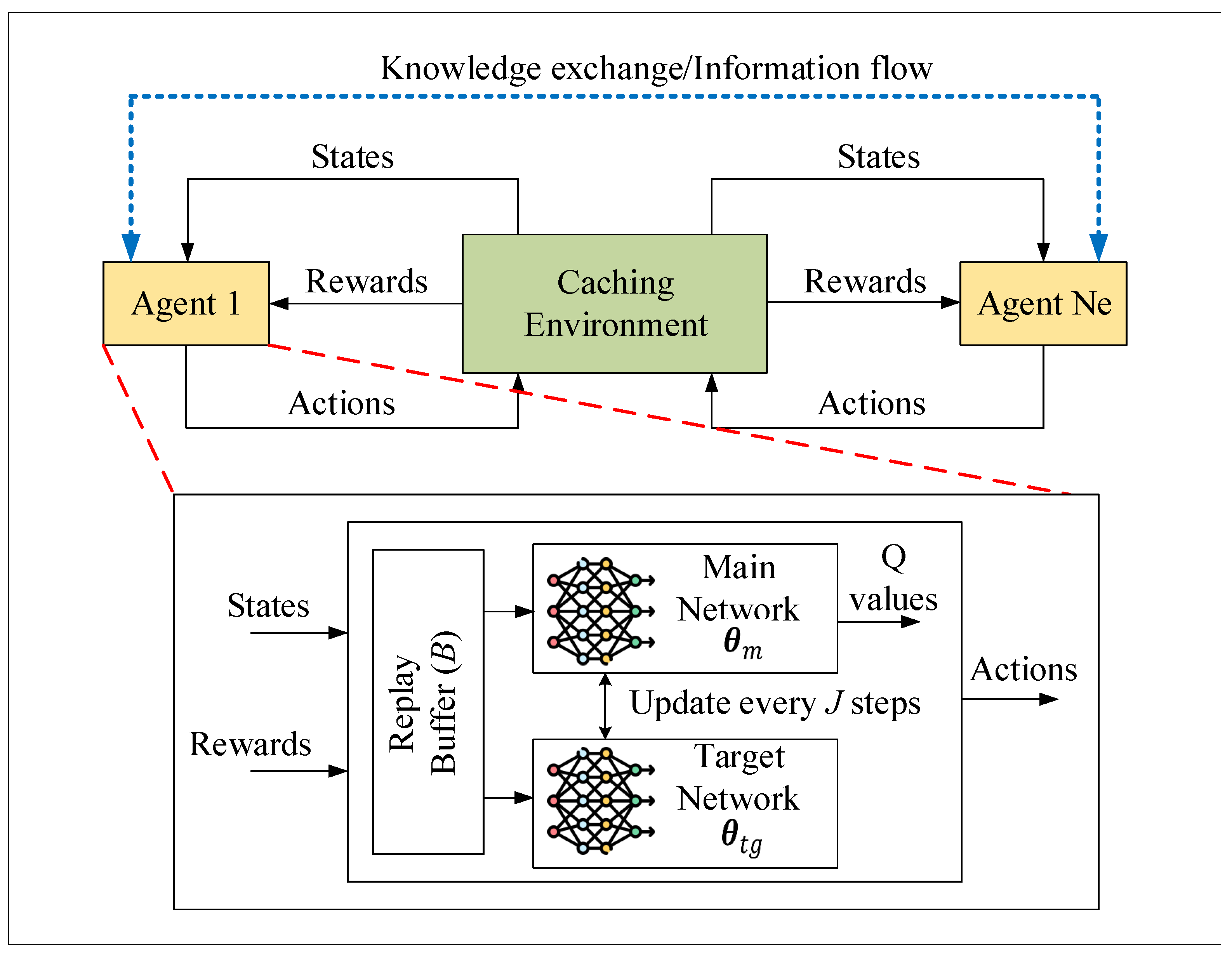
To address the curse of dimensionality problem, we propose a deep Q-learning-based approach where a neural network is used as a function approximator to generalize and approximate the value function. The proposed MADQN model is presented in
Figure 2. The MADQN model consists of multiple agents interacting with the caching environment and their neighboring nodes. In our case, each edge server is considered an agent.
In the multi-agent environment, each agent has a main network parameterized by () to estimate Q-values, a target network () that copies the main network to provide a stable target for learning, and a replay buffer to store the agent’s experiences. A deep neural network (DNN) can be implemented as a fully connected network consisting of an input layer, some hidden layers, and an output layer. The output layer produces the Q-values for all possible actions, and the action with the maximum Q-value is considered the optimal decision. Initially, at time t, agent i observes the content request and its states, exchanges information (states () and policies) with neighboring agents, and chooses an action (). Here, it should be noted that agent i selects the neighboring node with the minimum traffic cost. For instance, consider a case where the content request cannot be satisfied by agent i. Then, the agent will then look at the neighboring agents. Assume that the corresponding content is in two neighboring agents () with traffic costs and , where . In this case, the neighboring agent with traffic cost is selected.
The agent takes an action based on two methods: exploitation and exploration. Exploitation occurs when the agent selects the action with the maximum Q-value as the optimal decision. Active exploration is also integrated into our DQN agent. With a probability (
p) of
, the agent is encouraged to take a stochastic step, while with a probability of
, the agent follows a different cache replacement policy, such as LRU or LFU. Otherwise, the agent strictly follows the optimal action evaluated by the Q-values. The exploration policy can be written as
Additionally, we set
and
to decrease over time. Thus, the model will gradually opt for the optimal decision. If the agent performs poorly, exploration is encouraged. By keeping track of a set of recent rewards (
), we update
(where
) as follows:
where
is a reward threshold, and
and
are the step sizes for updating the probability
.
For the chosen action (
), the agent receives an immediate reward (
) based on (
3), transitions to the next state (
), and stores the transition in the replay buffer with a size of
. Throughout the training phase, agent
i chooses a mini-batch of size
B from the replay buffer and employs mini-batch gradient descent to train the main network. To ensure stability in learning, the target network duplicates the main network every
J steps.
The proposed MADQN algorithm is presented in Algorithm 1. MADQN enables the chosen edge server
i to act as an agent and initializes the main network, target network, and replay buffer in Steps 2 to 5. From Steps 7 to 9, it starts selecting neighboring agents and exchanging information. The action selection, reward calculation, storing experience, mini-batch training of the main network (
), computation of the target
over steps
, loss function calculation, and use of gradient descent to update the weights are presented in Steps 11 to 25. The target network parameters are updated every
J steps in Step 27. With the exchanged knowledge, the agent calculates the Q-value of the MADQN algorithm as follows:
where
is used to emphasize the impact of neighbor
j on agent
i and is modeled inversely proportional to the traffic cost (
) between
j and
i [
30].
| Algorithm 1 MADQN algorithm |
- 1:
Procedure: - 2:
Initialize agent i - 3:
Initialize main network - 4:
Initialize target network - 5:
Initialize replay buffer with size () - 6:
for episode = 1: do - 7:
Select neighboring agents - 8:
Send Q-value to neighboring agents - 9:
Receive from agent - 10:
Observe current state () - 11:
for do - 12:
Select action using ( 7) (exploration/exploitation) - 13:
Receive immediate reward and next state - 14:
Store experience in the replay buffer. The record () is saved. - 15:
Choose a mini-batch of experience (B) - 16:
for steps do - 17:
If episode ends then - 18:
- 19:
else - 20:
- 21:
end if - 22:
Calculate the loss function: - 23:
- 24:
Update Q value using gradient descent on main network parameters () - 25:
end for - 26:
Every J steps update - 27:
Update Q-value using Equation ( 9) - 28:
end for - 29:
end for - 30:
End Procedure
|
6. Experimental Results
The implementation details of our proposed cache replacement algorithm are presented in this section. We consider a mesh network with four edge servers, where each edge server is connected to other edge servers and the source server. The network configuration is assumed to be optimized. The source server slot capacity is set to
, and the edge servers’ capacities are specified in each simulation. A chosen
ith edge server has
neighboring edge servers. The link costs between the edge servers (
) and the source CDN server (
) are initialized randomly. This setup is used to investigate the capability of our algorithm in choosing the correct neighboring edge servers with the minimum traffic costs. The Zipf probabilistic distribution, which is used to generate content requests, has a distribution parameter set to 1.2 [
27,
28]. Typically,
requests are generated for each agent in the simulations unless stated otherwise.
We set the parameters of the reward function design in (
3) and (
5) as follows:
, and
,
, and
.
Each agent i has a main network and a target network. Both neural networks are implemented with one hidden layer consisting of 256 nodes. A deeper network is not adopted in order to accelerate the convergence of the network. Hyperparameter tuning via cross-validation is used to obtain the optimal DQN network parameters which are specified as follows: The learning rate and batch size are set to and , respectively. The size of the replay buffer is set to . The target network is updated every steps. The discount factor in (8) is set to . The probabilities for the exploration policies and are initialized at 0.1 and 0.3, respectively. Both parameters and are set to 0.005 for . For , and are set to 0.1 and 0.001, respectively.
We present our experimental results below. We evaluated our proposed cooperative MADQN with respect to several network parameters. Comparisons are presented to depict the performance enhancements achieved by our proposed algorithm. We compared our algorithm with existing non-cooperative heuristic cache replacement algorithms and a non-cooperative reinforcement learning-based algorithm. Moreover, we present how the number of cooperative nodes affects performance.
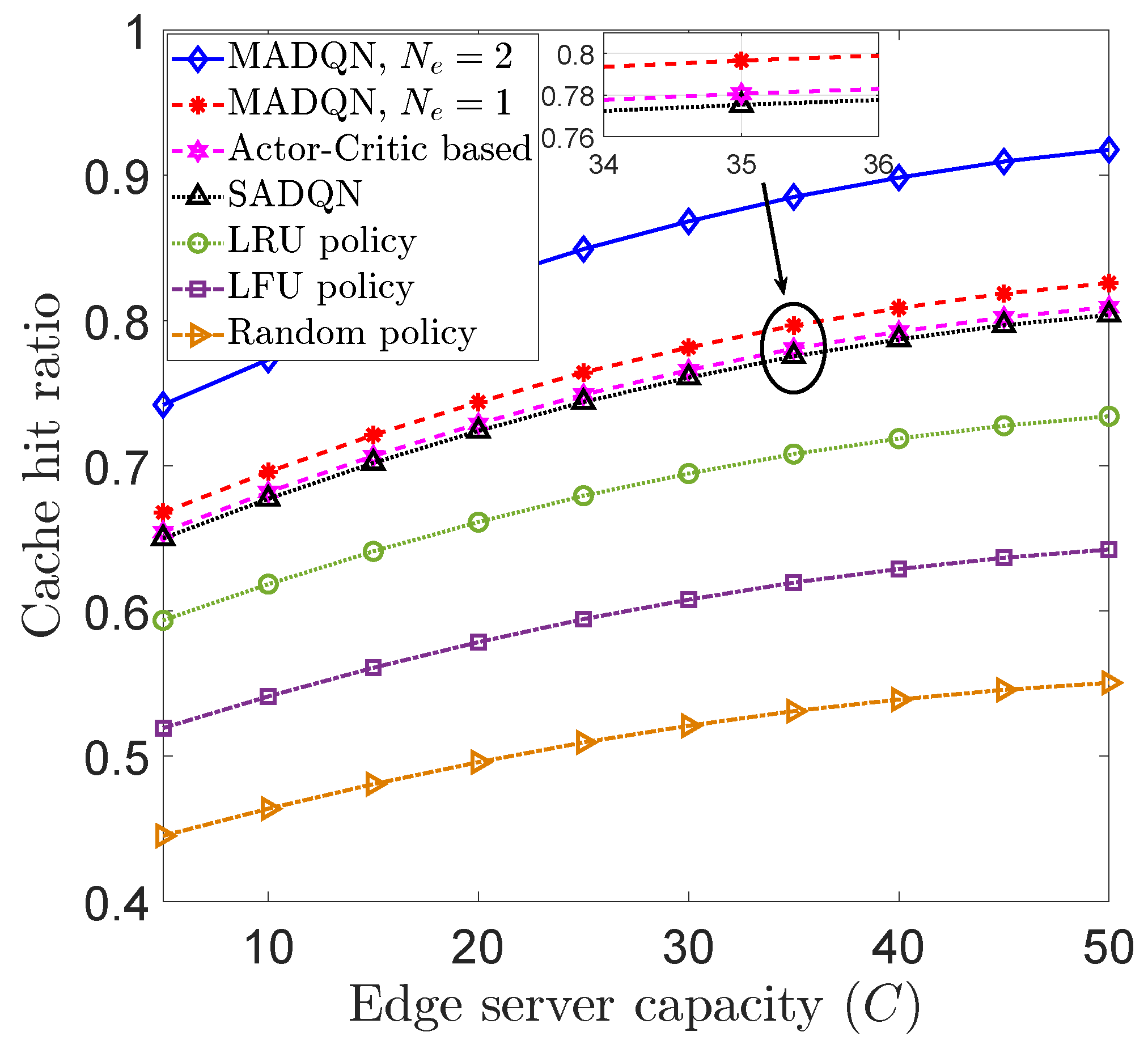
Figure 3 depicts the cache hit ratio with respect to the capacity of the
ith edge server for different cache replacement policies. We compared the performance of our MADQN approach with that of LRU, LFU, and random cache replacement policies. Furthermore, comparisons were made with a single-agent DQN (SADQN) and an actor-critic algorithm based on [
17] to show the performance differences. For instance, with an edge cache capacity of
, our MADQN approach with only one neighboring edge server achieved percentage increases of 2.74%, 3.33%, 12.51%, 28.569%, and 50.01% compared to SADQN, the algorithm based on [
17], LRU, LFU, and random cache replacement policies, respectively. Hence, compared to the reinforcement learning algorithm based on [
17] and SADQN, our cooperative MADQN algorithm achieved better performance in terms of the cache hit ratio. Moreover, it can be observed that with a higher number of neighboring edge servers (
), the cache hit ratio increased. For instance, MADQN with two neighboring edge servers (
) achieved a cache hit ratio increase of 0.08984 compared to MADQN with only one neighboring edge server (
) when the edge server capacity was
.
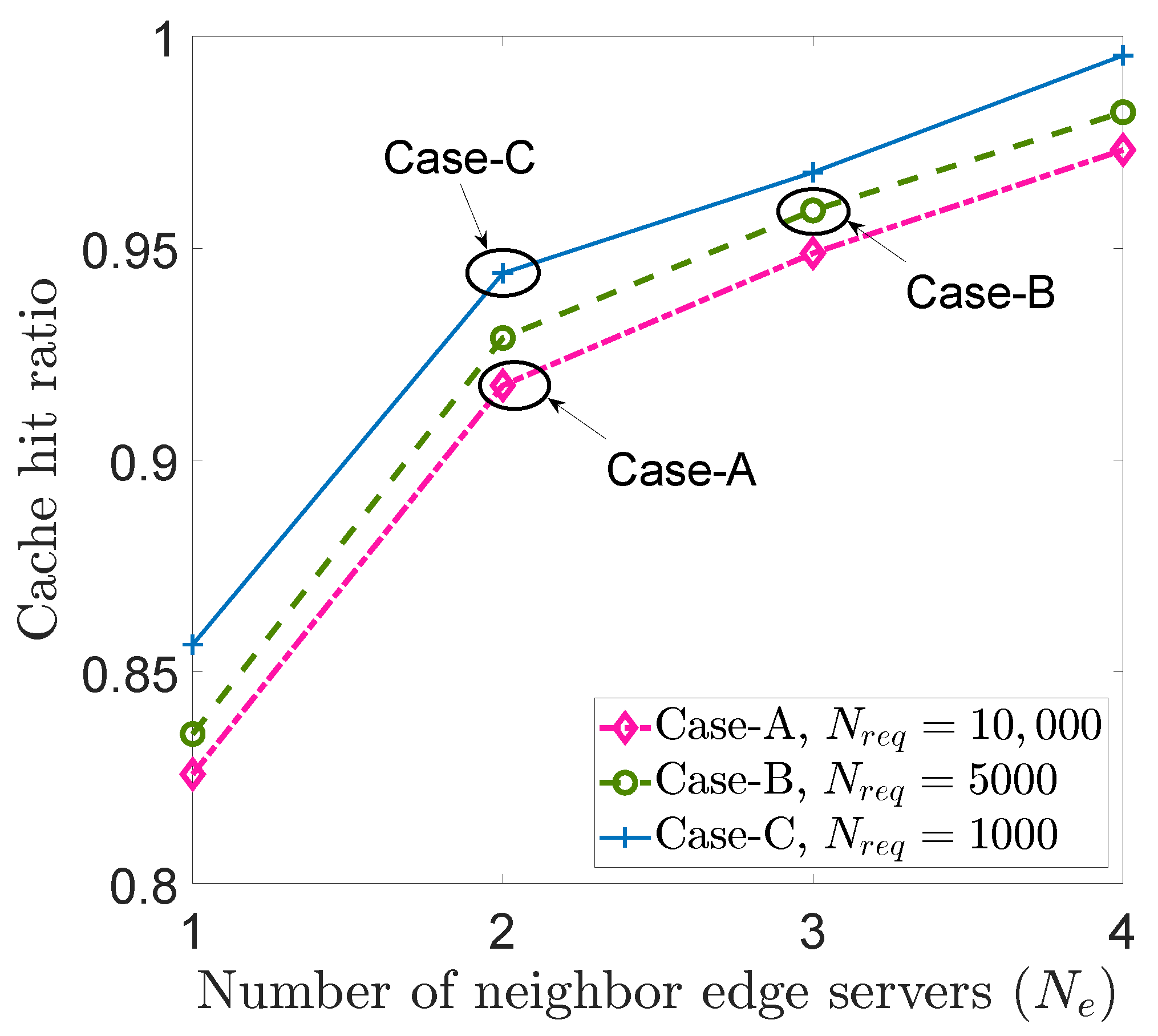
Figure 4 depicts the performance of our MADQN policy when varying the number of neighboring edge servers for three different cases:
. The
ith edge server capacity
C was set to 50 for all considered scenarios. The final cache hit ratio value after convergence, when all corresponding requests were satisfied, is depicted in
Figure 4. In
Figure 4, for all three cases, it can be seen that the cache hit ratio increased with the number of neighboring edge servers. Furthermore, when the
ith edge server worked cooperatively with three neighboring edge servers, compared to Case C, the cache hit ratios of Case B and Case A decreased by 0.009 and 0.0191, respectively. Another observation is that there was only a slight decrease in the cache hit ratio with an increased number of content requests (
) when employing our proposed MADQN algorithm.
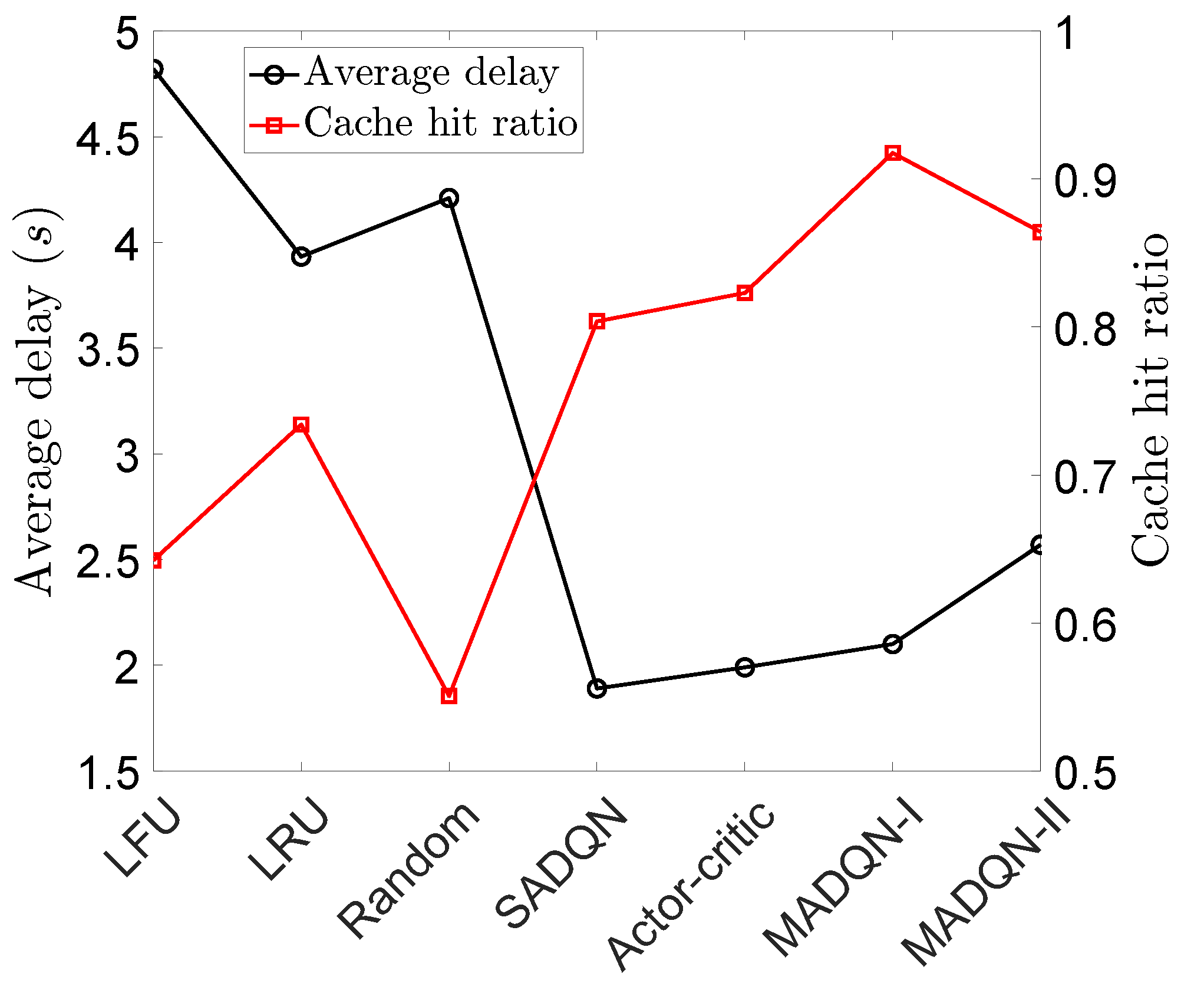
Figure 5 compares various caching algorithms in terms of the average delay and average cache hit ratio. We set
and simulated over ten episodes (
). The average delay was measured as the average time each policy took to cater to 5000 content requests over the ten episodes. It can be observed that traditional cache replacement policies had a higher average delay than our proposed MADQN policy. MDQN-I corresponds to the case where the neural network implemented in the
ith agent contained only one hidden layer, while MADQN-II contained two hidden layers. The average delay of the MADQN-II exhibited a slight increase compared to MADQN-I, as increasing the number of hidden layers in the neural network led to a longer convergence time in a dynamic environment. Moreover, it can be observed that the SADQN approach had a slightly lower delay (a difference of only 0.21 s) compared to MADQN-I, but it had a lower cache hit ratio compared to our MADQN approach. The algorithm based on [
17] achieved a cache hit ratio and average delay that fell between those of SQDQN and MQDQN-I. Finally, it can be highlighted that our proposed MADQN policy with cooperative learning outperformed traditional cache replacement policies and the algorithm based on [
17].
Figure 6 compares the performance of various caching algorithms with different sizes of
M content items on the source server. The capacity
C of the
ith edge server was set to 50. The sizes of the
M content items were chosen randomly, and the cache hit ratio was plotted against the size of the largest object. The largest possible size of a content item was set to half of the edge server capacity. It can be observed that the cache hit ratio decreased as the content size increased. Here, the cache size was fixed, so as the content item size increased, a smaller fraction of the total content could be stored in the cache at any given time. This increased the likelihood of a cache miss occurring. Moreover, with a larger content set, the cache needed to evict items more frequently to make space for new content, which led to a degradation in the cache hit ratio. However, compared with existing cache replacement algorithms, our proposed cooperative MADQN algorithm achieved better cache hit ratios as content item size increased.
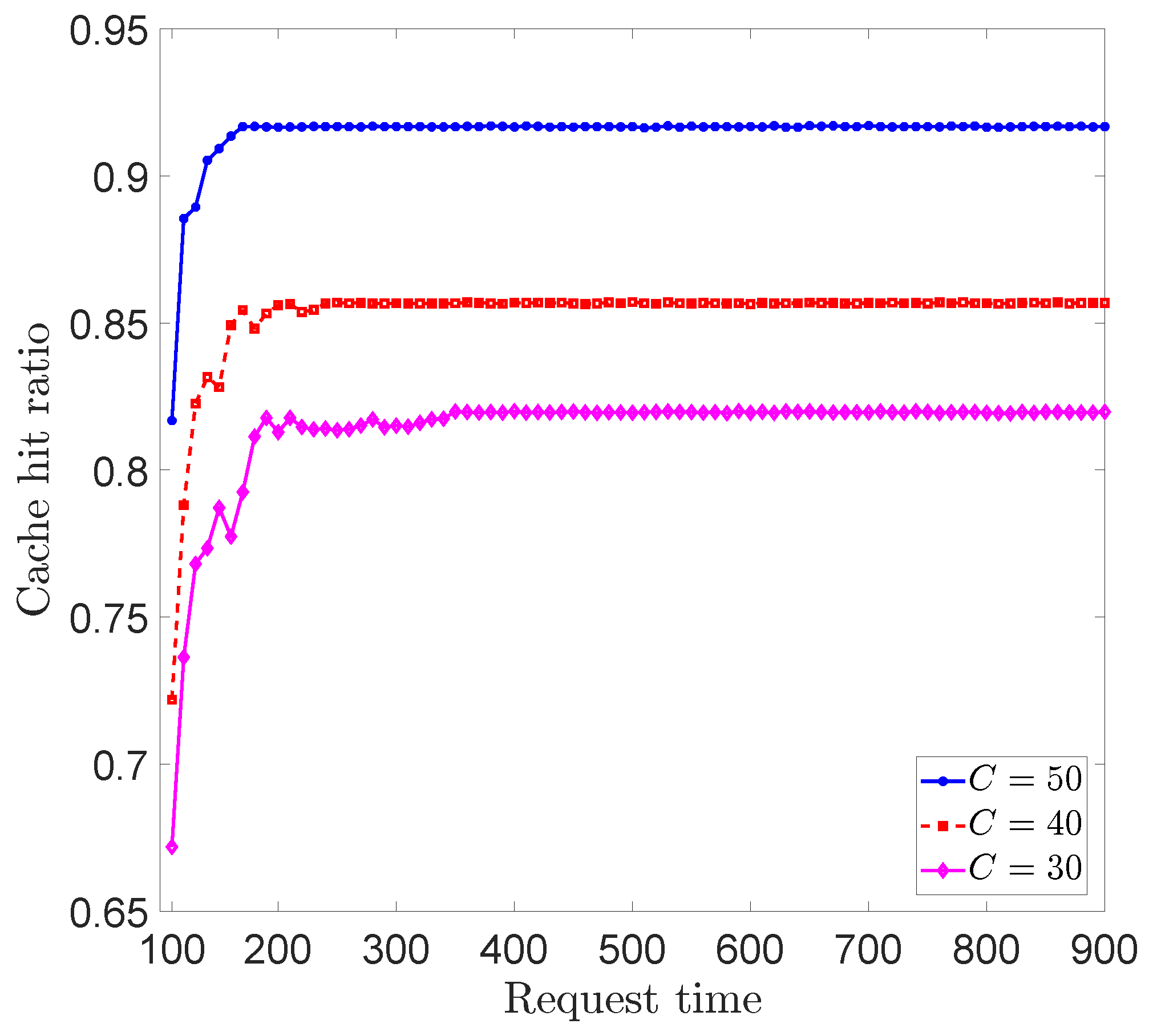
Figure 7 depicts the convergence of our algorithm when the cache capacity (
C) was varied. We utilized our algorithm with two neighboring nodes and simulated the network for 1000 requests. The cache hit rate was monitored from the 100th content request to the 1000th request. It can be observed that the convergence of our algorithm slightly depended on the cache capacity of the edge server. For instance, for the three edge cache capacities (
) investigated, the algorithm converged around 350th, 250th, and 150th requests, respectively. The convergence of our algorithm improved with the cache capacity of the edge server.
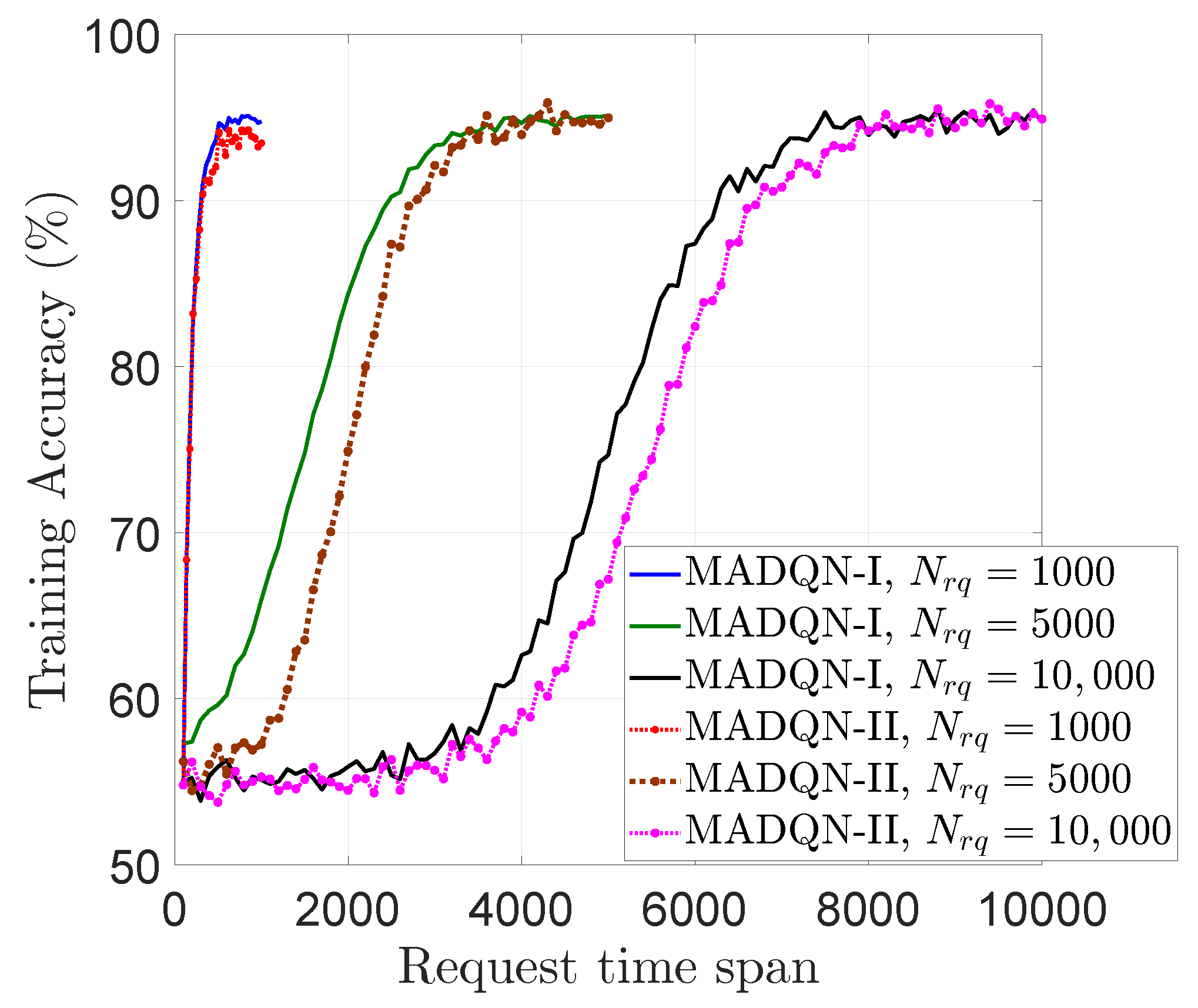
Figure 8 depicts how the training accuracy of our proposed algorithm varied over the request time span for three cases of the total number of requests (
). The solid lines and dotted lines correspond to cases with one hidden layer (MADQN-I) and two hidden layers (MADQN-II) in our DQN model, respectively. It can be seen that the accuracy of our algorithm increased gradually and settled around 95%, well before all the content requests were handled. Moreover, the MADQN model with two hidden layers was slower to converge compared to the model with one hidden layer. This is because having multiple hidden layers increased the convergence time of the model. The increasing accuracy and convergence of the model depict the stability of our well-tuned MADQN model.
7. Conclusions and Future Work
This paper introduces an innovative approach for maximizing the cache hit ratio of CDNs through an MADQN-based cache replacement policy. We consider a mesh CDN network with edge servers that cooperatively learn efficient cache replacement, aiming to maximize cache hit ratios. We compare the performance of our algorithm with that of heuristic caching policies like LFU, LRU, and random cache replacement policies. Moreover, the proposed algorithm is compared with non-cooperative reinforcement algorithms, such as SADQN and the actor-critic method. This study shows that our MADQN approach surpasses existing caching policies and achieves higher cache hit ratios and lower average delays. It is shown that, with a higher number of cooperative agents, our MADQN achieves higher cache hit ratios. Furthermore, it is shown that the proposed algorithm performs better than existing policies when the content item sizes are different in the network. Our experiments validate that using an MADQN reinforcement learning approach is more effective than traditional methods for improving cache replacement in CDNs by maximizing the cache hit ratio.
Author Contributions
Methodology, J.K.D., M.W. and M.Z.H.; software, J.K.D., M.W. and M.Z.H.; validation, J.K.D., M.W. and M.Z.H.; formal analysis, J.K.D., M.W. and M.Z.H.; investigation, J.K.D., M.W. and M.Z.H.; resources, J.K.D., M.W. and M.Z.H.; data processing, J.K.D., M.W. and M.Z.H.; writing—original draft preparation, J.K.D., M.W., M.Z.H. and N.Y.; visualization, J.K.D., M.W. and M.Z.H.; supervision, N.Y.; writing—review and editing, N.Y.; project administration, N.Y.; funding acquisition, N.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the US National Science Foundation under grant CC-2018919.
Data Availability Statement
Our work concentrates on the development and evaluation of the MADQN algorithm, specifically highlighting its application for cache replacement in CDNs. To demonstrate the performance of the MADQN algorithm, we employed a simulation environment modeled. Consequently, no actual dataset was used, as our approach relies solely on simulations.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| CDN | Content delivery networks |
| DNN | Deep neural network |
| DQN | Deep-Q network |
| MADQN | Multi-agent deep-Q network |
| SADQN | Single-agent deep-Q network |
| LRU | Least recently used |
| LFU | Least frequently used |
| FIFO | First-In-First-Out |
| RR | Random Replacement |
| MDP | Markov decision process |
| RL | Reinforcement learning |
| PoPs | Points of Presence |
References
- Gu, J.; Wang, W.; Huang, A.; Shan, H.; Zhang, Z. Distributed Cache Replacement for Caching-Enable Base Stations in Cellular Networks. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, NSW, Australia, 10–14 June 2014; pp. 2648–2653. [Google Scholar] [CrossRef]
- de Almeida, D.F.; Yen, J.; Aibin, M. Content Delivery Networks—Q-Learning Approach for Optimization of the Network Cost and the Cache Hit Ratio. In Proceedings of the IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), London, ON, Canada, 30 August–2 September 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Ma, G.; Wang, Z.; Zhang, M.; Ye, J.; Chen, M.; Zhu, W. Understanding Performance of Edge Content Caching for Mobile Video Streaming. IEEE J. Sel. Areas Commun. 2017, 35, 1076–1089. [Google Scholar] [CrossRef]
- Din, I.U.; Hassan, S.; Khan, M.K.; Guizani, M.; Ghazali, O.; Habbal, A. Caching in Information-Centric Networking: Strategies, Challenges, and Future Research Directions. IEEE Commun. Surv. Tutorials 2017, 20, 1443–1474. [Google Scholar] [CrossRef]
- Thomdapu, S.T.; Katiyar, P.; Rajawat, K. Dynamic cache Management in Content Delivery Networks. Comput. Netw. 2021, 187, 107822. [Google Scholar] [CrossRef]
- Shuja, J.; Bilal, K.; Alasmary, W.; Sinky, H.; Alanazi, E. Applying Machine Learning Lechniques for Caching in Next-Generation Edge Networks: A Comprehensive Survey. J. Netw. Comput. Appl. 2021, 181, 103005. [Google Scholar] [CrossRef]
- Wang, F.; Wang, F.; Liu, J.; Shea, R.; Sun, L. Intelligent Video Caching at Network Edge: A Multi-Agent Deep Reinforcement Learning Approach. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications, Toronto, ON, Canada, 6–9 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 2499–2508. [Google Scholar]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep Reinforcement Learning with Double Q-Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Luong, N.C.; Hoang, D.T.; Gong, S.; Niyato, D.; Wang, P.; Liang, Y.C.; Kim, D.I. Applications of Deep Reinforcement Learning in Communications and Networking: A Survey. IEEE Commun. Surv. Tutorials 2019, 21, 3133–3174. [Google Scholar] [CrossRef]
- Chen, F.; Sitaraman, R.K.; Torres, M. End-User Mapping: Next Generation Request Routing for Content Delivery. ACM SIGCOMM Comput. Commun. Rev. 2015, 45, 167–181. [Google Scholar] [CrossRef]
- Kirilin, V.; Sundarrajan, A.; Gorinsky, S.; Sitaraman, R.K. RL-Cache: Learning-Based Cache Admission for Content Delivery. In Proceedings of the 2019 Workshop on Network Meets AI & ML, Beijing, China, 23 August 2019; pp. 57–63. [Google Scholar]
- Li, L.; Zhao, G.; Blum, R.S. A Survey of Caching Techniques in Cellular Networks: Research Issues and Challenges in Content Placement and Delivery Strategies. IEEE Commun. Surv. Tutorials 2018, 20, 1710–1732. [Google Scholar] [CrossRef]
- Podlipnig, S.; Böszörmenyi, L. A Survey of Web Cache Replacement Strategies. ACM Comput. Surv. (CSUR) 2003, 35, 374–398. [Google Scholar] [CrossRef]
- Bilal, M.; Kang, S.G. Time Aware Least Recent Used (TLRU) Cache Management Policy in ICN. In Proceedings of the 16th International Conference on Advanced Communication Technology, Pyeongchang, Republic of Korea, 16–19 February 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 528–532. [Google Scholar]
- Tran, T.X.; Pompili, D. Octopus: A cooperative hierarchical caching strategy for cloud radio access networks. In Proceedings of the 2016 IEEE 13th International Conference on Mobile Ad Hoc and Sensor Systems (MASS), Brasilia, Brazil, 10–13 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 154–162. [Google Scholar]
- Wong, K.Y. Web cache replacement policies: A pragmatic approach. IEEE Netw. 2006, 20, 28–34. [Google Scholar] [CrossRef]
- Zhong, C.; Gursoy, M.C.; Velipasalar, S. A Deep Reinforcement Learning-Based Framework for Content Caching. In Proceedings of the 2018 52nd Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, USA, 21–23 March 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Sung, J.; Kim, K.; Kim, J.; Rhee, J.K.K. Efficient Content Replacement in Wireless Content Delivery Network with Cooperative Caching. In Proceedings of the 2016 15th IEEE International Conference on Machine Learning and Applications (ICMLA), Anaheim, CA, USA, 18–20 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 547–552. [Google Scholar]
- Jiang, F.; Yuan, Z.; Sun, C.; Wang, J. Deep Q-Learning-Based Content Caching with Update Strategy for Fog Radio Access Networks. IEEE Access 2019, 7, 97505–97514. [Google Scholar] [CrossRef]
- Avrachenkov, K.; Borkar, V.; Patil, K. Deep Reinforcement Learning for Web Crawling. In Proceedings of the 2021 Seventh Indian Control Conference (ICC), Mumbai, India, 20–22 December 2021; pp. 201–206. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Liang, X.; Zhao, D.; Huang, J.; Xu, X.; Dai, B.; Miao, Q. Deep Reinforcement Learning: A Survey. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 5064–5078. [Google Scholar] [CrossRef] [PubMed]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep Reinforcement Learning: A Brief Survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Malektaji, S.; Ebrahimzadeh, A.; Elbiaze, H.; Glitho, R.H.; Kianpisheh, S. Deep Reinforcement Learning-Based Content Migration for Edge Content Delivery Networks With Vehicular Nodes. IEEE Trans. Netw. Serv. Manag. 2021, 18, 3415–3431. [Google Scholar] [CrossRef]
- Guan, Y.; Zhang, X.; Guo, Z. Caca: Learning-Based Content-Aware Cache Admission for Video Content in Edge Caching. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; pp. 456–464. [Google Scholar]
- Alabed, S. RLcache: Automated Cache Management Using Reinforcement Learning. arXiv 2019, arXiv:1909.13839. [Google Scholar]
- Garetto, M.; Leonardi, E.; Traverso, S. Efficient Analysis of Caching Strategies under Dynamic Content Popularity. In Proceedings of the 2015 IEEE conference on computer communications (INFOCOM), Hong Kong, China, 26 April–1 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 2263–2271. [Google Scholar]
- Li, X.; Wang, X.; Wan, P.J.; Han, Z.; Leung, V.C. Hierarchical Edge Caching in Device-to-Device Aided Mobile Networks: Modeling, Optimization, and Design. IEEE J. Sel. Areas Commun. 2018, 36, 1768–1785. [Google Scholar] [CrossRef]
- Wang, C.; Wang, S.; Li, D.; Wang, X.; Li, X.; Leung, V.C. Q-Learning Based Edge Caching Optimization for D2D Enabled Hierarchical Wireless Networks. In Proceedings of the 2018 IEEE 15th International Conference on Mobile Ad Hoc and Sensor Systems (MASS), Chengdu, China, 9–12 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 55–63. [Google Scholar]
- Ibrahim, A.M.; Yau, K.L.A.; Chong, Y.W.; Wu, C. Applications of Multi-Agent Deep Reinforcement Learning: Models and Algorithms. Appl. Sci. 2021, 11, 10870. [Google Scholar] [CrossRef]
- Ge, H.; Song, Y.; Wu, C.; Ren, J.; Tan, G. Cooperative Deep Q-Learning with Q-Value Transfer for Multi-Intersection Signal Control. IEEE Access 2019, 7, 40797–40809. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).