Abstract
Data-based prognostic methods exploit sensor data to forecast the remaining useful life (RUL) of industrial settings to optimize the scheduling of maintenance actions. However, implementing sensors may not be cost-effective or practical for all components. Traditional preventive approaches are not based on sensor data; however, they schedule maintenance at equally spaced intervals, which is not a cost-effective approach since the distribution of the time between failures changes with the degradation state of other parts or changes in working conditions. This study introduces a novel framework comprising two maintenance scheduling strategies. In the absence of sensor data, we propose a novel dynamic preventive policy that adjusts intervention intervals based on the most recent failure data. When sensor data are available, a method for RUL prediction, designated k-LSTM-GFT, is enhanced to dynamically account for RUL prediction uncertainty. The results demonstrate that dynamic preventive maintenance can yield cost reductions of up to 51.8% compared to conventional approaches. The predictive approach optimizes the exploitation of RUL, achieving costs that are only 3–5% higher than the minimum cost achievable while ensuring the safety of critical systems since all of the failures are avoided.
1. Introduction
Proper maintenance planning is a complex task that requires interdisciplinary knowledge [1,2]. The significance of this field has garnered increasing attention due to its potential to mitigate a substantial portion of maintenance costs [3,4,5]. This interest is amplified by the widespread implementation of monitoring systems, which has stimulated research in prognostic methods for estimating the remaining useful life (RUL) of industrial assets [6]. Consequently, it is reflected in the maintenance scheduling field, since studies are focusing on integrating RUL prediction to optimize maintenance planning. While RUL prediction plays an important role in maintenance scheduling, it does not address all its challenges for the following reasons:
- Limitations of RUL estimation methods: Existing data-based methods for estimating RUL may rely on deep/machine learning approaches or statistical methods [6]. Machine and deep learning methodologies require run-to-failure data to train the models. However, such data may not be available in certain scenarios where maintenance actions are carried out with a high safety margin to prevent failures. On the other hand, statistical methods have ways to take into account right-censored data [7]; however, their accuracies are not as high as would be expected in some use cases.
- Technical and economical limitations in developing RUL models: It is not feasible to develop RUL models for every component in an industry due to technical constraints and complexities. Furthermore, it may not be economically advantageous to invest in monitoring systems for all of the parts of industrial equipment.
- Consideration of additional factors: Maintenance planning should not solely focus on RUL. Other factors, such as the availability of resources (experts, tools), need to be taken into account for effective maintenance planning.
- Accounting for uncertainty in RUL estimation: RUL estimation involves inherent uncertainty, i.e., there is not a perfect RUL estimation model that can make predictions with 100% accuracy. The errors in RUL estimation should be considered when planning maintenance actions, mainly to avoid the overestimation of the RUL near the point of failure, which may have a negative impact since a critical failure may occur.
These limitations highlight the need for a comprehensive approach to maintenance planning that goes beyond RUL prediction and that considers production planning [8] and technical limitations. In response to these challenges, this study presents a novel framework aimed at optimizing maintenance procedures in different scenarios. Building upon a previous work developed by [9], which introduced an RUL prognostic method based on the mixture of generalized fault trees (GFTs) and a k-fold ensemble of long short-term memory networks (k-LSTM), designated k-LSTM-GFT, this research proposes an innovative policy based on predictive maintenance. This exploits the failure probability estimated by the k-LSTM-GFT model to account for a safety margin for the RUL prediction, i.e., when the failure probability increases, the safety margin also increases, to reduce the risk of overestimating the RUL and at the same time exploit the useful life of industrial settings. Furthermore, recognizing that RUL methods may not always be feasible due to the lack of monitoring systems, we introduce an adaptive dynamic preventive maintenance (PMD) policy that dynamically calculates the time between interventions to account for changes in the distribution of the time between failures due to the increasing degradation of some parts or due to changes in working conditions.
The proposed framework is validated in two different use cases. The first one consists of sensor data of a fleet of aircraft engines until their failure and was obtained from a simulation software process by NASA [10]. This is a typical case where an RUL model can be developed since sensor data are available. The second use case is a friction welding process at BoschTermotechnology, where the welding tool should be replaced before failure to avoid damaging the working pieces. This case illustrates an opportunity where a dynamic preventive approach fits since the failure does not represent safety consequences, as in the case of the aircraft engines, and cost savings may be achieved even without sensor data. The primary contributions of this work are as follows:
- A PMD policy is proposed for cases where no sensor data are available. This proves effective in reducing maintenance costs since it can improve current PM policies by dynamically increasing or decreasing the time between interventions. The results indicate cost savings of up to 51.8% compared to static PM policies.
- A novel predictive maintenance (PdM) approach for maintenance scheduling with imperfect RUL prognostics (PdMI) is proposed. This novel method leverages sensor data and the k-LSTM-GFT, an RUL prognostic method presented by [9], to optimize maintenance planning. In contrast to the existing literature, our approach dynamically calculates a safety factor to account for the uncertainty in RUL estimation by utilizing the failure probability estimated by the k-LSTM-GFT method. The results of this approach are very promising, being only 3–5% above the minimum cost that can be achieved.
- A comprehensive comparative study of the proposed methods against traditional and idealistic maintenance scheduling policies is presented.
- The proposed framework showcases versatility as it can be applied even when no sensor data are available. The PdM policy with imperfect RUL predictions (PdMI) is employed when sensor data are available, while the PMD strategy is used in cases where sensor data are limited.
The remainder of this document is organized as follows: Section 2 presents the most recent works related to maintenance planning. Section 3 describes in detail the use cases adopted and formulates the problem. Section 4 presents the RUL prediction model that served as the base for one of the proposed maintenance scheduling approaches. Section 5 details the proposed framework for maintenance scheduling, while Section 6 describes other maintenance scheduling approaches used for comparison. Section 7 presents the main results and discusses them in detail. Finally, Section 8 summarizes the main findings of this work.
2. Related Work
Some studies have utilized linear programming to optimize maintenance costs, taking into consideration the RUL prediction [11,12,13,14], while others employed deep reinforcement learning (DRL) for the same purpose [15,16]. Multi-objective approaches were exploited by [17] to find solutions that represent a compromise between maintenance cost and equipment availability and by [18] to optimize maintenance costs, resource utilization, and reduce carbon footprint. The authors of [19] exploited an RUL estimation based on the visual monitoring of crack damages, while [20] used deep learning (DL) for RUL estimation, aiming to develop dynamic maintenance scheduling. Refs. [21,22] exploited an RUL model to group assets to be repaired to minimize maintenance costs. Most predictive maintenance (PdM) approaches currently adopt maintenance planning based on a static degradation threshold [4,23,24,25], which is utilized to determine the moment when an intervention should be performed. Determining the optimal threshold to minimize costs typically involves considering the RUL and an additional safety factor to account for imperfect RUL predictions [12], which often necessitates combining simulation with various optimization techniques.
Preventive maintenance (PM) can be utilized without a predictive model. It is widely adopted by enterprises since it only requires data concerning the time between failures. Commonly, in practical industrial scenarios, PM is scheduled in two ways: (1) maintenance actions are scheduled at equally spaced intervals based on the mean time between failures (MTBF), determined by the component’s supplier or historical data; (2) maintenance actions are programmed with a high safety factor to prevent any failures from occurring.
Scheduling interventions based on the MTBF aim to strike a balance between minimizing failures and utilizing the asset’s useful life. However, this approach may not be efficient in minimizing costs since it may allow several failures to occur. Furthermore, it fails to account for variations in operational conditions resulting from production changes or component degradation, which are crucial for the proper functioning of tools and equipment. For example, the degradation level of a given tool may be accelerated due to the age of the machine with which it is coupled. In this scenario, the majority of tools will fail before the MTBF calculated from historical data. Although there are proposed methods to overcome these issues [26,27], typically, these approaches need more data sources than the time between failures, which makes them more challenging to implement in practical scenarios. Adopting overly conservative maintenance schedules to avoid all failures, known as working in the safety zone, leads to the under-utilization of the asset’s useful life and, typically, is not cost-effective.
Some research has focused on optimizing PM actions, especially in scheduling interventions to avoid impacts on production [28,29,30,31,32] or in grouping maintenance tasks [33]. The uncertainty of the distribution of the time between failures (TBF) [34] is addressed by [35], who uses a Bayesian approach to estimate the strength of the population of replacement parts, and by [36], who considers the asset’s age to update the failure rate of parts. Some PM approaches also consider the health state of components by performing periodic inspections [37] or by using prediction models, such as the Wiener process model [38]. Other studies, such as [39,40,41,42], focused on optimizing PM actions of repairable systems by considering imperfect maintenance actions. Maintenance costs may be mitigated by considering opportunistic maintenance intervals with imperfect PM actions in systems whose unavailability caused by preparation time is considerable [43].
Despite recent efforts to optimize the scheduling of maintenance actions in the absence of a prognostic model, a persistent issue remains: the intervals between maintenance actions are maintained static. The optimal interval between interventions depends on the distribution of time between failures, a distribution that dynamically changes due to the increasing degradation of neighboring components or shifts in working conditions. Consequently, dynamically determining the optimal time between interventions can lead to significant cost savings in maintenance.
3. Problem Formulation and Use Case Description
3.1. Maintenance Scheduling Problem
Let us consider an industrial asset that contains at least one part that may be replaced. If the considered industrial asset is monitored by sensors whose signals are related to the degradation of the considered part, it is possible to develop an RUL prognostic model for the component, and an estimation of its RUL can be obtained at each day (or working cycle) by the k-LSTM-GFT model. Otherwise, the only data available for maintenance planning are the historical data of the time between failures observed until the current moment.
Each asset is allocated a set of maintenance slots that are equally distributed at intervals of m days. Periodic maintenance tasks and inspections may only be performed in these slots. If a given component v needs to be replaced at , this intervention should be planned at the latest in the previous maintenance slot, , to have a spare part available in stock. If the replacement of a given component is planned at a given slot, , to be performed during , the enterprise incurs an out-of-stock cost, , [20] since the replacement was not planned in advance.
A maintenance action can only be scheduled at each slot . Each proactive replacement (before the failure) costs , while a corrective action costs (a failure occurred). Note that . The objective of the maintenance schedule is to reduce the ratio between the total costs of maintenance and the number of working cycles performed by each component.
3.2. Friction Welding Use Case
Friction welding is a solid-state welding process in which heat is generated by the mechanical friction between a rotating tool and the workpieces to fuse the materials, as depicted in Figure 1. In addition, the tool has a lateral displacement in the direction of the X-axis to displace the materials.
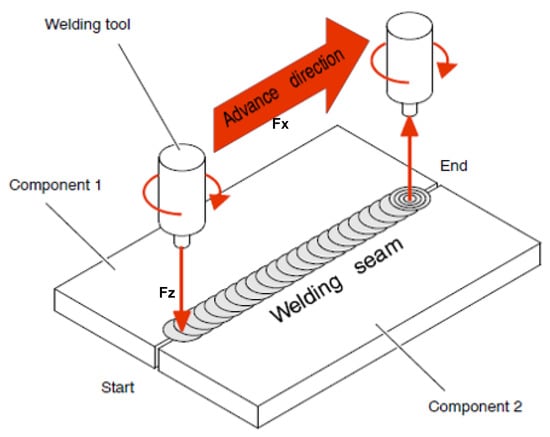
Figure 1.
Schematic of the friction welding process.
This process causes the degradation of the welding tools that must be regularly replaced. In this work, we address a real use case at BoschTermotechnology. For this purpose, the enterprise only performed corrective actions for one month to obtain the distribution of the time between failures for these components. During this period, a total of 54 tools were replaced due to failure. From these tools, the time between replacements of the first 34 were used for training, and the remaining were used for testing purposes.
When a tool fails before being replaced (corrective action), the workpieces are considered scrap, so there is an additional cost to the enterprise. The main objective in this use case is to minimize the cost per working cycle due to tool replacement.
3.3. Aircraft Engine Use Case
Typically, aircraft engines have five main components: the fan, the low-pressure compressor (LPC), the high-pressure compressor (HPC), the low-pressure turbine, and the high-pressure turbine (HPT). These aero-engines typically undergo different types of failure related to the degradation of their main components (LPC, HPC, LPT, HPT, and fan), which have to be replaced to avoid failures [44].
In this work, we use the C-MAPSS dataset, which is a benchmark dataset [10] for RUL estimation on aircraft engines, provided by NASA [10]. It was obtained through the commercial modular aero-propulsion system simulation (C-MAPSS) [45], and contains degradation trajectories of aero-engines, divided into four subsets (FD001–FD004), each one considering a specific number of failure modes and operating conditions, as shown in Table 1. Training instances contain run-to-failure sensor measurements, while testing instances include measurements up until a certain point before failure. When utilized to test the RUL prediction model, the goal is to predict the RUL in cycles for the last working cycle of each engine in the testing set. Each instance contains 26 columns, including the engine ID, cycle index, and three columns containing operational settings and sensor measurements.

Table 1.
C-MAPSS datasets description.
For this study, we focus exclusively on the subset FD001, which was utilized for the demonstration and validation of the maintenance scheduling framework. For these purposes, we need run-to-failure data. Therefore, we exclusively utilize the training instances, as they are the only ones that contain such data. To ensure that the approach is only validated on unseen data, we adopt an 80–20% split for training and testing, respectively. That is, the first 80 engines are used for training purposes, while the remaining 20 are reserved for testing the approach.
The main objective is to schedule maintenance interventions at a maintenance slot just before a failure occurs to optimize the useful life of the engines and to avoid failures, a critical requirement to ensure the safety of the aircraft staff.
4. k-LSTM-GFT Model for RUL Estimation
When sensor data are available, typically, it is possible to develop an RUL prediction model whose predictions may be exploited to optimize the scheduling of maintenance actions. The effectiveness of this process closely depends on the accuracy of predictions and on a mechanism to account for RUL prediction uncertainties, since no model is perfect. For this purpose, we exploit the k-LSTM-GFT model developed by [9]. This approach is depicted in Figure 2 and is clarified in the following paragraphs.
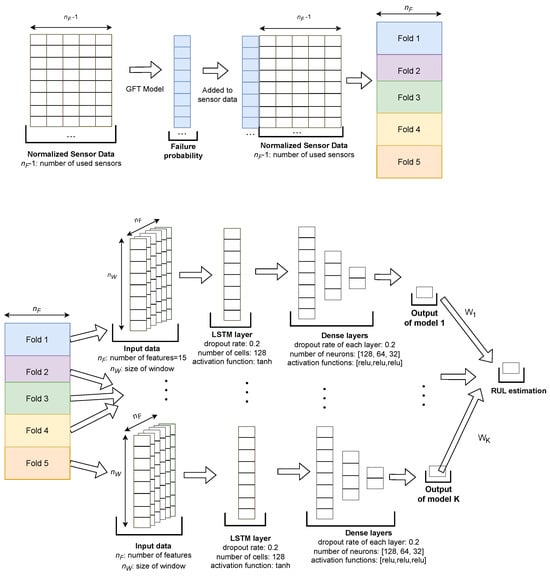
Figure 2.
Architecture of the k-LSTM-GFT [9].
The k-LSTM-GFT combines a reliability approach, the generalized fault tree (GFT) analysis, with an ensemble of k-fold LSTM (k-LSTM). The GFT is a data-driven generalization of the traditional fault tree analysis (FTA) proposed by [46] that graphically represents a failure event by a data-driven fault tree, whose basic events are derived from the categorization of the continuous sensor data [47]. The fault tree structure is obtained automatically from a training process, and enables the qualitative analysis of failures and estimates the failure probability based on the observed sensor data. Furthermore, during the training, a probability threshold is determined. This consists of a probability where it is recommended to take proactive action since the equipment or tool is near failure. Its value is the one that minimizes maintenance costs during the training process [46]. Additionally, the failure probability derived from GFT is integrated as a feature into the k-LSTM model, which estimates the RUL of the assets.
Figure 2 illustrates the architecture of the k-LSTM-GFT model. It fuses the GFT approach and LSTM by using the failure probability estimated by the GFT model and the probability of BEs as features for the LSTM. At the top of the figure, the input data are represented. They consist of normalized sensor data and the failure probability estimated by the GFT. These inputs are combined into a matrix with columns, representing the number of features (including the failure probability estimated by the GFT), and rows, representing the values from previous time steps. As we are working with the subset FD001, we chose , which corresponds to the minimum number of working cycles until failure, for an engine in the test subset [11].
The training data are divided into folds, each represented by a different color. In this setup, each fold is used as validation data, while the remaining folds serve as training data, resulting in the development of five distinct models. The final RUL prediction is generated by averaging the outputs of these individual models. As depicted at the bottom of Figure 2, the deep learning (DL) model comprises an LSTM layer, followed by three dense layers, each incorporating a dropout rate of 0.2. For more comprehensive details regarding the k-LSTM-GFT model, please refer to [9].
5. Proposed Framework for Maintenance Scheduling
5.1. Maintenance Scheduling with Imperfect RUL Estimation (PdMI)
Although the k-LSTM-GFT model has shown high accuracy in predicting the RUL of turbofan engines, as demonstrated by [9], effective maintenance scheduling goes beyond RUL predictions, as previously mentioned. This work presents an approach based on the k-LSTM-GFT model to schedule maintenance actions. This approach stands out from other PdM approaches by exploiting the failure probability estimated by the GFT to dynamically calculate a safety margin for RUL prediction, which is used to schedule maintenance actions.
The RUL estimation involves inherent uncertainty due to the imperfection of prognostic methods. Consequently, when using RUL predictions to schedule maintenance actions, it becomes necessary to account for this uncertainty by introducing a safety factor. In this study, we utilize the failure probability and the optimal threshold probability , estimated by the k-LSTM-GFT, to account for a safety margin for the RUL estimation. The new estimation with a safety factor, denoted as , is calculated as follows:
where is an underestimation of the initial estimation made by the k-LSTM-GFT at each day or cycle i. The safety margin increases as the estimated failure probability increases. It is a key feature since it is crucial to avoid the overestimation of the RUL when a given component or piece of equipment is near failure.
At each maintenance slot , a maintenance action may be triggered, and a replacement of a component may be performed. The proposed maintenance scheduling approach intends that a replacement is scheduled at time slot to be performed at if the estimated RUL considering the safety factor falls between m and . This scenario is represented in Case 1 in Figure 3. The replacement is planned m days ahead, thus, there is no cost associated with the action.
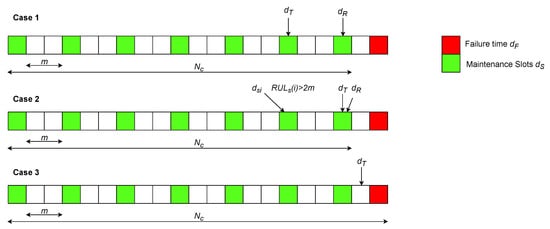
Figure 3.
Illustration of 3 hypothetical scenarios when scheduling maintenance based on the k-LSTM-GFT.
On the other hand, sometimes the estimated may be bigger than at slot , which is not sufficient for scheduling a replacement for ; however, at slot , the estimated may be lower than m. In this case, a replacement has to be performed in this maintenance slot ; otherwise, a failure is estimated to occur before the next maintenance slot, . This scenario is represented in Case 2 in Figure 3. Since the replacement was not planned, there is an associated out-of-stock cost of .
The most dangerous scenario occurs when a failure occurs but no maintenance action was triggered in the preceding maintenance slots. This is depicted by Case 3 in Figure 3. This occurs when the predictive model overestimates the RUL prediction. In such situations, corrective action with cost becomes necessary, and since it was not planned, the additional cost is also incurred. Note that in scenarios where safety is crucial, such as the case of aircraft engines, it is mandatory to avoid failures, highlighting the importance of an accurate RUL model and using a dynamic safety factor to account for RUL estimation uncertainties. This ensures that the safety factor increases when the equipment is near failure to avoid RUL overestimation while ensuring the exploitation of the useful life of components.
The cost of this policy for a set with n components is given by Equation (2), where and are, respectively, the time where a maintenance action is triggered within a maintenance slot and the failure time of each component, is a function defined as when x is true and , otherwise. is the number of cycles performed until the replacement, as illustrated in Figure 3.
5.2. Maintenance Scheduling with Dynamic PM Scheduling (PMD)
Consider a scenario where no RUL prognostic model exists for a given component and its replacement is currently scheduled at equally spaced intervals, . The proposed dynamic approach allows the first tools to reach failure. The parameter is initially set as the minimum time between failures observed for these tools and is dynamically updated after components are replaced, following these rules: If none of the components within the set have failed before being replaced, the new replacement interval, is adjusted to be , where . Conversely, if at least one component fails before being replaced, will be set to the shortest failure time observed for the last set of components, as depicted in Figure 4. A search grid on the parameters and is performed in the training data to find the optimal values based on the cost obtained for different values of these parameters.
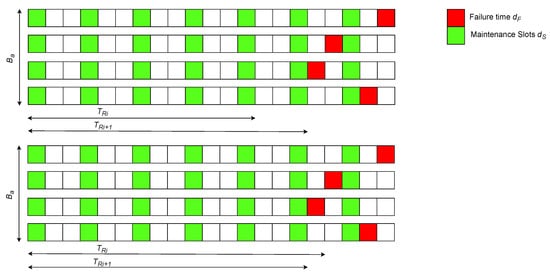
Figure 4.
Illustration of the proposed dynamic PM policy.
This adaptive updating of the replacement interval balances the exploitation of each component’s lifetime and the number of failures that occurred. The time between failures of a given component may depend on the degradation level of adjacent systems or changes in working conditions. The dynamic updating of the time between interventions allows these aspects to be considered since it is updated based on the last replacements.
In this case, the slots during which a maintenance action is triggered are known in advance since is predetermined. Consequently, the cost is only incurred when a failure occurs. As a result, the cost of this approach is calculated as follows:
If the replacement occurs before the failure, only the cost of a preventive action is present; otherwise, there is a cost of a corrective action and the out-of-stock cost since the replacement was not planned.
6. Other Maintenance Scheduling Approaches
6.1. PM Scheduling Based on Static Intervals between Interventions
While efforts are being presented on statistical methods in the field of maintenance [48], the majority of enterprises still rely on fixed intervals of time to perform proactive interventions. The main difference between the proposed dynamic PM scheduling approach and the most usual PM approaches currently used in the industry is that in the latter ones, the time between replacements or maintenance actions, , is constant over time. One of the most common strategies assumes the MTBF as the time between proactive interventions. The PM policy that uses the MTBF as the time between interventions is designated here as PMMTBF. Instead, a more conservative value may be used to avoid failures, whose approach is designated as PMC. In both situations, the cost of these approaches may be calculated by Equation (3), replacing by the MTBF or other constant values determined. In both situations, the value is calculated based on historical data concerning the time between failures.
6.2. Minimum Cost Achievable Using Perfect RUL Prognostics (PdMP)
This maintenance approach is based on the hypothesis that the RUL can be determined and the precise failure time is known two or more maintenance slots before it occurs. As a result, no failures or out-of-stock situations are incurred. The cost of this approach is calculated as follows:
Please note that this approach is not achievable since no RUL prognostic model is perfect. It is used solely for comparative purposes, serving as a reference for the minimal cost that may be achieved in a given use case.
7. Results and Discussion
The proposed framework comprises two distinct maintenance policies designed to be utilized in different scenarios. Firstly, a PdM maintenance policy with imperfect RUL prognostics (PdMI) based on the k-LSTM-GFT model is used when there is sufficient sensor data for developing the prognostic model. Secondly, for scenarios where constructing an RUL prognostic model is impractical, we propose a dynamic predictive maintenance policy (PMD). For this, we consider that the time between maintenance slots is days, and that the costs of maintenance actions may follow two distinct scenarios, A and B, represented in Table 2. These distinct scenarios are used to evaluate the different maintenance policies when the costs of maintenance actions change.

Table 2.
Costs for two different cases.
7.1. Static PM Approaches on the Friction Welding Use Case
The PM scheduling approaches described in Section 6 offer a significant advantage in some use cases, as they only rely on the data on the time between failures. In Figure 5, we illustrate these data for both training and testing instances of the friction welding use case. During the training phase, we use the distribution of the time between failures to define a replacement strategy, which is then applied to the testing data to evaluate the associated costs. It is noteworthy that the distribution of training instances varies from that of testing instances. This suggests that using a fixed value for the time between interventions may not be as cost-effective for the testing data as it was for the training data.
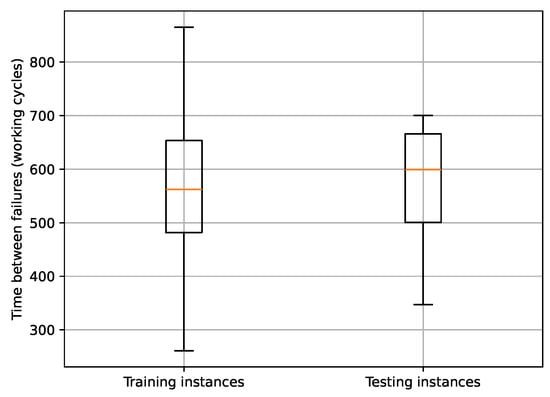
Figure 5.
Box plot of the performed cycles until failure for the friction welding use case. Note that outliers are not plotted.
Figure 6 displays the costs obtained when considering various static maintenance intervals for each case. It is important to note that the minimum time between failures in the training data is 119, while the MTBF is 608.82. Setting the time between interventions to values lower than 119 results in a conservative PM approach (PMC), which avoids all failures but may under-exploit the useful life of friction welding tools, leading to economic inefficiency. On the other hand, using the MTBF as the replacement interval allows for higher exploitation of the tools’ life cycle, but it may not necessarily be the best interval since a considerable number of failures may occur, resulting in higher costs. It is noteworthy that setting to a value lower than 119, which is the minimum observed in the training set, does not guarantee that all failures are avoided for the new instances. For this reason, in cases where safety is a major concern, the adopted value may be even more conservative to avoid all failures. Since these are not concerns for the friction welding use case, we focus solely on the economic costs of maintenance.
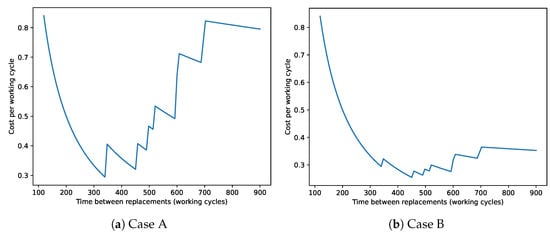
Figure 6.
Cost of traditional PM, varying the time between replacements, .
In Case A, the optimal is closer to the minimum time between failures compared with Case B, as shown in Figure 6a. Here, a conservative approach yields more interesting results, as significantly outweighs . However, in Case B, where the costs are more balanced, the optimal is closer to the MTBF, as can be seen in Figure 6b. The most widely used PM approaches, such as PMC or PMMTBF do not represent the optimal solution economically for different scenarios, which highlights the necessity of having a more flexible PM scheduling strategy.
7.2. Dynamic PM on the Friction Welding Use Case
The analysis of Cases A and B leads us to a crucial conclusion: the optimal depends on the costs associated with each maintenance action. Utilizing a static means the maintenance scheduling policies lack the flexibility to adapt to changes in the working environment or degradation of other components within the system, which could influence the time to failure of the friction welding tools. Moreover, adjusting from a conservative value to one closer to the MTBF may prove efficient if the cost of maintenance actions changes. However, with a conservative approach, estimating the actual MTBF for a given component becomes impossible as components are replaced before failure occurrence.
To address these challenges, the proposed PMD offers a dynamic solution by continuously adjusting . It is initially set at the minimum value observed in the first set of . This value dynamically changes each time, based on the time between failures of the last friction welding tools replaced, following the rules described in Section 5.2. The time between interventions, , increases when no tool within fails and decreases to the minimum time between failures observed if at least one tool in the set of the last fails before being replaced.
The values of and were set based on the costs obtained for the training set when using different combinations of these parameters. As seen in Figure 7, the optimal values for both scenarios A and B were and ; thus, these were the adopted values.
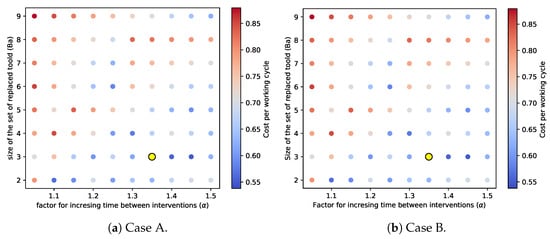
Figure 7.
Costs per working cycle on training data according to different values of and . The yellow point represents the minimum cost per working cycle obtained.
Figure 8 presents a visual representation of the costs associated with each PM policy for the testing instances under two distinct scenarios, denoted as A and B. The findings demonstrate the superior cost-effectiveness of the proposed PMD approach when compared to conventional PM strategies since, in both Cases A and B, the PMD approach achieves the lowest cost.
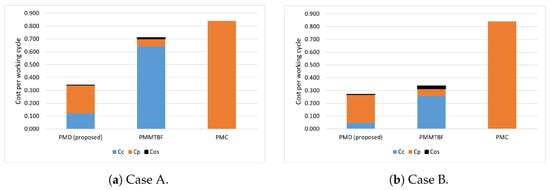
Figure 8.
Costs per working cycle of different PM maintenance policies for the testing engines.
In Case A, as the is much higher than , it was expected that the PMC strategy would have good results, but the minimum time between failures observed in the training instances (119 working cycles) is very conservative since the majority of friction welding tools failed after performing more than 500 working cycles. For this reason, the PMMTBF achieves better results than the PMC in both scenarios because the higher exploitation of the useful life of tools compensates economically for the higher number of failures. The dynamic adjustment of maintenance intervals in the PMD strategy emerges as a highly effective mechanism for striking a balance between exploiting assets’ lifetimes and minimizing the incidence of failures. As can be seen in Figure 8, this approach outperforms traditional preventive approaches for both cases, achieving cost savings of 19.5% and 51.8%, respectively, for Cases A and B.
Furthermore, the PMD policy’s adaptability shines through as it takes into account the impact of degradation in other system components or shifts in working conditions over time by dynamically adjusting itself based on recent failures and accounting for these evolving circumstances.
7.3. Maintenance Scheduling with Imperfect RUL Prognostics (PdMI) on the Aircraft Engine Use Case
The availability of monitoring data from sensors offers a significant advantage in enhancing maintenance actions. By utilizing these data, it becomes possible to develop RUL prognostic models that accurately estimate the current degradation state of assets based on sensor measurements. The number of cycles an aircraft engine can perform until failure depends on a lot of variables and working conditions; thus, its value may exhibit high variability. Consequently, implementing an effective PM strategy is challenging since the optimal time between interventions is not a trivial problem. Furthermore, for this specific use case, there is a major safety concern since aircraft engines must not fail during a flight. For this reason, a PdM policy for such components is highly advantageous, since the forecasting of the RUL of components has the potential to have a considerable impact in reducing the costs related to maintenance, while ensuring the safety and integrity of the engines.
The k-LSTM model was integrated into the maintenance scheduling framework to leverage the failure probability estimated by the GFT for calculating a dynamic safety margin in the RUL prediction. For testing and evaluation, the training set of FD001 was split, with 80 engines used for training the k-LSTM-GFT model and the remaining 20 engines for testing. The results of these test instances are presented in Figure 9a, displaying the RUL prediction outcomes. Additionally, Figure 9b illustrates the root-mean-squared-error (RMSE) as an evaluation metric plotted against the number of flights until failure. The RMSE of the model is lower when the actual RUL decreases, which means that the model is more accurate near the failure point. This occurs because the degradation patterns are more pronounced near failure when the model’s accuracy is more critical.
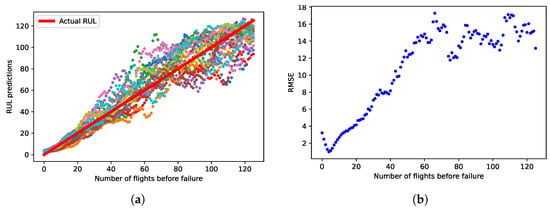
Figure 9.
Results of the k-LSTM-GFT for the 20 test engines. (a) RUL predictions over time for the 20 test engines in FD001. (b) RMSE of the RUL predictions for the 20 test engines.
The costs obtained with the proposed PdMI policy are presented in Figure 10 for both cases, A and B. With this policy, the useful life of components is exploited as close to the maximum as possible and no failure is incurred (see Figure 11). The perfect maintenance policy (PdMP) can be used as a bound that may be reached in terms of costs. The costs with the proposed approach are only 3% and 5% higher than the PdMP for Cases A and B, respectively. Note that the PdMP policy is not achievable since there is no perfect RUL prognostic model. This demonstrates the effectiveness of the PdMI approach in optimizing maintenance scheduling since the obtained costs are very close to the best that may be attainable in an idealistic situation.
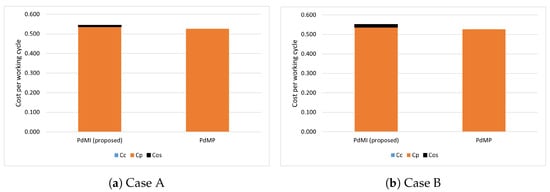
Figure 10.
Costs per working cycle: comparison of the proposed PdMI with the minimum maintenance cost that can be achieved.
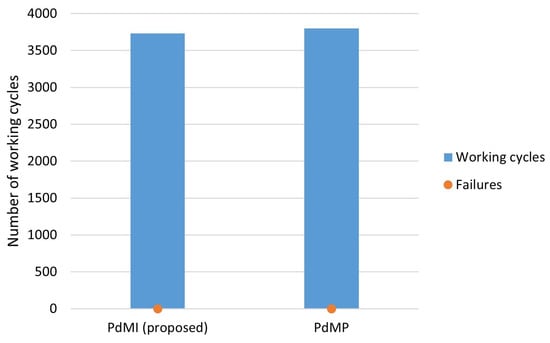
Figure 11.
Number of working cycles and failures obtained with each policy.
The main advantage of using the k-LSTM-GFT model in the proposed scheduling policy, compared to other RUL prognostic models, is the fact that, in addition to being very accurate in RUL prediction, the failure probability estimated by the GFT allows the calculation of a dynamic safety margin to mitigate RUL prediction errors. When the estimated failure probability is higher, typically near the point of failure, the safety margin to account for RUL uncertainties is also bigger, to ensure that the RUL is not overestimated when the engine is near failure. On the other hand, when the estimated failure probability is lower, the safety margin is also lower, allowing the exploitation of the engines’ useful life.
Table 3 shows an example of a testing engine. If using the estimated RUL by the model , at the maintenance slot available, when performing 190 flights, no immediate action would be taken since the falls between and , so a replacement would be scheduled for the next maintenance slot. However, the prediction in this case overestimates the actual RUL, and a failure would occur before the next maintenance slot if the engine was not replaced at the current time slot. In contrast, the predicted RUL with the safety margin suggests replacing the engine immediately, avoiding the cost associated with a failure and ensuring that the engine does not fail during the flight. Having the safety factor calculated dynamically allows a better exploitation of the useful life of components because it assumes higher values near the point of failure, ensuring the safety of components, and lower values far from the point of failure, according to the GFT failure probability estimation, optimizing the exploitation of the useful life of components.

Table 3.
Scenario for the engine with ID = 100 with the proposed PdMI policy.
8. Conclusions
Scheduling maintenance actions is a complex task, and the most suitable policy depends on the specific use case. A policy based on PdM is the optimal choice for reducing maintenance-associated costs; however, developing monitoring systems and RUL prognostic models for all components may not be feasible. In such cases, an alternative approach based on periodic maintenance actions may be a viable option to mitigate costs associated with equipment failures.
Some of the most widely used PM approaches in industry often employ static values for the time between replacements, which could be based on the MTBF calculated from historical data or overlying conservative values to prevent all failures. Such inflexible approaches can lead to sub-optimal cost-effectiveness, as maintenance costs may vary over time, affecting the compromise between asset lifetime exploitation and minimizing failures to obtain an optimal solution. Moreover, the time between failures and, consequently, the MTBF may dynamically change due to shifting working conditions or the degradation of other components within the system.
In this work, we propose two distinct maintenance policies: (1) The PMD, designed for scenarios where no RUL prognostic model is available. It dynamically calculates the time between interventions based on the occurrence of failures within the set of the last replaced components. (2) The PdMI policy, which leverages the RUL predictions and the failure probability estimated by the k-LSTM-GFT model to calculate a dynamic safety factor to account for the uncertainty of RUL predictions. This approach mitigates the impact of imperfect RUL predictions based on the estimated failure probability, which allows for the dynamic calculation of the safety factors.
The maintenance policies were tested on two distinct realistic use cases: one to highlight a scenario where sensor data are available and safety is a major concern (aircraft engines), and another where failures are allowed but no sensor data are available (friction welding use case). In the first use case, the proposed PdMI achieved a very good performance, achieving costs only 3–5% higher than the perfect maintenance plan, which is not achievable in practice since there is no perfect RUL prognostic model. Moreover, the PdMI approach successfully avoids failures, a crucial requirement for critical systems where safety is a crucial requirement.
In cases where an RUL prognostic model is not feasible, we employ the proposed PMD policy. The results demonstrate that this approach outperforms static PM policies in the friction welding use case in both cases, A and B, where the costs of maintenance actions are different. The improvement was 51.8% and 19.5%, respectively, for Cases A and B. In addition to being more cost-effective than traditional PM approaches, the PMD policy offers flexibility to adapt to changes that may affect the distribution of the time between failures, which may occur due to varying working conditions or the degradation of other components within the system.
The proposed maintenance approach aims to be deployed in a real industrial environment for future work. This deployment will involve integrating the company’s data, including the availability of resources for maintenance actions. By incorporating this information in real time, the scheduling process can be enhanced to consider additional parameters, such as work orders, thereby prioritizing maintenance tasks based on immediate necessity.
Author Contributions
Conceptualization, P.N. and E.R.; methodology, P.N., E.R. and J.S.; software, P.N.; validation, P.N., E.R. and J.S.; formal analysis, P.N.; investigation, P.N.; resources, E.R. and J.S.; data curation, P.N.; writing—original draft preparation, P.N.; writing—review and editing, P.N., J.S. and E.R.; visualization, P.N.; supervision, E.R. and J.S.; project administration, E.R. and J.S.; funding acquisition, E.R. and J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by FCT-Fundação para a ciência e Tecnologia through the PhD grant Ref. 2020.06926.BD.
Data Availability Statement
The data used for the aircraft engine use case are in the public C-MAPSS dataset [45]. The data used for the friction welding use case are confidential information of the Bosch company manufacturing system, so they are not publicly available.
Acknowledgments
The first author acknowledges the FCT—Fundação para a Ciência e a Tecnologia, I.P. for the PhD grant Ref. 2020.06926.BD. The first and second authors acknowledge the University of Aveiro, FCT/MCTES, for the financial support of the TEMA research unit (FCT Refs. UIDB/00481/2020 and UIDP/00481/2020) and CENTRO01-0145-FEDER-022083—Regional Operational Program of the Center (Centro2020), within the scope of the Portugal 2020 Partnership Agreement, through the European Regional Development Fund. The second author was partially supported by the Center for Research and Development in Mathematics and Applications (CIDMA) through the Portuguese Foundation for Science and Technology, reference UIDB/04106/2021. The present study was partially developed in the scope of the Project Augmented Humanity (PAH) [POCI-01-0247- FEDER-046103], financed by Portugal 2020, under the Competitiveness and Internationalization Operational Program, the Lisbon Regional Operational Program, and by the European Regional Development Fund.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Aghdam, S.S.; Fattahi, P.; Hosseini, S.M.H.; Babaeimorad, S.; Sana, S.S. Joint optimisation of the maintenance and buffer stock policies considering back orders. Int. J. Syst. Sci. Oper. Logist. 2023, 10, 2169054. [Google Scholar] [CrossRef]
- Zheng, R.; Zhao, X.; Hu, C.; Ren, X. A repair-replacement policy for a system subject to missions of random types and random durations. Reliab. Eng. Syst. Saf. 2023, 232, 109063. [Google Scholar] [CrossRef]
- Salonen, A.; Deleryd, M. Cost of poor maintenance: A concept for maintenance performance improvement. J. Qual. Maint. Eng. 2011, 17, 63–73. [Google Scholar] [CrossRef]
- Huynh, K.T.; Grall, A.; Berenguer, C. A Parametric Predictive Maintenance Decision-Making Framework Considering Improved System Health Prognosis Precision. IEEE Trans. Reliab. 2019, 68, 375–396. [Google Scholar] [CrossRef]
- Dui, H.; Zhang, H.; Wu, S. Optimisation of maintenance policies for a deteriorating multi-component system under external shocks. Reliab. Eng. Syst. Saf. 2023, 238, 109415. [Google Scholar] [CrossRef]
- Nunes, P.; Santos, J.; Rocha, E. Challenges in predictive maintenance—A review. CIRP J. Manuf. Sci. Technol. 2023, 40, 53–67. [Google Scholar] [CrossRef]
- Wan, Q.; Zhu, M.; Qiao, H. A joint design of production, maintenance planning and quality control for continuous flow processes with multiple assignable causes. CIRP J. Manuf. Sci. Technol. 2023, 43, 214–226. [Google Scholar] [CrossRef]
- Liu, X.; Wang, W.; Peng, R. An integrated preventive maintenance and production planning model with sequence-dependent setup costs and times. Qual. Reliab. Eng. Int. 2017, 33, 2451–2461. [Google Scholar] [CrossRef]
- Nunes, P.; Rocha, E.; Santos, J. Combining generalized fault trees and k-LSTM ensembles for enhancing prognostics and health management. 2024; submitted. [Google Scholar]
- Saxena, A.; Goebel, K.; Simon, D.; Eklund, N. Damage propagation modeling for aircraft engine run-to-failure simulation. In Proceedings of the 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–9. [Google Scholar]
- de Pater, I.; Mitici, M. Predictive maintenance for multi-component systems of repairables with Remaining-Useful-Life prognostics and a limited stock of spare components. Reliab. Eng. Syst. Saf. 2021, 214, 107761. [Google Scholar]
- de Pater, I.; Reijns, A.; Mitici, M. Alarm-based predictive maintenance scheduling for aircraft engines with imperfect Remaining Useful Life prognostics. Reliab. Eng. Syst. Saf. 2022, 221, 108341. [Google Scholar] [CrossRef]
- Hesabi, H.; Nourelfath, M.; Hajji, A. A deep learning predictive model for selective maintenance optimization. Reliab. Eng. Syst. Saf. 2022, 219, 108191. [Google Scholar] [CrossRef]
- Einabadi, B.; Mahmoodjanloo, M.; Baboli, A.; Rother, E. Dynamic predictive and preventive maintenance planning with failure risk and opportunistic grouping considerations: A case study in the automotive industry. J. Manuf. Syst. 2023, 69, 292–310. [Google Scholar] [CrossRef]
- Lee, J.; Mitici, M. Deep reinforcement learning for predictive aircraft maintenance using probabilistic Remaining-Useful-Life prognostics. Reliab. Eng. Syst. Saf. 2023, 230, 108908. [Google Scholar] [CrossRef]
- Wesendrup, K.; Hellingrath, B. Post-prognostics demand management, production, spare parts and maintenance planning for a single-machine system using Reinforcement Learning. Comput. Ind. Eng. 2023, 179, 109216. [Google Scholar] [CrossRef]
- Lee, J.; Mitici, M. Multi-objective design of aircraft maintenance using Gaussian process learning and adaptive sampling. Reliab. Eng. Syst. Saf. 2022, 218, 108123. [Google Scholar] [CrossRef]
- Wang, Y.; Limmer, S.; Van Nguyen, D.; Olhofer, M.; Bäck, T.; Emmerich, M. Optimizing the maintenance schedule for a vehicle fleet: A simulation-based case study. Eng. Optim. 2022, 54, 1258–1271. [Google Scholar] [CrossRef]
- Li, R.; Arzaghi, E.; Abbassi, R.; Chen, D.; Li, C.; Li, H.; Xu, B. Dynamic maintenance planning of a hydro-turbine in operational life cycle. Reliab. Eng. Syst. Saf. 2020, 204, 107129. [Google Scholar] [CrossRef]
- Nguyen, K.T.; Medjaher, K. A new dynamic predictive maintenance framework using deep learning for failure prognostics. Reliab. Eng. Syst. Saf. 2019, 188, 251–262. [Google Scholar] [CrossRef]
- Wang, Y.; Gogu, C.; Binaud, N.; Bes, C.; Haftka, R.T.; Kim, N.H. A cost driven predictive maintenance policy for structural airframe maintenance. Chin. J. Aeronaut. 2017, 30, 1242–1257. [Google Scholar] [CrossRef]
- Chang, F.; Zhou, G.; Zhang, C.; Xiao, Z.; Wang, C. A service-oriented dynamic multi-level maintenance grouping strategy based on prediction information of multi-component systems. J. Manuf. Syst. 2019, 53, 49–61. [Google Scholar] [CrossRef]
- Nielsen, J.S.; Sørensen, J.D. Computational framework for risk-based planning of inspections, maintenance and condition monitoring using discrete Bayesian networks. Struct. Infrastruct. Eng. 2018, 14, 1082–1094. [Google Scholar] [CrossRef]
- Shi, Y.; Zhu, W.; Xiang, Y.; Feng, Q. Condition-based maintenance optimization for multi-component systems subject to a system reliability requirement. Reliab. Eng. Syst. Saf. 2020, 202, 107042. [Google Scholar] [CrossRef]
- Cai, Y.; Teunter, R.H.; de Jonge, B. A data-driven approach for condition-based maintenance optimization. Eur. J. Oper. Res. 2023, 311, 730–738. [Google Scholar] [CrossRef]
- Nicolai, R.P.; Dekker, R. Optimal Maintenance of Multi-component Systems: A Review. In Complex System Maintenance Handbook; Springer: London, UK, 2008; pp. 263–286. [Google Scholar]
- Aramesh, M.; Shaban, S.Y.; Attia, M.H.; Kishawy, H.A.; Balazinski, M. Survival life analysis applied to tool life estimation with variable cutting conditions when machining titanium metal matrix composites (Ti-MMCs). Mach. Sci. Technol. 2016, 20, 132–147. [Google Scholar] [CrossRef]
- Rashidnejad, M.; Ebrahimnejad, S.; Safari, J. A bi-objective model of preventive maintenance planning in distributed systems considering vehicle routing problem. Comput. Ind. Eng. 2018, 120, 360–381. [Google Scholar] [CrossRef]
- Li, L.; Wang, Y.; Lin, K.Y. Preventive maintenance scheduling optimization based on opportunistic production-maintenance synchronization. J. Intell. Manuf. 2021, 32, 545–558. [Google Scholar] [CrossRef]
- van Staden, H.E.; Deprez, L.; Boute, R.N. A dynamic “predict, then optimize” preventive maintenance approach using operational intervention data. Eur. J. Oper. Res. 2022, 302, 1079–1096. [Google Scholar] [CrossRef]
- Wocker, M.M.; Ostermeier, F.F.; Wanninger, T.; Zwinkau, R.; Deuse, J. Flexible job shop scheduling with preventive maintenance consideration. J. Intell. Manuf. 2023. [Google Scholar] [CrossRef]
- Brenière, L.; Doyen, L.; Bérenguer, C. Optimization of preventive replacements dates and covariate inspections for repairable systems in varying environments. Eur. J. Oper. Res. 2023, 308, 1126–1141. [Google Scholar] [CrossRef]
- Urbani, M.; Brunelli, M.; Punkka, A. An approach for bi-objective maintenance scheduling on a networked system with limited resources. Eur. J. Oper. Res. 2023, 305, 101–113. [Google Scholar] [CrossRef]
- de Jonge, B.; Scarf, P.A. A review on maintenance optimization. Eur. J. Oper. Res. 2020, 285, 805–824. [Google Scholar] [CrossRef]
- Dursun, I.; Akçay, A.; van Houtum, G.J. Age-based maintenance under population heterogeneity: Optimal exploration and exploitation. Eur. J. Oper. Res. 2022, 301, 1007–1020. [Google Scholar] [CrossRef]
- Gong, Q.; Yang, L.; Li, Y.; Xue, B. Dynamic Preventive Maintenance Optimization of Subway Vehicle Traction System Considering Stages. Appl. Sci. 2022, 12, 8617. [Google Scholar] [CrossRef]
- Hanbali, A.A.; Saleh, H.; Ullah, N. Two-threshold control limit policy in condition-based maintenance. Qual. Reliab. Eng. Int. 2022, 38, 2170–2187. [Google Scholar] [CrossRef]
- Sedghi, M.; Bergquist, B.; Vanhatalo, E.; Migdalas, A. Data-driven maintenance planning and scheduling based on predicted railway track condition. Qual. Reliab. Eng. Int. 2022, 38, 3689–3709. [Google Scholar] [CrossRef]
- Mokhtar, E.H.A.; Laggoune, R.; Chateauneuf, A. Imperfect Preventive Maintenance Policy for Complex Systems Based on Bayesian Networks. Qual. Reliab. Eng. Int. 2017, 33, 751–765. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, H.; Zheng, B.; Li, Z.; Gao, H. Optimal maintenance period and maintenance sequence planning under imperfect maintenance. Qual. Reliab. Eng. Int. 2023, 39, 1548–1558. [Google Scholar] [CrossRef]
- Qiu, Q.; Cui, L.; Dong, Q. Preventive maintenance policy of single-unit systems based on shot-noise process. Qual. Reliab. Eng. Int. 2019, 35, 550–560. [Google Scholar] [CrossRef]
- Huang, Y.; Fang, C.; Wijaya, S. Condition-based preventive maintenance with a yield rate threshold for deteriorating repairable systems. Qual. Reliab. Eng. Int. 2022, 38, 4122–4140. [Google Scholar] [CrossRef]
- Truong-Ba, H.; Borghesani, P.; Cholette, M.E.; Ma, L. Optimization of condition-based maintenance considering partial opportunities. Qual. Reliab. Eng. Int. 2020, 36, 529–546. [Google Scholar] [CrossRef]
- Liu, X.; Lei, Y.; Li, N.; Si, X.; Li, X. RUL prediction of machinery using convolutional-vector fusion network through multi-feature dynamic weighting. Mech. Syst. Signal Process. 2023, 185, 109788. [Google Scholar] [CrossRef]
- NASA. Prognostics Health Management 8 (PHM08) Challenge. 2011. Available online: https://www.nasa.gov/intelligent-systems-division/discovery-and-systems-health/pcoe/pcoe-data-set-repository/ (accessed on 10 June 2024).
- Nunes, P.; Rocha, E.; Santos, J.; Antunes, R. Predictive maintenance on injection molds by generalized fault trees and anomaly detection. Procedia Comput. Sci. 2023, 217, 1038–1047. [Google Scholar] [CrossRef]
- Rocha, E.M.; Nunes, P.; Santos, J. Reliability Analysis of Sensorized Stamping Presses by Generalized Fault Trees. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Istanbul, Turkey, 7–10 March 2022. [Google Scholar]
- Roux, O.; Duvivier, D.; Quesnel, G.; Ramat, E. Optimization of preventive maintenance through a combined maintenance-production simulation model. Int. J. Prod. Econ. 2013, 143, 3–12. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).