CROWDMATCH: Optimizing Crowdsourcing Matching through the Integration of Matching Theory and Coalition Games

Abstract

This paper tackles the challenges inherent in crowdsourcing dynamics by introducing the CROWDMATCH mechanism. Aimed at enabling crowdworkers to strategically select suitable crowdsourcers while contributing information to crowdsourcing tasks, CROWDMATCH considers incentives, information availability and cost, and the decisions of fellow crowdworkers to model the utility functions for both the crowdworkers and the crowdsourcers. Specifically, the paper presents an initial Approximate CROWDMATCH mechanism grounded in matching theory principles, eliminating externalities from crowdworkers’ decisions and enabling each entity to maximize its utility. Subsequently, the Accurate CROWDMATCH mechanism is introduced, which is initiated by the outcome of the Approximate CROWDMATCH mechanism, and coalition game-theoretic principles are employed to refine the matching process by accounting for externalities. The paper’s contributions include the introduction of the CROWDMATCH system model, the development of both Approximate and Accurate CROWDMATCH mechanisms, and a demonstration of their superior performance through comprehensive simulation results. The mechanisms’ scalability in large-scale crowdsourcing systems and operational advantages are highlighted, distinguishing them from existing methods and highlighting their efficacy in empowering crowdworkers in crowdsourcer selection.

1. Introduction

The evolution in communication and computational technologies has facilitated the seamless aggregation of knowledge and efforts from a diverse population, giving rise to a novel online problem-solving paradigm known as crowdsourcing [1]. This entails the broad act of outsourcing tasks, traditionally handled by employees or contractors, to a vast internet population, often referred to as the wise crowd, through an open call [2]. Crowdsourcing finds extensive applications in various domains such as fundraising and urban sensing. Typically, a crowdsourcing platform receives microtasks that are uploaded by crowdsourcers and engages and organizes crowdworkers to perform these tasks iteratively or in parallel [3]. Essentially, human participants autonomously select tasks and contribute without direct interaction or collaboration with one another [4]. While conventional crowdsourcing platforms like Amazon’s Mechanical Turk primarily handle straightforward tasks, newer platforms like Upwork are tailored for more intricate assignments [5]. Consequently, the focus on crowdsourcing complex tasks has garnered substantial interest [6].

1.1. Related Work

1.1.1. Task Allocation

The challenge of task allocation between crowdsourcers and crowdworkers, or, conversely, the autonomous selection of a declared task by crowdworkers from crowdsourcers, has garnered attention from both academia and industry [7]. A set of novel algorithms for influence-aware task assignment in Spatial Crowdsourcing are introduced in [8], utilizing workers’ historical patterns, a historical acceptance approach, and a propagation optimization algorithm to maximize both task assignments and worker–task influence in the era of widespread smartphone use. A methodology for optimizing resource allocation in crowd-based cooperative computing is discussed in [9], focusing on evolutionary heuristics to balance matching rate and collaborative quality, supported by suitable metrics and multicriteria decision-making, demonstrating effectiveness through experiments on various scales of crowd-based cooperative task allocation problems. Focusing on the challenge of online task assignment with specific time windows for data collection, the authors in [10] formulated a profit maximization problem for the crowdsourcing system, proposing two heuristic algorithms whose effectivenesses were validated through simulation results. A mobile crowdsourcing mechanism for urban-scale monitoring is proposed in [11], addressing the cost-fair task allocation problem to balance sensing costs among mobile users, offering offline and online algorithms for efficient and fair task distribution. The concept of opportunistic mobile crowdsourcing is analyzed in [12] by addressing challenges related to uncertain worker trajectories, incorporating worker and task requester preferences and capacity constraints, and proposing novel task assignment algorithms that are proven to be optimal in terms of preference awareness. A game-theoretic approach for task allocation in crowdsourcing is presented in [13], addressing the challenge of optimizing crowdsourcing task assignment by incorporating trust evaluation, virtual currency incentives, and a bargaining game model.

1.1.2. Incentive Mechanisms

However, except for the problem of task allocation in crowdsourcing environments, motivating user participation is a critical challenge due to the inadequacy of satisfactory participants, leading researchers to actively explore incentive mechanisms to encourage diverse participant engagement in crowdsourcing [14]. A two-tiered social crowdsourcing architecture to address insufficient participation in budget-constrained online crowdsourcing is studied in [15], where three system models and corresponding incentive mechanisms are analyzed, demonstrating through analysis and simulations their effectiveness in achieving computational efficiency, individual rationality, and budget feasibility. An incentive mechanism for crowdsourcing is introduced in [16], tackling the challenge of unknown worker qualities by using a multi-armed bandit and three-stage Stackelberg game. Similarly, a multi-leader, multi-follower Stackelberg game for socially aware crowdsourcing is proposed in [17,18], addressing incentive design issues by integrating social influence and strategic interactions among service providers and users. The authors in [19] proposed innovative task diffusion models for large-scale crowdsourcing via social networks, introducing sealed reverse auction incentive mechanisms that achieve computational efficiency, truthfulness, and guaranteed approximation, with superior outcomes in social cost, overpayment ratio, and task completion rates. A crowdsourcing framework for user recruitment in Online Social Networks, employing a labor economics approach and formulating the competitive process as a Generalized Colonel Blotto game to determine optimal rewards, is proposed in [20]. Also, the authors in [21] applied psychological game theory to show that crowdsourcers can reduce costs in crowdsourcing by incorporating psychological payoffs, proving optimal incentive plans, and presenting a unique psychological model for improved incentive mechanism design.

1.1.3. Privacy and Trustworthiness

Nevertheless, challenges emerge in the crowdsourcing process concerning the privacy of crowdworkers and the trustworthiness of the information they provide to the crowdsourcers [22]. A novel crowdsourcing network architecture addressing location privacy concerns during task allocation is proposed in [23] by implementing a privacy-preserving, decentralized dispute arbitration protocol to handle payment disputes without revealing users’ private information, showcasing resistance to forgery attacks and efficient performance. A game-theoretic model is introduced in [24] to analyze the dissemination of user personal information in online social networks, considering factors like intimacy and subject popularity [25]. The authors in [26] focused on user privacy and data trustworthiness and proposed game-theoretic solutions, specifically revisiting coalitional game formation and subgame perfect equilibrium-based concepts.

1.1.4. Crowdworker Recruitment

Efficient crowdworker recruitment plays a pivotal role in the success of crowdsourcing campaigns [27]. Traditionally, crowdsourcing applications employ a direct approach, where the platform directly chooses and enlists suitable individuals for task execution [28]. Matching theory and coalition games have been widely used to support the crowdworker matching to tasks or crowdsourcers [29]. The crowdsourcing last-mile delivery problem is addressed in [30] involving orders with diverse destinations and time windows, crowdsourced drivers with preplanned trips, and introduction a non-cooperative game framework. The proposed algorithms efficiently find stable matches, demonstrating effectiveness through computational experiments and extending applicability to stochastic settings with random release times of orders. The authors in [31] introduce the Acceptance-aware Worker Recruitment (AWR) as a novel game in socially aware crowdsourcing, employing a random diffusion model for task invitation propagation on social networks, formulating the AWR game as an NP-hard combinatorial optimization problem to maximize overall task acceptance within a specified incentive budget, and presenting a meta-heuristic-based evolutionary approach, demonstrating its effectiveness and efficiency through comprehensive experiments on real-world datasets. A distributed team formation-based batch crowdsourcing for complex tasks is analyzed in [32], presenting two approaches—forming a fixed team for all tasks or a dynamically adjusted basic team for each task—demonstrating improved cost efficiency, requester payments, communication, task success rates, and scalability compared to previous benchmarks on a real-world dataset. Two crowdworker recruitment strategies are discussed in [33], i.e., platform-based and leader-based, optimizing team formation through an integer linear program considering expertise, social ties, cost, and confidence.

1.2. Contributions

In spite of the advancements made in prior research on the allocation of tasks to crowdworkers, examination of their privacy, trustworthiness in contributing information to crowdsourcers, and the recruitment of crowdworkers, the issue of facilitating crowdworkers to make selections of crowdsourcers based on provided incentives remains largely unexplored. Additionally, addressing externalities in the decision-making process of selecting a crowdsourcer, influenced by the decisions of other crowdworkers, poses an even more formidable challenge.

This paper aims to address these challenges. Specifically, our research introduces a crowdsourcing matching mechanism, named CROWDMATCH, aimed at empowering crowdworkers to select a suitable crowdsourcer and contribute information to a crowdsourcing task, taking into account the provided incentives, the availability and cost of information, and decisions made by other crowdworkers. An Approximate CROWDMATCH mechanism is initially developed, drawing on matching theory principles, to eliminate externalities from the decisions of other crowdworkers, allowing each crowdworker to maximize its utility while selecting a crowdsourcer. Simultaneously, all crowdsourcers also maximize their benefits. Subsequently, the Accurate CROWDMATCH mechanism is introduced, based on coalition game-theoretic principles, refining the selection process by accounting for externalities stemming from other crowdworkers’ decisions and incentives provided by other crowdsourcers. The distinctive contributions of this research, setting it apart from the existing literature, are succinctly outlined below:

• The CROWDMATCH system model is introduced, comprising a set of crowdsourcers such as Amazon Mechanical Turk, Upwork, CrowdFlower, Google Maps, etc., and a set of crowdworkers. Operational characteristics, including the availability and cost of information, provided incentives, and the assessment of crowdworkers’ benefits and crowdsourcers’ incentive costs, are encapsulated in utility functions that reflect the advantages derived by both crowdworkers and crowdsourcers in the context of the crowdsourcing process;
• The Approximate CROWDMATCH mechanism is initially devised based on matching theory principles, taking into account the absence of externalities in the decision-making process of crowdworkers as they select the most suitable crowdsourcer to contribute information to a corresponding crowdsourcing task. This mechanism converges to a stable matching of crowdworkers to crowdsourcers, optimizing the utility for both entities, and serves as input for the Accurate CROWDMATCH mechanism;
• Addressing the system’s externalities, the Accurate CROWDMATCH mechanism is proposed, based on coalition game-theoretic principles, to ascertain an optimal matching between crowdworkers and crowdsourcers, maximizing their respective utilities. The existence of a Nash–Individually stable matching of crowdworkers is analytically demonstrated;
• Comprehensive simulation results demonstrate the operational advantages of the CROWDMATCH mechanism, its scalability in large-scale crowdsourcing systems, and its superior performance compared to existing methods that empower crowdworkers in the selection of crowdsourcers.

1.3. Outline

The subsequent sections of this paper are structured as follows: Section 2 introduces the CROWDMATCH system model. The mechanisms of Approximate and Accurate CROWDMATCH are presented in Section 3 and Section 4, respectively. Simulation results are presented in Section 6. Finally, Section 7 concludes the paper.

2. System Model

In this section, the CROWDMATCH system model is presented. We consider a set of crowdsourcers, such as Amazon Mechanical Turk, Upwork, CrowdFlower, Google Maps, etc., $\mathcal{M}=\{1,\dots ,m,\dots ,M\}$, and a set of crowdworkers, denoted as $\mathcal{N}=\{1,\dots ,n,\dots ,N\}$. Each crowdsourcer has a total budget $P_m$$\left[\frac{\$}{\mathit{bits}}\right]$ that is provided as a reward to the crowdworkers in order to incentivize the latter to submit their information to crowdsourcing tasks announced by the crowdsourcer. Each crowdworker is characterized by an amount of information $I_n$ [bits], which can be composed of text, videos, photos, etc., and a corresponding cost $P_n\left[\frac{\$}{\mathit{bits}}\right]$ to collect the information. The crowdworker’s utility is defined as follows:

$$U_n=\frac{{\widehat{a}}_n({\widehat{P}}_m-{\widehat{P}}_n){\widehat{I}}_n}{{\displaystyle \sum _{\forall n^{\prime }\in {\mathcal{N}}_m}}{\widehat{I}}_{n^{\prime }}}$$

(1)

where $a_n\in R^{+}\left[\frac{\mathit{bits}}{\$}\right]$ denotes the evaluation of the crowdworker’s profit from uploading $I_n$ amount of information to the crowdsourcer m, and ${\mathcal{N}}_m$ denotes the set of crowdworkers that selected crowdsourcer m. The values have been normalized for presentation purposes and without loss of generality, as follows: ${\widehat{a}}_n=\frac{a_n}{max{\left\{a_n\right\}}_{\forall n\in \mathcal{N}}}$, ${\widehat{I}}_n=\frac{I_n}{max{\left\{I_n\right\}}_{\forall n\in \mathcal{N}}}$, ${\widehat{P}}_n=\frac{P_n}{max{\left\{P_n\right\}}_{\forall n\in \mathcal{N}}}$, and ${\widehat{P}}_m=\frac{P_m}{max{\left\{P_m\right\}}_{\forall m\in \mathcal{M}}}$. Also, it is noted that the crowdworker’s utility depends on the amount of information that all the crowdworkers upload to the selected crowdsourcer; if the crowdsourcer receives a large amount of information from other crowdworkers, then it is less incentivized to provide competitive rewards to the crowdworkers.

Focusing on the crowdsourcers’ benefit from the crowdsourcing process, the corresponding crowdsourcer’s utility is formulated as follows:

$$U_m=\frac{{\displaystyle \sum _{\forall n\in N_m}}{U}_n-{\widehat{\gamma }}_m{({\widehat{P}}_m-{\widehat{C}}_m)}^2}{{\widehat{\delta }}_m{\displaystyle \sum _{\forall m^{\prime }\in M}}{\widehat{P}}_{m^{\prime }}}$$

(2)

where $C_m\left[\frac{\$}{\mathit{bits}}\right]$ denotes the cost incurred by the crowdsourcer for executing its fixed operations, ${\gamma }_m$$\left[\frac{{\mathit{bits}}^2}{{\$}^2}\right]$ signifies the assessment of profit, and ${\delta }_m$$\left[\frac{\$}{\mathit{bits}}\right]$ represents the evaluation of the market impact. Analogously, in consideration of the crowdworker’s utility, we normalize the values for presentation purposes and without loss of generality, as follows: ${\widehat{C}}_m=\frac{C_m}{max{\left\{C_m\right\}}_{\forall m\in \mathcal{M}}}$ and ${\widehat{\delta }}_m=\frac{{\delta }_m}{max{\left\{{\delta }_m\right\}}_{\forall m\in \mathcal{M}}}$. The primary objective for each crowdworker is to select a crowdsourcer to upload its information, with the aim of maximizing its utility. Similarly, each crowdsourcer aims to recruit a group of crowdworkers to perform the designated crowdsourcing task while maximizing its utility. It is noted that each crowdsourcer can accommodate a maximum number of $N_m^{max}$ crowdworkers based on its available budget $P_m$ to provide rewards.

3. Approximate CROWDMATCH Based on Matching Theory

The crowdworkers seek to employ a strategic approach in selecting a crowdsourcer for uploading information, with the objective of maximizing their utilities. Conversely, the crowdsourcers endeavor to identify an optimal group of crowdworkers to enhance their utilities in a distributed fashion. This situation presents a many-to-one matching problem, wherein multiple crowdworkers are paired with a single crowdsourcer, and can be studied based on the matching theory.

Definition 1. 

(Matching) A set of crowdworkers, denoted as $\mathcal{N}=\{1,\dots ,n,\dots ,N\}$ and a set of crowdsourcers, denoted as $\mathcal{M}=\{1,\cdots ,M\}$ are regarded as two non-intersecting sets. The matching function Λ represents a mapping of elements from $\mathcal{N}$ to elements from $\mathcal{M}$, subject to the following conditions:

• (${\mathit{C}}_1$): $\forall n\in \mathcal{N}$, $|\Lambda (n\left)\right|\le 1$;
• (${\mathit{C}}_2$): $\forall m\in \mathcal{M}$, $|\Lambda \left(m\right)|\le N_m^{max}$;
• (${\mathit{C}}_3$): $\Lambda \left(n\right)\in \mathcal{M}\iff \Lambda \left(m\right)\in \mathcal{N}$;
• (${\mathit{C}}_4$): $n\in \Lambda \left(m\right)\iff \Lambda \left(n\right)=m$.

The magnitude of a matching, expressed as $|\Lambda (·\left)\right|$, signifies the cardinality of the matching. $N_{\max }$ denotes the maximum count of crowdworkers that a crowdsourcer can accommodate, contingent upon its available rewards. In cases where $\Lambda \left(n\right)=\varnothing$, crowdworker n remains unmatched to any crowdsourcer. Similarly, if $\Lambda \left(m\right)=\varnothing$, crowdsourcer m is not chosen by any crowdworker.

For each crowdworker $n\in \mathcal{N}$, preference is given to the crowdsourcer that yields the highest utility, as defined in Equation (1). The utility of crowdworker n, as expressed in Equation (1), is intricately tied not only to its individual decision, but also to the decisions of other crowdworkers, captured by the term ${\displaystyle \sum _{n^{\prime }\in {\mathcal{N}}_m}}{\widehat{I}}_{n^{\prime }}$. This phenomenon is commonly referred to as externality in matching theory.

In the initial phase of our analysis, we consider the absence of externalities in the matching process. Consequently, the reformulation of the crowdworker’s approximate utility is articulated as follows:

$${\widehat{U}}_n={\widehat{a}}_n({\widehat{P}}_m-{\widehat{P}}_n){\widehat{I}}_n$$

(3)

and the crowdsourcer’s approximate utility after omitting the externalities stemming from the rewards offered by the other crowdsourcers is formulated as follows:

$${\widehat{U}}_m={\displaystyle \sum _{\forall n\in {\mathcal{N}}_m}}\widehat{U_n}-{\widehat{\gamma }}_m{({\widehat{P}}_m-{\widehat{C}}_m)}^2$$

(4)

Definition 2. 

(Preference Relation) A preference relation < is a binary relation between elements of the set $\mathcal{N}$ and elements of the set $\mathcal{M}$ that is complete, self-referential, and transitive. The preference relation ${<}_n$ is formally defined as follows: for any crowdworker $n\in \mathcal{N}$ and any crowdsourcer $m,m^{\prime }\in \mathcal{M}$, where $m\ne m^{\prime }$, the relation is given by

$$m{>}_n{m}^{\prime }\iff {\widehat{U}}_n\left(m\right)>{\widehat{U}}_n\left(m^{\prime }\right)$$

(5)

Similarly, the preference relation ${<}_m$ is defined as follows: for any crowdsourcer $m\in \mathcal{M}$ and any pair of crowdworkers $n,n^{\prime }\in \mathcal{N}$ where $n\ne n^{\prime }$, the relation is given by

$$n{>}_m{n}^{\prime }\iff {\widehat{U}}_m\left(n\right)>{\widehat{U}}_m\left(n^{\prime }\right)$$

(6)

With Definition 2, preference lists for crowdsourcers and crowdworkers are established. Subsequently, based on these preference lists, crowdsourcers and crowdworkers are matched with their preferred partners through the Approximate CROWDMATCH algorithm, outlined in Algorithm 1.

Algorithm 1 Approximate CROWDMATCH Algorithm

1: Input: ${\{I_n,a_n,P_n\}}_{\forall n\in \mathcal{N}}$, $\mathcal{N}$, $\mathcal{M}$, ${\{N_m^{max},{\gamma }_m,{\delta }_m,P_m\}}_{\forall m\in \mathcal{M}}$   2: Output: Matching Results $\Lambda$   3: Initialization:   4: Initialize the unmatched set as ${\mathcal{N}}^{*}\leftarrow \mathcal{N}$ and the alternative crowdsourcers of crowdworkers as ${\mathcal{M}}_n\leftarrow \{m\mid m\in \mathcal{M}\}$ for all $n\in \mathcal{N}$   5: while ${\mathcal{N}}^{*}\ne ⌀$ and $\exists n\in {\mathcal{N}}^{*}:{\mathcal{M}}_n\ne ⌀$ do   6:    for $n\in {\mathcal{N}}^{*}$ do   7:      Crowdworker n selects their preferred crowdsourcers and sends an invitation based on Equation (5).   8:    end for   9:    for $m\in \mathcal{M}$ do 10:      if $|\Lambda \left(m\right)|\le N_m^{max}\wedge$ (m received invitation) then 11:         Crowdsourcer m selects the favorite crowdworkers to pair from the ones who sent a pair invitation based on Equation (6). 12:         Delete m from the alternative crowdsourcers of the crowdworkers that sent an invitation but were not accepted. 13:      end if 14:    end for 15: end while

The Approximate CROWDMATCH algorithm is based on a set of fundamental principles. Initially, all the crowdworkers participate in the competition for crowdsourcing tasks independently, without being paired with specific crowdsourcers. This approach provides flexibility, allowing the crowdworkers to be matched with any available crowdsourcer offering incentives. Unmatched crowdworkers take the initiative by extending invitations to pair with their preferred crowdsourcers. When a crowdsourcer possesses available rewards to accommodate crowdworkers, it consistently selects preferred crowdworkers for pairing from those who extended invitations. In instances where a crowdworker’s invitation to a crowdsourcer is not accepted, it signals that the crowdsourcer should consider a more favored crowdworker to maximize its utility, leading to the rejection of the initial pairing. Consequently, the rejected crowdworkers from a crowdsourcer strategically refrain from extending further invitations to disinterested crowdsourcers, preventing the wastage of time. The convergence of the Approximate CROWDMATCH algorithm occurs when either all crowdsourcers have recruited the maximum number of crowdworkers based on the available rewards they offer or when all the crowdworkers have been successfully paired.

4. Accurate CROWDMATCH Based on Coalition Games

Given the presence of an externality, the outcome derived from the matching outlined in Section 3 using the Approximate CROWDMATCH algorithm ensures an approximate optimality. The outcome of the stable matching derived from the Approximate CROWDMATCH algorithm acts as an initial input to the Accurate CROWDMATCH algorithm. Specifically, a coalition game has been formulated, along with the corresponding Accurate CROWDMATCH algorithm, to enhance the matching outcome. This approach is devised to address the externalities and achieve an improved result by building upon the findings of the initial matching outcome.

Definition 3. 

(Coalition Game) The coalition game is formally characterized by the triple ($\mathcal{N},\mathcal{M},{\left\{U_m\right\}}_{\forall m\in \mathcal{M}}$), where $\mathcal{N}$ denotes the set of players (crowdworkers), $\mathcal{M}$ represents the set of coalitions (crowdsourcers), and $U_m$ signifies the utility function associated with each coalition (i.e., crowdsourcer), as defined in Equation (2).

Definition 4. 

(Switching Rules) The following switching rules must be followed in the coalition game:

Rule 1:  For a crowdworker n who has not selected a crowdsourcer, n will join a crowdsourcer m, if $\exists m=arg{max}_{m^{*}\in \mathcal{M}}\{U_{m^{*}}(m^{*}\cup \left\{n\right\})-U_{m^{*}}\left(m^{*}\right)|U_{m^{*}}(m^{*}\cup \left\{n\right\})-U_{m^{*}}\left(m^{*}\right)>0\}$. The new set of coalitions is $\mathcal{M}=\{\mathcal{M}\setminus \{m\left\}\right\}\cup \{m\cup \{n\left\}\right\}$;

Rule 2:  For $n\in m$, n will leave crowdsourcer m if $U_m(m\setminus \left\{n\right\})>U_m\left(m\right)$. The new set of coalitions is $\mathcal{M}=\{\mathcal{M}\setminus \{n\left\}\right\}\cup \{m\setminus \{n\left\}\right\}$;

Rule 3:  For $n\in {\mathcal{N}}_m$ and crowdsourcer $m^{\prime }$, n will leave the original crowdsourcer m (where $m\ne m^{\prime }$) and join another crowdsourcer $m^{\prime }$ if and only if $U_m(m\setminus \left\{n\right\})+U_{m^{\prime }}(m^{\prime }\cup \left\{n\right\})>U_m\left(m\right)+U_{m^{\prime }}\left(m^{\prime }\right)$. The new set of coalitions is $\mathcal{M}=\{\mathcal{M}\setminus \{m,m^{\prime }\}\}\cup \{m\setminus \left\{n\right\}\}\cup \{m^{\prime }\cup \left\{n\right\}\}$;

Rule 4:  For $n\in m$ and $n^{\prime }\in m^{\prime }$, where $n\ne n^{\prime }$, n and $n^{\prime }$ switch crowdsourcers if $U_m((m\setminus \left\{n\right\})\cup \left\{n^{\prime }\right\})+U_{m^{\prime }}((m^{\prime }\setminus \left\{n^{\prime }\right\})\cup \left\{n\right\})>U_m\left(m\right)+U_{m^{\prime }}\left(m^{\prime }\right)$. The new set of coalitions is $\mathcal{M}=\{\mathcal{M}\setminus \{m,m^{\prime }\}\}\cup \{(m\setminus \left\{n\right\})\cup \left\{n^{\prime }\right\}\}\cup \{(m^{\prime }\setminus \left\{n^{\prime }\right\})\cup \left\{n\right\}\}$.

In accordance with the switching rules articulated in Definition 4, we have formulated the Accurate CROWDMATCH Algorithm, presented in Algorithm 2. This algorithm is strategically devised to streamline the formation of robust coalitions between crowdworkers and crowdsourcers within the context of the crowdsourcing process. Its core aim is to systematically enhance the utility for the crowdworkers, optimizing their contributions to crowdsourcers and facilitating the efficient execution of the crowdsourcing tasks. Simultaneously, it endeavors to improve the utility for the crowdsourcers, thereby establishing a mutually beneficial framework that supports their collaborative involvement in the crowdsourcing process.

Theorem 1. 

(Nash–Individually Stable Matching) The concept of Nash–Individually stable matching, represented as ${\Lambda }^{*}$, pertains to the allocation of crowdworkers to crowdsourcers. This allocation is considered stable when no individual crowdworker can improve their utility by switching to a different crowdsourcer. The Accurate CROWDMATCH algorithm is specifically crafted to ensure the existence of at least one Nash–Individually stable partition, denoted as ${\Lambda }^{*}$.

Proof. 

Initially, let us consider that the matching configuration of crowdworkers, denoted as ${\Lambda }^{*}$ and determined by the Accurate CROWDMATCH algorithm, does not exhibit Nash–Individual stability. In this context, the following conditions must be satisfied: (i) $\exists n\notin {\mathcal{N}}_m,\forall m\in \mathcal{M},m=arg{max}_{m^{*}\in \mathcal{M}}\{U_{m^{*}}(m^{*}\cup \left\{n\right\})-U_{m^{*}}\left(m^{*}\right)|U_{m^{*}}(m^{*}\cup \left\{n\right\})-U_{m^{*}}\left(m^{*}\right)>0\}$; (ii) $\exists n\in {\mathcal{N}}_m$, satisfying $U_m(m\setminus \left\{n\right\})>U_m\left(m\right)$; (iii) $\exists n\in {\mathcal{N}}_m,\exists m^{\prime },m\ne m^{\prime }$, satisfying $U_m(m\setminus \left\{n\right\})+U_{m^{\prime }}(m^{\prime }\cup \left\{n\right\})>U_m\left(m\right)+U_{m^{\prime }}\left(m^{\prime }\right)$; and (iv) $\exists n\in {\mathcal{N}}_m$, $\exists n^{\prime }\in {\mathcal{N}}_{m^{\prime }}$, and $m\ne m^{\prime }$, satisfying $U_m((m\setminus \left\{n\right\})\cup \left\{n^{\prime }\right\})+U_{m^{\prime }}((m^{\prime }\setminus \left\{n^{\prime }\right\})\cup \left\{n\right\})>U_m\left(m\right)+U_{m^{\prime }}\left(m^{\prime }\right)$. However, in the Accurate CROWDMATCH algorithm, if any of the aforementioned conditions holds true, the crowdworkers will adhere to the corresponding switching rules described in Definition 4. Consequently, the matching of the crowdworkers cannot be considered final, as they will persistently modify their associations with crowdsourcers by following these switching rules. This discrepancy challenges our initial assumption, leading to the deduction that the Accurate CROWDMATCH algorithm converges to a Nash–Individually stable matching among the crowdworkers and the crowdsourcers.    □

Algorithm 2 Accurate CROWDMATCH Algorithm

1: Input: ${\Lambda }_{\mathrm{initial}}$ from Approximate CROWDMATCH Algorithm   2: Output: Optimal Matching ${\Lambda }^{*}$   3: repeat   4:    Randomly select a crowdworker n and its crowdsourcer m   5:    if n does not belong to any crowdsourcer then   6:      $m=arg{max}_{m^{*}\in \mathcal{M}}\{U_{m^{*}}(m^{*}\cup \left\{n\right\})-U_{m^{*}}\left(m^{*}\right)|U_{m^{*}}(m^{*}\cup \left\{n\right\})-U_{m^{*}}\left(m^{*}\right)>0\}$   7:      $\mathcal{M}=\{\mathcal{M}\setminus \{m\left\}\right\}\cup \{m\cup \{n\left\}\right\}$   8:    else   9:      Another crowdsourcer $m^{\prime }$, $m^{\prime }\ne m$ is randomly selected 10:      if $N_m\le N_m^{max}$ then 11:         if $U_m(m\setminus \left\{n\right\})+U_{m^{\prime }}(m^{\prime }\cup \left\{n\right\})>U_m\left(m\right)+U_{m^{\prime }}\left(m^{\prime }\right)$ then 12:           $\mathcal{M}=\{\mathcal{M}\setminus \{m,m^{\prime }\}\}\cup \{m\setminus \left\{n\right\}\}\cup \{m^{\prime }\cup \left\{n\right\}\}$ 13:         end if 14:      else 15:         Randomly select a crowdworker $n^{\prime }$ of crowdsourcer $m^{\prime }$ 16:         if $U_m((m\setminus \left\{n\right\})\cup \left\{n^{\prime }\right\})+U_{m^{\prime }}((m^{\prime }\setminus \left\{n^{\prime }\right\})\cup \left\{n\right\})>U_m\left(m\right)+U_{m^{\prime }}\left(m^{\prime }\right)$ then 17:           $\mathcal{M}=\{\mathcal{M}\setminus \{m,m^{\prime }\}\}\cup \{(m\setminus \left\{n\right\})\cup \left\{n^{\prime }\right\}\}\cup \{(m^{\prime }\setminus \left\{n^{\prime }\right\})\cup \left\{n\right\}\}$ 18:         end if 19:      end if 20:    end if 21:    Update m to the current crowdsourcer of n 22:    if $U_m(m\setminus \left\{n\right\})>U_m\left(m\right)$ then 23:      $\mathcal{M}=\{\mathcal{M}\setminus \{n\left\}\right\}\cup \{m\setminus \{n\left\}\right\}$ 24:    end if 25: until no further updates of the crowdworkers

5. Complexity Analysis

The complexity of the Approximate CROWDMATCH Algorithm is $O(N·M+M)$. Specifically, the complexity of the Approximate CROWDMATCH Algorithm’s component where the crowdworkers select their preferred crowdsourcers is $O(N·M)$ and the complexity of the algorithm’s part where the crowdsourcers select their preferred crowdworkers is $O\left(M\right)$. The complexity of the Accurate CROWDMATCH Algorithm is $O\left(ite\right)$, where $ite$ denotes the number of iterations that the Accurate CROWDMATCH Algorithm needs to converge to the optimal matching ${\Lambda }^{*}$.

Specifically, the Approximate CROWDMATCH algorithm follows the matching theory and the Accurate CROWDMATCH algorithm follows the theory of coalition games. Specifically, focusing on the Approximate CROWDMATCH algorithm, given the calculation of the approximate utilities for the crowdworkers and the crowdsourcers, each crowdworker creates a sorted list of their preferred crowdsourcers based on their calculated approximate utility Equation (5). Initially, all the crowdworkers belong to the unmatched set ${\mathcal{N}}^{*}$, and they send their invitations to the crowdsourcers. Then, the crowdsourcers, considering that they still have capacity in terms of accommodating recruited crowdworkers (line 10 in the Approximate CROWDMATCH algorithm), select their most preferred crowdworkers by calculating their utility function and following the preference relation defined in Equation (6). Then, the crowdworkers that were not selected by a crowdsourcer delete that crowdsourcer from their alternative crowdsourcer list to avoid resending another matching invitation to a crowdsourcer that has already rejected them. This process is continued iteratively until all crowdworkers are matched to the crowdsourcers or until the crowdsourcers have reached their capacity in terms of crowdworkers that they can accommodate. In order for the Approximate CROWDMATCH algorithm to be implemented, the crowdworkers need to know the provided rewards $P_m$ by the crowdsourcers and the crowdsourcers require the information of the value of the utility of the crowdworkers that have sent a pair invitation to them. In a realistic implementation, this information can be exchanged in one packet transmitted in both directions that includes a very small amount of information, i.e., a single value. Focusing on the Accurate CROWDMATCH algorithm, the analysis is very similar in terms of the complexity and signaling that is needed, as the crowdworkers calculate their utility based on the announced rewards announced by the crowdsourcers, and then they follow the switching rules described in Definition 4 to converge to a stable matching. Based on the provided numerical results in Section 6, it is shown that, even for a large-scale setup, i.e., thousands of crowdworkers and tens of crowdsourcers, the Approximate and Accurate CROWDMATCH algorithms converge to a stable matching in a few seconds.

6. Numerical Evaluation

In this section, an exhaustive evaluative assessment is carried out for the proposed mechanisms, namely, Approximate and Accurate CROWDMATCH. The objective is to demonstrate their operational benefits and superior performance compared to contemporary methods. The primary focus is on presenting the self-managed matching between the crowdworkers and the crowdsourcers within the context of the crowdsourcing process. Section 6.1 provides a thorough exploration of the operational characteristics and effectiveness of the proposed framework for both the crowdworkers and the crowdsourcers. Moving on to Section 6.2, a scalability analysis is executed, progressively increasing the number of crowdworkers and crowdsourcers. This is undertaken to demonstrate the efficiency and resilience of the CROWDMATCH mechanism. Additionally, Section 6.3 conducts an all-encompassing comparative assessment of the CROWDMATCH mechanism in relation to other prevailing matching mechanisms found in the current literature. This comparative analysis aims to highlight CROWDMATCH mechanism’s superiority in concurrently meeting the requirements of both crowdworkers and crowdsourcers.

In the rest of the simulation results, we consider the following parameters: $N=15$, $I_n\in [1,8]$ Mbits, $P_n\in [5.0,9.5]·{10}^{-4}$ [$\frac{\$}{bits}$], $a_n\in [0.1,0.8]$ [$\frac{bits}{\$}$], $M=3$, $P_m=[3,3.5,4.5]·{10}^{-3}$ [$\frac{bits}{\$}$], ${\gamma }_m=[5,6,7]\left[\frac{bit{s}^2}{{\$}^2}\right]$, ${\delta }_m=[5,6,7]·{10}^{-2}$ [$\frac{\$}{bits}$], $C_m=[5,1,1.5]·{10}^{-4}$ [$\frac{\$}{bits}$], and $N^{max}=[5,6,7]$, unless otherwise explicitly stated. The values of the parameters are adopted from real crowdsourcers, such as Amazon Mechanical Turk [34]. The evaluation was performed on an HP Envy Desktop with Intel i7 8700 K 3.2 GHz processor, 24 GB available RAM.

6.1. Pure Operation Performance

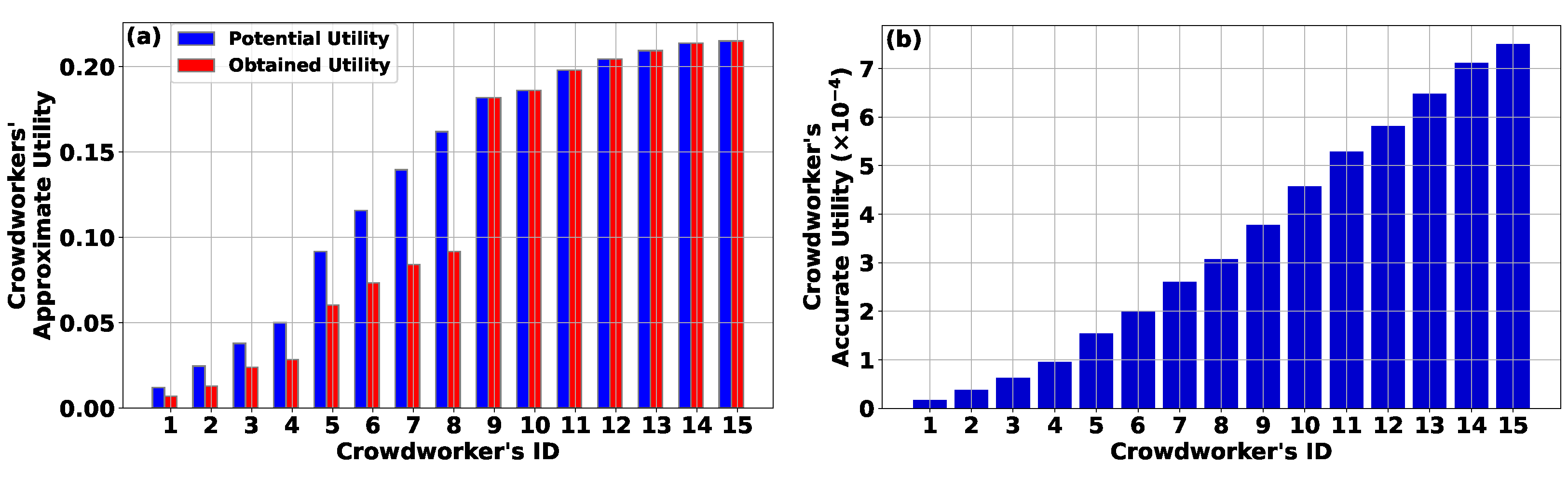
In this section, we present a comprehensive analysis of the performance and functionality of the Approximate and Accurate CROWDMATCH algorithms. Specifically, Figure 1a,b depicts the approximate and accurate utility of crowdworkers, respectively, with respect to their assigned IDs. The results highlight a direct correlation between higher crowdworker IDs, indicative of increased information availability for upload to crowdsourcers, and elevated levels of both approximate (Figure 1a) and accurate utility (Figure 1b) following the convergence of the Approximate and Accurate CROWDMATCH algorithms. Furthermore, the results reveal that the achieved accurate utility of the crowdworkers is lower compared to the corresponding approximate utility given the consideration of the externalities imposed in the crowdsourcing process, stemming from the other crowdworkers’ decisions and the crowdsourcer rewards’ availability.

Moreover, our findings reveal that the Approximate CROWDMATCH algorithm empowers crowdworkers to judiciously select the most suitable crowdsourcer, thereby maximizing their utility. This selection process takes into account the maximum capacity ($N_M^{max}$) of each crowdsourcer to accommodate crowdworkers based on the availability of rewards. Figure 1a specifically illustrates the potential approximate utility that the crowdworkers could receive when paired with their preferred crowdsourcer. However, the Approximate CROWDMATCH algorithm ensures a balanced approach by prioritizing crowdworkers characterized by higher information availability, allowing them to be selected first by crowdsourcers to facilitate the crowdsourcing process.

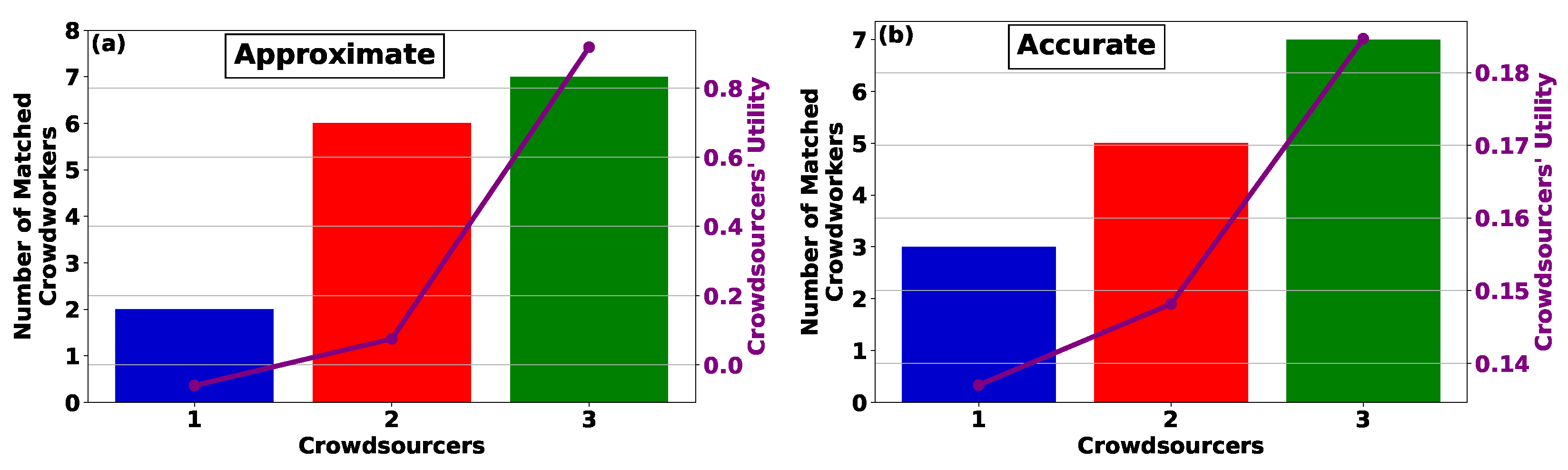
Figure 2a,b presents the number of matched crowdworkers and the crowdsourcers’ utility as a function of the crowdsourcers’ ID under the Approximate and Accurate CROWDMATCH algorithms, respectively. The findings indicate that an increase in crowdsourcers’ IDs, signifying greater reward availability, leads to the recruitment of a larger pool of crowdworkers for participation in the crowdsourcing process. This, in turn, results in higher utility, as evidenced in both the Approximate (Figure 2a) and Accurate (Figure 2b) CROWDMATCH algorithms. Furthermore, crowdsourcers with higher IDs, denoting enhanced rewards availability, demonstrate a heightened capacity for accommodating and recruiting crowdworkers. This capacity is initially exhausted, allowing lower-budget crowdsourcers to subsequently engage crowdworkers under the Approximate CROWDMATCH algorithm. On the other hand, the Accurate CROWDMATCH algorithm mitigates the disparity between higher- and lower-budget crowdsourcers, facilitating even the latter to secure a higher share of recruited crowdworkers.

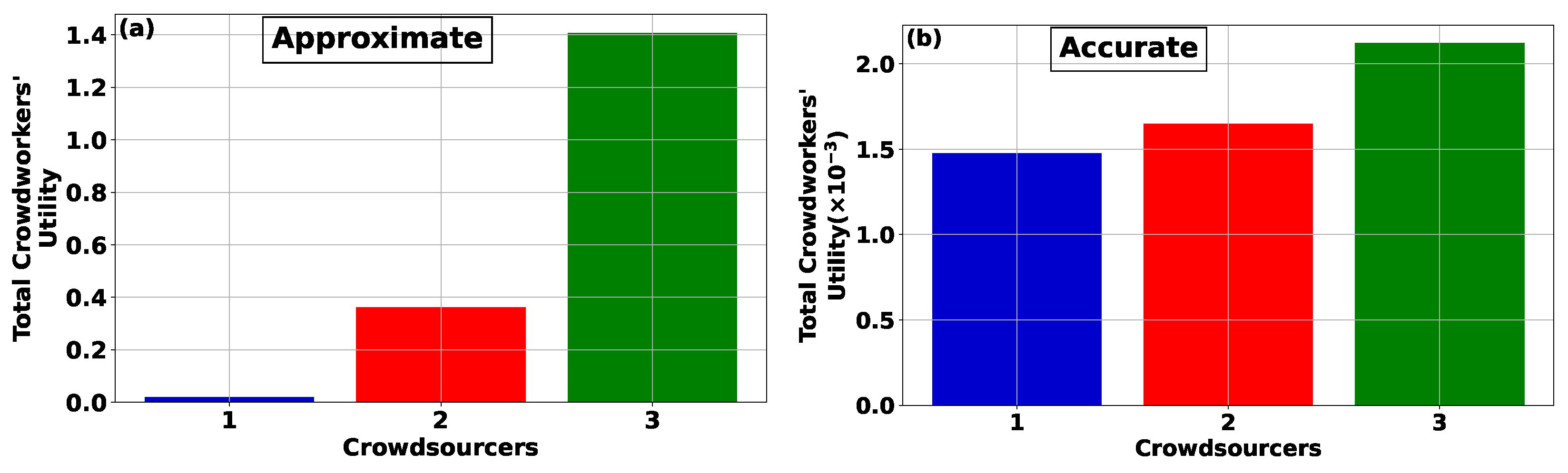
Focusing on the utility realized by crowdworkers when paired with crowdsourcers using the Approximate (Figure 3a) and Accurate (Figure 3b) CROWDMATCH algorithms, the results reveal that the utility experienced by the crowdworkers is contingent upon the selection of crowdsourcers. Specifically, within the framework of the Approximate CROWDMATCH algorithm, the crowdworkers possessing abundant information availability are matched with crowdsourcers offering the highest rewards in the crowdsourcing system. Conversely, the crowdworkers with low information availability are paired with crowdsourcers providing lower rewards. This imbalance leads to substantial variations in the overall utility achieved by the crowdworkers, associated with the crowdsourcers characterized by low versus high reward availability. This incongruity is alleviated by adhering to the Accurate CROWDMATCH algorithm, where crowdworkers with low information availability still have a favorable likelihood of being matched with crowdsourcers offering high rewards, thereby experiencing lower differences compared to the Approximate CROWDMATCH algorithm.

6.2. Scalability Analysis

In this section, an exhaustive scalability analysis is conducted, considering a progressive increase in the number of crowdworkers and crowdsourcers. A real online platform scenario is considered, consisting of crowdsourcers on the order of tens and crowdworkers on the order of thousands. The objective of this scalability analysis is twofold: first, to showcase the real-time viability of the CROWDMATCH mechanism, and, second, to elucidate the influence of an increasing number of crowdworkers and crowdsourcers on the utility experienced by the crowdworkers.

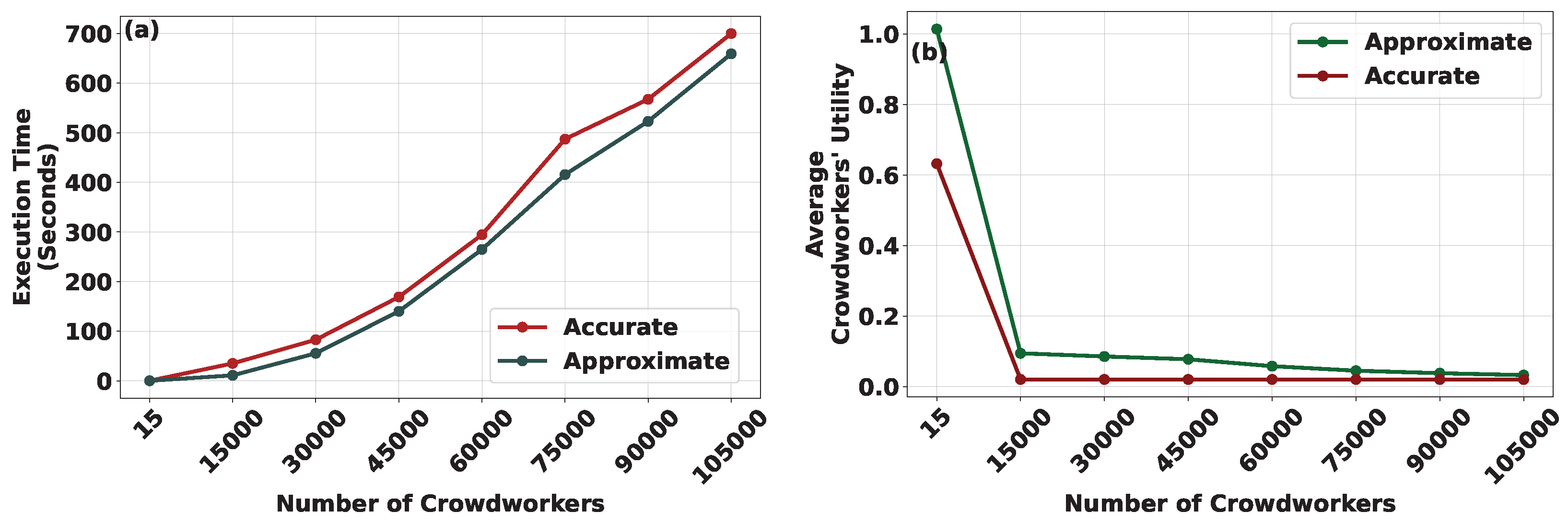
Figure 4a,b delineates the execution time and the average achieved utility of crowdworkers, respectively, in relation to the increasing number of crowdworkers involved in the crowdsourcing process. These analyses are conducted under both the Approximate and Accurate CROWDMATCH algorithms. For the sake of clarity in the presentation, we assume that a percentage increase in the number of crowdworkers results in an equivalent percentage decrease in the availability of their information. This approach ensures a consistent overall information pool within the system, irrespective of the number of engaged crowdworkers. The rationale behind this assumption lies in simplifying the presentation and modeling process. By assuming a proportional relationship between the increase in crowdworkers and the decrease in information availability, we aim to create a clear and comprehensible framework for our analysis. This assumption allows us to focus on the core aspects of our model without introducing unnecessary complexity.

Furthermore, considering that the uploaded information by crowdworkers to crowdsourcers remains constant, a percentage increase in the number of crowdworkers corresponds to an equivalent percentage increase in the number of crowdworkers that each crowdsourcer can accommodate, i.e., $N^{max}=[3,5,7]$. The results demonstrate that, with an escalating number of crowdworkers participating in the crowdsourcing process, the execution time of both the Approximate and Accurate CROWDMATCH algorithms follows a comparable upward trajectory, as depicted in Figure 4a.

Turning attention to the average utility achieved by crowdworkers, a discernible downward trend is observed under both the Approximate and Accurate CROWDMATCH algorithms. It should be highlighted that the decreasing trend becomes more pronounced under the Accurate CROWDMATCH algorithm, reflecting heightened competition among crowdworkers competing to be matched with the most rewarding crowdsourcer in terms of incentives.

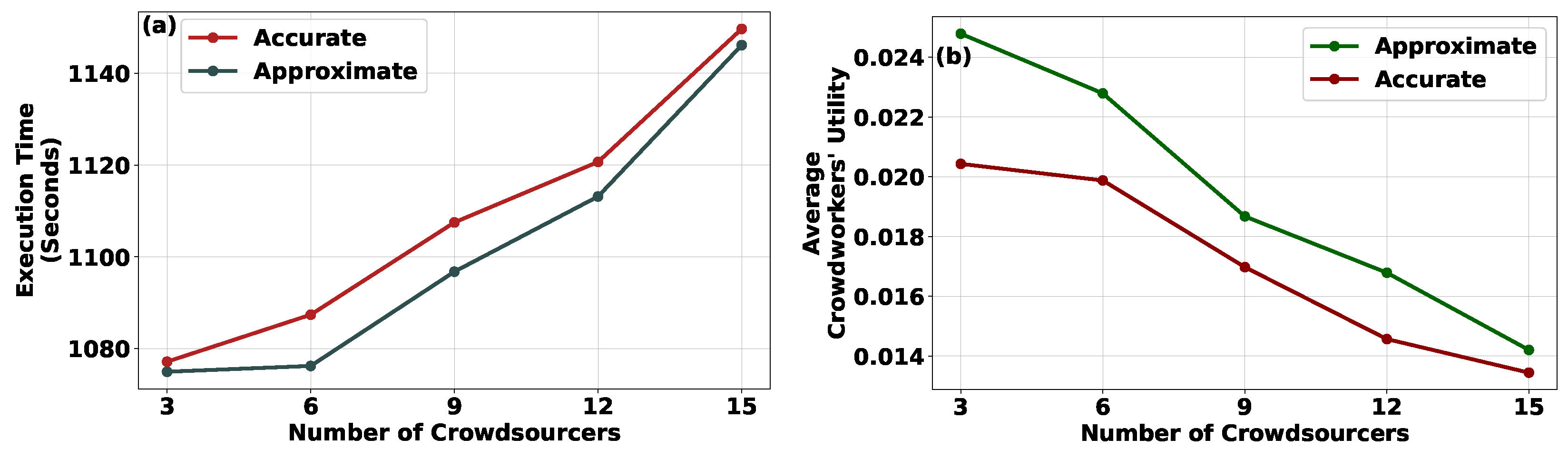
Focusing our scalability analysis on the scenario of increasing crowdsourcers, Figure 5a,b depicts the execution time and the average utility of the crowdworkers, respectively, in relation to the increasing number of participating crowdsourcers within the crowdsourcing process. The evaluation is conducted under the Approximate and Accurate CROWDMATCH algorithms. The results indicate that, with a growing number of crowdsourcers, the execution times of both the Approximate and Accurate CROWDMATCH algorithms exhibit a similar upward trend (Figure 5a). Nevertheless, the results affirm that, even with a substantial number of participating crowdsourcers, the execution time of the CROWDMATCH mechanism remains within the order of magnitude of sub-milliseconds. Furthermore, the outcomes reveal that an increasing number of crowdsourcers leads to a diminished average utility for crowdworkers. This is attributed to the constant overall number of rewards available in the system, which, when distributed among numerous crowdsourcers, results in smaller portions for individual crowdworkers.

6.3. Comparative Evaluation

In this section, a comprehensive comparative evaluation is conducted following the baseline scenario in terms of the number of crowdsourcers and crowdworkers for the proposed CROWDMATCH mechanism in comparison to three alternative models: (i) Highest Reward—wherein crowdworkers select crowdsourcers offering the highest rewards until their capacity is reached, subsequently moving to the next most rewarding crowdsourcer [35]; (ii) Random Matching—entailing a random allocation of crowdworkers to crowdsourcers; and (iii) Stochastic Learning Automata (SLA)—where the crowdworkers select a crowdsourcer following a reinforcement learning approach, based on the following probabilistic rules:

$$\begin{array}{c}\hfill P{r}_{\mathrm{n},\mathrm{m}}(ite+1)=P{r}_{\mathrm{n},\mathrm{m}}\left(ite\right)+b·{\widehat{r}}_n^{m\left(ite\right)}·(1-P{r}_{\mathrm{n},\mathrm{m}}\left(ite\right)),m^{(ite+1)}=m^{\left(ite\right)}\end{array}$$

(7a)

$$\begin{array}{c}\hfill P{r}_{\mathrm{n},\mathrm{m}}(ite+1)=P{r}_{\mathrm{n},\mathrm{m}}\left(ite\right)-b·{\widehat{r}}_n^{m\left(ite\right)}·P{r}_{\mathrm{n},\mathrm{m}}\left(ite\right),m^{(ite+1)}\ne m^{\left(ite\right)}\end{array}$$

(7b)

where ${\widehat{r}}_n^{m\left(ite\right)}=\frac{r_n^{m\left(ite\right)}}{max\left\{r_n^{m\left(ite\right)}\right\}}$ denotes the normalized reward, where

$$r_n^{m\left(ite\right)}=\left\{\begin{array}{cc}\frac{P_m}{N_m^{(ite-1)}{C}_m}\hfill & \mathrm{if}{N}_m^{(ite-1)}<N_m^{max}\hfill \\ 0\hfill & \mathrm{if}{N}_m^{(ite-1)}=N_m^{max}\hfill \end{array}\right.$$

(8)

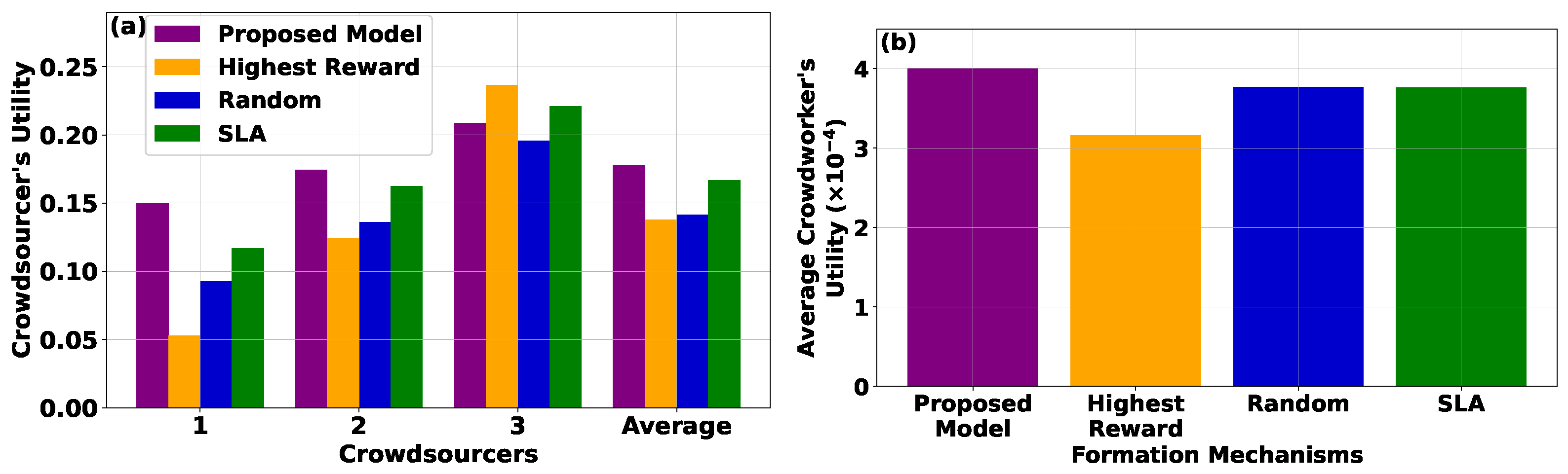
denotes the reward of crowdworker n after selecting crowdsourcer m, $b\in (0,1)$ (in this simulation, $b=0.8$) denotes the learning rate and $ite$ is the SLA algorithm’s iteration index [36,37]. Figure 6a,b depicts the utility of crowdsourcers based on their ID as well as their average utility and the average utility of crowdworkers across various matching mechanisms, respectively. The results indicate that, under the Highest Reward model, the crowdworkers tend to favor crowdsourcers with the highest rewards, resulting in diminished utility for crowdsourcers offering lower rewards. Moreover, the Random Matching model yields inferior results compared to the CROWDMATCH mechanism, attributable to its simplistic approach in matching crowdworkers with crowdsourcers. The SLA scenario achieves better results for the crowdsourcers compared to the Highest Reward and Random Matching models; however, it still performs worse than the CROWDMATCH mechanism.

When examining the utility achieved by crowdworkers, the CROWDMATCH mechanism outperforms the Highest Reward, Random Matching, and SLA models. This is derived from the observation that, under the Highest Reward model, the crowdworkers with greater information availability disproportionately select crowdsourcers that offer the highest rewards, thereby leaving other crowdworkers with suboptimal utility. Conversely, the Random Matching model achieves a mix of selections from crowdworkers with varying information availability, resulting in better outcomes compared to the Highest Reward model. In contrast, the proposed CROWDMATCH mechanism achieves superior average utility for crowdworkers, even compared to the SLA reinforcement learning-based model, as it strategically considers both crowdworkers’ and crowdsourcers’ characteristics. The CROWDMATCH approach enables a more effective and balanced allocation, enhancing the overall utility for both parties involved. Considering the complexity of the proposed models, the execution time of the CROWDMATCH mechanism was on the order of magnitude of 56 ms, while the execution time of the SLA model was double. The Highest Reward and Random Matching models had negligible execution time due to their non-iterative nature.

7. Conclusions

In conclusion, this paper introduces the CROWDMATCH mechanism as a novel solution to challenges in crowdsourcing. Specifically, our research presents an innovative approach that empowers crowdworkers to strategically select suitable crowdsourcers for information contribution, considering incentives (i.e., rewards), information availability, and information collection costs, while accounting for decisions made by other crowdworkers. The development of the Approximate CROWDMATCH mechanism, grounded in matching theory principles, eliminates externalities from crowdworkers’ decisions, allowing for individual utility maximization and simultaneous benefits for crowdsourcers. Building upon this, the Accurate CROWDMATCH mechanism incorporates coalition game-theoretic principles, refining the matching process to consider externalities, converging to an optimal and Nash–Individually stable matching. The unique contributions of this research include the introduction of the CROWDMATCH system model, the formulation of utility functions for the crowdworkers and crowdsourcers, and the proposal of two distributed matching mechanisms. Comprehensive simulation results demonstrate the operational advantages, scalability, and superior performance of the CROWDMATCH mechanism over different methods in empowering crowdworkers in crowdsourcer selection within large-scale crowdsourcing systems based on numerical evaluations.

Our current and future work includes the refinement and optimization of the CROWDMATCH mechanism to accommodate dynamic and evolving contexts, such as fluctuating incentive structures or varying information availability. Additionally, the integration of machine learning techniques could enhance the mechanism’s adaptability by learning from historical matching patterns and continuously improving its decision-making process. Exploring the application of CROWDMATCH across diverse domains and real-world platforms would provide valuable insights into its versatility and effectiveness in different contexts. Furthermore, investigating the implications of incorporating fairness and diversity considerations into the matching process could contribute to the development of more inclusive and equitable crowdsourcing systems.