Proximal Policy Optimization for Efficient D2D-Assisted Computation Offloading and Resource Allocation in Multi-Access Edge Computing

Abstract

In the advanced 5G and beyond networks, multi-access edge computing (MEC) is increasingly recognized as a promising technology, offering the dual advantages of reducing energy utilization in cloud data centers while catering to the demands for reliability and real-time responsiveness in end devices. However, the inherent complexity and variability of MEC networks pose significant challenges in computational offloading decisions. To tackle this problem, we propose a proximal policy optimization (PPO)-based Device-to-Device (D2D)-assisted computation offloading and resource allocation scheme. We construct a realistic MEC network environment and develop a Markov decision process (MDP) model that minimizes time loss and energy consumption. The integration of a D2D communication-based offloading framework allows for collaborative task offloading between end devices and MEC servers, enhancing both resource utilization and computational efficiency. The MDP model is solved using the PPO algorithm in deep reinforcement learning to derive an optimal policy for offloading and resource allocation. Extensive comparative analysis with three benchmarked approaches has confirmed our scheme’s superior performance in latency, energy consumption, and algorithmic convergence, demonstrating its potential to improve MEC network operations in the context of emerging 5G and beyond technologies.

1. Introduction

With the development of fifth-generation mobile networks (5G) and more advanced mobile communication networks, the number of mobile device users is expected to increase from 5.17 billion to 7.33 billion by the end of 2023, according to Statista [1]. In this rapidly evolving digital landscape, MEC servers, as a pivotal technology for enhancing the computational capabilities of mobile devices, offer users improved quality of service (QoS) and quality of experience (QoE). By decentralizing cloud computing, the MEC adeptly manages burgeoning data traffic, mitigates network congestion, and curtails latency, evolving to incorporate diverse technologies, including WiFi [2] and fixed access [3] (ETSI ISG [4]).

Amidst such advancements, MEC networks face the intricate challenge of efficient task management and coordination due to their compositional complexity and inherent variability. This complexity is further augmented in distributed layouts, which, unlike their centralized counterparts that optimize globally, offer escalated flexibility and scalability, essential for vast networks operating without central oversight.

Device-to-Device (D2D) communication has surfaced as a promising paradigm within MEC to bolster collaborative offloading efforts [5]. Studies [6,7] have exemplified enhancements in network capacity, energy efficiency, and latency reduction through D2D-facilitated offloading. In resource-constrained environments, Zhou et al. employed the game theory to devise a D2D-assisted offloading algorithm optimizing task computation time [8], while Xiao et al. tackled the content caching through an improved multi-objective bat algorithm [9]. Abbas et al. considered cooperative-aware task offloading to balance the number of completed tasks against energy and cost [10], and Li et al. proposed a security-conscious, energy-aware task offloading framework [11].

While the existing research has laid a robust groundwork for harnessing idle computational resources in MEC, optimizing the utilization of these resources remains a significant challenge. The integration of D2D technology introduces a spectrum of offloading modalities and platforms, enriching user services but also complicating offloading decisions with additional considerations like local computational capacities and the availability of proximate nodes.

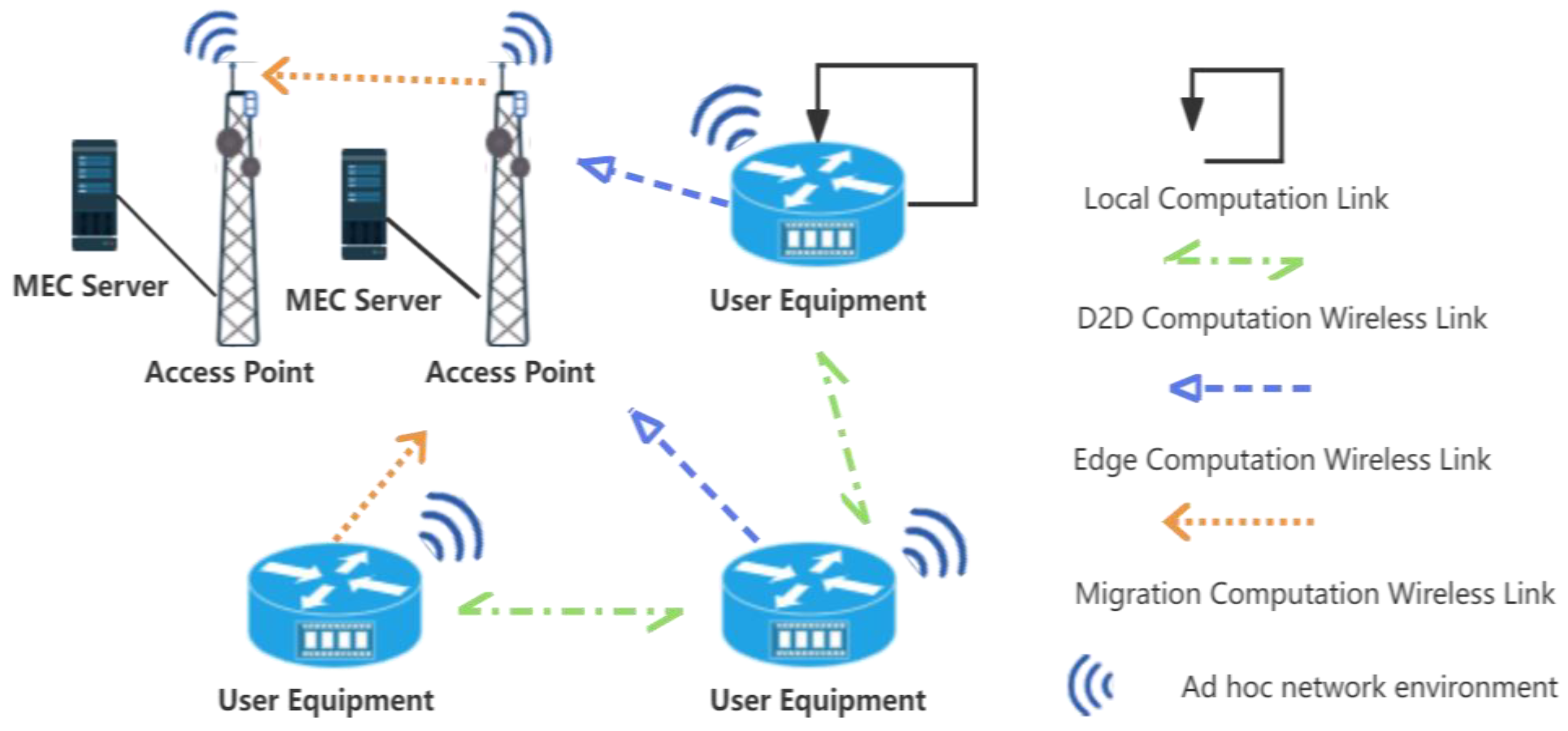
Addressing the dynamic, transient nature of D2D-integrated MEC networks, this paper proposes a PPO-based D2D-assisted computation offloading and resource allocation scheme. As shown in Figure 1, we consider a single unit in the MEC network, including two access points (APs) and multiple requesters and collaborators deployed at the edge of the network, where the user equipment (UE) can choose the appropriate computation method, such as local computation, edge computation, D2D computation, and migration computation, according to its own needs within the coverage of the APs. Our contribution is as follows:

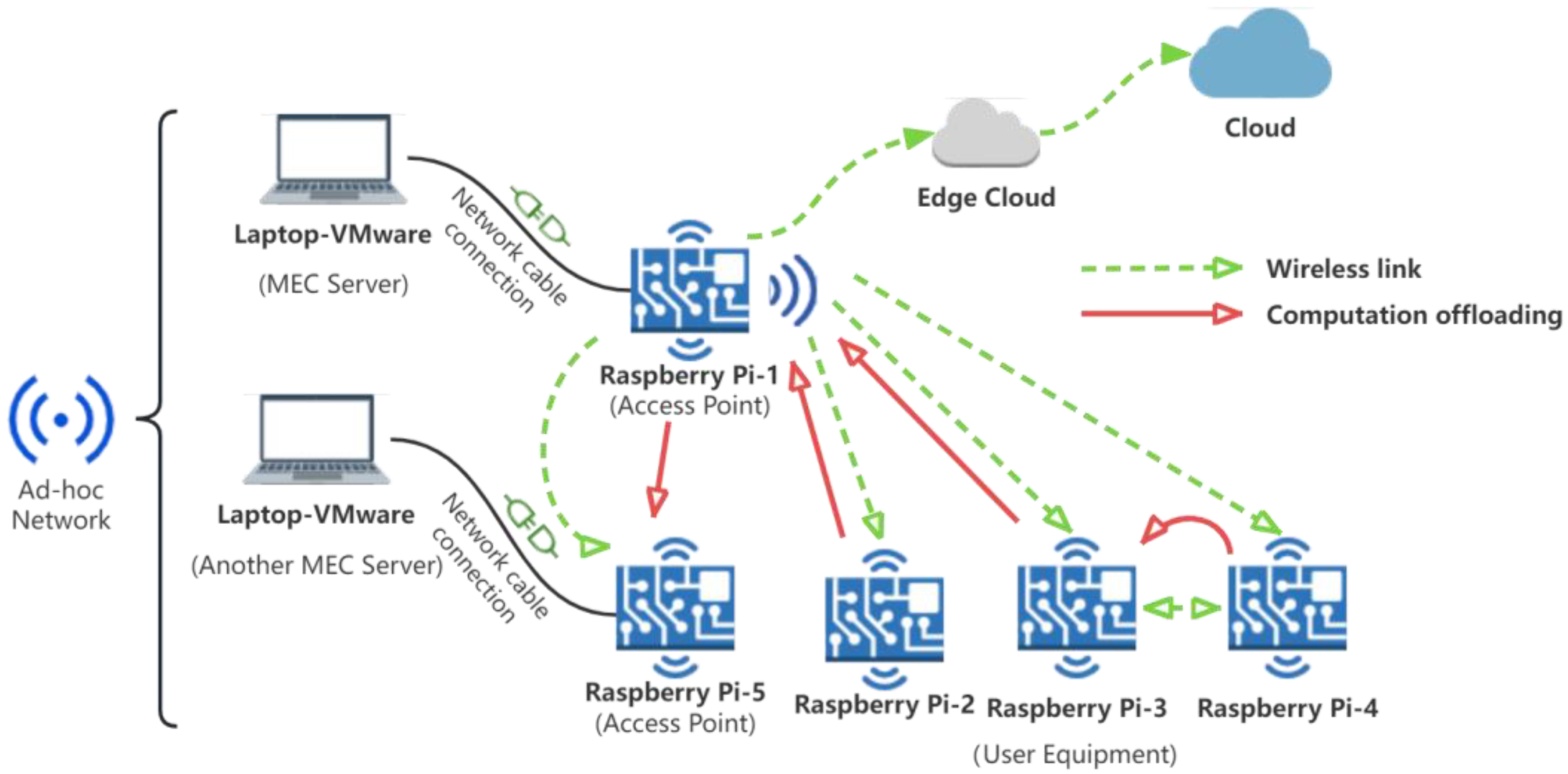
• We construct an authentic MEC network environment mirroring the actual MEC architecture, utilizing ad hoc wireless technology and computational devices, moving beyond mere simulation-based studies.
• Considering the MEC network’s complexity, dynamics, and randomness, we refine the neural network training features on the UE to include CPU utilization, transmission delay, task execution time, task count, and the aggregate of transmission and computation energy consumption.
• We introduce a PPO-based D2D-assisted computational offloading and resource allocation scheme to amplify terminal device resource utilization. By formulating a Markov decision process (MDP) model, we seek to minimize the time loss and energy consumption, deriving an optimal offloading strategy via PPO application.
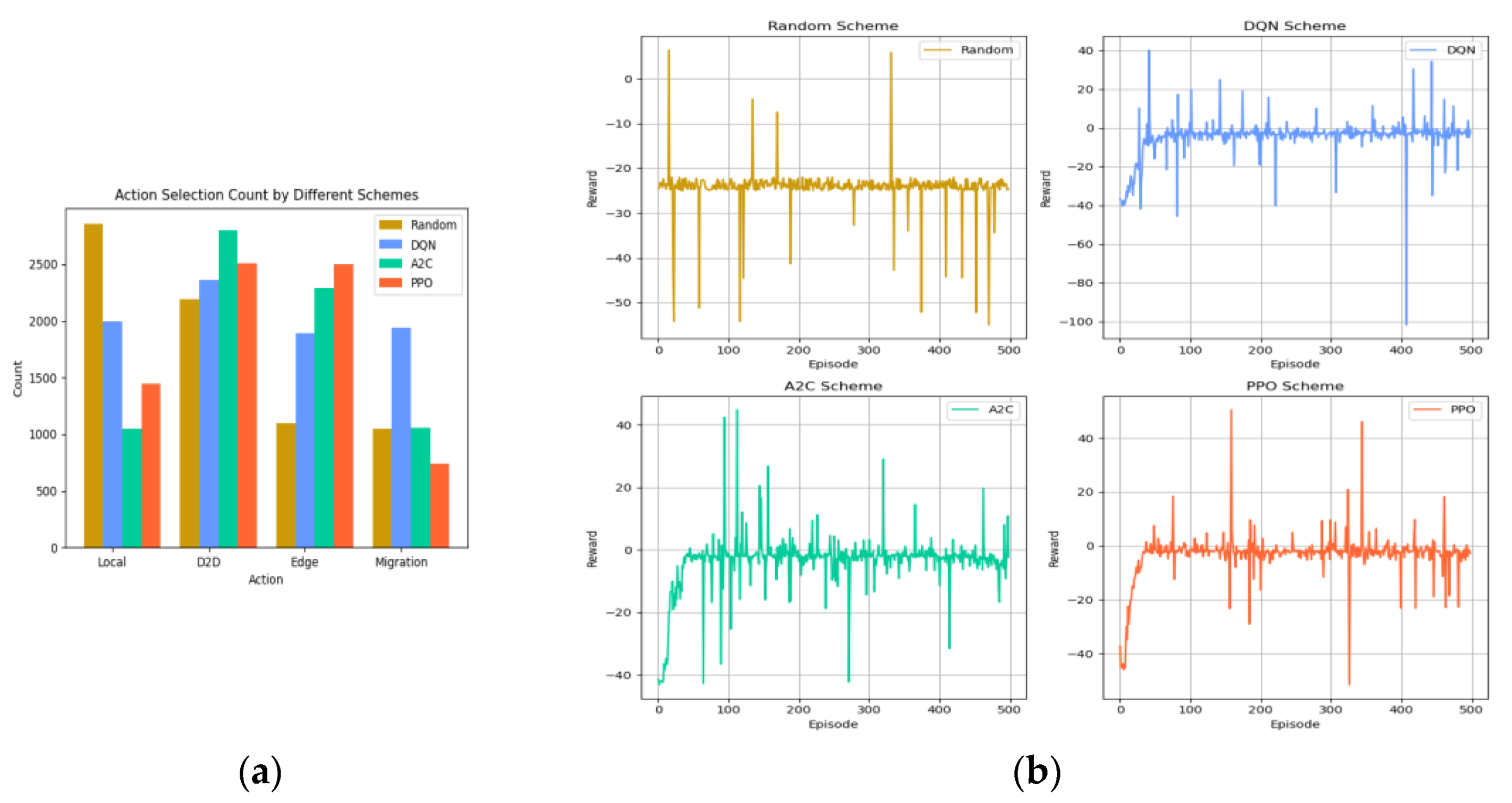
• The experimental results show that our scheme outperforms the other three baselines in terms of delay, energy consumption, and algorithm convergence.

The remaining sections are organized as follows. In Section 2, we review the related work. Section 3 defines the system model, including the communication and computation models, and formally defines the D2D auxiliary computation offloading and resource allocation problem. Section 4 describes the MDP model for this problem and the specific application of the PPO algorithm to this experiment. Section 5 describes the experimental environment and parameter settings and compares this scheme with three other baselines. Section 6 concludes the paper.

2. Related Work

In the multi-access edge computing (MEC) domain, computational offloading emerges as a multifaceted challenge, demanding innovative solutions [12,13,14], which are crucial for enhancing network efficiency. Research in this domain has predominantly concentrated on three approaches: mathematical optimization algorithms, control algorithms, and artificial intelligence (AI)-driven optimization algorithms. Among these, AI and machine learning (ML)-based algorithms have shown particular promise in dynamic and complex MEC environments due to their adaptability and learning capabilities [15].

The studies to date have focused on optimizing latency and energy consumption during computational offloading. Abbas et al. utilized meta-heuristic algorithms, such as ant colony, whale, and grey wolf optimization, to establish an offloading strategy aimed at minimizing energy and delay, albeit within the confines of a singular MEC server context [16]. While meta-heuristic algorithms are robust, their complexity and numerous parameters often complicate the tuning process. In the realm of control algorithms, Lin et al. proposed drone-assisted dynamic resource allocation leveraging Lyapunov optimization to ensure delay efficiency and reliability of offloading services [17]. Chang et al. contributed a balanced framework using SDN-based controller load balancing with Lyapunov optimization for improved offloading efficiency and reduced latency [18].

The precision of mathematical optimization for linear problems contrasts with its constrained adaptability to dynamic changes, whereas control algorithms excel in system stability and robustness but can be complex and less suitable for non-linear systems. Deep reinforcement learning (DRL), marrying deep learning with reinforcement learning, has emerged as a potent approach in MEC for managing dynamic tasks, with techniques like deep Q-network (DQN) and advantage actor–critic (A2C) algorithms gaining traction [19,20,21].

With the endeavor to overcome the limitations of mathematical optimization algorithms and control class algorithms, many researchers have used DRL methods for their self-learning and self-adaptation qualities in MEC resource allocation. In [19], the authors demonstrated the superiorities and applications of ML and deep learning (DL) methods in MEC environments for two key tasks: automatic identification and offloading of “untrusted tasks” and task scheduling on MEC servers, in particular using a flow-shop-like scheduling approach. Gao et al. developed an enhanced scheme based on the deep deterministic policy gradient (DDPG), which exhibited notable performance in reducing energy consumption, managing load status, and minimizing latency. However, this scheme did not adequately consider the involved behavioral characteristics of the devices [20]. To minimize the computing delay and energy consumption of UE, Liang et al. used DQN and DDPG to process large-scale state spaces and obtained the task offloading ratio and power allocation suitable for each UE. Silva et al. utilized A2C, empowered UEs to make intelligent offloading decisions, and demonstrated efficacy in simulated OpenAI Gym scenarios but did not fully capture the dynamism of mobile devices [21].

Although DRL demonstrates its superiority in resource management, the challenge of high user concurrency persists, often impacting QoS and QoE due to resource contention, and the challenge of high user concurrency persists, often impacting QoS and QoE due to resource contention [22]. D2D communication’s potential in offloading via high-speed, direct connections between devices has thus garnered academic focus. Li et al. addressed the energy consumption optimization problem for UE-assisted MEC computational offloading in mobile environments and proposed a DRL-based computational offloading model for D2D-MEC. Finally, they demonstrated that this scheme consumes the least amount of energy and cost in continuous time [23]. Lin et al. investigated a D2D collaborative computing offloading design for two users dynamically exchanging computational loads over a D2D link. The design achieved minimax optimization for a given finite time horizon [24]. Guan et al. studied the multi-user collaborative partial offloading and computational resource allocation problem, using a DQN algorithm to maximize the number of collaborative devices to maximize the computational resources under the maximum latency constraint of the application and limited computational resources [25]. Liu et al. investigated a computational offloading scheme in a multi-user UAV system, where a UAV with a computational task can offload part of the task to a nearby assistant to satisfy a latency constraint [26]. Fan et al. used the Lagrange multiplier method to solve the problem of computing resource allocation and adopted a greedy strategy to select D2D users, substantially reducing the average execution delay of the task [27]. They all increase the computing power by increasing the number of devices rather than fully utilizing the per-device computing resources.

D2D communication, a key component in enhancing MEC, has also received significant attention. Its ability to facilitate high-speed, short-range connections makes it a valuable asset in offloading tasks. However, research in this area has often focused on increasing the computational power through additional devices rather than optimizing per-device resource utilization. Our study contributes to this field by proposing a PPO-based D2D-assisted computation offloading and resource allocation scheme. This scheme not only addresses the dynamic nature of MEC networks but also optimizes resource utilization at a per-device level, filling a critical gap in the current research landscape.

3. System Model

In this study, we propose a D2D-assisted MEC server computation offloading and resource allocation scheme for multi-access edge computing scenarios. This model aims to minimize the total offloading cost, including task execution time and energy consumption. The proposed system model, as shown in Figure 2, is crucial to understanding how UE can optimize offloading decisions based on the device state, proximity to computational resources, and the nature of computational tasks. The system model consists of three parts: the network model, the communication model, and the computational model, which will be introduced in detail.

3.1. Network Model

The network model consists of multiple UEs and distributed MEC servers. In an ad hoc network [28,29] environment, each UE can generate computationally intensive tasks, while the MEC servers and available computing nodes nearby provide the necessary computational resources. $M$ represents the maximum workload of the MEC server and $C$ represents the maximum computational resources provided by the MEC server. Among the network entities, let $U=\{\mathrm{1,2},3,\dots ,i,\dots ,N\}$ as the set of all UEs in the network. All UEs can be represented as ${UE}_i=\{m_i,f_i,t_i,r_i,s_i\}$, where $m_i$ denotes the size of the user task. $f_i$ is the operating frequency of the CPU for processing computational tasks and $t_i$ represents the maximum tolerable time for the current UE transmission or computation. The variable $r_i$ represents the current computing state. When ${UE}_i$ executes a computation task, $r_i=1$; otherwise, $r_i=0$. The variables $s_i\in \{\mathrm{0,1},\mathrm{2,3}\}$ denote the system offloading decision set, representing different offloading strategies. The variables $S=\{s_i,i\in U\}$ represent the system offloading strategies, which represent different offloading decisions: $s_i=0$ for local computation, $s_i=1$ for offloading the task via D2D, $s_i=2$ for offloading the task via the current MEC, and $s_i=3$ for migrating the task to another MEC server, which is called migration calculation in this article.

3.2. Communication Model

The communication model defines the channels through which UEs and MEC servers interact. When an UE requires the edge server computation, the computation task for offloading must be transferred from the UE to the AP, and then the AP is assigned to the MEC server for computation. This process requires data transmission over the network, so the network bandwidth is one of the key factors affecting the overall system performance. To optimize the offloading process, we conceptualize a communication model that imposes a bandwidth limit between the UE and the AP. This measure is designed to ensure equitable bandwidth distribution among UEs, thereby mitigating potential network congestion. It simultaneously governs energy expenditure while striving to maintain an equilibrium between system performance and operational costs. The details are as follows: we take $B=\{\mathrm{1,2},... ,B\}$ as the set of communication links of the AP. $W_b$ is the bandwidth of the AP and we divide the available bandwidth resource of the AP into equal-width subchannels $W_{sub}$, then the bandwidth of each subchannel can be denoted as $W_{sub,b}={ W}_b/B.$ The matrix $M_b$ denotes the transmission state of the AP, $M_b=\left[\mathrm{0,1}\right],b\in B$, and $M_b=1$ indicates that the AP provides an offloading service on its communication link. $M_b=0$ indicates that no offloading service is being provided on its communication link. Thus, the bandwidth resource is denoted as:

$$\sum _{b\in B}{M}_b{W}_{sub,b}.$$

(1)

In the resource-constrained scenario, when the requester offloads the task to the MEC server, the task is first sent from the ${UE}_i$ to the AP via wireless transmission. We assume that the wireless channel state remains constant while each computational task is transmitted between the UE and the AP.$p_{i,b}$denotes the transmission power that requester i sends to the AP, $h_{i,b}$ denotes the channel gain during its transmission, ${\sigma }^2$ represents the power of the noise, $d_{i,b}$ denotes the distance between the requester${UE}_i$ and the AP, and $\theta$ is a standardized path loss propagation exponent so that the path loss can be denoted as $d_{i,b}^{-\theta }$; then, the signal-to-noise ratio (SNR) can be computed as:

$${SNR}_{i,b}=\frac{p_{i,b}{h}_{i,b}{d}_{i,b}^{-\theta }}{{\sigma }^2}.$$

(2)

After obtaining the SNR, the transmission rate from the requester to the AP can be calculated as

$$R_{i,b}=W_{sub,b}{log}_2\left(1+{SNR}_{i,b}\right).$$

(3)

In order to avoid the interference of UEs transmitting between D2D communication links, we assume that each D2D communication link can be obtained as an orthogonal subchannel; then, $W_{i,c}$ denotes the bandwidth of the subchannel. Similarly, we denote the signal-to-noise ratio of the D2D communication link, then the transmission rate of D2D communication between requester ${UE}_i$, and collaborator c is denoted as follows:

$$R_{i,c}=W_{i,c}{log}_2\left(1+{SNR}_{i,c}\right).$$

(4)

Since the executor that performs the task of the requester may be a MEC server or another UE (collaborator), based on the above expression, the transmission rate between the requester ${UE}_i$ and the executor may be expressed as $R_{i,b}$ or $R_{i,c}$.

3.3. Computational Model

We studied four computing models for devices to choose from under the MEC network environment: local computing, D2D peer devices computing, edge computing, and migration computing. The computation delay and energy consumption for each model are as follows.

3.3.1. Local Computing

If the computational requirements of the computing tasks are within the processing power of the UE, the device performs computing tasks locally. We assume that the CPU in ${UE}_i$ operates at a frequency of $f_i$, with $c_i$ representing the local computational power in terms of CPU cycles. Therefore, the local computation time can be calculated as follows:

$$t_i^{local}=\frac{c_i}{f_i}.$$

(5)

Parameter $k$ is based on the findings presented in reference [30]. Local energy consumption can be mathematically represented as

$$E_i^{local}=k{f}_i{(c}_i{)}^2.$$

(6)

Incorporating the influence of chip architecture [31], the effective switching capacitance κ is introduced in the equation. The total energy consumption is provided by the following expression ($\alpha ,\beta$ are loss factors):

$$C_i^{local}=\alpha t_i^{local}+\beta E_i^{local}.$$

(7)

3.3.2. Edge Computing

When the computing power of local devices is not enough to efficiently handle tasks or to handle tasks that require a fast response, edge computing can provide lower latency due to its proximity to the data source. The $m_i$ is the size of the task from the requester ${UE}_i$ and $R_{i,b}$ represents the rate at which ${UE}_i$ transmits tasks to the MEC server, transmission delay is

$$t_{i,b}^{tran}=\frac{m_i}{R_{i,b}}.$$

(8)

The time requirement of edge computing is

$$t_{i,b}^{edge}=\frac{c_i^{edge}}{f_i^{edge}}.$$

(9)

$p_{i,b}$ denotes the transmission power that requester ${UE}_i$ sends to the MEC server. The transmission energy loss is denoted as

$$E_{i,b}^{tran}=p_{i,b}{t}_{i,b}^{tran}.$$

(10)

Computation energy loss is denoted as

$$E_{i,b}^{edge}=p_{i,b}{t}_{i,b}^{edge}.$$

(11)

The total consumption, including the loss of time and energy, provides

$$C_i^{edge}=\alpha \left(t_{i,b}^{tran}+t_{i,b}^{edge}\right)+\beta \left(E_{i,b}^{tran}+E_{i,b}^{edge}\right).$$

(12)

3.3.3. Migrating the Computation

When the MEC server experiences an excessive workload or when neighboring servers have available resources, the ${UE}_i$ can migrate its computational tasks to the adjacent servers. This migration incurs additional transmission overhead for the ${UE}_i$, which involves transferring data between MEC servers. The magnitude of the transmission overhead is determined based on the allocated computational resources provided by the target server in response to the migration request from the ${UE}_i$. The $i,b^{\prime }$ in $t_{i,b^{\prime }}^{mig}$, $t_{i,b^{\prime }}^{{edge}^{\prime }},$ and $E_{i,b^{\prime }}^{mig}$ signifies the transmission from ${UE}_i$ to the AP where another MEC server is located; therefore, the transmission delay is

$$t_{i,b^{\prime }}^{mig}=\frac{m_i}{R_i^{mig}}+Z_i^{mig}.$$

(13)

Assuming that the migration cost only depends on the task size, which is denoted as $Z_i^{mig}=\delta m_i$, the transmission energy loss is

$$E_{i,b^{\prime }}^{mig}=p_{i,b^{\prime }}{t}_{i,b^{\prime }}^{mig}.$$

(14)

The computational delay and energy consumption of the ${UE}_i$ is computed based on the resource allocation strategy of the migration server, with the computational formula remaining unchanged. Consequently, the total cost of the migration computation is expressed as

$$C_i^{mig}=\alpha \left(t_{i,b^{\prime }}^{mig}+t_{i,b^{\prime }}^{{edge}^{\prime }}\right)+\beta E_{i,b^{\prime }}^{mig}.$$

(15)

3.3.4. D2D Device Computing

$m_i$ is the size of the task and $R_{i,c}$ represents the rate at which the requester, ${UE}_i$, transmits tasks to the collaborator; thus, the transmission delay is

$$t_{i,c}^{tran}=\frac{m_i}{R_{i,c}}.$$

(16)

$c_i^{collaborator}$ and $f_i^{collaborator}$ represent the number of CPU cycles required by the collaborator ${UE}_i$ to complete the computational task $m_i$ of the requester ${UE}_i$, and the current CPU working frequency, respectively. The time requirement of D2D computing is

$$t_{i,c}^{d2d}=\frac{c_i^{collaborator}}{f_i^{collaborator}}.$$

(17)

$p_{i,c}$ denotes the transmission power that requester ${UE}_i$ sends to the collaborator. The transmission energy loss is denoted as

$$E_{i,c}^{tran}=p_{i,c}{t}_{i,c}^{tran}.$$

(18)

Computation energy loss is denoted as

$$E_{i,c}^{d2d}=p_{i,c}{t}_{i,c}^{d2d}.$$

(19)

The total consumption provides

$$C_i^{d2d}=\alpha \left(t_{i,c}^{tran}+t_{i,c}^{d2d}\right)+\beta \left(E_{i,c}^{tran}+E_{i,c}^{d2d}\right).$$

(20)

3.4. Problem Formulation

To enhance the efficiency of computational task offloading, we constructed a mathematical model tailored to minimize the total execution cost within the MEC framework. This mathematical model integrates the inherent complexities of the network’s architecture, the communication resource in use, and the dynamics computation at play in MEC environments. Recognizing the finite nature of MEC server resources and the associated costs of server utilization, our model incorporates economic considerations. Specifically, due to MEC servers having limited resources, assuming that each strategy repeatedly selects an edge computing strategy will lead to a high cost. Therefore, we assigned very low rewards to successively select strategies for MEC as a main task processor; however, even if such a strategy emerges, it slowly disappears in the iterations.

We used the following equation to express the cost consumption of the four task offloading strategies of the UE:

$$C_i^{ue}=\left\{\begin{array}{c}{C}_i^{local}{s}_i\\ C_i^{d2d}{s}_i\\ C_i^{edge}{s}_i\\ C_i^{mig}{s}_i\end{array},\forall i\in U_i,s_i\in \left\{\mathrm{0,1},\mathrm{2,3}\right\}.\right.$$

(21)

Since the aim of this study was to minimize the total cost of delay and energy consumption of UEs, the bandwidth resources of AP should be satisfied:

$$\sum _{b\in B}{M}_b{W}_{sub,b}\le W_b,$$

(22)

where $W_b$ represents the bandwidth of AP. $C_{all}$ represents all UE devices, which can be calculated as

$$C_{all}=\sum _{n=1}^N{C}_i^{ue},\forall i\in U_i.$$

(23)

Under the constraints of maximum tolerable delay and energy consumption, the problem is expressed as

$$\begin{array}{l}Min{\mathrm{C}}_{\mathrm{all}}\\ C1:s_i\in 0,1,2,3,\forall i\in U{E}_i;\\ C2:t_i^{local}+t_{i,b}^{tran}+t_{i,b}^{edge}+t_{i,c}^{tran}+t_{i,c}^{d2d}+t_{i,b^{\prime }}^{mig}+t_{i,b^{\prime }}^{{edge}^{\prime }}<t_i,\forall i\in U_i;\\ C3:E_i^{local}+E_{i,b}^{tran}+E_{i,b}^{edge}+E_{i,c}^{tran}+E_{i,c}^{d2d}+E_{i,b^{\prime }}^{mig}+E_{i,b^{\prime }}^{{edge}^{\prime }}<E_i,\forall i\in U_i;\\ C4:{\displaystyle \sum {}_{n=1}^N{C}_i\le C_{all},\forall i\in U_i}.\end{array}$$

(24)

Based on satisfying the QoS and QoE required by users, the solution of this problem can be expressed as solving the minimum total offloading cost $C$ under the optimal offloading policy vector $S$.

4. Multi-Objective Deep Reinforcement Learning Based on the PPO Algorithm

In this section, we introduce the application of the proximal policy optimization (PPO) algorithm, a robust deep reinforcement learning approach, under the MEC environment. The PPO model was chosen for its notable benefits in multi-objective optimization, characterized by stability, adaptability, and efficient sample utilization, making it highly suitable for the dynamic and uncertain environments of MEC. The problem of computational offloading and resource allocation was first constructed as a Markov decision process (MDP) model, and the PPO algorithm was used to obtain the optimal solution.

4.1. Markov Decision Process

Our approach constructs the computational offloading and resource allocation problem as an MDP. The MDP is defined by a state space encompassing key metrics like transfer latency, computational delay, energy consumption, an action space for offloading strategies, and a reward function designed to minimize latency and energy consumption. This formulation is crucial for generating optimized offloading policies based on the current state of the network. In the context of computational offloading and resource allocation within the edge environments, we define the MDP as a quintuple, encompassing the state space ($S$), action space ($A$), state transition probability matrix ($P$), reward function ($R$), and the discount factor ($\gamma$). The crux of the MDP’s application in this scenario lies in its ability to generate a policy that dictates offloading decisions based on the current state.

• State: The state of the environment consists of several metrics for the local device, the MEC server, and the collaborator devices. Transfer latency used by the computational tasks, computational latency, transfer energy consumption, computational energy consumption, CPU utilization of the current device, and the number of computational tasks.
• Action: The action space consists of four offloading strategies: local computing, D2D computing, edge computing, and migration computing.
• Probability: The state probability transfer matrix can be expressed as

  $$P_{s{s}^{\prime }}^a=P\left[S_{t+1}=s^{\prime }|S_t=s,A_t=a\right].$$

  (25)
• Reward: The rewards are provided at each episode. Considering the goal of minimizing UE latency and energy consumption, the defined reward should be negatively correlated with this goal. It can be expressed as follows:

  $$R\left(s,a\right)=\sum _{n=i}^N\gamma \left(C_i^{local}-C_i^{d2d}-C_i^{edge}-C_i^{mig}\right),\forall i\in U_i.$$

  (26)
• $\gamma$: is the discount factor, $\gamma \in [0,1]$.

For the computational model of the system, the state can be composed of a number of metrics from the local device, the MEC server, collaborator devices, and the offloaded device. After executing each decision, the agent will receive an immediate reward to measure the goodness of the current decision [32]. The reward function is shown in Equation (26), and the value of the state is dependent on the current reward versus the possible future reward. The return of state is defined as follows:

$$G_t=R_{t+1}+{\gamma R}_{t+2}+{\gamma }^3{R}_{t+3}+\dots +{\gamma }^n{R}_{t+n}=\sum _{n=0}^{\mathrm{\infty }}{\gamma }^n{R}_{t+n+1}.$$

(27)

$\gamma$ is used to estimate the current value of future rewards, then the long-term payoff can be expressed as the expected value of $G_t$, defined as

$$V\left(s_t,\pi \right)=E_{\pi }\left[G_t\right]=E_{\pi }\left[R_{t+1}+\gamma V\left(s_{t+1},\pi \right)\right].$$

(28)

$V\left(s_t,\pi \right)$ denotes the value function of state $s$ under a given strategy $\pi$, $S_t$ denotes the next state, and $\pi$ denotes the strategy.

The problem is thus formulated as solving the optimal policy ${\pi }^{*}$ of the system model to maximize the long-term value of the model $V(s, \pi )$, expressed as follows:

$${\pi }^{\mathrm{*}}=\underset{\pi }{\underbrace{argmax}}V\left(\left(s_{t+1},\pi \right)\right).$$

(29)

4.2. PPO Algorithm Application

The application of the PPO algorithm is directed at optimizing the policy function using a neural network. This approach is particularly adapted to navigating the complexities of the non-convex optimization challenges characteristic of intricate MEC scenarios. PPO distinguishes itself by balancing the exploration of innovative strategies with the exploitation of established, efficacious actions facilitated by its distinct objective function and policy update methodology. This allows for effective handling of the non-convex optimization problem prevalent in complex MEC scenarios. The PPO algorithm, with its objective function and policy update mechanism, ensures a balance between the exploration of new strategies and the exploitation of known effective actions [33].

To evaluate the versatility of various reinforcement learning (RL) algorithms and to fine-tune hyperparameters for broader applicability, we decoupled the environmental module from the neural network. This separation enables the environmental module to focus exclusively on generating environmental feedback and computing rewards, a critical step in enhancing the scheme’s generality, as illustrated in Figure 3. The environmental module’s interfaces, namely reset and step, are integral to the RL process. The reset interface initializes or refreshes the environment to a baseline state, providing the initial observation post-training initiation or episode completion. In contrast, the step interface progresses the environment in response to the agent’s actions, delivering subsequent observations, instant rewards, termination flags, and additional context-specific data. This delineation of responsibilities ensures a coherent and systematic interaction between the PPO algorithms and the environment module, promoting an efficient learning cycle predicated on action-derived feedback.

Within the neural network module, the PPO algorithm updates the neural network parameters based on state returns by sampling historical offloading data. This process involves two distinct neural networks: the actor network, which is responsible for updating the current policy by determining action probabilities, and the critic network, which evaluates the policy’s expected returns. The functions of the actor and critic neural networks are to update and evaluate the current strategy, respectively. Upon receiving the current environment state as input, the actor network employs the neural network’s parameters, $\theta$, to ascertain the likelihood of undertaking a particular action within state s. Concurrently, the critic network computes the value of the current policy, effectively estimating the expected returns. This dual-structured approach enables the PPO algorithm to harmoniously balance the need for exploration, which involves experimenting with novel actions with the necessity of exploitation or optimizing known effective actions. Through this iterative interaction, the PPO algorithm learns and hones strategies, progressively navigating towards an optimal policy.

The objective function of the policy, denoted as$J \left(\theta \right)$ (Equation (30)), integrates with ${\widehat{A}}_t$, the estimator of the advantage function with time step $t$, and ${\pi }_{\theta }$is the strategy function.

$$J\left(\theta \right)=E_t\left[\frac{{\pi }_{\theta }\left(a_t|s_t\right)}{{\pi }_{{\theta }_{old}}\left(a_t|s_t\right)}{\widehat{A}}_t\right],$$

(30)

$$J\left(\theta \right)={\widehat{E}}_t\left[\min \left(r_t\left(\theta \right){\widehat{A}}_t,clip\left(r_t\left(\theta \right),1-ϵ,1+ϵ\right){\widehat{A}}_t\right)\right].$$

(31)

The PPO algorithm utilizes the principle of importance sampling to update the strategy with the experience generated by the old strategy. It solves the redundant process in reinforcement learning that requires recollecting experience after each policy update, thus effectively utilizing past experience and speeding up the learning process. The principle of importance sampling requires $r_t\left(\theta \right)$(expressed as Equation (32)) to be as close to 1 as possible, and here, a restriction is placed on the objective function of the online network, see Equation (31), in which $ϵ$ is generally taken to be 0.2 [34].

$$r_t\left(\theta \right)=\frac{{\pi }_{\theta }\left(a_t|s_t\right)}{{\pi }_{{\theta }_{old}}\left(a_t|s_t\right)}.$$

(32)

Optimal policies can be obtained by optimizing the metric based on gradient-based algorithms: ${\theta }_{t+1}={\theta }_t+\alpha {\nabla }_{\theta }J\left({\theta }_t\right)$, where ${\nabla }_{\theta }J$ is the gradient of $J$with respect to $\theta$, $t$ is the time step, and $\alpha$ is the optimization rate. Summarizing the above, the algorithm training process is presented in Algorithm 1.

Algorithm 1 Training the algorithm of PPO.

Initialize$\mathrm{Clip} \mathrm{factor} \mathsf{ϵ},$$\mathrm{discount} \mathrm{factor} \mathsf{\gamma },$$\mathrm{learning} \mathrm{rate} {\mathsf{\lambda }}_{\mathrm{a}}$$\mathrm{and} {\mathsf{\lambda }}_{\mathrm{c}}$, update times of each training step Rp,$\mathrm{actor} \mathrm{network} \mathsf{\theta },$$\mathrm{critic} \mathrm{network} \mathsf{\omega },$ and replay buffer; For episode = 1, …, 500, Obtain the Observation from the environment; Execute the action a[n]; Evaluate reward r[n], policy entropy S(s[n]), the log-probability of a[n], and store these variables in the experience buffer; Store the transition {s[n], a[n], r[n], s[n+1]} into experience buffer; If mod (n, N) = 0 then reset the training environment; end if n = n + 1; Calculate the advantage function A[n]; for up = 1, …, Rp do Calculate the current policy entropy S(s[n]) $\mathrm{Calculate} \mathrm{the} \mathrm{update} \mathrm{ratios} r_t\left(\theta \right)={\pi }_{\theta }\left(a_t\right|s_t)/{\pi }_{\theta old}\left(a_t\right|s_t)$   $\mathrm{Update} \mathrm{actor} \mathsf{\theta }$$\mathrm{and} \mathrm{critic} \mathsf{\omega }$$\mathrm{with} \mathrm{the} \mathrm{transitions} \mathrm{in} \mathrm{the} \mathrm{experience} \mathrm{buffer} \mathrm{according} \mathrm{to} \mathsf{\theta }\leftarrow \mathsf{\theta }-{\mathsf{\lambda }}_{\mathrm{a}}{\nabla }^{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}}\mathrm{J}\left(\mathsf{\theta }\right)$ and $\mathsf{\omega }\leftarrow \mathsf{\omega }-{\mathsf{\lambda }}_{\mathrm{b}}{\nabla }^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}}\mathrm{J}\left(\mathsf{\theta }\right)$;   Update the policy entropy and log probability in the experience buffer; end for Clear experience buffer; end for $\mathrm{Output} \mathrm{policy} \mathrm{parameters} \mathsf{\theta }$$\mathrm{and} \mathrm{critic} \mathrm{parameters} \mathsf{\omega }$.

5. Performance Evaluation

This section evaluates the performance of the proposed PPO-based D2D-assisted computation offloading and resource allocation scheme in a realistic MEC environment.

5.1. Experiment Setup

In this study, we deployed a real MEC network environment. As shown in Figure 4, this edge network consists of two APs, three UEs, and two MEC servers. The APs and UEs were all modeled by a Raspberry Pi 4B, which consumes an average of 6.4 W in operation and 2.7 W in idle mode [35]. All UEs were equipped with RPi Camera V2 model 8-megapixel external cameras and were randomly dispersed in an environment with a radius of approximately 5 m centered on the AP. The UEs had a local computational power of 1.5 GHz. The two MEC servers were simulated by personal laptops, which were configured with an 11th Intel(R) Core (TM) [email protected] CPU, NVIDIA 1650Ti GPU, and 16 GB RAM.

On top of putting the MEC environment in place, we introduced a real-time surveillance recognition system based on the YoloV5 algorithm [36] as a computational task for each UE, with the size of a computational task ranging from 370 kb to 450 kb, generating 20 unprocessed 256 × 256 images per second as a pending task. After testing, all UEs and MEC servers fulfilled the requirements for running the YOLOv5 object detection algorithm.

Subsequently, we analyzed the actual performance of the random scheme, DQN scheme, A2C scheme, and PPO scheme in edge computing. The network environment parameters and the training parameters of the four schemes are shown in

Table 1. Environment settings.

Description	Parameters	Values
The bandwidth of the wireless channel	$W$	10 MHz
The maximum transmission power of UEs	$P_i^{UE}$	14.5 dBm
The maximum transmission power of the MEC server	$P_i^{mec server}$	20 dBm
The data size of the task	$m_i$	370–450 kb
The computational power of UEs	$f_i^{UE}$	1.5 GHz/s
The computational power of the MEC server	$f_i^{mec server}$	4.2 GHz/s
Transmission rate of UEs	$R_{i,b}$	-
Transmission rate of the MEC server	$R_{i,c}$	-

. The user devices were uniformly distributed in an area with a radius of approximately 5 m. Our proposed PPO Scheme consists of the actor, a policy network responsible for generating actions, together with the critic, a value function network for estimating the value or the advantage of a state to guide the policy updates. The structure of the actor network consists of an input layer consisting of 15 neurons, two hidden layers containing (128, 64) neurons, and an output layer containing a fully connected layer. The weights of the actor network are updated by maximizing the agent’s objective function, whereas the weights of the critic network are updated by minimizing the loss of the mean-square error between the estimate of the value function and the true return. The activation function was ReLU, the current empirical data and the Adam optimizer were sampled during the weight update process, and the learning rates of the actor network and the critic network were set to $1\times {10}^{-4}$ and $5\times {10}^{-4}$, respectively.

We compared our PPO-based approach against three baseline algorithms: random scheme, DQN scheme, and A2C scheme. These comparisons aimed to demonstrate the superiority of our approach in various MEC scenarios. We compared the proposed PPO algorithmic scheme with a random offloading strategy, DQN strategy, and A2C strategy.

• Random Scheme: Each task randomly selects the execution device, including edge servers, migration to other edge server computation, D2D computation, and local computation.
• DQN Scheme: The DQN (deep Q-network) algorithm [37] is a deep reinforcement learning method that combines traditional Q-learning and deep learning techniques. Its core features include the use of deep neural networks to approximate the Q-function so as to learn strategies directly from the complex.
• A2C Scheme: The A2C (advantage actor–critic) algorithm is a widely used method in the field of reinforcement learning [38], which is a variant of the AC algorithm. The A2C algorithm improves this framework by introducing the advantage function, which improves learning efficiency and stability.
• PPO Scheme: PPO can be considered an improved version of the AC algorithm that introduces a limit on the magnitude of policy updates to prevent excessive policy changes in a single update [39]. This approach aims to avoid excessive jumps in the strategy space, thus improving the stability of the learning process.

For the above four frames, the training parameters are shown in

Table 2. Hyperparameters of algorithms.

Parameters	Values
$\mathrm{Learning} \mathrm{rate} {\lambda }_a,{\lambda }_c$ (PPO and A2C)	$1\times {10}^{-4}$$, 5\times {10}^{-4}$
$\mathrm{Learning} \mathrm{rate} \lambda$(DQN)	$1\times {10}^{-4}$
$\mathrm{Discount} \mathrm{factor} \gamma$	0.98
$\mathrm{Clipping} \mathrm{factor} ϵ$	0.2
$\mathrm{Entropy} \mathrm{factor} \psi$	0.01
Replay buffer size of DQN	10,000
Sample size in the empirical buffer	64
Activation functions and optimizers	ReLu, Adam
Hidden sizes	128, 64

.

5.2. Experimental Analysis

In this study, we analyzed the performance of four frameworks during the training process by recording their action selection and reward values, as illustrated in Figure 5a,b. Regarding convergence, the reward value of the PPO algorithm stabilized around step 340, while the A2C algorithm and the DQN algorithm showed stabilization at approximately steps 400 and 430, respectively. However, the random policy consistently demonstrated low reward values from the 57th step onward and was thus not considered for convergence analysis. Through an in-depth examination of the result, it became evident that reinforcement learning algorithms play a crucial role in offloading decisions. Notably, the PPO algorithm exhibited superior convergence compared to the other three benchmarked algorithms, as shown in Figure 5b.

Figure 6a shows the line graphs of the average reward value of the four schemes. The random scheme was in a low reward state compared with the other three schemes, and the average reward fluctuated slightly around −24 after 57 steps; the average reward value of the DQN scheme was around −5.0 after convergence, the average reward value of the A2C scheme was around −3.7 after convergence, and the average reward was still on the rise after 400 steps, while the average reward value of the PPO scheme was over −5.0 after convergence. The PPO scheme had an average reward value of around −3.3 after convergence and was relatively smooth, better than the other three baselines. In terms of training stability, the stability of the PPO algorithm was better than the other three baselines within 0–150 steps, DQN was more stable between 151 and 400 steps, and the A2C algorithm was smoother after 400 steps. Overall, DQN performed better in terms of stability. From Figure 5b and Figure 6a, we observed that the DRL algorithm effectively adapts to complex edge computing environments through end-to-end optimization and thus achieves better performance compared to the randomness strategy. Whereas the randomness strategy lacks targeted decisions, and its results do not provide meaningful information, we further focused on the DQN algorithm, A2C algorithm, and PPO algorithm.

Secondly, as shown in Figure 6b, we recorded the weighted average of the delay and energy consumption during the training process. Time cost represents the cumulative sum of transmission delay and computation delay. Energy cost encompasses the combined sum of transmission energy consumption and computation energy consumption. The ultimate average cost is the weighted sum of time cost and energy cost, with the respective weight parameters for time cost and energy cost determined by the neural network. PPO had the highest average total cost in 0–30 steps, and as the algorithms were trained, it became gradually smoother after 300 steps at around 2.87, which was the lowest average total cost compared to the other algorithms, and the overall view of the weighted average of the total cost was more stable.

As shown in Figure 7a,b, the performance metrics of delay and energy consumption were compared among the different algorithms. The DQN algorithm demonstrated relative stability in both delay and energy consumption; however, its learning efficacy was marginally outpaced by the A2C and PPO algorithms. After 300 steps, the A2C algorithm’s performance in the delay reduction closely approximated that of the PPO algorithm, yet it lagged slightly behind in energy consumption efficiency. Overall, when evaluating the learning outcomes, the PPO algorithm emerged as the superior performer in comparison to the DQN and A2C models, particularly in terms of optimizing the trade-off between the delay and energy consumption.

6. Conclusions

In this paper, we proposed a PPO-based D2D-assisted computation offloading and resource allocation scheme for multi-access edge computing environments. The proposed approach leverages the actor–critic based on the PPO method in reinforcement learning to optimize offloading decisions based on the task attributes and device performance, resulting in reduced latency and lower energy consumption. Additionally, the collaborative offloading strategy between the D2D and MEC servers greatly improved the utilization of the edge computational resources. The implementation of this scheme marks a significant advancement in addressing the complex challenges inherent in the MEC networks, particularly relevant in the evolving 5G landscape. However, we recognize the limitations in the current study: one being the time-varying nature of the communication model channel parameters as influenced by the environment and the other being the protection of sensitive user information and data during D2D communication. In the future, we will extend our work. On the one hand, we will use real-time monitoring and sensing techniques to accurately measure the dynamic characterization of channel parameters, and on the other hand, we will incorporate privacy-preserving aspects into the common offloading process within D2D-assisted MEC networks.