Analysis of Program Representations Based on Abstract Syntax Trees and Higher-Order Markov Chains for Source Code Classification Task
Abstract
:1. Introduction
- RQ1: How does the size of the dataset and the selected approach to source code transformation into vector-based representation affect the quality of different classification algorithms in the task detection problem?
- RQ2: Which of the considered approaches to source code transformation into vector-based representation is least sensitive to the used classification algorithm in the task detection problem?
2. Related Work
3. Task Detection Problem
4. Approaches to Source Code Transformation into Vector-Based Representations
4.1. word2vec
4.2. code2vec
4.3. Markov Chains for Abstract Syntax Trees
| Algorithm 1: Neighboring vertices merging in an AST | |
| Input: | ▷ AST with vertices represented as tuples. |
| 1. | , ▷ a set of vertices and a set of edges of a new tree. |
| 2. | For each edge do: |
| 3. | For each edge do: |
| 4. | , where ; is the last element of the tuple. |
| 5. | , where ; is the last element of the tuple. |
| 6. | . |
| 7. | . |
| 8. | End loop. |
| 9. | End loop. |
| 10. | Return ▷ AST-based tree with merged vertices. |
| Algorithm 2: Construction of an n-th order Markov chain from an AST | |
| Input: | ▷ program source code, ▷ Markov chain order. |
| 1. | Construct an AST for program using the ast.parse function [41]. |
| 2. | Delete from vertices belonging to set {Load, Store, alias, arguments, arg}. |
| 3. | Repeat n times: |
| 4. | Set to a new tree computed according to Algorithm 1. |
| 5. | End loop. |
| 6. | Define the mapping that maps a vertex to its type. |
| 7. | ▷ a set of edges of an n-th order Markov chain. |
| 8. | ▷ a set of vertices filled with AST node types from . |
| 9. | For each vertex type do: |
| 10. | ▷ multiset of descendant vertices of type . |
| 11. | ▷ types of descendants of vertices of type . |
| 12. | For each descendant vertex type do: |
| 13. | ▷ normed descendant count for . |
| 14. | ▷ add a new edge with weight . |
| 15. | End loop. |
| 16. | End loop. |
| 17. | Return the state transition graph of an n-th order Markov chain. |
4.4. Histograms of Assembly Language Instruction Opcodes
| Algorithm 3: Source code embedding into vector space based on opcode histograms | |
| Input: | ▷ a set of source codes to be converted into vector representations. |
| 1. | ▷ the ordered set of instruction type multisets. |
| 2. | ▷ the set of known instruction types. |
| 3. | For each source code do: |
| 4. | Construct an AST for program using the ast.parse function [41]. |
| 5. | Build a code object from the AST using the compile Python function. |
| 6. | Disassemble a multiset of instruction types from using dis [46]. |
| 7. | ▷ add the multiset of instruction types to . |
| 8. | ▷ add discovered instruction types to the set. |
| 9. | End loop. |
| 10. | ▷ the ordered set of vectors. |
| 11. | For each multiset of instruction types do: |
| 12. | . |
| 13. | For each known instruction type do: |
| 14. | ▷ instruction type occurrence frequency. |
| 15. | ▷ add a new component to the program vector. |
| 16. | End loop. |
| 17. | End loop. |
| 18. | Return the set of source code vector-based representations. |
4.5. Histograms of Abstract Syntax Tree Node Types
| Algorithm 4: Source code embedding based on AST node type histograms | |
| Input: | ▷ a set of source codes to be converted into vector representations. |
| 1. | ▷ the ordered set of node type multisets associated with source codes. |
| 2. | ▷ the ordered set of known node types. |
| 3. | For each source code do: |
| 4. | Construct an AST for the program using the ast.parse function [41]. |
| 5. | Extract a multiset of node types that are present in from . |
| 6. | ▷ add the multiset of node types to . |
| 7. | ▷ add discovered node types to the set. |
| 8. | End loop. |
| 9. | the ordered set of vectors. |
| 10. | For each multiset of node types do: |
| 11. | . |
| 12. | For each known node type do: |
| 13. | ▷ node type occurrence frequency. |
| 14. | ▷ add a new component to the program vector. |
| 15. | End loop. |
| 16. | End loop. |
| 17. | Return the set of source code vector-based representations. |
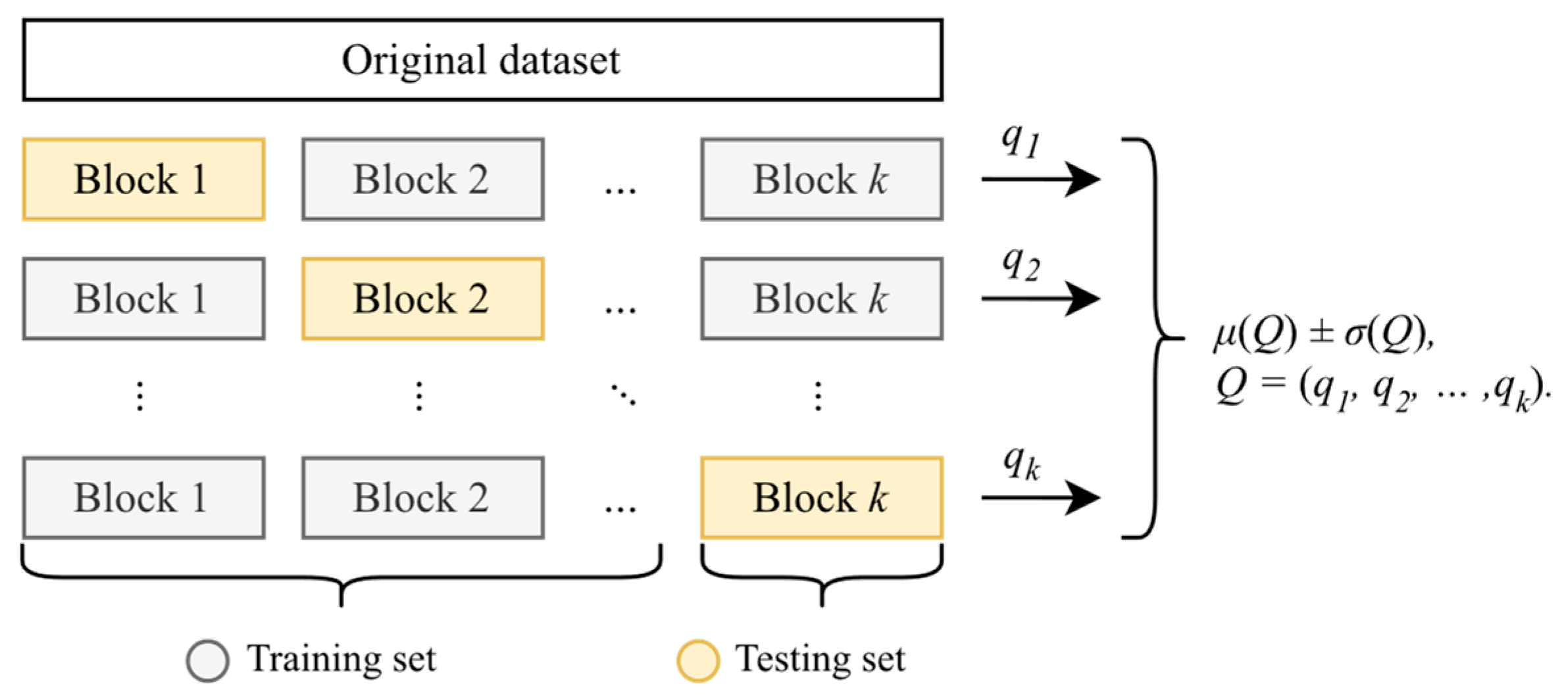
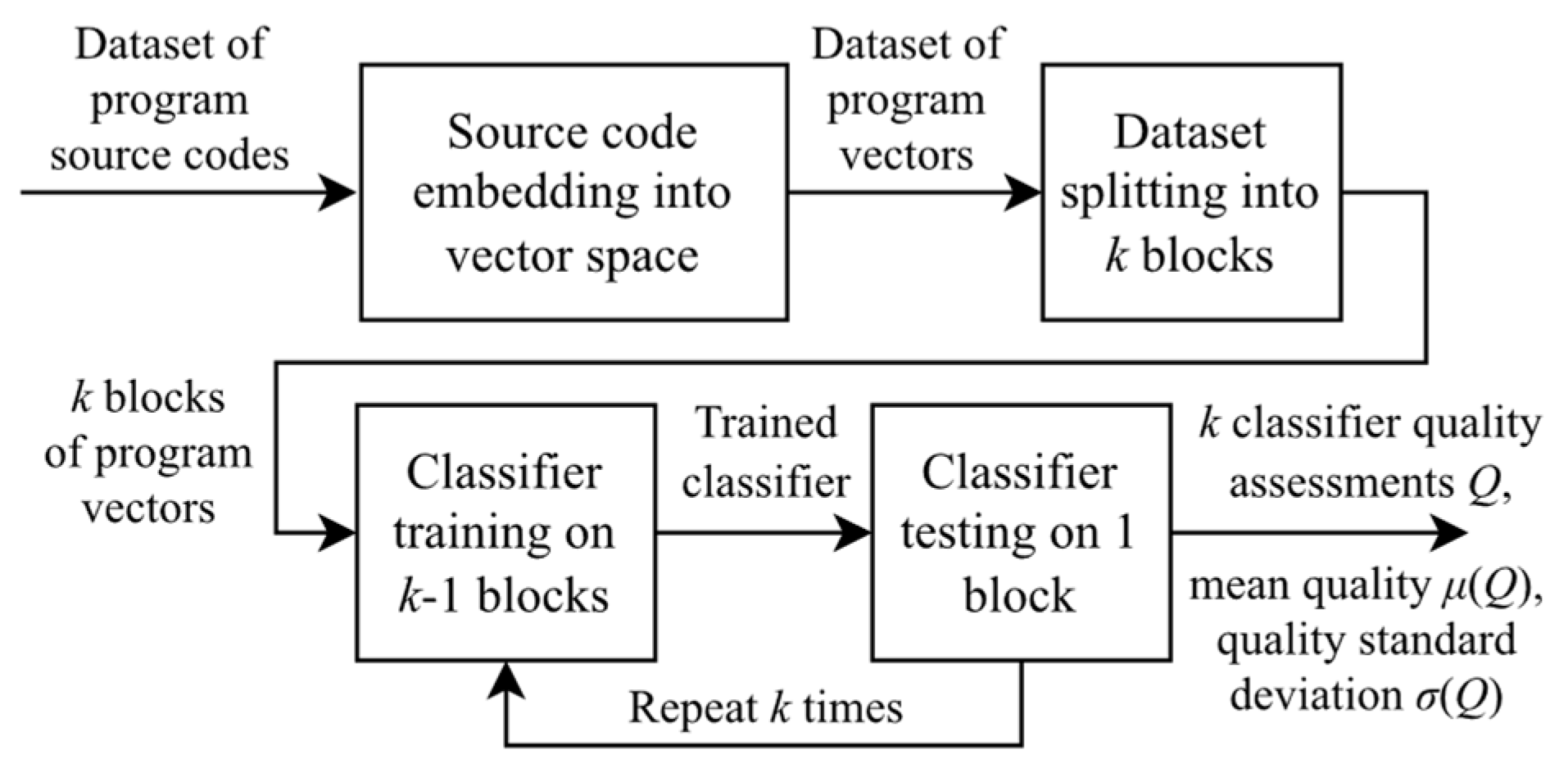
5. Experimental Studies
5.1. Experimental Setup
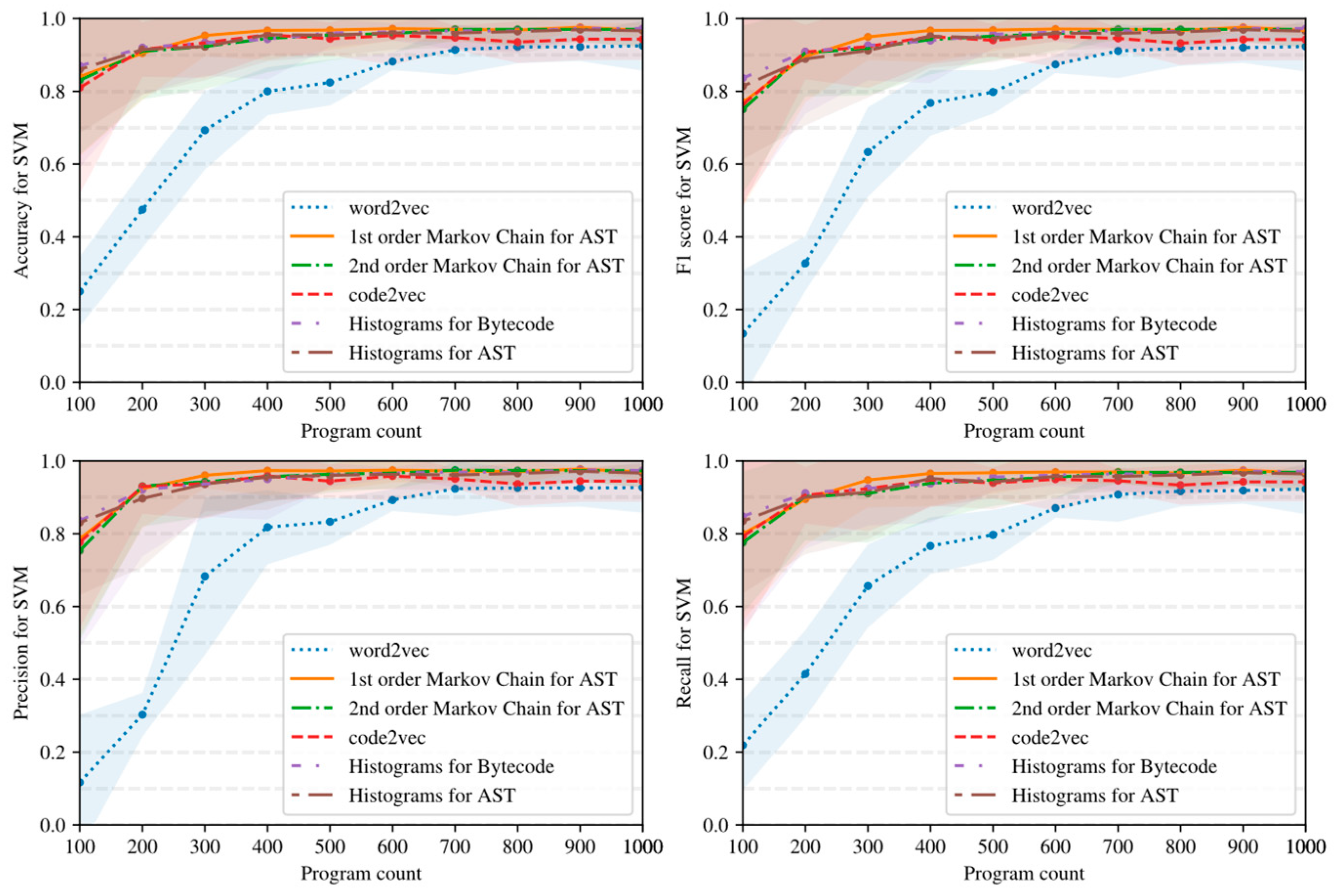
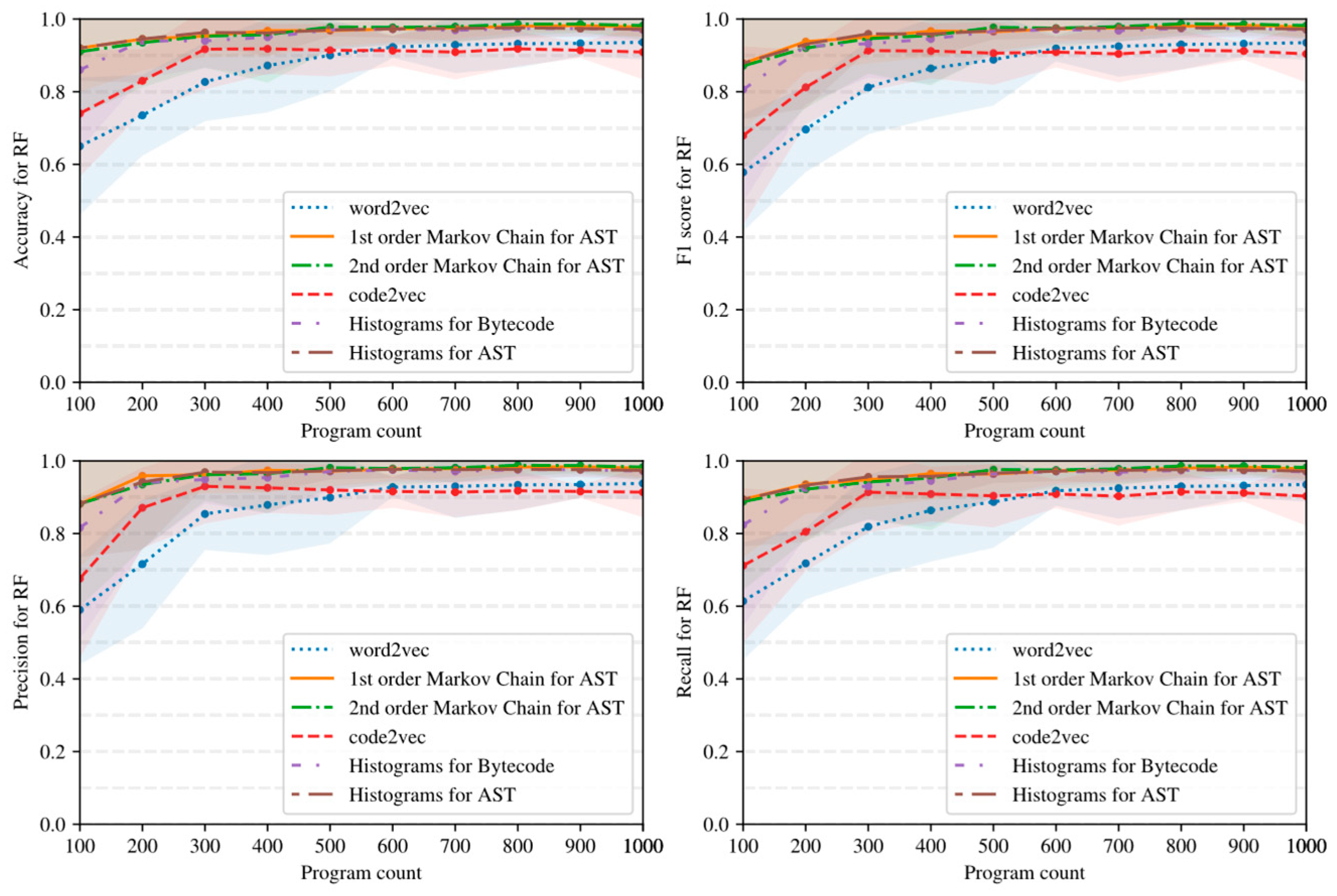
5.2. Influence of Dataset Size and Program Embedding on Classifier Quality
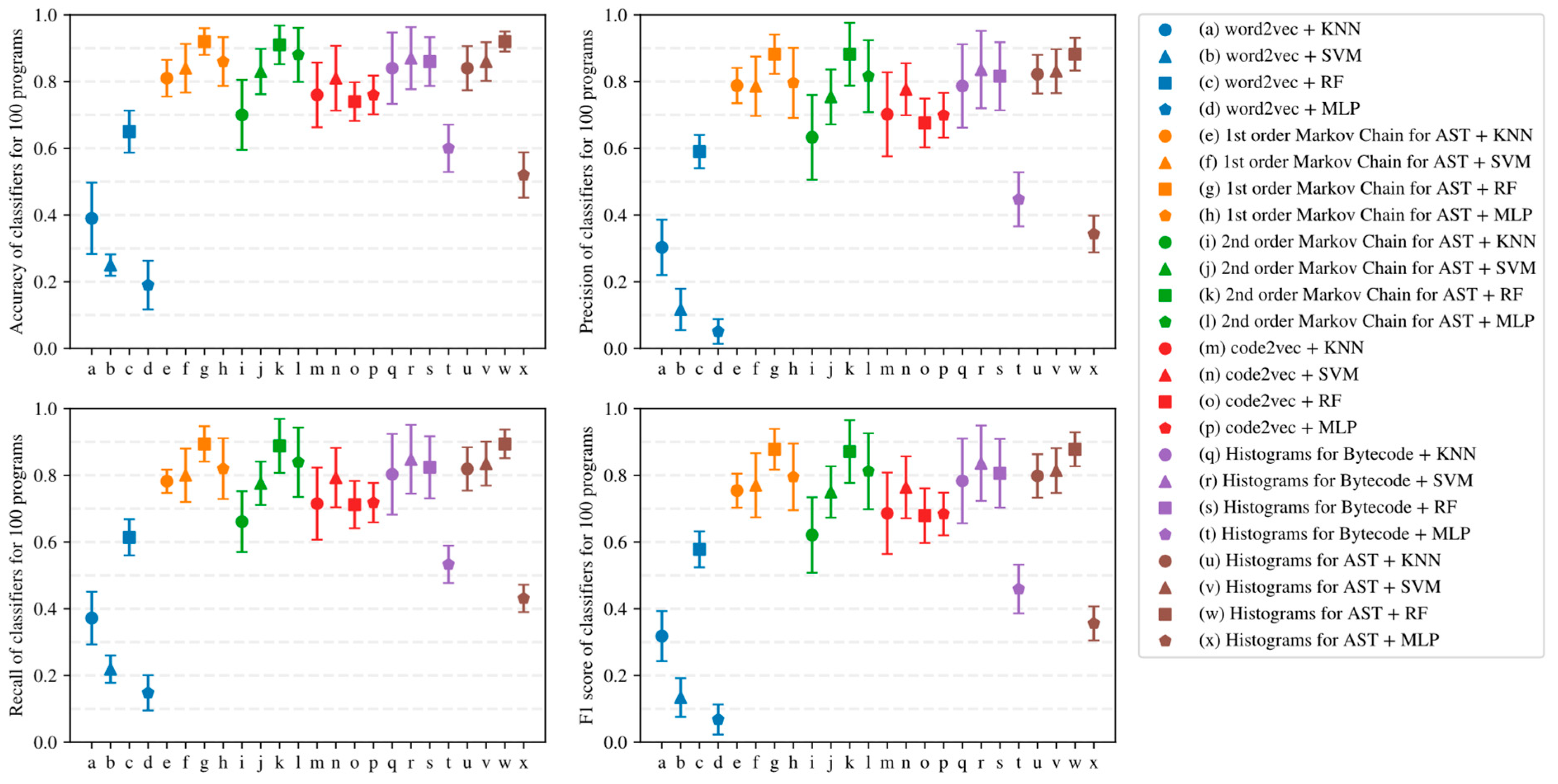
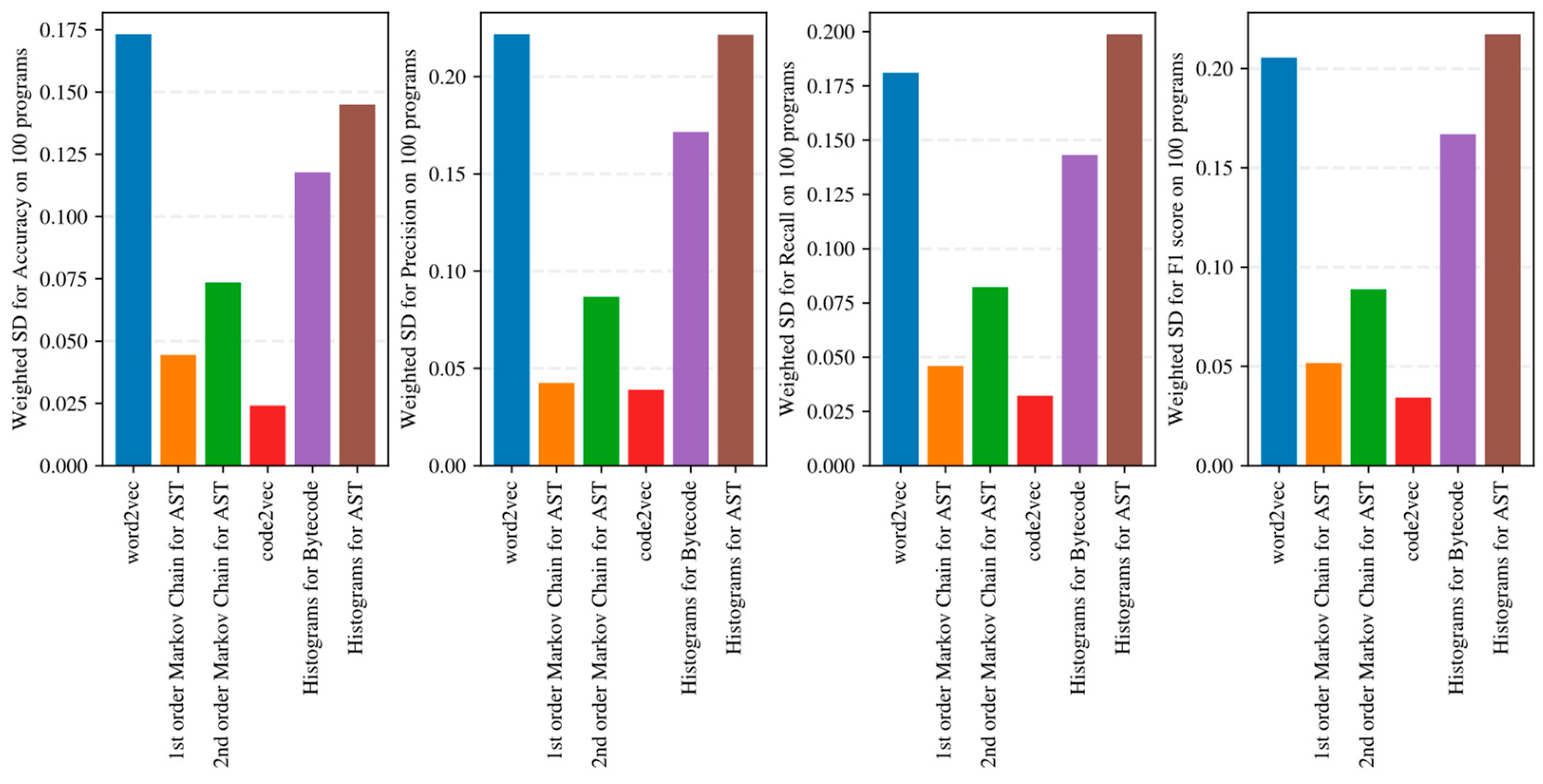
5.3. Sensitivity of Program Embeddings to the Used Classification Algorithm
6. Discussion
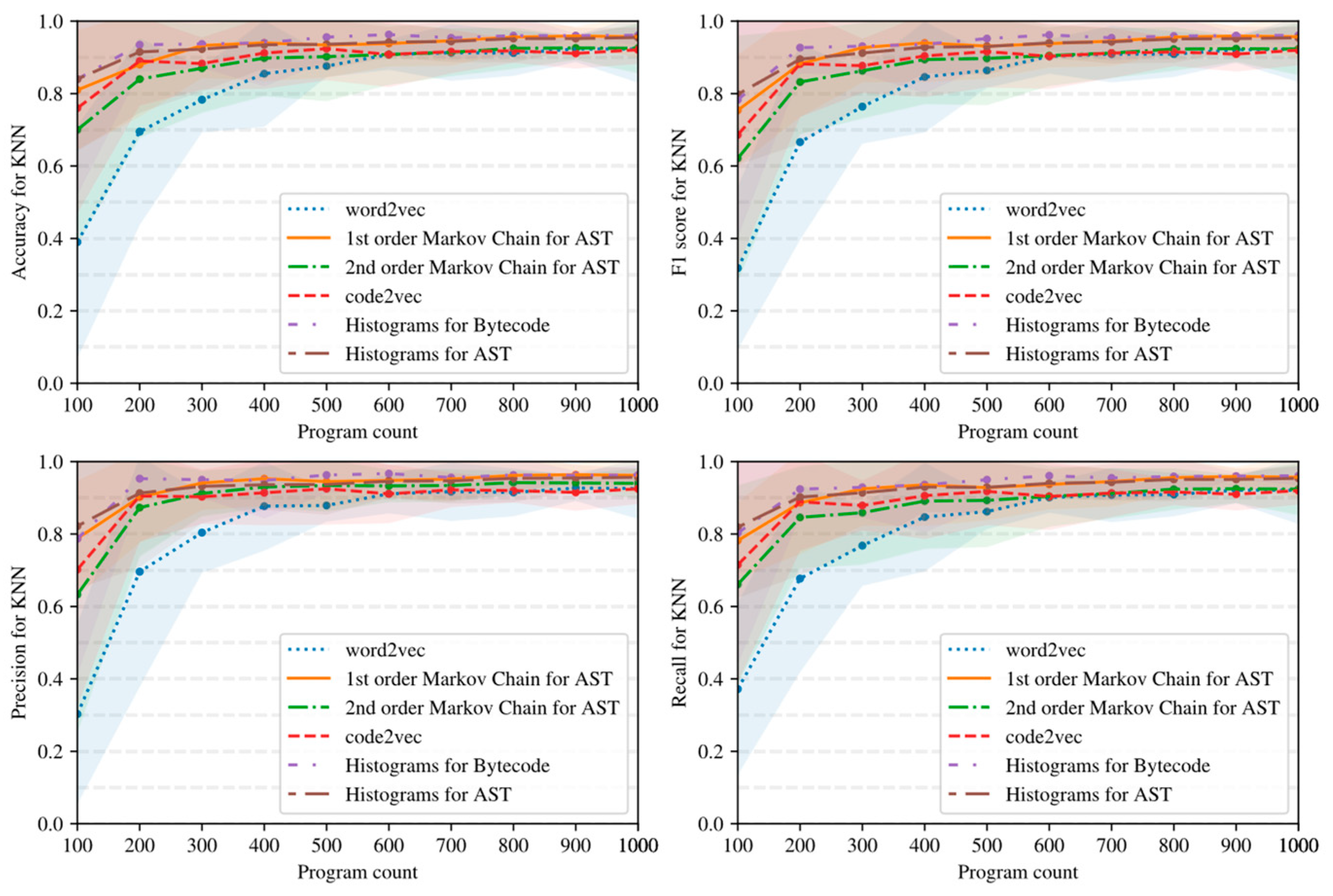
- Simple AST-based or bytecode-based representations of programs such as Markov chains and histograms outperform complex neural network-based embeddings with many hyperparameters in the considered task detection problem, especially when the amount of training data is limited (see Figure 15, Figure 16 and Figure 17).
- Embeddings of programs that are based on either AST or bytecode outperform token-based embeddings on small-sized datasets; however, with the increase in the dataset size, the difference in the quality of classifiers decreases and has the potential to vanish on larger datasets (see, for example, Figure 15 and Figure 16).
- Increasing the order of AST-based Markov chains offers no noticeable improvement in classifier quality in the sense of (13)–(16), and can even lead to quality degradation in the case of KNN (see Figure 19 and Figure 20); this makes AST-based Markov chains of order 1 most suitable for practical applications.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Simon, F.; Steinbruckner, F.; Lewerentz, C. Metrics based refactoring. In Proceedings of the 5th European Conference on Software Maintenance and Reengineering, Lisbon, Portugal, 14–16 March 2001; IEEE: Piscataway, NJ, USA, 2001; pp. 30–38. [Google Scholar]
- Campbell, G.A. Cognitive Complexity: An Overview and Evaluation. In Proceedings of the 2018 International Conference on Technical Debt, Gothenburg, Sweden, 27–28 May 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 57–58. [Google Scholar]
- Chen, Z.; Chen, L.; Ma, W.; Xu, B. Detecting Code Smells in Python Programs. In Proceedings of the 2016 International Conference on Software Analysis, Testing and Evolution (SATE), Harbin, China, 3–4 November 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 18–23. [Google Scholar]
- Zhang, Z.; Xing, Z.; Xia, X.; Xu, X.; Zhu, L. Making Python Code Idiomatic by Automatic Refactoring Non-Idiomatic Python Code with Pythonic Idioms. In Proceedings of the 30th ACM Joint European Software Engineering Conference and Symposium on the Foundations of Software Engineering, Singapore, 14–16 November 2022; Association for Computing Machinery: New York, NY, USA, 2022; pp. 696–708. [Google Scholar]
- Bruch, M.; Monperrus, M.; Mezini, M. Learning from Examples to Improve Code Completion Systems. In Proceedings of the 7th Joint Meeting of the European Software Engineering Conference and the ACM SIGSOFT Symposium on the Foundations of Software Engineering, Amsterdam, The Netherlands, 24–28 August 2009; Association for Computing Machinery: New York, NY, USA, 2009; pp. 213–222. [Google Scholar]
- Li, X.; Wang, L.; Yang, Y.; Chen, Y. Automated Vulnerability Detection in Source Code Using Minimum Intermediate Representation Learning. Appl. Sci. 2020, 10, 1692. [Google Scholar] [CrossRef]
- Shi, K.; Lu, Y.; Chang, J.; Wei, Z. PathPair2Vec: An AST path pair-based code representation method for defect prediction. J. Comput. Lang. 2020, 59, 100979. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Nguyen, T. A Context-based Automated Approach for Method Name Consistency Checking and Suggestion. In Proceedings of the 2021 IEEE/ACM 43rd International Conference on Software Engineering, Madrid, Spain, 22–30 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 574–586. [Google Scholar]
- Alon, U.; Zilberstein, M.; Levy, O.; Yahav, E. code2vec: Learning distributed representations of code. Proc. ACM Program. Lang. 2019, 3, 40. [Google Scholar] [CrossRef]
- Ziadi, T.; Frias, L.; Da Silva, M. Feature Identification from the Source Code of Product Variants. In Proceedings of the 2012 16th European Conference on Software Maintenance and Reengineering, Szeged, Hungary, 27–30 March 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 417–422. [Google Scholar]
- Rolim, R.; Soares, G.; D’Antoni, L.; Polozov, O.; Gulwani, S.; Gheyi, R.; Suzuki, R.; Hartmann, B. Learning Syntactic Program Transformations from Examples. In Proceedings of the 2017 IEEE/ACM 39th International Conference on Software Engineering (ICSE), Buenos Aires, Argentina, 20–28 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 404–415. [Google Scholar]
- Allamanis, M.; Sutton, C. Mining Idioms from Source Code. In Proceedings of the 22nd ACM Sigsoft International Symposium on Foundations of Software Engineering, Hong Kong, China, 16–21 November 2014; Association for Computing Machinery: New York, NY, USA, 2014; pp. 472–483. [Google Scholar]
- Iwamoto, K.; Wasaki, K. Malware Classification Based on Extracted API Sequences Using Static Analysis. In Proceedings of the 8th Asian Internet Engineering Conference, Bangkok, Thailand, 14–16 November 2012; Association for Computing Machinery: New York, NY, USA, 2012; pp. 31–38. [Google Scholar]
- Russell, R.; Kim, L.; Hamilton, L.; Lazovich, T.; Harer, J.; Ozdemir, O.; Ellingwood, P.; McConley, M. Automated Vulnerability Detection in Source Code Using Deep Representation Learning. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 757–762. [Google Scholar]
- Demidova, L.A.; Gorchakov, A.V. Classification of Program Texts Represented as Markov Chains with Biology-Inspired Algorithms-Enhanced Extreme Learning Machines. Algorithms 2022, 15, 329. [Google Scholar] [CrossRef]
- Wu, Y.; Feng, S.; Zou, D.; Jin, H. Detecting Semantic Code Clones by Building AST-based Markov Chains Model. In Proceedings of the 37th IEEE/ACM International Conference on Automated Software Engineering, Rochester, MI, USA, 10–14 October 2022; Association for Computing Machinery: New York, NY, USA, 2022; pp. 1–13. [Google Scholar]
- Wiem, B.; Marwa, H. Supervised Hardware/Software Partitioning Algorithms for FPGA-based Applications. In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020), Valletta, Malta, 22–24 February 2020; Springer: Berlin, Germany, 2020; Volume 2, pp. 860–864. [Google Scholar]
- Damásio, T.; Canesche, N.; Pacheco, V.; Botacin, M.; da Silva, A.F.; Pereira, F.M.Q. A Game-Based Framework to Compare Program Classifiers and Evaders. In Proceedings of the 21st ACM/IEEE International Symposium on Code Generation and Optimization, Montréal, QC, Canada, 25 February–1 March 2023; Association for Computing Machinery: New York, NY, USA, 2023; pp. 108–121. [Google Scholar]
- Demidova, L.A.; Andrianova, E.G.; Sovietov, P.N.; Gorchakov, A.V. Dataset of Program Source Codes Solving Unique Programming Exercises Generated by Digital Teaching Assistant. Data 2023, 8, 109. [Google Scholar] [CrossRef]
- Sovietov, P.N.; Gorchakov, A.V. Digital Teaching Assistant for the Python Programming Course. In Proceedings of the 2022 2nd International Conference on Technology Enhanced Learning in Higher Education (TELE), Lipetsk, Russia, 26–27 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 272–276. [Google Scholar]
- Qiao, Y.; Zhang, W.; Du, X.; Guizani, M. Malware classification based on multilayer perception and Word2Vec for IoT security. ACM Trans. Internet Technol. 2021, 22, 10. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef]
- Barchi, F.; Parisi, E.; Urgese, G.; Ficarra, E.; Acquaviva, A. Exploration of Convolutional Neural Network models for source code classification. Eng. Appl. Artif. Intell. 2021, 97, 104075. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Bagheri, A.; Hegedűs, P. A Comparison of Different Source Code Representation Methods for Vulnerability Prediction in Python. In Proceedings of the Quality of Information and Communications Technology: 14th International Conference, QUATIC 2021, Algarve, Portugal, 8–11 September 2021; Springer: Berlin, Germany, 2021; Volume 14, pp. 267–281. [Google Scholar]
- Fein, B.; Graßl, I.; Beck, F.; Fraser, G. An Evaluation of code2vec Embeddings for Scratch. In Proceedings of the 15th International Conference on Educational Data Mining, Durham, UK, 24–27 July 2022; International Educational Data Mining Society: Massachusetts, USA, 2022; pp. 368–375. [Google Scholar]
- Kovalenko, V.; Bogomolov, E.; Bryksin, T.; Baccheli, A. PathMiner: A Library for Mining of Path-Based Representations of Code. In Proceedings of the 2019 IEEE/ACM 16th International Conference on Mining Software Repositories (MSR), Montreal, QC, Canada, 26–27 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 13–17. [Google Scholar]
- Da Silva, A.F.; Borin, E.; Pereira, F.M.Q.; Queiroz, N.L., Jr.; Napoli, O.O. Program Representations for Predictive Compilation: State of Affairs in the Early 20’s. J. Comput. Lang. 2022, 73, 101171. [Google Scholar] [CrossRef]
- Fix, E.; Hodges, J. Discriminatory Analysis. Nonparametric Discrimination: Consistency Properties. Int. Stat. Rev. 1989, 57, 238–247. [Google Scholar] [CrossRef]
- Altman, N.S. An introduction to kernel and nearest-neighbor nonparametic regression. Am. Stat. 1992, 46, 175–185. [Google Scholar]
- Ho, T.K. Random Decision Forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 278–282. [Google Scholar]
- Grandini, M.; Bagli, E.; Visani, G. Metrics for Multi-class Classification: An Overview. arXiv 2020, arXiv:2008.05756. [Google Scholar]
- Taherkhani, A.; Malmi, L.; Korhonen, A. Algorithm Recognition by Static Analysis and Its Application in Students’ Submissions Assessment. In Proceedings of the 8th International Conference on Computing Education Research, Koli, Finland, 13–16 November 2008; Association for Computing Machinery: New York, NY, USA, 2008; pp. 88–91. [Google Scholar]
- Parsa, S.; Zakeri-Nasrabadi, M.; Ekhtiarzadeh, M.; Ramezani, M. Method name recommendation based on source code metrics. J. Comput. Lang. 2023, 74, 10117. [Google Scholar] [CrossRef]
- Bui, N.D.Q.; Jiang, L.; Yu, Y. Cross-Language Learning for Program Classification using Bilateral Tree-based Convolutional Neural Networks. arXiv 2017, arXiv:1710.06159. [Google Scholar]
- Alias, C.; Barthou, D. Algorithm Recognition based on Demand-Driven Dataflow Analysis. In Proceedings of the 10th Working Conference on Reverse Engineering (WCRE 2003), Victoria, BC, Canada, 13–16 November 2003; IEEE: Piscataway, NJ, USA, 2003; p. ensl01663748. [Google Scholar]
- Pérez-Ortiz, M.; Jiménez-Fernández, S.; Gutiérrez, P.A.; Alexandre, E.; Hervás-Martínez, C.; Salcedo-Sanz, S. A Review of Classification Problems and Algorithms in Renewable Energy Applications. Energies 2016, 9, 607. [Google Scholar] [CrossRef]
- Python Software Foundation. Tokenize—Tokenizer for Python Source. 2023. Available online: https://docs.python.org/3/library/tokenize.html (accessed on 10 July 2023).
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. arXiv 2013, arXiv:1301.3781. [Google Scholar]
- Rehurek, R.; Sojka, P. Gensim–Python Framework for Vector Space Modelling; NLP Centre, Faculty of Informatics, Masaryk University: Brno, Czech Republic, 2011; Volume 3. [Google Scholar]
- Python Software Foundation. AST—Abstract Syntax Trees. 2023. Available online: https://docs.python.org/3/library/ast.html (accessed on 15 July 2023).
- Gansner, E.R.; North, S.C. An Open Graph Visualization System and its Applications to Software Engineering. Softw. Pract. Exp. 2000, 30, 1203–1233. [Google Scholar] [CrossRef]
- Parr, T.J.; Quong, R.W. ANTLR: A predicated-LL (k) parser generator. Softw. Pract. Exp. 1995, 25, 789–810. [Google Scholar] [CrossRef]
- Canfora, G.; Mercaldo, F.; Visaggio, C.A. Mobile malware detection using op-code frequency histograms. In Proceedings of the 2015 12th International Joint Conference on e-Business and Telecommunications (ICETE), Colmar, France, 20–22 July 2015; IEEE: Piscataway, NJ, USA, 2015; Volume 4, pp. 27–38. [Google Scholar]
- Rad, B.B.; Masrom, M.; Ibrahim, S. Opcodes histogram for classifying metamorphic portable executables malware. In Proceedings of the 2012 International Conference on e-Learning and e-Technologies in Education (ICEEE), Lodz, Poland, 24–26 September 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 209–213. [Google Scholar]
- Python Software Foundation. Dis—Disassembler for Python Bytecode. 2023. Available online: https://docs.python.org/3/library/dis.html (accessed on 17 July 2023).
- Huang, S.; Wu, K.; Jeong, H.; Wang, C.; Chen, D.; Hwu, W.M. PyLog: An Algorithm-Centric Python-Based FPGA Programming and Synthesis Flow. IEEE Trans. Comput. 2021, 70, 2015–2028. [Google Scholar]
- Jiang, S.; Pan, P.; Ou, Y.; Batten, C. PyMTL3: A Python Framework for Open-Source Hardware Modeling, Generation, Simulation, and Verification. IEEE Micro 2020, 40, 58–66. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Pukelsheim, F. The Three Sigma Rule. Am. Stat. 1994, 48, 88–91. [Google Scholar]
- Jiang, Z.; Yang, M.Y.R.; Tsirlin, M.; Tang, R.; Dai, Y.; Lin, J. “Low-Resource” Text Classification: A Parameter-Free Classification Method with Compressors. In Proceedings of the Findings of the Association for Computational Linguistics: EACL 2023, Dubrovnik, Croatia, 2–6 May 2023; pp. 6810–6828. [Google Scholar]
- Demšar, J. Statistical Comparisons of Classifiers over Multiple Data Sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Curtis, J. Student Research Abstract: On Language-Agnostic Abstract-Syntax Trees. In Proceedings of the 37th ACM/SIGAPP Symposium on Applied Computing, Virtual, 25–29 April 2022; pp. 1619–1625. [Google Scholar]
- Sovetov, S.I.; Tyurin, S.F. Method for synthesizing a logic element that implements several functions simultaneously. Russ. Technol. J. 2023, 11, 46–55. [Google Scholar] [CrossRef]
- Arato, P.; Juhasz, S.; Mann, Z.A.; Orban, A.; Papp, D. Hardware-software partitioning in embedded system design. In Proceedings of the IEEE International Symposium on Intelligent Signal Processing, Budapest, Hungary, 6 September 2003; IEEE: Piscataway, NJ, USA, 2003; pp. 197–202. [Google Scholar]
- Demidova, L.A.; Sovietov, P.N.; Andrianova, E.G.; Demidova, A.A. Anomaly Detection in Student Activity in Solving Unique Programming Exercises: Motivated Students against Suspicious Ones. Data 2023, 8, 129. [Google Scholar] [CrossRef]
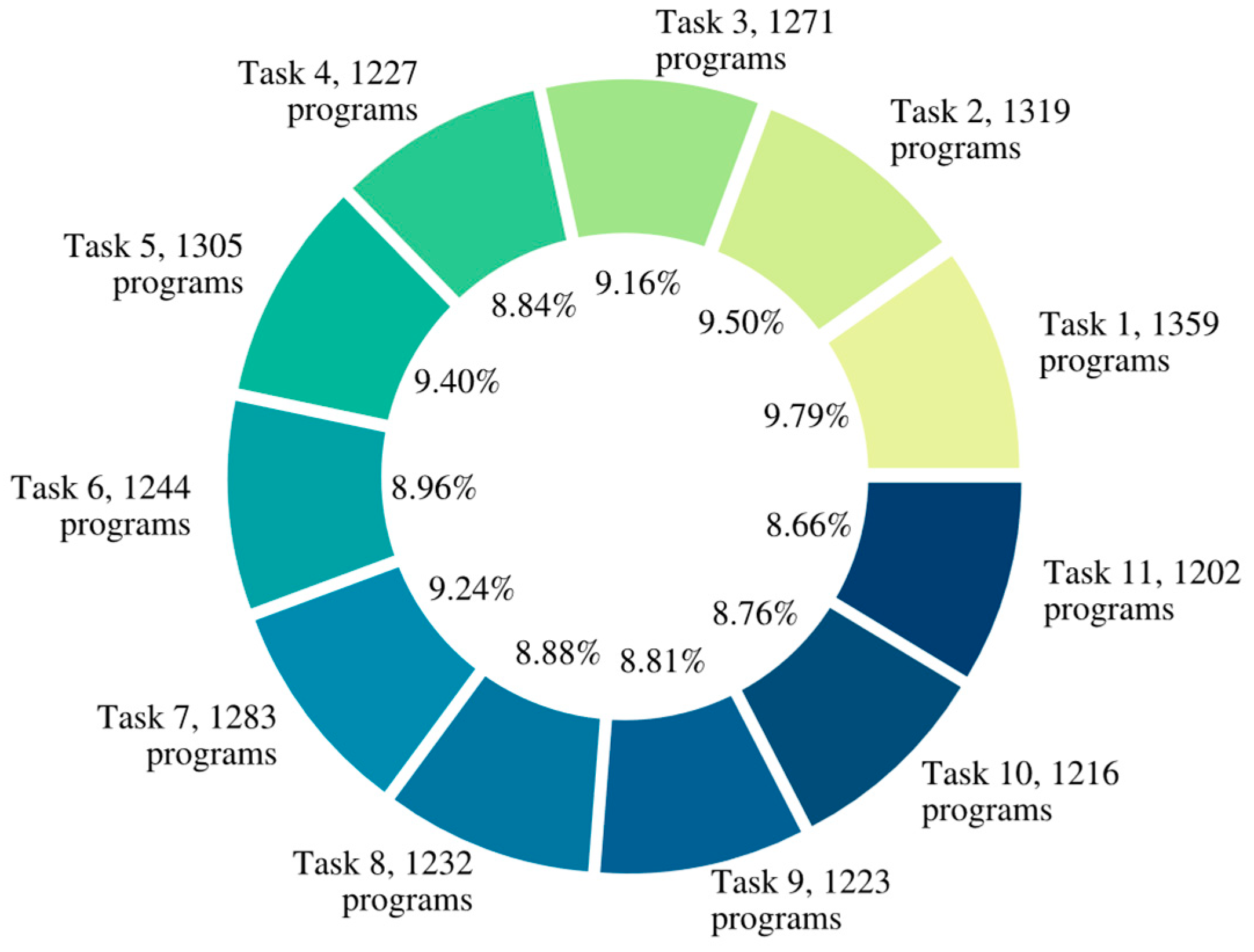



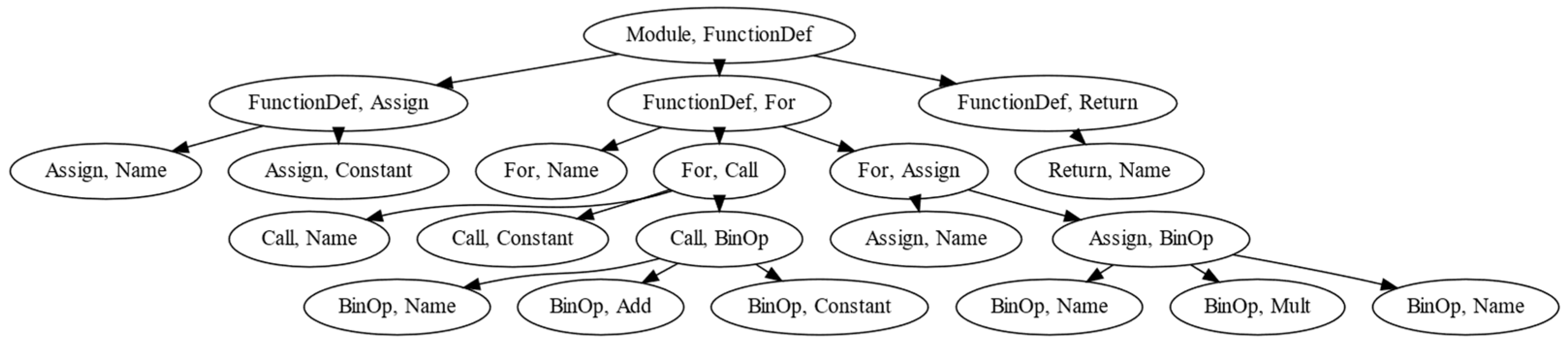
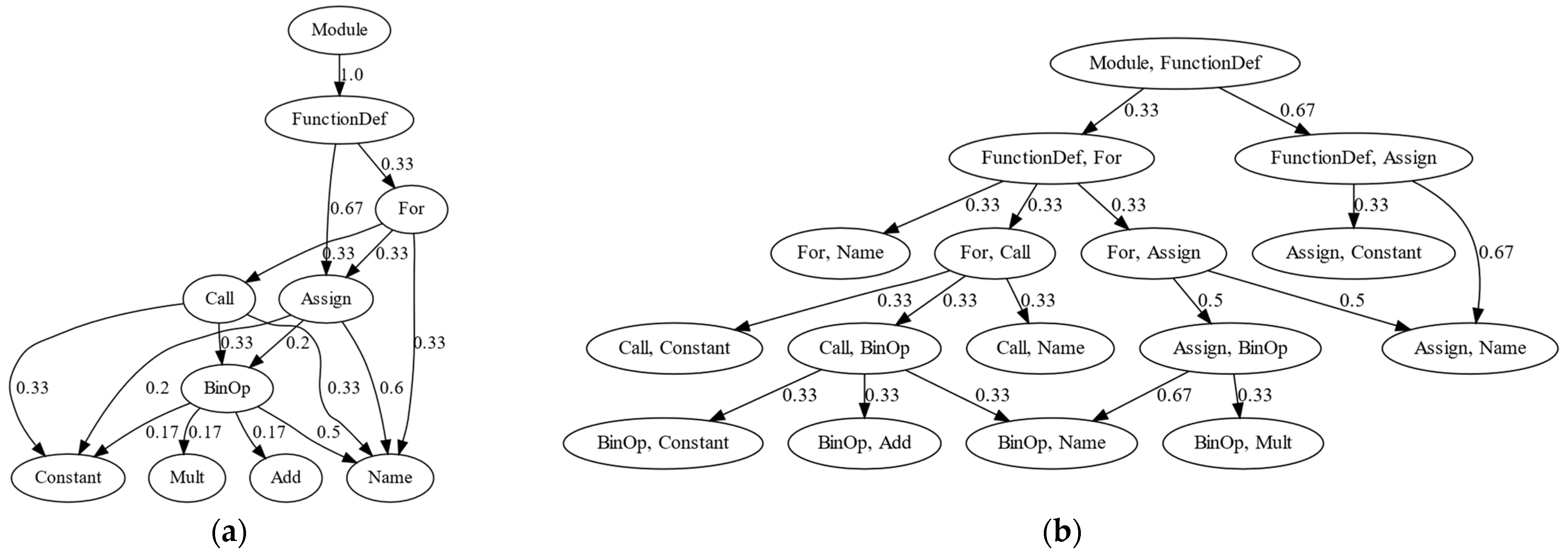

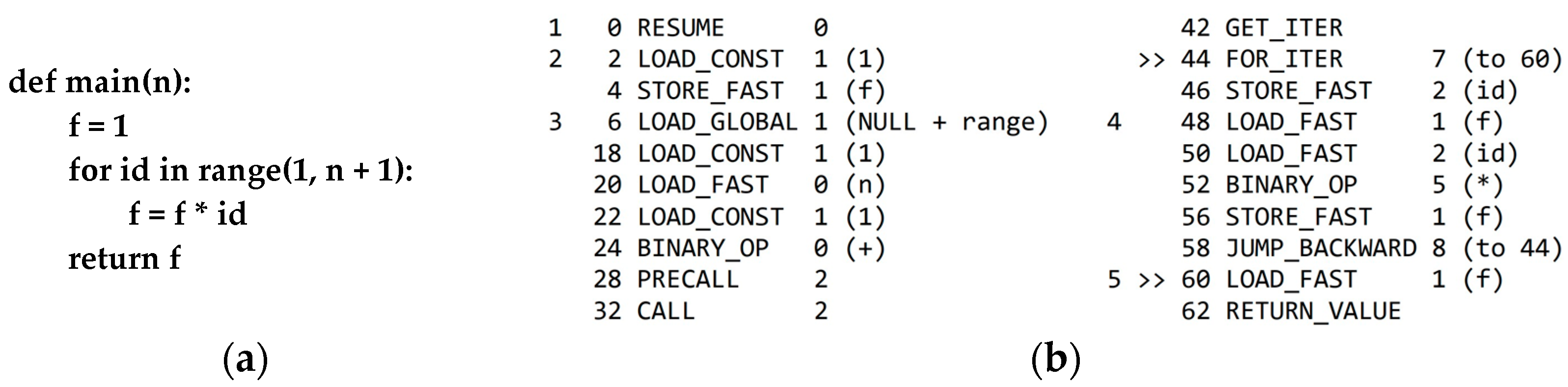






| Task | Description | Category |
|---|---|---|
| 1. | Implement a mathematical function | Notation into code translation |
| 2. | Implement a piecewise function formula | Notation into code translation |
| 3. | Implement an iterative formula | Notation into code translation |
| 4. | Implement a recurrent formula | Notation into code translation |
| 5. | Implement a function that processes vectors | Notation into code translation |
| 6. | Implement a function computing a decision tree | Notation into code translation |
| 7. | Implement a bit field converter | Conversion between data formats |
| 8. | Implement a text format parser | Conversion between data formats |
| 9. | Implement a finite state machine as a class | Notation into code translation |
| 10. | Implement tabular data transformation | Conversion between data formats |
| 11. | Implement a binary format parser | Conversion between data formats |
| Task | Approach 1 | Approach 2 |
|---|---|---|
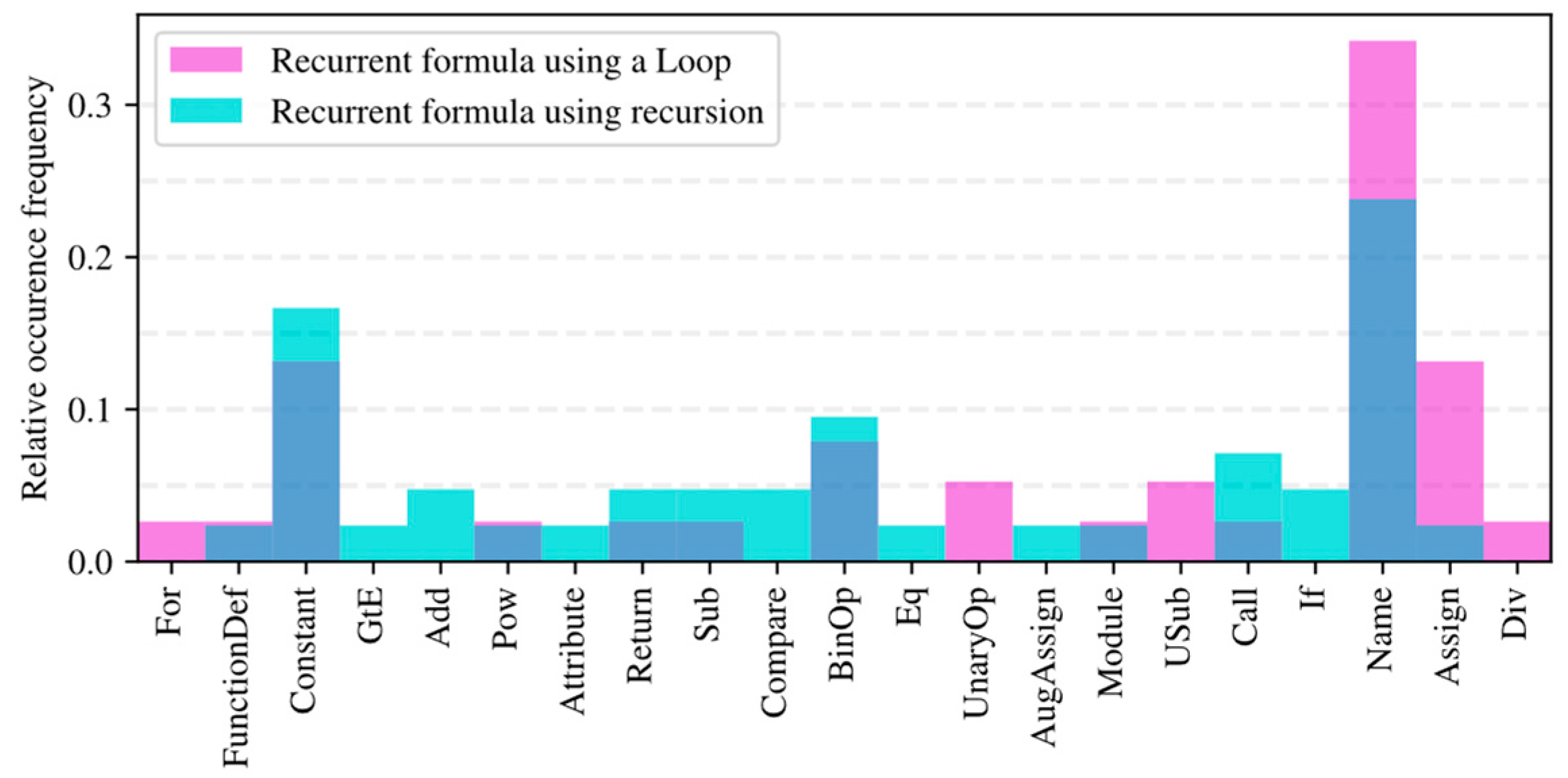
| 4. | def main(n): res1 = −0.31 res2 = −0.44 for i in range(1, n): temp = res1 − res2 ** 3/38 res1 = res2 res2 = temp return temp | def main(n): if n == 0: return 0.21 if n >= 1: ans = main(n − 1) + 1 ans += math.atan(main(n − 1)) ** 3 return ans |
| 11. | … def read_a(reader: BinaryReader): a1 = reader.read_uint16() a2 = read_array( source=reader.source, size=reader.read_uint32(), address=reader.read_uint32(), read=lambda reader: read_b(reader), structure_size=50) a3 = read_d(reader) a4 = [reader.read_int32(), reader.read_int32()] return dict(A1=a1, A2=a2, A3=a3, A4=a4) … | … def parse_c(buf, offs): c1, offs = parse(buf, offs, ‘float’) c2, offs = parse(buf, offs, ‘float’) c3, offs = parse(buf, offs, ‘uint16’) c4, offs = parse(buf, offs, ‘uint8’) c5size, offs = parse(buf, offs, ‘uint32’) c5offs, offs = parse(buf, offs, ‘uint16’) c5 = [] for _ in range(c5size): val, c5offs = parse(buf, c5offs, ‘uint8’) c5.append(val) return dict(C1=c1, C2=c2, C3=c3, C4=c4, C5=c5) … |
| Algorithm | Parameters |
|---|---|
| KNN | 4 neighbors, distance-based neighbor weighting. |
| SVM | Radial-basis function kernel, C = 30, one-vs-one strategy. |
| RF | Max. tree depth is 40, max. tree count is 300, gini criterion. |
| MLP | 100 hidden layer neurons, ReLU activation, Adam optimizer with learning rate = 0.001, , , . |
| word2vec | 100 vector components, window size = 5, 5 negative samples, = 0.025, 5 epochs. |
| code2vec | 384 vector components, dropout keep rate = 0.75, 20 epochs. |
| PathMiner | ANTLR Python parser, maximum path length = 30, maximum path width 15, maximum path contexts per entity = 300. |
| Embedding | Classifier | Accuracy (13) | Precision (14) | Recall (15) | F1 Score (16) |
|---|---|---|---|---|---|
| word2vec (See Section 4.1) | KNN | 39.0 ± 10.7 | 30.3 ± 8.3 | 37.2 ± 7.9 | 31.8 ± 7.5 |
| SVM | 25.0 ± 3.2 | 11.7 ± 6.2 | 21.9 ± 4.1 | 13.4 ± 5.8 | |
| RF | 65.0 ± 6.3 | 59.0 ± 5.0 | 61.4 ± 5.4 | 57.8 ± 5.4 | |
| MLP | 19.0 ± 7.3 | 5.1 ± 3.7 | 14.8 ± 5.3 | 6.8 ± 4.5 | |
| First-order AST-based Markov chain (See Section 4.3) | KNN | 81.0 ± 5.5 | 78.8 ± 5.3 | 78.2 ± 3.5 | 75.4 ± 5.1 |
| SVM | 84.0 ± 7.3 | 78.6 ± 8.9 | 80.0 ± 8.0 | 77.0 ± 9.6 | |
| RF | 92.0 ± 4.0 | 88.2 ± 5.9 | 89.4 ± 5.3 | 87.8 ± 6.1 | |
| MLP | 86.0 ± 7.3 | 79.6 ± 10.5 | 82.0 ± 9.1 | 79.5 ± 10.0 | |
| Second-order AST-based Markov chain (See Section 4.3) | KNN | 70.0 ± 10.5 | 63.3 ± 12.7 | 66.1 ± 9.1 | 62.1 ± 11.3 |
| SVM | 83.0 ± 6.8 | 75.4 ± 8.2 | 77.6 ± 6.5 | 75.0 ± 7.7 | |
| RF | 91.0 ± 5.8 | 88.2 ± 9.4 | 88.8 ± 8.1 | 87.1 ± 9.4 | |
| MLP | 88.0 ± 8.1 | 81.6 ± 10.8 | 83.9 ± 10.4 | 81.2 ± 11.4 | |
| code2vec (See Section 4.2) | KNN | 76.0 ± 9.7 | 70.2 ± 12.6 | 71.5 ± 10.8 | 68.6 ± 12.2 |
| SVM | 81.0 ± 9.7 | 77.7 ± 7.8 | 79.3 ± 8.9 | 76.4 ± 9.3 | |
| RF | 74.0 ± 5.8 | 67.6 ± 7.3 | 71.2 ± 7.1 | 67.9 ± 8.2 | |
| MLP | 76.0 ± 5.8 | 69.9 ± 6.7 | 71.8 ± 5.9 | 68.4 ± 6.4 | |
| Histograms for Bytecode (See Section 4.4) | KNN | 84.0 ± 10.7 | 78.7 ± 12.5 | 80.3 ± 12.1 | 78.3 ± 12.7 |
| SVM | 87.0 ± 9.3 | 83.6 ± 11.6 | 84.8 ± 10.3 | 83.6 ± 11.3 | |
| RF | 86.0 ± 7.3 | 81.6 ± 10.2 | 82.4 ± 9.3 | 80.6 ± 10.3 | |
| MLP | 60.0 ± 7.1 | 44.7 ± 8.1 | 53.3 ± 5.6 | 45.9 ± 7.3 | |
| Histograms for AST (See Section 4.5) | KNN | 84.0 ± 6.6 | 82.2 ± 5.8 | 81.9 ± 6.5 | 79.8 ± 6.5 |
| SVM | 86.0 ± 5.8 | 83.1 ± 6.6 | 83.5 ± 6.6 | 81.4 ± 6.7 | |
| RF | 92.0 ± 3.0 | 88.2 ± 4.9 | 89.4 ± 4.3 | 87.8 ± 5.1 | |
| MLP | 52.0 ± 6.8 | 34.3 ± 5.5 | 43.1 ± 4.1 | 35.6 ± 5.1 |
| Embedding | Classifier | Accuracy (13) | Precision (14) | Recall (15) | F1 Score (16) |
|---|---|---|---|---|---|
| word2vec (See Section 4.1) | KNN | 92.3 ± 3.1 | 92.6 ± 2.8 | 92.1 ± 3.1 | 92.2 ± 3.0 |
| SVM | 92.5 ± 2.3 | 92.7 ± 2.3 | 92.3 ± 2.3 | 92.3 ± 2.3 | |
| RF | 93.6 ± 1.6 | 93.8 ± 1.5 | 93.5 ± 1.6 | 93.5 ± 1.6 | |
| MLP | 91.0 ± 1.8 | 91.3 ± 2.1 | 90.7 ± 1.8 | 90.8 ± 1.8 | |
| First-order AST-based Markov chain (See Section 4.3) | KNN | 95.7 ± 1.9 | 96.2 ± 1.7 | 95.7 ± 1.9 | 95.7 ± 1.9 |
| SVM | 96.7 ± 0.7 | 97.0 ± 0.7 | 96.7 ± 0.6 | 96.7 ± 0.6 | |
| RF | 97.8 ± 0.9 | 98.0 ± 0.8 | 97.8 ± 0.9 | 97.8 ± 0.9 | |
| MLP | 97.9 ± 1.2 | 98.0 ± 1.2 | 97.9 ± 1.2 | 97.9 ± 1.2 | |
| Second-order AST-based Markov chain (See Section 4.3) | KNN | 92.5 ± 2.3 | 94.0 ± 1.4 | 92.4 ± 2.4 | 92.3 ± 2.4 |
| SVM | 97.0 ± 1.7 | 97.3 ± 1.5 | 96.9 ± 1.8 | 97.0 ± 1.7 | |
| RF | 98.2 ± 1.3 | 98.3 ± 1.2 | 98.2 ± 1.3 | 98.2 ± 1.3 | |
| MLP | 97.5 ± 0.8 | 97.7 ± 0.8 | 97.5 ± 0.7 | 97.5 ± 0.7 | |
| code2vec (See Section 4.2) | KNN | 92.1 ± 1.3 | 92.5 ± 1.4 | 92.0 ± 1.3 | 92.0 ± 1.4 |
| SVM | 94.3 ± 1.9 | 94.5 ± 1.9 | 94.3 ± 1.8 | 94.2 ± 1.9 | |
| RF | 90.9 ± 2.5 | 91.4 ± 2.3 | 90.3 ± 2.7 | 90.4 ± 2.6 | |
| MLP | 94.5 ± 1.2 | 94.6 ± 1.3 | 94.3 ± 1.3 | 94.2 ± 1.3 | |
| Histograms for Bytecode (See Section 4.4) | KNN | 96.1 ± 0.9 | 96.3 ± 0.9 | 96.1 ± 0.9 | 96.1 ± 0.9 |
| SVM | 97.2 ± 1.2 | 97.4 ± 1.1 | 97.1 ± 1.3 | 97.2 ± 1.2 | |
| RF | 97.0 ± 1.0 | 97.2 ± 0.8 | 97.0 ± 1.1 | 97.0 ± 1.0 | |
| MLP | 91.8 ± 1.6 | 92.4 ± 1.1 | 91.6 ± 1.7 | 91.6 ± 1.5 | |
| Histograms for AST (See Section 4.5) | KNN | 95.5 ± 0.9 | 95.7 ± 0.8 | 95.4 ± 1.1 | 95.4 ± 1.0 |
| SVM | 96.6 ± 1.4 | 96.7 ± 1.3 | 96.5 ± 1.4 | 96.5 ± 1.4 | |
| RF | 97.2 ± 0.7 | 97.4 ± 0.7 | 97.2 ± 0.8 | 97.2 ± 0.8 | |
| MLP | 88.4 ± 1.4 | 89.0 ± 1.3 | 87.8 ± 1.4 | 87.9 ± 1.4 |
| Classifier | KNN | SVM | RF | MLP | ||||
|---|---|---|---|---|---|---|---|---|
| Embedding | Sign | p-Value | Sign | p-Value | Sign | p-Value | Sign | p-Value |
| word2vec | + | 0.004 | + | 0.004 | + | 0.004 | + | 0.004 |
| Second-order AST-based Markov chain | + | 0.011 | = | 0.250 | = | 0.916 | = | 0.652 |
| code2vec | = | 0.820 | = | 0.359 | + | 0.004 | + | 0.008 |
| Histograms for bytecode | – | 0.019 | = | 0.359 | = | 0.207 | + | 0.004 |
| Histograms for AST | − | 0.004 | = | 0.164 | = | 0.498 | + | 0.004 |
| Classifier | KNN | SVM | RF | MLP | ||||
|---|---|---|---|---|---|---|---|---|
| Embedding | Sign | p-Value | Sign | p-Value | Sign | p-Value | Sign | p-Value |
| word2vec | + | 0.004 | + | 0.004 | + | 0.004 | + | 0.004 |
| Second-order AST-based Markov chain | + | 0.004 | = | 0.652 | = | 0.150 | + | 0.027 |
| code2vec | + | 0.004 | + | 0.004 | + | 0.004 | + | 0.004 |
| Histograms for bytecode | = | 0.570 | = | 0.359 | + | 0.027 | + | 0.004 |
| Histograms for AST | = | 0.426 | = | 0.074 | + | 0.042 | + | 0.004 |
| Program Embedding | Total Components | Non-Zero | Zero |
|---|---|---|---|
| word2vec | 100 | 100 | 0 |
| First-order Markov chain | 4096 | 17 | 4079 |
| Second-order Markov chain | 35,721 | 23 | 35,698 |
| code2vec | 384 | 384 | 0 |
| Histograms for bytecode | 73 | 15 | 58 |
| Histograms for AST | 75 | 19 | 56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gorchakov, A.V.; Demidova, L.A.; Sovietov, P.N. Analysis of Program Representations Based on Abstract Syntax Trees and Higher-Order Markov Chains for Source Code Classification Task. Future Internet 2023, 15, 314. https://doi.org/10.3390/fi15090314
Gorchakov AV, Demidova LA, Sovietov PN. Analysis of Program Representations Based on Abstract Syntax Trees and Higher-Order Markov Chains for Source Code Classification Task. Future Internet. 2023; 15(9):314. https://doi.org/10.3390/fi15090314
Chicago/Turabian StyleGorchakov, Artyom V., Liliya A. Demidova, and Peter N. Sovietov. 2023. "Analysis of Program Representations Based on Abstract Syntax Trees and Higher-Order Markov Chains for Source Code Classification Task" Future Internet 15, no. 9: 314. https://doi.org/10.3390/fi15090314
APA StyleGorchakov, A. V., Demidova, L. A., & Sovietov, P. N. (2023). Analysis of Program Representations Based on Abstract Syntax Trees and Higher-Order Markov Chains for Source Code Classification Task. Future Internet, 15(9), 314. https://doi.org/10.3390/fi15090314






