Distributed Average Consensus Algorithms in d-Regular Bipartite Graphs: Comparative Study
Abstract
1. Introduction
- ☐
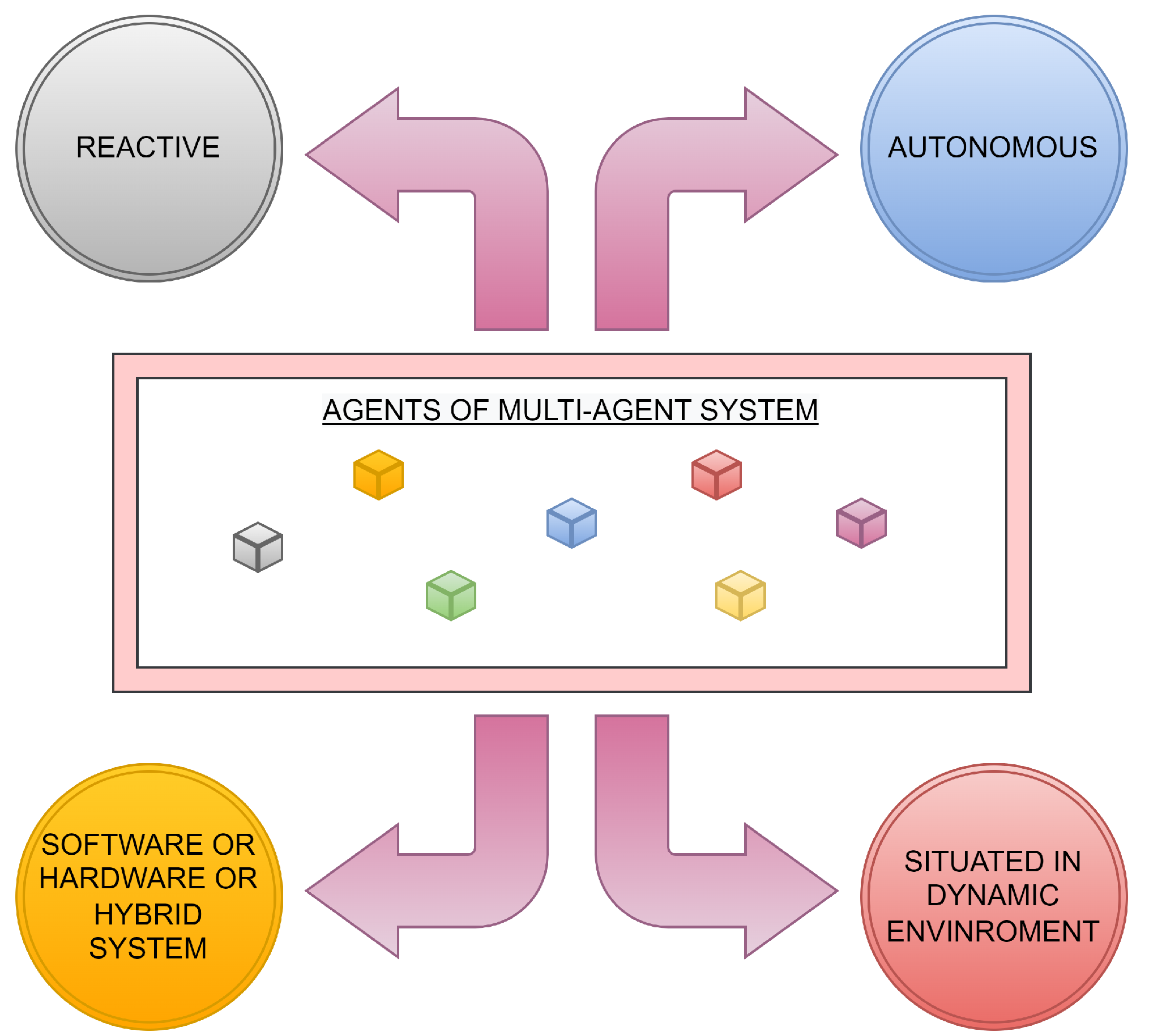
- Data Aggregation in Multi-Agent Systems: this subsection explains the importance of data aggregation, contains its definition and four-step process, discusses the benefits of its application, provides insight into multi-agent systems (MASs), and justifies the application of data aggregation mechanisms in these systems;
- ☐
- Distributed Consensus-Based Data Aggregation: in this subsection, we explain the general meaning of the term consensus, its meaning in the context of MASs, and the requirements for distributed consensus algorithms;
- ☐
- Theoretical Insight into d-Regular Bipartite Graphs: this subsection provides the definition of d-regular bipartite graphs, their graphical example, and examples of their applications;
- ☐
- Our Contribution: this subsection specifies our contribution presented in this paper and justifies the benefit of this manuscript compared to related papers;
- ☐
- Paper Organization: here, the paper structure is provided.
1.1. Data Aggregation in Multi-Agent Systems
- ■
- Phase 1: extracting data from independent sources;
- ■
- Phase 2: storing the extracted data;
- ■
- Phase 3: interpretation of the stored data;
- ■
- Phase 4: presenting the processed data in an appropriate form.
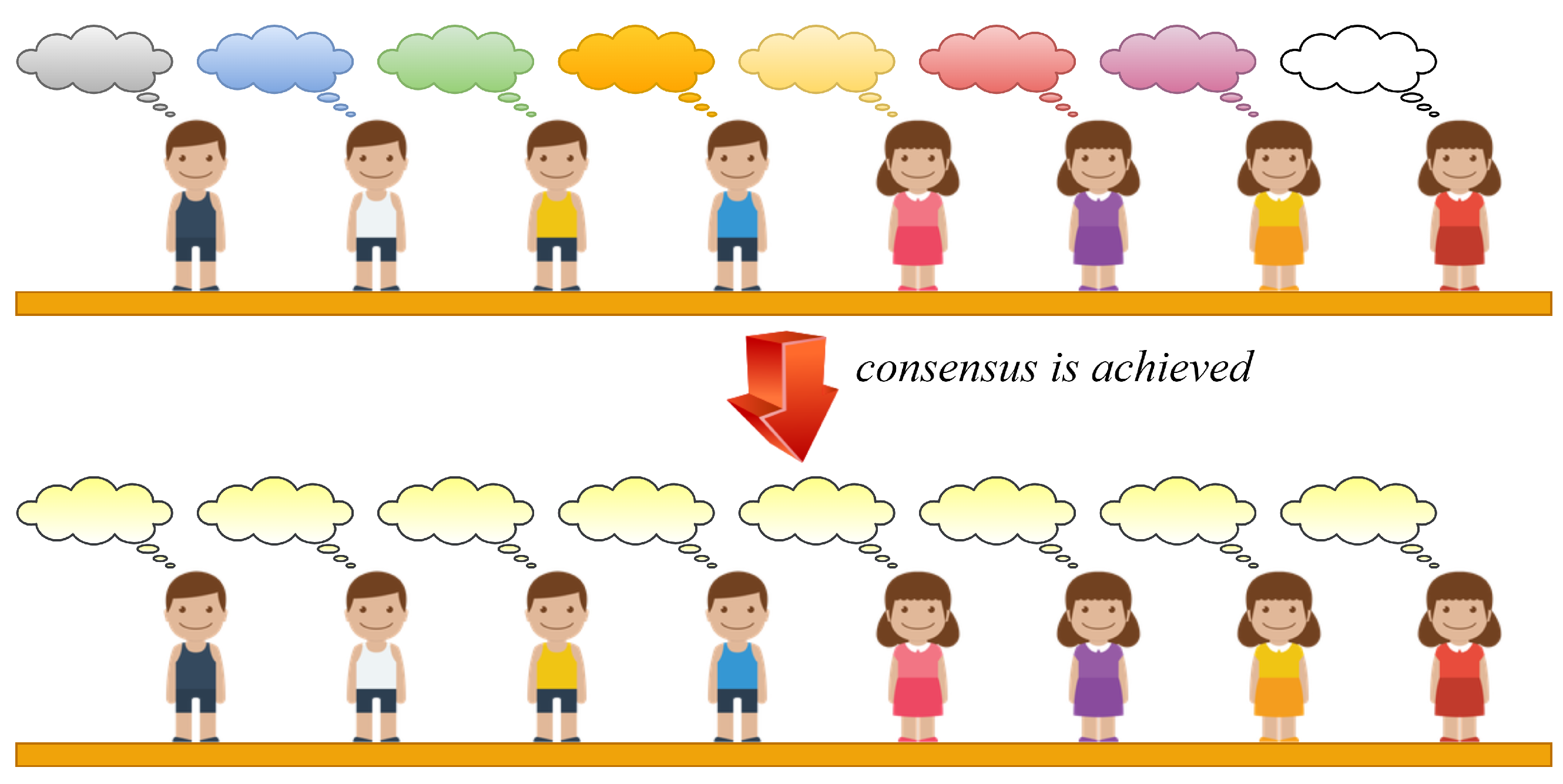
1.2. Distributed Consensus-Based Data Aggregation
- ■
- Agreement: all the non-faulty agents of MASs are required to agree on the same value (resp. on a precise estimate of this value);
- ■
- Validity: All the agents of MASs have to agree on a value suggested by the values of these agents. In other words, none of the non-faulty agents in MASs can decide on a value that is not suggested by the value of the agents in the system;
- ■
- Termination: the distributed consensus is achieved, provided that each non-faulty agent in MASs is in the agreement with all the other ones.
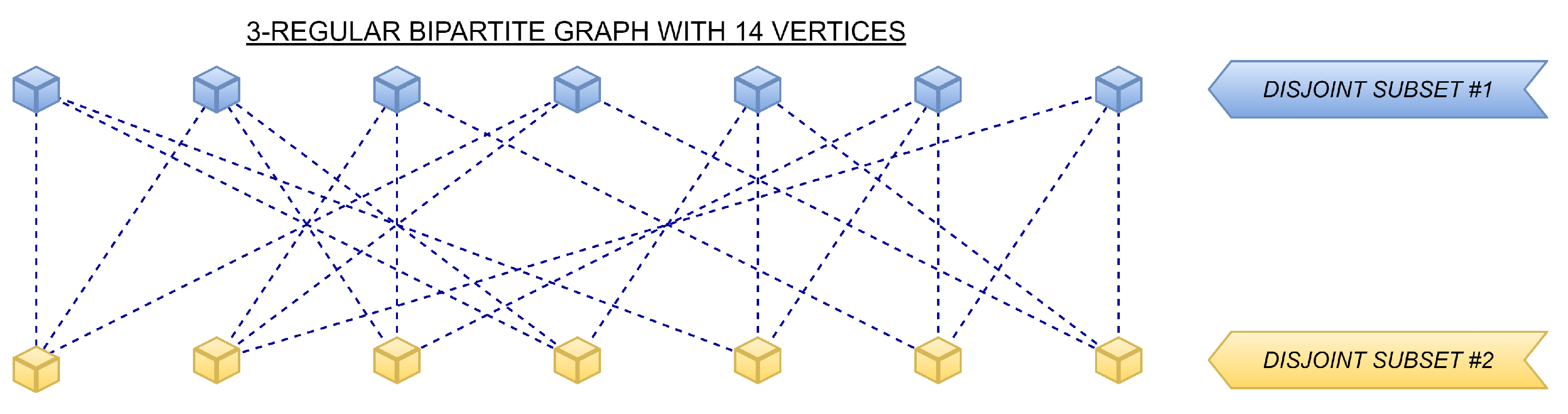
1.3. Theoretical Insight into d-Regular Bipartite Graphs
- ■
- Definition of d-regular graphs: the degree of each vertex from V is the same and equal to d;
- ■
- Definition of bipartite graphs: its vertex set V is splittable into two disjoint subsets such that two vertices from the same disjoint subset are not linked to one another.
1.4. Our Contribution
- ■
- Maximum-Degree weights (MD);
- ■
- Local-Degree weights (LD);
- ■
- Metropolis–Hastings algorithm (MH);
- ■
- Best-Constant weights (BC);
- ■
- Convex Optimized weights (OW);
- ■
- Constant weights (CW);
- ■
- Generalized Metropolis–Hastings algorithm (GMH).
1.5. Paper Organization
- ☐
- Section 2—Related Work: this is divided into two subsections and consists of topical and frequently cited papers addressing either consensus-based data aggregation in subjected/closely related graph topologies or the algorithms chosen for evaluation in non-regular non-bipartite graphs;
- ☐
- Section 3—Theoretical Background: this is divided into three subsections and provides the used mathematical model of MASs, a general definition of distributed consensus algorithms, and the weight matrices of the examined distributed average consensus algorithms;
- ☐
- Section 4—Experiments and Discussion: this is formed by three subsections again, consisting of the applied research methodology, experimental results, and a comparison of our conclusions with conclusions presented in papers where the selected algorithms are examined in non-regular non-bipartite graphs;
- ☐
- Section 5—Conclusions: this provides a brief summary of the contribution presented in this paper;
- ☐
- Appendix A—Appendix: this contains tables with the experimental results in numerical form.
2. Related Work
- ☐
- Distributed Consensus Algorithms in d-Regular Bipartite Graphs: this subsection introduces papers addressing consensus-based algorithms for data aggregation in regular bipartite graphs and related graphs;
- ☐
- Distributed Consensus Algorithms in non-Regular non-Bipartite Graphs: in this subsection, we provide an overview of papers concerned with a comparison of the chosen algorithms in non-regular non-bipartite graphs.
2.1. Distributed Consensus Algorithms in d-Regular Bipartite Graphs
2.2. Distributed Consensus Algorithms in Non-Regular Non-Bipartite Graphs
3. Theorethical Background
- ☐
- Applied Mathematical Model of Multi-Agent Systems: this subsection is concerned with the applied mathematical model of MASs;
- ☐
- General Definition of Average Consensus Algorithms: here, we provide general update rules of distributed average consensus algorithms and their convergence conditions;
- ☐
- Examined Distributed Consensus Algorithms: in this subsection, we introduce all the algorithms chosen for evaluation in d-regular bipartite graphs.
3.1. Applied Mathematical Model of Multi-Agent Systems
3.2. General Definition of Average Consensus Algorithms
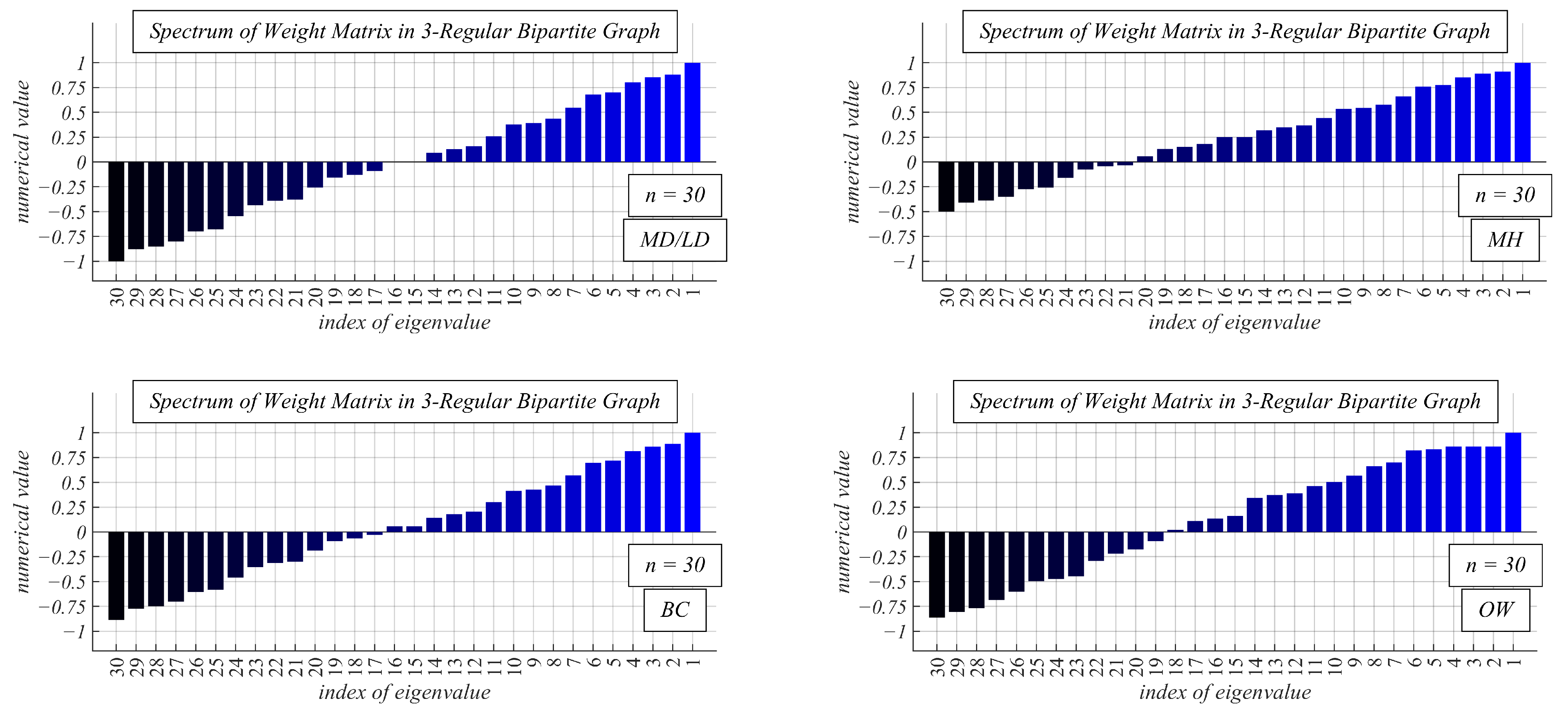
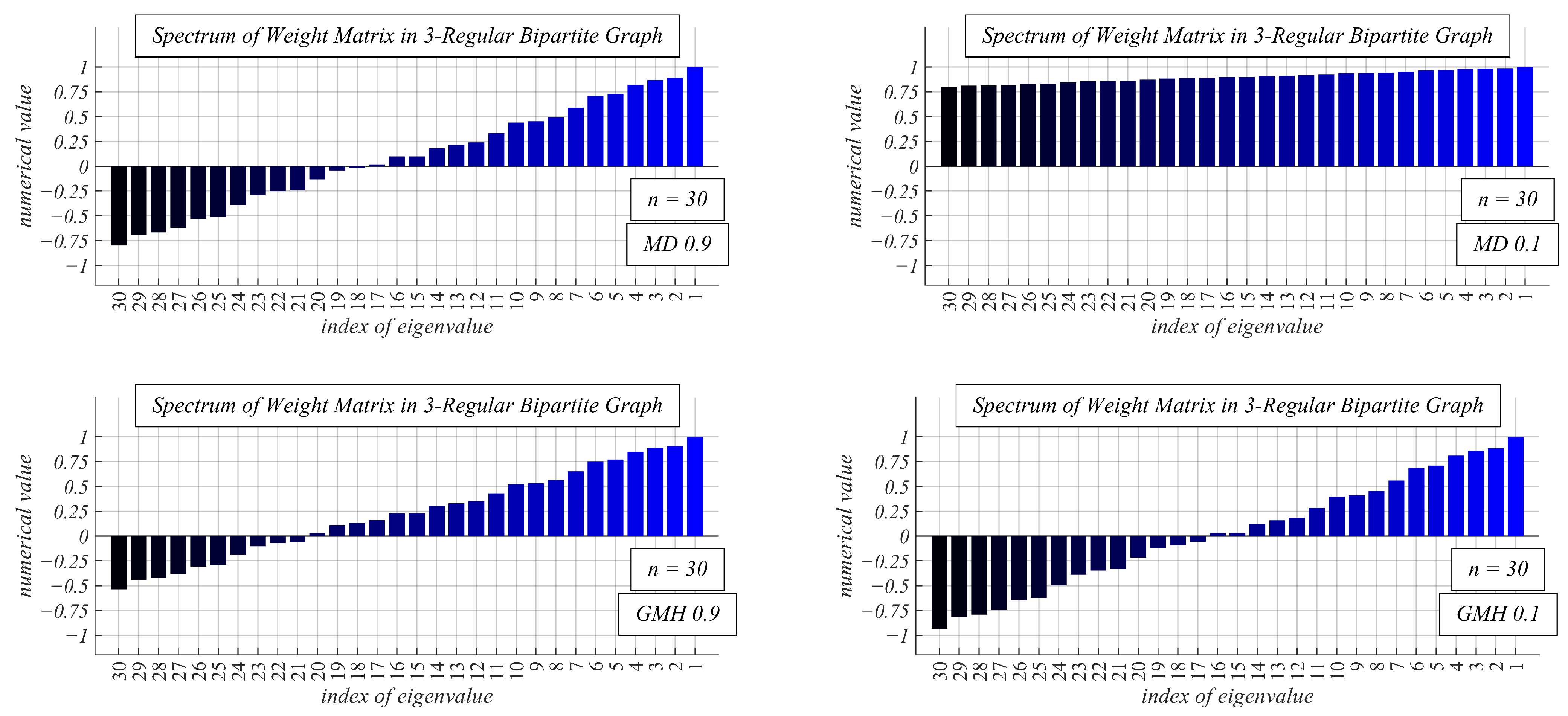
3.3. Examined Distributed Consensus Algorithms
4. Experiments and Discussion
- ☐
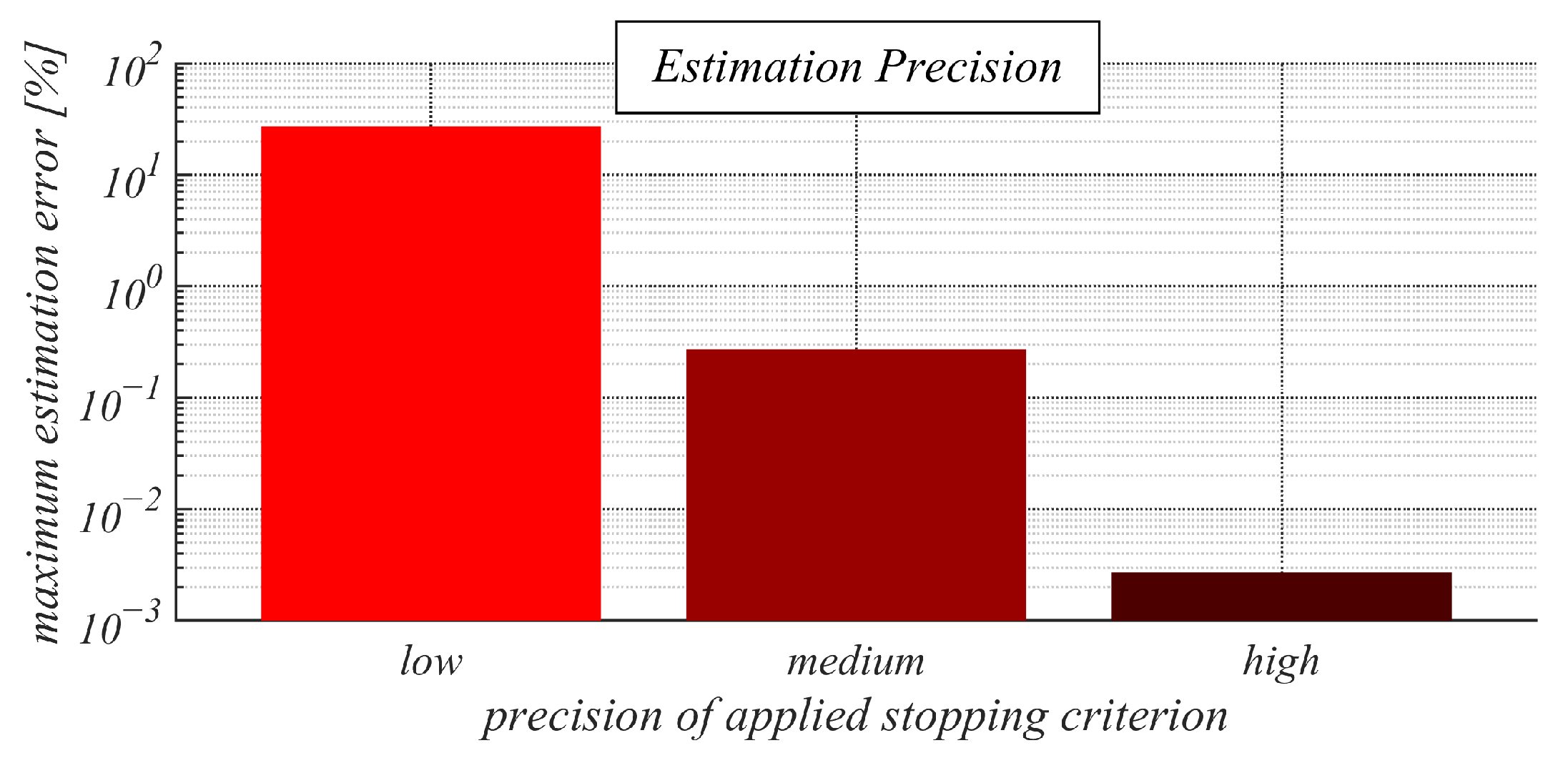
- Research Methodology and Applied Metric for Performance Evaluation: in this subsection, we introduce the simulation tool used, we specify the used d-regular bipartite graphs, and we provide the applied metric, the used stopping criterion, the method of generating the initial inner states, and the examined setups of CW and GMH;
- ☐
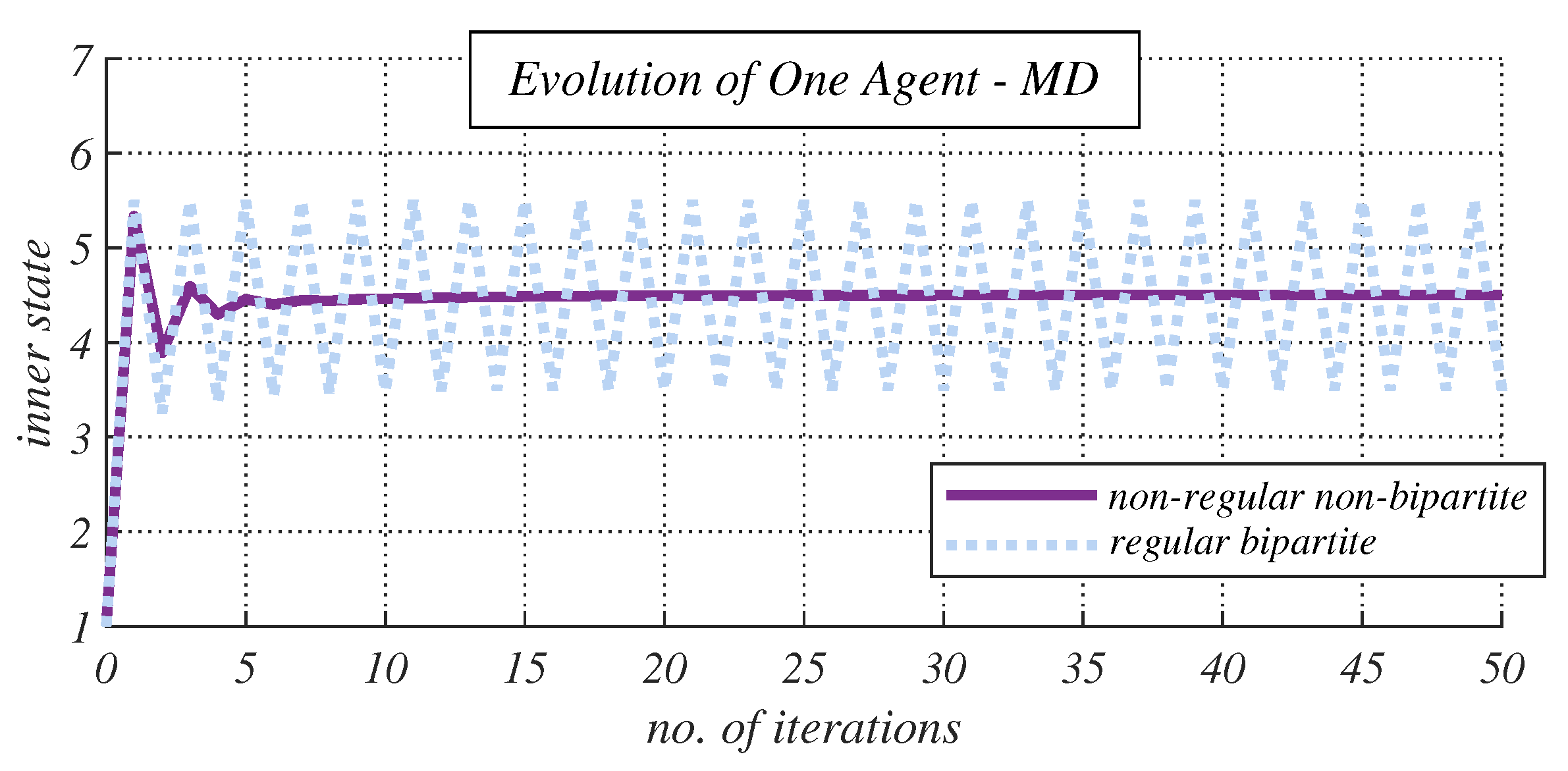
- Experimental Results and Discussion about Observable Phenomena: this subsection consists of the experimentally obtained results depicted in 15 figures and a subsequent discussion;
- ☐
- Comparison with Papers Concerned with Examined Algorithms in Non-Regular Non-Bipartite Graphs: here, we compare the contributions presented in this paper with manuscripts addressing the examined algorithms in non-regular non-bipartite graphs.
4.1. Research Methodology and Applied Metric for Performance Evaluation
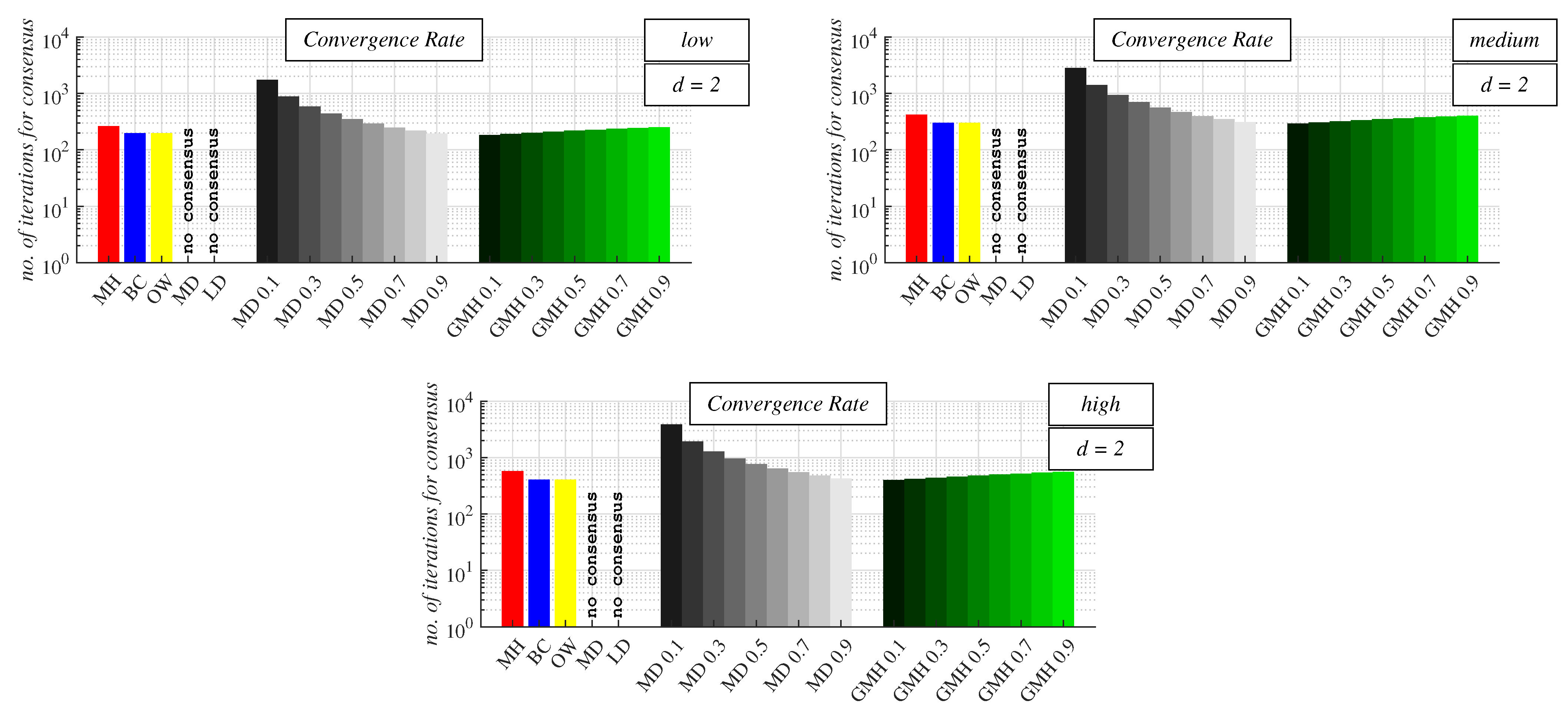
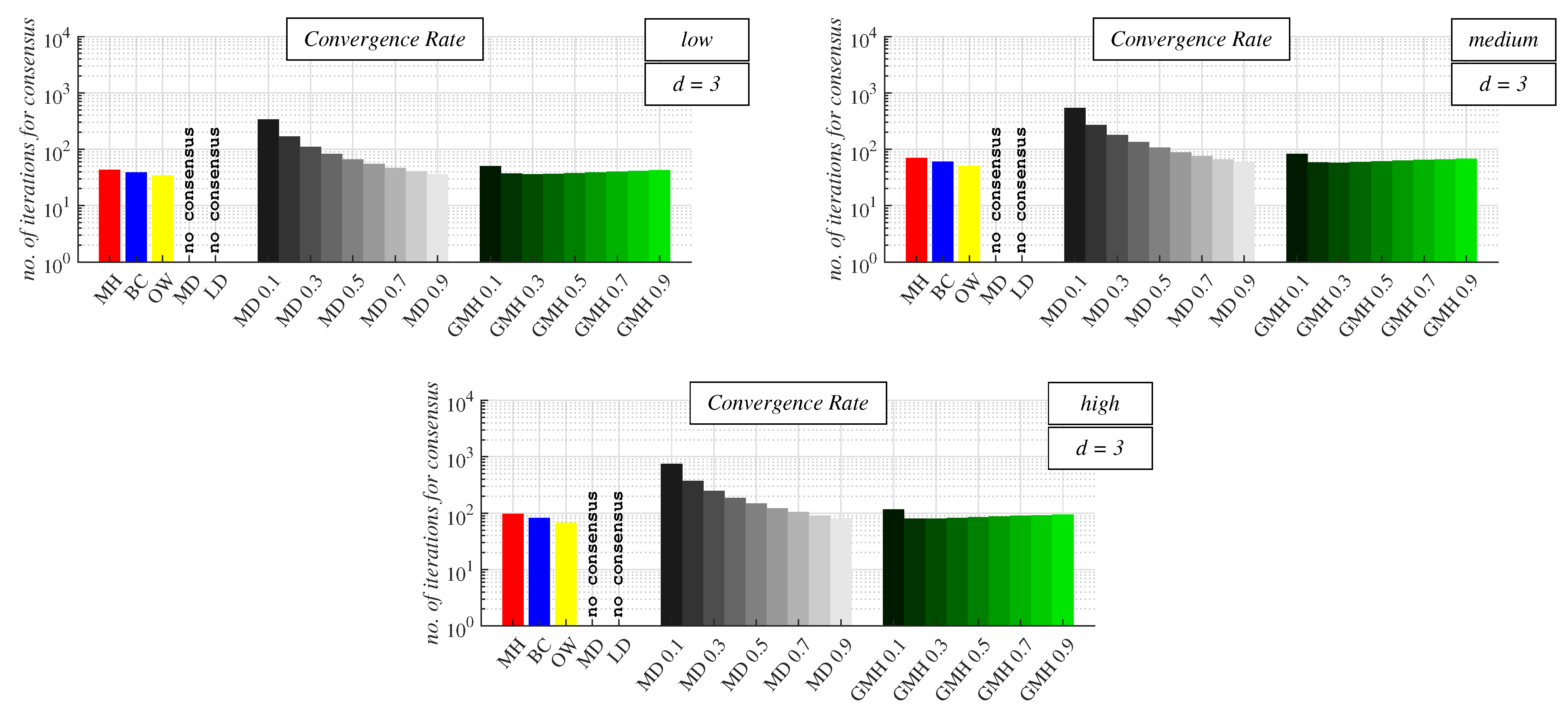
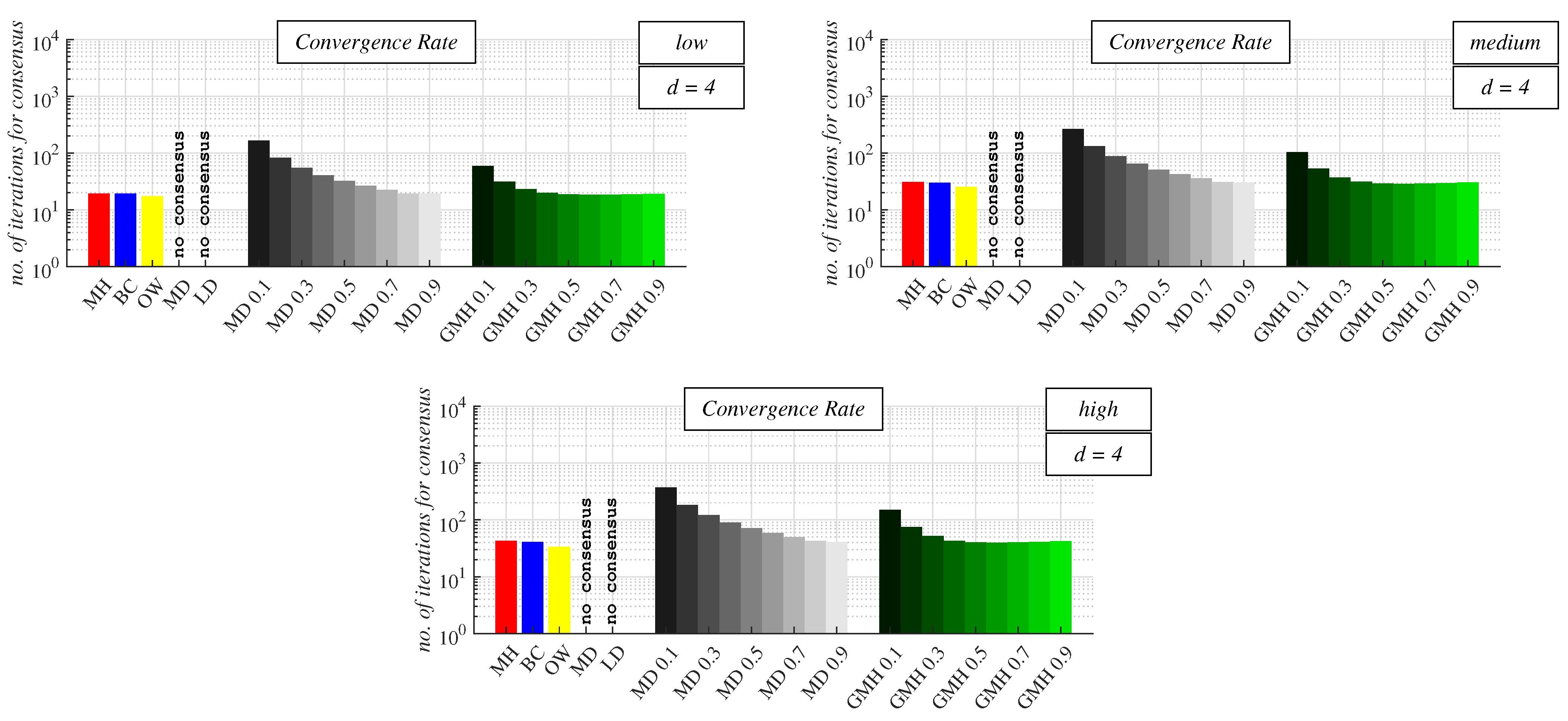
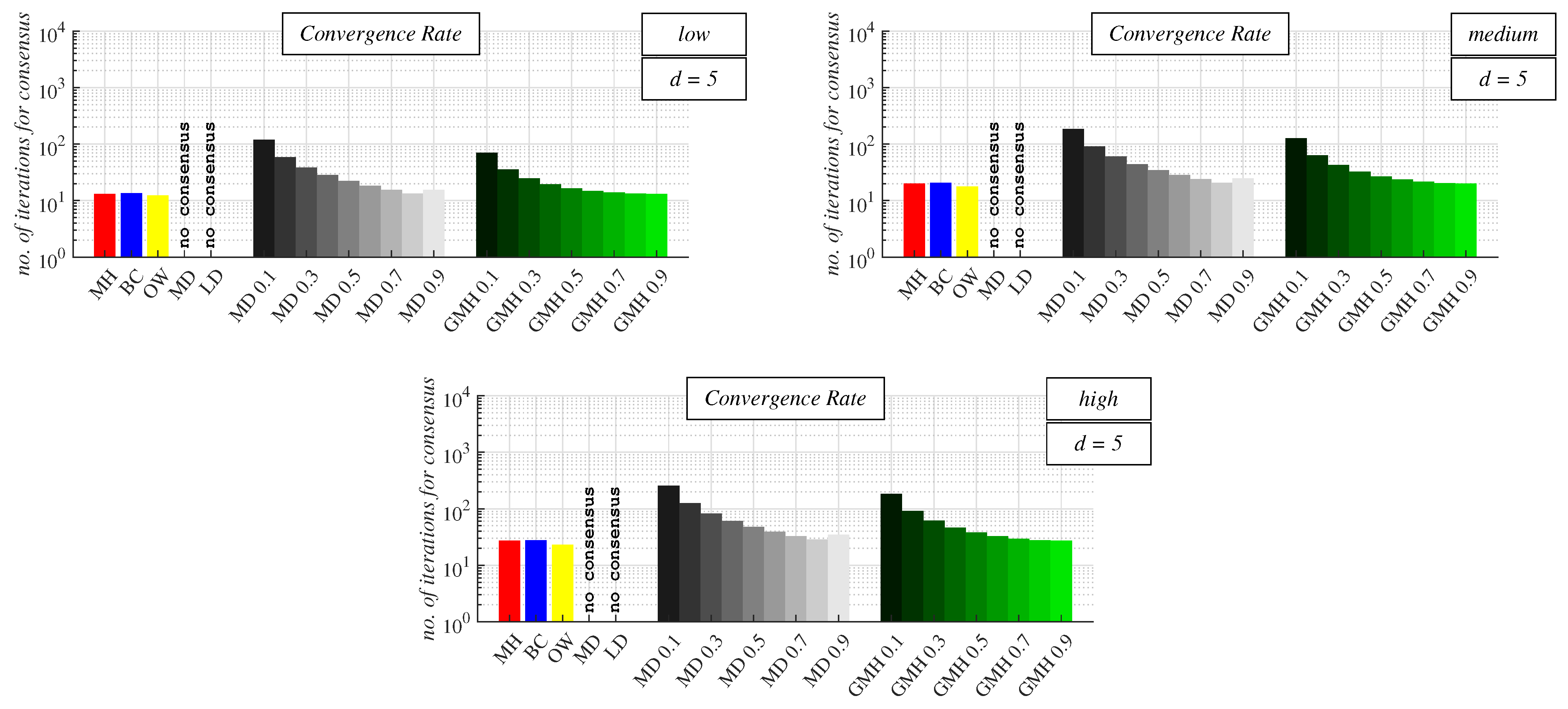
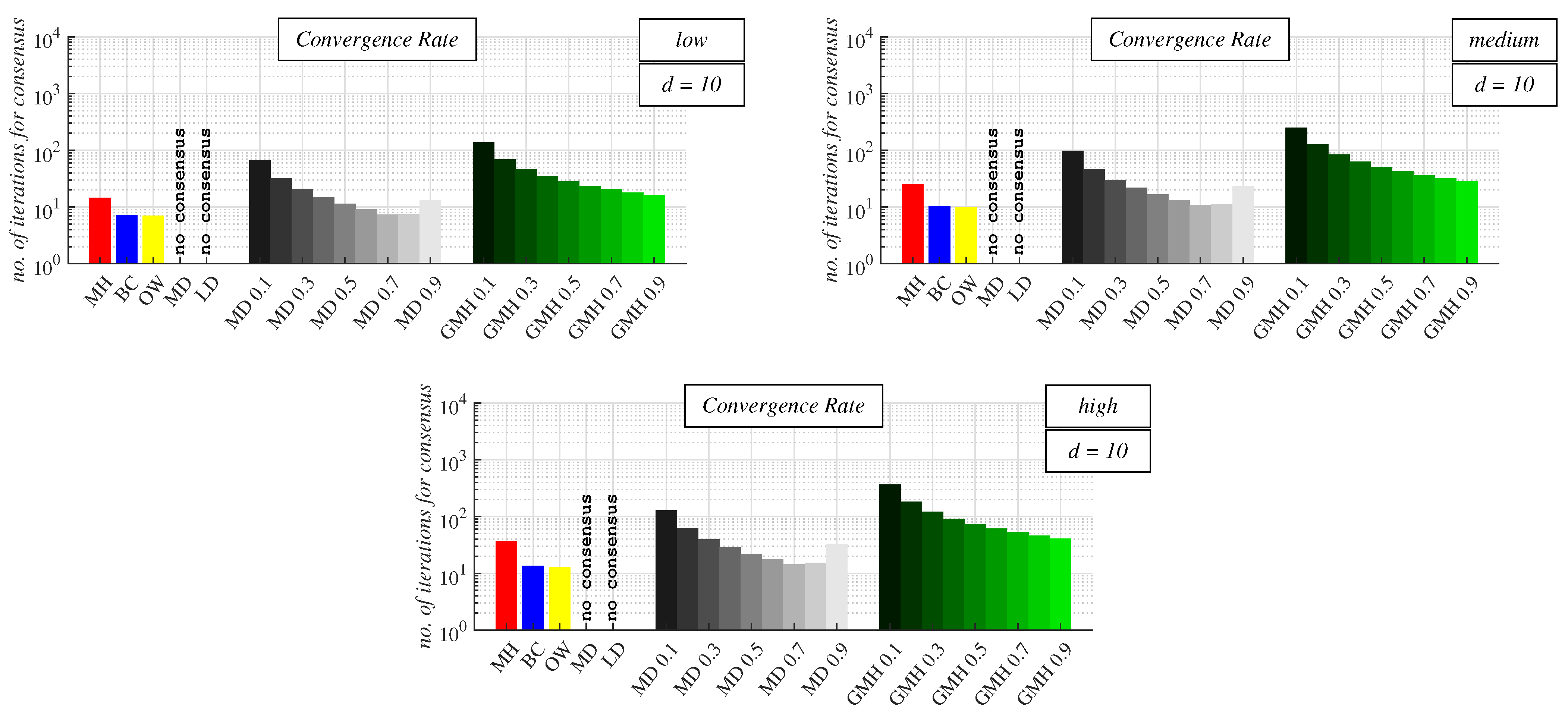
4.2. Experimental Results and Discussion about Observable Phenomena
4.3. Comparison with Papers Concerned with Examined Algorithms in Non-Regular Non-Bipartite Graphs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BC | Best constant weights |
| CW | Constant weights |
| GMH | Generalized Metropolis–Hastings algorithm |
| IID | Independent and identically distributed |
| LD | Local-degree weights |
| MAS | Multi-agent system |
| MD | Maximum-degree weights |
| MH | Metropolis–Hastings algorithm |
| OW | Convex optimized weights |
| QoS | Quality of service |
| UAV | Unmanned aerial vehicle |
Appendix A
| MH | BC | OW | CW | GMH | |
|---|---|---|---|---|---|
| Low | 261.69 it. | 196.75 it. | 196.75 it. | 193.47 it. | 182.78 it. |
| Medium | 418.54 it. | 301.86 it. | 301.86 it. | 309.40 it. | 292.16 it. |
| High | 575.45 it. | 407.27 it. | 407.27 it. | 425.36 it. | 401.74 it. |
| MH | BC | OW | CW | GMH | |
|---|---|---|---|---|---|
| Low | 43.52 it. | 39.03 it. | 34.35 it. | 36.31 it. | 36.11 it. |
| Medium | 70.10 it. | 60.39 it. | 50.88 it. | 58.07 it. | 57.67 it. |
| High | 97.18 it. | 81.85 it. | 67.66 it. | 80.48 it. | 79.70 it. |
| MH | BC | OW | CW | GMH | |
|---|---|---|---|---|---|
| Low | 19.47 it. | 19.43 it. | 17.50 it. | 19.31 it. | 18.38 it. |
| Medium | 31.02 it. | 30.08 it. | 25.44 it. | 30.08 it. | 28.83 it. |
| High | 42.99 it. | 40.68 it. | 33.33 it. | 41.16 it. | 39.61 it. |
| MH | BC | OW | CW | GMH | |
|---|---|---|---|---|---|
| Low | 13.12 it. | 13.54 it. | 12.40 it. | 13.32 it. | 13.19 it. |
| Medium | 20.07 it. | 20.58 it. | 17.72 it. | 20.69 it. | 20.10 it. |
| High | 27.27 it. | 27.79 it. | 23.11 it. | 28.35 it. | 27.27 it. |
| MH | BC | OW | CW | GMH | |
|---|---|---|---|---|---|
| Low | 14.56 it. | 7.12 it. | 7.05 it. | 7.33 it. | 16.11 it. |
| Medium | 25.57 it. | 10.21 it. | 10.02 it. | 10.82 it. | 28.37 it. |
| High | 36.86 it. | 13.46 it. | 13.03 it. | 14.31 it. | 41.03 it. |
References
- Pigozzi, G.; Hartmann, S. Aggregation in multiagent systems and the problem of truth-tracking. In Proceedings of the 6th International Joint Conference on Autonomous Agents and Multiagent Systems, Honolulu, HI, USA, 14–18 May 2007; pp. 219–221. [Google Scholar]
- Wang, J.; Yang, Y.; Wang, T.; Sherratt, R.S.; Zhang, J. Big data service architecture: A survey. J. Internet Technol. 2020, 21, 393–405. [Google Scholar]
- Vachkova, S.N.; Petryaeva, E.Y.; Kupriyanov, R.B.; Suleymanov, R.S. School in digital age: How big data help to transform the curriculum. Information 2021, 12, 33. [Google Scholar] [CrossRef]
- Stamatescu, G.; Chitu, C. Privacy-Preserving Sensing and Two-Stage Building Occupancy Prediction using Random Forest Learning. J. Sens. 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Bagha, H.; Yavari, A.; Georgakopoulos, D. Hybrid Sensing Platform for IoT-Based Precision Agriculture. Future Internet 2022, 14, 233. [Google Scholar] [CrossRef]
- Nicolae, M.; Popescu, D.; Merezeanu, D.; Ichim, L. Large scale wireless sensor networks based on fixed nodes and mobile robots in precision agriculture. Mech. Mach. Sci. 2019, 67, 236–244. [Google Scholar]
- Abbasian Dehkordi, S.; Farajzadeh, K.; Rezazadeh, J.; Farahbakhsh, R.; Sandrasegaran, K.; Abbasian Dehkordi, M. A survey on data aggregation techniques in IoT sensor networks. Wirel. Netw. 2020, 26, 1243–1263. [Google Scholar] [CrossRef]
- Guarino, S.; Mastrostefano, E.; Bernaschi, M.; Celestini, A.; Cianfriglia, M.; Torre, D.; Zastrow, L.R. Inferring Urban Social Networks from Publicly Available Data. Future Internet 2021, 13, 108. [Google Scholar] [CrossRef]
- Homaei, M.H.; Salwana, E.; Shamshirband, S. An enhanced distributed data aggregation method in the Internet of Things. Sensors 2019, 19, 3173. [Google Scholar] [CrossRef]
- Fan, H.; Liu, Y.; Zeng, Z. Decentralized privacy-preserving data aggregation scheme for smart grid based on blockchain. Sensors 2020, 20, 5282. [Google Scholar] [CrossRef]
- Dash, L.; Pattanayak, B.K.; Mishra, S.K.; Sahoo, K.S.; Jhanjhi, N.Z.; Baz, M.; Masud, M. A Data Aggregation Approach Exploiting Spatial and Temporal Correlation among Sensor Data in Wireless Sensor Networks. Electronics 2022, 11, 989. [Google Scholar] [CrossRef]
- Priyanka, E.B.; Thangavel, S.; Sagayam, K.M.; Elngar, A.A. Wireless network upgraded with artificial intelligence on the data aggregation towards the smart internet applications. Int. J. Syst. Assur. Eng. Manag. 2022, 13, 1254–1267. [Google Scholar] [CrossRef]
- Ozdemir, S.; Xiao, Y. Secure data aggregation in wireless sensor networks: A comprehensive overview. Comput. Netw. 2009, 53, 2022–2037. [Google Scholar] [CrossRef]
- Senderovich, A.; Shleyfman, A.; Weidlich, M.; Gal, A.; Mandelbaum, A. To aggregate or to eliminate? Optimal model simplification for improved process performance prediction. Inf. Syst. 2018, 78, 96–111. [Google Scholar] [CrossRef]
- Çam, H.; Özdemir, S.; Nair, P.; Muthuavinashiappan, D.; Sanli, H.O. Energy-efficient secure pattern based data aggregation for wireless sensor networks. Comput. Commun. 2006, 29, 446–455. [Google Scholar] [CrossRef]
- Femminella, M.; Reali, G. Gossip-based Monitoring Protocol for 6G Networks. IEEE Trans. Netw. Serv. Manag. 2023. early access. [Google Scholar] [CrossRef]
- Ionescu, L. Digital data aggregation, analysis, and infrastructures in fintech operations. Rev. Contemp. Philos. 2020, 19, 92–98. [Google Scholar]
- Sand, G.; Tsitouras, L.; Dimitrakopoulos, G.; Chatzigiannakis, V. A big data aggregation, analysis and exploitation integrated platform for increasing social management intelligence. In Proceedings of the 2014 IEEE International Conference on Big Data (Big Data), Washington, DC, USA, 27–30 October 2014; pp. 40–47. [Google Scholar]
- Li, C.T.; Shih, D.H.; Wang, C.C.; Chen, C.L.; Lee, C.C. A blockchain based data aggregation and group authentication scheme for electronic medical system. IEEE Access 2020, 8, 173904–173917. [Google Scholar] [CrossRef]
- Dhand, G.; Tyagi, S.S. Data aggregation techniques in WSN: Survey. Procedia Comput. Sci. 2016, 92, 378–384. [Google Scholar] [CrossRef]
- Dorri, A.; Kanhere, S.S.; Jurdak, R. Multi-agent systems: A survey. IEEE Access 2018, 6, 28573–28593. [Google Scholar] [CrossRef]
- Al-Doghman, F.; Chaczko, Z.; Jiang, J. A review of aggregation algorithms for the internet of things. In Proceedings of the 2017 25th International Conference on Systems Engineering (ICSEng), Las Vegas, NV, USA, 22–24 August 2017; pp. 480–487. [Google Scholar]
- Izadi, D.; Abawajy, J.H.; Ghanavati, S.; Herawan, T. A data fusion method in wireless sensor networks. Sensors 2015, 15, 2964–2979. [Google Scholar] [CrossRef]
- Stamatescu, G.; Stamatescu, I.; Popescu, D. Consensus-based data aggregation for wireless sensor networks. J. Control Eng. Appl. Inform. 2017, 19, 43–50. [Google Scholar]
- Huang, R.; Yang, X.; Ajay, P. Consensus mechanism for software-defined blockchain in internet of things. Internet Things Cyber-Phys. Syst. 2023, 3, 52–60. [Google Scholar] [CrossRef]
- Viriyasitavat, W.; Hoonsopon, D. Blockchain characteristics and consensus in modern business processes. J. Ind. Inf. Integr. 2019, 13, 32–39. [Google Scholar] [CrossRef]
- Ferdous, M.S.; Chowdhury, M.J.M.; Hoque, M. A survey of consensus algorithms in public blockchain systems for crypto-currencies. J. Netw. Comput. Appl. 2021, 182, 103035. [Google Scholar] [CrossRef]
- Claveria, O. A new consensus-based unemployment indicator. Appl. Econ. Lett. 2019, 26, 812–817. [Google Scholar] [CrossRef]
- Ullah, M.A.; Setiawan, J.W.; ur Rehman, J.; Shin, H. On the robustness of quantum algorithms for blockchain consensus. Sensors 2022, 22, 2716. [Google Scholar] [CrossRef] [PubMed]
- Alotaibi, R.; Alassafi, M.; Bhuiyan, M.S.I.; Raju, R.S.; Ferdous, M.S. A Reinforcement-Learning-Based Model for Resilient Load Balancing in Hyperledger Fabric. Processes 2022, 10, 2390. [Google Scholar] [CrossRef]
- Ji, X.; Zhang, W.; Chen, S.; Luo, J.; Lu, L.; Yuan, W.; Hu, Z.; Chen, J. Speeding up velocity consensus control with small world communication topology for unmanned aerial vehicle Swarms. Electronics 2021, 10, 2547. [Google Scholar] [CrossRef]
- Wang, C.; Mu, Z.; Mou, C.; Zheng, H.; Liu, J. Consensus-based clustering of single cells by reconstructing cell-to-cell dissimilarity. Briefings Bioinform. 2022, 23, bbab379. [Google Scholar] [CrossRef]
- Khan, D.; Jung, L.T.; Hashmani, M.A.; Waqas, A. A critical review of blockchain consensus model. In Proceedings of the 2020 3rd international conference on computing, mathematics and engineering technologies (iCoMET), Sukkur, Pakistan, 29–30 January 2020; pp. 1–6. [Google Scholar]
- Li, Y.; Tan, C. A survey of the consensus for multi-agent systems. Syst. Sci. Control Eng. 2019, 7, 468–482. [Google Scholar] [CrossRef]
- Moniz, H. The Istanbul BFT consensus algorithm. arXiv 2020, arXiv:2002.03613. [Google Scholar]
- Fan, Y.; Wu, H.; Paik, H.Y. DR-BFT: A consensus algorithm for blockchain-based multi-layer data integrity framework in dynamic edge computing system. Future Gener. Comput. Syst. 2021, 124, 33–48. [Google Scholar] [CrossRef]
- Ma, X.; Dong, L.; Wang, Y.; Li, Y.; Sun, M. AIRC: Attentive Implicit Relation Recommendation Incorporating Content Information for Bipartite Graphs. Mathematics 2020, 8, 2132. [Google Scholar] [CrossRef]
- Gao, W.; Aamir, M.; Iqbal, Z.; Ishaq, M.; Aslam, A. On Irregularity Measures of Some Dendrimers Structures. Mathematics 2019, 7, 271. [Google Scholar] [CrossRef]
- Tikhomirov, K.; Youssef, P. Sharp Poincaré and log-Sobolev inequalities for the switch chain on regular bipartite graphs. Probab. Theory Relat. Fields 2023, 185, 89–184. [Google Scholar] [CrossRef]
- Kulkarni, R. A New NC-Algorithm for Finding a Perfect Matching in d-Regular Bipartite Graphs When d Is Small. Lect. Notes Comput. Sci. 2006, 3998, 308–319. [Google Scholar]
- Chakraborty, S.; Shaikh, S.H.; Mandal, S.B.; Ghosh, R.; Chakrabarti, A. A study and analysis of a discrete quantum walk-based hybrid clustering approach using d-regular bipartite graph and 1D lattice. Int. J. Quantum Inf. 2019, 17, 1950016. [Google Scholar] [CrossRef]
- Arieli, I.; Sandomirskiy, F.; Smorodinsky, R. On social networks that support learning. arXiv 2020, arXiv:2011.05255. [Google Scholar] [CrossRef]
- Zehmakan, A.N. Majority Opinion Diffusion in Social Networks: An Adversarial Approach. In Proceedings of the 35th AAAI Conference on Artificial Intelligence (AAAI 2021), Online, 2–9 February 2021; pp. 5611–5619. [Google Scholar]
- Brandes, U.; Holm, E.; Karrenbauer, A. Cliques in regular graphs and the core-periphery problem in social networks. Lect. Notes Comput. Sci. 2016, 10043, 175–186. [Google Scholar]
- Rödder, W.; Dellnitz, A.; Kulmann, F.; Litzinger, S.; Reucher, E. Bipartite Structures in Social Networks: Traditional versus Entropy-Driven Analyses. Entropy 2019, 21, 277. [Google Scholar] [CrossRef]
- Galanter, N.; Silva, D., Jr.; Rowell, J.T.; Rychtář, J. Resource competition amid overlapping territories: The territorial raider model applied to multi-group interactions. J. Theor. Biol. 2017, 412, 100–106. [Google Scholar] [CrossRef]
- El-Mesady, A.; Romanov, A.Y.; Amerikanov, A.A.; Ivannikov, A.D. On Bipartite Circulant Graph Decompositions Based on Cartesian and Tensor Products with Novel Topologies and Deadlock-Free Routing. Algorithms 2023, 16, 10. [Google Scholar] [CrossRef]
- Pavlopoulos, G.A.; Kontou, P.I.; Pavlopoulou, A.; Bouyioukos, C.; Markou, E.; Bagos, P.G. Bipartite graphs in systems biology and medicine: A survey of methods and applications. GigaScience 2018, 7, 1–31. [Google Scholar] [CrossRef]
- Wieling, M.; Nerbonne, J. Bipartite spectral graph partitioning for clustering dialect varieties and detecting their linguistic features. Comput. Speech Lang. 2011, 25, 700–715. [Google Scholar] [CrossRef]
- Engbers, J.; Galvin, D. H-colouring bipartite graphs. J. Comb. Theory Ser. B 2012, 102, 726–742. [Google Scholar] [CrossRef]
- Schwarz, V.; Hannak, G.; Matz, G. On the convergence of average consensus with generalized Metropolis-Hasting weights. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 5442–5446. [Google Scholar]
- Kenyeres, M.; Kenyeres, J. DR-BFT: Distributed mechanism for detecting average consensus with maximum-degree weights in bipartite regular graphs. Mathematics 2021, 9, 3020. [Google Scholar] [CrossRef]
- Kenyeres, M.; Kenyeres, J. Examination of Average Consensus with Maximum-degree Weights and Metropolis-Hastings Algorithm in Regular Bipartite Graphs. In Proceedings of the 2022 20th International Conference on Emerging eLearning Technologies and Applications (ICETA), Stary Smokovec, Slovakia, 20–21 October 2022; pp. 313–319. [Google Scholar]
- Pandey, P.K.; Singh, R. Fast Average-consensus on Networks using Heterogeneous Diffusion. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 1–5. [Google Scholar] [CrossRef]
- Dhuli, S.; Atik, J.M. Analysis of Distributed Average Consensus Algorithms for Robust IoT networks. arXiv 2021, arXiv:2104.10407. [Google Scholar]
- Kibangou, A.Y.; Commault, C. Observability in connected strongly regular graphs and distance regular graphs. IEEE Trans. Control. Netw. Syst. 2014, 1, 360–369. [Google Scholar] [CrossRef]
- Kar, S.; Moura, J.M. Consensus based detection in sensor networks: Topology optimization under practical constraints. In Proceedings of the 1st International Workshop on Information Theory in Sensor Networks, Santa Fe, NM, USA, 18–20 June 2007; pp. 1–12. [Google Scholar]
- Yu, J.; Yu, J.; Zhang, P.; Yang, T.; Chen, X. A unified framework design for finite-time bipartite consensus of multi-agent systems. IEEE Access 2021, 9, 48971–48979. [Google Scholar] [CrossRef]
- Hu, J.; Zheng, W.X. Bipartite consensus for multi-agent systems on directed signed networks. In Proceedings of the IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 3451–3456. [Google Scholar]
- Han, T.; Guan, Z.-H.; Xiao, B.; Yan, H. Bipartite Average Tracking for Multi-Agent Systems with Disturbances: Finite-Time and Fixed-Time Convergence. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 4393–4402. [Google Scholar] [CrossRef]
- Muniraju, G.; Tepedelenlioglu, C.; Spanias, A. Consensus Based Distributed Spectral Radius Estimation. IEEE Signal Process. Lett. 2020, 27, 1045–1049. [Google Scholar] [CrossRef]
- Xiao, L.; Boyd, S. Fast linear iterations for distributed averaging. Syst. Control Lett. 2004, 53, 65–78. [Google Scholar] [CrossRef]
- Jafarizadeh, S.; Jamalipour, A. Weight optimization for distributed average consensus algorithm in symmetric, CCS & KCS star networks. arXiv 2010, arXiv:1001.4278. [Google Scholar]
- Schwarz, V.; Matz, G. Nonlinear average consensus based on weight morphing. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 3129–3132. [Google Scholar]
- Kenyeres, M.; Kenyeres, J.; Budinská, I. On performance evaluation of distributed system size estimation executed by average consensus weights. Recent Adv. Soft Comput. Cybern. 2021, 403, 15–24. [Google Scholar]
- Kenyeres, M.; Kenyeres, J. On Comparative Study of Deterministic Linear Consensus-based Algorithms for Distributed Summing. In Proceedings of the 2019 International Conference on Applied Electronics (AE), Pilsen, Czech Republic, 10–11 September 2019; pp. 1–6. [Google Scholar]
- Aysal, T.C.; Oreshkin, B.N.; Coates, M.J. Accelerated distributed average consensus via localized node state prediction. IEEE Trans. Signal Process. 2008, 57, 1563–1576. [Google Scholar] [CrossRef]
- Oreshkin, B.N.; Coates, M.J.; Rabbat, M.G. Optimization and analysis of distributed averaging with short node memory. IEEE Trans. Signal Process. 2010, 58, 2850–2865. [Google Scholar] [CrossRef]
- Schwarz, V.; Matz, G. Average consensus in wireless sensor networks: Will it blend? In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 4584–4588. [Google Scholar]
- Xiao, L.; Boyd, S.; Kim, S.J. Distributed average consensus with least-mean-square deviation. J. Parallel Distrib. Comput. 2007, 67, 33–46. [Google Scholar] [CrossRef]
- Fraser, B.; Coyle, A.; Hunjet, R.; Szabo, C. An Analytic Latency Model for a Next-Hop Data-Ferrying Swarm on Random Geometric Graphs. IEEE Access 2020, 8, 48929–48942. [Google Scholar] [CrossRef]
- Gulzar, M.M.; Rizvi, S.T.H.; Javed, M.Y.; Munir, U.; Asif, H. Multi-agent cooperative control consensus: A comparative review. Electronics 2018, 7, 22. [Google Scholar] [CrossRef]
- Erdös, P.; Fajtlowicz, S.; Hoffman, A.J. Maximum degree in graphs of diameter 2. Networks 1980, 10, 87–90. [Google Scholar] [CrossRef]
- Singh, H.; Sharma, R. Role of adjacency matrix & adjacency list in graph theory. Int. J. Comput. Technol. 2012, 3, 179–183. [Google Scholar]
- Van Nuffelen, C. On the incidence matrix of a graph. IEEE Trans. Circuits Syst. 1976, 23, 572. [Google Scholar] [CrossRef]
- Merris, R. Laplacian matrices of graphs: A survey. Linear Algebra Its Appl. 1994, 197, 143–176. [Google Scholar] [CrossRef]
- Mohar, B.; Alavi, Y.; Chartrand, G.; Oellermann, O.R. The Laplacian spectrum of graphs. Graph Theory Comb. Appl. 1991, 2, 12. [Google Scholar]
- Chen, X.; Huang, L.; Ding, K.; Dey, S.; Shi, L. Privacy-preserving push-sum average consensus via state decomposition. arXiv 2020, arXiv:2009.12029. [Google Scholar] [CrossRef]
- Merezeanu, D.; Nicolae, M. Consensus control of discrete-time multi-agent systems. U. Politeh. Buch. Ser. A 2017, 79, 167–174. [Google Scholar]
- Yuan, H. A bound on the spectral radius of graphs. Linear Algebra Its Appl. 1988, 108, 135–139. [Google Scholar] [CrossRef]
- Xiao, L.; Boyd, S.; Lall, S. A scheme for robust distributed sensor fusion based on average consensus. In Proceedings of the Fourth International Symposium on Information Processing in Sensor Networks, Boise, ID, USA, 15 April 2005; pp. 63–70. [Google Scholar]
- Strand, M. Strand, M. Metropolis-Hastings Markov Chain Monte Carlo; Chapman University: Orange, CA, USA, 2009. [Google Scholar]
- Avrachenkov, K.; El Chamie, M.; Neglia, G. A local average consensus algorithm for wireless sensor networks. In Proceedings of the 2011 International Conference on Distributed Computing in Sensor Systems and Workshops (DCOSS), Barcelona, Spain, 27–29 June 2011; pp. 1–6. [Google Scholar]
- Codes for the Paper “Distributed Average Consensus Algorithms in d-Regular Bipartite Graphs: Comparative Study”. Available online: https://github.com/kenyeresm/regularbipartite (accessed on 11 May 2023).
- Pereira, S.S.; Pagès-Zamora, A. Mean square convergence of consensus algorithms in random WSNs. IEEE Trans. Signal Process. 2010, 58, 2866–2874. [Google Scholar] [CrossRef]
- Skorpil, V.; Stastny, J. Back-propagation and k-means algorithms comparison. In Proceedings of the 2006 8th International Conference on Signal Processing (ICSP 2006), Guilin, China, 16–20 November 2006; pp. 374–378. [Google Scholar]
- Lee, C.S.; Michelusi, N.; Scutari, G. Finite rate distributed weight-balancing and average consensus over digraphs. IEEE Trans. Autom. Control 2020, 66, 4530–4545. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kenyeres, M.; Kenyeres, J. Distributed Average Consensus Algorithms in d-Regular Bipartite Graphs: Comparative Study. Future Internet 2023, 15, 183. https://doi.org/10.3390/fi15050183
Kenyeres M, Kenyeres J. Distributed Average Consensus Algorithms in d-Regular Bipartite Graphs: Comparative Study. Future Internet. 2023; 15(5):183. https://doi.org/10.3390/fi15050183
Chicago/Turabian StyleKenyeres, Martin, and Jozef Kenyeres. 2023. "Distributed Average Consensus Algorithms in d-Regular Bipartite Graphs: Comparative Study" Future Internet 15, no. 5: 183. https://doi.org/10.3390/fi15050183
APA StyleKenyeres, M., & Kenyeres, J. (2023). Distributed Average Consensus Algorithms in d-Regular Bipartite Graphs: Comparative Study. Future Internet, 15(5), 183. https://doi.org/10.3390/fi15050183







