Protecting Function Privacy and Input Privacy in the Publicly Verifiable Outsourcing Computation of Polynomial Functions

Abstract

With the prevalence of cloud computing, the outsourcing of computation has gained significant attention. Clients with limited computing power often outsource complex computing tasks to the cloud to save on computing resources and costs. In outsourcing the computation of functions, a function owner delegates a cloud server to perform the function’s computation on the input received from the user. There are three primary security concerns associated with this process: protecting function privacy for the function owner, protecting input privacy for the user and guaranteeing that the cloud server performs the computation correctly. Existing works have only addressed privately verifiable outsourcing computation with privacy or publicly verifiable outsourcing computation without input privacy or function privacy. By using the technologies of homomorphic encryption, proxy re-encryption and verifiable computation, we propose the first publicly verifiable outsourcing computation scheme that achieves both input privacy and function privacy for matrix functions, which can be extended to arbitrary multivariate polynomial functions. We additionally provide a faster privately verifiable method. Moreover, the function owner retains control over the function.

1. Introduction

With the explosive growth of data, the demand for data processing among users is constantly growing, which makes cloud services increasingly popular. These cloud services can help weak clients with limited resources store large-scale data or complete expensive computational tasks at a low cost. One of the most common applications of cloud services is outsourcing computation.

Consider a setting with three entities in the process of outsourcing the computation of functions as shown in Figure 1: a function owner, who possesses the function model and wants to outsource its computation to a cloud server; a series of request users, who need to obtain the function’s results on the private inputs; and a cloud server that performs the computation of the function based on the inputs and returns the results to the request users. In this process, the cloud server is untrusted. It should not learn anything about either the input or the function. Additionally, the correctness of the results should be verified. Thus, there are three requirements that need to be considered: function privacy, input privacy and public verifiability.

For example, in a medical predication scenario, a doctor, as the function owner, has developed an expensive disease prediction function model; in addition, some patients, as the request users, want to predict the probability of contracting this disease with their personal health data. It would be stressful for the doctor to perform the computation locally, so he wants to outsource the computation of the function to a cloud server. The cloud server would then compute the prediction function based on the inputs from the patients and return the predicted results to them.

The function parameters in this process are that private data owned by the doctor should remain confidential from the cloud server. Similarly, the health data of the patients should also be kept confidential. Since the cloud server is unreliable, it may compress the function model or simplify the computation for its own benefit, which can lead to a biased predicted result. Therefore, a fundamental requirement is that the patients can verify the correctness of the computed results. However, in many scenarios, individual verification is not sufficient. For example, patients may need to convince their insurance institutions to accept verification, which means that private verification cannot meet this requirement. Hence, we emphasize public verification, which allows anyone to verify the results of an outsourced function without learning anything about the sensitive data.

To address these requirements, researchers have proposed a series of solutions, such as Homomorphic Encryption (HE) [1,2,3], Secure Multi-Party Computation (SMPC) [4,5,6] and Publicly Verifiable Computation (PVC) [7,8,9]. Among them, homomorphic encryption can perform computations on ciphertexts. Secure multi-party computation can enable multiple parties to jointly complete a computing task without revealing their secret information. Publicly verifiable computation can verify the correctness of the computation results. It is important to combine privacy protection with verifiable computation.

Many works have been devoted to addressing one or more of the requirements in outsourcing the computation of functions [7,8,9,10,11,12,13,14,15,16,17,18,19], but none have achieved all of the above-mentioned requirements simultaneously. Our work aims to fill this gap, and the contributions of this study are listed below:

• We propose the first publicly verifiable outsourcing computation scheme that achieves both function privacy and input privacy for matrix functions, which can be extended to arbitrary polynomial functions (the extension method is provided).
• We additionally provide a faster privately verifiable method, which allows the request user to verify the results more efficiently than with public verification.
• The function owner retains control over the function. If they do not allow a user to use their function model, the cloud server cannot complete the computation.

The remainder of this paper is organized as follows. We present a brief overview of the related works in Section 2. We define the notation and review the necessary preliminaries in Section 3. We provide the system model and design goals in Section 4. In Section 5, we provide our publicly verifiable outsourcing computation scheme with privacy measures, and in Section 6, we analyze the performance of our scheme. Finally, Section 7 contains our conclusions and future works.

2. Related Works

There have been many works addressing one or more of the requirements mentioned above in outsourcing function computation. The schemes in [10,11,12] realize function privacy and input privacy based on FHE [2] or GCs [4]. However, they can only achieve private verification and not public verification. Additionally, the expensiveness of cryptographic primitives, such as GCs and FHE, limits their practical relevance. The schemes in [13,14,15] use lightweight algorithms for encryption and decryption instead of FHE to construct schemes with input privacy and function privacy. They reduce the system costs but still do not realize public verification.

The scheme in [16] shares the function model and input data among multiple servers using additive secret sharing [20] rather than encryption, and the results are obtained through the cooperation of these servers. Although it protects both function privacy and input privacy, it only provides private verification and not public verification. It also requires a strong assumption of non-collusion for the servers or the private data will be leaked.

Some works construct publicly verifiable computation schemes for specific functions. For instance, the works in [7,17,18,19] have constructed publicly verifiable computation schemes that are efficient for specific functions, such as univariate polynomial functions and matrix functions. In [8], a publicly verifiable computation scheme for Boolean functions was constructed based on key policy attribute-based encryption (KP-ABE) [21]. However, this scheme does not offer input or function privacy. Moreover, ref. [9] proposed a publicly verifiable scheme with privacy protection, but it can only protect one element between function privacy and input privacy, i.e., either a publicly verifiable computation scheme with function privacy or a publicly verifiable computation scheme with input privacy.

Table 1. Comparison of the proposed scheme with previous works.

Study Ref./No	Function Privacy/Input Privacy	Private Verification	Public Verification
[10,11,12]	✓/✓	✓	×
[13,14,15]	✓/✓	✓	×
[16]	✓/✓	✓	×
[7,8,17,18,19]	×/×	✓	✓
[9]	✓/× or ×/✓	✓	✓
Our scheme	✓/✓	✓	✓

Note: ✓—supported; and ×—not supported.

summarizes the requirements achieved in the surveyed literature, which can inform the research findings of our proposed scheme.

To improve efficiency, our work employs a partial homomorphic encryption scheme. The cloud server needs to perform a transformation on the ciphertexts from two different clients before computing. Several works have addressed this transformation on ciphertexts. For instance, Peter et al. [22] proposed a scheme that requires a participant to possess a strong private key that can decrypt any ciphertext in order to complete the transformation on ciphertexts. However, this approach poses a threat to data privacy and makes the data owner lose the right to control their data.

In contrast, our work ensures that the function owner retains control over their function, thereby strengthening data privacy. In [23], Ximeng Liu et al. split the strong private key in the BCP [24] scheme among multiple participants to decentralize the decryption power of the strong private key. However, their approach did not consider how to split the key securely. Additionally, their ciphertext transformation requires more cooperation among participants, which increases communication costs and decreases computing efficiency.

In contrast, our approach involves fewer participants, has lower communication costs and offers higher computing efficiency. In [25], Yutaka Kawai et al. proposed a homomorphic proxy re-encryption scheme that supports homomorphic operations for re-encrypted ciphertexts. However, this scheme requires a large number of computations of the discrete logarithm and group operations in bilinear groups, which increases the computational cost. Our approach is based on a lean homomorphic proxy re-encryption scheme, which makes computations more efficient.

3. Preliminaries

In this section, we review the basic notations and the primitives that are treated in this paper. The basic notations are shown in

Table 2. Summary of notations.

Notations	Descriptions
$\mathit{x}$	The lowercase bold letters denote vectors where $x_i$ indexes the i-th element
$\mathbf{M}$	The uppercase bold letters denote matrices where $M_{i,j}$ indexes the $(i,j)$-th element
${\mathit{x}}^{\top }$	The transpose of vector $\mathit{x}$
$\mathit{x},\dots ,\mathit{y}$	The dot product of two vectors, $\mathit{x}=(x_1,\dots ,x_n)$ and $\mathit{y}=(y_1,\dots ,y_n)$, where $\mathit{x}·\mathit{y}={\sum }_{i=1}^n{x}_i{y}_i$
$\mathbf{M}·\mathit{x}$	The matrix–vector multiplication of $\mathbf{M}$ and $\mathit{x}$
$x\stackrel{\$}{\leftarrow }S$	Uniformly sample x from a set S at random.
$\mathbb{N}$	The set of all natural numbers
$\left[n\right]$	The set $\{1,\dots ,n\}$, where $n\in \mathbb{N}$
$\lambda$	The security parameter
$p,q$	The odd primes
${\mathbb{Z}}_N$	A group under addition modulo N
${\mathbb{Z}}_N^{*}$	A group satisfies $gcd(b,N)=1$, where $b\in [N-1]$
$\mathcal{F}={\mathbb{Z}}_q^{m\times d}$	The set of all $m\times d$ matrices over ${\mathbb{Z}}_q$
$\mathbb{G}=\langle g\rangle$	The cyclic group with generator g
${\mathrm{\Phi }}_m\left(X\right)$	The m-th cyclotomic polynomial, where ${\mathrm{\Phi }}_m\left(X\right)=X^N+1$
$R:=\mathbb{Z}\left[X\right]/{\mathrm{\Phi }}_m\left(X\right)$	The ring of integer polynomials modulo ${\mathrm{\Phi }}_m$
$R_p$	The ring R with coefficients modulo p
$\chi$	The discrete Gaussian distribution over the ring
$(pk,sk)$	The key pair of public key and secret key

.

3.1. Additive Homomorphic Encryption (Additive HE)

Rivest et al. first proposed homomorphic encryption (HE) in 1978 [1], and this encryption performs homomorphic operations on ciphertexts without decryption. This is equivalent to performing the corresponding operations on plaintext, ensuring data privacy while also maintaining data availability.

Depending on the supported mathematical operations, HE can be classified into partial (additive or multiplicative) homomorphic encryption (PHE) [26,27], fully homomorphic encryption (FHE) [2] and somewhat homomorphic encryption (SWHE) [28,29,30]. PHE supports only one type of operation (either additive or multiplicative) on the ciphertext. FHE supports both additive and multiplicative operations but with high computational costs. SWHE supports limited multiplication and addition operations, with lower computational costs compared with FHE.

The following describes the additive homomorphic encryption scheme that we use based on [24], which contains five algorithms: $HE=(Setup,KeyGen,Enc,Dec,Eval)$. The details are as follows:

• $Setup\left(\lambda \right)\to pp$: The security parameter $\lambda$ is taken as input, and two $\lambda$-bit large prime numbers, $p^{\prime },q^{\prime }$, are chosen. Then, we have $N=pq$, where p = 2$p^{\prime }$ + 1 and q = 2$q^{\prime }$ + 1. A generator $g\in {\mathbb{Z}}_{N^2}^{*}$ is randomly sampled, and then the public parameters $pp=(N,g)$ are output.
• $KeyGen\left(pp\right)\to (pk,sk)$: The public parameters $pp$ are taken as input. According to $pp=(N,g)$, $a\stackrel{\$}{\leftarrow }{\mathbb{Z}}_{N^2}$ is randomly sampled. Then, the public/secret key pair $\left(pk=g^{a}mod{N}^2,sk=a\right)$ is output.
• $Enc(m,pk)\to c$: For a message $m\in {\mathbb{Z}}_N$, $r\stackrel{\$}{\leftarrow }{\mathbb{Z}}_{N^2}$ is sampled. The message m is encrypted with public key $pk=g^a$ and outputs ciphertext $c=(A,B)$, where $A=g^{ar}mod{N}^2,B=g^r\left(1+mN\right)mod{N}^2$.
• $Dec(c,sk)\to m$: For the ciphertext $c=(A,B)$, secret key $sk=a$ is used for decryption, and the output message is $m=\frac{B/\left(A^{\frac{1}{a}}\right)-1mod{N}^2}{N}$.
• $Eval(c_1,c_2)\to c_1\oplus c_2$: For two ciphertexts $c_1$ and $c_2$, whose corresponding plaintexts are $m_1,m_2$, where

  $$\begin{array}{ccc}\hfill c_1& =& Enc\left(m_1\right)=\left(A_1,B_1\right)=(g^{a{r}_1}mod{N}^2,g^{r_1}\left(1+m_{1}N\right)mod{N}^2)\hfill \end{array}$$

  (1)

  $$\begin{array}{ccc}\hfill c_2& =& Enc\left(m_2\right)=\left(A_2,B_2\right)=(g^{a{r}_2}mod{N}^2,g^{r_2}\left(1+m_{2}N\right)mod{N}^2),\hfill \end{array}$$

  (2)

  the additive homomorphism property is described as follows:

  $$\begin{array}{ccc}\hfill c_1\oplus c_2& =& Enc\left(m_1\right)\oplus Enc\left(m_2\right)\hfill \\ & =& (g^{a{r}_1}·g^{{ar}_2},g^{r_1}\left(1+m_{1}N\right)·g^{r_2}\left(1+m_{2}N\right))mod{N}^2\hfill \\ & =& (g^{a(r_1+r_{2)}},g^{r_1+r_2}\left(1+(m_1+m_2)N\right))mod{N}^2\hfill \\ & \to & Enc(m_1+m_2,pk).\hfill \end{array}$$

  (3)
  In particular, given a constant $\gamma$, we have $Eval(c_1,\gamma )\to c_1^{\gamma }$, where

  $$\begin{array}{ccc}\hfill c_1^{\gamma }& =& (g^{a\gamma r_1},g^{\gamma r_1}{\left(1+m_{1}N\right)}^{\gamma })mod{N}^2\hfill \\ & =& (g^{a\gamma r_1},g^{\gamma r_1}\left(1+\gamma m_{1}N\right))mod{N}^2\hfill \\ & \to & Enc(\gamma m_1,pk).\hfill \end{array}$$

  (4)

3.2. Linear Homomorphic Encryption (LHE)

Linear homomorphic encryption (LHE) [28,29,30] can support limited additive and multiplicative operations on ciphertexts. It is able to compute a linear combination of multiple ciphertexts, which has practical applications.

Given n plaintexts ($m_1,\dots ,m_n$), the corresponding ciphertext is ($c_1,\dots ,c_n$). Given n constant coefficients (${\gamma }_1,\dots ,{\gamma }_n$), the ciphertext of the linear combination ${\sum }_{i=1}^n{\gamma }_i·m_i$ can be computed by ${\left\{c_i\right\}}_{i=1}^n$ and ${\left\{{\gamma }_i\right\}}_{i=1}^n$. Next, we describe the LHE algorithms based on the private key version by Brakerski and Vaikuntanathan [3]. It contains five algorithms: $LHE=(Setup,KeyGen,Enc,Dec,Eval)$. The details are as follows:

• $Setup\left(\lambda \right)\to pp$: The security parameter $\lambda$ is taken as input. Two $\lambda$-bit large prime numbers q and $p\in {\mathbb{Z}}_q^{*}$ are chosen. Set $n=2^{\lfloor log\lambda \rceil -1}$, and there is a cyclotomic polynomial $f\left(x\right)=x^n+1$. $\chi$ is the discrete Gaussian distribution over the ring $R_q={\mathbb{Z}}_q\left[x\right]/\langle f\left(x\right)\rangle$. The public parameters $pp$={$n,f,q,\chi$} are obtained as outputs.
• $KeyGen\left(pp\right)\to sk$: The public parameter $pp$ is taken as input. A ring element $s\stackrel{\$}{\leftarrow }\chi$ is a sample, and the secret key $sk=s$ is obtained as an output.
• $Enc(sk,m)\to c$: For a message $m\in R_p$, $a\stackrel{\$}{\leftarrow }{R}_q,e\stackrel{\$}{\leftarrow }\chi$ is taken as a sample, and the output ciphertext is $c=(u,v)=(as+pe+m,-a)$.
• $Dec(sk,c)\to m$: The ciphertext $c=(u,v)$ is decrypted with the secret key $sk=s$, and the output $m=(u+v·sk)$ $\mathit{mod}p$ is obtained.
• $Eval(({\gamma }_1,\dots ,{\gamma }_d),\left((c^{\left(1\right)},\dots ,c^{\left(d\right)})\right)\to c$: Given d coefficients ${\gamma }_1,\dots ,{\gamma }_d\in {\mathbb{Z}}_q$ and d ciphertexts $c^{\left(1\right)},\dots ,c^{\left(d\right)}\in {\left(R_q\right)}^2$, the linear homomorphism property is described as follows:

  $$\begin{array}{ccc}\hfill c& =& \sum _{i=1}^d{\gamma }_i·c^{\left(i\right)}=\sum _{i=1}^d{\gamma }_i·{\left(u,v\right)}^{\left(i\right)}\hfill \\ & =& \left(\sum _{i=1}^d{\gamma }_i·u^{\left(i\right)},\sum _{i=1}^d{\gamma }_i·v^{\left(i\right)}\right)\hfill \\ & =& \left(\sum _{i=1}^d{\gamma }_{i}a·s+\sum _{i=1}^d{\gamma }_{i}pe+\sum _{i=1}^d{\gamma }_i{m}_i,-\sum _{i=1}^d{\gamma }_{i}a\right)\hfill \\ & \to & Enc\left(sk,\sum _{i=1}^d{\gamma }_i{m}_i\right).\hfill \end{array}$$

  (5)

3.3. Homomorphic Proxy Re-Encryption (HPRE)

Blaze, Bleumer and Strauss first proposed proxy re-encryption (PRE) [31] at EUROCRYPT 1998. The proxy can convert the ciphertext encrypted by the data owner into another ciphertext that can be decrypted by the specified data receiver. Homomorphic proxy re-encryption was introduced in [25], which combines the homomorphic property of HE and the “key-switching” property of PRE.

The following describes our homomorphic proxy re-encryption method, which consists of six algorithms: $PRE=(Setup,KeyGen,Enc,ReKeyGen,ReEnc,Dec)$. It is based on the additive homomorphic encryption above, and the details are as follows:

• $Setup\left(\lambda \right)\to pp$: The security parameter $\lambda$ is taken as input. $HE.Setup\left(\lambda \right)\to pp$ is run to generate $pp=(N,g)$. Then, the output $pp=(N,g)$ is obtained.
• $KeyGen\left(pp\right)\to ((p{k}_i,s{k}_i),(p{k}_j,s{k}_j))$: The public parameter $pp$ is taken as input. $HE.KeyGen\left(pp\right)\to (pk,sk)$ is run twice to generate $(p{k}_i=g^{a}mod{N}^2,s{k}_i=a)$, $(p{k}_j=g^{b}mod{N}^2,s{k}_j=b)$, which stands for the public/secret key pair of the data owner and data receiver, respectively. Then, the output $((p{k}_i,s{k}_i),(p{k}_j,s{k}_j))$ is obtained.
• $Enc(m,p{k}_i)\to c_i$: For a message $m\in {\mathbb{Z}}_N$, the data owner runs $HE.Enc(m,p{k}_i)\to c_i$ to output the ciphertext $c_i=(A_i,B_i)$, where $A_i=g^{ar}mod{N}^2,B_i=g^r\left(1+mN\right)mod{N}^2$. Then, the output is $c_i$.
• $ReKeyGen(s{k}_i,s{k}_j)\to r{k}_{i\to j}$: The data owner’s secret key $s{k}_i$ and the data receiver’s secret key $s{k}_j$ are taken as input, and the re-encryption key $r{k}_{i\to j}$ = $\frac{s{k}_j}{s{k}_i}$ = $\frac{b}{a}$ is the output.
• $ReEnc(r{k}_{i\to j},c_i)\to c_j$: The re-encryption key $r{k}_{i\to j}$ and the ciphertext $c_i$ are taken as inputs, and the re-encryption ciphertext $c_j$ is obtained as the output, where

  $$\begin{array}{ccc}\hfill c_j& =& (A_j,B_j)=(A_i^{{rk}_{i\to j}},B_i)\hfill \\ & =& \left(g^{ar\frac{b}{a}},g^r\left(1+mN\right)\right)mod{N}^2\hfill \\ & =& (g^{br},g^r\left(1+mN\right))mod{N}^2\hfill \\ & \to & Enc(m,p{k}_j).\hfill \end{array}$$

  (6)
• $Dec(c_j,s{k}_j)\to m$: The ciphertext $c_j=(A_j,B_j)=(g^{br},g^r(1+mN))$ is decrypted with the data receiver’s secret key $s{k}_j=b$, and the output is $m=\frac{B_j/\left({A_j}^{\frac{1}{b}}\right)-1mod{N}^2}{N}$.

3.4. Verifiable Matrix-Vector Multiplication (VerM)

Verifiable computation is a computational model that allows the client to delegate computational tasks to a computational entity and then to verify the correctness of the computed result without re-executing the entire computation task. The schemes in [32,33] propose a critical observation of matrix–vector multiplication, and the scheme in [9] proposes a solution for publicly verifiable matrix–vector multiplication computation.

The following describes the publicly verifiable matrix–vector multiplication scheme that we use based on [9], which consists of four algorithms: $VerM=(Setup,Prepare,Compute,Verify)$.

Table 3. Data size.

Data	Size
Matrix $\mathbf{F}$	$m\times d$
Verification data $\mathit{t}$	$1\times m$
Verification data $\mathit{s}$	$1\times d$
Vector $\mathit{x}$	$d\times 1$
The final result $\mathit{y}$	$m\times 1$

shows the data size in the scheme, and the details are given below:

• $Setup\left(\lambda \right)\to pp$: The security parameter $\lambda$ is taken as input, and a $\lambda$-bit large prime number q is chosen. Let ${\mathbb{Z}}_q$ be a finite field and $\mathbb{G}=\langle g\rangle$ be a cyclic group of generator g and order q. Let $m,d>0$ be integers, and then output $pp=(q,m,d,g)$.
• $Prepare\left(\mathbf{F}\right)\to \mathit{ver}$: The function owner takes their matrix $\mathbf{F}\in \mathcal{F}$, where $\mathcal{F}={\mathbb{Z}}_q^{m\times d}$ is the set of all $m\times d$ matrices over ${\mathbb{Z}}_q$ as input to generate the public verification data $\mathit{ver}$ (once and for all). A vector $\mathbf{t}=(t_1,\dots ,t_m)\stackrel{\$}{\leftarrow }{\mathbb{Z}}_q^m$ is uniformly sampled, and $\mathbf{s}=(s_1,\dots ,s_d)=\mathbf{t}·\mathbf{F}$ is computed. The obtained output is $\mathit{ver}=(\mathit{T},\mathit{S})$, where $\mathit{T}=g^{\mathbf{t}}=(g^{t_1},\dots ,g^{t_m})$, $\mathit{S}=g^{\mathbf{s}}=(g^{s_1},\dots ,g^{s_d})$.
• $Compute(\mathbf{F},\mathit{x})\to \mathit{y}$: The function $\mathbf{F}\in \mathcal{F}$ and the input $\mathit{x}={(x_1,\dots ,x_d)}^{\top }\in {\mathbb{Z}}_q^d$ are taken as inputs. The result $\mathit{y}=\mathbf{F}·\mathit{x}={(y_1,\cdots ,y_m)}^{\top }$ is obtained.
• $Verify(\mathit{ver},\mathit{x},\mathit{y})\to (0,1)$: The public verification data $\mathit{ver}$, the input $\mathit{x}$ and the result $\mathit{y}$ are taken as input. This convinces the user to accept the result if and only if

  $$\prod _{i=1}^d{g}^{s_i·x_i}=\prod _{i=1}^m{g}^{t_i·y_i}$$

  (7)
  If the equation is valid, then the output is 1; otherwise, the output is 0.

The correctness of the verification is as follows:

The left side:

$$\prod _{i=1}^d{g}^{s_i·x_i}=\prod _{i=1}^d{g}^{\left({\sum }_{j=1}^m{t}_j{\mathbf{F}}_{\mathbf{j},\mathbf{i}}\right)x_i}=g^{{\sum }_{i=1}^d{\sum }_{j=1}^m{t}_j{\mathbf{F}}_{\mathbf{j},\mathbf{i}}{x}_i}.$$

(8)

The right side:

$$\prod _{i=1}^m{g}^{t_i·y_i}=\prod _{i=1}^m{g}^{t_i·({\sum }_{j=1}^d{\mathbf{F}}_{\mathbf{i},\mathbf{j}}{x}_j)}=g^{{\sum }_{i=1}^m{\sum }_{j=1}^d{t}_j{\mathbf{F}}_{\mathbf{i},\mathbf{j}}{x}_j}.$$

(9)

If $\mathit{y}=\mathbf{F}·\mathit{x}$, then it is easy to verify that Equation (7) holds.

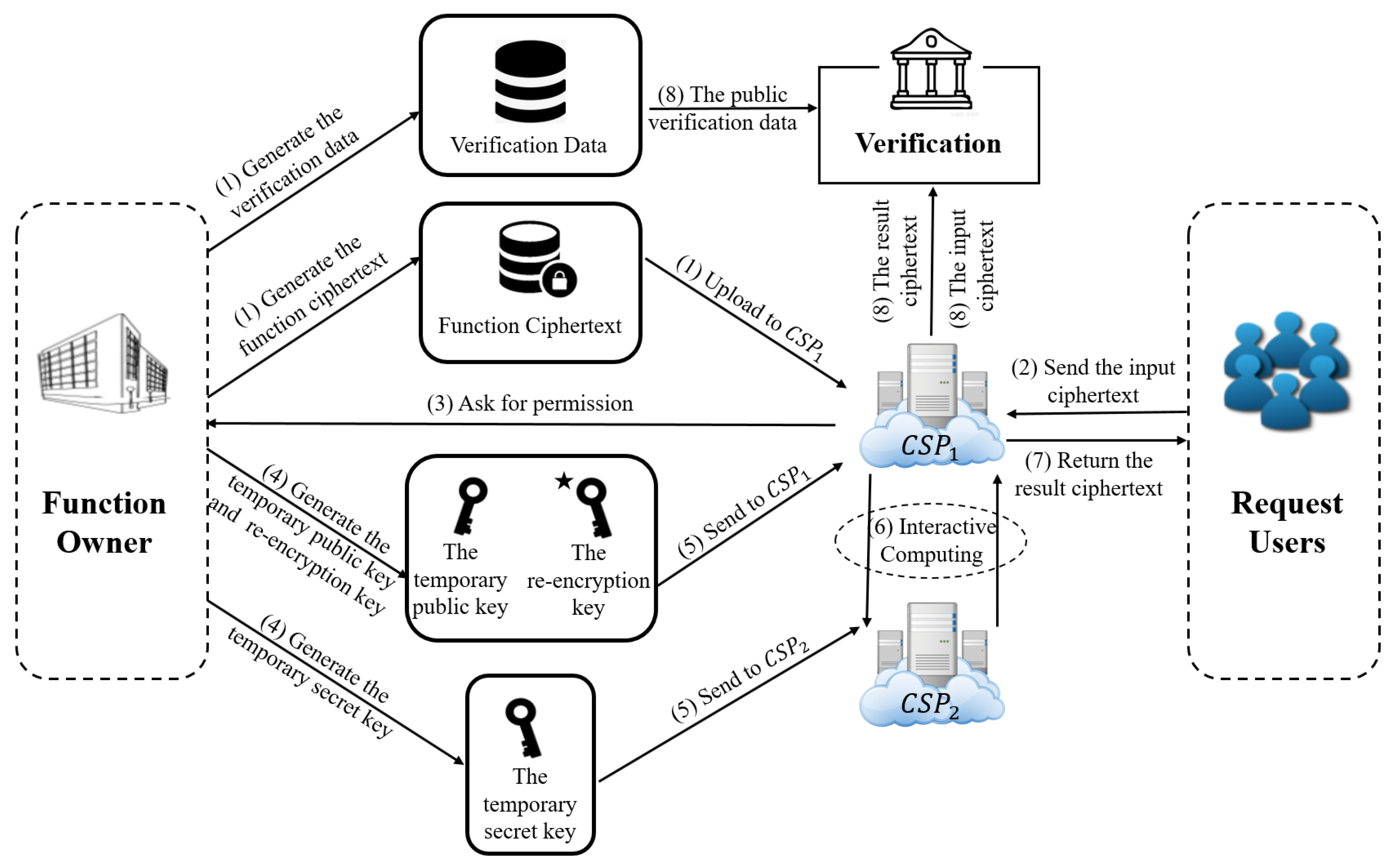
4. System Model and Design Goals

4.1. System Model

Consider a setting in our system model with three entities: a function owner who wants to outsource the function’s computation; two non-collusive cloud service providers $CS{P}_1$ and $CS{P}_2$ that collaborate to complete the computation; and a series of request users who want to obtain the computation results on their inputs. Figure 2 outlines a rough sketch of our system model. It consists of the following three phases: Preparation, Computation and Verification. The number before the text corresponds to Figure 2.

• Preparation:

  (1)

  The function owner encrypts the function parameters and prepares the public verification data. Then, they upload the function’s ciphertext to the cloud service provider $CS{P}_1$.

  (2)

  A request user encrypts their input when they request $CS{P}_1$ to perform the computation.

  (3)

  When $CS{P}_1$ receives the request from the user, it asks the function owner for permission.

  (4)

  The function owner generates a temporary public/secret key pair and a re-encryption key when they permit the use of their function.

  (5)

  The function owner sends the temporary public key and the re-encryption key to $CS{P}_1$ and sends the temporary secret key to $CS{P}_2$.

• Computation:

  (6)

  $CS{P}_1$ re-encrypts the original function ciphertext with a mask. Then, the new ciphertext can be decrypted by $CS{P}_2$ with the temporary secret key. $CS{P}_1$ then collaborates with $CS{P}_2$ to complete the computation.

  (7)

  $CS{P}_1$ returns the result ciphertext to the user.

• Verification:

  (8)

  The public verification is performed using the public verification data, the input ciphertext and the result ciphertext. Simultaneously, the user decrypts the result ciphertext and verifies the result privately in a fast way with the public verification data and the plaintexts of their input and result.

4.2. Design Goals

There are five goals that need to be achieved in our model:

• Maintain function privacy: The function ciphertext and public verification data cannot reveal any information about the function, so the encryption schemes that we use should be semantically secure so that no adversary can infer any information from the obtained ciphertext.
• Maintain input privacy. Similarly, the input ciphertext must not reveal information about the input. The encryption scheme for the input, thus, needs to be semantically secure.
• Maintain result privacy. No one should be able to obtain information about the result plaintext except for the request user. The result ciphertext cannot be distinguished from the random elements.
• Achieve public verification. Anyone can complete the verification with the publicly available information, and there is no malicious CSP that can persuade the public to accept an incorrect result with a non-negligible probability. We assume that the public has limited computational resources, and so verification must be efficient.
• Ensure the function owner’s control over the function. CSPs cannot complete the computation if the function owner does not allow the user to use their function model.

5. The Proposed Solution

We propose a scheme for the publicly verifiable outsourcing of computation with both input privacy and function privacy for matrix–vector multiplication in this section. The scheme can also be extended to various polynomial functions.

We provide the extension method in Section 5.4. In our setting, the function owner has a matrix $\mathbf{F}\in {\mathbb{Z}}_q^{m\times d}$, and the request user has a vector $\mathit{x}$. The user requests access from the cloud server for the result $\mathit{y}=\mathbf{F}·\mathit{x}$. Our scheme consists of three phases: Preparation, Computation and Verification, which are specified below.

5.1. Preparation

• The key pair of preparation steps for the function owner:

  -

  Run $HE.Setup\left(\lambda \right)\to p{p}_{he}$ to generate $p{p}_{he}=(N,g)$.

  -

  Run $HE.KeyGen\left(p{p}_{he}\right)\to (p{k}_f,s{k}_f)$ to generate $(p{k}_f,s{k}_f)$=$\left(g^a,a\right)$.

• The function owner encrypts the matrix and uploads it to $CS{P}_1$:

  -

  For each element $f_i$ in the matrix $\mathbf{F}\in {\mathbb{Z}}_q^{m\times d}$, $0<i\le m\times d$, run

  $HE.Enc(p{k}_f,f_i)\to c{t}_i$ to generate $c{t}_i=(g^{a{r}_i},g^{r_i}\left(1+f_{i}N\right))$, where $r_i\stackrel{\$}{\leftarrow }{\mathbb{Z}}_{N^2}$.

  -

  Upload $\mathit{ct}=(c{t}_1,\dots ,c{t}_{m·d})$ to $CS{P}_1$.

• The function owner generates the verification data $\mathit{ver}$:

  -

  Run $VerM.Prepare\left(\mathbf{F}\right)\to \mathit{ver}$ to generate $\mathit{ver}=(\mathit{T},\mathit{S})$. It holds that

  $\mathit{T}=g^{\mathit{t}}=(g^{t_1},\dots ,g^{t_m})$,

  $\mathit{S}=g^{\mathit{s}}=(g^{s_1},\dots ,g^{s_d})$,

  where $\mathit{t}\stackrel{\$}{\leftarrow }{\mathbb{Z}}_q^m$ and $\mathit{s}=(s_1,\dots ,s_d)=\mathit{t}·\mathbf{F}$.

• The request user encrypts the input vector and sends it to $CS{P}_1$:

  -

  Run $LHE.Setup\left(\lambda \right)\to p{p}_{lhe}$ to generate the public parameters $p{p}_{lhe}=(n,f,q,\chi )$ for the request user.

  -

  Run $LHE.KeyGen\left(p{p}_{lhe}\right)\to sk$ to generate the secret key $sk=s$ for the request user.

  -

  For each $x_i$ in the input vector $\mathit{x}={(x_1,\dots ,x_d)}^{\top },i\in \left[d\right]$, $x_i\in {\mathbb{Z}}_p\left[x\right]/\langle f\left(x\right)\rangle$, run $LHE.Enc(sk,x_i)\to c_i$ to generate the ciphertext $c_i=(u_i,v_i)=(a_{i}s+p{e}_i+x_i,-a_i)$, where $a_i\stackrel{\$}{\leftarrow }{R}_q,e_i\stackrel{\$}{\leftarrow }\chi$ and $c_i\in R_q^2$.

  -

  The user sends the ciphertext $\mathit{c}={(c_1,\dots ,c_d)}^{\top }$ to $CS{P}_1$ and requests computation.

• $CS{P}_1$ asks the function owner for permission.
• The function owner will generate a temporary key pair and a re-encryption key if permission is granted:

  -

  The function owner runs $HE.KeyGen\left(p{p}_{he}\right)\to (p{k}_f^{{}^{\prime }},s{k}_f^{{}^{\prime }})$ again to generate a temporary public/secret key pair $(p{k}_f^{{}^{\prime }}=g^{a^{{}^{\prime }}},{sk}_f^{{}^{\prime }}=a^{{}^{\prime }})$.

  -

  Run $PRE.ReKeyGen(s{k}_f,s{k}_f^{{}^{\prime }})\to r{k}_{f\to f^{{}^{\prime }}}$ to generate a re-encryption key ${rk}_{f\to f^{{}^{\prime }}}=\frac{{sk}_f^{{}^{\prime }}}{{sk}_f}=\frac{a^{{}^{\prime }}}{a}$.

  -

  The function owner sends $p{k}_f^{{}^{\prime }}$ and ${rk}_{f\to f^{{}^{\prime }}}$ to $CS{P}_1$ and sends $s{k}_f^{{}^{\prime }}$ to $CS{P}_2$.

5.2. Computation

• $CS{P}_1$ re-encrypts the matrix ciphertext:

  -

  For each element $c{t}_i$ in the matrix ciphertext $\mathit{ct}$, $0<i\le m\times d$, $CS{P}_1$ runs $PRE.ReEnc({rk}_{f\to f^{{}^{\prime }}},c{t}_i)\to c{t}_i^{{}^{\prime }}$ to re-encrypt $c{t}_i$ into $c{t}_i^{{}^{\prime }}$, where

  $c{t}_i=(A,B)=(g^{a{r}_i},g^{r_i}\left(1+f_{i}N\right))$, ${rk}_{f\to f^{{}^{\prime }}}=\frac{a^{{}^{\prime }}}{a}$.

  Then, ${ct}_i^{{}^{\prime }}=(A^{{rk}_{f\to f^{{}^{\prime }}}},B)=(g^{a^{{}^{\prime }}{r}_i},g^{r_i}\left(1+f_{i}N\right))mod{N}^2$.

• $CS{P}_1$ sends the re-encryption ciphertext with a mask to $CS{P}_2$:

  -

  For each element $c{t}_i^{{}^{\prime }}$ in ${\mathit{ct}}^{{}^{\prime }}={(c{t}_1^{{}^{\prime }},\dots ,c{t}_{m·d}^{{}^{\prime }})}^{\top }$, $0<i\le m·d$, $CS{P}_1$ samples $r_i^{{}^{\prime }}\stackrel{\$}{\leftarrow }{\mathbb{Z}}_{N^2}$ as the mask.

  -

  For each mask $r_i^{{}^{\prime }}$, run $HE.Enc(r_i^{{}^{\prime }},p{k}_f^{{}^{\prime }})\to {rct}_i^{{}^{\prime }}$ with the temporary key $p{k}_f^{{}^{\prime }}$ to generate ${rct}_i^{{}^{\prime }}=(g^{a^{{}^{\prime }}\widehat{r_i}},g^{\widehat{r_i}}\left(1+r_i^{{}^{\prime }}N\right))mod{N}^2$, where ${\widehat{r}}_i\stackrel{\$}{\leftarrow }{\mathbb{Z}}_{N^2}$.

  -

  For $i\in [m·d]$, run $HE.Eval({ct}_i^{{}^{\prime }},{rct}_i^{{}^{\prime }})\to {ct}_i^{{}^{\prime }}\oplus {rct}_i^{{}^{\prime }}$ to generate the masked ciphertext $m{ct}_i^{{}^{\prime }}={rct}_i^{{}^{\prime }}\oplus {ct}_i^{{}^{\prime }}\to Enc(f_i+r_i^{{}^{\prime }})$.

  -

  $CS{P}_1$ sends the masked ciphertext ${\mathbf{mct}}^{{}^{\prime }}={\left\{m{ct}_i^{{}^{\prime }}\right\}}_{i=1}^{m\times d}$ and the user’s input ciphertext $\mathit{c}={\left\{c_i\right\}}_{i=1}^d$ to $CS{P}_2$.

• $CS{P}_1$ computes the final result’s first part ${\mathit{res}}^{\mathbf{1}}$:

  -

  Parse ${\mathit{r}}^{{}^{\prime }}$ as a $m\times d$-size matrix and write $r_{i,j}^{{}^{\prime }}$ to index the $(i,j)$-th element.

  -

  For $i\in \left[m\right]$, run $LHE.Eval((r_{i,1}^{{}^{\prime }},\dots ,r_{i,d}^{{}^{\prime }}),(c_1,\dots ,c_d))\to re{s}_i^1$ to generate $re{s}_i^1={\sum }_{j=1}^d{r}_{i,j}^{{}^{\prime }}{c}_j$. The first part of the final result is ${\mathit{res}}^{\mathbf{1}}={[re{s}_1^1,...,re{s}_m^1]}^T$.

• $CS{P}_2$ performs the decryption for the masked ciphertext:

  -

  After receiving the masked ciphertext ${\left\{mc{t}_i^{{}^{\prime }}\right\}}_{i=1}^{m\times d}$, for $i\in [m·d]$, $CS{P}_2$ runs $HE.Dec(mc{t}_i^{{}^{\prime }},s{k}_f^{{}^{\prime }})\to f_i^{{}^{\prime }}$ to generate the masked matrix parameters ${\{f_i^{{}^{\prime }}=f_i+r_i^{{}^{\prime }}\}}_{i=1}^{m\times d}$.

  -

  Parse ${\mathbf{f}}^{{}^{\prime }}=(f_1^{{}^{\prime }},...,f_{m·d}^{{}^{\prime }})$ as an $m\times d$-size matrix and write $f_{i,j}^{{}^{\prime }}$ to index the $(i,j)$-th element. It holds that $f_{i,j}^{{}^{\prime }}$=$f_{i,j}+r_{i,j}^{{}^{\prime }}$.

• $CS{P}_2$ computes the second part of the final result ${\mathit{res}}^{\mathbf{2}}$:

  -

  For $i\in \left[m\right]$, run $LHE.Eval((f_{i,1}^{{}^{\prime }},\dots ,f_{i,d}^{{}^{\prime }}),(c_1,\dots ,c_d))\to re{s}_i^2$ to generate $re{s}_i^2={\sum }_{j=1}^d{f}_{i,j}^{{}^{\prime }}{c}_j$. Then, send the second part of the final result ${\mathit{res}}^{\mathbf{2}}={[re{s}_1^2,...,re{s}_m^2]}^T$ to $CS{P}_1$.

• $CS{P}_1$ computes the final result $\mathit{res}$ and returns it to the user:

  -

  For $i\in \left[m\right]$$,CS{P}_1$ computes $re{s}_i=re{s}_i^2-re{s}_i^1={\sum }_{j=1}^d{f}_{i,j}^{{}^{\prime }}{c}_j-{\sum }_{j=1}^d{r}_{i,j}^{{}^{\prime }}{c}_j={\sum }_{j=1}^d{f}_{i,j}{c}_j$. Then, the final result $\mathit{res}$=${[re{s}_1,\dots ,re{s}_m]}^T$ is returned to the user.

5.3. Verification

• Public Verification:

  -

  The public runs $VerM.Verify(\mathit{ver},\mathit{c},\mathit{res})\to (0,1)$. It outputs 1 if and only if

  $$\prod _{i=1}^d{g}^{s_i·c_i}=\prod _{i=1}^d{g}^{t_i·re{s}_i}.$$

  (10)

• Private Verification:

  -

  After the user receives the result ciphertext $\mathit{res}$=${(re{s}_1,...,re{s}_m)}^T$, for $i\in \left[m\right]$, they run $LHE.Dec(sk,re{s}_i)\to y_i$ to generate the plaintext $y_i$, where $y_i={\sum }_{j=1}^d{f}_{i,j}{x}_j$. The final result plaintext is $\mathit{y}={(y_1,\cdots ,y_m)}^{\top }=\mathbf{F}·\mathit{x}$.

  -

  Run $VerM.Verify(\mathit{ver},\mathit{x},\mathit{y})\to (0,1)$. It outputs 1 if and only if

  $$\prod _{j=1}^d{g}^{s_i·x_i}=\prod _{j=1}^d{g}^{t_i·y_i}.$$

  (11)

5.4. The Extension Method for Arbitrary Polynomial Functions

In the previous subsection, we described the verifiable matrix–vector multiplication. However, the function may be arbitrary. The scheme in [9] gives a solution for outsourcing these arbitrary polynomial functions based on the verifiable matrix–vector multiplication scheme.

This scheme decomposes the computation of arbitrary polynomials into a two-phase computation in which the heavy part is the matrix–vector multiplication that can be delegated to the cloud server, and the other part provides a substantially fast computation for the user. Then, we describe the decomposition scheme for univariate polynomials and arbitrary multivariate polynomials based on [9].

5.4.1. Univariate Polynomials

Let $\mathcal{F}$ be the set of all univariate polynomials of higher order over a finite field ${\mathbb{Z}}_q$. For any $f\left(x\right)\in \mathcal{F}$, suppose that $f\left(x\right)=f_0+f_{1}x+\cdots f_d{x}^d$. Let $m=\lceil \sqrt{d+1}\rceil$ and define

$$\begin{array}{c}\hfill \mathbf{F}=(\begin{array}{cccc}{f}_0& f_1& \cdots & f_{m-1}\\ f_m& f_{m+1}& \cdots & f_{2m-1}\\ ⋮& ⋮& \cdots & ⋮\\ f_{m^2-m}& f_{m^2-m+1}& \cdots & f_{m^2-1}\end{array})\end{array}$$

(12)

as a matrix of order m, where $f_i=0$ for all $i>d$. Set $\mathit{x}={(1,x,\dots ,x^{m-1})}^{\top }$ and $\mathit{y}=(1,x^m,\dots ,x^{m^2-m})$. Then, we have $f\left(x\right)=\mathit{y}·(\mathbf{F}·\mathit{x})$.

This is a two-phase computation: (i) the computation of $\mathit{u}=\mathbf{F}\mathit{x}$ and (ii) the computation of $f\left(x\right)=\mathit{y}·\mathit{u}$. The first phase is a matrix–vector multiplication function that can be delegated to a cloud server using our verifiable computation scheme. It requires $\mathit{O}\left(m^2\right)=\mathit{O}\left(d\right)$ arithmetic operations. The second phase is a substantially fast computation for the user that requires only $\mathit{O}\left(m\right)=\mathit{O}\left(\sqrt{d}\right)$ arithmetic operations locally.

5.4.2. Multivariate Polynomials

Let $\mathcal{F}$ be the set of all arbitrary multivariate polynomials over a finite field ${\mathbb{Z}}_q$. For any $f\left(x_1,\dots ,x_m\right)={\sum }_{i_1,\dots ,i_m=1}^d{f}_{i_1,\dots ,i_m}·x_1^{i_1}\cdots x_m^{i_m}\in \mathcal{F}$, $m\ge 2$, $l=⌊m/2⌋$, parse the parameters as a $d^l\times d^{m-l}$ matrix

$$\mathbf{F}=\left(F_{\left(i_1,\dots ,i_l\right),\left(i_{l+1},\dots ,i_m\right)}\right)$$

(13)

where $F_{\left(i_1,\dots ,i_l\right),\left(i_{l+1},\dots ,i_m\right)}=f_{i_1,\dots ,i_m}$. Set $\mathit{y}=\left(x_1^{i_1}\cdots x_l^{i_l}\right)\in {\mathbb{Z}}_q^{d^l}$ and $\mathit{x}={\left(x_{l+1}^{i_{l+1}}\cdots x_m^{i_m}\right)}^{\top }\in {\mathbb{Z}}_q^{d^{m-1}}$; then, we have $f\left(x_1,\dots ,x_m\right)=\mathit{y}·(\mathbf{F}·\mathit{x})$.

This is a two-phase computation: (i) the computation of $\mathit{u}=\mathbf{F}\mathit{x}$ and (ii) the computation of $f\left(x_1,\dots ,x_m\right)=\mathit{y}·\mathit{u}$. The first phase is a matrix–vector multiplication that can be delegated to a cloud server using our verifiable computation scheme. It requires $\mathit{O}\left(d^m\right)$ arithmetic operations. The second phase is a substantially fast computation for the user that requires $\mathit{O}\left(d^{\lceil m/2\rceil }\right)$ arithmetic operations locally.

6. Results

6.1. Correctness Analysis

• Correctness of the result ciphertext $\mathit{res}$ from $CS{P}_1$. Given the ciphertexts of the result $\mathit{res}$ and the input vector $\mathit{c}$, for $i\in \left[d\right]$, it holds that:

  $$\begin{array}{ccc}\hfill c_i& =& \left(u_i,v_i\right)=\left(a_{i}s+p{e}_i+x_i,-a_i\right)\hfill \\ \hfill re{s}_i& =& \left(\sum _{j=1}^d{f}_{i,j}{u}_j,\sum _{j=1}^d{f}_{i,j}{v}_j\right)\hfill \end{array}$$

  (14)

  $$\begin{array}{ccc}& =& \left(\sum _{j=1}^d{f}_{i,j}{a}_{i}s+\sum _{j=1}^d{f}_{i,j}p{e}_i+\sum _{j=1}^d{f}_{i,j}{x}_i,-\sum _{j=1}^d{f}_{i,j}{a}_i\right)\hfill \end{array}$$

  (15)
  Let ${\sum }_{j=1}^d{f}_{i,j}{a}_i=\widehat{a_i}$ and ${\sum }_{j=1}^d{f}_{i,j}{e}_i=\widehat{e_i}$, such that the following holds:

  $$\begin{array}{ccc}\hfill re{s}_i& =& \left(\widehat{a_i}s+p\widehat{e_i}+\sum _{j=1}^d{f}_{i,j}{x}_i,-\widehat{a_i}\right)\hfill \\ & \to & Enc\left(sk,\sum _{j=1}^d{f}_{i,j}{x}_i\right)\hfill \end{array}$$

  (16)
  We can see that the result $\mathit{res}$ corresponds to the multiplication of matrix $\mathbf{F}$ and vector $\mathit{x}$ in plaintext.
• Correctness of decryption for the result ciphertext $\mathit{res}$. Given the ciphertext of the result $\mathit{res}$, where

  $$\begin{array}{c}\hfill re{s}_i=\left(\sum _{j=1}^d{f}_{i,j}{u}_j,\sum _{j=1}^d{f}_{i,j}{v}_j\right)=\left(\widehat{a_i}s+p\widehat{e_i}+\sum _{j=1}^d{f}_{i,j}{x}_i,-\widehat{a_i}\right)\end{array}$$

  (17)

  for $i\in \left[d\right]$, it holds that:

  $$\begin{array}{ccc}\hfill y_i& =& \sum _{j=1}^d{f}_{i,j}{u}_j+\left(\sum _{j=1}^d{f}_{i,j}{v}_j\right)·skmodp\hfill \\ & =& \widehat{a_i}s+p\widehat{e_i}+\sum _{j=1}^d{f}_{i,j}{x}_i-\widehat{a_i}smodp\hfill \\ & =& \sum _{j=1}^d{f}_{i,j}{x}_i\hfill \end{array}$$

  (18)
  We can see that the decryption for the result ciphertext is correct.
• Correctness of public verification.
  Given the input vector ciphertext $\mathit{c}$, the result ciphertext $\mathit{res}$ and the public verification data $\mathit{ver}=(\mathit{T},\mathit{S})=((g^{t_1},\dots ,g^{t_m}),(g^{s_1},\dots ,g^{s_d}))$, where

  $$c_i=\left(u_i,v_i\right)$$

  (19)

  $$re{s}_i=\left(\sum _{j=1}^d{f}_{i,j}{u}_j,\sum _{j=1}^d{f}_{i,j}{v}_j\right)$$

  (20)

  $$s_i=\sum _{j=1}^m{t}_j{F}_{\mathbf{j},\mathbf{i}}$$

  (21)

  for $i\in \left[d\right]$, it convinces the public to accept the result if and only if:

  $$\prod _{i=1}^d{g}^{s_i·c_i}=\prod _{i=1}^d{g}^{t_i·re{s}_i}.$$

  (22)
  The left side is:

  $$\begin{array}{ccc}\hfill \prod _{i=1}^d{g}^{s_i·c_i}& =& \left(\prod _{i=1}^d{g}^{s_i·u_{\mathbf{i}}},\prod _{i=1}^d{g}^{s_i·v_i}\right)\hfill \\ & =& \left(\prod _{i=1}^d{g}^{\left({\sum }_{j=1}^m{t}_j{f}_{\mathbf{j},\mathbf{i}}\right)·u_{\mathbf{i}}},\prod _{i=1}^d{g}^{{\sum }_{j=1}^m{t}_j{f}_{\mathbf{j},\mathbf{i}}·v_i}\right)\hfill \\ & =& \left(g^{{\sum }_{i=1}^d{\sum }_{j=1}^m{t}_j{f}_{\mathbf{j},\mathbf{i}}{u}_i},g^{{\sum }_{i=1}^d{\sum }_{j=1}^m{t}_j{f}_{\mathbf{j},\mathbf{i}}{v}_i}\right)\hfill \end{array}$$

  (23)

  and the right side is:

  $$\begin{array}{ccc}\hfill \prod _{i=1}^d{g}^{t_i·re{s}_i}& =& \left(\prod _{i=1}^d{g}^{t_i·{\sum }_{j=1}^d{f}_{i,j}{u}_j},\prod _{i=1}^d{g}^{t_i·{\sum }_{j=1}^d{f}_{i,j}{v}_j}\right)\hfill \\ & =& \left(g^{{\sum }_{i=1}^m{\sum }_{j=1}^d{t}_j{f}_{i,j}{u}_j},g^{{\sum }_{i=1}^m{\sum }_{j=1}^d{t}_j{f}_{i,j}{v}_j}\right)\hfill \end{array}$$

  (24)
  If $\mathit{y}=\mathbf{F}·\mathit{x}$, then Equation (22) holds.
• Correctness of private verification.
  The correctness of private verification is consistent with the description provided in Section 3.4.

6.2. Security Analysis

In our two-server setup, we assume that $CS{P}_1$ and $CS{P}_2$ are non-collusive. Our security model allows for one or both servers to be malicious, as our verifiable computation scheme can detect the malicious behavior and reject the computation result. However, they cannot cooperate with each other. Under the non-collusion assumption, suppose one of the CSPs is malicious; then, the two CSPs cannot collaborate to perform the correct computation because the other CSP updates its data, causing the temporary ciphertext to not correspond to the temporary key. In this process, the malicious CSP does not learn any valuable information.

In our system, the function owner cannot obtain any additional information other than the function parameters. $CS{P}_1$ learns only the original ciphertext, the temporary ciphertext after re-encryption and the input ciphertext. $CS{P}_2$ learns only the temporary private key, the masked function parameters and the user’s input ciphertext. The request user only learns its own input and the computation result. Any public verification party can only learn the input ciphertext, the result ciphertext and the public verification data.

Next, we present the security analysis of our encryption schemes.

• HE. The scheme is based on the hardness of the Decisional Composite Residuosity Assumption and Decisional Diffie–Hellman Assumption, which is stated below:

  Definition 1.

  (Decisional Composite Residuosity Problem [26]) Given a composite n and an integer z, decide if z is an $n-residue$ modulo $n^2$ or not, namely, if there exists y such that $z=y^n\left(mod{n}^2\right)$.

  Definition 2.

  (Decisional Diffie–Hellman Problem [24]) Let g be an element of prime order in a cyclic group $\mathbb{G}$. Given $g^a,g^b,h\in \mathbb{G}$, decide whether or not $h=g^{ab}$.

  Theorem 1.

  The scheme is semantically secure if and only if the Decisional Composite Residuosity Assumption and Decisional Diffie–Hellman Assumption hold.
• LHE. The security is established in [3], and we state it below:

  Theorem 2.

  LHE is linearly homomorphic as long as $max\left\{\right|{\gamma }_1|,\dots ,|{\gamma }_d\left|\right\}·pr{n}^{1.5}<q/2$.

  Theorem 3.

  Let $r=poly\left(n\right)$ and $q=2^{n^{ϵ}}$ for some $0<ϵ<1$. The scheme is semantically secure under the worst-case hardness of approximating the shortest vectors on ideal lattices to within a factor of $O\left(2^{n^{ϵ}}\right)$.
• HPRE. It is based on the security of HE.
• VerM. It is based on the hardness of the Discrete Logarithm Assumption [9]. It will pass the verification by mistake with a probability of $1/q$ at most, which is negligible when q is a $\lambda$-bit prime. It is stated below:

  Definition 3.

  (Discrete Logarithm Problem) Let g be an element of prime order in a cyclic group $\mathbb{G}$. Given $h\in \mathbb{G}$, compute x such that $h=g^x$.

  Theorem 4.

  The scheme is semantically secure if and only if the Discrete Logarithm Assumption holds.

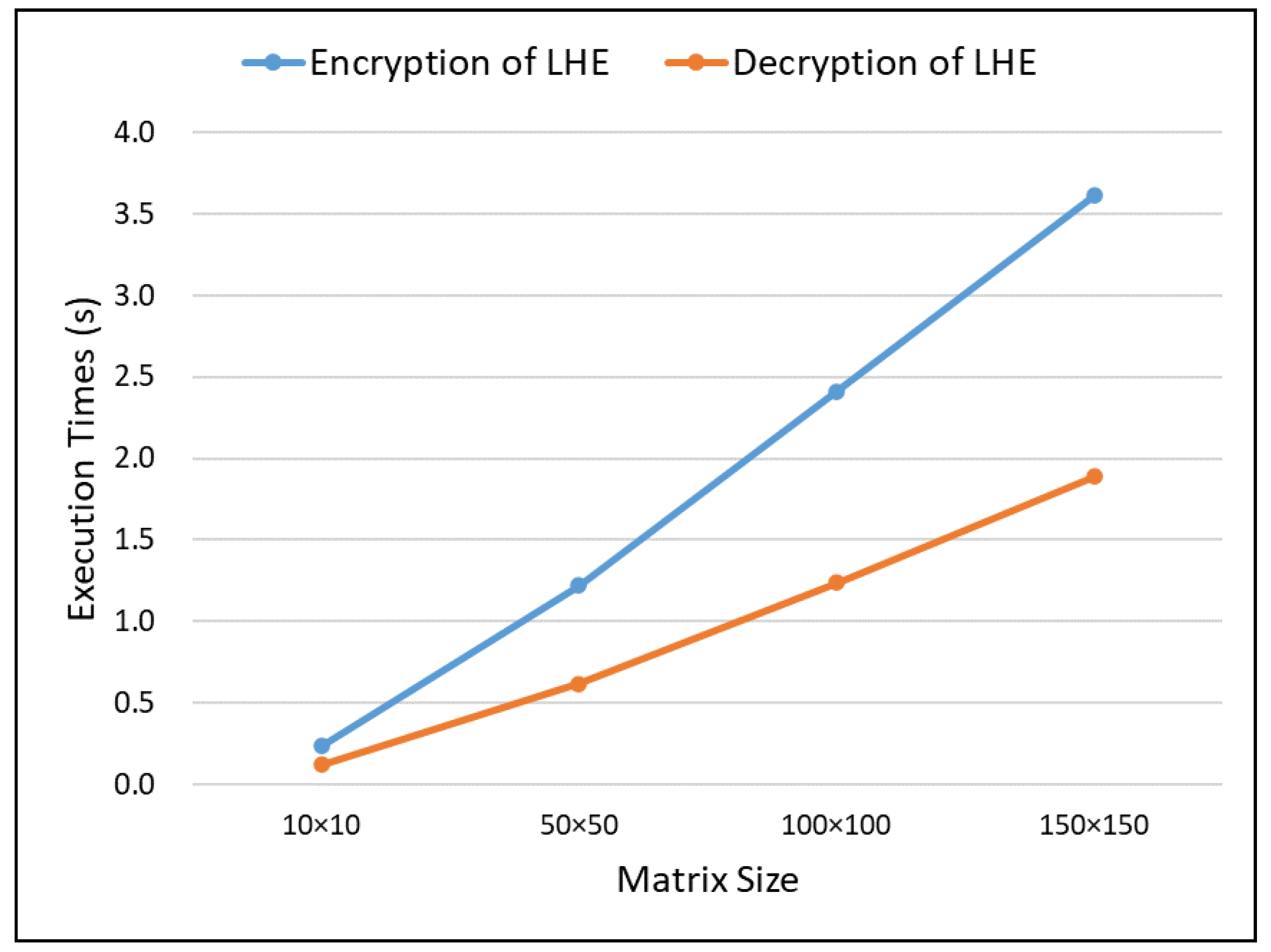
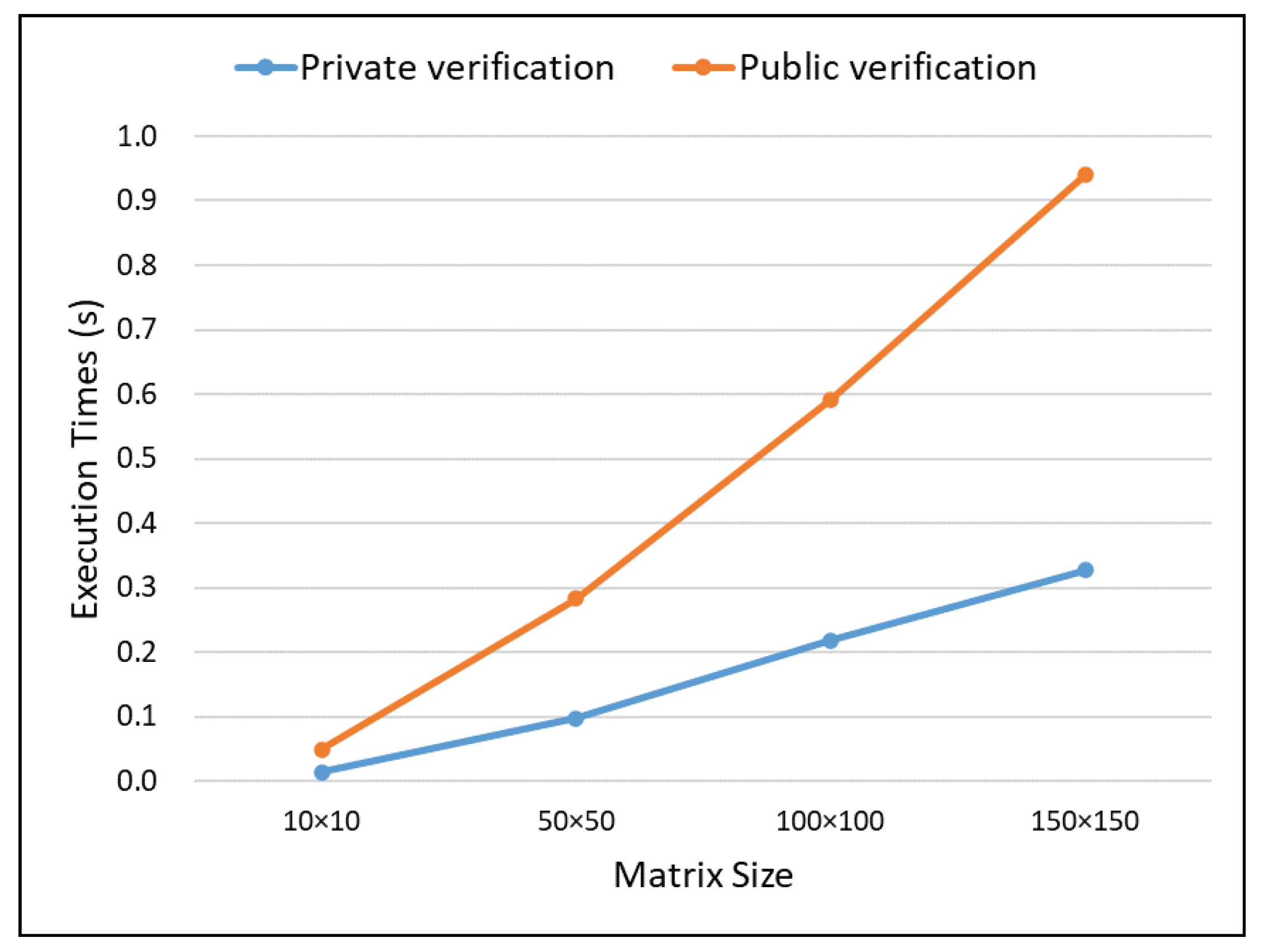
6.3. Experimental Results

To verify the efficiency, we performed our experiments on a personal computer with an AMD Ryzen 5 3600 3.6 GHz processor with 8 GB memory and running on the Ubuntu Desktop-20.04.1-LTS operating system using python language. We used the charm-crypto library to implement HE operations, PRE operations and VerM operations and used Microsoft SEAL to implement LHE operations. In the experiment, we set the security parameter of LHE to 4096 and that of HE to 1024. We tested the efficiency for the four entities when the matrix size was ($10\times 10,50\times 50,100\times 100,150\times 150$). The average time for each experiment was obtained by running it multiple times as shown in the graphs.

Figure 3 illustrates the time cost for the function owner, where the blue line presents the time for encrypting the matrix, the red line presents the time for preparing the generation of the verification data, and the gray line represents the time for the generation of the verification data. As shown in Figure 3, the function owner efficiently prepares the generation of verification data once for all parties. The primary overhead is the encryption of matrix parameters; however, since the function owner only needs to encrypt the function once for all parties, the computation cost can be amortized. Note that the vertical axis is on a logarithmic scale with a base of 10, and the same applies to Figure 4 and Figure 5.

Figure 4 illustrates the time cost for $CS{P}_1$. The blue line represents the time for re-encrypting the ciphertext, the red line represents the time for encrypting the mask, the gray line represents the time for generating the masked ciphertext, and the yellow line represents the time for computing the first part of the result ciphertext. As shown in Figure 4, the time for re-encryption and encrypting masks is nearly identical to that for the function owner to encrypt the matrix, and the homomorphic operations are highly efficient. The computation involving LHE ciphertexts is the most time-consuming, which would significantly burden the user if performed locally. Therefore, it was outsourced to the cloud server for computation.

Figure 5 illustrates the time cost for $CS{P}_2$, where the blue line represents the time for decrypting the masked ciphertext, and the red line represents the time computing the second part of the result ciphertext. As can be seen from Figure 5, the computation with LHE ciphertexts is the most time-consuming, which is the same as $CS{P}_1$, so it was outsourced to the cloud server.

Figure 6 illustrates the time cost for the request user, where the blue line represents the time for encrypting their input vector and the red line represents the time for decrypting the final result ciphertext. As shown in Figure 6, the encryption and decryption for users are very efficient.

Figure 7 illustrates the time cost for verification, where the blue line represents the time for private verification, and the red line represents the time for public verification. As shown in Figure 7, the process of private verification is quick and efficient. Public verification, on the other hand, may take more time but is still accessible for the public.

Next, we present the communication costs in

Table 4. Communication Costs.

Sender	Receiver	Phase	Communication Cost
Function owner	$CS{P}_1$	Preparation	$2·(m\times d)·{\mathbb{Z}}_{N^2}^{*}$ (Once for all)
Function owner	The public	Preparation	$(m+d)·{\mathbb{Z}}_q$ (Once for all)
Function owner	$CS{P}_1$	Preparation	$1·{\mathbb{Z}}_{N^2}+1·{\mathbb{Z}}_{N^2}^{*}$
Function owner	$CS{P}_2$	Preparation	$1·{\mathbb{Z}}_{N^2}$
Request User	$CS{P}_1$	Preparation	$d·{\left(R_q\right)}^2$
$CS{P}_1$	Function owner	Preparation	Permission Message
$CS{P}_1$	$CS{P}_2$	Computation	$2·(m\times d)·{\mathbb{Z}}_{N^2}^{*}+d·{\left(R_q\right)}^2$
$CS{P}_1$	Request User	Computation	$m·{\left(R_q\right)}^2$
$CS{P}_1$	The public	Verification	$(d+m)·{\left(R_q\right)}^2$
$CS{P}_2$	$CS{P}_1$	Computation	$m·{\left(R_q\right)}^2$

, where the matrix size is $m\times d$, N is the parameter in HE, and $R_p$ is the ring in LHE.

Compared with [9], our scheme achieves both function privacy and input privacy. In terms of computational complexity, our scheme is similar to their second scheme with only input privacy for the cloud server side, but we have two servers, which requires twice the computational overhead. At the same time, the two servers need to communicate with each other, which incurs additional communication overhead, but these additional costs provide privacy for the function.

7. Conclusions and Future Work

In this paper, we focused on the privacy-preserving and publicly verifiable outsourcing computation of matrix functions and polynomial functions. Our publicly verifiable computation scheme achieved both input privacy and function privacy for matrix functions, and it can be extended to arbitrary polynomial functions. Our scheme additionally provides a faster privately verifiable method and ensures the function owner’s control over access to the function. Our solution may be of interest to applications in oblivious polynomial evaluation or polynomial prediction model inference.

In the future, we plan to construct a publicly verifiable outsourcing computation scheme for nonlinear functions, such as for activation functions in convolutional neural networks. Furthermore, we will address how to identify malicious cloud servers if the verification fails.