A Comparative Study of Single and Multi-Stage Forecasting Algorithms for the Prediction of Electricity Consumption Using a UK-National Health Service (NHS) Hospital Dataset
Abstract
1. Introduction
- The use of a comparative study design and the inclusion of multiple forecasting algorithms allow for a robust analysis of the proposed technique.
- The impact of hybrid models and weather data on electricity demand forecasting is assessed.
- The use of an NHS hospital as the case study provides a relevant and practical application of the research, which could have important implications for hospital energy management and efficiency.
2. Data
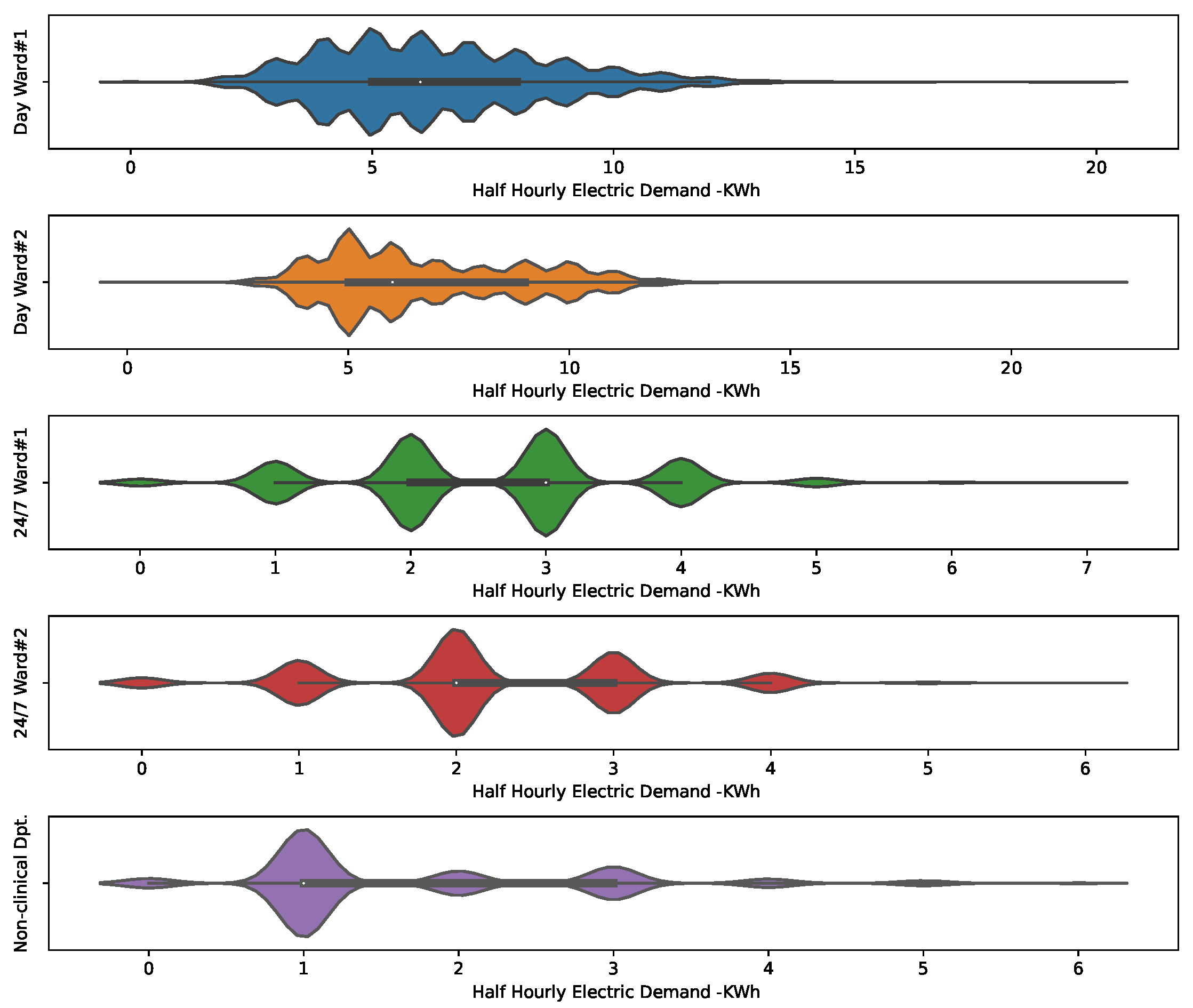
2.1. NHS Electricity Demand Dataset
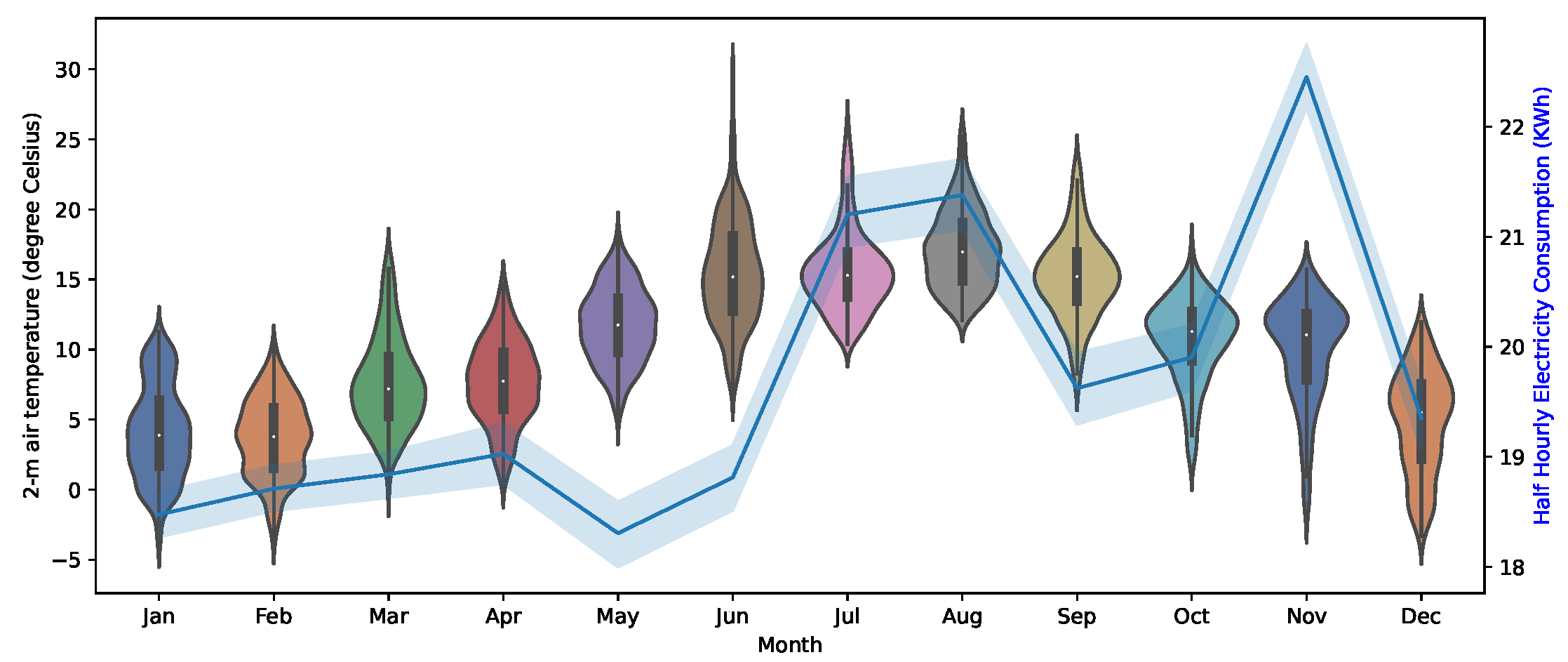
2.2. Weather Dataset
3. Forecasting Models and Evaluation Metrics
3.1. Forecasting Models
- FBP: The yearly, weekly, and daily seasonality are all set to increase forecasting accuracy and reliability.
- LSTM: The architecture used consists of one input, one hidden, and one output layer, with one, two hundred, and one nodes, respectively.
- SVR: The “RBF” kernel is used, due to its ability to deal with the high space complexity problem.
3.1.1. Multistage Forecasting
- Multistage models with similar algorithms
- SVR-SVR
- FBP-FBP
- Multistage models with hybrid algorithms
- FBP-SVR
- FBP-LSTM
- SVR-LSTM
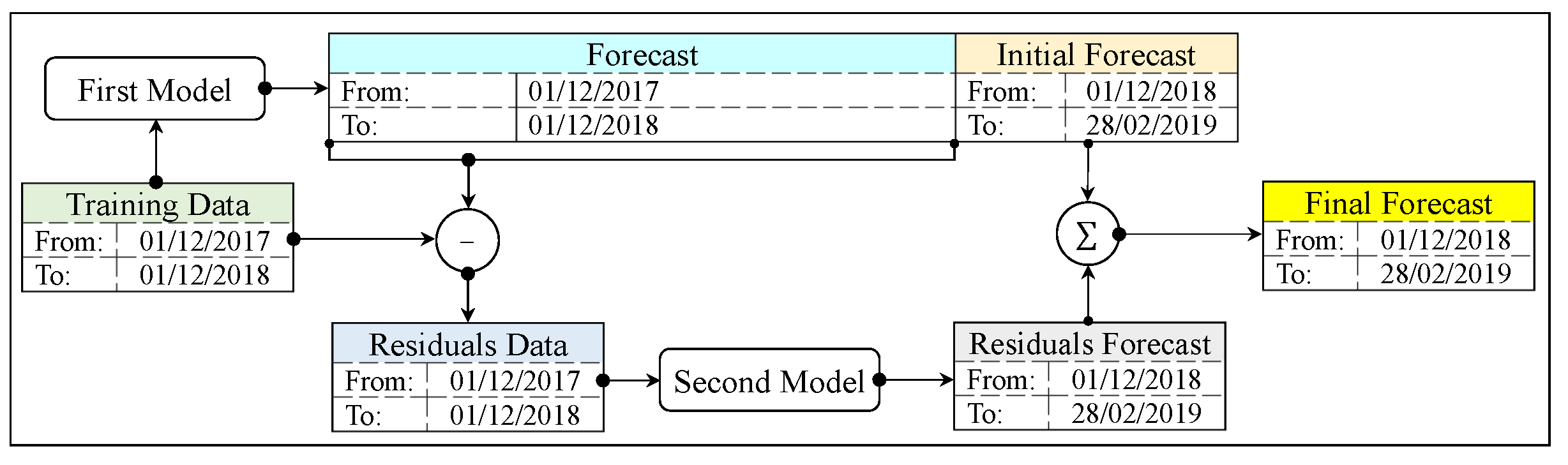
3.1.2. Limitations of Residual Forecasting
- Advantages
- −
- Simplicity: The method is easy to implement and requires minimal technical expertise.
- −
- Flexibility: The method can be applied to a wide range of forecasting problems, including time series forecasting and regression analysis.
- −
- Improved accuracy: By accounting for the residual errors in the forecasting model, the residual forecasting method can lead to more accurate predictions.
- −
- Transparency: The method is transparent and provides insight into the forecasting process, which can help decision-makers understand the sources of uncertainty in the forecasts.
- Limitations
- −
- Limited by time horizon: Residual forecasting is most effective in predicting outcomes over short to medium time horizons. Over longer time horizons, the accuracy of the predictions may decrease, particularly if there are significant changes in external factors that were not accounted for in the historical data.
- −
- Dependence on underlying model: The accuracy of the forecasts is heavily dependent on the accuracy of the underlying model used to estimate the residuals.
- −
- Assumption of stationarity: The method assumes that the residual errors are stationary over time, which may not always be the case.
- −
- Ignoring other sources of uncertainty: The method only accounts for residual errors and ignores other sources of uncertainty, such as measurement errors or random fluctuations.
3.2. Metrics to Evaluate the Forecasting Models
- The coefficient of determination ():where is the sum of squares of residuals, and is the total sum of squares.
- Mean Absolute Error (MAE):
- Root Mean Square Error (RMSE):where n is the number of samples, and y and are the predicted value and actual value, respectively.
4. Forecasting Results and Discussion
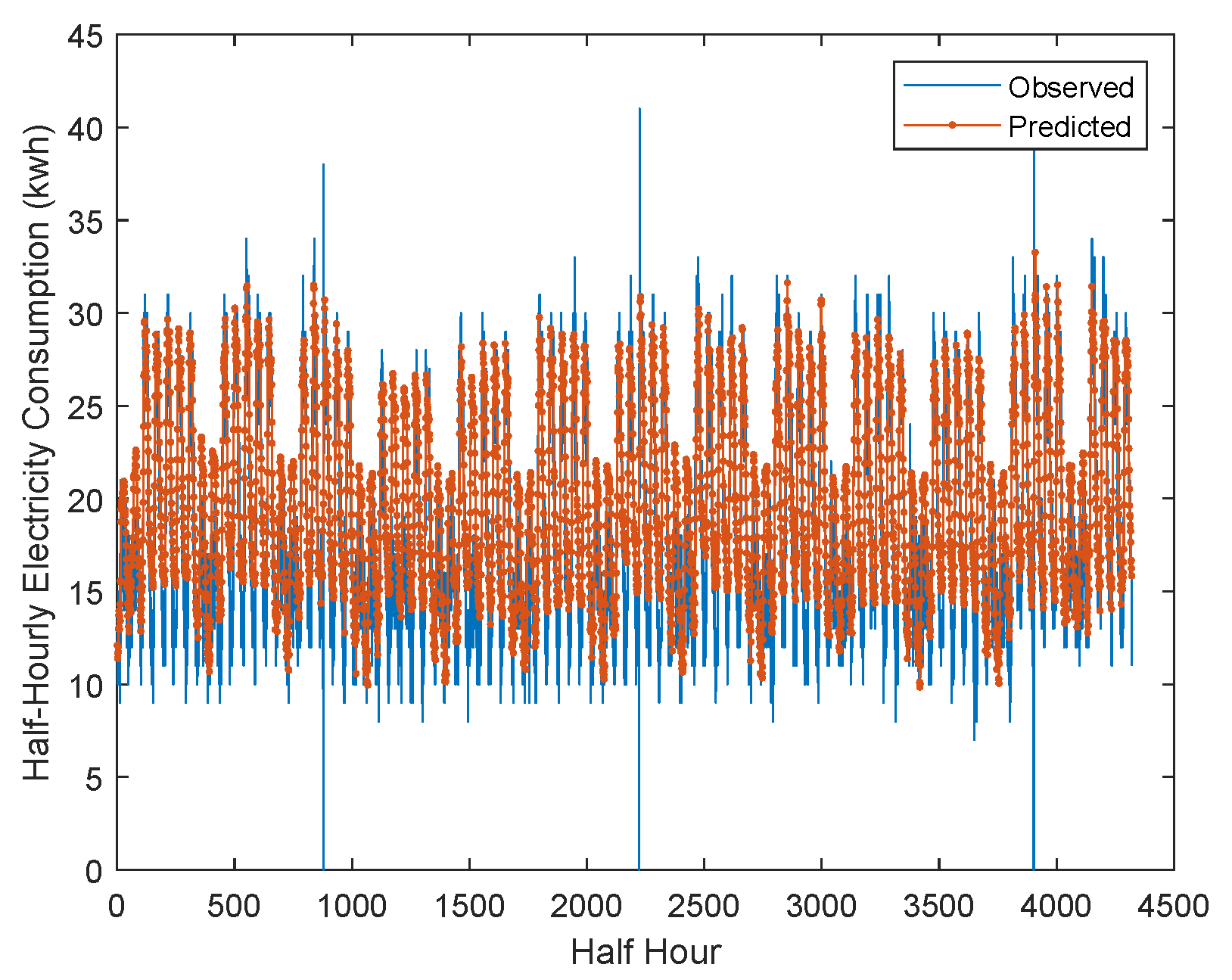
4.1. Single Models
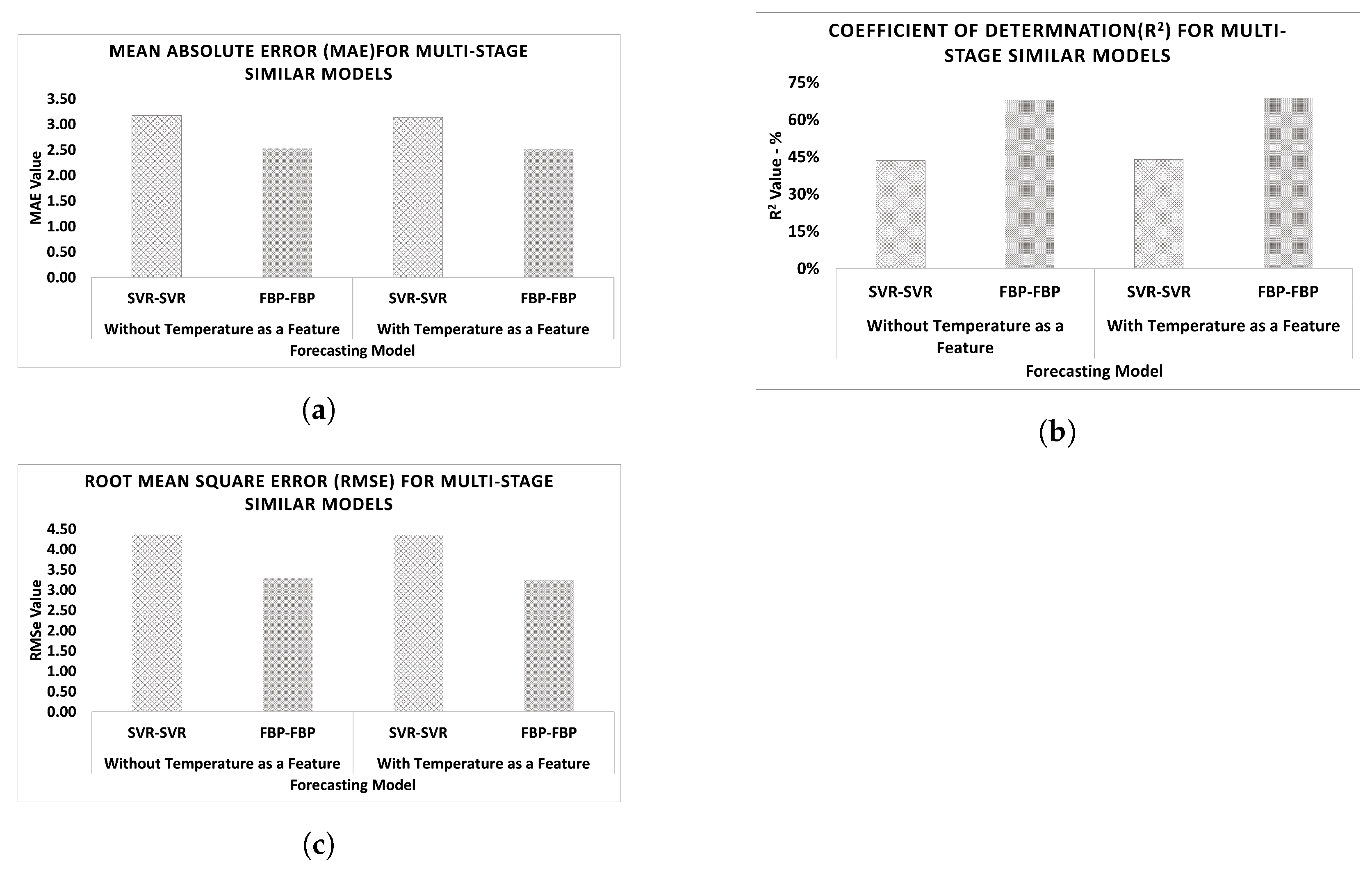
4.2. Multistage Models with Similar Algorithms
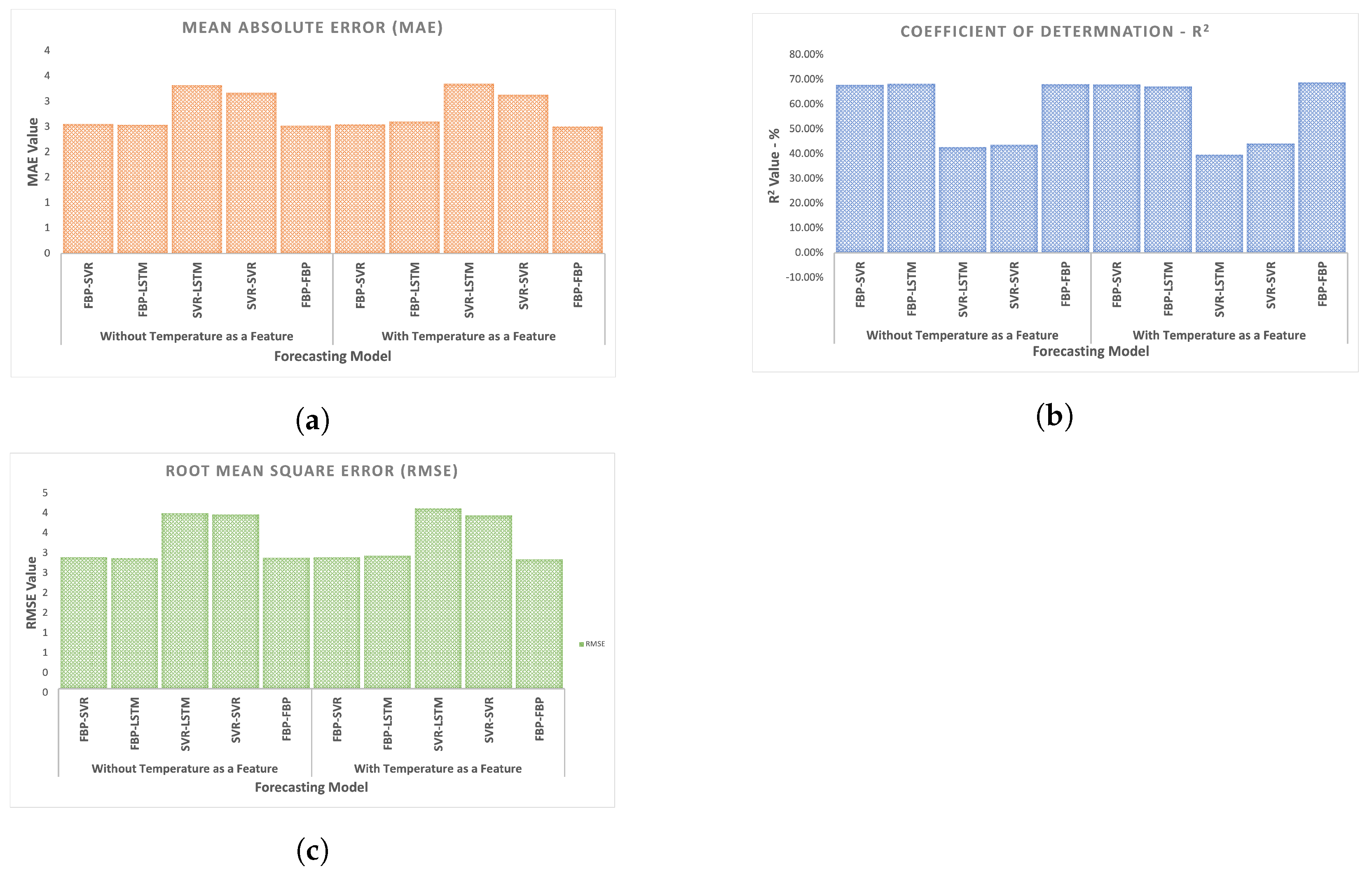
4.3. Multistage Models with Hybrid Algorithms
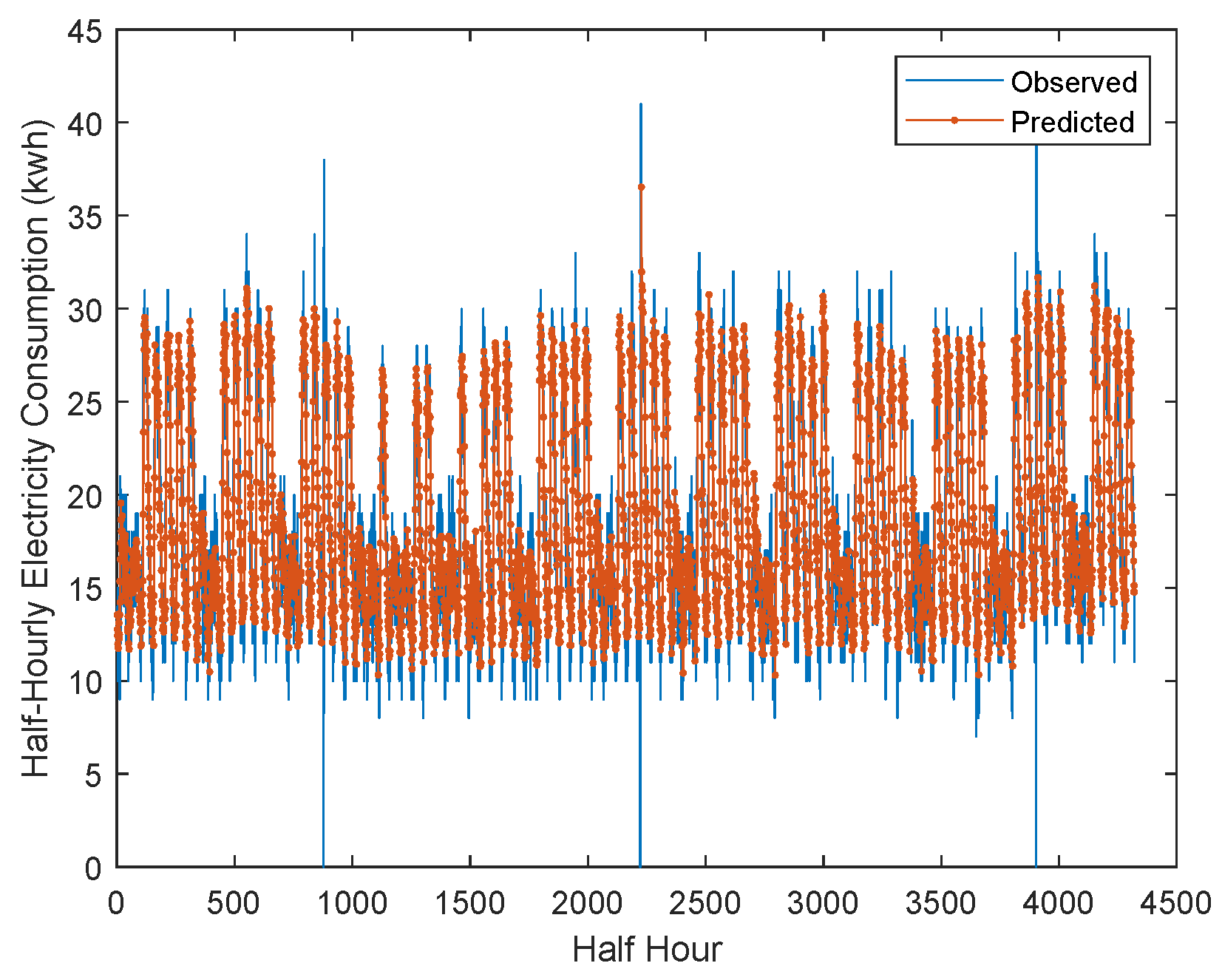
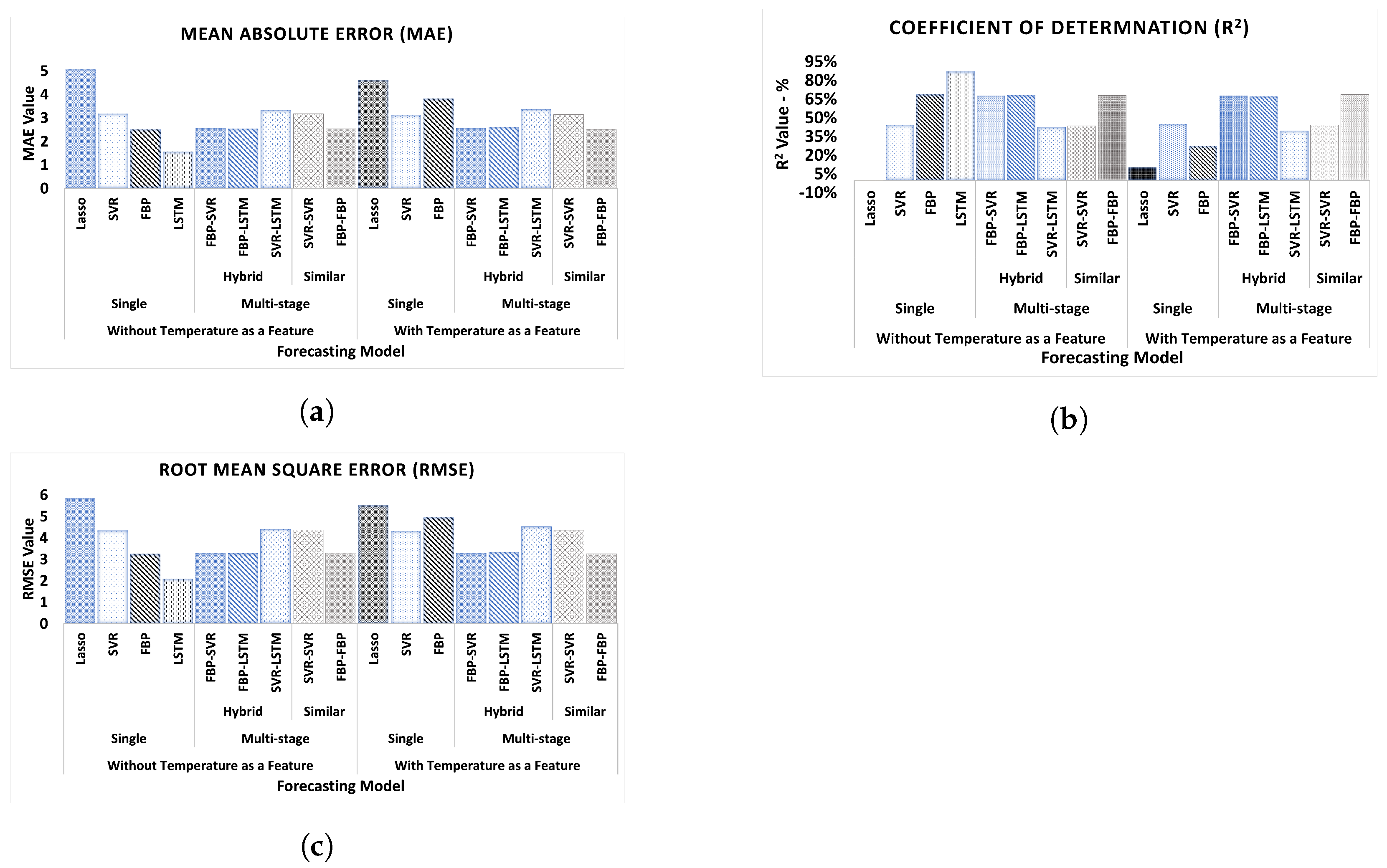
4.4. Evaluation and Discussions
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- NHS. Delivering a ’Net Zero’ National Health Service; Technical Report; National Health Service, NHS England and NHS Improvement: London, UK, 2020. [Google Scholar]
- NHS. NHS Energy Efficiency Fund-Final Report; Technical Report; National Health Service: London, UK, 2015. [Google Scholar]
- Suganthi, L.; Samuel, A.A. Energy models for demand forecasting—A review. Renew. Sustain. Energy Rev. 2012, 16, 1223–1240. [Google Scholar] [CrossRef]
- Hagan, M.T.; Behr, S.M. The Time Series Approach to Short Term Load Forecasting. IEEE Trans. Power Syst. 1987, 2, 785–791. [Google Scholar] [CrossRef]
- Fan, J.; McDonald, J. A real-time implementation of short-term load forecasting for distribution power systems. IEEE Trans. Power Syst. 1994, 9, 988–994. [Google Scholar] [CrossRef]
- Baliyan, A.; Gaurav, K.; Mishra, S.K. A Review of Short Term Load Forecasting using Artificial Neural Network Models. Procedia Comput. Sci. 2015, 48, 121–125. [Google Scholar] [CrossRef]
- Amjady, N. Short-term hourly load forecasting using time-series modeling with peak load estimation capability. IEEE Trans. Power Syst. 2001, 16, 498–505. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Aal, R.E.; Al-Garni, A.Z. Forecasting monthly electric energy consumption in eastern Saudi Arabia using univariate time-series analysis. Energy 1997, 22, 1059–1069. [Google Scholar] [CrossRef]
- Willis, H.L.; Tram, H.N. Load Forecasting for Trnasmission Planning. IEEE Trans. Power Appar. Syst. 1984, PAS-103, 561–568. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. A comparison of ARIMA and LSTM in forecasting time series. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1394–1401. [Google Scholar]
- Kumar, J.; Goomer, R.; Singh, A.K. Long short term memory recurrent neural network (LSTM-RNN) based workload forecasting model for cloud datacenters. Procedia Comput. Sci. 2018, 125, 676–682. [Google Scholar] [CrossRef]
- Dhiman, H.S.; Deb, D.; Guerrero, J.M. Hybrid machine intelligent SVR variants for wind forecasting and ramp events. Renew. Sustain. Energy Rev. 2019, 108, 369–379. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, P.; Chu, Y.; Li, W.; Wu, Y.; Ni, L.; Bao, Y.; Wang, K. Short-term electrical load forecasting using the Support Vector Regression (SVR) model to calculate the demand response baseline for office buildings. Appl. Energy 2017, 195, 659–670. [Google Scholar] [CrossRef]
- Ekonomou, L.; Christodoulou, C.A.; Mladenov, V. A short-term load forecasting method using artificial neural networks and wavelet analysis. Int. J. Power Syst. 2016, 1, 64–68. [Google Scholar]
- Karampelas, P.; Vita, V.; Pavlatos, C.; Mladenov, V.; Ekonomou, L. Design of artificial neural network models for the prediction of the Hellenic energy consumption. In Proceedings of the 10th Symposium on Neural Network Applications in Electrical Engineering (NEUREL 2010), Belgrade, Serbia, 23–25 September 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 41–44. [Google Scholar]
- Stratigakos, A.; Bachoumis, A.; Vita, V.; Zafiropoulos, E. Short-term net load forecasting with singular spectrum analysis and LSTM neural networks. Energies 2021, 14, 4107. [Google Scholar] [CrossRef]
- Aravazhi, A. Hybrid Machine Learning Models for Forecasting Surgical Case Volumes at a Hospital. AI 2021, 2, 512–526. [Google Scholar] [CrossRef]
- Bagnasco, A.; Fresi, F.; Saviozzi, M.; Silvestro, F.; Vinci, A. Electrical consumption forecasting in hospital facilities: An application case. Energy Build. 2015, 103, 261–270. [Google Scholar] [CrossRef]
- Tsakoumis, A.C.; Vladov, S.S.; Mladenov, V.M. Electric load forecasting with multilayer perceptron and Elman neural network. In Proceedings of the 6th Seminar on Neural Network Applications in Electrical Engineering, Belgrade, Yugoslavia, 26–28 September 2002; IEEE: Piscataway, NJ, USA, 2002; pp. 87–90. [Google Scholar]
- Barakat, B.; Taha, A.; Samson, R.; Steponenaite, A.; Ansari, S.; Langdon, P.M.; Wassell, I.J.; Abbasi, Q.H.; Imran, M.A.; Keates, S. 6G Opportunities Arising from Internet of Things Use Cases: A Review Paper. Future Internet 2021, 13, 159. [Google Scholar] [CrossRef]
- EnergyLogix. EnergyLogix Software, Helping to Manage Energy Consumption Information. 2019. Available online: https://energylogix.com/energy-monitoring/software/ (accessed on 9 February 2023).
- Science and Knowledge Service. JRC Photovoltaic Geographical Information System (PVGIS)-European Commission. 2020. Available online: https://europa.eu/capacity4dev/afretep/wiki/pvgis-photovoltaic-geographical-information-system (accessed on 9 February 2023).
- Wang, Y.; Shen, Y.; Mao, S.; Chen, X.; Zou, H. LASSO and LSTM Integrated Temporal Model for Short-Term Solar Intensity Forecasting. IEEE Internet Things J. 2019, 6, 2933–2944. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?–Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]





| Forecasting Techniques | Advantages | Disadvantages |
|---|---|---|
| Time Series Models (FBP, LSTM, SVR) | Easy to implement and interpret. Effective in dealing with strong seasonal effects. | Cannot capture complex relationships and nonlinearities in the data. Limited accuracy in long-term forecasting. |
| Regression Models | Easy to interpret and implement. Can capture linear relationships between variables. | Cannot capture nonlinear relationships in the data. Limited accuracy in long-term forecasting. |
| Econometric Models | Can capture complex relationships and nonlinearities in the data. | Can be difficult to interpret and implement. Limited accuracy in long-term forecasting. |
| Genetic Algorithms | Can capture complex relationships and nonlinearities in the data. Can optimise multiple objectives simultaneously. | Can be computationally expensive and difficult to interpret. Limited accuracy in long-term forecasting. |
| Algorithm | Advantages | Disadvantages |
|---|---|---|
| FBP | Simple and easy to implement. | Limited ability to capture complex patterns in data. |
| Can perform poorly when there are abrupt changes or irregularities in the data. | ||
| LSTM | Capable of capturing long-term dependencies in data. | Can be computationally expensive and require large amounts of data for training. |
| Can be computationally expensive and require large amounts of data for training. | Can be sensitive to the choice of kernel function. | |
| Able to handle nonlinear relationships between variables. | Can overfit if not properly regularised. | |
| SVR | Can handle nonlinear relationships between variables. | Can be computationally expensive and require large amounts of data for training. |
| Able to capture complex patterns in data. | Can be sensitive to the choice of kernel function. | |
| RNN | Capable of capturing long-term dependencies in data. | Can be computationally expensive and require large amounts of data for training. |
| Able to handle nonlinear relationships between variables. | Can suffer from the vanishing gradient problem. | |
| ANN | Can handle complex, nonlinear relationships between variables. | Can be computationally expensive and require large amounts of data for training. |
| Can suffer from the vanishing gradient problem. | ||
| ARIMA | Simple and widely used. Capable of capturing short-term dependencies in data. | Limited ability to capture long-term dependencies and nonlinear relationships between variables. |
| Can perform poorly when there are abrupt changes or irregularities in the data. | ||
| SARIMA | Extends ARIMA to handle seasonal patterns in data. | Limited ability to capture long-term dependencies and nonlinear relationships between variables. |
| Can perform poorly when there are abrupt changes or irregularities in the data. | ||
| LASSO | Able to handle high-dimensional data. | Can be sensitive to the choice of regularisation parameter. |
| Can perform feature selection and help with model interpretability. | May not perform well when there are nonlinear relationships between variables. | |
| MLP | Able to handle complex, nonlinear relationships between variables. | Can be sensitive to the choice of activation function. |
| Capable of capturing long-term dependencies in data. | Can suffer from the vanishing gradient problem. | |
| Can be used for both regression and classification problems. | Can be computationally expensive and require large amounts of data for training. | |
| Can suffer from the vanishing gradient problem. | ||
| May require careful tuning of hyperparameters to prevent overfitting. |
| Year | 2011 | 2015 | 2012 | 2016 | 2015 | 2015 | 2012 | 2012 | 2011 | 2012 | 2015 | 2012 |
| Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Model | MAE | RMSE | |||
|---|---|---|---|---|---|
| Without Temperature as a Feature | Single | LASSO | −0.76% | 5.05 | 5.83 |
| SVR | 44.35% | 3.17 | 4.34 | ||
| FBP | 68.68% | 2.51 | 3.25 | ||
| LSTM | 87.20% | 1.55 | 2.08 | ||
| With Temperature as a Feature | Single | LASSO | 10.15% | 4.61 | 5.51 |
| SVR | 44.99% | 3.12 | 4.31 | ||
| FBP | 27.61% | 3.82 | 4.94 | ||
| Model | MAE | RMSE | |||
|---|---|---|---|---|---|
| Without Temperature as a Feature | Multistage Similar | SVR-SVR | 43.57% | 3.17 | 4.37 |
| FBP-FBP | 68.06% | 2.52 | 3.28 | ||
| With Temperature as a Feature | Multistage Similar | SVR-SVR | 44.14% | 3.13 | 4.34 |
| FBP-FBP | 68.81% | 2.51 | 3.25 | ||
| Model | MAE | RMSE | |||
|---|---|---|---|---|---|
| Without Temperature as a Feature | Multistage Hybrid | FBP-SVR | 67.86% | 2.56 | 3.29 |
| FBP-LSTM | 68.22% | 2.54 | 3.28 | ||
| SVR-LSTM | 42.70% | 3.32 | 4.40 | ||
| With Temperature as a Feature | Multistage Hybrid | FBP-SVR | 67.97% | 2.55 | 3.29 |
| FBP-LSTM | 67.13% | 2.60 | 3.33 | ||
| SVR-LSTM | 39.62% | 3.35 | 4.52 | ||
| Model | MAE | RMSE | |||
|---|---|---|---|---|---|
| Without Temperature as a Feature | Single | LASSO | −0.76% | 5.05 | 5.83 |
| SVR | 44.35% | 3.17 | 4.34 | ||
| FBP | 68.68% | 2.51 | 3.25 | ||
| LSTM | 87.20% | 1.55 | 2.08 | ||
| Multistage Hybrid | FBP-SVR | 67.86% | 2.56 | 3.29 | |
| FBP-LSTM | 68.22% | 2.54 | 3.28 | ||
| SVR-LSTM | 42.70% | 3.32 | 4.40 | ||
| Multistage Similar | SVR-SVR | 43.57% | 3.17 | 4.37 | |
| FBP-FBP | 68.06% | 2.52 | 3.28 | ||
| With Temperature as a Feature | Single | LASSO | 10.15% | 4.61 | 5.51 |
| SVR | 44.99% | 3.12 | 4.31 | ||
| FBP | 27.61% | 3.82 | 4.94 | ||
| Multistage Hybrid | FBP-SVR | 67.97% | 2.55 | 3.29 | |
| FBP-LSTM | 67.13% | 2.60 | 3.33 | ||
| SVR-LSTM | 39.62% | 3.35 | 4.52 | ||
| Multistage Similar | SVR-SVR | 44.14% | 3.13 | 4.34 | |
| FBP-FBP | 68.81% | 2.51 | 3.25 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taha, A.; Barakat, B.; Taha, M.M.A.; Shawky, M.A.; Lai, C.S.; Hussain, S.; Abideen, M.Z.; Abbasi, Q.H. A Comparative Study of Single and Multi-Stage Forecasting Algorithms for the Prediction of Electricity Consumption Using a UK-National Health Service (NHS) Hospital Dataset. Future Internet 2023, 15, 134. https://doi.org/10.3390/fi15040134
Taha A, Barakat B, Taha MMA, Shawky MA, Lai CS, Hussain S, Abideen MZ, Abbasi QH. A Comparative Study of Single and Multi-Stage Forecasting Algorithms for the Prediction of Electricity Consumption Using a UK-National Health Service (NHS) Hospital Dataset. Future Internet. 2023; 15(4):134. https://doi.org/10.3390/fi15040134
Chicago/Turabian StyleTaha, Ahmad, Basel Barakat, Mohammad M. A. Taha, Mahmoud A. Shawky, Chun Sing Lai, Sajjad Hussain, Muhammad Zainul Abideen, and Qammer H. Abbasi. 2023. "A Comparative Study of Single and Multi-Stage Forecasting Algorithms for the Prediction of Electricity Consumption Using a UK-National Health Service (NHS) Hospital Dataset" Future Internet 15, no. 4: 134. https://doi.org/10.3390/fi15040134
APA StyleTaha, A., Barakat, B., Taha, M. M. A., Shawky, M. A., Lai, C. S., Hussain, S., Abideen, M. Z., & Abbasi, Q. H. (2023). A Comparative Study of Single and Multi-Stage Forecasting Algorithms for the Prediction of Electricity Consumption Using a UK-National Health Service (NHS) Hospital Dataset. Future Internet, 15(4), 134. https://doi.org/10.3390/fi15040134












