Abstract
We evaluate analysis results and approximations for the performance of basic caching methods, assuming independent requests. Compared with simulative evaluations, the analysis results are accurate, but their computation is tractable only within a limited scope. We compare the scalability of analytical FIFO and LRU solutions including extensions for multisegment caches and for caches with data of varying sizes. On the other hand, approximations have been proposed for the FIFO and LRU hit ratio. They are simple and scalable, but their accuracy is confirmed mainly through asymptotic behaviour only for large caches. We derive bounds on the approximation errors in a detailed worst-case study with a focus on small caches. The approximations are extended to data of different sizes. Then a fraction of unused cache space can add to the deviations, which is estimated in order to improve the solution.
1. Introduction: Basic Caching Methods and Their Evaluations
Caching strategies are essential for the performance of local caches in CPU, GPU and database systems [1] as well as for content delivery on the Internet [2,3]. A set of basic caching strategies, such as first-in-first-out (FIFO), least recently/frequently used (LRU/LFU) and clock-based caching [1,4,5,6,7,8,9], were studied in early caching approaches almost 50 years ago, and they are still preferably applied today. Other caching methods that include detailed properties, caching costs and values per data object can optimize the efficiency on the basis of score rankings [10,11] or machine-learning approaches [12,13]. However, FIFO and LRU are still attractive caching principles because of their simple and fast data management [3,14,15,16].
We compare analysis and approximation methods for the FIFO and LRU hit ratio evaluation, where RANDOM and clock-based caches are included, because their performance is partly equivalent to FIFO [6]. Moreover, simulation is a usual performance evaluation approach for caches. Simulations are flexibly applied for many caching methods and variants [2,11,17,18,19], but they are subject to random deviations, which require long runs for accurate results in narrow confidence intervals.
Exact analytic hit ratio solutions were derived long ago by W.F. King [8] and E. Gelenbe [6] for the independent reference model. In the past decade, the state of the art has advanced towards solutions for multisegment/multilevel caches [20], and for LRU caches with data objects of different sizes, including the cache startup or filling phase [21,22]. However, those exact solutions are tractable only for small caches.
In addition to exact analysis and simulation, approximation formulas form a third pillar for a simpler evaluation of basic caching methods, as proposed by Fagin [23] and Che et al. [24] for LRU as well as by Dan and Towsley [25] for FIFO. Recent research has approved asymptotical exactness of both LRU variants for large caches [26,27,28,29].
The motivation and purpose of this work is to present a complete picture of the currently available analysis and approximation results for FIFO and LRU. Our focus is mainly on FIFO results [14,16], which are only sparsely addressed in the literature, in contrast to LRU [9,18,21,22]. The product form solution of the FIFO hit ratio for independent requests [6,8] is scalable for large caches and applicable to clock-based caching (CpR: clock per request), in contrast to LRU analysis results. We show that the FIFO approximation [25] has similar properties, as confirmed for LRU [26,27,28,29] for data of unit size, and we extend the approaches for data of variable sizes as required for web content delivery.
An overview of the similarities and differences in the results for FIFO and LRU is provided in Table 1. The scope of the analysis methods is clarified in the main part, and the accuracy of the approximations is studied in an extensive quantitative investigation. On the basis of detailed insights and a comparison of the alternative cache performance evaluation methods, we finally recommend the most appropriate evaluation options for the considered caching use cases.

Table 1.
Overview of analytical and approximate cache performance results.
As new contributions of this work,
- product form solutions are extended to clock-based methods and combinations of those methods, with FIFO and RANDOM for single and multilevel caches,
- the scope of analytical solutions is clarified regarding scalable computation as well as the solutions’ applicability for data of different sizes, and
- quantitative evaluations of the accuracy of approximations identify the worst cases and error bound extensions for varying data sizes in caches.
We start with exact analysis results for the FIFO, CpR and RANDOM hit ratio and assess their scalability, in Section 2. The precision of approximations for FIFO and LRU caching strategies is evaluated in Section 3 and Section 4. Extensions to multisegment caches are addressed in Section 5. Section 6 focuses on FIFO solutions for objects of different sizes in comparison to LRU. Section 7 summarizes the main results and their limitations.
2. Markov Analysis Results for Basic Caching Strategies
W.F. King 8 provided steady state FIFO and LRU hit ratio formulas, assuming a limited cache size for M objects of unit sizes and an independent reference model (IRM). The latter is characterized by a fixed catalogue of N objects O1, …, ON, which are referenced with probabilities p1, …, pN in each request. The IRM request pattern with the Zipf-distributed popularity of the data has been confirmed manifold as a realistic model for web request traces [17,31,32]. Moderate correlation among requests and changes in the working set of relevant data are also relevant [31,32,33].
2.1. Common Hit Ratio Analysis of FIFO, RANDOM and Clock-Based Caching
FIFO caches replace the object that is present in the cache for the longest time with the requested object in the case of a cache miss. W.F. King [8] showed that FIFO caching follows a Markov process under IRM with a transition per request, whose steady state content distribution has a product form solution. The probability pFIFO(Ok1, ∙∙∙, OkM) to find the objects Ok1, ∙∙∙, OkM in positions 1, …, M of a FIFO cache is given by
pFIFO(Ok1, ∙∙∙, OkM) = c pk1 ∙ ∙∙∙ ∙ pkM (∀ j ≠ l: Okj ≠ Okl; M: cache size; c: norm. constant).
Gelenbe [6] proved the same product form solution to be valid also for a RANDOM caching strategy, which randomly chooses the eviction candidate with probability 1/M among the objects in the cache. Moreover, we confirm a broader scope of product form solutions, including clock-based caching and combinations of FIFO/RANDOM/clock.
Clock methods indicate an eviction candidate by a clock hand, which steps one position forward per request (CpR). Upon a cache miss, the requested object replaces the eviction candidate. Corbato [4] proposed several variants of the basic CpR method. Score-gated clock [11] is a clock scheme which admits new content only if it has a higher score than the eviction candidate. The steady state probabilities pCpR(Ok1, ∙∙∙, OkM) of CpR cache content follow the same product form as for FIFO and RANDOM:
pCpR(Ok1, ∙∙∙, OkM) = pFIFO(Ok1, ∙∙∙, OkM) = pRANDOM(Ok1, ∙∙∙, OkM) = c pk1∙ ∙∙∙ ∙pkM
As the main step of a proof, we insert this solution into the equilibrium equations of the underlying Markov chain for CpR cache content. Figure 1 illustrates which transitions are possible from previous states to the content Ok1, ∙∙∙, OkM.

Figure 1.
State transitions for CpR and FIFO to the cache content Ok1, ∙∙∙, OkM.
For a cache hit, a cyclic clock shift leads from content Ok2, ∙∙∙, OkM, Ok1 to Ok1, ∙∙∙, OkM with a corresponding transition probability pk1 + ∙∙∙ + pkM. Otherwise, a cache miss leads to Ok1, ∙∙∙, OkMif Ok1 is requested as an external object, i.e., with transition probability pk1 from a previous content state Ok2, ∙∙∙, OkM, Ol. We obtain the following equilibrium equations corresponding to one-step transitions per request to Ok1, ∙∙∙, OkM:
The product form solution is substituted and verified for those equilibrium equations:
This main step for proving the CpR steady state solution applies to FIFO and RANDOM strategies in a similar way [6,8]. Transitions in steady state are encountered only between content states representing a full cache, while states with less than M objects are transient. The proof of the product form solution, Equation (1), is completed by checking whether the Markov chain is ergodic; i.e., a transition path must lead from each content state Ok1, …, OkM to each other with nonzero probability. The underlying IRM Markov processes for the RANDOM and CpR strategies are generally ergodic if ∀k: pk > 0, whereas FIFO has a nonergodic exception if and only if N = M + 1. These results are covered by general criteria for ergodic caching networks derived by Rosensweig et al. [34].
Finally, the product form solution implies a common steady state hit ratio for the next request as the sum of request probabilities of all data objects stored in the cache [6,8]:
Moreover, the common solution extends to a broader class of variants and combined schemes. For example, when we alternate between FIFO, RANDOM and CpR in subsequent requests either in a periodic pattern or in a randomized pattern, the previous core verification step still applies per request. Variants of the clock-hand movement by skipping several objects per requests again leave the steady state solution unchanged, provided that the Markov process is still ergodic [34]. The FIFO product form solution has been derived in alternative ways via reversibility properties of the underlying Markov process by Marin et al. [35] and via fluid flow approximation by Tsukada et al. [36].
2.2. Scalable Iterative Evaluation of the Product Form Solution
An iterative evaluation of the product form (2) with scalable complexity O(MN) was proposed by Fagin and Price [30], which makes the FIFO hit ratio computations tractable even for large caches, in contrast to the LRU analysis formula of Equations (11)–(13). Equation (2) is evaluated in an extended format of intermediate results s(m, n) and h(m, n):
Next, the following scheme can be used to compute , etc. via Equation (3) [30]:
s(m, n + 1) = s(m, n) + s(m − 1, n) pn+1 with initialization s(0, n) = p1 +…+ pn ;
However, a direct implementation of this scheme is subject to numerical instability for large m, n, because the components s(m, n), h(m, n) of Equation (3) are partly extremely small, in a range below 10−100, 10−1000, etc. and thus below the usual CPU number representation. In order to improve numerical accuracy for large m, n, we sort the objects according to their request probabilities p1 ≤ p2 ≤ … ≤ pn and start summations with the smallest values. Moreover, we add a factor 10−20k (k ∈ N) to the real number representations of s(m, n) and h(m, n), such that the representation of y in the range (10−20(ky+1), 10−20ky) has an integer component ky ∈ N and a real component ry ∈ (10−20, 1), such that y = ry · 10−20ky. Thereafter, 10−1000 is included for (ry , ky) = (1, 50), etc. In this way, we finally achieve an accurate and scalable computation of the product form solution, as confirmed by a comparison with the simulation results of numerous examples, including the results in Figure 2 and Table 2.
3. Approximation of the IRM Hit Ratio for FIFO
Because the analytical FIFO solution of Equations (2) and (3) needs an extended number representation for large caches and the LRU solution of Equations (11)–(13) is not scalable, simpler approximations have been proposed. The FIFO hit ratio approximation refers to the time spans that an object Ok spends inside the cache (TInCache) and outside (TExtern,k), which are measured by the number of requests in both time spans. For independent requests, the external phase TExtern,k is geometrically distributed with mean = 1/pk until the next request to Ok.
When an object enters the cache, it starts from the top FIFO position and steps down by one place per cache miss. We assume a constant cache miss probability 1 −, independent of the current cache content. Next, the mean number of requests that an object spends in a FIFO cache is the same for all objects: ≈ M/(1 −). Finally, we obtain the hit ratio per object Ok: . In total,
This leads to the following iterative computation scheme for :
Starting from = 0 ⇒ = M, is monotonously increasing in each iteration step of Equation (5). There is a unique solution, and the iteration is converging towards this solution. The computation effort of Equation (5) is O(N) per iteration round.
The FIFO (RANDOM, CpR) hit ratio approximation of Equation (5) is equivalent to the approach by Dan and Towsley [25]. Based on a slightly more restrictive assumption of Poisson request processes per object, Garetto et al. [37] provide an alternative derivation by using queueing theory and Dehghan et al. [10] by using time-to-live caching.
3.1. Precision of the FIFO Approximation for Zipf-Distributed IRM Requests
We compare the exact FIFO hit ratio analysis with the approximation for cases of Zipf-distributed IRM requests [31] with pk = α k −β for k = 1, …, N; α = 1/Σ k k −β. Zipf-distributed request pattern has been reported manifold in content distribution on the Internet for the popularity of files, videos, etc. [31,32,33]. Figure 2 shows results for β = 1 and for varying object catalogue sizes N = 10, …, 106, with cache sizes M over the entire range [1, …, N]. The largest deviations of up to 1.7% are encountered for the smallest M, N. For large N, M, the deviations are often tiny, going down to the range of 10−6–10−7, where asymptotical exactness can be expected due to a statistical multiplexing effect. As a general trend, we experience the deviations to decrease with the variance of the popularity distribution. Thus, for independent Zipf-distributed requests, the deviations are increasingwith the shape parameter β and decreasing with M, N.
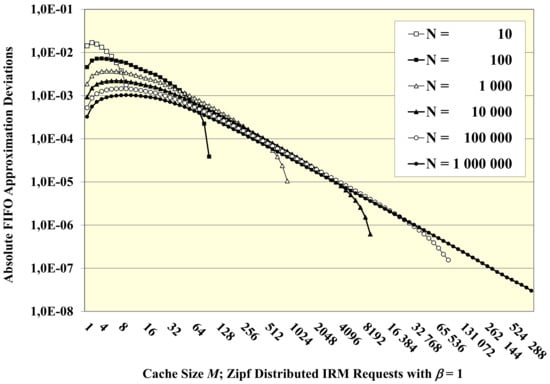
Figure 2.
Deviations of FIFO approximations of Equations (4) and (5) from exact results of Equations (2) and (3).
3.2. Maximum Error Cases of the FIFO Approximation for Small Cache Size M
The FIFO hit ratio approximation is highly accurate for large caches, but larger errors are encountered for small caches. In order to identify maximum error cases, the following approach aims to cover the entire range of IRM popularity distributions for small M, N.
In particular, we checked all 204 266 popularity distributions whose request probabilities are multiples of 1/50 = 2%, such that pk = ik/50 with integers ik for k ≤ N ≤ 50. The approximation of Equations (4) and (5) is compared to the product form analysis of Equation (2) for all those distributions and for all cache sizes M < N, yielding over a million deviation results. The computation required 2 days on a usual PC, but an exponential increase in the number of distributions will soon impede extensions to a finer raster of 1/51, 1/52, etc.
We separated the results for each cache size M and sorted them according to decreasing deviations. Finally, we obtained lists of the top-K largest deviations of the FIFO approximation for all popularity distributions in the 2% raster. They strongly suggest that maximum deviations are encountered for popularity distributions of the following type:
i.e., there are n data objects with the same popularity among many more objects with negligible request probabilities. The parameters n, p specify extreme distributions of the type (6) for different cache sizes M. In our study of popularity distributions in the 2% raster, a sorted list of the largest deviations starts with hundreds of cases which are closest to a specific case of the format of Equation (6).
p1 = p2 = ∙∙∙ = pn = p/n; pn+1 = ∙∙∙ = pN = (1 − p)/(N − n) → 0 for N → ∞,
The same behaviour has also been experienced by Fagin [23] and Che et al. [24] for maximum deviations of approximations to the LRU hit ratio; see Section 4. An example of the top-10 maximum error cases of approximations in the 2% raster is shown in Figure 4, which are all near the corresponding maximum error case of the format (6).
The distribution type (6) leads to simple direct solutions for the approximation Equation (5) and for the exact approach of Equation (2). A substitution of Equation (6) into Equations (4) and (5) results in a quadratic equation for and an explicit solution for :
The special format of Equation (6) also allows for computing the probabilities qm that we find m out of n popular objects in the cache for m = 0, …, min(n, M). In this way, we obtain the exact hit ratio result = Σm qm·m·p/n, especially for the format (6). We derive qm by collecting all the corresponding components from Equation (2):
A further evaluation of this expression in the limit N → ∞ yields the following simple scheme:
which leads to a direct evaluation of q0,···, qM and finally of .
qm+1/qm = (n − m)(M − m)p/[n(m + 1)(1 − p)],
In Table 2, the worst FIFO error cases are listed for M = 1, …, 10. The parameters p, n specify the probabilities p1 = ∙∙∙ = pn = p/n of the extreme format (6). The approximation is exact for uniform distributions, as confirmed by substituting = M/N and pk = 1/N into Equation (5). Moreover, we observe without proof that the errors are always negative, i.e., the approximation of Equations (4) and (5) seems to establish a lower bound. The main conclusions from Table 2 on the accuracy of the FIFO approximation are as follows:
- Considerable errors of up to 16.5% are encountered for small cache size M.
- They are reduced towards a fair accuracy with errors below 3% for M ≥ 10.

Table 2.
Maximum deviations of FIFO approximations of Equations (4) and (5) for cache size M.
Table 2.
Maximum deviations of FIFO approximations of Equations (4) and (5) for cache size M.
| Maximum Deviations of the FIFO, RANDOM & CpR Approximation for Cache Size M: Worst Cases Are Request Distributions of the Type (6) with n = M | ||||
|---|---|---|---|---|
| M | p1= ∙∙∙ = pn (n = M) | Exact Result of Equation (2) | Approximation of Equations (4) and (5) | Maximum Deviation |
| 1 | 0.8838 | 78.11% | 61.62% | –16.49% |
| 2 | 0.4705 | 84.13% | 73.30% | –10.83% |
| 3 | 0.3213 | 87.49% | 79.45% | –8.04% |
| 4 | 0.2440 | 89.75% | 83.37% | –6.38% |
| 5 | 0.1965 | 91.35% | 86.07% | –5.28% |
| 6 | 0.1645 | 92.51% | 88.00% | –4.51% |
| 7 | 0.1414 | 93.41% | 89.48% | –3.93% |
| 8 | 0.1240 | 94.10% | 90.62% | –3.48% |
| 9 | 0.1104 | 94.69% | 91.57% | –3.13% |
| 10 | 0.0995 | 95.14% | 92.30% | –2.84% |
4. Approximations of the LRU Hit Ratio
Because the exact LRU result of Equation (12) is tractable only for small caches, the proposed LRU approximations by Fagin [23] and Che et al. [24] are even more relevant. Both approaches are similar: each starts from an equation to determine the mean number of requests until an object O is handed over from the top LRU position to the bottom and leaves the cache if there are no further request to O. also characterizes the cache startup and LRU convergence time until an empty cache of fixed size M is filled [21].
can be determined from a coupon collection process until a series of requests has addressed M different objects. The exact computation of the probability distribution of this process for IRM requests is again scalable only for small caches [21,22,29]. Instead, Che’s approximation first determines and then the LRU hit ratio [24,28,37]:
- is approximated by the unique solution of the equation M =.
- Thereafter, the LRU hit ratio is obtained per object (hChe (Oj)) and in total (hChe):
Fagin’s earlier approach differs from Che’s by substituting e−pj with 1 – p :
Both approximations yield asymptotically exact results for large M, N, as shown in [26,27,28,29]. We complement the best-case analysis with a study of the worst-case errors of both approaches [21], similar to Section 3.2 for FIFO. All 204 266 popularity distributions in a 2% raster are checked with pk = ik/50 for integers ik (k ≤ N ≤ 50). The approximations hFagin and hChe are compared with the analysis results via Equation (12) and/or simulations for all cache sizes M < N. The study once more strongly suggests the format (6) for distributions with maximum errors of ∆hFagin = hFagin − hLRU and ∆hChe = hChe − hLRU.
Table 3 provides a list of the maximum deviations ∆hFagin and ∆hChe for M ≤ 10, similar to Table 2 for the FIFO deviations. We checked both parameters n, p of Equation (6) for extreme cases and adapted n, p for each M to maximize ∆hFagin and ∆hChe [21].

Table 3.
Maximum LRU approximation errors of Equations (7) and (8).
Note that Fagin’s approach [23] is exact for M = 1 and that Che et al. [24] report maximum errors of 2% for their approach compared with simulations. We conclude from Table 3:
- The maximum deviations ∆hChe of Che’s approximation are decreasing with the cache size M from 8.25% for M = 1 down to less than 1% for M ≥ 10.
- The maximum deviations ∆hFagin of Fagin’s approximation are decreasing with the cache size M from 5.2% for M = 2 down to less than 1.3% for M ≥ 10.
Figure 3 summarizes the encountered maximum errors for M = 1, …, 10:
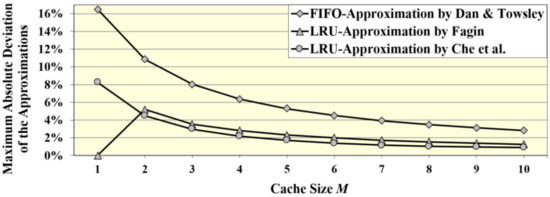
Figure 3.
Maximum errors of FIFO and LRU hit ratio approximations.
The LRU results in Table 3 are again based on the evidence from the check of 204 266 popularity distributions in a 2% raster. However, a proof that the distribution type (6) generally maximizes the errors of Fagin’s and Che’s approaches is open for future study.
We illustrate the evidence in the result max(|∆hChe|) ≈ 2.97% for M = 3. The top-10 error cases out of more than 2 × 105 popularity distributions in the 2% raster are shown in Figure 4. These cases are all in a close surrounding of the extreme case of the type (6), which is shown at the bottom of Figure 4. The top-100 error cases of the list are again in an extended surrounding of the same extreme case. A similar behaviour is observed for all maximum error cases for M = 1, …, 10 in Table 2 and Table 3.
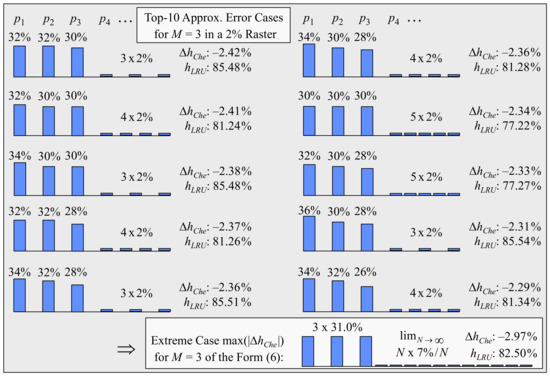
Figure 4.
Top-10 error cases for M = 3 in a 2% raster and extreme case ∆hChe ≈ −2.97%.
5. Extended Product Form Solution for Multisegment Caches
The product form solution (1–2) can be extended to caches composed of several levels (lists, partitions, segments) L1, …, LK. A requested object on cache level Lj (j ≥ 2) is then forwarded to level Lj−1 in exchange for an evicted object moving from Lj−1 to Lj, as illustrated in Figure 5. Cache segmentations can improve the hit ratio by collecting the most popular objects on high cache levels on account of slower adaptation to content changes. Many proposed caching strategies make use of two or more segments, such as ARC [18], segmented LRU [1], k-LRU [38], LRU(m) [12,38], half rank exchange [11], FB-FIFO [39], transposition relocation or CLIMB [7,40]. Distributed architectures also include spreading multilevel storage structures over several cache servers [41].
Garetto et al. [37] and Li et al. [12] include an LRU(K) variant with LRU on the first level L1. The mixing time is estimated [12] for adaptation to a changing request pattern. An extended product form solution is derived [20] for FIFO(K) and RANDOM(K) strategies when either FIFO or RANDOM is used on all levels. This solution extends to clock per request (CpR) and all variants, which were already included in the single-segment product form of Equations (1) and (2). The solution still remains valid when different strategy variants of the set {FIFO, RANDOM, CpR} are applied on different levels.

Figure 5.
Multisegment caches with FIFO, RANDOM or CpR strategy per segment.
Next, we confirm the generalized product form in an example of two-level caches where FIFO is applied on the first and RANDOM on second level. External objects enter the cache on the second level. Let p*(k1, …, km, km+1, …, km+n) denote the steady state IRM probability for content in the cache, where the first cache level ranges from positions 1, …, m, and the second from m + 1, …, m + n. Thereafter, we obtain
For a proof, we set up and check the solution (9) in Markovian equilibrium equations. All preceding states are considered on the right, which lead to the cache content in the next request. A request to an object in the first level keeps the state unchanged according to the FIFO rule. A request to an object on second level moves an object from a position m + i to the top; i.e., Ok1 is renewed by such a request with probability pk1, as illustrated in Figure 5. In exchange, the object on the bottom of level 1 moves to position m + i on level 2. Upon a cache miss, the requested external object replaces a RANDOM eviction candidate Okj in position m + i on the second level with transition probability pkm+i/n. We obtain (∀ j ≠ l: kj ≠ kl)
A check of the ergodicity preconditions is omitted, which would require more space, as well as a proof of the general result: the steady state IRM content distribution for K-level caches with arbitrary combinations of the strategies FIFO, RANDOM and CpR being applied on the levels follows the product form [20] (∀ j ≠ l: kj ≠ kl):
This result includes half rank exchange [11] as a special case with segment sizes lj = 2 j and M = 2K+1 − 1. As an extreme case, Climb [7,41] is covered by the multilevel LRU solutions [12,20] and by Equation (10), where ∀j: lj = 1. Climb is denoted as transposition relocation in a study by McCabe [7], who compared Climb with LRU in one of the first Markov analysis approaches for caching. Equation (10) still applies when the cache size covers k ≤ K levels, such that M = l1 + ··· + lk, and the K − k virtual levels are added outside of the cache. The result (10) can be evaluated via a recursive scheme with computational complexity O(N K 2(l1 + 1) ··· (lK+ 1)) [20]. Moreover, a mean-field approximation has been derived by Gast and Van Houdt [20] for simpler and faster evaluations.
6. FIFO and LRU Caching Analysis with Data of Different Sizes
The previous results apply to the cache support of CPU/GPU processing in a fixed, unit size data format, whereas web caches are storing files or data chunks of varying sizes. Therefore, we finally regard data objects Ok of different sizes sk. Then, the cache size M does not refer to the number of objects, but it is measured in bytes, and there is no 1:1 replacement of the data. Often, the caching strategy must perform several evictions until enough space for the new object becomes available. Small objects may be inserted without eviction into free cache space, or several evictions may be required to insert a large object.
To the best of the authors’ knowledge, hit ratio solutions for objects of varying sizes are rarely addressed in the literature and are thus open for future study. An extended Che approximation for LRU caches is proposed in Section 3.2 of [28] without further evaluation. We first summarize extended exact solutions for LRU and for the product form in Section 6.1 and Section 6.2. In Section 6.3, Section 6.4 and Section 6.5, we extend the FIFO approximation for varying data sizes with regard to unused cache space (UCS) as an additional source of deviations.
6.1. LRU Cache Hit Ratio Solution for Objects of Different Sizes
The IRM steady state probabilities pLRU (Ok1, …, OkM) of the LRU cache content and the LRU hit ratio have been derived by King [8] in the following format [12,25]:
The same result also characterizes cache-filling phases [21]. However, there is no scalable evaluation known for Equations (11) and (12), unlike the computation scheme for the FIFO product form of Section 2.2. Therefore, the solution can be applied only to small caches.
In the format (12), each term of the sum over m refers to hits contributed by the object On in LRU stack position m + 1. In addition, covers the hits for On in the top position. The solution with differentiation of LRU cache content per stack position is still valid for objects of different sizes, as far as they fit into the cache. This leads to a direct extension of Equation (12) for objects On of sizes sn (∀ j ≠ l: kj ≠ kl ; ∀ j: kj ≠ n) [21]:
6.2. No Common FIFO, RANDOM and CpR Solution for Objects of Different Sizes
In contrast to LRU, the common IRM product form solution of Equation (2) is restricted to a unit data size. Because we did not find an explicit statement on this limitation in the literature, we show that hit ratios of FIFO, RANDOM and CpR can differ already in a simple example for N = 3 objects A, B, C with sizes sA = 1; sB = 2; and sC = 3 and a cache size of M = 4. Then two objects fit together in the cache, except for B and C (sB + sC = 5 > M).
In this example, the IRM hit ratios of LRU, FIFO, RANDOM and CpR can be analysed by Markov chains, with states for the relevant cache content and state transitions according to the replacement principles of each strategy, as shown in Figure 6. There are six states with one (B or C) or two (A and B, A and C, B and A, C and A) objects as cache content in steady state. Other content states are ignored as transient states (A) or when they exceed the cache size (B and C, A and B and C). The top and bottom cache positions are not distinguished for random evictions, such that four states are sufficient for RANDOM.
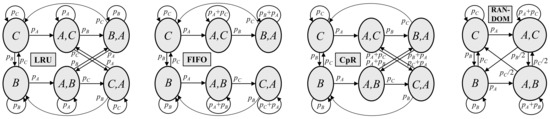
Figure 6.
Markov chains for steady state hit ratio analysis of the caching strategies.
The IRM hit ratio analysis first determines the steady state probabilities from equilibrium equations. State-specific hit ratios are given by the sum of the request probabilities of the objects in the cache. The total hit ratio is the sum of state-specific hit ratios weighted by their steady state probabilities. In the case of FIFO, we finally obtain = 1 − 2 pB pC/(pB + pC) − pA pB pC/(pA pB + pA pC + pB pC). In the case of LRU, the direct computation of the hit ratio via Equation (13) is simpler and equivalent.
The exact analysis shows differences in the hit ratios of the four caching strategies. In the example pA = 0.2, pB = 0.7 and pC = 0.1 we obtain the following:
The differences in the IRM hit ratio results are not large, but they indicate that several well-known results for unit object size do not hold for data of different sizes:
- (1)
- The FIFO, RANDOM and CpR hit ratios are different for variable data sizes. Their common product form solution (2) [6] is restricted to unit-size objects.
- (2)
- The proven “LRU is better than FIFO under IRM” result [40] is also restricted to unit data size and again violated in the previous example.
- (3)
- Moreover, a monotonous increase in the LRU, FIFO, RANDOM and CpR hit ratio curves (HRC) with the cache size M again holds only for unit data size.
Simulations of large caches with objects of different sizes still show results close to the unit size properties, with negligible differences between FIFO, RANDOM and CpR. However, LRU performance can largely deviate from FIFO, etc. for objects of different sizes. The LRU preference for popular objects leads to a higher hit ratio when those objects are small or to a lower hit ratio when they are large.
- Value and Byte Hit Ratio
Steady state Markov results are usually derived for the object hit ratio. We can include a caching value vk per object for the benefit of serving the object from the cache. vk may refer to measures for reduced link load and energy consumption on a transport network or to reduced delay, improved throughput and other QoS aspects from the user’s perspective. The value hit ratio (VHR) of a cache is defined as (∀ j ≠ l: kj ≠ kl)
where p (Ok1, …, OkM) again denotes the steady state probability of cache content for a considered strategy. This includes the byte hit ratio (BHR), i.e., the fraction of bytes delivered from the cache when the data size represents the caching value (vk = sk). In the example of Figure 6, we obtain
6.3. Extended Approximations for Objects of Different Sizes
We can straightforwardly extend the FIFO approximation (4) and (5) to data of different sizes sk:
In the fixed size case of Equations (4) and (5), the mean sojourn time of an object in a FIFO cache is determined by a step down of one position per cache miss in the FIFO queue when a new object enters on top. The extension of Equation (14) accounts for a shift down by the size sk when an object Ok enters the cache. The probability pEnter(k) that Ok is the next object to enter the cache is still assumed to be constant per request:
where represents the probability that Ok is outside of the cache. An iterative evaluation of in Equation (14) has similar properties of a monotonous convergence towards a unique solution, as in the unit size case of Equation (5).
The extended approximation of Equation (14) can be used for RANDOM and CpR as well. Their hit ratio slightly differs from FIFO for varying object sizes, where we encounter only minor differences between FIFO, RANDOM and CpR hit ratios, as in the example in Section 6.2, and it is even smaller for large caches.
Che’s and Fagin’s approximations for the LRU hit ratio are also extensible to objects of different sizes. Again, we have to modify only the iterative equations to determine in Equations (7) and (8) in order to account for object sizes sk, analogously to the FIFO case of Equation (14) with unchanged formulas for hChe and hFagin [21,28]:
6.4. Oversize Objects and Unused Cache Space (UCS)
When the cache is small, there may be oversize objects with sk > M, which cannot enter and therefore should be excluded from the set of relevant data objects in the computations of Equations (14)–(17). A fraction of unused cache space is another factor that is not regarded in those approximations. We estimate its mean value E[UCS] and then apply Equations (14)–(17) with a reduced cache size M* = M − E[UCS] = E[F], as the mean cache fill level E[F]. We transfer an UCS estimation scheme for LRU [21] to the FIFO approximation case. The concept of the estimation scheme is summarized in the next section.
6.5. Approximation Scheme for the Mean Unused Space in FIFO Caches
Let Fm denote the cache fill level before the m th request. The fill level stays unchanged for a cache hit: Fm+1 = Fm. In the case of a cache miss, Fm is increasing by the size of the requested object and decreasing by compensating evictions. We obtain
where denotes the size of the object of the m th request and are the sizes of eviction candidates. K is the number of required evictions until the requested object fits into the cache, where K = 0 if it fits into the currently empty space, i.e., if Fm + ≤ M. The size of objects that enter the cache has a discrete distribution s(j) for the number of bytes or kbytes, with a maximum size smax. We obtain s(j) = Σk pEnter(Ok) Prob(sk = j), where the probability pEnter(Ok) that an object Ok (re-)enters the cache is computed via Equation (15) on the basis of the FIFO approximation. We assign the same discrete distribution s(j) also as the size to the eviction candidates. Finally, the fill level Fm can be evaluated in the format of discrete distributions fm(j) = Prob(Fm = j), where M − smax ≤ Fm ≤ M.
The mean fill level E[F] is iteratively computed via Equation (18) until steady state is approached when the difference |E[Fm+1] − E[Fm]| < ε is becoming negligibly small:
E[F] = lim m → ∞E[Fm]; E[UCS] = M − E[F].
The entire computation scheme for the mean fill level E[F] versus unused cache space E[UCS] is described in detail in [21] for LRU caches. As the main difference in a transfer to FIFO, the probability pEnter(Ok) is obtained via Equation (15), with an impact also on the distribution of the object sizes s(j).
We compare FIFO approximations in the basic format (14) with the previously described scheme for UCS correction. Therefore, we consider an example with N = 50 objects with a uniform size distribution, i.e., s1 = 1, …, s50 = 50, and with independent and Zipf-distributed requests pk = αk−β for k = 1, …, 50, where α = 1/Σ k k−β [31]. Figure 7 shows the hit ratio curves (HRCs) for three examples:
- β = 0, i.e., for uniform requests among all data objects (p1 = … = p50 = 2%),
- β = 0.8 with a preference for small objects (p1 ≈ 15.3%, p2 ≈ 8.8%, …, p50 ≈ 0.67%), and
- β = 0.8 with a preference for large objects (p50 ≈ 15.3%, …, p1 ≈ 0.67%).
The mean object size per request is E(S) = 25.5 for uniform requests, and it is E(S) ≈ 14.1 or E(S) ≈ 36.9, respectively, when small or large objects are preferred. A preference for small objects yields the highest hit ratio, whereas uniform requests lead to the lowest hit ratio for cache sizes M ≥ 50. For M < 50, the caching efficiency is reduced because of oversize objects if sk = k > M, with the highest drawback in the third case. The three FIFO HRCs in Figure 7 are obtained via simulation, being accompanied by a curve for the basic FIFO approximation of Equation (14) as FIFO Approx.-1, marked with circles, and the approximation with UCS correction as FIFO Approx.-2, marked with triangles.
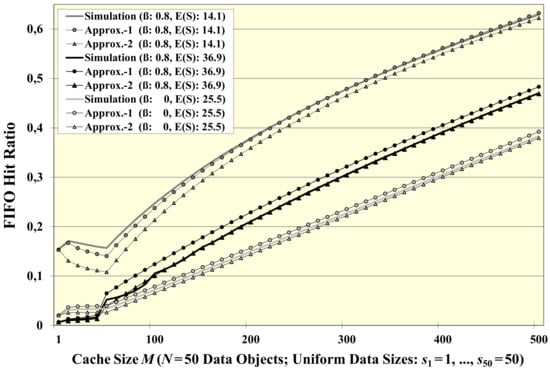
Figure 7.
FIFO approximation deviations for a case of uniform data-size distribution.
We conclude that the FIFO approximation can be subject to significant deviations when the cache size M is small in the starting part of the HRC and some popular data objects have a size close to M or larger. The UCS correction can only partly improve the basic FIFO approximation but indicates the extent of corresponding deviations.
We have evaluated the scenario of Figure 7 also for LRU with the basic extended Che approximation [28] and a variant with UCS compensation [21]. The results are very similar to the FIFO results in Figure 7. In the case of β = 0, the FIFO and LRU HRCs are identical, as are the HRCs for both approximation variants. In the third case with a preference for large objects, LRU and its approximations achieve a slightly higher hit ratio. Up to 6% higher LRU hit ratios are observed for the second case, with the same shape of relative deviations for the approximation variants for LRU as for FIFO.
Although LRU and FIFO caches are frequently applied, it has often been observed [2,17,18] that their web caching performance can be far below the optimum when compared with score- or utility-based methods [10,15]. The latter can use specific information about data items in their caching decisions. Then objects can be preferred in the cache with the highest ratio of popularity to size pk/sk as a score to maximize the IRM hit rate according to a knapsack solution.
7. Conclusions
For the exact hit ratio analysis of a cache of fixed size under independent (IRM) requests, the product form (1)–(2) provides the most general solution, which applies to FIFO, RANDOM and clock-based strategies, as well as to combinations of those methods. The product form solution can be computed by the scalable scheme of Equation (3) [30], but it needs an extended number representation, when there are many objects in the cache.
The solution extends to multilevel/multisegment caches [20] with the same set of methods (FIFO, RANDOM, CpR) being applied on each level. However, the hit ratio results differ for those methods if data in a cache is varying in size. The analytic solution 7 for LRU caches even extends to data of different sizes in the form of Equation (13). However, the LRU solutions are not scalable for large caches.
As an alternative, IRM hit ratio approximations have been proposed for LRU by Fagin [23] and Che et al. [24] as well as for FIFO by Dan and Towsley [25]. Those approaches were proven to be asymptotically exact for large caches with data of unit size [26,27,28,29]. Moreover, our quantitative analysis identifies the format of Equation (6) for request probabilities with maximum approximation error. The results of the quantitative evaluation lead to error bounds which are summarized as follows:
- The maximum absolute deviations |∆hChe| of Che’s approximation are decreasing with the cache size M from 8.25% for M = 1 down to less than 1% for M ≥ 10.
- The maximum absolute deviations |∆hFagin| of Fagin’s approximation are decreasing with the cache size M from 5.2% for M = 2 down to less than 1.3% for M ≥ 10.
- The maximum deviations of the FIFO approximation [25] are decreasing with the cache size M from 16.5% for M = 1 down to less than 3% for M ≥ 10.
Extensions of those approximations for data of different sizes are provided [21,28], which are still expected to yield asymptotic exact results for large caches. However, a fraction of unused cache space contributes to larger errors for small caches. Therefore, an exact analysis is recommended to avoid the largest approximation errors for small caches, as far as Markovian and other exact solutions are scalable.
The presented framework of analysis and approximation results provides a basic tool set for a performance evaluation of content delivery in current CDNs and cloud architectures, as well as in ICN, CCN and NDN concepts towards a future Internet. The limited scope of exact solutions and insufficient accuracy of approximations for varying data sizes are major challenges for future research.
Author Contributions
Formal analysis, G.H., K.N. and O.H.; software, F.H. and K.N.; methodology, G.H. and O.H.; writing—first draft, G.H.; writing—review and editing, all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable, the study does not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Podlipnik, S.; Böszörmenyi, L. A survey of web cache replacement strategies. ACM Comput. Surv. 2003, 35, 374–398. [Google Scholar] [CrossRef]
- Arlitt, M.; Williamson, C. Internet web servers: Workload characterization and performance implications. IEEE Trans. Netw. 1997, 5, 631–645. [Google Scholar] [CrossRef]
- Li, S.; Xu, J.; van der Schaar, M.; Li, W. Popularity-driven content caching. In Proceedings of the IEEE Infocom, San Francisco, CA, USA, 10–14 April 2016; pp. 1–9. [Google Scholar]
- Paschos, G.S.; Iosifidis, G.; Tao, M.; Towsley, D.; Caire, G. The role of caching in future communication systems and networks. IEEE JSAC 2018, 36, 1111–1125. [Google Scholar] [CrossRef]
- Corbato, F.J. A paging experiment with the Multics system. MIT Proj. MAC Rep. MAC-M-384 1968, 1–14. [Google Scholar]
- Gelenbe, E. A unified approach to the evaluation of a class of replacement algorithms. IEEE Trans. on Comp. 1973, 100, 611–618. [Google Scholar] [CrossRef]
- McCabe, J. On serial files with relocatable records. Oper. Res. 1965, 13, 609–618. [Google Scholar] [CrossRef]
- King, W.F., III. Analysis of demand paging algorithms. In Proceedings of the IFIP Congress, Ljubljana, Yugoslavia, 23–28 August 1971; pp. 485–490. [Google Scholar]
- Lee, D.; Choi, J.; Kim, J.H.; Noh, S.H.; Min, S.L.; Cho, Y.; Kim, C.S. LRFU: A spectrum of policies that subsumes the least recently used and least frequently used policies. IEEE Trans. Comput. 2001, 50, 1352–1361. [Google Scholar]
- Dehghan, M.; Massoulie, L.; Towsley, D.; Menasche, D.S.; Tay, Y.C. A Utility optimization approach to network cache design. IEEE/ACM Trans. Netw. 2019, 27, 1013–1027. [Google Scholar] [CrossRef]
- Hasslinger, G.; Ntougias, K.; Hasslinger, F.; Hohlfeld, O. Performance evaluation for new web caching strategies combining LRU with score-based selection. Comput. Netw. 2017, 125, 172–186. [Google Scholar] [CrossRef]
- Li, J.; Shakkottai, S.; Lui, J.C.S.; Subramanian, V. Accurate learning or fast mixing? Dynamic adaptability of caching algorithms. IEEE JSAC 2018, 36, 1314–1330. [Google Scholar] [CrossRef]
- Paschos, G.S.; Iosifidis, G.; Caire, G. Cache optimization models and algorithms. Found. Trends Commun. Inf. Theory 2020, 16, 156–345. [Google Scholar] [CrossRef]
- Eytan, O.; Harnik, D.; Ofer, E.; Friedman, R.; Kat, R. It’s time to revisit LRU vs. FIFO. In Proceedings of the 12th USENIX HotStorage Workshop, Berkeley, CA, USA, 13–14 July 2020; pp. 1–7. [Google Scholar]
- Hasslinger, G.; Ntougias, K.; Hasslinger, F.; Hohlfeld, O. Fast and efficient web caching methods regarding the properties per data. In Proceedings of the IEEE CAMAD, Limassol, Cyprus, 11–13 September 2019; pp. 1–7. [Google Scholar]
- Yang, J.; Yue, Y.; Rashmi, K.V. A large-scale analysis of key-value cache clusters at Twitter. ACM Trans. Storage 2021, 17, 1–35. [Google Scholar] [CrossRef]
- ElAarag, H. Web Proxy Cache Strategies: Simulation, Implementation and Performance Evaluation; Springer Publisher: Berlin/Heidelberg, Germany, 2013; pp. 1–103. [Google Scholar]
- Megiddo, N.; Modha, S. Outperforming LRU with an adaptive replacement cache algorithm. IEEE Comput. 2004, 37, 58–65. [Google Scholar] [CrossRef]
- Ntougias, K.; Papadias, C.B.; Papageorgiou, G.K.; Hasslinger, G.; Sorensen, T.B. Coordinated caching and QoS-aware resource allocation for spectrum sharing. Wirel. Pers. Comm. 2020, 112, 49–79. [Google Scholar] [CrossRef]
- Gast, N.; Van Houdt, B. Transient and steady-state regime of a family of list-based cache replacement algorithms. In Proceedings of the ACM Sigmetrics, Portland, OR, USA, 15–19 June 2015. [Google Scholar]
- Hasslinger, G.; Ntougias, K.; Hasslinger, F.; Hohlfeld, O. Analysis of the LRU cache startup phase and convergence time and error bounds on approximations by Fagin and Che. In Proceedings of the WiOpt Symposium, CCDWN workshop, Turin, Italy, 19 September 2022; pp. 1–8. [Google Scholar]
- Wong, K.Y.; Yeung, A.; Choi, K.C.; Lei, P.; Lam, C.T. Exact transient analysis on LRU cache startup for IoT. In Proceedings of the 9th International Conference on Information Technology: IoT and Smart City, New York, NY, USA, 22–25 December 2021; pp. 310–315. [Google Scholar]
- Fagin, R. Asymptotic miss ratios over independent references. J. Comp. Syst. Sci. 1977, 14, 222–250. [Google Scholar] [CrossRef]
- Che, H.; Tung, Y.; Wang, Z. Hierarchical web caching systems: Modeling, and experimental design. IEEE JSAC 2002, 20, 1305–1314. [Google Scholar]
- Dan, A.; Towsley, D. An approximate analysis of the LRU and FIFO buffer replacement schemes. In Proceedings of the ACM SIGMETRICS, Boulder, CO, USA, 22–25 May 1990; pp. 143–152. [Google Scholar]
- Berthet, C. Approximation of LRU caches miss rate: Application to power-law popularities. arXiv 2017, arXiv:1705.10738. [Google Scholar]
- Brenner, M. A Lyapunov analysis of LRU. Master Thesis, University of Illinois Urbana-Champaign, Champaign, IL, USA, 2020; pp. 1–42. [Google Scholar]
- Fricker, C.; Robert, P.; Roberts, J. A versatile, accurate approximation for LRU cache performance. In Proceedings of the ITC 24, Krakow, Poland, 4–7 September 2012; pp. 1–8. [Google Scholar]
- Poojary, P.; Moharir, S.; Jagannathan, K. A coupon collector based approximation for LRU cache hits for Zipf requests. In Proceedings of the 19th International Symposium on Modeling and Optimization in Mobile, Ad hoc, and Wireless Networks (WiOpt), Philadelphia, PA, USA, 18–21 October 2021; pp. 1–8. [Google Scholar]
- Fagin, R.; Price, T.G. Efficient calculation of expected miss ratios in the independent reference model. SIAM J. Comput. 1978, 7, 288–296. [Google Scholar] [CrossRef]
- Breslau, L.; Cao, P.; Fan, L.; Phillips, G.; Shenker, S. Web caching and Zipf-like distributions: Evidence and implications. In Proceedings of the IEEE Infocom, New York, NY, USA, 21–25 March 1999; pp. 126–134. [Google Scholar]
- Traverso, S.; Ahmed, M.; Garetto, M.; Giaccone, P.; Leonardi, E.; Niccolini, S. Unraveling the impact of temporal and geographical locality in caching systems. IEEE Trans. 2015, 17, 1839–1854. [Google Scholar]
- Hasslinger, G.; Kunbaz, M.; Hasslinger, F.; Bauschert, T. Web caching evaluation for Wikipedia request statistics. In Proceedings of the IEEE WiOpt Symposium, Paris, France, 15–19 May 2017; pp. 1–6. [Google Scholar]
- Rosensweig, E.J.; Menasche, D.S.; Kruose, J. On the steady-state of cache networks. In Proceedings of the IEEE Infocom, Turin, Italy, 14–19 April 2013; pp. 863–871. [Google Scholar]
- Marin, A.; Rossi, S.; Burato, D.; Sina, A.; Sottana, M. A product-form model for the performance evaluation of a bandwidth allocation strategy in WSN. ACM TOMACS 2018, 28, 1–23. [Google Scholar] [CrossRef]
- Tsukada, N.; Hirade, R.; Miyoshi, N. Fluid limit analysis of FIFO and RR caching for IRM. Perform. Eval. 2012, 69, 403–412. [Google Scholar] [CrossRef]
- Garetto, M.; Leonardi, E.; Martina, V. A unified approach to the performance analysis of caching systems. ACM Trans. Model. Perform. Eval. Comput. Syst. 2016, 1, 1–28. [Google Scholar] [CrossRef]
- Gast, N.; Van Houdt, B. TTL approximations of the cache replacement algorithms LRU(m) and h-LRU. In Performance Evaluation; Elsevier: Amsterdam, The Netherlands, 2017; pp. 33–57. [Google Scholar]
- Gomaa, H.; Messier, G.G.; Williamson, C.; Davies, R. Estimating instantaneous cache hit ratio using Markov chain analysis. IEEE/ACM Trans. Netw. 2013, 21, 1472–1483. [Google Scholar] [CrossRef]
- Van den Berg, J.; Gandolf, A. LRU is better than FIFO under the independent reference model. J. Appl. Probab. 1992, 29, 239–243. [Google Scholar] [CrossRef]
- Starobinsky, D.; Tse, D. Probabilistic methods for web caching. Perf. Eval. 2001, 46, 125–137. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).