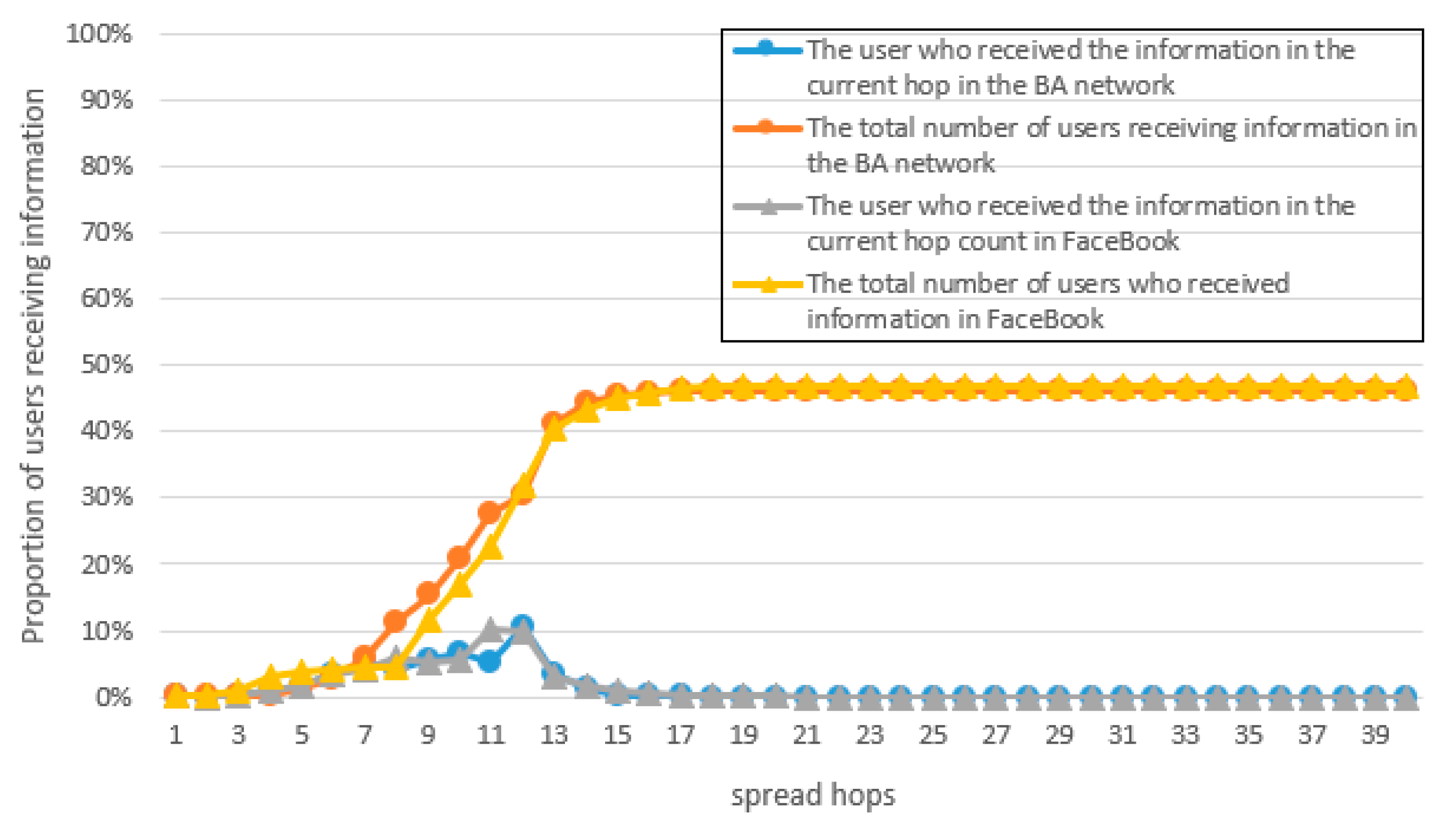
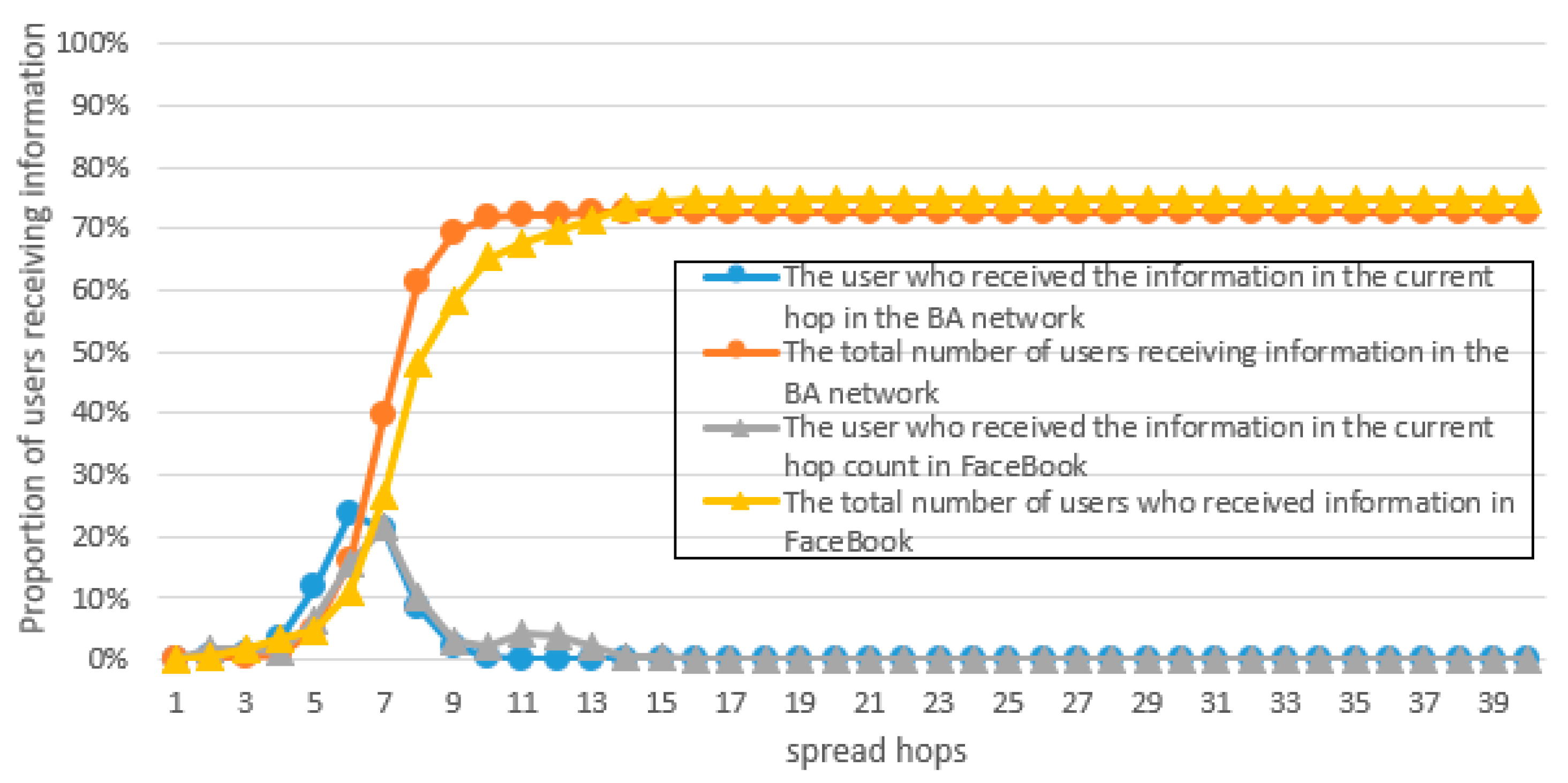
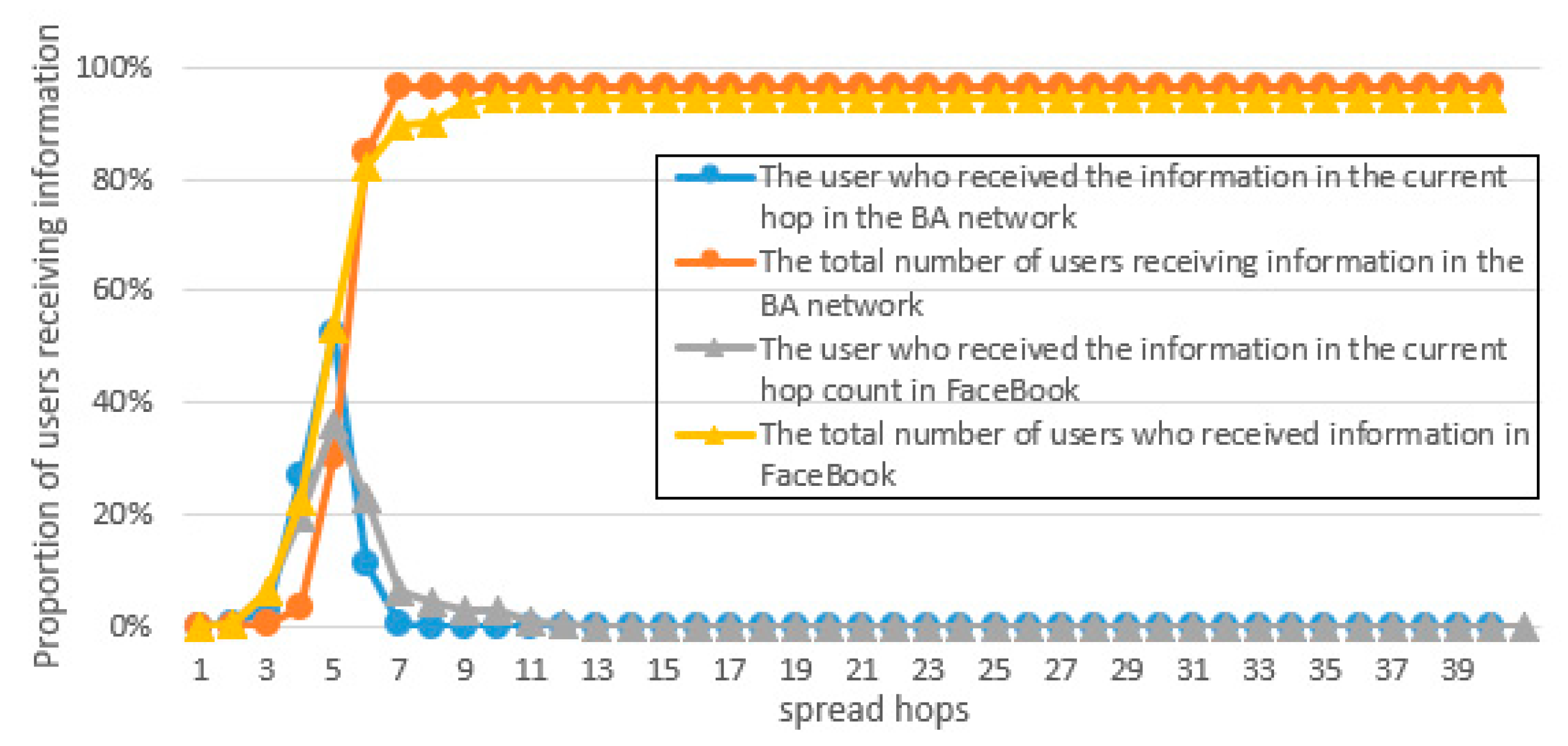
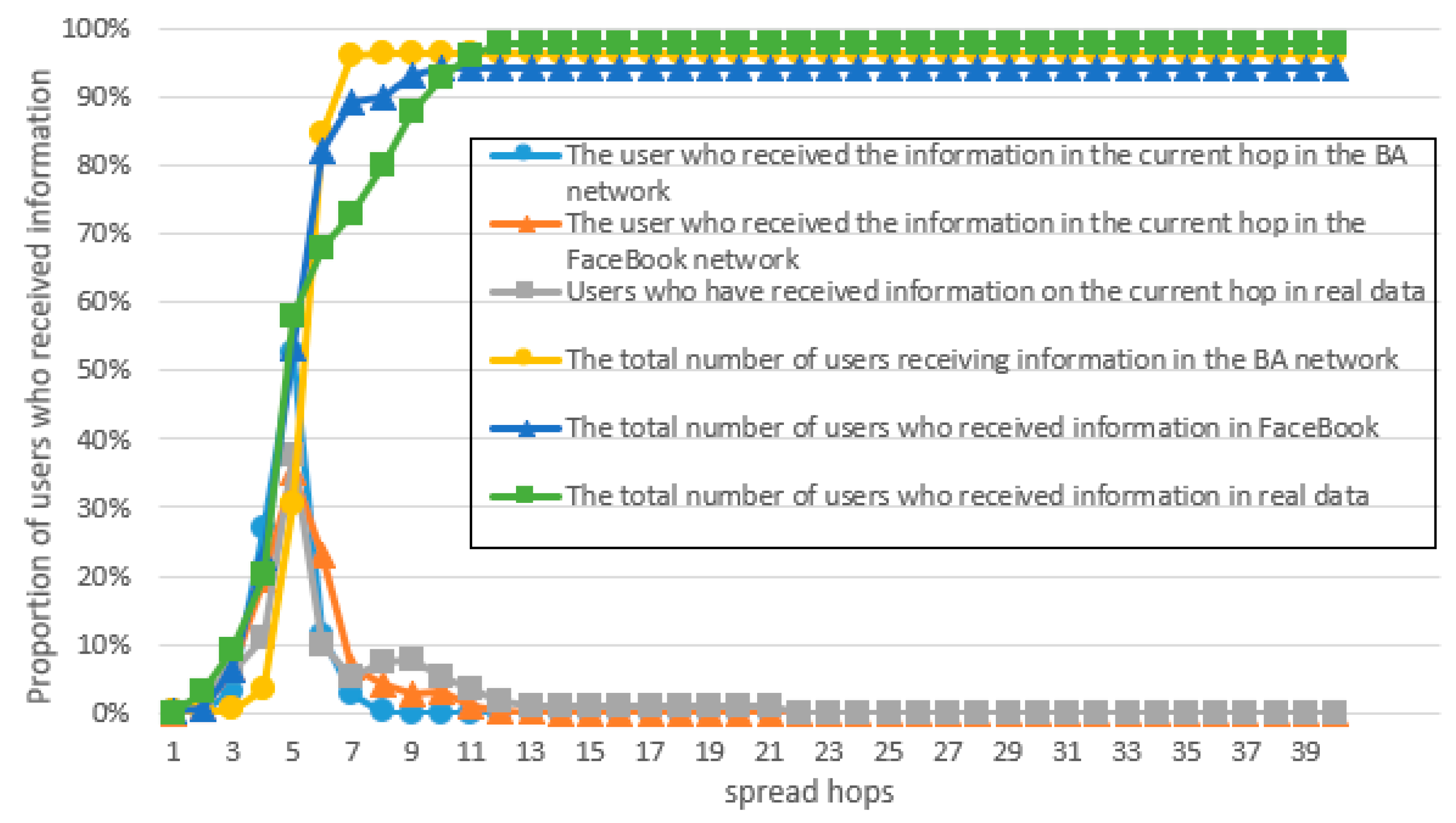
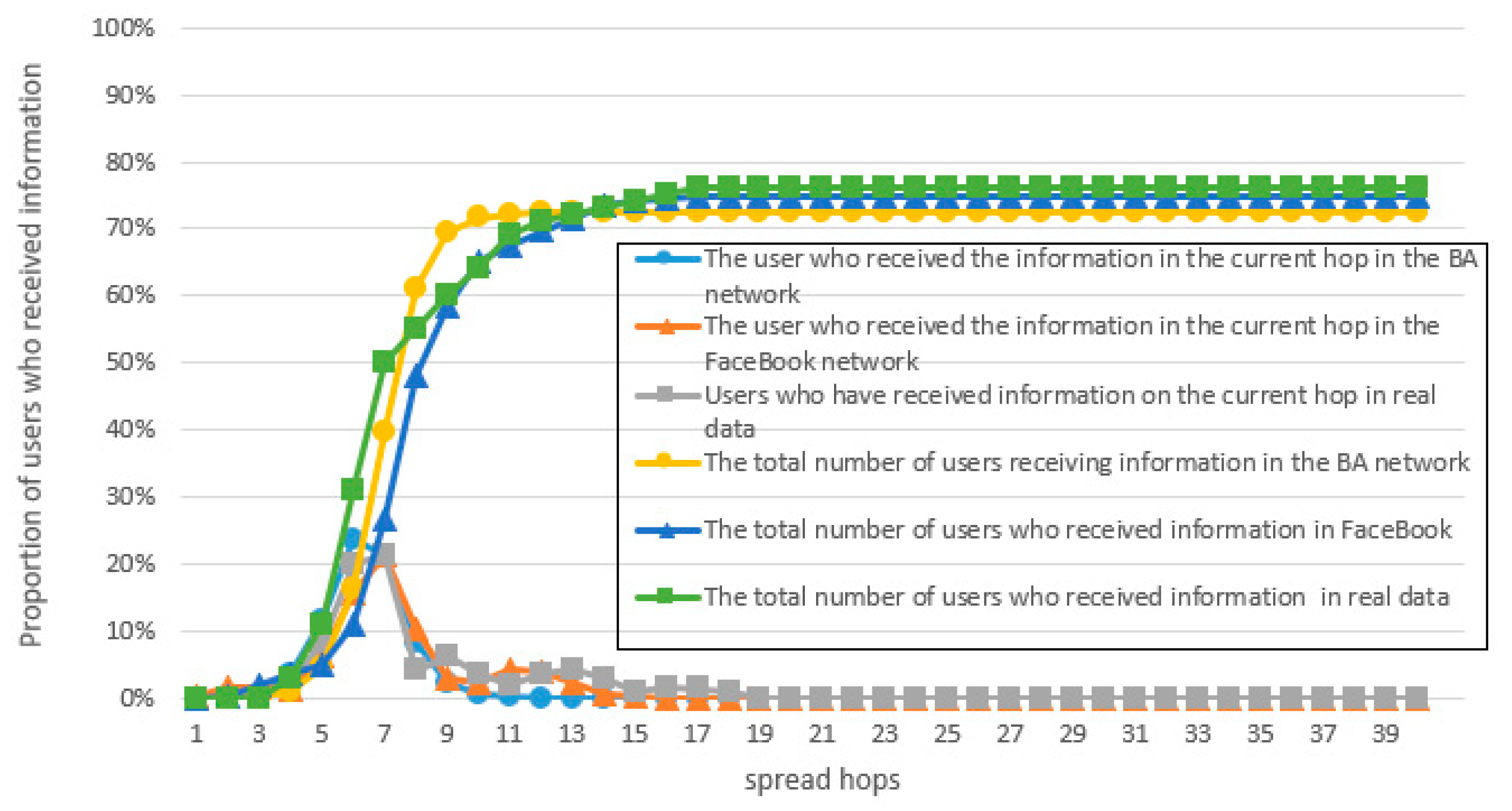
There are two major issues that need to be resolved in the construction of the model. The first is that after a user receives the privacy information, he/she needs to make a decision on whether to continue disseminating the information and on what probability to continue disseminating the information. The second is that after the user makes the decision to disseminate the privacy information, he/she needs to decide which neighboring user(s) to forward the privacy information. Based on the user’s microscopic point of view, the proposed model would establish the user’s sending probability and the user’s preference probability, which are jointly affected by the two parameters of intimacy and popularity, and determine the forwarding probability to solve the first problem. The second problem is then solved by constructing a sender–receiver game model where the sender and each receiver play a pairwise game to determine the probability of each receiver’s preference and the result of the Nash equilibrium threshold to determine whether the sender will send the privacy information. We assume that the dissemination of privacy information can be initiated by any node and that the privacy information has been obtained by the initiating node. We also assume that the privacy-concerning subject can be known by analyzing the content of the information. Privacy information dissemination in the proposed model can be schematically described as follows after a node obtains or receives a piece of privacy information.
(1) Check to see whether the information has already been received and processed. If yes, terminate the dissemination; if not, proceed to the next step.
(2) Calculate the probability of sending the information.
(3) Get the list of neighbor nodes, which are the potential receiving nodes.
(4) For each receiving node in the list, determine whether the information will be sent to the receiving node. If yes, the information is sent to the receiving node and the receiving node will become a sending node in the next round of dissemination; if not, terminate the dissemination.
(5) Repeat steps (1)–(4) until there is no more sending node, which would finish the dissemination of the privacy information.
3.1. Decision on Forwarding Privacy Information
Considering the importance of the micro-relationship between users on the spread of privacy information, our model incorporates two parameters: intimacy and popularity, to quantify the sender’s sending probability and the receiver’s preference probability and to be combined with a game theory model based on the receiver’s Nash equilibrium probability of the sending strategy of the sender.
3.1.1. Intimacy
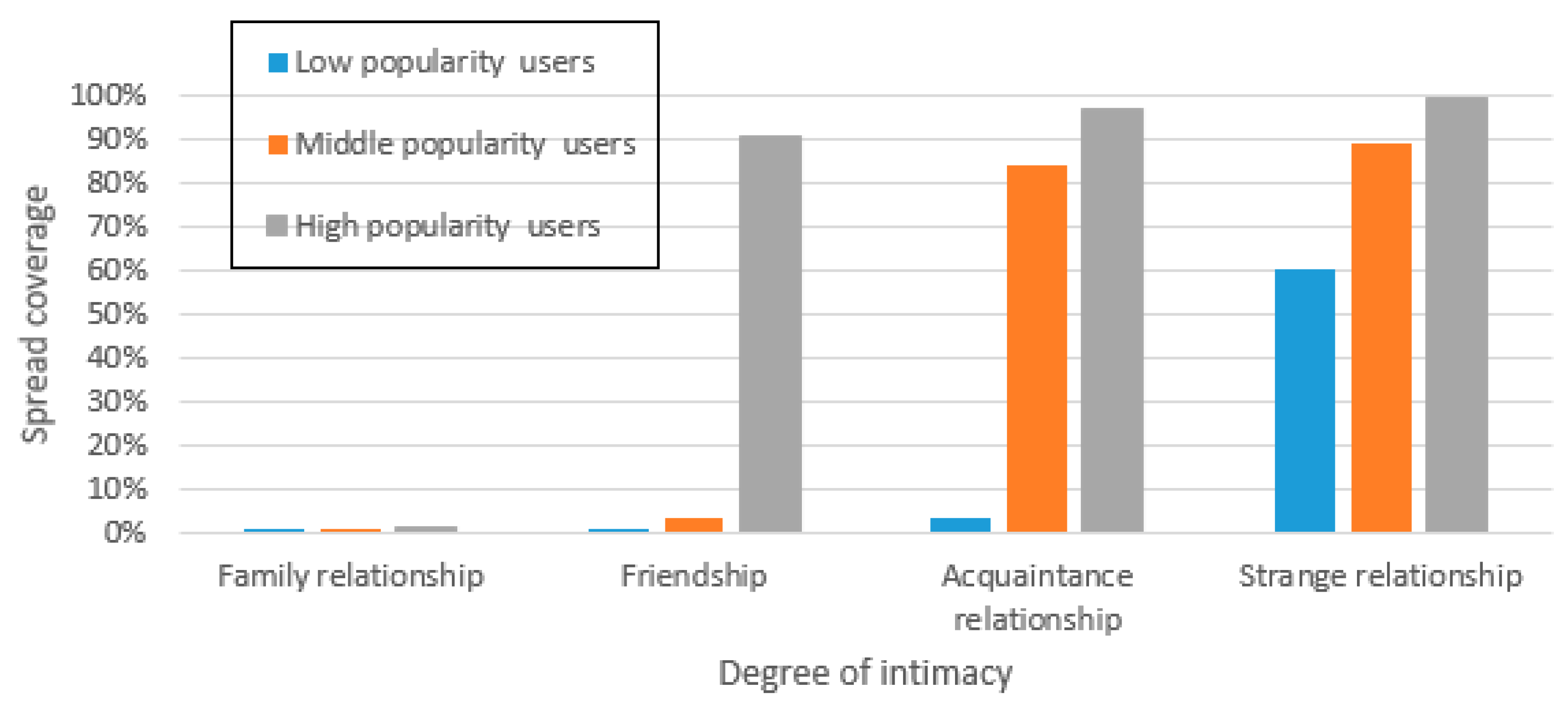
Intimacy is expressed as the degree of closeness between two users in an OSN. Studies have shown that intimacy plays a vital role in terms of with which users would share their privacy information. 95.24% of people will choose whether to communicate personal privacy information based on perceived intimacy. The most intuitive example is that users with a high degree of intimacy, such as parents and children, would tend to protect the privacy of each other, i.e., to stop the spreading of privacy information. On the other hand, users with a low degree of intimacy, such as ordinary colleagues or even strangers, would not care much about the protection of each other’s privacy and would, thus, have the tendency of spreading each other’s privacy information. These examples indicate that intimacy has a great influence on whether a user will be interested and participate in the dissemination of privacy information.
Intimacy is defined as the emotional experience when an individual gets along well with others according to “The Dictionary of Psychology”. It includes, but is not limited to, the affection between parents, brothers, and sisters, the love between men and women, the friendship between friends, and other different emotions. To facilitate our study, we classify intimacy into four levels in increasing order as shown in
Table 1.
3.1.2. Popularity
In OSNs, compared to the real social world, it is easier for someone to get the privacy of public figures and to participate in spreading it to others. The privacy exposure of public figures accounts for approximately 70% of the total privacy exposure on the Internet. On the contrary, the privacy information of ordinary people with a tiny number of fans will not receive widespread attention and people tend not to spread such privacy information. Therefore, dissemination of privacy information through examining popularity cannot be simply neglected.
The degree of a node in the network is the number of connections or edges between the nodes. In an OSN, the greater the degree of a user node, the more neighbor nodes the user has, and the higher the probability that the node is known in the network, the higher the popularity. The popularity of a node can be measured using Equation (1) in which degree(i) represents the degree of the current node, i.e., the number of fans in the network, and max degree is the largest degree of any node in the network.
The popularity distribution of nodes in the network can be obtained through calculation. Through repeated experiments, we can get the areas of the distribution of popularity with three different intervals. Based on the intervals, the popularity of the privacy subjects can be classified into the following three kinds:
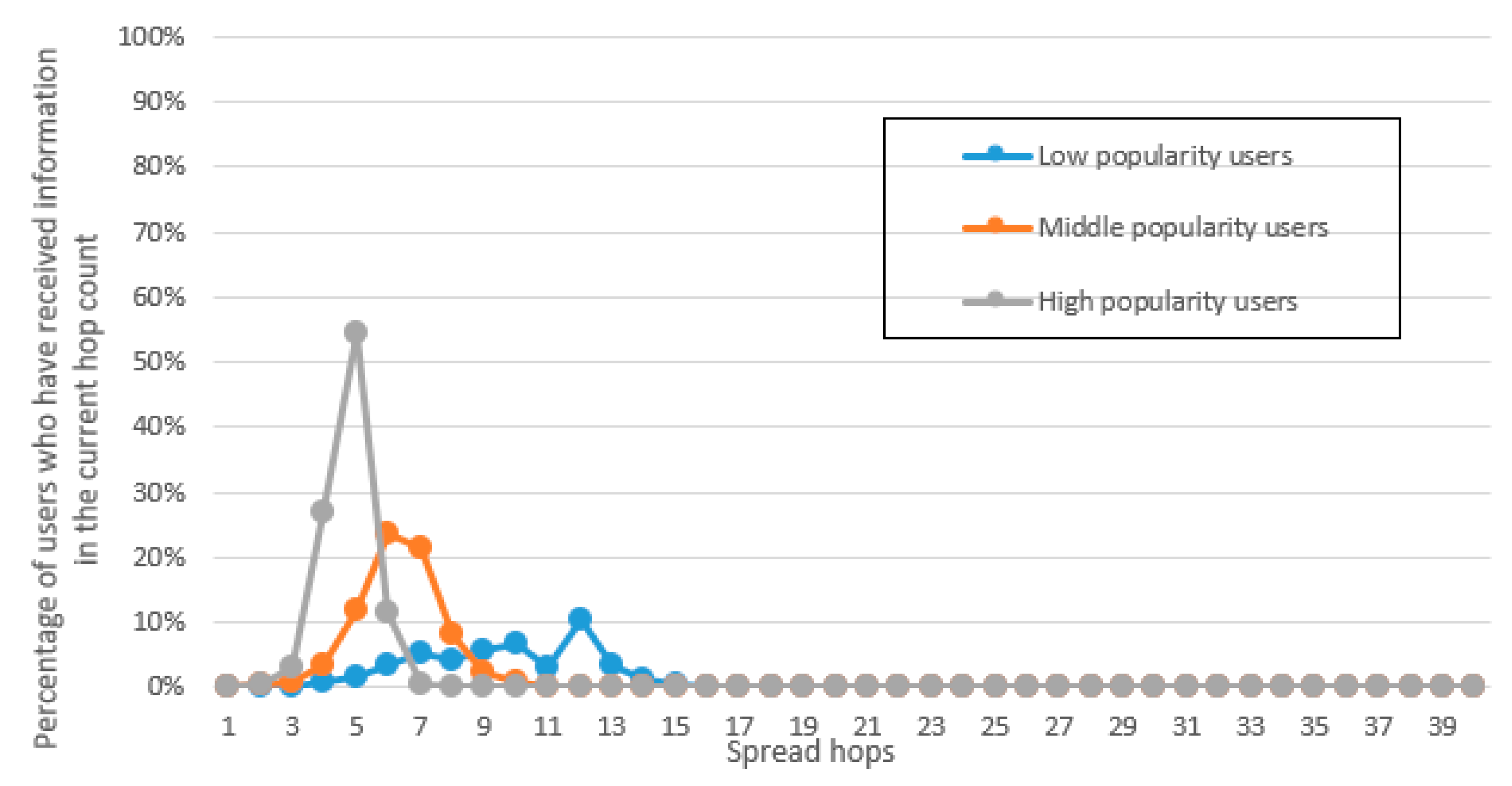
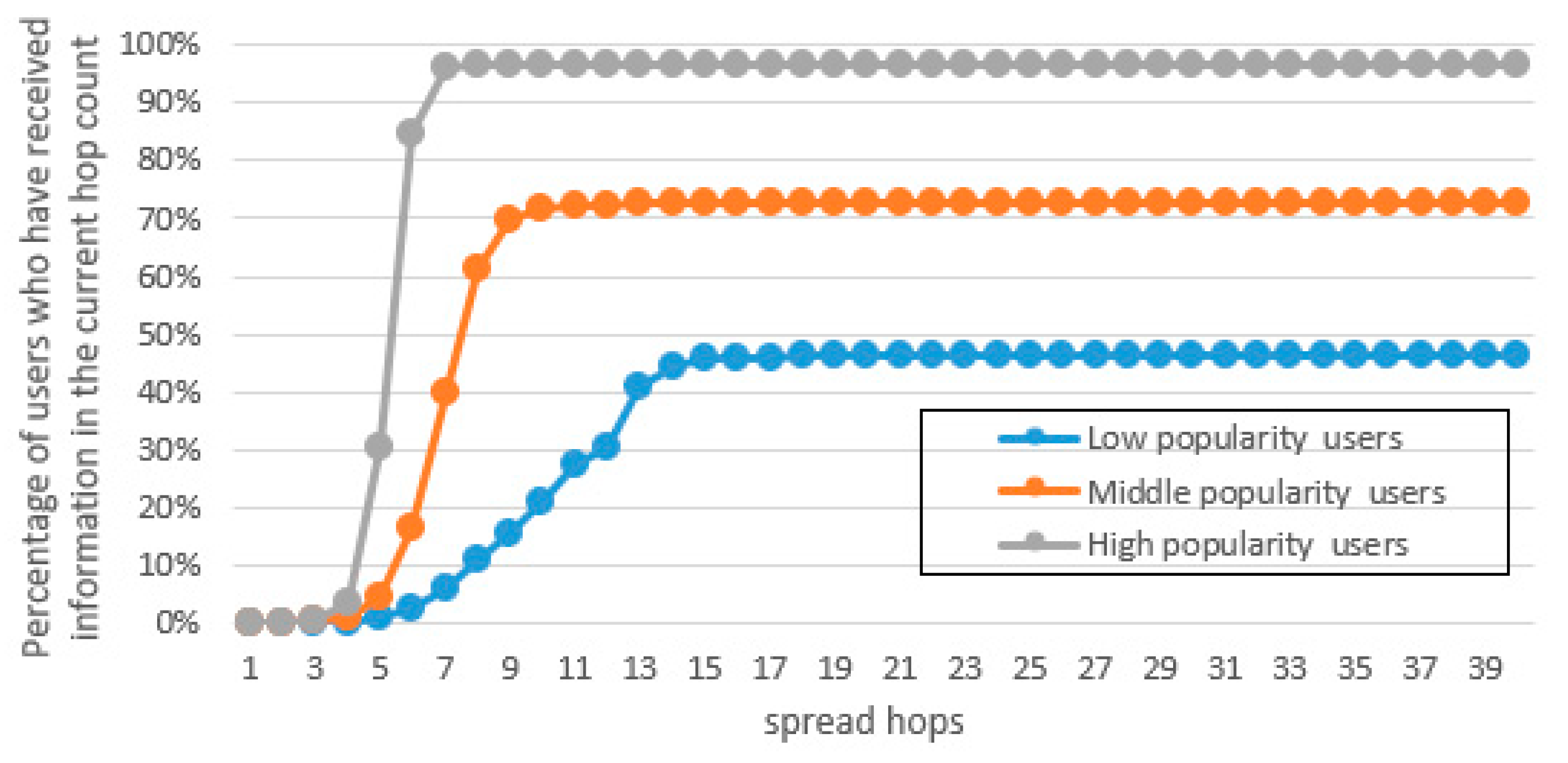
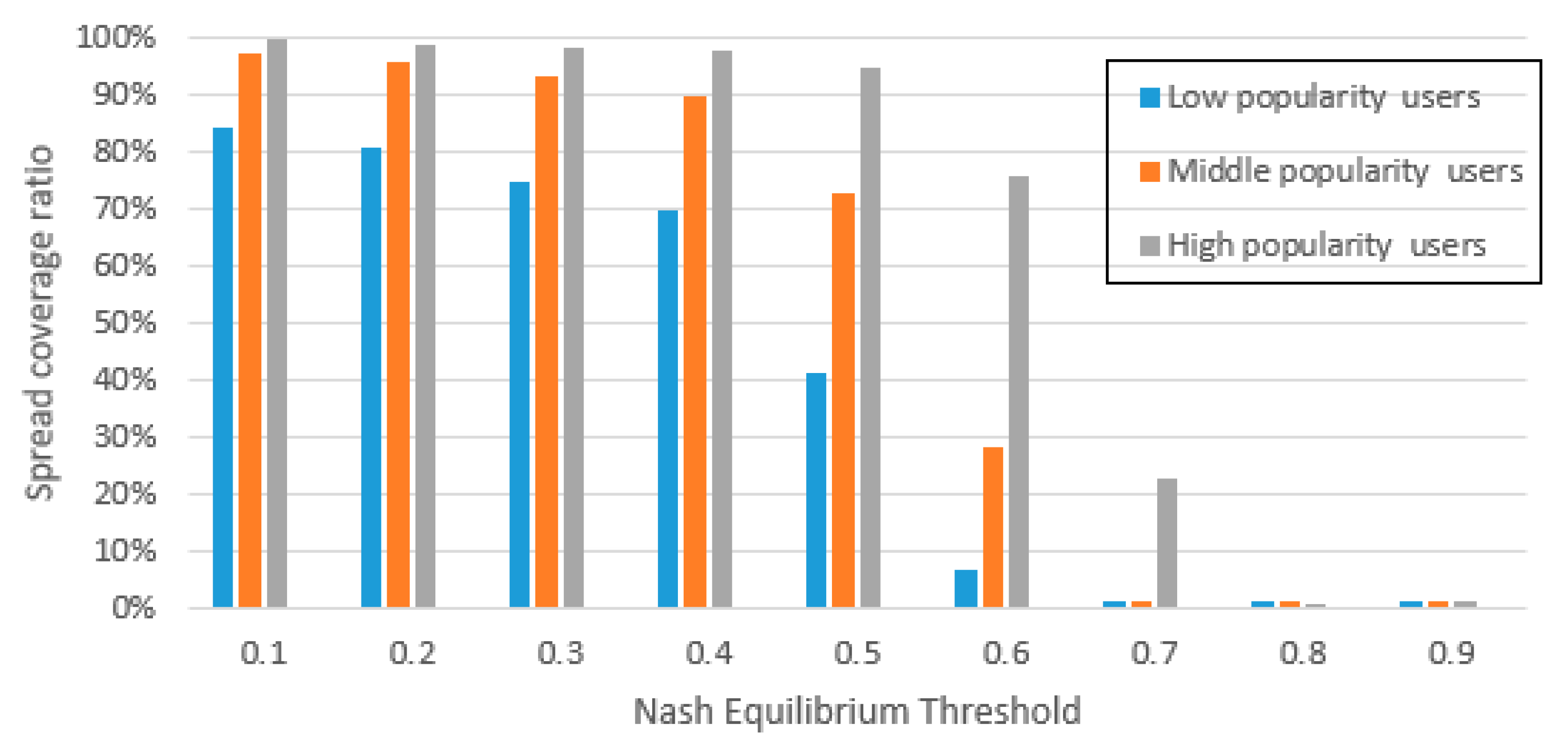
(1) High popularity users: This type of users each has a large number of fans. They are generally highly known and followed by a lot of people on the social network, such as celebrities and high-level politicians.
(2) Middle popularity users: This type of users each is usually well-known in a certain field or topic range of the social networks with a reasonable number of fans and followers in a specific field, such as food bloggers and game anchors.
(3) Low popularity users. This type of users are normally ordinary people with low levels of activity and only a few fans. Because of their low popularity, generally speaking, they do not attract much attention from other users.
3.1.3. Probability of Sending
The behavior of the sender is usually influenced by the degree of intimacy with the privacy subject and the popularity of the privacy subject. Then, sender 𝑣𝑖 can estimate its probability of forwarding the privacy information to other users based on the intimacy with the privacy subject and the popularity of the privacy subject, which is expressed in Formula (2), where
represents the intimacy between the sending node and the privacy subject,
represents the popularity of the privacy subject, and
will be used to determine the user’s forwarding behavior of the private information. The receiver also measures its interest in the privacy message based on the intimacy with the privacy subject and the popularity of the privacy subject, which is expressed in Equation (3), where
represents the intimacy between the receiving node and the privacy subject and
is used to determine how much the receiver would like the privacy information.
3.2. Decision on the Recipients of Privacy Information
The decision by sending a node to select a neighbor node is modeled using a game. At the micro level of the network structure, the game process is based on the interests of the nodes participating in the game. The whole process describes the strategy choices that the sending node sends to the receiver when the sending node has the privacy message. As shown in
Table 2, at the micro level of the network structure, for a sending node and a receiving node, the policies for both parties are “send privacy information” and “do not send privacy information”, respectively, and “like current privacy information” and “dislike current privacy information”, respectively, which depicts the possibility that the node would send the private messages. In the following, we use the game theory to analyze the strategy choices of both the sender and the receiver in the game.
First, we need to define the corresponding benefit when different strategies are adopted by the two sides of the game:
: This is the benefit to the sender when the receiver adopts strategy “like privacy information” and the sender adopts strategy “send privacy information”. The benefit can be viewed in the way that the sender gains more attention from the receiver by sending the privacy information, potentially making the relationship between the two parties closer.
: This is the benefit to the receiver when the receiver adopts strategy “like privacy information” and the sender adopts strategy “send privacy information”. The benefit can be viewed in the way that the receiver gets information to satisfy curiosity and pleasure.
: This is the loss to the sender when the receiver adopts strategy “do not like privacy information” and the sender adopts strategy “send privacy information”. The loss can be viewed in the way that the disclosure of some other’s privacy information by the sender causes some discomfort, which could result in bad feelings that may lead to the loss of attention or the consequence of some harm to the sender.
: This is the loss to the receiver when the receiver adopts strategy “do not like privacy information” and the sender adopts strategy “send privacy information”. The loss can be viewed in the way that the receiver may generate some sense of dissatisfaction and disgust when receiving a message that he/she does not like.
: This is the loss to the sender when the receiver adopts strategy “like privacy information” and the sender adopts strategy “do not send privacy information”. The loss can be viewed in the way that the sender loses an opportunity to gain more attention from the receiver.
: This is the loss to the receiver when the receiver adopts “like privacy information” and the sender adopts strategy “do not send privacy information”. The loss can be viewed in the way that the receiver misses receiving a message that he/she likes.
: This is the benefit to the sender when the receiver adopts strategy “do not like privacy information” and the sender adopts strategy “do not send privacy information”. The benefit can be viewed in the way that not sending a message that the receiver does not like can continue maintaining the receiver’s attention to the sender.
: This is the benefit to the receiver when the receiver adopts strategy “do not like privacy information” and the sender adopts strategy “do not send privacy information. The benefit can be viewed in the way that the receiver does not receive the message that he/she does not like.
Now, we need to analyze the game matrix in
Table 2. From the perspective of the receiver, when the sender chooses the strategy “send privacy information “, adopting the strategy “like privacy information” by the receiver can bring greater benefits, i.e.,
. When the sender chooses strategy “do not send privacy information”, adopting strategy “do not like privacy information” by the receiver can bring greater benefits, i.e.,
>
. From the perspective of the sender, when the receiver chooses strategy “like privacy information”, adopting strategy “send privacy information” by the sender can bring greater benefits, i.e.,
. When the receiver chooses strategy “do not like privacy information”, adopting strategy “send privacy information” brings less benefits than adopting strategy “do not send privacy information” by the sender, i.e.,
<
. From the above analysis, we can see that there is no pure strategy Nash equilibrium in the game matrix, so we need to calculate its mixed strategy Nash equilibrium.
and is set as the income matrix of the sender and the receiver, respectively. Assuming that the probability that the sender chooses strategy “send privacy information” is x, then the probability that the sender chooses strategy “do not send privacy information” is 1 − x and the mixed strategy probability of the sender is = (x,1 − x). Similarly, assuming that the probability that the receiver chooses strategy “like privacy information” is y, then the probability that the receiver chooses strategy “do not like privacy information” is 1 − y and the mixed strategy probability of the receiver is = (y,1 − y). The sender’s revenue function can be calculated by Equation (4):
By forcing Equation (5) to be equal to 0, we can obtain the value of y, which can be expressed using Equation (6):
Similarly, the receiver’s income can be calculated using Equation (7):
Taking the derivative of y, we can get Equation (8):
Forcing Equation (8) to be equal to 0, we can obtain the value of x, which can be expressed using Equation (9):
The resulting mixed strategy Nash equilibrium is then shown in Equations (10) and (11):
By deriving the above mixed strategy Nash equilibrium, the probability that the sender chooses strategy “sending privacy information” and the probability that the receiver chooses strategy “like privacy information” can be obtained. We can also see that the Nash equilibrium point of the receiver’s preference probability is as shown in Equation (12). If the probability that the receiver likes privacy information is lower than the threshold, the sender should not send the information to get more benefit, i.e., the sender should not send the privacy information to the receiver. On the other hand, if the probability that the receiver likes privacy information is higher than the threshold, the sender will send the information to get more benefit, i.e., the sender will send the privacy information to the receiver.