Dealing with Deadlocks in Industrial Multi Agent Systems

Abstract

Automated Manufacturing Systems (AMS) consisting of many cooperating devices incorporated into multiple cooperating production lines, sharing common resources, represent industrial Multi-Agent Systems (MAS). Deadlocks may occur during operation of such MAS. It is necessary to deal with deadlocks (more precisely said, to prevent them) to ensure the correct behavior of AMS. For this purpose, among other methods, methods based on Petri nets (PN) are used too. Because AMS are very often described by PN models, two PN-based methods will be presented here, namely based on (i) PN place invariants (P-invariants); and (ii) PN siphons and traps. Intended final results of usage these methods is finding a supervisor allowing a deadlock-free activity of the global MAS. While the former method yields results in analytical terms, latter one need computation of siphons and traps.

1. Introduction

Recent decades represent a huge evolution of Automated Manufacturing Systems (AMS), previously named Flexible Manufacturing Systems (FMS). We can even talk about the new industrial revolution. According to [1], this evolution is realized mainly by the development in four axes, namely products, technology, business strategies, and production paradigms. The edited book [2] offers a wide perspective on modern design and operation of production networks. The evolution of the manufacturing system in the future is presented in [3].

The operation of AMS often has a similar character to Discrete-Event Systems (DES), where the next state depends only on both the current state and the occurrence of discrete events. Petri nets (PN) [4,5] are frequently used for modeling and control of DES. The family of AMS is a typical representative of DES where many devices cooperate together—robots, machine tools, transport belts, automatically guided vehicles (AGV), etc. They are frequently called to be resources. They are shared by multiple production lines, robotized working cells, etc. These devices and their aggregates, in the form of lines and cells, can also be considered industrial agents and the whole AMS as a multi-agent system. The adequate resource allocation is very important in AMS in order to avoid deadlocks. A deadlock in general is a state in which two or more processes are each waiting for the other one to execute, but neither can go on. Hence, deadlock is undesirable and bad phenomenon. Due to deadlocks, either the entire plant or some of its parts remain stagnate. Thus, the primal intention of the production cannot be achieved. For a design of deadlock-free AMS discrete mathematics is necessary. PN-based discrete mathematical models of AMS yield a suitable background for this.

There exists a large number of publications interested in this topic. From the older ones, the following works should be mentioned in particular [6,7,8,9,10], as well as the UML (Unified Modeling Language)-based work [11] applied in software engineering. While in [6,9] foundations of the P-invariant-based method were laid, in [7,8] the method based on siphons and traps was elaborated. A generalized view on deadlocks in multi-agent systems is presented in [10]. Among the more recent works should be mentioned [12,13,14,15], as well as the author’s survey article [16]. While in [12] a comprehensive survey of Petri net siphons were presented, in [13,15] unreliable resources are investigated and the robust control for AMS containing such resources is designed. In [14], deadlocks in mobile agent systems are detected and resolved.

In relation to the elimination of deadlocks, in [16,17,18,19,20,21] three categories of strategies are distinguished: (i) deadlock detection and recovery—which is used in cases where deadlocks are infrequent and their consequences are not too serious; (ii) deadlock prevention—it imposes restrictions on the interactions among resources and their users to prevent resource requests that may lead to deadlocks; and (iii) deadlock avoidance—it grants a resource to a user only if the resulting state is not a deadlock.

Consequently, it is impossible to address to such a broad issue in one paper. In this paper, only two methods of deadlock prevention in AMS by means of PN-based models are introduced and compared. Both methods add monitors (additional places) into the original PN model of AMS in order to remove deadlocks. One method enumerates monitors and their interconnections with the original PN model using P-invariants and the other using siphons and traps.

1.1. Formal Methods in AMS

Formal methods for modeling, simulation, supervisory control, performance evaluation and fault diagnosis of AMS are very important part of global understanding of AMS. They yield an efficient help and knowledge at constructing and real implementation of AMS. A suitable review of such methods is presented in the e-book [22]. As to modeling AMS there are presented also models based on place/transition Petri nets (P/T PN), timed Petri nets (TPN), and hybrid Petri nets (HPN).

The supervisory control of AMS determined for the deadlock prevention and avoidance are presented by means of: (i) finite state automata (FSA); (ii) the Petri net view on AMS which are perceived as resource allocation systems (RAS); (iii) HPN-based inventory control systems; (iv) stochastic flow models (SFM); (v) the infinitesimal perturbation analysis (IPA); and (vi) the max-plus algebra.

The performance evaluation is watched by colored TPN, by continuous PN (CPN), by the timed process algebra, and by the Petri net-based complex system scheduling.

The fault diagnosis of AMS is analyzed by means of FSA, by the fault diagnosis of PN and by the control reconfiguration of discrete-event manufacturing systems modeled by non-deterministic input/output (I/O) automata.

Along with the development of information technologies, such as cloud computing, mobile Internet, information acquisition technology, and big data technology, traditional engineering knowledge and formal methods for knowledge-based software engineering undergo fundamental changes. Hence, networks also play an increasingly important role.

Within this context, it is necessary to develop new methodologies as well as technical tools for network-based approaches. The term “network” may have different meanings in different contexts. To resolve bottleneck problems in AMS, deadlock prevention and avoidance by means of Petri nets is crucial.

Although introduced topics cover a large set of formal methods in AMS it cannot be said that this set is complete. New methods are under development.

1.2. Agents Cooperation, Negotiation and Reentering in AMS

Important strategies in MAS (multi-agent systems) are cooperation and negotiation. A structural and Petri net-based approach to modeling of these strategies was elaborated in author’s older work [23] and in the chapter [24] where also the perspectives of learning in this area were analyzed.

In [25], a connection of the structural model of reenterable AMS on a computer-based supervisory controller for monitoring the status of jobs and regulating the part routing as well as the machine job selection by means of siphons of Petri nets as to resolving deadlocks was explored. Namely, there are many approaches to modeling and analysis of manufacturing systems. In addition to those ones mentioned above in the previous Subsection (i.e., automata, Petri nets, perturbation methods) there exist methods based on digraphs, alphabet-based approaches, control theoretic techniques, expert systems design, etc.

The so-called complex networks are an interdisciplinary area. Numerous natural and artificial systems are composed of a large number of individuals that interact with each other in various ways, and then perform surprising useful functions. Examples of such networks include, e.g., neural networks, social networks, and many others, but also MAS in general, including industrial MAS where AMS and RAS belong, and doubtlessly also PN that successfully model and analyze them.

1.3. The Paper Organization

In the following Section 2, preliminaries concerning theory of PN and the PN-based modeling of AMS will be concisely introduced. Then, Section 3 will be devoted to the presentation and illustration of the method of deadlock prevention, based on P-invariants. In Section 4, the method of deadlock prevention, based on PN siphons and traps, will be presented and illustrated. Section 5 will discuss and illustrate three PN models of AMS being more complicated from the computation point of view, namely problematic because of very long-lasting even impossible computations. In Section 6, the comparison of both methods will be introduced. Then, Section 7 contains a concise conclusions of this paper.

2. Preliminaries

Firstly, it is necessary to introduce several basic definitions. First, one is the author own definition extracted from knowledge published in [7,16], next three are the standard elementary definitions of P-invariants, siphons, and traps from the classical literature about Petri nets [4,5]. Last two definitions are taken over from [7].

Definition 1. 

A Petri net is a bipartite directed graph (BDG). It may be formally described by the quadruplet $N=(P,T,F,W)$. Here, P and T are finite nonempty sets, namely P is a set of places ($\left|P\right|=n$), representing the first kind of BDG nodes, and T is a set of transitions ($\left|T\right|=m$), representing the second kind of BDG nodes. It is valid that $P\cup T\ne \varnothing$ and $P\cap T=\varnothing$. The set $F=(P\times T)\cup (T\times P)$ is the flow relation of the net N. It is expressed by directed arcs from places to transitions and vice versa. The mapping $W:(P\times T)\cup (T\times P)\to \mathbb{N}$ assigns weights to directed arcs. The weight of an arc f: $W\left(f\right)>0$ if $f\in F$ and $W\left(f\right)=0$ otherwise. Here $\mathbb{N}=\{0,1,2,...\}$, i.e., it contains natural numbers plus zero. The Petri net $N=(P,T,F,W)$ is named ordinary and denoted as $N=(P,T,F)$ if $\forall f\in F, W\left(f\right)=1$. N is called generalized if $\exists f\in F, W\left(f\right)>1$. Petri net is called a state machine if, and only if, (iff) $\forall t\in T, |{}^{•}t|=|t^{•}|=1$, i.e., when each transition has only one input place and only one output place.

A mapping from P to $\mathbb{N}$ is a marking M of N. The marking $M\left(p\right)$ means the number of tokens located in the place p. Thus, we may say that the place p is marked by a marking M iff $M\left(p\right)>0$. In case of a subset $S\subseteq P$ we say that it is marked by M iff at least one place in S is marked by M. The sum of tokens located in all places of S is $M\left(S\right)={\sum }_{p\in S}M\left(p\right)$. S is empty at M iff $M\left(S\right)=0$. The pair $(N,M_0)$ is called the marked net or a net system. Here, $M_0$ is an initial marking of N.

PN marking is evolved as follows

$${\mathbf{M}}_{k+1}={\mathbf{M}}_k+\mathbf{N}.{\overrightarrow{\sigma }}_k, k\in \mathbb{N},$$

(1)

with ${\mathbf{M}}_0=(M_0\left(p_1\right),M_0\left(p_1\right),\dots ,M_0{\left(p_n\right)}^T$ being the $(n\times 1)$ initial marking. Here, $\mathbf{N}$ is the $(n\times m)$-dimensional incidence matrix based on the set F and ${\overrightarrow{\sigma }}_k$ is a $(m\times 1)$-dimensional firing vector (the binary vector, where its entry with the value 1 denotes the corresponding transition $t\in T$ able to be fired). $M\left(p\right)$ denotes (as it was already mentioned above) the number of tokens in place p. $(n\times 1)$ marking vectors $\mathbf{M}$ are sometimes named also as state vectors. $\mathbf{N}={\mathbf{N}}^{+}-{\mathbf{N}}^{-}$, where ${\mathbf{N}}^{+}=\mathbf{Post}$ and ${\mathbf{N}}^{-}=\mathbf{Pre}$ are, respectively, the output flow matrix and the input flow matrix. In other words, the matrix representing the output of transitions to places and the matrix representing the input of places to transitions.

For economy of space, in general, markings and vectors can be described by the formal sum notation. Thus, ${\sum }_{p\in P}M\left(p\right)p$ denotes the vector $\mathbf{M}$. For example, in a net with $P=\{p_1,\cdots ,p_5\}$ a marking where in $p_2$ are 3 tokens and in $p_3$ are 2 tokens may be written as $3p_2+2p_3$ instead of the vector notation ${(0, 3, 2, 0, 0)}^T$.

Definition 2. 

A vector $\mathbf{I}$ is a place invariant P (shortly, P-invariant) of PN iff $\mathbf{I}\ne \mathbf{0}$ and ${\mathbf{I}}^T.\mathbf{N}={\mathbf{0}}^T$. Here, $\mathbf{N}$ is the incidence matrix of N.

Definition 3. 

Any set $S\subseteq P, S\ne Ø$ with ${}^{•}S\subseteq S^{•}$ is said to be a siphon. Verbally said, if every transition having an output place in S has an input place in S. If a siphon does not contain another siphon, being its proper subset, it is said to be a minimal siphon. A proper subset is any subset of the set except itself. A minimal siphon S is called a strict minimal siphon (SMS) if ${}^{•}S⊊S^{•}$. In other words, if there is no siphon contained in it as a proper subset. A SMS does not contain a trap (the trap is defined below by Definition 4). When at the initial marking ${\mathbf{M}}_{\mathbf{0}}$$M_0\left(S\right)={\sum }_{p\in S}{M}_0\left(p\right)=0$, S is called an empty siphon.

Definition 4. 

Any set $Q\subseteq P, Q\ne Ø$ with $Q{}^{•}\subseteq {}^{•}Q$ is called a trap. In other words, if every transition having an input place in Q has an output place in Q.

Definition 5. 

A siphon S is said to be controlled in a net $(N,M_0)$ iff $\forall M\in R(N,M_0),M\left(S\right)>0$. Here, $R(N,M_0)$ expresses the reachability of markings from the initial marking. Consequently, any siphon containing a marked trap is controlled, since the marked trap can newer be emptied. Thus, in ordinary PN a controlled siphon does not cause any deadlock.

Definition 6. 

A siphon S in an ordinary PN $(N,M_0)$ is [7] invariant controlled by P-invariant $\mathbf{I}$ under the initial marking ${\mathbf{M}}_{\mathbf{0}}$ iff ${\mathbf{I}}^T.{\mathbf{M}}_{\mathbf{0}}>0$ and $\forall p\in P\backslash S,I\left(p\right)\le 0$, or equivalently, ${\mathbf{I}}^T.{\mathbf{M}}_{\mathbf{0}}>0$ and ${\left|\right|\mathbf{I}\left|\right|}^{+}\subseteq S$. Here, ${\left|\right|\mathbf{I}\left|\right|}^{+}=p\in P|I\left(p\right)>0$ is the positive support of $\mathbf{I}$.

Here, it is necessary to notify and emphasize that both methods examined in this paper require a rather wide mathematical background that cannot be either simplified nor abbreviated. Otherwise, the integrity of the interpretation of the methods would be violated. The mathematics used in examples should contribute to an accurate understanding of the application of both methods to particular cases of AMS.

2.1. Petri Nets and Resource Allocation Systems

Resource allocation systems (RAS) are a special class of concurrent systems, especially AMS. There, the attention is focused above all on resources. The set of Petri net-based models of RAS represent, in general, a subset of complete set of PN. Finite set of resources is shared in a competitive way by a finite set of processes. Such a competition induces (or may induce) existence of deadlocks. PN-based models of RAS are useful at synthesizing policies of deadlock prevention and/or deadlock avoiding. They make possible to design beforehand deadlock-free AMS, what is very useful especially preliminary to the creation of the final design of the structure of real AMS determined for application in production.

There are several standard paradigms of RAS [26,27,28,29]. Specific nomenclatures have been established for them—see, e.g., a survey made in [16], where also their mutual relations and their relations to PN as a whole, are displayed. Most frequently used paradigms of them are the following two: (i) S³PR (Systems of Simple Sequential Processes with Resources) suitable for AMS with flexible routing and the acquisition of the single-unit of the resource and (ii) S⁴PR (System of Sequential Systems with Shared Process Resources) which enables the modeling AMS with flexible routing and the acquisition of more units of the resource. The relation S³PR ≺ S⁴PR in this case expresses that systems S⁴PR model more complicated AMS than systems S³PR are able to model. In future, there may be S*PR (S³PR ≺ S⁴PR ≺ S*PR) paradigms suitable to model of yet more complicated AMS, where yet more copies of resources will be allowed. However, the asterix needs not always be just a greater integer than it was in previous two paradigms.

Some of the amount of paradigms, especially S³PR and S⁴PR, can be modeled and simulated in Matlab by means of the tool [30].

2.2. Methods for the Deadlock Prevention and Avoiding

As already mentioned, two main streams of methods are represented by methods based on: (i) reachability trees and P-invariants of PN and (ii) PN siphons and traps.

In the former case, it is necessary to mention the most principal contributions [6,8,9,31,32,33] important for the evolution of the P-invariants-based methods. The origin of this method consists in the effort to deal with the problem of the forbidden state in DES. Namely, it was shown in the literature that if a set $\mathcal{L}$ of legal PN markings is expressed by a set of s linear inequality constraints (so called General Mutual Exclusion Constraints (GMEC)) and if $\mathcal{L}$ is controllable, then the PN-based solution exists and it is maximally permissive. The controllability of $\mathcal{L}$ means that from any marking $M\in \mathcal{L}$ no forbidden marking is reachable by firing a sequence containing only uncontrollable transitions. In the opposite case, a general forbidden marking constraint may be enforced by PN-based controller only if the Petri net model of the system is safe. Hence, PN P-invariants are used in order to compute the feedback controller that enforces GMEC. They perform transformations on the system’s specifications to obtain constraints in the desired form. The controller is a set of control Petri net places. When the controller is added to the PN model of the plant, control places ensure a live and maximally permissive behavior of the closed loop system with respect to the forbidden states or markings. The controller design has a linear complexity in the number of system states. However, there are cases where such PN controller does not exist. Especially, when the set of legal markings $\mathcal{L}$ is not convex, there does not exist any PN place that can forbid the reachability of bad markings when allowing all legal ones. The concept of PN P-invariants was extended also to PN with uncontrollable and unobservable transitions. However, in this case maximally permissiveness cannot be guaranteed.

In the latter case, there are lots more such basal publications—[6,7,10,28,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57]. Siphons are tied to dead transitions whose existence leads to the loss of liveness of PN-based models of AMS. Siphon control is an effective way to prevent the occurrence of deadlocks. In a general case, particularly for models of AMS based on generalized PN, a siphon-based deadlock prevention policy cannot find an optimal (i.e., maximally permissive) supervisor. However, for PN models of AMS based on ordinary PN it is possible. Siphons in the PN model of a plant are divided into elementary and dependent ones. A monitor is added to the plant model for each elementary siphon, in such a way that the siphon will be invariant-controlled. The method guarantees that no further emptiable control-induced siphon is generated due to the addition of the monitors. When all elementary siphons are controlled, the controllability of a dependent siphon is ensured by properly setting the control depth variables of its related elementary siphons.

The explanation of the term invariant-controlled siphon, as well as the term control depth variable, will be explained and illustrated below in the Section 4.2. However, this is applicable only for S³PR paradigm of RAS. In case of S⁴PR paradigm (modeled by generalized PN), which uses multiple resource requirements and information about the weight of arcs, the concept of extended elementary siphons have to be used. Namely, due to the complicated utilization of resources, it is insufficient to represent the relationship between elementary and dependent siphons in generalized PN in such way as it is in case of ordinary PN. Extended elementary siphons are find by an iterative process—see, e.g., [58].

A methodology for modeling and analyzing fault-tolerant manufacturing systems that not only optimizes normal productive processes, but also performs detection and treatment of faults is presented in [59]. The coordination of cooperative multirobot system by means of PN is elucidated in [60].

The methodological framework yielded by the S⁴PR paradigm of RAS has raised considerable interest [61] on the grounds of a well-balanced compromise between modeling flexibility and the provision of sound and effective correction techniques.

In [62], a very general class of Petri nets are defined. This class has been called Petri nets of resource allocation (PNRA) to model as many kinds of RAS as possible. It not only focuses on the resources shared by processes, but also pays attention to the interaction/collaboration among processes.

At the solving of deadlock problems in AMS modeled with PN in [63], the attention is focused on adding a set of recovery transitions.

Here, in this paper, devoted to deadlock prevention and avoiding, it is not a sufficient space to analyze all introduced literature sources in details item by item. Namely, this area has many isolated particulars which are analyzed in detail in the above literature [6,7,8,9,10,28,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57].

Methods based on P-invariants are divided into many subclasses interested in deterministic and/or unreliable resources, methods suitable for ordinary and/or generalized PN, methods using linear and/or non-linear restrictions, methods applying optimization based on the linear programming (usually mixed integer linear programming (MILP)), etc.

Methods based on siphons and traps have still lots more such subclasses. The very good literature review of methods concerning the deadlock prevention is made in [26]. Likewise, in [53] a crucial literature review concerning the deadlock control is presented. A variety of deadlock-control policies is mentioned there. The optimization based on MILP is one of them. Such optimization can eliminate the need to compute completely all elementary siphons, which shorten the computational time for finding indispensably needed siphons.

In the following two sections, principles of both methods of the prevention of deadlocks will be introduced and mathematically described. Illustrative examples explaining the application of both methods in details will be introduced there as well.

3. P-Invariant-Based Method of Prevention Deadlocks

P-invariants are vectors $\mathbf{I}$ with the important property. The multiplication of such vectors with any marking (state) vector $\mathbf{M}$ reachable from a given initial marking ${\mathbf{M}}_0$ yields the same result. It is the relation of the state conservation, as follows

$${\mathbf{I}}^T.\mathbf{M}={\mathbf{I}}^T.{\mathbf{M}}_0$$

(2)

Taking into account the consecutive states obtained by firing of only one transition, we have for each transition t

$${\mathbf{I}}^T.{\overrightarrow{col}}_t\left(\mathbf{N}\right)=0,$$

(3)

where, ${\overrightarrow{col}}_t\left(\mathbf{N}\right)$ is the column of the incidence matrix $\mathbf{N}$ corresponding to the transition t. These vectors are solutions of the following equation

$${\mathbf{I}}^T.\mathbf{N}={\mathbf{0}}^T$$

(4)

what corresponds with the original Definition 2 of P-invariants introduced in the Section 2.

Consider the inequality representing linear combinations restricting behavior of marking $\mathbf{M}$

$$\mathbf{L}.\mathbf{M}\le \mathbf{b}$$

(5)

Here, $\mathbf{L}$ is a matrix of integers, $\mathbf{b}$ is an integer vector. An efficient help at creating $\mathbf{L}$ yields the reachability tree (RT) of the net N. After removing inequality by adding slack variables, we have

$$\mathbf{L}.\mathbf{M}+\mathbf{s}=\mathbf{b},$$

(6)

where entries of the $(n_s\times 1)$ vector $\mathbf{s}$ represents slack variables.

Just the Equation (4) represents the base of the method for the supervisor synthesis. Namely, when we force there $\left[\mathbf{L}\right|{\mathbf{I}}_s]$ instead of ${\mathbf{I}}^T$, we obtain (7) and some additional PN places (slacks) can be added to N. Thus, the extended (augmented) PN $N_1=N\circ N_s$ (where the symbol ∘ expresses a composition) will arise. $N_s$ is the PN which will (after finding its interconnections with N) ultimately create the supervisor. Then, slacks will create the places of the supervisor, frequently called monitors. In $N_1$ we have the following structure of (4) in the form

$$\left[\mathbf{L}\right|{\mathbf{I}}_s].\left[\begin{array}{c}\mathbf{N}\hfill \\ {\mathbf{N}}_s\hfill \end{array}\right]=\mathbf{0},$$

(7)

where ${\mathbf{I}}_s$ is $(n_s\times n_s)$-dimensional identity matrix; $n_s$ is the number of slacks; $\mathbf{L}$ is a $(n_s\times n)$-dimensional matrix which in a suitable form expresses the conditions imposed on marking (state) vectors of the original PN N, and ${\mathbf{N}}_s$ is the $(n_s\times m)$-dimensional matrix. After finding ${\mathbf{N}}_s$ from (7) by computing, we have the structure of the PN-based model of the supervisor—i.e., interconnecting arcs between N and $N_s$. Consequently, in general,

$$\begin{array}{ccc}\hfill \mathbf{L}.\mathbf{N}+{\mathbf{N}}_s& =& \mathbf{0}\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill {\mathbf{N}}_s& =& -\mathbf{L}.\mathbf{N}\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill {\mathbf{N}}_s& =& {\mathbf{N}}_s^{+}-{\mathbf{N}}_s^{-},\hfill \end{array}$$

(10)

where ${\mathbf{N}}_s^{+}$ is ${\mathbf{Post}}_s$ and ${\mathbf{N}}_s^{-}$ is ${\mathbf{Pre}}_s$ of ${\mathbf{N}}_s$.

The marking ${\mathbf{M}}_a$ of the supervised system $N_1$ consists of the state vector $\mathbf{M}$ of the N augmented with the state vector ${\mathbf{M}}_s$ of the supervisor $N_s$. Analogically, the incidence matrix ${\mathbf{N}}_a$ of the net $N_1$ consists of the incidence matrix $\mathbf{N}$ of N augmented with the incidence matrix ${\mathbf{N}}_s$ of the net $N_s$. The marking and the incidence matrix of the net $N_1$ are as follows

$${\mathbf{M}}_a=\left(\begin{array}{c}\mathbf{M}\hfill \\ {\mathbf{M}}_s\hfill \end{array}\right)$$

(11)

$${\mathbf{N}}_a^{-}=\left(\begin{array}{c}{\mathbf{N}}^{-}\hfill \\ {\mathbf{N}}_s^{-}\hfill \end{array}\right)$$

(12)

$${\mathbf{N}}_a^{+}=\left(\begin{array}{c}{\mathbf{N}}^{+}\\ {\mathbf{N}}_s^{+}\end{array}\right),$$

(13)

Here, ${\mathbf{N}}_a$, $\mathbf{N}$ and ${\mathbf{N}}_s$ are expressed by sub-matrices ${\mathbf{N}}_a^{+}$ and ${\mathbf{N}}_a^{-}$, ${\mathbf{N}}^{+}$ and ${\mathbf{N}}^{-}$, and ${\mathbf{N}}_s^{+}$ and ${\mathbf{N}}_s^{-}$.

Because of the prescribed conditions we have

$$[\mathbf{L} | {\mathbf{I}}_s].\left[\begin{array}{c}{\mathbf{M}}_0\hfill \\ {}^s{\mathbf{M}}_0\hfill \end{array}\right]=\mathbf{b},$$

(14)

where $\mathbf{b}$ is the $(n_s\times 1)$)-dimensional vector (see (5) and (6)). Its integer entries represent the limits for number of tokens in (5). Sometimes $\mathbf{b}=\mathbf{1}$ where $\mathbf{1}$ is the vector with all its entries equal to 1. Because

$$\mathbf{L}.{\mathbf{M}}_0+{}^s{\mathbf{M}}_0=\mathbf{b}$$

(15)

the initial state vector of the supervisor can be simply computed as follows

$${}^s{\mathbf{M}}_0=\mathbf{b}-\mathbf{L}.{\mathbf{M}}_0$$

(16)

Example 1

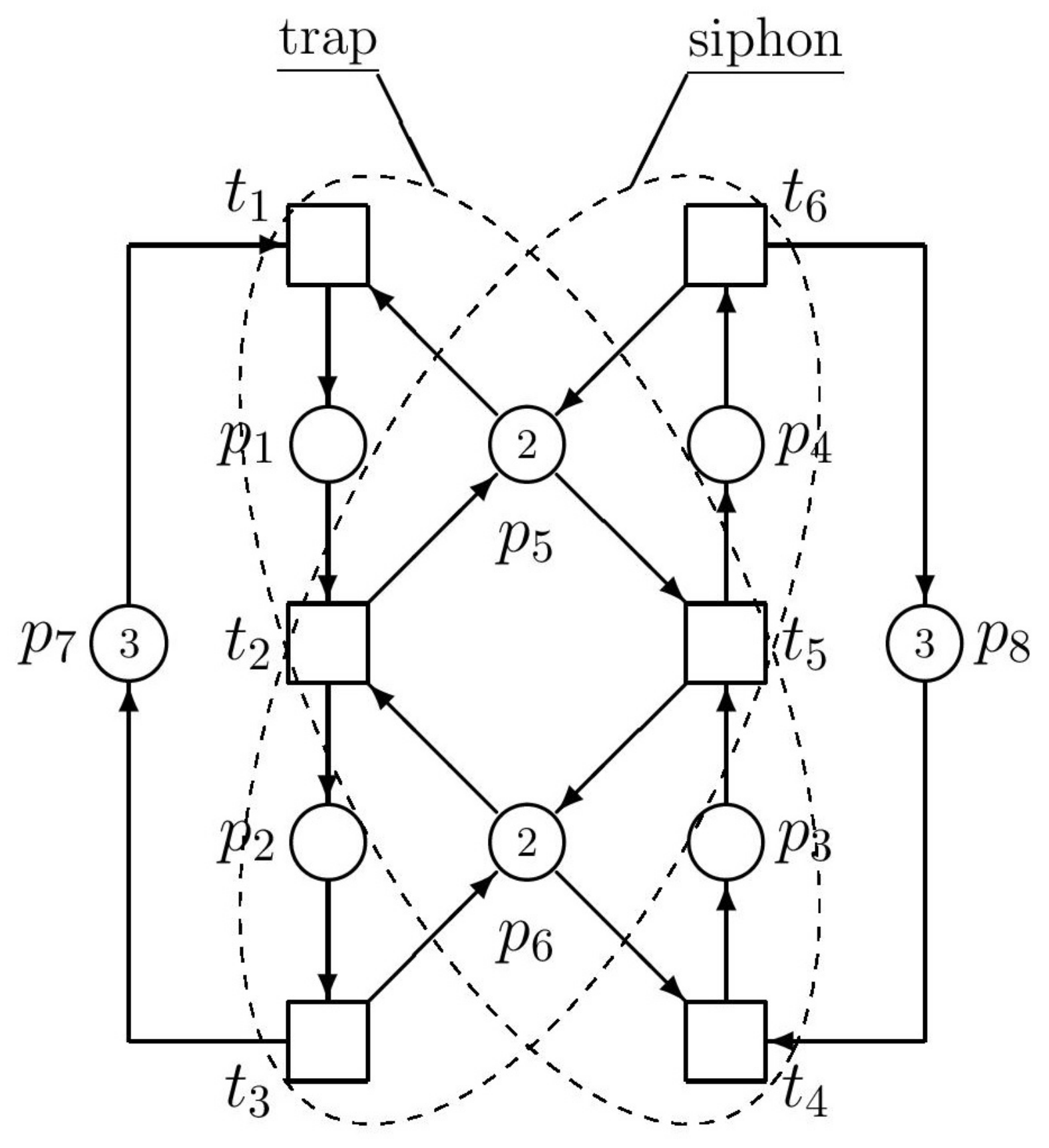
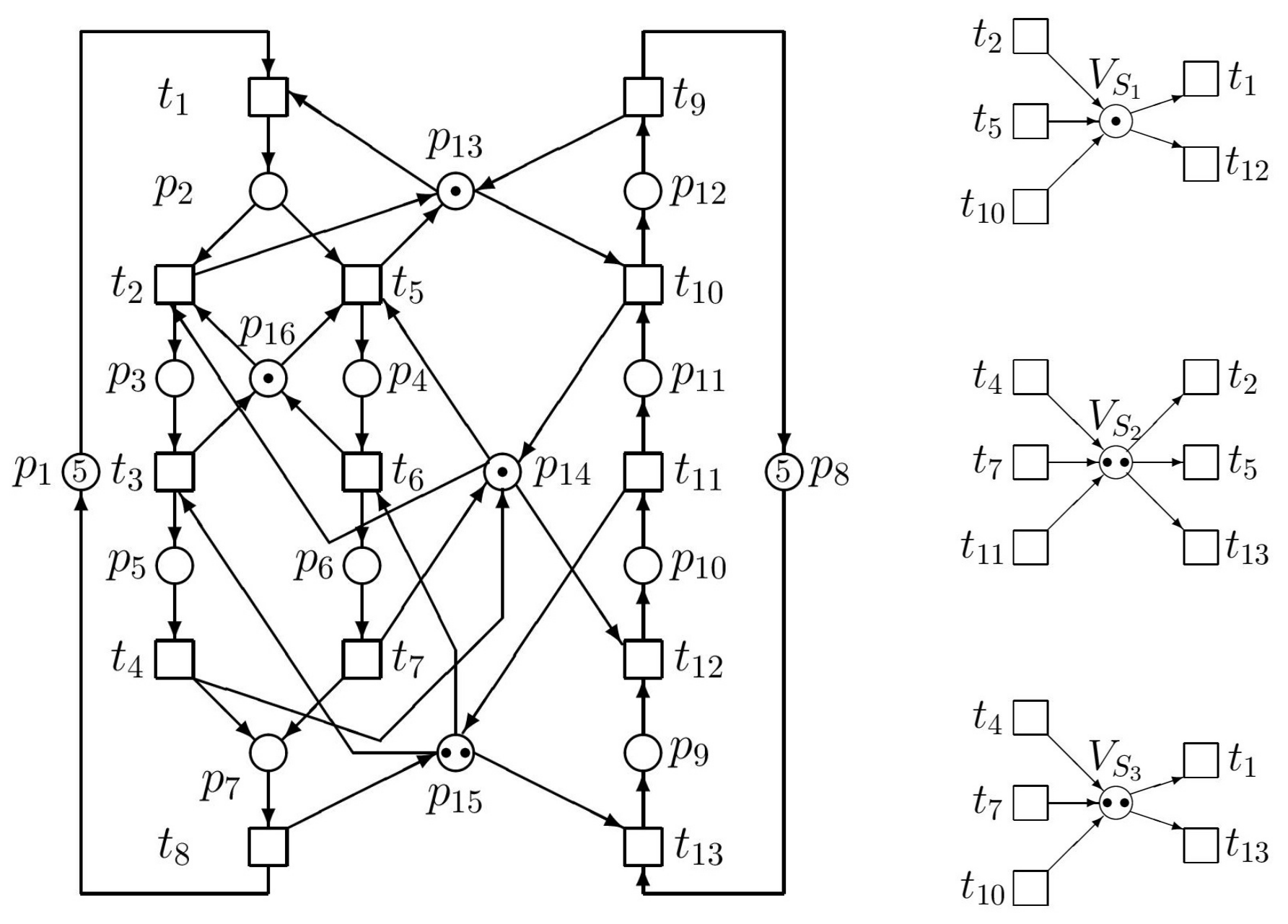
Consider the simple example of N modeling an AMS with two production lines {$p_7,t_1,p_1,t_2,p_2,t_3$} and {$p_8,t_4,p_3,t_5,p_4,t_6$} with two common resources $p_5$ and $p_6$, introduced in Figure 1. Places $p_7$ and $p_8$ are idle process places, $p_1$, $p_2$, $p_3$, and $p_4$ are active process places, and $p_5$ and $p_6$ are resource places. A token in an active process place models, e.g., a part being processed. In Figure 1, active process places are empty till firing $t_1$ and/or $t_4$. Tokens located in a resource place model, e.g., the available capacity of buffers. Tokens located in an idle place indicate the maximal number of concurrent activities that can occur in a process represented by the corresponding production line.

Parameters of N are as follows

$${\mathbf{N}}^{-}=\left(\begin{array}{cccccc}0& 1& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\\ 1& 0& 0& 0& 1& 0\\ 0& 1& 0& 1& 0& 0\\ 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0\end{array}\right){\mathbf{N}}^{+}=\left(\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 1& 0& 0& 0& 1\\ 0& 0& 1& 0& 1& 0\\ 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right)$$

(17)

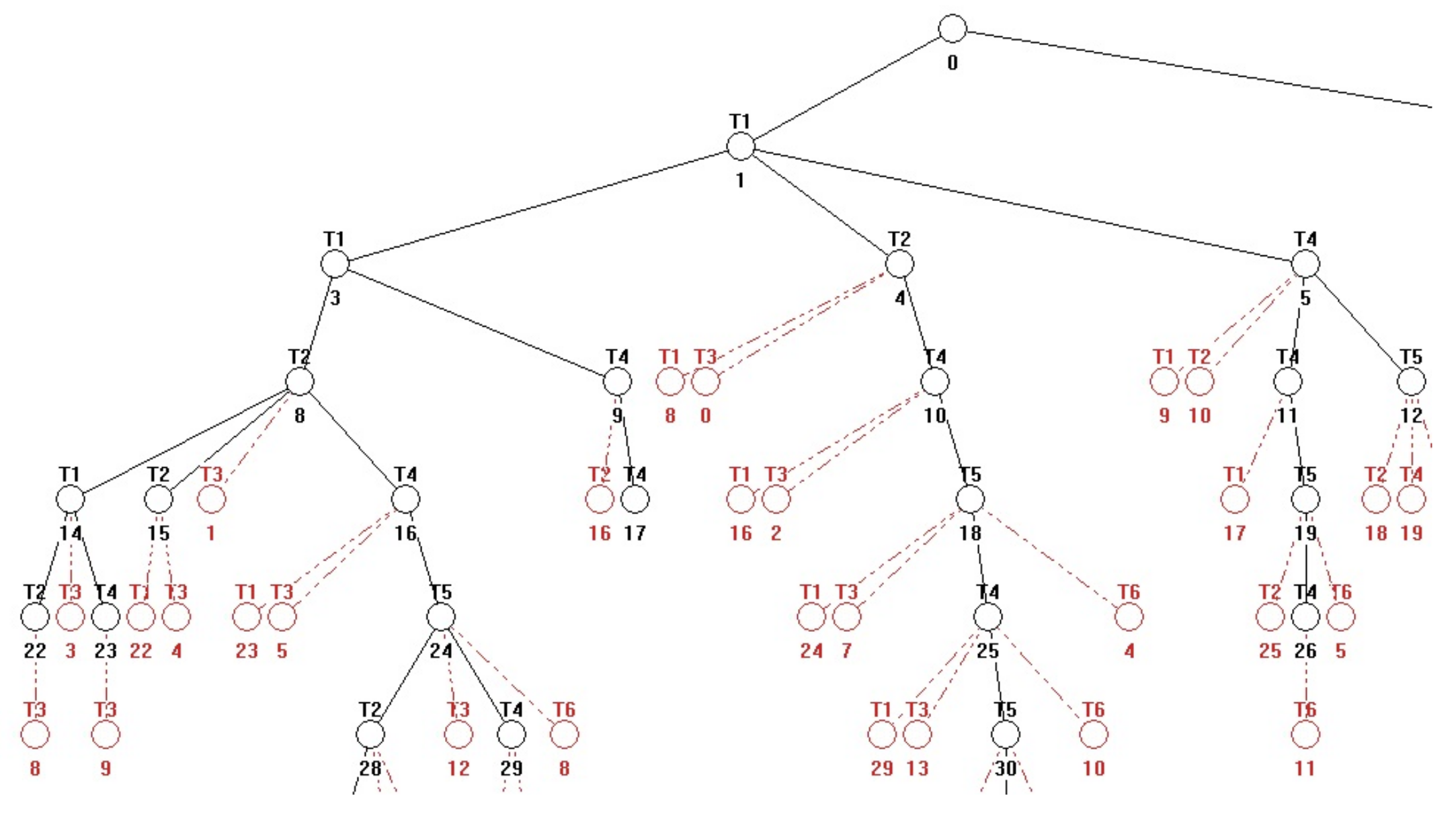
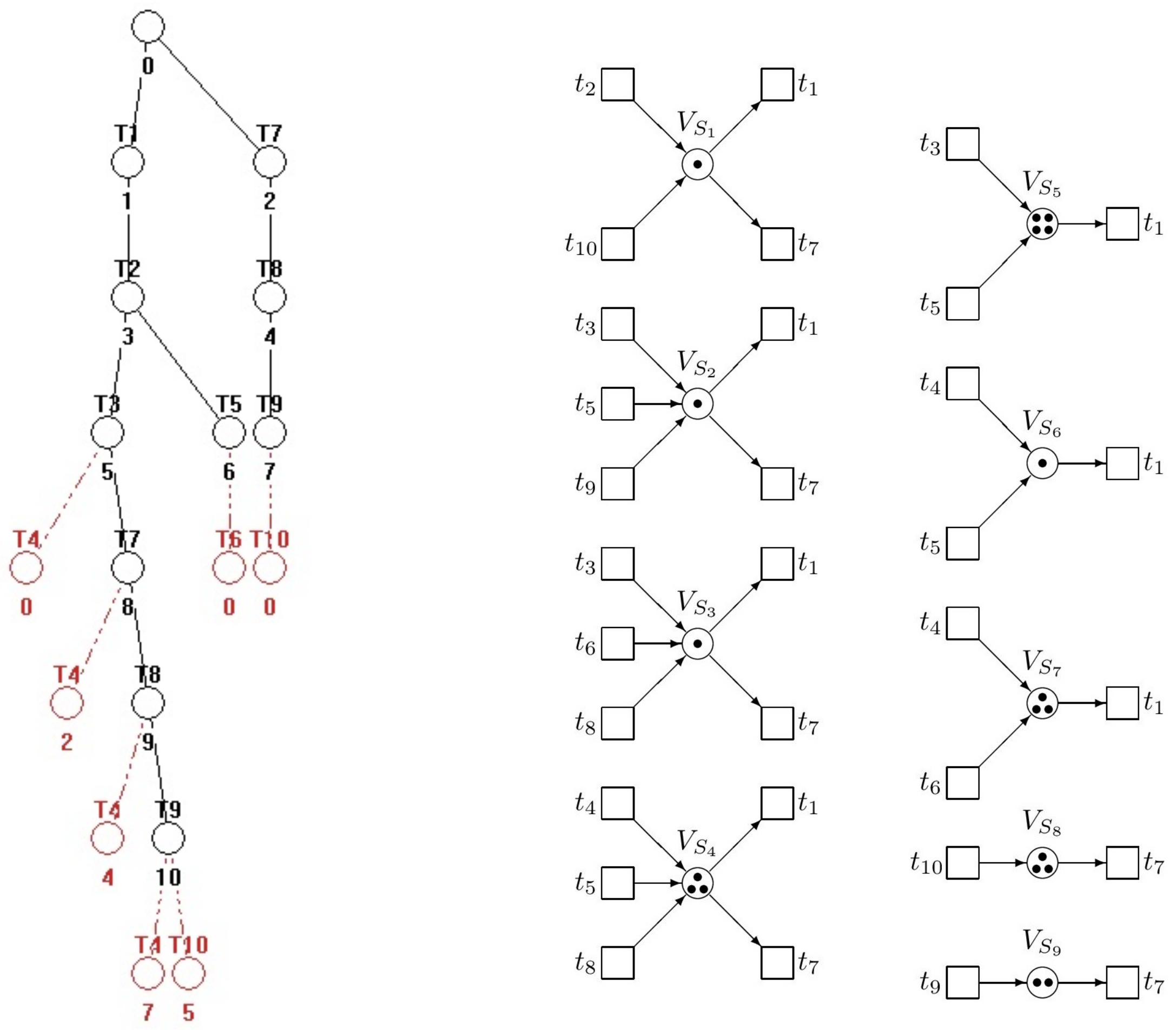
This N has, at the given initial state $M_0={(0, 0, 0, 0, 2, 2, 3, 3)}^T$, the fairly branched (patulous) reachability tree (RT) with 33 nodes (including $M_0$). All RT nodes, being the reachable markings $M_0,\dots ,M_{32}$ are the columns of the following matrix (in the ascending order):

$${\mathbf{X}}_r=\left(\begin{array}{ccccccccccccccccccccccccccccccccc}0& 1& 0& 2& 0& 1& 0& 0& 1& 2& 0& 1& 1& 0& 2& 0& 1& \left|2\right|& 0& 1& 0& 0& 1& 2& 1& 0& 1& 0& 0& 1& 0& 1& 0\\ 0& 0& 0& 0& 1& 0& 0& 0& 1& 0& 1& 0& 0& 0& 1& 2& 1& \left|0\right|& 1& 0& 0& 0& 2& 1& 1& 1& 0& 0& 2& 1& 1& 2& 1\\ 0& 0& 1& 0& 0& 1& 2& 0& 0& 1& 1& 2& 0& 1& 0& 0& 1& \left|2\right|& 0& 1& 2& 0& 0& 1& 0& 1& 2& 1& 0& 1& 0& 0& 1\\ 0& 0& 0& 0& 0& 0& 0& 1& 0& 0& 0& 0& 1& 1& 0& 0& 0& \left|0\right|& 1& 1& 1& 2& 0& 0& 1& 1& 1& 2& 1& 1& 2& 1& 2\\ 2& 1& 2& 0& 2& 1& 2& 1& 1& 0& 2& 1& 0& 1& 0& 2& 1& \left|0\right|& 1& 0& 1& 0& 1& 0& 0& 1& 0& 0& 1& 0& 0& 0& 0\\ 2& 2& 1& 2& 1& 1& 0& 2& 1& 1& 0& 0& 2& 1& 1& 0& 0& \left|0\right|& 1& 1& 0& 2& 0& 0& 1& 0& 0& 1& 0& 0& 1& 0& 0\\ 3& 2& 3& 1& 2& 2& 3& 3& 1& 1& 2& 2& 2& 3& 0& 1& 1& \left|1\right|& 2& 2& 3& 3& 0& 0& 1& 2& 2& 3& 1& 1& 2& 0& 2\\ 3& 3& 2& 3& 3& 2& 1& 2& 3& 2& 2& 1& 2& 1& 3& 3& 2& \left|1\right|& 2& 1& 0& 1& 3& 2& 2& 1& 0& 0& 2& 1& 1& 2& 0\end{array}\right)$$

(18)

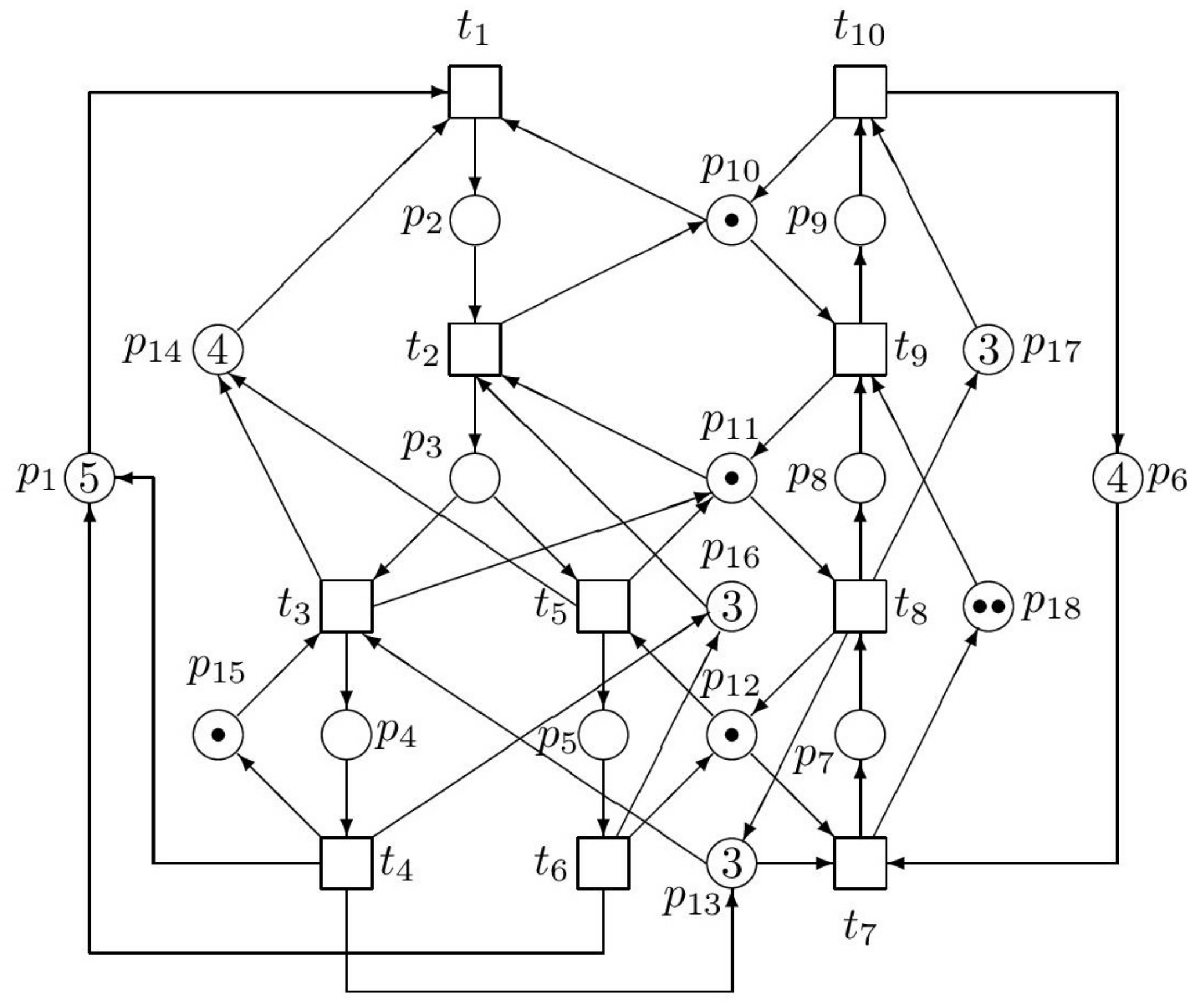
Because RT is too big, it cannot be introduced here full. In Figure 2, at least its principal fragment is introduced.

From the RT fragment we can find the solitary deadlock $M_{17}={(2, 0, 2, 0, 0, 0, 1, 1)}^T$—see (18), where it is separated. This deadlock can be reached by following paths:

$$\begin{array}{ccc}& & {\mathbf{M}}_0\stackrel{t_1}{⟶}{\mathbf{M}}_1\stackrel{t_1}{⟶}{\mathbf{M}}_3\stackrel{t_4}{⟶}{\mathbf{M}}_9\stackrel{t_4}{⟶}{\mathbf{M}}_{17}\hfill \end{array}$$

(19)

$$\begin{array}{ccc}& & {\mathbf{M}}_0\stackrel{t_1}{⟶}{\mathbf{M}}_1\stackrel{t_4}{⟶}{\mathbf{M}}_5\stackrel{t_1}{⟶}{\mathbf{M}}_9\stackrel{t_4}{⟶}{\mathbf{M}}_{17}\hfill \end{array}$$

(20)

$$\begin{array}{ccc}& & {\mathbf{M}}_0\stackrel{t_1}{⟶}{\mathbf{M}}_1\stackrel{t_1}{⟶}{\mathbf{M}}_3\stackrel{t_2}{⟶}{\mathbf{M}}_8\stackrel{t_1}{⟶}{\mathbf{M}}_{14}\stackrel{t_4}{⟶}{\mathbf{M}}_{23}\stackrel{t_3}{⟶}{\mathbf{M}}_9\stackrel{t_4}{⟶}{\mathbf{M}}_{17}\hfill \end{array}$$

(21)

$$\begin{array}{ccc}& & {\mathbf{M}}_0\stackrel{t_1}{⟶}{\mathbf{M}}_1\stackrel{t_1}{⟶}{\mathbf{M}}_3\stackrel{t_2}{⟶}{\mathbf{M}}_8\stackrel{t_4}{⟶}{\mathbf{M}}_{16}\stackrel{t_1}{⟶}{\mathbf{M}}_{23}\stackrel{t_3}{⟶}{\mathbf{M}}_9\stackrel{t_4}{⟶}{\mathbf{M}}_{17}\hfill \end{array}$$

(22)

Hence, we can see that in RT the node $M_9$ immediately precedes the node $M_{17}$ representing the deadlock. These nodes are marking vectors ${\mathbf{M}}_9={(2, 0, 1, 0, 0, 1, 1, 2)}^T$ (the 10th column of ${\mathbf{X}}_r$ because the first column is ${\mathbf{M}}_0$) and ${\mathbf{M}}_{17}={(2, 0, 2, 0, 0, 0, 1, 1)}^T$ (the 18th column of ${\mathbf{X}}_r$). After comparing entries of these vectors, from (19) follows the restriction $M\left(p_1\right)+M\left(p_3\right)<2$ (i.e., only one of them can be marked), i.e., $\mathbf{L}={(1, 0, 1, 0, 0, 0, 0, 0)}^T$ and $\mathbf{b}=\left(2\right)$. Consequently, ${\mathbf{N}}_s=(-1, 1, 0, -1, 1, 0)$ and ${}^s{\mathbf{M}}_0=\left(2\right)$ because in (16) $\mathbf{L}.{\mathbf{M}}_0=0$. Hence, with respect to (11)–(13) we have the augmented PN $N_a$ (i.e., the original uncontrolled net N together with the net $N_s$ representing the supervisor) and the augmented vector ${}^a{\mathbf{M}}_0$ of the initial marking as follows

$${\mathbf{N}}_a=\left(\begin{array}{cccccc}\hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill -1\\ \hfill -1& \hfill 1& \hfill 0& \hfill 0& \hfill -1& \hfill 1\\ \hfill 0& \hfill -1& \hfill 1& \hfill -1& \hfill 1& \hfill 0\\ \hfill -1& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 0& \hfill 1\\ \hfill -& \hfill -& \hfill -& \hfill -& \hfill -& \hfill -\\ \hfill -1& \hfill 1& \hfill 0& \hfill -1& \hfill 1& \hfill 0\end{array}\right){}^a{\mathbf{M}}_0={\left({\mathbf{M}}_0^T\right|{}^s{\mathbf{M}}_0^T)}^T=\left(\begin{array}{c}\hfill 0\\ \hfill 0\\ \hfill 0\\ \hfill 0\\ \hfill 2\\ \hfill 2\\ \hfill 3\\ \hfill 3\\ \hfill -\\ \hfill 2\end{array}\right)$$

(23)

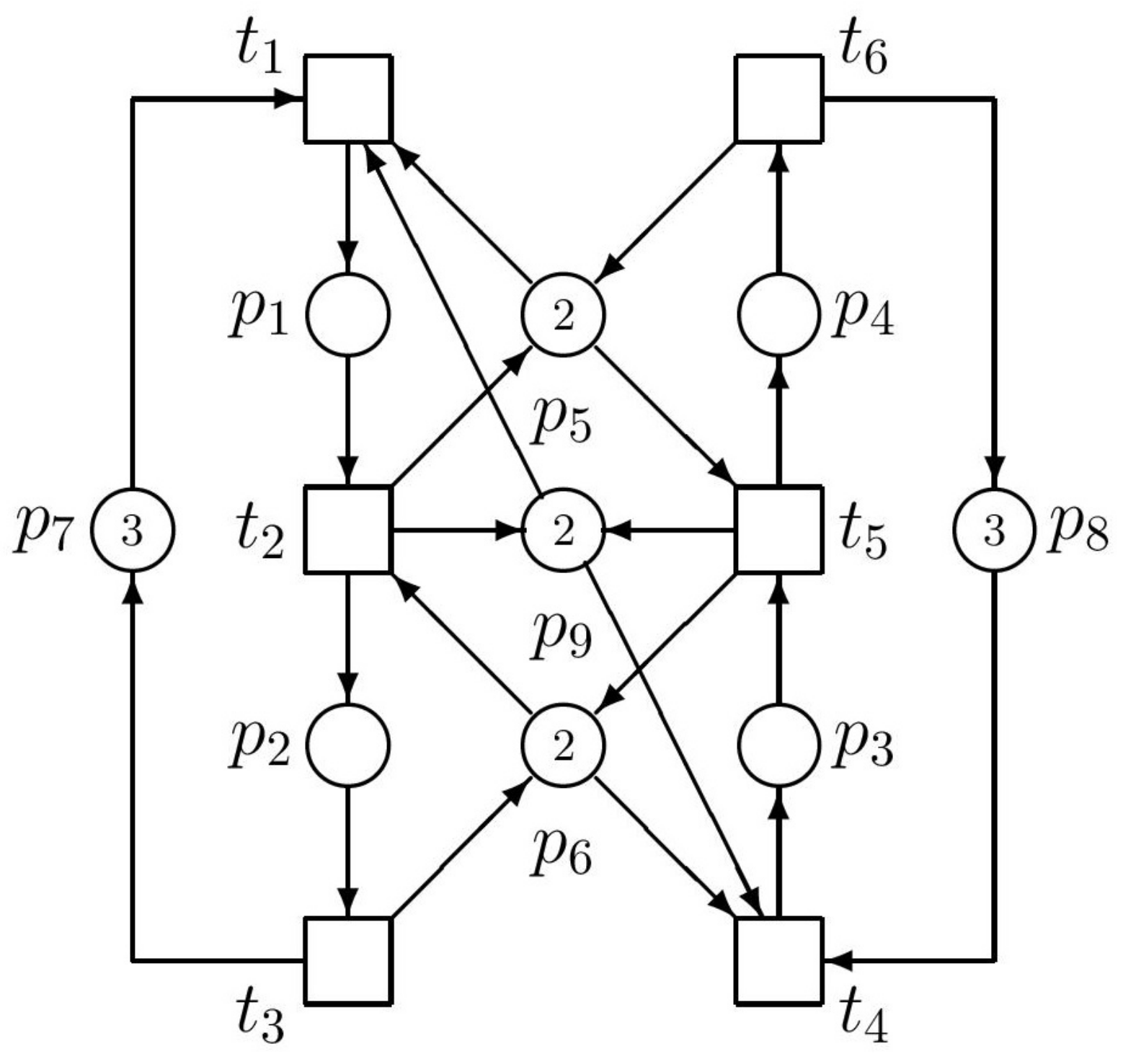
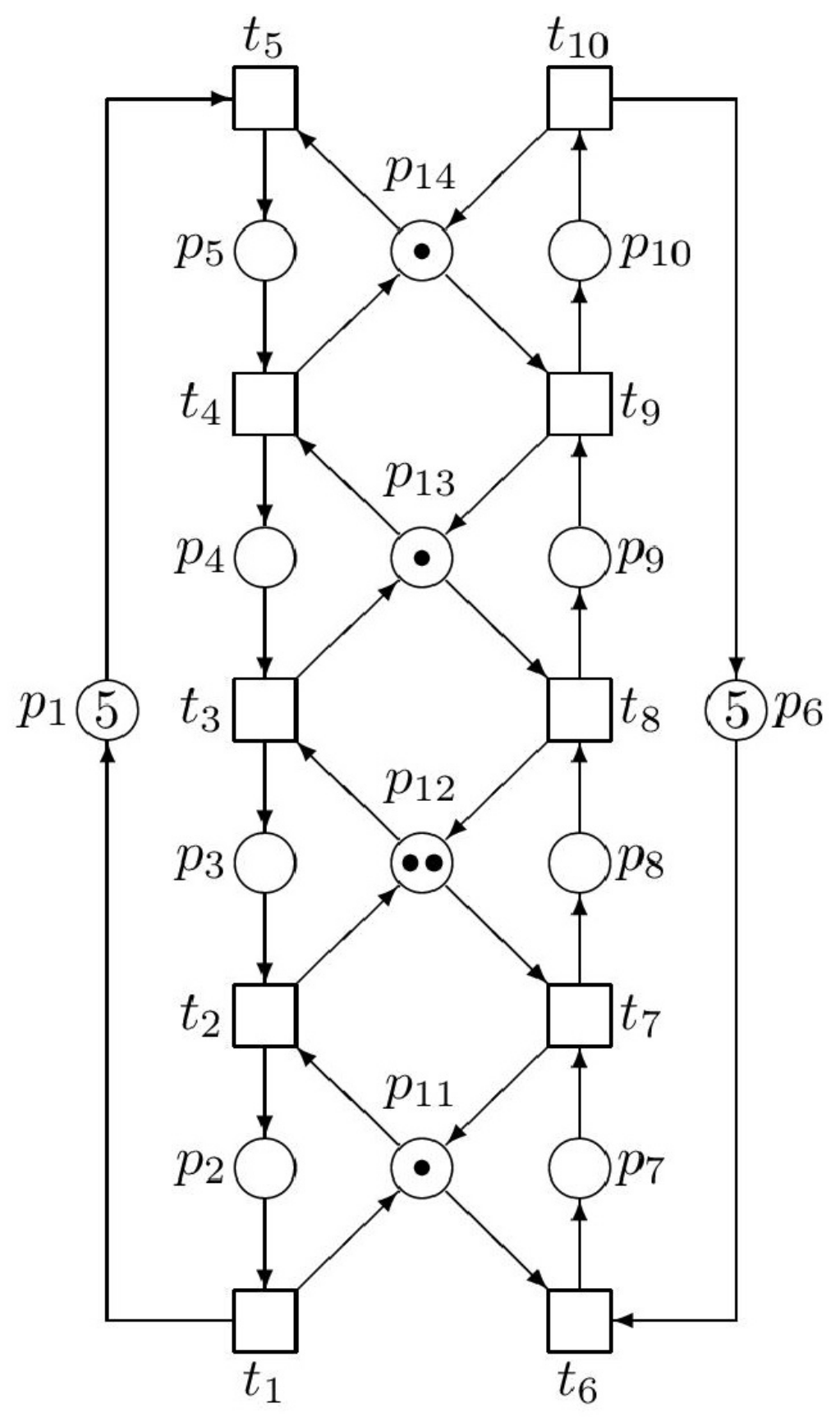
Thus, we have the supervisor represented by the single PN place $p_9$ (monitor) interconnected with the original PN model as it can be seen in Figure 3.

After computing RT of the augmented net, we can find that it contains 28 nodes and no deadlock exists there. It means that the augmented net works correctly.

4. Siphon and Trap-Based Method of Prevention Deadlocks

Such approaches are much more widespread than approaches based on P-invariants. There are many sources in literature. Let us mention at least some of them [7,8,12,13,16,29].

Invariants, siphons, and traps are structural entities of PN. All of them can be computed, e.g., by the Matlab-based tool presented in [30]. The problem of deadlock prevention in a concurrent system represented by N is equivalent to the problem of avoidance of empty siphons in the ordinary PN model of N. When at least one empty siphon occurs in ordinary PN N, the net is totally deadlocked [5].

At the supervisor synthesis it is sufficient to consider only minimal siphons. It is necessary to ensure that the sum of the number of tokens in each minimal siphon S is never less than one, namely in any reachable marking M. In such a case, the general condition ${\mathbf{S}}_i.\mathbf{M}\ge b$ for ith siphon can be replaced by the condition in the form ${\mathbf{S}}_i.\mathbf{M}\ge 1$. This can be derived as follows.

Consider the following formal specification in N

$${\mathbf{l}}^T.\mathbf{M}\ge b$$

(24)

where $\mathbf{l}$ is a ($n\times 1$)-dimensional vector, $\mathbf{M}$ is a marking and b is a scalar; b and the entries of $\mathbf{l}$ are integers. The relation (24) says that the weighted sum of the number of tokens in each place should be greater than or equal to a constant.

In [6], it was proved that if a Petri net $N=(P,T,F,W)$ with incidence matrix $\mathbf{N}$ and initial state ${\mathbf{M}}_0$ satisfies the following relation

$$b-{\mathbf{l}}^T.{\mathbf{M}}_0\le 0$$

(25)

then a control place $p_c$ can be added, that enforces (24). Let ${\mathbf{N}}_c:T\to \mathbb{Z}$ ($\mathbb{Z}$ is the set of integers) denotes the weight vector of arcs connecting $p_c$ with the transitions in the net N; ${\mathbf{N}}_c$ is obtained by ${\mathbf{N}}_c={\mathbf{l}}^T.\mathbf{N}$. In general, when there are more $p_c$ than one, ${\mathbf{N}}_c={\mathbf{L}}^T.\mathbf{N}$ with $\mathbf{L}$ being the matrix were rows represent particular ${\mathbf{l}}^T$ appertaining to particular $p_c$. The initial number of tokens in $p_c$ is $M_0\left(p_c\right)={\mathbf{l}}^T.{\mathbf{M}}_0-b\ge 0$ or, in general, ${\mathbf{M}}_c^0=\mathbf{L}.{\mathbf{M}}_0-\mathbf{b}\ge \mathbf{0}$.

The controlled Petri net is maximally permissive. The control process enforces just enough control to avoid all illegal markings. This is the basis for deadlock prevention, i.e., for the synthesis of the control algorithm based on siphons. Thus, the place invariant guarantees that for any marking $\mathbf{M}$ in the set of reachable markings of N

$${\mathbf{l}}^T.\mathbf{M}-M\left(p_c\right)=b$$

(26)

Here, as it was defined above, $M\left(p_c\right)$ is the number of tokens in the control place $p_c$. Due to the fact that $M\left(p_c\right)$ is non-negative, the inequality in (24) is satisfied. Equation (25) expresses the demand that (24) must be satisfied for ${\mathbf{M}}_0$, otherwise no solution exists there. ${\mathbf{b}}_c$ represents the row which extends the incidence matrix $\mathbf{N}$ of the uncontrolled net N with respect to the control place $p_c$. In general, for more additive places $p_1,\dots ,p_s$, it can be written

$$\mathbf{L}.\mathbf{M}\ge \mathbf{b},\mathrm{or}\mathbf{L}.\mathbf{M}-{\mathbf{M}}_c=\mathbf{b}$$

(27)

where $\mathbf{L}$ is ($n_s\times n$) matrix of positive integers greater than or equal to 0. $\mathbf{L}$ has the weighted vectors ${\mathbf{l}}_i^T$, $i=1,\dots ,s$, as its rows. The vector $\mathbf{b}$ is ($n_s\times 1$) vector of restrictions with entries being positive integers greater than or equal to 0; ${\mathbf{M}}_c$ is ($n_s\times 1$) vector of slacks with entries being positive integers greater than or equal to 0. Thus, we obtain the controlled PN model (with the incidence matrix ${\mathbf{N}}_{ex}$) consisting of original uncontrolled model (with the incidence matrix $\mathbf{N}$) and the siphon-based controller (with the incidence matrix ${\mathbf{N}}_c$) as follows

$$\begin{array}{ccc}\hfill {\mathbf{N}}_c& =& \mathbf{L}.\mathbf{N}\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill {\mathbf{M}}_c^0& =& \mathbf{L}.{\mathbf{M}}_0-\mathbf{b}\ge \mathbf{0}\hfill \end{array}$$

(29)

$${\mathbf{N}}_{ex}=\left(\begin{array}{c}\mathbf{N}\hfill \\ {\mathbf{N}}_c\hfill \end{array}\right);{\mathbf{M}}_{ex}^0=\left(\begin{array}{c}\hfill {\mathbf{M}}_0\\ \hfill {\mathbf{M}}_c^0\end{array}\right)$$

(30)

The controller consists of monitors and their interconnections with the original PN model.

Replacing ${\mathbf{l}}_i^T$ by the siphon ${\mathbf{S}}_i$, or, in general, replacing $\mathbf{L}$ by the matrix of siphons ${\mathbf{S}}_m$ (where particular siphons are its rows) we obtain

$${\mathbf{N}}_c={\mathbf{S}}_m.\mathbf{N}$$

(31)

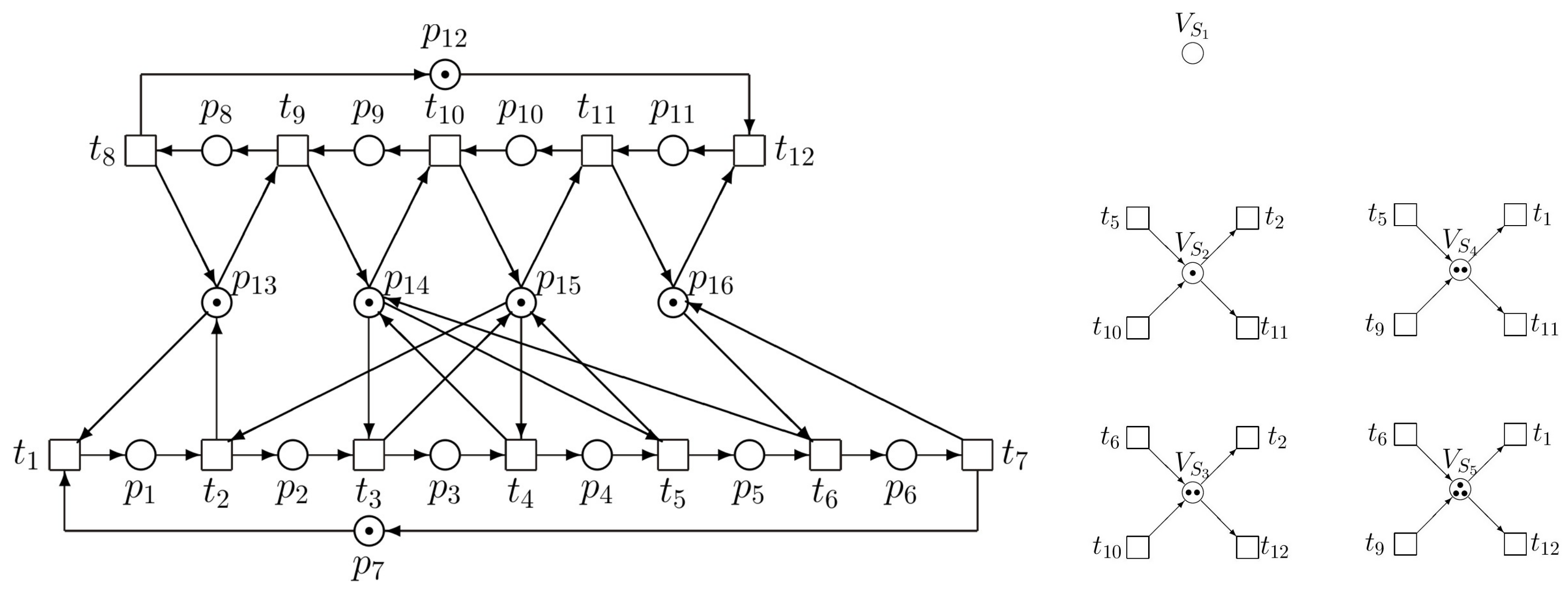
4.1. Example 2

Minimal siphons and traps of the PN model in Figure 1 are the following

$\sout{S_1=\{p_1,p_2,p_7\}}$	$\sout{T{r}_1=\{p_1,p_2,p_7\}}$
$\sout{S_2=\{p_2,p_3,p_6\}}$	$\sout{T{r}_2=\{p_2,p_3,p_6\}}$
$\sout{S_3=\{p_1,p_4,p_5\}}$	$\sout{T{r}_3=\{p_1,p_4,p_5\}}$
$\sout{S_4=\{p_3,p_4,p_8\}}$	$\sout{T{r}_4=\{p_3,p_4,p_8\}}$
$S_5=\{p_2,p_4,p_5,p_6\}$	$T{r}_5=\{p_1,p_3,p_5,p_6\}$

Denote $S=S_5$ and $T=T{r}_5$. In this simple example, the siphon and trap can be illustrated by Figure 4. Above introduced crossed siphons are equaled to traps. Such a siphon cannot be emptied once it is initially marked (this is ensured by the corresponding marked trap). Residual siphons are strict minimal siphons (SMS). Consequently, there is only one SMS, namely $S_5$. In a vector form it is denoted as $\mathbf{S}$ as follows

$$\mathbf{S}={\left(\begin{array}{cccccccc}0& 1& 0& 1& 1& 1& 0& 0\end{array}\right)}^T$$

(32)

The siphon corresponds with the Figure 4 as well as the trap $T{r}_5$. With respect to (31)

$${\mathbf{N}}_c=\mathbf{S}.\mathbf{N}=\left(\begin{array}{cccccccc}-1& 1& 0& -1& 1& 0& 0& 0\end{array}\right)$$

(33)

what is the same structure of the supervisor like in the previous approach based on P-invariants. Thus, the PN model of the controlled (supervised) AMS is in Figure 3. However, it must be said that such a coincidence of the results achieved by both methods occurs only rarely, not in general.

Figure 4. The siphon S and trap T in the PN model.

Figure 4. The siphon S and trap T in the PN model.

4.2. Invariant-Controlled Siphons and Setting the Marking of Monitors in the Siphon-Based Approach

The control places $p_c$ creating the supervisor are frequently named as monitors. Denote them as $V_{S_i}, i=1,\dots ,n_m$ ($n_m$ is a number of monitors). Now it is important to find a suitable marking of the monitors $V_{S_i}$. Namely, an inadequate setting of marking of monitors may cause other deadlocks in the controlled plant. In general, for setting the marking of monitors $V_{S_i}$, $i=1,n_m$ are valid the following general rules.

Let $S=\{p_i,p_j,\dots ,p_k\}$ be a strict minimal siphon (SMS) of an original (uncontrolled) ordinary net system $(N_0,M_0)$, where $N_0=(P_0,T_0,F_0)$. Add a monitor $V_S$ to $N_0$ to make the vector $\mathbf{I}={(0,\dots ,1i,\dots ,1j,\dots ,1k,\dots ,0,-1)}^T$ be a P-invariant of a new (controlled) net system $(N_1,M_1)$. Here, $\forall p\in P_0\backslash S, I\left(p\right)=0, I\left(V_S\right)=-1, \forall p\in P_0, M_1\left(p\right)=M_0\left(p\right)$, and ${\mathbf{N}}_1={\left[{\mathbf{N}}_0^T\right|{\mathbf{L}}_{V_s}^T]}^T$, where ${\mathbf{L}}_{V_s}$ is a row vector corresponding to adding the place $V_S$. Let $M_1\left(V_S\right)=M_0\left(S\right)-{\xi }_S$, where $1\le {\xi }_S\le M_0\left(S\right)$. Then S is an invariant-controlled SMS. Hence, it is always marked at any reachable marking of the net system $(N_1,M_1)$. Namely, $\mathbf{I}$ is a P-invariant and $\forall p\in (P_0\backslash \left\{V_S\right\})\backslash S,I\left(p\right)<0$. Note than ${\mathbf{I}}^T.{\mathbf{M}}_1={\mathbf{I}}^T.{\mathbf{M}}_0=M_0\left(S\right)-M_1\left(V_S\right)={\xi }_S>0$. Thus, S is an invariant-controlled siphon.

A siphon S is controlled in a net $(N,M_0)$ iff $\forall M\in R(N,M_0),M\left(S\right)>0$. Thus, any siphon that contains a marked trap is controlled. Namely, the marked trap can never be emptied. In ordinary PN a controlled siphon does not cause any deadlock.

A siphon S in an ordinary PN $(N,M_0)$ is [7] invariant-controlled by P-invariant I under $M_0$ iff ${\mathbf{I}}^T.{\mathbf{M}}_0>0$ and $\forall p\in P\backslash S,I\left(p\right)\le 0$, or equivalently ${\mathbf{I}}^T.{\mathbf{M}}_0>0$ and ${\left|\right|I\left|\right|}^{+}=p\in P|I\left(p\right)$ is the positive support of I.

More succinctly said, a siphon S is controlled if it can never be emptied, and invariant-controlled by P-invariant I if ${\mathbf{I}}^T.{\mathbf{M}}_0>0$ and ${\left|\right|I\left|\right|}^{+}\subseteq S$.

So that, to guarantee that a siphon S is always marked in a net system, it is necessary to keep at least one token being present at S at any reachable marking of the net system. Suppose that it was found such a control of a siphon S that S will never be emptied. Let ${\xi }_S$ is the least number of tokens being present at S. Such ${\xi }_S$ is called the siphon control depth variable. It is clear that the larger ${\xi }_S$ is, the more behavior of the modeled system will be restricted. However, it may means that more reachable states will be forbidden than it is necessary. Therefore, it is suitable when the siphon control depth variable is as small as possible, i.e., 1, if possible.

Setting the Marking of Monitors in Example 2

It is easy to check from Figure 3 with taking into account Figure 4 that $I=\{p_2, p_4, p_5,p_6\}-V_S$ is P-invariant of $N_1$. Clearly, $S=\{p_2, p_4, p_5, p_6\}$ is invariant-controlled by I, since ${\left|\right|I\left|\right|}^{+}=S$ and $M_0\left(S\right)-M_1\left(V_S\right)=4-2>0$. Here, ${\left|\right|I\left|\right|}^{+}$, is the positive support of I.

5. More Complicated Examples

5.1. Example 3

Consider a PN model in the form presented in Figure 5.

This PN model has RT with 77 nodes (including ${\mathbf{M}}_0$). There are three deadlocks in the PN, namely

$$\begin{array}{c}\hfill {\mathbf{M}}_{33}={(3, 1, 1, 0, 0, 0, 0, 3, 2, 0, 0, 0, 0, 0, 0, 0)}^T\end{array}$$

(34)

$$\begin{array}{c}\hfill {\mathbf{M}}_{36}={(3, 1, 0, 1, 0, 0, 0, 3, 2, 0, 0, 0, 0, 0, 0, 0)}^T\end{array}$$

(35)

$$\begin{array}{c}\hfill {\mathbf{M}}_{44}={(4, 1, 0, 0, 0, 0, 0, 2, 2, 0, 1, 0, 0, 0, 0, 1)}^T\end{array}$$

(36)

Because of the large RT it is difficult or practically impossible (by commonly available means) to analyze RT in order to find the matrix $\mathbf{L}$ and the vector $\mathbf{b}$ in (5). It remains to use the approach based on siphon and traps. Using the Matlab-based tool in [30] we obtain the following minimal siphons and traps

$\sout{S_1=\{p_3, p_4, p_{16}\}}$	$\sout{T{r}_1=\{p_3, p_4, p_{16}\}}$
$\sout{S_2=\{p_2, p_{12}, p_{13}\}}$	$\sout{T{r}_2=\{p_2, p_{12}, p_{13}\}}$
$\sout{S_3=\{p_8, p_9, p_{10}, p_{11}, p_{12}\}}$	$T{r}_3=\{p_2, p_{10}, p_{11}, p_{13}, p_{14}\}$
$\sout{S_4=\{p_5, p_6, p_7, p_9, p_{10}, p_{15}\}}$	$\sout{T{r}_4=\{p_8, p_9, p_{10}, p_{11}, p_{12}\}}$
$\sout{S_5=\{p_1, p_2, p_3, p_4, p_5, p_6, p_7\}}$	$\sout{T{r}_5=\{p_5, p_6, p_7, p_9, p_{10}, p_{15}\}}$
$S_6=\{p_3, p_4, p_5, p_6, p_{12}, p_{13}, p_{14}\}$	$\sout{T{r}_6=\{p_1, p_2, p_3, p_4, p_5, p_6, p_7\}}$
$\sout{S_7=\{p_3, p_4, p_5, p_6, p_{10}, p_{11}, p_{14}\}}$	$\sout{T{r}_7=\{p_3, p_4, p_5, p_6, p_{10}, p_{11}, p_{14}\}}$
$S_8=\{p_5, p_6, p_7, p_{10}, p_{11}, p_{14}, p_{15}\}$	$T{r}_8=\{p_2, p_9, p_{10}, p_{13}, p_{14}, p_{15}, p_{16}\}$
$S_9=\{p_5, p_6, p_7, p_{10}, p_{12}, p_{13}, p_{14}, p_{15}\}$	$T{r}_9=\{p_2, p_5, p_6, p_9, p_{10}, p_{13}, p_{14}, p_{15}\}$
	$T{r}_{10}=\{p_3, p_4, p_5, p_6, p_9, p_{10}, p_{14}, p_{15}\}$

Because $S_1=T{r}_1$, $S_2=T{r}_2$, $S_3=T{r}_4$, $S_4=T{r}_5$, $S_5=T{r}_6$, and $S_7=T{r}_7$, there are three minimal siphons where emptying must be prevented, namely $S_6$, $S_8$, and $S_9$. Rename $S_6$ to be $S_1$, $S_8$ to be $S_2$ and $S_9$ to be $S_3$. Consequently, we have

$$\mathbf{S}=\left(\begin{array}{cccccccccccccccc}0& 0& 1& 1& 1& 1& 0& 0& 0& 0& 0& 1& 1& 1& 0& 0\\ 0& 0& 0& 0& 1& 1& 1& 0& 0& 1& 1& 0& 0& 1& 1& 0\\ 0& 0& 0& 0& 1& 1& 1& 0& 0& 1& 0& 1& 1& 1& 1& 0\end{array}\right)$$

(37)

$${\mathbf{N}}_c=\mathbf{S}.\mathbf{N}=\left(\begin{array}{ccccccccccccc}\hfill -1& \hfill 1& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill -1& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill -1\\ \hfill -1& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill -1\end{array}\right)$$

(38)

where the incidence matrix of the PN model is the following

$$\mathbf{N}=\left(\begin{array}{ccccccccccccc}\hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill -1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill -1& \hfill 1& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill -1& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill 0& \hfill -1& \hfill 0& \hfill 0& \hfill -1& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill -1\\ \hfill 0& \hfill -1& \hfill 1& \hfill 0& \hfill -1& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right)$$

(39)

The uncontrolled PN model together with its supervisor is displayed in Figure 6. This form of the mutual interaction between the supervisor and the PN model is used in order to avoid intricate interconnections between the uncontrolled model and the supervisor in the same figure. Marking of monitors $V_{S_1}-V_{S_3}$ were established by the relation $M_0\left(S_i\right)-M_1\left(V_{S_i}\right)>0$ for $i=1,2,3$. Because $M_0\left(S_1\right)=2$ it is sufficient to put $M_1\left(V_{S_1}\right)=1$. Similarly, because $M_0\left(S_2\right)=3$ it is sufficient to put $M_1\left(V_{S_2}\right)=2$ and because $M_0\left(S_3\right)=4$ it is sufficient to put $M_1\left(V_{S_3}\right)=2$. In such a way controlled PN model (28) has RT with 56 nodes (it creates the state space of reachable markings) and no deadlocks. In case of putting $M_1\left(V_{S_3}\right)=3$ a new deadlock would occur in controlled system, namely ${\mathbf{M}}_{14}={(4, 1, 0, 0, 0, 0, 0, 3, 2, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0)}^T$.

5.2. Example 4

Consider the PN model given in Figure 7. There are 16 places and 12 transitions.

The transpose of the incidence matrix is the following

$${\mathbf{N}}^T=\left(\begin{array}{cccccccccccccccc}\hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill -1& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill -1& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 0\\ \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill -1\\ \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill -1\end{array}\right)$$

The siphons and traps are the following.

$\sout{S_1=\{p_{11}, p_{16}, p_6\}}$	$\sout{T{r}_1=\{p_{11}, p_{16}, p_6\}}$
$\sout{S_2=\{p_1, p_{13}, p_8\}}$	$\sout{T{r}_2=\{p_1, p_{13}, p_8\}}$
$S_3=\{p_{10}, p_{15}, p_2, p_4\}$	$T{r}_3=\{p_{10}, p_{14}, p_{15}, p_2\}$
$\sout{S_4=\{p_{14}, p_3, p_5, p_9\}}$	$T{r}_4=\{p_{10}, p_{15}, p_2, p_4\}$
$S_5=\{p_{14}, p_{15} p_5, p_9\}$	$\sout{T{r}_5=\{p_{14}, p_3, p_5, p_9\}}$
$S_6=\{p_{14}, p_{15}, p_{16}, p_6, p_9\}$	$T{r}_6=\{p_1, p_{10}, p_{13}, p_{14}, p_{15}\}$
$\sout{S_7=\{p_{10}, p_{11}, p_{12}, p_8, p_9\}}$	$T{r}_7=\{p_{11}, p_{14}, p_{15}, p_{16}, p_2\}$
$S_8=\{p_{13}, p_{14}, p_{15}, p_5, p_8\}$	$\sout{T{r}_8=\{p_{10}, p_{11}, p_{12}, p_8, p_9\}}$
$S_9=\{p_{13}, p_{14}, p_{15}, p_{16}, p_6, p_8\}$	$T{r}_9=\{p_1, p_{11}, p_{13}, p_{14}, p_{15}, p_{16}\}$
$\sout{S_{10}=\{p_1, p_2, p_3, p_4, p_5, p_6, p_7\}}$	$\sout{T{r}_{10}=\{p_1, p_2, p_3, p_4, p_5, p_6, p_7\}}$

Here, $S_1=T{r}_1$, $S_2=T{r}_2$, $S_4=T{r}_5$, $S_7=T{r}_8$, $S_{10}=T{r}_{10}$. Consequently, $S_1, S_2, S_4, S_7, S_{10}$ cannot be emptied. It is sufficient to prevent $S_3, S_5, S_6, S_8, S_9$ before emptying. Rename them to be, respectively, $S_1, S_2, S_3, S_4, S_5$. Hence,

$$\mathbf{S}=\left(\begin{array}{cccccccccccccccc}0& 1& 0& 1& 0& 0& 0& 0& 0& 1& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 1& 0& 0& 0& 1& 0& 0& 0& 0& 1& 1& 0\\ 0& 0& 0& 0& 0& 1& 0& 0& 1& 0& 0& 0& 0& 1& 1& 1\\ 0& 0& 0& 0& 1& 0& 0& 1& 0& 0& 0& 0& 1& 1& 1& 0\\ 0& 0& 0& 0& 0& 1& 0& 1& 0& 0& 0& 0& 1& 1& 1& 1\end{array}\right)$$

(40)

$${\mathbf{N}}_c=\mathbf{S}.\mathbf{N}=\left(\begin{array}{cccccccccccc}\hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill -1& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0\\ \hfill 0& \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill -1\\ \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill -1& \hfill 0\\ \hfill -1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill -1\end{array}\right)$$

(41)

Thus, we obtain five monitors $V_{S_1}-V_{S_5}$ (creating the supervisor) and their interconnections with the uncontrolled PN model. In order to establish marking of these monitors the following settings are necessary: $M_0\left(S_i\right)-M_1\left(V_{S_i}\right)>0, i=1,\dots ,5$. Because $M_0\left(S_1\right)=1$, $M_1\left(V_{S_1}\right)=0$. Analogically, $M_0\left(S_2\right)=2$, $M_1\left(V_{S_2}\right)=1$; $M_0\left(S_3\right)=3$, $M_1\left(V_{S_3}\right)=2$; $M_0\left(S_4\right)=3$, $M_1\left(V_{S_4}\right)=2$; $M_0\left(S_5\right)=4$, $M_1\left(V_{S_5}\right)=3$. With markings of monitors set in such a way, we obtain the controlled PN model without any deadlocks. RT of the controlled PN model has 54 nodes including the initial marking ${\mathbf{M}}_0={(0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1 | 0, 1, 2, 2, 3)}^T$. These nodes represent the space of reachable markings of the controlled PN model. The interconnection between original uncontrolled PN model and the supervisor represented by the set of monitors is realized by means of the incidence matrix ${\mathbf{N}}_c$, namely by ${\mathbf{N}}_c^{+}$ and ${\mathbf{N}}_c^{-}$. The supervisor is displayed in Figure 8 (right) together with the uncontrolled system (left).

5.3. Example 5

Consider the PN model displayed in Figure 9.

Its RT has 119 nodes (reachable markings) including the initial marking ${\mathbf{M}}_0={(5, 0, 0, 0, 0, 5, 0, 0, 0, 0, 1, 2, 1, 1)}^T$. There are five deadlocks in the model, namely ${\mathbf{M}}_{76}$, ${\mathbf{M}}_{85}$, ${\mathbf{M}}_{91}$, ${\mathbf{M}}_{96}$, ${\mathbf{M}}_{100}$ as follows,

$$\begin{array}{c}\hfill {\mathbf{M}}_{76}={(3, 0, 0, 1, 1, 2, 1, 2, 0, 0, 0, 0, 0, 0)}^T\end{array}$$

(42)

$$\begin{array}{c}\hfill {\mathbf{M}}_{85}={(2, 0, 1, 1, 1, 3, 1, 1, 0, 0, 0, 0, 0, 0)}^T\end{array}$$

(43)

$$\begin{array}{c}\hfill {\mathbf{M}}_{91}={(4, 0, 0, 0, 1, 1, 1, 2, 1, 0, 0, 0, 0, 0)}^T\end{array}$$

(44)

$$\begin{array}{c}\hfill {\mathbf{M}}_{96}={(1, 0, 2, 1, 1, 4, 1, 0, 0, 0, 0, 0, 0, 0)}^T\end{array}$$

(45)

$$\begin{array}{c}\hfill {\mathbf{M}}_{100}={(3, 0, 1, 0, 1, 2, 1, 1, 1, 0, 0, 0, 0, 0)}^T\end{array}$$

(46)

and the following siphon and traps

$\sout{S_1=\{p_2, p_7, p_{11}\}}$	$\sout{T{r}_1=\{p_2, p_7, p_{11}\}}$
$\sout{S_2=\{p_3, p_8, p_{12}\}}$	$\sout{T{r}_2=\{p_3, p_8, p_{12}\}}$
$\sout{S_3=\{p_4, p_9, p_{13}\}}$	$\sout{T{r}_3=\{p_4, p_9, p_{13}\}}$
$\sout{S_4=\{p_5, p_{10}, p_{14}\}}$	$\sout{T{r}_4=\{p_5, p_{10}, p_{14}\}}$
$S_5=\{p_2, p_8 p_{11}, p_{12}\}$	$T{r}_5=\{p_3, p_7, p_{11}, p_{12}\}$
$S_6=\{p_3, p_9, p_{12}, p_{13}\}$	$T{r}_6=\{p_4, p_8, p_{12}, p_{13}\}$
$S_7=\{p_4, p_{10}, p_{13}, p_{14}\}$	$T{r}_7=\{p_5, p_9, p_{13}, p_{14}\}$
$\sout{S_8=\{p_1, p_2, p_3, p_4, p_5\}}$	$\sout{T{r}_8=\{p_1, p_2, p_3, p_4, p_5\}}$
$S_9=\{p_2, p_9, p_{11}, p_{12}, p_{13}\}$	$T{r}_9=\{p_4, p_7, p_{11}, p_{12}, p_{13}\}$
$S_{10}=\{p_3, p_{10}, p_{12}, p_{13}, p_{14}\}$	$T{r}_{10}=\{p_5, p_8, p_{12}, p_{13}, p_{14}\}$
$\sout{S_{11}=\{p_6, p_7, p_8, p_9, p_{10}\}}$	$\sout{T{r}_{11}=\{p_6, p_7, p_8, p_9, p_{10}\}}$
$S_{12}=\{p_2, p_{10}, p_{11}, p_{12}, p_{13}, p_{14}\}$	$T{r}_{12}=\{p_5, p_7, p_{11}, p_{12}, p_{13}, p_{14}\}$

As we can see, $S_1=T{r}_1, S_2=T{r}_2, S_3=T{r}_3, S_4=T{r}_4, S_8=T{r}_8, S_{11}=T{r}_{11}$. As we already know, if a siphon contains a marked trap, it will never become empty. Therefore, we do not have to take the listed siphons into account. When synthesizing the supervisor, it is sufficient to use the remaining six siphons, i.e., $S_5, S_6, S_7, S_9, S_{10}, S_{12}$. After elimination of siphons being consensual to traps, rename the residual siphons in ascending order starting from $S_1$, i.e., $S_1=S_5$, $S_2=S_6$, $S_3=S_7$, $S_4=S_9$, $S_5=S_{10}$, and $S_6=S_{12}$. Thus, the matrix of siphons will have the following shape

$${\mathbf{S}}_m=\left(\begin{array}{cccccccccccccc}0& 1& 0& 0& 0& 0& 0& 1& 0& 0& 1& 1& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0& 1& 0& 0& 1& 1& 0\\ 0& 0& 0& 1& 0& 0& 0& 0& 0& 1& 0& 0& 1& 1\\ 0& 1& 0& 0& 0& 0& 0& 0& 1& 0& 1& 1& 1& 0\\ 0& 0& 1& 0& 0& 0& 0& 0& 0& 1& 0& 1& 1& 1\\ 0& 1& 0& 0& 0& 0& 0& 0& 0& 1& 1& 1& 1& 1\end{array}\right)$$

(47)

Since the incidence matrix $\mathbf{N}$ of the uncontrolled PN model directly follows from the model structure introduced in Figure 9, the incidence matrix of the supervisor will be as follows

$${\mathbf{N}}_c={\mathbf{S}}_m.\mathbf{N}=\left(\begin{array}{cccccccccc}\hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0& \hfill -1& \hfill 0& \hfill -1& \hfill 0& \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill -1& \hfill 0& \hfill -1& \hfill 0& \hfill 1& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill -1& \hfill -1& \hfill 0& \hfill 0& \hfill 1& \hfill 0\end{array}\right)$$

(48)

To set marking of particular monitors $V_{S_1}$, …, $V_{S_6}$, we will use the relation $M_0\left(S_i\right)-M_1\left(V_{S_i}\right)>0$ for $i=1,\cdots ,6$. Because $M_0\left(S_1\right)=M_0\left(S_2\right)=3$, $M_0\left(S_3\right)=2$, $M_0\left(S_4\right)=M_0\left(S_5\right)=4$, and $M_0\left(S_6\right)=5$. Hence, for $M_1\left(V_{S_1}\right)=M_1\left(V_{S_2}\right)=2$, $M_1\left(V_{S_3}\right)=1$, $M_1\left(V_{S_4}\right)=M_1\left(V_{S_5}\right)=2$, and $M_1\left(V_{S_6}\right)=2$ there are no deadlocks in the supervised PN model. The supervisor (the set of monitors) is displayed in Figure 10 right, in the neighborhood of the unsupervised PN model.

5.4. Example 6

In order to show that there may occur computational problems in case of PN models which need not be neither large nor structurally complicated consider the PN model in Figure 11.

In this case, it was not possible to calculate siphons and traps by the tool offered in [30] on PC (with Intel(R) Core(TM), i7-10700 CPU @ 2.90 GHz 2.90 GHz with 16 GB RAM and 64-bit operating system Windows 11) even after tens of hours (more than 24) of computation. So let us try to go back to the approach based on P-invariants RT of this uncontrolled PN model has 40 nodes (including the initial marking). There is only one deadlock ${\mathbf{M}}_{17}={(4, 1, 0, 0, 0, 2, 1, 1, 0, 0, 0, 0, 2, 3, 1, 3, 4, 4)}^T$, as we can see from the segment of RT displayed in Figure 12.

Let us try to find these paths in order to built the conditions necessary to the supervisor synthesis. As we can see in Figure 12,

$$\begin{array}{ccc}& & {\mathbf{M}}_{10}\stackrel{t_7}{⟶}{\mathbf{M}}_{17}\hfill \end{array}$$

(49)

$$\begin{array}{ccc}& & {\mathbf{M}}_4\stackrel{t_8}{⟶}{\mathbf{M}}_{10}\stackrel{t_7}{⟶}{\mathbf{M}}_{17}\hfill \end{array}$$

(50)

$$\begin{array}{ccc}& & {\mathbf{M}}_5\stackrel{t_1}{⟶}{\mathbf{M}}_{10}\stackrel{t_7}{⟶}{\mathbf{M}}_{17}\hfill \end{array}$$

(51)

$$\begin{array}{ccc}& & {\mathbf{M}}_5\stackrel{t_7}{⟶}{\mathbf{M}}_{11}\stackrel{t_1}{⟶}{\mathbf{M}}_{17}\hfill \end{array}$$

(52)

$$\begin{array}{ccc}& & {\mathbf{M}}_{27}\stackrel{t_7}{⟶}{\mathbf{M}}_{34}\stackrel{t_4}{⟶}{\mathbf{M}}_{17}\hfill \end{array}$$

(53)

Here,

$$\begin{array}{c}\hfill {\mathbf{M}}_4={(4, 1, 0, 0, 0, 3, 1, 0, 0, 0, 1, 0, 2, 3, 1, 3, 3, 3)}^T\end{array}$$

(54)

$$\begin{array}{c}\hfill {\mathbf{M}}_5={(5, 0, 0, 0, 0, 3, 0, 1, 0, 1, 0, 1, 3, 4, 1, 3, 4, 3)}^T\end{array}$$

(55)

$$\begin{array}{c}\hfill {\mathbf{M}}_{10}={(4, 1, 0, 0, 0, 3, 0, 1, 0, 0, 0, 1, 3, 3, 1, 3, 4, 3)}^T\end{array}$$

(56)

$$\begin{array}{c}\hfill {\mathbf{M}}_{11}={(5, 0, 0, 0, 0, 2, 1, 1, 0, 1, 0, 0, 2, 4, 1, 3, 4, 4)}^T\end{array}$$

(57)

$$\begin{array}{c}\hfill {\mathbf{M}}_{27}={(3, 1, 0, 1, 0, 3, 0, 1, 0, 0, 0, 1, 2, 3, 0, 2, 4, 3)}^T\end{array}$$

(58)

$$\begin{array}{c}\hfill {\mathbf{M}}_{34}={(3, 1, 0, 1, 0, 2, 1, 1, 0, 0, 0, 0, 1, 3, 0, 2, 4, 4)}^T\end{array}$$

(59)

After a short analysis of RT, we can set the constraints in the form:

$$\begin{array}{c}\hfill p_7+p_{11}<=2\end{array}$$

(60)

$$\begin{array}{c}\hfill p_7+p_{18}<=3\end{array}$$

(61)

$$\begin{array}{c}\hfill p_2+p_7<=1\end{array}$$

(62)

It means that

$$\mathbf{L}=\left(\begin{array}{cccccccccccccccccc}0& 0& 0& 0& 0& 0& 1& 0& 0& 0& 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1\\ 0& 1& 0& 0& 0& 0& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right); \mathbf{b}=\left(\begin{array}{c}2\\ 3\\ 1\end{array}\right)$$

(63)

$$\begin{array}{ccc}\hfill {\mathbf{N}}_s& =& -\mathbf{L}.\mathbf{N}=\left(\begin{array}{cccccccccc}\hfill 0& \hfill 1& \hfill -1& \hfill 0& \hfill -1& \hfill 0& \hfill -1& \hfill 2& \hfill -1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -2& \hfill 1& \hfill 1& \hfill 0\\ \hfill -1& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 1& \hfill 0& \hfill 0\end{array}\right)\hfill \end{array}$$

(64)

$$\begin{array}{ccc}\hfill {}^s{\mathbf{M}}_0& =& \mathbf{b}-\mathbf{L}.{\mathbf{M}}_0=\left(\begin{array}{c}\hfill 1\\ \hfill 1\\ \hfill 1\end{array}\right)\hfill \end{array}$$

(65)

Such supervisor indeed prevents the deadlock but RT of the supervised system has only 16 nodes. It means that its state space is (in comparison with the state space of uncontrolled system having RT with 40 nodes) considerably limited. Unfortunately, the right section (sub-net) in Figure 11 consisting of $p_6, p_7, p_8, p_9, p_{17}, p_{18}$ does not operate because it is eliminated by such supervisor.

Therefore, we have to find another supervisor which will be able to connect also this section in the activity. Consider the following constraints

$$\begin{array}{c}\hfill p_2+p_7+p_8+p_9\le 1\end{array}$$

(66)

$$\begin{array}{c}\hfill p_2+p_3+p_7+p_8\le 1\end{array}$$

(67)

$$\begin{array}{c}\hfill p_2+p_3+p_5+p_7\le 1\end{array}$$

(68)

$$\begin{array}{c}\hfill p_2+p_3+p_4+p_7\le 3\end{array}$$

(69)

$$\begin{array}{c}\hfill p_2+p_3\le 4\end{array}$$

(70)

$$\begin{array}{c}\hfill p_2+p_3+p_4\le 1\end{array}$$

(71)

$$\begin{array}{c}\hfill p_2+p_3+p_4+p_5\le 3\end{array}$$

(72)

$$\begin{array}{c}\hfill p_7+p_8+p_9\le 3\end{array}$$

(73)

$$\begin{array}{c}\hfill p_7+p_8\le 2\end{array}$$

(74)

or in the matrix form

$$\mathbf{L}=\left(\begin{array}{cccccccccccccccccc}0& 1& 0& 0& 0& 0& 1& 1& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 1& 0& 0& 0& 1& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 1& 0& 1& 0& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 1& 1& 0& 0& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 1& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 1& 1& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 1& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right); \mathbf{b}=\left(\begin{array}{c}1\\ 1\\ 1\\ 3\\ 4\\ 1\\ 3\\ 3\\ 2\end{array}\right)$$

(75)

$${\mathbf{N}}_s=-\mathbf{L}.\mathbf{N}=\left(\begin{array}{cccccccccc}\hfill -1& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 0& \hfill 0& \hfill 1\\ \hfill -1& \hfill 0& \hfill 1& \hfill 0& \hfill 1& \hfill 0& \hfill -1& \hfill 0& \hfill 1& \hfill 0\\ \hfill -1& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 1& \hfill 0& \hfill 0\\ \hfill -1& \hfill 0& \hfill 0& \hfill 1& \hfill 1& \hfill 0& \hfill -1& \hfill 1& \hfill 0& \hfill 0\\ \hfill -1& \hfill 0& \hfill 1& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill -1& \hfill 0& \hfill 0& \hfill 1& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill -1& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 0& \hfill 0& \hfill 1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 0& \hfill 1& \hfill 0\end{array}\right); {}^s{\mathbf{M}}_0=\mathbf{b}-\mathbf{L}.{\mathbf{M}}_0=\left(\begin{array}{c}\hfill 1\\ \hfill 1\\ \hfill 1\\ \hfill 3\\ \hfill 4\\ \hfill 1\\ \hfill 3\\ \hfill 3\\ \hfill 2\end{array}\right)$$

(76)

Applying the supervisor to the uncontrolled PN we obtain the controlled model without any deadlocks. Its RT, expressing the space of reachable states, has 11 nodes as it can be seen in Figure 13. In the same Figure right is displayed also the supervisor consisting of 9 monitors. As we can see, both of the sections (sub-nets) are active in this case.

6. Discussion

Two methods (approaches) how to avoid deadlocks in industrial multi-agent systems were presented in this paper, namely: (i) the approach based on P-invariants, and (ii) the approach based on siphons and traps. Let us compare them now.

Both approaches have their advantages and disadvantages.

The former approach represents the procedure in exact analytical terms. The supervisor synthesis is clear and simple. It is suitable especially for the S³PR paradigm of AMS. Thorough analysis of RT makes possible to find conditions how to mutually eliminate certain states (markings). In such a way it is possible to eliminate deadlocks. However, in a more complicated structure of the PN model with very branched RT the choice of the restriction inequality (5) (especially the matrix $\mathbf{L}$ and the vector $\mathbf{b}$) may be intricate or even impossible. Another disadvantage is that RT depends on the initial marking ${\mathbf{M}}_0$ of the uncontrolled PN. For another ${\mathbf{M}}_0$ RT is different.

The latter approach has not so exact analytically expressed procedure. This is due to the fact that siphons and traps are structural entities of the PN model. Their computation (notwithstanding that it may be realized by different algorithms) may sometimes take a very long time, especially in case of structurally complicated PN models. An advantage of this approach is that calculation of siphons and traps does not depend on the initial state of the PN model. This approach is able to deal with both paradigms of AMS—S³PR and S⁴PR.

As a summary it can be said that the weak point (shortcoming, weakness) in both approaches is computational complexity—at computing RT and handling it as well as at computation of siphons and traps—especially at large-scale and structurally complicated PN models.

Despite what has been said, the approach based on siphons and traps seems to be upon the whole more advantageous than the approach based on P-invariants. Apart from the time-consuming calculation of siphons and traps, it is also simpler. However, as it was demonstrated by the Example 6 in the Section 5.4, computational problems may be huge also in relatively simple and not very large PN models.

7. Conclusions

The presented paper is, in a broader sense, an overview paper concerning the deadlock prevention and avoidance in industrial MAS in general. RAS are very important subclass of AMS. Dealing with deadlocks in RAS has been the main topic of this paper. Benefits following from this are that deadlock free RAS can be designed off-line, preliminary to the construction of real manufacturing systems, still before their actual deployment in practice. Hence, this rapidly decreases a risk of defects in operation of AMS/RAS and prevents shutdowns of them. Thus, it is possible to avoid significant economic losses. Of course, another defects unrelated to deadlocks (e.g., some external disturbances) cannot be prevented in such a way. Attention has been paid to the present most frequently used RAS, in particular to their paradigms S³PR and S⁴PR.

A wide review of literature was introduced. A general view on formal methods used in AMS was presented in Section 1.1. A short comment about the agent cooperation and negotiation, as well as on reentering in AMS was introduced in Section 1.2. The most used Petri net-based paradigms of RAS were adduced in Section 2.1. A literature overview about deadlock prevention and avoiding was referred to in Section 2.2. Setting marking of monitors in case of the siphon-based method was described in details in Section 4.2. Two simple illustration examples introduced in Section 3 (Example 1) and in Section 4 (Example 2) were supplemented by four more complicated illustrative examples in Section 5 (Example 3–Example 6).

Two basic deadlock prevention techniques using Petri nets were presented in mathematical details, namely P-invariant-based method and the method based on siphons and traps. Although in Section 6 a rough comparison of both methods was introduced, in this closing section it is necessary to point out the principled difference between them. In

Table 1. Characteristics of both methods.

P-Invariant-Based Method	Siphon and Trap-Based Method
simple analytic method	Matlab-based computational method
it needs additional elaboration of RT	it does need any additional elaboration
it is more labored	—
it has analytical setting of the initial marking of monitors	it needs additional setting of the initial marking of monitors
—	it yields a possibility to control elementary siphons and to deal with dependent siphons by means of setting the siphon control depth variables
it is suitable above all for S3PR paradigm of AMS	it is suitable for S3PR as well as for S4PR paradigms of AMS
in the S4PR paradigm it cannot eliminate the origin of new deadlocks and requires new iterations of the deadlock prevention	it is able to preclude origin of new deadlocks in the S4PR paradigm

, the main characteristics of both methods are introduced. The ability to address the deadlock prevention in the S³PR and S⁴PR paradigms of RAS is also included there. After comparing those characteristics, the method based on siphons and traps unambiguously appears more advantageous than the method based on P-invariants. The same result follows also from

Table 2. Disadvantageous of both methods.

P-Invariant-Based Method	Siphon and Trap-Based Method
possible computational problems at finding RT	often long lasting computation of siphons
necessity to additionally analyze RT	—
dependence on the initial state of the PN model	—

(where disadvantageous of both methods are introduced) because long lasting computations can be accelerated, e.g., by using more powerful computing technique and/or by finding algorithms with a less computational complexity.

However, in spite of all, it must be said that even the method based on P-invariants should not be completely damned, especially in case of S³PR paradigm of AMS. As it was shown in Example 6 in the Section 5.4 this method has helped us to resolve a case where the siphon-based method was not able to give a result in a reasonable time.