Collaborative Storage and Resolution Method between Layers in Hierarchical ICN Name Resolution Systems
Abstract
1. Introduction
1.1. Name Resolution Systems in ICN
1.2. Collaborative Storage and Resolution Methods
- We analyze latency constraints required for inter-layer collaborative storage and resolution under the constraint of a deterministic service latency feature, and define the nodes that satisfy the above constraints as index neighbors. Then we propose an index neighbor construction method based on the MK-Mediod algorithm.
- We propose the collaborative storage and resolution method based on index neighbor structure, and conduct experiments to compare the latency measurement cost and computation cost of our index neighbor construction algorithm against several other approaches. Meanwhile, experiments are also conducted to compare the increase of total storage load and service latency when the constructed index neighbor structure is used to implement collaborative storage and resolution.
2. Materials and Methods
- A resolution node provides a name resolution service with deterministic service latency only to users in its service area.
- A user in the service area of a child node must also be in the service area of its parent node, a user in the service area of the parent node must also be in the service area of a particular child node of this parent node.
- Deterministic service latency value of name resolution nodes in the same level is the same, while the deterministic service latency value of high-level name resolution nodes is larger than that of low-level name resolution nodes.
2.1. System Model
2.2. Problem Statement
2.3. Collaborative Storage and Resolution Method with Index Neighbor Structure
2.3.1. Existence of Index Neighbor
| Algorithm 1: Index Neighbor Existence Validation |
Input: master node , child nodes , , Output: validation result |
 |
2.3.2. Index Neighbor Construction with MK-Mediod
MK-Mediod Algorithm
Index Neighbor Structure Construction Based on MK-Mediod Algorithm
2.3.3. Collaborative Storage and Resolution based on Index Neighbor Structure
| Algorithm 2: MK-Mediod-based index neighbor construction |
Input: master node , child nodes , , |
Output: index neighbor groups |
 |
| Algorithm 3: Collaborative Storage |
Input: master node , index neighbors set , mapping items for co-storage |
 |
| Algorithm 4: Collaborative Resolution |
Input: master node , name in the resolution request , user for this resolution request |
 |
3. Evaluation and Discussion
3.1. Experimental Setup
3.2. Construction of Index Neighbor Structure
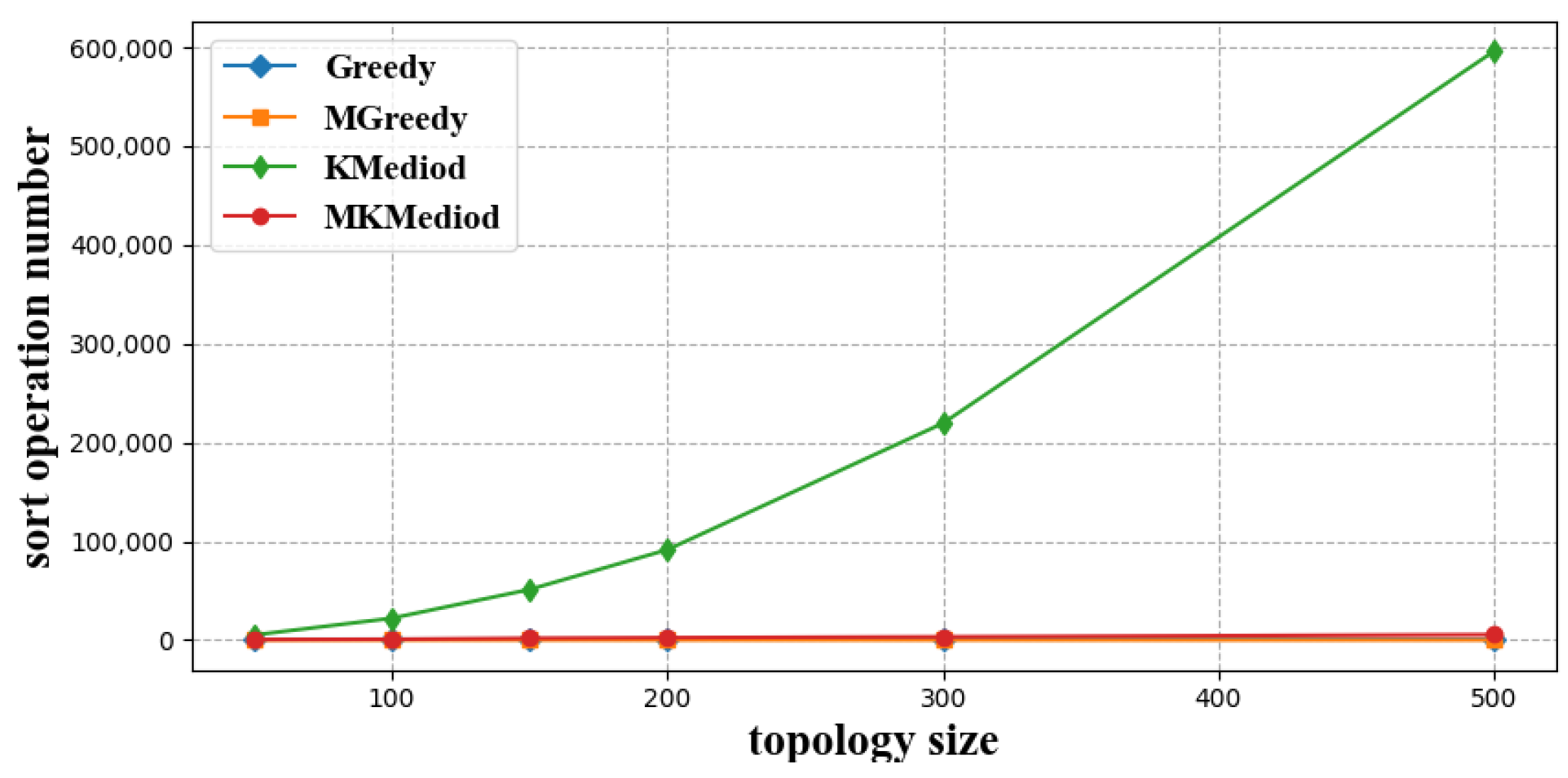
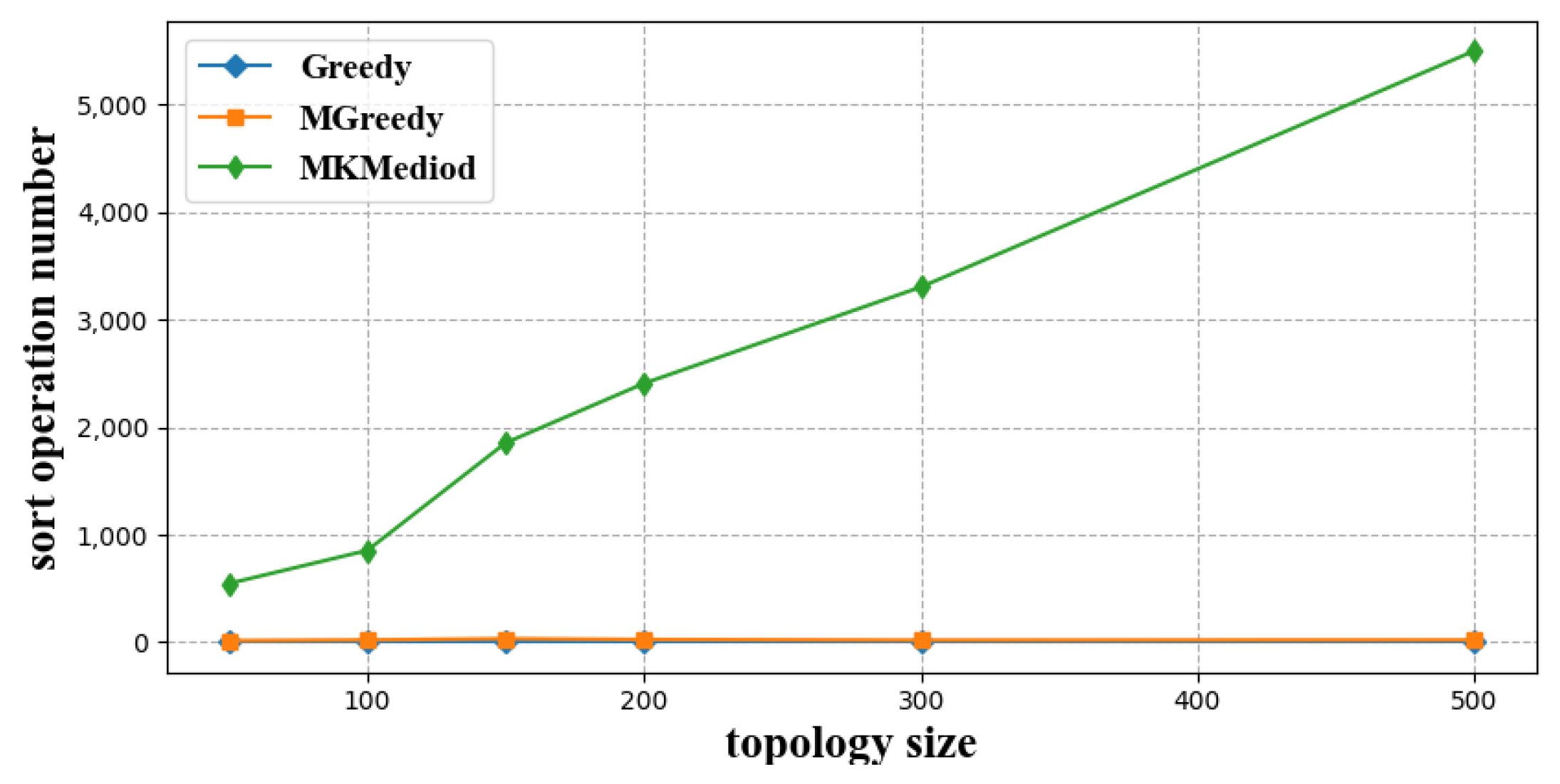
- Greedy algorithm [32]: This algorithm traverses each child node, uses the traversed child nodes to form an index neighbor group and tries to pull the rest of the child nodes into the group, this procedure is performed recursively until every child node resides in an index neighbor group.
- Modified Greedy algorithm: Different from the Greedy algorithm, this algorithm firstly sorts the child nodes by latency to the master node, and then greedily constructs index neighbor groups in the same manner with the Greedy algorithm in decent order of latency to the master node.
- K-Mediod algorithm [33]: Like our proposed MK-Mediod algorithm, this algorithm clusters the child nodes according to their latency to each other, and validates whether the clustering results meet the latency constraints defined by index neighbor groups. Clustering number increases one by one until a feasible resolution is found.
3.2.1. Latency Measure Times
3.2.2. Computation Cost
3.3. Collaborative Storage and Resolution
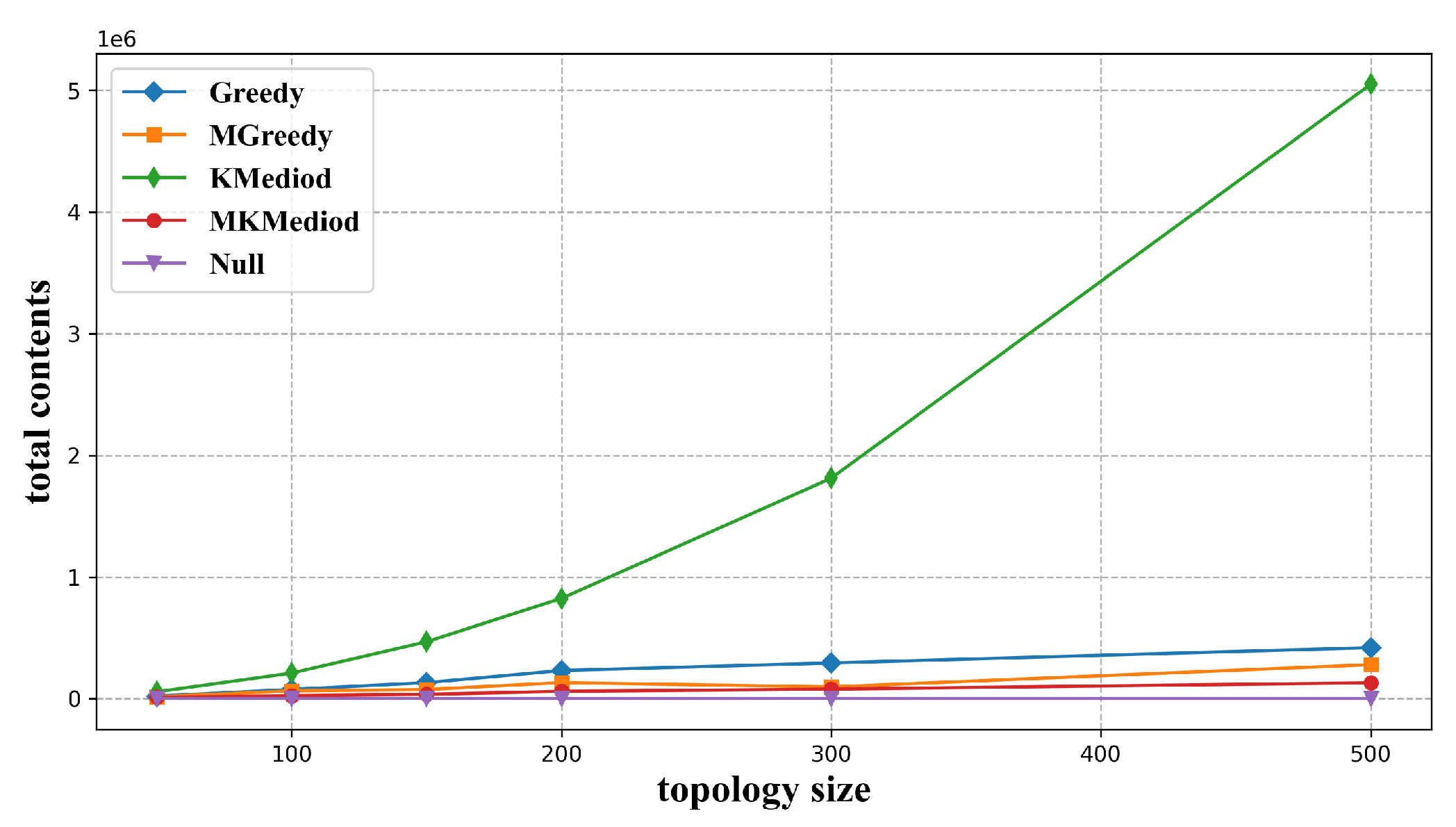
3.3.1. Total Storage Load
- (a)
- Impact of number of resolution nodes
- (b)
- Impact of numbers of mapping records for co-storage
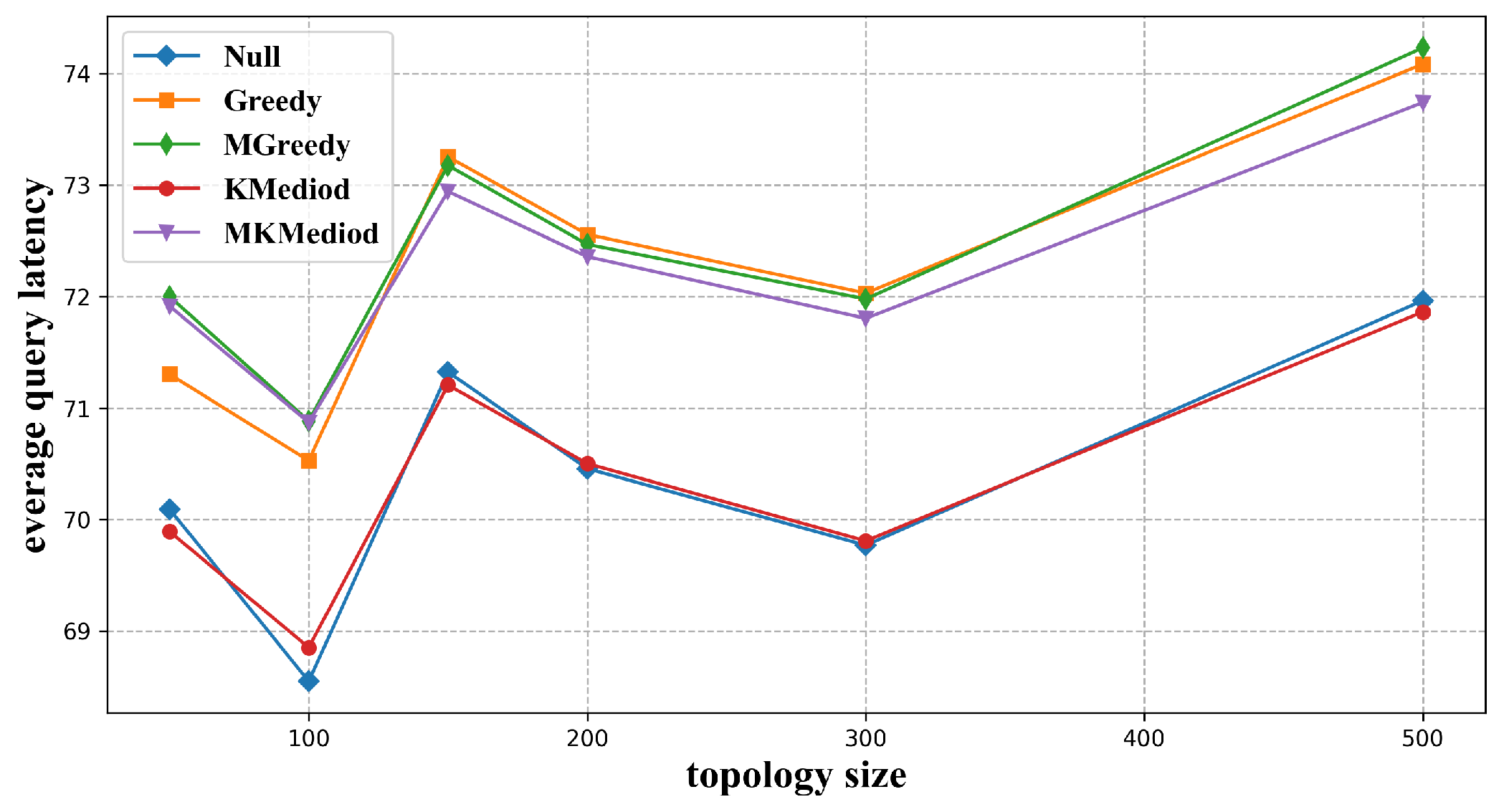
3.3.2. Average Service Latency and Maximum Service Latency
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huang, T.; Liu, J.; Wang, S.; Zhang, C.; Liu, R.J. Survey of the future network technology and trend. J. Commun. 2021, 42, 130–150. [Google Scholar]
- Ravindran, R.; Suthar, P.; Chakraborti, A.; Amin, S.O.; Azgin, A.; Wang, G. Deploying ICN in 3GPP’s 5G NextGen Core Architecture. In Proceedings of the 2018 IEEE 5G World Forum (5GWF), Santa Clara, CA, USA, 9–11 July 2018; pp. 26–32. [Google Scholar]
- Menth, M.; Hartmann, M.; Klein, D. Global locator, local locator, and identifier split (GLI-Split). Future Internet 2013, 5, 67–94. [Google Scholar] [CrossRef]
- Albalawi, A.; Garcia-Luna-Aceves, J.J. Named-Data Transport: An End-to-End Approach for an Information-Centric IP Internet. In Proceedings of the 7th ACM Conference on Information-Centric Networking, Online, 29 September–1 October 2020; pp. 136–148. [Google Scholar]
- Shannigrahi, S.; Fan, C.; Partridge, C. What’s in a Name?: Naming Big Science Data in Named Data Networking. In Proceedings of the 7th ACM Conference on Information-Centric Networking, Online, 29 September–1 October 2020; pp. 77–88. [Google Scholar]
- Handley, M. Why the Internet only just works. BT Technol. J. 2006, 24, 119–129. [Google Scholar] [CrossRef]
- Feldmann, A. Internet clean-slate design: What and why? ACM SIGCOMM Comput. Commun. Rev. 2007, 37, 59–64. [Google Scholar] [CrossRef]
- Parvez, I.; Rahmati, A.; Guvenc, I.; Sarwat, A.I.; Dai, H. A survey on low latency towards 5G: RAN, core network and caching solutions. IEEE Commun. Surv. Tutor. 2018, 20, 3098–3130. [Google Scholar] [CrossRef]
- Nasrallah, A.; Thyagaturu, A.S.; Alharbi, Z.; Wang, C.; Shao, X.; Reisslein, M.; ElBakoury, H. Ultra-low latency (ULL) networks: The IEEE TSN and IETF DetNet standards and related 5G ULL research. IEEE Commun. Surv. Tutorials 2019, 21, 88–145. [Google Scholar] [CrossRef]
- ITU Web Site. Available online: https://www.itu.int/en/ITU-T/focusgroups/net2030/Documents/White_Paper.pdf (accessed on 15 October 2022).
- Liu, H.; Azhandeh, K.; de Foy, X.; Gazda, R. A comparative study of name resolution and routing mechanisms in information-centric networks. Digit. Commun. Netw. 2019, 5, 69–75. [Google Scholar] [CrossRef]
- Barakabitze, A.A.; Xiaoheng, T.; Tan, G. A Survey on Naming, Name Resolution and Data Routing in Information Centric Networking (ICN). Int. J. Adv. Res. Comput. Commun. Eng. 2014, 3, 8322–8330. [Google Scholar] [CrossRef]
- Xylomenos, G.; Ververidis, C.N.; Siris, V.A.; Fotiou, N.; Tsilopoulos, C.; Vasilakos, X.; Katsaros, K.V.; Polyzos, G.C. A survey of information-centric networking research. IEEE Commun. Surv. Tutor. 2014, 16, 1024–1049. [Google Scholar] [CrossRef]
- Mathy, L.; Iannone, L. LISP-DHT: Towards a DHT to map identifiers onto locators. In Proceedings of the 2008 ACM CoNEXT Conference—4th International Conference on Emerging Networking EXperiments and Technologies, Madrid, Spain, 9–12 December 2008; pp. 1–6. [Google Scholar]
- Stoica, I.; Morris, R.; Karger, D.; Kaashoek, M.F.; Balakrishnan, H. Chord: A scalable peer-to-peer lookup service for internet applications. ACM SIGCOMM Comput. Commun. Rev. 2001, 31, 149–160. [Google Scholar] [CrossRef]
- Wang, P.; Lan, J.; Hu, Y.; Chen, S. Towards locality-aware DHT for fast mapping service in future Internet. Comput. Commun. 2015, 66, 14–24. [Google Scholar] [CrossRef]
- Hong, J.; Chun, W.; Jung, H. Demonstrating a scalable name resolution system for information-centric networking. In Proceedings of the ICN 2015—2nd International Conference on Information-Centric Networking, San Francisco, CA, USA, 30 September–2 October 2015; pp. 221–222. [Google Scholar]
- Wang, J.; Chen, G.; You, J.; Sun, P. SEANet: Architecture and Technologies of an On-site, Elastic, Autonomous Network. Netw. New Media 2020, 6, 1–8. [Google Scholar]
- Xie, W.; You, J.; Wang, J. A Tree Structure Protocol for Hierarchical Deterministic Latency Name Resolution System. Electronics 2022, 11, 2425. [Google Scholar] [CrossRef]
- TU-T Y. ICN-NMR Framework of Locally Enhanced Name Mapping and Resolution for Information Centric Networking in IMT-2020. Available online: https://www.itu.int/md/T17-SG13-C-1319/ (accessed on 15 October 2022).
- ITU Web Site. Requirements and Capabilities of Name Mapping and Resolution for Information Centric Networking in IMT-2020. Available online: https://www.itu.int/itu-t/recommendations/rec.aspx?rec=13890 (accessed on 15 October 2022).
- Luo, H.; Qin, Y.; Zhang, H. A DHT-based identifier-to-locator mapping approach for a scalable Internet. IEEE Trans. Parallel Distrib. Syst. 2009, 20, 1790–1802. [Google Scholar]
- Fuller, V.; Farinacci, D.; Meyer, D. LISP Alternative Topology (LISP+ALT). Available online: http://tools.ietf.org/id/draft-ietf-lisp-alt-10.txt (accessed on 15 October 2022).
- Dannewitz, C.; Kutscher, D.; Ohlman, B.; Farrell, S.; Ahlgren, B.; Karl, H. Network of information (NetInf)-An information-centric networking architecture. Comput. Commun. 2013, 36, 721–735. [Google Scholar] [CrossRef]
- Rajahalme, J.; Särelä, M.; Visala, K.; Riihijärvi, J. On name-based inter-domain routing. Comput. Netw. 2011, 55, 975–986. [Google Scholar] [CrossRef]
- Koponen, T.; Chawla, M.; Chun, B.G.; Ermolinskiy, A.; Kim, K.H.; Shenker, S.; Stoica, I. A data-oriented (and Beyond) network architecture. Comput. Commun. Rev. 2007, 37, 181–192. [Google Scholar] [CrossRef]
- Louati, W.; Ben-Ameur, W.; Zeghlache, D. A bottleneck-free tree-based name resolution system for Information-Centric Networking. Comput. Netw. 2015, 91, 341–355. [Google Scholar] [CrossRef]
- D’Ambrosio, M.; Dannewitz, C.; Karl, H.; Vercellone, V. MDHT: A hierarchical name resolution service for information-centric networks. In Proceedings of the ACM SIGCOMM Workshop on Information-Centric Networking, Toronto, ON, Canada, 15–19 August 2011. [Google Scholar]
- Dannewitz, C.; D’Ambrosio, M.; Vercellone, V. Hierarchical DHT-based name resolution for information-centric networks. Comput. Commun. 2013, 36, 736–749. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Sun, P.; Jiaqi, L.I. System for Providing Exact Communication Delay Guarantee of Request Response for Distributed Service. CN Patent 201910897838.8, 23 September 2021. [Google Scholar]
- Li, J.; Sheng, Y.; Deng, H. Two Optimization Algorithms for Name-Resolution Server Placement in Information-Centric Networking. Appl. Sci. 2020, 10, 3588. [Google Scholar] [CrossRef]
- Orenshtein, T.; Shinkar, I. Greedy Random Walk. Comb. Probab. Comput. 2014, 23, 269–289. [Google Scholar] [CrossRef]
- Chu, S.C.; Roddick, J.; Pan, J.S. A comparative study and extensions to k-medoids algorithms. In Proceedings of the Fifth International Conference on Optimization: Techniques and Applications, Hong Kong, China, 15–17 December 2001. [Google Scholar]





| Parameter | Value |
|---|---|
| Number of resolution nodes | 50/100/150/200/300/500 |
| Deterministic latency parameters | 50 ms, 25 ms |
| Latency scope from master node to nodes in level 2 | [0.5 ms, 25 ms) |
| Latency scope among child nodes | [5 ms, 30 ms) |
| Total number of contents | 100*(number of resolution nodes) |
| Ratio of contents to be co-stored | 2%/5%/10%/20% |
| Contents for resolution | all of the contents on master node |
| Latency scope from master node to users | [25 ms, 50 ms) |
| Latency scope from resolution nodes in level 2 to users | [0.5 ms, 25 ms) |
| 2% | 5% | 10% | 20% | |
|---|---|---|---|---|
| Null | 100,000 | 100,000 | 100,000 | 100,000 |
| MK-Mediod | 108,000 | 120,000 | 140,000 | 180,000 |
| MGreedy | 114,000 | 135,000 | 170,000 | 240,000 |
| Greedy | 198,000 | 255,000 | 590,000 | 1,080,000 |
| K-Mediod | 1,100,000 | 2,600,000 | 5,100,000 | 10,100,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, Y. Collaborative Storage and Resolution Method between Layers in Hierarchical ICN Name Resolution Systems. Future Internet 2023, 15, 74. https://doi.org/10.3390/fi15020074
Li Y, Li Y. Collaborative Storage and Resolution Method between Layers in Hierarchical ICN Name Resolution Systems. Future Internet. 2023; 15(2):74. https://doi.org/10.3390/fi15020074
Chicago/Turabian StyleLi, Yanxia, and Yang Li. 2023. "Collaborative Storage and Resolution Method between Layers in Hierarchical ICN Name Resolution Systems" Future Internet 15, no. 2: 74. https://doi.org/10.3390/fi15020074
APA StyleLi, Y., & Li, Y. (2023). Collaborative Storage and Resolution Method between Layers in Hierarchical ICN Name Resolution Systems. Future Internet, 15(2), 74. https://doi.org/10.3390/fi15020074




