MSEN: A Multi-Scale Evolutionary Network for Modeling the Evolution of Temporal Knowledge Graphs

Abstract

Temporal knowledge graphs play an increasingly prominent role in scenarios such as social networks, finance, and smart cities. As such, research on temporal knowledge graphs continues to deepen. In particular, research on temporal knowledge graph reasoning holds great significance, as it can provide abundant knowledge for downstream tasks such as question answering and recommendation systems. Current reasoning research focuses primarily on interpolation and extrapolation. Extrapolation research aims to predict the likelihood of events occurring in future timestamps. Historical events are crucial for predicting future events. However, existing models struggle to fully capture the evolutionary characteristics of historical knowledge graphs. This paper proposes a multi-scale evolutionary network (MSEN) model that leverages Hierarchical Transfer aware Graph Neural Network (HT-GNN) in a local memory encoder to aggregate rich structural semantics from each timestamp’s knowledge graph. It also utilizes Time Related Graph Neural Network (TR-GNN) in a global memory encoder to model temporal-semantic dependencies of entities across the global knowledge graph, mining global evolutionary patterns. The model integrates information from both encoders to generate entity embeddings for predicting future events. The proposed MSEN model demonstrates strong performance compared to several baselines on typical benchmark datasets. Results show MSEN achieves the highest prediction accuracy.

1. Introduction

Temporal knowledge graphs (TKGs) are a type of dynamic knowledge structure in which knowledge may change over time. Compared with traditional static knowledge graphs, TKGs take into account the influence of the time dimension. TKGs with multiple timestamps can be represented as a series of knowledge graph (KG) snapshots, where each snapshot contains all facts within the same timestamp.

For static knowledge graph completion, methods such as DiSMult [1], ComplEx [2], RGCN [3], ConvE [4], and RotatE [5] have been proposed. TKG reasoning tasks can perform temporal reasoning and evolution analysis of knowledge, mainly divided into interpolation and extrapolation [6]. Interpolation is to complete missing events based on existing facts; extrapolation is to predict future events based on past events. Predicting future events based on the evolution of historical knowledge graphs is very important and challenging. Obtaining possible future events in a timely manner based on temporal relations can support applications such as financial risk control, disaster relief, etc.

This paper focuses on extrapolation research. The challenge of this task is how to better obtain relevant historical information that can reflect future behaviors. Currently, there are two methods that can be used for TKG extrapolation, namely, query-specific and entire graph-based methods [7]. The former includes RE-NET [6], CyGNet [8], xERTE [9], TITer [10], CENET [11], etc., using high-frequency historical facts related to a query’s topics and relations to predict future trend, ignoring structural dependencies within snapshot; the latter includes RE-GCN [12], CEN 7, TANGO [13], TiRGN [14], L2TKG [15], etc., using historical knowledge graph as input to obtain the evolutionary patterns of TKG.

The above two methods do not consider the historical features from different perspectives, ignoring potentially useful information. Relying solely on either local or global knowledge graphs may result in information loss, affecting prediction results. However, future events may depend on both local structural dependencies and global temporal patterns. Historical knowledge from varying perspectives likely influences future occurrences to differing degrees.

In this work, we propose a model to capture multi-scale evolutionary features of historical information, called Multi-Scale Evolutionary Network (MSEN). Typically, different features manifest at different scales, providing diverse semantic information. The local memory focuses on contextual knowledge, while the global memory recalls long-range patterns. By integrating both scales, MSEN can better model TKG evolution for reasoning.

The main contributions are:

(1)

In the local memory encoder, a hierarchical transfer aware graph neural network (HT-GNN) is proposed to enriches structural semantics within each timestamp;

(2)

In the global memory encoder, a time related graph neural network (TR-GNN) is proposed to extract periodic and non-periodic temporal patterns globally across timestamps;

(3)

Through experiments on typical event-based datasets, the paper demonstrates the effectiveness of our proposed model MSEN.

2. Related Work

In this section, this paper reviews the existing methods for TKG Reasoning under the interpolation setting and the extrapolation setting, and summarizes the methods for event prediction.

2.1. TKG Reasoning under the Interpolation Setting

For the interpolation setting, models try to complete missing facts in the past timestamps. TTransE [16], TA-TransE [17], and TA-DistMult [17] embed temporal information into scoring functions and relations, respectively, to obtain the evolution information of facts; HyTE [18] proposes a time-aware model based on hyperplanes, and projects entities and subgraphs onto specific hyperplanes; TNTComplEx [19] introduces complex numbers to factorize a fourth-order tensor to generate timestamp embeddings. DE-SimplE [20] accomplishes the task of knowledge graph completion by making feature representations of temporal information; ChronoR [21] captures the rich interactions between time and multi-relational features in knowledge graphs by learning embeddings of entities, relations, and time; TempCaps [22] is a capsule network model that uses information retrieved through dynamic routing to construct entity embeddings. TKGC [23] maps entities and relations in TKG to multivariate Gaussian processes, thereby simulating overall and local trends. However, these models cannot obtain embeddings of future events.

2.2. TKG Reasoning under the Extrapolation Setting

Recently, several studies have attempted to infer future events, and existing methods can be divided into two categories: query-specific and entire graph-based methods [7] They all use historical information to predict future trends.

2.2.1. Query-Specific Models

The methods focus on obtaining historical information of a specific query. GHNN [24] predicts the occurrence of future events through obtaining the dynamic sequence of evolving graphs; xERTE [9] uses iterative sampling and attention propagation techniques to extract closed subgraphs around specific queries. Both CluSTeR [25] and TITer [10] are based on reinforcement learning to discover paths for specific queries in the historical KG; RE-NET [6] can effectively extract sequential and structural information related to a specific query in the TKG to solve the entity prediction task for a given query, but cannot model long-term KG information; CyGNet [8] combines two reasoning modes, copy mode and generation mode, making predictions based on repeated entities in the historical vocabulary or the entire entity vocabulary, but ignores higher-order semantic dependencies between co-occurring entities; CENET [11] proposes a novel historical comparative learning approach for knowledge graph reasoning that uses temporal reasoning patterns mined from historical knowledge graph versions to make more accurate predictions.

2.2.2. Entire Graph-Based Models

The methods focus on obtaining the history of the latest KG of fixed length. Glean [26] introduces unstructured event description information to enrich entity representations, but description information is not available for all events in real applications; TANGO [13] extends neural ordinary differential equations to multi-relational graph convolutional networks to model structural information, but the model’s utilization of long-distance information is still limited; RE-GCN [12] and CEN [7] both model the evolution of representations of all entities by capturing fixed-length historical information, but neither of these two models considers the evolutionary features of historical information from different perspectives; TiRGN [14] introduces a new recurrent graph network model that incorporates local and global historical patterns in temporal knowledge graphs to improve the accuracy of link prediction over time.

Some recent works have incorporated both local and global modeling for TKG reasoning. However, MSEN proposes new designs for each module and their integration, achieving better results. The hierarchical design in the local module enriches semantic learning, while the periodic and aperiodic temporal modeling in the global module improves temporal encoding.

3. The Proposed Method

In this section, this paper mainly introduces Temporal Knowledge Graph (TKG) Reasoning under the extrapolation setting and the proposed method.

Table 1. Important Symbols.

Symbol	Explanation
${\mathrm{G}}_{\mathrm{n}}$	KG at timestamp n
$\mathsf{{\rm E}},\mathrm{R}$	The set of entities, relations
${\mathsf{\Gamma }}_{\mathrm{t}}$	The set of facts at timestamp t
${\mathrm{h}}_{\mathrm{s},\mathrm{t}},{\mathrm{h}}_{\mathrm{r},\mathrm{t}}$	Embedding representation of entity s, relation r at timestamp t
${\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{e}\mathrm{n}\mathrm{t}}\right)}^{\mathrm{l}}$	Embedding representation of entity o at l-th layer
${\mathrm{H}}_{\mathrm{t}},{\mathrm{R}}_{\mathrm{t}}$	The set of entity embedding, relation embedding at time t
${\mathrm{T}}^{\mathrm{p}},{\mathrm{T}}^{\mathrm{a}\mathrm{p}}$	The periodic time vector, the non-periodic time vector
${\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}},{\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}$	Global memory embeddings, local memory embeddings

shows some of the important symbols of the paper and the corresponding explanations.

3.1. Problem Formulation

A TKG $\mathrm{G}=\{{\mathrm{G}}_0,{\mathrm{G}}_1,{\mathrm{G}}_2,{\mathrm{G}}_3,\cdots {\mathrm{G}}_{\mathrm{n}}\}$ is a KG sequence. In each KG, ${\mathrm{G}}_{\mathrm{t}}=\{\mathsf{{\rm E}},\mathrm{R},{\mathsf{\Gamma }}_{\mathrm{t}}\}$ is a directed multi-relational graph, where Ε is the set of entities; $\mathrm{R}$ is the set of relations; ${\mathsf{\Gamma }}_{\mathrm{t}}$ is the set of facts at timestamp t. A fact in ${\mathsf{\Gamma }}_{\mathrm{t}}$ can be expressed as a quaternion (s,r,o,t), where $\mathrm{s},\mathrm{o}\in \mathrm{E}$ and $\mathrm{r}\in \mathrm{R}$. The goal of the TKG entity reasoning task is to complete tail entity prediction (s,r,?,${\mathrm{t}}_{\mathrm{m}}$) or head entity prediction (?,r,o,${\mathrm{t}}_{\mathrm{m}}$) based on the historical knowledge graph sequence $\{{\mathrm{G}}_0,{\mathrm{G}}_1,{\mathrm{G}}_2,{\mathrm{G}}_3,\cdots {\mathrm{G}}_{{\mathrm{t}}_{\mathrm{m}}-1}\}$. For each quaternion (s,r,o,t), an inverse quaternion $(\mathrm{o},{\mathrm{r}}^{-1},\mathrm{s},\mathrm{t})$ is added to the KG. Therefore, the prediction of head entity (?,r,o,$\mathrm{t}$) can be transformed into the prediction of tail entity ($\mathrm{o},{\mathrm{r}}^{-1},?,\mathrm{t}$).

3.2. Model Overview

In this section, a Multi-Scale Evolutionary Network (MSEN) is proposed to solve the problem of feature extraction at different scales. The overall framework of a MSEN is illustrated in Figure 1. There are three parts in our model: (1) A local memory encoder that applies a hierarchical transfer-aware graph neural network (HT-GNN) to obtain structural features within each timestamp’s knowledge graph snapshot. The local encoder also performs temporal encoding of entities and relations using a gated recurrent unit (GRU); (2) a global memory encoder that employs a time-related graph neural network (TR-GNN) to mine temporal-semantic dependencies across the historical knowledge graph, yielding entity and relation embeddings; (3) a decoder that integrates the local and global encoder outputs and utilizes a scoring function to predict future entities.

Specifically, the input is a series of temporal knowledge graph snapshots. The local encoder extracts per-timestamp features using HT-GNN and temporal dynamics via the GRU. The global encoder identifies long-range patterns using TR-GNN. Finally, the decoder combines local and global embeddings to predict future entities using the scoring function. This multi-scale approach allows MSEN to capture both contextual knowledge and global evolutions for enhanced temporal reasoning.

3.3. Local Memory Encoder

The local memory encoder focuses on obtaining the memories of the m historical knowledge graphs adjacent to the query time. It aggregates each knowledge graph snapshot to capture structural dependencies within timestamps. Additionally, sequence neural networks are utilized to learn temporal features of entities and relations, enabling the model to better represent temporal dynamics across knowledge graphs.

3.3.1. HT-GNN

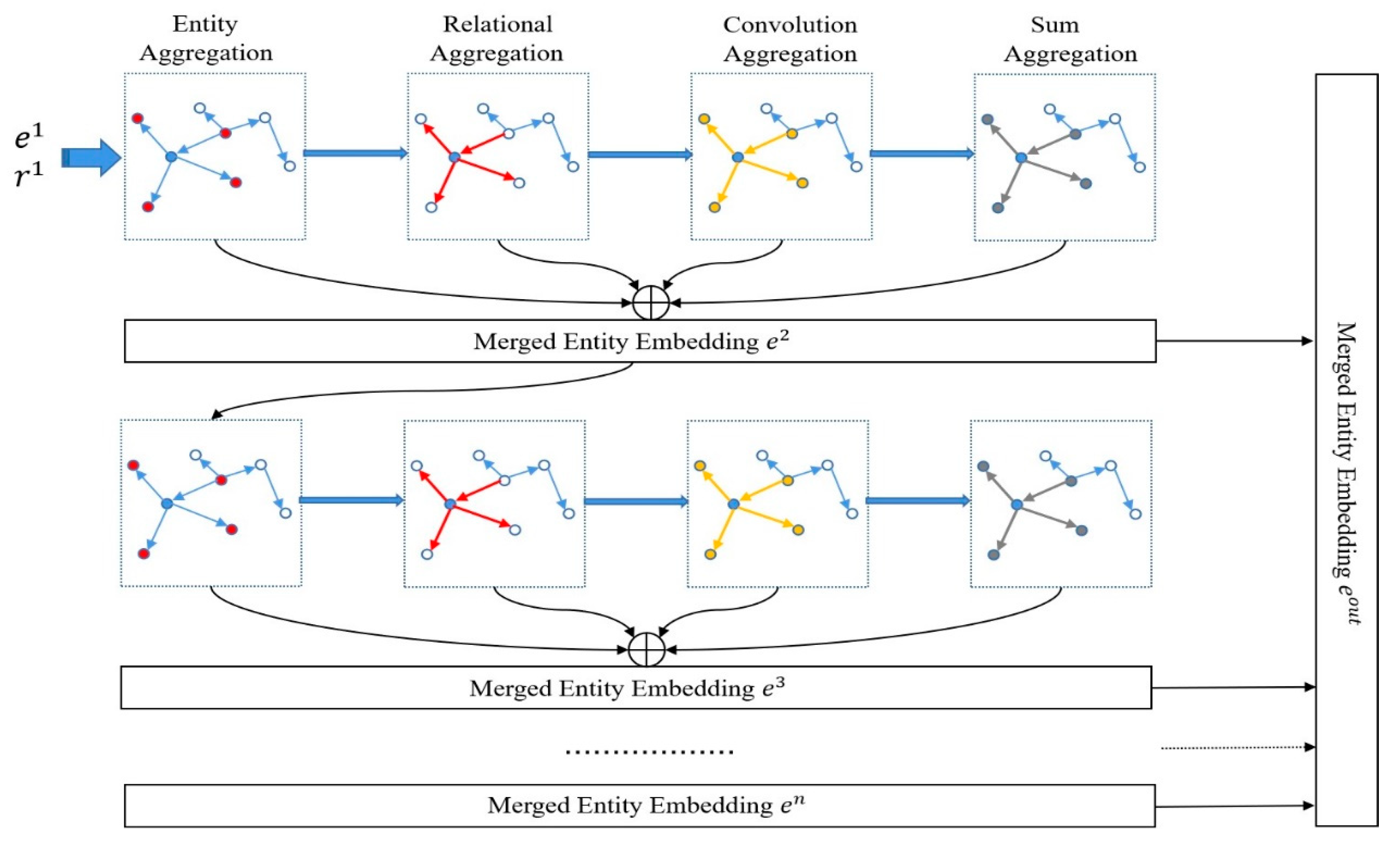
Obtaining informative embedding representations for each temporal knowledge graph is critical for effective local encoding. To better capture semantic information, we propose a novel graph neural network-based knowledge graph embedding method called Hierarchical Transfer-Aware Graph Neural Network (HT-GNN). As illustrated in Figure 2, HT-GNN performs sequential aggregation at each layer: entity aggregation, relation aggregation, convolution aggregation, and sum aggregation. The blue nodes serve as aggregation centers. Different aggregation results are merged as input to the next layer. Finally, the outputs from the multi-layer aggregations are combined as the overall model output.

Specifically, entity aggregation allows nodes to incorporate semantics from adjacent entities based on co-occurrence, capturing semantic dependencies. The entity aggregation function and weight calculation are:

$${\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{e}\mathrm{n}\mathrm{t}}\right)}^{\mathrm{l}}=\mathsf{\sigma }\left({\sum }_{\left(\mathrm{s},\mathrm{r}\right)\in {\mathrm{N}}_{\mathrm{t}}}{\mathsf{\alpha }}_{\mathrm{e}\mathrm{n}\mathrm{t}}^{\mathrm{l}}{\mathrm{w}}_{\mathrm{e}\mathrm{n}\mathrm{t}}^{\mathrm{l}}{\mathrm{h}}_{\mathrm{s},\mathrm{t}}^{\mathrm{l}}\right),$$

(1)

where ${\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{e}\mathrm{n}\mathrm{t}}$ is embedding representation of entity o. ${\mathrm{h}}_{\mathrm{s},\mathrm{t}}^{\mathrm{l}}$ is the embedding representation of entity s which is a neighboring node of entity o. ${\mathrm{w}}_{\mathrm{e}\mathrm{n}\mathrm{t}}^{\mathrm{l}}$ is a learnable weight matrix. ${\mathrm{N}}_{\mathrm{t}}$ represents the neighboring entities and relations of entity o. $\mathsf{\sigma }$ is a nonlinear activation function. ${\mathsf{\alpha }}_{\mathrm{e}\mathrm{n}\mathrm{t}}^{\mathrm{l}}$ is the aggregation weight, calculated as follows:

$${\mathsf{\alpha }}_{\mathrm{e}\mathrm{n}\mathrm{t}}^{\mathrm{l}}=\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{h}\left(\mathrm{L}\left(\left[{\mathrm{h}}_{\mathrm{s},\mathrm{t}}^{\mathrm{l}}‖{\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{l}}\right]\right)\right)\right)}{{\sum }_{\left(\mathrm{s},\mathrm{r}\right)\in {\mathrm{N}}_{\mathrm{t}}}\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{h}\left(\mathrm{L}\left(\left[{\mathrm{h}}_{\mathrm{s},\mathrm{t}}^{\mathrm{l}}‖{\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{l}}\right]\right)\right)\right)},$$

(2)

where $\mathrm{h}\left(·\right)$ is the LeakyRelu activation function. L$\left(·\right)$ represents the fully connected function. $\parallel$ represents the concatenation operation.

The result of entity aggregation is used as input to relation aggregation. The relation aggregation infuses relation semantics into the entity representations, thereby obtaining the co-occurrence of each node and relation in the knowledge graph. The relation aggregation function and corresponding weight calculation method used in the paper are as follows:

$${\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{r}\mathrm{e}\mathrm{l}}\right)}^{\mathrm{l}}=\mathsf{\sigma }\left({\sum }_{\left(\mathrm{s},\mathrm{r}\right)\in {\mathrm{N}}_{\mathrm{t}}}{\mathsf{\alpha }}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\mathrm{l}}{\mathrm{w}}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\mathrm{l}}{\mathrm{h}}_{\mathrm{r},\mathrm{t}}^{\mathrm{l}}\right),$$

(3)

where ${\mathrm{h}}_{\mathrm{r},\mathrm{t}}^{\mathrm{l}}$ is the embedding representation of the neighboring relation r of entity o. ${\mathrm{w}}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\mathrm{l}}$ is a learnable weight matrix. ${\mathsf{\alpha }}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\mathrm{l}}$ is the relation aggregation weight, calculated as follows:

$${\mathsf{\alpha }}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\mathrm{l}}=\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{h}\left(\mathrm{L}\left(\left[{\mathrm{h}}_{\mathrm{r},\mathrm{t}}^{\mathrm{l}}‖{\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{l}}\right]\right)\right)\right)}{{\sum }_{\left(\mathrm{s},\mathrm{r}\right)\in {\mathrm{N}}_{\mathrm{t}}}\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{h}\left(\mathrm{L}\left(\left[{\mathrm{h}}_{\mathrm{r},\mathrm{t}}^{\mathrm{l}}‖{\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{l}}\right]\right)\right)\right)}$$

(4)

The result of relation aggregation is used as input to convolution aggregation. For convolution aggregation, it obtains the hidden relation between entity s, relation r, and entity o, which enriches the semantic information of entities. The convolution aggregation function and weight calculation method used in the paper are as follows:

$${\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{c}\mathrm{o}\mathrm{n}}\right)}^{\mathrm{l}}=\mathsf{\sigma }\left({\sum }_{\left(\mathrm{s},\mathrm{r}\right)\in {\mathrm{N}}_{\mathrm{t}}}{\mathsf{\alpha }}_{\mathrm{c}\mathrm{o}\mathrm{n}}^{\mathrm{l}}{\mathrm{w}}_{\mathrm{c}\mathrm{o}\mathrm{n}}^{\mathrm{l}}\mathrm{c}\mathrm{o}\mathrm{n}\left(\mathrm{s},\mathrm{r},\mathrm{o}\right)\right),$$

(5)

where $\mathrm{c}\mathrm{o}\mathrm{n}\left(·\right)$ is the convolution operation. ${\mathrm{w}}_{\mathrm{c}\mathrm{o}\mathrm{n}}^{\mathrm{l}}$ is a learnable weight matrix. ${\mathsf{\alpha }}_{\mathrm{r}\mathrm{e}\mathrm{l}}^{\mathrm{l}}$ is the aggregation weight, calculated as follows:

$${\mathsf{\alpha }}_{\mathrm{c}\mathrm{o}\mathrm{n}}^{\mathrm{l}}=\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{h}\left(\mathrm{L}\left(\left[{\mathrm{h}}_{\mathrm{s},\mathrm{t}}^{\mathrm{l}}‖{\mathrm{h}}_{\mathrm{r},\mathrm{t}}^{\mathrm{l}}‖{\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{l}}\right]\right)\right)\right)}{{\sum }_{\left(\mathrm{s},\mathrm{r}\right)\in {\mathrm{N}}_{\mathrm{t}}}\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{h}\left(\mathrm{L}\left(\left[{\mathrm{h}}_{\mathrm{s},\mathrm{t}}^{\mathrm{l}}‖{\mathrm{h}}_{\mathrm{r},\mathrm{t}}^{\mathrm{l}}‖{\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{l}}\right]\right)\right)\right)}.$$

(6)

The result of convolution aggregation is used as input to sum aggregation. For sum aggregation, information is obtained through relational paths between entities, and sum-obtained information is similar to translation model TransE [27]. The sum aggregation function and corresponding weight calculation method used in the paper are as follows:

$${\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{s}\mathrm{u}\mathrm{m}}\right)}^{\mathrm{l}}=\mathsf{\sigma }\left({\sum }_{\left(\mathrm{s},\mathrm{r}\right)\in {\mathrm{N}}_{\mathrm{t}}}{\mathsf{\alpha }}_{\mathrm{s}\mathrm{u}\mathrm{m}}^{\mathrm{l}}{\mathrm{w}}_{\mathrm{s}\mathrm{u}\mathrm{m}}^{\mathrm{l}}\left({{\mathrm{h}}_{\mathrm{s},\mathrm{t}}^{\mathrm{l}}+\mathrm{h}}_{\mathrm{r},\mathrm{t}}^{\mathrm{l}}\right)\right),$$

(7)

where ${\mathrm{h}}_{\mathrm{s},\mathrm{t}}^{\mathrm{l}}$ and ${\mathrm{h}}_{\mathrm{r},\mathrm{t}}^{\mathrm{l}}$ are the embedding representations of neighboring entity s and relation r of entity o. ${\mathrm{w}}_{\mathrm{s}\mathrm{u}\mathrm{m}}^{\mathrm{l}}$ is a learnable weight matrix. ${\mathsf{\alpha }}_{\mathrm{s}\mathrm{u}\mathrm{m}}^{\mathrm{l}}$ is the relation aggregation weight, calculated as follows:

$${\mathsf{\alpha }}_{\mathrm{s}\mathrm{u}\mathrm{m}}^{\mathrm{l}}=\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{h}\left(\mathrm{L}\left(\left[{{\mathrm{h}}_{\mathrm{s},\mathrm{t}}^{\mathrm{l}}+\mathrm{h}}_{\mathrm{r},\mathrm{t}}^{\mathrm{l}}‖{\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{l}}\right]\right)\right)\right)}{{\sum }_{\left(\mathrm{s},\mathrm{r}\right)\in {\mathrm{N}}_{\mathrm{t}}}\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{h}\left(\mathrm{L}\left(\left[{{\mathrm{h}}_{\mathrm{s},\mathrm{t}}^{\mathrm{l}}+\mathrm{h}}_{\mathrm{r},\mathrm{t}}^{\mathrm{l}}‖{\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{l}}\right]\right)\right)\right)}.$$

(8)

Finally, the final entity embedding can be expressed as:

$${\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}\right)}^{\mathrm{l}+1}={\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{e}\mathrm{n}\mathrm{t}}\right)}^{\mathrm{l}}+{\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{r}\mathrm{e}\mathrm{l}}\right)}^{\mathrm{l}}+{\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{c}\mathrm{o}\mathrm{n}}\right)}^{\mathrm{l}}+{\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{s}\mathrm{u}\mathrm{m}}\right)}^{\mathrm{l}}.$$

(9)

3.3.2. Local Memory Representation

In order to obtain the temporal features of entities and relations in adjacent historical knowledge graphs, following RE-GCN [12], GRU is adopted to update the representations of entities and relations. The update of entity embedding representations is as follows:

$${\mathrm{H}}_{\mathrm{t}+1}=\mathrm{G}\mathrm{R}\mathrm{U}\left({\mathrm{H}}_{\mathrm{t}},{\mathrm{H}}_{\mathrm{t}}^{\mathrm{H}\mathrm{T}-\mathrm{G}\mathrm{N}\mathrm{N}}\right),$$

(10)

where ${\mathrm{H}}_{\mathrm{t}+1}$ is the entity embedding at time t + 1. ${\mathrm{H}}_{\mathrm{t}}^{\mathrm{H}\mathrm{T}-\mathrm{G}\mathrm{N}\mathrm{N}}$ is the entity embedding obtained after aggregating the knowledge graph using HT-GNN.

Similarly, in order to obtain the temporal embedding representation of the relationship, the following method is used for calculation:

$${\mathrm{R}}_{\mathrm{t}+1}=\mathrm{G}\mathrm{R}\mathrm{U}\left({\mathrm{R}}_{\mathrm{t}},\acute{\mathrm{R}}\right),$$

(11)

$$\acute{\mathrm{R}}=\mathrm{p}\mathrm{o}\mathrm{o}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{g}\left({\mathrm{H}}_{\mathrm{t}}\right),$$

(12)

where ${\mathrm{R}}_{\mathrm{t}+1}$ is the relation embedding at time t + 1. $\mathrm{p}\mathrm{o}\mathrm{o}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{g}\left(·\right)$ represents mean pooling operation to retain all entity embeddings related to the relationship r and average them.

3.4. Global Memory Encoder

To extract cross-timestamp entity dependencies, we construct a global knowledge graph by associating historical snapshots containing the same entities [28]. We introduce a Time-Related Graph Neural Network (TR-GNN) to effectively encode this global graph.

The global graph aggregates facts across timestamps, including periodic and non-periodic occurrences. To fully utilize this temporal information, we design separate periodic and aperiodic time vector representations:

$${\mathrm{T}}^{\mathrm{p}}=\mathrm{f}\left({\mathrm{w}}_1\mathrm{t}+{\mathsf{\phi }}_1\right),$$

(13)

$${\mathrm{T}}^{\mathrm{a}\mathrm{p}}={\mathrm{w}}_2\mathrm{t}+{\mathsf{\phi }}_2,$$

(14)

where ${\mathrm{T}}^{\mathrm{p}}$ is the periodic time vector; ${\mathrm{T}}^{\mathrm{a}\mathrm{p}}$ is the non-periodic time vector. $\mathrm{w}$ and $\mathsf{\phi }$ are learnable vectors, representing frequency and phase respectively. $\mathrm{f}\left(·\right)$ is a periodic activation function, which is sin function in the paper. t represents the time interval $\left|{\mathrm{T}}_{\mathrm{i}}-{\mathrm{T}}_{\mathrm{j}}\right|$ between two connected entities in the global knowledge graph.

To obtain the time-semantic dependencies between entities in the global knowledge graph, the paper designs TR-GNN to encode the knowledge graph:

$${\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}\right)}^{\mathrm{l}+1}=\mathsf{\sigma }\left({\sum }_{\left(\mathrm{s},\mathrm{r}\right)\in {\mathrm{N}}_{\mathrm{t}}}{(\mathsf{\alpha }}_1^{\mathrm{l}}{\mathrm{h}}_{\mathrm{s},\mathrm{t}}^{\mathrm{l}}+{\mathsf{\alpha }}_2^{\mathrm{l}}{\left({\mathrm{h}}_{\mathrm{r},\mathrm{t}}^{\mathrm{l}}\right)}^{\prime })+{{\mathrm{w}}_2\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}\right)}^{\mathrm{l}}\right),$$

(15)

$${\left({\mathrm{h}}_{\mathrm{r},\mathrm{t}}^{\mathrm{l}}\right)}^{\prime }={\mathrm{h}}_{\mathrm{r},\mathrm{t}}^{\mathrm{l}}+{\mathrm{T}}^{\mathrm{p}},$$

(16)

where ${\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}\right)}^{\mathrm{l}+1}$ is the encoded entity embedding. ${\mathrm{w}}_2$ is a learnable weight parameter. ${\mathsf{\alpha }}_1^{\mathrm{l}}$ and ${\mathsf{\alpha }}_2^{\mathrm{l}}$ are weights for entities and relations respectively, calculated as follows:

$${\mathsf{\alpha }}_1^{\mathrm{l}}=\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{h}\left(\mathrm{L}\left(\left[{\mathrm{h}}_{\mathrm{s},\mathrm{t}}^{\mathrm{l}}‖{\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{l}}‖{\mathrm{T}}^{\mathrm{a}\mathrm{p}}\right]\right)\right)\right)}{{\sum }_{\left(\mathrm{s},\mathrm{r}\right)\in {\mathrm{N}}_{\mathrm{t}}}\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{h}\left(\mathrm{L}\left(\left[{\mathrm{h}}_{\mathrm{s},\mathrm{t}}^{\mathrm{l}}‖{\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{l}}‖{\mathrm{T}}^{\mathrm{a}\mathrm{p}}\right]\right)\right)\right)},$$

(17)

$${\mathsf{\alpha }}_2^{\mathrm{l}}=\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{h}\left(\mathrm{L}\left(\left[{\mathrm{h}}_{\mathrm{r},\mathrm{t}}^{\mathrm{l}}‖{\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{l}}‖{\mathrm{T}}^{\mathrm{a}\mathrm{p}}\right]\right)\right)\right)}{{\sum }_{\left(\mathrm{s},\mathrm{r}\right)\in {\mathrm{N}}_{\mathrm{t}}}\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{h}\left(\mathrm{L}\left(\left[{\mathrm{h}}_{\mathrm{r},\mathrm{t}}^{\mathrm{l}}‖{\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{l}}‖{\mathrm{T}}^{\mathrm{a}\mathrm{p}}\right]\right)\right)\right)}.$$

(18)

Using the non-periodic time vector to compute weights for entities and relations better captures the temporal-semantic relationships between entities. Finally, the updated entity embeddings are nonlinearly transformed to obtain the embedding representations of each entity in the global knowledge graph.

3.5. Gating Integration

In order to better integrate the embeddings vectors obtained by the local memory encoder and the global memory encoder for reasoning, the paper applies a learnable gating function [29] to adaptively adjust the weights of local memory embeddings and global memory embeddings, finally obtaining a vector:

$${\mathrm{h}}_{\mathrm{o},\mathrm{t}}=\mathsf{\lambda }\left(\mathrm{g}\right)⊚{\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}+\left(1-\mathsf{\lambda }\left(\mathrm{g}\right)\right)⊚{\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}},$$

(19)

$${\mathrm{h}}_{\mathrm{r},\mathrm{t}}=\mathsf{\lambda }\left(\mathrm{g}\right)⊚{\mathrm{h}}_{\mathrm{r},\mathrm{t}}^{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}+\left(1-\mathsf{\lambda }\left(\mathrm{g}\right)\right)⊚{\mathrm{h}}_{\mathrm{r},\mathrm{t}}^{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}},$$

(20)

where $\mathsf{\lambda }\left(·\right)$ is the sigmoid function, aiming to restrict the range of each element to [0, 1]. g is the gate parameter to adjust the weights. $⊚$ is element-wise multiplication.

3.6. Scoring Function and Loss Function

In this section, the paper mainly introduces the details of scoring function and the loss function. In order to obtain the probability of an event occurring at timestamp t + 1 in the future, ConvTransE [12] is utilized as the decoder to calculate the probability of the existence between entities at timestamp t + 1 under the relation r:

$${\mathrm{P}}_{\mathrm{t}+1}\left(\mathrm{o}\left|\mathrm{s},\mathrm{r}\right.\right)=\mathsf{\lambda }\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}+1}\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{E}\left({\mathrm{h}}_{\mathrm{s},\mathrm{t}+1},{\mathrm{h}}_{\mathrm{r},\mathrm{t}+1}\right)\right),$$

(21)

where $\mathsf{\lambda }\left(·\right)$ is the sigmoid function. ${\mathrm{h}}_{\mathrm{s},\mathrm{t}+1}$ and ${\mathrm{h}}_{\mathrm{r},\mathrm{t}+1}$ are the embedding representations of entities and relations at timestamp t + 1. ${\mathrm{h}}_{\mathrm{o},\mathrm{t}+1}$ is the embedding representations of entities after global and local fusion.

Following RE-GCN [12], the loss function during training is defined as:

$${\mathrm{L}}_{\mathrm{e}}=-{\sum }_{\mathrm{t}=0}^{\mathrm{T}}{\sum }_{\left(\mathrm{s},\mathrm{r},0,\mathrm{t}+1\right)\in {\mathrm{G}}_{\mathrm{t}+1}}\mathrm{l}\mathrm{o}\mathrm{g}{\mathrm{P}}_{\mathrm{t}+1}\left(\mathrm{o}\left|\mathrm{s},\mathrm{r}\right.\right),$$

(22)

$${\mathrm{L}}_{\mathrm{r}}=-{\sum }_{\mathrm{t}=0}^{\mathrm{T}}{\sum }_{\left(\mathrm{s},\mathrm{r},0,\mathrm{t}+1\right)\in {\mathrm{G}}_{\mathrm{t}+1}}\mathrm{l}\mathrm{o}\mathrm{g}{\mathrm{P}}_{\mathrm{t}+1}\left(\mathrm{r}\left|\mathrm{s},\mathrm{o}\right.\right).$$

(23)

The final loss is $\mathrm{L}=\mathsf{\lambda }{\mathrm{L}}_{\mathrm{e}}+\left(1-\mathsf{\lambda }\right){\mathrm{L}}_{\mathrm{r}}+\mathsf{\mu }{‖\mathsf{\Theta }‖}_2$, where ${\mathrm{L}}_{\mathrm{e}}$ is the loss for predicting entities, ${\mathrm{L}}_{\mathrm{r}}$ is the loss for predicting relations, $\mathsf{\lambda }$ is the hyperparameter balancing different tasks. ${‖\mathsf{\Theta }‖}_2$ is ${\mathrm{L}}_2$ norm, and $\mathsf{\mu }$ is to control the penalty term. The overall training algorithm is shown in Algorithm 1.

Algorithm 1. Training of MSEN

Input: The train set: $\{{\mathbf{G}}_0,{\mathbf{G}}_1,{\mathbf{G}}_2,{\mathbf{G}}_3,\cdots {\mathbf{G}}_{{\mathbf{t}}_{\mathbf{m}}-1}\}$; the number of epoch n. Output: The minimum Loss on the train set.

$\mathsf{{\rm E}},\mathrm{R},{\mathsf{\Gamma }}_{\mathrm{t}}⟵$Init.normal_(), ${\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}_{\mathrm{m}\mathrm{i}\mathrm{n}}=0$ //Initialize the model’ parameters For each $\mathrm{i}\in [1,\mathrm{T}]$ do    /* Local Memory Encoder */      ${\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}\right)}^{\mathrm{l}+1}={\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{e}\mathrm{n}\mathrm{t}}\right)}^{\mathrm{l}}$ + ${\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{r}\mathrm{e}\mathrm{l}}\right)}^{\mathrm{l}}$ + ${\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{c}\mathrm{o}\mathrm{n}}\right)}^{\mathrm{l}}$ + ${\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{s}\mathrm{u}\mathrm{m}}\right)}^{\mathrm{l}}$//Obtaining the semantic information using HT-GNN      ${\mathrm{H}}_{\mathrm{t}+1}=\mathrm{G}\mathrm{R}\mathrm{U}\left({\mathrm{H}}_{\mathrm{t}},{\mathrm{H}}_{\mathrm{t}}^{\mathrm{H}\mathrm{T}-\mathrm{G}\mathrm{N}\mathrm{N}}\right)$//local memory representation    /* Global Memory Encoder */      Construct a global graph G;      ${\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}\right)}^{\mathrm{l}+1}=\mathsf{\sigma }\left({\sum }_{\left(\mathrm{s},\mathrm{r}\right)\in {\mathrm{N}}_{\mathrm{t}}}{(\mathsf{\alpha }}_1^{\mathrm{l}}{\mathrm{h}}_{\mathrm{s},\mathrm{t}}^{\mathrm{l}}+{\mathsf{\alpha }}_2^{\mathrm{l}}\left({\mathrm{h}}_{\mathrm{r},\mathrm{t}}^{\mathrm{l}}\right)\prime )+{{\mathrm{w}}_2\left({\mathrm{h}}_{\mathrm{o},\mathrm{t}}\right)}^{\mathrm{l}}\right)$ //Obtaining time-semantic dependencies using TR-GNN      ${\mathrm{h}}_{\mathrm{o},\mathrm{t}}=\mathsf{\lambda }\left(\mathrm{g}\right)⊚{\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}+\left(1-\mathsf{\lambda }\left(\mathrm{g}\right)\right)⊚{\mathrm{h}}_{\mathrm{o},\mathrm{t}}^{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}$//Gating Integration      ${\mathrm{P}}_{\mathrm{t}+1}\left(\mathrm{o}\left|\mathrm{s},\mathrm{r}\right.\right)⟵$ConvTranE()      Loss$⟵$Calculate the sum of ${\mathrm{L}}_{\mathrm{e}}$ and ${\mathrm{L}}_{\mathrm{r}}$      Update parameters End for Return Loss

4. Experiments

In this chapter, the paper compares MSEN with several baselines on two datasets. Meanwhile, ablation experiments are conducted to analyze the ability of acquiring semantic information at different scales. Comparison experiments evaluate the effects of different GCNs. In addition, the paper also studies the parameter settings of the model.

4.1. Datasets

To evaluate the effect of the MSEN model, experiments are conducted on two typical event-based datasets, including: ICEWS14 [17], ICEWS18 [6]. Both datasets are from the event-based dataset Integrated Crisis Early Warning System [30], with the time interval of 24 h. The statistical details of the datasets are listed in

Table 2. The statistical details of the datasets.

Datasets	Train	Valid	Test	Ent	Rel	Time Gap
ICEWS14	74,845	8514	7371	6869	230	24 h
ICEWS18	373,018	45,995	49,545	23,033	256	24 h

.

4.2. Baselines

The paper compares MSEN with two types of methods: static KG reasoning and TKG reasoning methods.

For static KG methods: DiSMult [1], ComplEx [2], RGCN [3], ConvE [4], and RotatE [5] are selected.

For TKG reasoning under the extrapolation setting: CyGNet [8], RE-NET [6], xERTE [9], RE-GCN [12], TITer [10], CENET [11], and TiRGN [14] are selected.

4.3. Evaluation Metrics

This paper adopts mean reciprocal rank (MRR) and Hit@k (k is 1 and 10) to evaluate the performance of models for entity prediction. For the fairness of the comparison, the ground truth is used when performing multi-step reasoning, and the experimental results are reported under the time-aware filtered setting. MRR is the average of the reciprocal ranks of all relevant candidate entities, measuring the rank of the highest-ranking relevant entity. Hit@k represents the proportion of cases where the true target entity is included in the top k predicted candidates, reflecting the model’s ability to contain the target entity within the top k.

4.4. Implementation Details

In the experiments, the embedding dimension was fixed at 200 for all methods. The Adam optimizer was used for parameter training with a learning rate of 0.001. The hyperparameter for balancing different tasks was set to 0.7. To ensure fairness of comparison with other models, for the local memory encoder, the number of adjacent historical knowledge graphs obtained was 3 and 6 on the ICEWS14 and ICEWS18 datasets respectively; for the global memory encoder, the number of adjacent historical knowledge graphs obtained was 10 and 10 on the ICEWS14 and ICEWS18 datasets, respectively. The number of layers in HT-GNN was 2 on both datasets. The number of layers in TR-GNN was 2 and 3 on the ICEWS14 and ICEWS18 datasets respectively. For the ConvTranE decoder, the number of channels used was 50 and the kernel size was 2 × 3.

5. Results

5.1. Performance Comparison

As shown in

Table 3. Performance on the ICEWS14 dataset in terms of MRR (%), Hit@1 (%), and Hit@10 (%).

Model	MRR	Hit@1	Hit@10
DistMult	25.31	17.93	42.22
ComplEx	32.33	23.21	52.37
RGCN	28.14	19.43	46.02
ConvE	30.93	21.74	50.18
RotatE	27.53	18.60	47.62
CyGNet	37.65	27.43	57.90
RE-NET	39.86	30.11	58.21
xERTE	40.79	32.70	57.30
TITer	41.73	32.74	58.44
RE-GCN*	41.99	32.93	61.92
CENET	41.30	32.58	58.22
TiRGN*	43.18	33.12	62.24
Our Method	46.68	35.29	68.96

The mark * in the table represents removing static information from models for fair comparison [15]. The best results are in bold.

and

Table 4. Performance on the ICEWS18 dataset in terms of MRR (%), Hit@1 (%), and Hit@10 (%).

Model	MRR	Hit@1	Hit@10
DistMult	16.59	10.01	31.69
ComplEx	18.84	11.41	25.78
RGCN	18.04	8.57	35.68
ConvE	24.28	15.61	44.59
RotatE	15.35	7.10	33.09
CyGNet	27.12	17.21	46.85
RE-NET	29.78	19.73	48.46
xERTE	29.31	21.03	46.48
TITer	29.98	22.05	44.83
RE-GCN*	30.13	19.11	48.86
CENET	29.65	19.98	48.23
TiRGN*	32.22	22.24	51.88
Our Method	34.05	22.83	56.80

The mark * in the table represents removing static information from models for fair comparison [15]. The best results are in bold.

, entity prediction experiments are conducted on facts at future timestamps. The tables list the predictive performance of MSEN and the baseline models on ICEWS14 and ICEWS18 datasets. The results of baseline models in the table are from [15].

In the experimental results, the MSEN model outperforms other baseline models. The results show the effectiveness of the MSEN model in predicting entities at future timestamps. Compared with TiRGN*, MSEN improves the MRR by 3.5 and 1.83 percentage points on ICEWS14 and ICEWS18, respectively.

Probing deeper, we evaluated recall capabilities against TiRGN* on ICEWS14. At recall@1, MSEN achieved 32.78%, while TiRGN* achieved 34.88%. For recall@10, the models achieved near identical results, with MSEN at 61.98% versus 62.21% for TiRGN*. While marginally behind in recall@k, MSEN still demonstrates competitive retrieval ability.

5.2. Ablation Study

The encoder of the MSEN model is mainly composed of two submodules: Local Memory Encoder (LME) and Global Memory Encoder (GME). To further analyze the effect of each module on the final entity prediction results, the paper reports the results of LME (HT-GNN) and GME (TR-GNN) on the ICEWS14 dataset using MRR and Hit@k (k = 1, 3, 10) metrics. LME (HT-GNN) represents removing the GME module from the MSEN model; GME (TR-GNN) represents removing the LME module from the MSEN model. As can be seen from

Table 5. Performance of GNN-based model in LME and GME in terms of MRR (%), Hit@1 (%), Hit@3 (%), and Hit@10 (%).

Model	ICEWS14
	MRR	Hit@1	Hit@3	Hit@10
LME (RGCN)	38.69	29.34	43.11	56.68
LME (KBGAT)	38.74	29.50	43.25	56.26
LME (CompGCN(add))	39.08	29.78	43.75	56.77
LME (HT-GNN)	39.91	30.45	44.48	57.91
GME (RGCN)	43.84	31.29	49.90	69.06
GME (KBGAT)	43.41	31.53	48.83	67.08
GME (CompGCN(add))	43.72	31.11	49.86	68.98
GME (HRGNN)	44.93	33.02	50.58	68.97
GME (TR-GNN)	45.24	33.36	50.88	69.22

, the performance of LME (HT-GNN) is worse than MSEN, because this part only extracts local features and the obtained embedding representations have less semantic information. The performance of GME (TR-GNN) has greatly improved compared to LME (HT-GNN), but integrating both using a gating function can further improve the accuracy of entity prediction.

To study the effects of HT-GNN and TR-GNN in LME and GME, respectively, the paper compares these two models with different types of GNN-based models on the ICEWS14 dataset using MRR and Hit@k (k = 1, 3, 10) metrics. In LME, RGCN [3], KBGAT [31], and CompGCN (add) [32] are used to replace the HT-GNN model; in GME, RGCN [3], KBGAT [31], CompGCN (add) [32], and HRGNN [28] are used to replace the TR-GNN model. The experimental results in Table 5 show that the MRR of HT-GNN is 0.83 percentage points higher than CompGCN (add); in GME, the MRR of TR-GNN is 0.31 percentage points higher than HRGNN. Overall, both can effectively improve the accuracy of entity prediction in LME and GME respectively. The improvement of HT-GNN may be due to the hierarchical transfer method that enriches the semantic information of entities in the final knowledge graph. The improvement of TR-GNN may be due to its full utilization of both periodic and non-periodic time in the global knowledge graph.

5.3. Sensitivity Analysis

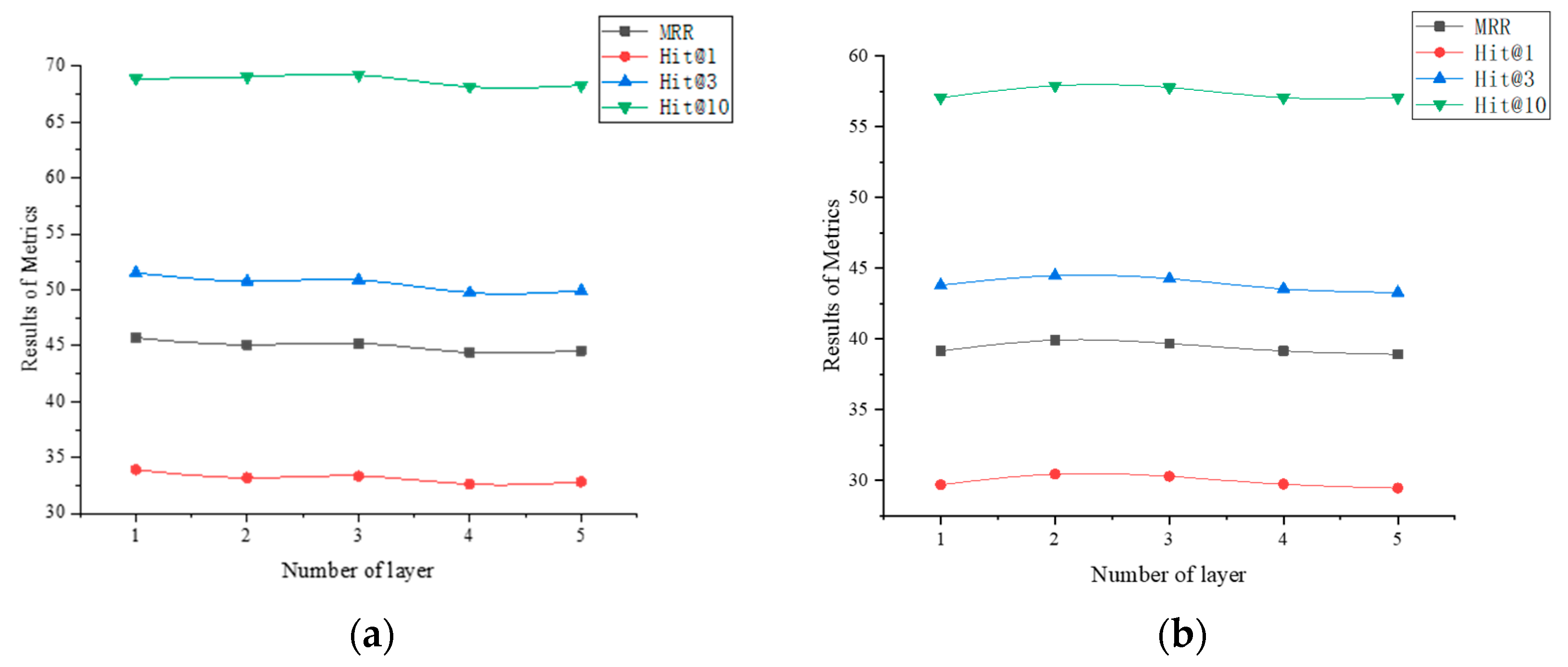
The paper further studied the effect of the number of layers in TR-GNN and HT-GNN on entity prediction performance for GME and LME modules using MRR and Hit@k (k = 1, 3, 10) metrics, respectively. Figure 3 show the experimental results with different numbers of layers on the ICEWS14 dataset. The experimental results show that with just 1 layer, the TR-GNN module can already effectively extract temporal-semantic information between entities. As the number of layers increases, the extracted features may interfere with entity embeddings. The HT-GNN model can extract sufficient semantic information with 2 layers, thus achieving higher entity prediction accuracy. Through experiments, it was proven that the different number of layers in TR-GNN and HT-GNN can affect the extraction of semantic information in the knowledge graph, thus influencing the effect of entity prediction.

5.4. Training Process Analysis

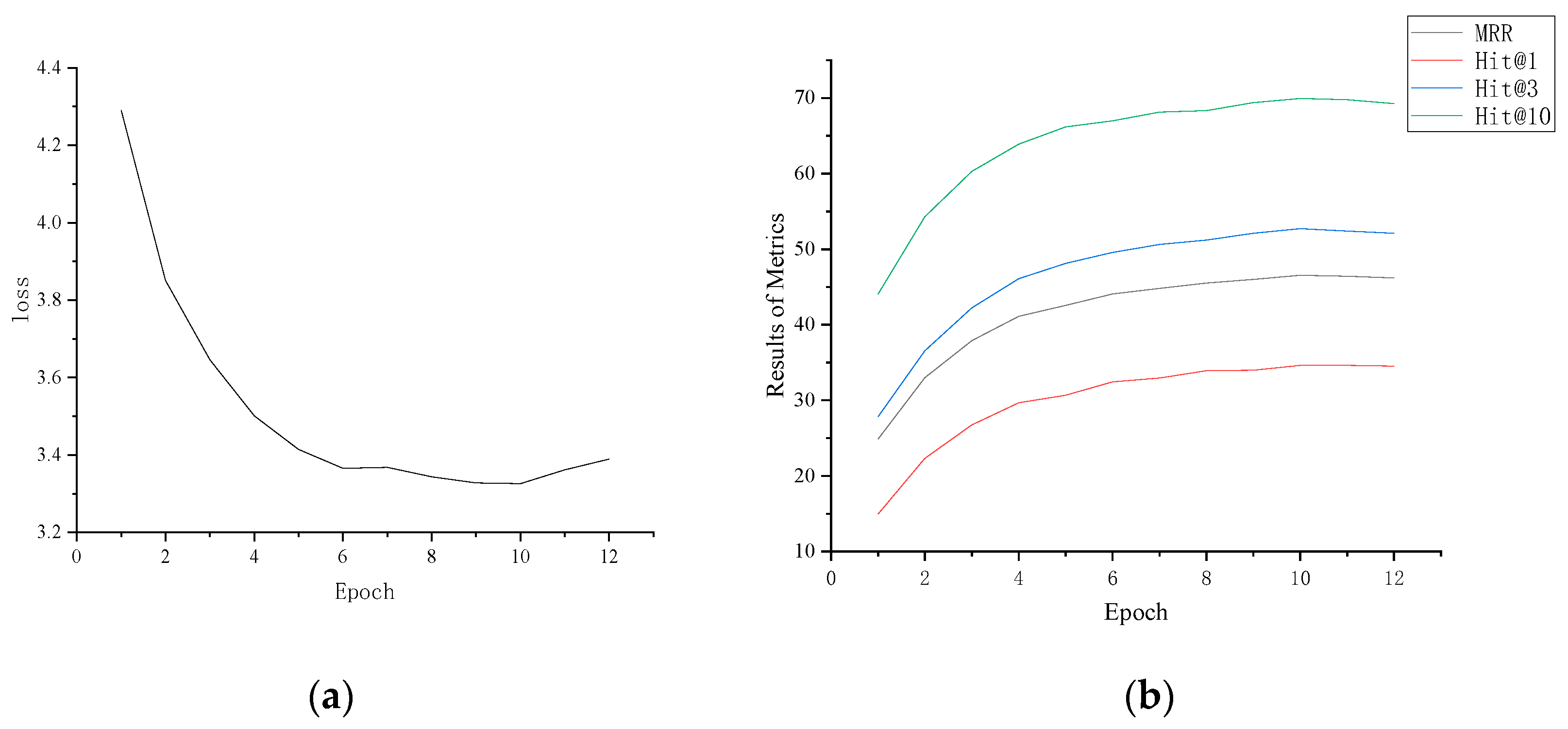
This paper studied the evolution of loss and evaluation metrics of the MSEN model during the training process. Figure 4 shows how the experimental results change with increasing epoch on the validation dataset of ICEWS14. The experimental results show that as the number of training epochs increases, the loss first gradually decreases, reaching the lowest point at the 10th epoch, and then slowly increases again; the values of the evaluation metrics MRR, Hit@1, Hit@3, and Hit@10 gradually increase, reaching a plateau after the 10th epoch. The results indicate that after 10 epochs of training on the ICEWS14 dataset, the model starts overfitting as evidenced by the increasing loss and stabilizing evaluation metrics. Therefore, 10 epoch is an appropriate number for training the MSEN model on the ICEWS14 dataset to achieve good performance without overfitting.

5.5. Statistical Analysis

In order to demonstrate the reliability of the results, both permutation tests and multiple repeated experiments were conducted in this study.

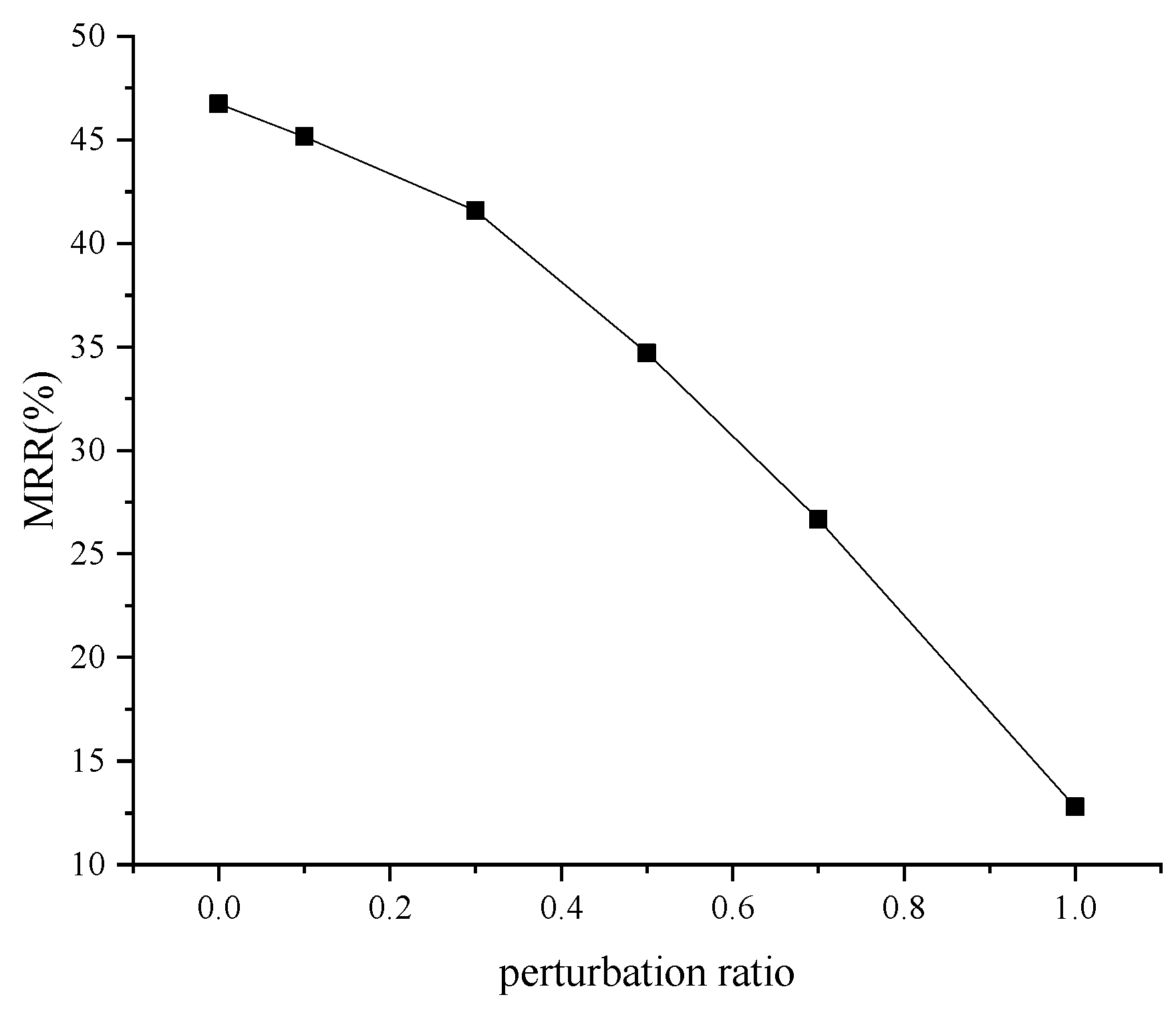
For the permutation test, we first trained the proposed MSEN model on the original training set and recorded the model’s performance (MRR) on the test set as the true observation. We then created perturbed training sets by replacing different proportions of head or tail entities in the original training set. The MSEN model was re-trained on these perturbed sets and achieved varying MRRs on the test set. The p-value was calculated using the following formula:

$$\mathrm{P}=\mathrm{M}/\mathrm{N}$$

(24)

where M is the number of times the MRR obtained using the perturbed datasets was greater than the true observation, and N is the number of experiments conducted with the perturbed datasets.

As illustrated in Figure 5, the MSEN model achieved lower MRRs when trained on more heavily perturbed sets, with p-values below the 0.05 significance level. This suggests the model has genuinely captured meaningful patterns in the training data.

Additionally, the experiment was repeated three times using the original training set, yielding consistent MRRs of 46.68%, 46.75%, and 46.72%, with an average of 46.72%. This further demonstrates the reliability and reproducibility of the proposed model.

6. Discussion

The experimental results demonstrate that the proposed MSEN model achieves superior performance compared to several baselines on typical benchmark datasets. The better results validate the effectiveness of modeling multi-scale evolutionary information for predicting future events in TKGs.

The ablation studies in Section 5.2 provide insights into the contribution of each module in MSEN. Removing the global memory encoder leads to a significant performance drop, showing the importance of capturing long-distance temporal dependencies. The local memory encoder also contributes steady improvements by aggregating rich semantics within each timestamp. Using HT-GNN and TR-GNN as the graph neural network encoders also leads to better results compared to alternative GNN models, demonstrating their capabilities in encoding structural and temporal patterns from TKGs.

The multi-scale modeling in MSEN aligns with findings from previous works such as TiRGN [14] which show combining local and global patterns is beneficial. However, MSEN proposes new designs for each module, leading to better results. The hierarchical design in HT-GNN enriches semantic learning, while the periodic and aperiodic temporal modeling in TR-GNN improves temporal encoding.

7. Conclusions and Future work

In this work, we propose a new method Multi-Scale Evolutionary Network (MSEN) to solve temporal knowledge graph (TKG) reasoning under the extrapolation setting. First, a hierarchical transfer graph neural network (HT-GNN) is designed in the local memory encoder to acquire rich semantic information from the local knowledge graph, and sequence neural networks are used to learn temporal features of entities and relations. Second, in the global memory encoder, a time-related GNN (TR-GNN) is designed to make full use of temporal information in the global knowledge graph, obtaining periodic and aperiodic temporal-semantic dependencies in the global knowledge graph, providing different weights for entities and relations, improving performance of downstream tasks. Finally, embeddings from different scales are integrated to complete entity prediction. Experimental results on a typical benchmark demonstrate the effectiveness of MSEN in solving TKG reasoning problems.

While MSEN achieves good results, there remain several promising directions for future investigation: (1) Model Compression: The current MSEN model entails relatively high computational complexity. To enable real-time inference and deployment under resource constraints, we can explore model compression techniques such as pruning and knowledge distillation. By simplifying the model while retaining predictive power, we can enhance its applicability to real-world systems. (2) Robustness to Noisy Data: Historical knowledge graphs often suffer from incomplete, biased, or noisy data. The robustness of MSEN’s predictions rely on the quality of the historical inputs. Advanced data filtering, denoising, and imputation methods can be studied to handle imperfect historical graphs. Techniques such as outlier detection and data estimation can help improve the model’s resilience against noise and missing facts. (3) Advanced GNN Architectures: Further improving the local and global graph neural network encoders with more sophisticated architectures such as graph attention networks is a promising direction. This can potentially capture more complex structural, semantic, and temporal patterns.

In the future, we will aim to enhance MSEN along these directions to make broader impacts in real-world applications of temporal knowledge graph reasoning.