Temporal-Guided Knowledge Graph-Enhanced Graph Convolutional Network for Personalized Movie Recommendation Systems

Abstract

Traditional movie recommendation systems are increasingly falling short in the contemporary landscape of abundant information and evolving user behaviors. This study introduced the temporal knowledge graph recommender system (TKGRS), a ground-breaking algorithm that addresses the limitations of existing models. TKGRS uniquely integrates graph convolutional networks (GCNs), matrix factorization, and temporal decay factors to offer a robust and dynamic recommendation mechanism. The algorithm’s architecture comprises an initial embedding layer for identifying the user and item, followed by a GCN layer for a nuanced understanding of the relationships and fully connected layers for prediction. A temporal decay factor is also used to give weightage to recent user–item interactions. Empirical validation using the MovieLens 100K, 1M, and Douban datasets showed that TKGRS outperformed the state-of-the-art models according to the evaluation metrics, i.e., RMSE and MAE. This innovative approach sets a new standard in movie recommendation systems and opens avenues for future research in advanced graph algorithms and machine learning techniques.

1. Introduction

The digital age has ushered in a revolutionary change in how humans interact with a broad spectrum of content. Social media platforms, streaming services, and e-commerce websites have grown in terms of their user base and have diversified the type of content they offer [1]. This proliferation has escalated the need for robust personalized movie recommendation systems to an unprecedented level, a need that is increasingly becoming a cornerstone for enhancing users’ engagement and satisfaction [2]. While traditional algorithms based on collaborative filtering and matrix factorization have set foundational standards, they come with inherent limitations. Most notably, they struggle with scalability and fail to adapt to dynamically evolving user preferences [3,4]. These limitations have prompted both the academic and industrial sectors to explore emerging technologies.

The integration of knowledge graphs (KGs) and graph neural networks (GNNs) into recommendation systems has become a recent focus [1,5]. Techniques such as hierarchical attentive knowledge graph embedding have shown promise in delivering more contextually relevant recommendations by capturing the semantic nuances and intricate relationships between users and items [6]. These advancements capture the semantic nuances and intricate relationships between users and items, which are usually overlooked in conventional systems.

Despite these advancements, a comprehensive solution that effectively combines these technologies while incorporating temporal dynamics remains elusive. This study aimed to fill this gap by introducing a novel algorithm that addresses user–item interactions’ static and dynamic aspects. As underscored by recent studies [7,8], the static nature of these advanced models hampers their ability to adapt to the dynamic shifts in users’ preferences. These shifts can be influenced by real-time events, seasonal changes, or trending topics, making the integration of temporal dynamics into recommendation algorithms an imperative rather than a luxury.

In addressing the identified gaps in the existing literature, this study introduced the temporal knowledge graph recommender system (TKGRS), an innovative algorithm that synergistically integrates matrix factorization, graph convolutional networks (GCNs), and temporal dynamics. TKGRS aims to overcome the limitations of the current algorithms while establishing a new benchmark in personalized recommendation systems [7,9]. Initially, TKGRS uses matrix factorization techniques to create initial embeddings for users and items, capturing their linear relationships. These embeddings serve as the foundation upon which GCNs act to update them, adding a layer of complexity by considering non-linear relationships and semantic connections in the user–item graph. To bring in the temporal aspect, a time decay factor is applied to user–item interactions, giving more weight to recent interactions while diminishing the impact of older ones. This multi-layered approach enables TKGRS to understand both the static and dynamic aspects of user–item interactions. The final recommendations are generated through a sequence of fully connected layers that map these updated embeddings to output the predictions.

The algorithm’s mathematical and computational foundations were explored rigorously. We validated its effectiveness using empirical evaluations, particularly focusing on the MovieLens 100K, 1M, and Douban datasets, and showed the best performance based on the evaluation metrics, i.e., RMSE and MAE. In addition, we used the t-test to show the significant difference between TKGRS and the best benchmark to justify the proposed algorithm. By harmonizing diverse technological advancements in matrix factorization, GCNs, and temporal modeling, TKGRS emerged as a versatile, robust solution for modern recommendation scenarios. Whether it captures the foundational user–item relationships, enriches these through semantic understanding via knowledge graphs, or adapts to real-time changes in users’ behavior, TKGRS provides a holistic perspective to the complex challenges faced by current movie recommendation systems.

The remainder of this study is organized as follows. Section 2 offers a detailed literature review, Section 3 delves into the intricacies of the TKGRS algorithm, Section 4 describes the experimental design and methodology, Section 5 presents the results and their broader implications, and Section 6 provides the concluding remarks.

2. Literature Review

As personalized recommendation systems have become more integral across various sectors, understanding their historical development, current capabilities, and limitations is crucial. This literature review aimed to offer an exhaustive overview of these facets. It started by tracing the evolution of personalized recommendation systems and then delved into their application in specific domains. We also discussed the current challenges and prospective directions in this field.

2.1. Personalized Recommendation Systems

The domain of personalized recommendation systems has undergone a significant transformation since its inception. What began as rudimentary algorithms have evolved into complex computational models that leverage machine learning, data analytics, and neural networks. This shift has fundamentally changed users’ interactions with digital platforms, making personalized recommendations pervasive in today’s digital experience. In the initial stages, recommendation systems largely relied on simple algorithms using user–item filtering techniques. These rudimentary methods, however, were quickly found to be lacking in scalability and adaptability. This led to the incorporation of machine learning algorithms that were adept at capturing the non-linear patterns in users’ behavior, providing a nuanced approach to personalization.

The utility of recommendation systems has spread across various sectors, from e-learning to crowdfunding platforms. In educational settings, algorithms analyze a multitude of factors, such as student engagement and performance metrics, to deliver personalized course suggestions [10]. In financial platforms such as crowdfunding, machine learning algorithms evaluate market conditions, investment risks, and historical behaviors to tailor investment suggestions [11].

Recent advancements in machine learning techniques, particularly deep learning, have enabled these systems to analyze users’ historical behavior and predict their future actions with greater accuracy [12]. Additionally, the rise of big data technologies has empowered these systems to process enormous datasets in real time, enhancing the efficiency and effectiveness of recommendations [13].

However, the increasing capabilities of personalization also bring forth challenges related to data privacy. Given the sensitive nature of users’ data, there is an urgent need for robust encryption methods and decentralized data storage solutions to safeguard privacy [14]. Ethical considerations around users’ consent and data usage are also gaining prominence in research. Evaluation metrics for recommendation systems have undergone a paradigm shift. They are no longer solely focused on accuracy but now encompass fairness and interpretability, providing a more comprehensive assessment of a system’s performance. Fairness addresses algorithmic biases, while interpretability focuses on the explainability of the recommendations.

While advances have been made, challenges remain, notably in scalability and real-time recommendations. Potential solutions could include adopting more efficient algorithms, particularly those based on deep learning, and using high-performance computing resources.

2.2. GNNs for KG

The integration of GNNs with knowledge graphs has revolutionized the field of recommendation systems, offering a sophisticated approach to understanding the complex relationships among various entities. Traditional recommendation systems have limitations when capturing these complexities, a gap that GNNs have efficiently filled.

The advent of time-sensitive GNNs has been a significant step forward, particularly in dynamic sectors such as e-commerce. These models adapt to the ever-changing relationships between entities by incorporating time-based decay functions, providing a more nuanced approach to personalization [15]. Beyond recommendation systems, GNNs have found a myriad of applications, including (but not limited to) legal case recommendations [16], analyzing art through knowledge graphs [17], and even in the biomedical sector for the extraction of events [18].

Challenges remain in the realm of scalability and handling high-dimensional data. Scalability issues often arise in processing large graphs, necessitating increased computational resources. Emerging solutions such as DistDGL promise to scale GNNs across multiple GPUs [19]. These challenges set the stage for our study, which aimed to address both scalability and adaptability through the TKGRS algorithm. The interaction between GNNs and knowledge graphs has introduced innovative approaches in recommendation systems. These approaches include hybrid models that can harness both structured and unstructured data. Future research will likely focus on developing more efficient graph traversal and analysis algorithms, which could pave the way for more robust and versatile recommendation systems.

2.3. Considering Temporal Aspects in Recommendation Systems

Temporal dynamics have emerged as an essential factor in the development of recommendation systems. A recent comprehensive survey by [20] described how these dynamics can influence the system’s performance. For instance, time-weighted algorithms can adjust the recommendations on the basis of seasonality or users’ activity cycles, ushering in a new era of personalized and context-aware recommendations. These insights are particularly relevant to our study, which aimed to integrate temporal dynamics into the TKGRS algorithm for enhanced performance.

The methodology for incorporating temporal aspects into recommendation systems has seen remarkable evolution. Early work by [21] used matrix factorization techniques to treat different temporal aspects individually, paving the way for more nuanced models. In contrast, recent advancements such as hierarchical temporal convolutional networks [22] have ushered in capabilities of dynamic learning. These models can adapt to short-term and long-term changes in users’ behavior, offering a more comprehensive solution.

Multi-aspect models such as MAPS [23] have also gained attention, fusing categorical, temporal, social, and spatial aspects into a single recommendation model. These holistic models ensure that all potential influences on users’ preferences are considered, adding complexity and effectiveness to recommendation systems. Research by [24] has further explored time- and session-aware diversification, adding another layer of complexity and effectiveness to recommendation systems.

Scalability and high dimensionality continue to pose challenges, especially when processing large volumes of temporal data. A systematic review by [25] emphasized these challenges and suggested future avenues such as efficient data structures and parallel processing techniques. These challenges and suggestions are directly relevant to the current study, which aimed to address issues of scalability through the TKGRS algorithm.

Potential future research avenues include exploring the concept of temporal bias in point-of-interest recommendations, as suggested by [26]. Additionally, examining how temporal processes such as information gathering and decision-making impact users’ interactions could offer valuable insights [27]. These research questions are particularly relevant to our study, which aimed to address similar challenges through the TKGRS algorithm.

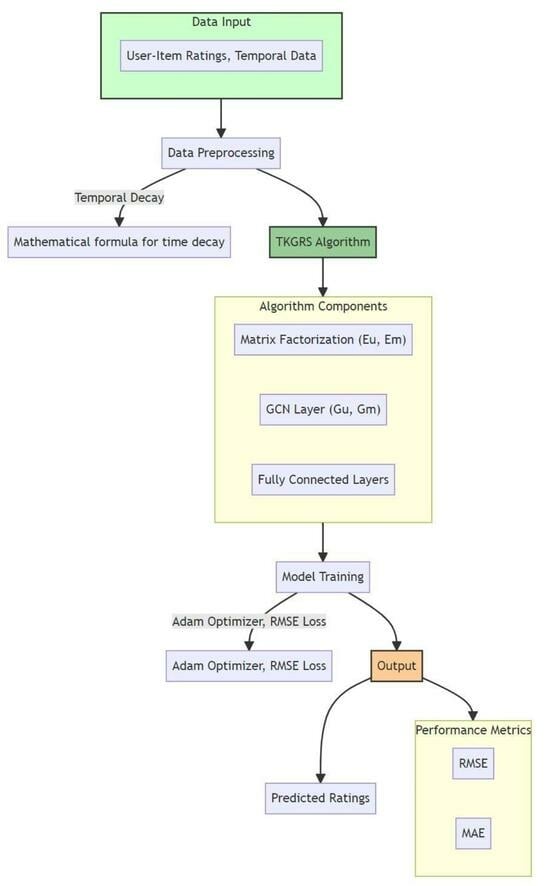
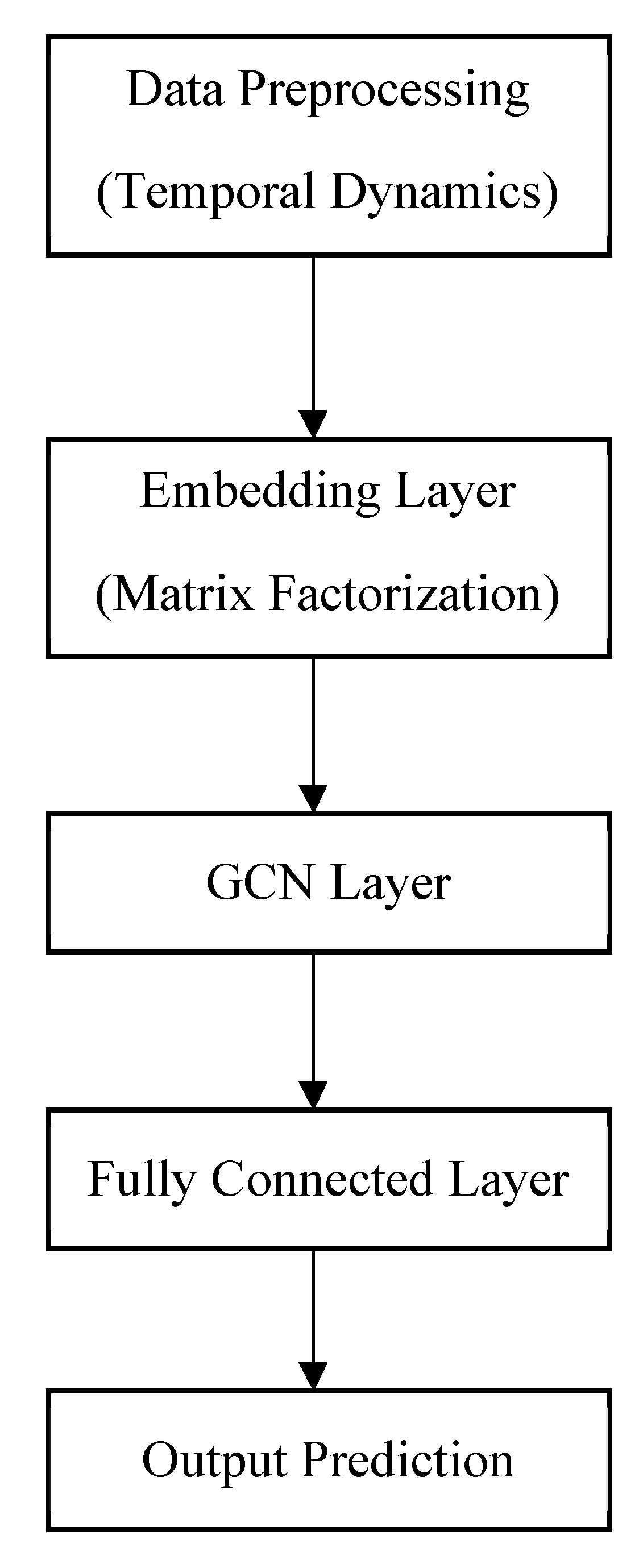
3. The Temporal Knowledge Graph Recommender System

The increasing complexity of user–item interactions has necessitated more sophisticated recommendation systems in recent years. Conventional methods have been found to fall short, especially in accounting for temporal dynamics and intricate user–item relationships. This need for advancement has been emphasized in seminal studies such as those by [20,21]. Our study aimed to address these limitations by introducing the TKGRS algorithm, which makes novel contributions to capturing both temporal and contextual nuances.

The TKGRS algorithm uses a multi-faceted approach to enhance movie recommendations’ accuracy and contextual relevance. Specifically, it starts with matrix factorization techniques for the initial embeddings of the user and item. This captures the linear relationships effectively. The algorithm then utilizes GCNs to update these embeddings, offering a nuanced understanding of complex, non-linear relationships. Additionally, a time decay factor is incorporated to prioritize more recent interactions, adding a temporal dimension to the recommendation process. The TKGRS algorithm aims to provide robust movie recommendations by combining these diverse techniques. It is uniquely positioned to address the static and dynamic aspects of user–item interactions, setting a new benchmark in personalized movie recommendation systems.

Data preprocessing serves as a foundational step in the TKGRS algorithm. One key aspect is the incorporation of a temporal decay factor, set at 0.9, to emphasize more recent user–item interactions. This value was chosen on the basis of preliminary testing and aligns with best practices in the field. The decay factor modifies the original ratings, thereby allowing the model to prioritize newer interactions over older ones.

Mathematically, the updated rating r′ is computed as follows:

$$r^{\prime }=r\times {\mathrm{decay}\text{\_}\mathrm{factor}}^{\left(\max \text{\_}\mathrm{timestamp}-\mathrm{timestamp}\right)}$$

(1)

The model’s architecture is a neural network with three primary components:

• Embedding layer (matrix factorization): This converts the users’ and movies’ IDs into fixed-size vectors (Eu and Em).
• GCN layer: This updates the embeddings using GCN. The mathematical representation for a single-layer GCN is:

$$H_u^{\left(1\right)}=GCN\left(E_u\left(u\right),G_u\right)\mathrm{and}{H}_m^{\left(1\right)}=GCN\left(E_m\left(m\right),G_m\right)$$

3.

Fully connected layers: A fully connected layer sequence maps the updated embeddings to the output prediction.

The model is trained using the Adam optimizer with a learning rate and weight decay. The loss function is RMSE and is defined as

$$RMSE=\sqrt{1/N{{\displaystyle \sum }}_{i=1}^N{\left(r_i-{\widehat{r}}_i\right)}^2}$$

(2)

where $r_i$ is the real rating and ${\widehat{r}}_i$ is the predicted rating.

Next, we can depict our algorithm as shown in Figure 1.

Next, we detail each component of the proposed algorithm as follows.

• Embedding layer: The embedding layer uses matrix factorization through embeddings for users and movies. The embeddings are then used to predict the rating a user would give to a movie. Let R be the original user–item interaction matrix, where R_ij represents the rating given by user i to item j. The neural collaborative filtering step aims to approximate R by learning two matrices, U and M, for users and movies, respectively. Each row in U and M represents the latent factors of a user and a movie to satisfy the equation:

$$\mathit{R}\approx \mathit{U}\times {\mathit{M}}^T$$

(3)

More specifically, given a user u or a movie m, their corresponding embeddings E_u(u) and E_m(m) are looked up from the embedding matrices U and M, respectively, such that

$$E_u\left(u\right)=\mathit{U}\left[u,:\right]$$

(4)

$$E_m\left(m\right)=\mathit{M}\left[m,:\right]$$

(5)

where $\mathit{U}$ is a $n_{users}\times d$ matrix, $\mathit{M}$ is a $n_{movies}\times d$ matrix, and $d$ is the dimensionality of the embedding space.

2.

GCN layer: The GCN layer updates the initial embeddings E_u(u) and E_m(m) by incorporating the topology and features of the respective graphs Gu and Gm, denoting the graph structures for users and movies, respectively. The initial embeddings E_u(u) for users and E_m(m) for movies serve as the initial node features H⁽⁰⁾ for the GCN layer, where a single GCN layer can be represented as

$${\mathit{H}}^{\left(l+1\right)}=\sigma \left({\mathit{D}}^{-\frac{1}{2}}\mathit{A}{\mathit{D}}^{-\frac{1}{2}}{\mathit{H}}^{\left(l\right)}{\mathit{W}}^{\left(l\right)}\right)$$

(6)

where H^(l) is the matrix of the node features at the lth layer, A is the adjacency matrix, D is the degree matrix, W^(l) is the weight matrix at the lth layer, and σ is the activation function, which is ReLU here. The GCN layer calculates the weighted sum of its neighbors’ features for each node. The aggregated features are transformed by a weight matrix and passed through an activation function. The embeddings are updated for subsequent layers or the final prediction.

3.

Fully connected layers: The updated embeddings ${\mathit{H}}_{\mathit{u}}{}^{\left(l\right)}$ and ${\mathit{H}}_m{}^{\left(l\right)}$ are concatenated along the feature dimension. This results in a new feature vector F for each (user, movie) pair, such that:

$$\mathit{F}=\mathrm{Concat}\left({\mathit{H}}_{\mathit{u}}{}^{\left(l\right)};{\mathit{H}}_m{}^{\left(l\right)}\right)\in {\mathbb{R}}^{2d}$$

(7)

Before feeding F into the fully connected layers, it is often subject to dropout layers and non-linear activations to introduce regularization and complexity. F is then passed through one or more fully connected layers. Each layer can be represented mathematically as

$${\mathit{Y}}^{l+1}=\sigma \left({\mathit{W}}^{\left(l\right)}\mathit{F}+{\mathit{b}}^{\left(l\right)}\right)$$

(8)

where ${\mathit{Y}}^{l+1}$ is the output of the fully connected layer l + 1, ${\mathit{W}}^{\left(l\right)}$ is the weight matrix, ${\mathit{b}}^{\left(l\right)}$ is the bias term, and $\sigma \left(·\right)$ is an activation function.

The final layer is a single unit with a sigmoid activation function, scaled to the range of the ratings, to make the final prediction, and is represented as

$$\widehat{\mathit{r}}=\sigma \left({\mathit{W}}^{\left(L\right)}{\mathit{Y}}^L+{\mathit{b}}^{\left(L\right)}\right)$$

(9)

where $\widehat{\mathit{r}}$ is the predicted rating and L is the final layer.

The pseudo-codes of the proposed Algorithm 1 can be described as follows.

Algorithm 1: Pseudo-codes

Input: User IDs Movie IDs User graph data Movie graph data Stopping criterion (maximum epochs, patience for early stopping) Output: Predicted ratings Initialize: Best Loss ←∞ No Improvements ←0 Steps: Initial embedding User_Embeddings = Embedding(nusers,nfactors)(User_IDs)) Movie_Embeddings = Embedding(nmovies,nfactors)(Movie_IDs) GCN layer Updated_User_Embeddings = GCNConv(nfactors,gcn_output)(User_Embeddings,User_Graph_Data.edge_index) Updated_Movie_Embeddings = CNConv(nfactors,gcn_output)(Movie_Embeddings,Movie_Graph_Data.edge_index) Concatenation of updated embeddings Concatenated_Embeddings = Concatenate([Updated_User_Embeddings,Updated_Movie_Embeddings]) Fully connected layers Hidden_Layer_Outputs = σ(Concatenated_Embeddings) Final output layer Predicted_Ratings = σ(Hidden_Layer_Outputs) Compute loss Current_Loss = LossFunction(Predicted_Ratings,True_Ratings) Stopping criterion If Current_Loss < Best Loss Best Loss←Current_Loss No Improvements←0 Else No Improvements+=1 If No Improvements ≥ Patience or Epoch = Max Epochs Stop and return Best Loss

The TKGRS model addresses the static and dynamic aspects of user–item interactions, setting a new standard in personalized recommendation systems. The model prioritizes more recent interactions by applying a decay factor to historical ratings. The GCN layer enhances the quality of recommendations by capturing complex relationships and dependencies between users and movies.

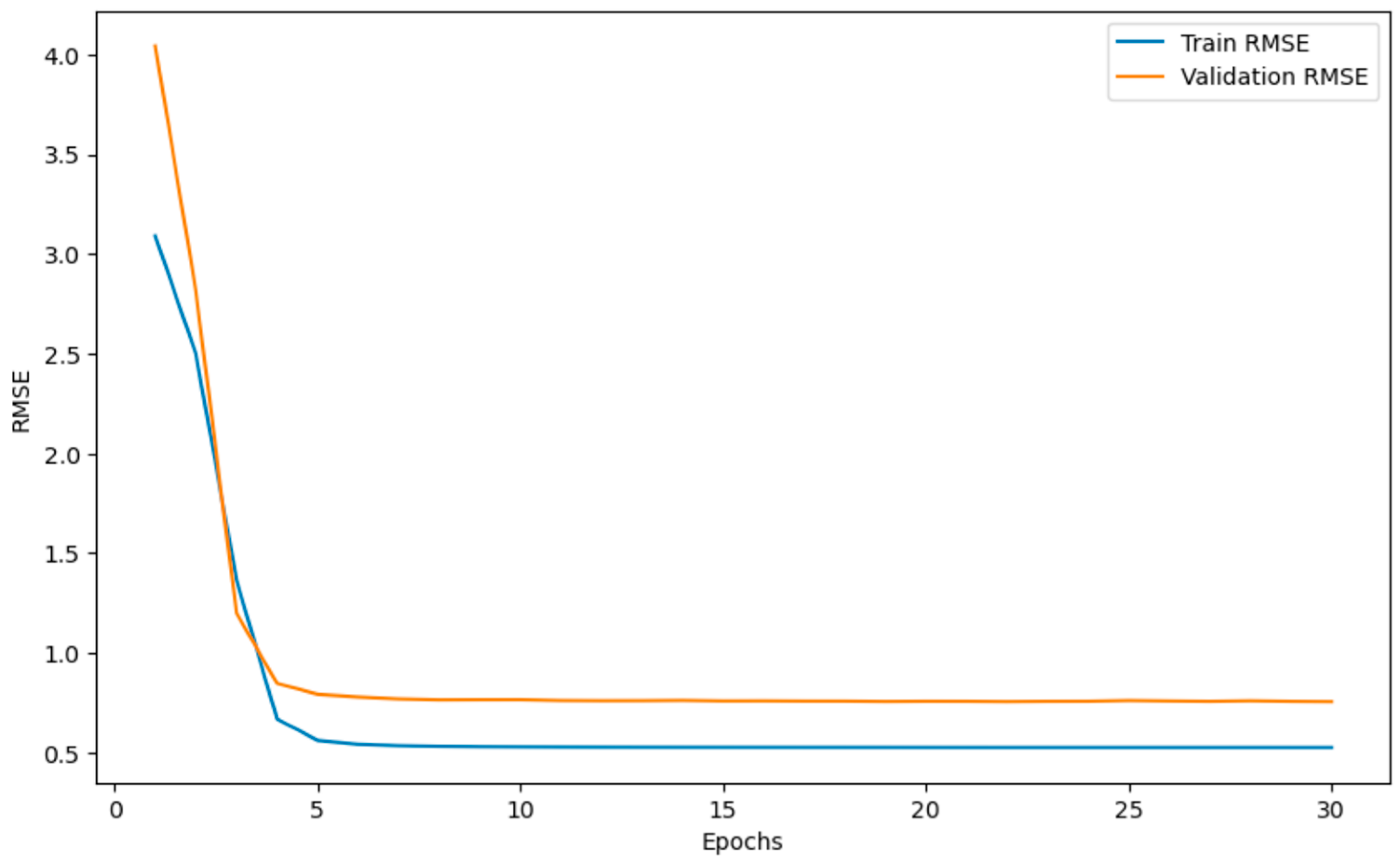
4. Experiments

Movie recommendation systems are indispensable tools in today’s digital world, particularly in the era of information overload. While traditional recommendation methods such as collaborative filtering and content-based filtering have their merits, they lack the sophistication to adapt to the dynamic and evolving nature of users’ preferences and interactions with items. The present study aimed to address these limitations by evaluating the TKGRS, an innovative algorithm that synergistically integrates matrix factorization, GCNs, and temporal decay factors.

The experiments utilized three well-established movie datasets: MovieLens 100K, MovieLens 1M, and the Douban Conversation Corpus. The MovieLens 100K and 1M datasets consist of 100,000 and 1 million movie ratings by users, respectively. These datasets stand as seminal benchmarks in the movie recommendation systems domain. In contrast, the Douban Conversation Corpus was purpose-built for retrieval-based chatbots, and encompasses 1 million session–response pairs in the training set, 50,000 in the validation set, and 10,000 in the test set. Each dataset offers unique challenges and complexities, making them ideal for evaluating the TKGRS algorithm, which notably incorporates a temporal decay factor to adapt to dynamic user–item interactions.

Table 1. Model parameters.

Parameter	Value
Number of factors	50
Hidden layers	50
Dropout rate	0.2
Batch size	4096
Learning rate	$1\times {10}^{-3}$
Weight decay	$1\times {10}^{-5}$
Number of epochs	30
Optimizer	Adam
Loss Function	RMSE, MAE

outlines the selected hyperparameters, determined through extensive preliminary testing to optimize the performance.

The datasets were divided into 80% for training and 20% for the validation subset. We used the Adam optimizer for training, which spanned 30 epochs. An early-stopping criterion was also implemented to prevent overfitting.

Next, with the dataset MovieLens 100K dataset as an example, the training and validation’s RMSE can be shown as in Figure 2. As depicted in Figure 2, the training and validation RMSE for the MovieLens 100K dataset showed consistent improvement over epochs, validating the effectiveness of the TKGRS algorithm.

We benchmarked TKGRS against the existing state-of-the-art models, i.e., LFM-SPE [28] GHRS [29], Glocal-K [30], MG-GAT [31], T-ULVD [32], JK-DMC [33], SparseFC [34], and CF-NADE [35], as shown in

Table 2. The comparison of different algorithms.

MovieLens 100K	Model	RMSE	MAE	p-Value
	LFM-SPE	0.795	0.661
	GHRS	0.887	0.685
	GLocal-K	0.889	0.690
	MG-GAT	0.890	0.692
	T-ULVD	0.892	0.701
	Proposed model	0.757	0.590	0.000
MovieLens 1M	Model	RMSE	MAE	p-value
	LFM-SPE	0.736	0.638
	GLocal-K	0.823	0.640
	SparseFC	0.824	0.643
	CF-NADE	0.829	0.645
	T-ULVD	0.848	0.669
	Proposed model	0.722	0.565	0.0174
Douban	Model	RMSE	MAE	p-value
	JK-DMC	0.718	0.517
	GLocal-K	0.721	0.521
	MG-GAT	0.737	0.541
	SparseFC	0.745	0.551
	Proposed model	0.712	0.511	0.000

. As indicated in Table 2, TKGRS not only validated the efficacy of integrating GCNs and temporal decay factors but also set a new performance standard. In addition, we also used the t-test to compare the difference in the mean RMSE between the best benchmark and the proposed algorithms with 10 runs. The P-values were all below the significance level, i.e., 0.05, and hence confirmed that TKGRS performs best, according to the RMSE criterion.

TKGRS demonstrated competitive performance when compared with state-of-the-art models. Its true potential, however, lies in its capacity to integrate GCNs and temporal decay factors effectively. This opens up avenues for further enhancements, such as incorporating more advanced graph algorithms and exploring additional optimization techniques.

Table 3. Comparison between different algorithms.

Models	Pros	Cons
GHRS	The hybrid approach combines multiple features, providing robust recommendations	Lacks a temporal component, thereby not accounting for users’ recent behavior
GLocal-K	Focuses on both local and global patterns, providing balanced recommendations	Not as sophisticated in capturing complex relationships
MG-GAT	Captures complex relationships through multiple graphs	Does not account for temporal dynamics
SparseFC	Requires fewer parameters than traditional fully connected layers, making it computationally efficient	The performance is highly dependent on the choice of the kernel function, which may require expertise to select appropriately
CF-NADE	Specifically designed for collaborative filtering tasks where data sparsity is a common issue, providing a more nuanced model	The algorithm’s time complexity can be high, especially when the hidden representation’s dimensions and the number of possible ratings are large
TKGRS	Incorporates a time decay factor, thus adding a temporal dimension. Utilizes graph convolutional networks (GCNs) for a sophisticated understanding of the complex relationships between users and items	The complexity may be higher due to the incorporation of GCNs, which could make it slower for larger datasets

presents a theoretical assessment of each algorithm’s advantages and disadvantages.

In summary, TKGRS distinguished itself through its incorporation of a time decay factor and the use of GCNs, enabling the capture of complex non-linear relationships between users and items. Although computationally more intensive than some alternatives, its performance metrics justify its resource requirements, especially when juxtaposed with fully connected graph-based models such as MG-GAT. It remains a compelling option for systems where a balance between accuracy and computational efficiency is paramount. Nonetheless, the computational demands may escalate for exceedingly large graphs, a challenge that is not unique to TKGRS but is intrinsic to graph-based models.

5. Discussion

Recent research in movie recommendation systems has made significant strides, exploring various domains such as IoT scenarios [36], multi-task learning [37], and deep learning [38]. While these studies offer substantial advances, they frequently overlook the importance of temporal dynamics in user–item interactions. TKGRS fills this research gap by seamlessly integrating a temporal decay factor alongside GCNs and matrix factorization.

The TKGRS makes a transformative contribution to the field of recommendation system. By uniquely incorporating temporal dynamics through a decay factor, it adds a dynamic layer to the process of recommendation. This feature, validated through RMSE and MAE metrics on the MovieLens and Douban datasets, surpassed existing models and provided a more robust alternative for research into recommendation systems. TKGRS not only outperformed the others in terms of the RMSE and MAE metrics but also stood strong when qualitatively compared with existing state-of-the-art models. The algorithm uniquely incorporates temporal dynamics through a decay factor, adding a dynamic layer to the recommendation process.

Despite its strengths, TKGRS has limitations. The computational complexity associated with GCNs might limit its scalability, especially for large datasets. Future research could focus on enhancing the algorithm’s robustness against adversarial attacks and exploring its scalability. Moreover, while the choice of hyperparameters has been optimized, it has not been exhaustively explored, leaving room for potential improvements. Studies could also focus on addressing data sparsity issues and extending its applicability across diverse sectors such as healthcare, e-commerce, and smart cities.

TKGRS not only outperformed the others in terms of RMSE and MAE metrics but also stood strong when qualitatively compared with existing state-of-the-art models, such as those discussed in the survey on knowledge graph-based recommendation systems by [39]. Unlike these models, TKGRS addresses the challenges of users’ dynamic preference, offering a more comprehensive solution. In conclude, TKGRS provides a more holistic solution that takes the temporal changes in users’ behavior into account, thereby standing strong both quantitatively and qualitatively when compared with existing models.

6. Conclusions

In an era of information overload and rapidly evolving user behavior, the shortcomings of traditional movie recommendation systems have become increasingly glaring. This study introduced TKGRS, an innovative algorithm that effectively addresses these challenges by incorporating GCNs, matrix factorization, and temporal dynamics. TKGRS exhibits a unique capability to capture both the static and dynamic aspects of user–item interactions. It revolutionizes the recommendation process by adding a dynamic layer through a temporal decay factor, ensuring that recent interactions hold greater weight. Further, integrating GCN layers significantly enhances the model’s understanding of the complex relationships between users and items. Empirical validation on the MovieLens 100K, 1M, and Douban datasets confirmed its robust performance, outperforming existing state-of-the-art models.

In conclusion, TKGRS marks a significant advancement in personalized recommendations. It offers a comprehensive solution to the multi-faceted challenges of user–item interactions, setting a new benchmark in the field. As such, it provides a robust foundation for future research, including exploring more advanced graph algorithms and machine learning techniques to advance recommendation system’s capabilities continually.