A Bayesian Analysis of the Inversion of the SARS-COV-2 Case Rate in the Countries of the 2020 European Football Championship
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Bayesian Changepoint Detection and Analysis
3. Results
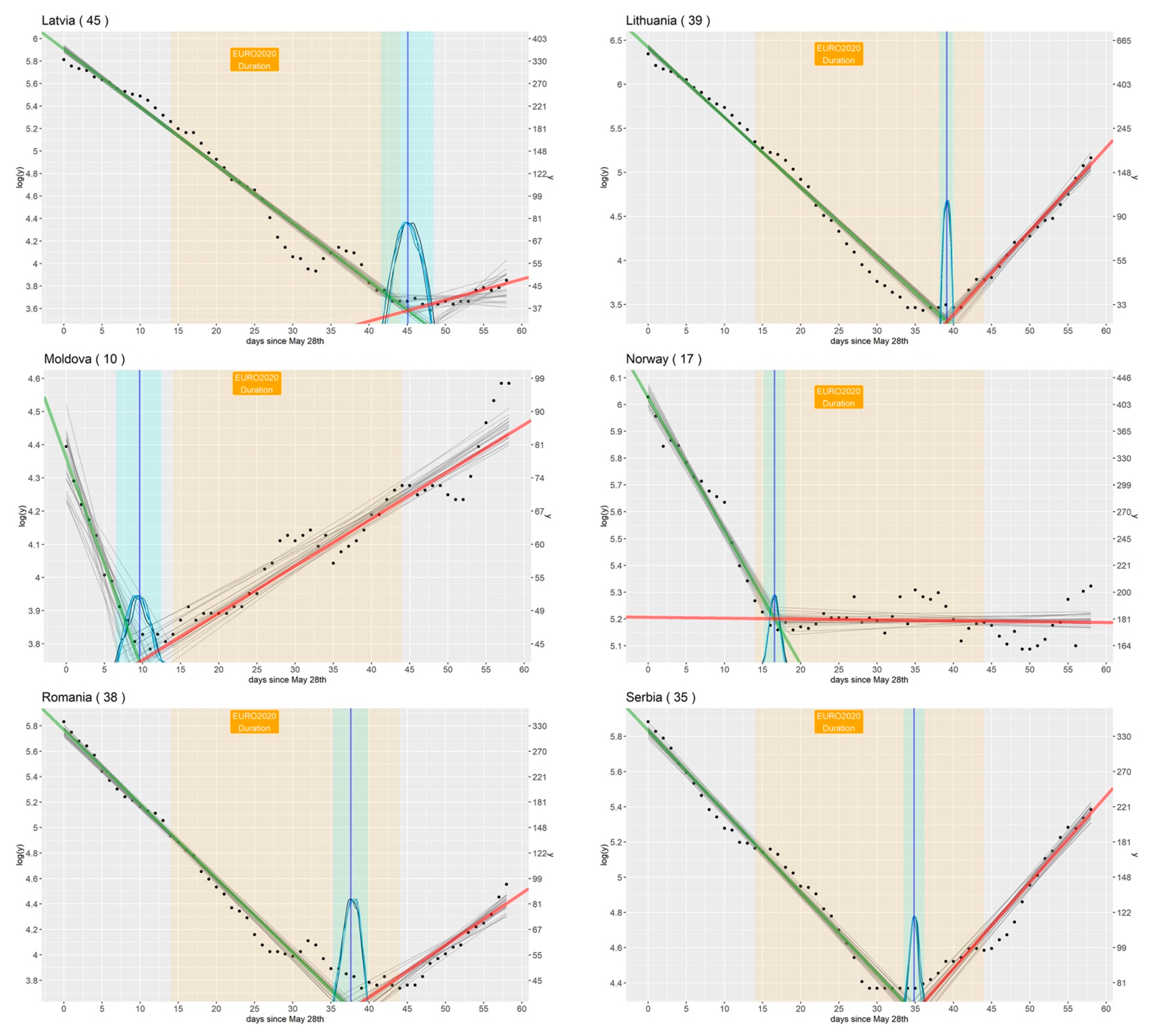
3.1. Countries That Participated in the Tournament
3.2. Countries That Did Not Participate in the Tournament
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Thomasson, E. German Minister Chides ‘Irresponsible’ UEFA over Euro 2020 Crowds. Reuters. 2021. Available online: https://www.reuters.com/world/europe/german-minister-slams-uefas-decision-fuller-stadiums-2021-07-01/ (accessed on 28 July 2021).
- World Health Organization. Statement by Dr Hans Henri P. Kluge, WHO Regional Director for Europe. 2021. Available online: https://www.euro.who.int/en/media-centre/sections/statements/2021/statement-covid-19-the-stakes-are-still-high (accessed on 28 July 2021).
- Henley, J.; Rankin, J. COVID: Euro 2020 Crowds ‘a Recipe for Disaster’, Warns EU Committee”, The Guardian. 2021. Available online: https://www.theguardian.com/world/2021/jul/01/covid-euro-2020-crowds-a-recipe-for-disaster-warns-german-minister0 (accessed on 28 July 2021).
- UEFA. Euro 2020 Key Information for Spectators. 2021. Available online: https://www.uefa.com/uefaeuro-2020/news/025b-0ef33753d7d0-100629325be2-1000--key-information-for-euro-spectators/ (accessed on 28 July 2021).
- Italian Associated Press Agency (ANSA). Cluster of 91 COVID-19 Cases Linked to Euro 2020 Game. 2021. Available online: https://www.ansa.it/english/news/general_news/2021/07/16/cluster-of-91-covid-19-cases-linked-to-euro-2020-game_84349124-e130-453b-ade2-8b7136bd8993.html (accessed on 28 July 2021).
- Kington, T. Italy’s Euro 2020 Victory Tour Sent Rome Cases Rocketing. The Times. 22 July 2021, pp. 1–4. Available online: https://www.thetimes.co.uk/article/italys-euro-2020-victory-tour-sent-rome-cases-rocketing-r6m667r0b (accessed on 28 July 2021).
- Peltier, E. Crowds for European Championship Soccer Games Are Driving Infections, the W.H.O. Says. New York Times. 1 July 2021, pp. 1–2. Available online: https://www.nytimes.com/2021/07/01/world/europe/euro-2020-covid-outbreak.html (accessed on 28 July 2021).
- Skydsgaard, N.; Gronholt-Pedersen, J. Euro 2020 Crowds Driving Rise in COVID-19 Infections, Says WHO. Reuters. 2021. Available online: https://www.reuters.com/world/europe/who-warns-third-coronavirus-wave-europe-2021-07-01/ (accessed on 28 July 2021).
- Schumacher, Y.O.; Tabben, M.; Hassoun, K.; Al Marwani, A.; Al Hussein, I.; Coyle, P.; Abbassi, A.K.; Ballan, H.T.; Al-Kuwari, A.; Chamari, K.; et al. Resuming professional football (soccer) during the COVID-19 pandemic in a country with high infection rates: A prospective cohort study. Br. J. Sports Med. 2021, 1–11. [Google Scholar] [CrossRef]
- Kochańczyk, M.; Grabowski, F.; Lipniacki, T. Super-spreading events initiated the exponential growth phase of COVID-19 with 0 higher than initially estimated. R. Soc. Open Sci. 2020, 7, 200786. [Google Scholar] [CrossRef] [PubMed]
- Weed, M.; Foad, A. Rapid Scoping Review of Evidence of Outdoor Transmission of COVID-19. medRxiv 2020, 1–16. Available online: https://www.medrxiv.org/content/10.1101/2020.09.04.20188417v2 (accessed on 16 August 2021).
- Cereda, D.; Tirani, M.; Rovida, F.; Demicheli, V.; Ajelli, M.; Poletti, P.; Trentini, F.; Guzzetta, G.; Marziano, V.; Barone, A.; et al. The early phase of the COVID-19 outbreak in Lombardy, Italy. arXiv 2020, arXiv:2003.0932. [Google Scholar]
- Mercker, M.; Betzin, U.; Wilken, D. What influences COVID-19 infection rates: A statistical approach to identify promising factors applied to infection data from Germany. medRxiv 2020, 1–12. Available online: https://www.medrxiv.org/content/10.1101/2020.04.14.20064501v1 (accessed on 16 August 2021).
- Signorelli, C.; Odone, A.; Riccò, M.; Bellini, L.; Croci, R.; Oradini-Alacreu, A.; Fiacchini, D.; Burioni, R. Major sports events and the transmission of SARS-CoV-2: Analysis of seven case-studies in Europe. Acta Biomed. 2020, 91, 242–244. [Google Scholar] [CrossRef]
- El Hassan, N. Deloitte’s Sports Business Group Estimates That Football Money League Clubs Will Miss out on Revenue of over €2 Billion by End of the 2020/21 Season Due to the COVID-19 Pandemic. 2021. Available online: https://www2.deloitte.com/xe/en/pages/about-deloitte/articles/deloittes-sports-business-group-estimates-football-money-league-miss-out-revenue-over-2euros-billion-end-202021-due-covid.html (accessed on 28 July 2021).
- Our World in Data. COVID-19 GitHub Repository. 2021. Available online: https://github.com/owid/covid-19-data/blob/master/public/data/README.md (accessed on 28 July 2021).
- Wikipedia. European Football Championship 2020. Available online: https://en.wikipedia.org/wiki/UEFA_Euro_2020 (accessed on 28 July 2021).
- Lindeløv, J.K. mcp: An R Package for Regression with Multiple Change Points. 2020. Available online: https://osf.io/fzqxv/ (accessed on 28 July 2021).
- Sebastiani, G.; Palù, G. COVID-19 and School Activities in Italy. Viruses 2020, 12, 1339. [Google Scholar] [CrossRef] [PubMed]
- Casini, L.; Roccetti, M. Reopening Italy’s schools in September 2020: A Bayesian estimation of the change in the growth rate of new SARS-CoV-2 cases. BMJ Open 2021, 11, e051458. [Google Scholar] [CrossRef]
- Tosi, D.; Campi, A. How Data Analytics and Big Data Can Help Scientists in Managing COVID-19 Diffusion: Modeling Study to Predict the COVID-19 Diffusion in Italy and the Lombardy Region. J. Med. Internet Res. 2020, 22, e21081. [Google Scholar] [CrossRef] [PubMed]
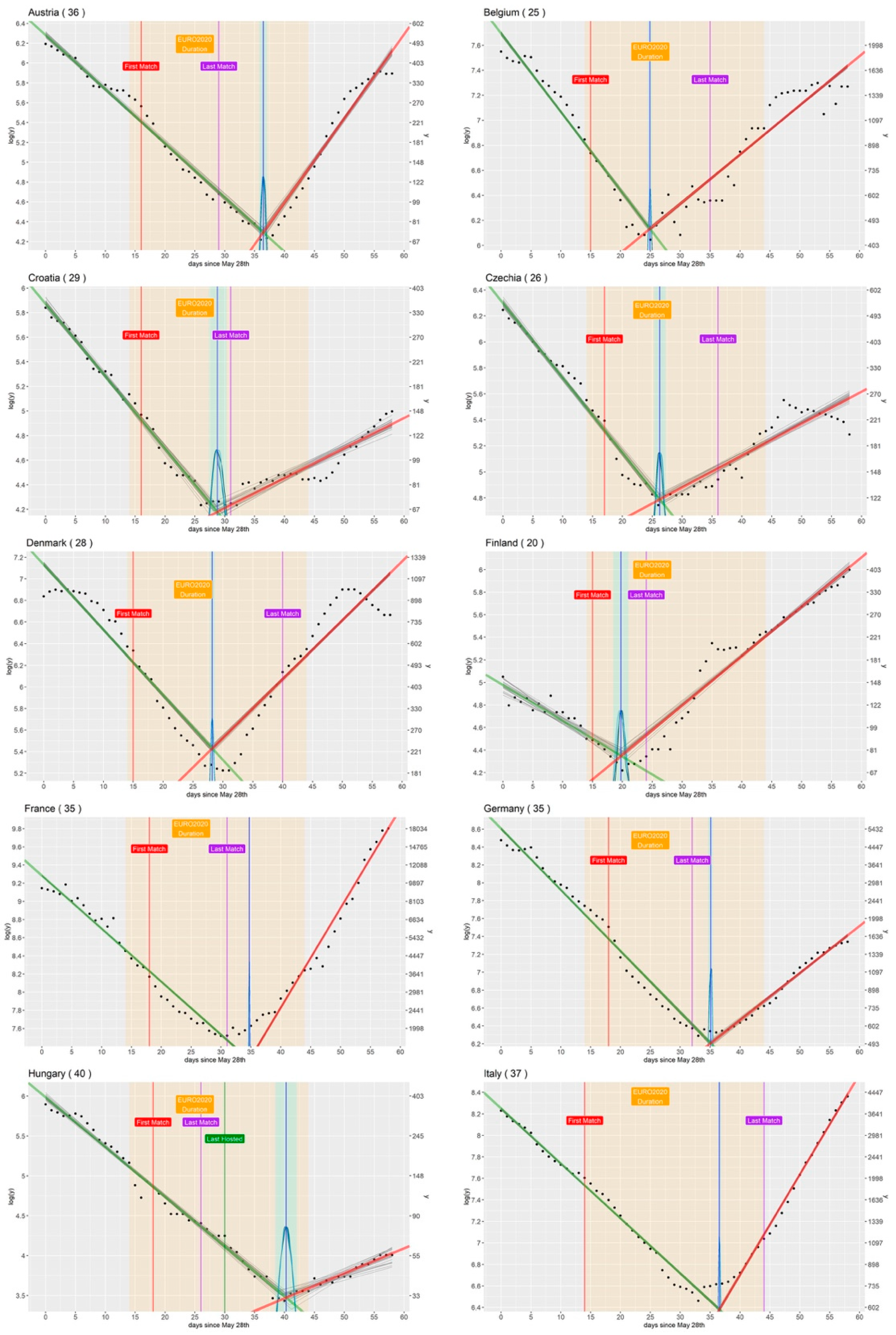
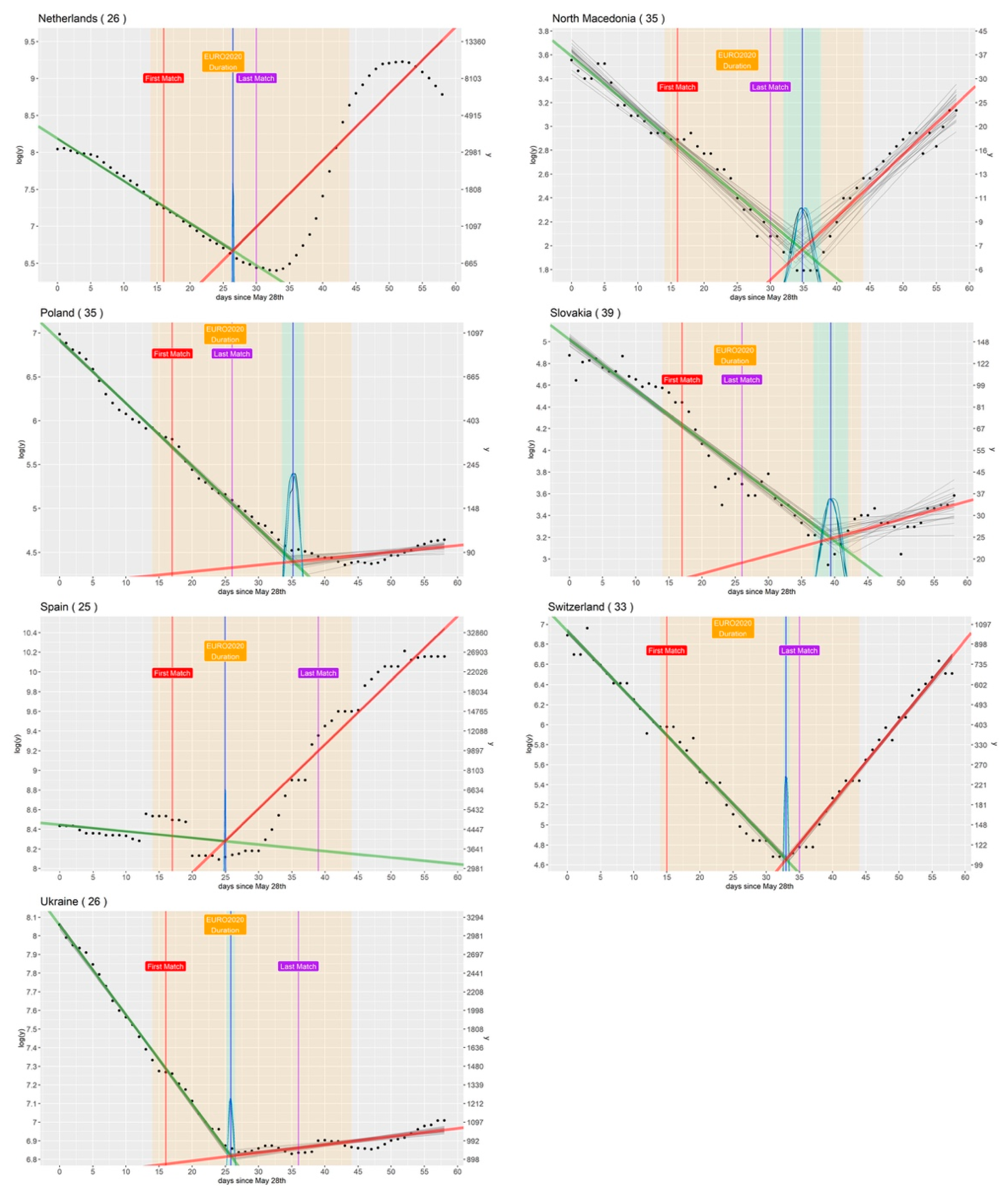
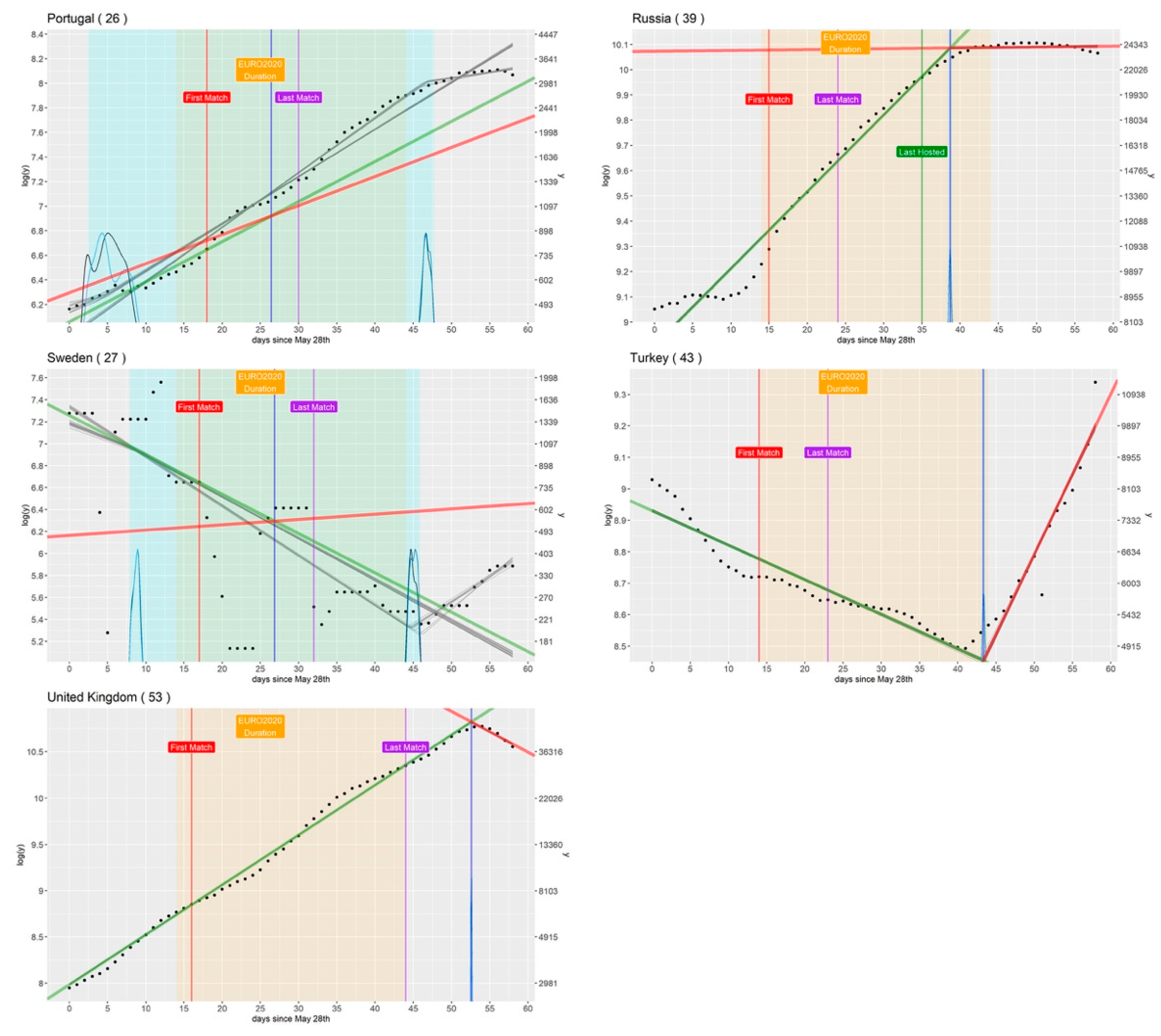
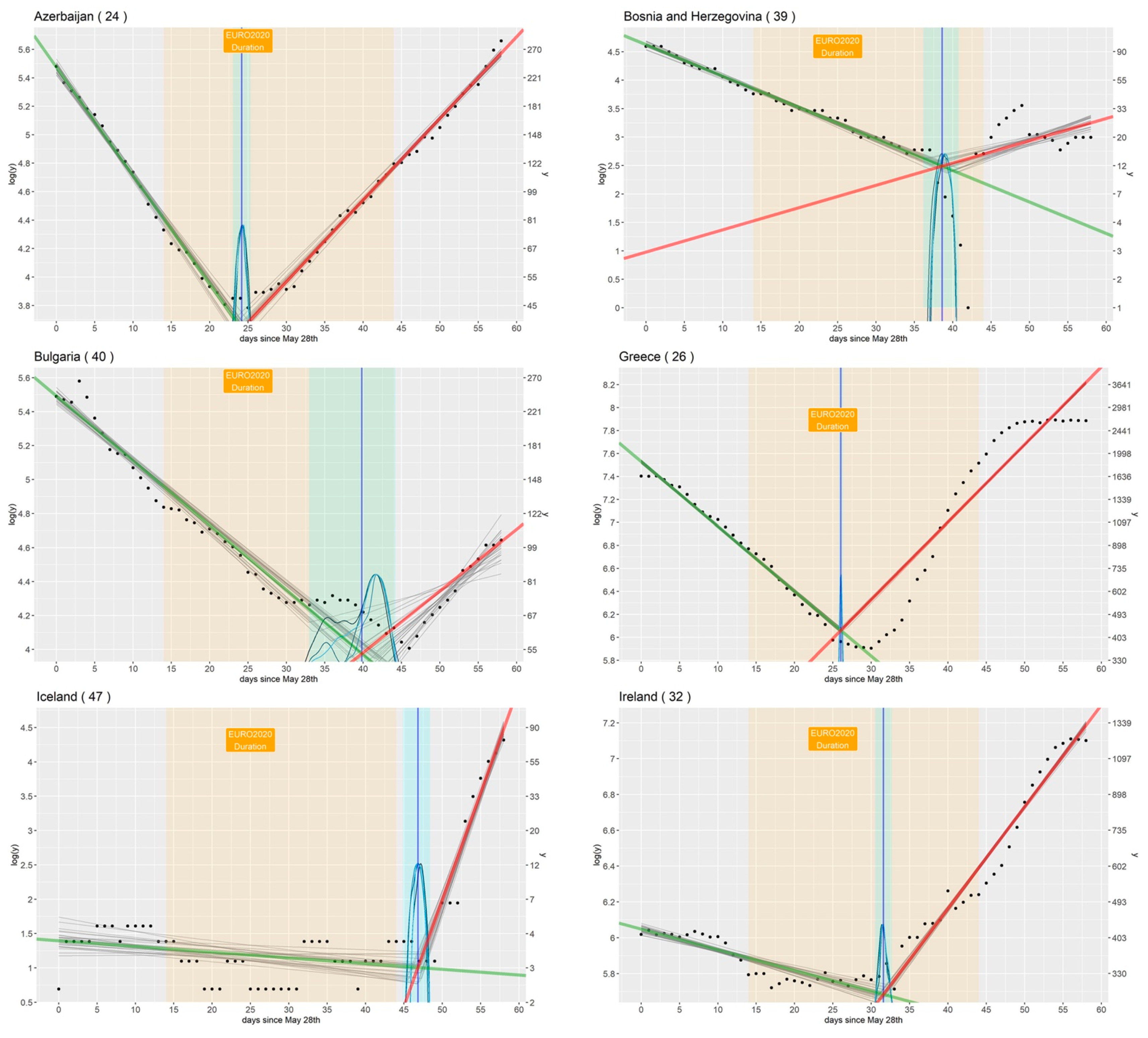
| Country (Participating in the Tournament) | τ (Changepoint, avg. Value and 95% CI) | Diff (Days Separating τ from First Match) | b1 (Angular Coefficient before τ, avg. Value and 95% CI) | b2 (Angular Coefficient after τ, avg. Value and 95% CI) | a1 (Intercept before τ, avg. Value and 95% CI) |
|---|---|---|---|---|---|
| Austria | 36.4 (35.8, 37.1) | 20 | −0.05 (−0.06, −0.05) | 0.08 (0.08, 0.09) | 6.28 (6.25, 6.32) |
| Belgium | 24.9 (24.6, 25.2) | 10 | −0.06 (−0.06, −0.06) | 0.04 (0.04, 0.04) | 7.70 (7.68, 7.71) |
| Croatia | 28.7 (27.4, 30.3) | 13 | −0.06 (−0.06, −0.06) | 0.02 (0.02, 0.03) | 5.87 (5.83, 5.92) |
| Czechia | 26.2 (25.3, 27.2) | 9 | −0.06 (−0.06, −0.05) | 0.02 (0.02, 0.03) | 6.30 (6.26, 6.34) |
| Denmark | 28.2 (27.8, 28.6) | 13 | −0.06 (−0.06, −0.06) | 0.05 (0.05, 0.06) | 7.13 (7.11, 7.15) |
| Finland | 19.8 (18.4, 21.0) | 5 | −0.03 (−0.04, −0.03) | 0.04 (0.04, 0.05) | 4.98 (4.90, 5.05) |
| France | 34.7 (34.6, 34.8) | 17 | −0.06 (−0.06, −0.06) | 0.11 (0.11, 0.11) | 9.28 (9.28, 9.29) |
| Germany | 35.1 (34.6, 35.5) | 17 | −0.07 (−0.07, −0.07) | 0.05 (0.05, 0.05) | 8.60 (8.59, 8.62) |
| Hungary | 40.3 (38.4, 42.0) | 22 | −0.06 (−0.06, −0.06) | 0.03 (0.02, 0.05) | 5.99 (5.95, 6.03) |
| Italy | 36.5 (36.3, 36.8) | 23 | −0.05 (−0.05, −0.05) | 0.09 (0.09, 0.10) | 8.25 (8.24, 8.26) |
| Netherlands | 26.4 (26.2, 26.6) | 10 | −0.06 (−0.06, −0.06) | 0.09 (0.09, 0.09) | 8.18 (8.17, 8.20) |
| N. Macedonia | 34.8 (31.9, 37.6) | 19 | −0.05 (−0.05, −0.04) | 0.05 (0.04, 0.07) | 3.59 (3.46, 3.72) |
| Poland | 35.2 (33.5, 36.8) | 18 | −0.07 (−0.07, −0.07) | 0.01 (−0.00, 0.01) | 6.92 (6.89, 6.94) |
| Slovakia | 39.4 (36.8, 42.1) | 22 | −0.05 (−0.05, −0.04) | 0.02 (0.00, 0.03) | 5.02 (4.96, 5.08) |
| Spain | 24.9 (24.8, 25.0) | 8 | −0.01 (−0.01, −0.01) | 0.07 (0.06, 0.07) | 8.45 (8.44, 8.46) |
| Switzerland | 32.9 (32.5, 33.5) | 18 | −0.07 (−0.07, −0.07) | 0.08 (0.08, 0.08) | 6.93 (6.91, 6.96) |
| Ukraine | 25.8 (25.1, 26.5) | 10 | −0.05 (−0.05, −0.05) | 0.00 (0.00, 0.01) | 8.06 (8.04, 8.07) |
| Country | Days Needed to Halve the Number of Cases (before τ) | Days Needed to Double the Number of Cases (after τ) |
|---|---|---|
| Austria | 12.69 | 8.18 |
| Belgium | 11.05 | 17.60 |
| Croatia | 11.77 | 28.32 |
| Czechia | 12.05 | 28.22 |
| Denmark | 11.49 | 12.71 |
| Finland | 21.81 | 15.84 |
| France | 11.86 | 6.32 |
| Germany | 10.14 | 13.17 |
| Hungary | 11.10 | 22.10 |
| Italy | 13.56 | 7.43 |
| Netherlands | 12.11 | 7.69 |
| N. Maced. | 14.88 | 13.20 |
| Poland | 9.67 | 92.80 |
| Slovakia | 14.91 | 41.59 |
| Spain | 103.50 | 10.62 |
| Switzerland | 10.03 | 8.56 |
| Ukraine | 14.43 | 159.00 |
| Country (Participating in the Tournament) | τ (Changepoint, avg. Value and 95% CI) | Diff (Days Separating τ from First Match) | b1 (Angular Coefficient before τ, avg. Value and 95% CI) | b2 (Angular Coefficient after τ, avg. Value and 95% CI) | a1 (Intercept before τ, avg. Value and 95% CI) |
|---|---|---|---|---|---|
| Portugal | 26.4 (2.4, 47.7) | 8 | 0.03 (0.01, 0.05) | 0.08 (0.08, 0.09) | 6.28 (6.25, 6.32) |
| Russia | 38.7 (38.4, 39.0) | 24 | 0.03 (−0.03, −0.03) | 0.00 (0.00, 0.00) | 8.91 (8.90, 8.91) |
| Sweden | 26.9 (7.9, 45.8) | 10 | −0.04 (−0.05, −0.02) | 0.00 (−0.04, 0.05) | 7.26 (7.15, 7.36) |
| Turkey | 43.4 (43.1, 43.6) | 29 | −0.01 (−0.01, −0.01) | 0.05 (0.05, 0.06) | 8.93 (8.92, 8.94) |
| UK | 52.6 (27.8, 28.6) | 37 | 0.05 (0.05, −0.05) | −0.04 (−0.05, −0.04) | 7.99 (7.98, 7.99) |
| Country (Participating in the Tournament) | τ (Changepoint, avg. Value and 95% CI) | Diff (Days Separating τ from Beginning of Tournament) | b1 (Angular Coefficient before τ, avg. Value and 95% CI) | b2 (Angular Coefficient after τ, avg. Value and 95% CI) | a1 (Intercept before τ, avg. Value and 95% CI) |
|---|---|---|---|---|---|
| Moldova | 9.63 (6.52, 12.52) | −4 | −0.06 (−0.10, −0.03) | 0.01 (0.01, 0.02) | 4.36 (4.21, 4.50) |
| Norway | 16.56 (15.09, 17.98) | 3 | −0.05 (−0.06, −0.04) | −0.00 (−0.00, 0.00) | 6.03 (5.98, 6.07) |
| Azerbaijan | 24.16 (23.00, 25.32) | 10 | −0.08 (−0.08, −0.07) | 0.06 (0.05, 0.06) | 5.47 (5.41, 5.54) |
| Greece | 26.03 (25.77, 26.31) | 12 | −0.06 (−0.06, −0.06) | 0.07 (0.07, 0.07) | 7.53 (7.51, 7.55) |
| Ireland | 31.58 (30.53, 32.68) | 18 | −0.01 (−0.01, −0.01) | 0.06 (0.05, 0.06) | 6.05 (6.01, 6.08) |
| Serbia | 34.84 (33.49, 36.20) | 21 | −0.05 (−0.05, −0.04) | 0.05 (0.04, 0.06) | 5.83 (5.79, 5.87) |
| Lithuania | 39.12 (38.17, 40.08) | 25 | −0.08 (−0.08, −0.08) | 0.09 (0.08, 0.10) | 6.42 (6.39, 6.45) |
| Latvia | 45.07 (41.54, 48.44) | 31 | −0.05 (−0.05, −0.05) | 0.02 (−0.01, 0.05) | 5.91 (5.87, 5.94) |
| Romania | 37.60 (35.21, 39.90) | 24 | −0.06 (−0.06, −0.06) | 0.04 (0.03, 0.05) | 5.77 (5.72, 5.82) |
| Bosnia and Herzegovina | 38.61 (36.16, 40.76) | 25 | −0.06 (−0.06, −0.05) | 0.04 (0.02, 0.06) | 4.63 (4.55, 4.70) |
| Bulgaria | 39.82 (32.97, 44.20) | 26 | −0.04 (−0.04, −0.03) | 0.04 (0.01, 0.06) | 5.49 (5.44, 5.55) |
| Iceland | 46.82 (44.85, 48.43) | 33 | −0.01 (−0.02, 0.00) | 0.31 (0.27, 0.36) | 1.40 (1.11, 1.70) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casini, L.; Roccetti, M. A Bayesian Analysis of the Inversion of the SARS-COV-2 Case Rate in the Countries of the 2020 European Football Championship. Future Internet 2021, 13, 212. https://doi.org/10.3390/fi13080212
Casini L, Roccetti M. A Bayesian Analysis of the Inversion of the SARS-COV-2 Case Rate in the Countries of the 2020 European Football Championship. Future Internet. 2021; 13(8):212. https://doi.org/10.3390/fi13080212
Chicago/Turabian StyleCasini, Luca, and Marco Roccetti. 2021. "A Bayesian Analysis of the Inversion of the SARS-COV-2 Case Rate in the Countries of the 2020 European Football Championship" Future Internet 13, no. 8: 212. https://doi.org/10.3390/fi13080212
APA StyleCasini, L., & Roccetti, M. (2021). A Bayesian Analysis of the Inversion of the SARS-COV-2 Case Rate in the Countries of the 2020 European Football Championship. Future Internet, 13(8), 212. https://doi.org/10.3390/fi13080212







