Abstract
With the rapid proliferation of wireless traffic and the surge of various data-intensive applications, the energy consumption of wireless networks has tremendously increased in the last decade, which not only leads to more CO2 emission, but also results in higher operating expenditure. Consequently, energy efficiency (EE) has been regarded as an essential design criterion for future wireless networks. This paper investigates the problem of EE maximisation for a cooperative heterogeneous network (HetNet) powered by hybrid energy sources via joint base station (BS) switching (BS-Sw) and power allocation using combinatorial optimisation. The cooperation among the BSs is achieved through a coordinated multi-point (CoMP) technique. Next, to overcome the complexity of combinatorial optimisation, Lagrange dual decomposition is applied to solve the power allocation problem and a sub-optimal distance-based BS-Sw scheme is proposed. The main advantage of the distance-based BS-Sw is that the algorithm is tuning-free as it exploits two dynamic thresholds, which can automatically adapt to various user distributions and network deployment scenarios. The optimal binomial and random BS-Sw schemes are also studied to serve as benchmarks. Further, to solve the non-fractional programming component of the EE maximisation problem, a low-complexity and fast converging Dinkelbach’s method is proposed. Extensive simulations under various scenarios reveal that in terms of EE, the proposed joint distance-based BS-Sw and power allocation technique applied to the cooperative and harvesting BSs performs around 15–20% better than the non-cooperative and non-harvesting BSs and can achieve near-optimal performance compared to the optimal binomial method.
1. Introduction
Massive growth in the number of mobile users and mobile user equipment (UE) has sown the seeds of data hunger and severely high traffic congestion, especially in cellular networks. This problem has been aggravated by the emerging 5G technologies, which leads to increasingly dense network deployments to cater for growing user demands. The densification of base stations (BSs) within a geographical area has led to the emergence of a new network architecture known as a heterogeneous network (HetNet), which employs multiple BSs with different transmit power capabilities [1]. The unprecedented network densification through HetNets deployment has resulted in a scarcity of radio resources (particularly spectrum) and a tremendous increase in energy consumption. Over the years, many radio resource management techniques have been proposed to better utilise radio resources, which has cost the mobile service providers (MSPs) billions of dollars yearly. Recently, it has been reported that, other than the costly radio resources, the MSPs have also spent as much as half of their annual operating expense on energy costs [2]. Hence, making HetNets spectrally and energy-efficient not only can result in a tangible positive environmental impact, but also help MSPs in attaining long-term profitability.
Undoubtedly, the energy consumption of cellular systems is highly dependent on the mobile users’ characteristics. The user activities and data usage patterns in a large cellular network can be modelled statistically using a Markov model with tri-non-negative matrix factorisation [3]. This work has demonstrated that data usage across mobile users are severely uneven for a cellular network. From this report, we can infer that the data usage and user activities for a HetNet will follow this pattern and may demonstrate a more uneven and unpredictable trend due to irregular cell sizes in HetNet. One observation from this work implies that around-the-clock, not every hour is considered a peak hour in terms of data usage. Indeed, during non-peak hours, the excess radio resources are being wasted together with the energy used to power the various networking devices in a HetNet [4]. Studies suggest that most of the power consumption (about 58%) of a communication system is mainly contributed by the base station (BS) [5]. Thus, to reduce wastage of radio resources and save energy, certain small-cell BSs with low spectrum utilisation in a HetNet can be switched off; however, it is noteworthy that it does not mean there are no mobile users at all during off-peak hours. On the other hand, there might be a small number of users who still need to access the services of the BSs; therefore, shutting down any small-cell BS in this scenario is unwise and it may lead to a coverage hole where the affected small-cell users could lose connection to any BS services permanently. Fortunately, HetNet architecture can fill the coverage hole by allowing macro BS (MBS) to serve the affected small-cell users [6].
Nevertheless, deployment of multiple cells within a HetNet leads to inter-cell interference (ICI) since the coverage area of small-cell BSs overlaps with the coverage of MBS. The ICI effect can be mitigated by using a coordinated multi-point joint-processing (CoMP-JP) technique [7]. In a HetNet equipped with a CoMP-JP mechanism, the MBS and small-cell BSs share their channel state information (CSI) and data to coordinate the transmission process and hence avoiding interference. As specified in the CoMP standards of 3GPP Release 9, 10 and Beyond [8], apart from increasing a particular UE’s date rate, the appropriate coordination of signals received from multiple interfering cells also improves the performance of the overall network with enhanced coverage area. Anyhow, the BSs that are isolated geographically should have proper synchronisation to avoid performance collision.
Switching off BSs in a HetNet may not be sufficient to reduce energy consumption; therefore, a more energy-efficient solution needs to be sought urgently because increasing energy consumption due to the massive deployment of HetNets has contributed significantly to greenhouse gases emission (GHGE) as well as pollutants related to global warming. According to the studies performed by the authors in [9], GHGE contribution by information and communication technology (ICT) would surpass half of the current transportation sector contribution by 2040 and about 14% of the total global carbon footprint. Thus, substituting non-renewable energy with renewable energy (energy harvesting) in HetNets is seen as one of the possible solutions to reduce brown energy consumption by HetNets, leading to lower carbon emission; therefore, energy sustainability is important in order to maintain the equilibrium between the degrading environmental factor and increasing HetNet user demand. In addition, energy harvesting also improves the energy efficiency (EE) of a HetNet by reducing the grid power consumption (GPC) as suggested by the studies conducted in [10]. Undoubtedly, GPC is also regarded as one of the factors contributing to increasing carbon footprints.
Apart from energy efficiency, hybrid power source also greatly contributes to communication during emergency situations. Wireless communication by itself is considered an emergency communication strategy [11]. Nevertheless, depending solely on grid power source can backfire during grid power outages caused by natural or man-made disasters, i.e., earthquake, landslide, war and so on; therefore, it is very crucial to have a back-up plan, such as renewable energy sources during emergency situations.
Nevertheless, irregular patterns of energy harvesting should be taken into consideration while evaluating their contribution to the EE of a HetNet. In spite of improving just a single-cell EE, sharing the excess harvested energy (HE) among the coordinating BSs would further enhance the EE of the overall HetNet [12]. This can be explained by comparing the available energy per BS and its user strength and /or distribution, which rarely compensates one another. Several technologies, such as power lines and smart grids, are being studied for energy cooperation among the connected BSs. The research conducted in [13] discusses safe and reliable architectures and current implementations of the smart grid; therefore, it is clear that utilising this technology in this work has the potential for significant and reliable contribution. In recent works [14], less complex and simplified smart grid applications are designed specifically for communication systems. In this work, a smart grid is considered to coordinate the transfer of the excess HE among different BSs and also as an energy storage medium. As the case studies carried out in [15] suggest, energy storage management for smart grids is a vast separate topic and was not taken into consideration in this work.
The remainder of this paper is structured as follows. Section 2 describes some existing work related to this research and the contributions of this work. Section 3 illustrates the CoMP-based hybrid-powered HetNet model together with an explanation of the problem. In Section 4, the proposed algorithm is described in detail and the principal algorithm is explained in parts for better insight. Next, Section 5 presents the performance evaluation results and the discussions. Finally, the conclusions and potential future research directions are drawn in Section 6.
2. Related Work and Contributions
The survey carried out by authors in [16] highlights the predominant contribution of BSs to the total power consumption of cellular networks. This work also studies the integration of smart grids to the RE-powered cellular networks, including analyses on architecture and challenges that could be faced in the implementation; however, BS-Sw is not considered as an additional factor to enhance the EE of the system. Similarly, research conducted in [17] discusses the feasibility and benefits of integrating RE resources into the smart grid but again disregarding BS-Sw. There are also several works that study real-time BS control or BS-Sw to maximise energy savings. For instance, in [18], the authors employed the Markov decision process (MDP)-based algorithm to develop such a system. The operational mode of the BSs switches according to the capricious state (arrival and departure) of the active UEs; however, frequent and unexpected switching of BSs may not be efficient in practice [19].
BS-Sw is also studied from the perspective of energy cost in [20] where the energy expenditure can be reduced at the expense of poorer QoS. Moreover, the main concern in this work is communication cost reduction based on real-time energy pricing. Similarly, the studies in [21] focus on monetary-related issues such as operational and energy cost saving among the mobile network operators. In this work, a Markovian model is used as an RE generator and manager. The work in [5] studies BS coordination-based switching design for a green cellular network by making use of a self-adaptive scheduling algorithm without utilising energy harvesting. This work also suggests that BSs are the prime contributors to the total power consumption of the cellular network through the chart shown in Figure 1. Authors in [22] also studied the methods to reduce the grid power consumption of cellular networks through renewable energy without affecting user service quality by utilising a coalitional technique to manage the association between the user and the BS; however, BS-Sw was not considered in this work.
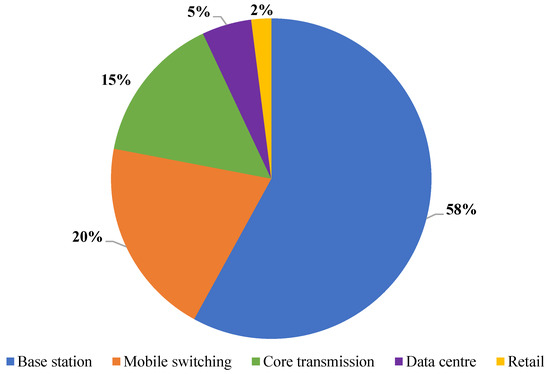
Figure 1.
Cellular network power consumption profile [5].
Thus far, the existing works related to BS-Sw for HetNets have not been integrated with RE, smart grid, power control and data cooperation under a single objective. A general review of some recent relevant works that employ BS-Sw is presented in Table 1. The work in [23] optimises energy performance and offloads macrocell traffic without considering power allocation and energy sharing. In [24], the system EE is maximised by incorporating power control and data cooperation but there is no RE harvesting facility. On the other hand, the work in [25] looks into minimising the total power consumption by utilising power management and RE sharing disregarding data cooperation. The work in [26] contributes to maximising on-grid energy savings through energy sharing but no data cooperation or power allocation has been considered. Furthermore, the authors of [27] have enhanced the network EE by employing data cooperation discounting energy harvesting and sharing. Unlike the existing work, the proposed algorithm in this paper maximises the energy efficiency by utilising data cooperation and power allocation that mitigates the interference while employing renewable energy source to reduce the grid power consumption. Subsequently, excess energy is shared among the BSs through smart-grid and BS-Sw is applied to manage the underutilised BSs, which causes unnecessary energy and resource wastage.

Table 1.
Summary of the relevant work that employs BS-Sw.
Motivated by the above mentioned problems, in this paper, we propose an algorithm to efficiently allocate transmit powers to all BSs and/or switch-off an optimal set of BSs to improve the EE of a HetNet consisting of CoMP-enabled hybrid-powered BSs subject to a minimum quality-of-service (QoS) for all mobile users. Hybrid power in this context implies that the BSs are powered by both the grid power source as well as the energy harvesting source. Energy exchange is enabled via the smart grid among different BSs so that BSs with excess harvested energy can channel out the energy to other BSs demanding for extra energy. To the best of our knowledge, this is the first work to incorporate base station switching (BS-Sw) into a CoMP-enabled hybrid-powered BS connected to a smart grid. Unlike the work in [12], which proposes a joint power allocation and energy cooperation for a CoMP-enabled HetNet, this work extends the previous works further by considering the BS-Sw and power allocation in a CoMP-enabled HetNet, which employs smart grid for energy cooperation. The problem formulated is more challenging by taking BS-Sw into account because the strategy to switch off the BS has a direct impact on the power allocation and energy cooperation. In short, the main contributions of this paper are summarised as follows:
- Develop a HetNet infrastructure with CoMP-enabled hybrid-powered BSs framework by incorporating BS-Sw technique to improve the EE of the smart grid based HetNet and hence reducing the GPC and mitigating interference among the cells.
- Formulate an EE optimisation problem for a CoMP-enabled hybrid-powered HetNet that allows BSs to cooperatively allocate their transmit powers and optimally switch off subject to the minimum QoS requirement.
- Design an optimal binomial and two sub-optimal heuristic optimisation methods to solve BS-Sw problem in order to maximise EE and simultaneously reduce the total GPC by utilising the harvested renewable energy (RE).
- Propose an energy-efficient joint power allocation and BS-Sw algorithm by incorporating the sub-gradient method into the proposed binomial or heuristic methods to reduce computational complexity. Along with it, Dinkelbach’s algorithm is adopted additionally to ensure faster convergence speed while solving the EE problem.
3. System Model and Problem Formulation
Figure 2 illustrates the downlink transmission of hybrid-powered HetNet infrastructure considered in this work, which consists of a macrocell overlaid by multiple small cells. Each cell is served by a BS capable of harvesting RE; therefore, it can be powered by both grid power and an RE source. The power lines of all the BSs are connected to a smart grid that facilitates the energy exchange among the BSs. More specifically, if there is excess HE at any BS, the excess HE will be transferred to the smart grid to share. It is also assumed that the BSs coordinate among each other to eliminate interference through CoMP-JP technique to serve the users.
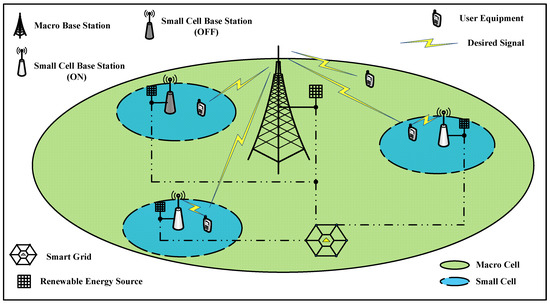
Figure 2.
CoMP-enabled hybrid-powered MBS and SBSs connected to a smart grid in HetNet architecture.
For simplicity, Table 2 lists the notations of the main variables and parameters used throughout the paper. The data rate of user i and the total grid power consumed are denoted by and , respectively, which can be represented as follows:
where is a Boolean value indicating association of user i with BS j where = 1 if the user i is associated with BS j, and otherwise. Similarly, is also a Boolean value representing the on/off status of BS j where = 1 if BS j is on, and otherwise. represents the HE of BS j and denotes the HE efficiency. The EE is maximised by optimising the transmit power allocation and BS switching of SBSs. It is noteworthy that MBS is always ON, and therefore, is always 1.

Table 2.
List of main variables and parameters.
The system EE is maximised by formulating an optimisation problem aiming to reduce total GPC. In this case, EE is defined as ratio of system total throughput to the total grid power consumption. Hence, the objective function and the constraints are shown as follows:
Constraint (3b) limits the transmit power of the BS to . Constraint (3c) guarantees that every user can achieve a minimum SNR denoted by the threshold . Constraint (3d) ensures that each UE is served by at least one BS. Constraint 5 enforces the BS-Sw condition by evaluating the ratio of harvested energy to BS transmit power. Only if the SBS fulfils the condition, where the ratio equals to at least the threshold value, it will be allowed to be switched on.
4. Proposed Technique
The problem formulation given in (3a) is a non-deterministic polynomial-time (NP)-hard combinatorial optimisation problem where determining its optimal solution within a given time is very challenging. Performing a direct exhaustive search at each BS would incur a prohibitive computational burden, which is not feasible due to the rapid variations of wireless channels. In certain cases, it may be solvable in polynomial time, but would require using an impractically slow algorithm; therefore, for practical implementation, the problem formulation in (3a) can be decomposed into two sub-problems, i.e., (1) power allocation (PA) problem and (2) BS-Sw problem. Binomial or heuristic methods can be used to solve the former problem while the latter can be modelled as a Lagrange dual problem.
4.1. Combinatorial Optimisation Algorithm
Furthermore, the formulated EE problem in (3a) is classified as a non-linear fractional programming, thus, solving the problem by applying general mathematical approaches greatly increases its complexity; therefore, a significantly less-complex iterative algorithm, based on Dinkelbach’s method can be utilised to obtain the solution as presented in Algorithm 1. Dinkelbach’s theorem is generally used to simplify the non-linear complex fractional problem into a simpler iterative algorithm [28]. First, the objective function is converted from fractional into a non-fractional function with a parameter (refer to Appendix A for derivation). Initially, the parameter is set to 0 as stated in step 1 of Algorithm 1. Along with it, the maximum number of iterations and convergence condition are also initialised accordingly. The optimal EE is only achievable upon fulfilment of convergence condition, otherwise, the obtained EE value is used in the following iteration to solve the problem as shown in steps 10–15 of Algorithm 1.
The Lagrangian function is evaluated in each iteration as indicated in step 7 of Algorithm 1 based on the BS On/Off statuses and updated transmit power allocation values. Along with the dual decomposition method, steps 4–9 in Algorithm 1 show the combined application of sub-gradient method to obtain the optimal power allocation value. Simple characteristics, i.e., pre-defined constant step size, of sub-gradient method make it more preferable to be applied compared to the gradient method, which uses a computed instantaneous step size [29]. Once the formulated problem is divided into sub-problems with the aid of Lagrange duality, each subgradient is updated iteratively with a constant step size as indicated in step 8 of Algorithm 1. Consequently, each of the Lagrange multiplier values is also updated in every iteration and the convergence condition is evaluated each time. The condition is violated only if the difference between the previous and current values of the Lagrangian function drops below the convergence threshold as can be seen in step 9 of the algorithm.
| Algorithm 1 PABS-Sw algorithm. |
|
4.2. BS-Sw Techniques
While the dual decomposition method is applied to solve the PA part of the formulated problem, three other methods are proposed to determine the BS switching status. One of them evaluates an optimal set of sleeping SBSs by adopting binomial theorem to maximise the EE function, whereas the other two proposed heuristic methods (i.e., distance-based and random BS-Sw schemes) provide a sub-optimal solution as shown in step 3 of Algorithm 1. The computational complexity of the optimal technique (binomial theorem) increases exponentially as the number of SBSs is increased while the heuristic techniques have a constant and smaller computational complexity. Since the BS-Sw and PA are intertwined problems where their optimisations are interdependent, the PA and BS-Sw schemes can be integrated as a single algorithm (PABS-Sw). Depending on the BS on/off status attained through the BS-Sw method, the transmit power allocation is evaluated. Thereafter, the EE is determined through Dinkelbach’s method. These processes are carried out until an optimal EE value is achieved through the iterative algorithm as shown in step 10–16 of Algorithm 1.
The binomial theorem is used to obtain the BS on/off statuses where all possible combinations (i.e., ) of SBS on/off is evaluated as shown in Algorithm 2. It is worth noting that the MBS is always on in this work, i.e., . The best output that yields the highest EE is chosen from the results as indicated in step 6 of Algorithm 2; therefore, this method is regarded as the optimal BS-Sw technique.
| Algorithm 2 Binomial method. |
|
In order to satisfy the target QoS of the user with higher channel gain, allocating less transmit power is sufficient [30]. Consequently, the total power consumption will be decreased, leading to a higher EE. Higher channel gain is viable through decreased path loss, which is achievable through shorter distance between BS and user [31]. The example shown in Figure 3 consists of four small cells (SCs) located randomly within the coverage of the MBS. The distance of SBS j from MBS is indicated by , whereas represents the distance of user i from MBS and is the sum of distances of all users of the particular SBS j to MBS. The SBS with lowest value is considered to be switched off. As the number of users per cell increases, the possibility for the SBS to be switched off will be consequently reduced, in other words, the number of users per cell is taken into consideration while switching off the SBSs.
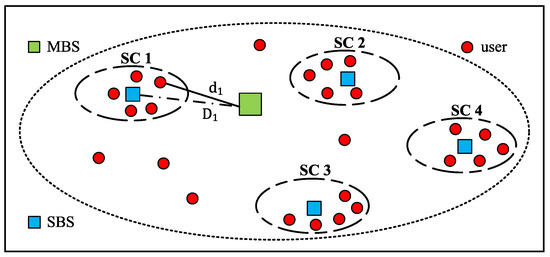
Figure 3.
Example of system model consisting of four randomly distributed SBSs and users.
The proposed BS-Sw strategy employs two distance-based thresholds, and , to determine the on/off state of an SBS.
If or or both of the conditions are satisfied, then the SBSs that fall in the category and the combination of the SBSs are shortlisted to be switched off as shown in step 4 of Algorithm 3. Thereafter, the EE of those combinations are evaluated and the combination that provides the best EE among them is chosen to be switched off, i.e., . For instance, in Table 3, the highlighted cells indicate the SBSs that fulfil the value less than the threshold value for the example shown in Figure 3. From Table 3, we can deduce that SBS 1 or SBS 2 or both SBS 1 and SBS 2 can be considered to be switched off. Thus, after evaluating the highest EE obtained by switching off the mentioned combinations of SBSs, the switching decision is made.
| Algorithm 3 Distance-based method. |
|

Table 3.
SBSs ordered from highest to lowest possibility to be switched off.
This heuristic method is proven to be effective through analysis and observation of thousands of realisations (realisations here refers to the EE evaluation and comparison performed for the binomial and distance-based BS-Sw methods for different settings of SBSs and UEs distribution within the macrocell to prove the accuracy of the distance-based method), but for the sake of clarity, we only show 100 realisations in Figure 4. The plot illustrates the comparison between the EE of binomial and distance-based switching techniques, where the binomial method is around 5% better than the latter. Furthermore, Figure 4 also indicates the matching rate of distance-based method with the binomial method in terms of SBSs switching statuses. It is observed that around 80% realisations of distance-based method matches the binomial method (Boolean representation: the status “1” indicates that the switching decision of distance-based method matches that of the binomial technique and the status “0”, otherwise). Algorithm 4 shows the steps to obtain the accuracy or EE matching percentage. The EE of the distance-based method is displayed as a stacked line for a distinct comparison. The analyses were carried out using different numbers of SBSs and UEs per cell as shown in Figure 4 to validate the performance of the proposed distance-based strategy. It is noteworthy that the EE difference and matching rate of all the considered scenarios are similar.
| Algorithm 4 Distance-based performance validation method. |
|
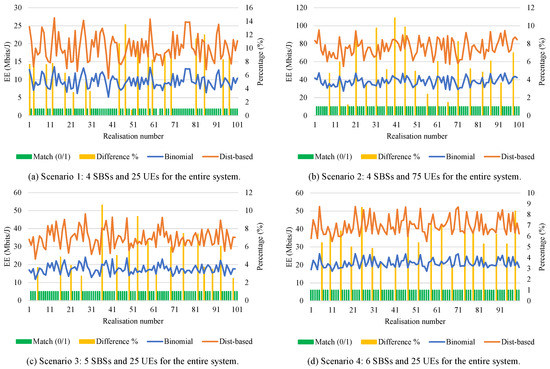
Figure 4.
EE observation of 100 realisations to compare between binomial and distance-based BS-Sw techniques for different scenarios.
Random SBS based on discrete uniform distribution is set to off as shown in Algorithm 5. This distribution follows an equal likelihood to switch off the SBSs (the probability of each SBS to be switched off is the same, e.g., if the number of SBS = 3, then the switch off probability of each SBS is 1/3).
| Algorithm 5 Random method. |
|
4.3. Dual Decomposition
To obtain the optimal transmit power, the PA problem can be converted into Lagrangian optimisation and the problem can be solved using the Lagrangian dual method. It is worth noting that this method was used in the author’s previous work to solve a similar problem [12]. First, the Lagrangian function of the PA optimisation problem is formed as in Equation (5). Then, the dual problem is developed accordingly as shown in Equation (6). Due to its convex characteristic, the dual decomposition method is used to solve the Lagrange function. Consequently, the dual problem is determined by solving the corresponding Karush–Kuhn–Tucker (KKT) conditions [32] as in Equation (8). Finally, the optimal transmit power, which is obtained by applying the dual decomposition method, is expressed in Equation (9).
where and are nonnegative Lagrange multipliers and denotes EE based on Dinkelbach’s method [28] (see Appendix A).
To obtain an optimal power allocation for BS j serving user i, Equation (5) is derived with respect to and equated to zero:
where represents the optimal power allocation.
5. Simulation Results and Analysis
There are three BS-Sw techniques investigated in this work, namely binomial (optimal), distance-based (heuristic) and random (heuristic) methods. Furthermore, the proposed binomial BS-Sw method was simulated for three different scenarios, i.e., (1) CoMP-enabled harvesting; (2) CoMP-enabled non-harvesting; (3) non-CoMP harvesting scenarios (the legends of the graphs are abbreviated as follows: Binomial BS-Sw technique for CoMP-enabled harvesting system (Bin-CoMP-H), distance-based BS-Sw technique for CoMP-enabled harvesting system (Dist-CoMP-H), random BS-Sw technique for CoMP-enabled harvesting system (Rand-CoMP-H), Binomial BS-Sw technique for Non-CoMP harvesting system (Bin-Non-CoMP-H) and Binomial BS-Sw technique for CoMP-enabled non-harvesting system (Bin-CoMP-NoH)).
5.1. Simulation Setting
For a CoMP-enabled system, the macrocell UEs are served solely by the MBS while small cell UEs are served by both MBS and their respective SBS. On the other hand, for a Non-CoMP system, each UE is served only by its respective BS. Unless specified otherwise, the network considered in this work typically consists of an MBS, three SBSs and five UEs per cell. Algorithm 6 shows the simplified simulation steps of EE evaluation. The model was simulated for non-peak hours to observe the energy wastage caused by the BSs serving in under-loaded cells. The performance gain used in the evaluation is based on the average of the difference between the compared techniques, which is the reason a single value is used instead of a series of values (i.e., The explanation of Figure 5 shows that EE performance of random BS-Sw technique is 25% worse than the binomial BS-Sw method. The number of SBSs vary from 2 to 8. So, the EE performance gain is measured at each x-axis point and averaged as 25% instead of choosing just one point.). Table 4 tabulates the simulation settings and parameters used in this work.
| Algorithm 6 EE evaluation. |
|
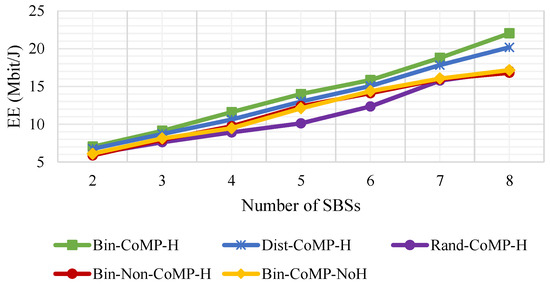
Figure 5.
EE for various number of SBSs analysed for different BS-Sw methods and BS coordination techniques with dB and dB.

Table 4.
Setting of the simulation parameters.
5.2. Simulation Results and Discussions
Table 5 summarises the complexity of the three BS-Sw methods proposed in this work based on the example given in Figure 3. The complexity term in this context means the number of choices to be considered or computed before deciding which SBSs are to be switched off. Generally, the computational complexity of the binomial technique increases exponentially as the number of SBSs increases. Whereas, the random switching technique induces a constant trivial complexity regardless of the number of SBSs. On the other hand, a distance-based technique incurs a medium computational complexity depending on the distance of SBSs and UEs from the MBS. In the given example with four SBSs, the binomial method is 80% more complex compared to the distance-based method. Additionally, the complexity of different number of SBSs are determined and compared by assuming similar threshold conditions as the former example. While the number of SBSs is 8, the binomial method results in more than 90% complexity compared to the distance-based method. It is proven that the rise in number of SBSs drastically increases the computational complexity of the binomial BSS technique.

Table 5.
Computational complexity of the proposed BS-Sw techniques.
Figure 5 depicts the impact of the number of SBSs on the EE of the system. Generally, the EE improves as the number of SBSs increases owing to the fact that the total sum rate rises at a rate faster than the consumed power. The EE of the CoMP-enabled binomial method performs around 5% better than the CoMP-enabled distance-based method but at the expense of much higher computational complexity. As the number of SBSs increases, the complexity rises exponentially since the EE of all the possible combinations of SBSs need to be evaluated before selecting the optimal EE. On the contrary, the sub-optimal method provides a near-optimal (95% of the optimal performance) result at much lower constant computational complexity as the number of SBSs increased. Further, random BS-Sw performs much worse, about 25% worse, than the binomial method in terms of EE, making it a poorer choice of switching technique. The binomial method was further investigated for a CoMP-enabled non-harvesting as well as Non-CoMP harvesting techniques where both the trends coincide with each other and its EE is nearly 20% lower than that of the CoMP-enabled harvesting technique. Both energy harvesting and data cooperation contribute fairly to EE but combining both techniques produce a much higher EE.
Figure 6 depicts the impact of the threshold value of the ratio of the SBS harvested energy to the transmit power on the EE of the system. In general, the increase in the number of UEs leads to a rise in EE of the system owing to the fact that the sum rate inflates more rapidly than the total power consumption. When the threshold value is set to 0.7, the EE of the system is around 5% better than setting it to 0 or 1.2. A threshold value less than 1 indicates that the SBS transmits more power than the harvested energy and vice versa. If the ratio of SBS harvested energy to transmit power is greater than the threshold value, the SBS will be considered to be switched on. In that case, setting the threshold to a higher value limits the potential SBSs that can be switched on, hence leading to a lower EE. Adjustment of this ratio greatly aids in enhancing the EE of the system, which consists of SBSs that harvest at an inconsistent rate.
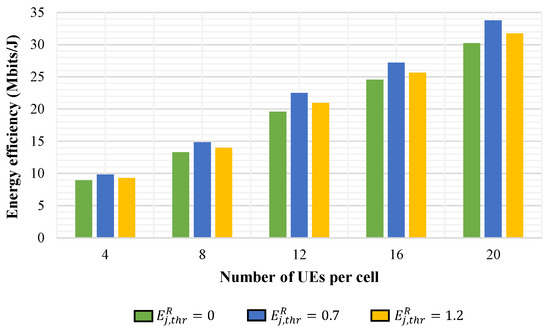
Figure 6.
Impact of on EE for a different number of users per cell with dB and ranges randomly from 0 dB to 2 dB.
Figure 7 illustrates the system EE for different HE of SBSs using different BS-Sw algorithms. In general, the EE rises as the HE of the SBSs increases, as a result of the GPC reduction and in turn more HE is used by the system. The proposed binomial method was investigated for both CoMP and Non-CoMP techniques. BS-Sw for the CoMP technique using the binomial method generates an optimal EE solution, but again at the cost of higher computational complexity. On the other hand, CoMP-enabled distance-based solution, which is a sub-optimal method, still yields a satisfactory EE performance that was about 5% lower than the binomial method, but at a much lower complexity. The near-optimal performance gained by the proposed distance-based solution is mainly due to switching off the SBSs nearer to the MBS, which leads to a smaller power requirement by the latter to serve the users. On the other hand, random BS-Sw, which is the least complex scheme, only achieves 85% of the performance achieved by the distance-based method. In fact, the BS-Sw of the Non-CoMP technique using the binomial method performs around 5% better than the CoMP-enabled random BS-Sw.
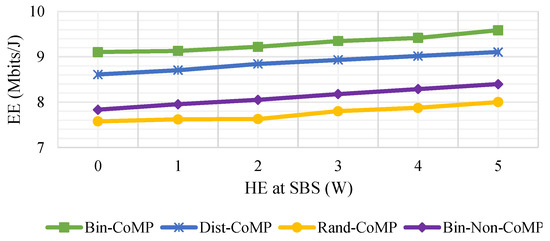
Figure 7.
EE for different HE of SBSs with dB.
Figure 8 shows the effect of the number of users per cell on the EE of the system. It is observed that the increase in the number of users enhances the EE of the system because the system throughput increases at a higher rate than the increase in the total power consumption in the scenarios with sufficient bandwidths. The average difference between the optimal and sub-optimal method is around 5% whereas the random method performs around 25% lower than the optimal method. Serving the SBS users with sum distance shorter from the MBS boosts the EE performance as the required power is lesser. Since the random method switches off the BSs arbitrarily, it results in an inferior performance. Both the CoMP-enabled non-harvesting as well as Non-CoMP harvesting techniques increase at similar trends and on average, nearly 20% worse than the CoMP-enabled harvesting technique in terms of EE. Once again, it is proven that both data and energy cooperation play a vital role in improving the EE of the system.
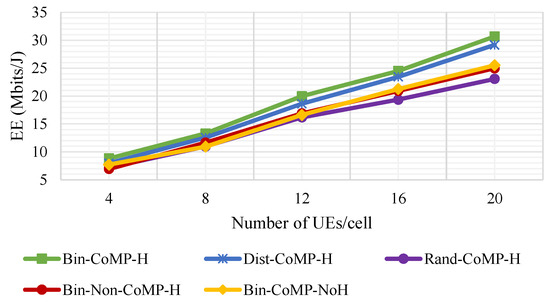
Figure 8.
EE for increasing number of UEs per cell analysed for different BS-Sw methods and BS coordination techniques with dB and dB.
Figure 9 shows the impact of HE efficiency on the EE of the system. From the figure, it is worth noting that higher HE results in improved EE. Under different HE efficiency, it is noticed that the EE of the binomial method is around 5% higher than the distance-based method and nearly 15% better than the random method. Typically, while users are near to the serving BS and the number of UEs served by the BS is fewer, the system provides a better EE. The random method does not necessarily switch off the nearest serving SBS or the SBS with fewer UEs, it can even be the other way round, which is the reason for yielding a worse EE. HE efficiency typically comprises RE source efficiency as well as the energy transfer efficiency, which takes into account the line losses; therefore, in the high efficiency region, the energy transferred through the line with little loss yields a higher optimisation margin for EE.
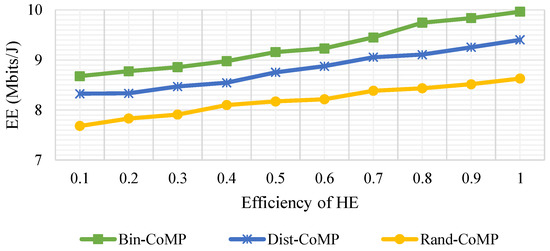
Figure 9.
Impact of the efficiency of HE on the EE of the system analysed for diverse BS-Sw methods with dB and dB.
In the following figure, we demonstrate the effects of switching off all the SBSs so that the users are only served by the MBS. Figure 10 displays the impact of MBS HE on the EE performance for various number of UEs per cell in the absence of SBSs. In general, the EE of the system rises 5% on average as the MBS HE is increased. As MBS becomes the sole access point for all of the users, it requires more energy to serve the users. Thus, more HE aids in reducing the GPC and hence leading to a better EE. Furthermore, adding more users per cell increases the EE of the system about 5% on average. This proves that the MBS can still handle the increasing number of UEs with the aids of HE.
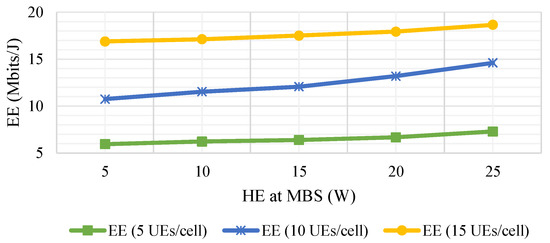
Figure 10.
Effects of the MBS as sole access point on EE for various MBS HE and number of UEs per cell.
As some of the analyses above suggest that the total sum rate rises at a higher rate compared to the total power consumed, further investigation was carried out to prove the hypothesis. While the simulation conditions used for results in Figure 10 were adopted for this analysis, the inference is still applicable for other conditions as well. Figure 11 illustrates the increase rate (for power consumption, the graph trend is not increasing as sum rate, it fluctuates, but for ease of readability, ‘increase rate’ is used instead of ‘variation rate’) of the sum rate and total power consumption as the MBS HE is varied. On average, the increased rate of total power consumed is around 5% whereas for sum rate, rate increased by about 20%. Moreover, the sum rate increases almost steadily while the total power consumed fluctuates at certain points as the system regulates the power to maintain a high EE; therefore, it can be inferred that an increase in UEs/cells or the number of SBSs leads to a higher EE.
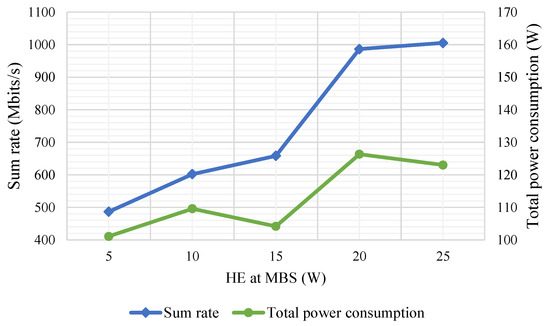
Figure 11.
Sum rate and total power consumption for various MBS HE with UEs/cell = 5 and all SBSs are in off condition.
Figure 12 shows the analysis of convergence behaviour of Dinkelbach’s algorithm as suggested in theory. On average, the convergence is achieved within three to five iterations for all the methods that were analysed. According to the analysis, it is proven that Dinkelbach’s algorithm possesses a fast converging characteristic, which is why it is preferred to be utilised in such complex non-factional problem.
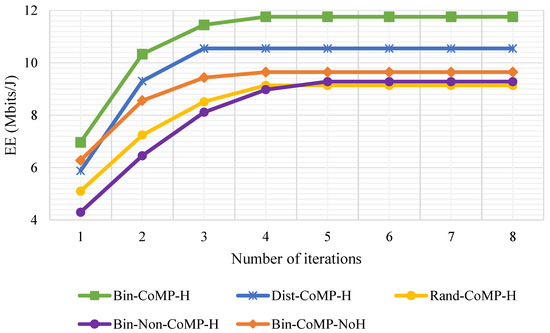
Figure 12.
Convergence behaviour of Dinkelbach’s algorithm for dB and four SBSs with dB.
6. Final Remarks
EE has recently attracted the attention of researchers in the mobile communication field due to the increasingly disastrous impact on the environment caused by less energy-efficient applications. Generally, increasing the QoS of the users or throughput increases the grid power consumption of the communication system. On the other hand, a massive number of users leads to interference issues as well as increased energy demand. Further, the number of users is not always significant, leading to energy wastage during off-peak hours. Hence, it is crucial to switch off underutilised BSs and allocating UE power, which simultaneously solves throughput as well as power consumption issues. This work proposes an energy-efficient joint BS-Sw and power allocation scheme for a CoMP-based Het-Net architecture with hybrid power sources. By using a combinatorial (sub-gradient-binomial or sub-gradient-heuristic) optimisation technique, joint BS-Sw and power allocation yields about 15–20% higher EE compared to the non-cooperative or non-harvesting systems. The proposed distance-based BS-Sw method is proven to perform better in terms of EE compared to the random method in all tested scenarios. Though its EE performance is around 5% poorer than the optimal binomial method, the computational complexity is proven to be much lesser than the former. Overall, the distance-based BS-Sw method of the cooperative harvesting system performs the best in terms of both performance gain and computational complexity. The application of BS-Sw to MBS would greatly enhance the EE of the system, but in order to avoid a coverage hole, techniques such as cell zooming have to be employed, which is left for future work. Apart from that, the application of a smart grid is not limited to only energy sharing, it can be extended to more advanced time-series-based energy and traffic management. The energy harvesting and traffic model used in this work is based on instantaneous values. For more practical applications, the trending machine learning techniques can be utilised to learn the energy and traffic pattern sampled through the time-series. Consequently, the overall system performance can be enhanced with reduced complexity caused by real-time computations.
Author Contributions
Conceptualisation, S.E.; methodology, S.E.; software, S.E.; validation, S.E.; formal analysis, S.E.; investigation, S.E.; resources, S.E.; data curation, S.E.; writing—original draft preparation, S.E.; writing—review and editing, Y.H.N. and C.K.T.; visualisation, S.E.; supervision, Y.H.N. and C.K.T.; project administration, Y.H.N. and C.K.T.; funding acquisition, Y.H.N. and C.K.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Multimedia University grant number MMUI180002.02. and the APC was funded by Multimedia University.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy considerations.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CoMP-JP | Coordinated multi-point joint processing |
| CSI | Channel state information |
| EE | Energy efficiency |
| GHGE | Greenhouse gas emission |
| GPC | Grid power consumption |
| HE | Harvested energy |
| HetNet | Heterogeneous network |
| ICI | Inter-cell interference |
| ICT | Information and communication technology |
| KKT | Karush-Kuhn-Tucker |
| MBS | Macro base station |
| MDP | Markov decision process |
| MSP | Mobile service provider |
| PA | Power allocation |
| QoS | Quality of service |
| RE | Renewable energy |
| SBS | Small cell base station |
| SC | Small cell |
| SNR | Signal-to-noise ratio |
| UE | User equipment |
Appendix A. Application of Dinkelbach’s Method
Non-linear fractional programming problem transformation:
where , and denotes optimal EE, optimal PA and optimal BS on/off statuses, respectively.
References
- Yang, J.; Pan, Z.; Guo, L. Coverage and energy efficiency analysis for two-tier heterogeneous cellular networks based on matérn hard-core process. Future Internet 2020, 12, 1. [Google Scholar] [CrossRef] [Green Version]
- Ismail, M.; Shakir, M.Z.; Qaraqe, K.A.; Serpedin, E. Green Heterogeneous Wireless Networks; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Jin, Y.; Duffield, N.; Gerber, A.; Haffner, P.; Hsu, W.L.; Jacobson, G.; Sen, S.; Venkataraman, S.; Zhang, Z.L. Characterizing data usage patterns in a large cellular network. In Proceedings of the 2012 ACM SIGCOMM Workshop on Cellular Networks: Operations, Challenges, and Future Design, Helsinki, Finland, 13 August 2012; pp. 7–12. [Google Scholar] [CrossRef]
- Dahal, M.S.; Shrestha, J.N.; Shakya, S.R. Energy saving technique and measurement in green wireless communication. Energy 2018, 159, 21–31. [Google Scholar] [CrossRef]
- Dutta, U.K.; Razzaque, M.A.; Al-Wadud, M.A.; Islam, M.S.; Hossain, M.S.; Gupta, B. Self-adaptive scheduling of base transceiver stations in green 5g networks. IEEE Access 2018, 6, 7958–7969. [Google Scholar] [CrossRef]
- Yang, J.; Pan, Z.; Xu, H.; Hu, H. Joint Optimization of Pico-Base-Station Density and Transmit Power for an Energy-Efficient Heterogeneous Cellular Network. Future Internet 2019, 11, 208. [Google Scholar] [CrossRef] [Green Version]
- Khoriaty, J.; Artail, H.; Nasser, Y. Coordinated multipoint in dense heterogeneous networks with overlapping microcell expanded regions and its effect on backhaul links. Phys. Commun. 2018, 29, 230–244. [Google Scholar] [CrossRef]
- Qamar, F.; Dimyati, K.B.; Hindia, M.N.; Noordin, K.A.B.; Al-Samman, A.M. A comprehensive review on coordinated multi-point operation for LTE-A. Comput. Netw. 2017, 123, 19–37. [Google Scholar] [CrossRef]
- Belkhir, L.; Elmeligi, A. Assessing ICT global emissions footprint: Trends to 2040 & recommendations. J. Clean. Prod. 2018, 177, 448–463. [Google Scholar] [CrossRef]
- Özbuğday, F.C.; Erbas, B.C. How effective are energy efficiency and renewable energy in curbing CO2 emissions in the long run? A heterogeneous panel data analysis. Energy 2015, 82, 734–745. [Google Scholar] [CrossRef]
- Bordel Sánchez, B.; Alcarria, R.; Robles, T. Managing Wireless Communications for Emergency Situations in Urban Environments through Cyber-Physical Systems and 5G Technologies. Electronics 2020, 9, 1524. [Google Scholar] [CrossRef]
- Euttamarajah, S.; Ng, Y.H.; Tan, C.K. Energy-Efficient Joint Power Allocation and Energy Cooperation for Hybrid-Powered Comp-Enabled HetNet. IEEE Access 2020, 8, 29169–29175. [Google Scholar] [CrossRef]
- Sestrem Ochôa, I.; Augusto Silva, L.; De Mello, G.; Garcia, N.M.; de Paz Santana, J.F.; Quietinho Leithardt, V.R. A cost analysis of implementing a blockchain architecture in a smart grid scenario using sidechains. Sensors 2020, 20, 843. [Google Scholar] [CrossRef] [Green Version]
- Viel, F.; Augusto Silva, L.; Leithardt, V.R.Q.; De Paz Santana, J.F.; Celeste Ghizoni Teive, R.; Albenes Zeferino, C. An Efficient Interface for the Integration of IoT Devices with Smart Grids. Sensors 2020, 20, 2849. [Google Scholar] [CrossRef]
- Kolokotsa, D.; Kampelis, N.; Mavrigiannaki, A.; Gentilozzi, M.; Paredes, F.; Montagnino, F.; Venezia, L. On the integration of the energy storage in smart grids: Technologies and applications. Energy Storage 2019, 1, e50. [Google Scholar] [CrossRef] [Green Version]
- Hassan, H.A.H.; Pelov, A.; Nuaymi, L. Integrating cellular networks, smart grid, and renewable energy: Analysis, architecture, and challenges. IEEE Access 2015, 3, 2755–2770. [Google Scholar] [CrossRef]
- Rehmani, M.H.; Reisslein, M.; Rachedi, A.; Erol-Kantarci, M.; Radenkovic, M. Integrating renewable energy resources into the smart grid: Recent developments in information and communication technologies. IEEE Trans. Ind. Inform. 2018, 14, 2814–2825. [Google Scholar] [CrossRef]
- Elsherif, F.; Chong, E.K.; Kim, J.H. Energy-Efficient Base Station Control Framework for 5G Cellular Networks Based on Markov Decision Process. IEEE Trans. Veh. Technol. 2019, 68, 9267–9279. [Google Scholar] [CrossRef]
- Park, J.W.; Yoo, D.S.; Oh, S.J. User-Number Threshold Based Small-Cell On/Off Control Scheme: Performance Evaluation and Optimization. IEEE Trans. Wirel. Commun. 2019, 19, 367–379. [Google Scholar] [CrossRef]
- Vallero, G.; Deruyck, M.; Meo, M.; Joseph, W. Accounting for energy cost when designing energy-efficient wireless access networks. Energies 2018, 11, 617. [Google Scholar] [CrossRef]
- Renga, D.; Hassan, H.A.H.; Meo, M.; Nuaymi, L. Energy management and base station on/off switching in green mobile networks for offering ancillary services. IEEE Trans. Green Commun. Netw. 2018, 2, 868–880. [Google Scholar] [CrossRef]
- Masero, E.; Fletscher, L.A.; Maestre, J.M. A coalitional model predictive control for the energy efficiency of next-generation cellular networks. Energies 2020, 13, 6546. [Google Scholar] [CrossRef]
- Yaacoub, E. RESCUE: Renewable energy small cells for utility enhancement in green LTE HetNets. IEEE Syst. J. 2015, 11, 2356–2365. [Google Scholar] [CrossRef]
- Feng, M.; Mao, S.; Jiang, T. BOOST: Base station on-off switching strategy for green massive MIMO HetNets. IEEE Trans. Wirel. Commun. 2017, 16, 7319–7332. [Google Scholar] [CrossRef]
- Ghazzai, H.; Farooq, M.J.; Alsharoa, A.; Yaacoub, E.; Kadri, A.; Alouini, M.S. Green networking in cellular hetnets: A unified radio resource management framework with base station on/off switching. IEEE Trans. Veh. Technol. 2016, 66, 5879–5893. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Zhao, Z.; Cheng, X.; Ying, J.; Qu, J.; Xu, G. Base Station Sleeping Strategy for On-Grid Energy Saving in Cellular Networks With Hybrid Energy Supplies in IoT Environment. IEEE Access 2018, 6, 45578–45589. [Google Scholar] [CrossRef]
- Jahid, A.; Shams, A.B.; Hossain, M.F. Green energy driven cellular networks with JT CoMP technique. Phys. Commun. 2018, 28, 58–68. [Google Scholar] [CrossRef]
- Chen, F.; Huang, G.; Fan, Y. A linearization and parameterization approach to tri-objective linear programming problems for power generation expansion planning. Energy 2015, 87, 240–250. [Google Scholar] [CrossRef]
- Rahim, S.; Javaid, N.; Khan, R.D.; Nawaz, N.; Iqbal, M. A convex optimization based decentralized real-time energy management model with the optimal integration of microgrid in smart grid. J. Clean. Prod. 2019, 236, 117688. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, G.; Zhou, W.; Li, L.; Wu, G.; Liang, Y.C.; Li, S. Primary channel gain estimation for spectrum sharing in cognitive radio networks. IEEE Trans. Commun. 2017, 65, 4152–4162. [Google Scholar] [CrossRef]
- Cai, S.; Che, Y.; Duan, L.; Wang, J.; Zhou, S.; Zhang, R. Green 5G heterogeneous networks through dynamic small-cell operation. IEEE J. Sel. Areas Commun. 2016, 34, 1103–1115. [Google Scholar] [CrossRef] [Green Version]
- Huo, L.; Jiang, D.; Lv, Z. Soft frequency reuse-based optimization algorithm for energy efficiency of multi-cell networks. Comput. Electr. Eng. 2018, 66, 316–331. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).