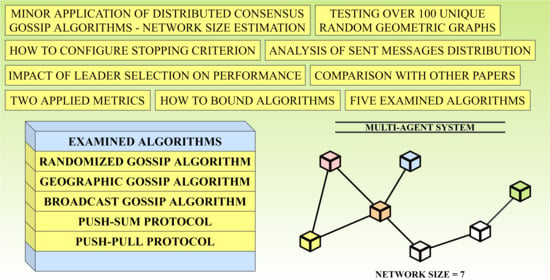
Comparative Study of Distributed Consensus Gossip Algorithms for Network Size Estimation in Multi-Agent Systems
Abstract
1. Introduction
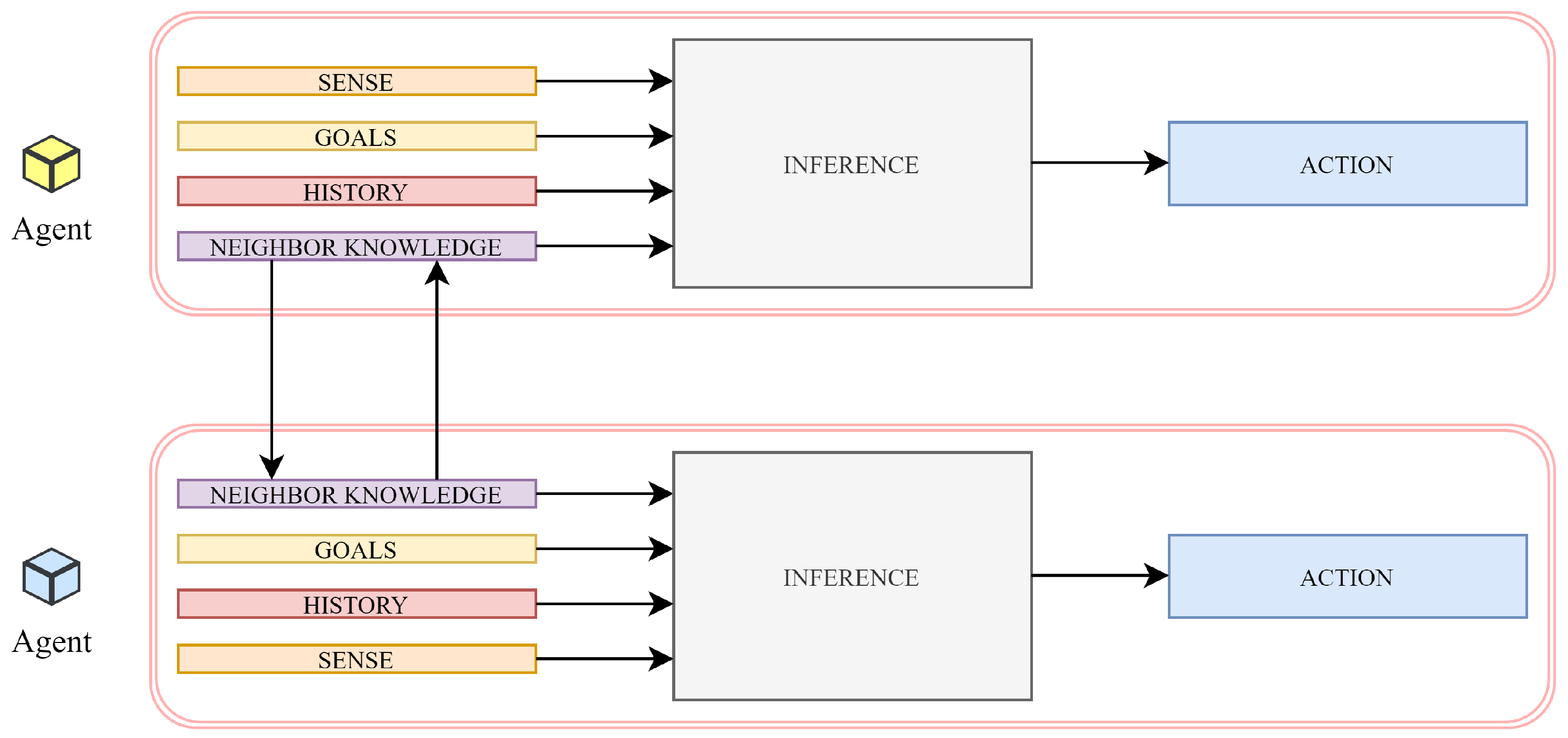
1.1. Theoretical Background into Multi-Agent Systems
- □
- Autonomy is the ability to operate without any human interaction and to control its own actions/inner state.
- □
- Reactivity is the ability to react to a dynamic surrounding environment.
- □
- Social ability is the ability to communicate with other agents or human beings.
- □
- Pro-activeness is the ability to act as an initiative entity and not only to respond to an external stimulus.
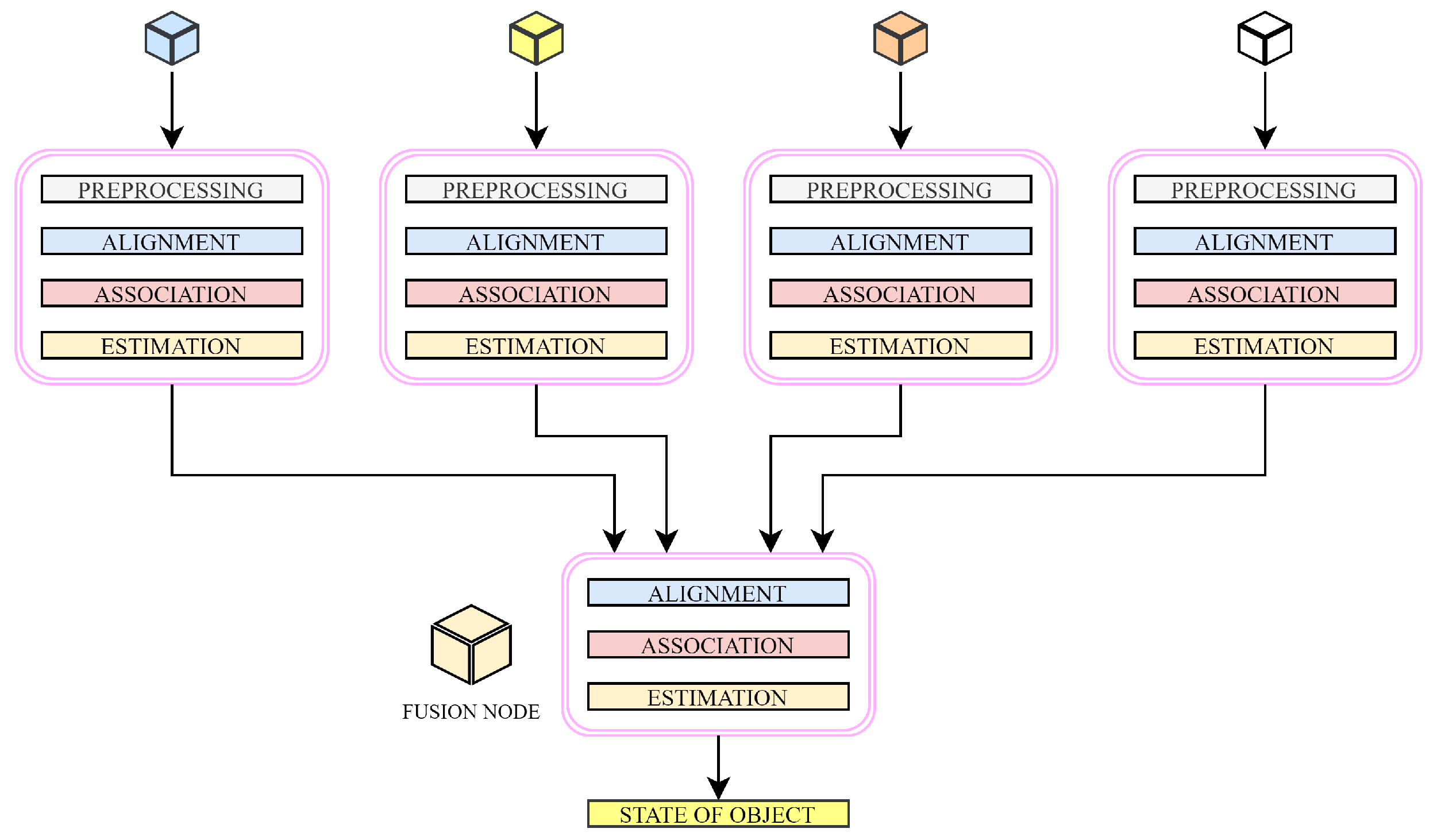
1.2. Data Aggregation in Multi-Agent Systems
- □
- Centralized architecture: Data aggregation is carried out by the fusion node, which collects the raw data from all the other agents in the system. Thus, all the agents measure the quantity of interest and are only required to deliver this information to the fusion node subsequently. Therefore, this approach is not too appropriate for real-world systems since it is characterized by a significant time delay, a massive transmitted information amount, high vulnerability to potential threats, etc.
- □
- Decentralized architecture: In this approach, there is no single point of data aggregation in contrast to the centralized architecture. In this case, each agent autonomously aggregates its local information with data obtained from its peers. Despite many advantages, decentralized architecture also has several shortcomings, e.g., communication costs, poor scalability, etc.
- □
- Distributed architecture: Each agent in a system independently processes its measurement; therefore, the object state is executed only according to the local information. This approach is characterized by a significant reduction of communication and communication cost, thereby gaining in popularity and finding a wide application in real-world systems over recent years [13,14,15,16].
- □
- Hierarchical architecture: This architecture (also referred to as hybrid architecture) is a combination of the decentralized and the distributed architecture, executing data aggregation at different levels at the hierarchy.
1.3. Consensus Theory
- □
- Deterministic algorithms include the Metropolis–Hastings algorithm, the Max-Degree weights algorithm, the Best Constant weights algorithm, the Convex Optimized weights algorithm, etc.
- □
- Gossip algorithms include the Push-Sum protocol, the Push-Pull protocol, the Randomized gossip algorithm, the Broadcast gossip algorithm, etc.
1.4. Our Contribution
- □
- Randomized gossip algorithm (RG);
- □
- Geographic gossip algorithm (GG);
- □
- Broadcast gossip algorithm (BG);
- □
- Push-Sum protocol (PS); and
- □
- Push-Pull protocol (PP).
1.5. Paper Organization
2. Related Work
3. Mathematical Model of Multi-Agent Systems
4. Examined Distributed Consensus Gossip-Based Algorithms
- □
- Randomized gossip algorithm (RG): see Section 4.1.
- □
- Geographic gossip algorithm (GG): see Section 4.2.
- □
- Broadcast gossip algorithm (BG): see Section 4.3.
- □
- Push-Sum protocol (PS): see Section 4.4.
- □
- Push-Pull protocol (PP): see Section 4.5.
4.1. Randomized Gossip Algorithm
4.2. Geographic Gossip Algorithm
4.3. Broadcast Gossip Algorithm
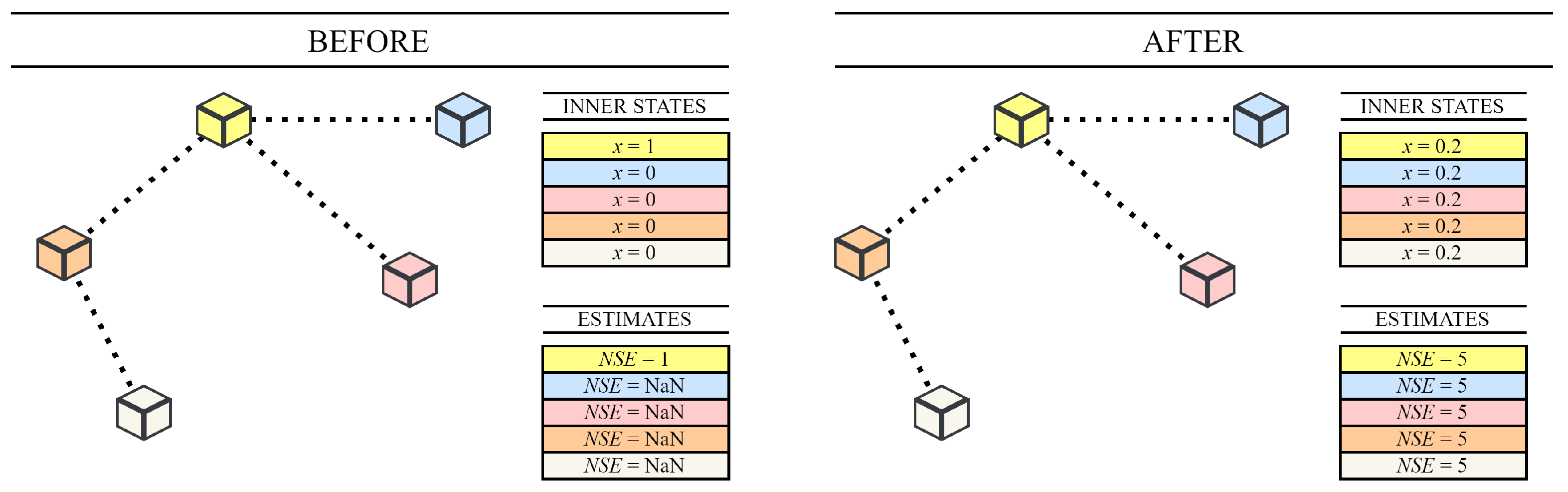
4.4. Push-Sum Protocol
- □
- sum s (initiated with either “1” (leader) or “0” (other agents) when the network size is estimated); and
- □
- weight w (each agent sets its value to “1”).
4.5. Push-Pull Protocol
4.6. Comparison of Distributed Gossip Consensus Algorithms with Deterministic Ones
5. Applied Research Methodology
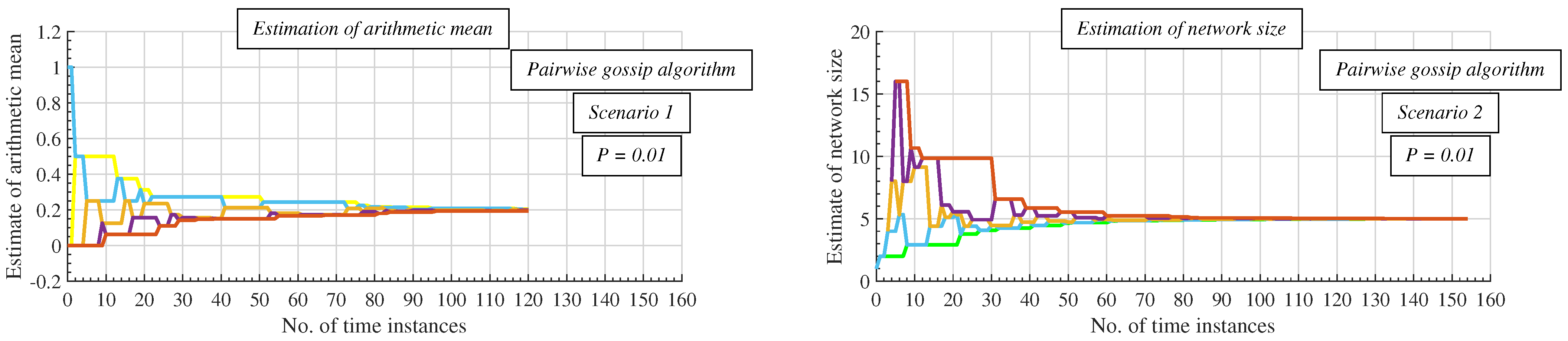
- □
- Scenario 1: In this scenario, the value of the current inner states is relevant in the decision about whether or not to stop an algorithm at the current time instance. This stopping criterion is defined in (10), meaning that an algorithm is stopped at the time instance when (10) is met for the first time.
- □
- Scenario 2: In the case of applying the other applied stopping criterion, the values of the current network size estimates are checked instead of the inner states. In this scenario, the consensus is considered to be achieved when (11) is met.
- □
- The best-connected agent is the leader.
- □
- The worst-connected agent is the leader.
6. Experiments and Discussion
- □
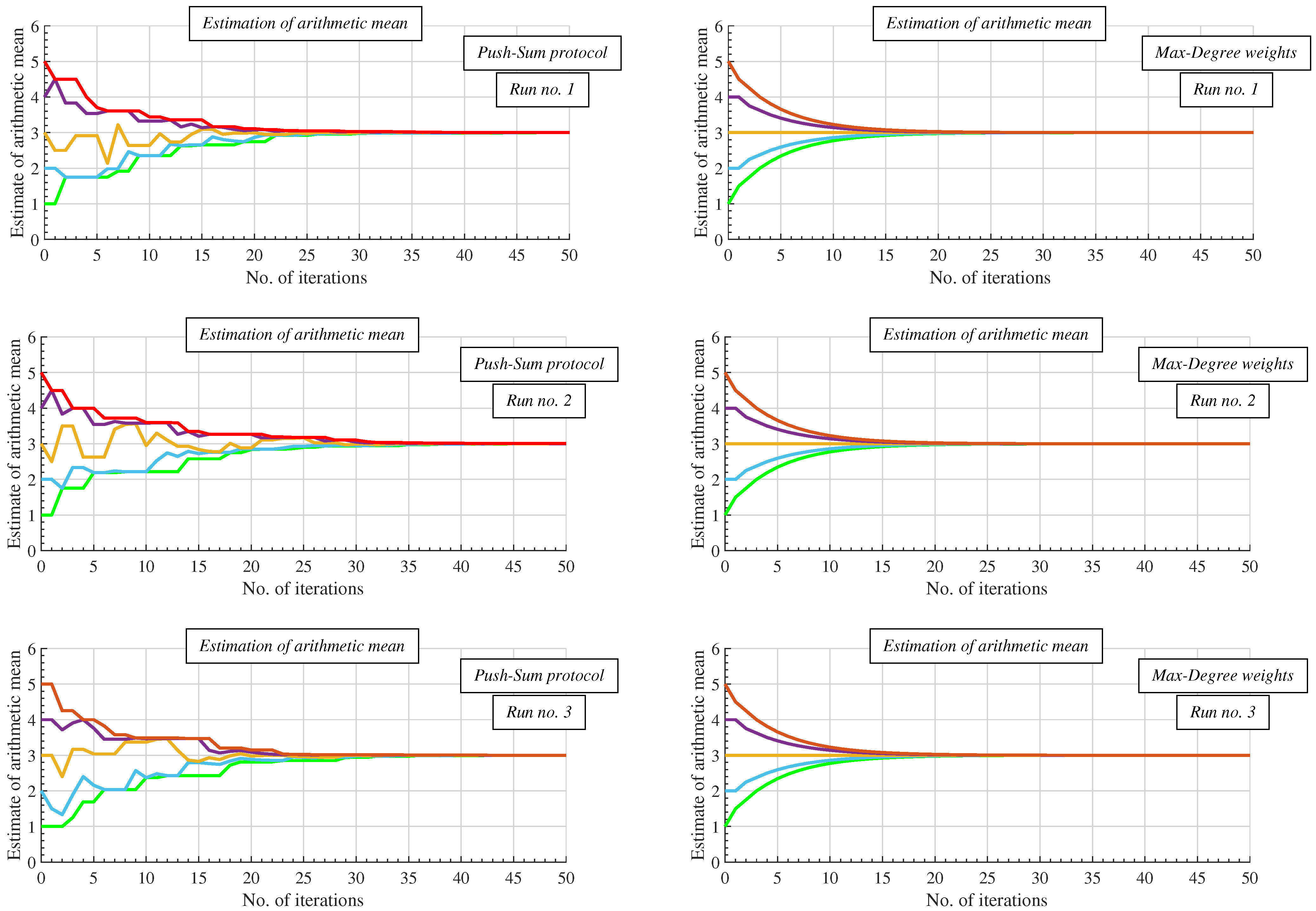
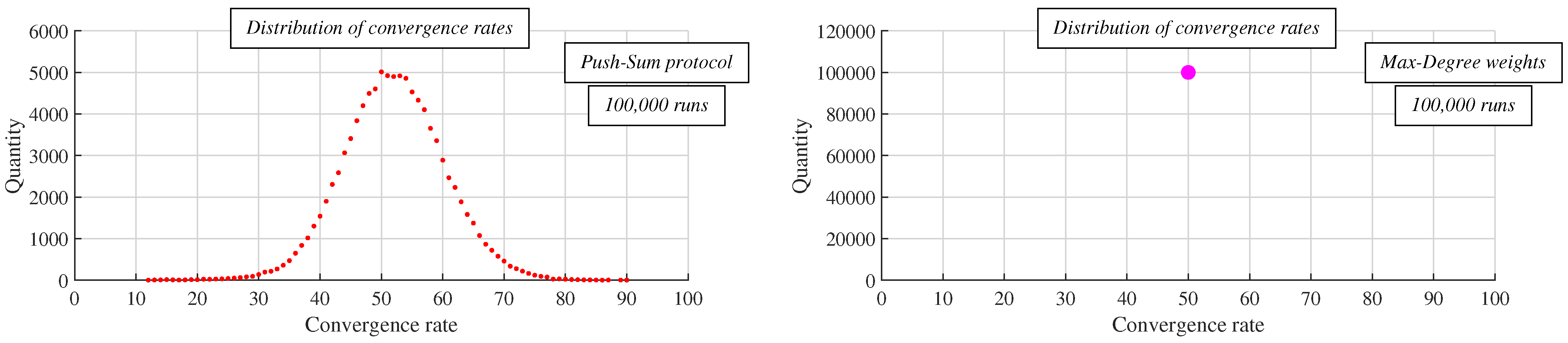
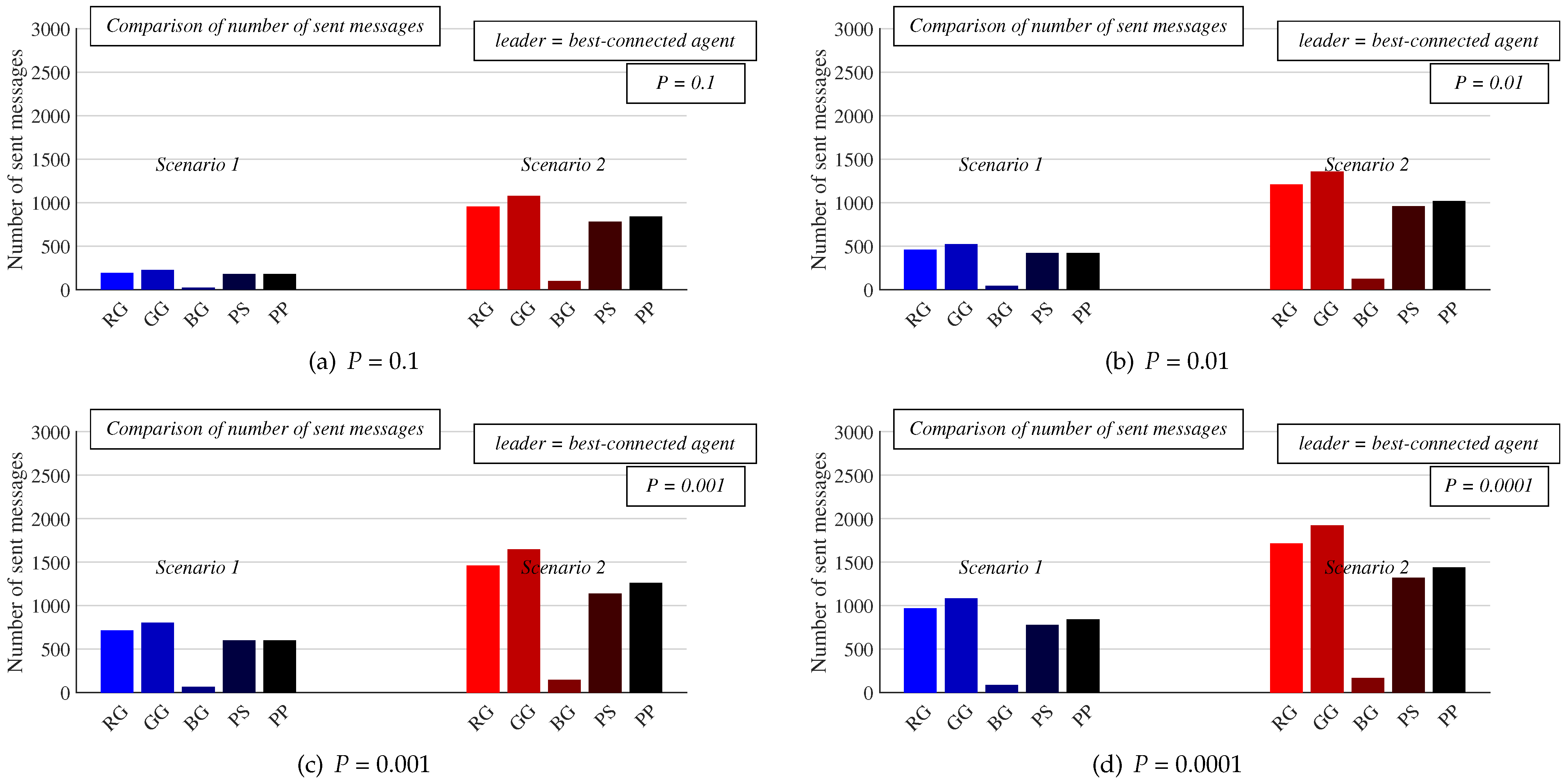
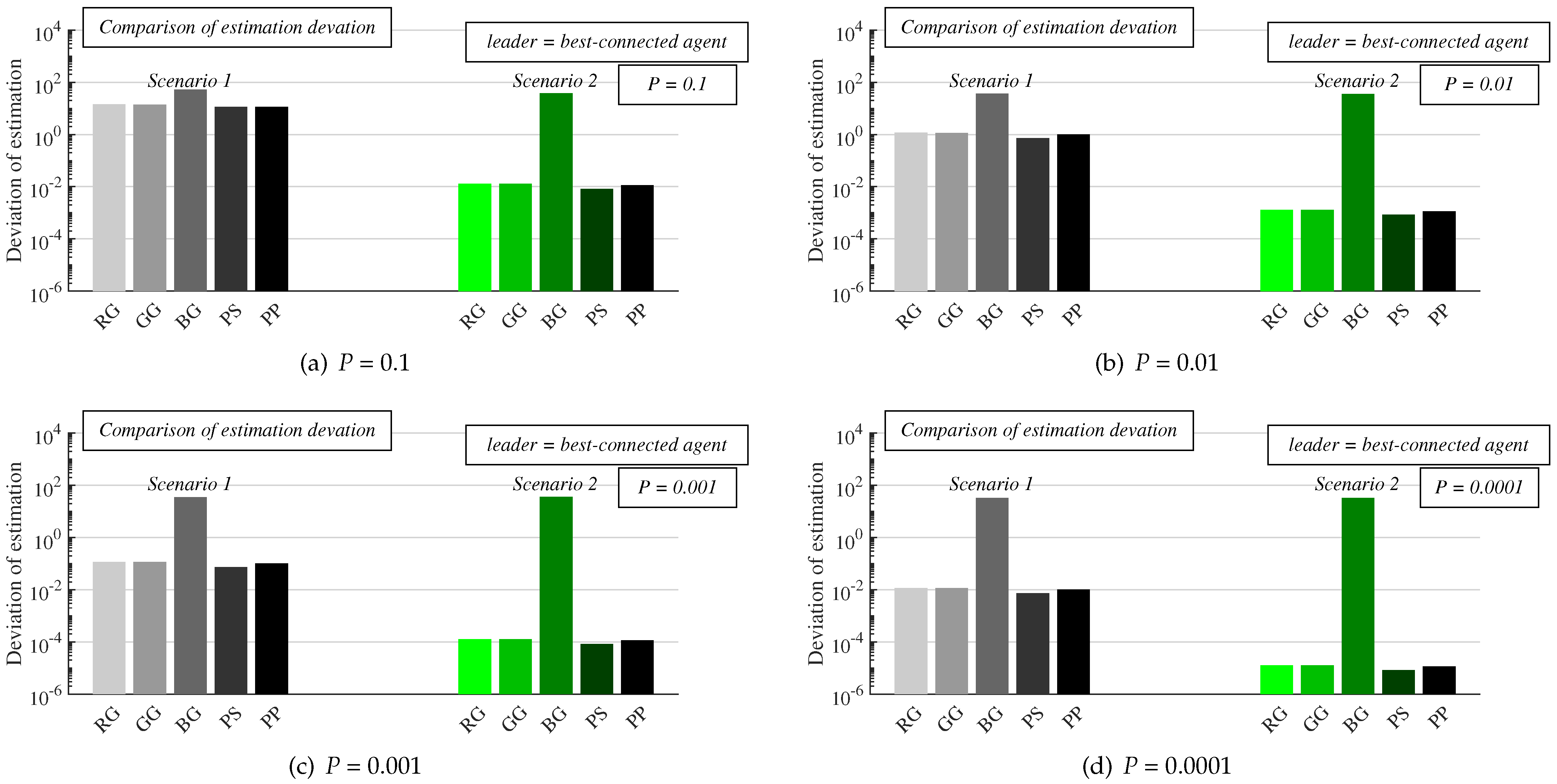
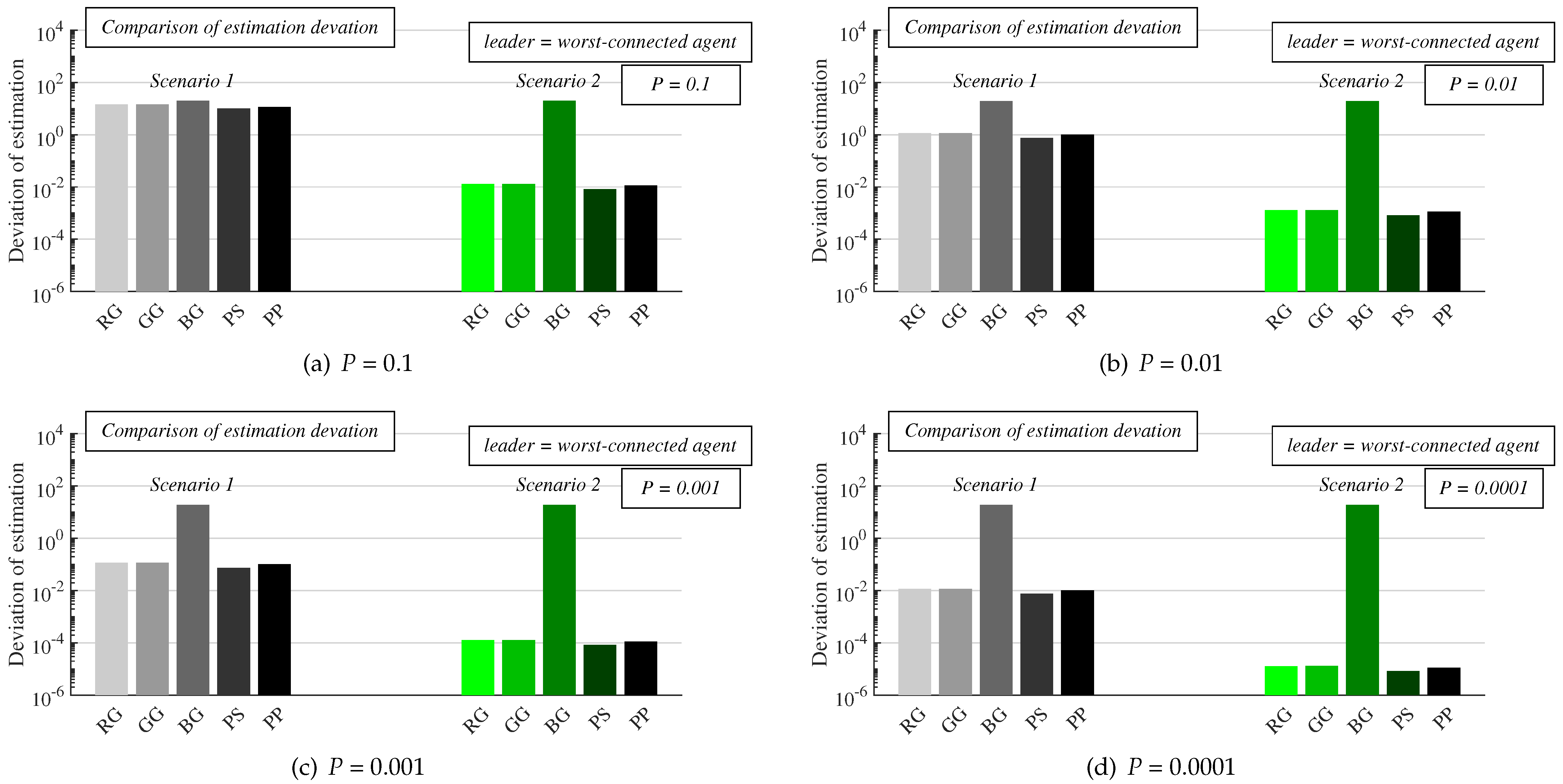
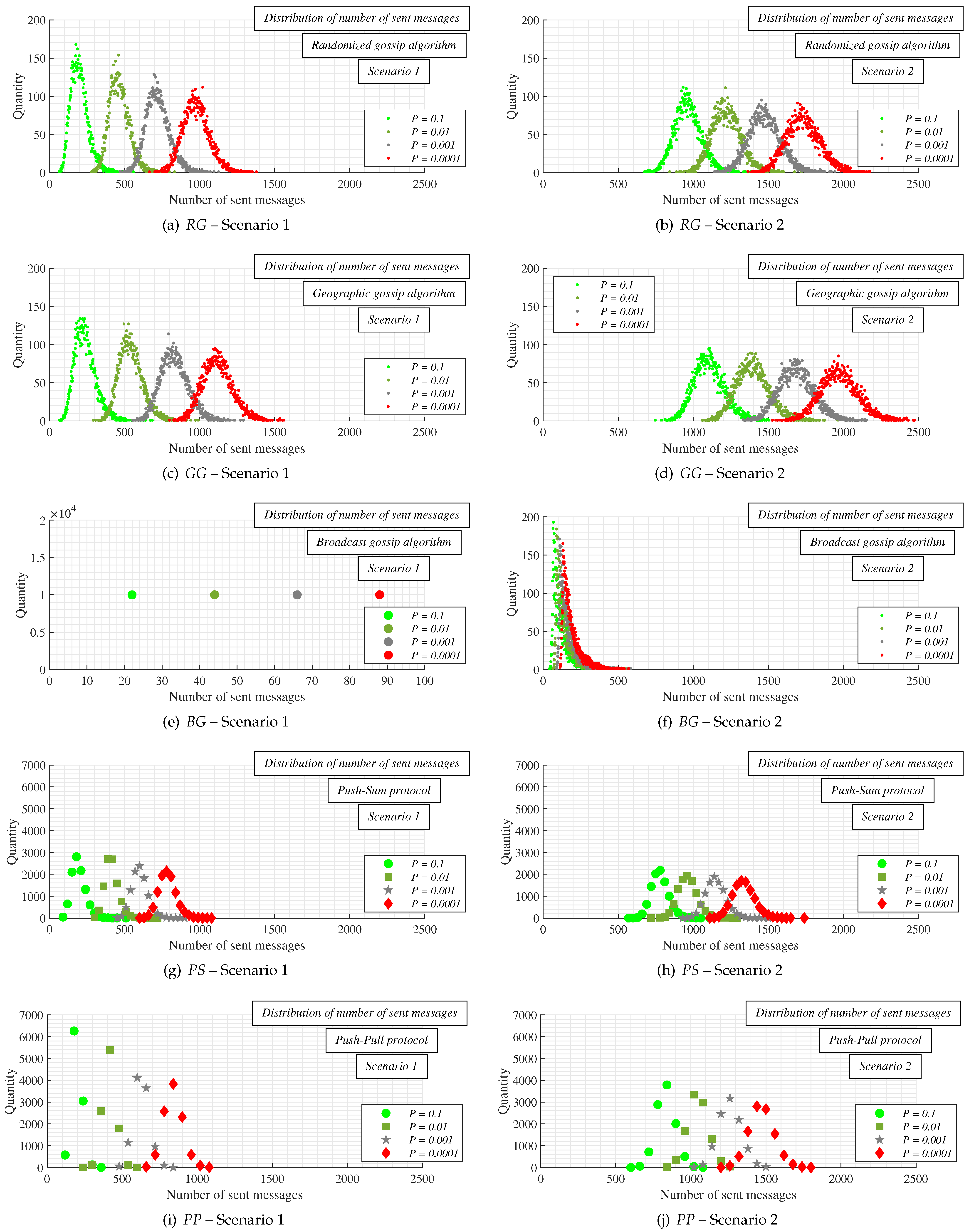
- Experiments: In this subsection, we present the results from numeral experiments for each examined algorithm. In Figure 10 and Figure 11, we provide the number of sent messages for consensus and the estimation precision, respectively, in both scenarios, for four values of the parameter P, and with the best-connected agent selected as the leader. In Figure 12 and Figure 13, the results obtained in experiments with the worst-connected agent as the leader are provided. In Figure 14, the distribution of the sent messages over 10,000 runs for each algorithm, in both scenarios, for each value of P, and with the best-connected agent selected as the leader is provided.
- □
- Discussion: In this subsection, we compare the results presented in Section 6.1 with conclusions presented in the papers from Section 2.
6.1. Experiments
6.2. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BG | Broadcast gossip algorithm |
| GG | Geographic gossip algorithm |
| MAS | Multi-agent system |
| NaN | Not a Number |
| PP | Push-Pull protocol |
| PS | Push-Sum protocol |
| RG | Randomized gossip algorithm |
| RGG | Random geometric graph |
References
- Zheng, Y.; Zhao, Q.; Ma, J.; Wang, L. Second-order consensus of hybrid multi-agent systems. Syst. Control Lett. 2019, 125, 51–58. [Google Scholar] [CrossRef]
- McArthur, S.; Davidson, E.M.; Catterson, V.M.; Dimeas, A.L.; Hatziargyriou, N.D.; Ponci, F.; Funabashi, T. Multi-agent systems for power engineering applications—Part I: Concepts, approaches, and technical challenges. IEEE Trans. Power Syst. 2007, 22, 1743–1752. [Google Scholar] [CrossRef]
- Shames, I.; Charalambous, T.; Hadjicostis, C.N.; Johansson, M. Distributed Network Size Estimation and Average Degree Estimation and Control in Networks Isomorphic to Directed Graphs. In Proceedings of the 50th Annual Allerton Conference on Communication, Control, and Computing, Allerton, Monticello, IL, USA, 1–5 October 2012; pp. 1885–1892. [Google Scholar]
- Seda, P.; Seda, M.; Hosek, J. On Mathematical Modelling of Automated Coverage Optimization in Wireless 5G and beyond Deployments. Appl. Sci. 2020, 10, 8853. [Google Scholar] [CrossRef]
- Wooldridge, M.; Jennings, N.R. Intelligent agents: Theory and practice. Knowl. Eng. Rev. 1995, 10, 115–152. [Google Scholar] [CrossRef]
- Dorri, A.; Kanhere, S.S.; Jurdak, R. Multi-Agent Systems: A Survey. IEEE Access 2018, 6, 28573–28593. [Google Scholar] [CrossRef]
- Rocha, J.; Boavida-Portugal, I.; Gomes, E. Introductory Chapter: Multi-Agent Systems. In Multi-Agent Systems; IntechOpen: Rijeka, Croatia, 2017. [Google Scholar]
- Li, M.; Zhang, X. Information fusion in a multi-source incomplete information system based on information entropy. Entropy 2017, 19, 570. [Google Scholar] [CrossRef]
- Castanedo, F. A review of data fusion techniques. Sci. World J. 2013, 2013, 704504. [Google Scholar] [CrossRef]
- Skorpil, V.; Stastny, J. Back-propagation and k-means algorithms comparison. In Proceedings of the 2006 8th International Conference on Signal Processing, ICSP 2006, Guilin, China, 16–20 November 2006; pp. 374–378. [Google Scholar]
- Zacchigna, F.G.; Lutenberg, A. A novel consensus algorithm proposal: Measurement estimation by silent agreement (MESA). In Proceedings of the 5th Argentine Symposium and Conference on Embedded Systems, SASE/CASE 2014, Buenos Aires, Argentina, 13–15 August 2014; pp. 7–12. [Google Scholar]
- Zacchigna, F.G.; Lutenberg, A.; Vargas, F. MESA: A formal approach to compute consensus in WSNs. In Proceedings of the 6th Argentine Conference on Embedded Systems, CASE 2015, Buenos Aires, Argentina, 12–14 August 2015; pp. 13–18. [Google Scholar]
- Merezeanu, D.; Nicolae, M. Consensus control of discrete-time multi-agent systems. U. Politeh. Buch. Ser. A 2017, 79, 167–174. [Google Scholar]
- Antal, C.; Cioara, T.; Anghel, I.; Antal, M.; Salomie, I. Distributed Ledger Technology Review and Decentralized Applications Development Guidelines. Future Int. 2021, 13, 62. [Google Scholar] [CrossRef]
- Merezeanu, D.; Vasilescu, G.; Dobrescu, R. Context-aware control platform for sensor network integration. Stud. Inform. Control 2016, 25, 489–498. [Google Scholar] [CrossRef]
- Vladyko, A.; Khakimov, A.; Muthanna, A.; Ateya, A.A.; Koucheryavy, A. Distributed Edge Computing to Assist Ultra-Low-Latency VANET Applications. Future Int. 2019, 11, 128. [Google Scholar] [CrossRef]
- Xiao, L.; Boyd, S.; Lall, S. A Scheme for robust distributed sensor fusion based on average consensus. In Proceedings of the 4th International Symposium on Information Processing in Sensor Networks, IPSN 2005, Los Angeles, CA, USA, 25–27 April 2005; pp. 63–70. [Google Scholar]
- Hlinka, O.; Sluciak, O.; Hlawatsch, F.; Djuric, P.M.; Rupp, M. Likelihood consensus and its application to distributed particle filtering. IEEE Trans. Signal Process. 2012, 60, 4334–4349. [Google Scholar] [CrossRef]
- Xiao, L.; Boyd, S. Fast linear iterations for distributed averaging. Syst. Control. Lett. 2004, 53, 65–78. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; Oyedeji, M.O.; Xia, Y. Advanced Distributed Consensus for Multiagent Systems; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Kenyeres, M.; Kenyeres, J. Average consensus over mobile wireless sensor networks: Weight matrix guaranteeing convergence without reconfiguration of edge weights. Sensors 2020, 20, 3677. [Google Scholar] [CrossRef]
- Gutierrez-Gutierrez, J.; Zarraga-Rodriguez, M.; Insausti, X. Analysis of Known Linear Distributed Average Consensus Algorithms on Cycles and Paths. Sensors 2018, 18, 968. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.Y.; Rabbat, M. Performance comparison of randomized gossip, broadcast gossip and collection tree protocol for distributed averaging. In Proceedings of the 5th IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, CAMSAP 2013, Montreal, QC, Canada, 15–18 December 2013; pp. 93–96. [Google Scholar]
- Liu, Z.W.; Guan, Z.H.; Li, T.; Zhang, X.H.; Xiao, J.W. Quantized consensus of multi-agent systems via broadcast gossip algorithms. Asian J. Control 2012, 14, 1634–1642. [Google Scholar] [CrossRef]
- Baldi, M.; Chiaraluce, F.; Zanaj, E. Performance of gossip algorithms in wireless sensor networks. Lect. Notes Electr. Eng. 2011, 81, 3–16. [Google Scholar]
- Aysal, T.C.; Yildiz, M.E.; Sarwate, A.D.; Scaglione, A. Broadcast gossip algorithms for consensus. IEEE Trans. Signal Process. 2009, 57, 2748–2761. [Google Scholar] [CrossRef]
- Aysal, T.C.; Yildiz, M.E.; Sarwate, A.D.; Scaglione, A. Broadcast gossip algorithms. In Proceedings of the IEEE Information Theory Workshop, ITW, Porto, Portugal, 5–9 May 2008; pp. 343–347. [Google Scholar]
- Dimakis, A.A.G.; Sarwate, A.D.; Wainwright, M.J.; Scaglione, A. Geographic gossip: Efficient averaging for sensor networks. IEEE Trans. Signal Process. 2008, 56, 1205–1216. [Google Scholar] [CrossRef]
- Aysal, T.C.; Yildiz, M.E.; Sarwate, A.D.; Scaglione, A. Broadcast gossip algorithms: Design and analysis for consensus. In Proceedings of the 47th IEEE Conference on Decision and Control, CDC 2008, Cancun, Mexico, 9–11 December 2008; pp. 4843–4848. [Google Scholar]
- Jesus, P.; Baquero, C.; Almeida, P.S. Dependability in Aggregation by Averaging. arXiv 2010, arXiv:1011.6596. [Google Scholar]
- Jesus, P.; Baquero, C.; Almeida, P.S. A study on aggregation by averaging algorithms (poster). In Proceedings of the EuroSys 2007–2nd EuroSys Conference, Lisbon, Portugal, 21–23 March 2007; p. 1. [Google Scholar]
- Blasa, F.; Cafiero, S.; Fortino, G.; Di Fatta, G. Symmetric push-sum protocol for decentralised aggregation. In Proceedings of the 3rd International Conference on Advances in P2P Systems, AP2PS 2011, Lisbon, Portugal, 20–25 November 2011; pp. 27–32. [Google Scholar]
- Huang, W.; Wang, Y.; Provan, G. Comparing Asynchronous Distributed Averaging Gossip Algorithms Over Scale-free Graphs. Available online: http://www.cs.ucc.ie/~gprovan/Provan/comparegossip.pdf (accessed on 16 May 2021).
- Cardoso, J.C.S.; Baquero, C.; Almeida, P.S. Probabilistic Estimation of Network Size and Diameter. In Proceedings of the 4th Latin-American Symposium on Dependable Computing, LADC 2009, Joao Pessoa, Brazil, 1–4 September 2009; pp. 33–40. [Google Scholar]
- García-Magariño, I.; Palacios-Navarro, G.; Lacuesta, R.; Lloret, J. ABSCEV: An agent-based simulation framework about smart transportation for reducing waiting times in charging electric vehicles. Comput. Netw. 2018, 138, 119–135. [Google Scholar] [CrossRef]
- García-Magariño, I.; Sendra, S.; Lacuesta, R.; Lloret, J. Security in Vehicles with IoT by Prioritization Rules, Vehicle Certificates, and Trust Management. IEEE Internet Things J. 2019, 6, 5927–5934. [Google Scholar] [CrossRef]
- Baquero, C.; Almeida, P.S.; Menezes, R.; Jesus, P. Extrema Propagation: Fast Distributed Estimation of Sums and Network Sizes. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 668–675. [Google Scholar] [CrossRef]
- Kennedy, O.; Koch, C.; Demers, A. Dynamic Approaches to In-Network Aggregation. In Proceedings of the 25th IEEE International Conference on Data Engineering, ICDE 2009, Shanghai, China, 29 March–2 April 2009; pp. 1331–1334. [Google Scholar]
- Jesus, P.; Baquero, C.; Almeida, P.S. A Survey of Distributed Data Aggregation Algorithms. IEEE Commun. Surveys Tuts. 2015, 17, 381–404. [Google Scholar] [CrossRef]
- Nyers, L.; Jelasity, M. A comparative study of spanning tree and gossip protocols for aggregation. Concurr. Comp. 2015, 27, 4091–4106. [Google Scholar] [CrossRef]
- Nyers, L.; Jelasity, M. Spanning tree or gossip for aggregation: A comparative study. In Proceedings of the European Conference on Parallel Processing, Euro-Par 2014, Porto, Portugal, 25–29 August 2014; pp. 379–390. [Google Scholar]
- Nyers, L.; Jelasity, M. A practical approach to network size estimation for structured overlays. Lect. Notes Comput. Sci. 2008, 5343, 71–83. [Google Scholar]
- Fraser, B.; Coyle, A.; Hunjet, R.; Szabo, C. An Analytic Latency Model for a Next-Hop Data-Ferrying Swarm on Random Geometric Graphs. IEEE Access 2020, 8, 48929–48942. [Google Scholar] [CrossRef]
- Gulzar, M.M.; Rizvi, S.T.H.; Javed, M.Y.; Munir, U.; Asif, H. Multi-agent cooperative control consensus: A comparative review. Electronics 2018, 7, 22. [Google Scholar] [CrossRef]
- Qurashi, M.A.; Angelopoulos, C.M.; Katos, V.; Munir, U.; Asif, H. An Architecture for Resilient Intrusion Detection in IoT Networks. In Proceedings of the 2020 IEEE International Conference on Communications, ICC 2020, Dublin, Ireland, 7–11 June 2020; pp. 1–7. [Google Scholar]
- Mustafa, A.; Islam, M.N.U.; Ahmed, S. Dynamic Spectrum Sensing under Crash and Byzantine Failure Environments for Distributed Convergence in Cognitive Radio Networks. IEEE Access 2021, 9, 23153–23167. [Google Scholar] [CrossRef]
- Kempe, D.; Dobra, A.; Gehrke, J. Gossip-based computation of aggregate information. In Proceedings of the 44th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2003, Cambridge, MA, USA, 11–14 October 2003; pp. 482–491. [Google Scholar]
- Boyd, S.; Ghosh, A.; Prabhakar, B.; Shah, D. Randomized gossip algorithms. IEEE Trans. Inf. Theory 2006, 52, 2508–2530. [Google Scholar] [CrossRef]
- Avrachenkov, K.; Chamie, M.E.; Neglia, G. A local average consensus algorithm for wireless sensor networks. In Proceedings of the 7th IEEE International Conference on Distributed Computing in Sensor Systems, DCOSS’11, Barcelona, Spain, 27–29 June 2011; pp. 1–6. [Google Scholar]
- Kenyeres, M.; Kenyeres, J.; Budinska, I. On Performance Evaluation of Distributed System Size Estimation Executed by Average Consensus Weights. Fuzziness Soft Comput. 2021, 403, 15–24. [Google Scholar]
- Shang, Y.; Bouffanais, R. Consensus reaching in swarms ruled by a hybrid metric-topological distance. Eur. Phys. J. B 2014, 87, 1–7. [Google Scholar] [CrossRef]
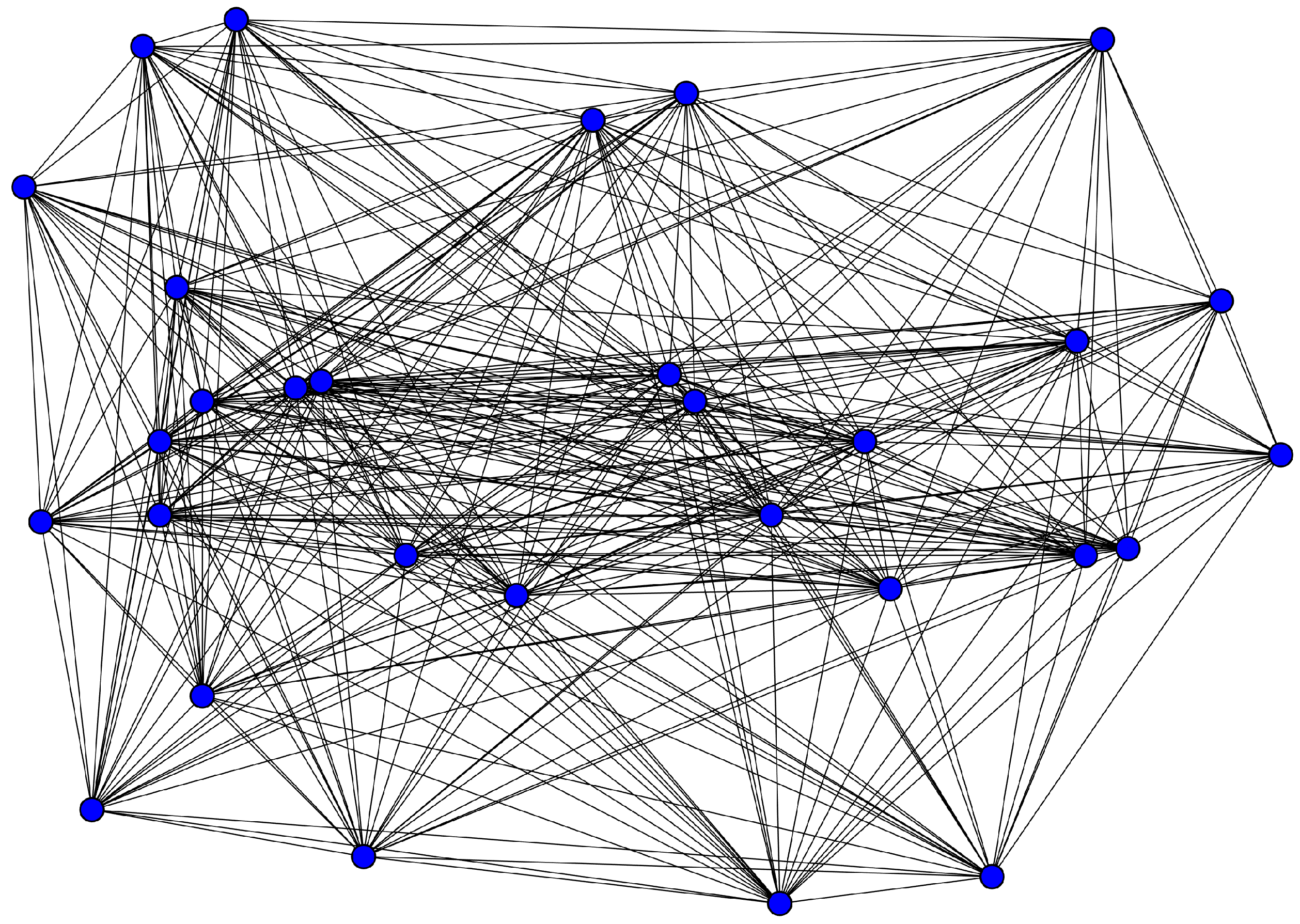
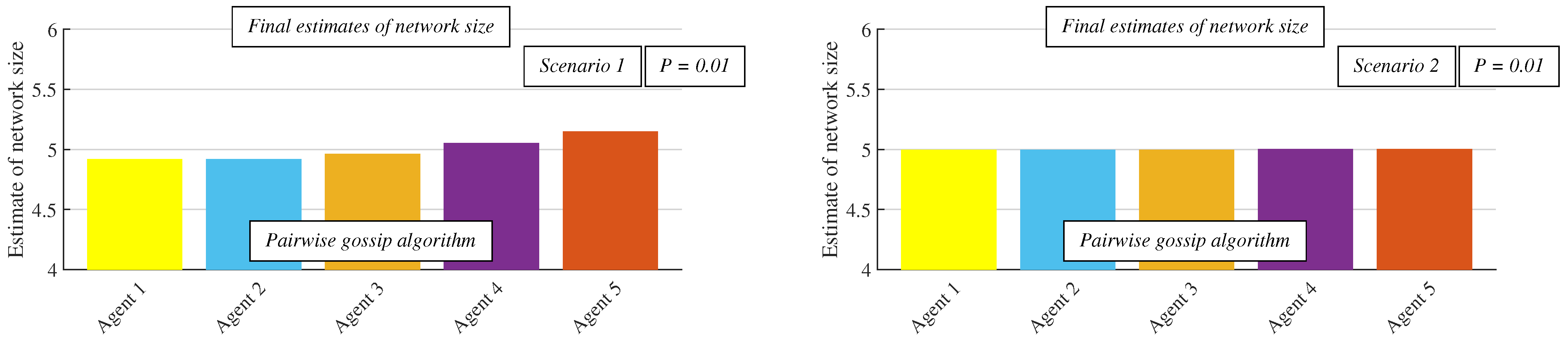

| Graph Parameter | Numerical Value |
|---|---|
| Graph order | 30 |
| Median degree | 25.21 |
| Max degree | 29 |
| Min degree | 16.17 |
| Diameter | 2 |
| Graph size | 371.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kenyeres, M.; Kenyeres, J. Comparative Study of Distributed Consensus Gossip Algorithms for Network Size Estimation in Multi-Agent Systems. Future Internet 2021, 13, 134. https://doi.org/10.3390/fi13050134
Kenyeres M, Kenyeres J. Comparative Study of Distributed Consensus Gossip Algorithms for Network Size Estimation in Multi-Agent Systems. Future Internet. 2021; 13(5):134. https://doi.org/10.3390/fi13050134
Chicago/Turabian StyleKenyeres, Martin, and Jozef Kenyeres. 2021. "Comparative Study of Distributed Consensus Gossip Algorithms for Network Size Estimation in Multi-Agent Systems" Future Internet 13, no. 5: 134. https://doi.org/10.3390/fi13050134
APA StyleKenyeres, M., & Kenyeres, J. (2021). Comparative Study of Distributed Consensus Gossip Algorithms for Network Size Estimation in Multi-Agent Systems. Future Internet, 13(5), 134. https://doi.org/10.3390/fi13050134