Abstract
Complex systems are fully described by the connectedness of their elements studying how these develop a collective behavior, interacting with each other following their inner features, and the structure and dynamics of the entire system. The forthcoming 6G will attempt to rewrite the communication networks’ perspective, focusing on a radical revolution in the way entities and technologies are conceived, integrated and used. This will lead to innovative approaches with the aim of providing new directions to deal with future network challenges posed by the upcoming 6G, thus the complex systems could become an enabling set of tools and methods to design a self-organized, resilient and cognitive network, suitable for many application fields, such as digital health or smart city living scenarios. Here, we propose a complex profiling approach of heterogeneous nodes belonging to the network with the goal of including the multiplex social network as a mathematical representation that enables us to consider multiple types of interactions, the collective dynamics of diffusion and competition, through social contagion and evolutionary game theory, and the mesoscale organization in communities to drive learning and cognition. Through a framework, we detail the step by step modeling approach and show and discuss our findings, applying it to a real dataset, by demonstrating how the proposed model allows us to detect deeply complex knowable roles of nodes.
1. Introduction
The ongoing process of telecommunications evolution towards 6G, along with the growing number of mobile users and the demand of bandwidth-intensive services and high data-rate applications, are creating a large volume of traffic, making a complex dare which needs to be addressed with innovative approaches [1,2]. The worldwide research activity is focused on defining the next-generation 6G systems in order to take into consideration a confluence of trends as densification, higher rate, massive antenna and emerging trends that include innovations in terms of services and devices, complexity and artificial intelligence (AI), computing and sensing [3]. Ranging from simple sensors to sophisticated devices, and including different network scenarios as cellular, vehicular, Wi-Fi, Internet of Things (IoT) and Internet of Everything (IoE) systems which connect millions of people and billions of machines, we expected that the sixth generation systems will meet the demands for a fully connected and intelligent network. Taking into consideration the forthcoming 6th generation (6G) communication networks, it will address the constraints and the performance requirements of the applications and innovative services which need highly increasing resources, introducing new approaches and technologies as well as revolutionary network features [2,4].
The designing and modeling processes of 6G network need new paradigms to move the system from closed hierarchical structures towards open and distributed networks, including self-organization, self-adaptation and optimization of interactions and functions of nodes. Thus, it can be achieved through the introduction of a complex systems approach. The traditional attributes applied to measure and characterize communication networks such as interference, coverage, throughput, robustness and costs are not able to describe dynamics and crucial aspects of future wireless and mobile networks. That is why there is growing interest in studying communication networks from a complex systems perspective, taking into account methodologies and tools built to analyze emerging behaviors, and cooperative and collaborative dynamics, among the elementary units of the system [2,5,6]. The upcoming 6G has the ambition to introduce heterogeneous interconnected elements which can dynamically interact with each other as well as with their environment in an unpredictable and unplanned way. Human beings, their devices and, consequently, their behaviors are active elements of the networks, becoming a sort of heterogeneous and aggregated things, with a crucial role in technical systems and in the design of the networking functions, representing the interacting part of a complex socio-technical ecosystem [7,8]. From the mobile users and their devices (from wearable to hand-held) or the heterogeneous smart devices that form the IoT networks to the plethora of entities of each sub-network that constitute a 6G environment, these can be represented by nodes of a multiplex social network, as shown in Figure 1.
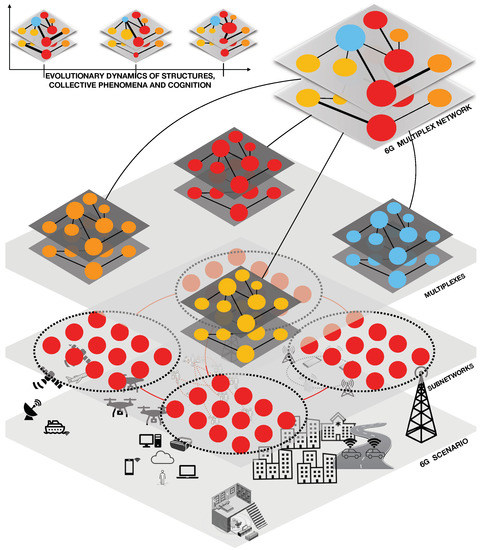
Figure 1.
Multiplex representation mined from 6G subsystems. This figure shows the schematic representation through the multiplex network of a 6G scenario, including different types of sub-networks, various interactions and the evolutionary dynamics of collective phenomena.
The multiplex dimension offers a key change in perspective for the structural analysis, and it represents the suitable representation to study the emergence of complex properties of the network [9,10]. The 6G network is intrinsically suitable to be modeled as the multidimensional relational systems of different sub-networks, represented by various graphs that embed interacting elements in different ways [2].
The designing, modeling and monitoring of the behavior of these systems will be challenges to address. Since we are rapidly moving from a closed to an open and distributed system, and to a completely dynamic topology that will be characterized by a vast heterogeneity, this requires an intelligence at the node level. The node, in a fully user-centric network architecture, plays a key role in content diffusion, learning, computation and organization, and consequently, a new characterization is becoming necessary. For this reason, we propose a node profiling process based on a complex network approach, which embeds, step by step, the knowledge extracted from the introduction of the multiplex dimension, the analysis of the dynamics of collective phenomena as diffusion and competition, applying the epidemics spreading modeling and the evolutionary game theory, from the mesoscale hierarchical organization of the network in communities. We detail the profiling technique through the introduction of metrics and parameters that enables the analysis of three different aspects, structural, collective dynamical and community-based. The paper is organized as follows: in Section 2 we briefly introduce background and methods. In Section 3, we detail the modeling approach to the profiling, in terms of structural, collective and community analysis. After, we show and discuss our findings in Section 4 to conclude in Section 5.
2. Materials and Methods
2.1. Multiplex Social Network and Mesoscale Structure
In order to show the hidden dynamics of complex systems it is useful to rely on multi-dimensional network representation, which is able to unveil interesting structural properties and interdependence. A single graph representation, where elementary units are mapped into network nodes and their interactions into links, can result in a loss of knowledge about the structural complexity and connectivity [9,11]. Representing all the links in an equivalent way can lead to a loss in details and information, and so, to an incomplete description about phenomena of real-world networks. Multilayer networks embody a generalization of traditional network theory, representing a novel framework to study graphs, in which nodes have different layers of connectivity [12]. These networks are able to properly describe the complex connectivity, by distinguishing in the different layers the several channels of interactions, which can be different for relevance, context and meaning [9,10,13]. The concept of multilayer networks extends to other mathematical objects, such as multiplex networks, that describe a large number of real networks, including biological [14], social and technological systems, social networks and relationships [15], epidemic and social contagions [16], air transportation networks and brain computing [5,17,18,19,20].
The multiplexity constitutes an additional dimension of analysis which makes the full characterization of behavior in complex systems possible, unveiling crucial structural properties [21]. Furthermore, an even deeper analysis of complexity in connections can be done characterizing interactions by a given cost, a distance or a weight, reflecting their intensity in the different layers, like in the case of weighted multiplex networks [13].
Moreover, a multiplex network has a rich structure that is often reflected in its community [22]. In the literature, there are several algorithms proposed to detect communities in complex networks [23]. Since there is a tendency of nodes of the networked systems to cluster together in groups, triggering a non-trivial structure, it is interesting to analyze the mesoscale structure [22]. The aim is to unveil a hidden organization of nodes and its interplay with the structure of multiplex network, nodes profile, nature of links, and layers existence.
2.2. Collective Dynamics of Diffusion and Competition
The multiplex networks lead us to explore in what measure the heterogeneous nodes and their ties in the different layers have an impact on emerging phenomena like cascading failures, super-diffusion, spreading and epidemic dynamics [15,17,18,19,20,21,24]. The diffusion dynamics can be modeled as a spreading process of diseases [5,25], social contagion of behaviors in networks [15] or misinformation and emotions spreading [26]. These processes, based on classical epidemiological models [25], find applications in many fields, from smart cities to healthcare [6,27], characterizing different collective phenomena that spread inter-personally through the social networks [16,28]. The nature of social ties has a pivotal role in shaping the structure, the heterogeneity of nodes and the diffusion in the network. There is an upsurge of social and communication technologies and an increasing in the need to embody what is traced about the activity of networked individuals. It is interesting to investigate the effect of the diffusion processes that co-evolve in the network, based on content exposure, event dynamics, collective attention and awareness, shifting the dynamics of social behaviors, also impacting on the nature of nodes and ties [5,28]. To study the evolutionary dynamics of competition, we use the Evolutionary Game Theory (EGT), which is an extension of the traditional Game Theory, and it was applied to the study of genetics, adaptation, and frequency of gene’s appearance [29]. The focus is the dynamic of changing strategies, and games are a way to investigate which behavior emerges from the interaction among individuals and if it is able to persist. The purpose of these theories is to use mathematical models to describe and predict what will happen, through games, in real situations.
Games are defined by a set of N players who can choose among a set of available strategies; with each strategy, players receive a payoff, which acts as a feedback and scores the preference [30]. EGT is useful to study the collective dynamics of cooperation and competition, through the so-called social dilemmas. In these dilemmas, there are two players and two possible strategies: cooperation and defection. They model conflict situations in which the most profitable strategy for individuals does not correspond to the most convenient for the entire social community. Thus, the players and the society would benefit more from mutual cooperation, receiving a higher benefit than in the case of mutual defection. Each of them is described by its payoff matrix representing the interactions’ rules [14].
Players will both receive a reward R in correspondence of mutual cooperation and a punishment P in the case of mutual defection. A defector will get the temptation payoff T when playing against a cooperator, while the cooperator obtains the so-called sucker payoff S. Here, we consider different social dilemmas as the Prisoner’s Dilemma (PD), Snowdrift Game (SD), Stag-Hunt Game (SH), and Harmony Game (HG) [31,32], for the investigation of the evolutionary dynamics of the cooperation.
3. Results
3.1. Scenario
We propose a nodes’ profiling technique based on a modeling framework, as we presented in Figure 2. The scheme put in evidence the introduction of the multiplex dimension to detect a profiling in structural terms, also enabling the analysis of the diffusion and the competition dynamics with the aim at analyzing the collective contribution to the characterization of nodes. Finally, the clustering techniques for the community detection enable us to track down an added value to the nodes’ role linked to a mesoscopic point of view.
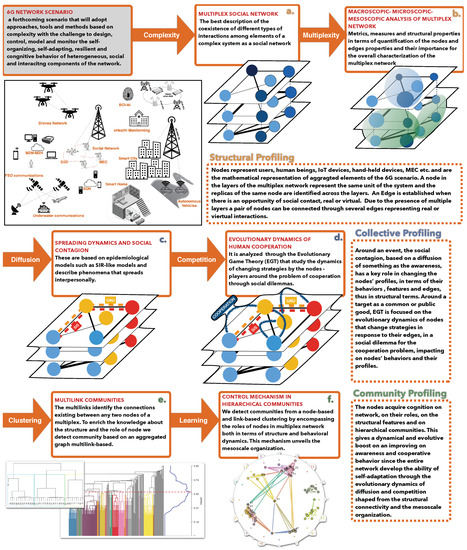
Figure 2.
Modeling Approach: a technical scheme of nodes’ profiling in a 6G network scenario. The figure graphically describes the various steps and the key aspects to profile the elements that constitute the 6G scenario into a complex network heterogeneous environment of cognitive elements. The approach starts from the application of the complexity and the multiplex representation and analysis to extract structural features as detailed, respectively, in (a,b). The scheme shows the collective profiling based on the analysis of diffusion and competition, representing two co-evolving and interdependent dynamics, as, respectively, detailed in (c,d). The community profiling, as in (e,f), is characterized by the detection of communities based on node and link hierarchical clustering obtained through a multilink graph.
3.2. Structural Profiling
A complex network involves basic units connected to each other with multiple kinds of relationships among them. Embedding the interactions in different layers in accordance to their types, we can consider the multiplex social network representation and analysis [5,9,10,15]. Following the scheme presented in Figure 2, we consider a multiplex social network M, assuming that it can represent a 6G sub-network and it is referred to different kinds of interactions among nodes. A node represents an aggregation of different basic units of the network (as wearable or hand-held devices, IoT systems, etc.). The multiplex network consists of a population of N nodes and layers. Here, we consider layers, where the layer is referred to a real contact network, extracted from a real case [33], while the second one is referred to a virtual layer following a theoretical scheme as, for example, a Scale-Free network [34] or a Small-World network [35]. In the literature, the multiplex network is defined as a set of graphs G, with , with vertices V and edges E. The set of nodes N is the same for each layer, whereas the set of links E changes according to the layer [9]. Each network is described by the adjacency matrix, denoted by with elements , where , if the node i and the node j are connected through a link on a layer l, otherwise . Alternatively, in the weighted case, , if there is a link between i and j with a weight , otherwise , with a real positive number, namely the weight of the link between i and j. In this case, a weighted multiplex network is completely specified by the weighted adjacency matrix , with elements [13]. With , we indicate the degree of the node i in a given layer l, that considers the total number of connections. Moreover, other basic features that we include in the profiling are represented by the edge overlap , that take into consideration the fact that a pair of nodes can be connected by ties in different layers, and the overlapping degree [9]. In the case of weighted multiplex networks, the latter are, respectively, expressed as weighted overlap and weighted overlapping degree [9,13]. The weights, which can be distributed heterogeneously, are strongly correlated with the structure [13], shedding light on the relevance of the links in a layer of the multiplex network representation. For that reason and with the aim at embodying social aspects into structural profiling, we apply the definition of the weights of the links as function of some key metrics, as follows:
where indicates the tendency to interact with similar nodes (as equal devices) or with that ones that are in similar conditions (capacity, resources, etc.) [5,9,13]. Furthermore, we include the gap value, between i and j, of the node awareness . In a fixed time T, in which we observe the network and its activity, we define as the awareness level of a node i, that represents acquired knowledge on the sub-network to which it belongs, that is about activity about task requests, as a result of a complex discovering process. For that reason, we estimate the awareness of a node i as function of the participation coefficient , and the attention level, as follows:
The multiplex participation coefficient ponders the awareness since it measures the heterogeneity of the number of neighbors across the layers of each node at the edge of the weighted link, measuring the probability of acquiring more knowledge as a result of different interactions distributed across the layers of the multiplex network [5,9]. The value is added to incorporate the richness of the knowledge extracted from the introduced multiplex dimension. Furthermore, the awareness can be computed as the result of the monitoring of the attention level, traced through the analysis of the user-generated data [28,36]. Data can be produced by devices in terms of willingness to cooperate for a set of tasks in IoT cognitive systems or it can represent the activity of nodes produced in social media during collective phenomena of interest, impacting on the widespread participation of networked users, on the behaviors of each node and its interactions and decisions in the dynamical evolution of the concerned phenomena [5]. We show the multiplex network M in Figure 3.
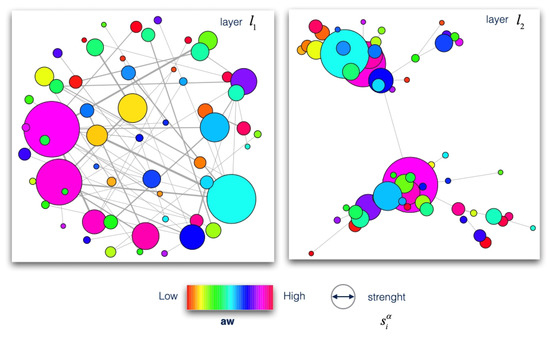
Figure 3.
Multiplex Network Representation. The figure describes both layers of the multiplex network M. The layer is obtained from a real contact case, as explained in Section 3.2, while the layer , follows a theoretical scheme. Here, is represented as a scale-free network. We shed light on the strength of each node (as the nodes’ size), and the awareness of each node (as the nodes’ color).
A complete list of parameters and defined metrics with its fair meaning, referring to the structural profiling, is summarized in Table 1.

Table 1.
Structural Profiling Parameters and Defined Metrics. Here, we summarize the general formalism of the multiplex networks nodes’ parameters and some defined statistical estimators, used to draw up the structural profiling of nodes in a 6G scenario represented and analyzed through the proposed framework and the mentioned above mathematical methods and tools, based on complex systems and networks.
3.3. Collective Profiling
Multiplex networks representation, as showed in Figure 3, constitutes the most suitable network structure to understand and investigate on collective dynamical processes and their complex interdependence [37]. In this second step, we consider key features extracted from the analysis of parameters and statistical estimators of two interdependent and co-evolving spreading processes and the evolutionary dynamics of the cooperation among nodes. Firstly, we study the spreading of two interdependent processes in the multiplex network M, modeled as disease spreading process [15] and thought of as “composed-SIR” models, that is as an extension of the classical SIR epidemic model [38]. One process is referred to a specific phenomenon as epidemic [5], collective attention [28] or a social contagion [16], while the second one is related to the diffusion of the awareness on what is transmitted through the first one [15,39]. Heterogeneity and awareness, for each node, are included in order to describe the impact of the diffusion and competition into the structural connectivity and the evolutionary dynamics. Each node has a different awareness , representing the acquired knowledge from an interest or participation on a collective phenomena. As a consequence, each node, will be heterogeneously prone to join a diffusion process, since the awareness acquired has an influence on the behaviors of nodes. Firstly, we analyze two co-evolving spreading processes in the multiplex network M. The first one is based on the content shared or a phenomena of interest. Taking into consideration the nature of the phenomena or content, we can diagrammatically express the first process, in terms of reaction-diffusion equations, following two different hypothesis as indicated below as the or spreading processes:
The can occurs when a node, based on its interactions, becomes prone to participate to the diffusion, and after that it returns in the condition to the starting pools of nodes. Differently, in the the last transition is replaced by the step which occurs when a node have acquired a permanent condition and it is not available to participate again in the diffusion. Both models are characterize by the states , defined as “heterogeneous susceptible state”, where a node is predisposed to be involved in the spreading process [15]. The state I indicates the condition in which a node is involved or infected, while R represents the recovered state. The probability of call off the diffusion is equal to , while the is the diffusion rate for each node i at each layer in the multiplex network M. The latter represents the probability that a node i in the layer is predisposed or susceptible to be involved in the diffusion process. We assume that, the involvement for a node in the network means that a node i is in the state of informed or infected. The heterogeneous diffusion rate depends on the weighted structural connectivity through the measures of inverse participation ratio [13] and the rate of awareness , defined in Equation (8).
Similarly, the second spreading process, focused on awareness diffusion, is diagrammatically expressed in terms of reaction–diffusion equation also in two possible different cases, as follows:
with and , defined as transition rates. We distinguish between the rate of awareness for each node i at each layer of the multiplex M and the rate of awareness after being aware. The state expresses a condition in which a node is heterogeneously unaware, while in A, it is aware about the phenomena that spreads inter-personally in the network. In the second case, the state F is introduced as the “faded state”, in which a node decreases the attention and the interest to improve its knowledge about the phenomena of interest. The rate of awareness is expressed as follows:
where is the strength of node i in the layer of the multiplex network M [13].
Starting from the assignment of a state probability for each node i in M, to be in one of the initial states as (SU)-(SA)-(IA), and choosing the suitable spreading models for the co-evolution process, as indicated in Figure 4 and expressed in Equations (3) and (4), we add, in the profiling process, some features extracted from the analysis of the co-evolution in the multiplex network considered. To obtain the contagion threshold, we need to apply the MMCA method, investigating the steady state of the system, indicated as . The Dynamic Microscopic Markov Chain Approach (MMCA) enables us to explore the dynamics of the co-evolution on a weighted multiplex network. Following the mathematical approach, as expressed in [5], we get the density of involved nodes :
where are the probabilities of being involved and aware. On this matter, it is important to underline that the threshold model depends on the complex dynamical interplay between social contagion and the awareness spreading in M and the values of that change in accordance with the awareness state , the network structure of M, and the double heterogeneity expressed in S state and U state. Consequently, the awareness of a node as expressed in Equation (2) also depends on the and value in terms of attention which represents the social-aware factor that varies in function of the two rates. Both processes co-evolve modeling the sharing or participation in terms of content, interests, attention and awareness, and in terms of active or passive involvement [6,16,39]. Furthermore, we inspect the cooperative behaviors and its dynamics among nodes, which include social factors in their aggregated nature, by introducing the game theoretical approach [14]. We introduce different dilemmas as the iterated forms of Prisoner’s Dilemma game (PD), Snowdrift game (SD), Stag-Hunt game (SH) and Harmony game (HG) [31]. In the analysis of the interdependent collective dynamics, we run and compare the dilemmas for a number of rounds such that a dynamical steady state is reached, in order to describe not only the problem of cooperation, but also its evolution. Nodes are treated as players that, in each elementary round of the game can decide to change or maintain its strategy, playing the game with all its neighbors in both layers of the multiplex M, in line with the Fermi function , expressed as follows:
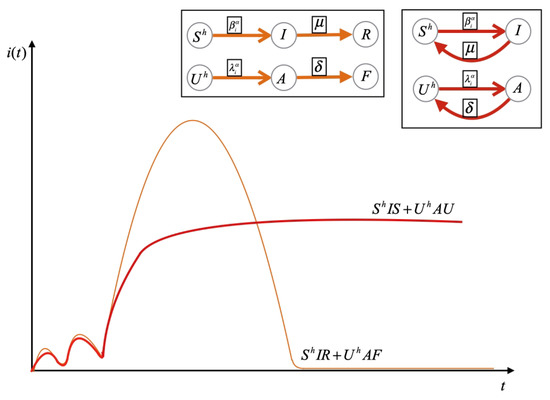
Figure 4.
Density of Involved Nodes versus time , on the two processes in co-evolution. The outbreak of spreading in time is subjected to statistical variability. After a common exponential growth, we shed light on how the density of involved (“involved” means informed or infected) nodes change in two different cases (respectively, orange and red) of the co-evolving processes that can converge to zero () or to a constant number ().
Firstly, with this function we take into account the payoff difference , the homophily measure , a communicability measure and a noise factor K to evaluate the probability that a player i on the layer decides to adopts the strategy of node j playing on the layer [14]. Accounting for that, at time step t, each node can occupy one state of the co-evolving spreading processes, and considering that, represents the probability of node i not being involved and with the probability of unaware node i staying unaware at the same time step t, we include in the Fermi function the dependency from the factor, defined as follows:
This includes the joint impact of the co-evolving spreading processes and the evolutionary dynamics of the cooperation among nodes in the multiplex network M, assessed in the temporal window T. We summarize parameters and defined metrics of the collective dynamics aspects in Table 2.

Table 2.
Collective Profiling Parameters and Defined Metrics. Here, we summarize the general formalism linked to the analysis of the collective dynamics of diffusion and competition that involve the networks nodes in the multiplex network M. We list the key parameters and some defined statistical estimators used to compose the collective profiling of nodes in a 6G scenario represented and analyzed through the proposed framework and the mentioned above mathematical tools, based on complex systems and networks.
3.4. Community Profiling
The whole multiplex network M can be also described via its multilink [22] with the aim at describing a mesoscopic dimension. Every pair of nodes in M is connected by a multilink with and , layers of the multiplex M, with indicating the set of all links connecting these nodes in the different layers [22]. If there are no interactions between the two nodes in the multiplex M. This measure shows the basic motif [9] that contributes to the unveiling of correlations between structure and function of a network [12]. We construct a weighted aggregated network , based on the multilink , with the adjacency matrix , with a step function [22]. For detecting community, we introduce the multidegree for each node i of the population, showing how many multilinks are incident on the node i [13]. In line with the previous steps of profiling, we propose two community detection methods introducing the mesoscopic analysis of the network. The resulting hierarchy embeds both the richness of the structure and the collective dynamics in the cognitive profiling since each node belongs to a community with a specific role that dynamically tunes in response to the changes in behaviors and social factors. Thus, we combine the different interdependent steps of profiling and we apply two hierarchical clustering technique to the multiplex network, respectively, a node-based and a link-based technique. The node-based hierarchical clustering analyzes a set of dissimilarities through the application of an agglomeration method. We define a dissimilarity structure based on the distance between each pair of nodes in function of the number of cooperations , the social dilemma, the between-ness centrality , and the multidegree [9,22]. We construct a dendrogram via hierarchical clustering method containing information about the structure and based on the dissimilarity matrix. More specifically, we evaluate a defined score function for each pair of nodes to estimate the distance between them, as indicated below:
With this approach, each node belongs to a community with a role in the hierarchical organization of the multiplex network M. Similarly, by constructing the aggregated graph multilink-based , we furthermore apply a hierarchical clustering by grouping instead the links in different communities showing a hidden mesoscale structural organization, highlighting how nodes can belong, at the same time, to different link-based communities. We summarize parameters and defined metrics of the community profiling aspects in Table 3. We detail the output of these methodologies in the next section.

Table 3.
Community Profiling Parameters and Defined Metrics. Here, we summarize the general formalism linked to the mesoscale analysis applied to the multiplex network M. We list the key parameters and some defined metrics used to compose the community profiling of nodes in a 6G scenario represented and analyzed through the proposed framework and the mentioned above mathematical tools, based on complex systems and networks.
4. Discussion
Simulations have been performed considering a weighted multiplex network M as explained in Section 3. To build the model, do computation and obtain our results, we used the programming language R and the IDE RStudio. The figures were generated thanks to the package Plotly and Linkcomm [40,41,42,43]. We consider a population in the two layers representing two distinct kinds of weighted interactions and connectivity between nodes. In the first layer , the interactions are based on the graph extracted from a real contact network [33], while in , we consider a theoretical scheme for the same population of nodes N. In Figure 5, we can observe how the structural heterogeneity in the multiplex representation of the networks leads to highlight several key aspects for the structural roles of nodes. For a heterogeneous weighted multiplex network, we study how certain metrics are distributed across different layers and in the whole structure. We have computed the degree , the strength and the overlapping degree as indicated in the two heath-map plots. Both plots display metrics for the multiplex M composed by the first layer based on real contact network while through the second layer we can compare the case of a scale-free network (in the top-left plot) with a small-world network (in top-right plot). For the sake of clarity, we indicate the first resulting multiplex M as , and the second one as . As shown in Figure 5, our findings exhibit two different levels of heterogeneity. We can notice how in the case, there is a small heterogeneity due to a high clustering and modularity, meaning that there are groups of nodes more highly connected than the rest of the network with an abundance of high degree nodes that act as hubs of the network. Instead, in the case, there are few hubs in the network since it exhibits a highly heterogeneous and high degree correlations. In the other two panels below in Figure 5, the curves correspond to the distribution of the participation coefficient , in the range , considering this variation in function of the Z-score of the overlapping degree, . We extract profiling features structurally classifying the nodes of the multiplex in three classes, focused, mixed and multiplex nodes, putting in evidence the fitness based on the two cases and , the awareness distribution of and the homophily distribution of the values , in accordance with the modeling approach. Our findings highlight an increasing of the value in both cases (–), and a higher density of regular multiplex nodes. Decreasing the homophily (from the left plot to the right plot below), the findings exhibit a decreasing of for the case that has a more homogeneous distribution with a higher density of regular mixed nodes. Differently, in the same condition, in the , the findings show an increasing of and a higher density in the multiplex hubs, since, although there is a higher value of homophily, the structural heterogeneity of the topology produces a more heterogeneous distribution of nodes’roles.
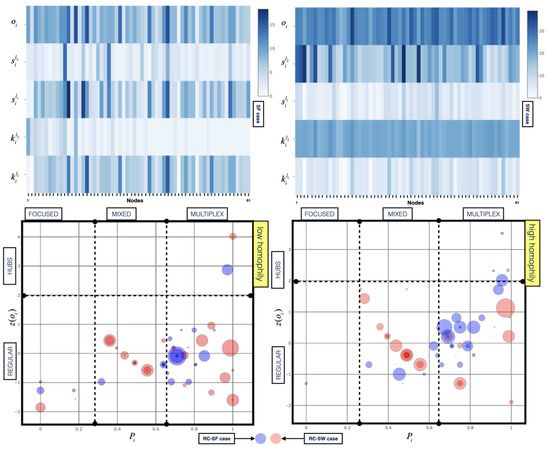
Figure 5.
Roles of Nodes from Structural Analysis. We show four panels to shed light on the roles of each node in M as a result of the structural profiling. At the top, the two heat-maps show with a color-code the value of degree , strength and overlapping degree for each node, from the largest (darkest) to the smallest (brightest) in both cases of scale-free (SF) and small-world networks (SW) as assumption for the graph of the second layer of the multiplex that describes a social-based interaction graph, jointly with the first layer based on a real contact network (RC). Below, the other two panels show two cartography obtained by plotting, for each node, the multiplex participation coefficient versus the Z-score of the total overlapping degree in the cases of a theoretical distribution with high standard deviation for low homophily and low standard deviation for high homophily, referring to the distribution of similarity features among nodes. In both plots, comparing the cases and , we identify specific roles of nodes put in evidence by the plots, in terms of focused, mixed, multiplex, regular or hubs nodes.
Figure 6 points out the profiling features embedding a measure of how a node of the multiplex structure is involved in the collective dynamics. We show the findings of diffusion and competition dynamics, by displaying the trend of infection rate in function of the awareness rate jointly with our modeling approach presented in Section 3.
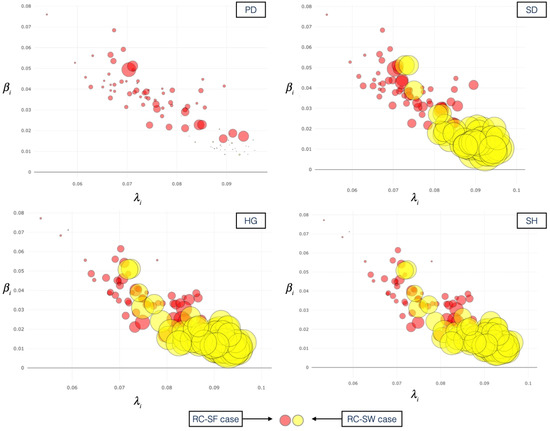
Figure 6.
Roles of Nodes from Collective Dynamics Analysis. We show four plots to shed light on the roles of each node of the population considered for the multiplex network M as a result of the collective profiling. The plots display, in the plane -, the trend of involved rate in function of the awareness rate, comparing both cases of scale-free (SF) and small-world (SW) networks as assumption for the graph of the second layer of the multiplex that describe a social-based interaction graph, jointly with the first layer based on a real contact network (RC), showing in red color the case, while in yellow the case. In accordance with the model and the interdependence between the evolutionary dynamics linked to the co-evolving spreading processes and the evolutionary game theory, we set and compare the four social dilemmas (PD-SD-HG-SH) displaying the trend of the spreading dynamics in relation to the number of cooperation for each node (as dot size variation) of the multiplex network M.
The plots show the resulting trend, in the plane -, of the spreading dynamics in conjunction with the cooperative behavior of nodes in the multiplex M, taking into consideration the two cases and , and the four social dilemmas PD-SD-HG-SH. Since the diffusion dynamics impact on the evolutionary dynamics of cooperation, we compare the modeling of the conflict situations with the different dilemmas. We find out how the increasing of the awareness rate , and the consequently decreasing of infections rate produce an impact on the collective cooperation dynamics. Namely, in case of social dilemmas in which the cooperation dominates the defection as SD, HG and SH, a more homogeneous number of cooperations for each node is more evident in the case of . Differently, in the plot referred to the PD game, in case of we detect a more heterogeneous distribution of cooperative behavior. In addition, in the PD, the increasing of results in a decreasing of , in both cases and , while in the other social dilemmas cases, this impact is stronger in then in . What is more, in the case and SD-HG-SH, the decreasing of with the increasing of is up to a specific threshold, resulting in a change in strategy, in accordance with the Fermi function as expressed in Equation (10), shedding light on the increased size of nodes in line with the increasing average in number of cooperation for each node.
In Figure 7, we show four panels linked to the community profiling detailed in the Section 3.4. By defining the dissimilarity between nodes based on Equation (12) we apply a hierarchical clustering of nodes as showed in the (a), (b) plots of Figure 7, that, respectively, exhibits the dendrogram and the graph based colored partitions of the six different communities. The detected groups of nodes based on a complex score function that take into consideration the structural and collective dynamical properties, show a community connectivity lower than the multiplex one. This unveils how the multiple interactions in the multiplex structure of each node represent a key point in a hierarchical characterization of the nodes’ roles. In the plot (c) and (d) (produced through the R package “linkcomm” [43]) of Figure 7, we find out results linked to the multilink and the link-based hierarchical clustering to reveal the richness of the network at the mesoscale level. We show in (c) the cluster dendrogram and the sixteen communities detected, and in (d) a graph visualization of the multilink-based aggregated graph . This methodology sheds light on in what measure the nodes of the multiplex structure, independently of its layer activity, can belong to different communities, revealing the hidden information extracted from the mesoscale structure organized in communities. The findings demonstrate that since the nodes belongs to multilinks communities, on average they have a high community activity, suggesting that the network can be expanded in many layers of different interactions. Moreover, the plot (d) of Figure 7 also underlines the brokering function of certain nodes among whose belonging to many communities (dots with multiple colors), playing a pivotal role in the cognitive collective dynamics.
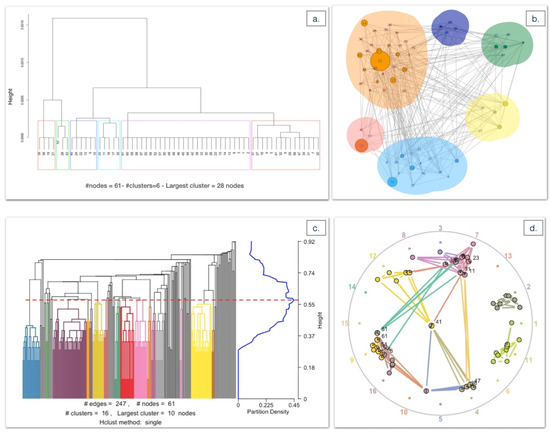
Figure 7.
Roles of Nodes from Community Analysis. In the (a,b) panel, we display the findings of the hierarchical clustering of nodes based on the score function . In (a), we show the cluster dendrogram, with each colored square shedding lights on different node communities, determined by cutting the dendrogram at a specific height. In panel (b), we display the visualization of nodes communities using graph highlighting the six communities of the weighted aggregated graphs , whose interaction are referred to existing multilinks between a pair of nodes, and it is extracted from the multiplex network M. Moreover, we underline the multidegree values for each node in accordance with their size. In the panel (c,d), we exhibit the findings of a link-based clustering of the graph of the multiplex M, to detect the links communities. In (c), we show the cluster dendrogram highlighting the sixteen clusters detected. In (d), we illustrate the visualization of links communities using graph. Panel (d) shows a Spencer circle layout with numbers around the circumference of the circle that are referred to community ID.
5. Conclusions
Over the last few years, the analysis and modeling of communication networks as complex dynamical systems has attracted high interest, especially in the interdisciplinary research. The 6G network is intrinsically suitable to be modeled as a multidimensional relational system of different sub-networks, represented by various graphs which embed elements that interact in different ways. These elements represent connected heterogeneous things that can share resources, archives, and tasks to provide services. These ecosystems involve devices with constrained resources and computational capabilities and call for novel algorithms and a new characterization for dynamically managing lightweight and simple services as a microservice. It represents a task for a physical edge element of the network, that in a virtual space is connected with other elements, seen as resources able to perform different tasks with the aim at providing an application that is in line with the consumer’s requirements. Heterogeneous things and devices (as sensors or hand-held devices), virtualized in edge cloud represent data and computational resources for tasks. In the proposed work, the elements are physical, virtual and concatenated resources. The interest mainly falls on the fact that those systems can be effectively described as complex networks, leveraging on the complex systems theory to engineer, design and model a 6G network. The complex approach for 6G systems will envision distributed artificial intelligence, to implement a fully user-centric network architecture. Introducing complexity through the proposed profiling approach, in 6G network, allows nodes to acquire cognition ability, as the results of processes able to disentangle grades of knowledge on their connectivity and behaviors on multiple different channels by deepening the investigation of structural and social aspects of the network, the collective dynamics of diffusion and competition, and the learning of belonging to various communities. In this paper, we propose a node profiling process that, step-by-step, allows defining of different aspects extracted from a complex network analysis, to shape a profile which embeds macroscopic, microscopic, mesoscopic, dynamical and learning properties. Our proposed profiling framework describes a set of inter-operable abstract classes referred to processes which constitute a cognitive level for nodes and community of nodes in network. We detail metrics and parameters, theory and analytical tools to study the coexistence of various type of interaction among nodes, the multiplex dimension of the network and the interplay of collective dynamics and the mesoscale organization.
Author Contributions
All the authors (M.S., B.A., A.L.C.) have equally contributed to the conceptualization, methodology, software, validation, formal analysis, investigation, resources, data curation, writing—original draft preparation and funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not Applicable, the study does not report any data.
Acknowledgments
This work was partially supported by the Research Grants: Italian Ministry of University and Research (MIUR)—PON REC 2014—2020 within the project ARS01 01116 “TALIs-MAN”—University of Catania.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Giordani, M.; Polese, M.; Mezzavilla, M.; Rangan, S.; Zorzi, M. Toward 6G networks: Use cases and technologies. IEEE Commun. Mag. 2020, 58, 55–61. [Google Scholar] [CrossRef]
- Sergiou, C.; Lestas, M.; Antoniou, P.; Liaskos, C.; Pitsillides, A. Complex Systems: A Communication Networks Perspective Towards 6G. IEEE Access 2020, 8, 89007–89030. [Google Scholar] [CrossRef]
- Saad, W.; Bennis, M.; Chen, M. A vision of 6G wireless systems: Applications, trends, technologies, and open research problems. IEEE Netw. 2019, 34, 134–142. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Kak, A.; Nie, S. 6G and beyond: The future of wireless communications systems. IEEE Access 2020, 8, 133995–134030. [Google Scholar] [CrossRef]
- Scatá, M.; Attanasio, B.; Aiosa, G.V.; La Corte, A. The Dynamical Interplay of Collective Attention, Awareness and Epidemics Spreading in the Multiplex Social Networks During COVID-19. IEEE Access 2020, 8, 189203–189223. [Google Scholar] [CrossRef]
- Scatà, M.; Di Stefano, A.; La Corte, A.; Liò, P. A Multiplex Social Contagion Dynamics Model to shape and discriminate D2D content dissemination. IEEE Trans. Cogn. Commun. Netw. 2020. [Google Scholar] [CrossRef]
- Mordacchini, M.; Conti, M.; Passarella, A.; Bruno, R. Human-centric data dissemination in the IoP: Large-scale modeling and evaluation. ACM Trans. Auton. Adapt. Syst. (TAAS) 2020, 14, 1–25. [Google Scholar] [CrossRef]
- Scatà, M.; Di Stefano, A.; Giacchi, E.; La Corte, A.; Liò, P. The bio-inspired and social evolution of node and data in a multilayer network. In Proceedings of the 2014 5th International Conference on Data Communication Networking (DCNET), Vienna, Austria, 28–30 August 2014; pp. 1–6. [Google Scholar]
- Battiston, F.; Nicosia, V.; Latora, V. The new challenges of multiplex networks: Measures and models. Eur. Phys. J. Spec. Top. 2017, 226, 401–416. [Google Scholar] [CrossRef]
- Boccaletti, S.; Bianconi, G.; Criado, R.; Del Genio, C.I.; Gómez-Gardeñes, J.; Romance, M.; Sendiña-Nadal, I.; Wang, Z.; Zanin, M. The structure and dynamics of multilayer networks. Phys. Rep. 2014, 544, 1–122. [Google Scholar] [CrossRef]
- De Domenico, M.; Nicosia, V.; Arenas, A.; Latora, V. Structural reducibility of multilayer networks. Nat. Commun. 2015, 6, 1–9. [Google Scholar] [CrossRef]
- Battiston, F.; Nicosia, V.; Chavez, M.; Latora, V. Multilayer motif analysis of brain networks. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 047404. [Google Scholar] [CrossRef] [PubMed]
- Menichetti, G.; Remondini, D.; Panzarasa, P.; Mondragón, R.J.; Bianconi, G. Weighted multiplex networks. PLoS ONE 2014, 9, e97857. [Google Scholar] [CrossRef]
- Di Stefano, A.; Scatà, M.; Vijayakumar, S.; Angione, C.; La Corte, A.; Liò, P. Social dynamics modeling of chrono-nutrition. PLoS Comput. Biol. 2019, 15, e1006714. [Google Scholar] [CrossRef] [PubMed]
- Scatà, M.; Di Stefano, A.; La Corte, A.; Liò, P. Quantifying the propagation of distress and mental disorders in social networks. Sci. Rep. 2018, 8, 5005. [Google Scholar] [CrossRef] [PubMed]
- Christakis, N.A.; Fowler, J.H. Social contagion theory: Examining dynamic social networks and human behavior. Stat. Med. 2013, 32, 556–577. [Google Scholar] [CrossRef]
- Nicosia, V.; Skardal, P.S.; Arenas, A.; Latora, V. Collective phenomena emerging from the interactions between dynamical processes in multiplex networks. Phys. Rev. Lett. 2017, 118, 138302. [Google Scholar] [CrossRef]
- Battiston, F.; Perc, M.; Latora, V. Determinants of public cooperation in multiplex networks. New J. Phys. 2017, 19, 073017. [Google Scholar] [CrossRef]
- Santoro, A.; Nicosia, V. Algorithmic complexity of multiplex networks. Phys. Rev. X 2020, 10, 021069. [Google Scholar] [CrossRef]
- De Domenico, M.; Granell, C.; Porter, M.A.; Arenas, A. The physics of spreading processes in multilayer networks. Nat. Phys. 2016, 12, 901–906. [Google Scholar] [CrossRef]
- Bianconi, G. Multilayer Networks: Structure and Function; Oxford University Press: Oxford, UK, 2018. [Google Scholar] [CrossRef]
- Mondragon, R.J.; Iacovacci, J.; Bianconi, G. Multilink communities of multiplex networks. PLoS ONE 2018, 13, e0193821. [Google Scholar] [CrossRef]
- Iacovacci, J.; Wu, Z.; Bianconi, G. Mesoscopic structures reveal the network between the layers of multiplex data sets. Phys. Rev. E 2015, 92, 042806. [Google Scholar] [CrossRef]
- Bródka, P.; Musial, K.; Jankowski, J. Interacting spreading processes in multilayer networks: A systematic review. IEEE Access 2020, 8, 10316–10341. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Castellano, C.; Van Mieghem, P.; Vespignani, A. Epidemic processes in complex networks. Rev. Mod. Phys. 2015, 87, 925. [Google Scholar] [CrossRef]
- Xian, J.; Yang, D.; Pan, L.; Wang, W.; Wang, Z. Misinformation spreading on correlated multiplex networks. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 113123. [Google Scholar] [CrossRef] [PubMed]
- Attanasio, B.; La Corte, A.; Scatá, M. Syncing a Smart City within an Evolutionary Dynamical Cooperative Environment. In Proceedings of the 2020 AEIT International Conference of Electrical and Electronic Technologies for Automotive (AEIT AUTOMOTIVE), Turin, Italy, 18–20 November 2020; pp. 1–6. [Google Scholar]
- He, X.; Lin, Y.R. Measuring and monitoring collective attention during shocking events. EPJ Data Sci. 2017, 6, 30. [Google Scholar] [CrossRef]
- Newton, J. Evolutionary game theory: A renaissance. Games 2018, 9, 31. [Google Scholar] [CrossRef]
- Iyer, S.; Killingback, T. Evolution of cooperation in social dilemmas on complex networks. PLoS Comput. Biol. 2016, 12, e1004779. [Google Scholar] [CrossRef] [PubMed]
- Matamalas, J.T.; Poncela-Casasnovas, J.; Gómez, S.; Arenas, A. Strategical incoherence regulates cooperation in social dilemmas on multiplex networks. Sci. Rep. 2015, 5, 9519. [Google Scholar] [CrossRef]
- Guo, D.; Fu, M.; Li, H. Cooperation in Social Dilemmas: A Group Game Model with Double-Layer Networks. Future Internet 2021, 13, 33. [Google Scholar] [CrossRef]
- Magnani, M.; Micenkova, B.; Rossi, L. Combinatorial analysis of multiple networks. arXiv 2013, arXiv:1303.4986. [Google Scholar]
- Barabási, A.L. Scale-free networks: A decade and beyond. Science 2009, 325, 412–413. [Google Scholar] [CrossRef]
- Barrat, A.; Weigt, M. On the properties of small-world network models. Eur. Phys. J. B-Condens. Matter Complex Syst. 2000, 13, 547–560. [Google Scholar] [CrossRef]
- Mazumdar, S.; Thakker, D. Citizen science on twitter: Using data analytics to understand conversations and networks. Future Internet 2020, 12, 210. [Google Scholar] [CrossRef]
- Yang, L.; Yu, Z.; El-Meligy, M.A.; El-Sherbeeny, A.M.; Wu, N. On Multiplexity-Aware Influence Spread in Social Networks. IEEE Access 2020, 8, 106705–106713. [Google Scholar] [CrossRef]
- Vespignani, A. Modelling dynamical processes in complex socio-technical systems. Nat. Phys. 2012, 8, 32–39. [Google Scholar] [CrossRef]
- Granell, C.; Gómez, S.; Arenas, A. Competing spreading processes on multiplex networks: Awareness and epidemics. Phys. Rev. E 2014, 90, 012808. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- RStudio Team. RStudio: Integrated Development for R; RStudio, Inc.: Boston, MA, USA, 2015; Volume 42, p. 14. Available online: http://www.rstudio.com (accessed on 19 May 2021).
- Sievert, C. Plotly for R. R Package Version. 2018, Volume 4. Available online: https://plotly.com/r/ (accessed on 19 May 2021).
- Kalinka, A.T.; Tomancak, P. linkcomm: An R package for the generation, visualization, and analysis of link communities in networks of arbitrary size and type. Bioinformatics 2011, 27, 2011–2012. [Google Scholar] [CrossRef]
Short Biography of Authors
 | Marialisa Scatá received her B.S. (2005) and M.S. degrees (2009) in Telecommunication Engineering, from the Department of Electrical, Electronic and Computer Engineering (DIEEI), University of Catania, Italy. She received the Ph.D. in Computer Science and Telecommunication Engineering from University of Catania, in 2012, under the supervision of Prof. Aurelio La Corte, with whom she has been collaborating since 2009. Currently, she works as Postdoctoral Researcher at DIEEI, University of Catania. She serves as reviewer for several top-tier journals. She has an interdisciplinary approach to research and her interests include bio-inspired models, ICT, telecommunications, social networks, complex networks, multi-layer networks, social contagion and epidemic spreading, evolutionary game theory, data mining, machine learning, healthcare applications and cognitive networks. |
 | Barbara Attanasio received her B.S. degree in Computer engineering (2016) and M.S. degree in Telecommunications engineering (2018) from the Dipartimento di Ingegneria Elettrica, Elettronica e Informatica (DIEEI) at University of Catania, Italy. She is currently a Ph.D. student in Systems, Energy, Computer and Telecommunications Engineering at DIEEI, University of Catania. Her research interests Multi Access Edge Computing, Evolutionary Game Theory, Multi-layer networks, Data Science and IoT. |
 | Aurelio La Corte is Associate Professor in Telecommunication Engineering at the University of Catania, Italy. He received the degree in electrical engineering in 1988, and the Ph.D. in Electronic Engineering and Computer Science in 1994. He has more than 25 years of experience in scientific and teaching activity and specific experience in designing telecommunications networks and systems and in managing complex projects. Responsible for various ICT-related activities at the University of Catania, he has been involved in coordinating, designing and developing networks and ICT services.His scientific interests include telecommunication systems and integrated services, innovative ICT services and technological innovation. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).