Policy-Engineering Optimization with Visual Representation and Separation-of-Duty Constraints in Attribute-Based Access Control
Abstract
1. Introduction
- (1)
- To reduce the mining scale and enhance the interpretability of policy mining, we use the visual technique with Hamming distance to rearrange, portray, and partition an original authorization matrix and discover a minimal set of authorization rules from rearranged submatrices. We present a policy mining algorithm and compare its performance to the existing methods.
- (2)
- To verify whether SOD constraints can be satisfied in a constructed policy engineering system, we convert the SOD constraints into SOAR constraints using the method of SAT-based model counting. We construct MEAR constraints from the SOAR constraints to implicitly enforce the given SOD constraints and evaluate the performance of the PEO_VR&SOD.
2. Related Work
2.1. Research on Policy Engineering in ABAC
2.2. Research on Constraints in ABAC
2.3. Research on Visual Representation for Access Information
2.4. Characteristics of Our Work
3. Preliminaries
3.1. Basic Components of ABAC
- (1)
- U represents a finite set of requesting users. Each element of the set is denoted as ui, where 1 ≤ i ≤ |U|.
- (2)
- O represents a finite set of requested objects. Each element of the set is denoted as oi, where 1 ≤ i ≤ |O|.
- (3)
- OP represents a finite set of the operations allowed to be performed on the objects in an ABAC system. Each element of the set is denoted as opi, where 1 ≤ i ≤ |OP|. For instance, if there are only two operations allowed in a system: read and write, then we represent OP = {read, write}.
- (4)
- E represents a finite set of environments in which authorizations are made, such as time and locations. These authorizations are independent of users and objects. Each element of the set is denoted as ei, where 1 ≤ i ≤ |E|.
- (5)
- UA represents a finite set of attribute names of users. Each element of the set is denoted as uai, where 1 ≤ i ≤ |UA|. User attribute uai can associate several values. If we use to represent the one-to-many mapping of uai onto a set of attribute values, it can be formalized as:where null indicates that the corresponding attribute values of the user is unknown or uncertain. For instance, user attribute Role in a hospital can take values of Doctor, Nurse, and Patient, and then we represent ValRole = {Doctor, Nurse, Patient}.
- (6)
- UAV represents a finite set of all the possible attribute name–value pairs of users. Each element of the set is denoted in the form of the equality uai = xi, where uai ∊ UA, xi ∊ . For instance, if there are two attributes of users: Role and Specialty, where Role can take values of Doctor, Nurse and Patient, and Specialty can take values of Cardiology, Medicine, and Pediatrics, then UAV is represented as: {Role = Doctor, Role = Nurse, Role = Patient, Specialty = Cardiology, Specialty = Medicine, Specialty = Pediatrics}.
- (7)
- UUAV ⊆ U × UAV represents a many-to-many assignment of users to their attribute name-value pairs. It can be formalized as:
- (8)
- OA represents a finite set of attribute names of objects. Each element of the set is denoted as oai, where 1 ≤ i ≤ |OA|. The object attribute oai is also associated with several values. If we use to represent the one-to-many mapping of oai onto a set of attribute values, it can be formalized as:where null indicates that the corresponding attribute values of the object is unknown or uncertain. For instance, object attribute Department in a hospital can take values of Cardiology, Dermatology, and Gynecology, and then we represent ValDepartment = {Cardiology, Dermatology, Gynecology}.
- (9)
- OAV represents a finite set of all the possible attribute name-value pairs of objects. Each element of the set is denoted in the form of the equality oai = yi, where oai ∊ OA, yi ∊ . For instance, if there are two attributes of objects: Department and RecordOf, where Department can take values of Cardiology, Dermatology, and Gynecology, and RecordOf can take values of Doctor, Nurse, Patient, and Staff, then OAV is represented as: {Department = Cardiology, Department = Dermatology, Department = Gynecology, RecordOf = Doctor, RecordOf = Nurse, RecordOf = Patient, RecordOf = Staff}.
- (10)
- OOAV ⊆ O × OAV represents a many-to-many assignment of objects to their attribute name–value pairs. It can be formalized as:
3.2. Basic Policy-Mining Problem in ABAC
- (1)
- A represents a set of all possible authorizations that occur in an ABAC system. Each element of the set is represented as a = <u,o,op>, which allows user u to perform operation op on object o, where u ∊ U, o ∊ O, op ∊ OP.
- (2)
- P represents an ABAC policy, which is also referred to as a set of authorization rules AR. Each element ar in AR is denoted in a 3-tuple form <UAV’,OAV’,OP’>, where UAV’ ⊆ UAV, OAV’ ⊆ OAV, OP’ ⊆ OP.
3.3. Enforcement of SOD Constraints in ABAC
3.4. Hamming Distance
3.5. SAT-Based Model Counting
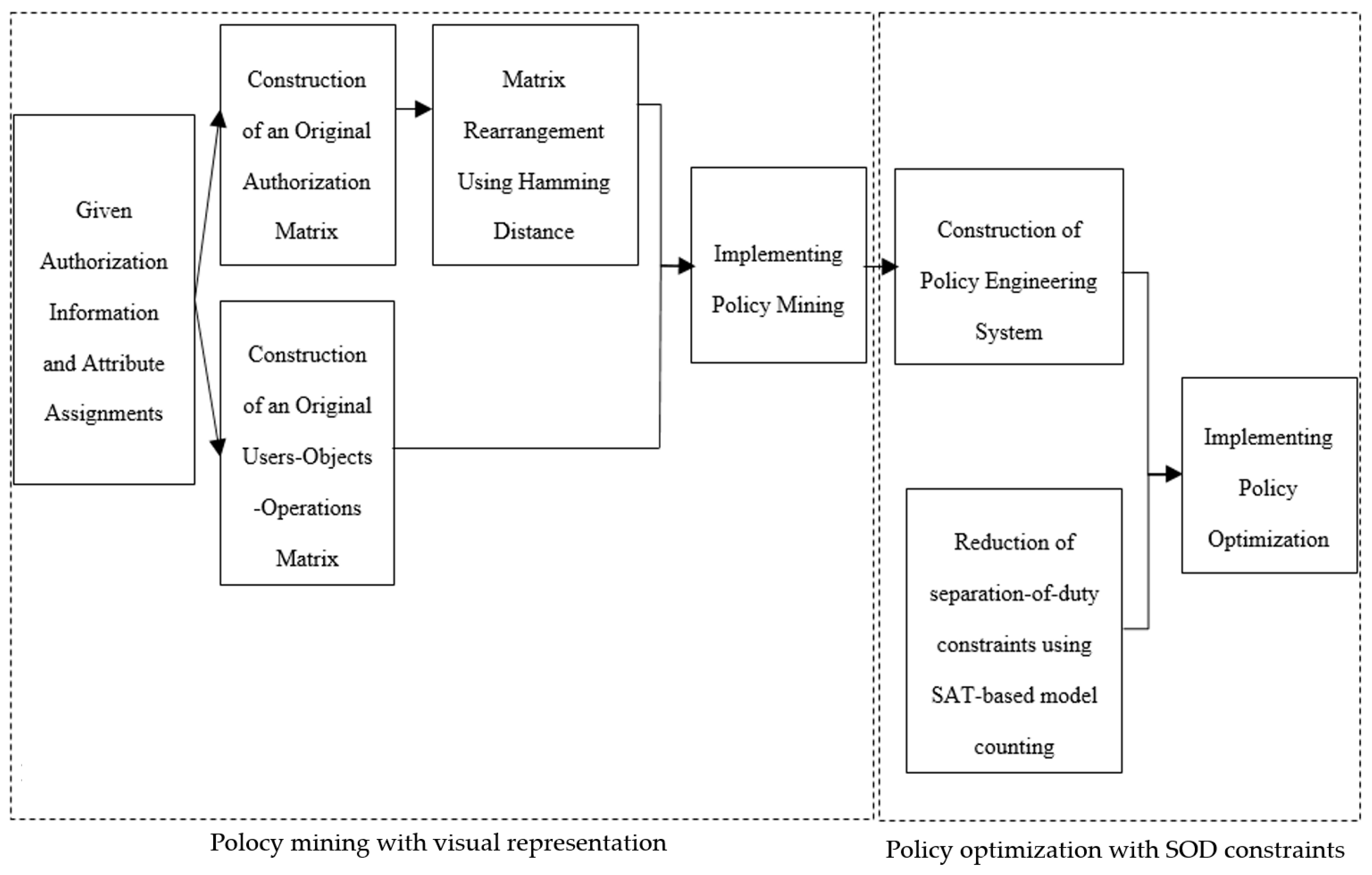
4. Proposed Method
4.1. Policy Mining with Visual Representation
4.1.1. Preprocessing
- (1)
- Principle 1: Assume that k1 and k2 are two different combinations of attribute-value pairs included in rules ar1 and ar2, respectively. If k1 ⊆ k2 (that is, the number of attribute-value pairs in k2 is greater than that in k1), then the authorizations covered by k2 can also be covered by k1; moreover, k2 is more restricted than k1. The authorizations covered by rule ar increase in number as the number of attribute-value pairs in ar decreases. Thus, we should choose short-length rules for the number of attribute-value pairs in any rule.
- (2)
- Principle 2: To discover a minimal set of rules while ensuring a short length in any rule, we decompose the UOP into two submatrices that consist of operation columns with values of 1 and 0. We denote these columns as UOPop=1 and UOPop=0 and sort UOPop=1 in ascending order according to the number of values of 1 in any row. We attempt to mine rules to cover all the authorizations corresponding to UOPop=1.
4.1.2. Visual Representation for Authorizations
| Algorithm 1 Matrix rearrangement |
| Input: original matrix Aop Output: rearranged matrix Aop’ 1. Initialize Aop’ = Aop; 2. Represent Aop’ as a list of row vectors: Aop’[1], Aop’[2], …; 3. Identify matrix Dr of the Hamming distances between any two row vectors such that ∀i,j: Dr[i][j] = Dis(Aop’[i], Aop’[j]); 4. for each Aop’[i] in Aop’ do 5. if (∃Aop’[j]: Dr[i][j] < Dr[i][i + 1]) then 6. swap(Aop’[i + 1], Aop’[j]); 7. end if 8. end for |
4.1.3. Policy Mining
| Algorithm 2 Policy mining |
| Input: rearranged matrix Aop’, matrices UUA and OOA Output: set AR of authorization rules 1. Identify the number of visual submatrices in Aop’ as k; 2. Based on the visual submatrices, separate Aop’ into n partitions: Aop’1, Aop’2, …, and Aop’k. In each partition, the columns correspond to the same set of objects, and the rows correspond to different sets of users; 3. According to k sets of users in different partitions, separate UUA into k partitions: UUA1, UUA2, …, and UUAn; 4. Define and initialize the sets of rules: Initial_rules = ø, Uninitial_rules = ø, Candidate_rules = ø; 5.for each Aop’i in {Aop’1,Aop’2,…,Aop’k} do 6. Construct matrix using the Cartesian product of the UUAi and OOA, and decompose it into and ; 7. Identify combinations of the different attribute-value pairs present in all rows of and sort them in ascending order according to the number of attribute-value pairs. Consider them as initial rules and insert them into Initial_rules; 8. Identify the combinations of different attribute-value pairs present in all rows of . Do not consider them as rules and insert them into Uninitial_rules; 9. for each combination of attribute-value pairs ar in Candidate_rules do 10. for each combination of attribute-value pairs ar’ in Initial_rules do 11. if (ar is not null)∧(ar ⊆ ar’) then 12. continue;/*authorizations covered by ar’ has been covered by ar*/ 13. else 14. if (ar∩ar’) ∉ Uninitial_rules then/*authorizations covered by both ar and ar’ are allowed*/ 15. Candidate_rules = (Candidate_rules\{ar})∩{ar∩ar’}; 16. else /*authorizations covered by ar’ are only allowed*/ 17. Candidate_rules = Candidate_rules∩{ar’}; 18. end if 19. end if 20. end for 21. end for 22. for each rule car in Candidate_rules do 23. for each attribute-value pair a in car do 24. if (car\{a}) ∉ Uninitial_rules then 25. car = car\{a}; 26. end if 27. end for 28. AR = AR∪{car}; 29. end for 30.end for |
4.2. Policy Optimization with Separation-of-Duty Constraints
- (1)
- user_rulesγ(u) represents a set of authorization rules that allows user u to perform operations on objects under the system status γ;
- (2)
- tuple_rulesγ(t) represents a set of authorization rules that allows access to tuple t for a given SOD constraint under the system status γ;
- (3)
- user_tuplesγ(u) represents a set of tuples of a given SOD constraint that is authorized to user u under the system status γ. It can be formalized as
4.2.1. Construction of k-n SOAR Constraints from k-n SOD Constraints
- (1)
- The process of the conversion does not take value k of the constraint into consideration because, for each k’-n SOAR constraint constructed, k’ takes the value of k in the following process of constructions.
- (2)
- AR’ in CIF does not contain the rules in (AR\AR’) because the rules not in AR’ are not relevant to the construction of the SOAR constraints.
4.2.2. Construction of t-m MEAR Constraints from k-n SOAR Constraints
| Algorithm3 Construction of t-m MEAR constraints |
| Input:k-n SOAR constraint soar = <{ar1,ar2,…arn},k>, where 2 ≤ k ≤ n Output: set ψ of t-m MEAR constraints 1. Initialize ψ = ø; 2. if k == 2 then 3. ψ = {<{ar1,ar2,…arn},n>}; 4. else if k == n then 5. ψ = {<{ar1,ar2,…arn},2>}; 6. else 7. for t = 2 to do 8. m = (k-1) × (t-1)+1; 9. for any subset {ar1,ar2,…arm’} in {ar1,ar2,…arn} do 10. ψ = ψ∪{<{ar1,ar2,…arm’},t>}; 11. end for 12. end for 13.end if |
5. Experimental Evaluations
5.1. Performance Comparison with the Xu-Stoller and VisMAP in Real Datasets
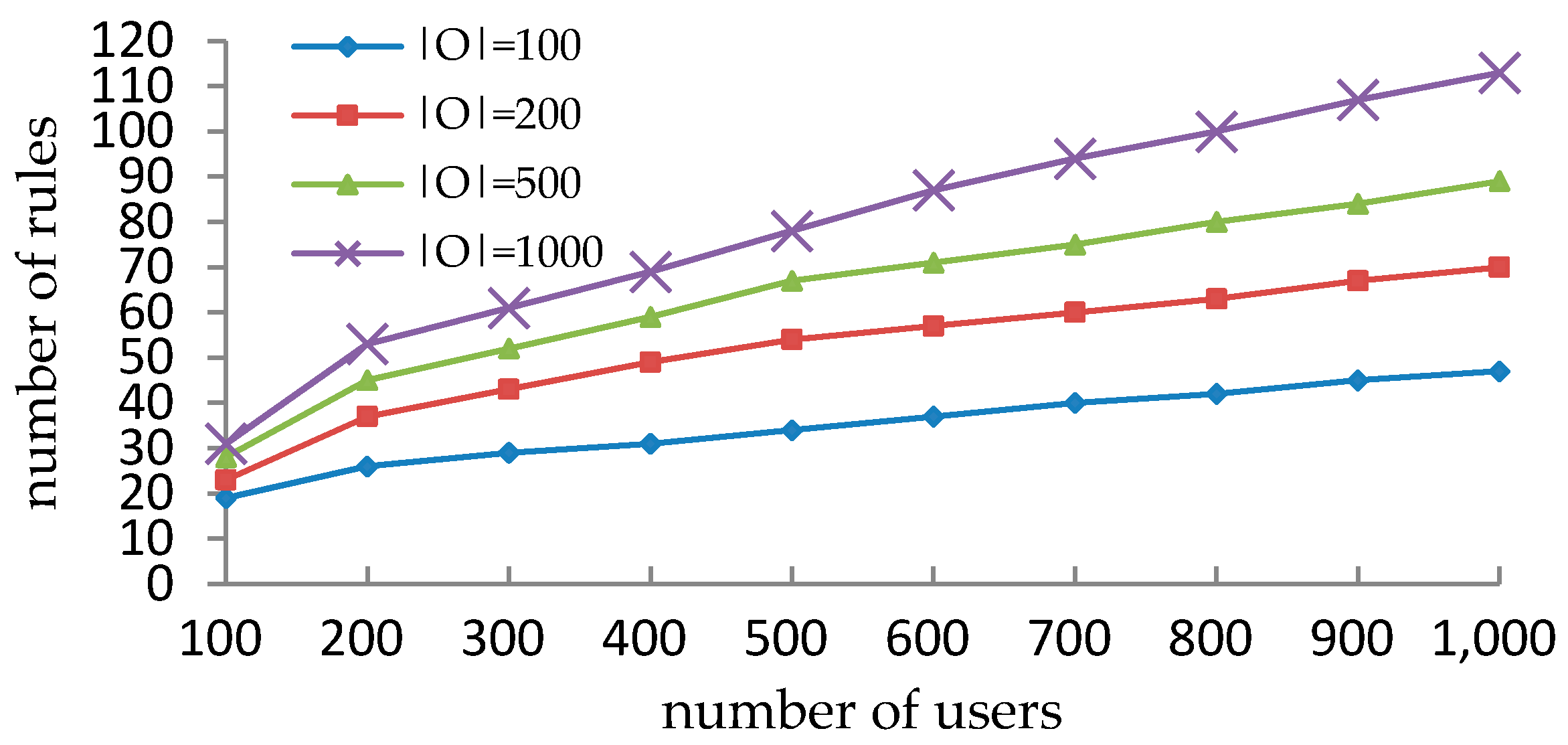
5.2. Performance Comparison with VisMAP in Synthetic Datasets
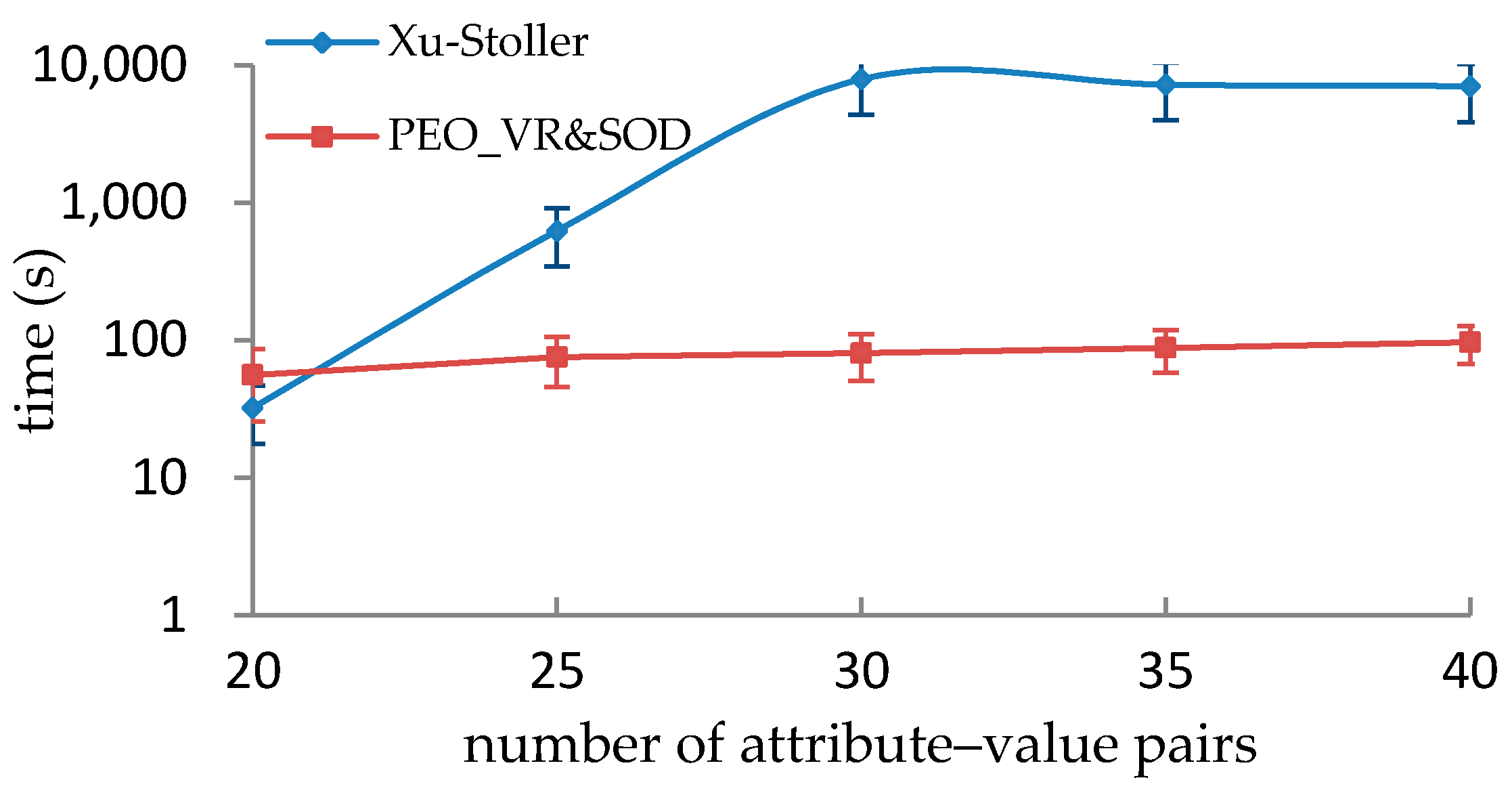
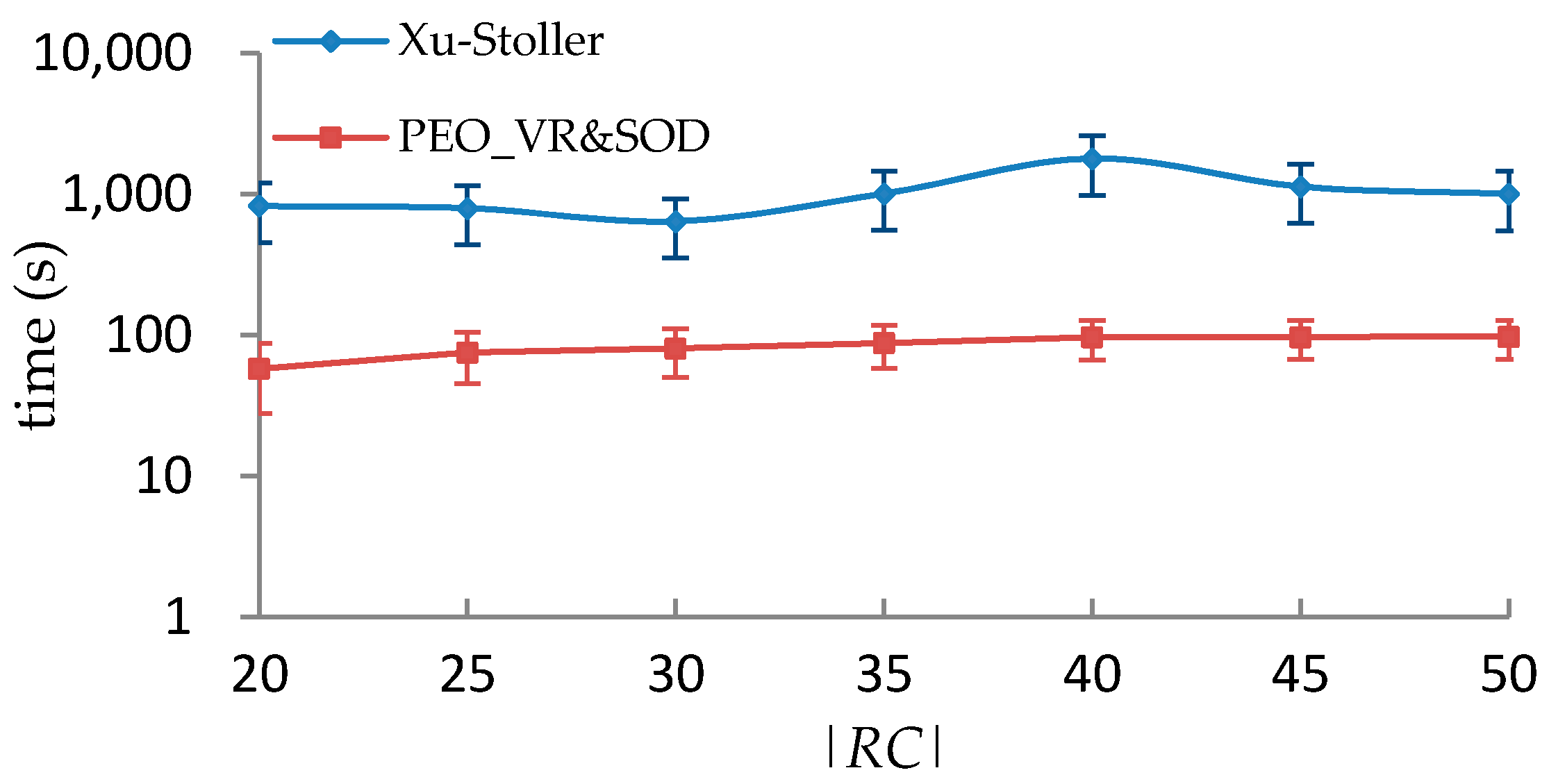
5.3. Performance Comparison with Xu-Stoller on Synthetic Datasets
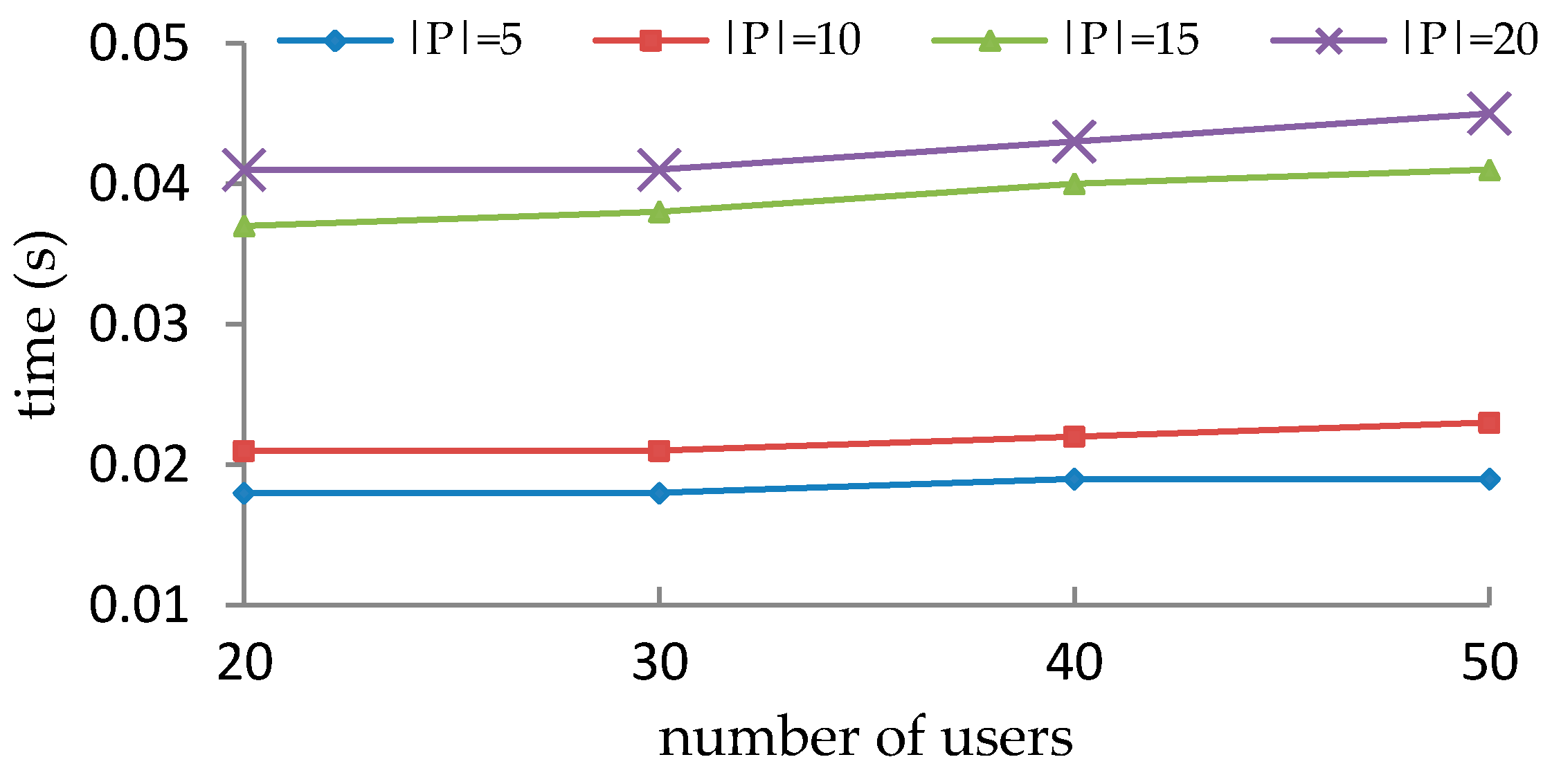
5.4. Performance Evaluation of Enforcement of SOD Constraints
5.5. Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sun, W.; Su, H.; Liu, H. Role-Engineering Optimization with Cardinality Constraints and User-Oriented Mutually Exclusive Constraints. Information 2019, 10, 342. [Google Scholar] [CrossRef]
- Batra, G.; Atluri, V.; Vaidya, J.; Sural, S. Deploying ABAC Policies Using RBAC Systems. J. Comput. Secur. 2019, 27, 483–506. [Google Scholar] [CrossRef] [PubMed]
- Narouei, M.; Takabi, H. A Nature-Inspired Framework for Optimal Mining of Attribute-Based Access Control Policies. In International Conference on Security and Privacy in Communication Systems; Springer: Cham, Switzerland, 2019; pp. 489–506. [Google Scholar]
- Servos, D.; Osborn, S.L. Current Research and Open Problems in Attribute-Based Access Control. ACM Comput. Surv. 2017, 49, 1–45. [Google Scholar] [CrossRef]
- Chakraborty, S.; Sandhu, R.; Krishnan, R. On the Feasibility of Attribute-Based Access Control Policy Mining. In Proceedings of the 20th IEEE International Conference on Information Reuse and Integration for Data Science, Los Angeles, CA, USA, 30 July–1 August 2019; pp. 245–252. [Google Scholar]
- Narouei, M.; Khanpour, H.; Takabi, H.; Parde, N.; Nielsen, R.D. Towards a Top-down Policy Engineering Framework for Attribute-based Access Control. In Proceedings of the 22nd ACM on Symposium on Access Control Models and Technologies, Indianapolis, IN, USA, 21–23 June 2017; pp. 103–114. [Google Scholar]
- Medvet, E.; Bartoli, A.; Carminati, B.; Ferrari, E. Evolutionary Inference of Attribute-Based Access Control Policies. In Proceedings of the 8th International Conference on Evolutionary Multi-Criterion Optimization, Guimarães, Portugal, 29 March–1 April 2015; pp. 351–365. [Google Scholar]
- Mocanu, D.; Turkmen, F.; Liotta, A. Towards ABAC policy mining from logs with deep learning. In Proceedings of the 18th International Multiconference, Ljubljana, Slovenia, 12–13 October 2015; pp. 124–128. [Google Scholar]
- Benkaouz, Y.; Erradi, M.; Freisleben, B. Work in progress: K-nearest neighbors techniques for ABAC policies clustering. In Proceedings of the 2016 ACM International Workshop on Attribute Based Access Control, New Orleans, LA, USA, 11 March 2016; pp. 72–75. [Google Scholar]
- Xu, Z.; Stoller, S.D. Mining Attribute-Based Access Control Policies. IEEE Trans. Dependable Secur. Comput. 2015, 12, 533–545. [Google Scholar] [CrossRef]
- Das, S.; Mitra, B.; Atluri, V.; Vaidya, J.; Sural, S. Policy Engineering in RBAC and ABAC. In From Database to Cyber Security; Springer: Cham, Switzerland, 2018; pp. 24–54. [Google Scholar]
- Roy, A.; Sural, S.; Majumdar, A.K.; Vaidya, J.; Atluri, V. Enabling Workforce Optimization in Constrained Attribute Based Access Control Systems. IEEE Trans. Emerg. Top. Comput. 2019, 7, 1. [Google Scholar] [CrossRef]
- Jha, S.; Sural, S.; Atluri, V.; Vaidya, J. Enforcing Separation of Duty in Attribute Based Access Control Systems. In Proceedings of the 11th International Conference on Information Systems Security, Kolkata, India, 16–20 December 2015; pp. 61–78. [Google Scholar]
- Krautsevich, L.; Lazouski, A.; Martinelli, F.; Yautsiukhin, A. Towards Attribute-Based Access Control Policy Engineering Using Risk. In Proceedings of the 1st International Workshop on Risk Assessment and Risk-Driven Testing, Istanbul, Turkey, 12 November 2013; pp. 80–90. [Google Scholar]
- Biswas, P.; Sandhu, R.; Krishnan, R. Label-Based Access Control: An ABAC Model with Enumerated Authorization Policy. In Proceedings of the 2016 ACM International Workshop on Attribute Based Access Control, New Orleans, LA, USA, 11 March 2016; pp. 1–12. [Google Scholar]
- Iyer, P.; Masoumzadeh, A. Mining positive and negative attribute-based access control policy rules. In Proceedings of the 23nd ACM on Symposium on Access Control Models and Technologies, Indianapolis, IN, USA, 13–15 June 2018; pp. 161–172. [Google Scholar]
- Das, S.; Sural, S.; Vaidya, J.; Atluri, V. HyPE: A Hybrid Approach toward Policy Engineering in Attribute-Based Access Control. IEEE Lett. Comput. Soc. 2018, 1, 25–29. [Google Scholar] [CrossRef] [PubMed]
- Gautam, M.; Jha, S.; Sural, S.; Vaidya, J.; Atluri, V. Poster: Constrained policy mining in attribute based access control. In Proceedings of the 22nd ACM on Symposium on Access Control Models and Technologies, Indianapolis, IN, USA, 21–23 June 2017; pp. 121–123. [Google Scholar]
- Das, S.; Sural, S.; Vaidya, J.; Atluri, V. Poster: Using Gini Impurity to Mine Attribute-based Access Control Policies with Environment Attributes. In Proceedings of the 23nd ACM on Symposium on Access Control Models and Technologies, Indianapolis, IN, USA, 13–15 June 2018; pp. 213–215. [Google Scholar]
- Talukdar, T.; Batra, G.; Vaidya, J.; Atluri, V.; Sural, S. Efficient bottom-up mining of attribute based access control policies. In Proceedings of the 3rd IEEE International Conference on Collaboration and Internet Computing, San Jose, CA, USA, 15–17 October 2017; pp. 339–348. [Google Scholar]
- John, J.C.; Sural, S.; Gupta, A. Authorization Management in Multi-Cloud Collaboration Using Attribute-based Access Control. In Proceedings of the 15th International Symposium on Parallel and Distributed Computing, Fuzhou, China, 8–10 July 2016; pp. 190–195. [Google Scholar]
- John, J.C.; Sural, S.; Gupta, A. Optimal Rule Mining for Dynamic Authorization Management in Collaborating Clouds using Attribute-based Access Control. In Proceedings of the 10th IEEE International Conference on Cloud Computing, Honolulu, HI, USA, 25–30 June 2017; pp. 739–742. [Google Scholar]
- John, J.C.; Sural, S.; Gupta, A. Attribute-based access control management for multicloud collaboration. Concurr. Comput. Pract. Exp. 2017, 29, e4199. [Google Scholar] [CrossRef]
- Jin, X.; Krishnan, R.; Sandhu, R. A unified attribute-based access control model covering DAC, MAC and RBAC. In Proceedings of the 26th Annual IFIP WG 11.3 Conference on Data and Applications Security and Privacy XXVI, Paris, France, 11–13 July 2012; pp. 41–55. [Google Scholar]
- Bijon, K.Z.; Krishnan, R.; Sandhu, R. Towards an attribute based constraints specification language. In Proceedings of the 2013 International Conference on Social Computing, Washington, DC, USA, 8–14 September 2013; pp. 108–113. [Google Scholar]
- Helil, N.; Rahman, K. Attribute based access control constraint based on subject similarity. In Proceedings of the 2014 IEEE Workshop on Advanced Research and Technology in Industry Applications, Ottawa, ON, Canada, 29–30 September 2014; pp. 226–229. [Google Scholar]
- Jha, S.; Sural, S.; Atluri, V.; Vaidya, J. Specification and Verification of Separation of Duty Constraints in Attribute-Based Access Control. IEEE Trans. Inf. Forensics Secur. 2018, 13, 897–911. [Google Scholar] [CrossRef]
- Alohaly, M.; Takabi, H.; Blanco, E. Towards an Automated Extraction of ABAC Constraints from Natural Language Policies. In Proceedings of the 34th IFIP TC 11 International Conference on ICT Systems Security and Privacy Protection, Lisbon, Portugal, 25–27 June 2019; pp. 105–119. [Google Scholar]
- Colantonio, A.; Pietro, R.D.; Ocello, A.; Verde, N.V. Visual Role Mining: A Picture Is Worth a Thousand Roles. IEEE Trans. Knowl. Data Eng. 2012, 24, 1120–1133. [Google Scholar] [CrossRef]
- Verde, N.V.; Vaidya, J.; Atluri, V.; Colantonio, A. Role engineering: From theory to practice. In Proceedings of the Second ACM Conference on Data and Application Security and Privacy, San Antonio, TX, USA, 7–9 February 2012; pp. 181–192. [Google Scholar]
- Das, S.; Sural, S.; Vaidya, J.; Atluri, V.; Rigoll, G. VisMAP: Visual Mining of Attribute-Based Access Control Policies. In Proceedings of the 15th International Conference on Information Systems Security, Hyderabad, India, 16–20 December 2019; pp. 79–98. [Google Scholar]
- Zheng, G.; Xiao, Y. A Research on Conflicts Detection in ABAC Policy. In Proceedings of the 7th International Conference on Computer Science and Network Technology, Dalian, China, 19–20 October 2019; pp. 408–412. [Google Scholar]
- Hu, V.C.; Ferraiolo, D.; Kuhn, D.R.; Schnitzer, A.; Sandlin, K.; Miller, R.; Scarfone, K. Guide to Attribute-Based Access Control (ABAC) Definition and Considerations; Technical Report; NIST Special Publication; National Institute of Standards and Technology: Gaithersburg, MA, USA, 2014. [Google Scholar]
- Ernvall, J.; Katajainen, J.; Penttonen, M. NP-completeness of the Hamming sales-man problem. BIT Numer. Math. 1985, 25, 289–292. [Google Scholar] [CrossRef]
- Gomes, C.P.; Kautz, H.A.; Sabharwal, A.; Selman, B. Satisfiability Solvers. In Handbook of Knowledge Representation; Elsevier: Amsterdam, The Netherlands, 2008; pp. 89–134. [Google Scholar]
- Huang, H.; Khan, L.; Zhou, S. Classified enhancement model for big data storage reliability based on Boolean satisfiability problem. Clust. Comput. 2020, 23, 483–492. [Google Scholar] [CrossRef]
- Bayardo, J.R., Jr.; Roberto, J.; Robert, S. Using CSP look-back techniques to solve real-world SAT instances. In Proceedings of the Fourteenth National Conference on Artificial Intelligence and Ninth Innovative Applications of Artificial Intelligence Conference, Providence, RI, USA, 27–31 July 1997; pp. 203–208. [Google Scholar]



| User | Object | Operation |
|---|---|---|
| u1 | o1 | op1 |
| u2 | o1 | op1 |
| u2 | o1 | op2 |
| u3 | o2 | op1 |
| u3 | o2 | op2 |
| u4 | o2 | op1 |
| User | uav1 | uav2 | uav3 | uav4 |
|---|---|---|---|---|
| u1 | 0 | 1 | 1 | 0 |
| u2 | 1 | 0 | 1 | 0 |
| u3 | 1 | 0 | 0 | 1 |
| u4 | 0 | 1 | 0 | 1 |
| Object | oav1 | oav2 | oav3 |
|---|---|---|---|
| o1 | 1 | 0 | 1 |
| o2 | 0 | 1 | 1 |
| User-Object | uav1 | uav2 | uav3 | uav4 | oav1 | oav2 | oav3 | op1 | op2 |
|---|---|---|---|---|---|---|---|---|---|
| u1-o1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| u2-o1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| u3-o1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| u4-o1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| u1-o2 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| u2-o2 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| u3-o2 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| u4-o2 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| o1 | o2 | o3 | o4 | o5 | o6 | o7 | o8 | o9 | o10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| u1 | 1 | 1 | 1 | |||||||
| u2 | 1 | 1 | 1 | |||||||
| u3 | 1 | 1 | 1 | 1 | ||||||
| u4 | 1 | 1 | 1 | 1 | ||||||
| u5 | 1 | 1 | ||||||||
| u6 | 1 | 1 | 1 | |||||||
| u7 | 1 | 1 | ||||||||
| u8 | 1 | 1 | 1 | 1 | ||||||
| u9 | 1 | 1 | 1 | 1 | ||||||
| u10 | 1 | 1 | 1 |
| o5 | o9 | o3 | o4 | o7 | o8 | o6 | o1 | o2 | o10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| u8 | 1 | 1 | 1 | 1 | ||||||
| u9 | 1 | 1 | 1 | 1 | ||||||
| u3 | 1 | 1 | 1 | 1 | ||||||
| u4 | 1 | 1 | 1 | 1 | ||||||
| u5 | 1 | 1 | ||||||||
| u7 | 1 | 1 | ||||||||
| u1 | 1 | 1 | 1 | |||||||
| u2 | 1 | 1 | 1 | |||||||
| u6 | 1 | 1 | 1 | |||||||
| u10 | 1 | 1 | 1 |
| Aop’[1] | Aop’[2] | Aop’[3] | Aop’[4] | Aop’[5] | Aop’[6] | Aop’[7] | Aop’[8] | Aop’[9] | Aop’[10] | |
|---|---|---|---|---|---|---|---|---|---|---|
| Aop’[1] | 0 | 0 | 7 | 7 | 3 | 0 | 3 | 7 | 7 | 0 |
| Aop’[2] | 0 | 0 | 7 | 7 | 3 | 0 | 3 | 7 | 7 | 0 |
| Aop’[3] | 7 | 7 | 0 | 0 | 6 | 7 | 6 | 0 | 0 | 7 |
| Aop’[4] | 7 | 7 | 0 | 0 | 6 | 7 | 6 | 0 | 0 | 7 |
| Aop’[5] | 3 | 3 | 6 | 6 | 0 | 3 | 0 | 6 | 6 | 3 |
| Aop’[6] | 0 | 0 | 7 | 7 | 3 | 0 | 3 | 7 | 7 | 0 |
| Aop’[7] | 3 | 3 | 6 | 6 | 0 | 3 | 0 | 6 | 6 | 3 |
| Aop’[8] | 7 | 7 | 0 | 0 | 6 | 7 | 6 | 0 | 0 | 7 |
| Aop’[9] | 7 | 7 | 0 | 0 | 6 | 7 | 6 | 0 | 0 | 7 |
| Aop’[10] | 0 | 0 | 7 | 7 | 3 | 0 | 3 | 7 | 7 | 0 |
| o1 | o2 | o3 | o4 | o5 | o6 | o7 | o8 | o9 | o10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| u8 | 1 | 1 | 1 | 1 | ||||||
| u9 | 1 | 1 | 1 | 1 | ||||||
| u3 | 1 | 1 | 1 | 1 | ||||||
| u4 | 1 | 1 | 1 | 1 | ||||||
| u5 | 1 | 1 | ||||||||
| u7 | 1 | 1 | ||||||||
| u6 | 1 | 1 | 1 | |||||||
| u1 | 1 | 1 | 1 | |||||||
| u2 | 1 | 1 | 1 | |||||||
| u10 | 1 | 1 | 1 |
| o1 | o2 | o3 | o4 | o8 | o7 | o6 | o5 | o9 | o10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| u8 | 1 | 1 | 1 | 1 | ||||||
| u9 | 1 | 1 | 1 | 1 | ||||||
| u3 | 1 | 1 | 1 | 1 | ||||||
| u4 | 1 | 1 | 1 | 1 | ||||||
| u5 | 1 | 1 | ||||||||
| u7 | 1 | 1 | ||||||||
| u6 | 1 | 1 | 1 | |||||||
| u1 | 1 | 1 | 1 | |||||||
| u2 | 1 | 1 | 1 | |||||||
| u10 | 1 | 1 | 1 |
| o1 | o9 | o3 | o4 | o7 | o8 | o6 | o5 | o2 | o10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| u8 | 1 | 1 | 1 | 1 | ||||||
| u9 | 1 | 1 | 1 | 1 | ||||||
| u3 | 1 | 1 | 1 | 1 | ||||||
| u4 | 1 | 1 | 1 | 1 | ||||||
| u5 | 1 | 1 | ||||||||
| u7 | 1 | 1 | ||||||||
| u6 | 1 | 1 | 1 | |||||||
| u1 | 1 | 1 | 1 | |||||||
| u2 | 1 | 1 | 1 | |||||||
| u10 | 1 | 1 | 1 |
| o5 | o9 | o3 | o4 | o8 | o7 | o6 | o1 | o2 | o10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| u8 | 1 | 1 | 1 | 1 | ||||||
| u9 | 1 | 1 | 1 | 1 | ||||||
| u3 | 1 | 1 | 1 | 1 | ||||||
| u4 | 1 | 1 | 1 | 1 | ||||||
| u5 | 1 | 1 | ||||||||
| u7 | 1 | 1 | ||||||||
| u6 | 1 | 1 | 1 | |||||||
| u1 | 1 | 1 | 1 | |||||||
| u2 | 1 | 1 | 1 | |||||||
| u10 | 1 | 1 | 1 |
| User | Rules |
|---|---|
| u1 | {ar1, ar2, ar4, ar5} |
| u2 | {ar3, ar7} |
| u3 | {ar1, ar2, ar4, ar5} |
| u4 | {ar6} |
| Tuple | Rules |
|---|---|
| t1 | {ar7} |
| t2 | {ar3} |
| t3 | {ar1,ar2} |
| Tuple | Rules |
|---|---|
| t4 | {ar4, ar5, ar6} |
| t5 | {ar3} |
| t6 | {ar1, ar2} |
| Tuple | Rules |
|---|---|
| t1 | {ar4} |
| t2 | {ar2} |
| t3 | {ar1, ar3} |
| t4 | {ar2, ar3, ar4} |
| Soar | Mears |
|---|---|
| <{ar2, ar3, ar4}, 3> | {<{ar1, ar2, ar4}, 2>} |
| <{ar1, ar3, ar4}, 3> | {<{ar2, ar3, ar4}, 2>} |
| <{ar1, ar2, ar3, ar4}, 3> | {<{ar1, ar2, ar3}, 2>, <{ar2, ar3, ar4}, 2>, <{ar1, ar2, ar4}, 2>, <{ar1, ar3, ar4}, 2>} |
| <{ar1, ar3, ar4, ar5}, 3> | {<{ar1, ar3, ar4}, 2>, <{ar3, ar4, ar5}, 2>, <{ar1, ar3, ar5}, 2>, <{ar1, ar4, ar5}, 2>} |
| <{ar2, ar3, ar4, ar5}, 3> | {<{ar2, ar3, ar4}, 2>, <{ar3, ar4, ar5}, 2>, <{ar2, ar3, ar5}, 2>, <{ar2, ar4, ar5}, 2>} |
| <{ar1, ar2, ar3, ar4, ar5}, 3> | {<{ar1, ar2, ar3}, 2>, <{ar1, ar2, ar4}, 2>, <{ar1, ar2, ar5}, 2>, <{ar1, ar3, ar4}, 2>, <{ar1, ar3, ar5}, 2>, <{ar1, ar4, ar5}, 2>, <{ar2, ar3, ar4}, 2>, <{ar2, ar3, ar5}, 2>, <{ar2, ar4, ar5}, 2>, <{ar3, ar4, ar5}, 2>, <{ar1, ar2, ar3, ar4, ar5}, 3>} |
| Dataset | |U| | |UA| | |O| | |OA| | |Val| | |A| | Xu-Stoller | VisMAP | Our Method | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |P| | T(s) | |P| | T(s) | |P| | T(s) | |||||||
| University | 20 | 6 | 34 | 5 | 76 | 168 | 10 | 0.02 | 10 | 0.02 | 10 | 0.02 |
| Healthcare | 21 | 6 | 16 | 7 | 55 | 51 | 11 | 0.02 | 7 | 0.02 | 7 | 0.02 |
| Project Management | 16 | 7 | 40 | 6 | 77 | 189 | 19 | 0.03 | 12 | 0.03 | 12 | 0.03 |
| |U| | |O| | |Partitions| | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 4 | 1 | 2 | 4 | ||||||||
| VisMAP | PEO_VR&SOD | ||||||||||||
| |P| | T(s) | |P| | T(s) | |P| | T(s) | |P| | T(s) | |P| | T(s) | |P| | T(s) | ||
| 100 | 100 | 19 | 0.59 | 38 | 0.72 | 62 | 0.35 | 19 | 0.59 | 22 | 0.84 | 30 | 0.93 |
| 200 | 100 | 26 | 1.77 | 55 | 1.11 | 84 | 1.03 | 26 | 1.77 | 31 | 1.98 | 42 | 2.14 |
| 500 | 100 | 34 | 10.18 | 76 | 5.38 | 108 | 5.9 | 34 | 10.18 | 42 | 10.73 | 53 | 11.95 |
| 1000 | 100 | 47 | 43.28 | 96 | 20.46 | 197 | 10.92 | 47 | 43.28 | 56 | 43.61 | 74 | 44.17 |
| 100 | 200 | 23 | 1.63 | 48 | 1.57 | 78 | 0.95 | 23 | 1.63 | 26 | 1.87 | 34 | 2.02 |
| 200 | 200 | 37 | 4.25 | 77 | 3.33 | 114 | 2.14 | 37 | 4.25 | 42 | 5.01 | 53 | 5.61 |
| 500 | 200 | 54 | 21.54 | 96 | 12.36 | 146 | 10.78 | 54 | 21.54 | 56 | 22.34 | 62 | 23.24 |
| 1000 | 200 | 70 | 100.4 | 145 | 43.01 | 197 | 39.77 | 70 | 100.4 | 81 | 105.34 | 98 | 106.11 |
| 100 | 500 | 28 | 8.27 | 50 | 9.78 | 89 | 4.72 | 28 | 8.27 | 33 | 8.77 | 43 | 9.07 |
| 200 | 500 | 45 | 17.64 | 91 | 16.41 | 156 | 9.39 | 45 | 17.64 | 50 | 18.13 | 65 | 18.55 |
| 500 | 500 | 67 | 75.23 | 141 | 49.92 | 224 | 33.57 | 67 | 75.23 | 74 | 76.02 | 87 | 76.93 |
| 1000 | 500 | 89 | 334.98 | 207 | 163.96 | 304 | 115.50 | 89 | 334.98 | 99 | 335.44 | 115 | 336.01 |
| 100 | 1000 | 31 | 33.84 | 60 | 47.46 | 109 | 10.09 | 31 | 33.84 | 35 | 34.11 | 47 | 34.89 |
| 200 | 1000 | 53 | 62.47 | 100 | 70.63 | 180 | 33.43 | 53 | 62.47 | 58 | 62.88 | 68 | 63.56 |
| 500 | 1000 | 78 | 248.87 | 175 | 174.30 | 282 | 100.21 | 78 | 248.87 | 87 | 249.19 | 103 | 250.17 |
| 1000 | 1000 | 113 | 1052.78 | 218 | 695.67 | 335 | 452.52 | 113 | 1052.78 | 126 | 1053.11 | 155 | 1053.88 |
| |U| | |O| | |UAV| | |OAV| | |RCmax| | |RLmax| | |PXu-Stoller| | |PPEO_VR&SOD| |
|---|---|---|---|---|---|---|---|
| 1000 | 100 | 20 | 20 | 30 | 5 | 27 | 26.31 |
| 1000 | 100 | 25 | 25 | 30 | 5 | 25.67 | 25.67 |
| 1000 | 100 | 30 | 30 | 30 | 5 | 26.67 | 25.11 |
| 1000 | 100 | 35 | 35 | 30 | 5 | 26.67 | 25.37 |
| 1000 | 100 | 40 | 40 | 30 | 5 | 27.53 | 26.89 |
| 1000 | 100 | 25 | 25 | 20 | 5 | 17.67 | 17.53 |
| 1000 | 100 | 25 | 25 | 40 | 5 | 36 | 35.31 |
| 1000 | 100 | 25 | 25 | 50 | 5 | 43 | 42.83 |
| 1000 | 100 | 25 | 25 | 30 | 4 | 25.67 | 25.39 |
| 1000 | 100 | 25 | 25 | 30 | 3 | 24.67 | 24.64 |
| 1000 | 100 | 25 | 25 | 30 | 2 | 24 | 24 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Su, H.; Xie, H. Policy-Engineering Optimization with Visual Representation and Separation-of-Duty Constraints in Attribute-Based Access Control. Future Internet 2020, 12, 164. https://doi.org/10.3390/fi12100164
Sun W, Su H, Xie H. Policy-Engineering Optimization with Visual Representation and Separation-of-Duty Constraints in Attribute-Based Access Control. Future Internet. 2020; 12(10):164. https://doi.org/10.3390/fi12100164
Chicago/Turabian StyleSun, Wei, Hui Su, and Huacheng Xie. 2020. "Policy-Engineering Optimization with Visual Representation and Separation-of-Duty Constraints in Attribute-Based Access Control" Future Internet 12, no. 10: 164. https://doi.org/10.3390/fi12100164
APA StyleSun, W., Su, H., & Xie, H. (2020). Policy-Engineering Optimization with Visual Representation and Separation-of-Duty Constraints in Attribute-Based Access Control. Future Internet, 12(10), 164. https://doi.org/10.3390/fi12100164





