Coverage and Energy Efficiency Analysis for Two-Tier Heterogeneous Cellular Networks Based on Matérn Hard-Core Process
Abstract
:1. Introduction
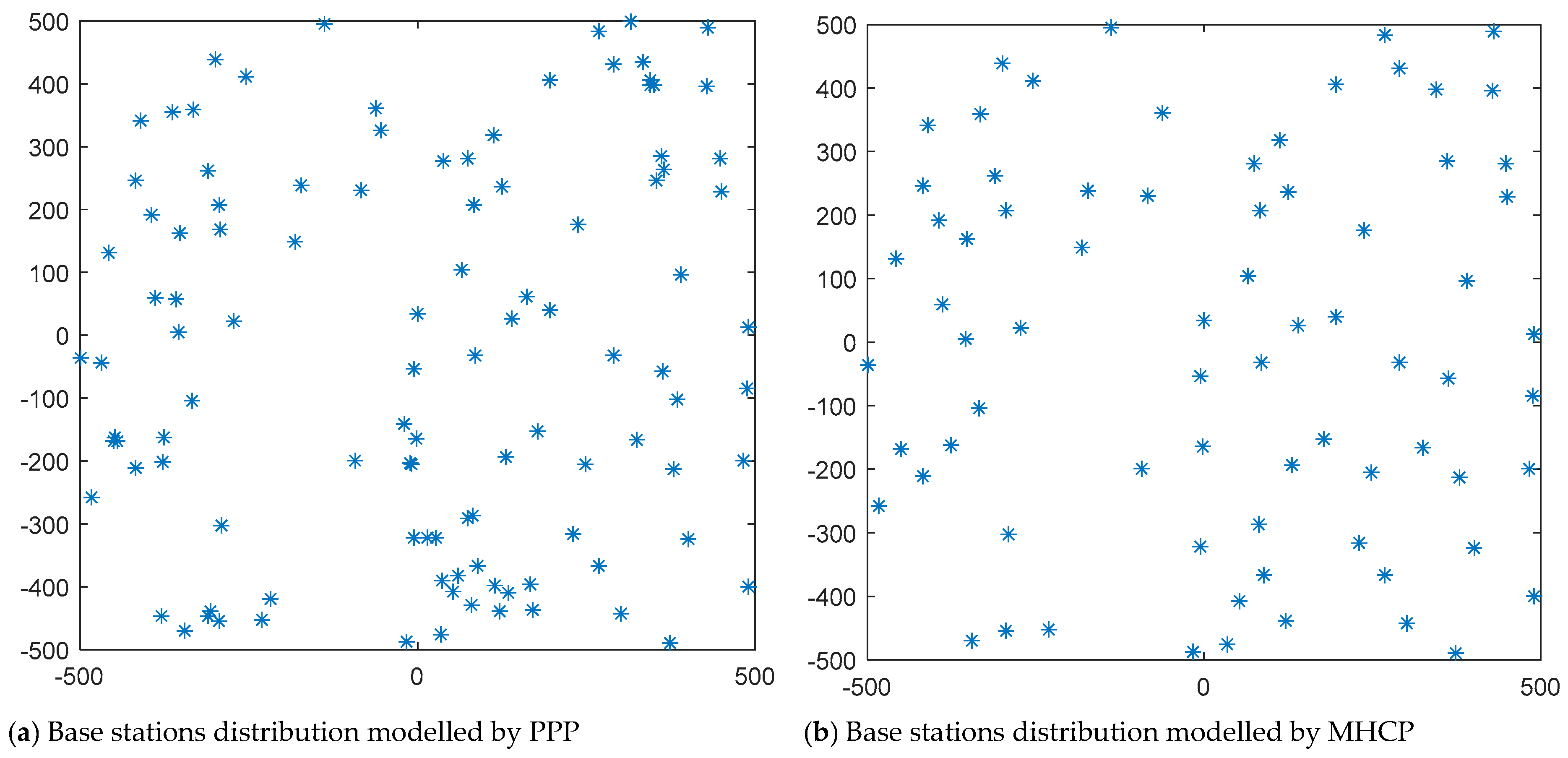
2. System Model
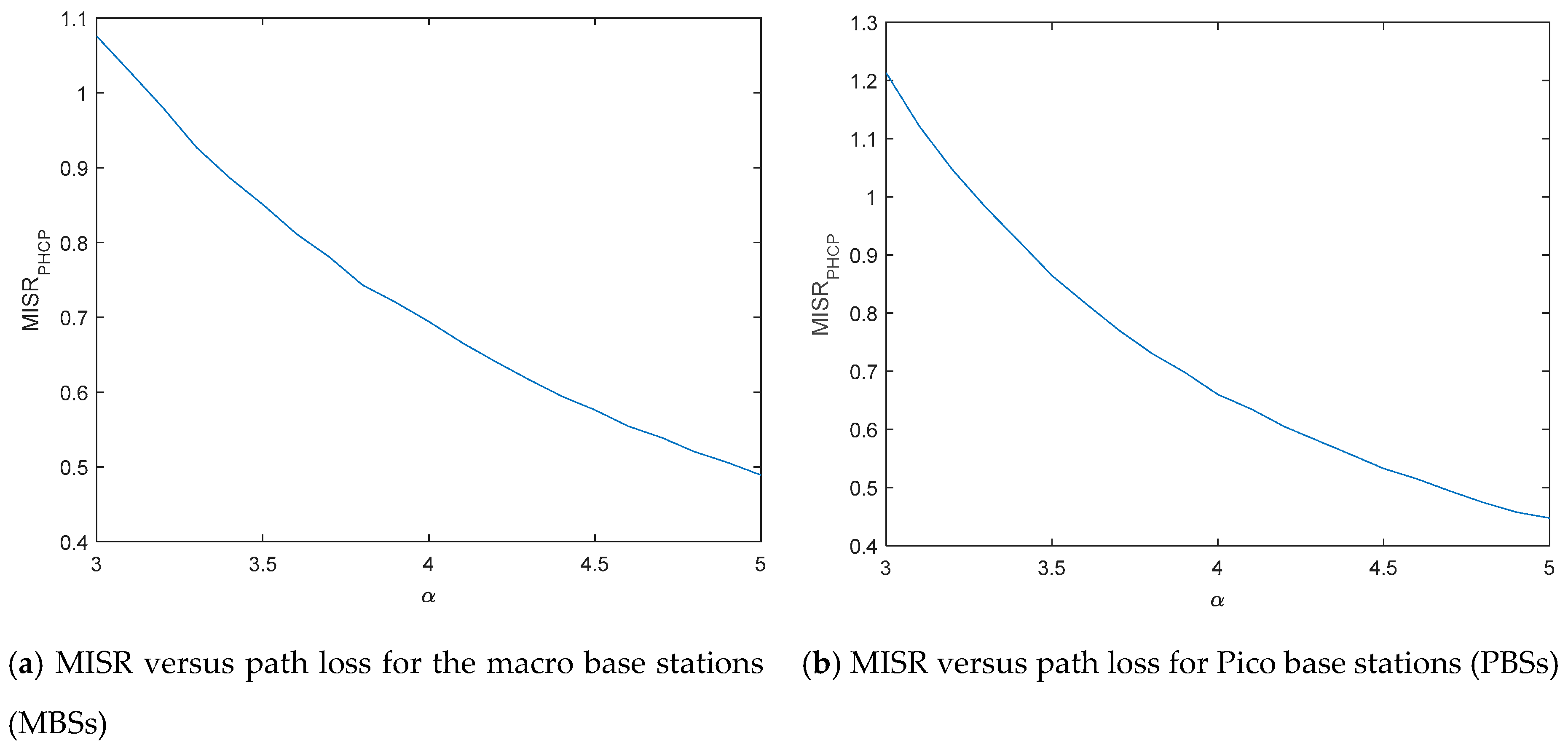
3. The ASAPPP Approach for Single-Tier MHCP Network
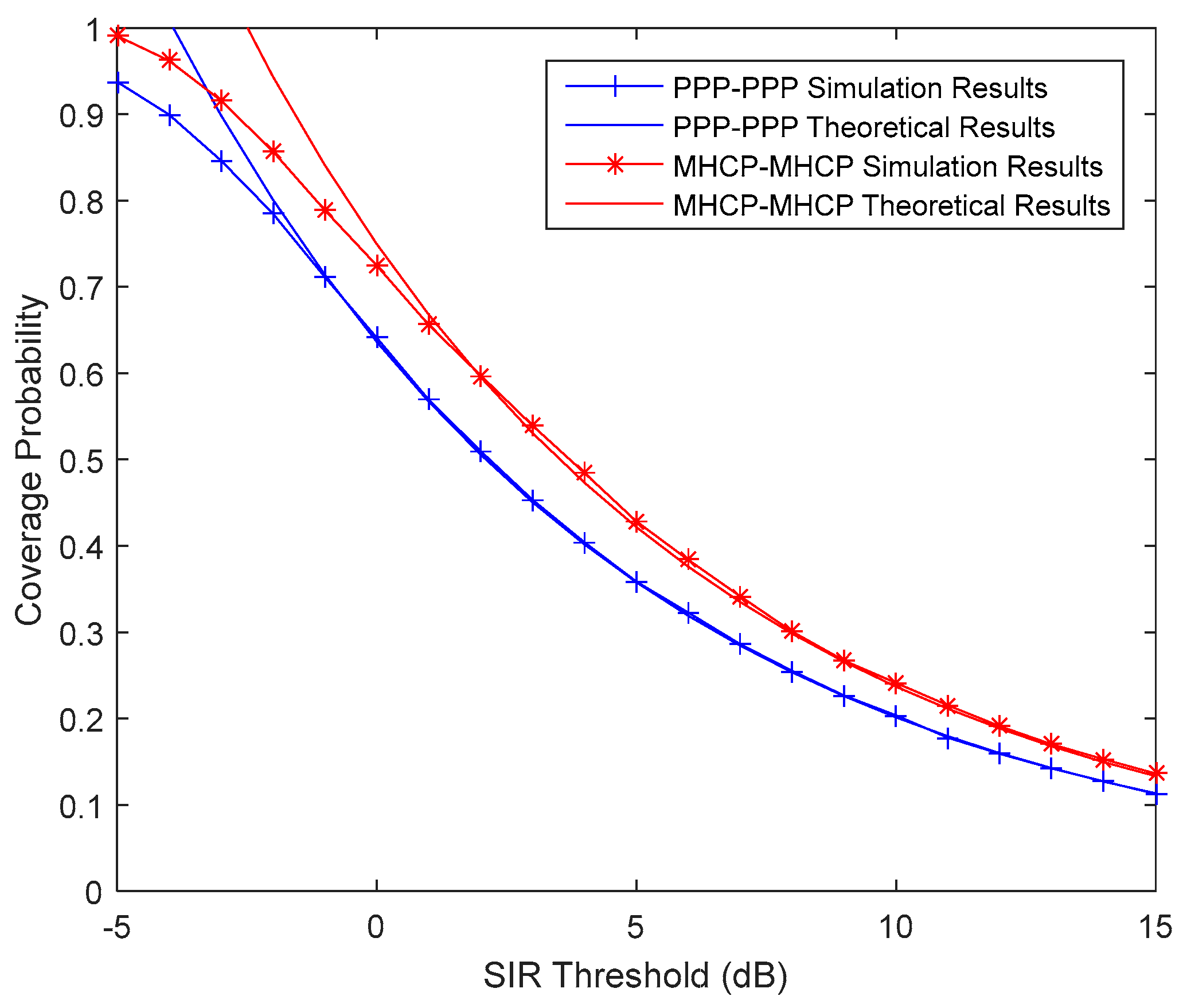
4. Coverage Probability of MHCP-MHCP Network
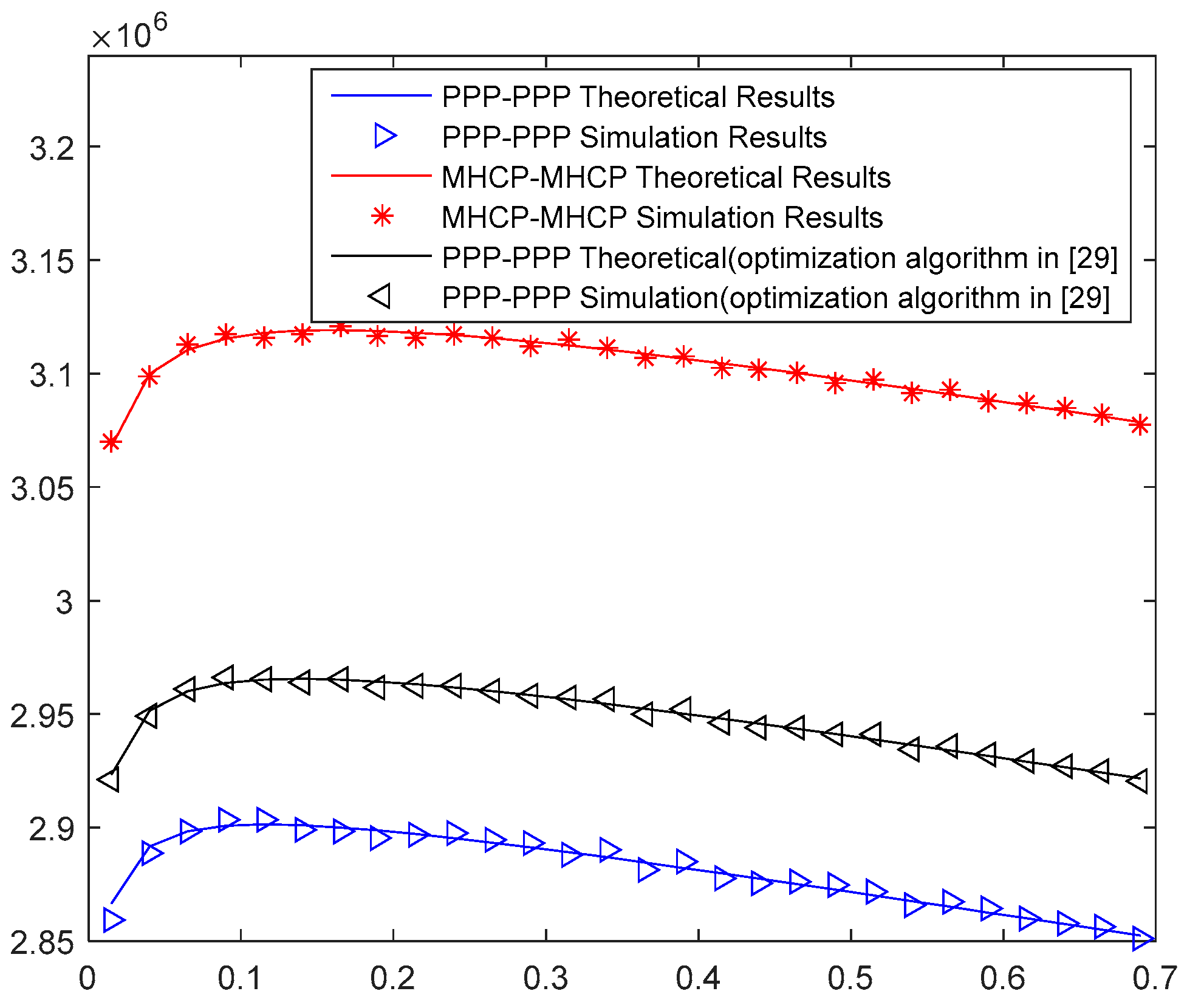
5. Energy Efficiency of the MHCP-MHCP Network
5.1. Downlink Channel Capacity
5.2. Total Power Consumption
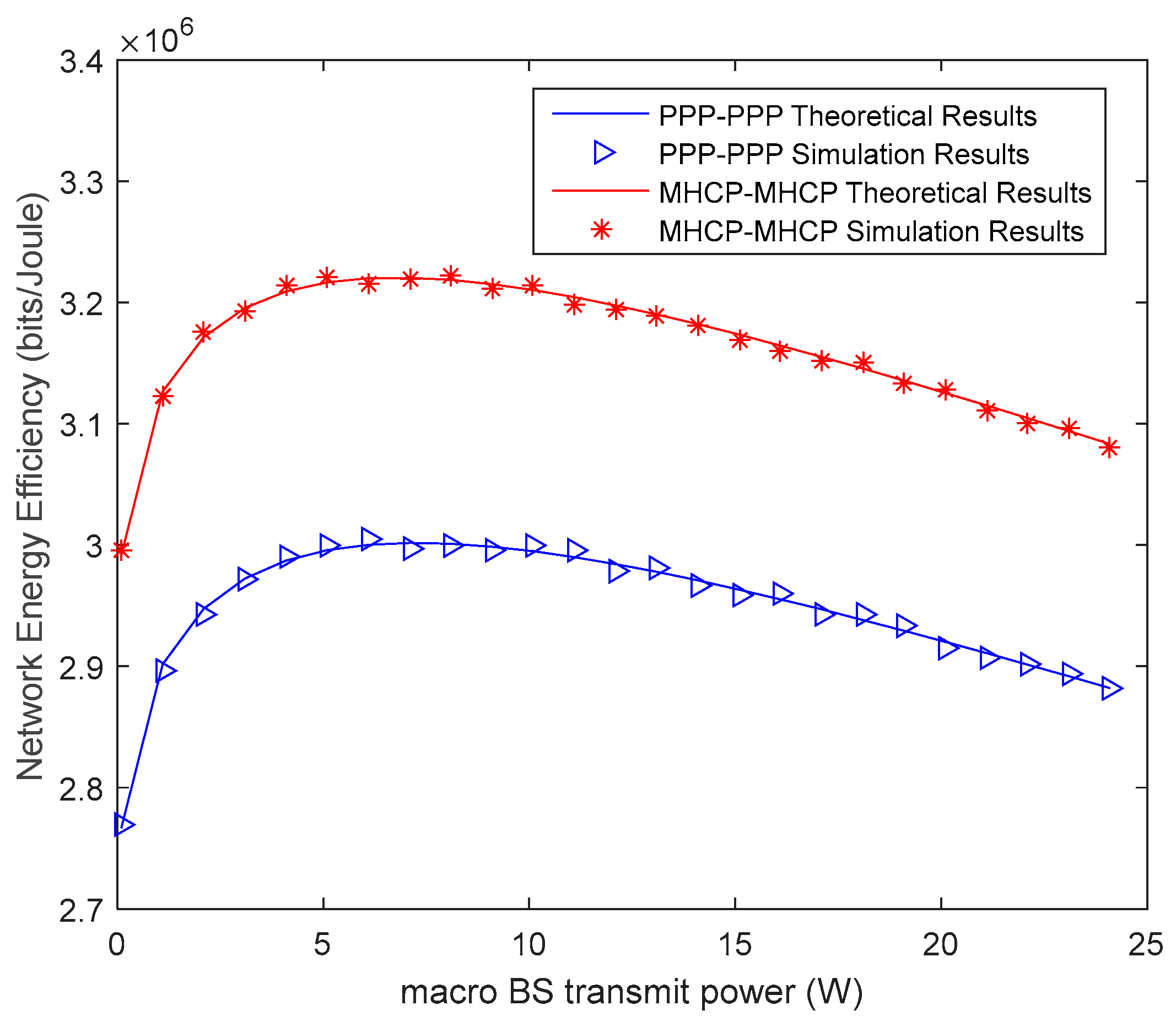
6. Data Fitting and Simulation Analysis
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kamel, M.; Hamouda, W.; Youssef, A. Ultra-Dense Networks: A Survey. IEEE Commun. Surv. Tutor. 2016, 18, 2522–2545. [Google Scholar] [CrossRef]
- Wang, H.; Leung, S.; Song, R. Uplink Area Spectral Efficiency Analysis for Multichannel Heterogeneous Cellular Networks with Interference Coordination. IEEE Access 2018, 6, 14485–14497. [Google Scholar] [CrossRef]
- Saha, C.; Afshang, M.; Dhillon, H.S. Enriched K-Tier HCN Model to Enable the Analysis of User-Centric Small Cell Deployments. IEEE Trans. Wirel. Commun. 2016, 16, 2835–2849. [Google Scholar]
- Dhillon, H.S.; Ganti, R.K.; Baccelli, F.; Andrews, J.G. Modeling and Analysis of K-Tier Downlink Heterogeneous Cellular Networks. IEEE J. Sel. Areas Commun. 2012, 30, 550–560. [Google Scholar] [CrossRef] [Green Version]
- Madhusudhanan, P.; Restrepo, J.G.; Liu, Y.; Brown, T.X. Analysis of Downlink Connectivity Models in a Heterogeneous Cellular Network via Stochastic Geometry. IEEE Trans. Wirel. Commun. 2016, 15, 3895–3907. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, Q. Modeling and Analysis of Small Cells Based on Clustered Stochastic Geometry. IEEE Commun. Lett. 2016, 21, 576–579. [Google Scholar] [CrossRef]
- Saha, C.; Afshang, M.; Dhillon, H.S. 3GPP-Inspired HetNet Model Using Poisson Cluster Process: Sum-Product Functionals and Downlink Coverage. IEEE Trans. Commun. 2018, 66, 2219–2234. [Google Scholar] [CrossRef]
- Deng, N.; Zhou, W.; Haenggi, M. The Ginibre Point Process as a Model for Wireless Networks with Repulsion. IEEE Trans. Wirel. Commun. 2015, 14, 107–121. [Google Scholar] [CrossRef]
- Flint, I.; Kong, H.; Privault, N.; Wang, P.; Niyato, D. Analysis of Heterogeneous Wireless Networks Using Poisson Hard-Core Hole Process. IEEE Trans. Wirel. Commun. 2017, 16, 7152–7167. [Google Scholar] [CrossRef]
- Kong, H.B.; Flint, I.; Wang, P.; Niyato, D.; Privault, N. Modeling and analysis of wireless networks using poisson hard-core process. In Proceedings of the IEEE International Conference on Communications, Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Kalamkar, S.S.; Haenggi, M. A Simple Approximation of the Meta Distribution for Non-Poisson Cellular Networks. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Haenggi, M. The Mean Interference-to-Signal Ratio and Its Key Role in Cellular and Amorphous Networks. IEEE Wirel. Commun. Lett. 2014, 3, 597–600. [Google Scholar] [CrossRef]
- Ganti, R.K.; Haenggi, M. Asymptotics and Approximation of the SIR Distribution in General Cellular Networks. IEEE Trans. Wirel. Commun. 2016, 15, 2130–2143. [Google Scholar] [CrossRef] [Green Version]
- Guo, A.; Haenggi, M. Asymptotic Deployment Gain: A Simple Approach to Characterize the SINR Distribution in General Cellular Networks. IEEE Trans. Commun. 2015, 63, 962–976. [Google Scholar] [CrossRef]
- Takahashi, Y.; Chen, Y.; Kobayashi, T.; Miyoshi, N. Simple and Fast PPP-based Approximation of SIR Distributions in Downlink Cellular Networks. IEEE Wirel. Commun. Lett. 2018, 7, 898–901. [Google Scholar] [CrossRef]
- Yang, J.; Pan, Z.Y.; Hu, H.; Bao, Z.Y. Approximate Coverage Analysis of Heterogeneous Cellular Networks Modelled by Poisson Hole Process. In Proceedings of the 2018 IEEE 18th International Conference on Communication Technology (ICCT), Chongqing, China, 8–11 October 2018; pp. 424–427. [Google Scholar]
- Miyoshi, N. Downlink Coverage Probability in Cellular Networks with Poisson–Poisson Cluster Deployed Base Stations. IEEE Wirel. Commun. Lett. 2018, 8, 5–8. [Google Scholar] [CrossRef] [Green Version]
- Haenggi, M. The meta distribution of the SIR in Poisson bipolar and cellular networks. IEEE Trans. Wirel. Commun. 2016, 15, 2577–2589. [Google Scholar] [CrossRef]
- Kalamkar, S.S.; Haenggi, M. Simple Approximations of the SIR Meta Distribution in General Cellular Networks. IEEE Trans. Commun. 2019, 67, 4393–4406. [Google Scholar] [CrossRef]
- Wei, H.; Deng, N.; Zhou, W.; Haenggi, M. Approximate SIR Analysis in General Heterogeneous Cellular Networks. IEEE Trans. Commun. 2016, 64, 1259–1273. [Google Scholar] [CrossRef]
- Chen, Z.; Qiu, L.; Liang, X. Area Spectral Efficiency Analysis and Energy Consumption Minimization in Multiantenna Poisson Distributed Networks. IEEE Trans. Wirel. Commun. 2016, 15, 4862–4874. [Google Scholar]
- Logambigai, R.; Kannan, A. Energy conservation routing algorithm for wireless sensor networks using hybrid optimisation approach. Int. J. Commun. Netw. Distrib. Syst. 2018, 20, 352–371. [Google Scholar] [CrossRef]
- Su, L.; Yang, C.; Chih-Lin, I. Energy and Spectral Efficient Frequency Reuse of Ultra Dense Networks. IEEE Trans. Wirel. Commun. 2016, 15, 5384–5398. [Google Scholar] [CrossRef]
- Thompson, J.; Ge, X.; Wu, H.C.; Irmer, R.; Jiang, H.; Fettweis, G.; Alamouti, S. 5G WIRELESS COMMUNICATION SYSTEMS: PROSPECTS AND CHALLENGES PART 2. IEEE Commun. Mag. 2014, 52, 24–26. [Google Scholar] [CrossRef]
- Zhang, T.; Zhao, J.; An, L.; Liu, D. Energy Efficiency of Base Station Deployment in Ultra Dense HCNs: A Stochastic Geometry Analysis. IEEE Wirel. Commun. Lett. 2016, 5, 184–187. [Google Scholar] [CrossRef]
- Jie, Y.; Zhenjian, T.; Han, H.; Yonghong, C. Energy-efficient picocell base station power control in heterogeneous cellular network. In Proceedings of the IEEE 17th International Conference on Communication Technology (ICCT), Chengdu, China, 27–30 October 2017; pp. 553–557. [Google Scholar]
- Di Renzo, M.; Zappone, A.; Lam, T.T.; Debbah, M. System-Level Modeling and Optimization of the Energy Efficiency in Cellular Networks—A Stochastic Geometry Framework. IEEE Trans. Wirel. Commun. 2018, 17, 2539–2556. [Google Scholar] [CrossRef]
- Lorincz, J.; Matijevic, T. Energy-efficiency analyses of heterogeneous macro and micro base station sites. Comput. Electr. Eng. 2014, 40, 330–349. [Google Scholar] [CrossRef]
- Li, L.; Peng, M.; Yang, C.; Wu, Y. Optimization of Base-Station Density for High Energy-Efficient Cellular Networks with Sleeping Strategies. IEEE Trans. Veh. Technol. 2015, 65, 7501–7514. [Google Scholar] [CrossRef]
- Coskun, C.C.; Ayanoglu, E. Energy- and Spectral-Efficient Resource Allocation Algorithm for Heterogeneous Networks. IEEE Trans. Veh. Technol. 2018, 67, 590–603. [Google Scholar] [CrossRef]
- Aydin, O.; Jorswieck, E.A.; Aziz, D.; Zappone, A. Energy-Spectral Efficiency Trade-Offs in 5G Multi-Operator Networks with Heterogeneous Constraints. IEEE Trans. Wirel. Commun. 2017, 16, 5869–5881. [Google Scholar] [CrossRef]
- Zhao, G.; Chen, S.; Zhao, L.; Hanzo, L. Energy-Spectral-Efficiency Analysis and Optimization of Heterogeneous Cellular Networks: A Large-Scale User-Behavior Perspective. IEEE Trans. Veh. Technol. 2018, 67, 4098–4112. [Google Scholar] [CrossRef] [Green Version]
- Zhao, G.; Chen, S.; Qi, L.; Zhao, L.; Hanzo, L. Mobile-Traffic-Aware Offloading for Energy- and Spectral-Efficient Large-Scale D2D-Enabled Cellular Networks. IEEE Trans. Wirel. Commun. 2019, 18, 3251–3264. [Google Scholar] [CrossRef]
- Luo, Y.; Shi, Z.; Bu, F.; Xiong, J. Joint Optimization of Area Spectral Efficiency and Energy Efficiency for Two-Tier Heterogeneous Ultra-Dense Networks. IEEE Access 2019, 7, 12073–12086. [Google Scholar] [CrossRef]
- Krauss, R.; Brante, G.; Rayel, O.K.; Souza, R.D.; Onireti, O.; Imran, M.A. Energy Efficiency of Multiple Antenna Cellular Networks Considering a Realistic Power Consumption Model. IEEE Trans. Green Commun. Netw. 2019, 3, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Ni, Y.; Zhang, J.; Zhao, S.; Zhu, H. Energy efficiency and spectrum efficiency in underlay device-to-device communications enabled cellular networks. China Commun. 2019, 16, 16–34. [Google Scholar]
- Mollahasani, S.; Onur, E. Density-Aware, Energy- and Spectrum-Efficient Small Cell Scheduling. IEEE Access 2019, 7, 65852–65869. [Google Scholar] [CrossRef]
- 3GPP. Study on Future Railway Mobile Communication System. Technical report/Specification #: 22.889. Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3162 (accessed on 18 December 2019).
- Vamvakas, P.; Tsiropoulou, E.E.; Papavassiliou, S. Dynamic Spectrum Management in 5G Wireless Networks: A Real-Life Modeling Approach. In Proceedings of the IEEE INFOCOM 2019—IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; pp. 2134–2142. [Google Scholar]
- Lin, S.; Kong, L.; Gao, Q.; Khan, M.K.; Zhong, Z.; Jin, X.; Zeng, P. Advanced Dynamic Channel Access Strategy in Spectrum Sharing 5G Systems. IEEE Wirel. Commun. 2017, 24, 74–80. [Google Scholar] [CrossRef]
- Vamvakas, P.; Tsiropoulou, E.E.; Papavassiliou, S. Dynamic provider selection & power resource management in competitive wireless communication markets. Mob. Netw. Appl. 2018, 23, 86–99. [Google Scholar]
- Ding, Z.; Lei, X.; Karagiannidis, G.K.; Schober, R.; Yuan, J.; Bhargava, V.K. A Survey on Non-Orthogonal Multiple Access for 5G Networks: Research Challenges and Future Trends. IEEE J. Sel. Areas Commun. 2017, 35, 2181–2195. [Google Scholar] [CrossRef] [Green Version]
- Vamvakas, P.; Tsiropoulou, E.E.; Papavassiliou, S. On Controlling Spectrum Fragility via Resource Pricing in 5G Wireless Networks. IEEE Netw. Lett. 2019, 1, 111–115. [Google Scholar] [CrossRef]
- Stoyan, D.; Kendall, W.; Mecke, J. Stochastic Geometry and Its Applications, 2nd ed.; John Wiley and Sons: Hoboken, NJ, USA, 1996; pp. 54–66. [Google Scholar]
- Singh, S.; Dhillon, H.S.; Andrews, J.G. Offloading in Heterogeneous Networks: Modeling, Analysis, and Design Insights. IEEE Trans. Wirel. Commun. 2013, 12, 2484–2497. [Google Scholar] [CrossRef] [Green Version]
- Sui, X.; Zhao, Z.; Li, R.; Zhang, H. Energy Efficiency Analysis of Heterogeneous Cellular Networks with Downlink and Uplink Decoupling. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–7. [Google Scholar]
- Lorincz, J.; Matijevic, T.; Petrovic, G. On interdependence among transmit and consumed power of macro base station technologies. Comput. Commun. 2014, 50, 10–28. [Google Scholar] [CrossRef]
- Auer, G.; Giannini, V.; Desset, C.; Godor, I.; Skillermark, P.; Olsson, M.; Imran, M.A.; Sabella, D.; Gonzalez, M.J.; Blume, O.; et al. How much energy is needed to run a wireless network? IEEE Wirel. Commun. 2011, 18, 40–49. [Google Scholar] [CrossRef]
| Parameters Name | Values |
|---|---|
| Bandwidth | 107 Hz |
| MHCP-MHCP network area | 1000 × 1000 m2 |
| density of MUs, λu | 0.15 m−2 |
| density of MBSs, λ1-MHCP | 2 * 10−5 m−2 |
| density of PBSs, λ2-MHCP | 2 * 10−4 m−2 |
| repulsion radius of MBSs | 100 m |
| repulsion radius of PBSs | 50 m |
| path-loss exponent, α | [3, 5] |
| circuit power consumption of MBS, PC1 | 130 W |
| transmit power of MBS, PT1 | 20 W |
| number of transmit antenna elements of MBS, NTR1 | 6 |
| slope of power consumption depends on load of MBS, θ1 | 4.7 |
| circuit power consumption of PBS, PC2 | 6.8 W |
| transmit power of PBS, PT2 | 0.13 W |
| number of transmit antenna elements of PBS, NTR2 | 2 |
| slope of power consumption depends on load of PBS, θ2 | 4.0 |
| Coefficients Name | a | b | c |
|---|---|---|---|
| 1-th tier network (MBSs) | 5.917 (5.55, 6.285) | −1.551 (−1.641, −1.461) | 0.001449 (−0.04122, 0.04412) |
| 2-th tier network (PBSs) | 18.09 (16.82, 19.36) | −2.602 (−2.678, −2.527) | 0.1721 (0.1558, 0.1883) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Pan, Z.; Guo, L. Coverage and Energy Efficiency Analysis for Two-Tier Heterogeneous Cellular Networks Based on Matérn Hard-Core Process. Future Internet 2020, 12, 1. https://doi.org/10.3390/fi12010001
Yang J, Pan Z, Guo L. Coverage and Energy Efficiency Analysis for Two-Tier Heterogeneous Cellular Networks Based on Matérn Hard-Core Process. Future Internet. 2020; 12(1):1. https://doi.org/10.3390/fi12010001
Chicago/Turabian StyleYang, Jie, Ziyu Pan, and Lihong Guo. 2020. "Coverage and Energy Efficiency Analysis for Two-Tier Heterogeneous Cellular Networks Based on Matérn Hard-Core Process" Future Internet 12, no. 1: 1. https://doi.org/10.3390/fi12010001




