Abstract
After a lengthy debate within the scientific community about what constitutes the problem solving approach of computational thinking (CT), the focus shifted to enable the integration of CT within compulsory education. This publication strives to focus the discussion and enable future research in an educational setting with a strong focus on the Austrian circumstances and the goal to allow wide international adoption later on. Methodically, a literature review was conducted to gain knowledge about the current strands of research and a meta study to show the diversity of proposed and materialized studies. Three main questions were answered, establishing that CT as an idea is rooted in scientific literature dating back to the 1980s and grew in popularity after Wing introduced the concept to a broader audience. A number of authors contributed to the current state of the field, with the most cited review coming from Grover and Pea. The challenge to integrate CT in curricula around the world was met by many experiments and case studies but without a conclusive framework as of yet. Ultimately, this paper determines that expert integration is a blank spot in the literature and aims to create a strong, inclusive path to CT education by inviting practitioners.
1. Introduction
The skillset proposed by the problem solving approach computational thinking (CT) is an incredibly important asset for today’s students [1]. Young adults are growing up in an increasingly complex and interesting world filled with a multitude of opportunities and challenges. CT enables every learner to “bend computation to (their) needs”. Not everybody needs to become a master computer programmer but, in our digital world, everybody should be enabled to understand the basics of computing and the principles that allow tech savvy experts to tackle the complex problems our generation encounters [2] (p. 25). Carnegie Mellon University (CMU) scholar Jeannette Wing proposes that, ultimately, CT “is becoming the new literacy of the 21st century” [3] (p. 4). Her ideas led to a flood of experiments and case studies exploring the ways and methods these important skills are currently taught, ranging from young kids [4] to adult lifelong learners [5]. Experiments are conducted inside formal school settings, as well as makerspaces and after school events, all around the world [6].
This set of skills is incredibly valuable far outside the technical community and allows scholars to make sense of the ever changing world around us as CT “draws on skills and professional practices that are fundamental to computing and computer science” [7] (p. 3). This research study adopts the definition of Csizmadia et al. wherein CT “is the process of recognizing aspects of computation in the world that surrounds us and applying tools and techniques from computing to understand and reason about natural, social, and artificial systems and processes. It allows pupils to tackle problems, to break them down into solvable chunks, and to devise algorithms to solve them” [8] (p. 5).
Based on this definition and according to Wing [3], everybody should be able to:
- understand which aspects of a problem can be solved with a tool,
- evaluate if a specific tool can solve a problem,
- understand the limitations of computational tools,
- adapt a computational tool to a new use,
- recognize new ways to use tools, and
- apply computational strategies in any domain.
The goal of this study is to determine what has been researched and implemented to teach CT on and below the K-12 level. This term includes primary and secondary education and signifies an age range between kindergarten and twelfth grade, ending with a high school diploma or in the Austrian system a “Matura”.
To create a baseline, this literature review first pinpoints what CT actually is and what the scientific community makes of the term. Furthermore, this article attempts to answer three main research questions, while allowing for a solid overview of the field. The first part of this research presents a historical breakdown, pinpoints what the scientific community makes of the term, and answers the question “When was CT first described and what happened since then?”. The second part of this work looks for literature reviews conducted in the field of CT and outlines its significance in an educational and institutional context, answering “What were the most important literature review works in the field?”. A third part looks more specific into how CT has been taught and evaluated in K-12 education, within institutional settings and makerspaces with a focus on EU research, asking “What has been tried to integrate CT in K-12 education?”.
This research builds the basis for our attempt to experiment within an exemplary Austrian K-12 classroom setting with the ideas and principles present in makerspaces around the world to allow for a more practical and fun learning experience inside our established educational institutions.
2. Materials and Methods
This literature review was conducted by using the well respected search engine Web of Science (webofknowledge.com). We based our first search on publications between 2016 and 2019 to show what significant progress has been made in the field of CT. The wording is critical and different in some countries, so searchterms included computational thinking, computer programming and coding. The sole term programming is intertwined with different meanings, thus not suitable to gain an overview if computer programming is the expected focus. Regional specificities are also at play, as in the UK current curricula use the term coding. It is also important that most of the work is written with a focus on younger generations and beginners, excluding university students from this literature review. The keywords K-12, children, and school were added to achieve this goal.
2.1. Search Terms
The first simple query was to look for all papers including “computational thinking” in the subject field which yielded 1175 papers as an initial result. This study focuses on school settings; thus, “K-12” or “school” need to appear in the topic, making the query TS = (K-12 or school) and TI = Computational Thinking, where TS looks in the fields title, abstract, and keywords of the record, and TI looks at the title separately. Within our specified time range of 2016 to 2019, this leads to 151 potential publications, while TI = (“computational thinking” and K-12) leads to only ten appropriate articles which were added to our potential candidates. The search also focused on the subject matter, where querying for TS = (“computational thinking” and K-12) lead to 114 results. Probing the search terms without bracketing the publication years lead to 196 results. Sorted by citations, it was determined that all papers cited more than ten times were within our candidate range. To cross-check our findings, more complex queries were also explored, e.g., TI = (“computational thinking” and school); TS = (“computational thinking” and making); and TI = (“computational thinking” or “computer programming” or coding) and TI = (K-12 or school). To determine significance, all potential papers were sorted by number of citations, all included counts were last updated in August 2019.
Making sure no important work was missed during our initial search, a number of search queries in the google scholar database (scholar.google.com) were evaluated. This is one sample query used: (computational thinking or programming or coding or programmieren) and (K-12 or school or schule or makerspace or workshop). Some of our keywords are based on a data driven analysis conducted with the visualisation tool “CiteSpace” that found a significant clustering between these terms “Computational thinking, education, k12, programming, Scratch, computer science education, problem solving, teaching, learning, secondary education” [9]. For future reference, this includes the full list of search terms linked by “and” and “or” statements: beginner, case study, children, coding, computational thinking, computer programming, education, K-12, kids, learning, making, makerspace, programmieren, programming, pupils, school, schule, secondary education, teacher, teaching, undergraduate, workshop.
2.2. Selection Process
Obviously not applicable results were redacted from the list of potential candidates. Thi process looked at the abstracts to determine if the connection to K-12 education is suitable. Furthermore, publications that share our understanding that CT is beyond merely computer programming were prioritised. Lastly, the number of citations from other researchers were taken into account to qualify the studies impact. Two categories were selected; on the one hand, case studies and experiments conducted with young people to determine what worked in the field, and on the other hand, related work that conducted solid literature reviews. After this process, most cited papers were ranked to determine important resources in the field. This also allows a historical perspective to understand what work had been influential.
There is a noticeable regional gap, with the USA leading (415 publications) and the EU (351 publications) on the forefront of CT research (Figure 1). The focus of this research is on the EU and, specifically, the Austrian educational system, which were primarily chosen.
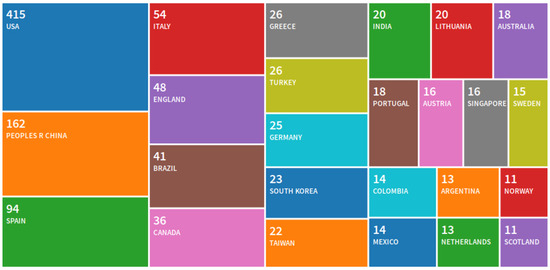
Figure 1.
Computational thinking (CT) research papers published by country as generated on Web of Science.
To qualify this review, the authors note that publications exist which do not mention CT explicitly but feature the same goals and principles. As can be seen in the historical breakdown, higher order thinking skills have been explored in philosophy, maths, and many other fields. An overview of different ways of thinking in computer science (CS) can be found in a recent study published by the HCI group at UT Vienna describing the “Ways of thinking in informatics” [10].
3. Results
3.1. Historical Breakdown
The term computational thinking was first coined by Jeannette Wing in 2006 and better defined in 2008 [1,11]. In her seminal paper, she proposed a “universally applicable attitude and skill set” to utilize “abstraction and decomposition” to tackle complex tasks with the mindset of a computer scientist. This first detailed mention of CT started a movement to integrate it into curricula and educational institutions around the world. Her ultimate goal to “inspire the public’s interest in the intellectual adventure” and “spread the joy, awe and power of computer science” was met with much enthusiasm, signified by the number of citations, according to Google Scholar as many as 4971 (September 2019). Based on this success, Carnegie Mellon University funded the now defunct “Center for Computational Thinking” that hosted seminars from 2007 to 2012. As a response to some of the critiques, Wing authored a second paper clarifying the objectives and methods CT encompasses. She posed the challenge that triggered this work and a host of scientific research by asking “What are effective ways of learning (teaching) computational thinking by (to) children?”. She envisioned that CT “will be an integral part of childhood education”, thus anchoring it within K-12 or even K-9 education. Lastly, she explicitly argues that learning in informal settings should be explored to better empower young people [1].
Potential precursors are put forward by diSessa with the idea of “computational literacy” [12] and Pea and Grover, who link the 1980 concept of “procedural literacy” [13]. The term CT was first mentioned by Seymour Papert in his book “Mindstorms: Children, Computers, and Powerful Ideas” in 1980 [14], reoccured 1996 in his publication “An Exploration in the Space of Mathematics Educations” [15] and defined by Jeannette Wing [11] in the aforementioned publication of the same name. Papert proposed the goal of CT is “to forge ideas that are at least as ‘explicative’ as the Euclid-like constructions (and hopefully more so) but more accessible and more powerful”, which aligns well with the programming environment he co-developed to teach the basic concepts of programming. The programming environment Logo, with its iconic turtle, as well as the LEGO Mindstorm learning tools pioneered by Seymour Papert, are still widely known and regarded as the precursors to Scratch. The work of MIT media labs lifelong kindergarten group and Mitchel Resnick on the programming environment Scratch and its concepts to use constructivist views and a community of makers and creators shaped current educational premises. Within this envelope of constructionism, different patterns of thinking and problem solving have emerged, most prominent in current education is algorithmic thinking, design thinking and computational thinking [16].
More recently, Dagiene and Futschek made the case that CT “presents a chance to bring more constructionist learning to schools”. In their editorial paper, the link between constructionist learning and CT education is established, proposing their goal to “situate constructionism in connection to CT within the wider educational discourse”. They end with the plea to create “more examples of constructionist learning at school” [17]. Despite the initial success, critical voices have been heard, for example, Chenglie Hu noted that, if CT “is thinking about process abstraction, then Jean Piaget’s Stages of Cognitive Development may suggest that this thinking skill cannot be effectively taught until adolescence age”, making it unsuitable for K-12 education. His argument is that CT is a mixture of different ways of thinking, mainly comprised from mathematical thinking [18]. In addition, proposing a stronger link to mathematical abstractions, a definition of CT is added by Alfred Aho who focuses on the close ties between algorithmic thinking and CT and simplifies “CT to be the thought processes involved in formulating problems so their solutions can be represented as computational steps and algorithms.” He states that “finding or devising appropriate models of computation to formulate problems is a central and often non-trivial part of CT” [19] (p. 2).
A Google Trends analysis, featured in Figure 2, shows that computational thinking has grown in importance over time, especially if compared to other ways of thinking in informatics.
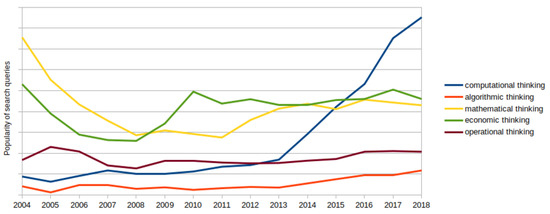
Figure 2.
Google Trends analysis comparing ways of thinking from 2004 to 2018.
“When was CT first described and what happened since then?” To answer our first research question, it is important to note that CT has evolved from earlier concepts dating back to the 1980s. Since then, a lot of effort has been spent to define clear goals and, starting around 2010, steps were taken to implement CT in nationwide curricula and international policies.
Between CS and CT, It’s Complicated
Most reviewed publications note the complicated relationship between computer science (CS) in general and the concept of CT. Wing felt the need to explicitly say in the paragraph “What it is, and isn’t” that “Computer science is not computer programming” [11], and Resnick stated that CT “is more than programming” [20]. Historically, CS education taught to program mainframe computers and this meant to write cryptic lines of textual code that can be executed. Learning a low-level programming language, like the 1964-established BASIC, meant to memorize commands and work in a strictly text-based environment without feedback or assistance. That learning to think like a software developer can be made simpler and more playful was proven by Papert, who envisioned the programming environment Logo in 1967 and leveled the ground for the ongoing success of Scratch. It made learning to code more intuitive with the LEGO-like brick user interface, more participatory with the Scratch community, and ultimately more mobile with the smartphone application “Pocket Code”.
In 2009, Peter Denning wrote a very important and thoughtful piece to the CS community, stating that the close linkage between CS and programming is a problematic outside perspective [21]. He cautions to merely “repackage” and “replace that older notion with ‘CS = CT’”, reminding readers that CS is a wide and diverse field and should be presented and understood as such. He reiterates that the seven great principles of CS allow for a much broader conception of our surroundings. In his words, “Computation is more fundamental than CT. For this reason alone, CT seems like an inadequate characterization of CS”. Hemmendinger concurred that the goal of CT “is to teach them how to think like an economist, a physicist, an artist, and to understand how to use computation to solve their problems, to create, and to discover new questions that can fruitfully be explored” [22] (p. 4). Barr and Stephenson also tried to determine what role the CS community plays in “bringing computational thinking to K-12”. They highlight the complex and sometimes contradictory relationship between these fields, on the one hand, allowing CT to act as “a problem solving methodology that can be automated and transferred and applied across subjects” to solve complex problems on a global scale, while on the other hand, the very wording that entangles the fields and somehow links CT to CS and, specifically, programming [23]. As the paper at hand shows, this complex relation is still disputed, as some showcased articles treat CT as a subfield of programming education. The authors also point out the politicized nature of K-12 CS education, where any “effort to achieve systemic change in this environment requires deep understanding of the realities of the system”, further arguing “embedding CT in K-12 requires a practical approach, grounded in an operational definition”. Ultimately, Barr and Stephenson show that the greater CS community can assist in achieving systematic change by giving “clear examples of ways it applies to and can be integrated into a range of curricular areas”. Luckily, this is happening already; as an example, this book featuring the BBC micro:bit (microbit.eeducation.at) can be downloaded as an open educational resource (OER) and used to teach K-12 students CT skills with hands-on projects.
3.2. Related Work
One metric to gauge the popularity of CT in research and academia is to evaluate the sheer quantity of literature reviews and meta studies conducted in the mere 13 years since its inception. The chosen publications are grouped by main focus and sorted by newest publication date first, if applicable.
3.2.1. A Closer Look at Definitions
A recent paper published in Turkey [24] tries to give an overview of definitions and practices. The authors found that conflicting theories have been problematic to the establishment of a concise integration in formal education. They combine and contrast definitions, as well as defining components proposed to be key ingredients, of CT. Ultimately, the paper cautions to integrate CT in educational curricula without succumbing to populist notions and overboarding simplifications. Before that, USA researchers evaluated all current definitions of CT and added their spin to the growing field [25]. Earlier publications tried to disentangle the different definitions CT entails and map them to “the big ideas of computing” [13,26]. CT research can be grouped in 19 classifications of thinking steps, where not all steps are included in every definition. Most researcher groups these steps to follow, in broad terms, Wing’s understanding of what CT can and should be [27].
3.2.2. Interdisciplinary Education
A meta-review conducted by Hsu et al. was based on quantifying prior research (116 papers) published between 2006 and 2017. Their findings show that, unsurprisingly, 75 papers state CS education (including computer programming courses) was the applicable subject to conduct CT training. Within the K-12 range, the study found a strong focus in problem-based learning, as well as game-based learning. The papers showed that 74 percent of research is related to formal learning scenarios, highlighting the obvious move to integrate CT into national curricula. They end by showing five suggestions for future research one being the necessity to “Adopt the cross-domain teaching mode” [27] (p. 13). The need to infuse CT into other subject areas of the curricula to “operate within the constraints of available resources” was also emphasized by Yadav et al. To empower students and allow the cross disciplinary approach of CT to be embedded in different subject areas is their key goal [28]. While a few examples of integration are given, the authors state that ongoing teacher development opportunities are needed to enable and reinforce capabilities, reiterating the need to train in-service teachers, as well as preservice teachers. In a related study featuring 134 pre-service teachers, the authors found them to be “limited to simplified conceptions of the idea and … not show case an in-depth understanding of what computational thinking involves”, driving home the point that “to be successfully implemented in classrooms across the globe, preservice teacher education has to be the focus of researchers, teacher educators, and policy makers” [29] (p. 14).
Similar conclusions were reached by a Swedish paper asking how CT and CS can be introduced in K-12 education by first comparing published papers by year and highlighting ten countries. They identify a common trend within all models “to introduce computing into primary education either in multiple subjects … or as cross cutting theme”. As current information and communications technology (ICT) teachers are pushed into teaching CT, “there is a need to develop the digital competencies of the teachers and make school more modern and relevant”. Within their publication, they observe that the “common struggle among all the countries is pre-service and in-service training of teachers”. Ultimately, the authors conclude that CT, programming, and digital competencies are often integrated into primary education, while broader courses in CS are developed for secondary education [30]. Researchers Barcelos and Silveira explored the proposal that CT, as “a way of reasoning and problem solving”, builds an inherent relationship between maths and CS. The authors aim to map the fields competencies and argue that it is possible to link different disciplinary treats to CT competencies, reiterating the importance of interdisciplinary education for a better future exchange. Based on the example of mathematics, especially in the Brazilian and Chilean system, the authors argue that “to incorporate CT to the basic education is to analyze its relationship with other knowledge areas already present in the basic education level” [31] (p. 7). One of the biggest challenges faced in CT is the lack of cooperation between different countries and disciplines [9].
3.2.3. Teaching the Teachers
A look specifically at the challenges teachers face showed that the integration into curricula and research on this integration is scarce and mostly based on CS contributions with inadequate focus on teacher education. It finds that a lack of confidence linked with a low self-efficacy in the subject matter in some teachers might cause a problematic correlation and could be remedied by a focus primarily on educating teachers. The authors ran full-day workshops geared towards Australian K-8 teachers, and a total of 75 educators participated in the post workshop survey. The lack of knowledge and time in class was presented as the major factors why CT was not taught more. They propose that “schools could organize support groups that include peer learning and teaching buddies” and also point out the role of academia and industry to fill this obvious gap. By attending the workshop, teachers gained a better understanding and the authors argue “it is possible for teachers to build up their confidence level … in quite a short period of time” [32] (p. 15). To understand the importance of CT in schools, training should start in early educational grades; only then the basic concepts of CT can be fully understood and appreciated [33]. A great starting point for educators is provided by Lockwood and Mooney, who answered the question “Where does (CT) fit?” by conducting a thorough review of the literature body. They showed testing possibilities, the importance for institutional adoption, and the interdisciplinary implementation [34].
3.2.4. Learning Through Programming
Focusing on engineering education, Gross et al. published a well defined list of challenges and best practices for educators. The authors see a “widespread and consequent introduction of computational tools to support the students in acquiring knowledge and developing problem-solving skills”. This paper links tools, software (MATLAB), and hardware (LEGO Mindstorms) very tightly to CS skills, thus negating the interdisciplinary notion of the definition first introduced by Wing [35]. In the same spirit, Lye et al. explored a different angle on CT skills with their review “on teaching and learning … through programming”. This study lays a significance on the relation between CT and programming skills, evaluating 27 studies with nine focusing on K-12 education. The researchers found a problematically low percentage of studies in this age bracket combined with the lack of representative studies in classroom settings critiquing that there “seems to be an implicit assumption that learners can exhibit such computational practices and perspectives through pure self-discovery”. The focus on visual programming languages, like Scratch, is widespread, and the use of authentic problem “pertinent to the students” is very well received and should be added to rigorous reflection activities [36]
3.2.5. Qualifying Cultural Impact
An initial review of the academic and grey literature was given by Bocconi as part of the European Commission CompuThink study. The takeaways from this paper are, on the one side, the underdeveloped methods to assess students CT skill, and, on the other side, the overwhelming focus on programming as the method used to teach CT in a classroom setting [37]. This paper concluded in a study focusing on concrete pointers for practical implementation of CT. While reiterating the promise of CT within an interdisciplinary context, they also see the paramount importance of solid teacher education, proposing massive open online courses (MOOCs) as a possible short term solution. To successfully integrate CT in national curricula, the authors argue that cooperation and “the exchange of experience and lessons learned at both European and international levels will become crucial” [2] (p. 52). The current implementation of CT in compulsory education was also highlighted by Voogt et al. in their 2015 paper. They present a historical overview on the early stages of CT and its basis in math. Offering a host of possible definitions and tracing back most of them to their origins, this article gives one of the best overviews on research in CT until 2015. In Section 4, it shows what can be taught and how CT is implemented in education, ultimately proposing a draft curriculum framework. Their prominent call for more research asks if “developing CT … increases students’ ability to be able to deal with complex and open-ended problems” [38] (p. 12). Kalelioglu et al. shine a light on the inherent shortcomings of the concept and current research in the field of CT. A big part of reviewed papers (39 of 125) are classified as “Idea paper”, based on personal views about the topic. Ultimately, the researchers also propose a sound draft for a framework to incorporate the work and findings of ten years of CT research. It is worth reiterating that this framework applies one of the broadest possible definitions, thus its ability to incorporate a large number of prior definitions. They define five major columns comprising CT as a problem solving process, namely: identify the problem, gather data, plan a solution, implement, and assess the progress made [39]. The research conducted in CT had a profound impact in the scientific community but has not yet reached broader implementation in classroom settings.
“What were the most important literature review works in the field?” All evaluated publications are important contributions to the state of the art in CT education, where Grover and Pea, Lye and Koh, Sengupta, Kalelioglu, Denning, and Yadav became the most prominently cited researchers.
3.3. Fieldwork and Integration
The current focus of scientific debate lies within the question how computational thinking can be included in already packed curricula in schools and universities alike. One of the many innovative institutions trying to remedy that “public schools do not always cover this demand (for CT education) adequately” is the “Teaching-Learning-Lab” (TLL) established at Alpen-Adria-University in Austria. Their research, in line with most initiatives, “focuses on how to create a setting, which is fruitful to disseminate the idea of computational thinking as a fundamental skill”. The TLL defines the following three main opportunities for future research. The assessment of CT skills “regardless of programming software” is a much needed improvement, reiterating the problematic marriage between CS and CT. To successfully teach CT as a higher order thinking skill, “indicators measuring the level of CT” are necessary. A second opportunity highlighted is the need for interdisciplinary education, with the widespread dissemination of CT knowledge outside of CS education. The last opportunity is to integrate CT into common teacher education curricula for a sustainable, long-term effect [40]. By hosting two children’s congresses (2016 and 2017), they succeeded in bringing CT concepts into schools (K-8) and were able to demonstrate the effect of project driven education [41]. The authors determined that participating students and teachers were interested in migrating the knowledge and lessons from the congress setting into their own learning and teaching environments. By using a relatively open problem description and the goal to present the developed solutions, they also found no difference in gender participation often visible in CS education. In the same realm of action-based research, game jams are a well known and documented method to create enthusiasm in young learners. To use this challenging informal setting for CT education was pioneered by Boulton et al. in their 2016 paper “The Role of Game Jams in Developing Informal Learning of CT: A Cross-European Case Study”. Using the smartphone application “Pocket Code”, the authors conducted two game jams with participants between 11 and 18 years old (K-12). They found learners to be engaged and motivated, more so than in a regular classroom setting, and concluded that a community with wider social and cultural perspectives enriched the learning experience [42].
3.3.1. Maker Education
A recurring critique leveled against CT education is its failure to engage diverse student bodies. At the same time, the maker and DIY (do it yourself) culture enables learners of different backgrounds, genders, and age brackets to interact with and learn from each other [25]. A 2015 article makes a case to move from CT to a computational making approach to “consider the potential of tangible interfaces to support learning”, evaluating the learning experience of primary school children working with e-textiles in Germany. To transform CT into computational making, the authors propose five key factors to extend CT, namely aesthetics, creativity, constructing, representations, and materials. While it is clear that CT “is a core skill to making in that it speaks to individual creativity, collaboration and problem solving”, the researchers believe there is more to it. The ideas incorporated in making allow CT to become deeply integrated into STEAM (Science, Technology, Engineering, Arts, and Mathematics) education and aim to “benefit from the diversity that making allows” [43]. “To create programmable objects as art projects” [44] (p. 13) is obviously bleeding over in current trends to form “do it yourself” communities, hackerspaces, and makerspaces. The authors propose to keep this crucial form of education inside the classrooms and institutions, reminding us all that “code should be embraced as a form of critical digital making” [44] (p. 14). The concepts of tinkering, creating, debugging, persevering, and collaborating are not yet fully explored in an educational context “due to constraints of time, misconceptions, and over-emphasis on examination” [45] (p. 10).
A valuable concept sometimes inadvertently used utilizes the three-stage progression of use, modify, and create to assist learning in steps and also emphasizes how every new invention is based on the efforts of countless female and male engineers, artists, thinkers, and makers. This study highlights how CT can be applied in K-12 education by showcasing after school programs and concludes that more efforts are required to allow teachers the time and possibilities to do so [46]. The same progression is used by Giovanni Serafini, who explored the possibility to teach coding to K-8 children. His argument is that CT “can be introduced and taught on an appropriate and adequate level of abstraction at all school stages”. They used the programming environment Logo at workshop events and found this to be valuable to keep the cognitive load of younger students down, and the feedback received confirmed the success of this approach [47,48]. An Austrian study notes that teachers need to work with a diverse set of students and concludes that interaction between learners is an underestimated factor in solving CT challenges [49]. Focusing more on the social aspects of maker education, Kafai and Burke described the impact they experienced when using a participatory programming environment named Scratch as a tool to develop CT skills in K-12 education. Teaching by allowing students to “create authentic applications” and remix the work of their peers on the well received Scratch platform has been described as a constructionist way to develop new skills [50].
3.3.2. Common Tools in CT Education
The idea that programming, and specifically CT, is a skill that needs to be taught to a broader audience was pioneered by Seymour Papert et al. with the 1967 advent of the Logo programming environment, a baseline for a visually appealing tool to learn the basics of computer programming. His notion to utilize an environment with a low floor to enter and high ceilings for longevity still lives on to this day, as the iconic turtle graphic remains in use in education. The lifelong kindergarten group around Mitch Resnick added, in their 2009 paper “Scratch: Programming for All” [16], a third principle they coined “wide walls”, to allow learners a wide range of potential projects to be attempted and learned from. These three principles inform the widely used and, with, according to scratch.mit.edu/statistics, 45 million registered users in August 2019, very popular visual coding environment, Scratch. The three principles described translate well to other popular coding tools and inform CS teaching efforts in general. The smartphone variant of the LEGO-like Scratch building blocks interface is realized by the tool “Pocket Code” (catrobat.org) developed at Graz University of Technology. In addition, widely used with 8.2 million users and offering the possibility to easily author smartphone applications, with students is the MIT “App Inventor” (appinventor.mit.edu). Other tools used by researchers are Python, Minecraft, MATLAB, Java, and the simplified ScratchJr.
A lot of research studies the implications of unplugged tools and methods for CT education. This paper differentiates between mixed and solely unplugged approaches, where the mixed approach utilizes robotics or microcontroller boards, like Arduino, LEGO Mindstorms, BBC micro: bit, or Calliope mini, to translate algorithms into a more haptic environment. The solely unplugged tools encountered during this study were, for example, drawing, board games, LEGO, braiding, dancing, and the Bebras tasks (bebras.org), allowing learners to access CT skills without linking to software development. Some research suggests this leads to a more diverse reception among female and male students alike.
“What has been tried to integrate CT in K-12 education?” Our third research question makes the push to introduce CT into schools and informal education obvious. Unplugged initiatives that utilize, for example, board games, as well as game development, coding, and other plugged in experiments, are conducted by researchers around the globe. It is an ongoing effort to streamline CT education, and the implementation is a long way from international coverage.
4. Discussion
The work done leading up to this publication shows that CT is a very timely concept and valuable for a future-proof educational system. Studies are conducted all over the globe in a decentralized manner, highlighting the diverse educational settings young people grow up in and become curious adults. In the field of CT, a host of well documented approaches exist without conclusive evidence of what leads to repeatable success viable in an institutional setting. Despite the solidified definition of CT, it is still unclear, and an open debate exists on how to best teach the foundational ideas in an institutional setting. The literature shows different problematic angles, on the one hand, the challenges involved in teaching and learning a way of thinking and problem solving in a hierarchical and time constrained system, and on the other hand, the inherently slow way teachers are prepared for an ever-changing classroom setting. More recently, a third leg gained traction because testing and evaluating success in education is a key concept for policymakers and stakeholders. These interlinked challenges make CT a hard to grasp but particularly worthwhile concept.
Imagining a Future
There is a big claim that computational thinking skills allow students to better deal with complexity and the open ended non-trivial problems posed by a world ever more uncertain and unpredictable. This research can and will lead to a generation more adept to tackle the imminent challenges posed by the climate crisis, automation and artificial intelligence (AI). To understand and evaluate the knowledge students possess, we propose a series of self-motivated project-based and practical use cases. Solving trivial tasks is not the skill people need in a future work nor academic environment. Creativity and higher order thinking skills are necessary and powerful tools within an ever changing world.
“Today’s students will be confronted with a never-ending stream of unknown, uncertain, and unpredictable situations throughout their lives. Their success and happiness will depend upon their ability to think and act creatively.”—Mitchel Resnick [51]
Based on the current work done in the field of CT, the problematic stance is obvious, and as long as teacher education and institutional willingness is not fully invested in integration, it seems that progress can be quicker made outside of the rigid school systems. Multiple studies show possibilities to integrate CT by outreach programs and engaging students in sustainable solution, ways of thinking, and ultimately, in the STEAM professions. This research and the subsequent case studies propose a path to address this blank spot, exploring to bring experts with practical CT problem solving skills into institutional settings and classrooms of the world. Constructionism and the problem solving methods of maker education are closely linked to the potential of CT, so STEAM disciplines should be looking to align resources and expertise. We strive to develop methods and a framework to bring practitioners into the classrooms, allowing young students to make sense of the implications and learn the skills they need from querying people with practical knowledge. This massive potential is underdeveloped while schools struggle to raise teachers awareness and efficacy. Our goal is to test methods of professional interaction and find ways to integrate outside knowledge, practical expertise and useful technologies into our school settings.
By allowing youth to solve problems in ways experts and engineers around the world do, they learn to utilize the most powerful tool—their brain. Informal learning is important but to solve massively interesting challenges like the climate crisis, our young minds need to be given the best tools and skills within the powerful structures of our public educational system.
Author Contributions
Conceptualization, M.E. and M.P.; Methodology, M.P.; Writing—Original Draft Preparation, M.P.; Writing—Review & Editing, M.E. and M.P.; Visualization, M.P.; Supervision, M.E.
Funding
This research received no external funding, the APC was funded by TU Graz.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CS | Computer Science |
| CT | Computational Thinking |
| K-12 | Learners between kindergarten and twelfth grade |
| MOOC | Massive Open Online Course |
| OER | Open Educational Resources |
| STEAM | Science, Technology, Engineering, Arts, and Mathematics |
| TLL | Teaching-Learning-Lab |
References
- Wing, J. Computational thinking and thinking about computing. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2008, 366, 3717–3725. [Google Scholar] [CrossRef] [PubMed]
- Bocconi, S.; Chioccariello, A.; Dettori, G.; Ferrari, A.; Engelhardt, K. Developing Computational Thinking in Compulsory Education—Implications for Policy and Practice; JRC Working Papers; Joint Research Centre: Seville, Spain, 2016. [Google Scholar]
- Wing, J. Research Notebook: Computational Thinking—What and Why? Link Mag. 2011, 8, 20–23. [Google Scholar]
- Grandl, M.; Ebner, M. Kissed by the Muse: Promoting Computer Science Education for All with the Calliope Board. In Proceedings of the EdMedia: World Conference on Educational Media and Technology, Amsterdam, The Netherlands, 25–29 June 2018; pp. 606–615. [Google Scholar]
- Wolf, D.; Ebner, M. From Refugee to Programmer? An Action-Based Learning Approach for Teaching Coding to Refugees. In Proceedings of the EdMedia: World Conference on Educational Media and Technology, Amsterdam, The Netherlands, 25–29 June 2018. [Google Scholar]
- Menon, D.; Bp, S.; Romero, M.; Viéville, T. Going Beyond Digital Literacy to Develop Computational Thinking in K-12 Education. Available online: https://hal.inria.fr/hal-02281037/document (accessed on 13 December 2019).
- Sengupta, P.; Kinnebrew, J.S.; Basu, S.; Biswas, G.; Clark, D. Integrating computational thinking with K-12 science education using agent-based computation: A theoretical framework. Educ. Inf. Technol. 2013, 18, 351–380. [Google Scholar] [CrossRef]
- Csizmadia, A.; Curzon, P.; Dorling, M.; Humphreys, S.; Ng, T.; Selby, C.; Woollard, J. Computational Thinking—A Guide for Teachers; Computing at School: Swindon, UK, 2015. [Google Scholar]
- Chen, P.; Tian, Y.; Zhou, W.; Huang, R. A systematic review of computational thinking: Analysing research hot spots and trends by CiteSpace. In Proceedings of the 26th International Conference on Computers in Education, Manila, The Philppines, 26–30 November 2018; p. 3. [Google Scholar]
- Purgathofer, P.; Frauenberger, C. Ways of Thinking in Informatics. Commun. ACM 2019, 62, 58–64. [Google Scholar]
- Wing, J. Computational Thinking. Commun. ACM 2006, 49, 33–35. [Google Scholar] [CrossRef]
- DiSessa, A.A. Changing Minds: Computers, Learning, and Literacy; Massachusetts Institute of Technology: Cambridge, MA, USA, 2000; ISBN 978-0-262-04180-5. [Google Scholar]
- Grover, S.; Pea, R. Computational Thinking in K–12 A Review of the State of the Field. Educ. Res. 2013, 42, 38–43. [Google Scholar] [CrossRef]
- Papert, S. Mindstorms: Children, Computers, and Powerful Ideas; Basic Books: New York, NY, USA, 1980; ISBN 978-0-465-04627-0. [Google Scholar]
- Papert, S. An exploration in the space of mathematics educations. Int. J. Comput. Math. Learn. 1996, 1, 95–123. [Google Scholar] [CrossRef]
- Resnick, M.; Silverman, B.; Kafai, Y.; Maloney, J.; Monroy-Hernández, A.; Rusk, N.; Eastmond, E.; Brennan, K.; Millner, A.; Rosenbaum, E.; et al. Scratch: Programming for all. Commun. ACM 2009, 52, 60. [Google Scholar] [CrossRef]
- Dagienė, V.; Futschek, G. On the Way to Constructionist Learning of Computational Thinking in Regular School Settings. Constr. Found. 2019, 14, 231–233. [Google Scholar]
- Hu, C. Computational thinking—What it might mean and what we might do about it. In Proceedings of the 16th Annual Joint Conference on Innovation and Technology in Computer Science Education, Darmstadt, Germany, 27–29 June 2011; pp. 223–227. [Google Scholar]
- Aho, A.V. Computation and Computational Thinking. Comput. J. 2012, 55, 832–835. [Google Scholar] [CrossRef]
- Council, N.R. Report of a Workshop on the Scope and Nature of Computational Thinking; National Academies Press: Washington, DC, USA, 2010; ISBN 978-0-309-14957-0. [Google Scholar]
- Denning, P.J. The profession of IT Beyond computational thinking. Commun. ACM 2009, 52, 28–30. [Google Scholar]
- Hemmendinger, D. A plea for modesty. ACM Inroads 2010, 1, 4–7. [Google Scholar] [CrossRef]
- Barr, V.; Stephenson, C. Bringing computational thinking to K-12: What is Involved and what is the role of the computer science education community? Inroads 2011, 2, 48–54. [Google Scholar] [CrossRef]
- Kursat Cansu, F.; Kilicarslan Cansu, S. An Overview of Computational Thinking. Int. J. Comput. Sci. Educ. Sch. 2019, 3, 3. [Google Scholar]
- Shute, V.J.; Sun, C.; Asbell-Clarke, J. Demystifying computational thinking. Educ. Res. Rev. 2017, 22, 142–158. [Google Scholar] [CrossRef]
- Gretter, S.; Yadav, A. Computational Thinking and Media & Information Literacy: An Integrated Approach to Teaching Twenty-First Century Skills. TechTrends 2016, 60, 510–516. [Google Scholar]
- Hsu, T.-C.; Chang, S.-C.; Hung, Y.-T. How to learn and how to teach computational thinking: Suggestions based on a review of the literature. Comput. Educ. 2018, 126, 296–310. [Google Scholar] [CrossRef]
- Yadav, A.; Hong, H.; Stephenson, C. Computational Thinking for All: Pedagogical Approaches to Embedding 21st Century Problem Solving in K-12 Classrooms. TechTrends 2016, 60, 565–568. [Google Scholar] [CrossRef]
- Yadav, A.; Gretter, S.; Good, J.; McLean, T. Computational Thinking in Teacher Education. In Emerging Research, Practice, and Policy on Computational Thinking; Rich, P.J., Hodges, C.B., Eds.; Educational Communications and Technology: Issues and Innovations; Springer International Publishing: Cham, Switzerland, 2017; pp. 205–220. ISBN 978-3-319-52691-1. [Google Scholar]
- Heintz, F.; Mannila, L.; Farnqvist, T. A review of models for introducing computational thinking, computer science and computing in K-12 education. In Proceedings of the 2016 IEEE Frontiers in Education Conference (FIE), Erie, PA, USA, 12–15 October 2016; pp. 1–9. [Google Scholar]
- Barcelos, T.; Silveira, I. Teaching Computational Thinking in initial series An analysis of the confluence among mathematics and Computer Sciences in elementary education and its implications for higher education. In Proceedings of the XXXVIII Conferencia Latinoamericana En Informatica (CLEI), Medellin, Colombia, 1–5 October 2012; pp. 1–8. [Google Scholar]
- Bower, M.; Wood, L.; Lai, J.; Howe, C.; Lister, R.; Mason, R.; Highfield, K.; Veal, J. Improving the Computational Thinking Pedagogical Capabilities of School Teachers. Aust. J. Teach. Educ. 2017, 42, 4. [Google Scholar] [CrossRef]
- Qualls, J.A.; Sherrell, L.B. Why Computational Thinking Should Be Integrated into the Curriculum. J. Comput. Sci. Coll. 2010, 25, 66–71. [Google Scholar]
- Lockwood, J.; Mooney, A. Computational Thinking in Education: Where does it Fit? A systematic literary review. arXiv 2017, arXiv:1703.07659. [Google Scholar]
- Gross, S.; Kim, M.; Schlosser, J.; Lluch, D.; Mohtadi, C.; Schneider, D. Fostering computational thinking in engineering education: Challenges, examples, and best practices. In Proceedings of the 2014 IEEE Global Engineering Education Conference (EDUCON), Istanbul, Turkey, 3–5 April 2014; pp. 450–459. [Google Scholar]
- Lye, S.; Koh, J. Review on teaching and learning of computational thinking through programming: What is next for K-12? Comput. Hum. Behav. 2014, 4, 51–61. [Google Scholar] [CrossRef]
- Bocconi, S.; Punie, Y.; Dettori, G. Developing Computational Thinking: Approaches and Orientations in K-12 Education. In Proceedings of the EdMedia: World Conference on Educational Media and Technology, Vancouver, BC, Canada, 28–30 June 2016. [Google Scholar]
- Voogt, J.; Fisser, P.; Good, J.; Mishra, P.; Yadav, A. Computational thinking in compulsory education: Towards an agenda for research and practice. Educ. Inf. Technol. 2015, 20, 715–728. [Google Scholar] [CrossRef]
- Kalelioglu, F.; Gulbahar, Y.; Kukul, V. A Framework for Computational Thinking Based on a Systematic Research Review. Balt. J. Mod. Comput. 2016, 4, 583–596. [Google Scholar]
- Demarle-Meusel, H.; Sabitzer, B.; Sylle, J. The Teaching-Learning-Lab-Digital Literacy and Computational Thinking for Everyone. In Proceedings of the 9th International Conference on Computer Supported Education (CSEDU), Porto, Portugal, 21–23 April 2017. [Google Scholar]
- Sabitzer, B.; Demarle-Meusel, H. A Congress for Children and Computational Thinking for Everyone. In Proceedings of the 13th Workshop in Primary and Secondary Computing Education, Potsdam, Germany, 4–6 October 2018; pp. 25:1–25:6. [Google Scholar]
- Boulton, H.; Spieler, B.; Petri, A.; Schindler, C.; Slany, W.; Beltrán-Jaunsarás, M. The role of game jams in developing informal learning of computational thinking: A cross-european case study. arXiv 2016, arXiv:1805.04458. [Google Scholar]
- Rode, J.A.; Weibert, A.; Marshall, A.; Aal, K.; von Rekowski, T.; El Mimouni, H.; Booker, J. From Computational Thinking to Computational Making. In Proceedings of the 2015 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Osaka, Japan, 7–11 September 2015. [Google Scholar]
- Knochel, A.D.; Patton, R.M. If Art Education Then Critical Digital Making: Computational Thinking and Creative Code. Stud. Art Educ. 2015, 57, 21–38. [Google Scholar] [CrossRef]
- Zaharin, N.L.; Sharif, S.; Mariappan, M. Computational Thinking: A Strategy for Developing Problem Solving Skills and Higher Order Thinking Skills (HOTS). Int. J. Acad. Res. Bus. Soc. Sci. 2018, 8, 1265–1278. [Google Scholar] [CrossRef]
- Lee, I.; Martin, F.; Denner, J.; Coulter, B.; Allan, W.; Erickson, J.; Malyn-Smith, J.; Werner, L. Computational Thinking for Youth in Practice. Inroads 2011, 2, 32–37. [Google Scholar] [CrossRef]
- Serafini, G. Teaching Programming at Primary Schools: Visions, Experiences, and Long-Term Research Prospects. In Proceedings of the International Conference on Informatics in Schools: Situation, Evolution, and Perspectives, Bratislava, Slovakia, 26–29 October 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 143–154. [Google Scholar]
- Tsarava, K.; Moeller, K.; Pinkwart, N.; Butz, M.; Trautwein, U.; Ninaus, M. Training Computational Thinking: Game-Based Unplugged and Plugged-in Activities in Primary School. In Proceedings of the 11th European Conference on Game-Based Learning (ECGBL 2017), Graz, Austria, 5–6 October 2017. [Google Scholar]
- Standl, B. A case study on cooperative problem solving processes in small 9th grade student groups. In Proceedings of the 2016 IEEE Global Engineering Education Conference (EDUCON), Abu Dhabi, UAE, 10–13 April 2016; pp. 961–967. [Google Scholar]
- Kafai, Y.; Burke, Q. The social turn in K-12 programming: Moving from computational thinking to computational participation. In Proceedings of the 44th ACM Technical Symposium on Computer Science Education, SIGCSE 2013, Denver, CO, USA, 6–9 March 2013. [Google Scholar]
- Mitchel Resnick’s Open edX Opening Keynote. Available online: https://www.youtube.com/watch?v=J5swKv1V5_Y (accessed on 27 August 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).